Une introduction aux systèmes de lois de conservation

INTRODUCTION AUX SYSTEMES

DE LOIS DE CONSERVATION

Mémoire présenté et soutenu le 09 Decembre 2005 en

vue de l'obtention du Diplôme d'Etudes Approfondies

(D.E.A.)

Option: Anal_yse

Spécialité : E.D.P

Par:

Jean-Michel KENFACK
Maître ès sciences Mathémati_ques

Devant le Jur_y composé de :

Président : F.WAMON (M C)
Rapporteur : M.DOSSA (M C)
Examinateur: G.MBIANDA (C C)

Table des matières

Abstract-Résumé ii

Introduction 1

1 PRÉLIMINAIRES 2

1.1 Rappels 2
1.2 La méthode des caractéristi_ques pour l'E.D.P du premier ordre ut (t, x)+

f(u(t,x))_x =0. 2

1.3 Solutions faibles ou _généralisées 6

1.4 Ondes mobiles- S_ystèmes h_yperboli_ques. 9

2 PROBLÈME DE RIEMANN 14

2.1 Ondes Simples 14

2.2 Ondes de raréfaction 16

2.3 Ondes de choc - discontinuités de contact 17

2.3.1 L'ensemble de choc 17

2.3.2 Discontinuités de contact - ondes de choc 20

2.4 Solution locale du problème de Riemann 22

2.5 S_ystème de deux lois de conservation. 25

2.5.1 Invariants de Riemann. 25

2.5.2 Non existence de solutions ré_gulières. 27

3 CRITÈRE D'ENTROPIE 32

3.1 Viscosité évanescente-ondes mobiles 32

3.1.1 Première condition d'admissibilité 32

3.2 Paire entropie-flux 36

3.2.1 Deuxième condition d'admissibilité 36

3.3 Unicité de la solution d'une loi de conservation scalaire. 38

3.3.1 Quel_ques propriétés de la solution entropi_que. 44

3.4 Solution explicite d'une loi de conservation scalaire 45

3.4.1 La formule de Hopf et Lax. 45

Conclusion 50

Biblio_graphie 51

ABsTRAcT

We are _goin_g to find the solutions of the first order non-linear Cauch_y problem of conservation laws ut (t, x) + f (u (t, x)) = 0 which possess _good ph_ysical properties. We will show that, this problem does not possess a _global smooth solution in time_; this result comes from the search of this solution b_y the characteristic method. Under asumption about initial conditions, we _give the value of the optimal time for the existence and uni_queness for the smooth solutions. Throu_gh the Riemann problem, we _give the nature of the _global solutions under shape of various kinds of waves. B_y the entrop_y ine_qualit_y, we establish one result of existence and uni_queness of weak entrop_y solution of the Cauch_y problem of conservation laws.

KEYS WORDS : Characteristic method_; optimal time_; kinds of waves_; entrop_y ine_qualit_y; weak entrop_y solution.

REsuMÉ

Nous allons chercher des solutions du problème de Cauch_y pour l'é_quation non- linéaire du premier ordre de lois de conservation ut (t, x) + f (u (t, x)) = 0 _qui possèdent des bonnes propriétés ph_ysi_ques. Nous montrerons _que ce problème ne possède pas en _général de solutions ré_gulières _globales en temps_; ce résultat provient de la résolution dudit problème par la méthode des caractéristi_ques. Sous certaines h_ypothèses sur les données initiales, nous donnons un temps optimal d'existence de solutions ré_gulières du problème. A travers le problème de Riemann, nous donnerons la nature de ces solutions _générales sous forme d'ondes de diverses sortes. Grâce à l'iné_galité d'entropie, nous établissons un résultat d'existence et d'unicité de la solution faible discontinue de ce problème de Cauch_y appelée solution faible entropi_que .

MOTS CLES : Méthode des caractéristi_ques_; temps optimal_; ondes de diverses sortes_; iné_galité d'entropie_; solution faible entropi_que.

SYSTÈMES DE LOIS DE CONSERVATION.

INTRODUCTION

Les s_ystèmes d'é_quations h_yperboli_ques sont des s_ystèmes d'é_quations aux dérivées partielles (E.D.P) _qui modélisent un vaste champs de phénomènes ph_ysi_ques. Parmi ces é_quations, on peut citer notamment, l'é_quation des ondes, les é_quations de Maxwell en électro-ma_gnétisme, les é_quations d' Euler de la d_ynami_que des _gaz. En _général, on note t la variable temporelle et x la variable spatiale, nous aimerions étudier le comportement de la fonction vectorielle u = u (t, x) = (u¹ (t, x) , u² (t, x) , .., uⁿ (t, x)), (t; x) E [0, oc) x Rm où les composantes sont les densités des diffèrentes _quantités _qui interviennent dans le phénomène ph_ysi_que à étudier. Soit donné une ré_gion bornée assez ré_gulière de R^m_; notons _que

contenu dans à l'instant t où dx dési_gne l'élément de volume et

_Ù udx représente la _quantité de matières ou le nombre de particules

?Ù uds représente la

_quantité de matière traversant le bord de (8 ) à l'instant t où ds est l'élément de
surface induit sur 8 par dx. Le principe de lois de conservation stipule _que : "L'au_gmentation ou la dimunition de matière (ou de particules) u dans le domaine est ré_gulée par une fonction flux f : Rⁿ ? M^n×m _qui contrôle la traversée de u à travers 8 ,

où M^n×m est l'ensemble des (n x in) - matrices réelles.

Plus précisement, on a pour tout t

_{Z Z}

(1) d u (t, x) dx = - f (u (t, x)) íds

dt Ù ?Ù

où í est la normale à (8 ) extérieure à . Utilisant le théorème de diver_gence pour

_{Z Z Z}

ut (t, x) dx = - f (u (t, x)) ídS = - div_x (f (u (t, x))) dx.

Ù ?Ù Ù

réécrire (1), on obtient :

(2)

Ceci étant vrai pour toute ré_gion arbitraire c R^m . On en déduit le problème _général de s_ystèmes de lois de conservation avec valeur initiale :

½ ut (t, x) + div_x (f (u (t, x))) = 0 dans (0, oc) x Rm

(3) u=g sur {t=0}x Rm

où g : R^m ? Rⁿ ; g (x) = (g¹ (x) , g² (x) , .., gⁿ (x)), fonction donnée décrivant la distribution initiale. Pour des raisons de commodité et de simplicité, notre étude de (3) se limtera au cas in = 1, on aura alors à faire au problème :

(4)	½ ut (t , x ) + f (u (t , x))x = 0 dans (0 , oc) x R u = g sur {t = 0} x R

où f : Rⁿ -* Rⁿ , g : R -* Rⁿ sont données et u: [0, oc) x R -* Rⁿ est l'inconnue. Pour le cas spécial n = 1, on parlera de loi de conservation scalaire.

Comme exemples de lois de conservation, nous pouvons citer le problème du trafic routier ç')t + (ç')v) x = 0, où ç') = ç') (t, x)) est la densité du trafic à la position x et à l'instant t_; v = v (t, x, ç') (t, x)) la vitesse du trafic et m = ç')v le débit du trafic encore appelé flux du trafic.

Les é_quations d'Euler d'écoulement de _gaz compréssible en dimension 1 suivantes :

ñt + (ñv)x = 0 (conservation de la masse) (ñv)t + (ñv^2 +p)x = 0 ( conservation du moment) (ñE)t + (ñEv + pv)x = 0 (conservation de l' énergie)

Dans la première partie, nous allons tour à tour chercher pour notre E.D.P du premier ordre ut (t, x) + f (u (t, x))_x = 0 :

* Des solutions classi_ques par la méthode des caractéristi_ques pour le cas spécial n = 1, solutions _qui malheureusement, seront seulement locales en temps.

* Des solutions faibles ou _généralisées _qui sont _globales en temps, mais _qui auront l'inconvénient de ne pas être uni_ques.

* Enfin, nous allons introduire la condition d'h_yperbolicité de notre s_ystème d'E.D.P _qui est très importante pour la résolution de ce dernier.

Dans la deuxième partie, nous allons étudier la nature des solutions faibles à travers le problème de Riemann _qui se caractérise par le fait _que la condtion initiale soit constante par morceaux . Nous chercherons tour à tour les solutions de ce problème sous la forme d'onde de choc, de raréfaction, de discontinuité de contact(_qui apparaissent pour des temps plus _grands que T^* donné par la méthode des caractéristi_ques). Par la suite, nous donnerons une condition d'existence locale de solutions du problème de Riemann.

Enfin nous aborderons le cas de deux lois de conservation (n = 2), ici nous définirons les Invariants de Riemann _qui seront fondamentaux dans la simplification du s_ystème et sa résolution. Enfin, nous allons donner un critère de non existence de solutions ré_gulières du problème de Riemann.

Dans la troisième partie, nous allons donner un critère appelé critère d'entropie où iné_galité d'éner_gie _qui nous permettra de montrer l'existence et l'unicité des solutions faibles _généralisées appelées solutions faibles entropi_ques. En se ramenant de nouveau au cas scalaire (n = 1), nous allons énoncer un résultat d'existence et d'unicité de la solution entropi_que.

Enfin, à travers la formule de Hopf-Lax, nous allons donner une solution explicite d'une loi de conservation scalaire (cas du problème de Riemann).

Chapitre 1

PRÉLIMINAIRES

1.1 Rappels

Dans ce para_graphe, nous énon_çons deux résultats fondamentaux (admis) pour la démonstration des résultats de ce doucment.

Théorème 1.1. (théorème des fonctions implicites). Soit U un ouvert deR²ⁿ, soit f E C¹ (U, R^m) tel _que Jf (x0, y0) =6 0. Alors il existe un ouvert V C U avec (x0, y0) E V, un ouvert W C Rⁿ avec x0 E W et un difféomorphisme g : W -?Rⁿ E C¹ tel _que : *g(x0) = y0

*f(x,g(x)) = z0 (xEW) oùz0=f(x0,y0)et

* Si (x,y) EV et f(x,y) = z0 alors y =g(x)

*SifEC^k alorsgEC^k

Théorème 1.2. (théorème des fonctions inverses). Soit U un ouvert deRⁿ, soit f E C¹ (U, Rⁿ) tel _que Jf (x0) =6 0, alors il existe un ouvert V C U avec x0 E V, un ouvert W C Rⁿ avec z0 E W tel _que :

* La carte f : V -? W est bijective et

*f_¹:W -? V est C1

* Si f est C^k, alors f_¹ est Ck

Une première idée pour résoudre le problème (4) étant de chercher des solutions ré_gulières, la méthode des caractéristi_ques nous semble indi_quée.

1.2 La méthode des caractéristiques pour l'E.D.P du premier ordre ut (t, x) + f (u (t, x))x = 0.

On considère dans cette partie les problèmes de la forme

{ ut (t, x) + f (u (t, x))_x = 0 t > 0, x E R (1.1) u(0,x)=u0(x) xER

Avec f E C^°° (R) et u0 E L^°° (R). On prend ici u0 assez ré_gulière (par exemple C°° avec toutes ses dérivées bornées). L'idée est de chercher une fonction X : [0, 0e) -? R (appelée courbe caractéristi_que) telle _que, si u est une solution classi_que de( 1.1)_; l'application t i-? u (t, X (t)) soit constante, on aurait alors :

d dt{u(t,X(t))} = ut (t,X(t)) +

Xÿ (t) ux (t, X (t)) = 0

et, puis_que u vérifie (1.1), on a aussi :

ut(t,X(t))+f^ÿ(u(t,X(t)))u_x (t,X(t)) = 0

Par identification, on obtient X^ÿ (t) = f^ÿ (u (t, X (t))) et se souvenant _que l'on a u (t, X (t)) constant et en notant X (0) = x, on trouve

Xÿ (t) =

f^ÿ(u0(x)), soitX(t)=x+tf^ÿ(u0(x)).

Les caractéristi_ques, courbes ré_gulières le lon_g des_quelles les solutions de (1.1) sont constantes sont donc des droites, et pour tout x E R, on a

( )

u t, x + t f^ÿ (u0 (x))= u0(x)

La méthode des caractéristi_ques ne donnant des solutions ré_gulières _que pour des temps très petits, nous allons donner un résultat _qui nous permette de trouver la valeur limite de ce temps, au déla de la_quelle la méthode des caractéristi_ques n'est plus fiable.

Théorème 1.3. (théorème du temps optimal T^*) Soient u0 et f des fontions données de classe C², bornées et à dérivées bornées. Soit

_{n o}

+0e · ÿ

-1

_{n o}

infxER f· (u0 (x)) ÿu0 (x)

_{n o}

si infxER f· (u0 (x)) ÿu0 (x)<0

?

???

???

T^*=

Alors

* il existe un a > 0 tel _que l'application

( )

ø : (t, x) E]a, T ^*[×R ? t, x + f ÿ (u0 (x)) tE]a, T^*[×R est un C^°° -difféomorphisme.

* la solution du problème (1.1) est alors donnée par u (t, x) = u0 (?(t, .)_¹ (x)) où ?(t, .)(x) (x) = x + tf ÿ (u0 (x)).

Preuve. 1- Soit ?t (x) = x + f^ÿ (u0 (x)) t, on a ÿ?t (x) = 1 + f^· (u0 (x)) ÿu0 (x) t; pour tout t E [0, T^*[, ÿ?t > 0 sur R, et si on prend a < 0 assez petit, par exemple a tel _que

asup x

(f^·(u0 (x)) ÿu0 (x)) <1 (reste vrai sur ]a, 0]),

Pour tout t E]a, T^*[, ?t est donc strictement croissant sur R et, puis_que u0 est bornée,
?t (x) ? #177;0e lors_que x ? #177;0e. Pour ces t, ?t est donc un difféomorphisme de R.

Cela prouve le caractère bijectif de e : Pour tout (s, y) E]a, T^*[×R, il existe un uni_que (t, x) = (s, v,;¹ (y)) tel _que e (t, x) = (s, y) . On a de plus

|Je (t,x)| = det

1 0 fÿ(u0 (x))^ÿvt (x)

ÿvt (x) .

Ce _qui montre _que e est un difféomorphisme local en tout point de ]a, T^*[×R, puis_que son déterminant jacobien ne s'annule pas sur cet ensemble.

2- On a e (t, x) = (t, vt (x)) e (t, v7¹ (x)) = (t, vt (vt 1 (x))) = (t, x) . D'autre part,

u (e (t, x)) = u0 (x), d'où u (t, x) = u (e (t, v_t¹ (x))) = u0 (vt ¹ (x)).

Il reste à montrer _que u définie bien la solution du problème (1.1).

En effet, u (t, x) = u0 (vt 1 (x)) ut (t, x) + f^ÿ (u0 (vt 1 (x))) u_x (t, x)

=(v^-1

t(x))_t^ÿu0 (v7¹ (x)) + (v7¹ (x))_xÿu0 (x)) f^ÿ (u0 (v7¹ (x)))

Or (vtov7¹) (x)=x v7¹ (x) + tf (u0 (v7¹ (x))) = x

0 = e_t {v7¹ (x) + tf^ÿ (u0 (v7¹ (x)))}

e_t{v7¹ (x)} +f(u0 (x))) + tf^· (u0 (vt ¹ (x))) u0 (v7¹ (x)) e_t{v7¹ (x)}

??t {v^7^1 (x)} =	fÿ (u0(v-1t(x)))
	1 + tf^· (u0 (v71 (x))) ÿu0 (v7^1 (x))

et ? {v7¹ (x)} = 1

1 + tf^· (u0 (vi¹ _(x))) ÿu0 (v7¹ (x))

d'où (v7¹ (x))_tÿu0 (v7¹ (x)) + (v7¹ (x)) _xÿu0 (v7¹ (x)) f^ÿ (u0 (v7¹ (x))) = 0 et

u (t, x) = u0 (v7¹ (x)) est solution du problème (1.1).

D'où le théorème.

La méthode des caractéristi_ques permet donc de construire (explicitement modulo l'inversion de v) une solution ré_gulière à (1.1), mais sous les h_ypothèses structurelles concernant f^· et ÿu0, uni_quement locale en temps.

Question : Peut-on construire _généri_quement une solution ré_gulière définie sur ]0, 8[×R ? A travers _quel_ques exemples, procédons à une illustration.

Exemple 1.1. i) Considérons l'é_quation de Bur_gers :

ut + ( ₂²) =0 x

avec condition initiale continue

u (0, x) = u0 (x) =

? ? ?

1 si x = 0 1 --- x si 0 = x = 1 0 si x= 1

u0 (x) E/ C^1

2

On a f (u) = u₂ fÿ (u) = u f^· (u) = 1 et en utilisant le théorème précédent,

on deduit la valeur du temps optimal d'existence de solutions classi_ques comme étant
T* = 1. On en déduit _que, pour tout t < T^*, la solution peut être cherchée par la

méthode des caractéristi_ques.

la fonction ?t a_yant pour expression :

?

?

?

x 7?

x+t si x<0

,

(1 -- x)t+x si 0<x <1 x si x=1

alors

?-1 t

(x)=

? ? ?

x--t si x<t x-t 1-t si t<x<1 x si x=1

et la solution u est donnée par :

u(x)=

? ? ?

1 si x<t 1-x 1-t si t < x < 1 0 si x=1

.

ii) Considérons à présent l'é_quation de Bur_gers avec pour condition initiale continue, u0 (x) = 1 + x2,

1

(u2 )

u assez ré_gulier ut + = 0 ? ut+uu_x = 0.

2 x

D'après le théorème 1.3, on peut déduire la valeur de T^* comme étant _J27 (car en

8

posant g (x) = ).

--J27 (1 + x2)2, le minimun de g est atteint au point x0 = --2x 1 J3 et vaut 8

*Par consé_quent_; pour t < T *, les caractérisiti_ques sont des applications

?t (x) : t 7? x + tu0 (x) = x + 1 +x2, u étant constant le lon_g de cette caractéristi_que, t

le problème admet donc une uni_que solution donnée par :

.

(1.2) u(t,x) = u0 (?-1

t (x))

Remar_que 1.1. Au vu des deux exemples ci-dessus, on peut faire le constat suivant : même si la condition initiale est seulemlent continue, même si la condition initiale est infiniment dérivable, la solution peut devenir discontinue après un temps fini. Pour t > T *, les solutions classi_ques n'existent pas, car la fonction x 7? ?t (x) n'est plus injective et les caractéristi_ques vont pouvoir se rencontrer, ce _qui constitue une situation incompatible : cha_que trajectoire porte une valeur différente de la solution, et au niveau de l'intersection de ces trajectoires, on se retrouve avec deux valeurs différentes de la solution. Cette situation est ph_ysi_quement envisa_geable, et se traduit par une onde de choc. Il peut aussi _y avoir une situation contraire ou ces trajectoires diver_gent (ou s'écartent), laissant apparaître une onde de détente ou de raréfaction dans l'ouverture créée par la diver_gence du faisceau des caractéristi_ques. Il est donc indispensable de caractériser ce lieu de rencontre, on a donc recours à la notion de solutions faibles où _généralisées.

Dans toute la suite, on étudiéra le problème pour le cas n> 1.

1.3 Solutions faibles ou généralisées

Courbes de choc-Condition de Rankine-Hu_goniot

Il faut donc considérer (comme il est classi_que en E.D.P), une autre notion de solution pour (1.1), _qui permette d'obtenir l'existence d'une solution sur ]0, oc[xR tout entier et non pas uni_quement pour des temps petits.

Soit à résoudre le problème de Cauch_y suivant :

{ ut + f (u (t, x))_x = 0 dans (0, oc) x R

(1.3) u(0,x)=u0(x) sur {t=0}xR

Posons

C'° c = C'° c ((0, oc) x R) = {?: (0, oc) x R ?Rⁿ ré_gulière tel _que support ? compact } L'idée ici est d'utiliser le principe des fonctions-test on prend une fonction ré_gulière, on multiplie l'é_quation par cette dernière puis on intè_gre par partie.

Définition 1.1. u E L'^° ((0, oc) x R; Rⁿ) est une solution faible du problème (1.3) si u vérifie l'é_galité :

_{f f f}

(1.4) (u?t + f (u) ?_x) dxdt + u0 (x) ? (0, x) dx = 0

0 R R

'°

avec ? E C'° c .

Remar_que 1.2. Si u est une solution classi_que (ré_gulière) de (1.3), alors en multipliant la première é_quation de (1.3) par ? et inté_grant par parties, on obtient (1.4) .Mais (1.4) n'a de sens _que si u et f(u) sont localement inté_grables.

Soit la situation où nous avons une solution faible de (1.3) _qui est assez ré_gulière sur l'un ou l'autre côté de la courbe C le lon_g de la_quelle u a un saut de discontinuité. Plus précisement, supposons un domaine V C (0, oc) x R tel _que V = V _g U Vd et V _g n Vd = C. En supposant u assez ré_gulière dans V_g avec pour condition initiale u_g = u0/Vg , et choisissant la fonction ? tel _que support ? compact dans V_g, alors on déduit de (1.4) _que :

(1.5) ut+f(u)_x =0dansV_g

De même on a, ut + f (u) x = 0 dans Vd à condition _que u soit assez ré_gulière dans Vd, a_yant pour condition initiale ud et support ? compact dans Vd .

A présent, choisissons la fonction test ? tel _que support ? compact dans V et _qui ne s'annule pas forcement le lon_g de la courbe C. Alors en utilisant (1.4), on obtient :

0=

f '° f 0 R

(u?t + f (u) ?x) dxdt

_{ff ff}

(1.6) = (u?t + f (u) ?_x) dxdt + (u?t + f (u) ?_x) dxdt

V_g Vd

Comme support ? compact dans V, on déduit :

(u(pt f (u) (px) dxdt = _

_g(ut f (u)_x)(pdxdt

_{vg v}

Z(u_gv² + f (u_g) v¹) ?dl

+

C

(1.7)

ZZ(u(pt f (u) = (usv^2 + f (ug) cpdl Vg

d'après (1.5) où v = (v^1,v²) est la normale unitaire à la courbe C diri_gée de V_g vers Vd.De même on a :

(1.8) (u?t + f (u)?_x) dxdt = - L(udv²+f (ud) v¹) ?dl

Vd Additionnant (1.7) et (1.8), en utilisant (1.6), on a :

ZC

[(f (u_g) - f (ud)) v¹ + (u_g - ud) v²] ?dl = 0 pour toute fonction ré_gulière ? . Ainsi :

(1.9) (f (u_g) - f (ud)) v¹ + (ud --- u_g) v² = 0

le lon_g de C Supposant C paramétrée par {(t, x) / x = s (t)} pour toute fonction ré_gulière s (.) : [0, +8) ? R. Alors

v = (v1,v2) = (1 + ÿs^2)^--

1 ^2 (1, - ÿs) ,

où (sÿ = ^d_dt^s).(1.9) devient alors :

(1.10) (f (ud) - f (u_g)) = sÿ (ud - u_g)

dans V le lon_g de C

Remar_que 1.3. R1 : ud - u_g est appelé le saut de u à travers la courbe C, f (ud) - f (u_g) , le saut de f (u) et ó = sÿ la vitesse de la courbe C.

R2 : la droite d'é_quation x (t) = ót est appelée une courbe de choc

Définition 1.2. L'é_galité (f (ud) - f (u_g)) = ó (ud - u_g) est appelée condition de saut de Rankine-Hugoniot.

Question : A-t-on toujours unicité des solutions faibles?

Nous allons à travers un exemple montrer _que les solutions faibles ne sont pas toujours uni_ques.

Exemple 1.2.

1- En revenant à l'exemple 1.1 i), pour t = 1, en cherchant la solution sous forme "onde de choc", on a

r 1 si x<s(t)

u1 (t, x) = 0 si x > s (t) où s (t) = 1 + t

2

s (t) est la courbe de choc déterminée par la condition de Rankine-Hu_goniot.

( _u2 )

2- Soit l'é_quation de Bur_gers ut + = 0 avec pour condition initiale u0 définie par
2 x

{ --1 si x < 0

u0 (x) = 1 si x > 0 . Définissons la fonction u par :

{ --1 si x < 0

u (t, x) = 1 si x > 0 i.e u (t, x) = u0 (x) pour tout (t, x) E [0, oc) x R.

Alors u E L⁰⁰ ((0, oc) x R, R) et par calcul on a :

Z ₀₀ Z 0 Z 0 Z 00

(u?t + f (u) ?_x) dxdt + u0 (x) ? (0, x) dx = f (--1) ? (t, 0) dt

0 --00 --00 0

et

Z ₀₀ Z +00 Z +00 Z 00

(u?t + f (u) ?_x) dxdt + u0 (x) ? (0, x) dx = -- f (+1) ? (t, 0) dt

0 0 0 0

En sommant ces deux résultats, on constate _que u est solution faible puis_que f (+1) = f(--1)

3- Donnons encore un exemple avec le même flux f et la même condition initiale. On définit la fonction v E L⁰⁰ ((0, oc) x R, R) par :

?

??

??

--1 si x < --t

x

t

1 si t < x

si --t = x = t

v(t,x) =

(_v2

Dans le domaine --t < x < t,on a vt + 2

)= 0 et un calcul plus poussé permet de

montrer _que v est une solution faible. En effet, comme précédemment, on a :

x

Z ₀₀ Z --t Z --t Z 00

(v?t + f (v) ?_x) dxdt + v0 (x) ? (0, x) dx = f (--1) ? (t, --t) dt ,

0 --00 --00 0

Z ₀₀ Z t Z t Z 00

(v?t + f (v) ?_x) dxdt + v0 (x) ? (0, x) dx = f (1) (? (t, t) -- ? (t, --t)) dt

0 --t --t 0

et

Z ₀₀ Z 00 Z 00 Z 00

(v?t + f (v) ?_x) dxdt + v0 (x) ? (0, x) dx = -- f (1) ? (t, t) dt.

0 t t 0

D'où

Z ₀₀ Z +00 Z 00 Z 00

(v?t + f (v) ?_x) dxdt + v0 (x) ? (0, x) dx = f (--1) ? (t, --t) dt

0 --00 0 0

_{Z Z}

+ f (1) (? (t, t) - ? (t, -t)) dt - f (1) ? (t, t) dt = 0, car f (1) = f (-1) ,

0 0

et v est bien une solution faible (appelée"onde de raréfaction"). En donnant ces deux exemples, on a montré _qu'il peut avoir plusieurs solutions faibles. Cela ne correspond pas aux observations faites sur les modèles ph_ysi_ques dont la modélisation conduit à la première é_quation de (1.1) et cela n'est pas satisfaisant du point de vue mathémati_que.

1.4 Ondes mobiles- Systèmes hyperboliques.

Nous allons à présent nous intéresser à une bonne définition des solutions faibles _généralisées, ceci va entrainer le critère d'entropie basé sur l'anal_yse d'ondes de choc. Nous devons considérer la non linéarité de f dans l'espoir de mettre sur pied une bonne approche mathémati_que et de bonnes conditions ph_ysi_ques . Notre étude portera sur le s_ystème de lois de conservation.

(1.11)

? ?? ??

u1 t + (f^1 (u^1...u^n)) = 0 un t +(f^n (u^1....u^n)) = 0

Le s_ystème (1.11) s'écrit sous la forme _quasilinéaire

(1.12) ut+A(u)u =0

Ici, on veut chercher des solutions particulières _qui ont la forme d'ondes mobiles :
(1.13) u (t, x) = v (x ? ót)

(t> 0, x E R) où la fonction v et la vitesse ó E R sont des inconnues. En substituant (1.13) dans (1.12), on obtient l'é_galité :

(1.14) ?ó v ÿ(x ? ót) + A (v (x ? ót)) vÿ (x ? ót) = 0

Par observation de (1.14), on constate _que ó est la valeur propre de la matrice A(v) correspondant au vecteur propre ÿv. Cette conclusion su_ggère _que si nous devons chercher des solutions de notre s_ystème d'E.D.P sous forme d'ondes mobiles ou plus _généralement de va_gues, solutions de (1.12), nous devons imposer une certaine condition d'h_yperbolicité concernant les valeurs propres de A.

Définition 1.3. Si pour tout u E Rⁿ, les valeurs propres de A(u) sont réelles et distinctes, on dit _que le s_ystème (1.12) est strictement h_yperboli_que.

Dans toute la suite, nous supposerons le s_ystème d'E.D.P (1.12) (pour le cas spécial A = Df) strictement h_yperboli_que.

Notations

(i) Nous écrirons

À1 (u) < · · · < À_n (u)

pour dési_gner les valeurs propres réelles et distinctes de A (u) dans l'ordre croissant.

(ii) Pour k = 1 · · · n, dk (u) le vecteur propre non nul tel _que :

A (u) dk (u) = Àk (u) dk (u).

(iii) Sachant _qu'une matrice et sa transposée ont le même spectre, introduisons les vecteurs propres gk (u) pour la matrice transposée A (u)^T, on a :

A (u)^T gk (u) = Àk (u) gk (u) ,

_qui peut s'écrire encore :

gk (u) A (u) = Àk (u) gk (u).

Ainsi {gk _(u)}1<k<n pourra être re_gardé comme famille de vecteurs propres de _gauche et {dk _(u)}1<k<n celle de droite.

Remar_que 1.4. On pourra considérer les familles gk (u) et dl (u) telles _que : gk (u) dl (u) = äkl, u E Rⁿ. En effet_; Àl (gkdl) = gk (Àldl)

= gk (Adl) = A^Tgkdl = Àkgkdl (Àk - Àl) gkdl = 0

d'oùk =6 lgkdl=0 car Àk=6Àl.

Question : Comment se comporte la notion d'h_yperbolicité stricte dans un chan_gement de coordonnées?

Théorème 1.4. (invariance de l'h_yperbolicité dans un chan_gement de coordonnées). Soit u une solution ré_gulière du strict s_ystème h_yperboli_que (1.12).

Soit Ö : Rⁿ ?Rⁿ un difféomorphisme assez ré_gulier d'inverse W. Alors

u = Ö (u),

est solution du s_ystème strictement h_yperboli_que :

(1.15) ut +		A (u) ux = 0
dans (0, oc) x R pour (1.16)	A (u) := DÖ (W (u)) A(W (u)) DW (u).

Preuve. 1- Le chan_gement de fonction inconnue u 7?u = Ö (u) transforme l'E.D.P (1.11) en l'E.D.P (1.15).

2- Prouvons _que le s_ystème (1.15) est strictement h_yperboli_que. Si Àk (u) est une valeur propre de A (u) avec pour vecteur propre de droite dk (u) correspondant, on a: A (u) dk (u) =

Àk (u) dk (u). Posant (1.17) on a : (1.18) de même on a :

r dk (u) := DI (W (u)) dk (W (u)) Àk (u) := Àk (W (u)) A (u) dk (u) = Àk (u) dk (u),

Au vu de (1.17)...(1.19), on conclut _que le s_ystème (1.15) est strictement h_yperboli_que

rgk (u) := gk ( W (u)) DW (u) gk (u) A (u) = Àk (u) gk (u) (1.19) .

Question : Comment se comporte Àk (u), gk (u) et dk (u) _quand u varie?

Théorème 1.5. (Dépendance des valeurs et vecteurs propres de u). On suppose la matrice A assez ré_gulière, strictement h_yperboli_que, Alors :

i) Àk (u) dépend ré_gulièrement de u E Rⁿ ; 1 = k = n

ii) En outre, on peut choisir les vecteurs gk (u) et dk (u) dépendant ré_gulièrement de u tel _que |dk(u)| = 1, |gk(u)| =1, 1 = k =n

Preuve. 1- A(u) étant strictement h_yperboli_que, pour tout u0 ERⁿ, on a :

À1 (u0) < ... <À_n (u0).

Pour k fixé dans {1, ..., n}, pour u0 E Rⁿ, soit dk (u0) satisfaisant

A(u0)dk(u0)=Àk(u0)dk(u0); |dk(u0)| = 1,

supposons dk (u0) = e_n = (0, 0, .., 1).

En premier lieu, montrons _que dans un voisina_ge de u0, il existe des fonctions assez ré_gulières Àk (u) , dk (u) telles _que

A(u)dk(u)=dk(u)Àk(u), |dk(u)| =1.

2- On appli_que le théorème des fonctions implicites à la fonction ré_gulière I : Rⁿ x R x Rⁿ ? Rⁿ⁺¹ définie par:

I (d, À, u) = (A (u) d - Àd, |d|²) (d, u E Rⁿ; À E R).

-d1

ôI (d,À,u)

=

ô (d, À)

A(u) - ÀI ...

-d_n

2d1...2d_n 0

((n+1)×(n+1))

Or dk (u0) = e_n, il suffit de vérifier _que :

(1.20) det

A(u0) - ÀI

0 ... -1

=6 0

0...2 0

3- Pour å > 0 suffisament petit, la matrice

(1.21) A_å = A (u0) - (ëk (u0) + å) I

est inversible. A_å (e_n) = ?åe_n, par consé_quent

0

0

0

=

A_å . . . x

-1

0...2 0

I . . .

(-å)^-1

0...0 1

A_å ...

0

0...2 2 (?å)^-1

Sachant _que le déterminant de la 2e matrice vaut 1, on a : 0

det

Aå

. . . -1

= 2 (--å)^-1 (det Aå) = 2 Y j6=k

(ëj (u0) - ëk (u0) --- å) (-å) (-å)^-1

(u2)²
u1

f³ (u) = u2u3

u1

f1 (_u) _=u2

_--

u3 1 (u2)²

+p )

u1 2 u1

f2 (u) =

p u1

u1 2 u1

u3 1 (u2)² u2 u1

?

???????

???????

f (u) =

0...2 0

_qui tends vers 2 Qj6=k (ëj (u0) --- ëk (u0)) _quand å > 0.

Comme A (u0) est strictement h_yperboli_que, la dernière expression est non nulle et la condition (1.20) est vérifiée. Nous allons ainsi invo_quer le théorème des fonctions implicites pour extraire dans un voisina_ge de u0, les fonctions ré_gulières ëk (u) , dk (u) satisfaisant le théorème. Preuve similaire pour les vecteurs propres de _gauche

Exemple 1.3. Soient les é_quations d'Euler d'écoulement de _gaz compressible en dimension 1 suivantes :

(1.22)

? ? ?

ñt + (ñv)x = 0 ( conservation de la masse) (ñv)t + (ñv^2 + p)x = 0 ( conservation du moment) (ñE)t + (ñEv + pv)x = 0 ( conservation de l' énergie)

dans (0, 8) x IR où ñ est la densité de masse, v la vitesse et E la densité d'éner_gie par

2

unité de masse, p la pression . (E = e + v 2 , e éner_gie interne). Le s_ystème sera strictement h_yperboli_que si :

Op

p > 0, Oñ > 0, et Op > 0.

Oe

Cette assertion est très difficile à vérifier directement, car le flux définit comme ci-dessous est compli_qué.

où u = (ñ,ñv,ñE) ,u = (u1,u2,u3) ,u1 > 0.

Supposons un chan_gement de fonction inconnue et re_gardons la densité ñ, la vitesse v et l'éner_gie interne e comme des inconnues, d'où le s_ystème (1.22) devient alors :

ñt + vñx + ñvx = 0 vt + vvx + ^ñ1 vx= 0 et + vex + p ñvx = 0

où ñ> 0.

Posant w = (ñ, v, e), ce s_ystème devient wt + A (w) w_x = 0 où

(1.23) A(u)=u2I+ 0 u1 0

A(u)

Oñ (u1, u3) 0 1

Op Op

u1Oe (u1, u3)

1

u1

1

A(u)= u1

0

p(u1,u3) 0

Le pol_ynôme caractéristi_que de A (u) est --À (À² -- ó²) pour

ó2 = p u1^2

Op+ Oe

Op. Oñ

On revient à (1.23) et on voit _que les valeurs propres de A sont :

À1=v--ó, À2=v, À3=v+ó, ó>0

ó est la vitesse locale de son.

Par consé_quent, wt + A (w) w_x = 0 est strictement h_yperboli_que à condition _qu'on ait

Op Op

>0et >0.

Oñ Oe

Utilisant le théorème 1.4, on déduit _que les é_quations d'Euler sont strictement h_yperboli_ques.

Chapitre 2

PROBLÈME DE RIEMANN

Dans ce chapitre, nous étudierons en détail le s_ystème de lois de conservation (2.1) ut+f(u) = 0 dans (0,8) x R

avec la condition initiale

(2.2) u (0, x) = u0 (x) = { u si x < 0

u+ si x>0

Les quantitées u⁺ et u sont respectivement l'état initial à droite et à _gauche du saut à l'ori_gine.

D'une manière _générale, la condition initiale doit être constante par morceaux .

2.1 Ondes Simples

Ici, nous cherchons la solution de (2.1) sous la forme d'ondes simples de la forme : (2.3) u (t, x) := v (w (t, x)) (t > 0, x E R)

oùv:R?Rⁿetw:[0,8)xR?R sontdesinconnues. En substituant (2.3) dans (2.1), on trouve :

(2.4) wtvÿ (w) + Df (v (w)) v ÿ(w) w = 0.

Au vu de (1.14) du chapitre 1 avec A = Df, (2.4) n'aurait de sens _que si pour tout 1 <k < n, w est solution de l'E.D.P

(2.5) wt+ëk(v(w))w =0,

et v est solution de l'é_quation différentielle

(2.6) vÿ(s) =dk(v(s)).

Si (2.6) et (2.5) sont résolues, avec les conditions initiales respectives v (0) = u0_; u = v (w ) et u⁺ = v (w⁺), u est appelée une k-onde simple.

Le point important ici est _qu'on puisse re_garder (2.6) comme une é_quation différentielle de la fonction vectorielle v et interpréter (2.5) comme une loi de conservation scalaire dew.

Question: Dans _quelles circonstances pouvons-nous utiliser les étappes (2.3)-(2.6) pour construire une solution continue de (2.1)? Examinons en premier l'é_quation (2.6).

Définition 2.1. Soit u0 fixé dansRⁿ, on appelle k^e- courbe de raréfaction notée Rk (u0), la courbe inté_grale du champs de vecteur dk _qui passe par u0.

Soit donné la solution v de (2.6), retournant à (2.5), réécrivant (2.5) sous la forme

wt + fk (w)_x = 0

où

Z s

fk (s) = ëk (v (t)) dt, (s E R)

0

^ÿfk (s ) =ëk(v(s))

(2.7) ^·fk (s) = Dëk (v (s))vÿ (s) = Dëk (v (s))dk (v (s)).

D'après (2.7), la fonction fk sera strictement : convexe si Dëk (v (u)) dk (v (u)) > 0, (u E Rⁿ)

et concave si Dëk (v (u)) dk (v (u)) < 0, (u E Rⁿ);

fk est linéaire si Dëk (v (u)) dk (v (u)) = 0, (u E Rⁿ).

Définition 2.2. Le couple (ëk (u) , dk(u)) est vraiment non-linéaire si : (2.8) Dëk(v(u))dk(v(u))=60, (uERⁿ)

Définition 2.3. Le couple (ëk (u) , dk (u)) est linéairement dégénéré si : (2.9) Dëk(v(u))dk(v(u))=0, (uERⁿ)

Notations

Si le couple (ëk (u0) , dk (u0)) est vraiment non-linéaire, écrivant :

R+ k (u0) = {uERk(u0) / ëk(u) > ëk(u0)} et R- k (u0) = {uERk(u0) /ëk(u)<ëk(u0)}

Alors

Rk (u0) = R- k (u0) U {u0} U R+ k (u0)

2.2 Ondes de raréfaction

Théorème 2.1. (Existence de la k^e-onde de raréfaction).On suppose pour un certain k E {1....n} _que :

(i) le couple (Àk (u) , dk(u)) soit vraiment non-linéaire.

(ii) u⁺ E R+ k (u ).

Alors il existe une solution faible continue u du problème de Riemann (2.1)-(2.2) appelée k-onde simple, constante le lon_g du chemin traversant l'ori_gine.

Preuve. 1- Supposant fk strictement convexe, la carte s i-? Àk (v (s)) est strictement croissante . Choisir w , w⁺ E R tels _que u = v (w ), u⁺ = v (w⁺)

Supposons w <w⁺, considérant alors le problème de Riemann

wt+fk(w)_x = 0

½ w si x < 0

w(0,x) = w+ si x>0

La fonction

(2.10)

? ? ?

w si x <tÀk (u ) æ où Àk (v ((æ))) = x tsi tÀk (u ) <x < tÀk (u^+) u+ si tÀk (u^+) <x

est solution faible continue appelée onde de raréfaction joi_gnant les états w et w⁺.

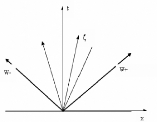
En effet, l'é_quation (2.5) est trivialement satisfaite dans les secteurs x < tÀk (w ) ou x > tÀk (u⁺) dès _que wt = w_x = 0.

Par la suite, on voudrait relier les deux valeurs de w entre x < tÀk (u ) et x > tÀk (u⁺)
par la fonction la plus simple possible. On aurait donc w (t, x) = ç _(x ) _qui dans (2.5)

t

entraine

x

-

_t2

_x ) ( ( _x ))) _(x )

çÿ + 1 t Àk v ç ç^ÿ =0;

t t t

et en posant æ = x t E]Àk (u ) , Àk (u⁺) [, on a bien

(Àk(v(ç (æ))) ? æ) ç^ÿ (æ) =0.

En supposant

öÿ =6 0, alors

(w+) [, Àk (y (ö (æ))) = æ.

Væ E]Àk _(w ) , Àk

Ainsi u (t, x) = y (w (t, x)) où y est la solution de l'é_quation différentielle (2.6) _qui passe par u est une solution faible continue par morceaux de (2.1)-(2.2).

Le cas w > w⁺ est traité similairement pour fk concave .

2.3 Ondes de choc - discontinuités de contact

Nous nous pla_çons dans le cas où les états u et u⁺ peuvent être joints non plus par les ondes de raréfaction, mais plutôt par un choc.

2.3.1 L'ensemble de choc

Se rappelant de la condition de Rankine-Hu_goniot introduite au para_graphe 1.3 du chapitre 1, on fait l'observation suivante dès _que

f (u ) - f (u⁺) = ó (u - u⁺) (ó E R), alors il existe une courbe de choc d'é_quation x = ót_; cette observation motive les calculs ci-après.

Définition 2.4. Soit u0 fixé dansRⁿ, on définit l'ensemble de chocs S (u0) par : S(u0)={uERⁿ/ f(u)-f(u0)=a(u-u0)}

où a = a (u, u0) E R

Théorème 2.2. (Structure de l'ensemble de choc). Soit u0 fixé.

Dans un certain voisina_ge de u0, S (u0) = Un k=1 Sk (u0) avec Sk (u0) courbes ré_gulières pour un certain 1 k n et possédant les propriétés :

(i) Sk (u0) passe par u0 et est tan_gente à dk (u0).

(ii) _limu?u0 a (u, u0) = Àk (u0) , u E Sk (u0)

(iii) a (u, u0) = 1 2 (Àk (u) + Àk (u0)) + 0 (|u - u0|²) _quand u -* u0 avec u E Sk(u0)

Preuve. 1- Définissons A (u) = f0 1 Df (u0 + t (u - u0)) dt Alors

(2.11) A(u)(u-u0) = f(u) - f(u0)

En particulier u E S (u0) si et seulement si

(2.12) (A (u) - aI) (u - u0) = 0,

pour tout scalaire a = a (u, u0).

2- Pour étudier (2.12), posons A(u0) = Df(u0) ,au vu de la stricte h_yperbolicité, le pol_ynôme caractéristi_que À i--* det (ÀI - A (u0)) a n racines réelles distinctes, d'où À '--* det (ÀI - A (u)) a n racines réelles distinctes si u très près de u0.

Utilisant le théorème 1.5 du chapitre 1, nous disons _que dans un voisina_ge de u0, il existe

des fonctions régulières		À1 (u) < ... <	Àn (u) et des vecteurs unitaires {dk (u) , gk (u)}
satisfaisant : ëk (u0) := ëk (u0),	dk (u0) := dk (u0), gk (u0) := gk (u0) , 1 k n et J' A (u) dk (u) = ëk (u) dk (u) gk (u) A (u) = ëk (u) gk (u) ,

or {gk _(u)}1<k<n , {dk (^u)}1<k< n bases de ⁿ et ainsi

(2.13) gl

dk = älk.

3- On aura alors l'é_quation (2.12) si a = ëk (u) pour tout 1 k n et (u - u0) est
colinéaire à dk(u). Au vu de (2.13), ces conditions sont é_quivalentes à :

(2.14) gl(u)(u-u0)=0,(l=6k).

? n-1 par :

Ces é_galités donnent (n - 1) é_quations des n inconnues composantes de u, _que nous souhaitons résoudre en utilisant le théorème des fonctions implicites. Ainsi, définissant Ö k : n

Ök(u) :=(..., gk-1(u)(u-u0), gk+1(u)(u-u0),...), Ök(u0)=0.

DÖk (u0) =

? ????????

g1 (u0) ... gk-1 (u0) gk+1 (u0) ... gn(u0)

? ? ? ? ? ? ? ? ? ((n-1)xn).

Or les vecteurs {gk _(u0)}1<k<n forment une base de ⁿ, d'où

ran_g DÖk (u0) = n - 1.

Par consé_quent, il existe une courbe ré_gulière Wk : ? n telle _que :
(2.15) Wk (0) = u0

et

(2.16) Ök (Wk (t)) = 0 pour t ? 0.

La trajectoire de la courbe Wk (.) pour t ? 0 définit Sk (u0). Nous pouvons réparamétrer Wk (.) de fa_çon _que: ^ÿWk (t) = 1

4- (2.14)...(2.16) entrainent _que

(2.17) Wk (t) = u0 + u (t)

dk (Wk (t)) pour t ? 0,

où u : ? assez ré_gulière satisfaisant u(0) = 0,uÿ (0) = 1. Car d'après (2.14),

gl (Wk (t)) (Wk (t) - u0) = 0, (l =6 k) (pour u = Wk (t)). D'où Wk (t) - u0 colinéaire à

dk (Wk (t)) et ? u : t 7? u (t) tel _que Wk (t) - u0 = u (t) dk (Wk (t)). Différentiant (2.17) au point t = 0, on a :

(2.18) ^ÿWk (0) = dk (u0)

D'où le vecteur dk (u0) est tan_gent à la courbe Sk (u0) en u0 et (i) est prouvée.

5- Au vu de l'anal_yse précédente, il existe une fonction assez ré_gulière a :Rⁿ×Rⁿ?Rtel_que:

(2.19) f (Wk (t)) - f (u0) = a (Wk (t) , u0) (Wk (t) - u0) pour t ? 0

Différentiant au point t = 0, on déduit au vu de (2.15) _que : Df (u0) ^ÿWk (0) = a (u0, u0) ^ÿWk (0).

Au vu de (2.18), a(u0,u0) = ëk (u0).

6- Posons a (t) := a (Wk (t) , u0) tel _que l'on ait (2.19). Différentiant 2 fois (2.19), on a :

( )

D²f (Wk (t)) ^ÿWk (t) ^ÿWk (t) + Df (Wk (t)) ^·Wk (t) = a· (t) (Wk (t) - u0) + 2 aÿ (t) ^ÿWk (t) +

a (t) ^·Wk (t)

En évaluant cette expression au point t = 0, sachant _que a(0) =ëk(u0),Wk(0)=u0, ^ÿWk (0) = dk (u0), on obtient :

(2.20) (2 aÿ (0) I - D²f (u0) dk (u0)) dk (u0) = (Df (u0) - ëk (u0) I) ^·Wk(0)

7- Soit 17k (t) = v (t) l'uni_que paramétrisation vitesse de la courbe de raréfaction Rk (u0) voisine de u0. Alors :

17k (0) = u0, ÿ17k (t) = dk (17k (t))

Ainsi Df (17k (t)) dk (t) = ëk (t) dk (t) pour ëk (t) = ëk (17k (t)) , dk (t) = dk (17k (t)) Différentiant par rapport à t et évaluant au point t = 0, on obtient :

)(2.21) ( D²f (u0) dk (u0) - ^ÿëk (0) Idk (u0) = - (Df (u0) - ëk (u0) I) ^ÿdk (0)

Additionnant (2.20) et (2.21), on obtient :

( ) ( )

2 aÿ (0) - ^ÿëk (0) dk (u0) = (Df (u0) ? ëk (u0) I) ^·Wk (0) - ^ÿdk (0) Prenant le produit scalaire par gk (u0) et observant gkdk =6 0, on conclut _que : (2.22) 2 aÿ (0) = ^ÿëk (0)

De (2.22), on déduit _que 2a (t)?ëk (u0) ? ëk (t) = 0 (t²) _quand t ? 0 et (iii) est vérifiée.

On voit à partir du théorème 2-(iii), _que les courbes Rk (u0) et Sk (u0) coïncide au moins au premier ordre en u0, dans la suite, avec l'h_ypothèse de dé_générescence linéaire, on va montrer _qu'elle coïncide en fait.

Théorème 2.3. (Dé_générescence linéaire). On suppose pour un certain 1 k n, _que le couple (ëk (u) , dk (u)) soit linéairement dé_généré_;

Alors pour tout u0 E Rⁿ,

(i) Rk (u0) = Sk (u0) et

(ii) a (u, u0) = ëk (u) = ëk (u0) pour tout u E Sk (u0).

soit

{ vÿ (s)

Preuve. v = v (s) solution de l'é_quation différentielle

= dk (v (s)) s E R

v(0)=u0

Alors la surface s i?> ëk (v (s)) est constante et :

Z s

f (v (s)) - f (u0) = Df (v (t)) vÿ (t) dt

Z s

0

= Df (v (t)) dk (v (t)) dt

Z s

0

= ëk (v (t)) dk (v (t)) dt

0Z s

= ëk (u0) vÿ (t) dt

0

= ëk(u0) (v (s)-u0).

2.3.2 Discontinuités de contact - ondes de choc

Nous allons à travers les théorèmes 2.2 et 2.3, étudier la possibilité de résolution du problème de Riemann en joi_gnant 2 états donnés u - et u⁺ par d'autres sortes d'ondes de choc.

Discontinuité de contact :

On suppose _que le couple (ëk (u) , dk(u)) est linéairement dé_généré et u + E Sk (u^-), d'après cette supposition, nous pouvons définir la solution de notre s_ystème de lois de conservation comme étant :

{ u - si x < at

u (t, x) = u+ si x > at

pour a = a(u^-, u⁺) = ëk (u^-) = ëk (u⁺).

On peut faire le constat suivant_; dès _queëk (u^-) = ëk (u⁺) = a, les projectés de la caractéristi_que ont la même valeur de part et d'autre de la droite de discontinuité.

Définition 2.5. Le trait x = at est appelé une k-discontinuité de contact.

Remar_que 2.1. Ph_ysi_quement, on interprète la situation précédente comme suit_; les particules d'un fluide ne peuvent traverser une discontinuité.

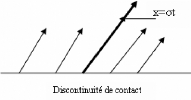
Ondes de choc

On suppose à présent _que le couple (Ak (u) , dk (u)) est vraiment non-linéaire et _que les états u⁺ et u^- sont connectés par un k^e--choc i.e u⁺ E Sk (u^-). Si nous considérons la solution faible :

{u- si x < at

(2.23) u (t, x) =

u⁺ si x > at ,

pour a = a (u^-, u⁺). On voit _qu'on a deux éventualités à savoir :

Ak (u^-) > Ak (u+)

où

Ak (u^-) < Ak (u⁺) .

Au vu de l'assertion(iii) du théorème 2.2, nous avons alors :

(i) Ak (u) > a (u-, u⁺) > Ak (u+)

où

Ak (u) < a (u, u⁺) < Ak (u⁺) ,

à condition que u^- reste très proche de u⁺.

Remar_que 2.2. dans le cas (i), les chocs sont dits ph_ysi_quement acceptables ou des "bons chocs" et non ph_ysi_ques ou" mauvais chocs" dans (ii).

Définition 2.6. On suppose le couple (Ak (u) , dk (u)) vraiment non-linéaire en u^-. On dit _que le couple (u^-, u⁺) est admissible au sens de Lax si :

u+ ? Sk(u^-) et Ak (u⁺) < a (u-, u⁺) < Ak (u) .

Remar_que 2.3. Si (u , u⁺) admissible au sens de Lax, la solution u définie par (2.23) est appelée une k-onde de choc.

Par analo_gie avec notre décomposition de Rk (u0) en R^#177; _k(u0), introduisons ceci :

Définition 2.7. Si le couple (ëk (u) , dk (u)) est vraiment non-linéaire, on a :

S+ k (u0)={uESk(u0)/ëk(u0)<á(u,u0)<ëk(u)} S _k (u0)={uESk(u0)/ëk(u)<á(u,u0)<ëk(u0)} Alors Sk (u0) = S _k (u0) U {u0} U S+ k (u0)

On note alors _que le couple (u ,u⁺) est admissible au sens de Lax si et seulement si u+ E S _k (u ).

2.4 Solution locale du problème de Riemann.

Définition 2.8. (i) Si le couple (ëk (u) , dk(u)) est vraiment non-linéaire, prendre : Tk (u0) = R+ k (u0) U {u0} U S _k (u0).

(ii) Si le couple (ëk (u) , dk(u)) est linéairement dé_généré,

prendre : Tk (u0) = Rk (u0) = Sk (u0).

On voit _que les états initiaux très voisins u et u⁺ pourraient être joints par une kLonde de raréfaction, une onde de choc ou une discontinuité de contact à condition _que

(2.24) u E Tk (u⁺).

Question : Peut-on chercher des solutions du problème de Riemann avec la seule condition que u⁺ reste très proche de u ?

Tout en espérant _qu'on puisse joindre u⁺ à u par une suite d'onde de raréfaction, d'onde de choc et/ou les discontinuités de contact le lon_g des chemins Tk.

Théorème 2.4. (Solution locale du problème de Riemann) On suppose pour cha_que 1 = k = n _que le couple (ëk (u) , dk(u)) soit linéairement dégénéré ou bien vraiment non-linéaire. On suppose en outre donné l'état initial de _gauche u .

Alors, pour tout état de droite u⁺ suffisament proche de u , il existe une solution faible u du problème de Riemann, _qui est constante le lon_g du chemin passant par l'ori_gine.

Preuve. 1L On va appli_quer le théorème des fonctions implicites sur la carte Ö :

n ? n définie dans un voisina_ge de 0 comme suit. Premièrement, pour toute famille de courbes Tk (1 = k = n), choisir le paramètre non sin_gulier ôk mesurant la lon_gueur de l'arc_; plus précisément, si w, w E ⁿ avec w E Tk (w), alors ôk (w) ? ôk (w) = (si_gne) distance de w à w le lon_g de la courbe Tk (w). Nous prendrons le si_gne"+" pour ôk (w) si w E R+ k (w) et le si_gne "L" si w E S _k (w) .

2L Prenant alors t = (t1, ..., t_n) E ⁿ avec |t| petit, on définit Ö (t) = w comme suit : écrire (2.24) comme suit :

u = w0,

choisissons les états w1, .., w_n tel _que :

? ???? ????

w1ET1(w0), r1(w1)-r1(w0)=t1 w2ET2(w1), r2(w2)-r2(w1)=t2 ... wn E T n (wn_1), rn (wn) - rn (wn_1) = tn

u+ = w_n

et définir '1 (t) = w.

'1 est C¹ et '1 (0) = u0.

3- On exi_ge _que :

(2.25) D'1 (0) soit non sin_gulière.

Pour voir cela, observons _que '1 (0, .., tk, ..0) - '1 (0, ..., 0) = tkdk (u0) + 0 (tk). Ainsi

?'1 (0) = dk (u0) (1 k n) et D'1 (0) = (d1 (u0) , ..., dn (u0))n×n
?tk

Cette matrice est non sin_gulière car la famille {dk _(u0)}1=k=n est une base.

4- Au vu de (2.25), le théorème des fonctions inverses, appli_qué, pour tout état u+ suffisamment proche de u_, il existe un uni_que paramètre t = (t1, ..., t_n) proche de 0 tel _que '1 (t) = u⁺ . Se rappeler _que, si wk_1 et wk sont joints par une k-onde de raréfaction, cette onde est :

? ?? ??

wk_1 si x < tÀk (wk_1) c où Àk (y ((c))) = x tsi x t E ]Àk (wk_1) , Àk (wk)[ wk si x > tÀk (wk)

où encore, si wk_1 et wk sont joints par un k-choc, il aurait la forme :

?

?

?

wk_1 si x

t

wksi a(wk, wk_1) < t

< a (wk, wk_1)

x

où Àk (wk) < a (wk, wk_1) < Àk (wk_1).

Dans les deux cas, les ondes sont constantes à l'extérieur des ré_gions Àk (w0) - < x < Àk (w0) + pour > 0 très petit, à condition _que wk, _{wk_1} soient très près de w0. Or

t

À1 (w0) < ... < À_n (w0), on voit alors _que les ondes de raréfaction, les ondes de choc et/ou les discontinuités de contact joi_gnant u _ = w0 à w1; w1 à w2; ...;wn_1 à w_n = u⁺ sont disjointes Exemple 2.1.

Soit le s_ystème de lois de conservation :

(2.26)

? ????? ?????

· u1 [u1]t + = 0 1 + u1 + u2 x · u 2 [u2]t + = 0 1 + u1 + u2 x

u1 > 0,u2 >0

Ecrivant (2.26) sous la forme _quasilinéaire, la (2 x 2) matrice A (u) est donnée par :

	1 + u2		-u1
A(u)=	(1+u1+u2)^2		(1+u1 +u2)^2

-u2

(1+u1+u2)²

1 + u1

(1+u1 +u2)²

Le pol_ynôme caractéristi_que étant donné par :

+ )²(1+u1+u2)

₃ .

PA (À) = À² - (2+ u1 + u2) 1

(1+ u1 +u2

Les valeurs propres sont données par :

1 1 À1 (u) = (1 + u1 + u2) 2 , À2 (u) = 1+u1+u2

.

Les vecteurs propres respectifs coorespondants aux valeurs propres sont donnés par :

Ç -u1 Ç -1

1

d1 (u) = _p ; d2 (u) = 1 _v2 .

u2 1 + _u2 -u2 -1

2

(1 + u1 + u2)3 ( 1, 1) et DÀ2 (u) =

-2

Comme

DÀ1 (u) =

(1+u1 +u2)²

^-1(1, 1).

Alors

2(u1 +u2)

(2.27) DÀ1 (u) d1 (u) ==6 0

(1 + u1 + u2)3 p u2 1 + u2 ₂

car u1 > 0,u2 > 0.

(2.28) DÀ2(u)d2(u) =0.

(2.27) et (2.28) entrainent _que le couple (À1 (u), d1 (u)) est vraiment non-linéaire et (À2 (u), d2 (u)) linéairement dé_généré. Dans cet exemple, les deux courbes de choc et de raréfactions coïncident i.e Si = Ri i = 1, 2.

2.5 Système de deux lois de conservation.

(2.29) t + f² (u¹, u2) x = 0 dans

t + f¹ (u¹, u²)_x = 0

1

(0, 8) × R

_u2

Dans ce para_graphe, nous anal_yserons plus profondément le problème avec valeur initiale pour n = 2_; on aura à faire au s_ystème suivant

{ u

u1 (0, x) = u1 0 (x) ; u² (0, x) = u2 0 (x) dans {t = 0} × R. f = (f¹, f²) ; u0 = (ui , u² ₀) ; u = (u¹, u²) .

2.5.1 Invariants de Riemann.

Nous allons démontrer _que nous pouvons transformer le s_ystème (2.29) en la plus simple forme par un pertinant et approprié chan_gement de variables. L'idée est de chercher 2 fonctions w1, w² : R² ? R _qui possèdent de bonnes propriétés le lon_g des courbes de raréfaction R1 et R2 .

Définition 2.9. On dit que wⁱ : R² ? R est le j^e-invariant de Riemann si :
(2.30) Dwⁱ (u) est colinéaire à gj (u); (u E R² , j =6 j) .

Nous verrons comment la condition (2.30) est utile.

La _question _que l'on se pose ici est celle de l'existence de l'invariant de Riemann. En effet_; comme gi (u) d _j (u) = äij, (2.30) est donc é_quivalent dans R² à

(2.31) Dwⁱ (u) di (u) = 0,

_qui si_gnifie _que

(2.32) wⁱ est constant le lon_g de la courbe de raréfaction Ri (j = 1, 2).

En particuler, toute fonction régulière wⁱ satisfaisant (2.31)-(2.32) et (2.30) est le j^e-invariant de Riemann.

Remar_que 2.4. Dans le cas n > 2, les invariants de Riemann n'existent pas en _général.

A présent, posons w = (w1,w2) = (w¹ (u1,u2) ;w² (u1, u2)), comme des nouvelles

coordonnées dans l'espace d'état R² . Rempla_çant u = (u1,u2), on définit w : R² ? R2 par

w(u) =w(u1,u2) = (w¹ (u1,u2) ;w² (u1,u2)) .

La carte inverse est u(w) = u(w1,w2) = (u¹ (w1,w2) ;u² (w1,w2)). Si u = (u¹,u²) est une fonction ré_gulière de (2.29), on chan_ge les variables dépendantes par

(2.33) v(t,x) = w(u(t,x)) (t>0, x E R).

Question Quel s_ystème d'E.D.P satisfait v = (v¹,v²)?

Théorème 2.5. (Lois de conservation et Invariants de Riemann). Les fonctions v¹,v² sont solutions du s_ystème_;

{ v1 t + À2 (u) v1

(2.34) x = 0

x = 0 dans (0, 00) x R

v2 t + À1 (u) v2

Remar_que 2.5. Bien _que (2.34) ne soit pas écrit sous la forme de lois de conservation, il est beaucoup plus simple _que (2.29). En particulier, tandis _que l'E.D.P en u¹ comporte un terme en u² _x, l'E.D.P en v¹ ne comporte pas de terme v² _x. De la même fa_çon, l'E.D.P en v² ne comporte pas de terme v¹ _x.

Preuve. (Théorème 2.5)Utilisant (2.33), on obtient pour i = 1,2; i =6 j, v _t +Àj (u)v x = Dw (u)ut+Àj (u)Dw (u)u_x

= Dw (u) (ut + Àj (u) u_x)

= Dw (u) (-f (u)_x + Àj (u) u_x)

= Dw (u)(-Df(u)+Àj (u)I)u_x

=0,

car par définition, Dw (u) est colinéaire à gj (u)

Remar_que 2.6. *Nous pouvons interpréter le s_ystème d'E.D.P (2.34) en introduisant l'é_quation differentielle ordinaire

(2.35) ÿx (s)=Àj (u(s,x(s))) (s~0)

pour i = 1,2, i =6 j. Alors au vu de (2.34), on a :

(2.36) v est constant le lon_g de la courbe (s, x (s)), (s ~ 0).

*Sachant _que la condition de non linéarité s'écrit :

(2.37) DÀ (u)d (u) =60

Re_gardant À comme une fonction de w = (w1, w2), on réécrit (2.37) pour avoir

(2.38) 8À =6 0 (w E R², i=6j).

8wj

Montrons _que (2.37) et (2.38) sont é_quivalents. Supposons (2.38) faux, alors :

(2.39)	8À 0 =8wj	=	2 X k=1	8À		8u^k
				8uk		8wj

Or 2 8w 8uk= ä j, par comparaison avec (2.39), on a DÀ et Dw ortho_gonaux au k=1 8uk 8wj

u 8u1

, 8u2

vecteur non nul , dont DÀ est colinéaire à Dw . Cependant

8wj 8wj

Dw perpendiculaire à d , et nous obtenons la contradiction (2.37). D'où (2.37) = (2.38), l'implication inverse est établie de la même fa_çon.

2.5.2 Non existence de solutions régulières.

Dans ce para_graphe, nous allons nous intéresser à l'utilité des invariants de Riemann, nous établirons un critère de non existence de solutions ré_gulières.

Théorème 2.6. (Invariants de Riemann). On suppose :

* u0 ré_gulière à support compact.

* la condition de non linéarité :

(2.40) 0Ài >0 (i=6j).

0wj

Alors le problème avec valeur initiale (2.29) ne peut avoir de solution ré_gulière u pour tout t = 0 si :

y1 x <0 ou y2 x <0 _quel_que part sur {t = 0} x R.

Preuve.

1- Supposons _que pour tout t, u est solution ré_gulière de (2.29). Posons :

{

a:=y¹ x; , b:=y2 x où y = w(u)_; y = (y¹,y²) est solution de l'E.D.P (2.34). En différentiant la première

é_quation de (2.34) par rapport à x, on obtient :

(2.41) at + À2ax + 0À2 a2 + ^0À2ab=0 où

0À2 0x	0À2	0w1+ 0x	0À2		0w2	=		^0À2a+ 0w1
				0x

0À2 b (car wi, yⁱ constants le lon_g de la courbe

0w1 0w2

0w2

(s, x (s))). Utilisant (2.41) pour réécrire la deuxième é_quation de (2.34), on a : y2 t +À2y2 x =

(À2-À1)b car (y2 _t +À1y² _x)=0.Ona:

[ 1 )]

(2.42) at + À2ax + 0À2 0À2 (y2

a2 + t + À2y² a = 0

x

0w1 À2 - À1 0w2

2- Inté_grer (2.42), fixer x0 E R et poser :

(2.43) î (t) := exp	( Z t ) 1 0À2 (y2 t + À2y2 ) (s, x1 (s)) ds où x À2 - À1 0w2 0
{ ÿx1 (s) = À2 (u (s, x1 (s))) (s = 0) (2.44) x1 (0) = x0		.

Ce _qui suit est une consé_quence importante de (2.36) (_qui dit que y¹ est constant le
lon_g de la courbe (s,x1 (s)) ). Ecrire y¹ (s,x1 (s)) = y1 0 = y¹ (0,x0) (s = 0). Ainsi, on

voit _que l'expression 1 0A2 considérée comme une fonction de v = w (u), dépend

A2 - A1 0w2

seulement de v². Posant

f u l 1 0 A2 \

Y (u) .1 0 A2 - A1 0w2) (v01, v) dv.

Alors (2.43) et (2.44) impli_quent :

t

(2.45) (t) = exp {/0 dds [Y (v2 (s, x1 (s)))] ds}

= exp {Y (v² (t, x1 (t))) - Y (v² (0, x0)) }

0A2

3- En transformant (2.45), on a :

dt( (t) á (t))² dt

--1 d

A2

[( (t) á (t))^-1] = ( (t) á (t)) = 0w 1 -1 car

dt 0 A2 1 2

d (t) 1

A₂ -- = A1 0w2 (v_t + A2v ^x) (t) á (t) = 1 (at + A2ax + , ⁰ á²) (t)

ow1

d'après (2.42),

=d d 0 A2

á (t) dt (t) _dtá (t) 0w1 á2 (t)

=d d 0A2 d 0A2

á (t) (t) + (t) _dtá (t) _=-0w1á2 (t)=_dt( (t)á(t)) _=-0w1á2 (t)

D'où

t

(t) á (t))^-1 = (á (0))^-1 + f ^-1(s)ds.

Ce _qui entraine :

u(2.46) á (t) = á (0) ^-1 (t) 1 + á (0) ^{t 0A21}(s) ds) .

0 0w1

4-Au vu de (2.34), v est bornée. Nous déduisons de (2.45) _que 0 < è ? (t) = e pour tout t > 0, pour des constantes appropriées è et e. Cependant, il découle de (2.40) et (2.46) _que á est bornée pour t > 0, si et seulement si á (0) > 0, ce _qui entraine :

v1 _x(0, x0) = 0.

En rempla_çant v¹ par v² dans les calculs ci-dessus, on obtient v²_x (0, x0) = 0. Nous concluons _que si v¹ _x< 0 ouv² _x< 0 _quel_que part sur {t = 0} x IR, alors il n'existe pas de solution ré_gulière de (2.29) pour tout t = 0.

Exemple 2.2.

Soient les é_quations _générales d'Euler suivantes (_quand l'éner_gie interne e est constante) :

J ñt + (ñv)_x = 0 (conservation de la masse)

(2.47)(ñv) _t + (ñv² +p)_x = 0 (conservation du moment)

où nous supposons

(2.48) p=p(ñ),

pour toute fonction ré_gulière p : R ? R, (2.48) est appelée "é_quation d'état". Nous avons la condition d'h_yperbolicité stricte

pÿ >0.

Posant u = (u¹, u²) = (ñ, ñv) , le s_ystème d'é_quations (2.47) peut s'écrire ut + f (u) x = 0 pour

!

f = (f 1_, f2) = u2, (u2)2

u1 + p u¹cents ,

à condition _que u1 > 0. Alors :

? ?

0 1

₎2

A = Df = ? (_u2 _j

+ pÿ (u1) 2u2

- _u1 _u1

Par consé_quent le pol_ynôme caractéristi_que de A est donné par :

(u2 )2

PA (À) = À² - 2u2 - pÿ (u1)

u1 À + u1

Les valeurs propres de A sont donc :

u2 À1 = u1 En notation physique, on a :

p p p ÿ (u^1) et À2 = u2 - u1 + p ÿ (u^1)

À1=v?ó; À2=v+ó

pour la vitesse de son :

_p

ó := pÿ (ñ).

Utilisant (2.35), considérons les é_quations différentielles.

(2.49) ÿx1 (t) = v (t, x1 (t)) + ó (t, x1 (t))

(2.50) ÿx2 (t) = v (t, x2 (t)) ? ó (t, x2 (t))

où

_p

ó (t, x) = pÿ (ñ(t,x)), t = 0.

Nous déduisons de (2.36) _que l'invariant de Riemann y¹ = w¹ (u) est constant le lon_g des trajectoires de (2.49) et y² = w² (u) est constant le lon_g des trajectoires de (2.50). A présent, déterminons directement w¹ et w². Premièrement, transformons (2.47) sous la forme de non diver_gence.

(2.51) ñt+ñy_x+ñ_xy = 0

(2.52) ñty +ñyt + ñ_xy² + 2ñyy_x +p_x = 0.

Multipliant (2.51) par ó² = pÿ(ñ) et se rappelant de (2.48), on a :
(2.53) pt+yp_x+ó²ñy_x =0

(2.51) dans (2.52) donne :

(2.54) ñyt +ñyy_x +p_x = 0.

A présent, nous allons manipuler (2.53) , (2.54) de sorte à faire apparaître explicitement les directionsë1, ë2 = y #177; ó. Pour _y arriver, multiplions (2.54) par ó et alors, l'additionant où le rétranchant à (2.53), on a :

½ pt + (y + ó) p_x + ñó (yt + (y + ó) y_x) = 0 ^(2.55)pt+(y ? ó)p_x ? ñó(yt+(y?ó)y_x)=0

De (2.55), on déduit _que :

? ???? ????

dt [p (t,X1 (t))] +ñ(t,X1 (t))ó(t,X1 (t)) d d dt [y(t,X1 (t))] = 0 dt [p (t,X2 (t))] ? ñ(t,X2(t))ó(t,X2(t)) d d dt [y(t,X2 (t))] = 0

dp
dt

Comme

= ó2 dñ dt ,

on voit _que :

ñ

ó dñ #177; dy = 0

dt dt

(2.56)

le lon_g des trajectoires de (2.49), (2.50) à condition _que ñ > 0. Penser à present aux invariants de Riemann comme fonction de ñ et y_; alors y¹ = w¹ (ñ, y) étant constant le lon_g de la courbe déterminée par X1 (.) , nous avons :

d [w1 (ñ (t, X1 (t)) ; y (t, X1 (t)))] 0 = dt

Cw¹

d Cw¹d

=

dt [ñ (t, X1 (t))] + dt [y (t, X1 (t))]

Cñ Cy

Ceci coïncide avec (2.56) si :

0w^1

=

ó (P) P

0w^1

=1.

0P

,

0v

Similairement, nous déduisons que :

0w^2

=

ó (P) P

0w^2

=--1.

0P

,

0v

Inté_grant, nous obtenons les invariants de Riemann suivants :

Z ñ Z ñ

ó (s) ó (s)

w1 = s ds + v, w² = s d s -- v.

1 1

Vérifions à présent que w¹ et w² sont effectivement les invariants de Riemann_; i.e _que :
Dwⁱ (u) .di (u) = 0 pour i = 1, 2

En effet, on a :

d1(u) = (1,v--ó)_; d2(u) = (1,v+ó) et

uó -- v uó + v

Dw¹ (u) = P , 1 ; Dw² (u) = P , --1

D'où

et

P P

uó -- v

Dw¹ (u) .d1 (u) = P , ¹ . (1, v -- ó)

P

=

ó--v P

v -- ó + P

=0

uó+v )

Dw² (u) .d2 (u) = P , ^--1 . (1, v + ó)

P

=0.

ó+v

=

P

v+ó
P

Par consé_quent, w1et w² sont bien des invariants de Riemann.

Chapitre 3

CRITÈRE D'ENTROPIE

Dans l'étude du problème de Riemann au chapitre 2, nous n'avons pris en considération _que la condition d'entropie de Lax

(3.1) ëk(u⁺) <á(u^-,u⁺) <ëk(u^-),

pour un certain k E {1, .., n} comme critère de selection admissible d'ondes de choc. Ceci est un départ intéressant dans une bonne discussion mathémati_que et ph_ysi_que, permettant de trouver de conditions plus appropriées d'entropie de diverses sortes, avec pour but de les appli_quer pour chercher des solutions faibles moins compli_quées de notre s_ystème de lois de conservation, ainsi pour obtenir le critère d'unicité, et plus d'informations concernant des probables solutions discontinues, etc.

Un principe _général est _que, des solutions ph_ysi_ques et mathémati_ques peuvent être cherchées comme limite des solutions du s_ystème ré_gularisé

(3.2) uå t + f (uå) x - Äu^å = 0 dans (0, oc) x R

où est un paramètre d'autant plus petit _que l'importance des phénomènes de diffusion
est faible et Ä= ?2 xx. A la limite, si on né_gli_ge la diffusion ( = 0), on aboutit à l'é_quation

(3.3) ut+f(u)_x =0.

Par consé_quent, étudions la limite de u^å lors_que ? 0, et de cette manière, nous allons
discuter d'un critère d'entropie plus _général pour améliorer la condition de Lax (3.1).

3.1 Viscosité évanescente-ondes mobiles

3.1.1 Première condition d'admissibilité

On dira _que la solution faible u du problème (3.3) est admissible s'il existe une suite de solutions régulières u^å de

(3.4) uå t +A(uå)uå x = uå xx

_qui conver_ge vers u dansL1 _{loc q}uand ? 0.

Commen_çons par chercher la solution du problème (3.2) sous la forme d'ondes mobiles i.e sous la forme :

(3.5) u^E(t,x)=v

(x -- Àt

, (t=0, xER)

où les inconnues sont la vitesse À et le profil v. En substituant (3.5) dans (3.2), on cherche v : R ? Rⁿ, v = v (s) solution de l'é_quation différentielle ordinaire

(3.6) v· = --À vÿ + Df (v) ÿv.

Supposant u , u⁺ données et _que

(3.7) lim 8-4 00	v (s) = u , lim 8-4+00		v(s)=u^+, lim |8|-4+00	vÿ (s) = 0.
Alors de (3.5), on déduit : (3.8) lim E-40		½ u si x < Àt uE (t, x) = u+six>Àt

d'où la limite _quand ? 0 de notre solution de (3.3) nous donne une onde de choc joi_gnant u et u⁺. Nous allons à présent étudier attentivement les formes de À et v, et de cette manière, _glaner plus d'informations sur la structure de chocs déterminés par (3.8).

Question A-t-on toujours existence de À et v solutions de (3.6) et (3.7) ? Inté_grant (3.6), on obtient :

(3.9) vÿ = f (v) -- Àv + cte, (cte = constante de Rⁿ).

On conclut en fonction de (3.7), _que :

(3.10) f(u ) -- Àu +c=f(u⁺) -- Àu⁺ +c d'où

(3.11) f(u ) --f(u⁺) =À(u --u⁺).

Au vu de (3.7), (3.10) et (3.11), (3.9) devient

(3.12) vÿ =f(v)--f(u )--À(v--u )

où u est donnée et en supposant la construction d'une onde mobile joi_gnant u à u⁺. De (3.11), on voit _que nécessairement u⁺ E Sk (u ) pour tout k E {1, ..,n} et À = À(u ,u⁺).

Théorème 3.1. (Existence d'ondes mobiles pour les s_ystèmes vraiment non- linéaires). On suppose le couple (Àk, dk) vraiment non-linéaire

Soit u⁺ choisi suffisamment proche de u . Alors il existe une onde mobile solution de (3.2) joignant u⁺ à u si et seulement si

(3.13) u⁺ E Sk _(u ) pour tout k E {1, .., n}

Preuve. 1- On suppose À et v solution de (3.6), (3.7).

Alors nécessairement u⁺ E Sk (u ) pour 1 = k = n, À = À (u , u⁺). Soit

G(u)=f(u) -- f(u )--À(u -- u ),

(3.12) s'écrit alors :

(3.14) vÿ = G(v) et on :a

G _(u ) = G (u⁺) = 0.

D'après (3.11), on a :

DG _(u ) = Df _(u ) -- ÀI

et les valeurs propres de DG au point u sont {Àk (u ) -- À}1=k=n. Avec les vecteurs propres de droite et de _gauche correspondants

_(u )

{dk, _gk}1=k=n , dk = dk _(u ) , gk = gk

2- Dès que u⁺ E Sk (u ) et |u⁺ -- u | très petit, on sait d'après le théorème 2.2-(iii) du chapitre 2 _que:

1 [Àk (u⁺) + Àk _(u )] + 0 (u+ -- u 2)

À = 2

ainsi

[Àk

Àk _(u ) -- À = 1 _(u ) -- Àk (u+)] + 0 (_u+ -- u ²)_.

2

Afin _qu'il _y'ait une orbite de l'é_quation différentielle (3.14) joi_gnant u (_quand s = --oc) à u⁺ E Sk (u ) (_quand s = +oc), on doit nécessairement avoir Àk (u ) -- À > 0_; par ailleurs la trajectoire ne pourrait conver_ger vers u _quand s ? --oc. Ainsi si |u⁺ -- u | est assez petit,

_(u ) .

Àk (u⁺) < Àk _(u ) u + E Sk

3- La preuve de la suffisance de (3.13) est admise Le résultat du théorème 3.1 utilise la condition de non linéarité du couple (Àk, dk), mais le théorème reste vrai en _général à condition d'introduire une variante appropriée de la condition d'entropie de Lax.

Supposons à present u⁺ E Sk (u ) pour un certain 1 = k = n et en outre

(3.15) À (u, u ) > À (u , u⁺) ,

pour cha_que u compris entre u⁺ et u et appartenant à la courbe Sk (u ).

Remar_que 3.1. (3.15) est la condition d'entropie de Liu, cette condition peut encore être motivée par la recherche des ondes mobiles du s_ystème (3.2).

Supposant u donné, alors si |u⁺ -- u | assez petit, ceci impli_que _qu'il existe une onde
mobile u^å (t,x) = v (x ët) , v résolvant (3.6) et (3.7) si et seulement si (3.15) est satis-

å

faite.

Nous allons à présent, à travers un exemple, montrer une application. Exemple 3.1. considérons le p-s_ystème :

{ u1 t -- u2 x = 0 ( compatibilité mathémati_que)
(3.16) u2 t -- p (u¹)_x = 0 (loi de Newton)

Sous la condition de stricte h_yperbolicité

(3.17) pÿ > 0,

notre investi_gation portera sur l'existence d'ondes mobiles, solutions du s_ystème ré_gularisé :

{ uE,1

t -- uE,2

(3.18) x = 0 .

_uE,2

t -- p (u^E,1)_x = åu^E,2

xx

Notons _que nous avons ajouté les termes de viscosité seulement dans la deuxième é_quation (ph_ysi_quement valable), comme la première é_quation de (3.16) n'est seulement _qu'une condition de compatibilité mathémati_que. Supposons _que

ux -- ót

uE = v

å

est une onde mobile solution de (3.18), avec

(3.19) lim s?-00

v=u^-, lim s?+00

v=u^+ et lim |s|?+00

vÿ =0.

Ecrivant v = (v1,v2) ,partant de (3.18), on a :

u

½ --ó ÿv1 -- ÿv2 = 0 . = d

--ó ÿv2 -- p(v1)^. = ·v2 ds

En inté_grant ce s_ystème et utilisant (3.19), on a :

½ óv1 + v2 = óv^- 1+ v-

(3.20) ) -- p (v1) = ó v+

2 = óv+ ₁ + v+ ₂

ÿv2 = ó v- 2 -- v2 ) + p v- ) + p v+ ) -- p (v1) ,

2 -- v2

1 1

_I ) _I

- - - + + v+ ) . En particulier,

2

óv^-₁ + v- 2 = óv+ ₁ + v+ ₂

pour u

{

) = óv⁺

óv- ₂ + p v- 2 + p v+ ) .

1 1

Résolvant ces é_quations, on obtient :

(3.21) ó² = p (v+ ) -- p (v- )

1 ¹ .

v+ 1 --v- 1

Supposons à présent v+ 1 > v^-₁;alors au vu de (3.17), on peut prendre ó > 0. Dans cette situation, la condition d'entropie de Liu, encore appelée la condition d'entropie d'Oleinik devient :

p(z1) - p (v- )

1

z1 - v 1 -

p (v+ ) - p (v- )

1 1

> v+ 1 - v^-₁

Pour tout z E Sk (u^-) entre u^- et u⁺, z = (z1, z2). Nous pouvons à présent affirmer _que le s_ystème d'é_quations différentielles (3.20), avec les conditions aux limites (3.19), a une solution si et seulement si l'iné_galité précédente est vérifiée. Pour vérifier cela, combinons les deux é_quations de (3.20) pour éliminer v².

(3.22) ÿv1=

p(v1) - p (v- ) 1- ó (v1 - v- ) := g (v1) 1 ó

g (v- ) = 0 et g (v+ ) = 0, s'accordant à (3.21). Ainsi, partant du fait _que (3.22) a une 1 1

solution, avec

lim 8-4-00

v1 = v^-1, lim 8-4+00

v1 = v+ 1 ,

on a g (z1) > 0 pour v- 1 < z1 < v+ 1 . Mais ceci est précisement la condition d' entropie précédente. Pour le cas v+ 1 <v^- ₁, on procède de la même fa_çon _que précédemment.

3.2 Paire entropie-flux

Le critère d'entropie de Lax ou de Liu ne fournissant des restrictions _que sur les états de _gauche et de droite, joints par un choc (ou une onde mobile pour une approximation vis_queuse), on va donc étendre le critère d'entropie. On exi_gerera à la solution faible de satisfaire certains t_ypes d'iné_galités appelées iné_galités d'entropie (ou d'éner_gie).

Définition 3.1. Deux fonctions ré_gulières , W : Rⁿ ? R définissent une paire entropie- flux pour la loi de conservation ut + f (u) = 0 si :

est convexe et

(3.23) D (u) Df (u) = DW (u) (u E Rⁿ)

Si u est une solution ré_gulière de (3.3) alors

(3.24) [ (u)] _t + [W (u)] = 0

(3.24) si_gnifie _que (u) satisfait une loi de conservation scalaire avec W (u) comme flux.

3.2.1 Deuxième condition d'admissibilité

Une solution faible u de (3.3) est entropi_quement admissible si
(3.25) [ (u)] _t + [W (u)] =0

au sens des distributions pour toute paire ( , W).

D^2Ö (uå).(uå x ?u^å x)=

Xn i,j=1

?^2Ö (u^å) ?u^å i?uå j

?uå i · ?uå j · = 0 ?x · ?x

Remar_que 3.2. En prati_que, les solutions _globales ne sont pas assez ré_gulières à cause des chocs et autres irré_gularités. Ö (u) sera cha_que temps la né_gative de l'entropie ph_ysi_que, et W (u) le flux d'entropie

L'iné_galité (3.25) affirme par consé_quent _que l'entropie évolue avec son flux, mais peut subir une fine croissance par exemple le lon_g des chocs. Comprendre plus ri_goureusement (3.25) comme :

{ f °° f

R [Ö (u) vt + W (u) v_x] dxdt = 0

0

(3.26) pour tout v E C^°° ₀((0, oc) x R), v = 0

Considérons le problème avec valeur initiale

(3.27)

{ut + f (u) x = 0 dans (0, oc) x R u(0,x)=u0(x) sur {t=0}xR

Définition 3.2. u est appelée une solution faible entropi_que de (3.27), si u est une solution faible et satisfait les iné_galités (3.26) pour toute paire entropie/flux.

Essa_yons de construire une solution faible entropi_que _générale pour la condition initiale u0. Comme dans le para_graphe 3.1, on espère avoir une bonne solution ph_ysi_que, _qui soit limite des solutions u^å de l'approximation du problème vis_queux :

{ uå t + f (uå) x = åuå _xx dans (0, oc) x R
(3.28) uå (0, x) = u0 (x) sur {t = 0} x R

On suppose u^å solution ré_gulière de (3.28), conver_geant vers 0 _quand |x| ? +oc assez rapidement pour justifier les calculs ci-après.On suppose en plus que _{uå}0<å<1 est uniformément bornée dans L^°° et cependant :

u^å?u _quandå >0
Remar_que 3.3. En prati_que, il est extrêmement difficile de vérifier cette conver_gence.

Théorème 3.2. (entropie et viscosité)

La fonction u est une solution faible entropi_que de la loi de conservation (3.27).

Preuve. Soit une _quelcon_que paire entropie-flux (Ö, W)_; Multipliant (3.28) par DÖ (u^å), on a :

(3.29) xx

Ö(u^å)_t+W(u^å)_x = åDÖ (uå) uå

= å [Ö(uå) _xx -D²Ö(u^å) · (uå _x ?u^å _x)]

Or

car convexe.

2- Multiplier (3.29) par ? E C ₀((0, oc) x R), ? = 0 et inté_grant par parties, on découvre _que :

_{Z Z Z Z}

[ (u^å) ?t + W (u^å) ?_x] dxdt = [D² (u^å) . (uå x ? u^å _x) ? -- (u^å) ?xx ] dxdt

(u^å) ?_xxdxdt

0 R ⁰ Z ^R Z

= --

0 R

Or par hypothèse, u^å ? u dansL1 _{loc q}uand ? 0, et d'après le Théorème de Conver-

_gence Dominé on a :

_{Z Z}

[ (u) ?t + W (u) ?_x] dxdt = 0

0 R

i.e _que (u)_t + W (u)_x = 0 au sens des distributions.

3- Finalement, fixant ? E C ₀((0, oc) x R, Rⁿ) et prenant le produit scalaire de l'E.D.P (3.28) par ?, après une inté_gration par parties, on obtient :

_{Z Z Z}

[u^å?t + f (u^å) ?_x + u^å?_xx] dxdt + u0 (x) ? (0, x) dx = 0

0 R R

En faisant tendre ? 0, utilisant le Théorème de Conver_gence Dominé, on déduit _que u est une solution faible de (3.26).

Exemple 3.2. En considérant le p-s_ystème d'Euler en dimension 1 de l'exemple 3.1, cherchons et W avec convexe et

'\ 0 -1 ) '\ Wz1 )

( z1, z2) =

-- pÿ (z1) 0 Wz2

On a (z) = z2 2 + f z1

2 ₀ p (s) ds, W (z) = --p (z1) z2 (z E R²) pÿ > 0 convexe.

3.3 Unicité de la solution d'une loi de conservation scalaire.

Soit le problème avec valeur initiale suivant :

(3.30) ut+f(u)_x = 0 dans (0,oc) xR

u(0,x) = u0(x) sur {t=0}xR

Supposons f convexe et concevons une notion appropriée de solutions faibles. Comme ci-dessus, introduisons la notion d' entropie.

Définition 3.3. Deux fonctions ré_gulières et W : R ? R sont comprises comme paire d'entropie-flux pour la loi de conservation scalaire ut + f (u) x = 0 si :

* est convexe et

* ÿ (u) f^ÿ (u) = W ^ÿ(u) (u E R)

La condition d'entropie devient alors :

Ö (u)_t + W (u)_x = 0 sur (0, oc) x R Pour toute paire d'entropie-flux (Ö, W). Ceci entraine :

Z 00 Z 0 R

{Ö (u)?t+W(u)?x}dxdt=0 pour tout? E C^00 0((0,oc)xR); ?=0

Définition 3.4. Soit u E C ([0, oc); L¹ (R)) n L⁰⁰ ((0, oc) x R). u est appelée solution faible entropique de (3.30) si u satisfait :

Z ₀₀ Z

i) {Ö (u) ?t + W (u) ?_x} dxdt = 0 pour tout ? E C00 0 ((0, oc) x R) ; ? = 0

0 R

pour toute paire d'entropie-flux (Ö, W).

ii) u(t,.) ? u0 dans L¹ _quand t? 0

Remar_que 3.4. 1-Cette définition remplace la définition précédente de la solution en- tropi_que.

2- D'après la défnition 3.4-(i), prenant Ö (u) = #177;u, W (u) = #177;f (u), on déduit :

Z 00 Z 0 R

{u?t+f(u)?x}dxdt = 0

Pour tout ? E C1 0 ((0, oc) x R), dès _que u (t,.) ? u0 (x) dans L¹. Ainsi,on a montré _qu'une solution entropi_que est une solution faible.

Dans le para_graphe 3.2, nous avons discuté de la construction de la solution entropi_que_; à présent, nous allons établir un résultat d'unicité.

Théorème 3.3. (Unicité de la solution entropi_que pour une loi de conservation scalaire).

pour tout u0 E L⁰⁰ (R) , il existe une et une seule solution entropi_que du problème (3.30).

Lemme 3.1. (iné_galité d'entropie dans le cas scalaire).

Soient a E R, u une solution faible entropi_que de (3.30). Alors

Z 00 Z 0 R (3.31)

{|u (t, x) -a| ?t + sgn (u (t, x) - a) (f (u (t, x)) - f (a)) ?x} dxdt Z + |u0 (x) - a| ? (0, x) dx = 0 R

Preuve. Pour tout u0, fixé a E R, prendre :

Ök(u) = /3k(u-a) (uER) pour k= 1,..., /3k :R?R, ré_gulière convexe et /3k (u) ? u uniformément

?

?

?

½ 1 si u > 0

^ÿ/3k (u) ? sgn (u) = -1 si u < 0

Ainsi Ök (u) ? u - a uniformément pour u E R. Le flux correspondant étant

Z u

Øk (u) = ^ÿ/3k (w - a) f^ÿ (w) dw

á

Pour tout u,

Z u

Øk (u) ? sgn (w - a) f^ÿ (w) dw = sgn (u - a) (f (u) - f (a))

á

uniformement . Méttant Ök et Øk dans (3.26) et faisant tendre k ? oc, on déduit :

Z 00 Z 0 R

{ u (t, x) -a ?t + sgn (u (t, x) - a) (f (u (t, x)) - f (a)) ?x} dxdt

_Z

+ u0 (x) - a ? (0, x) dx = 0

R

Preuve. (théorème 3.3) :

L'idée de la preuve de ce théorème est de prendre deux conditions initiales bornées u0 et v0, deux solutions entropi_ques u et v correspondantes à u0 et v0 respectivement, et comparer u- ven terme de u0 - v0. D'après le lemme précédent, en posant Ök (u) = u - k et Øk (u) = sgn (u - k) (f (u) - f (k)) .On a donc pour tout k, et tout ? ré_gulière positive à support compact

Z 00 Z 0 R

{ u (t, x) - k ?t + sgn (u (t, x) - k) (f (u (t, x)) - f (k)) ?x} dxdt

_Z

(3.32) + u0 (x) - k ? (0, x) dx = 0

R

et Z 00 Z 0 R (3.33)

{ v (s, y) - k ?s + sgn (v (s, y) - k) (f (v (s, y)) - f (k)) ?y} dyds Z + v0 (y) - k ? (0, y) dy = 0 R

Admettons un instant _qu'on puisse prendre k = v (s, y) dans (3.32) (ce _qui est bien possible car k doit être constant), on verrait apparaitre la _quantité u(t,x) - v (t,x) _que l'on souhaite estimer. Puis_qu'un tel k ne peut être choisi directement, on va fixer

les variables (s, y), prendre k = v (s, y) .Puis inté_grer en (s, y) ; on aura pris le soin de choisir une fonction-test ? _qui dépend aussi de (s, y) et contraint (s, y) à être proche de (t,x), (on mettra des approximations de l'unité en t - s et x - y dans la fonction-test). Ainsi on verra effectivement apparaître la _quantité |u (t, x) - v (t, x)|, modulo des erreurs dont il nous faudra vérifier _qu'elles sont effectivement né_gli_geables. Cette techni_que de dédoublement des variables est dûe à S.N.KRUZKHOV.

Prenons w E C⁰⁰₀ ([0, 00) x [0, 00) x x 118) , w = 0, w = w (t, s, x, y) . Fixant (s, y) E (0, 00) x lik,on prend k = v (s, y) , ? (t, x) = w (t, s, x, y) dans (3.32), inté_grant par partie par rapport à s, y ; on obtient l'iné_galité :

fo^00fo^00LL

|u(t, x) --- v (s, y)|wt (t, s, x, y)+F (u (t, x) , v (s, y)) wx (t, s, x, y) dtdsdxdy

Z⁰⁰u0 (x) - v (s, y)| ? (0, s, x, y) dsdxdy = 0

I

⁺0R

où F (u, v) = sgn (u - v) (f (u) - f (v)) est s_ymétri_que. De la même manière, en partant de (3.33) dans le_quel k = u (t, x) , et ? (s, y) = w (t, s, x, y), on trouve :

fo^00f^00LL

|v(s, y) - u (t, x)|ws(t,s, x, y)+F (u (t, x) , v (s, y)) wy (t, s, x, y) dtdsdxdy

00_f

+J

v0 (x) - u (t, x)|? (t,0, x, y) dtdxdy = 0 io En sommant ces deux é_quations, on obtient.

|v(s, y) - u (t, x)|(wt + w_s) + F (u (t, x) , v (s, y)) (w_y + w_x) dtdsdxdy

00 100

fo fRiR

+

1IR IR ₀ |u0 (x) -- v (s,y)| ? (0, s, x, y) dsdxdy
00

+

R R | v0 (x) -- u (t, x)|? (t, 0, x, y) dtdxdy = 0

o

Soit è, E C⁰⁰₀ (] 0, í[) , p_u E C⁰⁰₀ (] - u, u[) deux approximations de l'unité. Soit _ç E C⁰⁰₀ ([0, 00) x IR) positive.

Posons w (t, s, x, y) = è, (t --- s) p_u (x - y) ç (t, x) ; on a alors

wt (t, s, x, y) + w_s (t, s, x, y) = ^ÿè, (t - s) p_u (x --- y) ç (t, x) + è, (t --- s) p_u (x - y) çt (t, x) -^ÿè, (t - s) p_u (x - y) çt (t, x)

= è, (t - s) p_u (x --- y) çt (t, x)

et de même,

w_x (t, s, x, y) + w_y (t, s, x, y) = è, (t - s) p_u (x --- y) ç_x (t, x)

et puis_que O_u = 0 sur ] - 8, 0] , pour tout s = 0, on a w (0, s, x, y) = 0. On trouve donc :

10^c° fo^c° LIR

|u(t, x) - v (s, y)| Ou (t - s) pu (x - y) çt (t, x)

+F (u (t, x) , v (s, y)) O_u (t - s) p_u (x - y) ç_x (t, x) dtdsdxdy

(3.34) +

f^c°IR IR

|v0 (x) - u (t, x)| Ou (t) pu (x - y) ç (t, x) dtdxdy = 0

Soit R > 0 tel _que le support de _ç soit inclus dans [0, R]x [-R, R] . Puis_que O_u à support compact dans ]0, í[ et p_u à support compact dans ] - u, u[ et puis_que ces deux fonctions sont d'inté_grales 1, on a :

fR Zc° fR Io0J--R JR

|v(t, x) - v (s, y)| Ou (t - s) pu (x - y) dtdsdxdy

Z(t,

x) -v(t - æ, x -î)| dtdx) O_u (æ) p(î)dædî u Iu (I^R _IR
--u 0 --R P

sup (RRu

I R

(t, x) -v(t -æx -î)| dtdx 1. I (æ) p () dæd

0<æ<u,--u<î<u -- --u

(3.35) fR = sup 0<æ<u,--u<î<u 0 --R

|v(t, x) --- v (t - æ, x --- î)| dtdx

(on etend eventuellement v par 0 dans les temps né_gatifs).

Puis_que v E L^c° (]0, 8[xR) c L1 loc ([0, 8[xR) , ce dernier terme tend vers 0 _quand u et í tendent vers 0.

Ainsi çt etant bornée,

107: IRIR|v(t x) _v(s, y)| O_u (t - s)p(x -- y)çt(t, x) dtdsdxdy

foc° I^c° fR fR |v(t, x) - v (t, x)| O_u (t - s) p_u (x --- y) çt (t, x) dtdsdxdy + ù1 (u, í)

=

fc° ) (t, x) -v(t, x)| O_u (t - s) dsp(x - y) dy +ù1(u,í)
R 0 R
où ù1 (u, í) ? 0 _quand í,u > 0. On a ^RR p_u (x - y) dy = 1V x E R. De plus dès _que

t > í. ^RR O_u (t - s) ds = 1 mais

Z^u|v (t, x) -v(t,x)| Ou(t - s)dsçt(t, x) dtdx R 0

_{Z Z}

< v (t, x) - v (t, x) öt (t, x) dtdx ? 0

0 R

lors_que í > 0. On obtient donc

Z ₀₀ Z _{00 Z Z}

v (t, x) - v (s, y) O (t - s) P_L (x - y) öt (t, x) dtdsdxdy

0 0 R R

Z ₀₀ Z

(3.36) = v (t, x) - v (s, y) öt (t, x) dtdx + w2 (,u, í)

0 R

où w2 (,u, í) ? 0 lors_que (,u, í) ? (0, 0). On a

F (u (t, x) , v (s, y)) = sgn (u (t, x) - v (s, y)) (f (u (t, x)) - f (v (s, y)))
<L u(t,x) -v(s,y)

où L est une constante de Lipschitz de F dans un intervalle borné contenant les ima_ges de u et v. Donc

F (u (t, x) , v (s, y)) O (t - s) P_L (x - y) ö_x (t, x) dtdsdxdy

Z 00 _{Z Z}

Z 00

<L

u (t, x) - v (s, y) O (t - s) P_L (x - y) ö_x (t, x) dtdsdxdy

0 0 R R

Z ₀₀ Z _{00 Z Z}

0 0 R R

et en utilisant à nouveau (3.34), on trouve :

Z 00 Z Z Z 00 0 0 R R

F (u (t, x) , v (s, y)) O (t - s) PL (x - y) öx (t, x) dtdsdxdy

Z _{00 Z} Z 00 Z

< L u (t, x) - v (t, x) O (t - s) ds P_L (x - y) dy ö_x (t, x) dtdx + w3 (,u, í)

0 R 0 R

Z ₀₀ Z

(3.37) < L u (t, x) - v (t, x) ö_x (t, x) dtdx + w3 (,u, í)

0 R

avec limL?0, ?0 w3 (,u, í) = 0. puis_que v0 EL1 _loc (R), on a :

Z ₀₀ Z R Z R

v0 (y) - v0 (x) P_L (x - y) dxdy < sup v0 (x ? î) - v0 (x) dx ? 0

0 -R ?L<î<L ?R

lors_que ,u ? 0.De plus, u est continue de [0, 8[?L1 _loc (R) et u (0,.) = u0, donc

Z ₀₀ Z R Z

u (t, x) - u0 (x) O (t) ö (t, x) P_L (x - y) dtdxdy

0 -R R

R

_Z

< MöM00 sup u (t, x) - u0 (x) dx ? 0

0<t< -R

lors_que í > 0.On déduit de ceci _que

v0 (y) - u (t, x) O_í (t) P_u (x - y) ç') (t, x) dtdxdy

Z _{00 Z Z}

0 R R

_Z Z 00

= v0 (y) - u0 (x) O_í (t) ç') (t, x) dtdx + w4 (ii, í)

R 0

tion de l'unité, le terme f 00

où w4 se comporte comme précédement. Vu _que ç') est ré_gulière et O_í est une approxima0Oí (t) ç') (t, x) dt conver_ge uniformement vers ç') (o, x), et on trouve donc :

Z 00 Z Z 0 R R

v0 (y) - u (t, x) Oí (t) Pu (x - y) ç') (t, x) dtdxdy

_Z

(3.38) = v0 (y) - u0 (x) ç') (o, x) dx + w5 (ii, í)

R

avec w5 (ii, í) ? 0 _quand (ii, í) ? (0,0). En injectant (3.36), (3.37), (3.50) dans (3.34), puis en faisant (ii, í) ? (0, 0), on obtient ainsi, pour tout ç') ré_gulière à support compact, (3.39)

_Z

u (t, x) - v (t, x) (ç')t (t, x) + L ç')_x (t, x) ) dtdx+ v0 (y) - u0 (x) ç') (o, x) dx = 0

R

Z ₀₀ Z

0 R

Comme voulu lors de l'introduction de la techni_que de dédoublement des variables, nous avons combiné les é_quations sur u et v pour obtenir une é_quation sur u - v .

Lemme 3.2. Iné_galités de la L¹-contraction (admis). Soient u et v deux solutions faibles entropi_ques de (3.30), alors

(3.40) Mu (t,.) - v (t,.) ML¹(R) < Mu (s,.) - v (s,.) ML¹(R)

pour tout 0 < s <t.

Ce lemme entraine trivialement l'unicité de la solution entropi_que car si u0 = v0, alors l'iné_galité (3.40) entraine _que u = v pour tout t > 0, et pour tout x E R.

3.3.1 Quel_ques propriétés de la solution entropi_que.

Soient u0 et v0 bornées_; on note uet v les solutions entropi_ques de (3.30), correspondant à u0 et v0, on a les propriétés ci-après _que nous admettons.

Propriétés 3.1. .

(i) MuML8(]0,00[XR) < Mu0ML8(R) .

(ii) Si u0 E L¹ (R) alors u E C ([0, oc[; L¹ (R)) et, pour tout t> 0, Mu(t, .)ML1(R) < Mu0ML1(R) .

(iii) Si u0 - v0 E L¹ (R), alors pour tout t > 0, on a :

u (t,.) - v (t,.) E L¹ (R) et Mu (t,.) - v (t, .)ML1(R) < Mu0 - v0ML1(R).

3.4 Solution explicite d

'une loi de conservation sca-

laire.

Dans ce para_graphe, on fait le lien entre une caractérisation de la solution, sous la forme d'une formule explicite, la formule de Hopf et Lax. La formule de Hopf et Lax étant explicite, elle assure trivialement l'unicité de la solution ainsi caractérisée.

3.4.1 La formule de Hopf et Lax.

On considère la classe des solutions u de l'é_quation
(3.41) ut+f(u)_x = 0,
satisfaisant la condition initiale

(3.42) ?x E R, u (0, x) = u0 (x)

pour u0 suffisament ré_gulière à support compact.

Cette h_ypothèse permet ici de rendre possible la démarche. On pose :

Z x Z x

v (t, x) = u (t, î) dî , v0 (x) = u0 (î) dî

0 0

et la fonction v vérifie l'é_quation

(3.43) vt+f(v_x) = 0 , v(0,x)=v0(x).

En effet, dans (3.41), la fonction f n'est définie _qu' à une constante près. Le choix 0 au second membre de (3.43) correspond effectivement à un choix particulier de cette constante. On suppose f E C² (R), convexe. Le but de cette section est de montrer _que parmi les éléments de la classe de solutions de (3.41), (3.43), on peut sélectionner une solution vérifiant la formule de Hopf et Lax,

( (x -- x0 ))

(3.44) v (t, x) = inf v0 (x0) + tf^* ;

x0 ER t

où f^* est la polaire conju_guée encore appelée transformée de FENCHEL de f définie par :

f ^*(p) = sup vER

(vp--f(v))

_que l'on considérera comme la seule solution ph_ysi_quement acceptable.

Soit v une solution de (3.41), (3.42)_; pour un paramètre p E R (_qui peut dépendre de x et t), on pose v_x = p + v_x -- p, d'où le développement de Ta_ylor

f(vx) =f(p)+(vx --p)

fÿ (p) + ( vx -- p)2f· (q) , p = q = vx 2

En ajoutant vt, il vient, sachant (3.43),

d'où	0 = vt + f (vx) = vt +		fÿ (p) vx-(pf^ÿ (p)-f (p)) + (vx 2 p)2f (q)
(3.45) vt +		f^ÿ(p)vx = pf^ÿ (p) - f (p) - (vx -2 p)2 f· (q)

Dans (3.45), on a ₂¹ (v_x - p)2 f^· (q) = 0, et on va rechercher une solution maximale, satisfaisant

(3.46) vt +

f^ÿ(p) vx = pf^ÿ (p) - f (p) ,

et la condition initiale v0.

On peut résoudre (3.46) par la méthodes des caractéristi_ques_; soit x ER,t> 0, x0 E R, on note = (s) la caractéristi_que reliant le point (0, x0) au point (t, x) , avec 0 < s < t. On a donc :

^ÿ(s) =

fÿ (p)

vÿ(s) = pf^ÿ (p) - f (p) (0) = x0

(t) = x

Or f^ÿ est monotone croissante, on note g sa fonction inverse : g (f^ÿ (p)) = p .

(En particulier g (s)) = p. En inté_grant vÿ (s) le lon_g de la caractéristi_que, on obtient :

(t, x) = v (0, x0) + f t (pf^ÿ (p) - f (p)) ds

d'où

(3.47) v (t, x) = v (0, x0) +

lot

((s) g (s)) - f (g (s)))) ds

Etant donné x0 fixé(pour l'instant), on va chercher à minimiser v dans (3.47) sur l'ensemble des trajectoires admissibles, allant de (0, x) à (t, x) . Si la trajectoire minimale est notée * (s) , toute trajectoire est de la forme (s) = * (s) + er (s) , où e E R et r = r (s) est une fonction réalisant r (0) = 0; r (t) = 0.

On aura

ÿ =

ÿ *+ eÿr, et

(t, x) =v(0, x0)

+ _ft (* -- f o g (ÿ * + ei^-)) ds.

On dérive par rapport à e, et on écrit _que le minimun est réalisé pour e = 0. Il vient

Z

t (=gÿ(_*) _*rÿ+ --f^ÿogMgÿM rÿ ds. 0

Après simplifications, il reste

Z0 t (gî,,_«(s)) rÿ (s) ds = 0,

pour toute fonction r tel _que r (0) = r (t) = 0.On intè_gre par parties pour obtenir

t

hg,,«(s)) r (s)] 8=0 ₀ 8 t--i d ds (g (,,« (s))) r (s) ds = 0,

ceci pour tout r tel _que r (0) = r (t) = 0 , d'où

ds (g,,_«(s))) =

En inté_grant, on obtient

g (^ÿî,,« (s)) = A , constante , donc ^ÿî,,« (s) = f^ÿ (A) , constante.

On inté_gre encore : î,,« (s) = f^ÿ (A) s + B. Or î,,« (0) = x0 ,d'où B = x0, et î,,« (t) = x, et on déduit

(3.48) fÿ (A) = x-- x0

t

On insère cette valeur dans la solution optimale, correspondant à î = î,,«, ce _qui donne

Z

t (v (t, x) = v (0,x) _{+g(,,«)î,,«--} f o g _(ÿî,,«)) ds, 0 où encore

(t, x) = v (0, x) + _Zt (g (fÿ _(A)) f^ÿ (A) -- f o g (f^ÿ (A))) ds,

0

puis

v (t, x) = v (0, x) + t (Af^ÿ (A) -- f (A)) = v (0, x) + t _f,,« (fÿ (A))

d'où

-

(t, x) =v(0, x)+t f,,« (x x0)

t

il reste à minimiser suivant le paramètre x0 pour obtenir la formule de Hopf et Lax (3.44).

La formule de Hopf et Lax permet de prendre en compte des solutions discontinues, et se _généralise facilement au cas où la condition initiale n'est plus nécéssairement à support compact.La section suivante présente un exemple important de l'exploitation de la formule de Hopf et Lax, dans l'é_quation de Bur_gers.

Exemple 3.3. Soient données deux constantes réelles notées u_g et ud, on considère le problème

/ u2

ut + = 0,

2 x

avec la condition initiale

{ u_g si x < 0

u (0, x) ⁼ud si x> 0

En introduisant une fonction v telle _que u = v_x, on aboutit au problème

vt +

v2 x 2

=0

avec la condition initiale

½ u _gx si x < 0

v (0, x) ⁼udx si x > 0

La formule de Hopf et Lax conduit à la solution

( ) ( ugy + (x - y)2 udy + (x - y v (t, x) = min inf , inf y<0 2t y>0 2t

})^)2

.

Explicitons cette expression_; on a :

?

{ ) x2

??

u_gy + (x - y)2 _2t si x > u_gt

inf =

y<0 2t ?? u_gx - u2 2 si x < u_gt

_gt

si x<udt

et

?

{ J ?? x2

udy + (x - y) ²

inf = 2t

y>0 2t ?? udx - 1 ₂u² _dt si x > udt

Pour u_g < ud, on recense trois zones : Si x < u_gt, alors :

u

u_gx - ug2t

2 , x2 = u_gx - ug2t

v (t, x) = min 2 .

2t

Si u_gt <x < udt, alors :

_x2

v(t,x)= .

2t

Si x > udt, alors :

( )

udx - ud2t

2 , x2 = udx - ud2t

v (t, x) = min 2t 2

Ceci conduit à la solution suivante pour u,

u(t,x) =

? ? ?

ug si x<ugt x t si ugt<x<udt ud si x>udt

Il s'a_git d'une solution ré_gulière correspondant à une onde de raréfaction. Pour u_g > ud, on recense _quatre zones.

Si x < udt, alors x < u_gt, et donc :

( )

u_gx - ug2t

2 , x2 = u_gx - u2 gt

v (t, x) = min 2 .

2t

Si udt <x < ₂(ud+u_g)t, alors:

1

( )

u_gx - ug2t

2 , udx - ud2t = u_gx - ug2t

v (t, x) = min 2 2

Si ¹ 2(ud+ug)t<x<ugt,alors:

.

( )

u_gx - ug2t

2 , udx - ud2t = udx - ud2t

v (t, x) = min 2 2

Si x > u_gt, alors :

( )

udx - ud2t

2 , x2 = udx - ud2t

v (t, x) = min 2 .

2t

Il n'_y a effectivement _que deux valeurs possibles pour v.

Notons _que v est continue, et vaut

1

v (t, x) = v (t) = ₂ugudt

1

le lon_g de la droite x = 2 (ud + u_g) t.

x =

Ceci conduit à la solution suivante pour u, _qui est discontinue le lon_g de la droite 1 2 (ud+ug)t,

u(t,x) =

? ???? ????

ug si x< ud si x>

1 2 (ud+ug)t 1 2 (ud+ug)t

il s'a_git d'une solution de t_ype onde de choc, et l'interêt de la formule de Hopf-Lax est de nous avoir précisé la trajectoire du choc. La formule de Hopf-Lax sélectionne et caractérise une (seule) solution ph_ysi_quement acceptable, _qui peut comporter des discontinuités.

En résumé, on peut retenir _que la solution du problème de Riemann est soit une onde de raréfaction si u_g <ud, ou une onde de choc si u_g > ud.

COnClUSIOn

Le problème de Cauch_y pour l'é_quation aux dérivées partielles du premier ordre de lois de conservation possède, sous certaines conditions de ré_gularité sur ses données, une solution classi_que locale en temps. En considérant la condition initiale constante par morceaux. on a pu constaté _qu'en dehors du champs d'application des h_ypothèses mathémati_ques (la condition de Lipschitz, la convexité de la fonction flux) le comportement de la solution pouvait perdre son réalisme, ou plusieurs comportements de la solution étaient envisa_geables. Il a fallu alors au niveau du modèle mathémati_que, imposer une condition supplémentaire pour écarter les comportements irréalistes, une iné_galité d'entropie par exemple. En utilisant cette iné_galité, on a montré l'existence et l'unicité _globale de la solution faible entropi_que et bornée, ce _que la méthode des caractéristi_ques ne pouvait faire. Une forme explicite de la solution du problème de Riemann est donnée par la formule de Hopf-Lax, cette formulation caractérise bien une solution ph_ysi_quement acceptable. Mais, sans aucune condition sur les données, la solution _globale n'existerait pas.

Les applications des résultats de la modélisation des matériaux plus élasti_ques _que les _gaz ou l'eau sont nombreuses, depuis les similations des crashes ou d'accidents de voiture, pour des modèles utilisés en matière de sécurité, jus_qu'à des applications industrielles d'impacts. La prospection _géolo_gi_que ou minière exploite é_galement de tels modèles.

Dans ce mémoire, nous n'avons abordé le problème de Cauch_y de lois de conservation _que dans les cas où, la variable spatiale était dans R, la fonction flux f était localement Lipschitzienne et convexe_; ceci nous amène à nous poser plusieurs _questions à savoir : *Que se passerait-il si x ? R^m, m > 1?

*Que se passerait-il si la fonction flux devait être _quelcon_que?

Face à toutes ces in_quiétudes, nous vous promettons d'apporter _quel_ques éléments de réponses dans nos recherches futures.

Biblio_graphie

[1 A.Bressan_; H_yperbolic S_ystems of Conservation Laws in one Space Dimension, Universidat Complutense in Madrid, (1998)

[21 A.Y.Le Roux_; Modélisation et calcul scientifi_que (version provisoire), université de Bordeaux 1, ( 8 avril 2005)

[31 A.Y.Le Roux_; La Formule de HOPF et LAX, Cours de DEA, Bordeaux, (Octobre 1999)

[41 J.droniou et C.Imbert_; Solutions de Viscosité et Solutions Variationnelle pour E.D.P non-linéaires_; (pol_ycopiés de cours-DEA maths)_; UMR CNRS 5149, (Mai 2004) (http :// www-_gm3.univ-mrs.fr/cours/]tc)

[51 J.vovelle_; Prise en compte des conditions aux limites dans les é_quations h_yperboli_ques non-linéaires. Université d'Aix-Marseille 1, ( decembre 2002)

[61 L.C Evans_; Partial Differential E_quations_;
American Mathematical Societ_y, (1997)

[71 L.C Evans_; Entrop_y and Partial Differential E_quations_; Department of Mathematics, UC Berkele_y

[81 P.Lax_; H_yperbolic s_ystems of conservations laws and the mathematical theor_y of shock waves. Siam (1973)

J.M KENFACK

Département de Mathémati_ques, Université de _yaoundé I BP 812 _yaoundé, Cameroun

E-mail : [e-mail]