Analyse de l'accès à l'éducation à Kinshasa

CONCLUSION GENERALE :

L'un des plus grands défis majeurs du monde moderne est d'atteindre le plus haut niveau d'éducation de la population car aucun pays n'a atteint le développement et la croissance économique et sociale sans une population suffisante en qualité d'abord puis en quantité.

L'éducation, comme les ressources géologiques, climatiques et autres, est capable de favoriser le développement de n'importe quel pays du monde, même les plus démunis et les plus pauvres.

Beaucoup de pays ont compris que l'éducation est le seul moyen d'accroître le bien être social et économique quoique ses retombées se situent à long terme. L'éducation comme moyen qui s'offre à toutes les nations d'asseoir une démocratie durable comme d'aucuns le veulent est aussi le seul moyen de propager les valeurs au sein de la population en général et de la jeunesse en particulier.

En effet, malgré tous les bienfaits que propose l'éducation maximum de la population d'un pays, beaucoup de pays ne cessent de sombrer dans des situations chaotiques du secteur de l'éducation avec comme conséquence « l'analphabétisme » et le bas niveau intellectuel de la majeure partie de la population. Cela est le cas de République Démocratique du Congo.

Bien que la situation de l'éducation soit chaotique dans ce pays pris dans son ensemble, dans la ville province de Kinshasa la situation s'avère du moins acceptable bien que la majeure partie de la population de ce pays soit pauvre, par conséquent présumée ne pas être à même de supporter tous les coûts qu'engage une éducation meilleure, dans des écoles (universités) de qualité acceptable.

La population à scolariser ne cesse de s'accroître ; mais se presse aux portes des écoles déjà démunies du fait des crises de deux dernières décennies passées dans les désordres politiques qui ont occasionné des déséquilibres socioéconomiques.

Le travail que nous avons voulu présenter au public chercheur s'était fixé pour l'un des objectifs d'identifier les contraintes d'ordre socioéconomiques et démographiques liés à l'accès à l'éducation des enfants dans les ménages de Kinshasa. Pour y arriver, nous avons utilisé les données de l'enquête nationale 1-2-3 réalisée en 2004.

Dans l'échantillon sous études, il s'est avéré qu'il n'y a pas des disparités entre sexes des enfants dans l'ensemble de ménages. L'âge des enfants est compris entre 5 et 25 ans et de ces enfants, 63,1% sont issus des familles pauvres. Dans l'ensemble de la population, la déperdition est souvent due à l'impossibilité financière des chefs de ménages.

En effet, tout au long de cette étude, nous avons cherché à expliquer les facteurs qui favorisent l'accès à l'éducation dans tous les degrés formel et non formel en RDC. Pour ce faire, le niveau d'étude atteint par l'enfant dans le ménage a été choisi comme variable endogène de notre étude. L'économiste étant un homme qui fait parler les chiffres, les données de l'enquête nationale 1-2-3 ont été soumises à trois analyses empiriques (régressions logistiques binaires, de choix multiple et l'arbre de régression par la méthode CART).

De ces analyses, il est ressorti la conclusion selon laquelle, il y a réellement des facteurs socioéconomiques et démographiques qui influencent l'éducation des enfants au sein des ménages et cela à tous les sens selon les niveaux d'étude atteint par l'enfant. Ces facteurs sont : la taille du ménage, la télévision, le sexe de l'enfant, la religion du chef de ménage, le type d'école fréquenté par l'enfant, l'éducation du chef de ménage, l'âge du chef du ménage, les dépenses journalières du ménage, le statut d'occupation du logement et la part du revenu consacrée à l'enseignement. Bien que de façon générale ces facteurs expliquent l'éducation prise globalement, c'est-à-dire tous les niveaux confondus, du point de vue empirique cette étude confirme l'existence des déterminants différenciés selon le niveau d'étude atteint par l'enfant.

Nous devons soulignés que contrairement à la plupart de travaux qui ont fait l'objet de notre revue de littérature , qui se sont limités seulement à détecter les facteurs explicatifs de l'éducation, dans notre étude, en plus de ce qu'ont fait nos prédécesseurs et loin de ne se limiter qu'à la simple détection des différentes variables explicatives, nous avons construit un arbre de régression par la méthode CART, méthode peu utilisée, on peut même dire jamais utilisée à l'Université de Kinshasa. Cet arbre nous a permis de classifier ces facteurs selon l'ordre d'importance des variables dans l'explication du phénomène « éducation des enfants » dans les ménages.

Par ailleurs, on retiendra par exemple qu'au primaire les facteurs déterminants sont la taille du ménage, la télévision, le sexe de l'enfant, la religion du chef de ménage, le sexe et l'âge du chef de ménage, le type d'école fréquenté par l'enfant et l'éducation du chef de ménage. A ce niveau le privilège pour restructurer le secteur d'éducation primaire doit être accordé d'abord à l'âge du chef de ménage, à la télévision et la taille du ménage respectivement.

Au niveau secondaire, les déterminants ne sont pas très différents du primaire, sauf que les signes de ceux - ci diffèrent parfois du fait des différentiations qu'on peut établir entre les enfants de divers âges dans la perception des phénomènes. Les facteurs déterminants sont  la taille du ménage, la télévision, le sexe du chef de ménage, l'âge du chef de ménage et le niveau de pauvreté du ménage. Parmi ces facteurs, les plus déterminants sont respectivement l'âge du chef de ménage, la télévision et le niveau de pauvreté du ménage (dépense journalière du ménage).

Au niveau universitaire, les facteurs déterminants sont : la télévision, la religion et l'âge du chef de ménage, le type d'école fréquentée, l'éducation du chef de ménage, la part du revenu consacré à l'éducation et le niveau de pauvreté. Au programme non formel par ailleurs, ce sont l'âge du chef de ménage, le statut d'occupation du logement et la part du revenu consacré à l'éducation. La relation entre l'éducation et la pauvreté se fait sentir plus au niveau universitaire et au programme non formel ; A ces deux niveaux, le revenu du ménage conditionne l'éducation : positivement au niveau universitaire et négativement au programme formel.

L'éducation ayant pour l'une des finalités la formation de l'élite nationale, ce qui est un atout majeur pour le développement et la croissance d'un pays, l'Etat doit intervenir pour accroître l'efficacité du système éducatif congolais. Aussi, les ménages et les autres partenaires doivent - ils accompagner les efforts de l'Etat pour la réussite de la rénovation du système éducatif et de l'éducation au sein des ménages et des familles, cellules de base d'une nation.

Ainsi, nous avons vérifié les hypothèses de notre étude et les objectifs assignés sont atteints.

· Suggestions et recommandations :

La tâche de l'éducation de la population et de la formation du capital humain d'un pays revient à l'Etat qui a le monopole de préparer la relève pour pérenniser le développement et la croissance économique et sociale de la nation.

A l'issu de toutes les assises nationales et internationales sur l'éducation qui ont connu la participation de la RDC, il s'est avéré que celle-ci a pris les engagements de mettre en oeuvre tous ses moyens possibles pour atteindre l'éducation pour tous tel que prévu par la conférence de Jomtien ; mais jusqu'à ces jours, la RDC est encore loin d'atteindre l'éducation pour tous et pire, le taux d'analphabétisation va crescendo. Ce qui n'est pas une bonne alerte pour le développement tant attendu par plus d'un. D'où, l'implication de l'Etat doit devenir une réalité et non plus un slogan de bonnes intentions.

L'Etat doit assurer au préalable l'éducation, surtout au niveau primaire, à défaut la rendre gratuite afin de permettre à toutes les couches sociales d'y avoir accès pour mener au maximum le taux d'alphabétisation.

L'Etat en tant que chef d'orchestre de l'organisation des secteurs sociaux dans un pays se voit attribuer une lourde et grande responsabilité dans le redressement du système éducatif. La responsabilité de ses partenaires à l'éducation est aussi nécessaire.

Dans l'accomplissement de ces responsabilités qui incombent en grande partie à l'Etat, les autres partenaires doivent mener leurs actions dans le sens d'apporter leurs contributions tant soit peu à la redynamisation de ce secteur. C'est pourquoi nos recommandations sont formulées à l'endroit de l'Etat et de ses partenaires.

1. A l'Etat nous recommandons et suggérons ce qui suit :

· Comme il existe un lien entre la scolarisation et le niveau de pauvreté, son intervention doit être accrue au sens d'augmenter le niveau de vie des ménages qui supportent les coûts de l'éducation ;

· suite à la discrimination des sexes des enfants dans la scolarisation au primaire, son intervention est exigée pour briser ce déséquilibre ;

· Il existe une forte relation entre la scolarisation et la religion des parents au niveau primaire ; l'Etat doit encourager les confessions religieuses à offrir plus en matière d'éducation tout en les encadrant et en accompagnant leurs actions.

· Pour améliorer l'accès à l'éducation, l'Etat doit veiller à ce que l'offre ne dépende pas de la demande d'éducation car celle-ci est déjà confrontée à une infrastructure vétuste et insuffisante.

· Enfin, L'Etat doit mettre en place une politique d'habitat adéquate vu qu'il y a relation entre le logement et l'éducation ; ce qui peut faciliter la probabilité de scolariser les enfants au sein des ménages.

2. Aux chefs de manages :

· Il doivent veiller à ce que le nombre d'enfants dans les ménages dépende de leur revenu et moyens de survie ;

· Ils doivent mettre les jeunes enfants à l'abri des méfaits de la télévision ;

· Ils doivent éviter d'avoir les enfants au début du troisième âge.

3. Aux autres partenaires nationaux et internationaux, Ils doivent accompagner et suivre les actions de l'Etat car il gère très mal le secteur social, porteur du bien-être de la population.

ANNEXES :

Tableau 1 : Raisons d'arrêt des études

Raisons d'arrêt des études		Fréquence	Pourcentage
	Impossibilité financière parents	288	43,3
	Préférence pour un apprentissage	34	5,1
	Grossesse, mariage	26	3,9
	Handicap, maladie	19	2,9
	Echec scolaire	16	2,4
	Trop jeune	212	31,9
	Ecoles trop éloignées	3	,5
	Etudes achevées	43	6,5
	Autres	24	3,6
	Total	665	100,0

Tableau 2 : Pauvreté et accès à l'école

Pauvreté par les dépenses alimentaires		Avez-vous été au moins à l'école primaire ?		Total
		Oui	Non
	Pauvres	1188	191	1379
	Non pauvres	723	84	807
Total		1911	275	2186

Tableau 3 : Pauvreté et raison d'arrêt des études

Pourquoi avez-vous arrêté vos études ?		Pauvreté par les dépenses alimentaires		Total
		Pauvres	Non pauvres
	Impossibilité financière parents	225	63	288
	Préférence pour un apprentissage	22	12	34
	Grossesse, mariage	20	6	26
	Handicap, maladie	174	76	250
	Echec scolaire	23	20	43
	Autres	14	10	24
Total		478	187	665

Tableau 4 : fréquentation et religion de l'individu

Religion Pratiquée		Avez-vous été au moins à l'école primaire ?		Total
		Oui	Non
	Catholique	610	80	690
	Protestant	356	46	402
	Kimbanguiste	82	13	95
	Musulman	20	4	24
	Autre chrétien	701	108	809
	Animiste	17	7	24
	Sans religion	110	17	127
	Autre religion	15	0	15
Total		1911	275	2186

Tableau 5 : fréquentation et taille du ménage

Taille de ménage		Avez-vous été au moins à l'école primaire ?		Total
		Oui	Non
	2	9	0	9
	3	36	1	37
	4	71	9	80
	5	182	24	206
	6	250	42	292
	7	291	45	336
	>8	1072	154	1226
Total		1911	275	2186

Graphique 1 : pauvreté et niveau d'étude atteint par l'enfant

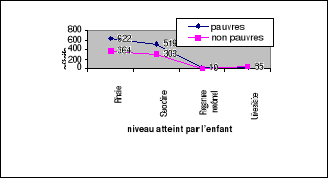
Graphique 2 : sexe de l'enfant et raison de déperdition

Tableau 6 : Test Khi-deux de la relation éducation- pauvreté

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	12,656	2	,002
Rapport de vraisemblance	12,228	2	,002
Association linéaire par linéaire	4,241	1	,039
Nombre d'observations valides	1911

Tableau 7 : Tests du Khi-deux déperdition et sexe de l'enfant

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	31,034	7	,000
Rapport de vraisemblance	41,117	7	,000
Association linéaire par linéaire	,965	1	,326
Nombre d'observations valides	665

Tableau 8 : Test Khi-deux déperdition et pauvreté du ménage

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	16,768	5	,005
Rapport de vraisemblance	16,199	5	,006
Association linéaire par linéaire	11,224	1	,001
Nombre d'observations valides	665

Tableau 9 : Tests du Khi-deux déperdition et sexe du chef de ménage

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	50,601	4	,000
Rapport de vraisemblance	54,441	4	,000
Association linéaire par linéaire	37,540	1	,000
Nombre d'observations valides	665

Tableau 10 : Tests du Khi-deux déperdition et type d'école fréquenté

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	7,499	2	,024
Rapport de vraisemblance	7,672	2	,022
Association linéaire par linéaire	3,067	1	,080
Nombre d'observations valides	390

Tableau 11: Tests du Khi-deux déperdition et sexe du chef de ménage

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	52,085	3	,000
Rapport de vraisemblance	53,820	3	,000
Association linéaire par linéaire	40,959	1	,000b
Nombre d'observations valides	634

.

Tableau 12 : Tests du Khi-deux de fréquentation et éducation du chef de ménage

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	5,951	3	,014
Rapport de vraisemblance	6,213	3	,102
Association linéaire par linéaire	2,612	1	,106
Nombre d'observations valides	2128

Tableau 13 : Tests du Khi-deux radio et faire au moins l'école primaire

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	2,062	1	,151
Correction pour la continuité	1,846	1	,174
Rapport de vraisemblance	2,132	1	,144
Test exact de Fisher
Association linéaire par linéaire	2,061	1	,151
Nombre d'observations valides	2186

Tableau 14 : Tests du Khi-deux téléviseur et faire au moins l'école primaire

	Valeur	ddl	Signification asymptotique (bilatérale)
Khi-deux de Pearson	10,448	1	,001
Correction pour la continuité	10,023	1	,002
Rapport de vraisemblance	10,239	1	,001
Test exact de Fisher
Association linéaire par linéaire	10,443	1	,001
Nombre d'observations valides	2186

Tableau 15 : statistiques descriptives des variables quantitatives des modèles

	Taille du ménage	Part du revenu consacré à l'enseignement	Dépenses journalières	Age du chef de ménage
Mean	8.213175	0.056144	0.071308	49.07136
Median	8.000000	0.040000	0.050000	48.00000
Maximum	20.00000	0.440000	0.700000	77.00000
Minimum	2.000000	0.000000	0.010000	24.00000
Std. Dev.	2.845741	0.060727	0.068866	9.118916
Skewness	0.881488	1.627696	4.691033	0.363267
Kurtosis	4.320187	6.319517	35.88695	3.053240
Jarque-Bera	441.8433	1968.927	106528.8	48.33671
Probability	0.000000	0.000000	0.000000	0.000000
Observations	2186	2186	2186	2186

1. régression du primaire :

. logit m13b_ens1 q17_tmen e5_tele m3_sexe m8b_reli parensg cmsex cmage m15_tec2 m15_tec3 cmeduc2 cmeduc3 cmeduc4 pauvrali

Logistic regression Number of obs = 1894

LR chi2(13) = 305.96

Prob > chi2 = 0.0000

Log likelihood = -1159.2304 Pseudo R2 = 0.1166

------------------------------------------------------------------------------

m13b_ens1 | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

q17_tmen | -.0382064 .0187238 -2.04 0.041 -.0749045 -.0015084

e5_tele | -.5190149 .1123722 -4.62 0.000 -.7392603 -.2987695

m3_sexe | .2170805 .1002847 2.16 0.030 .0205262 .4136349

m8b_reli | .0444016 .0254002 1.75 0.080 -.0053819 .0941851

parensg | -.0080365 .0090871 -0.88 0.376 -.0258469 .0097739

cmsex | -1.186294 .148573 -7.98 0.000 -1.477492 -.8950967

cmage | -.0873491 .0069137 -12.63 0.000 -.1008998 -.0737984

m15_tec2 | .2812516 .1193654 2.36 0.018 .0472997 .5152035

m15_tec3 | .0475517 .1392544 0.34 0.733 -.2253818 .3204853

cmeduc2 | -.6152853 .1562376 -3.94 0.000 -.9215054 -.3090652

cmeduc3 | -1.139606 .341499 -3.34 0.001 -1.808932 -.47028

cmeduc4 | -.9130472 .1851638 -4.93 0.000 -1.275962 -.5501328

pauvrali | .0668372 .1097204 0.61 0.542 -.1482109 .2818854

_cons | 6.430455 .5447657 11.80 0.000 5.362733 7.498176

------------------------------------------------------------------------------

. test m15_tec2 m15_tec3

( 1) m15_tec2 = 0

( 2) m15_tec3 = 0

chi2( 2) = 6.54

Prob > chi2 = 0.0381

. test cmeduc2 cmeduc3 cmeduc4

( 1) cmeduc2 = 0

( 2) cmeduc3 = 0

( 3) cmeduc4 = 0

chi2( 3) = 27.78

Prob > chi2 = 0.0000

. estat ic

------------------------------------------------------------------------------

Model | Obs ll(null) ll(model) df AIC BIC

-------------+----------------------------------------------------------------

. | 1894 -1312.212 -1159.23 14 2346.461 2424.111

------------------------------------------------------------------------------

. mfx compute, dydx at(mean)

Marginal effects after logit

y = Pr(m13b_ens1) (predict)

= .51583395

------------------------------------------------------------------------------

variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

q17_tmen | -.009542 .00468 -2.04 0.041 -.018707 -.000377 8.23865

e5_tele*| -.1284758 .02738 -4.69 0.000 -.182144 -.074808 .633052

m3_sexe | .0542157 .02505 2.16 0.030 .005126 .103305 1.49947

m8b_reli | .0110893 .00634 1.75 0.080 -.001344 .023523 3.21595

parensg | -.0020071 .00227 -0.88 0.376 -.006455 .002441 5.83433

cmsex | -.2962762 .0371 -7.99 0.000 -.368987 -.223565 1.17159

cmage | -.0218154 .00173 -12.64 0.000 -.025198 -.018433 49.4857

m15_tec2*| .070091 .02963 2.37 0.018 .012012 .12817 .44773

m15_tec3*| .0118703 .03474 0.34 0.733 -.056224 .079964 .238648

cmeduc2*| -.1523415 .03804 -4.00 0.000 -.226896 -.077787 .537487

cmeduc3*| -.2637565 .0665 -3.97 0.000 -.394091 -.133422 .032207

cmeduc4*| -.2229315 .04294 -5.19 0.000 -.307085 -.138778 .249736

pauvrali*| .0166865 .02738 0.61 0.542 -.036976 .070349 .37962

------------------------------------------------------------------------------

. mfx compute, dyex at(mean)

Elasticities after logit

y = Pr(m13b_ens1) (predict)

= .51583395

------------------------------------------------------------------------------

variable | dy/ex Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

q17_tmen | -.0786134 .03853 -2.04 0.041 -.154122 -.003105 8.23865

e5_tele | -.0820584 .01776 -4.62 0.000 -.116877 -.04724 .633052

m3_sexe | .0812949 .03756 2.16 0.030 .007687 .154903 1.49947

m8b_reli | .0356625 .0204 1.75 0.080 -.004323 .075648 3.21595

parensg | -.0117102 .01324 -0.88 0.376 -.037662 .014241 5.83433

cmsex | -.3471156 .04346 -7.99 0.000 -.432303 -.261928 1.17159

cmage | -1.07955 .08541 -12.64 0.000 -1.24695 -.912147 49.4857

m15_tec2 | .0314496 .01335 2.36 0.018 .005289 .05761 .44773

m15_tec3 | .0028342 .0083 0.34 0.733 -.013433 .019102 .238648

cmeduc2 | -.082594 .02097 -3.94 0.000 -.123694 -.041494 .537487

cmeduc3 | -.0091666 .00275 -3.34 0.001 -.014551 -.003782 .032207

cmeduc4 | -.056948 .01155 -4.93 0.000 -.079578 -.034318 .249736

pauvrali | .0063368 .0104 0.61 0.542 -.014052 .026725 .37962

------------------------------------------------------------------------------

. estat gof

Logistic model for m13b_ens1, goodness-of-fit test

number of observations = 1894

number of covariate patterns = 1117

Pearson chi2(1103) = 1292.27

Prob > chi2 = 0.1520

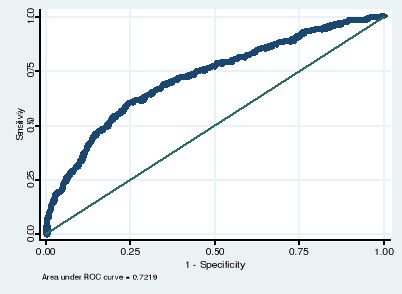
. lroc

Logistic model for m13b_ens1

number of observations = 1894

area under ROC curve = 0.7219

. logistic m13b_ens1 q17_tmen e5_tele m3_sexe m8b_reli parensg cmsex cmage m15_tec2 m15_tec3 cmeduc2 cmeduc3 cmeduc4 pauvrali

Logistic regression Number of obs = 1894

LR chi2(13) = 305.96

Prob > chi2 = 0.0000

Log likelihood = -1159.2304 Pseudo R2 = 0.1166

------------------------------------------------------------------------------

m13b_ens1 | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

q17_tmen | .9625142 .018022 -2.04 0.041 .9278321 .9984928

e5_tele | .5951065 .0668734 -4.62 0.000 .477467 .7417304

m3_sexe | 1.242444 .1245981 2.16 0.030 1.020738 1.512305

m8b_reli | 1.045402 .0265534 1.75 0.080 .9946325 1.098763

parensg | .9919957 .0090144 -0.88 0.376 .9744842 1.009822

cmsex | .3053507 .0453669 -7.98 0.000 .2282093 .4085681

cmage | .9163572 .0063355 -12.63 0.000 .9040236 .9288589

m15_tec2 | 1.324787 .1581337 2.36 0.018 1.048436 1.673979

m15_tec3 | 1.0487 .1460361 0.34 0.733 .7982114 1.377796

cmeduc2 | .5404867 .0844443 -3.94 0.000 .3979196 .7341329

cmeduc3 | .3199451 .1092609 -3.34 0.001 .1638291 .6248273

cmeduc4 | .4012995 .0743062 -4.93 0.000 .2791624 .5768732

pauvrali | 1.069121 .1173045 0.61 0.542 .8622493 1.325627

------------------------------------------------------------------------------

2. Regression du secondaire:

. logit m13b_ens2 q17_tmen e5_tele m15_tec cmsex cmage cmeduc2 cmeduc3

Logistic regression Number of obs = 1894

LR chi2(7) = 161.50

Prob > chi2 = 0.0000

Log likelihood = -1214.9894 Pseudo R2 = 0.0623

------------------------------------------------------------------------------

m13b_ens2 | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

q17_tmen | .0353505 .0173722 2.03 0.042 .0013016 .0693994

e5_tele | .3593313 .1035805 3.47 0.001 .1563173 .5623453

m15_tec | .116865 .0666612 1.75 0.080 -.0137885 .2475185

cmsex | .8583547 .1343492 6.39 0.000 .5950351 1.121674

cmage | .0598274 .0060049 9.96 0.000 .048058 .0715968

cmeduc2 | .0964395 .1012973 0.95 0.341 -.1020995 .2949785

cmeduc3 | .5136868 .2904684 1.77 0.077 -.0556207 1.082994

_cons | -5.068405 .4505342 -11.25 0.000 -5.951436 -4.185374

------------------------------------------------------------------------------

. test cmeduc2 cmeduc3

( 1) cmeduc2 = 0

( 2) cmeduc3 = 0

chi2( 2) = 3.56

Prob > chi2 = 0.1687

. estat ic

------------------------------------------------------------------------------

Model | Obs ll(null) ll(model) df AIC BIC

-------------+----------------------------------------------------------------

. | 1894 -1295.738 -1214.989 8 2445.979 2490.35

------------------------------------------------------------------------------

. mfx compute, dydx at(mean)

Marginal effects after logit

y = Pr(m13b_ens2) (predict)

= .42798042

------------------------------------------------------------------------------

variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

q17_tmen | .0086543 .00425 2.04 0.042 .00032 .016988 8.23865

e5_tele*| .087102 .02478 3.52 0.000 .038542 .135662 .633052

m15_tec | .0286101 .01632 1.75 0.080 -.003374 .060595 1.92503

cmsex | .2101365 .03288 6.39 0.000 .145693 .27458 1.17159

cmage | .0146465 .00147 9.98 0.000 .011769 .017524 49.4857

cmeduc2*| .023593 .02476 0.95 0.341 -.024933 .072119 .537487

cmeduc3*| .1276425 .07182 1.78 0.076 -.013118 .268403 .032207

------------------------------------------------------------------------------

. mfx compute, dyex at(mean)

Elasticities after logit

y = Pr(m13b_ens2) (predict)

= .42798042

------------------------------------------------------------------------------

variable | dy/ex Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

q17_tmen | .0712995 .03503 2.04 0.042 .00264 .139959 8.23865

e5_tele | .055689 .01605 3.47 0.001 .024238 .08714 .633052

m15_tec | .0550752 .03141 1.75 0.080 -.006496 .116646 1.92503

cmsex | .2461948 .03852 6.39 0.000 .170693 .321697 1.17159

cmage | .7247946 .07265 9.98 0.000 .582406 .867183 49.4857

cmeduc2 | .0126899 .01333 0.95 0.341 -.013434 .038813 .537487

cmeduc3 | .0040503 .00229 1.77 0.077 -.00044 .00854 .032207

------------------------------------------------------------------------------

. estat gof

Logistic model for m13b_ens2, goodness-of-fit test

number of observations = 1894

number of covariate patterns = 709

Pearson chi2(701) = 906.54

Prob > chi2 = 0.3080

. logistic m13b_ens2 q17_tmen e5_tele m15_tec cmsex cmage cmeduc2 cmeduc3

Logistic regression Number of obs = 1894

LR chi2(7) = 161.50

Prob > chi2 = 0.0000

Log likelihood = -1214.9894 Pseudo R2 = 0.0623

------------------------------------------------------------------------------

m13b_ens2 | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

q17_tmen | 1.035983 .0179973 2.03 0.042 1.001302 1.071864

e5_tele | 1.432371 .1483657 3.47 0.001 1.169197 1.754783

m15_tec | 1.123968 .074925 1.75 0.080 .9863061 1.280843

cmsex | 2.359276 .3169668 6.39 0.000 1.813095 3.06999

cmage | 1.061653 .0063751 9.96 0.000 1.049232 1.074222

cmeduc2 | 1.101243 .1115529 0.95 0.341 .9029397 1.343097

cmeduc3 | 1.671442 .4855011 1.77 0.077 .9458978 2.95351

3. Regression du Programme formel

. logit m13b_ens3 h5_stocu parensg cmage

Logistic regression Number of obs = 1911

LR chi2(3) = 30.30

Prob > chi2 = 0.0000

Log likelihood = -52.553122 Pseudo R2 = 0.2237

------------------------------------------------------------------------------

m13b_ens3 | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

h5_stocu | .3696359 .1490812 2.48 0.013 .0774421 .6618296

parensg | -1.030176 .4197563 -2.45 0.014 -1.852883 -.2074688

cmage | .0524278 .0317072 1.65 0.098 -.0097171 .1145727

_cons | -7.343024 1.891926 -3.88 0.000 -11.05113 -3.634917

------------------------------------------------------------------------------

. estat ic

------------------------------------------------------------------------------

Model | Obs ll(null) ll(model) df AIC BIC

-------------+----------------------------------------------------------------

. | 1911 -67.70063 -52.55312 4 113.1062 135.3278

------------------------------------------------------------------------------

. mfx compute, dydx at(mean)

Marginal effects after logit

y = Pr(m13b_ens3) (predict)

= .00004548

------------------------------------------------------------------------------

variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

h5_stocu | .0000168 .00004 0.43 0.666 -.00006 .000093 2.03977

parensg | -.0000468 .00009 -0.52 0.606 -.000225 .000131 5.82698

cmage | 2.38e-06 .00001 0.42 0.678 -8.9e-06 .000014 49.471

------------------------------------------------------------------------------

. mfx compute, dyex at(mean)

Elasticities after logit

y = Pr(m13b_ens3) (predict)

= .00004548

------------------------------------------------------------------------------

variable | dy/ex Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

h5_stocu | .0000343 .00008 0.43 0.666 -.000122 .00019 2.03977

parensg | -.000273 .00053 -0.52 0.606 -.00131 .000764 5.82698

cmage | .000118 .00028 0.42 0.678 -.000439 .000675 49.471

------------------------------------------------------------------------------

. estat gof

Logistic model for m13b_ens3, goodness-of-fit test

number of observations = 1911

number of covariate patterns = 554

Pearson chi2(550) = 513.47

Prob > chi2 = 0.8658

. logistic m13b_ens3 h5_stocu parensg cmage

Logistic regression Number of obs = 1911

LR chi2(3) = 30.30

Prob > chi2 = 0.0000

Log likelihood = -52.553122 Pseudo R2 = 0.2237

------------------------------------------------------------------------------

m13b_ens3 | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

h5_stocu | 1.447208 .2157514 2.48 0.013 1.08052 1.938335

parensg | .3569441 .1498295 -2.45 0.014 .1567845 .8126386

cmage | 1.053826 .0334139 1.65 0.098 .9903299 1.121394

------------------------------------------------------------------------------

4. Regression du niveau universitaire:

. logit m13b_ens4 e5_tele m8b_reli m15_tec parensg depjour_ cmage cmeduc4

Logistic regression Number of obs = 1894

LR chi2(7) = 190.75

Prob > chi2 = 0.0000

Log likelihood = -272.62019 Pseudo R2 = 0.2592

------------------------------------------------------------------------------

m13b_ens4 | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

e5_tele | 1.493721 .4204463 3.55 0.000 .6696616 2.317781

m8b_reli | -.1748045 .067927 -2.57 0.010 -.3079391 -.04167

m15_tec | -1.046007 .1883571 -5.55 0.000 -1.41518 -.6768337

parensg | .0729207 .0158001 4.62 0.000 .0419531 .1038882

depjour_ | .031578 .0123555 2.56 0.011 .0073617 .0557943

cmage | .0884656 .0151252 5.85 0.000 .0588207 .1181104

cmeduc4 | .7862451 .289286 2.72 0.007 .219255 1.353235

_cons | -7.734486 1.019479 -7.59 0.000 -9.732628 -5.736344

------------------------------------------------------------------------------

. estat ic

------------------------------------------------------------------------------

Model | Obs ll(null) ll(model) df AIC BIC

-------------+----------------------------------------------------------------

. | 1894 -367.997 -272.6202 8 561.2404 605.612

------------------------------------------------------------------------------

. mfx compute, dydx at(mean)

Marginal effects after logit

y = Pr(m13b_ens4) (predict)

= .01576813

------------------------------------------------------------------------------

variable | dy/dx Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

e5_tele*| .0207837 .0054 3.85 0.000 .010203 .031365 .633052

m8b_reli | -.0027129 .00109 -2.48 0.013 -.004856 -.00057 3.21595

m15_tec | -.0162335 .00356 -4.56 0.000 -.023212 -.009255 1.92503

parensg | .0011317 .00031 3.69 0.000 .00053 .001733 5.83433

depjour_ | .0004901 .00021 2.33 0.020 .000078 .000902 7.32105

cmage | .0013729 .00028 4.95 0.000 .00083 .001916 49.4857

cmeduc4*| .0150929 .007 2.16 0.031 .001373 .028812 .249736

------------------------------------------------------------------------------

. mfx compute, dyex at(mean)

Elasticities after logit

y = Pr(m13b_ens4) (predict)

= .01576813

------------------------------------------------------------------------------

variable | dy/ex Std. Err. z P>|z| [ 95% C.I. ] X

---------+--------------------------------------------------------------------

e5_tele | .0146753 .0039 3.77 0.000 .007041 .022309 .633052

m8b_reli | -.0087245 .00352 -2.48 0.013 -.015617 -.001832 3.21595

m15_tec | -.0312499 .00685 -4.56 0.000 -.044685 -.017815 1.92503

parensg | .0066027 .00179 3.69 0.000 .003093 .010112 5.83433

depjour_ | .0035879 .00154 2.33 0.020 .000574 .006601 7.32105

cmage | .067941 .01372 4.95 0.000 .041052 .09483 49.4857

cmeduc4 | .0030473 .00119 2.57 0.010 .000722 .005373 .249736

------------------------------------------------------------------------------

. estat gof

Logistic model for m13b_ens4, goodness-of-fit test

number of observations = 1894

number of covariate patterns = 805

Pearson chi2(797) = 870.69

Prob > chi2 = 0.3353

. logistic m13b_ens4 e5_tele m8b_reli m15_tec parensg depjour_ cmage cmeduc4

Logistic regression Number of obs = 1894

LR chi2(7) = 190.75

Prob > chi2 = 0.0000

Log likelihood = -272.62019 Pseudo R2 = 0.2592

------------------------------------------------------------------------------

m13b_ens4 | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

e5_tele | 4.453638 1.872515 3.55 0.000 1.953576 10.15312

m8b_reli | .8396211 .057033 -2.57 0.010 .7349601 .9591863

m15_tec | .3513379 .066177 -5.55 0.000 .2428819 .5082236

parensg | 1.075645 .0169953 4.62 0.000 1.042846 1.109476

depjour_ | 1.032082 .0127519 2.56 0.011 1.007389 1.05738

cmage | 1.092497 .0165242 5.85 0.000 1.060585 1.125368

cmeduc4 | 2.195138 .6350228 2.72 0.007 1.245149 3.869926

------------------------------------------------------------------------------

5. Regression logistique de choix multiple :

. ologit m13b_ens3 h5_stocu parensg cmage cmage

Ordered logistic regression Number of obs = 1911

LR chi2(3) = 30.30

Prob > chi2 = 0.0000

Log likelihood = -52.553123 Pseudo R2 = 0.2237

------------------------------------------------------------------------------

m13b_ens3 | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

h5_stocu | .3696359 .1490812 2.48 0.013 .0774422 .6618296

parensg | -1.030177 .4197529 -2.45 0.014 -1.852878 -.2074768

cmage | .0524278 .0317072 1.65 0.098 -.0097171 .1145727

-------------+----------------------------------------------------------------

/cut1 | 7.343023 1.891926 3.634917 11.05113

------------------------------------------------------------------------------