|
DYNAMIQUE NON LINEARE DU
PULSE DANS UNE FIBRE OPTIQUE
DJINGUE JEAN PIERRE
yaoundé le 25 avril 2007
Table des matières
Dédicaces ii
Remerciements iii
Abstract - Résumé 1
0.1 Abstract 1
0.2 Résumé 1
Introduction Générale 1
|
1 Généralités sur la fibre optique
et la méthode de Lax
|
3
|
|
1.1
|
La fibre optique
|
3
|
|
1.1.1
|
Description de la fibre optique
|
3
|
|
1.1.2
|
Mode de fabrication et différents types de fibres
|
4
|
|
1.2
|
Propagation d'une impulsion lumineuse dans la fibre optique
|
5
|
|
1.2.1
|
Réponse d'un milieu à une excitation
électrique extérieure
|
5
|
|
1.2.2
|
Polarisation induite
|
6
|
|
1.2.3
|
Équation d'onde
|
7
|
|
1.2.4
|
Équation de propagation
|
7
|
|
1.2.5
|
L'équation de Schrödinger non linéaire
|
9
|
1.3 La méthode de Lax 10
1.4 Conclusion 12
2 Solution soliton de l'équation de
Schrödinger non linéaire d'ordre supérieur 13
|
|
2
|
|
2.1
|
Le soliton
|
13
|
|
2.2
|
Conditions d'Hirota
|
15
|
|
2.3
|
Construction de la paire de Lax associée à
l'équation de Schrödinger non linéaire
|
|
|
d'ordre supérieur
|
17
|
|
2.4
|
Solution Soliton
|
20
|
|
2.5
|
Solution soliton en absence du mode linéaire
|
26
|
|
2.6
|
Conclusion
|
29
|
3 Construction de la paire de Lax pour les modèles
couplés 30
3.1 Équations couplées de Schrödinger non
linéaires 30
3.2 Phénomènes décrits par un
système couplé d'équations de Schrödinger non li-
néaires 31
3.2.1 Propagation de deux ondes de couleurs différentes
31
3.2.2 Autres phénomènes 32
3.3 Construction de la paire de Lax 32
3.4 Conclusion 36
Conclusion générale et perspectives
38
Bibliographie 40
Table des figures
|
1.1
|
Structure d'une fibre optique
|
3
|
|
1.2
|
Quelques types de fibre optique
|
5
|
|
2.1
|
Interaction de deux solitons [6].
|
14
|
|
2.2
|
volution de l'amplitude (2.63) en fonction de la distance Z, pour
les cas g1 =
|
|
|
0.05, g2 =
0.01; g1 = 0.01,
g2 = 0.05 et g1 =
g2 = 0.01 ( avec
Ac = 1,ã1 =
ã2 =
|
|
|
1,o1 = 0.05,o2
= -0.04 et ó = 5)
|
25
|
|
2.3
|
volution de l'amplitude Ac en
fonction de l'amplitude As pour L
= 8, 9, 10, 11
|
|
|
et 12
|
26
|
|
2.4
|
volution de la largeur à mi-hauteur en fonction de la
distance z
|
28
|
|
2.5
|
volution de l'énergie en fonction de la distance z
|
28
|
Dédicaces
Je dédie ce mémoire à :
? Ma mère TEUPE Alice pour les encouragements,
les efforts incessants et l'attention portée envers moi. Ce travail est
le fruit de l'éducation que vous avez toujours su m'apporter
? Mon oncle NGAYAP Eloi qui par ses conseils sans
relâche a fait de moi ce que je suis.
? Ma tante LEUNA Catherine pour ses conseils sans
relâche.
? Mes frères et soeurs Mme NGOUAMBE, Mme YOUBI,
Mme WETCHEBEWE, Mme FOTSO, Mlle KOUEYAP et M. NGANDEU pour leur
patience et leur soutien durant de longues années.
Remerciements
Aujourd'hui l'opportunité m'est offerte de
témoigner ma profonde gratitude à l'endroit de ceux qui de
près ou de loin ont contribué à l'élaboration de ce
mémoire. Je tiens tout d'abord à remercier :
* Le Professeur Claude Marie NGABIRENG, pour la
confiance qu'elle a placé en moi en acceptant de diriger ces travaux. Je
ne peux que louer affectueusement son entière disponibilité, ses
remarques et le sentiment de bienveillance exprimé à mon
égard.
* Le Professeur Timoléon Crépin KOFANE,
responsable du Laboratoire de Mécanique, pour les enseignements
édifiants.
* Le Professeur Paul WOAFO, pour son sérieux
dans l'exécution de sa tâche d'éducateur.
* À M. FEWO Serge pour tous les conseils, la
disponibilité et les interventions énergiques tout au long de ce
travail. Qu'il trouve ici ma sincère reconnaissance.
* Au Professeur. LU Li, du Département de
Physique de l'Université de Shanxi (Taiyuan). Je dis merci pour la
collaboration que nous avons eue.
* À tous les membres du jury pour l'honneur qu'ils
me font en acceptant de participer au jury.
* À tous mes enseignants du Département
de Physique , en particulier Dr C. TCHAWOUA, Dr S. ZEKENG, Pr E. MANGUELLE, Pr
F. KAMGA qui sont les principaux acteurs de ma formation
académique.
Mes remerciements vont également :
* À M. WETCHEBEWE André pour la peine qu'il
a pu se donner pour ma réussite.
* À M.YOUMBI Jean Paul pour ses conseils sans
relâche. * À madame NGAYAP Christine.
* À ma cousine FADJIE NGAYAP Chimène pour
son soutien financier et moral.
* Aux familles NGOUAMBE, FOTSO et NGADEU
* À DJUIDJE Prudence et WOUKOUWE Grâce ,
jamais vous ne m'avez abandonné pendant les moments
difficiles.
* À mes frères et scours MONGOUE, NOUBEU,
SIWE, TANKEBOU, LIATOU, NGAYAP et NKOULIHEU
* À mes camarades et amis KASSE, TANGA,
TCHEUMAGOU, HAPPI, TACHIM, SAH, TANSEM, PEDIER, YAKADA, FEZEU, NANA, LIMI,
DAMO, ONGUENE, BEDGA, GATCHOUSSI, AHOUDOU, GAMBO et TOGUEU pour les
échanges bénéfiques depuis plusieurs années et tout
au long de ce travail.
* À tous mes camarades de promotion de classe de
D.E.A ; Année Académique 2006 -2007, pour les débats
édifiants de tous les jours.
* À tous ceux qui de près ou de loin ont
contribué à l'élaboration de ce travail.
Abstract - Résumé
0.1 Abstract
The aim of This report is look for solution of some
systems in nonlinear optics using the reduction of a nonlinear problem to a
linear one, using the Lax pair construction. We determine initially, when the
conditions of Hirota are verified, the pulses 's soliton solution of the
nonlinear Schrödinger equation with higher order terms which models
propagation of signals in optical fibers. Finally, we are interested on a
coupled nonlinear Schödinger equation in order to construct the associated
Lax pair.
0.2 Résumé
Ce mémoire traite de la recherche des solutions
de quelques systèmes Physiques grâce à la reduction d'un
problème non linéaire en un problème linéaire
à travers la construction de Lax. Nous déterminons dans un
premier temps, lorsque les conditions d'Hirota sont vérifiées, la
solution soliton du type pulse de l'équation de Schrödinger non
linéaire d'ordre supérieur qui modélise la propagation des
impulsions dans une fibre optique. Enfin, nous nous interessons à
l'équation de Schödinger non linéaire couplée par sa
construction de Lax associée en vue de rechercher ses solutions
éventuelles.
Introduction Générale
Le monde des télécommunications a connu
une importante évolution depuis la mise au point du
télégraphe (sur câble électrique) en 1837 par Samuel
Morse et l'invention du téléphone en 1875 par Alexander Graham
Bell [1, 2]. En effet, grâce à la théorie de
l'électromagnétisme de James Clerck Maxwell qui prédit
l'existence des ondes radio en 1864, Heinrich Hertz a prouvé
expérimentalement l'existence de ces ondes en 1887 [1, 2]. Par la suite,
Olivier James a établi une communication sans fil sur une distance de
140 mètres en 1894 et Guglielmo Marconi a effectué la
première transmission transatlantique en 1901 [2]. Un grand pas a
été effectué durant les deux derniers siècles avec
le développement des systèmes de transmission sur câbles et
sur ondes hertziennes, mais la qualité et le débit de la
transmission sont restés toujours d'une grande importance. L'idée
de se servir de la lumière dans la communication remonte aux feux de
bois utilisés par les Grecs et les Perses ainsi qu'aux torches
enflammées utilisées par les Romains. En 1958, et avec
l'invention du laser, l'idée d'utiliser l'optique surgit de nouveau. Le
laser(ligt amplification by stymulated émission of radiation) pouvait
remplir dans le domaine lumineux le même rôle que l'oscillateur
radioélectrique dans le cas des ondes hertziennes. Les premières
expériences de transmission étaient dans l'atmosphère, qui
s'est révèlé un milieu de transmission dispersif et
absorbant [2]. L'idée de guider la lumière sur de grandes
distances avec un très faible taux d'atténuation a conduit
à la contruction d'un support révolutionnaire de transmission
qui
est la fibre optique.
De nos jours, la fibre optique tend à remplacer
progressivement le câble coaxial dans la transmission des données.
Celle-ci se fait au moyen d'impulsions générées à
l'entrée de la fibre, et repose sur la modulation binaire de
l'intensité d'une onde lumineuse de très haute fréquence
appelée onde porteuse. sous certaines conditions particulières,
les impulsions générées peuvent être des solitons.
Les solitons se définissent comme des ondes solitaires qui, au cours de
leur propagation conservent leurs formes et leurs énergies [3, 4]. La
géneration d'impulsions à très hauts débits dans le
domaine des femtosecondes fait apparaître des effets d'ordre superieur
influençant fortement la propagation des dites impulsions. Entre autres,
nous avons la dispersion d'ordre trois et l'effet d'auto-raidissement. Ces
differents effets seront pris en compte dans l'équation de
Schrödinger non linéaire (SNL) en vue de l'obtention des solutions
par la méthode Abowitz, Kaup, Newell et Segur (AKNS), incluant les
conditions d'Hirota et la représentation de la paire Lax. Ceci fera
l'objet de notre travail. Ce mémoire s'articule autour de trois
axes.
La première partie, présente quelques
généralités sur la fibre optique. Nous montrons comment
l'équation de Schrödinger non linéaire d'ordre
supérieur modélise la propagation des ondes dans les
systèmes optiques. Par la suite nous présentons la méthode
AKNS.
La résolution de l'équation de
Schrödinger non linéaire d'ordre supérieur par la
méthode AKNS est présentée dans la deuxième
partie.
L'essentiel de la troisième partie est basé
sur la construction de la paire de Lax de l'équation de Schrödinger
non linéaire couplée.
Notre travail s'achève par une conclusion
générale et des perspectives pour des travaux futurs.
CHAPITRE PREMIER
GENERALiTEs suR LA FiBRE opTiQuE ET LA METHoDE DE LAX
1.1 La fibre optique
1.1.1 Description de la fibre optique

FIG. 1.1 - Structure d'une fibre optique
La fibre optique est un fil transparent très
fin qui guide la lumière ; Entourée d'une gaine protectrice, elle
est utilisée pour conduire la lumière entre deux lieux distants
de plusieurs centaines, voir milliers de kilomètres. Le signal lumineux
codé par une variation d'intensité est capable de transmettre une
grande quan-
tité d'information. La fibre trouve son
utilisation principale dans les réseaux de transmission pour les
télécommunications; C'est un guide d'ondes
électromagnétiques. La fibre optique est constituée d'une
partie centrale appelée coeur, ayant un indice de réfraction
légèrement supérieur à celui de la gaine entourant
le coeur. L'ensemble coeur-gaine étant couvert d'une couche
protectrice.
1.1.2 Mode de fabrication et différents types de
fibres
La fabrication d'une fibre optique passe par la
réalisation d'une préforme cylindrique en barreau de silice [51;
La silice est un composé dioxyde du silicium, présent dans un
grand nombre de minéraux, tels que le quartz, la calcédoine et
l'opale. Le barreau subit ensuite un étirage en plaçant
l'extrémité dans un four porté à une
température voisine de 2000 degrés celsus [51. Il est alors
transformé en fibre de plusieurs centaines de kilomètres à
une vitesse de l'ordre du kilomètre par minute. La fibre est ensuite
revêtue d'une double couche de résine protectrice avant
d'être enroulée sur une bobine. L'écart d'indice entre le
coeur et la gaine est obtenue en incorporant des dopants, tels que
:
- Le germanium et le phosphore qui accroissent l'indice
dans le coeur, - Le bore et le fluor qui font décroître l'indice
dans la gaine.
L'étude de la propagation dans un guide
électromagnétique fait apparaître la notion de mode de
propagation, quantifiée par les paramètres du guide. Dans le cas
de la fibre optique, cette quantification conduit à une première
classification: on distingue les fibres monomodes, dans lesquelles un seul mode
de propagation est possible, et les fibres multimodes oil plusieurs modes
(quelques centaines ou milliers) peuvent coexister.
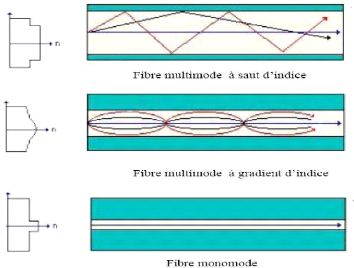
FIG. 1.2 - Quelques types de fibre optique
1.2 Propagation d'une impulsion lumineuse dans la fibre
optique
1.2.1 Réponse d'un milieu à une excitation
électrique extérieure
Un matériau peut être essentiellement
considéré comme un ensemble de particules chargées (ions
et électrons); Soumises à un champ électrique, les charges
tendent à se déplacer : Les charges positives dans le sens du
champ électrique, les charges négatives dans le sens
opposé. Dans un milieu conducteur, les électrons peuvent se
déplacer à travers le matériau aussi longtemps que le
champ électrique est appliqué, donnant lieu à un courant
électrique. Dans le cas d'un diélectrique, qui est d'un usage
beaucoup plus courant en optique, les particules chargées sont
liées fortement les unes aux autres, bien que leurs liens conservent une
certaine " élasticité ". Ainsi, en présence d'un champ
électrique, les charges ont un mouvement uniquement transitoire et
s'éloignent légèrement de leur position
d'origine.
Ces petits déplacements
élémentaires (charges positives d'un côté, charges
négatives de l'autre) se traduisent par l'apparition dans le
matériau de moments dipôlaires électriques
induits. En d'autres termes l'effet d'un champ électrique sur
un diélectrique est d'induire une polarisation. Sous l'action du
champ électrique d'une onde laser, les charges d'un
diélectrique sont soumises à un mouvement
oscillant de même fréquence formant un ensemble de
dipôle oscillant. La réponse du matériau
à ce champ laser devient donc non linéaire.
|
1.2.2 Polarisation induite
Pour le cas d'une fibre optique, le vecteur polarisation
induit
|
?-
P est une fonction
|
|
non linéaire du champ électrique
appliqué
|
?- E ainsi que suit [6]
|
?-P =
å0[÷(1)-?E
+ ÷(2)-?E?-E +
÷(3)-? E ?- E ?- E +
...], (1.1)
|
qui est une combinaison d'une partie linéaire
(
|
-? PL) et d'une partie non linéaire
|
|
( PNL) tel que :
|
?-
P=
|
PL + PNL, (1.2)
|
avec
PL =
å0÷(1)-?
-? E , (1.3)
PNL =
å0[÷(2)-?
--? E ?- E +
÷(3)-? E ?- E ?- E +
...]. (1.4)
Où
÷(j)(j =
1, 2, ...) est la
susceptibilité d'ordre j. En général,
÷(j) est un
tenseur de rang (j+1). La
susceptibilité linéaire ÷(1)
représente la contribution dominante ?-
de P . Ces effets sont inclus
à travers l'indice de réfraction n et le coefficient
d'atténuation. La susceptibilité d'ordre 2 (
÷(2)) est responsable d'effets non
linéaires tels que la génération de
second harmonique. Cependant, elle est non nulle, seulement si le milieu ne
présente pas une symétrie d'inversion au niveau
moléculaire. La fibre optique étant
constituée de molécule de dioxyde de silicium, le
tenseur ÷(2) s'annule du fait que cette
molécule est centro-symétrique.
Les effets non linéaires dans les fibres
optiques ont pour principale origine la susceptibilité d'ordre 3
(÷(3)), qui est responsable de nombreux
phénomènes tels que la génération de
troisième harmonique, la réfraction non
linéaire,...[7].
1.2.3 Equation d'onde
A partir des équations bien connues de Maxwell
[8], l'équation d'onde d'un
|
champ électrique
|
?-E est donnée par:
|
-? E - 1
c2
= -u0(?2-? PL
?t2 +
?
?2 PNL
?t2 ), (1.5)
?2
?2
-?E
?t2
oil u0 et c sont respectivement la
pérméabilité du vide et la vitesse de la
lumière.
Nous supposons dans la suite que le milieu est
homogène, isotrope et centrosymétrique. Ces conditions initiales
permettent de considérer une approche selon une seule composante des
champs, en supposant que le champ électrique maintienne sa polarisation
pendant la propagation, permettant ainsi une approche scalaire de
l'équation. Pour développer cette équation, on
s'intéresse en particulier à la propagation selon l'axe z dans un
système invariant axialement.
1.2.4 Equation de propagation
|
La polarisation étant une fonction non
linéaire de
|
?-E, nous considérons
dans
|
un premier temps une réponse purement
linéaire; L'équation d'onde devient dans ce cas :
?2 Ee +
å(ù)k0
Ee = 0 (1.6)
avec å = (n +
iá/2k0)2, n
l'indice et á le coefficient d'atténuation.
|
?-E et nous prenons l'impulsion
électrique
|
|
E est la transformée de Fourier de sous la forme
:
|
E(z, t) =
q(z, t)
expi(â0z -
ù0t) + cc. (1.7)
En remplaçant (1.7) dans (1.6) et en
considérant l'enveloppe q(z, t)
lentement variable suivant la coordonnée z,
c'est-à-dire;
|?2eq
?z2| «
|â0ù0 ?eq
?z|, (1.8)
l'équation (1.6) se met sous la forme
:
?eq
2iâ0+
(eâ2 -
â2 0)eq = 0,
(1.9)
?z
avec eâ2 =
å(ù)k2
0.
Les effets de la dispersion dans la fibre sont pris en
compte à travers le développement en série de Taylor de la
constante de propagation â(ù)
autour de la fréquence ù0
â(ù) =
â0 + â1(ù -
ù0) + 2â2(ù -
ù0)2 + 1
1 6â3(ù -
ù0)3 + ..., (1.10)
oil âm = dmâ
dtm |ù=ù0
(m =
1,2,3,...).
En prenant la transformation de Fourier inverse de
l'équation (1.9) et en utilisant un référentiel se
déplaçant avec notre signal à la vitesse de groupe
Vg = 1/â1, avec la
transformation T = t - â1z on obtient
:
|
?q
=
?z
|
i ?2q 1
?3q á
2â2 ?T2 +
6â3 ?T 3 - 2
q, (1.11)
|
qui est l'équation de la propagation de
l'enveloppe dans le cadre linéaire.
Si nous tenons compte d'une réponse non
linéaire instantanée, ceci entraîne
|
que la dépendance de PNL par rapport au temps et
en fonction de par la relation [6] :
|
?-E est donnée
|
PNL(z, t) =
o0÷(3)E(z,
t)E(z,
t)E(z, t).
(1.12)
Nous remplaçons par la suite l'équation
(1.7) dans l'équation (1.12), la polarisation non linéaire se met
sous la forme suivante :
PNL(z, t) =
o0÷(3)[3|qq|q(z,
t)expi(-ù0t
+ â0z)
+q3(z,t)exp3i(-ù0t
+ â0z) +
cc]. (1.13)
Dans cette équation, on peut donc observer un
terme oscillant à ù0 mais également un
autre terme oscillant à la troisième harmonique
3ù0. Ce deuxième terme peut
entraîner la génération de troisième harmonique s'il
est en accord de phase avec l'onde pompée. Ce qui n'est pas envisageable
dans les fibres optiques [7]. Il est habituellement négligé dans
la modélisation basée sur la propagation de l'enveloppe du
champ.
1.2.5 L'équation de Schrödinger non
linéaire
En remplaçant l'équation (1.13) dans
(1.5) et en tenant compte de l'équation (1.11), l'équation
traduisant la propagation d'une onde lumineuse dans une fibre optique suivant
une direction z et possédant un champ électrique dont l'enveloppe
est lentement variable avec la fréquence ù est définie
par
|
?q
=
?z
|
i ?2q 1
?3q á
2â2 ?T 2 +
6â3 ?T 3 - 2 q
+ iã|q|2q.
(1.14)
|
Cette équation qui est l'équation de
Schrödinger non linéaire.
Sous certaines conditions, des effets non
linéaires influencent la propagation des solitons, et le modèle
est celui Schrödinger non linéaire avec les termes d'ordre
supérieur donné par l'équation
iqz =
-d2(z)qtt -
2r(z)|q|2q
+ id3(z)qttt +
iá(z)(|q|2q)t
+if(z)q(|q|2)t
+ i(z)q, (1.15)
oil
- Le deuxième terme de l'équation
décrit la dispersion d'ordre 2.
- Le troisième terme décrit l'auto
modulation de phase.
- Le quatrième terme décrit la dispersion
d'ordre 3.
- Le cinquième terme décrit la dispersion
kerr
- Le sixième terme décrit
l'auto-raidissement de la fréquence.
- Le septième terme décrit les pertes dues
aux phénomènes d'absorption.
Cette dernière forme d'équation de
propagation d'impulsion lumineuse dans la fibre est encore appelée
équation de Schrödinger non linéaire d'ordre
supérieur. De nombreuses méthodes analytiques ont
été utilisées en vue de rechercher les solutions de
l'équation de Schrödinger non linéaire. Nous nous servirons
de la méthode AKNS à trvers la construction de Lax pour
rechercher les solutions du modèle de Schrödinger d'ordre
superieur.
1.3 La méthode de Lax
La méthode de Lax [4, 9] permet de traiter
toute une variété de système non linéaire
totalement intégrable. Son principe consiste à
réécrire l'équation non linéaire sous la forme
d'une équation linéaire avec les opérateurs qui agissent
dans un espace de Hilbert différent de l'espace fonctionnel dans lequel
on résout l'équation différentielle. Connaissant la
condition initiale, la résolution du problème linéaire
nous permet de déduire la solution de l'équation non
linéaire. Une généralisation de Cette méthode a
été introduite en 1974 par Abowitz, Kaup, Newell et Segur (
méthode AKNS) [4, 10, 11], qui est une forme matricielle de la
méthode de Lax.
La construction du problème linéaire passe
par la détermination de deux opérateurs L et M appelés
paire de Lax et definis comme suit :
L est un opérateur linéaire
dépendant de deux fonctions q(z, t) et
r(z, t) tel
que
|
?
L = ?
|
?z -q(z,t)
r(z,t)
-?z
|
?
?,
|
(1.16)
|
et agit sur un espace dont la fonction
ø(z, t) =
(ø1(z, t),
ø2(z, t)) forme un ensemble de deux
fonctions. Les valeurs propres ë de l'opérateur L sont
définies de la manière suivante :
Lø = -iëø,
(1.17)
ces valeurs propres ë sont indépendantes du
temps et les fonctions propres en dépendent selon la loi
øt = Mø,
(1.18)
oil M est un opérateur linéaire agissant
sur le même espace.
La compatibilité des deux équations (1.16)
et (1.17) limite les choix pour l'opérateur M. En effet on peut
réécrire l'équation (1.17) sous la forme
øz = Rø,
(1.19)
avec
?
?.
-ië q(z, t)
r(z,t) ië
?
R = ?
Pour avoir une compatibilité entre
øz = Rø et øt =
Mø. Il faut que les deux conditions suivantes soient
vérifiées :
øzt = Rtø +
Røt = Rtø + RMø,
(1.20)
øtz = Mxø
+ Møx =
Mxø + MRø, (1.21)
cela impose la condition
Rt - Mz - [M,R] =
0. (1.22)
L'équation (1.22 ) est une équation de
compatibilité entre les deux opérateurs L et M et nous permet,
connaissant L de déterminer l'opérateur M. En
générale l'opérateur L est connu et dépend du type
de problème non linéaire à résoudre. Ainsi, pour
l'équation de SNL on utilise la matrice [4, 11].
|
?
R = ?
|
ë -u
u -ë
|
?
?,
|
(1.23)
|
oil u est la fonction conjuguée de u.
1.4 Conclusion
Ce chapitre nous a permis de présenter la fibre
optique, de mettre en évidence les équations nécessaires
à l'établissement de l'équation de l'enveloppe non
linéaire décrivant la propagation d'impulsions dans la fibre
optique. Enfin, nous avons présenté la méthode AKNS qui
est une généralisation de la methode de Lax. Cette méthode
nous permettra dans la suite de pouvoir retrouver les solutions analytiques de
l'équation de Schrödinger non linéaire d'ordre
supérieur.
CHAPITRE DEUX
SoLuTioN SoLiToN DE L'EQuATioN DE ScHRODiNGER NoN
LiNEAiRE
D'oRDRE SupERiEuR
Dans cette partie, nous recherchons les solutions de
type soliton par la méthode AKNS présentée dans la
première partie. Pour cela, nous allons dans un premier temps
établir une relation entre les coefficients de l'équation de
Schrödinger non linéaire d'ordre superieur ( conditions d'Hirota) ;
Par la suite, nous construirons la paire de Lax de cette équation , et
au moyen de la transformation de Darbourx, nous rechercherons les solutions de
cette équation non linéaire de Schrödinger d'ordre
supérieur.
2.1 Le soliton
Dans le domaine de la propagation des impulsions dans
les fibres optiques, le soliton se définit de façon simple comme
une impulsion dont le profil et l'énergie sont conservés au cours
de la propagation [3]. Néanmoins, la notion de soliton va au-delà
de cette définition. En effet, si l'on injecte dans la fibre un soliton
rapide à la suite d'un soliton lent, les deux impulsions vont interagir
durant un certain temps car leur régime de propagation est non
linéaire. Cependant, au terme de cette interaction, on retrouvera en
ordre inversé deux impulsions de même profils, énergies et
vitesses qu'avant l'interaction. Le seul témoin de l'interaction sera la
phase des impulsions qui aura varié. La figure (2.1) suivante
présente l'interaction
de deux solitons oil nous observons que les profils
d'amplitude sont identiques avant et après l'interaction. nous
constatons aussi que chaque soliton est décalé de sa trajectoire
rectiligne du fait de l'interaction. C'est la seule marque
révélant que la collision a eu lieu.
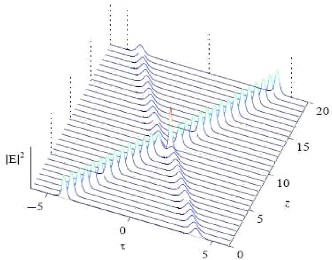
FIG. 2.1 - Interaction de deux solitons [6].
Un tel comportement lors des interactions incite
à voir les impulsions impliquées comme s'il s'agissait des
particules conservant leurs énergies, quantités de mouvements et
formes. C'est ce caractère de particule que l'on tente de
refléter par l'appellation " soliton " qui englobe donc une notion de
stabilité forte des impulsions qui en sont qualifiées [3, 4I.
Quand on veut désigner une impulsion qui conserve son profil mais ne
présente pas une telle robustesse vis-à-vis des collisions, on
parle plutôt d'"onde solitaire" [4I. Néanmoins, l'usage a
consacré certaines appellations qui s'opposent à cette
règle. L'exemple type est celui des " solitons de parois de domaines "
qui ne sont en réalité que des ondes solitaires
[4]; Quels que soient les abus de langage commis, il
est certain que la notion de soliton ne peut être attribuée
qu'à une impulsion stable et conservant son profil et l'énergie
lors de sa propagation. Néanmoins, plusieurs effets indésirables
peuvent affecter le soliton lors de sa propagation dans la fibre optique. Entre
autres, nous avons les pertes, la dispersion,...etc
La propagation des solitons dans le domaine des
femtosecondes est modelisée par l'équation non linéaire de
Schrödinger d'ordre superieur. A la suite des conditions imposées
aux coefficients de cette équation, nous établirons les solutions
exactes par la construction de la paire de Lax.
2.2 Conditions d'Hirota
Nous rappelons l'équation de SNL avec les termes
d'ordre superieur obtenue dans la premiere partie.
iqz =
-d2(z)qtt -
2r(z)|q|2q
+ id3(z)qttt +
iá(z)(|q|2q)t
+if(z)q(|q|2)t
+ i(z)q. (2.1)
Cette équation n'étant
généralement pas intégrable, nous l'analysons en
considérant la solution approchée donnée par l'expression
[12] :
r
d2
q1(z, t) =
ç1(z) r
exp(iö1)sechè1,
(2.2)
avec
è1 =
ç1(z)[t +
ñ(z)],
ö1 = î1t
+ ù(z).
(2.3)
Où ç1(z),
ñ(z), î1 et
ù(z) sont rattachés
respectivement à l'inverse de la largeur, la vitesse de groupe, la
fréquence propre et la phase de l'onde. En substituant
l'équation (2.2) dans l'équation (2.1) et
en posant g = Vd2/r, on obtient
une équation de la forme :
G + iH = 0,
(2.4)
avec
G = (î't
+ ù')çg
cosh2 è +
d2çî2g
cosh2 è -
d2ç3g(-1
+ sinh2 è) -
2rç3g3
+d3çç3g
cosh2 è -
3d3ç3îg(-1
+ sinh2 è) -
áç3îg3,
(2.5)
H =
(ç'g+çg'-Fçg)
cosh2
è-[(ç't+ç'ñ+ñ'ç)çg+2d2ç2îg+3d3ç2î2g]
sinh è cosh2 è
-(5d3ç4g
-
3áç4g3
-
2fç4g3)
sinh è +
d3ç4g
sinh3 . (2.6)
Nous linéarisons l'équation (2.5) et (2.6),
et nous obtenons les équations suivantes :
ç'g +
çg' - Fçg =
0, (2.7)
(ç't
+ç'ñ
+ñ'ç)çg
+2d2ç2îg
+3d3ç2î2g
-d3ç4g =0,
(2.8)
(ç't
+ç'ñ+ñ'ç)çg
+2d2ç2îg
+3d3ç2î2g
-d3ç4g
+5d3ç4g
-3áç4g3
-2fç4g3
=0,
|
(2.9)
|
|
(î't +
ù')çg +
d2çî2g
+ d3çî3g -
d2ç3g -
3d3ç3îg
= 0,
(î't +
ù')çg +
d2çî2g
+
d3çî3g
+ d2ç3g +
3d3ç3îg -
2rç3g3
- áç3g3 =
0.
|
(2.10)
(2.11)
|
|
En posant ç constant l'équation (2.7) nous
conduit à :
|
|
|
F= d2,zr - rzd2
|
(2.12)
|
|
.
2rd2
|
Nous sommons les équations (2.8) et (2.9) et nous
faisons la difference des équations (2.10) et (2.11).
Nous obtenons respectivement les relations suivantes :
6rd3 = (3á +
2f)d2, (2.13)
f + á = 0.
(2.14)
Les équations
(2.12), (2.13)
et (2.14) encore appelées
conditions d'Hirota. Ces conditions montrent que l'absorption (ou
l'amplification) peut être contrôlée à travers les
autres coefficients d2, d3 et r.
.
2.3 Construction de la paire de Lax associée à
l'équation de Schrödinger non linéaire d'ordre
supérieur
En tenant compte des conditions d'Hirota données
par les équations (2.12),
(2.13) et
(2.14), que nous remplaçons dans
l'équation (2.1) et en faisant le changement de variable
V r
E = q, (2.15)
d2
l'équation (2.1) se met sous la forme
:
iEz = -d2Ett
- 2d2|E|2E
+ id3Ettt +
6id3|E|2Et.
(2.16)
La paire de Lax associée à
l'équation (2.16) est construite ainsi qu'il suit :
|
?
?
?
|
øt = Uø
øz = V ø
|
(2.17)
|
où ø =
(ø1,ø2)T
represente la fonction propre associée à la valeur propre ë
(T étant la transposée); U et V étant deux matrices
definies par :
|
?
U = ?
|
ë -E E -ë
|
?
?,
|
(2.18)
|
et
?
V=?
A B C --A
oil E est la conjuguée de E ; A, B et C des
polynômes définis par :
{
A = a0 +
ëa1 + ë2a2
+ ë3a3
(2.20)
B = b0 +
ëb1 + ë2b2
+ ë3b3
C = c0 +
ëc1 + ë2c2
+ ë3c3
oil les coefficients ai, bi et ci
(i = 0, 1,
2, 3) sont à déterminer.
Les matrices U et V vérifient l'équation de
compatibilité donnée par la relation :
Uz -- Vt + [U, V ] = 0.
(2.21)
(
Nous remplaçons U et V par leurs valeurs
données par les équations
(2.18) et (2.19) et
tenons compte du fait que [U, V ] = UV -- V
U. L'équation de compatibilité se met donc sous la forme
:
At Bt -- Ez
Ct + Ez --At )
+ ( --CE -- BE 2Bë + 2EA )
( 0 0 )
2EA -- 2Cë EB + EC
0 0 . (2.22)
Nous remplaçons A, B et C par leurs expressions
données par l'équation
(2.20), ainsi l'équation de
compatibilité permet d'obtenir :
--a0t --
ëa1t --
ë2a2t --
ë3a3t --
E(c0 + ëc1 +
ë2c2 +
ë3c3)
--E(b0 +
ëb1 + ë2b2
+ ë3b3) = 0,
(2.23)
Ez -- b0t --
ëb1t --
ë2b2t --
ë3b3t +
2ë(b0 + ëb1
+ ë2b2 +
ë3b3)
+2E(a0 +
ëa1 + ë2a2
+ ë3a3) = 0,
(2.24)
Ez -- c0t --
ëc1t --
ë2c2t --
ë3c3t +
2E(a0 + ëa1 +
ë2a2 +
ë3a3)
--2ë(c0
+ ëc1 +
ë2c2 +
ë3c3) = 0.
(2.25)
Nous regroupons les équations
(2.23), (2.24)
et (2.25) en puissance de ë
et
nous posons par la suite que les différents
coefficients associés à ëi
(i = 0, 1,
2, 3) sont nuls. nous obtenons les équations
suivantes :
a0t +
c0E + b0E =
0 (2.26)
a1t +
c1E + b1E =
0 (2.27)
a2t +
c2E + b2E =
0 (2.28)
a3t +
c3E + b3E =
0 (2.29)
Ez -- b0t +
2Ea0 = 0 (2.30)
b1t + 2b0 +
2Ea1 = 0 (2.31)
b2t + 2b1 +
2Ea2 = 0 (2.32)
b3t + 2b2 +
2Ea2 = 0 (2.33)
b3 = 0 (2.34)
Ez -- c0t +
2Ea0 = 0 (2.35)
c1t +
2Ea1 -- 2c0 = 0
(2.36)
c2t +
2Ea2 -- 2c1 = 0
(2.37)
c3t +
2Ea3 -- 2c2 = 0
(2.38)
c3 = 0 (2.39)
Nous résolvons ces équations et
déterminons les valeurs de ai, bi, et ci (i =
0, 1, 2, 3) ainsi
qu'il suit :
?
??????????????????????????????? ?
????????????????????????????????
a0 = d3(EEt -
EEt) + id2|E|2
a1 =
2d3|E|2
a2 = 2id2
a3 = 4d3
b0 = -d3Ett -
2d3|E|2E -
id2Et
(2.40)
b1 =
-2d3Et -
2id2E
b2 =
-4d3E
b3 = 0
c0 = d3Ett +
2d3|E|2E -
id2Et
c1 =
-2d3Et +
2id2E
c2 = 4d3E
c3 = 0
Nous obtenons ainsi les éléments de la
matrice V :
{ A = d3(EEt -
EEt) + id2|E|2 +
2d3ë|E|2 +
2id2ë2 +
4d3ë3
(2.41)
B = -d3Ett -
2d3|E|2E -
id2Et - 2d3ëEt
- 2id2ëE -
4d3ë2E
C = d3Ett +
2d3|E|2E -
id2Et - 2d3ëEt
+ 2id2ëE -
4d3ë2E
Ainsi nous avons ramené notre problème
non linéaire représenté par
l'équation
(2.1) en un problème
linéaire grâce à la construction de la paire de Lax
associée.
2.4 Solution Soliton
Une des solutions simples de l'équation (2.1) est
une solution onde plane définie par [13].
r(z) i4,
(2.42)
q =
Acld2(z)
exp[zwet
+k(
. ik(z)],
ø1,z,z
Aø101
Bø20 (2.50
ø2,t24
Cø1O - Aø202
oil
k(z) =
(2A2c -
ù2c)D2(z)
+
ùc(6A2c
-
ù2c)D3(z),
(2.43)
D2,3(z)
= f0z
d2,3(î)dî
représente la dispersion totale accumulée ; Ac et
ùc représentant les coefficients arbitraires
d'amplitude et de fréquence, respectivement.
L'équation (2.17) se met sous la forme :
{
q r
ø1,t =
ëø1 -
d2qø2
(2.44)
ø2,t =
\/cr
i2 qø1 - ëø2
ceci nous conduit à l'équation
différentielle de second dégré définie par la
relation suivante
r r
1,tt =
ëø1,t - qtø2 -
qø2,t (2.45)
d2 d2
En tenant compte de l'équation (2.42),
l'équation (2.45) se met sous la forme :
ø1,tt -
iùcø1,t +
(iùcë +
Ac2 -
ë2)ø1 = 0
(2.46) qui est une équation différentielle de
second d'ordre à coefficient constant. La recherche des
solutions de cette équation nous donne :
ø1 =
(ä1exp(iMR +
iMI
2 ) +
ä2exp(-iMR +
iMI
2 ))exp(iùct +
k
2 ), (2.47)
De même,, nous déduisonss
ø22 sous la forme :
ø22 =
(D1exp(iMRR
+iMI) )+
+D2exp(-iMR
R+
+iMI))exp(-iùct
t+ +kk2 2), '(2.48))2 22
2
oil
1 (ë - iùc 2 -
iMR + iMI
D1 = 2
)ä1,
Ac 2
1(ë - iùc 2 +
iMR + iMI
D2 = 2 )ä2,
(2.49)
Ac
La recherche des constante
ä181 e
ä262 se fai à l'aidede d
l'équationon (2.17) qu s'écritit
L'insertion des solutions ø1 et
ø2 dans l'équation (2.50) conduit aux
équations différentielles
vérifiées par ä1 et
ä2 suivantes :
|
oil
|
|
ä1,z
=[-ikz2 + Ð1 + Ð2
1Ac(ë -
iùc2 - i
MR-rinä1
ä2,z
= [-ikz 2+ Ð1 + Ð2
1Ac(ë -
iùc2 +
iMRrnä2
|
(2.51)
|
Ð1 =
(iA2c +
2ië2)d2 +
(2iA2cùc
+
2A2cùcë
+ 4ë3)d3,
Ð2 = (Acùc -
2iëAc)d2 +
(Acù2c
- 2iëAcùc -
4ë2Ac)d3.
(2.52)
La résolution du système d'équation
(2.51) nous donne :
ä1 =
ä01exp(â1
2 D2 + â2 2
D3 - iâ3 2
D2 + â4 2
D3 + ã),
ä2 =
ä02exp(-â1
2 D2 - â2 2
D3 + iâ3 2
D2 - â4 2
D3 + ã), (2.53)
avec
zrã =
=[ikzzÐ1 i+
+ !lÐ2(ë -
iù)]dæ..11
02 22
2ëA =
-As/2+iùs/2,,
a =
-2AcAs/(A2s
+M2R),,
b =
-2AcMR/(A2s2+M2R),,
c =MI/As, â11
= AsMRR + (ùss +
ùc)MI,, â22 =
(ùcc + 2ùs)AsMRR ---
mMI,,
â33 =
(ùss +
ùc)MRR --- AsMI â44 =
mMR + (ùce +
2ùs)AsMI,,
m
= 2Ac2+#177;A2 s
-ùcùss ---
ù2c2---
ù2s,,
MR
+ iMII = [(ùce ---
ùss --- iAs) 2 +
4Ac2]1/2
Les constantes d'intégrationn
ä01, et
ä022 sont prises sous la forme
ä01, =
exp(è00 ---
i?0oè0
0- --i?0o2
2
), ,
ä02
2
=
=
exp(
( 2 ),'
oil è00 et ?0o
sont des constantes réelless arbitraires.
En substituant les expressions ä16
et ä16 dans (2.47) et (2.48) nous avons en
definitive :
ø1. =
eã22
[exp((MItt --- â1D22
- â2D33 - è0)
--- i(MRt --- â3D22 +
â4D33 - ?0)))
+exp(-(MIt -
â1D2 -
â2D3 - è0) +
i(MRt - â3D2 +
â4D3 - ?0))],
(2.54)
et
7 , 1 i 2 2
--As + MI ùs -
ùc - MR
ø2 = e 2
[A i
)exp((MIt-O1D2 -
â2D3 - è0) -
i(MRt
cl
1 (-As - MI +
iùs - ùc
+ MR
-â3D2 +
â4D3 - ?0)) + 2
)exp(-(MIt -
â1D2
Ac
2-â2D33 ---
è0)) + i(MRt ---
â3D22 +
â4D33 ---
?0))].. (2.55)
Les solutions (2.54) et (2.55), étantt ainsi
obtenues, nous déterminonss la solution de l'équationn de
Schrödingerr non linéairee d'ordree supérieurr en utilisant
la transformation de Darboux définiee par [13, 14] :\I
q1 i= =q q- --2
2d2(z))(ë
A+
+ë))øTTø22(2.56))øoø0r(z)
)
oil
øøTT =
|ø1|22
+|ø2|2..
En remplaçantt (2.54) et (2.55) dans
l'équationn (2.56) tout en tenant compte de (2.42),
nous obtenons la nouvelle solution q1i donnée& par
la relation :
|
avec
|
q1i =
|
\I
d2(z)QQ(zz,,t)exp(ii?)),
,(2.57))r(z) )
|
acoshè1 + cos?1 +
i(bsinhè1 +
csin?1)
coshè1 O+
acos?1p,
Q(z, t) =
Ac + A
è101 = M -
â1D2(z)z -
â2D3(z)z -
è0,o, (2.58
?1P1 = MR -
â3D2(z)z)
â4D3(z)z -
?0,o
?cp ùctet
k(z). .
Pour une amplitud évanescentet (c'ests à a
dir AcA, = 0) d l'ondede plane, la
solution
( 2.57) s réduiti à a la solution
solitoqsol o=
AsAd2(z)z)
r(z
sech(ès)exp(i?s),),
(2.59
avec
ès =
As[t -
2ùsD2(z) -
(3ù2 s -
A2
s)D3(z)] -
è0,
?s =
ùst - (ù2 s
- A2
s)D2(z) +
ùs(3A2 c -
ù2
s)D3(z) -
?0.
qui est une fonction sécante hyperbolique
caractéristique des solutions solitons de l'équation SNL.
L'amplitude maximale et la vitesse de groupe du soliton (2.59) /sont
données respectivement par As
d2(z)/r(z)
et Vs =
2ùsd2(z) +
(3ù2 s - A2
s)d3(z).
Il vient que sous la généralisation des
conditions d'Hirota les termes d'ordre supérieur affectent la vitesse et
par conséquent la phase du soliton. L'expression de l'amplitude
révèle que les termes d'ordre superieur sont sans influence sur
l'amplitude de la solution soliton. Nous pouvons donc contrôler la
vitesse du soliton en jouant sur les paramètres
d2(z) et
d3(z), l'amplitude à partir des
paramètres d2(z) et
r(z).
Dans le souci de se rapprocher de la pratique, et de
mieux décrire la dynamique de la solution soliton, les coefficients
d2(z),
d3(z), et r(z)
sont pris sous la forme [13] :
|
d2(z) =
ã1[1 +
o1sin(óz)]exp(-g1z)
|
(2.60)
|
|
r(z) =
ã2[1 +
o2sin(óz)]exp(-g2z)
|
(2.61)
|
|
d3(z) =
ã3[1 +
o3sin(óz)]exp(-g3z)
|
(2.62)
|
oil ãi, oi et gi sont des constantes pour i
= 1, 2, 3.
Dans le cas oil o1 = o2 =
o3 = 0 les équations (2.60), (2.61) et (2.62)
correspondent au contrôle par modulation exponentielle des
paramètres [12, 13, 16]. L'amplitude du soliton (2.59) se met alors sous
la forme :
j
ã1[1 +
o1sin(óz)]
A(z) = As
ã2[1 +
o2sin(óz)]exp[(g2
- g1)z/2], (2.63)
La courbe suivante présente l'évolution de
l'amplitude (2.63) pour des cas g1 >
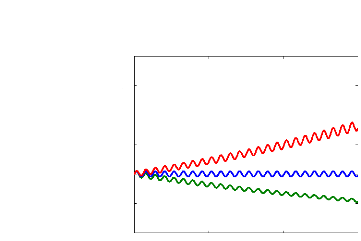
g2,; g1 <
g2 et g1 = g2.
0 5 10 15 20 25 30
Amplitude
2.5
0.5
1.5
2
3
0
1
Distance z
FIG. 2.2 - Évolution de l'amplitude (2.63) en fonction
de la distance Z, pour les cas g1 = 0.05,
g2 = 0.01; g1 =
0.01, g2 = 0.05 et
g1 = g2 = 0.01 ( avec
Ac = 1,ã1 =
ã2 = 1,o1 =
0.05, o2 =
-0.04 et ó = 5)
Pour une situation beaucoup plus
générale oil Ac =6 0
avec la pulsation de la solution soliton égale à la
pulsation de l'onde plane initiale (ùc =
ùs = ù ) et A2 c >
A2
s/4, l'équation (2.57)
s'écrit encore
|
avec
|
q1 =
|
sd2(z)
r(z)
QMI(z,t)exp(i?),
(2.64)
|
QMI(z,t) =
Ac + As
Ascoshè1 -
2Accos?1 +
iMRsinhè1
2Accoshè1 -
Ascos?1
,
(2.65)
oil
è1 =
AsMR[D2(z) +
3ùD3(z)] -
è0,
?1 = MRt -
MR[2ùD2(z) +
(3ù2 - 2A2
c - A2
s)D3(z)] -
?0,
? = ùt +
(2A2 c -
ù2)D2 +
ù(6A2 c -
ù2)D3,
/MR =
4A2c -
A2s.
La solution donnée par l'équation (2.64)
avec les coefficients donnés en (2.65) montre que cette solution est
périodique suivant t et de période L définie
par
2ð
L = . (2.66)
MR
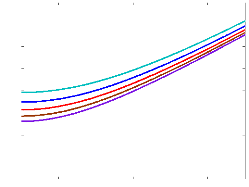
Ainsi, le contrôle de la période peut
s'effectuer à partir des amplitudes Ac et As. la
figure (2.3) montre l'évolution de l'amplitude Ac en fonction
de l'amplitude As pour diverses valeurs de la
période.
0 0.2 0.4 0.6 0.8 1 1.2
Amplitude Ac
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Amplitude As
FIG. 2.3 - Évolution de l'amplitude
Ac en fonction de l'amplitude
As pour L = 8,
9, 10, 11 et 12
2.5 Solution soliton en absence du mode linéaire
La propagation dans les fibres optiques s'accompagne
le plus souvent des modes linéaires. Ces modes linéaires sont
indésirables pour la propagation [13]. Pour mieux décrire la
dynamique de la solution de l'équation de Schrödinger
d'ordre
supérieur, la solution correspondante au mode
linéaire doit être soustraite de la solution
(2.64). Ce mode linéaire est pris sous la forme [13],
qB = \Id2
(z)
QB(z,t)exp(i?),
(2.67)
r(z)
oil
Ascoshè1 +
2Ac - iMRsinhè1
QB(z, t) =
Ac - As, (2.68)
2Accoshè1 +
As
on obtient
d2 (z)
qT = \I r(z)
QT(z,t)exp(i?),
(2.69)
oil
AsMR(MRcoshè1
+ iAssinhè1)(1 +
cos?1)
QT(z,t)
=.(2.70) (2Accoshè1 +
As)(2Accosh?1 -
Ascos?1)
L'énergie E(z)
et la largeur à mi-hauteur (full-width at half-maximum "FWHM")
ô(z) de la solution
donnée par l'équation (2.69) sont données respectivement
par les expressions suivantes :
(2.71)
E(z) =
qT(z,t)|2dt
=
2ðMRd2(z)
I(z)
r(z)
0
oil
I z =
2Accohè1 -
As2Accohè1
- 2As
(2.72
()
)
2Accohè1 + As V
4i*osh2è1
- A2s
et
2 1 2(v2 -
1)Accoshè1 +
As,
ô(z) =
cos- [ j (2.73)
MR 2Accoshè1
+ (v2-
1)As.
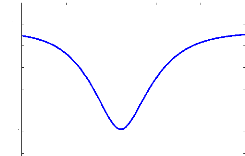
Les figures (2.4) et (2.5) présentent
respectivement l'évolution de la largeur à mihauteur et de
l'énergie en fonction de la distance z pour As =
1.1, As =
0.65, ù = 0,
è0 = 0, ?0 = 0, ã1 =
ã2 = 0.5,ã3 =
0.01, g1 = g2 =
g3 = 0.001, ó =
5, å1 = 0.05,
å2 = -0.04 et
å3 = 0.02.
FWHM
3.5
2.5
0.5
1.5
4
3
2
1
0
0 5 10 15 20 25
Distance z
FIG. 2.4 - Évolution de la largeur à mi-hauteur
en fonction de la distance z
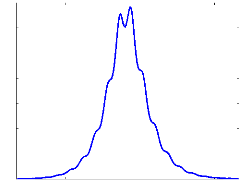
Energie E
4
2
7
6
5
3
0
1
0 5 10 15 20
Distance z
FIG. 2.5 - Évolution de l'énergie en fonction de
la distance z
Il ressort de ces deux courbes que pour z =
11, la largeur à mi-hauteur est minimale et qu'en ce même
point l'énergie se trouve dans un état stable. Nous pouvons donc
déduire que la solution donnée par l'équation (2.69)
présente une forte stabilité à la distance z =
11.
2.6 Conclusion
Cette partie nous a permis dans un premier temps de
retrouver les conditions d'Hirota satisfaites par l'équation de
Schrödinger non linéaire d'ordre supérieur. La
méthode AKNS nous a permis par la suite et au moyen de la transformation
de Darboux de trouver la solution analytique de cette équation et sous
certaines conditions la solution soliton. Enfin, il ressort de la solution
soliton obtenue que les termes d'ordre supérieur affectent la vitesse et
la phase du soliton mais sont sans effet sur l'amplitude du
soliton.
Nous nous intéresserons dans la suite à
rechercher les solutions solitons dans les modèles à deux
dimensions, modèlisés par les équations couplées de
Schrödinger non linéaires.
CHAPITRE TROIS
CoNsTRuCTioN DE LA pAiRE DE LAX pouR LEs MoDELEs CoupLEs
3.1 Equations couplées de Schrödinger non
linéaires
Lorsque la lumière se déplace dans le
guide d'onde formé par la fibre optique, divers
régimes de propagation correspondant à divers modes coexistent.
Afin d'éviter la dispersion modale en télécommunication
par fibres optiques, le choix est de restreindre la taille du
coeur de la fibre de sorte qu'à la longueur d'onde
considérée, seul le mode fondamental existe. En
réalité, il subsiste encore deux modes de
polarisations orthogonales et deux équations sont nécessaires
pour décrire leur évolution. Pour parvenir
à ces équations, on effectue les hypothèses qui
suivent.
- Les effets non linéaires peuvent être
traités comme une perturbation qui ne modifie pas
profondément la distribution transverse des modes de la
fibre.
- L'étalement du spectre est fortement
limité par rapport à la valeur de sa
fréquence centrale. Cette supposition permet de pratiquer
l'approximation de l'" enveloppe lentement variable " le long
de la distance de propagation.
- La réponse du milieu est instantanée. De
plus, nous supposons que le modèle ignore donc l'effet
Raman.
En tenant compte de ces hypothèses,
l'équation modélisant la propagation dans une
fibre optique se met sous la forme du modèle couplé [15]
:
|
iuz =
-d2(z)utt -
2á(z)(|u|2
+ |v|2)u +
i(z)u
(3.1)
ivz =
-d2(z)vtt -
2á(z)(|u|2
+ |v|2)v +
i(z)v
|
|
?
U = ?
|
ëI-Q R-ëI
|
?
?,
|
(3.9)
|
oil u et v représentent les champs se propageant
dans le modèle.
Le paramètre d2
représente le coefficient de la dispersion de la vitesse de
groupe. Il est dû à la variation de vitesse entre les diverses
composantes de fréquence constituant l'impulsion. á est le
coefficient de non linéarité et le coefficient
de perte ou d'amplification.
3.2 Phénomènes décrits par un
système couplé d'équations de Schrödinger non
linéaires
Les équations (3.1) décrivent aussi la
propagation optique dans d'autres milieux que les fibres optiques isotropes.
Dans cette section, nous en présenterons quelques uns. Pour le premier,
nous resterons dans le domaine des fibres optiques mais nous lèverons
l'hypothèse d'isotropie. Ensuite, nous évoquerons d'autres
domaines oil des phénomènes pourront être
modélisés par les équations de Schrödinger non
linéaires couplées.
3.2.1 Propagation de deux ondes de couleurs
différentes
Le cas qui se rapproche sans doute le plus de celui
que nous avons présenté ci-dessus est celui oil l'on injecte dans
une fibre optique deux ondes différentes et qu'on étudie leur
propagation dans l'approximation scalaire. En régime de propagation
linéaire, les deux fréquences n'interagiraient pas. Lorsque les
effets non linéaires sont pris en compte, on peut montrer qu'il
apparaît un terme d'intermodulation de phase (modulation de phase
croisée). Les équations décrivant la propagation peuvent
se ramener à un système de la forme (3.1) [15].
3.2.2 Autres phénomènes
Les premiers résultats concernant les
équations de Schrödinger non linéaires furent obtenus dans
le cadre de la théorie des plasmas [4, 15]. Dans ce cadre, ces
équations décrivent la propagation d'ondes
électromagnétiques dans un plasma homogène et isotrope
à température nulle [4, 15]. Cette dernière
hypothèse permet de négliger le mouvement des ions et de
considérer une non linéarité d'origine
électronique. En restant dans ce domaine de la physique, on peut
mentionner que les équations de Schrödinger non linéaires
cubiques couplées décrivent l'interaction entre deux ondes de
polarisations transverses orthogonales dans un plasma. Ces équations
s'appliquent aussi à un système de deux fermions à une
dimension spatiale et permettent de décrire la fonction d'onde des
condensas de Bose-Einstein [4, 15].
3.3 Construction de la paire de Lax
Le système d'équations (3.1) n'est en
général pas intégrable. Néanmoins, sous certaines
conditions cette équation devient totalement
intégrable.
En tenant compte de la condition d'Hirota definie par
:
d2,zr - rzd2
= , (3.2)
2rd2 / /
et en faisant le changement de variable q =
á/d2u et r =
á/d2v le systéme d'équations
(3.1) se met sous la forme :
|
iqz =
-d2(z)qtt -
2á(z)(|q|2
+ |r|2)q
(3.3)
irz =
-d2(z)rtt -
2á(z)(|q|2
+ |r|2)r
|
Cette dernière forme (équation 3.3) est
totalement intégrable [16, 17] pour d2 =
á
(après analyse de Painlevé). Sous cette
condition en déterminant les équations
vérifiées par les fonctions q et r
conjuguées on obtient le système d'équation :
|
En posant
|
?
???????
???????
|
iqz =
-d2(z)qtt -
2d2(z)(|q|2
+ |r|2)q irz =
-d2(z)rtt -
2d2(z)(|q|2
+ |r|2)r -iqz =
-d2(z)qtt -
2d2(z)(|q|2
+ |r|2)q -irz =
-d2(z)rtt -
2d2(z)(|q|2
+ |r|2)r
|
; (3.4)
|
? ?
q r
Q
= ?) , (3.5)
r -q
|
?
R = ?
|
q r
r -q
|
?
?.
|
(3.6)
|
le système d'équation (3.4) peut se mettre
sous la forme matricielle donnée par l'équation suivante
:
iQz =
-d2(z)Qtt -
2d2(z)QRQ =
0. (3.7)
Etant donné que R = Q, l' équation (3.7)
vérifiée par Q est une équation non linéaire
cubique de Schrödinger de la forme:
iQz =
-d2(z)Qtt -
2d2(z)|Q|2Q
. La paire de Lax se constuit en posant :
øt = Uø
øz = V ø
(3.8)
Où ø =
(ø1,ø2)T
représente la fontion propre associée à la valeur propre
ë (T étant la transposée); U et V deux matrices
définies par :
|
V = (A B ? .
C --A
|
(3.10)
|
Oil I est la matrice unité d'ordre deux ; A, B et
C les matrices définies par :
|
{
|
A = a0 +
ëa1 + ë2a2
B = b0 +
ëb1 +
ë2b2
C = c0 +
ëc1 + ë2c2
|
(3.11)
|
Les matrices U et V vérifient l'équation de
compatibilité donnée par la relation : Uz --
Vt + [U, V ] = 0. (3.12)
Nous remplaçons U et V par leurs expressions
données par les équations (3.9)
et (3.10) et tenons compte du fait
que [U,V ] = UV -- V U. L'équation de
compatibilité se met donc sous la forme :
At Bt -- Qz Ct
+ Rz --At
?
?

. (3.13)
? --CQ -- BR 2B+ 2QA
0 0( 2RA -- 2Cë RB
+ QC ) ( 0 0 )
Nous remplaçons A, B et C par leurs expressions
données par l'équation
(3.11), ainsi l'équation de
compatibilité permet d'obtenir :
--a0t --
ëa1t --
ë2a2t --
Q(c0 + ëc1 +
ë2c2) --
R(b0 + ëb1 +
ë2b2) = 0 (3.14)
Qz -- b0t -- ëb1t --
ë2b2t +
2ë(b0 + ëb1
+ ë2b2) +
2Q(a0 + ëa1 +
ë2a2) = 0 (3.15)
Rz -- c0t -- ëc1t --
ë2c2t +
2R(a0 + ëa1 +
ë2a2) --
2ë(c0 + ëc1
+ ë2c2) = 0
(3.16)
Nous regroupons les équations
(3.14),(3.15)
et (3.16) en puissance de ë et
nous posons par la suite que les différents coefficient
à ëi (i = 0,
1, 2, 3) sont nuls. On
obtient les équations suivantes :
a0t +
c0E + b0R =
0 (3.17)
a1t +
c1Q + b1R =
0 (3.18)
a2t +
c2Q + b2R =
0 (3.19)
-Qz - b0t +
2Qa0 = 0 (3.20)
-b1t + 2b0 +
2Qa1 = 0 (3.21)
-b2t + 2b1 +
2Qa2 = 0 (3.22)
b2 = 0 (3.23)
Rz - c0t +
2Ra0 = 0 (3.24)
-c1t + 2Ra1
- 2c0 = 0 (3.25)
-c2t + 2Ra2
- 2c1 = 0 (3.26)
c2 = 0 (3.27)
Nous résolvons ces équations et
déterminons les valeurs de ai, bi, et ci (i =
1, 2, 3) ainsi qu'il suit
:
?
?????????????????????? ?
???????????????????????
a0 = id2QR
a1 = 0
a2 = 2id2I
b0 = -id2Qt
(3.28)
b1 =
-2id3Q
b2 = 0
c0 = -id2Rt
c1 = 2id2R
c2 = 0
Nous obtenons ainsi les éléments de la
matrice V :
?
????
????
A = id2QR +
2ië2d2I
(3.29)
B = -id2Qt -
2iëd2Q
C = -id2Rt +
2iëd2R
Nous remplaçons les expressions des matrices A,
B et C dans la paire (U, V) et en tenant compte des
expressions de Q et R données par les équations (3.5) et
(3.6), nous obtenons finalement les matrices U et V suivantes
:
|
U =
|
[
|
ë 0 -q -r
0 -ë -r q
q r -ë 0
r -q 0 ë
|
]
|
(3.30)
|
|
V =
|
[
|
id2(|q|2 +
|r|2) 0 -id2qt
-id2rt
0 id2(|q|2 +
|r|2) -id2rt
id2qt
- id2qt
-id2rt -id2(|q|2 +
|r|2) 0
- id2rt id2qt
0 -id2(|q|2
+|r|2)
|
]
|
|
+ë
|
[
|
0 0 -2id2q
-2id2r
0 0 -2id2r
2id2q
2id2q
2id2r 0 0
2id2r
-2id2q 0 0
|
]
|
+ ë2
|
[
|
2id2 0 0 0 0 2id2 0 0
0 0 0 0
0 0 0 0
|
]
|
. (3.31)
|
Où U est une matrice carrée d'ordre 4,
de même que la marice V. À la suite de cette
construction, une recherche éventuelle des solutions de
l'équation couplée de Schrödinger non
linéaire est envisageable.
3.4 Conclusion
Dans cette partie nous avons présenté
l'équation de Schrödinger non linéaire
couplée comme une équation modélisant la
propagation des solitons dans les fibres optiques dans le cas
où on tient compte de deux modes de polarisations. Par la
suite, nous avons énuméré quelques
phénomènes physiques pouvant être
modélisés
par le modèle couplé. Enfin la
construction de la paire de Lax de l'équation de Schrödinger non
linéaire couplée dans le cas oil elle est totalement
intégrable est une avancée dans la recherche des solutions
analytiques de ce modèle couplé par la méthode
AKNS.
Conclusion générale et perspectives
Au cours de cette étude, nous avons dans un
premier temps modélisé la propagation de l'onde solitaire dans la
fibre optique, ceci en partant des équations de Maxwell. Il ressort que
le système est modélisé par l'équation de
Schrödinger non linéaire d'ordre supérieur. La recherche de
la solution de cette équation par la méthode AKNS nous a conduit
à un soliton du type pulse. L'analyse de cette solution soliton montre
que les effets d'ordre supérieur influence sa vitesse et sa phase et est
sans action sur son amplitude. Nous avons aussi montré que dans le cas
oil la pulsation de la solution soliton est égale à celle de
l'onde plane initiale (ùc =
ùs = ù) et A c > A
s/4; La solution soliton est périodique suivant t
et de période L donnée par L = 2ð/MR. Cette
période peut être modulée à partir des amplitudes de
la solution onde plane (Ac) et de la solution soliton
(As).
Après ce premier travail nous nous sommes
intéressés à la construction de la paire de Lax
associée à l'équation de Schrödinger non
linéaire couplée. Ceci constitue un point de départ dans
la recherche de la solution soliton de cette dernière équation
par la méthode AKNS. Il est à noter que cette équation
modélise la propagation de l'onde solitaire dans la fibre lorsqu'on
tient compte des deux composantes du champ électrique.
Au terme de ce travail, nous pouvons dire que bien
d'autres aspects restent inconnus. C'est ainsi qu'il serait intéressant
dans un avenir proche de rechercher les solutions de l'équation de
Schrödinger non linéaire couplée. On pourra
aussi
examiner un cas beaucoup plus général
modélisé par les équations couplées de
Ginzburg-Landau complexe. Enfin notre étude pourra être
étendue à d'autres domaines aussi variés oil de nombreux
phénomènes Physiques peuvent être modélisés
par les équations précédemment
mentionnées.
Bibliographie
[1] René Parfait "Les réseaux de
télécomunications" Lavoisier, Paris, Hermes (2002).
[2] A. Hasegawa and Y. Tappert, Appl. Phys. Lett. 23
(1973) 142.
[3] T.C. Kofane "Excitation non linéaire et
Structures cohérentes" cours de DEA de Physique, Université de
Yaoundé I (2007).
[4] M. Perard, and T. Dauxois "Physique des Solitons"
Ed. EDP Sciences CNRS (2004) 254.
[5] G.P. Agrwal, Nonlnear Fiber Optics, Academic press,
New York (1995).
[6] B. Dya " Etude de la propagation optique dans une
structure de fibre optique en presence des microdéformations
périodiques" Université de Batna (1998).
[7] L. Li, Z. Li, Z. Xu, Z. Li and G. Zhuo , J. phys. A.
Math. Gen. 36 (2003) 817.
[8] S. Zekeng "Électromagnétisme et
relativité restreinte" cours de DEUG de Physique, Université de
Yaoundé I (2003).
[9] P. Lax "Integrals of nonlinear equations of
evolution and solitary waves" Commun. Appl. Math. 21 (1968) 467.
[10] M.J. Ablowitz and P.A. Clarkson "Soliton, Nonlinear
Evolution Equations and Inverse Scarttering" Cambridge University Press,
Cambridge (1991).
[11] Y.S. Kivshar and B. Malomed , Review of Modern
Physics 61 (1989) 763.
[12] R.Y. Hao, L. Li, and S. Zhou, Phys.Rev. E 70 (2004)
066603.
[13] J. Wang, L. Li, Z. Li , G. Zhou, D. Mihalache and
B. Molomed, Opt Commun 263 (2006) 328.
[14] Z.Y. Xu, L. Lu, Z. Li and S. Zhou, Opt Commun 210
(2002) 375.
[15] M. Haelterman " Dynamique non linéaire
vectorielle de la propagation lumineuse en fibre optique" Université
libre de Bruxelles (2000 - 2001).
[16] V.I. Kruglov, A.C. Peacock and J.D. Harvey, Phys.
Rev. Lett. 90 (2003) 113902.
[17] T. Tsuchida and M. Wadati, J. Phys. Soc. Jpn. 67
(1998) 1175.
| 


