Dynamique non lineaire du pulse dans une fibre optique

2.2 Conditions d'Hirota

Nous rappelons l'équation de SNL avec les termes d'ordre superieur obtenue dans la premiere partie.

iq_z = -d2(z)qtt - 2r(z)|q|²q + id3(z)qttt + iá(z)(|q|²q)t

+if(z)q(|q|²)t + i(z)q. (2.1)

Cette équation n'étant généralement pas intégrable, nous l'analysons en considérant la solution approchée donnée par l'expression [12] :

_r

d2

q1(z, t) = ç1(z) r exp(iö1)sechè1, (2.2)

avec

è1 = ç1(z)[t + ñ(z)],

ö1 = î1t + ù(z). (2.3)

Où ç1(z), ñ(z), î1 et ù(z) sont rattachés respectivement à l'inverse de la largeur, la vitesse de groupe, la fréquence propre et la phase de l'onde. En substituant

l'équation (2.2) dans l'équation (2.1) et en posant g = Vd2/r, on obtient une équation de la forme :

G + iH = 0, (2.4)

avec

G = (î^'t + ù^')çg cosh² è + d2çî²g cosh² è - d2ç³g(-1 + sinh² è) - 2rç³g³

+d3çç³g cosh² è - 3d3ç³îg(-1 + sinh² è) - áç³îg³, (2.5)
H = (ç^'g+çg^'-Fçg) cosh² è-[(ç^'t+ç^'ñ+ñ^'ç)çg+2d2ç²îg+3d3ç²î²g] sinh è cosh² è

-(5d3ç⁴g - 3áç⁴g³ - 2fç⁴g³) sinh è + d3ç⁴g sinh³ . (2.6)

Nous linéarisons l'équation (2.5) et (2.6), et nous obtenons les équations suivantes :

ç^'g + çg^' - Fçg = 0, (2.7)

(ç^'t +ç^'ñ +ñ^'ç)çg +2d2ç²îg +3d3ç²î²g -d3ç4g =0, (2.8)

(ç^'t +ç^'ñ+ñ^'ç)çg +2d2ç²îg +3d3ç²î²g -d3ç⁴g +5d3ç⁴g -3áç⁴g³ -2fç4g3 =0,

	(2.9)
(î^'t + ù^')çg + d2çî^2g + d3çî^3g - d2ç^3g - 3d3ç^3îg = 0, (î^'t + ù^')çg + d2çî^2g + d3çî^3g + d2ç^3g + 3d3ç^3îg - 2rç^3g^3 - áç^3g^3 = 0.	(2.10) (2.11)
En posant ç constant l'équation (2.7) nous conduit à :
F= d2,zr - rzd2	(2.12)
. 2rd2

Nous sommons les équations (2.8) et (2.9) et nous faisons la difference des équations (2.10) et (2.11). Nous obtenons respectivement les relations suivantes :

6rd3 = (3á + 2f)d2, (2.13)

f + á = 0. (2.14)

Les équations (2.12), (2.13) et (2.14) encore appelées conditions d'Hirota. Ces conditions montrent que l'absorption (ou l'amplification) peut être contrôlée à travers les autres coefficients d2, d3 et r. .

2.3 Construction de la paire de Lax associée à l'équation de Schrödinger non linéaire d'ordre supérieur

En tenant compte des conditions d'Hirota données par les équations (2.12), (2.13) et (2.14), que nous remplaçons dans l'équation (2.1) et en faisant le changement de variable

V r

E = q, (2.15)

d2

l'équation (2.1) se met sous la forme :

iE_z = -d2Ett - 2d2|E|²E + id3Ettt + 6id3|E|²Et. (2.16)

La paire de Lax associée à l'équation (2.16) est construite ainsi qu'il suit :

? ? ?

øt = Uø øz = V ø

(2.17)

où ø = (ø1,ø2)^T represente la fonction propre associée à la valeur propre ë (T étant la transposée); U et V étant deux matrices definies par :

? U = ?

ë -E E -ë

? ?,

(2.18)

et

?

V=_?

) .

(2.19)

A B C --A

oil E est la conjuguée de E ; A, B et C des polynômes définis par :

{

A = a0 + ëa1 + ë²a2 + ë³a3

(2.20)

B = b0 + ëb1 + ë²b2 + ë³b3

C = c0 + ëc1 + ë²c2 + ë³c3

oil les coefficients ai, bi et ci (i = 0, 1, 2, 3) sont à déterminer.

Les matrices U et V vérifient l'équation de compatibilité donnée par la relation :

Uz -- Vt + [U, V ] = 0. (2.21)

(

Nous remplaçons U et V par leurs valeurs données par les équations (2.18) et (2.19) et tenons compte du fait que [U, V ] = UV -- V U. L'équation de compatibilité se met donc sous la forme :

At Bt -- E_z

Ct + E_z --At ) + ( --CE -- BE 2Bë + 2EA ) ( 0 0 )

2EA -- 2Cë EB + EC 0 0 . (2.22)

Nous remplaçons A, B et C par leurs expressions données par l'équation (2.20), ainsi l'équation de compatibilité permet d'obtenir :

^--a0t -- ëa1t -- ë²a2t -- ë³a3t -- E(c0 + ëc1 + ë²c2 + ë³c3)

--E(b0 + ëb1 + ë²b2 + ë³b3) = 0, (2.23)

E_z -- b0t -- ëb1t -- ë²b2t -- ë³b3t + 2ë(b0 + ëb1 + ë²b2 + ë³b3)

+2E(a0 + ëa1 + ë²a2 + ë³a3) = 0, (2.24)

E_z -- c0t -- ëc1t -- ë²c2t -- ë³c3t + 2E(a0 + ëa1 + ë²a2 + ë³a3)

--2ë(c0 + ëc1 + ë²c2 + ë³c3) = 0. (2.25)
Nous regroupons les équations (2.23), (2.24) et (2.25) en puissance de ë et

nous posons par la suite que les différents coefficients associés à ëⁱ (i = 0, 1, 2, 3) sont nuls. nous obtenons les équations suivantes :

a0t + c0E + b0E = 0 (2.26)

a1t + c1E + b1E = 0 (2.27)

a2t + c2E + b2E = 0 (2.28)

a3t + c3E + b3E = 0 (2.29)

E_z -- b0t + 2Ea0 = 0 (2.30)

b1t + 2b0 + 2Ea1 = 0 (2.31)

b2t + 2b1 + 2Ea2 = 0 (2.32)

b3t + 2b2 + 2Ea2 = 0 (2.33)

b3 = 0 (2.34)

E_z -- c0t + 2Ea0 = 0 (2.35)

c1t + 2Ea1 -- 2c0 = 0 (2.36)

c2t + 2Ea2 -- 2c1 = 0 (2.37)

c3t + 2Ea3 -- 2c2 = 0 (2.38)

c3 = 0 (2.39)

Nous résolvons ces équations et déterminons les valeurs de ai, bi, et ci (i = 0, 1, 2, 3) ainsi qu'il suit :

?

??????????????????????????????? ?

????????????????????????????????

a0 = d3(EEt - EEt) + id2|E|²

a1 = 2d3|E|²

a2 = 2id2

a3 = 4d3

b0 = -d3Ett - 2d3|E|²E - id2Et

(2.40)

b1 = -2d3Et - 2id2E

b2 = -4d3E

b3 = 0

c0 = d3Ett + 2d3|E|²E - id2Et

c1 = -2d3Et + 2id2E

c2 = 4d3E

c3 = 0

Nous obtenons ainsi les éléments de la matrice V :

{ A = d3(EEt - EEt) + id2|E|² + 2d3ë|E|² + 2id2ë² + 4d3ë³

(2.41)

B = -d3Ett - 2d3|E|²E - id2Et - 2d3ëEt - 2id2ëE - 4d3ë²E

C = d3Ett + 2d3|E|²E - id2Et - 2d3ëEt + 2id2ëE - 4d3ë²E

Ainsi nous avons ramené notre problème non linéaire représenté par l'équation
(2.1) en un problème linéaire grâce à la construction de la paire de Lax associée.

2.4 Solution Soliton

Une des solutions simples de l'équation (2.1) est une solution onde plane définie par [13].

r(z) i4, (2.42)

q = A_cl^d2(z) exp[zw_et +k(

. ik(z)],

ø1,z,z Aø101 Bø20 (2.50

ø2,t24 Cø1O - Aø202

oil

k(z) = (2A²_c - ù²_c)D2(z) + ù_c(6A²_c - ù²_c)D3(z), (2.43)

D2,3(z) = f0z d2,3(î)dî représente la dispersion totale accumulée ; A_c et ù_c représentant les coefficients arbitraires d'amplitude et de fréquence, respectivement. L'équation (2.17) se met sous la forme :

{

q r

ø1,t = ëø1 - d2qø2

(2.44)

ø2,t = _\/_c^r i2 qø1 - ëø2

ceci nous conduit à l'équation différentielle de second dégré définie par la relation suivante

r r

1,tt = ëø1,t - qtø2 - qø2,t (2.45)

d2 d2

En tenant compte de l'équation (2.42), l'équation (2.45) se met sous la forme :

ø1,tt - iùcø1,t + (iù_cë + A_c² - ë²)ø1 = 0 (2.46) qui est une équation différentielle de second d'ordre à coefficient constant. La recherche des solutions de cette équation nous donne :

ø1 = (ä1exp(iMR + iMI

2 ) + ä2exp(-iMR + iMI

2 ))exp(iùct + k

2 ), (2.47)

De même,, nous déduisonss ø22 sous la forme :

ø22 = (D1exp(iMRR ^+iMI) )+ +D2exp(-iMR ^R+ +iMI))exp(-iùct t+ +kk2 ₂), '(2.48))2 22 2

oil

1 (ë - iùc 2 - _iMR + iMI

D1 = 2 )ä1,

A_c 2

¹(ë - iùc 2 + _iMR + iMI

D2 = 2 )ä2, (2.49)

A_c

La recherche des constante ä181 e ä262 se fai à l'aidede d l'équationon (2.17) qu s'écritit

L'insertion des solutions ø1 et ø2 dans l'équation (2.50) conduit aux équations différentielles vérifiées par ä1 et ä2 suivantes :

oil

ä1,z =[-ikz2 + Ð1 + Ð2 1Ac(ë - i^ùc2 - i^MR^-r^inä1 ä2,z = [-i^kz 2+ Ð1 + Ð2 1Ac(ë - i^ùc2 + i^MRrnä2

(2.51)

Ð1 = (iA²_c + 2ië²)d2 + (2iA²_cù_c + 2A²_cù_cë + 4ë³)d3,

Ð2 = (Acùc - 2iëA_c)d2 + (A_cù²_c - 2iëA_cù_c - 4ë²A_c)d3. (2.52)

La résolution du système d'équation (2.51) nous donne :

ä1 = ä01exp(â1 ₂ D2 + â2 2 D3 - iâ3 2 D2 + â4 2 D3 + ã),

ä2 = ä02exp(-â1 ₂ D2 - â2 2 D3 + iâ3 2 D2 - â4 2 D3 + ã), (2.53)

avec

zrã = =[i^kzzÐ1 i+ + _!lÐ2(ë - i^ù)]dæ..¹¹

₀2 22 ²ëA = -A_s/2+iù_s/2,, a = -2A_cA_s/(A²_s +M²_R),, b = -2A_cMR/(A²_s²+M²_R),,

c =MI/A_s, â11 = AsMRR + (ùss + ùc)MI,, â22 = (ùcc + 2ùs)AsMRR --- mMI,,

â33 = (ù_ss + ùc)MRR --- AsMI â44 = mMR + (ùce + 2ùs)AsMI,,
m = 2Ac2+#177;A2 s -ù_cù_ss --- ù²_c²--- ù²_s,,
MR + iMII = [(ù_ce --- ù_ss --- iA_s) ² + 4A_c²]¹/²

Les constantes d'intégrationn ä01, ^et ä022 sont prises sous la forme

ä01, = exp(è00 --- i?0oè0 ^0- --i?0o2

₂

), ,

ä0₂

₂

=

=

exp(

( 2 ),'

oil è00 et ?0o sont des constantes réelless arbitraires.

En substituant les expressions ä16 et ä16 dans (2.47) et (2.48) nous avons en definitive :

ø1. = e^ã22 [exp((MItt --- â1D22 - â2D33 - è0) --- i(MRt --- â3D22 + â4D33 - ?0)))

+exp(-(MIt - â1D2 - â2D3 - è0) + i(MRt - â3D2 + â4D3 - ?0))], (2.54)

et

7 , 1 i 2 2 --A_s + MI ù_s - ù_c - MR

ø2 = e 2 [_A i )exp((MIt-O1D2 - â2D3 - è0) - i(MRt

_cl

1 ₍-As - MI + _iùs - ù_c + MR

-â3D2 + â4D3 - ?0)) + 2 )exp(-(MIt - â1D2

Ac ²-â2D33 --- è0)) + i(MRt --- â3D22 + â4D33 --- ?0))].. (2.55)

Les solutions (2.54) et (2.55), étantt ainsi obtenues, nous déterminonss la solution de l'équationn de Schrödingerr non linéairee d'ordree supérieurr en utilisant la transformation de Darboux définiee par [13, 14] :\I

q1 i= =q q- --2 2^d2(z))(ë A+ +ë))øTTø22(2.56))øoø0r(z) )

oil

øø^TT = |ø1|²² +|ø2|²..

En remplaçantt (2.54) et (2.55) dans l'équationn (2.56) tout en tenant compte de (2.42), nous obtenons la nouvelle solution q1i donnée& par la relation :

avec

q1i =

\I d2(z)QQ(zz,,t)exp(ii?)), ,(2.57))r(z) ^)

acoshè1 + cos?1 + i(bsinhè1 + csin?1)

coshè1 O+ acos?1p^,

Q(z, t) = A_c + ^A

è101 = M - â1D2(z)z - â2D3(z)z - è0,o, (2.58

?1P1 = MR - â3D2(z)z) â4D3(z)z - ?0,o

?cp ù_ct_et k(z). .

Pour une amplitud évanescentet (c'ests à a dir A_cA, = 0) d l'ondede plane, la solution

( 2.57) s réduiti à a la solution ^solitoq_sol o= AsAd2(z)z) r(z sech(è_s)exp(i?_s),), (2.59

avec

è_s = A_s[t - 2ù_sD2(z) - (3ù2 s - A² _s)D3(z)] - è0,
?_s = ù_st - (ù2 s - A² _s)D2(z) + ùs(3A2 c - ù² _s)D3(z) - ?0.

qui est une fonction sécante hyperbolique caractéristique des solutions solitons de l'équation SNL. L'amplitude maximale et la vitesse de groupe du soliton (2.59) /sont données respectivement par A_s d2(z)/r(z) et V_s = 2ù_sd2(z) + (3ù2 s - A2 s)d3(z).

Il vient que sous la généralisation des conditions d'Hirota les termes d'ordre supérieur affectent la vitesse et par conséquent la phase du soliton. L'expression de l'amplitude révèle que les termes d'ordre superieur sont sans influence sur l'amplitude de la solution soliton. Nous pouvons donc contrôler la vitesse du soliton en jouant sur les paramètres d2(z) et d3(z), l'amplitude à partir des paramètres d2(z) et r(z).

Dans le souci de se rapprocher de la pratique, et de mieux décrire la dynamique de la solution soliton, les coefficients d2(z), d3(z), et r(z) sont pris sous la forme [13] :

d2(z) = ã1[1 + o1sin(óz)]exp(-g1z)	(2.60)
r(z) = ã2[1 + o2sin(óz)]exp(-g2z)	(2.61)
d3(z) = ã3[1 + o3sin(óz)]exp(-g3z)	(2.62)

oil ãi, oi et gi sont des constantes pour i = 1, 2, 3.

Dans le cas oil o1 = o2 = o3 = 0 les équations (2.60), (2.61) et (2.62) correspondent au contrôle par modulation exponentielle des paramètres [12, 13, 16]. L'amplitude du soliton (2.59) se met alors sous la forme :

_j

ã1[1 + o1sin(óz)]

A(z) = As ã2[1 + o2sin(óz)]exp[(g2 - g1)z/2], (2.63)

La courbe suivante présente l'évolution de l'amplitude (2.63) pour des cas g1 >

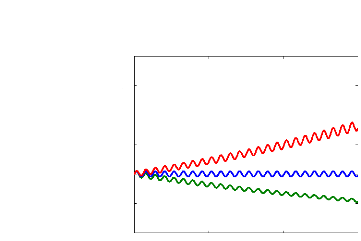
g2,; g1 < g2 et g1 = g2.

0 5 10 15 20 25 30

Amplitude

2.5

0.5

1.5

2

3

0

1

Distance z

FIG. 2.2 - Évolution de l'amplitude (2.63) en fonction de la distance Z, pour les cas g1 = 0.05, g2 = 0.01; g1 = 0.01, g2 = 0.05 et g1 = g2 = 0.01 ( avec A_c = 1,ã1 = ã2 = 1,o1 = 0.05, o2 = -0.04 et ó = 5)

Pour une situation beaucoup plus générale oil A_c =6 0 avec la pulsation de la solution soliton égale à la pulsation de l'onde plane initiale (ù_c = ù_s = ù ) et A2 c > A² _s/4, l'équation (2.57) s'écrit encore

avec

q1 =

sd2(z) r(z) QMI(z,t)exp(i?), (2.64)

QMI(z,t) = A_c + A_s A_scoshè1 - 2A_ccos?1 + iMRsinhè1

2A_ccoshè1 - A_scos?1

,

(2.65)

oil

è1 = A_sMR[D2(z) + 3ùD3(z)] - è0,
?1 = MRt - MR[2ùD2(z) + (3ù² - 2A2 c - A² _s)D3(z)] - ?0,

? = ùt + (2A2 c - ù²)D2 + ù(6A2 c - ù²)D3,

/MR = 4A²_c - A²_s.

La solution donnée par l'équation (2.64) avec les coefficients donnés en (2.65) montre que cette solution est périodique suivant t et de période L définie par

2ð

L = . (2.66)

MR

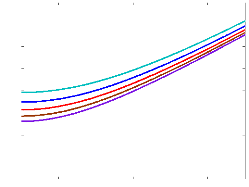
Ainsi, le contrôle de la période peut s'effectuer à partir des amplitudes A_c et A_s. la figure (2.3) montre l'évolution de l'amplitude A_c en fonction de l'amplitude A_s pour diverses valeurs de la période.

0 0.2 0.4 0.6 0.8 1 1.2

Amplitude Ac

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

Amplitude As

FIG. 2.3 - Évolution de l'amplitude A_c en fonction de l'amplitude A_s pour L = 8, 9, 10, 11 et 12