Résolution des équations de Navier Stokes bidimensionnelle par méthode des différences finies et méthode spectrale

4.4 Exemple :

On considère une fonction f(x) avec x E [--l,l]

Soit

f(x) = x-il -- x²

Dans ce cas oil on a une fonction qui n'est pas périodique donc on utilise un développement polynomial et puisque le problème est posé en domaine borné, on utilise polynôme de Tchebychev.

Soit

N
fN = / f^~k Tk

k=0

Pour la méthode de collocation, le résidu est exactement nul en certains points (points de collocation) par contre la méthode de Gallerkin, le résidu est nul au moyenne.

RN(xi) = 0

Avec : xi = cos (^s_N) j = 0, ...., N

Ce qui implique :

N

/ f^~k Tk(xi) = f(xi)

k=0

On obtient donc un système algébrique de N+1 équations à N+1 inconnues f^~k , l'existence de la solution pour ce système implique que :

det (Tk(xj)) * 0

C'est une première condition que doivent satisfaire les points de collocation. Faisons une application numérique pour le cas oil on prend N=4 :

4

/ f^~k Tk(x*) = f(xJ)

k=0

Sous la forme matricielle : El Y = b Avec :

£r	£~~~~~	£~~~~~	£€~~~~
£r~~r~	£~r	£~r	£€~~r~
£r ~	£~~~~~	£~~~~~	£€~~~~
£r~	£~~~~~	£~~~~~	£€~~~~
£r~~€~	£~~~€~	£~~~€~	£€~~€~

Æfa)

~~~ É

É Æ Æ£

É

r Å ~ Z!"# ^À €[ È

È r £r

Å È Å È Å

~~~ È , ~ , et Á ~

Å ~~~~~ È ~ È £~~~~~

Å

Y=

Å ~ Z!"# ^À ~[

~~~ È Å ~~~~~ È Å £~~~~~

È ~ Z!"# ~À È Å

€ [

~~€Ç Ä ~~~€~Ç Å È Ä £~~~€~

Ä ~~!"# ° Ç

Application numérique :

1 0.7071 0 0.7071 --1

1 0 --1 0 1

1 0.7071 0 0.7071 --1

1

1

Å

El = 1

Å 1
Ä 1

1 É

--1.7071

È

0 È

--0.2929 È 3 Ç

Et puis que : Y=M^-1b Implique et finalement :

~

f ~ É

Æ G

r È GIFËF É

~~~ È ~ G

ÅÅ^Å ÈÈ^È

~~~ È 3GIFËF

È Ä

0 Ç

f4

Dans le cas oil on ne veut pas inverser la matrice du système, on peut utiliser la relation discrète d'orthogonalité pour les polynômes de Tchebychev pour exprimer explicitement les valeurs desfk.

Soit

Avec

~ fk =

N !Ì = ; Ck J=^0

f(ci)Tk(xi) k = 0, · · , N

2 si j = 0

ci = Í1 si 1 j < --1 2 si j = N

Appliquons maintenant la méthode spectrale à la résolution des équations de Navier Stokes.

4.5 Projection de la méthode spectrale

Problème à résoudre ;

0(uw)

7
Ox

0(vc) 1

= V²c (4.15)

ay R_e

aco at 7

4.5.1 L'intégration temporelle

co = a2ip7 ax^2

a^2* (4.16) 0y^2

Le schéma d'intégration temporelle que nous avons utilisés est de type semi-implicite à pas multiples. Pour illustrer ceux-ci, considérons l'équation:

Ow
at

= ,C(w) 7 N(w) (4.17)

Ou L et N sont des operateurs respectivement linéaire et non linéaire. Les déférentes
discrétisations des trois termes de l'équation, permettant de construire le système linéaire à
résoudre pour déterminer c^"l(c.-`a-d.: le champ au temps présent: (n+1).At, en fonction

des valeurs aux temps précédents n.At, (n - 1).At, . . .). Adams-Bashforth Crank-Nicholson (ordre 2 en temps)

Ow

at Ð

1 1

_co(n+1) _{3 co}(n) (4.18)

At At

1 1

£(w)2 L(6)(n+1)) 7 2 46)(n)) (4.19)

3 1

~~%~ Ð ; ~H%^~~J 3 ; ~H%^~qr~J (4.20)

d d d7= d3=

= =

~~ %d7= 3 ~~ %d ~ ^ ; %d7= 7 ^ ; %^d 3 F ; >~ ?% 7 ~ ?% @ 7 ; = N ?% 7 ~ ?% O

?~ ?~ Ox ay

_~	d d d7= d3= ^~~` %d7= ~ 3 ; ; ^~~ %d 3 %^d 7 F ^ >~ ?% 7 ~ ?% @ 3 ^ = N ?% 7 ~ ?% O ?~ ?~ ?~ ay

Après application du schéma temporel, le champ c0(n+1) est tel que:

0 3 oco⁽ⁿ⁺ⁱ⁾ = s^(l+i)

2

Oil k =_vAT est une constante (positive) et Sⁿ⁺¹ un terme source ^(connu).

Ce système est d'abord réduit aux points de collocation intérieurs (procédure d'injection des Conditions aux limites), puis résolu (via les diagonalisations successives de l'opérateur), avec reconstruction des valeurs aux frontières.

4.5.2 Les conditions aux limites

Les conditions aux limites pour chaque variable, suivant chaque direction peuvent s'écrire sous la forme :

OC

aC + 13 an = y

Les six coefficients sont, dans l'ordre: a_, a₊,13_, 13+, y_ety+ Les indices -- et + font

référence aux frontières en --1 et +1. -les conditions aux limites sur la vitesse :
a_ = 1, 13_	= y_ =	0	--> U(x = --1)	= 0
a+ = 1, 13+	= y+ =	0	--> U(x = +1)	= 0
a_ = 1, 13_	= y_ =	0	--> U(y = --1)	= 0
a+ = 1,13+	= y+ =	1	--> U(y = +1)	= 1
a_ = 1, 13_	= y_ =	0	--> V(x = --1)	= 0
a+ = 1,13+	= y+ =	0	--> V(x = +1)	= 0
a_ = 1, 13_	= y_ =	0	--> V(y = --1)	= 0
a+ = 1,13+	= y+ =	0	--> V(y = +1)	= 0

Les conditions aux limites pour la fonction courant sont les même que celle de V. Par contre pour la fonction tourbillon ig est toujours nul et y change à chaque itération puisqu'il est fonction de * .

-paroi supérieure x E [--1,1], Y = ¹

o(i, NY) =			^2*(i, NY) -- *(i, NY -- 1)
			Dye
-paroi inférieure E [-1,1],y = --1
w(i3 O) = -paroi droite				2m(i3O) 3 m(i,1)
				ïb^~
	w(NX,j) =	2m(NX,j) 3 m(ÙÚ 3 1,])
-paroi gauche		LX 2
w(O,j) =				2m(O,j) 3 m= Û
				LX 2

4.5.3 Procédures de résolutions des équations de Navier-Stokes

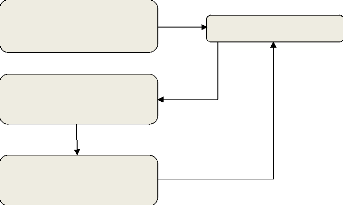
Condition initiales pour la
La fonction courant et tourbillon

Résolution de l'équation de
poisson

Obtention les composantes

u et v

L'équation de transport

Visualisation des résultats

Fig. (4.2) : Procédures de résolutions des équations de Navier-stokes

Les résultats que nous allons présenter dans le chapitre qui va suivre concernent :

1) La résolution des équations de Navier Stokes bidimensionnelles dans une cavité carrée à paroi supérieure entrainée en variables fonction de courant fonction tourbillon par la méthode des différences finies d'ordre (O(H2)-O(H4)).

2) La résolution des équations de Navier Stokes bidimensionnelles dans une cavité carrée à paroi supérieure en variables vitesse pression par méthode spectrale de collocation Tchebychev.

3) La résolution des équations de Navier Stokes bidimensionnelles dans une cavité carrée à paroi supérieure en variables fonction de courant fonction tourbillon par méthode spectrale de collocation Tchebychev.