Etude du prix spot du Gaz naturel

Etude des Prix Spot du Gaz naturel

Yasmine Abbas et Wissem Bentarzi

Faculté de Mathématiques,
Université des Sciences et de la Technologie Houari Boumediene,
U. S. T. H. B..

i

Table de Matières

Introduction générale 1

Chapitre 1: Généralités sur le marché gazier 7

1.1. Origine et histoire 8

1.2. Description et caractéristiques techniques 10

1.3. Description des opérations de transformation du gaz naturel 12

1.4. Secteur d'utilisation 14

1.5. Prix 17

1.6. Marché 18

1.7. La libéralisation du marché du gaz 22

Chapitre 2: Processus stochastiques et séries chronologiques 24

2.1. Introduction 24

2.2. Processus stochastiques 25

2.2.1. Classification des processus stochastiques 25

2.2.2. Distribution de probabilité d'un processus aléatoire 26

2.2.3. Caractéristiques d'un processus stochastique 26

2.2.4. Processus du second ordre 26

2.2.5. Fonction d'autocovariance d'un processus stochastique 26

2.2.6. Processus stationnaires 27

2.2.7. Propriétés et estimation empirique de la fonction d'autocovariance 29

2.2.8. Fonction d'autocorrélation 30

2.3. Opérateurs et opérateur de différence 31

2.4. Séries chronologiques 33

2.4.1. Analyse des séries chronologiques 33

2.5. Modélisation des séries chronologiques 35

2.5.1. Décomposition de Wold 36

2.5.2. Formule de convolution 37

2.6. Classe des modèles ARMA(p, q) 38

2.6.1. Processus autoregressif 39

2.6.2. Processus moyenne mobile 45

2.6.3. Modèles ARMA 49

2.6.4. Modèles ARIMA 50

2.6.4. Modèles saisonniers SARIMA 57

Chapitre 3: Méthodologie de Box et Jenkins 58

3.1. Introduction 58

3.2. Identification du modèle 61

3.3. Estimation des paramètres 62

3.4. Validation 65

3.5. Prévision 67

3.5.1. Méthodes de prévision à court et à moyen terme 69

3.5.2. Méthodes d'extrapolation 69

Chapitre 4: Application de la méthodologie de Box et Jenkins 72

4.1. Etude du prix spot du gaz naturel à Pensylvania 72

4.1.1. Identification et estimation 72

4.1.2. Validation 80

4.1.3. Prévision 83

4.2. Etude du prix spot du gaz naturel au Texas 86

4.2.1. Identification et estimation 86

4.2.2. Validation 90

4.2.3. Prévision 94

4.3. Etude du prix spot du Brent 97

4.3.1. Identification et estimation 97

4.3.2. Validation 101

4.3.3. Prévision 105

4.4. Etude du prix spot du WTI 108

4.4.1. Identification et estimation 108

4.4.2. Validation 112

4.4.3. Prévision 115

Chapitre 5 : Modélisation multivariée 118

5.1. Processus multivariés stationnaires du second ordre 119

5.1.1. Fonction d'autocorrélation 121

5.2. Classe des modèles VARMA(p, q) 122

5.2.1. Processus autoregressif multivarié VAR(p) 123

Chapitre 6: Cointégration et modèles à correction d'erreur 126

6.1. La cointégration 126

6.1.1. Définition de la cointégration 127

6.2. Modèle à correction d'erreurs 128

6.2.1. Représentation des modèles à correction d'erreurs (ECM) 128

6.3. Estimation des modèles à correction d'erreurs et test de cointégration: 129

approche de Engle et Granger

6.3.1. Méthode d'estimation en deux étapes 129

6.3.2. Test de cointégration 129

6.4. Approche multivariée de la cointégration: l'analyse de Johanson 130

Chapitre 7: Application de la théorie de cointégration 134

7.1. Etude de l'évolution du prix du gaz naturel et du brut sur le marché Américain 134

7.2. Etude de l'évolution du prix du WTI et du prix du Brent 140

Conclusion générale 150

Annexe A 151

Annexe B. 156

Introduction générale

Grâce à ses vertus économiques et écologiques, le gaz naturel est devenu l'une des sources d'énergie les plus utilisées dans le monde, sinon la plus prometteuse. L'Algérie en est un principal producteur et exportateur à plusieurs pays dans le monde, dont parmi les principaux clients figure l'USA et l'Europe. Traditionnellement, les contrats de transaction du gaz se font à long terme, avec des prix stables. Cependant, ils existent de plus en plus des contrats à comptant (spot), en raison de la libéralisation de l'industrie du gaz naturel, bien que la majeure partie du gaz naturel échangé sur le plan international reste dans le cadre de contrats à terme. Comme par ailleurs l'industrie du gaz naturel est un secteur vaste et réclame des capitaux importants, la société Sonatrach (société nationale de transport et de commercialisation des hydrocarbures), exploiteur exclusif de cette matière, se doit d'étudier et analyser l'évolution du prix de cette matière stratégique, aux marchés américain et européen, afin de tirer des informations et des conclusions utiles pour la phase de prise des décisions liées à la réalisation des projets gaziers.

Les prix du gaz dans le temps, aux marchés américain et européen, constituent ce qu'on appelle des séries chronologiques (séries temporelles, chroniques), mathématiquement considérées comme trajectoires particulières prises par des processus stochastiques. L'étude de la série des prix revient à celle de son processus générateur, via l'analyse des séries chronologiques. L'analyse des séries chronologiques regroupe un ensemble de techniques et de méthodes permettant de détecter la structure de corrélation (dépendance) entre les composantes d'un processus générateur, qu'on induit à travers une série sous étude. Cette structure une fois captée, sera exploitée, entres autres, sous l'hypothèse fondamentale que les valeurs futures de la série restent une réalisation du processus, pour faire des prédictions. Pour induire le processus générateur à partir de sa réalisation, l'analyse des séries chronologiques

offre un ensemble d'outils permettant de construire le modèle (i.e. un processus, le plus souvent solution d'une équation aux différences stochastique) le plus adéquat.

Bien qu'ils ne représentent souvent qu'une vision partielle de la réalité, les modèles linéaires autoregressifs moyenne mobile (AutoregRessive Moving Average, ARMA) sont les plus utilisés en analyse des séries chronologiques. Cette classe de modèles a connu un développement remarquable grâce au théorème de Wold (1938) qui a été popularisé plus tard, dans les années 70, avec l'apparition du fameux ouvrage de Box et Jenkins ((1970) deuxième édition (1976)). Ouvrage dans lequel ces deux auteurs proposent une méthodologie pour la construction du modèle adéquat. Cette méthodologie part de l'identification du modèle à sa validation, en passant par l'estimation de ses paramètres.

La quasi-totalité des résultats et des méthodes utilisées dans l'analyse des séries temporelles sont fondés sur l'hypothèse de stationnarité du second ordre du processus générateur (ou par abus de notation, de sa série générée), hypothèse qu'on accepte pour peu que la série étudiée présente une allure dénudée de tendance et/ou de saisonnalité apparentes. Cependant, dans les phénomènes économiques, on est souvent confronté à des chroniques "non stationnaires", auxquelles on fait subir des transformations adéquates (différence ordinaire, différence saisonnière, différence mixte, transformation de Box-Cox...) afin d'obtenir, éventuellement, des séries stationnaires. L'efficacité de ces transformations est conditionnée par la nature de la non-stationnarité de la série étudiée.

Parmi les processus stochastiques non stationnaires pouvant être rendus stationnaires, via des transformations adéquates, on distingue principalement les processus saisonniers (lesquels, après des transformations saisonnières appropriées peuvent être rendus stationnaires) et les processus à tendance. Cette dernière classe comporte quant à elle deux grandes catégories particulières a savoir la classe des processus à tendance déterministe (Trend Stationnary, TS) et la classe des processus à tendance stochastique (Difference Stationnary, DS). La perception entre ces deux classes de processus linéaires non stationnaires est d'une grande importance du fait que dans la première classe (TS), l'intervention d'un choc à un instant t n'a aucune influence sur l'erreur de prévision de la série à l'instant t + h, et que dans la seconde (DS) chaque perturbation aléatoire est persistante et possède un effet durable sur le comportement de la série. Pour détecter le type de tendance (stochastique ou

déterministe) que possède une série, plusieurs tests de racines unitaires ont été mis au point, dont les plus répandus sont les tests de Dickey-Fuller simple et augmenté (1979) et le test de Phillips-Perron.

L'approche de modélisation via la méthodologie de Box-Jenkins est qualifiée d'univariée dans le sens où l'on suppose qu'un phénomène stochastique n'est influencé que par son propre passé, à un bruit blanc près, et que l'influence d'un ou de plusieurs autres phénomènes est du moins négligeable. Cette hypothèse est par trop insuffisante dans la réalité économique et particulièrement, en ce qui concernent les prix du gaz qui dépendent non seulement de leurs passés mais aussi de certains d'autres facteurs tels que les prix du pétrole, la consommation d'énergie... Ainsi le recours à une approche multivariée, qui tient en compte de l'interdépendance d'un phénomène avec certains d'autres, s'avère primordiale. Les modèles ARMA multivariés ( VARMA), dans le cas où les séries présenteraient une allure stationnaire (dénudées de tendance, de saisonnalité et de cyclicité), en sont de bons instruments. Cependant si les séries sont non stationnaires, en particulier nanti d'une tendance stochastique, les transformations usuelles même si elles rendent chacune des séries stationnaires peuvent casser l'interdépendance entre les processus générateurs, et détruire par là même une relation à long terme. En effet, à court terme, plusieurs séries peuvent avoir des tendances stochastiques différentes et évoluent d'une façon plus ou moins divergente, mais à long terme on s'attend à ce qu'elles convergent vers un même itinéraire de sorte qu'il est possible de trouver une combinaison linéaire stationnaire, mesurant les erreurs d'ajustement d'une série par rapport aux autres, et ce, autour d'une relation d'équilibre. Les modèles classiques tels que les modèles VARMA sont incapables de mettre en évidence une telle relation d'équilibre. Il existe cependant une classe particulière de modèles, directement liés à la théorie de cointégration à savoir les modèles à correction d'erreurs. Ces modèles permettent de modéliser les ajustements qui conduisent à une situation d'équilibre de long terme en intégrant à la fois les évolutions de court, moyen et long terme des séries sous-jacentes.

La théorie de cointégration a été introduite par Granger (1981) et le lien entre le modèle de cointégration et les modèles à correction d'erreurs a été explicité par Granger (1981, 1983), Granger et Weiss (1983) et Engle et Granger (1987). Ces derniers ont mis en oeuvre une procédure en deux étapes permettant de tester la présence d'une cointégration. L'inconvénient de cette procédure est qu'elle ne permet pas d'estimer une relation d'équilibre entre plus

de deux variables. Johansen (1988) a proposé une approche multivariée de la cointégration fondée sur la méthode du maximum de vraisemblance.

Soucieuse de préserver et d'améliorer ses productions, la société Sonatrach nous nous confié la tâche d'étudier et d'analyser les prix du gaz naturel aux marchés américain et européen dans le but de promouvoir ses projets gaziers.

Notre projet de fin d'étude porte sur la modélisation et la prévision du prix du gaz naturel sur le marché Américain et Européen, ainsi que sur l'étude des relations qui peuvent éventuellement exister entre le prix du gaz naturel et le prix du pétrole. Cette étude repose sur l'analyse des séries chronologiques représentant l'évolution du prix de ces énergies au cours du temps.

Le document de notre mémoire contient sept chapitres. Le premier chapitre est consacré aux caractéristiques du gaz naturel et de ces propriétés. Le chapitre suivant porte sur l'étude des notions de base des processus stochastiques et les séries chronologique. Dans le troisième et le quatrième chapitre, nous exposons respectivement la méthodologie de Box et Jenkins et son application. Le chapitre suivant est consacré à la modélisation multivariée, et le sixième et septième chapitre contient respectivement la théorie de cointégration et les modèles à correction d'erreur et leur application. Une conclusion achève notre travail

0.3. Présentation de l'organisme d'accueil

Suite à l'indépendance de l'Algérie en 1962, l'industrie pétrolière précédemment détenue par Total, Sell, Mobil,.. .(sociétés françaises) à été totalement ré-attribuée à ce pays. De ce fait, elle a pu développer son indépendance économique. L'état se dota alors d'un instrument permettant la mise en oeuvre de sa politique énergique, en Evian le 31 décembre 1963 par le décret N^°63/491 la société nationale de transport des hydrocarbures. La mission de cette dernière s'est étendue en 1966 à l'ensemble des activités pétrolières tels que la recherche, la production, la transformation et la distribution.

Les années 70 ont été marquées par la nationalisation des hydrocarbures ce qui a engendré des investissements massifs ayant pour objectifs :

Augmenter les capacités de rafiunage.

Créer des usines de liquéfaction.

Développer la pétrochimie.

Etendre le réseau de transport par canalisation.

Intensifier l'exploration.

Suite à une décision politique et à la réorganisation de l'économie nationale dans les années 80, la SONATRACH (société nationale de transport et commercialisation des hydrocarbures) a subi une restructuration et un essangeage qui ont donné lieu à des naissances de filiales telles que : NAFTAL, ENPL, ENPI... . L'état décida ainsi de décentrer l'activité de la société par décret présidentiel (11/02/98) elle a donc adapté le statut de société par action(SPA), organisée de manière suivante:

Assemblée générale, conseil d'administration, président directeur général (nommé par décret présidentiel)). Son capital social est de 40 milliards de dinars, répartis en 245000 actions (entièrement et exclusivement souscrites et libérées par l'état). L'économie du pays dépend essentiellement de l'industrie des hydrocarbures dans la mesure où :

95% des recettes en devises du pays sont issues de l'exportation des hydrocarbures. La fiscalité pétrolière couvre prés de 60% du budget de l'état.

L'approvisionnement des pays en hydrocarbures à moyen et à long terme.

Optimiser la valeur des ressources d'hydrocarbures de l'Algérie à long terme.

Elle a également d'autres missions, dictées par l'article 7 du journal officiel de la R.A.D.P(du 07 au 15/07/98)

Prospection, recherche et exploitation des hydrocarbures.

Développement, exploitation, gestion des moyens de transport, de stockage et de chargement des hydrocarbures.

Transformation et raffinage des hydrocarbures. Commercialisation des hydrocarbures.

Développement de toutes formes d'actions conjointes en Algérie et hors Algérie avec des sociétés algériennes ou étrangères, prises de participation et autres valeurs mobilières de toutes les sociétés existantes crées en Algérie ou à l'étranger.

L'approvisionnement du pays en hydrocarbures à moyen et long terme.

Développement par tous les moyens de toute action pouvant engendrer des intérêts pour la société et généralement toute opération de qu'elle soit sa nature pouvant se rattacher à son activité.

Chapitre 1

Généralités sur le marché gazier

Le gaz naturel est la source d'énergie fossile qui a connu la plus forte progression depuis les années 70. En effet, elle représente la cinquième de la consommation énergétique mondiale.

En raison de ses avantages économiques et écologiques, le gaz naturel devient chaque jour plus attractif pour beaucoup de pays. Les propriétés de ce produit, comme par exemple le faible intervalle de combustion le caractérisant, en font l'une des sources d'énergies les plus fiables connue à ce jour.

D'après l'EIA, du département américain de l'énergie, la part du gaz naturel dans la production énergétique mondiale était de 23% en 1999 et les perspectives de développement de la demande sont excellentes. Il est considéré comme le combustible fossile du siècle, comme le pétrole l'était lors du siècle précédent et le charbon il y a deux siècles.

Le gaz naturel présente un avantage concurrentiel par rapport aux autres sources d'énergie car, seuls 10% (environ) du gaz naturel produit sont perdus avant d'arriver chez le consommateur final. En outre, les progrès technologiques améliorent constamment l'efficacité des techniques d'extraction, de transport et de stockage ainsi que le rendement énergétique des équipements fonctionnant à base de gaz naturel. Le gaz naturel est considéré comme un combustible plus propre et plus respectueux de l'environnement que la plus part des autres combustibles fossiles. Son avantage comparatif en matière d'environnement par rapport au charbon ou au pétrole réside dans le fait que les émissions de dioxyde de soufre son négligeables et que les niveaux d'oxydes d'azote et de dioxyde de carbone sont plus faibles. Un plus grand recours à cette source d'énergie permettrait notamment de limiter les impacts

négatifs sur l'environnement tels que : les pluies acides, la détérioration de la couche d'ozone ou les gaz à effet de serre.

Le gaz naturel est également une source d'énergie très sûre tant en ce qui concerne son transport et son stockage, que son utilisation.

Bien que les réserves de gaz naturel soient limitées et qu'il s'agisse d'une source d'énergie non-renouvelable, les réserves exploitées sont importantes à travers le monde et augmentent au fur et à mesure que de nouvelles techniques d'exploration et d'extraction permettant un forage plus large ou plus profond ses découvertes.

Les niveaux des investissements consacrés à l'industrie du gaz naturel montre l'importance grandiloquence de ce produit. Ce secteur fait preuve d'un dynamisme important au lendemain de ce nouveau millénaire. Une demande en progression et le niveau des prix au cours d'un passé récent ont conduit à de nouveaux projets d'expansion et d'exploration. Des projets de construction de nouveaux gazoducs sont développés et planifiés à travers le monde. En outre, les gouvernements incluent progressivement le gaz naturel à l'ordre du jour de leur politique énergétique, notamment par la poursuite de politiques de libéralisation du marché (en particulier depuis les crises pétrolières des années 70). De plus en plus, les utilisateurs finaux montrent une préférence pour le gaz naturel du fait de sa propreté, de sa sécurité, de sa fiabilité et de son intérêt économique. Le gaz naturel peut être employé pour le chauffage, la réfrigération (cooling) et plusieurs autres applications de type industriel. Dans le même temps, il tend à devenir le combustible préféré pour la production d'électricité.

1.1 Origine et histoire

Le gaz naturel a été découvert au Moyen-Orient au cours de l'antiquité. Il y a de cela quelques milliers d'années, l'apparition soudaine de gaz naturel s'enflammant brutalement était assimilée à des sources ardentes. En Perse, en Grèce ou en Inde, les Hommes ont érigé des temples autour de ces feux pour leurs pratiques religieuses. Cependant ils n'évaluèrent pas immédiatement l'importance de leurs découvertes. C'est la Chine qui autour de 900 avant Jésus-Christ, comprit l'importance de ce produit et fora le premier puits aux alentours de 211 avant Jésus-Christ.

En Europe, il a fallut attendre jusqu'à 1659 pour que la Grande-Bretagne découvre le gaz naturel et le commercialise à partir de 1790. En 1821, à Fredonia (Etats-Unis), les habitants ont découvert le gaz naturel dans une crique par l'observation de bulles de gaz qui remontaient jusqu'à la surface. William Hart est considéré comme le "père du gaz naturel". C'est luit qui creusa le premier puits nord-américain.

Au cours du XIX ième siècle, le gaz naturel a presque exclusivement été utilisé comme source de la lumière. Sa consommation demeurait très localisée en raison du manque d'infrastructures de transport qui rendait difficile l'acheminement de grandes quantités de gaz naturel sur de longues distances. En 1890, un changement important intervient avec l'invention des joints à l'épreuve des fuites. Cependant, les techniques existantes n'ont pas permis de transporter le gaz naturel sur plus de 160 Kilomètres et ce produit a été gaspillé pendant des années car brûlé sur place. Le transport du gaz naturel sur de longues distances s'est généralisé au cours des années 1920, grâce aux progrès technologiques apportés aux gazoducs. Après la seconde guerre mondiale, la consommation de gaz naturel s'est développée rapidement en raison de l'essor des réseaux de canalisation et des systèmes de stockage.

Dans les premiers temps de l'exploration du pétrole, le gaz naturel était souvent considéré comme un sous produit sans intérêt entravant le travail des ouvriers forcés de s'arrêter pour laisser échapper les poches de gaz naturel découvertes lors du forage. Aujourd'hui, et en particulier depuis les crises pétrolières des années 70, le gaz naturel est devenu une source importante d'énergie dans le monde.

L'industrie du gaz naturel a été fortement régularisée pendant de nombreuses années car elle était considérée comme un monopole d'Etat. Au cours des 30 dernières années, il y eut un mouvement vers une plus grande libéralisation des marchés du gaz naturel et une forte déréglementation des prix de ce produit. Cette tendance eut pour conséquence d'ouvrir le marché à une plus grande concurrence et de rendre l'industrie du gaz naturel plus dynamique et plus innovante. En outre, grâce à de nombreux progrès technologiques, la découverte, l'extraction et le transport du gaz naturel vers les consommateurs peut se faire d'une manière plus aisée. Ces innovations ont également permis d'améliorer les applications existantes et d'en imaginer de nouvelles. Le gaz naturel est de plus en plus utilisé pour la production d'électricité.

1.2 Description et caractéristiques techniques

Le gaz naturel est incolore, inodore, insipide, sans forme particulière et plus légère que l'aire. Il se présente sous sa forme gazeuse au-dessus de - 161^°C. Pour des raisons de sécurité, un parfum chimique, le mercaptan, qui lui donne une odeur d'oeuf pourri, lui est souvent ajouté de sorte qu'une fuite de gaz puisse ainsi être détectée.

Le gaz naturel est un mélange d'hydrocarbures légers comprenant du méthane, de l'éthane, du propane, des butanes et des pentanes. D'autres composés tels que le CO2, l'hélium, le sulfure d'hydrogène et l'azote peuvent également y être trouvés. La composition du gaz naturel n'est jamais la même. Cependant, on peut dire que son composant principal est le méthane (au moins 90%). Il possède une structure d'hydrocarbure simple, composé d'un atome de carbone et de quatre atomes d'hydrogène (CH4). Le méthane est extrêmement inflammable. Il brûle facilement et presque totalement et n'émet qu'une faible pollution. Le gaz naturel n'est ni corrosif ni toxique, sa température de combustion est élevée et il possède un intervalle restreint d'inflammabilité, ce qui en fait un combustible fossile sûre comparé à d'autres sources d'énergie. En outre, en raison de sa densité de 0.60, inférieure à celle de l'air (1.00), le gaz naturel a tendance à s'élever et peut, par conséquent, disparaître facilement du suite où il se trouve par n'importe quelle fissure.

Il est généralement admis que le carbone et l'hydrogène contenus dans le gaz naturel proviennent des restes de plantes et d'animaux qui se sont trouvés rassemblés au fond des lacs et des océans durant des millions d'années. Après avoir été recouverts par des couches importantes d'autres sédiments, le matériel organique s'est transformé en pétrole brut et en gaz naturel sous l'effet de la pression exercée par les couches de sédiments et la chaleur émise par le noyau terrestre. Le pétrole et le gaz ont alors été expulsés hors de schistes argileux marins dans lesquels ils s'étaient déposés, et de là, ont pénétré les roches sédimentaires poreuses. Le pétrole et le gaz remontent alors à travers la roche, car moins dense que l'eau, qui remplit les pores.

On trouve du gaz naturel partout dans le monde, dans des réservoirs situés en profondeur sous la surface terrestre, ou des océans. Des poches de gaz peuvent se former au-dessus des dépôts de pétrole brut, ou être emprisonnées au sein de roches poreuses.

A la pression atmosphérique, si le gaz naturel est refroidi à une température de -161^°C environ, il se condense sous la forme d'un liquide appelé le gaz naturel liquéfié (GNL). Un volume de ce liquide occupe environ le six centième d'un volume de gaz naturel et est deux fois moins lourd que l'eau, (45% environ). La réduction de volume permet de transporter et de stocker le gaz naturel de façon beaucoup plus économique. Le GNL est :

a) Incolore : le GNL est clair et incolore comme l'eau.

b) Extrêmement froid : il faut porter des vêtements protecteurs lorsqu'il y a risque de contact direct avec du GNL ou lors de la manutention de conteneurs non isothermes de GNL.

c) Non toxique : l'exposition du GNL vaporisé n'a pas d'effet toxique sur les humains et les animaux.

d) Non corrosif: l'exposition au GNL durant une longue période n'entraîne ni dommage ni corrosion à l'équipement conçu pour ce service.

e) Plus léger que l'eau : le GNL pèse moins de la moitié d'un volume d'eau équivalent, de sorte qu'il flotte à la surface.

f) Inerte : contrairement au gaz naturel, le GNL n'explose pas lorsqu'il est exposé à une source d'inflammation dans un espace clos. Aussi, le GNL n'est pas sous pression lorsqu'il est dans les conteneurs d'expédition ou les réservoirs de stockage; la perforation d'un conteneur n'entraînera donc pas d'explosion.

g) Ininflammable : Comparativement au gaz naturel qui est inflammable lorsqu'il est mélangé avec une partie appropriée d'air, le GNL n'est pas combustible.

Pour reconvertir le GNL en gaz naturel, il faut le réchauffer. Trois procédés sont couramment employés pour réchauffer le GNL et le regazifier :

Vaporisation par échange de chaleur avec l'eau de mer ce procédé utilise de grands volumes d'eau pour chauffer le gaz, puis l'eau, après qu'elle a été refroidi, est retournée à sa source, par exemple un fleuve.

Vaporisation par combustion submergée ce procédé consiste à brûler une petite quan tité de gaz pour chauffer un bain d'eau qui permet de réchauffer le GNL. L'eau circule dans un circuit fermé et n'est pas submergée seront installés au terminal et

agiront comme seule source de chaleur pour la regazification, ou comme source d'appoint si une centrale de co-génération est construite.

Centrale de co-génération : une centrale de co-génération au gaz naturel située sur le site fournirait de l'énergie résiduelle pour réchauffer le GNL, tout en produisant de l'électricité pour les consommateurs. Cette option économie énergétique fait actuellement l'objet d'une évaluation dans le cadre de ce projet.

Le transport du GNL commence outre-mer dans les endroits où le gaz naturel est produit. Le gaz naturel est d'abord transporté par un réseau de gazoducs vers des endroits où il est transformé en GNL. Le GNL est transporté dans des réservoirs de stockage. Au terminal, le GNL est pompé au moyen de vaporisateurs où il retourne à son état gazeux. Il est ensuite acheminé par gazoduc vers sa destination finale.

Le gaz naturel est considéré comme un combustible propre. Sous sa forme commercialisable, il ne contient presque pas de soufre et ne produit pratiquement aucun dioxyde de soufre (8O2). Ses émissions d'oxyde d'azote (NOx) sont plus faibles que celles du pétrole ou du charbon et celles de gaz carbonique (CO2) inférieures à celles des autres combustibles fossiles (selon Eurogaz de 40 à 50% de moins que le charbon et de 25 à 30% de moins que le pétrole).

1.3 Description des opérations de transformation du gaz naturel

Le processus de production du gaz naturel est très simple et très proche de celui du pétrole. Le gaz naturel est tout d'abord extrait du sol ou des océans par forage, puis transporté par pipeline (sur terre) ou tankers (par mer) jusqu'à une installation de nettoyage et de transformation pour être ensuite acheminé vers une zone de stockage ou des cavités creusées dans le sol.

exploration

L'exploration est une étape très importante du processus. Au cours des premières années de l'industrie du gaz naturel, lorsque les connaissances dans ce domaine étaient encore limitées, les puits étaient uniquement creusés à l'intuition. Aujourd'hui, au regard des coûts

d'extraction très élevés, les compagnies ne peuvent pas prendre le risque de forer n'importe ou. Les géologues jouent alors un rôle essentiel en identifiant les poches de gaz naturel. Pour trouver une zone où du gaz naturel est susceptible d'être découvert, ils analysent la composition du sol, et comparent les échantillons prélevés avec ceux d'autres zones où du gaz naturel a déjà été trouvé. Puis ils réalisent des tests spécifiques comme l'étude des formations rocheuses des couches supérieures où du gaz naturel pourrait être formé. Les techniques de prospection ont évolué au cours du temps et fournissent aujourd'hui des informations d'une grande fiabilité sur l'existence possible de dépôts de gaz naturel. Plus précises sont ces techniques, plus forte sera la probabilité de découvrir du gaz lors du forage.

Extraction

Le gaz naturel est extrait en creusant un trou dans la roche. Le forage peut être effectué sur terre ou en mer. Le matériel employé est fonction de la localisation de la poche de gaz et de la nature de la roche. Si c'est une formation peu profonde des câbles de forage peuvent être utilisés. Un mouvement de va et vient est effectué à plusieurs reprises à l'aide d'une mèche en métal dans le sol. Pour des prospections plus en profondeur, des plates-formes de forage rotatives sont nécessaires. Elles sont les plus répandues aujourd'hui. Cette méthode se compose d'une mèche pointue qui permet de passer à travers la terre et la roche.

Une fois le gaz naturel trouvé il doit être prélevé efficacement. Le taux de recouvrement le plus efficace est donné par la quantité maximum de gaz naturel pouvant être extraite sur une période de temps donné sans endommager la formation. Plusieurs tests doivent être effectués à ce stade du processus.

Le plus souvent, le gaz naturel sous pression, sortira du puits sans intervention extérieure. Toutefois, il est parfois nécessaire de faire appel à des pompes ou d'autres méthodes plus compliquées. La méthode d'extraction la plus répandue est basée sur les équipements de

pompage.

Traitement

processus implique tout d'abord une extraction des éléments en phase liquide dans le gaz naturel, puis un fractionnement de ces différents éléments.

Transport et stockage

Une fois le gaz naturel traité, il va être acheminé vers son lieu d'utilisation. Il peut être transporté par voie terrestre à travers des gazoducs qui sont constitués de tubes d'acier de 20 à 42 pouces de diamètre. Le gaz étant acheminé sous haute pression des stations de compression disposées tout au long de la canalisation maintiennent la pression du gaz au niveau souhaité.

Comparé à d'autres sources d'énergie, le transport du gaz naturel est très efficace étant donnée la faible part d'énergie perdue entre le départ et l'arrivé. Les gazoducs sont les moyens les plus sûrs de distribution de l'énergie car elles sont fixes et souterraines.

Le gaz naturel peut également être transporté par mer dans des tankers. Dans ce cas, il est transporté en gaz naturel liquéfié (GNL). Le procédé de liquéfaction permet d'en retirer l'oxygène, le dioxyde de carbone, les composés de soufre et l'eau. Les éléments principaux de ce processus sont : une usine de liquéfaction, des bateaux de transport pressurisés et à température faible et des installations de regazification.

Avant d'arriver chez le consommateur, le gaz naturel passe parfois par une phase de stockage (dans des réservoirs souterrains) de sorte que l'industrie du gaz naturel puisse faire face aux fluctuations saisonnières de la demande. Ces réservoirs son habituellement situés à proximité des marchés consommateurs afin de permettre aux compagnies de distribution de gaz naturel de faire face à des pics de la demande et d'approvisionner leurs clients sans délai. Elles peuvent également vendre le gaz naturel sur le marché physique pendant les périodes

creuses.

1.4 Secteur d'utilisation

Le gaz naturel est une source d'énergie polyvalente qui peut être employée dans des domaines très variés. La production de chauffage et d'électricité en sont ses débouchés traditionnels principaux. En outre, les préoccupations grandissantes liées à la protection de

l'environnement devraient conduire à un plus grand recours au gaz naturel dans le transport.

Utilisateurs domestiques

Les applications domestiques sont les principaux débouchés du gaz naturel. Ce dernier peut être utilisé pour cuisiner, laver, sécher, faire chauffer une maison, la climatisation. En outre, les appareils ménagers sont sans cesse améliorés afin d'être aptes à utiliser du gaz naturel plus économiquement et de manière plus sûre. Les frais d'exportation du matériel fonctionnant au gaz naturel sont généralement plus faibles que ceux liés à d'autres formes d'énergie.

Applications commerciales

Les principaux utilisateurs commerciaux de gaz naturel sont des fournisseurs de services tels que les restaurants, les hôtels, les équipements des services médicaux ou les bureaux. Les applications commerciales du gaz naturel incluent la climatisation (air conditionné et réfrigération), la cuisine ou le chauffage.

Industrie

Le gaz naturel entre dans la fabrication de la pâte à papier, du papier, de certains métaux, produits chimiques, pierres, argile, verre et dans la transformation de certaines denrées. Il peut également être employé pour le recyclage des déchets, pour l'incinération, le séchage, la déshumidification, le chauffage, la climatisation et la co-génération.

Production d'électricité

Les compagnies d'électricité et les fournisseurs d'énergie indépendants emploient de plus en plus le gaz naturel pour alimenter leurs centrales du fait de son coût d'exploitation. En général, les centrales fonctionnant au gaz naturel coûtent moins chères, elles sont construites plus rapidement, travaillent plus efficacement et rejettent moins de pollution dans l'atmosphère que des centrales utilisant d'autres combustibles fossiles. Les améliorations technolo-

giques en matière de conception, d'efficacité et d'emploi de turbines à cycles combinés ainsi que de processus de co-génération encouragent l'emploi de gaz naturel dans les industries de création d'énergie. Les centrales à cycles combinés (CCGT) utilisent la chaleur perdue pour produire davantage d'électricité, alors que la co-génération de gaz naturel fournit en même temps de la puissance et de la chaleur utile aussi bien pour l'industrie que pour les utilisateurs commerciaux. Cette co-génération réduit très fortement le rejet de gaz polluant dans l'atmosphère.

Industrie automobile

Le gaz naturel peut être utilisé comme combustible pour les véhicules à moteur de deux manières :

En tant que gaz naturel comprimé (GNC), qui est la forme la plus répondue, ou en tant que gaz naturel liquéfié.

Le parc des véhicules fonctionnant au gaz naturel est d'environ 1.5 millions d'automobiles à travers le monde (selon l'association internationale des véhicules à gaz naturel). Les interrogations concernant la qualité de l'air dans la plupart des régions du monde renforcent l'intérêt pour le gaz naturel dans ce secteur. On estime que les voitures utilisant ce type de combustible émettent 20% de gaz à effet de serre en moins que les véhicules à essence ou diesel. Contrairement à une idée reçue, l'emploi de gaz naturel dans les véhicules à moteur n'est pas une nouveauté, puisqu'il était déjà utilisé dans les années 30. Dans beaucoup de pays, ce type de véhicules est présenté comme un substitut aux bus, taxis et autres transports publics. Il représente un système peu onéreux et pratique.

Piles à combustible

La pile à combustible est un dispositif électrochimique qui permet de combiner l'hydrogène et l'oxygène contenus dans l'air afin de produire de l'électricité, de la chaleur et de l'eau. Les piles à combustible fonctionnent sans combustion. Elles ne polluent donc pratiquement pas. Une pile à combustible peut être utilisée à des rendements beaucoup plus élevés que les moteurs à explosion puisque le combustible est directement transformé en électricité et qu'elle produit plus d'énergie à partir de la même quantité de combustible. La pile à com-

bustible ne possède aucune pièce mobile, ce qui en fait une source d'énergie relativement silencieuse et fiable. Le gaz naturel est un des multiples combustibles à partir desquels les piles à combustibles peuvent fonctionner.

1.5 Prix

Référence et mécanismes de formation des prix

Le marché international du gaz naturel se compose de différents marchés régionaux. Il est donc difficile de parler d'un prix mondial pour ce produit. Bien qu'il existe une tendance vers une certaine libéralisation du marché, celui-ci reste néanmoins très réglementé sur beaucoup de marché. Ces divers degrés de libéralisation expliquent en partie les différences des prix qu'ils existent entre les différents Etats. En Amérique du nord par exemple, où le marché est fortement libéralisé, les prix sont très concurrentiels et fluctuent en fonction de l'offre et de la demande. A la suite de la libéralisation, les prix ont connu une baisse significative. Au contraire, au sein de la fédération de la Russie, où il existe encore un certain monopole, les prix internes sont maintenus artificiellement bas tandis que le gaz est devenu sur les marchés étrangers à différents prix plus élevés afin de compenser les pertes. En Europe, le prix de vente du gaz naturel est le plus souvent influencé par la concurrence des combustibles alternatifs.

Les prix du gaz naturel peuvent être évalués dans différents stades de la filière. On distingue alors le prix pour le consommateur domestique, commercial, industriel ou les compagnies d'électricité. En général, les principaux composants du prix du gaz naturel sont : le prix de tête de puits (le coût du gaz naturel lui-même), le coût du transport sur une longue distance, le coût de la distribution locale.

En Amérique du Nord, les prix de tête de puits ont été libéralisés. Les coûts relatifs au transport sont encore gérés par des offices gouvernementaux, alors que les organes locaux, les "local regulator boards" s'intéressent eux aux coûts locaux de distribution.

Les facteurs principaux qui déterminent la demande sont l'influence et l'activité économique. En raison de l'importance du premier facteur: les conditions climatiques, la demande de gaz naturel est caractérisée par une forte saisonnalité. Les mouvements de population et

l'attrait des utilisateurs pour le gaz naturel affectent également la demande. Les évolutions de la législation relative à la pollution atmosphérique pourraient conduire à une croissance de la demande pour ce combustible considéré comme propre. L'offre est influencé par la disponibilité et l'accessibilité au transport et l'accessibilité ainsi que par la quantité physique de gaz naturel produit et le niveau des stocks.

Le gaz naturel est en compétition avec d'autres formes d'énergie telles que le pétrole, l'électricité ou le charbon. Le gaz et le pétrole étant des produits très proches et substituables, leur offre est liée et leur prix sont fortement corrélés.

Comme la plupart des produits de base, les prix du gaz naturel sont cycliques. Leurs mouvements à la hausse est la conséquence d'une demande plus forte, qui va encourager l'exploration et le forage (comme cela c'est produit en 2000). Le temps de réponse de l'industrie à l'effet induit par les prix peut être plus ou moins long lorsque la production commence à croître, les prix vont tendre à chuter.

1.6 Marché

Structure de marché

La structure du marché du gaz naturel subit des mutations importantes à l'heure de la libéralisation. L'industrie traverse une phase de restructuration fondamentale, associée à une ouverture des marchés à travers le monde aux grandes entreprises du secteur, pour qui le gaz jouera un rôle clé. Il existe, une concurrence intense entre les compagnies pour pénétrer les marchés et contrôler les ressources d'exploitation.

Sur le marché Américain, le processus de libéralisation est déjà bien avancé puisqu'il est loin d'être un marché dont les prix sont stabilisés et contrôlés et dont les contrats sont à long terme. Ce marché est aujourd'hui un cadre dynamique et fortement concurrentiel caractérisé par des fluctuations de prix, un marché physique actif et une utilisation plus large des contrats à moyen terme. Ceci a eu pour résultante de changer fondamentalement la manière dont chacun des acteurs traditionnels de l'industrie opèrent : producteurs, entreprises de transport, entreprises étatiques et utilisateur industriel. De nouveaux acteurs émergent comme les intermédiaires assurant l'interface entre les acheteurs et les vendeurs de

gaz naturel.

Réserves et consommation du gaz naturel

Les principaux pays producteurs en 2000 sont les Etats-unis et la fédération de Russie avec respectivement 22,9% et 22,5% de la production mondiale. D'autres Etats possèdent également une certaine importance tels que la Canada, le Royaume-Uni, l'Algérie, l'Indonésie, l'Iran, les pays bas, la Norvège et l'Uzbekistan. Ces pays ont représenté à eux plus de 86% de la production totale de gaz naturel en 2000. A noter que l'Amérique du nord et l'ex Union soviétique produisent 59% de la production globale.

La production mondiale totale en 2000 était de 2422,3 milliards de mètres cubes en croissance de 43% par rapport à l'année précédente. Bien que la production ait augmenté dans toutes les régions, la croissance la plus rapide a été enregistre au Moyen-Orient et en Afrique. Pendant la décennie 90, la production a progressé dans toutes les régions sauf en ex Union soviétique. Une hausse de la production de gaz naturel dans le monde est anticipée en raison des projets d'exploration et d'expansion planifiée en prévision d'une demande future haussière.

Le gaz naturel représente près du quart de la consommation énergétique mondiale. Les principaux pays consommateurs de gaz naturel en 2000 sont les Etats-Unis, avec 27,2% de la consommation totale et la Fédération de Russie, avec 15,7%. L'Amérique du nord et l'ex Union soviétique ont consommé ensemble environ 55% du gaz naturel produit. La part de l'Europe dans la consommation totale de gaz naturel était de 19,1%. Ces trois zones représentent à elles seules les trois quarts de la consommation globale.

La croissance de la consommation était 4,8% en 2000, avec des taux plus élevés en Afrique (12,8%) et en Asie (7,8%). La consommation mondiale totale a représenté 2404,6 milliards de mètres cubes.

Le commerce international

Selon Cedigaz, seul 26,3% de la production commercialisée a fait l'objet d'échanges internationaux. Le commerce par tankers de GNL a représenté 21% du commerce international total.

La proportion très faible des échanges internationaux s'explique notamment par l'éloignement des sites de production par rapport aux lieux de consommation et aux coûts élevés du transport. C'est un secteur qui exige des investissements importants, la construction et l'exploitation des gazoducs et qui posent également de nombreux problèmes juridiques et logistique.

Les principaux pays exportateurs qui utilisent les gazoducs comme mode de distribution en 2000 sont la Fédération de Russie, le Canada, la Norvège, les Pays-Bas, l'Algérie et le Royaume-Uni. La première zone d'importation par gazoduc, indépendamment des Etats- Unis qui ont absorbé toutes les exportations canadiennes, est l'Europe.

La plus grande part du commerce international de GNL était représentée par les régions Asie-Pacifique, avec l'Indonésie, la Malaisie et l'Australie pour les pays exportateurs et le Japon comme principal pays importateur. L'Algérie et le Qatar sont également des exportateurs majeurs de GNL.

La filière mondiale du GNL selon le "World LNG Source Book 2001(Gaz Technology Institute)" est la suivante :

Douze pays possèdent des équipements de liquéfaction: Abou Doubai, l'Algérie, l'Australie, Brunei, l'Indonésie, la Libye, la Malaisie, le Nigeria, Oman, le Qatar, Trinité et Tobago et les Etats-Unis.

Trente-huit terminaux receveurs fonctionnent dans dix pays dont 23 au Japon, 3 en Espagne, 3 aux Etats-Unis, 2 en Corée, et 1 en Belgique, en Grèce en Italie, dans la Province chinoise de Taiwan, en Chine et en Turquie.

Le commerce régional

En raison de la faible proportion de gaz naturel échangée par rapport à la quantité produite, il n'existe pas véritablement de marché global, mais des marchés régionaux, qui possèdent des organisations différences. Les principaux débouchés sont l'Amérique de Nord, l'Europe de l'Ouest et l'ex Union Soviétique. D'autres marchés régionaux prennent de l'importance, tels que la région Asie-Pacifique et l'Amérique Latine. La demande en provenance d'Afrique, d'Asie du sud et de Chine est principalement satisfaite par des sources internes ou régionales. Le Moyen-Orient est essentiellement une région productrice.

Amérique du Nord

L'Amérique du nord est un marché presque autosuffisant. Le processus de libéralisation de ce marche a débuté dans les années 70, au Canada et aux Etats-Unis et ce sont ces pays qui ont été le plus loin dans l'ouverture de ce secteur à la concurrence.

Les Etats-Unis sont le premier producteur mondial et le premier consommateur de gaz naturel. Selon l'étude de l'USEA (United States Energy Association) "Vers une stratégie nationale de l'énergie", le nombre des consommateurs de gaz naturel aux Etats-Unis a augmenté depuis quelques années et représente environ 175 millions en 2001.

Europe de l'Ouest

Les réserves de gaz naturel en Europe de l'Ouest sont limitées. Elles comptent pour moins de 5% des ressources globales. Actuellement, le marché Européen est marqué par des changements structurels importants du processus de libéralisation. Les pays producteurs principaux sont les Pays-Bas, la Norvège et le Royaume-Uni. L'industrie du gaz naturel en Europe consiste principalement en des activités situées en aval de la production tels que le transport ou la distribution.

Plus de 30% de la consommation de gaz naturel à travers de gazoducs, par des importations en provenance d'ex Union soviétique et d'Algérie à travers des gazoducs ainsi que par du GNL en provenance d'Afrique du Nord. On s'attend à une progression de la dépendance face aux importations dans le futur, bien que l'offre soit considérée comme étant à une distance géographique raisonnable.

Ex Union soviétique

L'ex Union soviétique possède les plus grandes réserves mondiales de gaz naturel prouvées. La Fédération de Russie est le deuxième pays producteur et le premier exportateur. Le gaz naturel est le combustible prédominant en Russie, où il représente près de la moitié de la consommation intérieure. La fédération de Russie exporte entièrement le gaz qui n'est pas consommé par les domestiques. Avant la dissolution de l'Union soviétique, la majeure partie de ce gaz était exportée vers l'Europe de l'Est. Depuis lors, la Russie a continué de fournir la

CET et l'Europe de l'Est tout en essayant de diversifier géographiquement ses exportations, avec plus de 62% du volume exporté en dehors des zones traditionnelles. Outre la Russie, le Turkménistan est le seul exportateur significatif. L'industrie russe de gaz naturel est un monopole dominé par la société Gzprom, qui contrôle plus de 95% de la production.

Principaux marchés physiques

Traditionnellement, les contrats sur le gaz naturel étaient passés à long terme entre les compagnies de gaz naturel et les utilisateurs, avec des prix stables. Ils présentaient un niveau de risque très faible tant en ce qui concernaient l'offre que le prix, mais permettaient peu de flexibilité. L'importance de ces contrats a diminué notamment en raison de la libéralisation de l'industrie, alors que les marchés au comptant ont accentué leur présence. Ces derniers proposent une plus grande flexibilité en matière de compensation de l'offre et de la demande et une meilleure adaptabilité aux conditions du marché. Les acteurs du marché peuvent alors se constituer un portefeuille de contrats à court ou à plus long terme. Toutefois, il est à noter qu'encore aujourd'hui, la majeure partie du gaz échangé sur le plan international, l'est dans le cadre de contrats à long terme.

Les marchés au comptant sont généralement créés dans des zones où sont concentrés un grand nombre d'acheteurs, de vendeurs et de transporteurs. Ils sont situés près des grandes régions de consommation ou de production de gaz naturel. Des prix au comptant sont alors fixés en divers lieux. Les principales références en matière de prix spot en Amerique du nord sont : New York City Gate, Henry Hub Louisiana, Chicago City Gate, Katy Hub Texas, So. Calif. Border, AECO Hub (Canada).

1.7 La libéralisation du marché du gaz

Au cours des deux dernières décennies, la principale tendance du marché du gaz naturel s'est orientée vers la libéralisation, aussi bien dans les pays développés, qu'en voie de développement. On appelle souvent ce processus : le déréglementation, bien qu'il ne s'agisse pas d'une absence totale de règles.

secteur stratégique et trop important pour le laisser entre les mains du marché. Le gaz naturel était regardé comme un monopole naturel et des entreprises d'Etat contrôlaient en général cette industrie. Suite aux crises énergétiques des années 1970, le secteur a subi des réformes structurelles afin d'ouvrir le marché à la concurrence et de réduire les coûts, améliorer la performance économique et l'efficacité. Ces politiques de libéralisation prennent différentes formes et ne sont pas à la même vitesse selon les pays. Elles peuvent englober la privatisation, l'introduction de la concurrence basée sur l'accès des tiers à l'infrastructure d'offre de gaz, le démantèlement des monopoles d'Etat ou les réformes législatives. Le but est de réduire l'action directe des gouvernements sur les marchés et de fournir du gaz naturel à des prix fiables, transparents et concurrentiels.

Le processus de libéralisation a été initié, quelques années auparavant par des pays comme les Etats-Unis, le Canada, le Royaume-Uni ou l'Australie. Il est toujours en cours dans l'Union Européenne ainsi que dans divers autres pays.

Aux Etats-Unis, l'industrie de gaz naturel a traversé une phase de profonde mutation avec l'établissement du "Natural Gaz Policy Act" en 1978. L'industrie est passée d'un marché presque totalement réglementé à un marché libéralisé. L'Order 636 de 1992 de la "Federal Energy Regulatory Commission" exige que les entreprises de gazoducs séparent leurs activités de transport, de vente et de stockage, ce qui fut très important. Ainsi ces entreprises ont réduit leur champ d'activités : de vendeurs elles sont devenues transporteurs de gaz. De plus, les producteurs, les filiales des sociétés en charge des gazoducs, les distributeurs et les négociants ont la possibilité de jouer un plus grand rôle en matière d'approvisionnement en gaz naturel des utilisateurs.

Au sein de l'Union européenne, les gouvernements sont en train de réfléchir au cadre juridique à donner à l'industrie du gaz naturel. Dans le contexte de la Directive du Gaz Naturel 98/30 relative à l'ouverture de ce marché, des règles communes pour la transmission, la distribution, l'approvisionnement et le stockage du gaz naturel sont établies. Cette industrie devrait progressivement s'ouvrir à la concurrence afin d'atteindre d'ici 2008 au moins 33% de la consommation totale de gaz. Les niveaux de libéralisation en Europe sont différents d'un pays à l'autre. Par exemple, le Royaume-Uni étant le plus libéralisé et la France le moins.

Chapitre 2

Processus stochastiques et séries

chronologiques

2.1 Introduction

Un processus stochastique est une famille de variables aléatoires indexées par le temps dont l'objectif principal est la représentation des phénomènes aléatoires qui évoluent dans le temps. A à titre d'exemple, l'évolution des prix (Spot ou à Terme) du Gaz naturel ou d'autres biens sur leurs marchés appropriés peut être représentée par un processus stochastique. Une trajectoire (ou une réalisation) prise par un processus aléatoire représentant certain phénomène (physique, économique, écologique, biologique,...), constitue une série chronologique dont l'analyse a pour but la description des principales propriétés du processus générateur de cette dernière. Analyser une série chronologique revient à trouver un modèle mathématique adéquat décrivant le mécanisme ayant donné lieu à cette série temporelle. Le modèle adéquat obtenu sera par la suite utilisé selon les objectifs désirés, tels que la prévision ou le contrôle.

On constate ainsi que le concept des processus stochastiques joue un rôle primordial dans

la modélisation des séries chronologiques. Pour cela, allons présenter, dans un premier temps, les notions de base et les propriétés essentielles des processus aléatoires, en particulier celles de la famille des processus dits faiblement stationnaires ou encore de ceux qui peuvent être ramenés au cas stationnaire par le biais d'une transformation adéquate (ajustement d'une tendance déterministe, différence ordinaire, différence saisonnière, ...).

2.2 Processus stochastiques

Dans la suite (e, A, P) désigne un espace de probabilité et (E, .7) un espace probabilisable.

Définition 2.2.1

Un processus aléatoire ou encore stochastique noté {Xt, t E T} est une famille de

variables aléatoires, définies sur un même espace probabilisé (e, A, P) et à valeur dans l'espace (E, .7) appelé "espace d'états du processus stochastique" .

2.2.1 Classification des processus stochastiques

Les processus aléatoires sont généralement classés selon la dimension de leurs espaces des états, la dénombrabilité de leurs ensembles des indices T ou la dénombrabilité de leurs espaces des états

Ainsi, le processus {Xt, t E T} est dit scalaire si E C R et multivarié si E C R^r,m E N* -- {1}. De même, {Xt, t E T} est dit processus à temps discret si T est dénombrable et à temps continu si T est non dénombrable.

Remarques

1. Notons qu'une trajectoire du processus {Xt, t E T} est une suite de réalisations des variables aléatoires Xt, t E T.

2. Pour t fixé, Xt représente une variable aléatoire à valeurs dans E.

3. Lorsqu'on fixe l'issue w E e, Xt (w) est une fonction définie sur T.

4. Dans la suite de notre travail, nous considérons T = Z. Le processus {Xt, t E Z} est souvent appelé suite aléatoire.

2.2.2 Distribution de probabilité d'un processus aléatoire

La distribution de probabilité d'un processus aléatoire {Xi, t E Z} est caractérisée par les lois de toute sous-famille finie _Xi1, :::, Xin, n E N*, t1,
·.., tn E Z. Elle est généralement définie à travers la fonction de répartition d'une variable aléatoire

Définition 2.2.2

La fonction de répartition d'un processus aléatoire {Xi, t E Z} est définie pour tout

n E N*, (t1, :::, t_n) E Zⁿ₍ et (x1, ..., x_n) E Rⁿ, par :

Fxt₁,...,xt_r, x1, :::, xn) = P (Xi1 < x1, :::, Xin < xn)

2.2.3 Caractéristiques d'un processus stochastique

Parmi les caractéristiques les plus importantes d'un processus aléatoire, on distingue : la moyenne et la variance.

On appelle moyenne d'un processus, la fonction définie sur Z par :

m_i= E (Xi) t E Z.

De même la variance d'un processus est définie sur Z par :

2 X(t) = V (Xi) = E [(Xi --m_i)²] t E Z

2.2.4 Processus du second ordre

Un processus stochastique {Xi, t E Z} est dit de second ordre si son moment d'ordre deux est fini ; i. e. :

Vt E Z, E (X²_i) < oo

2.2.5 Fonction d'autocovariance d'un processus stochastique

La fonction d'autocovariance d'un processus aléatoire est donnée par : Cov (Xi, X_s) = E [(Xi -- m_i) (X_s -- m_s)] t, s E Z

2.2.6 Processus stationnaires

La notion de stationnarité joue un rôle crucial dans la théorie des processus aléatoires et particulièrement en analyse des séries chronologiques. Dans plusieurs problèmes du monde réel, on rencontre des processus aléatoires qui évoluent dans un état "d'équilibre statistique" dans le sens où les propriétés probabilistes et statistiques du processus ne changent pas dans le temps. De tels processus sont dits stationnaires. On distingue cependant deux modes de stationnarité, à savoir la stationnarité stricte et la stationnarité faible (du second ordre).

Processus strictement stationnaire (la stationnarité forte)

Grossièrement, un processus aléatoire est dit strictement stationnaire si sa loi de probabilité est invariante par translation dans le temps. Mathématiquement, le concept de stationnarité stricte est donné par la définition suivante:

Définition 2.2.3

Un processus stochastique IXt, t E Z} est dit strictement (ou fortement) sta-

tionnaire si pour tout n E N*, et pour tout n-uplet (t1, t2,..., t_n) E Z, i = 1, n , la distribution de probabilité conjointe du vecteur _(Xt1+h, ..., Xt_n+h) est la même que celle de (Xt₁, ..., Xt_n) Vh E Z. Autrement dit, si on a :

P (Xt1 < x1, ..., Xt_n < x_n) = P (Xt1+h < x1, ..., Xt_n+h < x_n) , V (x1, x2_,..., x_n) E Rⁿ, Vh E Z.

On note que toutes les caractéristiques (c'est à dire tous les moments) d'un processus strictement stationnaire sont invariantes dans le temps. Cette définition de la stationnarité est, cependant, trop forte et très exigeante et repose sur la connaissance de la loi conjointe du processus qui ne peut être connue en pratique, sauf dans des cas très spéciaux. Toutefois, plusieurs propriétés essentielles des processus aléatoires peuvent être obtenues juste à partir des moments de premier et du second ordre. La stationnarité de ces deux moments peut donc être suffisante pour expliquer la stationnarité du processus. Pour cette raison, on a besoin d'un concept de stationnarité moins fort et qui peut être rencontré dans la pratique.

Processus faiblement stationnaire (du second ordre)

Considérons un processus stochastique de second d'ordre IXt, t E Z} .

Définition 2.2.4

Le processus stochastique IXt, t E Z} est dit faiblement stationnaire si on a :

1) E (Xi) = E (Xi+h) = ~ (de moyenne constante), Vt E Z,

2) Cov (Xi, Xi+h) = E [(Xi - t_i) _(Xi+h - Ili+h)] = 'h, Vt, h E Z.

La fonction 'Yh est dite fonction d'autocovariance du processus.

Remarques

1. La fonction d'autocovariance d'un processus faiblement stationnaire dépend seulement de la différence des instants.

2. Dans les processus du second ordre, il est clair que la stationnarité stricte implique la stationnarité faible (la réciproque n'est pas vraie, sauf pour les processus Gaussiens).

Un processus {Xi, t E Z} est dit Gaussien si toute sous-famille finie du processus constitue un vecteur Gaussien. Autrement dit, pour tout n E N^* et (t1, t2_,..., t_n) E Zⁿ, le vecteur (Xi1, ..., _Xin) est Gaussien.

Processus bruit blanc(White noise)

Selon la théorie du signal, un bruit blanc est un bruit à intensité égale par rapport à toutes les fréquences dans une large bande. Par exemple, la musique Rock, le hurlement d'un moteur d'un gicleur, le bruit dans un super marché et le chuchotement de vilains étudiants dans une classe bruyante sont juste quelques exemples de bruits blancs. On emploie le mot "blanc" pour décrire ce genre de bruit en raison de sa similitude avec la "lumière blanche" qui se compose de toutes les différentes couleurs (fréquences) de lumière combinées ensemble.

En science appliquée le bruit blanc est souvent pris comme idéalisation pour représenter les phénomènes de fluctuations soudaines et extrêmement grandes. Mathématiquement, un bruit blanc est le processus de second ordre faiblement stationnaire le plus simple et le plus utilisé, en analyse des séries chronologiques dont la définition est la suivante

Définition 2.2.5

Un processus bruit blanc {€i, t E Z}, est une suite de variables aléatoires non corrélées de moyenne nulle et de variance constante, g². Un processus bruit blanc est donc caractérisé par la fonction d'autocovariance particulière suivante :

(

², h=0,

'Yh = E(€isi+h) = 0, h =6 0. Vt 2 Z

Lorsque de plus {€i} est une suite de variables aléatoires indépendantes alors {€i, t 2 Z} est dit bruit blanc fort.

2.2.7 Propriétés et estimation empirique de la fonction d'autocovariance

Rappelons que la fonction d'autocovariance d'un processus stochastique faiblement stationnaire {Xi, t 2 Z}, notée 'Yh, est définie par :

'Yh = cov (Xi, Xi_h) = E [(Xi - E (Xi)) _{(Xi_h} - E _{(Xi_h))],} Vh, t 2 Z,

On remarque que pour h = 0, l'autocovariance se réduit à la variance du processus Xi notée 'Y0.

Propriétés 2.2.6

a) La fonction d'autocovariance 'Yh satisfait la propriété suivante

'Y_h = 'Yh, Vh 2 Z, (fonction paire)

Donc, on peut dans la pratique, se restreindre aux autocovariances aux retards positifs, c'est-à-dire on peut, sans perte de généralité, prendre h 2 N.

b) On peut facilement, en utilisant l'inégalité de Cauchy-Shwarz, vérifier la propriété suivante

j'Yhj ~ 'Y0=Var(Xi) Vh,t2Z.

Autocovariance empirique

En pratique, la fonction d'autocovariance n'est pas connue, cependant elle peut être estimée, sur la base d'un vecteur aléatoire (X1, ..., XT)^', de taille T, par le biais de l'estimateur convergent ~b (.) dit autocovariance empirique, défini par:

b'Yh =	1 T--h	T P_h i=1		PT (Xi -- Xi ) (Xi_h -- Xi ) , avec Xi = 1 Xi Ti=1
b'Yh =	1 T--h	T P_h i=1	1 PT (Xi - Xi) (Xi_h - Xi), avec Xi = Xi. T i=1

Bien entendu, pour une série temporelle X1, X2, ..., XT, on a l'estimation empirique b'Yh :

2.2.8 Fonction d'autocorrélation

La fonction d'autocorrélation de retard h, Ph, h 2 Z, d'un processus, du second ordre, faiblement stationnaire de moyenne E (xi) = ~ et de variance Var (xi) = 'y0, notée Ph est définie par:

Ph =	Cov (xi, xi-h)	'yh 'y0	, Vh2Z.
	/V (xi)pV (xi-h)

Il est facile de vérifier que la fonction d'autocorrélation satisfait les deux propriétés suivantes, qui découlent directement des deux propriétés a) et b) de la fonction d'autocovariance Propriétés 2.2.7

1) Ph = P-h Vh2Z,

Donc on peut dans la pratique se restreindre aux autocorrélations pour h ~ 0.

2) P0 = 1, Vh2Z,

jPhj ~ 1, Vh2Z.

Autocorrélation empirique

L'estimateur de la fonction d'autocorrélation, bPh, est obtenu en remplaçant, dans l'expression de Ph, 'y0 et 'yh par leurs estimateurs b'y0 et b'yh, respectivement. En effet, on a

b'yh

, Vh2Z

bPh =

b'y0

Ce qui peut s'écrire, en tenant compte de la définition de l'estimateur empirique de la fonction d'autocovariance, sous la forme explicite suivante :

(x i - )

xi ) (xi-h - xi

, Vh2Z

T _P-h
i=1

T
T--h

(xi - )2

xi

_PT
i=1

b'yh

=

b'y₀

bPh =

Remarques

1. La représentation graphique de Ph est appelée "corrélogramme".

2. Si Ph décroît rapidement quand le nombre de retard augmente, cela signifie que la série est stationnaire, sinon elle est sans doute non stationnaire ou de mémoire longue.

2.3 Opérateurs et opérateurs de différence

Dans ce paragraphe on passe en revue les différents opérateurs et les différents opérateurs de différence, fréquemment utilisés en analyse des séries chronologiques, ainsi que leurs propriétés essentielles.

Opérateurs retard (Backward ) et avance (Forward)

Un opérateur retard B est une application dans l'ensemble des processus du second ordre qui associe à un processus {Xt, t E Z} le processus {Yt, t E Z} tel que :

Yt = B Xt = Xt_1.

Cet opérateur est linéaire et vérifie :

Bi Xt = Xt_i

De plus il est inversible (application bijective) et son inverse B_¹ = F appelé opérateur "avance" (Forward) est défini par :

FXt = Xt#177;1

On a également, Fⁱ Xt = Xt#177;i

Propriétés 2.2.8

1) B⁰Xt = Xt,

2) Si Xt = c, Vt E Z (c E R) : Bⁱ Xt = Bⁱ c=c VjE Z,

3) BⁱBⁱ Xt = B^i#177;i Xt = Xt_i_i V(i, j) E Z²,

4) B_ⁱXt = Xt#177;i Vi E Z; B_¹ = F,

5) (Bⁱ + Bⁱ)Xt = BⁱXt + Bi Xt = Xt_i + Xt_i V(i, j) E Z²,

1) _En

i=1

aiXt_i = (E aiBⁱ) Xt
·

i=1

_~00 00 00

7) E iXt_i = E Xt à condition que la série E j soit absolument

i=0 i=0 i=0

convergente.

On note que les propriétés précédentes sont satisfaites aussi par l'opérateur avance F. Opérateur de différence ordinaire

L'opérateur de différence première ordinaire noté V, associé au processus{Xt, t E Z} est défini par :

VXt = (1 -- B) Xt = Xt -- Xt_1, Vt E Z.

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 32 et par construction on obtient l'opérateur de différence d'ordre d (d E N), noté V^d tel que :

V^dXt=(1--B)^dXt, oùdEN,VtEZ. Opérateur de différence saisonnière

De même, on définit l'opérateur de différence saisonnière de saison S, noté VS, par: VSXt = (1 -- B^S) Xt, où S E N^*, Vt E Z.

Par construction, on obtient l'opérateur de différence saisonnière, de saison S, et d'ordre D (D E N), d'ordre S, noté VD S , donné par:

VD SXt = (1-- B^S)^DXt, 8t E Z.

2.4 Séries chronologiques

Les enregistrements, habituellement faits à des intervalles de temps souvent réguliers, des observations d'un phénomène économique, météorologique, biologique, démographique ... , sont fréquemment rencontrés en pratique. Ces données prises en ordre chronologique constituent une série chronologique ou encore une série temporelle. Cette série temporelle est souvent l'objet d'une analyse afin d'obtenir des renseignements sur le processus qui génère le phénomène observé, et de tirer par la suite des conclusions concernant les problèmes liés à ce phénomène.

Définition 2.4.1 :

Une série chronologique (ou temporelle) est une suite finie d'observations (xt)t=1;:::;T. Mathématiquement, une série chronologique est une réalisation (tra-

jectoire) d'un processus aléatoire.

2.4.1 Analyse des séries chronologiques

Le but d'une analyse statistique peut être descriptif qui consiste à dégager les caractéristiques particulières et désirables de la série, ou explicatif en essayant d'induire le mécanisme générateur de la série à l'aide des modèles mathématiques construits pour représenter au mieux les observations. La frontière entre le descriptif et l'explicatif n'est pas claire, puisque un modèle explicatif trop simple peut n'avoir qu'une valeur descriptive, et une analyse descriptive très poussée peut contenir une part d'explication. Le but final de l'analyse statistique peut être la prévision qui consiste à prédire des valeurs futures de la série à l'aide des observations présentes ou passées et cela n'est possible que si on dispose d'un modèle adéquat.

L'analyse statistique des séries chronologiques est souvent précédée par un traitement préliminaire de la série brute, et donc le premier pas d'une analyse statistique consiste à tracer le graphe représentatif de la série, ce qui est d'une grande importance car il nous permet d'avoir une idée générale sur le comportement de la série.

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 35 Composantes principales d'une série chronologique

Une série chronologique peut être considérée comme la "superposition" de plusieurs composantes : tendance, cyclicité, saisonnalité, aléas.

Tendance (T) : qui marque l'allure générale du phénomène(l'évolution générale de la série); elle se représente comme une fonction linéaire ou non linéaire du temps.

Cycle ou cycle conjoncturel (C) : regroupe les variations autour de la tendance avec des alternances d'époques ou de phases d'expansion et de contraction.

Variations saisonnières : Ce sont les variations liées au rythme imposé par les saisons

météorologiques, que ce soit directement ou indirectement par les activités économiques avec une période égale à l'année.

Variations accidentelles ou erreurs (€) : qui résultent de multiples causes et dont l'effet est souvent de faible intensité et de courte durée; elles sont de nature aléatoire.

Ces différentes composantes peuvent être combinées selon un des trois modèles (descriptifs) suivants:

Modèle additif: qui est sous la forme suivante :

Yt = Tt + St + Ct + "t. t2Z

Modèle multiplicatif:

Yt = Tt:St:Ct:"t:t 2 Z

Modèle mixte:

Tout autre modèle où additions et multiplications sont utilisées.

2.5 Modélisation des séries chronologiques

L'objectif de la modélisation explicative est de développer des modèles probabilistes permettant de décrire le comportement d'une ou de plusieurs séries chronologiques et de résoudre les problèmes liés à la prévision.

classe de modèles probabilistes suffisamment vaste. Une classe particulière de modèles fortement utilisés en pratique est la classe des modèles Autoregressifs moyenne mobile (ARMA). Cette classe de modèle n'est rien d'autre qu'une approximation d'une décomposition très connue des processus stationnaires, dite décomposition de Wold.

2.5.1 Décomposition de Wold

Avant de présenter brièvement, les modèles de séries chronologiques linéaires existants dans la littérature et les plus fréquemment utilisés dans la modélisation des séries chronologiques, il nous est paru indispensable, pour la bonne compréhension de la performance de ces modèles, d'énoncer le théorème de Wold (1938) qui établie une décomposition de chaque processus, de second d'ordre, faiblement stationnaire. Ce théorème, qui donne une justification théorique de l'utilité de la classe des modèles linéaires à coefficients constants, a donné un grand essor à la modélisation des séries chronologiques. En effet, le théorème de Wold (1938) est un théorème fondamental pour l'analyse des séries chronologiques stationnaires ou qui peuvent être stationnarisées par des transformations adéquates. Nous commencerons par donner l'énoncé de ce théorème, puis nous discuterons l'importance pratique de cette décomposition.

Théorème (Décomposition de Wold (1938))

Tout processus, du second ordre, faiblement stationnaire {Yt, t Z} possède une décomposition unique donnée par :

Yt = Ct + Xt,

telle que

Les deux processus Ct et Xt sont orthogonaux de plus le processus C _t est purement déterminable (singulier) et Xt est purement indéterminable (régulier). De plus ce dernier processus stochastique peut être représenté par une combinaison linéaire, du présent et du passé d'un processus bruit blanc, convergente (en moyenne quadratique) unique de la forme :

oùf"t_; t E Z} est un processus du second ordre bruit blanc dit processus d'innovation du processus.

Remarques

a) En notant _{Ht_1} Xt la projection orthogonale de Xt sur le sous-espace de Hilbert,H²(Xt_1, t)', l'innovation normée du processus n'est que l'erreur de prévision à l'horizon 1, c'est-à-dire elle peut s'exprimer comme suit :

"t=Xt^--Ht_1Xt; tEZ.

b) La composante Ct est une fonction déterministe qui peut être ajustée mathématiquement sans difficulté. Ainsi, l'intérêt d'un analyste de séries chronologiques va vers l'étude stochastique de la composante stochastique (non déterministe) Xt de la décomposition de Wold.

c) Dans le théorème de Wold, la condition de convergence en moyenne quadratique s'exprime par la condition suivante dite condition de sommabilité :

_P 1O.J1 <oc,avecO0=1.

i=0

d) D'après le théorème de Wold, si nous omettons la composante déterministe Ct, tout pro-

cessus faiblement stationnaire peut s'écrire comme une somme pondérée infinie conver-

gente, en moyenne quadratique, de chocs à l'instant présent et aux instants passés, ces chocs étant représentés par un bruit blanc de variance finie.

f) L'implication forte de ce théorème est que, si nous connaissons les pondérations Oj, et si nous connaissons la variance o-², nous pouvons proposer une représentation de n'importe quel processus stationnaire. Cette représentation est aussi qualifiée de moyenne mobile infinie.

2.5.2 Formule de convolution

Le théorème de Wold montre que tout processus, de second d'ordre, faiblement stationnaire, peut s'écrire sous la forme moyenne mobile infinie dite représentation de Wold. Néanmoins, on montre que cette forme est équivalente à la forme suivante dite formule de convolution (forme d'un modèle autorégressif infini), qui exprime le processus bruit blanc en

¹L'ensemble des variables aléatoires de carrée intégrable (dont les moments d'ordre deux existent) consti-

.,/

tue un espace vectoriel normé, dont la norme 11X11 = V ar (X). Il est également "complet" et constitue donc une structure d'un espace de Hilbert.

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 38 terme du présent et du passé du processus stochastique sous-jacent :

00

Et = _P P. Xt_ = Xt + P1 Xt_1 + P2 Xt_2 + P3 Xt_3 + ... , avec P0 = 1, (2.5.2)

i=0

00

où la suite infinie _P P_{j Xt_j,} avec P₀ = 1, est convergente en moyenne quadratique, au-

i=0

trement dit les coefficients P₁, P₂, P₃, P4, ..., satisfont la condition

00

_P ~~P7 ~~ <oc, avecP0=1.

i=0

On conclue donc qu'un processus faiblement stationnaire peut toujours s'écrire de façon équivalente sous la forme d'un modèle moyenne mobile infini ou un modèle autorégressif infini.

2.6 Classe de modèles ARMA (p, q)

On a vu que tout processus, de second ordre purement déterminable, stationnaire peut être représenté, d'après le fameux théorème de Wold, par l'une de deux formes équivalentes à savoir, la forme d'un modèle autorégressif d'ordre éventuellement infini et la forme d'un modèle moyenne mobile d'ordre éventuellement infini, données respectivement, par:

Et = Xt + P1 Xt_1 + P2 Xt_2 + P3 Xt_3 + ..., t E Z, Modèle autorégresif d'ordre infini

et

Xt = Et + 01 Et_1 + 02 Et_2 + 03 Et_3 + ..., t E Z, Modèle moyenne mobile d'ordre infini

Chacune de ces deux représentations nécessite éventuellement l'utilisation d'un nombre infini de paramètres qui sont, en pratique, inconnus et qu'on a à estimer, sur la base d'une série de taille finie; ce qui n'est pas possible en pratique. Par ailleurs, ces deux représentations s'expriment à travers des séries convergentes dont les termes sont necessairement convergent vers zéro. Il est donc possible qu'à partir d'un certain rang suffisamment grand,on puisse tronquer ces séries infinies en négligeant les restes. Ainsi deux représentations particulières et intéressantes de ces deux formes peuvent être évoquées, la première représentation particulière correspond au P _p =6 0 et P = 0, Vi ~ p + 1, dans la première représentation, ce qui

donne le modèle suivant dit modèle autorégressif d'ordre p, noté AR (p) :

et la deuxième représentation particulière correspond à 0_q =6 0 et 0i = 0, Vj > q + 1, dans la seconde représentation, ce qui donne le modèle suivant dit modèle moyenne mobile d'ordre q, noté MA (q) :

Xt = Et + 01 Et-1 + 02 Et-2 + 03 Et-3 + .. . + 0 q Et-q, t E Z, (2.6.2)

Il est clair que si on exprime un processus stochastique satisfaisant le modèle (2.6.1) sous la forme de Wold, on obtient une représentation moyenne mobile d'ordre infini. De même si on exprime un processus stochastique satisfaisant le modèle (2.6.2) sous la forme de convolution, on obtient une représentation autorégressive d'ordre infini.

Dans le cas où le modèle autorégressif (réciproquement modèle moyenne mobile) est d'ordre infini, on peut, pour satisfaire au principe de parcimonie (ce principe consiste à trouver le modèle d'ordre le plus petit possible), utiliser un modèle de série chronologique qui contient en même temps la partie autorégressif d'ordre p et la partie moyenne mobile d'ordre q, ce qui donne le modèle dit autorégressif moyenne mobile d'ordre (p, q) donné par :

Xt -- (1 Xt-1 -- '2 Xt-2 -- ... -- ç_p Xt-p = Et -- 01 Et-1 -- 02 Et-2 -- ... -- 0_q Et-q, (2.6.3)

Le reste de ce chapitre est consacré à l'étude des propriétés et les caractéristiques essentielles des modèles autorégressifs purs d'ordre p (AR (p)), des modèles moyenne mobile purs d'ordre q (MA (q)) et les modèles autorégressifs moyenne mobile d'ordre (p, q) (ARMA (p, q)).

2.6.1 Processus autoregréssif

La définition d'un processus autoregréssif d'ordre p, noté AR (p) est la suivante : Définition 2.6.1 :

Un processus du second ordre {Xt, t E Z} est dit admettre une représentation AR d'ordre p, s'il est solution de l'équation aux différences stochastique suivante : Xt -- ~1Xt-1 -- 02Xt-2 --
·
·
· -- OpXt-p = Et (2.6.4)

où Et est un processus bruit blanc de moyenne nulle et de variance u²

En introduisant l'opérateur de retard B dans l'équation (2.6.4) peut se réécrire comme suit : (1) (B) Xt = Et,

où (1)(B) est le polynôme de retard, de degré p, donné par :

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 40 ~ (B) = 1 ~ _Pp çbjB^j avec çbj 2 , et çb _p =6 0,

j=1

Notion de causalité

Définition 2.6.2

Un modèle de série chronologique (linéaire ou non linéaire) de la forme : Xt = g (Xt_1, Xt_2, ... Xt_p; t, et_1, et_2, ... _{Et_q)} ,

où Et est un bruit blanc, est dit causal si, et seulement si, on peut exprimer le
processus stochastique Xt sous forme d'une combinaison linéaire (finie ou infinie)
convergente, en moyenne quadratique, du présent et du passé du bruit blanc €t.

Remarques

? 1. La causalité n'est pas une propriété du processus {Xt} à lui seul mais plutôt de la relation avec {€t}. Ainsi si le modèle est causal, le processus {Xt}, puisque s'exprimant en fonction de bruit blanc stationnaire, est stationnaire.

? 2. On remarque, d'après la définition du concept de causalité, qu'un modèle moyenne mobile d'ordre fini est toujours causal.

Condition nécessaire et suffisante de causalité d'un AR (p)

Le théorème suivant établi une condition nécessaire et suffisante pour q'un modèle autorégressif d'ordre p, soit causal.

Théorème 2.6.1

Une condition nécessaire et suffisante pour que le modèle autorégressif Xt - _{~1Xt_1} - _{~2Xt_2} - ~ ~ ~ - ÇbpXt_p = "t,

soient causal est que les racines de l'équation caractéristique

zp - Çb1z ^p_1 - Çb2z ^p_2 - ~
·. - çb p = 0,

soient en valeurs absolues strictement supérieurs à 1, i. e., z > 1.

Fonction d'autocorrélation d'un AR

Soit {Xt} un processus stochastique autoregressif d'ordre p vérifiant l'équation aux différences stochastiques

Xt = q1Xt_1 + q2Xt_2 + ... + çbpXt_ p + Et, Vt 2 Z, (2.6.5)

où {€t} est bruit blanc de moyenne nule et de variance finie cr² (non corréléXt_j, j ~ 1) :

Equations de Yule-Walker

Les équations de Yule-Walker sont des relations (équations) qui lient les paramètres d'un modèle AR aux autocovariances du processus {Xt} figurant dans le modèle. Elles peuvent être exploitées, par exemple, pour l'estimation des paramètres lorsque des estimations des autocovariances sont disponibles et vice-versa.

Multiplions l'équation (2.6.5) par _Xt-h et prenons l'espérance des deux côtés, on obtient :

E(XtXt-h) = 01E(Xt-1Xt-h) + 02E(Xt-2Xt-h) + ... + 0pE(Xt-pXt-h) + E(EtXt-h),

a) Pour h = 0, on trouve :

-₀ = 01^-Y1 + 02~2 + 0₃~₃ + ... + 0_p~_p + a2

b) pour h > 0, on obtient le système d'équations :

^-Yh = 01-h-1 + 02'h-2 + 03'h-3 + . .. + 0p~h-p, 1 < h < p

en divisant les deux cotés de l'égalité précédente par -y0 on obtient :

Ph = 01Ph-1+ 02Ph-2+ 03Ph-3+ ... + 0pPh-p, 1 < h < p. (2.6.6)

Si nous réitérons l'équation (2.6.6) pour h = 1, p, nous obtenons le système d'équations suivant dit système de Yule-Walker :

{

P1 = 01+ 02P1+ ... + 0pPp-1, P2 = 01P1+ 02 + ... + 0pPp-2, . . . Pp = 01P1 + 02P2 + ... + 0p,

(2.6.7)

Ce système peut s'écrire sous la forme matricielle suivante :

[

11

01 02 03 ... 0p

]

=

[

P1 P2 P3 ... Pp

]

1 P1 P2
·
·
· Pp-1

P1 1 P1
·
·
· Pp-2

P1 P2 1
·
·
· Pp-3

... ... ...

. .

. .

. .

Pp-1 Pp-2 Pp-3
·
·
· 1

1 P1 P2
·
·
· Pp-1

P1 1 P1
·
·
· Pp-2

P2 P1 1
·
·
· Pp-3

. . .

. . .

Pp-1 Pp-2 Pp-3
·
·
· 1

1 _-1 0

_{C B}

_{C B}

_{C B}

_{C B}

_{C B}

_A @

... ... ...

₀
B B B B B @

=

₀
B B B B B @

01

02

03

₁
AC C C C C

...

0_p

P₁

P2

P3

...

₁
AC C C C C

Pp

pourvu que la matrice du système soit inversible.

Estimation de Yule-Walker

Dans la pratique les autocorrélations, P1, P2, , P_p, du processus générateur de la série chro-
nologique sous-jacente, sont inconnues. Néanmoins, sur la base d'une série x1, ..., xT, en les
remplaçant, dans le système d'équations de Yule-walker par leurs estimations empiriques bP₁,

bP2, -,

bPp, et en résolvant les équations obtenues, on obtient les estimations,

^b01,

^b02, :::,

^b0p,

dites estimations de Yule-Walker des paramètres inconnus, 01, 02,:::, 0_p

₀
B B B B B B @

=

₀
B B B B B @

01

02

03

₁
AC C C C C C

...

^b0_p

1 bP1bP2
·
·
· Pp-1'./Ô1 1 bP₁
·
·
· Pp-2

P2 bP1 1
·
·
· Pp-3

...

...

Pp-1 Pp-2

...

. . .

. . .

^bPp-3
·
·
· 1

1 _-1 0

bP1

P2

.

P3

₁
AC C C C C

...
Pp

_{C B}

_{C B}

_{C B}

_{C B}

_{C B}

_A @

pourvu que la matrice du système précédent soit inversible.

La résolution des équations de Yule-walker peut être accomplie récursivement, de façon élégante et rapide, en appliquant l'algorithme récursif de Durbin-Levinson qui est présenté dans la section suivante.

Fonction d'autocorrélation partielle

Soit {Xt; t E Z} un processus stochastique, du second ordre, faiblement stationnaire, donné par l'équation aux différences stochastique suivante :

Xt =(k,1Xt-1 + ::: + (Pk,kXt^-k + E?⁾, t E Z

où ne^e)o est un processus bruit blanc, de variance constante c²k et cp k_,i, i = 1, 2, ..., k, est le

i--ième paramètre du modèle autorégressif d'ordre k. En considérant une suite de modèles autoregressifs {AR (k) , k = 1, 2, 3, _:}, d'ordre k, donnés par l'équation aux différences précédente, on peut établir la suite de système de Yule-Walker lui correspondant donnée par :

Pj = (Pk1Pj-1 +(Pk2Pj-2 + ... +(Pkk, j= 1, k

où _çbkj est le j ième coefficient du processus autoregréssif d'ordre k. Ce système d'équations, en (Pk1, (Pk2, ..., _(Pkk, peut s'écrire sous la forme matricielle suivante :

₀
B B B B B @

₁
AC C C C C

₀
B B B B B @

=

(Pk,1
(Pk,2

(Pk,3
...

(Pk,k

...

...

...

1 P1 P2
·
·
· Pk-1

P1 1 P1
·
·
· Pk-2

P2 P1 1
·
·
· Pk-3

. . .

. . .

Pk-1 Pk-2 Pk-3
·
·
· ¹

1 _-1 0

_{C B}

_{C B}

_{C B}

_{C B}

_{C B}

_A @

P1

P2

P3

...

₁
AC C C C C

Pk

1 P1
·
·
· Pk-2 P1

P1 ¹
·
·
· Pk-3 P2

P2 P₁
·
·
· Pk-4 P3

. .

. .

. .

Pk-1 Pk-2
·
·
· P1 Pk

~~~~~~~~~~~~~~~~

~~~~~~~~~~~~~~~~

... ... ...

,avec			~~~~~~~~~~~
~~~~~~~~~~~	=6 0.

Il est important, dans l'étape de l'identification de la méthodologie de Box et Jenkins, comme on le verra ultérieurement, de connaître le dernier coefficient, _(Pkk, k = 1, 2, 3, ..., K, où K est un entier positif suffisamment grand, de chaque modèle autorégressif de la suite considérée. Il est connu que ce coefficient est donné par :

(Pkk =

~~~~~~~~~~~~~~~~

~~~~~~~~~~~~~~~~

1 P1 P2
·
·
· Pk-1

P1 1 P1
·
·
· Pk-2

P2 P1 1
·
·
· Pk-3

... ... ...

. .

. .

. .

Pk-1 Pk-2 Pk-3
·
·
· ¹

1 P1 P2
·
·
· Pk-1

P1 1 P1
·
·
· Pk-2

P2 P1 1
·
·
· Pk-3

... ... ...

. .

. .

. .

Pk-1 Pk-2 Pk-3
·
·
· ¹

k= 1, 2,3, ...,K

₈

<>>>>>>>>>>>>> >

>>>>>>>>>>>>>>:

(Pk,k =

...

...

...

~~~~~~~~~~~~~

,

...

...

...

1 P1 P2
·
·
· Pk-1

P1 1 P1
·
·
· Pk-2

. .

. .

. .

Pk-1 Pk-2 Pk-3
·
·
· ¹

1, k = 1,

~~~~~~~~~~~~~

(

k => 2, (2.6.8)

~~
Pk

~~~

=

Pk

1 P₁
·
·
· Pk-2 P₁

P1 ¹
·
·
· Pk-3 P2

. .

. .

. .

Pk-1 Pk-2
·
·
· P1 Pk

~~~~~~~~~~~~~

~~~~~~~~~~~~~

Définition 2.6.3

Le dernier coefficient, d'un modèle autorégressif d'ordre k, k = 1, 2, 3, ..., K, noté (Pkk, comme étant une fonction, en k, est par définition la fonction d'autocorrélation partielle de retard k. Il est donné par :

~~

où ~ _k et ~

~ est le déterminant de la matrice _k est donnée par :

k

1 P1 ~ ~ ~ Pk_2 P1

P1 1 ~ ~ ~ Pk_3 P2

...

. ..

Pk_1 Pk_2 ~ ~ ~ P1 Pk

... ... ...

₀
^BB_B@

~ k =

, k= 2, 3, ..., K;

_1
AC_C^C

~ k est ainsi la matrice _k dans laquelle on a remplacé la dernière colonne par le vecteur

[P₁....Pk1^', k= 2, 3, ..., K.

On remarque que la fonction d'autocorrélation partielle mesure la corrélation linéaire entre Xt et _{Xt_k,} après avoir retirer l'effet deXt_1, Xt_2, ..., Xt_(k_1).

Remarques

On constate facilement de la définition de la fonction de corrélation partielle qu'un modèle autoregressif pur d'ordre p, AR (p), est caractérisé par un "cut-off" dans sa fonction de corrélation partielle, après son vrai ordre p. Autrement dit, la fonction de corrélation partielle, 'kk, d'un modèle autoregréssif pur d'ordre p vérifie :

'kk=0, Vk~p+1

Algorithme récursif de Durbin

La fonction d'autocorrélation partielle joue, comme la fonction d'autocorrélation simple, un rôle prédominant dans l'étude du problème de l'identification des ordres des modèles de séries chronologiques linéaires. Le calcul de la fonction d'autocorrélation partielle, _'k;k, à

partir de (2.6.8), est très lourd, car il nécessite, pour chaque ordre, le calcul de deux déterminants de dimension k x k. Cependant, cette fonction peut être calculée, facilement, en utilisant la méthode de calcul récursif établie par Levinson (1947) et Durbin (1960). Théorème 2.6.2. Algorithme de Durbin (1960)

Les paramètres 'k,1, 'k,2, ..., 'k,k, solutions des équations de Yule-Walker, du modèle autorégressif (1.6.4), sont donnés par les formules récursives suivantes :

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 45 Pk,j = 'k-1_;j -- Pk,k Vk-1,k-j, j = 1, ..., k; k = 2, ..., K,

p(k) -- (Pk,k =		k-1 Ei1 p(k	, k = 2, ..., K, avec (,01,1 = p(1).
		k-1 Ei1 p(i)
1 --

0^-j_c = Cfjc (1 -- C_IOL_k) ; a0 = '7₀

Bien entendu, dans la pratique les autocorrélations, p1, p2, ..., p_p, sont remplacées par leurs estimations, 791,^-P2, ..., o_p, alors en appliquant l'algorithme récursif de Durbin-Levison on obtient les estimations, ça 1, ça2, ..., ça_p, de Yule-Walker des paramètres autorégressifs inconnus, 4⁰1,(1)2, ..., Vp
·

Ça'k,j = ^b'k-1_;j -- ^b'k_;k ^b'k-1_;k-j,j = 1, ..., k; k = 2, ..., p,

Ça.k,k =

^b'k-1_;iî)k-i

, k = 2, ..., p, avec i;c31_,1 = 79(1).

k-1 1-- E i=1

^bPk-1,i pi

k-1

E

i=1

î)k --

b0²k = b~2k (1 k) ;₀= '7₀

2.6.2 Processus moyenne mobile

La définition d'un processus moyenne mobile d'ordre q, noté MA (q) est la suivante :

Définition 2.6.4 :

Le processus du second ordre {Xt, t E Z} est dit admettre une représentation MA

d'ordre q, noté MA (q), s'il est solution de l'équation aux différences stochastique suivante :

Xt = Et -- 01 Et-1 -- 02 Et-2 --
·
·
· -- 0_q Et-q, (2.6.9)

où Et est un processus bruit blanc de moyenne nulle et de variance u².

En introduisant l'opérateur de retard B le modèle précédent peut se réécrire comme suit : Xt = 0 (B) Et,

où 0 (B) est le polynôme de retard, de degré q, donné par :

q

0 (B) = 1 -- 0j B^j où 0j E R, et 0_q =6 0,

j=1

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 46 Notion d'inversibilité

Définition 2.6.5

Un modèle de série chronologique (linéaire ou non linéaire) de la forme : Xt = g (série

Xt-2, ... Xt-p; Et, Et-1, Et-2, ... _Et-q) ,

où {Et} est un bruit blanc, est dit inversible si, et seulement si, on peut exprimer le processus {Et} comme combinaison linéaire (finie ou infinie) convergente, en moyenne quadratique, du présent et du passé du processus stochastique {Xt}.

Remarques

On remarque, d'après la définition du concept d'inversibilité, qu'un modèle autoregréssif d'ordre fini est toujours inversible.

Condition nécessaire et suffisante d'inversibilité d'un MA (q)

Le théorème suivant établi une condition nécessaire et suffisante pour q'un modèle moyenne mobile d'ordre q, soit inversible.

Théorème 2.6.3

Une condition nécessaire suffisante pour que le modèle moyenne mobile

Xt - _01Xt-1 - _02Xt-2 -
·
·
· - 0qXt-q = Et,

soit inversible est que les racines de l'équation caractéristique zp - 01z^p-1 - 02z^p-2 -
·
·
· - 0_q = 0,

sont en valeurs absolues strictement supérieures à 1, i.e., 1z1 > 1.

Fonction d'autocorrélation d'un MA

Soit {Xt} un processus stochastique moyenne mobile d'ordre q vérifiant l'équation aux différences stochastique

Xt = Et - 01 Et-1 - 02 Et-2 -
·
·
· - 0_q Et-q, Vt E z, (2.6.10)

où {Et} est bruit blanc de moyenne nulle et de variance finie u² (qui est non corrélé avec le passé du processus).

La fonction d'autocovariance de {Xt} est donnée par :

'Yh =

(1 + 0q + 0²+ ... + 0²_q) o^-2, h = 0,

(-0h + 010h+1+ ... + 0q-h0q)0², 0 < h < q,

0, h > q.

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 47 D'où on obtient la fonction d'autocorrélation de ce processus :

Ph =

'Yh 'Y0

=

8 <>> >>:

1, h = 0,

-0h + 010h+1 + ... + 0q_h0q , 0 <h q,

1+02 ₁ +02 ₂ +...+02 q

0, h > q.

On remarque que la fonction d'autocorrélation s'annule à partir d'un décalage supérieur à q, on dit qu'elle est tronquée au-delà du retard q. Donc on peut identifier un MA(q) à partir du corrélogramme qui s'annule à partir d'un retard supérieur à q.

Fonction d'autocorrélation partielle d'un modèle MA(q)

Afin de calculer les autocorrélations partielles d'un processus stochastique satisfaisant à un modèle moyenne mobile pur d'ordre q, MA(q), on doit, d'abord, exprimer le processus d'innovation (bruit blanc), Et, de ce modèle en terme du processus Xt et de son passé Xt_1, Xt_2, ..., _{Xt_} ,....Il est connu que l'innovation Et, d'un modèle moyenne mobile inversible, s'écrit sous forme d'une combinaison linéaire infinie, convergente en moyenne quadratique, du processus et de son passé :

00

Et = a0 Xt + a1 _{Xt_1+} ^a2 Xt_2 + a3 Xt_3 + ... = _P ai Xt_i.

i=0

Ainsi un processus moyenne mobile pur d'ordre fini q, peut s'écrire sous forme d'un modèle autoregressif d'ordre infini. D'où, selon le résultat obtenu concernant la fonction de corrélation partielle d'un modèle autoregressif, la fonction d'autocorélation d'un modèle moyenne mobile pur d'ordre fini q, montre une décroissance mais pas de cut-off comme dans le cas d'un modèle autoregressif pur.

Prenons par exemple le processus MA(1) suivant

Xt = Et - 0Et_1,

avec 0 < 1, et Et un bruit blanc de moyenne nulle et de variance u².

On peut, facilement, vérifier par récurrence que cette expression est équivalente à l'expression suivante qui est convergente en moyenne quadratique :

00

Et =Xt+0Xt_1+0²Xt_2+0³Xt_3+... = _P 0i Xt_i.

i=0

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 48 Afin de calculer les autocorrélations partielles d'un processus MA, on utilise l'algorithme récursif de Durbin. On sait par ailleurs que la fonction d'autocorrélation de ce processus est donnée par

₈

<> >

>>:

Ph =

1, h = 0,

0

-1+02, h=1,

0, h > 2.

Les autocorrélations partielles sont donc données récursivement par l'algorithme de Durbin, en effet, on a en première itération :

0

011 = P1 = - 1 + 02,

022 =

P2 - 011P1 P²₁

= - ,

¹ - 0111P1 1 - P²₁

P3 - P21P2 022P1 022P1

= - .

¹ - 021P1 ^-022P2 ¹ - 021P1

033 =

et

P1

021 = 011 - 022011 = 011(¹ - 022) = 1 - P²1

Ainsi on en déduit la valeur de l'autocorrélation partielle d'ordre 3

3

P₁

033 = 1 -P21

On peut ensuite poursuivre les calculs pour déterminer les autocorrélations partielles d'ordre

supérieur, en exprimant les autocorrélations partielles en fonction de 0 pour obtenir une suite récurrente.

Après calcul, on montre que la formule de récurrence pour les autocorrélations partielles

d'un MA (1) est alors donnée par :

0kk =

0^k (1 - 0^2) 1 -02(k+1)

Deux cas peuvent se présenter

a) Si 0 > 0, alors les valeurs de _0kk sont négatives

b) Si 0 < 0, alors les autocorrélations alternent de signe.

2.6.3 Modèles ARMA

Un modèle ARMA est une composition d'un modèle autoregréssif AR et d'un modèle moyenne mobile MA.

Définition :

Le processus du second ordre {Xt, t E Z} est dit admettre une représentation ARMA, d'ordre p et q notée ARMA (p, q), s'il est solution de l'équation aux différences stochastique suivante :

Xt -

Pp j=1

ojXt-j= et -

q j=1

Ojet-j,

ou encore :

4) (B) Xt = 0 (B) et.

où {et} est bruit blanc de moyenne nulle et de variance o^-2

Ainsi nous constatons que les processus AR (p) et MA(q) sont des cas particuliers du processus ARMA (p, q). Un AR (p) n'est qu'un ARMA (p, 0) et un MA(q) n'est qu'un ARMA (0, q).

Condition de causalité et d'inversibilité

Théorème :

Soit {Xt, t E Z} un processus ARMA (p, q) défini par

4) (B) Xt = 0 (B) et.

tel que les polynômes 4) (.) et 0 (.) d'ordres respectifs p et q n'ont pas de racines communes. Alors, le modèle précédent est dit inversible si et seulement si les racines de l'équation caractéristique associée à 0 :

z^q - 01 z^q-1 - 02 z^q-2 -
·
·
· - B_q = 0

sont en module strictement supérieures à l'unité, i. e., jzj > 1. Et il est causal si et seulement si les racines de l'équation caractéristique associée à 4) :

zp - o1 z^p-1 - o2 ^zp-2 -
·
·
· -o_p =0.

sont en valeurs absolues strictement supérieures à 1, i.e., jzj > 1

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 50 Fonction d'autocorrélation d'un ARMA (p, q)

Pour calculer les autocorrélations d'un modèle ARMA, on procède comme dans le cas des modèles AR. En effet, en multipliant les deux membres de l'égalité suivante

Xt - _{O1Xt_1} - 02Xt_2 -
·
·
· - O_pXt__p = Et - 01Et_1 - _{02"t_2} -
·
·
· - 0 qEt_q par Xt_h et en prenant l'espérance, on obtient :

1

'0

[E (XtXt_h) - çb1E (Xt_1Xt_h) - - ç_pE (Xt__pXt_h)] =

1

'0

[E (etXt_h) - 01E (Et_1Xt_h) - - 0_qE (et__qXt_h)]

Puisque let} est un bruit blanc et par conséquent non corrélé avec le passé du processus Xt, i.,e, E (etXt_h) = 0, Vh =6 0, on obtient

Ph - _{O1Ph_1} - - OpPh_p = 0, Vh > q

Soit finalement

Ph = E^pi=1 OiPh_i,Vh > q.

Fonction d'autocorrélation partielle d'un modèle ARMA (p, q)

La fonction d'autocorrélation partielle d'un processus stochastique satisfaisant à un modèle autoregréssif moyenne mobile d'ordre (p, q) , ARMA (p, q) , peut être calculée en écrivant d'abord le modèle sous forme d'un AR (oo) :

Et = 0 Xt + Q1 Xt_1 + ,82 Xt_2 + ~3 Xt_3 + ::: =

00 E i=0

ei Xt_i.

De l'expression précédente on remarque que la fonction autocorélation d'un modèle autoregressif moyenne mobile d'ordre (p, q) ne montre pas un cut-off comme dans le cas d'un modèle autoregressif pur.

2.6.4 Modèles ARIMA(p,q)

cette hypothèse n'est pas tenable. Pourtant, si l'on considère, par exemple, les différences premières (ou en général les différences d'ordre d) d'une série, l'hypothèse de stationnarité devient plus plausible; auquel cas, il existe un modèle ARMA (p, q) qui représente adéquatement une telle série. Ainsi, il est naturel de considérer une nouvelle classe de modèles, dite ARMA, intégrée d'ordre d, dont la différence d'ordre d est un ARMA. Une telle classe est notée par ARIMA (p, d, q).

Un processus du second ordre {Xt, t Z} est dit admettre une représentation ARIMA d'ordre p, d, q s'il est solution de l'équation aux différences stochastique :

~ (B)V^dX _t =e(B) "t

où {€t} est un bruit blanc de variance cr², VXt = Xt - _{Xt_1;} et où les racines de CI" (.) et e (.) sont en module supérieures à 1

La relation précédente peut s'écrire également comme :

' (B)Xt =e(B) "t

avec: ço(B) = ~ (B)(1 -B)^d = (1 -ço₁B -::: - op+dB^p+d)

Cette dernière équation est analogue à l'équation de définition d'un modèle ARMA (p + d, q) avec toutefois la différence fondamentale que le polynôme ço (.) admet 1 comme racine multiple d'ordre d (cette racine est dite racine unitaire).

Les modèles ARIMA sont préconisés pour la modélisation des séries chronologiques présentant une tendance marquante. Cependant il y a lieu de distinguer entre deux types de tendances dont l'amalgame conduit à des modélisations aberrantes. Parmi les processus non stationnaires à tendance, on cite deux grandes catégories à savoir, la classe des processus à tendance déterministe (notée TS, Trend Stationary) et la classe des processus à tendance stochastique (DS, Difference Stationary).

Les processus TS sont des processus non stationnaires que l'on peut écrire sous la forme suivante :

Xt =ft+Yt

où {Xt} est le processus en question, {Yt} est un processus stationnaire et ft est une fonc-
tion déterministe de t, qui peut être l'équation d'une droite, une parabole,.. .L'estimation
de ft conduit à un processus stationnaire. On constate donc que la non-stationnarité d'un

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 52 processus TS est de type "déterministe".

Un modèle est dit à tendance stochastique s'il contient au moins une racine unitaire. Dans ce cas, la non-stationnarité du processus est de type stochastique.

Caractéristiques des processus TS

Supposons qu'un processus peut s'écrire comme la somme d'une fonction déterministe du temps fi et d'un élément stochastique stationnaire €i (bruit blanc).

Xi = fi + "i

Si par exemple, fi est une fonction polynomiale d'ordre 1 alors

Xi = + !3t + E:i

Supposons en outre que €irBB (0, u²). On a alors les propriétés suivantes :

a) E (Xi) = E (a + !3t + €i) = a + !3t,

b) V(Xi) = E(Xi - E(Xi))² = u2

c) cov (Xi, Xi+h) = E [(Xi - E (Xi)) E _(Xi+h - E (Xi+h))] = E ("i"i+h) = 0. Nous constatons dans ce cas que le processus TS est caractérisé par une espérance mathématique à tendance déterministe, une variance constante et des covariances nulles. Dans un tel modèle, la réalisation des prévisions est délicate, du fait que l'intervention d'un choc à un instant t n'a aucune influence sur l'erreur de prévision de la série à l'instant t + h (les effets d'un choc sur Xi sont transitoires)

Caractéristiques des processus DS

Considérons un processus DS de la forme

Xi _=pXi-1 +!3+ "i,

où {€i} est un processus bruit blanc de variance u² avec p = 1.

Nous pouvons écrire ce processus sous une autre forme :

Xi =p² Xi-2+p!3+ p"i-1 +!3+ "i,

Xi = p³Xi-3 + p²!3 + p²"i-2 + p!3 + pei-1 + !3 + "i.

Par récurrence on obtient

Xi = p^TXi-~ + !3 P-1

j=0 pj + P-1

j=0 p^j"i-j.

Si l'on suppose maintenant que p = 1 et que r = t on aura donc Xi =X0+t!3+Pi j=1€j.

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 53 où X0 désigne le premier terme du processus {Xt}.

Passons maintenant à l'étude des caractéristiques de ce processus

( )

X0 + t~ + Pt

a) E (Xt) = E j=1 "j= X0 + tj,

Pt 2 tP )

_Pt

b) V (Xt) = E (Xt -- E (Xt))² = E j=1 "j = E "i "j ,

i=1 j=1

=

"2 i +

_Pt
i=1

"i"j

_Pt
i=1

_Pt
i=1

_1
AC

_Pt
j=1

i6=j

₀

_B

= E @

E(€2 _i )+0 =to² ",

c) cov(Xt,X₅) = E[(Xt -- E(Xt))E(X₅ -- E (X_s))] ; [( Pt ) eP )]

= E sj "j ;

i=1 j=1

=Min(t,s)a² Vt=6s

Nous constatons que le processus DS est caractérisé non seulement par une non-stationnarité de type déterministe, provenant du fait que son espérance est une fonction évolutive dans le temps, mais aussi par une non-stationnarité de nature stochastique par le biais des perturbations dont la variance est une fonction affine du temps et dont le coefficient est la variance du processus bruit blanc; de ce fait nous pouvons conclure que dans ce type de processus, chaque perturbation aléatoire est persistante et possède un effet durable et cumulatif sur le comportement de la série.

Connaissant les différences qui existent entre les processus TS et DS, nous concluons que la distinction entre ces deux types de processus est d'une grande importance, puisque si l'on est en présence d'un processus TS et que l'on traite comme un processus DS, et vice versa, on aboutit à une mauvaise stationnarisation.

Conséquences sur un processus TS, d'une stationnarisation de type DS Considérons un processus TS

Xt=a+/Jt+€t où "teBB(0,a²)

Appliquons à ce processus un filtre aux différences première

zXXt =(1--B)Xt =Xt --Xt_1 =j+ "t-- "t_1

Analysons les caractéristiques de LÏX

a) E (~Xt) = E (/ + €t - €t_1) = /3,

( ₎2

b) V (~Xt) = E ~Xt - E (~Xt)= E (€t - €t_1)² = 2a2 " = 'y0,

c) cov(~Xt, IXt_h) = E [(~Xt - E (zXt)) E _{(IXt_h} - E (IXt_h))], = E [(€t - €t_1) (€t_h - _{€t_h_1)]} ,

₈

<

:

=

2a², h=0,

-², h =+_ 1,

0, h=60.

d'où la fonction d'autocorrélation suivante

₈

<>

>:

Ph =

1, h=0,

1

-₂, h=#177;1,

0, h=60.

On remarque que LïXt n'a pas les caractéristiques d'un bruit blanc, on conclue donc qu'un
filtre aux différences a créé une perturbation artificielle puisqu'il apparaît une autocorrélation

1

des erreurs à l'ordre 1 égale à -₂.

Tests de racine unitaire

La perception des processus TS et DS n'est pas une tâche facile, c'est pour cette raison qu'on a recours aux tests de racine unitaire. Ces tests, et comme l'indique leur nom, portent sur l'existence ou non d'une racine unitaire de la fonction caractéristique du modèle de série chronologique candidat à décrire le processus sous-jacent. Si une telle racine existe, alors la transformation adéquate pour la stationnarisation de ce processus est bien la différence ordinaire, et dans ce cas on dit qu'on est face à un processus non stationnaire de type DS. Le principe de ces tests consiste à tester l'hypothèse nulle de racine unitaire (le processus est non stationnaire DS) contre l'hypothèse alternative d'absence de racine unitaire.

Il existe un grand nombre de test de racine unitaire, parmi ces tests nous allons citer les tests de Dickey-Fuller simple et augmenté (1979).

Test de Dickey-Fuller simple (DF)

Trois modèles de base pour la série Xt ont été proposé par Dickey et Fuller. Modèle (1) : modèle sans constante ni tendance déterministe

Xt = PXt_1 + €t

CHAPITRE 2. PROCESSUS STOCHASTIQUES ET SÉRIES CHRONOLOGIQUES 55 Modèle (2) : modèle avec constante sans tendance déterministe

Xt = c + pXt_1 + E:t

Modèle (3) : modèle avec constante et tendance déterministe

Xt = c+bt+pXt_1 + "t

Le but de ce test est de tester l'hypothèse nulle de racine unitaire contre l'hypothèse alternative d'absence de racine unitaire.

L'hypothèse du test est la suivante

{

H0:p=1, H1 : p <1 En pratique, on estime les modèles suivants

Modèle (1)^'

lxXt _{=qXt_1} + "t

Modèle (2)^'

1XXt _{=c+qXt_1} + "t

Modèle (3)^'

~Xt=c+bt+qXt_1+€t, avecq=p--1

( ) On compare la t--statistique t ~ , associée à q, à la valeur critique ttabul~e avec t ~ = tel que si {t ~ <ttabul^~e = on rejette H0, t ~ ~ttabul~e= on accepte H0

^bq--1 b"

Notons que ces tests ne seront pas effectué sur les trois modèles (1)^', (2)^' et (3)^'. En pratique on adapte une stratégie séquentielle en trois étapes

Etape 1 : Dans cette étape on estime le modèle (3)^' et on teste la signification de la tendance déterministe.

Si la tendance n'est pas significativement différente de zéro (t--statistique de la tendance est inférieure aux valeurs critiques de la tendance tabulées par Dickey-Fuller) on passe à l'étape 2

Si la tendance est significativement différente de zéro, on teste l'hypothèse nulle de

racine unitaire en comparant t ~ aux valeurs tabulées par Dickey-Fuller. Si on accepte H0, Xt est non stationnaire de type DS.

Si on rejette H0, Xt est de type TS.

Etape 2 : Cette étape n'est applicable que si la tendance n'est pas significative, donc on estime le modèle (2)^' et on teste la signification de la constante.

Si la constante n'est pas significative on passe à l'étape 3

Si la constante est significative, on teste l'hypothèse de racine unitaire.
Si H0 est acceptée, donc Xt est non stationnaire de type DS.

Si H0 n'est acceptée, Xt est stationnaire.

Etape 3 : Cette étape n'est applicable que si la constante dans le modèle n'est pas significative. On estime dans ce cas le modèle (1)^' et on teste l'hypothèse nulle de racine unitaire. Si H0 est acceptée, Xt est non stationnaire de type DS.

Si H0 est rejetée, Xt est stationnaire.

Test de Dickey-Fuller augmenté (ADF)

Les tests ADF s'éffectuent exactement comme les tests DF sur les modèles suivants : Modèle (1) :

LXt = ~Xt_1+ X ^p çbj¹XXt_ + €t

j=1

Modèle (2) :

/XXt _{=c+çbXt_1} + X ^p çbj/XXt_ + €t

j=1

Modèle (3)

lxXt =c+bt+çbXt_1 + X ^p çbj/XXt_ + €t

j=1

Remarques

? 1. Avant d'appliquer le test ADF il faut préciser l'ordre de décalage p tel que le critère

d'Akaïke soit minimum.

? 2. Les tables de Dickey-Fuller figurent dans l'annexe A.

2.6.5 Modèles saisonniers SARIMA

Il est bien connu que certaines séries peuvent être caractérisées par une allure périodique; par exemple, les données relatives à un même mois de différentes années ont tendance à se trouver de façon analogue par rapport à la moyenne annuelle. Ainsi, il serait intéressant de faire intervenir, dans un modèle ARIMA, des retards multiplesde 12. Pourtant si rien n'empêche à ce que l'on prenne des valeurs de p et q suffisamment grands pour que ces retards soient pris en compte, il n'en demeure pas moins que le nombre de paramètres soit très grand, de sorte qu'il est impossible d'estimer un tel modèle. Box et Jenkins (1970), ont cependant proposé une classe particulière de modèles dites : classe de modèles ARIMA saisonniers dont la forme est du type suivant :

Vd p (B) VD S P (B) Xt = e_q (B) eQ (BS) "t

où {€t} est un bruit blanc de variance ² et où:

S : période de la saisonnalité.

V = 1 - B; VS = 1 - B^S; _p, p, e_q, eQ sont des polynômes de degrés p, P, q, Q dont les racines sont de module superieur à 1.

Un processus {Xt} satisfaisant la relation précédente est appelée processus SARIMAS ((p, d, q) , (P, D, Q)). On note par ailleurs que les séries saisonnières peuvent être détectées en examinant les fonctions d'autocorrélation d'autocorrélation partielle empiriques, dès lors que celle-ci, prennent des grandes valeurs en module pour les indices multiples de S.

L'identification de S se fait généralement à travers des connaissances à priori, des type des données.. .Par exemple, souvent S = 12 pour des données mensuelles, S = 7 pour des données hebdomadaires, S = 4 pour des données trimestrielles...

Chapitre 3

Méthodologie de Box et Jenxins

3.1 Introduction

Bien qu'ils ne représentent souvent qu'une approximation simplifiée de la réalité, les modèles stochastiques stationnaires (ou ceux qui peuvent être rendus stationnaires à travers certaines transformations) tels que les modèles ARIMA, SARIMA, VARMA, etc., sont les plus répandus et les plus utilisés dans l'analyse des séries chronologiques. A partir du début des années 70 et avec l'apparition du fameux livre de Box et Jenkins (1970) ces modèles ont fait l'objet d'une littérature surabondante propulsée par les travaux de ces deux auteurs qui ont rendu célèbres ce genre de modèles, en proposant un ensemble de techniques permettant la construction du meilleur modèle susceptible de représenter adéquatement la série chronologique sous étude. Depuis, l'ensemble des méthodes impliquées dans la construction du modèle stochastique est connu sous le nom de méthodologie de Box-Jenkins. Schématiquement, cette méthodologie englobe trois phases essentielles à savoir : l'identification du modèle paramétrique, l'estimation de ses paramètres et les tests permettant la validation du modèle construit.

Celui-ci étant obtenu,il peut être exploité entres autres pour la prévision et le contrôle. Si la série montre une allure stationnaire, on montre qu'il existe toujours deux entiers p et q tels que le modèle ARMA(p, q) dont les paramètres sont bien spécifiés soit le plus adéquat. Lorsque la série exhibe une non-stationnarité apparente, par exemple quand le graphe associé contient une tendance globale ou une périodicité apparente, des transformations peuvent dans certains cas la ramener à une série à caractère stationnaire, et là on dit que la série a été stationnarisée. Ainsi, la recherche d'un modèle ARMA(p, q) se fait de manière séquentielle.

La première phase d'identification consiste à déterminer des valeurs vraisemblables des ordres p et q du modèle ARMA que l'on veut construire. Bien entendu des opérations préliminaires, si nécessaires, doivent être précédemment effectuées pour ramener la série à une allure stationnaire. Par exemple, une transformation logarithmique pour atténuer les grandes variations de la série, une différentiation ordinaire dans le cas de présence d'une tendance et une différentiation saisonnière s'il y a lieu d'une saisonnalité. A la sortie de cette étape, plusieurs couples de valeurs de p et q peuvent être retenus. Une fois le modèle identifié, l'estimation de ses paramètres est sûrement l'étape la plus importante dans la construction de celui-ci. Elle constitue la partie mécanique de la méthodologie. Plusieurs méthodes d'estimations sont envisageables en fonction des ordres du modèle retenu et des caractéristiques du processus ARMA postulés, pour justement optimiser et la vitesse de calcul et la précision des estimations. L'étape d'estimation étant achevée, le modèle est complètement spécifié et doit subir des test de validité à travers la troisième étape pour justement vérifier s'il représente assez bien la série. Après avoir vu globalement en quoi consiste la méthodologie de Box-Jenkins, il convient à présent d'exposer avec un peu plus de détail chacune de ses étapes en commençant par la phase d'identification.

3.2 Identification du modèle

En premier lieu, on examine le graphe représentatif de la série chronologique sous-jacente. Ceci peut nous donner une idée préliminaire sur le comportement de la série (stationnarité, tendance, saisonnalité...). Comme cité plus haut, si par exemple, la série exhibe une tendance et/ou une saisonnalité, des transformations adéquates doivent être appliquées à cette série afin de la stationnariser, car la méthodologie de Box-Jenkins est conditionnée par la stationnarité de la série. L'idée générale de l'identification consiste à comparer la structure des corrélations estimées que présente la série à travers le corrélogramme (diagrame représentatif des autocorrélations estimées simples et partielles) avec la structure de corrélation théorique exhibée par des modèles bien connus. Ainsi l'étude du corrélogramme est trés utile pour la détermination des ordres p et q, puisque les fonctions d'autocorrélation simple et partielle peuvent indiquer la présence d'un modèle moyenne mobile ou autoregressif respectivement. Plus précisément si la fonction d'autocorélation simple décroît rapidement vers zéro et la fonction d'autocorrélation partielle présente un cut-off après p retard, on peut conclure que la série provient d'un processus autorégressif d'ordre p (AR(p)). Par contre si l'autocorrélation simple présente un cut-off après un q retards et que l'autocorrélation partielle décroît rapidement vers zéro, alors on peut en déduire que la série est générée à partir d'un modèle moyenne mobile d'ordre q, MA(q). Evidemment, il se peut aussi que les fonctions d'auto- corrélation simple et d'autocorrélation partielle ne présentent aucune forme spécifique, on constate alors dans ce cas qu'on est en présence d'un processus autoregréssif moyenne mobile ARMA(p, q). On note que cette étape dite identification à priori, n'est pas une tache aisée tant et demande beaucoup d'expertise ce qui révèle une part de subjectivité. Il existe cependant des méthodes d'identification (voir plus bas) plus effectives, basée sur des critères d'information.

Critères d'information

Ils existent des critères d'informations qui sont utilisés, comme guide, dans le choix du modèle, ce qui nous permet d'éviter la sélection arbitraire des paramètres p et q du modèle. parmi ces critères, ils existent les critères d'information qui mesurent l'écart entre la vraie loi inconnue et le modèle proposé. Les estimateurs de la quantité d'information qui ont été proposés sont :

1.AIC = log b² + 2(p+ q)

N (Akaïke 1969)

2.BIC = log b² + (p + q)log ^NN (Akaïke 1977)

Le critère de choix consiste à minimiser AIC et/ou BIC.

3.3 Estimation des paramètres

Il existe un grand nombre de méthodes d'estimation qui peuvent être classées en deux grandes catégories générales : les méthodes d'estimation utilisant directement les données et les méthodes qui n'utilisent les données qu'à travers des transformations de celles-ci en résumés statistiques. Parmi les méthodes de la première classe nous citons en particulier la méthode du maximum de vraisemblance et ses différentes approximations (ces approximations sont astreintes à préserver quelques propriétés asymptotiques telles que la convergence et l'efficacité asymptotique) et la méthode des moindres carrés et ses variantes. La méthode du maximum de vraisemblance est conditionnée par l'hypothèse de normalité des processus sous-jacents. Si cette hypothèse n'est pas vérifiée, il est possible d'utiliser cette méthode comme si l'hypothèse de normalité était vérifiée, l'estimateur ainsi obtenu est dit estimateur du quasi (ou pseudo) maximum de vraisemblance. Parmi les méthodes de la seconde classe, probablement l'approche commune consiste à transformer les données en un ensemble fini de résumés statistiques (moyenne empirique, covariance empirique) sur la base de quoi on estime les paramètres du modèle (estimateur de Yule-Walker, estimateur de Durbin-Levinson,...). Concernant l'estimation des modèles ARMA, la méthode des moindres carrés (conditionnelle et non conditionnelle) fut l'une des premières utilisées et avait montré des résultats satisfaisants, mais le besoin croissant de l'analyse des séries chronologiques a eu pour conséquence, la naissance de nouveaux problèmes pour lesquels cette méthode est devenue aussi loure qu'imprécise. Avec l'amélioration des performances des ordinateurs ainsi que l'apparition de nouveaux algorithmes, la méthode du pseudo maximum de vraisemblance s'est révélée d'une importance capitale grâce à ces propriétés désirables tant du point de vue théorique que pratique. En effet, cette méthode a donné beaucoup de satisfaction aussi bien pour la précision des résultats obtenus que pour la stabilité et la rapidité des calculs. Son principe consiste à optimiser, donc à évaluer plusieurs fois, une fonction non linéaire dont l'expression explicite

n'est pas connue, en inversant à chaque itération une certaine matrice. Plusieurs algorithmes ont vu le jour, afin de palier aux carences dû à l'inversion des grandes matrices, pour justement réduire le temps de calcul et l'espace mémoire. Le schéma 3:1 donne un aperçu sur les différentes méthodes d'estimation utilisées (maximum de vraisemblance, moindre carrés, critère Bayesien...) et les modèles identifiés (AR, MA, ARMA,...).

3.4 Validation

Au début de cette étape on dispose de plusieurs modèles, dont on a estimé les paramètres, que l'on doit valider. Pour ce faire, il existe plusieurs type de tests que l'on peut les regrouper comme suit :

a) Tests numériques : ces tests concernent la procédure numérique d'optimisation utilisée pour l'estimation des paramètres. En général la fonction critère (maximum de vraisemblance, moindres carrés, critère Bayesien...) sur laquelle se fonde l'estimation est très complexe pour pouvoir l'optimiser à travers une méthode analytique. Donc l'emploi des routines d'optimisation numériques est nécessaire. Cependant ces méthodes peuvent ne pas converger et même si elles convergent, elles atteignent des optimums locaux seulement. Les tests numériques permettent justement de répondre à ce genre de questions.

b) tests sur le modèle

Le premier test qu'on peut effectuer est le test de l'hypothèse nulle p^' = p - 1 et q^' = q, i.e., qu'on cherche à savoir si on peut diminuer l'ordre du processus autoregréssif d'une unité. Autrement dit, on test l'hypothèse nulle du processus ARMA(p - 1, q) (i.e.ç p = 0) contre l'hypothèse alternative de processus ARMA(p, q) (i.e.ç _p =6 0). Ce test est très simple puisqu'il s'agit de tester la significativité du coefficient çb_p.

_p

Pour cela, on calcul la statistique de Student de q : t p = , et la règle du test est la

b~_p

suivante :

~~ --Si ~ ~~ --Si ~

~~ t p ~ <t1_ 2 , on accepte l'hypothèse nulle de processus ARMA(p - 1, q). ~~ t p ~ ~ t1_ 2 , on rejette l'hypothèse nulle et retient un processus ARMA(p, q).

( 1 - ~ ~

Où t1_ 2 est le quantile d'ordre de la loi de Student à (T - h) degrés de liberté. h

2

étant le nombre de paramètres estimés.

Remarque

Il est aussi possible de tester l'hypothèse nulle p^' = p et q^' = q - 1, ou encore l'hypothèse

' '

p= p + 1 et q= q, ou l'hypothèse p^' =p et q^' =q+1.

c) tests sur les résidus

Ces tests aident à vérifier si les résidus estimés forment un bruit blanc. Parmi ces tests on cite les tests suivants :

-- test "portmanteau" (Box-Pierce 1970)

Ce test est fondé sur la statistique Q = T _XH bP2 _h (be). où bPh (be) est le coefficient d'autocorré-

h=1

lation d'ordre h des résidus estimés, et H est le nombre maximal de retard.

Les hypothèses de ce test sont les suivantes :

J

H0 : P₁ = ::
·Ph = 0, non significativement différent de zéro H1 : j tq P₇ =6 0, significativement différent de zéro
Les règles du test sont :

--Si Q <x2 _{(1_a)} (H - p - q) on accepte H0

--Si Q > x2 (1_a) (H - p - q) on refuse H

Avec x2 (1_a) (H - p - q) est le quantile d'ordre (1 - a) de la loi x² à (H - p - q) degrès de liberté.

-- test de Durbin-Watson

Le test de Durbin-Watson permet de détecter une autocorrélation des résidus d'ordre 1, sous la forme

bet = P^bet_1+71t

où _t r' N(0, o-² ~) et bet = yt - byt est le résidu de l'estimation du modèle, avec byt est la prévision de yt faite à t - 1. Les hypothèses du test s'écrivent comme :

J

H0: P=0 H1 P=60 Pour tester l'hypothèse H0, la statistique de Durbin-Watson utilisée est :

_PT (- et - - et_1)²

DW=

t=2

_PT be2 t

t=1

Cette statistique est comprise entre 0 et 4 et vaut 2 lorsque P = 0. Durbin et Watson ont tabulé les valeurs critiques de DW au seuil 5% en fonction de la taille de la série et du nombre de variables explicatives.

d) Test de normalité des résidus (Test de Jaques-Béra (1984)) :ce test plus récent, ne
figurent pas dans la méthodologie proposée par Box et Jenkins (1970). Il est basé sur la
notion d'applatissement et de symétrie (Kurtosis et skewness). Soit jUk le moment d'ordre

k de la distribution postulée. On appelle skewness, le coefficient S = 3 2/3 2 coefficient K = 4 . Alors sous l'hypothese de normalité on a: 2 2 r ) r ) S ~ N 0; T6 24T et K ~ N 3; Le test de Jarque-Bera repose sur la statistique		et Kurtosis le
T JB= 6	S2+ 24 (K_3)2 T

pour tester les hypothèses suivantes :

H0 : La distribution des résidus suit une loi Normale au seuil a

H1 : La distribution des résidus ne suit pas une loi normale au seuil a

Ainis les règles du test sont les suivantes : Si JB <X2 _{(1_a)} alors on accepte H0 Si JB ~~2 _{(1_)} alors on accepte H0

3.5 Prévision

Les organismes et les établissements des secteurs de développement sont confrontés à planifier pour le futur dans une atmosphère d'incertitude. Cette incertitude provient du fait que les évènements aléatoires futurs influent considérablement sur les facteurs essentiels sur lesquels se basent leurs plans d'action.

Il existe une diversité de méthodes de prévision. Le choix de l'utilisation d'une méthode de prévision, que ce soit parmi les plus simples ou les plus sophistiquées, dépend essentiellement de la spécificité des données et de la nature de l'information disponible concernant la grandeur aléatoire à prédire.

3.5.1 Méthodes de prévision à court et à moyen terme

Critères d'optimalité de la prévision

Soit _Xt+h la valeur future à prévoir, à partir de l'instant présent t, de la variable Xt+h. Notons _bxt+h la valeur prédite, à partir de l'instant t, à l'horizon h, de la vraie valeur inconnue Xt+h en se basant sur l'ensemble d'information disponible It.

La variable aléatoire _et;h exprimant l'erreur commise en estimant la valeur de _Xt+h par

la valeur de prévision

b Xt+h est donnée par : et;h = Xt+h -

^bXt+h.

L'erreur quadratique moyenne de la prévision est donnée par:

[( _)2] [( ₎2_] ( ₎2

Q = E _Xt+h - ^bXt+h = E _Xt+h - E( ^bXt+h) + ^bXt+h - E( ^bXt+h)

Prévision optimale (au sens des moindres carrées)

La prévision optimale, au sens du critère des moindres carrées est donnée par l'espérance conditionnelle suivante ^bXt+h = E(Xt+h/It)

En pratique, la loi de probabilité conditionnelle est rarement connue, et même si elle était connue, le calcul de cette espérance est souvent très compliqué et peut donner une fonction non linéaire complexe. Pour surmonter ces difficultés, on se restreint à la recherche de la fonction de prévision dans la classe des fonctions linéaires en les observations présentes et passée, c'est à dire qu'on cherche une fonction de prévision optimale parmi les fonctions linéaires des données de It.

3.5.2 Méthodes d'extrapolation (méthodes de prévision en séries chronologiques)

Généralités sur la prévision (à court et moyen terme)

Les différentes méthodes de prévision ne permettent pas de prévoir un changement d'évolution dû à un changement dans les structures économiques, puisque rien dans le passé ne l'indique. La qualité de prévision dépend de l'horizon h et est meilleure lorsque h est petit.

Considérons le modèle ARIMA(p, d, q) écrit sous la forme suivante :

(B) Xt = e (B) Et, (4.3.1)
où (B) = ~ (B)V^d

La prévision optimale Xt+h, h > 0 faite à la date t est notée Xt+h ou ^bXt(h), avec t l'origine de la prévision et h son horizon. Une observation _Xt+h générée par le processus (4.3.1) peut être exprimé par l'une des trois formules suivantes :

--1. Formule déduite de la forme autoregressive moyenne mobile du processus L'équation (4.3.1) peut s'écrire sous la forme suivante :

Xt = O1Xt-1 + 02Xt-2 -
·
·
· + 0p+dXt-p-d + Et - _O1Et-1 - 02Et-2 -
·
·
· - OqEt-q

Donc

Xt+h = O1Xt+h-1 + 02Xt+h-2 -
·
·
· + OpXt+h-p-d + Et+h - _611Et+h-1 - 02Et+h-2 -
·
·
· - OqEq

2. Formule déduite de la forme moyenne mobile du processus

D'après le théorème de Wold (1938) (voir paragraphe 2.5.1), Xt+h peut s'écrire comme suit :

cx,

Xt+h = _P j Et+h-j, où 0 = 1 j=0

D'une manière équivalente, le modèle peut s'écrire sous la forme tronquée suivante : Xt+h = Et+h + 1 Et+h-1 Et+h-q_q

q

Xt+h = j Et+h-j

j=0

-- 3. Formule déduite de la forme autoregressive du processus

La forme autoregressive permet d'avoir la relation suivante :

Xt+h = Et+h -			cx, j=1	7r^.X 3 t+h-j
pour h > 1 on a : Xt+h=-	cx, j=1	7r X 3 t+h-j

Nous pouvons donc dire que pour faire la prévision d'un processus à la date t pour la date t+ h, Box et Jenkins ont proposé trois formes de base de prévision : la première forme de base s'obtient en se basant sur la forme autoregressive moyenne mobile du processus, la seconde et la troisième s'obtiennent en se basant respectivement sur les forme moyenne mobile et

autoregressive du processus.

b

Notons que la prévision Xt(h ) est aussi l'espérance mathématique de _Xt+h conditionnelle en Xt, _Xt-1, :::donc les trois modèles de base de prévision s'écrivent comme suit :

a) Première forme de base : ^bXt (h) = E _(Xt+h/ Xt, Xt-1..) ^bXt(h) = O1E _(Xt+h-1 Xt, ..) + ::: + Op+dE (Xt+h-p-d/ Xt, ..) -- O1E (Et+h-1/Xt, ..) - :::

-- OqE (Et+h-q/ Xt,
·
·) + E (Et+h/ Xt,
·
·)

b) Deuxième forme de base : ^bXt(h) = E (Xt+h/ Xt, Xt-1
·
·)

^bXt(h) = 1E( Et+h-1/ Xt, ..) +
·
·
· + _{h-1E(Et+1/Xt,..)} + hE(EtiXt,..)+... + h+1E(Et-1iXt,)+
·..+E(Et+hiXt, --)

c) Troisième forme de base : ^bXt(h) = E (Xt+h/ Xt, Xt-1..)

^bXt(h) =

cx, j=1

~jE(Xt+h-j I Xt, Xt-1..) + E (et+h I Xt, Xt-1..)

Pour calculer les espérances conditionnelles figurant dans les trois modèles de base, il faut savoir que :

8 E (Xt-j I Xt, Xt-1)= Xt-j <> > E (Xt+j I Xt, Xt-1::) =^bXt(j) >>: E (Et-j/Xt, Xt-1 · ·) = Et-j = Xt-j -- ^bXt-j-1(j) E (et+j I Xt, Xt-1..) = 0

j = 0,1, ... j = 1, 2, ... j = 0,1, ... j = 1, 2, ...

Remarque

Dans ce qui suit nous allons utiliser la première forme de base de prévision pour sa simplicité.

Chapitre 4

Application de la méthodologie de

Box et Jenkins

4.1 Etude de la série des prix spot du gaz naturel à Pensylvania (Pi)

4.1.1 Identification et estimation

Considérons la série Pt qui représente le prix du gaz naturel sur le marché régional de Pensylvania de Janvier 1989 à Février 2004 (les données ont pour unité de mesure le dollar par mettre cube ($/m³)). En observant la représentation graphique de cette (Figure 1.1) série nous constatons qu'elle possède une tendance à la hausse avec une variabilité qui paraît de plus en plus grande . Afin de dissiper les variations ou encore de stabiliser la variance de cette série, nous proposons de lui appliquer une transformation logarithmique. La série ainsi transformée, notée LP _t (Figure 1.2) garde la même allure que la série Pt exhibant ainsi une tendance à la hausse, et semblant donc non stationnaire au sens de la moyenne.

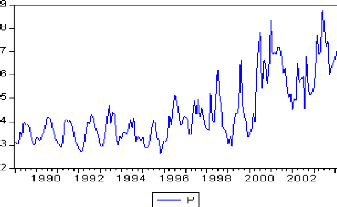
Figure (1.1)

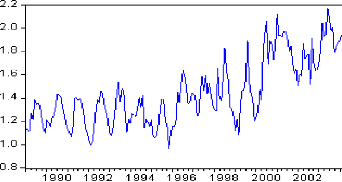
Figure (1.2)

En analysant le corrélogramme associé à la série LP _t (Figure 1.3) nous constatons que la série n'est pas stationnaire puisque sa fonction d'autocorrélation simple et partielle diminuent lentement et qu'elle possède une saisonnalité d'ordre 12 puisque la fonction d'autocorrélation simple possède des valeurs importantes aux retards 1, 12, 24... .

Afin de traiter l'effet de saisonnalité sur notre série ou encore de la stationnariser nous lui avons appliqué la différence saisonnière d'ordre 12, la série ainsi désaisonnalisée est notée

SLPt.

Figure (1.3)

Nous remarquons que la fonction d'autocorrélation simple de la série désaisonnalisée SLP _t diminue rapidement, nous pouvons donc dire qu'elle est stationnaire (Figure 1.4).

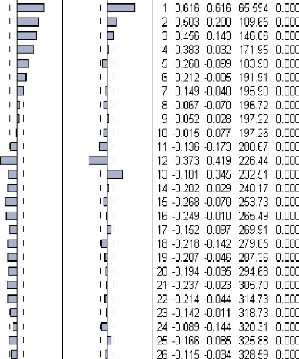
Figure (1.4)

Pour confirmer ou infirmer notre hypothèse consistant à ce que la série désaisonnalisée est stationnaire, nous avons appliqué le test de Dickey-Fuller sur la série SLP _t qui nécessite tout d'abord de sélectionner le nombre de retard p, nous avons alors choisi le retard qui minimise le critère d'Akaïke et qui est 2. Nous avons commencé par l'estimation du modèle (3)

2

Modèle (3) : LXSLP t = c + bt + çbSLPt_1 + _X çbjLXSLPt_j + Et

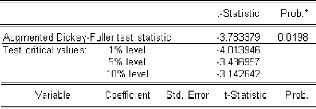
De la table ci-dessus nous constatons que la tendance n'est pas significativement différente de zéro puisque sa t-statistic (0.956) est inférieure aux valeurs critiques 3.46, 2.78 et 2.38 tabulées par Dickey-Fuller respectivement aux seuils 1%, 5% et 10%. Nous avons donc par la suite estimé le modèle (2)

2

Modèle (2) : LXSLP t = c + çbSLPt_1 + _X çbjLXSLPt_j + Et

j=1

Des résultats de l'estimation du modèle (2), reportés dans la table 1.1, nous constatons que la constante n'est pas significativement différente de zéro puisque sa t-statisique (1.06) est inférieure aux valeurs tabulées par Dickey-Fuller aux seuils 1%, 5% et 10% qui sont respectivement égales à 3.18, 2.52 et 2.16.

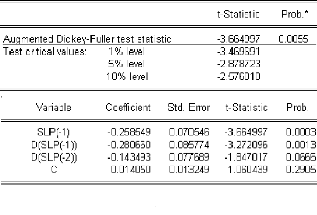
Table (1.1)

Du fait que l'estimation de la constante est statistiquement nulle, nous avons estimé le modèle sans intercept, autrement dit nous avons estimé le modèle (1) dont les résultats sont présentés dans la table (1.2).

Nous procédons au test de racine unitaire, la valeur estimée de la statistique ADF est égale à --4.368 (voir la table ci-dessus). Cette valeur est inférieure aux valeurs critiques --2.57879, --1.9427 et --1.6154 aux seuils 1%, 5% et 10%. Par conséquent, nous rejetons l'hypothèse nulle de racine unitaire : la série SLP _t est stationnaire, c'est à dire intégrée d'ordre 0, ce qui est cohérent avec l'étude du corrélogramme de SLPt.

2

Modèle (1) : LXSLP t = çbSLPt_1 + _X çbjLXSLPt_j + Et

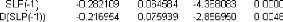
Table (1.2)

Après avoir stationnarisé la série, il convient à présent d'estimer le modèle susceptible à la représenter. En observant le corrélograme simple et partiel de la série stationnaire SLPt (Figure 1.4) nous remarquons que la fonction d'autocorrélation simple possède des valeurs importantes aux retards q = 1, 12, 13, ..., et que la fonction d'autocorrélation partielle possède des valeurs importantes aux retards p = 1, 2, 6, 9, 20, .., alors nous avons estimé plusieurs modèles parmi lesquels nous avons sélectionné deux modèles: SARIMA(13, 0, 0) x (1, 1, 0)12 et SARIMA(13, 0, 9) x (1, 1, _0)12, les résultats de l'estimation de ces deux modèles sont donnés respectivement par les tables 1.3 et 1.4.

Parmi ces deux modèles nous devons choisir un seul, le plus adéquat. Pour faire ce choix nous nous somme basés sur les critères de pouvoir prédictif (à savoir : R² qui est à maximiser

et R², AIC à minimiser), et nous avons à la fin choisi le modèle SARIMA(13, 0, 9) x (1, 1, 0)12 puisqu'il est le plus adéquat. Les valeurs des critères de pouvoir prédictif des deux modèles sont données dans la table suivante

	SARIMA(13,0,9) x (1,1,0)12	SARIMA(13,0,0) x (1, 1,0)12
R2	0.642	0.632
R2	0.6328	0.625
AIC	--1.1536	--1.1389

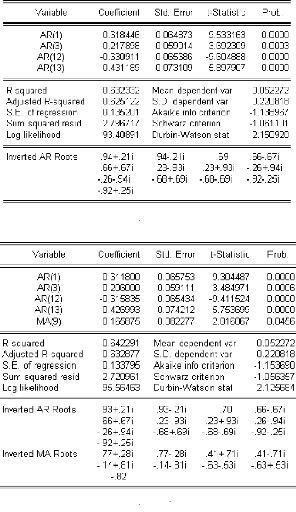
Table (1.3)

Table (1.4)

4.1.2 Validation

Tests sur les paramètres

? 1. Nous remarquons que tous les paramètres du modèle sont significativement différents de zéro. En effet les rapports des coefficients du modèle sont en valeur absolue supérieurs à

1.96, ce qui est confirmé par les probabilités de nullité des coefficients qui sont tous inférieurs à 0.05.

? 2. De la représentation graphique des inverses des racines des polynômes de retards

moyenne mobile et autoregressif (Figure 1.5) nous constatons qu'ils sont tous supérieurs à 1 en module (leurs inverses fournis par l'Eviews 5 sont, en module, inférieurs à 1).

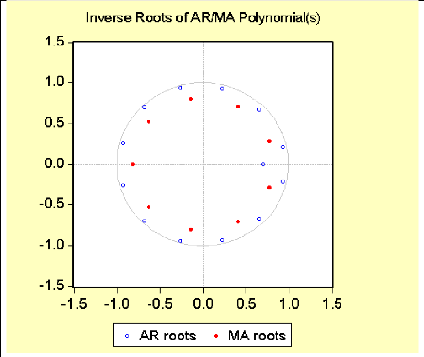
Figure (1.5)

Tests sur les résidus

1. A partir de la représentation graphique des séries résiduelle, actuelle et estimée (Figure 1.6) nous constatons que le modèle a bien expliqué la série. En effet, le coefficient R² de cette estimation est fort (égale à 0.642)

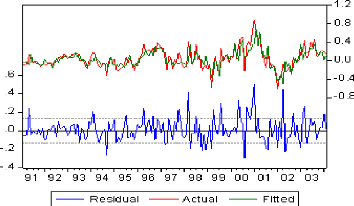
Figure (1.6)

? 2. Le corrélogramme des résidus du modèle (Figure 1.7) montre que les résidus forment un bruit blanc puisque tous les termes ne sont pas significativement différents de zéro. Nous remarquons aussi que la statistique de Ljung-Box (Q - stat) est inférieure à la valeur théorique de X²(h - 5) quelque soit h, en particulier pour h = 25, on a Q - stat (25) = 19.679 est inférieure à X²(20) = 31.41 au seuil 5%. Donc le modèle SARIMA(13, 0, 9) x (1, 1, 0)12

est valide et il s'écrit sous la forme suivante :

(1 - 0.61B - 0.2B³ + 0.62B¹² - 0.43B¹³)(1 - B¹²)LP t = (1 - 0.17B⁹)€t

? 3. De la statistique de Durbin-Watson (1.78 DW = 2.125 2.22) nous constatons que les résidus ne sont pas corrélés.

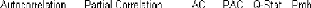
Test de Skewness : 'Y1 =	~~~~~ ~~^1=2 1 ~ 0		j0.769 - 0j	= 3.93> 1.96
	r^6ii		r^6157

j2 ~ 3j

Test de Kurtosis : 'Y2 =

j4.498 - 3j

r²⁴157

= 3.83> 1.96

/²⁴ii

(Figure 1.7)

Test de normalité sur les résidus de SARIMA(13, 0,9) x (1, 1,0)

CHAPITRE 4. APPLICATION DE LA MÉTHODOLOGIE DE BOX ET JENKINS 83 Berra= 30:19 > 5:911_; donc les résidus forment un bruit blanc non gaussien.

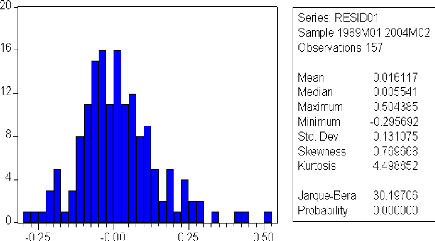
4.1.3 Prévision

Nous avons trouvé que le modèle générateur de la série LTt s'écrit sous la forme suivante : LPt = 0.61LPt_1 - 0.2LPt_3 + 0.38LPt_12 - 0.18LPt_13 - 0.2LPt_15 +

0.62LPt_24 - 0.43LPt_25 + Et - 0.17Et_9-

Donc pour faire la prévision à un horizon h, on n'a qu'à remplacer t par t+ h dans l'équation du modèle (nous allons faire la prévision pour h = 10).

Pour h = 1

^cLPt(1) = 0.61LPt - 0.2LPt_2 + 0.38LPt_11 - 0.18LPt_12 - 0.2LPt_14 +

0.62LPt_23 - 0.43LPt_24 - 0.17Et_s.

Pour h = 2

^cLPt(2) = 0:61 ^cLPt(1) - 0.2LPt_1 + 0.38LPt_10 - 0.18LPt_11 - 0.2LPt_13 + 0.62LPt_22 - 0.43LPt_23 - 0.17Et_7.

- Pour h = 3 ^cLPt(3) = 0:61 ^cLPt(2) - 0.2LPt + 0.38LPt_9 - 0.18LPt_10 - 0.2LPt_12 +

0.62LPt_21 - 0.43LPt_22 - 0.17Et_6.

- Pour h = 4 ^cLPt(4) = 0:61 ^cLPt(3) - 0:2^cLPt(1) + 0.38LPt_8 - 0.18LPt_9 - 0.2LPt_11 + 0.62LPt_20 - 0 .⁴3LPt_21 - _{0.17Et_5} -

- Pour h = 5 ^cLPt(5) = 0:61 ^cLPt(4) - 0:2^cLPt(2) + 0.38LPt_7 - 0.18LPt_8 - 0.2LPt_10 + 0.62LPt_19 - 0 .43LPt_20 - _{0.17Et_4} .

- Pour h = 6 ^cLPt(6) = 0:61 ^cLPt(5) - 0:2^cLPt(3) + 0.38LPt_6 - 0.18LPt_7 - 0.2LPt_9 + 0.62LPt_18 - 0 .⁴3LPt_19 - _{0.17Et_3} -

- Pour h = 7 ^cLPt(7) = 0:61 ^cLPt(6) - 0:2^cLPt(4) + 0.38LPt_5 - 0.18LPt_6 - 0.2LPt_8 + 0.62LPt_17 - 0 .43LPt_18 - _{0.17Et_2} .

- Pour h = 8 ^cLPt(8) = 0:61 ^cLPt(7) - 0:2^cLPt(5) + 0.38LPt_4 - 0.18LPt_5 - 0.2LPt_7 + 0.62LPt_16 - 0.43LPt_17 - 0.17Et_1.

- Pour h = 9 ^cLPt(9) = 0:61 ^cLPt(8) - 0:2^cLPt(6) + 0.38LPt_3 - 0.18LPt_4 - 0.2LPt_6 + 0.62LPt_15 - 0.43LPt_16 - 0.17Et
·

- Pour h = 10 ^cLPt(10) = 0:61 ^cLPt(9) - 0:2^cLPt(7) + 0.38LPt_2 - 0.18LPt_3 - 0.2LPt_5 + 0.62LPt_14 - 0.⁴3LPt_15-

- Pour h > 10 ^cLPt(h) = 0:61 ^cLPt(h - 1) - 0:2^cLPt(h - 3) + 0.38LPt+h_12 - 0.18LPt+h_13 - 0.2LPt+h_15 + 0.62LPt+h_24 - 0.⁴3LPt+h_25-

Le tableau suivant donne les valeurs prédites de la série LPt

Mars 2004	1:958274
Avril 2004	2:066585
Mai 2004	1:93495
Juin 2004	2:001217
Juillet 2004	1:998913
Août 2004	1:762774
Septembre 2004	1:978006
Octobre 2004	1:707491
Novembre 2004	1:655169
Decembre 2004	1:703825

Au départ nous avons transformé les données en appliquant une transformation logarithmique sur la série brute, donc il faut recolorer les prévisions issues du processus SARIMA (13,0, 9) x (1, 1, 0)₁₂ en prenant leur exponentielle. Ainsi nous obtenons le graphe représentant la série brute Pt et la série prévue PF _t suivant :

4.2 Etude de la série des prix spot du gaz naturel au

Texas (Te)

4.2.1 Identification et estimation

Considérons la série Tt représentant l'évolution du prix spot du gaz naturel au Texas de Janvier 1989 à Janvier 2004 (les données ont pour unité de mesure le dollar par mettre cube ($/m³). Cette série transformée en logarithme possède une tendance à la hausse (voir Figure 2.1) et semblant donc non stationnaire.

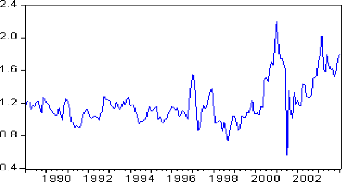
Figure (2.1)

Le corrélogramme associé à la série LT _t (Figure (2.2)) confirme l'hypothèse que nous avons fait en ce qui concerne la non-stationnarité de la série. En effet, nous remarquons que la fonction d'autocorrélation diminue lentement.

Figure (2.2)

Afin de détecter la nature de la non-stationnarité de la série nous avons appliqué le test de Dickey-Fuler augmenté (ADF) sur le modèle (3) avec un décalage de 1. Le résultat du test est le suivant :

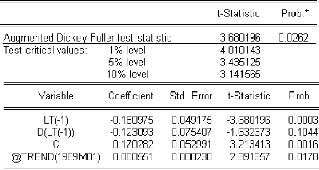
CHAPITRE 4. APPLICATION DE LA MÉTHODOLOGIE DE BOX ET JENKINS 88 Modèle (3) : LXLT t = c + bt + qTt_1 + çbLXLTt_1 + Et

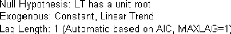
De l'estimation de ce modèle nous remarquons que la tendance déterministe est significativement différente de zéro puisque sa statistique qui vaut 2.39 est supérieure à la valeur critique tabulée par Dickey-Fuller aux seuil 10% (égale à 2.38), la statistique ADF est supérieure (égale à --3.68) à la valeur critique aux seuils 1%. Nous constatons donc que la série possède une racine unitaire et est donc non stationnaire (non-stationnarité de type stochastique). Pour stationnariser notre série nous proposons de la différencier une fois, la série ainsi différenciée est notée DLTt. Le corrélogramme de la série DLT _t (Figure 2.3) montre qu'elle est stationnaire. En effet, l'application du test de Dickey-Fuller (Table2.1) confirme la stationnarité de la série DLT _t puisque la valeur estimée de la statistique ADF est égale à --16.56 est inférieure aux valeurs critiques --2.578, --1.94 et --1.615 aux seuils 1%, 5% et 10% respectivement. Par conséquent, nous rejetons l'hypothèse nulle de racine unitaire : la série DLT _t est stationnaire c'est à dire intégrée d'ordre 0.

(Figure 2.3)

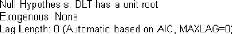
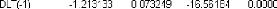
(Table 2.1)

En observant le corrélograme simple et partiel (Figure 2.3) nous remarquons que la fonction d'autocorrélation simple possède des valeurs importantes aux retards p = 1, 6, 9, ..., et que la fonction d'autocorrélation partielle possède des valeurs importantes aux retards q = 1, 2, 6, 11, 15.., alors nous avons estimé plusieurs modèles parmi lesquels nous avons choisie le plus adéquat : ARIMA(8, 1, 20), les estimations des paramètres de ce modèle sont données par la table (2.2)

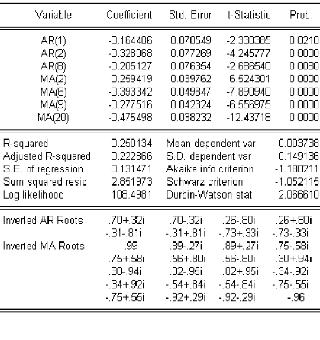
Table (2.2)

4.2.2 Validation

Tests sur les paramètres

1. Nous remarquons que tous les paramètres du modèle sont significativement différents de zéro (Table 3.2). En effet, les rapports des coefficients du modèle sont en valeur absolue supérieurs à 1.96, ce qui est confirmé par les probabilités de la nullité des coefficients qui sont tous inférieurs à 0.05.

2. Nous remarquons que les inverses des racines des polynômes de retards moyenne mobile et autoregressif (Table 2.3) nous constatons qu'ils sont tous supérieurs en module à 1 (leurs inverses fournis par l'Eviews 5 sont en module inférieurs à 1)

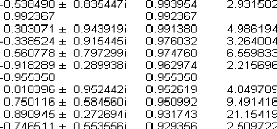
(Table 2.3)

Tests sur les résidus

1. A partir de la représentation graphique des séries résiduelle, actuelle et estimée (Figure 2.4) nous constatons que le modèle n'a pas bien expliqué la série. En effet, le coefficient de détermination R² de cette estimation est faible (égal à 0.25)

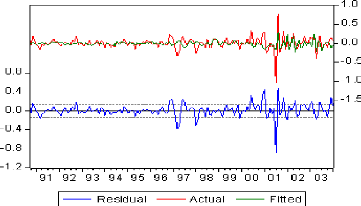
Figure (2.4)

.

? 2. Le corrélogramme des résidus du modèle (Figure 2.5) montre que les résidus forment un bruit blanc puisque tous les termes ne sont pas significativement différents de zéro. Nous remarquons aussi que la statistique de Ljung-Box (Q - stat) est inférieure à la valeur théorique de X²(h - 7) quelque soit h, en particulier pour h = 25, on a Q - stat (25) = 14.82 est inférieure à X²(18) = 28.87 au seuil 5%. Donc le modèle ARIMA(8, 1, 20) est valide et il s'écrit sous la forme suivante :

(1 +0.164B +0.328B² +0.205B⁸)(1 - B)LT t = (1- 0.259B² +0.39B⁶ +0.277B⁹ +0.475B²⁰)€t

? 3. De la statistique de Durbin-Watson ( DW = 2.06 2) nous constatons que les résidus ne sont pas corrélés.

Test de Skewness : 'Y1 =	~~~~~ ~~^1=2 1 ~ 0		j--0.71 - 0j			= 3.80> 1.96
	r^6ii		r^6172

Test de Kurtosis : 'Y2 = j₂ ~ 3j

= 20.35> 1.96

j10.53 - 3j

r²⁴172

/²⁴ii

Figure (2.5)

Test de normalité sur les résidus de ARIMA(8, 1,20)

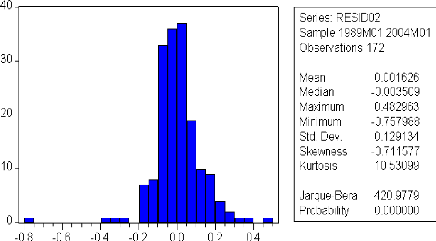
4.2.3 Prévision

Nous avons trouvé que le modèle générateur de la série LTt s'écrit sous la forme suivante : LTt = 0.836LTt_1 - 0.164LTt_2 + 0.32LTt_3 - 0.205LTt_8 + 0.205LTt_9 + et - 0.259et_2 + 0.39et_6 + _{0.277et_9} + 0.⁴75et_20-

Donc pour faire la prévision à un horizon h, on n'a qu'à remplacer t par t + h dans l'équation du modèle (nous allons faire la prévision pour h = 10).

- Pour h = 1 LTt(1) = 0.836LTt -0.164LTt_1 +0.32LTt_2-0.205LTt_7+0.205LTt_8-0.259et_1+ 0.39et_5 + 0.277et_8 + 0.475et_19
·

- Pour h = 2 LTt(2) = 0:836 LTt(1) - 0.164LTt + 0.32LTt_1 - 0.205LTt_6 + 0.205LTt_7 -

0.259et + 0.39et_4 + 0.277et_7 + 0.⁴75et_18-

- Pour h = 3 LTt(3) = 0:836 LTt(2) - 0:164LTt(1) + 0.32LTt - 0.205LTt_5 + 0.205LTt_6 + 0.39et_3 + 0.277et_6 + 0.475et_17
·

- Pour h = 4 ^cLTt(4)= 0:836 LTt(3) - 0:164LTt(2) + 0:32LTt(1) - 0.205LTt_4 + 0.205LTt_5 + 0.39et_2 + 0.277et_5 + 0.475et_16
·

- Pour h = 5 ^cLTt(5) = 0:836 LTt(4) - 0:164LTt(3) + 0:32LTt(2) - 0.205LTt_3 + 0.205LTt_4 + 0.39et_1 + 0.277et_4 + 0.⁴75et_15
·

Pour h = 6

LTt(6) = 0.836LTt(5) - 0.164LTt(4) + 0.32LTt(3) - 0.205LTt_2 + 0.205LTt_3 + 0.39et + 0.277et_3 + 0.475et_14
·

- Pour h = 7 LTt(6) = 0.836LTt(6) - 0:164^cLTt(5) + 0.32LTt(4) - 0.205LTt_1 + 0.205LTt_2 + 0.277et_2 + 0.⁴75et_13
·

- Pour h = 8 LTt(8) = 0.836LTt(7) - 0.164LTt(6) + 0.32LTt(5) - 0.205LTt + 0.205LTt_1 + 0.277et_1 + 0.⁴75et_12

- Pour h = 9 LTt(9) = 0.836LTt(8) - 0.164LTt(7) + 0.32LTt(6) - 0.205LTt(1) + 0.205LTt + 0.277et + 0.475et_11

- Pour h = 10 LTt(10) = 0.836LTt(9) - 0.164LTt(8) + 0.32LTt(7) - 0.205LTt(2) + 0.205LTt(1) + 0.⁴75et_10

- Pour 10 < h < 20

LTt(h) = 0:836 LTt(h - 1) - 0:164LTt(h - 2) + 0:32LTt(h - 3) - 0:205LTt(h - 4) +

0:205LTt(h - 5) + 0.⁴75et+h_20

- Pour h > 20

LTt(h) = 0.836LTt(h - 1) - 0.164LTt(h - 2) + 0.32LTt(h - 3) - 0.205LTt(h - 4) +

0.205LTt(h - 5)

Le tableau suivant donne les valeurs prédites de la série LTt

Février 2004	1:605608
Mars 2004	1:586944
Avril 2004	1:705234
Mai 2004	1:819836
Juin 2004	1:903985
Juillet 2004	1:925679
Août 2004	1:914119
Septembre 2004	1:994605
Octobre 2004	2:196437
Novembre 2004	2:108767

Au départ nous avons transformé les données en appliquant une transformation logarithmique sur la série brute, donc il faut recolorer les prévisions issues du processus ARIMA (8, 1,20) en prenant leur exponentielle. Ainsi nous obtenons le graphe représentant la série brute Tt et la série prévue TF _t suivant :

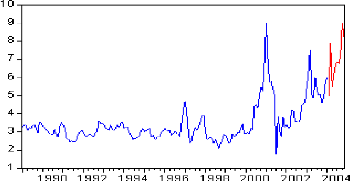
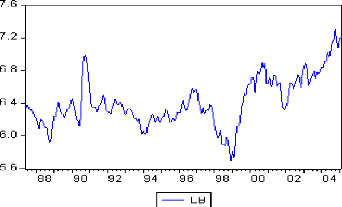
4.3 Etude de la série du prix du Brent (Bi

) 4.3.1 Identification et estimation

Considérons la série B représentant l'évolution du prix du Brent de Juin 1987 à Février 2005 (les donnée sont pour unité de mesure le dollar par baril : $.US.BL). Cette série transformée en logarithme, notée LB , possède une tendance à la hausse (voir Figure 3.1), elle est donc non stationnaire.

Figure (3.1)

Le corrélogramme associé à la série LB (Figure (3.2)) confirme l'hypothèse que nous avons fait en ce qui concerne la non-stationnarité de la série. En effet, nous remarquons que la fonction d'autocorrélation diminue lentement.

Figure (3.2)

Afin de détecter la nature de la non-stationnarité de la série nous avons appliqué le test de Dickey-Fuler augmenté (ADF) sur les trois modèles (avec tendance et constante, avec constante et sans constante ni tendance) avec un décalage de 1. Le résultat du test sur le modèle (1) a montré que la série possède une racine unitaire (ADF = 0.407 supérieur aux valeurs critiques) et donc la série est non stationnaire.

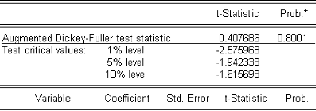
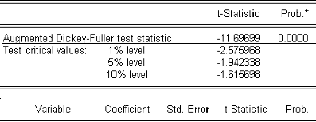
CHAPITRE 4. APPLICATION DE LA MÉTHODOLOGIE DE BOX ET JENKINS 99 Modèle (1) : 1XLB = çbLB _{_1} + çb/XLB _{_1} + "

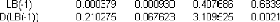
Pour stationnariser notre série nous proposons de la différencier une fois, la série ainsi différenciée est notée DLB . Le corrélogramme de la série DLB (Figure 3.3) montre qu'elle est stationnaire. En effet l'application du test de Dickey-Fuller sur le modèle (1) confirme la stationnarité de la série DLB (voir table 3.1) puisque la valeur estimée de la statistique ADF est égale à --11.69 est inférieure aux valeurs critiques --2.57, --1.94 et --1.615 aux seuils 1%, 5% et 10%. Par conséquent, nous rejetons l'hypothèse nulle de racine unitaire: la série LB est stationnaire c'est à dire intégrée d'ordre 0.

(Table 3.1)

Figure (3.3)

A partir du corrélogramme associé à la série stationnaire DLB (Figure 3.3) nous avons estimé plusieurs modèles, parmi lesquels nous avons choisi le modèle le plus adéquat ARIMA (27, 1, 15) dont l'estimation des paramètres est donnée par la table (3.2)

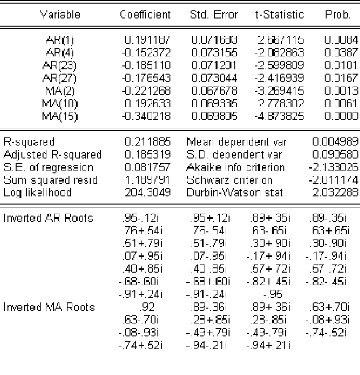
Table (3.2)

4.3.2 Validation

Tests sur les paramètres

? 1. Nous remarquons que tous les paramètres du modèle sont significativement différents de zéro. En effet les rapports des coefficients du modèle sont en valeur absolue supérieurs à

1.96, ce qui est confirmé par les probabilités de nullité des coefficients qui sont tous inférieurs à 0.05.

? 2. De la représentation graphique des inverses des racines des polynômes de retards

moyenne mobile et autoregressif (Figure 3.4) nous constatons qu'ils sont tous supérieurs à 1 en module (leurs inverses fournis par l'Eviews 5 sont en module inférieurs à 1).

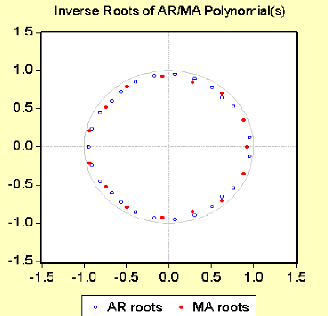
Figure (3.4)

Tests sur les résidus

1. A partir de la représentation graphique des séries résiduelle, actuelle, et estimée (Figure 3.5) nous constatons que le modèle n'a pas bien expliqué la série. En effet, le coefficient R2 de cette estimation est faible (égal à 0.21)

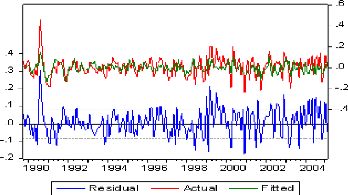
Figure (3.5)

.

? 2. Le corrélogramme des résidus du modèle (Figure 3.6) montre que les résidus forment

un bruit blanc puisque tous les termes ne sont pas significativement différents de zéro. Nous remarquons aussi que la statistique de Ljung-Box (Q - stat) est inférieure à la valeur théorique de X²(h - 7) quelque soit h, en particulier pour h = 25, on a Q - stat (25) = 14:93 est inférieure à X²(18) = 33:92 au seuil 5%. Donc le modèle ARIMA(27, 1, 15) est valide et il

s'écrit sous la forme suivante :

(1 - 0:19B² + 0:15B⁴ + 0:18B²³ + 0.17B²⁷)(1 - B)LB = (1 + 0:22B² - 0:19B¹⁰ + 0.34B¹⁵)€

? 3. De la statistique de Durbin-Watson (DW = 2:03 2) nous constatons que les résidus ne sont pas corrélés.

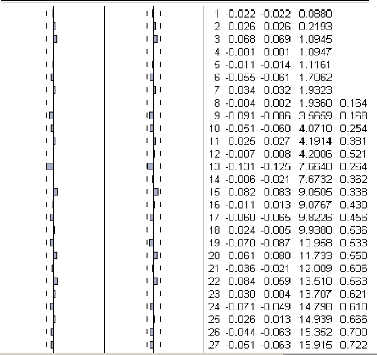
Test de Kurtosis : 'Y2 = j₂ - 3j

j3.27-3j

r²⁴185

/²⁴ii

= 0.75 < 1.96

Figure (3.6)

Test de normalité sur les résidus de ARIMA(27, 1,15)

Test de Skewness : 'Y1 =	~~~~~ ~~^1=2 1 - 0		j0.265 - 0j			= 1.47 < 1.96
	r^6ii		r^6185

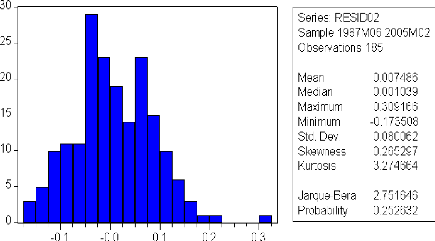
4.3.3 Prévision

Nous avons trouvé que le modèle générateur de la série LBt s'écrit sous la forme suivante : LBt = 1.19LBt_1 -0.19LBt_2 -0.15LBt_4+0.15LBt_5 -0.18LBt_23+0.18LBt_24 - - 0.17LBt_27 + 0.17LBt_28 + Et + 0.22Et_2 - 0.19Et_10 + 0.3⁴Et_15.

Donc pour faire la prévision à un horizon h, on n'a qu'à remplacer t par t + h dans l'équation du modèle (nous allons faire la prévision pour h = 10).

- Pour h = 1

LBt(1) = 1.19LBt - 0.19LBt_1 - 0.15LBt_3 +0.15LBt_4 - 0.18LBt_22 +0.18LBt_23 -

0.17LBt_26 + 0.17LBt_27 + 0.22Et_1 - 0.19Et_9 + 0.3⁴Et_14.

- Pour h = 2

LBt(2) =1.19^dLBt(1)- 0.19LBt - _{0.15LBt_2} +0.15LBt_3 - 0.18LBt_21 +0.18LBt_22 ^-0.17LBt_25 + 0.17LBt_26 + 0.22Et - _{0.19Et_8} + 0.3⁴Et_13.

- Pour h = 3

LBt(3) = 1.19^dLBt(2)-0.19^dLBt(1)-0.15LBt_1+0.15LBt_2-0.18LBt_20+0.18LBt_21- 0.17LBt_24 + 0.17LBt_25 - 0.19Et_7 + 0.34Et_12.

- Pour h = 4

LBt(4) =1.19^dLBt(3)-0.19^dLBt(2)-0.15LBt+0.15LBt-1 - 0.18LBt-19 +0.18LBt-20 - 0.17LBt-23 + 0.17LBt-24 - 0.19et-6 + 0.34et-11.

- Pour h = 5

LBt(5) = 1.19^dLBt(4)-0.19^dLBt(3)-0.15^dLBt(1)+0.15LBt-0.18LBt-18+0.18LBt-19- 0.17LBt-22 + 0.17LBt-23 - _0.19et-5 + 0.3⁴et-10-

- Pour h = 6

LBt(6) = 1.19LBt(5)-0.19LBt(4)-0.15LBt(2)+0.15LBt(1)-0.18LBt-17+0.18LBt-18- 0.17LBt-21 + 0.17LBt-22 - 0.19et-4 + 0.34et-9.

- Pour h = 7

LBt(7) = 1.19^dLBt(6)-0.19^dLBt(5)-0.15^dLBt(3)+0.15^dLBt(2)-0.18LBt-16+0.18LBt-17- 0.17LBt-20 + 0.17LBt-21 - 0.19et-3 + 0.3⁴et-8-

- Pour h = 8

LBt(8) = 1.19^dLBt(7)-0.19^dLBt(6)-0.15^dLBt(4)+0.15^dLBt(3)-0.18LBt-15+0.18LBt-16- 0.17LBt-19 + 0.17LBt-20 - 0.19et-2 + 0.34et-7.

- Pour h = 9

LBt(9) = 1.19^dLBt(8)-0.19^dLBt(7)-0.15^dLBt(5)+0.15^dLBt(4)-0.18LBt-14+0.18LBt-15- 0.17LBt-18 + 0.17LBt-19 - 0.19et-1 + 0.3⁴et-6-

- Pour h = 10

LBt(10) = 1:19LBt(9)-0.19LBt(8)-0.15LBt(6)+0.15LBt(5)-0.18LBt-13+0.18LBt-14-

0.17LBt-17 + 0.17LBt-18 - 0.19et + 0.3⁴et-5.

- Pour 10 < h < 15

LBt(h) = 1.19LBt(h - 1) - 0.19LBt(h - 2) - 0.15LBt(h - 4) + 0.15LBt(h - 5)

- 0.18LBt+h-23+0.18LBt+h-24-0.17LBt+h-27+0.17LBt+h-28+0.34et+h-15.

- Pour h > 15

LBt(h) = 1.19LBt(h - 1) - 0.19LBt(h - 2) - 0.15LBt(h - 4) + 0.15LBt(h - 5)

- 0.¹8LBt+h-23 + 0.18LBt+h-24 - 0.17LBt+h-27 + 0.¹7LBt+h-28. Le tableau suivant donne les valeurs prédites de la série LBt

Mars 2005	7:211504
Avril 2005	7:244381
Mai 2005	7:205962
Juin 2005	7:216676
Juillet 2005	7:255771
Août 2005	7:282994
Septembre 2005	7:262662
Septembre 2005	7:289575
Novembre 2005	7:299444
Decembre 2005	7:300837

Au départ nous avons transformé les données en appliquant une transformation logarithmique sur la série brute, donc il faut recolorer les prévisions issues du processus ARIMA (27, 1, 15) en prenant leur exponentielle. Ainsi nous obtenons le graphe représentant la série brute B et la série prévue TB suivant :

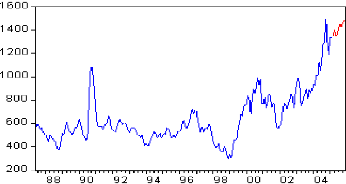
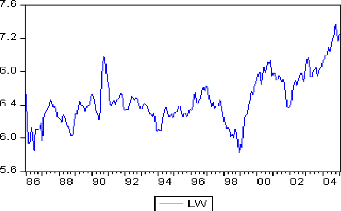
4.4 Etude de la série du prix du WTI (Wt)

4.4.1 Identification et estimation

Considérons la série W _t représentant l'évolution du prix WTI (West Texas Intermediate) de Janvier 1986 à Février 2005 (les données ont pour unité de mesure le dollar par baril $/US.BL). Cette série transformée en logarithme, notée LWt, possède une tendance à la hausse (Figure 4.1), elle est donc non stationnaire.

Figure (4.1)

En analysant le corrélogramme associé à la série LW _t (Figure 4.2) nous confirmons que la série n'est pas stationnaire. En effet, la fonction d'autocorrélation diminue lentement.

Figure (4.2)

Afin de détecter la nature de la non-stationnarité de la série nous avons appliqué le test de Dickey-Fuler augmenté (ADF) sur les trois modèles (avec tendance et constante, avec constante et sans constante ni tendance) avec un décalage de 1. Nous avons trouvé que ni la tendance déterministe ni la constante n'étaient significatives. Le résultat du test sur le modèle (1) (Table 4.1) montre que la série possède une racine unitaire (ADF = 0.709 supérieur aux valeurs critiques) et donc la non-stationnarité de la série est de type stochastique.

CHAPITRE 4. APPLICATION DE LA MÉTHODOLOGIE DE BOX ET JENKINS 110 Modèle (1) : LXLW t = çbLWt_1 + çbLXLWt_1 + €t

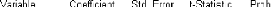
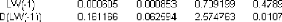
Table (4.1)

Pour stationnariser notre série nous proposons de la différencier une fois, la série ainsi différenciée est notée DLWt. Le corrélogramme de la série DLW _t (Figure 4.3) montre bien qu'elle est stationnaire.

En effet, l'application du test de Dickey-Fuller confirme la stationnarité de la série DLWt puisque la statistique ADF associée au modèle (1) est inférieure aux valeurs critiques aux seuils 1%, 5% et 10% (égale à --11.44)

Figure (4.3)

A partir du corrélogramme associé à la série stationnaire DLW _t nous avons estimé plusieurs modèles, parmi lesquels nous avons choisi le modèle le plus adéquat ARIMA(15, 1,27) dont l'estimation des paramètres est donné par :

4.4.2 Validation

Tests sur les paramètres

? 1. Nous remarquons que tous les paramètres du modèle sont significativement différents de zéro. En effet les rapports des coefficients du modèle sont en valeur absolue supérieurs à

1.96, ce qui est confirmé par les probabilités de nullité des coefficients qui sont tous inférieurs à 0.05.

? 2. Les racines des polynômes de retards moyenne mobile et autoregressif sont supérieurs

à 1 en module (leurs inverses fournis par l'Eviews 5 sont en module inférieurs à 1).

Tests sur les résidus

? 1. Le corrélogramme des résidus du modèle (Figure 4.4) montre que les résidus forment un bruit blanc puisque tous les termes ne sont pas significativement différents de zéro. Nous remarquons aussi que la statistique de Ljung-Box (Q - stat) est inférieure à la valeur théorique de X²(h - 7) quelque soit h, en particulier pour h = 25, on a Q - stat (25) = 16:528 est inférieure à X²(18) = 28:87 au seuil 5%.

? 2. De la statistique de Durbin-Watson (DW = 1:99 2) nous constatons que les résidus sont non corrélés.

Figure (4.4)

Donc nous retenons le modèle ARIMA(15, 1, 27) comme étant le modèle générateur de la série LWt.Ce modèle s'écrit sous la forme suivante :

(1 - 0.24B + 0.16B¹⁵)(1 - B)LW t = (1 + 0:12B² + 0:25B¹³ - 0:26B²⁰ + 0:16B²⁶ + 0.23B27)€t

Graphe des séries réelle, estimée et résidus

En analysant le graphe (Figure 4.5) nous remarquons que le modèle ARIMA(15, 1,27) explique d'une manière générale, bien la série LWt.

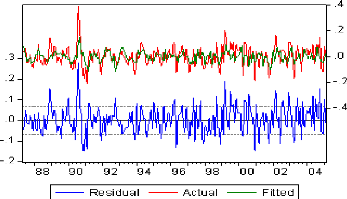
Figure (4.5)

Test de normalité sur les résidus de ARIMA(15, 1,27)

Test de Skewness : 'Y1 =	~~~~~ ~~^1=2 1 ~ 0		j0.329 - 0j	= 0.167 < 1.96
	r^6ii		r^6214

j₂ ~ 3j

Test de Kurtosis : 'Y2 =

j3.469 - 3j

r²⁴214

= 1.42 < 1.96

/²⁴ii

Ainsi nous acceptons l'hypothèse de normalité, ce qui est confirmé par la statistique de Jaque-Berra= 5.846 <5.911, donc les résidus forment un bruit blanc gaussien.

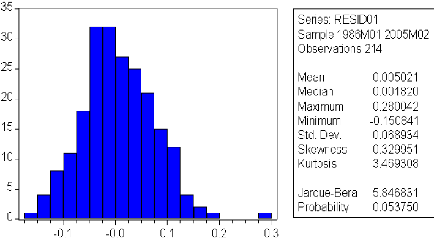
4.4.3 Prévision

Nous avons trouvé que le modèle générateur de la série LWt s'écrit sous la forme suivante :

LWt = 1.24LWt_1 - 0.24LWt_2 - 0.16LWt_15 + 0.¹6LWt_16 +

et + 0.12et_2 + 0.25et_13 - 0.26et_20 + 0.16et_26 + 0.23et_27
·

Donc pour faire la prévision à un horizon h, on n'a qu'à remplacer t par t+ h dans l'équation du modèle (nous allons faire la prévision pour h = 10).

- Pour h = 1 LWt(1) = 1.24LWt - 0.24LWt_1 - 0.16LWt_14 + 0.16LWt_15 +

0.12et_1 + 0.25et_12 - 0.26et_19 + 0.16et_25 + 0.23et_26
·

- Pour h = 2 LWt(2) = 1:24^dLWt(1) - 0.24LWt - 0.16LWt_13 + 0.16LWt_14 +

0.12et + _{0.25et_11} - 0.26et_18 + 0.16et_24 + 0.23et_25-

- Pour h = 3 LWt(3) = 1:24^dLWt(2) - 0:24^dLWt(1) - 0.16LWt_12 + 0.16LWt_13 +

0.25et_10 - 0.26et_17 + 0.16et_23 + 0.23et_24

- Pour h = 4 LWt(4) = 1:24^dLWt(3) - 0:24^dLWt(2) - 0.16LWt_11 + 0.16LWt_12 +

0.25et_9 - 0.26et_16 + 0.16et_22 + 0.23et_23
·

- Pour h = 5 LWt(5) = 1:24^dLWt(4) - 0:24^dLWt(3) - 0.16LWt_10 + 0.16LWt_11 +

0.25et_8 - 0.26et_15 + 0.16et_21+ 0.23et_22
·

Pour h = 6

LWt(6) = 1:24^dLWt(5) - 0:24^dLWt(4) - 0.16LWt_9 + 0.16LWt_10 +

0.25et_7 - 0.26et_14 + 0.16et_20 + 0.23et_21.

- Pour h = 7 LWt(7) = 1:24^dLWt(6) - 0:24^dLWt(5) - 0.16LWt_8+ 0.16LWt_9+

0.25Et_6 - 0.26Et_13+ 0.16Et_19+ 0.23Et_20

- Pour h = 8 LWt(8) = 1:24^dLWt(7) - 0:24^dLWt(6) - 0.16LWt_7 + 0.16LWt_8 +

0.25et_5 - 0.26et_12 + 0.16et_18 + 0.23et_19
·

- Pour h = 9 LWt(9) = 1:24^dLWt(8) - 0:24^dLWt(7) - 0.16LWt_6 + 0.16LWt_7 +

0.25et_4 - 0.26et_11 + 0.16et_17 + 0.23et_18

- Pour h = 10 LWt(10) = 1:24^dLWt(9) - 0:24^dLWt(8) - 0.16LWt_5 + 0.16LWt_6 +

0.25et_3 - 0.26et_10 + 0.16et_16 + 0.23et_17

- Pour 10 < h < 27

LWt(h) = 1:24 LWt(h - 1) - 0:24LWt(h - 2) - 0.16LWt+h_15 +

0.16LWt+h_16 + 0.25et+h_13 - 0.26et+h_20 + 0.16et+h_26 +

0.23Et+h_27-

- Pour h > 27 LWt(h) = 1:24^dLWt(h - 1) - 0:24^dLWt(h - 2) - 0.16LWt+h_15 +

0.16LWt+h_16.

Les prévisions sont données dans le tableau suivant :

Mars 2005	7:327918
Avril 2005	7:352893
Mai 2005	7:377470
Juin 2005	7:369183
Juillet 2005	7:352715
Août 2005	7:381418
Septembre 2005	7:404471
Octobre 2005	7:398639
Novembre 2005	7:412903
Décembre 2005	7:403311

Le graphe représentant la série brute W _t et la série prévue WF _t est le suivant :

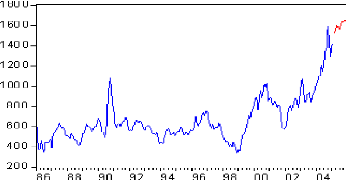
Après avoir modélisé les séries représentant le prix du gaz naturel ( à Pensylvania et au Texas) et le prix du brut sur les marchés américain et européen, par la méthodologie de Box et Jenkins, nous avons constaté que les modèles obtenus n'étaient pas vraiment satisfaisant. Pour cette raison, nous avons soupçonné qu'une étude multivariée pourra améliorer nos modèles.

Chapitre 5

Modélisation multivariée

Nous avons vu plus haut que l'analyse des séries chronologiques consiste principalement à détecter la structure de corrélation (dépendance) entre les composantes du processus générateur {Xt, t E Z} de la série sous étude X1, ..., XT. Cette structure sera exploitée entres autres, sous l'hypothèse fondamentale que les valeurs futures de la série restent une réalisation du processus, pour faire des prédictions dans le futur. Dans ce cas, l'approche permettant de révéler la structure de dépendance est qualifiée d'univariée dans le sens où l'on suppose que les variables du processus générateur {Xt, t E Z} ne sont corrélées qu'entre elles seulement et qu'il n'existe pas (ou du moins on néglige) de corrélation avec d'autres processus générateurs de d'autres séries. Cependant, plusieurs chroniques rencontrées dans la pratique, et spécialement en économie, peuvent être considérées comme composantes d'une série chronologique multivariée X1, ..., XT issue d'un processus multvarié {Xt, t E Z} dont la spécification inclu non seulement la structure de "dépendance" de chaque composante{Xti, t E Z}, mais aussi l'interdépendance entre différentes composantes{Xti, t E Z} et{Xtj, t E Z}. Par exemple, on a vu que la série des prix spot du gaz naturel au Texas (T) peut être considérée comme réalisation d'un processus ARIMA(8, 1, 20). Ainsi on peut dire grossièrement que ce prix à une période donnée dépend du prix aux huit périodes précédentes et du passé, à l'ordre 20, d'un processus bruit blanc. Cependant, la théorie économique nous montre que le prix du gaz est fortement lié au prix du pétrole et que le comportement des consommateurs vis-à-vis du gaz est conditionné par celui du pétrole. La prise en compte de l'effet du pétrole sur le gaz décrit mieux la série des prix du gaz et peut donc améliorer leurs prévisions.

D'un point de vue du second ordre, un processus multivarié stationnaire {Xt, t E Z} est déterminé par sa moyenne vectorielle p = E (Xt) et sa fonction d'autocovariance matricielle

Ph = E [(Xt+h -- E _(Xt+h)) (Xt -- E (Xt))^'~ = E (XtX^'_t) -- pp^'. La plus part des résultats relatifs aux processus univariés sationnaires du second ordre peuvent être généralisés au cas de processus multivariés. Cependant de nouveaux problèmes surgissent. Dans ce qui suit nous allons présenter brièvement les principaux résultats concernant les processus multivariés faiblement stationnaires et les modèles VAR qui les representent.

5.1 Processus multivariés stationnaires du second ordre

Dans la suite on considère un processus m-varié {Xti, t E Z}, i = 1, ..,m, du second ordre, i.e., E (Xt) < oo et E (XtX^'_t) < oo Vt E Z. La stationnarité d'un processus est liée à l'invariance d'une de ses propriétés par translation dans le temps. Cette propriété représente la distribution de probabilité dans le cas de stationnarité forte et la moyenne et la covariance dans le cas de stationnarité faible (ou du second ordre).

Définition 5.1.1

Un processus stochastique m-varié {Xt, t E Z} est dit strictement stationnaire si pour tout n E N^*, et pour tout n-uplet (t1,t2,...,t_n) E Zⁿ, la distribution de probabilité conjointe du vecteur _(Xt1+h, , Xt_n+h) est la même que celle de (Xt₁, , Xt_n) Vh E Z. Autrement dit, si on a :

P(Xt₁< x1, :::,Xt_n < x_n) = P (Xt1+h < x1, :::, Xt_n+h < xn) ,

n E N^*, V (t1, t2,..., t_n) E Zⁿ, Vx1,x2_;:::, x_n E R^m, Vh E Z.

Définition 5.1.2

Le processus stochastique {Xt, t E Z} est dit faiblement stationnaire si on a :

1) E (Xt) = E (Xt+h) = p (de moyenne le vecteur constant), Vt E Z,

2) Cov (Xt, Xt+h) = E [(Xt -- p_t) (Xt+h -- pt+h)'] = Vt, h E Z.

La fonction matricielle Ph = (yii(h))i je{1,..,m} est dite fonction d'autocovariance du

Remarques

? 1. Les mêmes propriétés de la fonction d'autocovariance étudiée dans le chapitre 2 restent valables dans le cas multivarié. Cependant la fonction d'autocovariance dans le cas multivarié n'est pas symétrique et on a

F_h = F0 h

De plus, F est définie non négative

? 2. Comme pour le cas univarié, il est clair que la stationnarité stricte implique la stationnarité faible (la réciproque n'est pas vraie, sauf pour les processus Gaussiens), pourvu que le processus sous étude soit du second ordre.

Processus bruit blanc multivarié (Multivariate White noise)

Le processus de second ordre, multivarié, faiblement stationnaire de base (à partir duquel on peut générer d'autres processus multivariés stationnaires par combinaison linéaire infinie, convergente en moyenne quadratique), est le processus bruit blanc multivarié dont la définition est la suivante.

Définition 5.1.3

Un processus bruit blanc {"t, t E Z}, est un processus stochastique non corrélé de moyenne nulle et de matrice de covariance finie . Autrement dit :

{

E ("t) = 0,

Vt E Z,

E ("t"⁰ _t) = :

et par la fonction d'autocovariance particulière suivante :

{

, h = 0,

Fh = E ("t "t+h) = Vt E Z

0, h=60.

pour des raisons théoriques on suppose que est non singulière.

Estimateur empirique

Dans la pratique la fonction d'autocavariance n'est pas connue, néanmoins, elle est estimée par la statistique suivante dite estimateur empirique :

^bh = 1 T - h	T P-h t=1	(Xt - ) , Xt ) (Xt+h - Xt+h
avec Xt-h =			1 T - h	T P- h t=1	Xt h ~ 0

Bien entendu, pour une série temporelle multivariée x1, x2, ..., x_n, on a l'estimation empirique ^b['h:

b['h= 1 T - h	T P-h t=1	(xt - xt) (xt+h - xt+h),
avec xt-h =			1 T - h	T P- h t=1	xt h ~ 0

5.1.1 Fonction d'autocorrélation

La fonction d'autocorrélation de retard h, h E Z, d'un processus multivarié, du second ordre, faiblement stationnaire de moyenne E (Xt) = p. et de matrice de covariance ['h, notée Rh = (p_ij(h)) est définie par

pij(h) = 'yij (h)

\/Yii (0) _jj (0)

ou encore sous forme matricielle

Rh = D^-1['hD^-1, Vh E Z.

où D^-1 = diag

) 1 \/_Yii (0)

. Il est facile de vérifier que la fonction d'autocorrélation satisfait

les deux propriétés suivantes, qui découlent directement des propriétés précédentes de la fonction d'autocovariance

Propriétés 4.1.4

1) R-h=R^'h VhEZ,

Donc on peut dans la pratique se restreindre aux autocorrélations pour h ~ 0.

Estimateur empirique

L'estimateur empirique ^bRh de la fonction d'autocorrélation, Rh, est obtenu en remplaçant,

dans l'expression de Rh, D et ['h par leurs estimateurs empiriquesD^b et En effet, on
	['h, respectivement.

^bRh= D-1 ^b['h D^-1, VhEZ

Remarques

? 1. La représentation graphique de p _j (h) est appelée"corrélogramme" pour chaque i,j=1,. .. ,m.

? 2. Si p _j (h) décroît rapidement quand le nombre de retard augmente, cela signifie que la série est stationnaire, sinon elle est sans doute non stationnaire ou de mémoire longue.

5.2 Classe de modèles VARMA (p, q)

Le théorème de Wold reste valable dans le cas multivarié, et donc on admet les réultats déjà énoncés dans le chapitre 2. C'est à dire que tout processus multivarié, du second ordre purement indéterminable, stationnaire peut être représenté par l'une de deux formes équivalentes à savoir, la forme d'un modèle autorégressif d'ordre éventuellement infini et la forme d'un modèle moyenne mobile d'ordre éventuellement infini, données respectivement, par:

"t = Xt - _41Xt-1 - _42Xt-2 - _43Xt-3 +..., t E Z, Modèle autorégresif d'ordre infini

et

Xt = "t- _1"t-1 - _2"t-2 - _83"t-3 +..., t E Z, Modèle moyenne mobile d'ordre infini

Chacune de ces deux représentations nécessite éventuellement l'utilisation d'un nombre infini de paramètres qui sont en pratique inconnus et qu'on a à estimer sur la base d'une série de taille finie. Ceci n'est donc pas possible en pratique. C'est pourquoi on utilise plutôt une approximation des représentations en tronquant les séries infinies, tout en supposant la décroissance géométrique vers zéro des termes à tronquer. Deux représentations particulières et intéressantes de ces deux formes peuvent être évoquées, la première représentation particulière correspond au cas où 4, =6 0 et 4 = 0, Vi ~ p + 1, ce qui donne le modèle suivant

dit modèle autorégressif d'ordre p, noté VAR (p) :

Et = Xt - 1 Xt-1 - ² _Xt-2 - ... - _{p Xt-p,} t E Z,

et la deuxième représentation particulière correspond au 8_p =6 0 et 8j = 0, Vj > q + 1, dans la seconde représentation, ce qui donne le modèle suivant dit modèle moyenne mobile d'ordre q, noté VMA (q) :

Xt = Et - 81 _Et-1 - 82 _Et-2 - ... - 8_{q Et-q,} t E Z,

Le reste de ce chapitre est consacré seulement à l'étude des propriétés et les caractéristiques essentielles des modèles autorégressifs mutivarié purs, d'ordre p (VAR(p)).

5.2.1 Processus autoregréssif multivarié VAR(p)

La définition d'un processus autoregréssif multivarié d'ordre p, noté VAR (p) est la suivante :

Définition 5.2.1

Le processus stationnaire m-varié {Xt, t E Z} est dit admettant une représentation autoregressive vectorielle d'ordre p, noté VAR (p), s'il est solution de l'équation aux différences stochastiques suivante :

Xt - 1 _Xt-1 - (1^,2 _Xt-2 - ... - + _p Xt-p = Et (5.2.1)

où {Et, t E Z} est un bruit blanc vectoriel de matrice de covariance E. En introduisant l'opérateur retard B le modèle précédent peut s'écrire sous la forme symbolique suivante :

ou encore (I - e1B - e2B² -
·
·
· - e_pB^p) Xt = Et,

4' (B) Xt = Et,

où 4' (B) est le polynôme de retard, de degré p, donné par :

(B) = I -

Pp j=1

4j B^j où (j sont des matrices réelles avec ep =6 0,

Un modèle VAR particulier mais très important dans l'étude des propriétés théoriques des
modèles autoregressifs est le modèle VAR d'ordre 1. On montre facilement que tout modèle
VAR d'ordre p peut se mettre sous la forme (appelée souvent forme espace d'état) d'un

modèle VAR(1). En effet, en introduisant le processus m x p-varié {Yt, t Z} défini par

Yt = (X' t_1, X' t_2, ..., X' t_p+1)'

et la matrice mp x mp

₀
B_B@

~ =

_1
ACC

1 2 ~ ~ ~ _p I000 0I00 00I0

alors le modèle VAR(p) (5.2.1) peut se mettre sous la forme VAR(1) suivante

Yt = ⁴'Yt_1 + _t (5.2.2)

où

_t = (e^' _t,0^', 0^', ..., 0^')^'

Ainsi l'étude des propriétés théoriques du modèle VAR(p) (5.2.1) se ramènent à celle du modèle VAR(1) (5.2.2).

La notion de causalité qui caractérise la relation entre le processus (Xt) et le bruit (et) est également liée aux processus multivariés. Bien entendu lorsqu'un processus est causal, c'est à dire qu'il s'exprime comme fonction du présent et du passé d'un processus bruit blanc (qui est stationnaire), il est donc stationnaire. La stationnarité est cependant une propriété qui ne concerne que le processus (Xt) et non sa relation avec un autre processus. Ainsi dans le cas de modèles stationnaires, par abus de langage, on confond souvent entre causalité et stationnarité tout en sachant que les deux notions très complètement différentes.

Définition 5.2.2

Un modèle multivarié de série chronologique (linéaire ou non linéaire) de la forme:

Xt = g (Xt_1, Xt_2, ... _{Xt_p;} ^et, et_1, et_2, ... _{et_q)} ,

où et est un bruit blanc, est dit causal si, et seulement si, on peut exprimer le processus stochastique Xt sous forme combinaison linéaire (finie ou infinie) convergente, en moyenne quadratique, du présent et du passé du bruit blanc vectoriel et.

Le théorème suivant établi une condition nécessaire et suffisante pour q'un modèle autorégressif d'ordre p, soit causal.

Théorème 4.2.3

Le modèle VAR défini par la définition (5.2.2) est causal si et seulement si les racines de l'équation déterminantale suivante

det [I -- B] = 0

ou de manière équivalente

det[I-- 1B-- 2B²--...-- "B"]=0

sont à l'intérieur du cercle unité.

On remarque que la condition précédente est nécessaire et suffisante pour la causalité mais suffisante seulement pour la stationnarité.

Chapitre 6

Cointégration et modèles à correction

d'erreurs

Le point de départ de la théorie de la cointégration lors de la mise en oeuvre du problème des régressions fallacieuses (Spurious régressions) par Granger et Newbold en 1974 : soient { Xt} et {Yt} deux processus intégrées d'ordre 1 suivant chacune une marche aléatoire

Xt = Xt_1 - Et Yt = Yt_1^- _t

où Et et _t sont deux bruits blancs indépendants. Si l'on effectue la régression Y t = a + /3Xt + Wt, on devrait avoir /3 = 0, mais Granger et Newbold ont montré que /3 était différent de zéro, ce qui veut dire qu'il existe une relation entre les deux séries Xt et Yt et qui sont par hypothèse indépendantes, donc ils ont abouti à une contradiction.

6.1 La cointégration

Nous avons vu, dans le cadre univarié, que la distinction entre les processus à tendance déterministe et les processus à tendance stochastique est d'une grande importance, car elle mène à des propriétés de long terme complètement différentes : persistance des chocs dans le cas d'une racine unitaire et amortissement des chocs dans le cas alternatif. Dans ce chapitre nous allons faire l'étude des séries chronologiques de façon conjointe, ce qui ouvre de nouveaux horizons.

On peut dire que la notion de racine unitaire n'a vraiment d'intérêt que dans le cadre multivarié. Dans le cadre de la cointégration, les variables peuvent avoir des tendances stochastiques communes, par exemple si l'évolution des prix de deux biens ont chacune une tendance stochastique, comment va évoluer ce couple de variables ? économiquement, on s'attend à ce qu'elle évoluent de façon plus ou moins parallèle, dans ce cas il est possible de trouver une combinaison linéaire de ces deux variables qui ne possède plus de tendance, mais qui mesure les erreurs d'ajustement d'une variable par rapporte à l'autre autour d'une relation d'équilibre.

Les premiers papiers sur les concepts d'intégration et de la cointégration remontent à Granger (1981,1983) et Granger et Weiss (1983). Le premier document fondamental est de Engel et Granger.

6.1.1 Définition de la cointégration

Si {Xt} et {Yt} sont deux processus intégrés d'ordre d (I(d)) alors en général la combinaison linéaire Zt telle que Zt = Xt -- aYt est aussi I(d)

Remarques

1. Si Xt rs^, I(d) alors a + bXt rs^, I(d) où a et b sont des constantes avec b =6 0.

2. Si Xt rs^, I(0) et Yt rs^, I(0) alors aXt + bYt rs^, I(0) où a et b sont des constantes.

3. Si Xt rs^, I(0) et Yt rs^, I(1) alors aXt + bYt rs^, I(1) où a et b sont des constantes avec b =6 0.

4. Si Xt rs^, I(d1) et Yt rs^, I(d2) alors en général aXt + bYt rs^, I [Max(d1, d2)] où a et b sont des composantes non nulles.

Définition

Les m composantes du vecteur Xt sont dites cointégrées à l'ordre (d, b) (Xt rs^, CI (d, b)) avec 0<b < d, si

toutes les composantes ses composantes sont intégrées d'ordre d

il existe un vecteur a (a =6 0) de taille (m, 1) tel que Zt = a^' Xt soit intégré d'ordre (d -- b). Le vecteur a est appelé vecteur de cointégration.

Remarque

Si Xt a m composantes, et s'ils existent r (r m -- 1) vecteurs de cointégration indépendants, alors Xt est dit cointégré de rang r, r désigne le rang de cointégration.

6.2 Modèle à correction d'erreur

Les modèles à correction d'erreur ont été proposés par Davidson, Hendry, Sbra et Yeo (1978) sous le nom de l'approche DHSY et développés et renommés ECM par Hendry (1980).

Ces modèles permettent de modéliser les ajustements qui conduisent à une situation d'équilibre de long terme en intégrant à la fois les évolutions de court terme et de long terme des variables.

6.2.1 Représentation des modèles à correction d'erreur (ECM)

Soient Xt et Yt CI (1, 1). Le modèle à correction d'erreur s'écrit sous la forme suivante

₈

<>>

>>:

_X

/3iLXt_i +

j

_X

LXt = 'y1Zt_1 +

i

LYt = 'y2Zt_1 + _X ~' iLXt_i + _X

i j

8LYt_ + d1(B)E:xt ~' jLYt_j + d2(B)€:Yt

où"Xt et _Yt sont deux bruits blancs. Z t = Xt--aY _t est le résidu de la relation de cointégration entre Xt et Yt, d1 et d2 sont des polynômes finis en B.

Définition

Un processus vectoriel {Xt} possède une représentation à correction d'erreur s'il peut être écrit sous la forme :

A(B)LXt = 'yZt_1 + d(B)€t

où {€t} est un bruit blanc, A(0) = I, A(1) ne comporte que des termes finis, Zt = a^'Xt où a est le vecteur de cointégration et 'y =6 0.

6.3 Estimation des modèles à correction d'erreur et test de cointégration: approche de Engel et Gran-

ger (1987)

6.3.1 Méthode d'estimation en deux étapes

Cette méthode, proposé par Engel et Granger (1987), et développée par phillips (1991), permet d'estimer en deux étapes les coefficients d'une représentation à correction d'erreur.

Remarque

Cette technique n'est valable que pour les séries CI (1, 1).

Première étape

Cette étape consiste à estimer la relation de long terme suivante : Yt = ~ + ~Xt + Z

où Zt est le terme d'erreur.

Deuxième étape

Dans cette étape on estime le modèle à correction d'erreur par la méthode des moindre carrés ordinaires.

~Yt='Y ^bZt_1+ _X XaiIXt_ + bjzYt_ + €t

i j

b

où {€t} est un bruit blanc et Zt_1 est le résidu estimé de la relation de long terme retardé

d'une pèriode

^bZt_1 = Yt_1^- b - b Xt_1.

6.3.2 Test de cointégration

Au cours de la première étape de la procédure de Engel et Granger, il est nécessaire de vérifier si les deux variables sont cointégrées, autrement dit, vérifier si les résidus de la relation de long terme sont stationnaires.

A cette fin, Engel et Granger ont proposé plusieurs tests tels que lest tests CRDW (Coin-
tégration régression Durbin Watson), lest tests de Dickey-Fuller simple (DF) et augmenté
(ADF)..., parmi ces tests, Engel et Granger (1987) recommandent l'utilisation des tests de

Dickey-Fuller.

Tests de Dickey-Fuller DF et ADF :

^bZt de la

Cest tests sont basés sur l'existence d'une racine unitaire dans les résidus estimés relation de long terme

Zt=I't-b~-

b ^b/3Xt.

Dans le test DF, on estime la relation :

zx^bZt = ç _{bZt_1+} ut

Dans le test ADF, on estime la relation :

XL^bZt=ç^bZt_1+ çi¹X^bZt_j + ut.

i

avec {ut} BB.

b

On test l'hypothèse nulle H0 : Zt non stationnaire (ç = 0) traduisant le fait que {Xt} et {I't}

sont non cointégrées, contre l'hypothèse alternative H1 : ^bZt stationnaire (ç < 0) indiquant que {Xt} et {I't} sont cointégrées.

b

Ce test de cointégration est basé sur les résidus estimés Zt et non pas sur les vraies valeurs

Zt. Donc on utilise les valeurs critiques tabulées par Engel et Yoo (1987) ou par McKinnon (1991) (voir annexe A)

La règle de décision est la suivante :

Si t ~ < valeur critique, on rejette H0

Si t ~ ~ valeur critique, on accepte H0.

6.4 Approche multivariée de la cointégration : l'analyse de Johansen

La méthodologie de Johansen (1991) est fondée sur un modèle véctoriel autorégressif (VAR). Elle permet a la fois d'estimer et de tester les relations d'equilibres des séries non stationnaires.

Considérons un modèle VAR d'ordre p de la forme suivante :

Yt = A0 + A1Yt~1 + :::::::: + ApYt~p + Et (1)

avec:

Yt : vecteur de dimension (k x 1)

A0 : vecteur de dimension (k x 1)

A : matrice de dimension (k x k) qui contient les paramètres du vecteur autorégressif VAR(p).

dans ce modèle, chaque composante I't est exprimée par ces p valeurs retardées. On peut réécrire le modèle (1) en différence premiere sous la forme suivante :

vYt= A0 + p--1_P F vYt_ + irYt~1 + Et (2)

=1

avec: F = -(A ₊₁ + .....+ A_p)

~ = -I + A1 + :::: + A_p

Si on a K variables endogènes, toutes ayant une racine unitaire (c'est a dire stationnaires en différences), on peut avoir (K - 1) relations de cointégration linéaires indépendantes.

les différentes étapes de test de Johansen sont :

Première étape

Cette étape consiste à calculer les résidus _t et Ut en effectuant les régressions suivantes : vYt = ^b0+ ^b~1vYt~1+ ^b~2vYt~2+ .... :: + ^b~pvYt~p + _t

Yt-1= ^bO0 + ^bO1vYt~1+ ^bO2vYt~2+ .......+ ^bOpvYt~p + Ut

On a les mêmes variables explicatives, seule la spécification du bloc de la variable à expliquer est modifiée.

^bçb et ^bO sont des matrices d'ordre (n, n), _t et Ut sont les matrices des résidus de dimension (k, n) avec k est le nombre de variables, et n le nombre d'observations.

Deuxième étape

Dans cette étape on calcul la matrice permettant le calcul des valeurs propres.

A partir des résidus 'i_t et Ut, on calcule les quatre matrices des variances-covariances de dimension (k, k) suivantes.

P d ~~ = 1n _Xn /t/^'t Pd z,z, = 1n _Xn UtU' t

i=1 i=1

P d iv = 1n _Xn /tU^'t P d vp = n 1 _Xn Ut/' t

i=1 i=1

Troisième étape

On extraie les k valeurs propres de la matrice M, de dimension (k, k), calculée de la manière suivante:

[P1 P

M = ~~ P d ^[_P1

~~ d ~~

Quatrième étape

A partir des valeurs propres de la matrice ir, on calcule la statistique À

Àtrace = -n _Xk Ln(1 - Ài)

i=r+1

où r est le rang de la matrice ir, k est le nombre de variables et Ài est la ^jieme plus grande valeur propre de la matrice ir.

Cette statistique suit une loi de probabilité (similaire à un x²) tabulée à l'aide de simulations par Johansen et Juselius (1990).

Ce test procède comme suit :

r = 0 : la matrice ir est nulle, le modèle (2) est un modèle vectoriel autorégressif sur les variables prises en différence première.

r = k : les variables sont intégrées d'ordre zéro et le modèle VAR est stationnaire. 0 < r < k : il existe une représentation de ir de la forme ir = a^'/5) où la matrice /3 de

taille (k, r) dite matrice de cointégration contient r colonnes appelées vecteur de

cointègration.

Cinquième étape

Après avoir déterminer le rang de cointégration au pas 4, ir peut être écrite sous la forme

~ = ~a

avec:

a : est une (k x r) matrice dont les colonnes sont les vecteurs propres calculés à l'étape

précédente et qui représentent les estimateurs, par le maximum de vraisemblance, des

vecteurs cointégrants.

/3: est une (k x r) matrice des facteurs de pondération (ainsi appelés) qui contient des poids associés à chaque vecteur cointégrant.

Chapitre 7

Application de la théorie de

coint égrat ion

Dans le chapitre 4 nous avons étudié les séries représentant l'évolution du prix du gaz naturel sur la marché américain (marché régional du Texas), et l'évolution du prix du brut sur le marché américain et Europen. Cette étude, menée dans un cadre univarié, n'explique pas l'influence du prix du brut sur le prix du gaz naturel. Afin de trouver la relation qui existe entre ces deux séries, nous avons proposé de faire une étude dans le cadre bivarié par le biais de la théorie de la cointégration qui exige que les séries soient intégrées d'ordre 1, ce qui est vérifié (voir le chapitre 4).

7.1 Etude de l'évolution du prix du gaz naturel et du brut sur le marché américain

Considérons les séries mensuelles du prix du gaz naturel (transformée en logarithme) LTt, et du prix du brut (transformée en logarithme) LW _t sur la période allant de Janvier 1989 à Janvier 2004. Ces deux séries exhibent une tendance commune à la hausse (Figure 1.1).

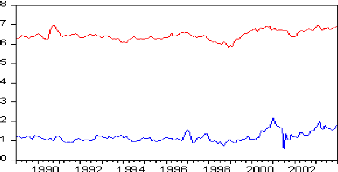
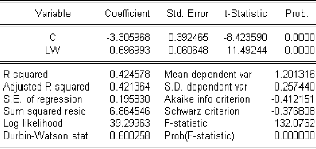
Figure (1.1)

Afin de trouver la relation de cointégration entre ces deux séries, nous avons appliqué la procédure en deux étapes de Engle et Granger.

Estimation de la relation statique entre LT et LW

Cette étape consiste à estimer la relation de long terme suivante :

LT =/3+aLW +Z (1)

L'estimation des paramètres de la relation (1) est donnée par la table suivante :

5% car leurs statistiques de Student relatives sont en valeurs absolues supérieures à 1.96. Donc la relation de long terme s'écrit sous la forme suivante :

LT t = --3.306+0.7LWt +Zt

avec Z _t les résidus de la relation estimée.

Notons que la condition nécessaire pour que la relation (1) soit une relation de cointégration est que la série de ces résidus soit stationnaire (dans le cas contraire on dit que qu'il s'agit d'une régression fallacieuse). En analysant le corrélogramme des résidus Z _t (Figure 1.2) nous constatons que la séries Z _t est stationnaire. pour confirmer la stationnarité des résidus notés Z1 nous avons appliqué le test ADF dont les résultats sont reportée dans la table de la Figure 1.3.

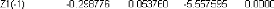
Afin d'interpréter ces résultats nous utilisons les tables de valeurs critiques de Engle et Yoo ou de MacKinnon (voir Annexe A). Nous constatons que la statistique ADF estimée (-5.557) est inférieure à la valeur tabulée par Engle et Yoo au seuil 5% (-3.37). Nous en déduisons donc que les résidus de la relation entre LT _t et LW _t sont stationnaires. Par conséquent, les séries du gaz naturel et du brut sur le marché américain sont cointégrées.

Après avoir estimé la relation de long terme entre les séries LT _t et LWt, il convient à présent d'estimer le modèle à correction d'erreur.

Estimation du modèle à correction d'erreur

Dans cette étape nous avons modélisé le taux de croissance du prix du gaz naturel (LTt) en fonction des résidus retardés d'une période, du taux de croissance du prix du brut (LWt) retardé d'une période et du taux de croissance du prix du gaz naturel retardé d'une période, c'est à dire que nous avons estimé le modèle suivant :

DLT t = ~ ^dZt~1+ aDLWt~1 + /3DLTt~1 + _t

A partir du résultat de cette estimation (Table 1.1) nous constatons que le coefficient associé à la force de rappel est négatif (-0.303) est significativement différent de zéro au seuil 5% puisque son t de Student (-5.89) est supérieur à 1.96 en valeur absolue. De plus les résidus associés à ce modèle forment un bruit blanc (Figure (1.3)), donc Il existe bien un mécanisme à correction d'erreur.

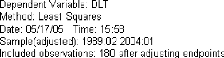
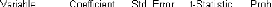
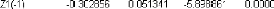
Table (1.1)

Nous retenons alors le modèle à correction d'erreur qui s'écrit sous la forme suivante : DLT = --0:303^bZt_1 + _t

ou encore

LT t = --1+ _{0.7LTt_1} + _{0.21LWt_1} + _t

avec _t les résidus du modèle à correction d'erreur estimé.

Graphe des séries réelle, estimée et résidus

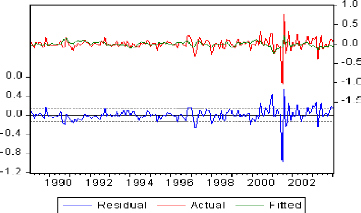
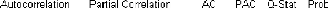
Figure (1.3)

Prévision :

Le modèle à correction d'erreur de la série LT _t s'écrit sous la forme suivante : LT t = --1+ _{0.7LTt_1} + _{0.21LWt_1} + _t.

D'où la prévision de la valeur de la série LT _t à un horizon h ~ 1 est donnée par la formule suivante:

{ --1 + 0.7LTt + 0.21LWt, h = 1

^cLT _t (h)= --1 + 0:7 ^cLT _t (h -- 1) + 0:21 ^dLWt(h -- 1), h ~ 2

Les prévisions de la série LTtsont données dans le tableau suivant :

Février 2004	1.782404
Mars 2004	1.786546
Avril 2004	1.794689
Mai 2004	1.805551
Juin 2004	1.811414
Juillet 2004	1.812060
Août 2004	1.818540
Septembre 2004	1.827917
Octobre 2004	1.833256
Novembre 2004	1.839989

Le graphe représentant la série brute Tt et la série prévue TF _t est le suivant :

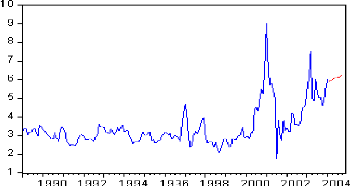
7.2 Etude de l'évolution du prix du WTI et du Brent

Considérons les séries mensuelles du prix du Brent (transformée en logarithme) LBt, et du prix du WTI (transformée en logarithme) LW _t sur la période allant de Juin 1987 à Février 2005. Ces deux séries exhibent une tendance commune à la hausse (Figure 2.1).

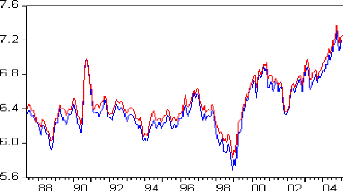
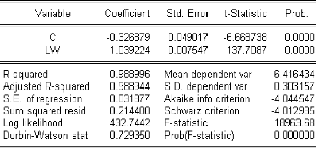
Figure (2.1)

Pour trouver la relation de cointégration entre ces deux séries, nous avons appliqué la procédure en deux étapes de Engle et Granger.

Estimation de la relation statique entre LB et LW

Cette étape consiste à estimer la relation de long terme suivante :

LB =/3+aLW +Z (1)

L'estimation des paramètres de la relation (1) est donnée par la table suivante :

Nous remarquons que les coefficients /3 et a sont significativement différents de zéro au seuil 5% car leurs statistiques de Student relatives sont en valeurs absolues supérieures à 1.96. La relation de long terme s'écrit sous la forme suivante :

LB = --0.33 + 1.04L W + Z

avec Z les résidus de la relation estimée.

En observant le corrélogramme des résidus Z (Figure 2.2) nous constatons que la série Z est stationnaire. Pour confirmer la stationnarité des résidus notés Z nous avons appliqué le test ADF dont les résultats sont reportée dans la table 2.1.

Figure (2.2)

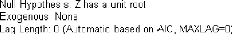
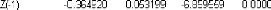
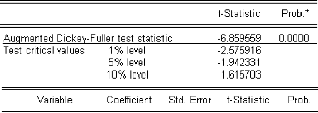
Table (2.1)

Afin d'interpréter ces résultats nous utilisons les tables de valeurs critiques de Engle et Yoo ou de MacKinnon. Nous constatons que la statistique ADF estimée (-6.86) est inférieure à la valeur tabulée par Engle et Yoo au seuil 5% (-3.37). Nous en déduisons donc que les résidus de la relation entre LB et LW sont stationnaires. Par conséquent, les séries LB et LW sont cointégrées. Après avoir estimé la relation de long terme entre les séries LB et LW , il convient à présent d'estimer le modèle à correction d'erreur.

Estimation du modèle à correction d'erreur

Dans cette étape nous avons modélisé le taux de croissance du prix du Brent en fonction des résidus retardés d'une période, du taux de croissance du prix WTI retardé d'une période et du taux de croissance du prix du Brent retardé d'une période, c'est à dire que nous avons estimé le modèle suivant :

DLB = ~ dZ ~1+ aDLW _~1 + /3DLB _~1 + ~

A partir du résultat de cette estimation (Table 2.2) nous constatons que le coefficient associé à la force de rappel est négatif (-0.51) et significativement différent de zéro au seuil 5% puisque son t de Student (-2.72) est supérieur à 1.96 en valeur absolue. De plus les résidus associés à ce modèle forment un bruit blanc (Figure 2.3), donc Il existe bien un mécanisme à correction d'erreur.

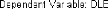
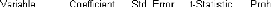
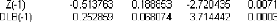
Table (2.2)

Nous retenons alors le modèle à correction d'erreur qui s'écrit sous la forme suivante : DLB = --0.51 dZ _1+ 0.25DLB _{_1} + ~

ou encore

LB = --0.17 + 0.74LB _1 -- 0.25LB _{_2} + 0.53LW _{_1} + ~

avec ~ les résidus du modèle à correction d'erreur estimé.

Graphe des séries réelle, estimée et résidus

Figure (2.3)

Prévision :

Le modèle à correction d'erreur de la série LB s'écrit sous la forme suivante : LB = -0.17 + 0.74LB _{_1} - 0.25LB _{_2} + 0.53LW _{_1} + ~ .

D'où la prévision de la valeur de la série LB à un horizon h > 1 est donnée par la formule suivante:

^dLB (h) =

8 < :

-0.17 + 0.74LB - 0.25LB _1 + 0.53LW , -0.17 + 0.74^dLB (1) - 0.25LB + 0.53 ^dLW (1), -0.17 + 0.74^dLB (h - 1) - 0.25^dLB (h - 2) + 0.53 ^dLW (h - 1),

h=1 h=2 h>3

Les prévisions de la série LB sont données dans le tableau suivant :

Mars 2005	7:207824
Avril 2005	7:247234
Mai 2005	7:288030
Juin 2005	7:315420
Juillet 2005	7:307897
Août 2005	7:277292
Septembre 2005	7:267395
Octobre 2005	7:282051
Novembre 2005	7:291229
Décembre 2005	7:295082

Le graphe représentant la série brute B et la série prévue BF est le suivant :

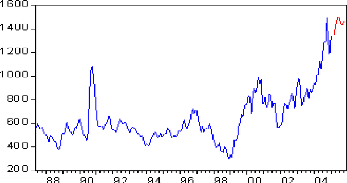
Comparaison entre la méthodologie de Box-Jenkins et de la théorie de coitégration en terme de prévision

Après avoir fait les prévisions sur le prix du gaz naturel (sur le marché régional du Texas) par la méthodologie de Box-Jenkins et par la théorie de cointégration, il convient de juger laquelle de ces deux approches est meilleure en terme de prévision.

Pour ce faire, nous nous somme basé sur la somme des carrées des résidus obtenue par chaque approche. Ainsi, une méthode est jugée meilleure qu'une autre son RMSE(e) est plus faibles. Le RMSE(e) est donné par la formule suivante :

_r

RMSE(e) = e ²

n1 Pn _t où et = (Xt - bxt).

t=1

Pour savoir laquelle des deux approches est meilleure en terme de prévision pour la série du prix du gaz naturel au Texas, nous avons réestimé son modèle générateur en négligeant les dix dernières valeurs (le modèle obtenu par la méthodologie de Box et Jenkins et par la théorie de cointégration), et nous avons constaté que le modèle est resté le même (pour les deux approches). Après avoir réestimé les modèles nous avons calculé les prévisions à un horizon h = 10, en suite nous avons calculé le RMSE(e) associé à chaque méthode. La table suivante donne les résultats pour la méthodologie de Box et Jenkins :

Données LT	t	Prévisions ^cLT t	e2 t
01/04/2003	1:615420	2:087036	0:222422
01/05/2003	1:583094	1:816601	0:054525
01/06/2003	1:795087	1:875996	6:5404 x	10^~3
01/07/2003	1:667707	2:034125	0:134262
01/08/2003	1:612430	2:080196	0:217870
01/09/2003	1:623341	1:887394	0:069724
01/10/2003	1:528228	1:939636	0:169256
01/11/2003	1:589235	1:954421	0:134107
01/12/2003	1:735189	1:970983	0:055598
01/01/2004	1:796747	2:125774	0:108226
RMSE(e)			0:342422

De la même manière nous avons calculé le RMSE(e) associé à la prévision par la théorie de cointégration et nous avons trouvé:

RMSE(e) = 0:2031:

Ainsi nous constatons que la théorie de cointégration révèle la meilleure, en terme de prévision.

Bibliographie

[1] Akaike, H. (1974). A new look at the statistical model identification. IEEE. Trans. Automat. Contr,19, pp 716-723.

[2] Box, G.E.P. et Jenkins, G. M.(1976). Time Series Analysis, Forecasting and Control, Holden-Day, (revised edition). San Francisco, CA.

[3] Davidson, J. E. H., Hendry, D. F., Sbra, F. et Yeo, S. (1978). Econometric Modelling of the Aggregate Time Series Relationship between Consumers, Expenditure and Income in the United Kingdom, Journal Economique, 88, pp 661-692.

[4] Dickey,D. A. et Fuller,W. A. (1979). Distibution of the Estimation for Autoregressive Time Series with a Unit Root. Journal of Monetery Economics. 28. pp 221-254.

[5] Durbin, J. (1960) .The fitting of time series models. Revue international of institut of Statistics, 28, pp 233.

[6] Engel, R. F. et Granger, C. W.J. (1987). Co-Integration and Error Correlation : Representation, Estimation and Testing. Econometrica, 55, pp 251-276.

[7] Gourieuroux, C. et Monfort, M. (1995). Séries temporelles et modèles dynamiques Economica..

[8] Granger, C.W.J. (1983). Co-Integrated Variables and Error-Correcting Models. Unpublished University of California, San Diego, Discussion Paper 83-13..

[9] Granger, C.W.J. et Newbold, P. (1974). Spurious Regressions in Econometrics. Journal of Econometrics, 2, pp 111-120.,

[10] Johansen, S. (1991). Estimating and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica, 59, pp1551-1580.

[11] Johansen, S. et K, Juselius, (1990). Maximum likehood estimation and inference on cointegration-with applications to the demand for money. Oxford Bulletin of Economics and Statistics 52(2), pp 169-210.

[12] Lardic. S. et Mingnon, V. (2002). Econométrie des Séries Temporelles Macroéconomiques et Financières. Economica.

[13] Ljung, G. M. et Box, G. E. P. (1979). The likelihood Function of stationary autoregressive-moving average models. Journal of the Royal Society. Series C Applied. Statistics, 24, pp 255-259.

[14] Mélard, G. (1990). Méthodes de prévision à court terme. Ellipses.

[15] Phillips, P.C.B.(1991). Optimal Inference in Cointegrated Systems. Econometrica 59 :283-306.

[16] Schwarz, G. (1978). Estimating the dimension of the model. Ann. Stat, 6, pp 461-664.

[17] Wold, H. (1938). A study in the stationary time series, Almqvist and Wiksell, Stockholm (2nd edition :1954).

[18] Caractéristiques du gaz naturel: http ://r0, unctad.org/infocomm/francais/ gaz/descript .htm.