Chapitre 4
Application de la méthodologie de
Box et Jenkins
4.1 Etude de la série des prix spot du gaz
naturel à Pensylvania (Pi)
4.1.1 Identification et estimation
Considérons la série Pt qui représente le
prix du gaz naturel sur le marché régional de Pensylvania de
Janvier 1989 à Février 2004 (les données ont pour
unité de mesure le dollar par mettre cube ($/m3)). En
observant la représentation graphique de cette (Figure 1.1) série
nous constatons qu'elle possède une tendance à la hausse avec une
variabilité qui paraît de plus en plus grande . Afin de dissiper
les variations ou encore de stabiliser la variance de cette série, nous
proposons de lui appliquer une transformation logarithmique. La série
ainsi transformée, notée LP t (Figure 1.2) garde la
même allure que la série Pt exhibant ainsi une tendance à
la hausse, et semblant donc non stationnaire au sens de la moyenne.
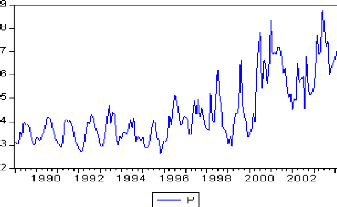
Figure (1.1)

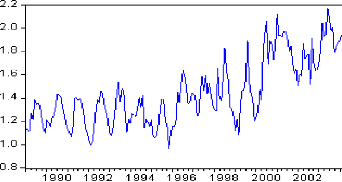
Figure (1.2)
En analysant le corrélogramme associé à
la série LP t (Figure 1.3) nous constatons que la
série n'est pas stationnaire puisque sa fonction
d'autocorrélation simple et partielle diminuent lentement et qu'elle
possède une saisonnalité d'ordre 12 puisque la fonction
d'autocorrélation simple possède des valeurs importantes aux
retards 1, 12, 24... .
Afin de traiter l'effet de saisonnalité sur notre
série ou encore de la stationnariser nous lui avons appliqué la
différence saisonnière d'ordre 12, la série ainsi
désaisonnalisée est notée
SLPt.


Figure (1.3)
Nous remarquons que la fonction d'autocorrélation simple
de la série désaisonnalisée SLP t diminue
rapidement, nous pouvons donc dire qu'elle est stationnaire (Figure 1.4).

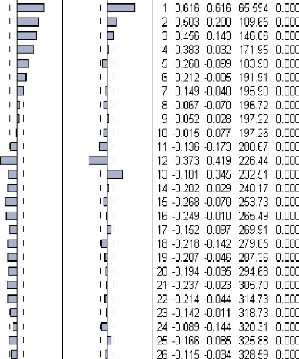
Figure (1.4)
Pour confirmer ou infirmer notre hypothèse consistant
à ce que la série désaisonnalisée est stationnaire,
nous avons appliqué le test de Dickey-Fuller sur la série SLP
t qui nécessite tout d'abord de sélectionner le nombre
de retard p, nous avons alors choisi le retard qui minimise le critère
d'Akaïke et qui est 2. Nous avons commencé par l'estimation du
modèle (3)
2
Modèle (3) : LXSLP t = c + bt + çbSLPt_1 +
X çbjLXSLPt_j + Et


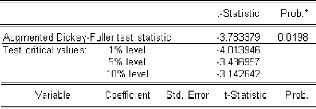
De la table ci-dessus nous constatons que la tendance n'est
pas significativement différente de zéro puisque sa t-statistic
(0.956) est inférieure aux valeurs critiques 3.46, 2.78 et 2.38
tabulées par Dickey-Fuller respectivement aux seuils 1%, 5% et 10%. Nous
avons donc par la suite estimé le modèle (2)
2
Modèle (2) : LXSLP t = c + çbSLPt_1 + X
çbjLXSLPt_j + Et
j=1
Des résultats de l'estimation du modèle (2),
reportés dans la table 1.1, nous constatons que la constante n'est pas
significativement différente de zéro puisque sa t-statisique
(1.06) est inférieure aux valeurs tabulées par Dickey-Fuller aux
seuils 1%, 5% et 10% qui sont respectivement égales à 3.18, 2.52
et 2.16.
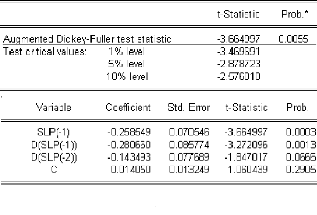
Table (1.1)
Du fait que l'estimation de la constante est statistiquement
nulle, nous avons estimé le modèle sans intercept, autrement dit
nous avons estimé le modèle (1) dont les résultats sont
présentés dans la table (1.2).
Nous procédons au test de racine unitaire, la valeur
estimée de la statistique ADF est égale à --4.368 (voir la
table ci-dessus). Cette valeur est inférieure aux valeurs critiques
--2.57879, --1.9427 et --1.6154 aux seuils 1%, 5% et 10%. Par
conséquent, nous rejetons l'hypothèse nulle de racine unitaire :
la série SLP t est stationnaire, c'est à dire
intégrée d'ordre 0, ce qui est cohérent avec
l'étude du corrélogramme de SLPt.
2
Modèle (1) : LXSLP t = çbSLPt_1 + X
çbjLXSLPt_j + Et


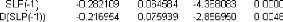
Table (1.2)
Après avoir stationnarisé la série, il
convient à présent d'estimer le modèle susceptible
à la représenter. En observant le corrélograme simple et
partiel de la série stationnaire SLPt (Figure 1.4) nous remarquons que
la fonction d'autocorrélation simple possède des valeurs
importantes aux retards q = 1, 12, 13, ..., et que la fonction
d'autocorrélation partielle possède des valeurs importantes aux
retards p = 1, 2, 6, 9, 20, .., alors nous avons estimé plusieurs
modèles parmi lesquels nous avons sélectionné deux
modèles: SARIMA(13, 0, 0) x (1, 1, 0)12 et SARIMA(13, 0, 9) x (1, 1,
0)12, les résultats de l'estimation de ces deux
modèles sont donnés respectivement par les tables 1.3 et 1.4.
Parmi ces deux modèles nous devons choisir un seul, le
plus adéquat. Pour faire ce choix nous nous somme basés sur les
critères de pouvoir prédictif (à savoir : R2
qui est à maximiser
et R2, AIC à minimiser), et nous avons
à la fin choisi le modèle SARIMA(13, 0, 9) x (1, 1, 0)12
puisqu'il est le plus adéquat. Les valeurs des critères de
pouvoir prédictif des deux modèles sont données dans la
table suivante
|
SARIMA(13,0,9) x (1,1,0)12
|
SARIMA(13,0,0) x (1, 1,0)12
|
|
R2
|
0.642
|
0.632
|
|
R2
|
0.6328
|
0.625
|
|
AIC
|
--1.1536
|
--1.1389
|
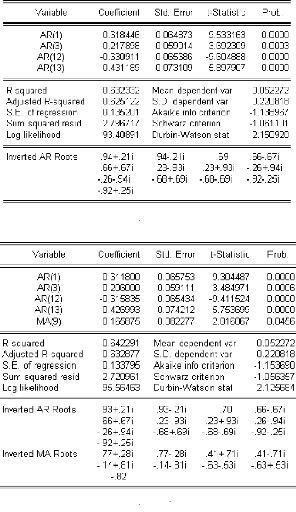
Table (1.3)
Table (1.4)
| 


