Variables linguistiques et propositions floues

REPUBLIQUE DU CAMEROUN
Paix - Travail - Patrie

UNIVERSITE DE YAOUNDE I THE UNIVERSITY OF YAOUNDE I

ECOLE NORMALE SUPERIEURE

HIGHER TEACHERS TRAINING

COLLEGE

N

E

S

DEPARTEMENT DE MATHEMATIQUES
DEPARTMENT OF MATHEMATICS

MA 510 : LOGIQUE FLOUE

THEME:

VARIABLES LINGUISTIQUES ET PROPOSITIONS FLOUES

Filière : MATHEMATIQUES Niveau : 5

Sous la direction de : Dr FOTSO SIMEON

Année académique 2009- 2010

LISTE DES MEMBRES DU GROUPE

N°	NOMS ET PRENOMS	Matricule
1	AMANG GUEBEDIANG Stéphanie A.	98M012
2	LONLACK TCHOFFO Alain Isidore	02U184
3	MINLEND Ignace Aristide	03T192
4	NGONO AMOA Madeleine Flora	99Y469
5	NJIFON Ousseni	03V253
6	NTSAFACK DONGMO Frank Wilson	01S296
7	TAGUEDONG Raoul Bernard	02U060

TABLE DES MATIERES

INTRODUCTION 3

I. THEORIE DES ENSEMBLES FLOUS 3

PROPRIPTIS 4

OPERATIONS SUR LES ENSEMBLES ELOUS 5

II. THEORIE DES POSSIBILITES - VARIABLES LINGUISTIQUES - PROPOSITIONS

FLOUES 7

A. LA THEORIE DES POSSIBILITES 7

B. VARIABLES LINGUISTIQUES ET PROPOSITIONS FLOUES 8

DISTRIBUTION DE POSSIBILITES ASSOCIEE A UNE PROPOSITION FLOUE 9

CONCLUSION 10

LEXIQUE 10

BIBLIOGRAPHIE 10

INTRODUCTION

La modélisation est devenue un outil important dans l'ingénierie et la science. Les approches traditionnelles de modélisation insistaient énormément sur la précision et la description exacte des systèmes. L'utilisation des outils mathématiques comme les équations différentielles, équations aux différences, fonction de transfert, etc... est appropriée et justifiée pour les systèmes bien définis. Mais quand la complexité augmente, ces outils deviennent moins efficaces. Le traitement des systèmes complexes nécessite souvent la manipulation d'informations vagues, imprécises, incertaines ou à la fois imprécises et incertaines.

Depuis longtemps, l'homme recherche donc à maîtriser les incertitudes et les imperfections inhérentes à cette nature des choses. C'est pourquoi, au lieu de réfléchir en termes mathématiques, l'être humain décrit le comportement [mathématiques] à l'aide du système par les propositions linguistiques. Afin de pouvoir représenter ce type d'informations, ZADEH a proposé de modéliser le mécanisme de la pensée humaine par un raisonnement approximatif basé sur les variables linguistiques et les propositions floues.

Il convient pour mieux comprendre les concepts de variables linguistiques et de propositions floues, d'explorer avec beaucoup d'attention la théorie des ensembles flous qui constitue une interface entre les mondes numériques et linguistiques.

Dans la suite, notre tâche consistera donc à faire un rappel des définitions de base et concepts concernant les sous ensembles flous (noyau, hauteur, support, a-coupe...), les opérations sur ces sous ensembles flous (intersection, réunion complémentaire, etc...) d'une part, d'autre part nous étudierons la théorie des possibilités pour voir les variables linguistiques et les propositions floues.

I. THEORIE DES ENSEMBLES FLOUS

Les sous-ensembles flous (ou parties floues) ont été introduits afin de modéliser la représentation humaine des connaissances, et améliorer les performances des systèmes de décision qui utilisent cette modélisation.

Les sous ensembles flous sont utilises soit pour modéliser les incertitudes et l'imprécision, soit pour représenter des informations précises sous forme lexicale assimilable par un système expert.

Définition :

Une partie A d'un ensemble E est usuellement associée à sa fonction caractéristique. Celle-ci s'applique sur les éléments x de E. Elle prend la valeur 0 si x n'appartient pas à A et 1 si x appartient à A.

ì_A : E? { 0,1}

0 si			xA ?
x
1 si		x A ?



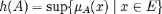
On souhaite définir une partie A floue de E en attribuant aux éléments x de E un degré d'appartenance, d'autant plus élevé qu'on souhaite exprimer avec certitude le fait que x est élément de A. Cette valeur vaudra 0 si on souhaite exprimer que x de façon certaine n'est pas

élément de A, elle vaudra 1 si on souhaite exprimer que x appartient à A de façon certaine, et elle prendra une valeur comprise entre 0 et 1 suivant qu'on estime plus ou moins certain l'appartenance de x à A. On est donc amené à définir une partie floue de la façon suivante :

Une partie floue (ou sous-ensemble flou) d'un ensemble E est une application de E dans [0,1].

Plus généralement, si L est un treillis complet, distributif et complémenté, on définit une partie L-floue comme étant une application de E dans L. Si L = [0,1], on retrouve la

définition précédente de partie floue, et si L = {0,1}, on retrouve la notion usuelle de partie de E.

PROPRItTtS

P1 : Une partie floue A de E est caractérisée par une application de E dans [0,1]. Cette application, appelée fonction d'appartenance et notée EiA représente le degré de validité de la proposition « x appartient à A » pour chacun des éléments x de E. Si EiA(x) = 1, l'objet x appartient totalement à A, et si EiA(x) = 0, il ne lui appartient pas du tout. Pour

un élément x donné, la valeur de la fonction d'appartenance EiA(x) est appelée ^degréd'appartenance de l'élément x au sous-ensemble A.

P2 : L'ensemble E est donné par la fonction d'appartenance identiquement égale à 1.

L'ensemble vide est donné par la fonction d'appartenance identiquement nulle.

P3 : Le noyau d'une partie floue A est l'ensemble des éléments qui appartiennent totalement à A c'est-à-dire dont le degré d'appartenance à A vaut 1.



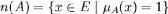
P4 : Le support d'une partie floue A est l'ensemble des éléments appartenant, même très peu, à A c'est-à-dire dont le degré d'appartenance à A est différent de 0.



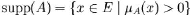
P5 : La hauteur d'un sous-ensemble flou A de E est définie par

P6 : a-coupe

Une partie floue A de E peut aussi être caractérisée par l'ensemble de ses á-coupes. Une

á-coupe d'une partie floue A est le sous-ensemble net (classique) des éléments ayant un degré d'appartenance supérieur ou égal à á.



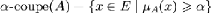
P7 : Un ensemble fini possède un nombre fini de sous-ensembles L-flous si et seulement si le treillis L est fini³. Si L = [0,1], un ensemble fini possède une infinité de sous-ensembles flous.

OP~R~~IONS SUR LES I ~EMBLES FLOUS

En observant comment les opérations usuelles se comportent vis-à-vis des fonctions caractéristiques de parties, on étend ces opérations aux fonctions d'appartenance des parties floues.



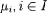
O1. Réunion

Soient une famille de parties floues d'un ensemble E, données par leur

fonction d'appartenance. On définit la réunion de ces parties au moyen de la fonction d'appartenance suivante :

, ce qui sera noté



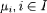
O2. Intersection

Soient une famille de parties floues d'un ensemble E, données par leur

fonction d'appartenance. On définit la réunion de ces parties au moyen de la fonction d'appartenance suivante :

, ce qui sera noté

Réunion et intersection restent distributives l'une par rapport à l'autre. C'est-à-dire

ì₁
ì₁

U fl

( ) ( ) ( )

ì ì ì ì ì ì

= U fl u

2 3 1 2 1 3

fl U

( ì ₂ ì ì ì ì ì

3 ) ( 1

= fl U fl

2 ) ( 1 3 )

O3. Complémentaire

Soit A une partie floue d'un ensemble E, donné par sa fonction d'appartenance i. Alors le complémentaire de A donnée par sa fonction d'appartenance JL est la partie floue dont la fonction d'appartenance est 1 - jt.

Notons que :

· Le complémentaire d'une intersection reste égal à la réunion des complémentaires.

· Le complémentaire d'une réunion est égal à l'intersection des complémentaires.

· Le complémentaire du complémentaire redonne la partie initiale.

On notera cependant que :

· La réunion d'une partie floue et de son complémentaire ne donne pas l'ensemble E

· L'intersection d'une partie floue et de son complémentaire ne donne pas l'ensemble vide.

O4. Image directe

Soient E et F deux ensembles et f une application de E dans F. Considérons une partie floue de E donnée par sa fonction d'appartenance p.. On appelle image directe de cette partie floue par f la partie floue de F donnée par la fonction d'appartenance suivante, notée f(p) :



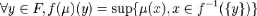
O5. Image réciproque

Soient E et F deux ensembles et f une application de E dans F. Considérons une partie floue de F donnée par sa fonction d'appartenance p.. On appelle image réciproque de cette partie floue par f la partie floue de E donnée par la fonction d'appartenance suivante, notée f - ¹(p.) :



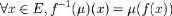
Après avoir donné les origines et rappelé quelques généralités sur la logique floue, nous venons de définir quelques propriétés des ensembles flous ou parties floues d'une part, et de rappeler les opérations sur les parties floues d'autre part.

Nous allons dans le paragraphe suivant, étudier la théorie des possibilités, les variables linguistiques et les propositions floues.

II. THEORIE DES POSSIBILITES - VARIABLES
LINGUISTIQUES - PROPOSITIONS FLOUES

A. LA THEORIE DES POSSIBILITES

Si la théorie des sous-ensembles flous assouplit le cadre de la théorie classique des ensembles pour pouvoir traiter l'imprécision, la théorie des possibilités propose un cadre permettant de traiter les incertitudes difficiles, voire impossibles à traiter par la théorie des probabilités. C'est une théorie mathématique basée sur la théorie classique des ensembles, correspondant à l'introduction de la nouvelle notion de distribution de possibilité. En effet, raisonner en termes de probabilités suppose de pouvoir définir la probabilité de chaque événement. C'est donc un moyen de dire dans quelle mesure la réalisation évènement est possible et à quel point on en est certain sans toute fois avoir à sa disposition l'évaluation de sa probabilité. Pour cela, il faut en avoir une bonne connaissance. Si cette connaissance n'est pas disponible, alors on raisonne en termes de possibilité (et de son dual, nécessité). La théorie des possibilités comme la théorie des ensembles flous est basée sur les fonctions d'appartenance

1. Définition : Fonction de possibilité

La fonction de possibilité ð associe à chaque évènement d'un univers 1~ une valeur entre 0 et1 qui définit le degré de possibilité de l'événement :

ð : u ? Ù-ð(u)? [0,1]

Il ne faut pas confondre possibilité et probabilité car même si les deux notions traitent des incertitudes évènementielles, certaines différences très importantes séparent ces deux

0 0

concepts .Par exemple, si A est événement contraire de A, on a P ( A ) = 1- P(A) mais il n'y a

0

aucune raison que (A)

ð soit égale à 1- t(A).

Nous allons à présent définir les notions de mesure de probabilité, distribution de possibilité, mesure de nécessite et donner une propriété essentielle de la mesure de nécessite.

Définition : Une mesure de possibilité est une fonction ð : P ( X ) ? [ 0,1] vérifiant les propriétés :

(i) t ({}) = 0, t (X) = 1

(ii) ? ? ?

( )

A P X

( ), ( ) sup ( )

ð U =

A ð A où I est un ensemble

i i I i i

i I

i I

?

quelconque d'indices.

Propriété : t (A U B) = Max (t (A), t (B)) Définition :

?

On appelle distribution de possibilité ou fonction de possibilité, une fonction ð : X ? [ 0,1] qui vérifie la condition de normalité ( ) = 1

Sup x

ð

x X

La mesure de possibilité de possibilité associée est définie par :

ð ( ) = ð ( ) A Sup x x ? A

Définition : Une mesure de nécessité est une fonction N définie de P(X) dans [0,1] et vérifiant :

(i) N ({}) = 0, N(X) = 1

(ii) N n A_i = Inf N A ( _i ) où I est un ensemble quelconque d'indices.

i I

?

i I

?

Propriété : cette propriété est vérifiée par la mesure de nécessité.

Pour tous A et B éléments de P(X), nous avons N (AnB) = min (N (A), N (B))

En outre, en l'absence de P (A) (évaluation de la probabilité de l'évènement A), on se sert du couple (N (A), ð (A)) pour représenter l'incertitude sur l'occurrence de l'évènement A. La nécessité et la probabilité d'un évènement quelconque encadrent sa possibilité inconnue.

La théorie des ensembles flous fournit une base naturelle à la théorie des possibilités. Une contrainte souple ou floue sur les valeurs que peut prendre une variable x induit une distribution de possibilité sur les valeurs que peut prendre cette variable .On associe donc à une variable dont les valeurs sont floues,une distribution de possibilité de la même manière qu'on associe à une variable aléatoire dont les valeurs stochastiques ont une distribution de probabilité .On peut interpréter donc toute distribution de possibilité comme une restriction floue élastique sur les valeurs que peut prendre une variable .La distribution de possibilité devient alors une fonction d'appartenance d'un ensemble flou représentant cette contrainte.

B. VARIABLES LINGUISTIQUES ET PROPOSITIONS FLOUES

L'expression « variable linguistique » introduite par ZADEH, propose que les valeurs de cette variable ne soient pas numériques mais symboliques comme les mots du langage courant. Une variable linguistique est donc une variable prenant ses valeurs dans un ensemble de mots symboliques (sous-ensemble flous) définissant certaines catégories d'un ensemble de référence.

Définition : Variable linguistique

On appelle Variable linguistique un triplet (V, X, Tv) tel que :

(i) X est un ensemble de référence

(ii) V est une variable symbolique définit sur X.

(iii) T V = { A₁ , A ₂,..., A _n ,... } ensemble fini ou dénombrable de sous ensembles flous

normalisés, utilisés pour caractériser V.

Rappelons qu'un sous ensemble flou est normalisé s'il est non vide et identique a son support et a son noyau ou bien sa hauteur est 1.

Définition : Modificateur linguistique

Un Modificateur linguistique est un opérateur qui permet a partir de toute caractérisation floue A de produire une nouvelle caractérisation.

Nous allons a présent définir les deux types de propositions floues : la proposition floue élémentaire et la proposition floue générale.

Définition: Proposition floue élémentaire

Elle est définie à partir d'une variable linguistique (V, X, Tv) par la qualification « V

, où M (Tv) l'ensemble des caractérisations nouvelles obtenues en

A T ou

? V

est A » avec

A ?

M T

( _V )

appliquant les modificateurs linguistiques.

La formation d'une proposition floue est possible a partir de l'utilisation conjointe de proposition floue élémentaires « V est A », « W est B » pour des variables V, W supposées non interactives, ceci en utilisant des connecteurs comme la conjonction (?), la disjonction (? ) et l'implication .

Définition : Proposition floue générale

Elle est obtenue par disjonction (?), conjonction (?), négation (+) et implication de proposition floues quelconques

Exemple : Soient « V est A » et « W est B » deux propositions floues élémentaires, par des variables V et W.

· « V est A » « W est B »

· « V est A » ? « W est B »

· « V est A » ? « W est B »

· #172; (« V est A ») sont 4 propositions floues générales.

Définition : (Règle floue)

Entre deux propositions floues quelconques p et q, on peut utiliser une implication. On obtient ainsi une proposition floue de la forme « si p alors q », appelée règle floue.

DISTRIBUTION DE POSSIBILITES ASSOCIEE A UNE PROPOSITION FLOUE

Etant donnée une proposition floue « V est A », une distribution de possibilité lui est associée, donnée par ð V , A ( x ) = f_A (x )

La distribution de possibilités associée à une proposition floue générale peut être calculée en appliquant les opérations ensemblistes de la théorie des ensembles flous ; les distributions de possibilités étant considérées comme des fonctions d'appartenance. Souvent

dans le langage naturel, on utilise des qualifications linguistiques et des quantificateurs symboliques, agissant sur des propositions floues. Ces opérations induisent des distributions de possibilités de différentes natures.

CONCLUSION

Dans le cadre de la maîtrise des incertitudes et des imperfections liées à sa nature, l'homme trouve dans les variables linguistiques et les propositions floues des outils importants dans l'étude du raisonnement approximatif, qui est une grande alternative au raisonnement extra rigide. Pour le raisonnement les variables sont manipulées par les termes linguistiques ainsi définis, et les ensembles flous assurent la correspondance avec l'univers numérique.

LEXIQUE

Modélisation: c'est la conception d'un modèle. En mathématiques appliquées, et en pratique en chimie, en physique, en informatique, en météorologie ou en sciences de la vie et de la terre, la modélisation permet d'analyser des phénomènes réels et de prévoir des résultats à partir de l'application d'une ou plusieurs théories à un niveau d'approximation donné.

Equations différentielles : En mathématiques, une équation différentielle est une relation entre une ou plusieurs fonctions inconnues et leurs dérivées.

Equations aux q différences : Les équations aux q-différences forment une famille d'équations fonctionnelles dont l'étude est apparentée à celle des équations différentielles.

Fonction de transfert : Une fonction de transfert est une représentation mathématique de la relation entre l'entrée et la sortie d'un système linéaire invariant.

BIBLIOGRAPHIE

www.wikipedia.org/wiki/logique_floue www.math-info.univ-paris5.fr/~hachama/dossier/.../r_sum_-magister.pdf