4.8. Détermination des para mètres de l'a
todé harg
u c e par
spectroscop ie d'impédance
4.8.1. Réponse en fréquence de
l'impédance de l'autodécharge
Les phénomènes électrochimiques rapides
se produisent à haute fréquence et correspondent aux transferts
de charges. Les phénomènes lents correspondant à des
transports de matière par diffusion se produisent à basse
fréquence.
L'impédance électrochimique de
l'autodécharge par processus de diffusion lié à
l'oxydoréduction Zrp représentée par
le circuit RrpCrp sur la figure 4-12, peut être
caractérisée, ainsi que l'impédance de la double couche,
par spectroscopie d'impédance électrochimique.
Selon la nature des impuretés, le processus de
diffusion lié à l'oxydoréduction est
quasiréversible [137], c'est-à-dire que les charges
diffusées vers les électrodes pendant cette autodécharge
ne sont pas dissipées parfaitement mais elles peuvent être
récupérées. Ceci nous permet en principe de
caractériser l'impédance équivalente. La fréquence
f correspond au phénomène de l'autodécharge par
diffusion est comprise entre 30 uHz à 0.3 mHz (une heure à une
dizaine d'heure).
Le schéma donné sur la figure 4-12
représente le comportement temporel du supercondensateur. En très
basse fréquence, le circuit de la figure 4-12 p eut être
réduit au schéma montré sur la figure 4-37, car les
circuits ont une constante de temps très faible par rapport à la
branche constituée f C1 :
par R
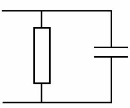
Rf
C1
Fig. 4-37 : Circuit équivalent du
supercondensateur à très basse fréquence
La réponse en fréquence du circuit
équivalent peut être déduite comme suit :
4-25
1 1 j C
= + ù 1
f
Z R
? - 1 2
? 1 R f ù R f C
1
Z = ?? + ù
j C ?? = - j 4-26
1 1 2 2 2 2 2 2
? R R C 1 R C
f ? + ù + ù
f 1 f 1
Rf
Re( )
Z = 4-27
2 2 2
1 + ù f
R C 1
- ùR 2C
f 1
Im( )
Z = 4-28
2 2 2
1 + ù R C
f 1
Nous montrons sur la figure 4-38 le tracé de Nyquist
correspondant au circuit RfC1 à très basse
fréquence. Nous constatons que la réponse en fréquence du
circuit équivalent du supercondensateur à une fréquence de
l'ordre de quelques nHz, est un demi-cercle de rayon de Rf/2. La
fréquence correspondant au centre du demi-cercle est égale
à ff = 1/(2ðRfC1). Nous constatons donc qu'il y a deux
limites de l'impédance : à basse fréquence Z = Rf
et à haute fréquence Z = 0. La fréquence
intéressante qui permet théoriquement de déterminer la
valeur de la résistance de fuite est de l'ordre de la fréquence
ff.
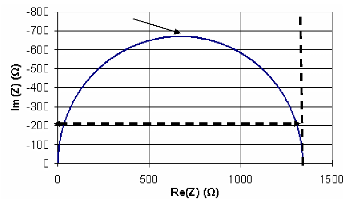
2.5 nHz
Rf
Fig. 4-38 : Simulation du circuit RfC 1 en
tracé de Nyquist
| 


