4.9. Phénomène de la
récupération de tension
A une température de 25 °C et pour une tension
initiale de 0,5 V, l'autodécharge conduit pendant les premières
heures à diminuer la tension aux bornes des supercondensateurs comme le
montre la figure 4-41. Un phénomène de récupération
de tension est ensuite observé. Un accroissement lent de la tension a
lie e t probablem û ersion de la taille des
u. C ci es ent d à la disp
pores [116] : une redistribution de la charge entre les pores se
produit lorsque les potentiels des différents pores ne so nt pas
égaux. De plu , la quasi-réversibilité du processus de
diffus
s ion due
aux impuretés peut être l'une des causes de la
récupération de charge.
La remontée de la tension observée sur la
figure est de l'ordre de plusieurs dizaines de jours et est très
supérieure à celle de la redistribution de charges. Ceci nous a
conduit à réétudier la théorie de
l'autodécharge du processus de diffusion dû à
l'oxydoréduction.
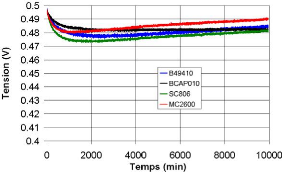
Fig. 4-41 : Tension aux bornes des supercondensateurs
étudiés à une tension initiale de 0. 5V
4.10. Impédance électrochimique de
l'autodécharge de diffusion
Nous proposons dans ce paragraphe d'étudier d'un point
de vue théorique le comportement temporel et fréquentiel de
l'impédance électrochimique de l'autodécharge due au
processus de diffusion. Ceci va nous permettre de mieux comprendre les
phénomènes observés expérimentalement tels que la
récupération de tension.
A partir de l'équation de diffusion de concentration
de charges aux interfaces charbon- électrolyte, nous pouvons
déduire le courant et la tension de diffusion dus à
l'oxydoréduction. Le courant parcourant les surfaces
charbon-électrolyte d'épaisseur 2.h dû à la
diffusion à l' instant t peut être écrit
par l'équation suivante [138] :
idiff D ( t ) = m .C .
exp
-
D t ?4-29
2
où,
m et D sont respectivement le paramètre
et le coefficient de diffus ion (cf. eq. 4-5), C la capacité
totale du supercondensateur.
du
C . = - diff 4-30
i ( t )
dt
A partir de l'équation 4-30 en considérant une
capacité C non dépendante de la tension, la tension aux
bornes du supercondensateur peut donc être donnée par la relation
suivante [138] :
? ? ? - h 2 ? ? ? h ? ?
u t U m t
( ) 0
= - ? ?? 1 exp

- ? ? ?? + h D erfc ?? ?? ?
4-31
? D t ?
? ? ? ? D t
? ? ? ?
erfc étant la fonction erreur de Gauss (Error
Function)
Pour expliquer le phénomène
d'autodécharge dû au processus de diffusion, nous
présentons l'évolution du courant et de la tension sur les
figures 4-42-a et b avec un paramètre h donné dans le
document [138].
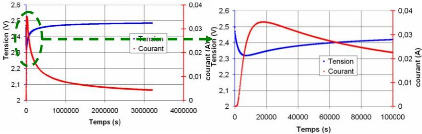
(a)
(b)
Fig. 4-42 : Evolution du courant et de la tension de
l'autodécharge de diffusion
D'après ces figures, nous observons d'une part que la
durée de cette autodécharge est de quelques heures (cf. fig.
4-42-b) comme nous l'avons déterminé expérimentalement,
d'autre part que la tension aux bornes du supercondensateur remonte très
lentement après être descendue. Ce phénomène de
récupération de tension n'est pas visible
expérimentalement à court terme pour les tensions initiales
élevées (cf. fig. 4-19). En effet les équations 4-29 et
4-31 ne considèrent que le courant et la tension de diffusion dus
à l'oxydoréduction. Le courant de fuite intrinsèque
important pour des tensions élevées n'est pas pris en compte dans
ces équations. Ce phénomène de récupération
de tension est donc masqué expérimentalement par le courant de
fuite intrinsèque. Par contre, pour une tension initiale de 0,5 V (cf.
fig. 4-42) le courant de fuite intrinsèque est faible et donc ce
phénomène visible.
Nous proposons de calculer l'impédance de diffusion
électrochimique de l'autodécharge. L'impédance temporelle
z(t) (cf. eq. 4-32) peut être déduite de l'expression de
la tension et du courant 4-29, 4-31, en négligeant l'erreur de Gauss
erfc.
2
u t
( ) ?? ?? + h
?? ??
z t
( ) = t
= - . exp -1 4-32
i( t ) ? ? Dt ? ?
Nous réécrivons l'impédance de
l'équation 4-29 dans le domaine fréquentiel en employant la
transformation de Laplace.
4. Etude, caractérisation et modélisation de
l'autodécharge des supercondensateurs
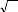
??
? 2 . ù ??
h j ù ? h j
2 .
? 1, ? jh BesselI
2 . 0 ,
?? D ?? ?? D
? ?
-
h BesselI .

jù.
= - 4-33
C
z ( )
ù
D
D . ù
h Dirac j
2 . ( ù
D
)
+
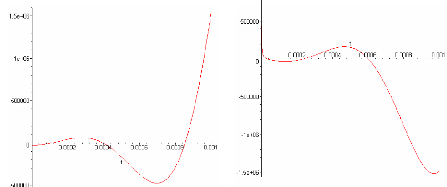
Nous présentons sur les figures 4-43 la partie imaginaire
et réelle de l'impédance électrochimique de
l'autodécharge du processus de diffusion en fonction de la
fréquence
Re(Z'
Im(Z)
f (Hz)
f (Hz)
Fig. 4-43 : Partie imaginaire et réelle de
l'impédance électrochimique de l'autodécharge de
diffusion
Ces différents résultats montrent qu'il n'est
pas aisé de modéliser finement l'ensemble des comportements lors
d'une autodécharge du supercondensateur avec des circuits
électriques équivalent RC.
Le circuit équivalent que nous avons établi dans
ce chapitre (cf. fig. 4-12) ne prend pas en compte le phénomène
de la récupération de tension.
| 


