Conception d'un pro logiciel interactif sous r pour la simulation de processus de diffusion

2.2 Construction du mouvement brownien

Ce processus de diffusion peut être construit par differentes approches. Les definitions les plus usuelles du mouvement brownien sont les suivantes.

2.2.1 Construction par un processus gaussien

Un processus stochastique Wt est un mouvement brownien ou un processus de Wiener si W0 = 0 (on dit que Wt est issu de 0) et si pour tous reels 0 < t1 < t2 < ··· < t_n, les variables aleatoire Wt1 -Wt0, . . . ,Wt_n -Wtn-1 sont independants et suivent une distribution gaussienne centree reduite (on dit que le mouvement brownien est standard si m = 0 et ó = 1) telle que :

{

E(Wt+h -Wt) = ⁰ E(Wt+h -Wt)² = h

Dans le cas general, lorsque le mouvement brownien n'est pas centre reduit, on a :

E(Wtk - Wtk-1) = m(tk - tk-1)

{

E((Wt+h -Wt - m(tk -tk-1))2 = ó²(tk -tk-1)

le vecteur (Wt0,Wt1,...,Wt_n) est un vecteur gaussien. Le processus Wt suit une loi gaussienne de moyenne mt et de variance ó²t. On peut facilement simuler une trajectoire de mouvement brownien dans un intervalle de temps [0,T], il suffit de fixee un pas de temps Ät > 0 et d'ecrire

v

W(Ät) = W(Ät) -W(0) ~ N(0,Ät) ~ ÄtN(0,1)

Les accroissements (WnÄt -W(n-1)Ät) etant independants et gaussiens, il suffit donc de simuler une loi gaussienne

Wt+Ät - Wt ~ N(0, Ät) ~ vÄtN(0, 1)

Ainsi, nous pouvons simuler facilement une seule trajectoire brownienne de la façon suivante. On considère la subdivision de l'intervalle de temps [0,T] suivante 0 = t1 < t2 < ··· < tN < tN+1 = T, avec _ti+1 -ti = Ät, pour i = 1 on a W(0) = W(t1) = 0. On donne l'algorithme suivant :

1. Generee un nouveau variable aleatoire Z de la distribution gaussienne N(0,1).

2. i = i+1.

3. W(ti) = W(ti-1)+ZvÄt.

4. Si i = N + 1, reiterez a l'etape 1.

La fonction BMN permet de simuler un mouvement brownien standard {Wt,t = 0} dans l'intervalle de temps [t0,T] avec un pas Ät = (T -t0)/N, et la fonction BMNF permet de simuler un flux brownienne standard (C = ó²)

R> BMN(N = 1000, t0 = 0, T = 1, C = 1)

R> BMNF(N = 1000, M = 100, t0 = 0, T = 1, C = 1)

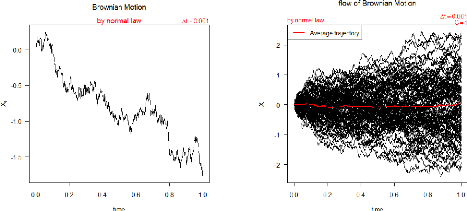
FIGURE 2.1 - Trajectoire brownienne simulée a partir d'une distribution gaussienne.

FIGURE 2.2 - Flux de trajectoires brownienne simulées a partir d'une distribution gaussienne.

2.2.2 Construction par une limite d'une marche aléatoire

Une caractérisation du mouvement brownien indique qu'il peut voir en tant que limite d'une marche aléatoire dans le sens suivant. Considérons une suite de variables aléatoires indépendants Xi centrées de variance ó² et la marche aléatoire S_n = X1 +X2 + ··· +X_n, où

(

+1 si p = 1/2

Xi =

-1 si p = 1/2

On définit une suite de variables Y_n par la formule suivante :

	Yn(t) =	S[nt] + (nt - [nt])X[nt]+1
où [.] est la partie entière.		óvn

Ce résultat fondamental est donné par le théorème de Donsker (1951) et est, en fait, au niveau des processus, une version du théorème usuel de la limite centrale

Théorème 2.1 (Principe d'invariance de Donsker) Soit (Xn)n=1 une suite de variables aléatoires réelles indépendantes, identiquement distribuées, avec E(X_n) = 0 et E(X² _n) = 1. Soit S_n = Y.1=i=nXi avec S0 = 0.

Les processus des sommes normalisées Yⁿ_t = 1 vnS[nt] (oil [nt] désigne la partie entière de nt) convergent en loi, en tant que processus, vers le mouvement brownien.

Cette convergence donne une définition du mouvement brownien comme l'unique limite (en loi) de marches aléatoires.

Le code 1, permettre de simulée un mouvement brownien standard comme l'unique limite de marche aléatoire. La figure 2.3 donne une représentation de l'approximation d'un mouvement brownien par une marche aléatoire pour n = 10,n = 100 et n = 1000.

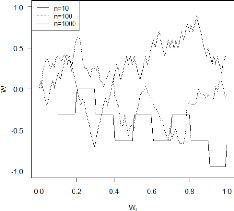
FIGURE 2.3 - Trajectoire brownienne comme limite d'une marche aléatoire.