3.3.2 Existence et unicité des solutions de
l'ÉDS
Soit T > 0, u(t,x) une
fonction mesurable de [0,T] × Rn dans
Rn et a(t,x) une fonction mesurable de
[0,T] × Rn dans Rn
vérifiant :
(1) Condition de croissance : il existe une constante
C telle que
|u(t,x)| + |a(t,x)|
= C(1 + |x|)
(2) Condition de Lipschitz : il existe une constante
K telle que
|u(t,x)
-u(t,y)| + |a(t,x)
-a(t,y)| = K|x-y|
< 0°,
(3) X0 est une variable indépendante de la tribu
a(Ws,s = 0) et E X2 0
Alors l'équation différentielle stochastique
d'Itô (3.14) admet une solution unique Xt dont presque toutes
les réalisations sont continues, qui est un processus de Markov de loi
initiale X0 et de probabilité de transition
p(s,x,t,A) =
P(Xt ? A|Xs = x)
De plus, si les fonctions u et a sont continues,
alors Xt est un processus de diffusion de dérive
u(t,x) et de matrice de diffusion
aaT (symétrique et semi-définie positive). En
particulier lorsque u et a sont lipschitziennes, l'équation
(3.14) admet une solution unique.
Remarque 3.3 (1) Une équation peut
admettre une solution locale sans admettre de solution globale. Par exemple sur
[0,1], l'équation
dXt
dt
= X2 t , X0 = 1
admet une solution unique locale sur [0,1[
Xt = 1 -t , t ? [0,1[
1
mais n'admet pas de solution globale sur l'intervalle [0,1].
(2) La condition de croissance évite que les solutions
explosent, i.e. que les solutions |Xt| tendent vers l'infini en un
temps fini. L'équation
dXt = 2aX3
1 t dt, Xt = y 1 et y >
0
admet une solution
Xt =
1
\/
y2 - at
qui diverge dans la direction y2 =
at. Si la condition de croissance n'est pas satisfaite,
l'équation peut quand même avoir une solution.
(3) La condition de Lipschitz garantit l'unicité.
L'équation
dXt = 3X2/3
t dt, X0 = 0
admet plus d'une solution
Xt =
(t-a)31t>a
car la fonction u(t,x) =
3x2/3 ne vérifie pas la condition de
Lipschitz.
3.3.3 Equation de Langevin
Des particules dans un fluide sont soumises à une force
de frottement proportionnelle à la vitesse de ces
particules et à une force aléatoire. La vitesse des particules
est processus aléatoire. L'équation fondamentale
de la dynamique s'écrit
dv
dt
= -av + c(t)
avec a = 6mir/m, la masse d'une
particule étant m et i désigne la viscosité du
fluide. Les particules sont assimilées à des
petites sphères de rayon r. La force aléatoire
c(t) est un bruit blanc, son espérance est
nulle et sa fonction de corrélation est constant, D est
appelé coefficient de diffusion d'Einstein.
E(c(t)) = 0 R(s,t) =
2D8(t -s)
En termes mathématiques, ce problème s'écrit
sous la forme d'une équation d'Itô
dXt = -aXtdt +v2DdWt (3.17)
t
Xt = X0e-at +
v2D f
ea(t-s)dWs
o
Wt est un processus de Wiener standard. Appliquons la
formule d'Itô (3.7) à Yt = Xteat, en
posant f (t,x) =
xeat, on a at f =
axeat, ax f
=eat et axx f = 0. On en
déduit que la solution est le processus de diffusion,
markovien, gaussien Xt donné par
De cette expression, on posant x0 = E(X0), on
trouve l'espérance
E(Xt) = x0e-at
et la variance du processus
var(Xt) = D(1 -e-2at)
a
La fonction de corrélation du processus est
En supposant que var(X0) < 00, il s'en suit que
lorsque t ? 00, on a
E(Xt) ---? 0
et
var(Xt) ---? D/a
La distribution de Xt approche de la loi
N (0, Da ) lorsque t ? 00. Ainsi,
quelque soit la distribu-
tion initiale, la solution de l'équation
différentielle stochastique pour des temps très grands
suit
approximativement une loi gaussienne centrée et
de variance D/a (Chapitre 4 exemple 4.2), qui
représente un équilibre entre la force
aléatoire de perturbation dWt (que nous avons appelé
dans l'introduction un bruit blanc) et la force de frottement -aXt.
Le code 6 permet de simulée une seule trajectoire de
l'équation de Langevin Xt avec un pas Ät =
10-4 (peut être fixé par l'utilisateur),et les deux
paramètres a = 2 et D = 1, qui est
présentée par la figure 3.4. Et le code 7 permet de
simulée l'équation de Langevin en deux dimensions avec les
conditions initiales x0 = 5 et y0 = 6, comme c'est
illustré par la figure 3.5. C'est-à-dire que on a système
d'équation différentielle stochastique de la forme suivante :
( v
dXt = -aXtdt + 2DdW1
t , X0 = x0
v
dYt = -aYtdt + 2DdW2
t , Y0 = y0
Avec W1
t et W2
t deux mouvements browniens standards
indépendants, a = 2 et D = 1.
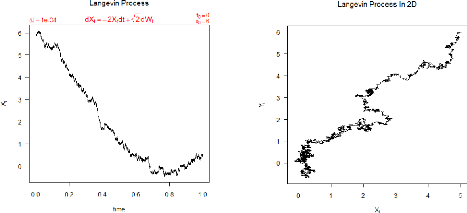
FIGURE 3.4 - Trajectoire simulée de l'équation de
Langevin avec a = 2 et D = 1.
FIGURE 3.5 - L'équation de Langevin en deux dimensions
avec a = 2 et D = 1.
| 


