Conception d'un pro logiciel interactif sous r pour la simulation de processus de diffusion

3.4.2 Relation entre le schéma d'Euler et Milstein

L'approximation de schéma de Milstein (3.24) a un ordre fort de convergence égal à 1. Cette méthode améliore donc les instabilité numériques par rapport à la méthode d'Euler (3.23). Toutefois, il y a un lien entre les deux méthodes dans le cas où on peut réaliser une transformée de Lamperti (3.21) de l'équation différentielle stochastique de départ. En effet, dans le cas où l'équation stochastique de départ n'a pas de bruit multiplicatif, comme par exemple dans l'exemple du processus d'Ornstein-Uhlenbeck, la méthode d'Euler a un ordre de convergence fort qui devient égal à 1. Or, avec une transformée de Lamperti (si g(Xt) est indépendante du temps), on peut transformer l'équation stochastique en une autre équation sans bruit multiplicatif. Ainsi, on peut montrer que le schéma d'Euler de l'équation transformée est identique au schéma de Milstein

sur l`équation originale. Dans le cas où la transformée de Lamperti est difficile à obtenir analytiquement, il est utile d'utiliser le schéma de Milstein qui est plus précis.

Preuve Soit le schéma de Milstein de l'équation différentielle stochastique (3.22)

1

Xn+1 = X_n + f_nÄt +g_nÄW_n +

₂gn⁰gn((ÄWn)² - Ät)

Soit la fonction y = F(x) et l'inverse x = G(y), appliquons la transformée de Lamperti (3.21) à Yt = F(Xt), on trouver

0

dYt = (fn gn - 1 2gn) dt +dWt

En suite appliquons le schéma d'Euler (3.23) a l'équation Yt

~ fn ~

- 1

ÄY = Yn+1 -Y_n = ₂g⁰ Ät + ÄW_n

n

g_n

Et en appliqué le développement de Taylor à l'inverse de la transformation de Lamperti, i.e. à Xt = G(Yt), on trouver

G(Y_n +ÄY) = G(Y_n)+ G⁰(Y_n)ÄY + 21 Of (Y_n) (Ä11² + O (ÄY³)

Notons

d

G⁰(Y_n) = F^-1(y) = 1

F0(G(y)) = g_n

dy

et

Gⁿ(Yn) = G⁰(Y_n)g'_n = gngn^'

Donc finalement, on a

G(Y_n +ÄY) - G(Y_n) = g_nÄY + 21 gngn^' (ÄY)² + O(ÄY³)

~~ fn ~ ~ ~~ fn ~ _~2

- 1 - 1

= g_{n 2}g⁰ + 1

Ät + ÄW_{n 2}gng⁰ ₂g⁰ Ät + ÄW_n

n n n

g_n g_n

+ O(ÄY³)

~ ~~ fn ~ ~~~~ fn ~ ~

g_n + 1

= ₂gng⁰ - 1 ₂g⁰ - 1

Ät + ÄW_{n 2}g⁰ Ät + ÄW_n

n n n

g_n g_n

+ O(ÄY³) ~ ~ ~ ~

g_n + 1

= ₂gng⁰ f_n - 1

_nÄWn ÄW_n + ₂gng⁰ Ät + O(Ät³/²)

n

= f_nÄt + gnÄWn +

₂g_n⁰gn((ÄWn)² - Ät)+ O(Ät³/²)

Puisque on a ÄW_n = î_n,1(Ät)¹/² et (ÄW_n)² = î2 n,1Ät, d'où on trouver le schema de Milstein

G(Y_n +ÄY) -G(Y_n) = Xn+1 -X_n = f_nÄt + _gnÄWn + 21 g_n⁰ g_n((ÄW_n)² - Ät) + O(Ät³/²)

Exemple 3.6 (Transformation de modèle Cox-Ingersoll-Ross (CIR)) Le modèle Cox-IngersollRoss (CIR) est utilisé en mathématiques financières pour modéliser l'évolution des taux d'intérêt court terme. Il s'agit de la solution de l'équation différentielle stochastique

dXt = (è1 - è2Xt)dt + è3vXtdWt, X0 = x0 > 0. (3.29)

oil sous cette forme

dXt = ê(è - Xt)dt + óvXtdWt, X0 = x0 > 0. (3.30)

Notons que la solution de cette de l'équation (3.30) reste strictement positive sous la condition 2êè > ó². Le paramètre è donne la moyenne à long terme, et ê > 0 donne la vitesse à laquelle le processus va converger vers cet équilibre.

Appliquons le schéma de Milstein (3.24) à l'équation (3.29), on a :

ÄX = ( (è1 - è2Xn) - 41 èi) Ät + è3 vX_nÄW_n + ⁴¹ è3 (ÄW_n)² (3.31)

Maintenant appliquons la formule d'Itô (3.7) à Yt = vXt pour l'équation (3.29), en posant y = f(t,x) = vx, on a ?t f = 0, ?_x f = 1/2vx et ?xx f = -1/4x³/². On obtient :

dYt =

2Yt , 1 4 2 1 ((è1 - è2Y`t^,) - è^,1) dt + 2 è3dWt -

(3.32)

Appliquons le schéma d'Euler (3.23) à Yt, on a

ÄY =	2Ynn 1 1 ( (è1 - è2Y^2) - 4 è32 ) Ät + 2 è3ÄWn

Et en appliquant le développement de Taylor à l'inverse de y = vx, c'est-à-dire à G(y) = x², on obtient :

G(Y_n +ÄY) - G(Y_n) = (Yn + ÄY)² -Y²_n

= (ÄY)² + 2Y_nÄY

= [ 2Yn ((è1 - è2Y 4

2) -- 1 è32 ) Ät + ²¹ è3ÄWn1 2

+ ( (è1 - è2Y2 ) - 41 èi) Ät + Ynè3ÄWn

= ( (è1 - è2Y2 ) - 14 è3²) Ät + _è3YnÄWn + ₄ è3 (ÄW_n)² + O (Ät²) On remplace Yt = vXt, on trouve la même résultat (3.31).

Exemple de simulation

Le code 8 nous permettre de comparée entre le processus origine Xt (3.29) avec son transformation Yt (3.32), qui est illustré par le graphie 3.11. Posons (è1,è2,è3) = (0.1,0.2,0.05), avec un pas Ät = 0.1 et x0 = 1. (2è1 > è2 3 est vérifie)

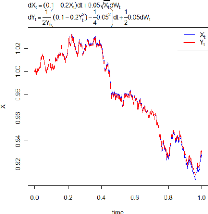
FIGURE 3.11 - Transformation de modèle Cox-Ingersoll-Ross (CIR) dXt = (0.1 - 0.2Xt)dt + 0.05vXtdWt .