Analyse comparative de modèle d'allocation d'actifs dans le plan Moyenne-Var relative

Université Claude Bernard - Lyon 1 INSTITUT DE SCIENCE FINANCIERE ET D'ASSURANCES

Mémoire présenté

devant l'Institut de Science Financière et d'Assurances

le

pour l'obtention du Master Recherche

Sciences Actuarielle et Financière

Par : Faleh Alaeddine

Titre : Analyse comparative de modèle d'allocation d'actifs dans le plan Moyenne-VaR relative

Confidentialité :

Composition du jury des mémoires : Entreprise :

Membres du jury des mémoires

M. AUGROS Jean-Claude Directeur de mémoire :

M. LAURENT Jean-Paul

M. LEBOISNE Nicolas

M. LOISEL Stéphane

M. PLANCHET Frédéric

M. QUITTARD-PINON François

M. RULLIERE Didier

M. TCHAPDA Idriss

Invité : Secrétariat :

Mme BARTHELEMY Diane Mme BRUNET Marie

Mme GARCIA Marie-José

Mme GHAZOUANI Soundous Mme MOUCHON Marie-Claude Bibliothèque :

Mme SONNIER Michèle

50 avenue Tony Garnier

69366 LYON cedex 07

Mes sincères Remerciements a

Monsieur Jean Claude Augros

qui m'a donné sa confiance tout au long de ce travail de recherche

Monsieur Didier Rullière

qui m'a soutenu à travers ses précieux conseils, critiques et suggestions

Toute l'équipe administrative de l'ISFA

qui m'a gentiment accueilli et orienté tout au long de l'année universitaire

Mots clés: allocation d'actifs, Valeur à Risque, Normalité, modèle GARCH, modèle GPD

Résumé

Dans ce travail, on présente un modèle de sélection du portefeuille optimal dans le cadre de la Value-at-Risk (VaR). Le modèle de base maximise l'espérance de rendement du portefeuille sous la contrainte d'un niveau de VaR limite préfixé par l'investisseur. Pour cela, différents modèles d'estimation de la VaR sont utilisés : le modèle Empirique, le modèle GARCH, le modèle GPD. L'étude empirique se base sur deux actifs risqués : le Nasdaq 100 et le S&P 500 et ce pour une période de dix ans (1997-2007). Dans le cadre d'une période de prévision, on détermine les recommandations optimales journalières en terme de montant à emprunter ou à prêter ainsi que les poids optimaux des deux indices dans le portefeuille risqué. On compare ensuite la performance des trois modèles en se référant au critère de taux d'échec minimal et au critère de la richesse finale maximale. Les résultats montrent la dominance du modèle GPD pour le premier critère et la supériorité du modèle Empirique pour le deuxième critère.

Keywords: portfolio selection, Value-at-Risk, Normality, GARCH model, GPD model

Abstract

In this work, we propose an optimal portfolio selection model in a Value-at-Risk (VaR) framework. The general model allocates financial assets by maximising expected returns subject to the constraint that expected maximum loss should meet the Value-At-Risk limits set by the investor. Different models for the estimation of the VaR are used: Empirical model, GARCH model and GPD model. We provide an empirical analysis using two risky assets: Nasdaq100 and S&P 500 over ten years (1997-2007). In an out-of-sample context, we determine the best daily recommendations in terms of the wealth to borrow or lend and the optimal weights of the assets in the risky portfolio. We compare the three models performance using the failure rate and the wealth achieved as instruments to determine the best model. Results show that the GPD model outperforms other models relative to the first criterion. We also find that Empirical model is preferred to other models relative to the second criterion.

Introduction p 5

I- La Value at Risk et la gestion de portefeuille

I-1 Le concept de la Value at Risk p 8

I-2 Les paramètres de la Value at Risk .p 11

I-3 Les principaux méthodes de mesure de la Value at Risk p 15

I-4 La Value at Risk dans la littérature de la gestion de portefeuille p 21

II- L'allocation optimale dans le plan Moyenne - VaR relative

II-1 La modélisation du problème d'optimisation du portefeuille p 25

II-2 Le cadre de l'étude empirique p 30

II-3 L'application des méthodes de mesure de la Value at Risk p 33

II-4 La construction des frontières d'efficience p 34

II-5 L'allocation optimale dans le cadre statique ..p 34

II-6 L'allocation optimale dans le cadre dynamique .p 37

Conclusion p 41

Annexes p 42

Bibliographie ..p 56

L'optimisation d'allocation d'actifs devient de plus en plus un enjeu important sur les marchés financiers. Les coûts relatifs à une mauvaise gestion de portefeuille et à un erreur de prévision des tendances du marché peuvent engendrer des situations financières précaires pour les sociétés voir même les exposer au risque de faillite.

En théorie moderne de portefeuille, l'allocation optimale de la richesse initiale se base sur la maximisation de la prime de risque espéré par unité de risque. L'approche traditionnelle de mesure de ce dernier est celle de la Moyenne Variance. Dans ce cas, le risque est définie en terme de variation possible des espérances de rendement du portefeuille dans les deux sens, celui de la hausse et de la baisse: on parle de la volatilité des actifs financiers. Elle est égale à la racine carrée de la variance des rendements. Néanmoins, cette approche présente des inconvénients. Le principal inconvénient est qu'elle considère l'investisseur comme indifférent devant l'évolution de la valeur du portefeuille dans le sens de la hausse ou dans le sens de la baisse. Il est supposé que pour lui, il s'agit toujours d'un risque à assumer. Un deuxième inconvénient important est l'hypothèse implicite de la symétrie de la distribution des rendements et plus précisément la normalité de cette distribution. En pratique, il est bien montré que la distribution de plusieurs séries de rendements financiers est non normale avec un coefficient d'asymétrie (skewness) et un coefficient d'aplatissement (kurtosis) trop élevés. De même, les agents économiques traitent évidemment les pertes et les gains d'une façon asymétrique. Il existe pas mal d'études sur l'aversion à la perte (voir par exemple, Kahneman et al.1990).

Le choix de l'approche Moyenne Variance apparaît ainsi comme une stratégie inefficiente pour optimiser l'espérance de rendement tout en minimisant le risque. Il sera plus intéressant de chercher une mesure de risque qui peut incorporer n'importe quel non linéarité dans la distribution des rendements des actifs financiers tout en se focalisant sur la valeur potentielle à perdre plutôt que sur l'évolution en valeur absolue. Dans ce cas on aura l'avantage de pouvoir considérer des payoff non normal tel que ceux des produite dérivés et ainsi un cadre d'étude plus générale. Cependant, il faut signaler qu'en finance la déviation à

l'hypothèse de normalité suggère des critiques dont on peut citer principalement la perte de l'opportunité de passage d'un cadre discret à un cadre continue.

Dans ce cadre de recherche, la notion relativement récente de la Valeur à risque (Value at Risk) apparaît être capable de répondre à la problématique présentée ci dessus. D'une part, l'estimation de cette mesure de risque peut incorporer la composante de non normalité de la distribution des rendements du portefeuille. D'autre part, cette mesure s'intéresse directement au montant de la perte potentielle à subir sur l'investissement. En effet, la Value at Risk (VaR) peut se définir simplement comme la perte potentielle maximale que l'investisseur peut subir dans un horizon de temps donné et pour un niveau de probabilité fixé. La Value at Risk mesure directement et en terme monétaire la perte future dans la valeur de portefeuille. Le résultat additionnel résultant d'une non normalité peut être inclut et absorbé dans l'estimation de la Value at Risk. Cette mesure semble à ce jour s'imposer comme le standard pour la mesure des risques de marché dans l'industrie financière et surtout bancaire.

L'objectif de ce travail est d'analyser un modèle d'allocation optimale de la richesse en se référant à la VaR comme la mesure du risque. On cherche aussi à valider les méthodes d'estimation de la VaR incorporé dans ce modèle. Dans le premier chapitre, on s'intéresse à la présentation de la VaR, de ses paramètres et des méthodes pratiquées pour son estimation. On étudie aussi le concept de la VaR ainsi que sa relation avec la gestion de portefeuille tel que cité en littérature financière.

Dans le second chapitre, on commence par présenter le modèle permettant de déterminer la répartition optimale entre les actifs risqués d'un portefeuille. Ce modèle permet aussi de calculer le montant de prêt emprunt nécessaire pour ramener la VaR du portefeuille optimal à un niveau prédéterminé. Ceci nous rappelle du théorème de séparation de Tobin (1958) dans l'approche traditionnelle de gestion de portefeuille. Ensuite, on élabore le cadre empirique de notre étude avec des hypothèses sur les différents facteurs. Cette étude empirique sera composé de trois parties : Dans la première partie, on applique et on analyse les différentes méthodes d'estimations de la VaR cités dans le chapitre précédent. Dans la seconde partie, on applique et on analyse les résultats de notre modèle dans un cadre statique. Les méthodes d'estimation de la VaR retenue sont la méthode empirique, la méthode de l'hypothèse de normalité et la méthode de la théorie des valeurs extrêmes (TVE ou aussi GPD en se référant à la distribution de Pareto Généralisé). Dans la troisième partie, on passe à un

cadre dynamique. L'objectif est de tester les trois approches d'estimation de la VaR dans notre modèle générale. Pour cela, on procède à l'application de ce dernier pour une gestion quotidienne sur 465 jours. On se réfère ensuite à un Backtesting en comparant les pertes effectives des portefeuilles optimaux constitués quotidiennement avec les VaR limites prévues par les investisseurs. Le critère retenu dans ce cas est donc le taux d'échec des prévisions pour les trois approches. Un deuxième critère peut être retenu qui est celui de la richesse finale obtenue à la fin de la période de gestion (après les 465 jours). Le modèle choisi sera celui qui maximise cette richesse.

I-1 Le concept de la Value at Risk :

Selon Berdin et Hyde (2001) la VaR est définie comme étant la mesure qui fournit une estimation statistique de la perte potentielle sur un actif ou un portefeuille qui peut survenir avec une probabilité donnée suite à des mouvements de prix ou de taux relativement adverses. Ceci est valable sous l'hypothèse que pendant une période de temps (l'horizon de calcul de la VaR) la composition du portefeuille resterait inchangée. D'après A. Louis Calvet (2000) la VaR d'un portefeuille d'actifs financiers correspond au montant de pertes maximales sur un horizon de temps donné, si l'on exclut un ensemble d'évènements défavorables (worst case scénarios) ayant une faible probabilité de se produire. Une autre définition de la VaR peut être avancée : il s'agit de la perte maximale par rapport à la valeur espérée du portefeuille et non par rapport à la valeur initiale. Dans ce cas, on parle de la VaR relative. La figure 1 illustre la notion de la VaR dans le cas d'une distribution normale centrale réduite des rendements du portefeuille étudié. Dans ce cas, dire que la VaR à 95% pour un jour est égale à -1,645% signifie qu'au maximum on aura 5 rendements sur 100, dans le jour suivant, qui soient inférieures à -1,645%.

Figure 1 : Un exemple de la Value-at-Risk sous la distribution normale

Selon Paul Glasserman et al.(2000), deux événements ont concouru à l'adoption généralisée de la VaR sur le secteur financier et un autre a favorisé son développement dans les entreprises surtout américaines.

> Le premier date de 1995. Réunis en comité à la banque des règlements internationaux à Bale, les représentants des banques centrales de dix grandes économies de l'ouest proposent de nouvelles règles amendant l'accord de Bale de 1988 et imposant aux établissements financiers un niveau de fonds propres proportionnels aux risques résultant de leurs engagements. Officiellement adoptés en 1996, cette proposition incite les banques à développer des modèles internes sophistiqués pour calculer leurs VaR. En effet, elles peuvent ainsi espérer une diminution des fonds propres qu'elles doivent détenir par rapport aux montants des fonds propres exigés sur les autres banques qui se fondent sur les modèles standard (édictés par les autorités de tutelle pour déterminer les besoins des banques en capitaux propres). Ainsi, dès le départ, la recherche d'un allègement des obligations règlementaires est un important facteur de la croissance de la VaR.

> Le deuxième évènement s'est produit sur Internet. En 1994, la banque américaine JP Morgan a mis gratuitement son système RiskMetrics à la disposition de tous sur Internet. Ce système fournissait les données financières et la méthodologie nécessaire au calcul de la VaR d'un portefeuille. Les autres établissements financiers et les entreprises peuvent utiliser le calculateur de VaR de RiskMétrics ou télécharger les données sur leurs propres systèmes de gestion des risques. Très vite, sont apparus de nouveaux fournisseurs de programmes de gestion des risques exploitant RiskMetrics, transformant cette méthodologie en une référence incontournable.

Un troisième évènement a probablement moins d'impact à ce jour, mais c'est l'un des grands facteurs d'expansion de la VaR parmi les entreprises américaines. En 1997 aux EtatsUnis, la Securities and Exchange Commission (SEC), préoccupée des risques cachés derrière les instruments hors bilan, a émis des règles de communication relative aux produits dérivés employés par les entreprises : celles-ci ont trois solutions pour faire état des risques associés

aux instruments dérivés : tableau des valeurs de marché, mesure de sensibilité ou VaR. C'est la raison pour laquelle les rapports annuels de Microsoft, de Philip Morris et de bien d'autres grandes sociétés présentent maintenant des calculs de la VaR. Récemment, les recommandations du comité Bale II publié en 2004 ont renforcé l'utilité de cette notion.

En ce qui concerne la littérature, plusieurs articles évaluent le risque de marché en se basant sur la technique de la Valeur à Risque et ses différentes méthodes. La VaR donne lieu à différents modèles d'évaluation qui lient le rendement des différents actifs aux différents facteurs de risque :

Le premier type de modèle repose sur la méthode des Variances Covariances développée et diffusée par JP Morgan grâce à son système RiskMetricsTM en 1996. Cette méthode qui se base sur une évaluation locale des positions est appelée aussi delta normal (Jorion 2001).

Le deuxième type de modèle utilisant une évaluation complète regroupe les méthodes de simulation historique et de Monte Carlo.

Il existe une quatrième méthode complémentaire aux trois précédentes appelée " Stress testing " recommandée par le régulateur pour évaluer la qualité des modèles de contrôle interne. Lopez (1996) compare ces méthodes et répartit les aptitudes de chacune. Jackson et al. (1997) examinent la possibilité de prédire la variance des facteurs de risque (taux d'intérêt, prix de l'actif et taux de change). Ils comparent les méthodes paramétriques et non paramétriques de la mesure de la VaR.

CrnKovic et Drahmann (1996) examinent la possibilité de prédire tous les paramètres de distribution des facteurs de risque. Kupiec (1995) étudie le Backtesting pour le modèle de la VaR et il examine la période du temps passé jusqu'au premier échec de l'estimation. A un niveau plus tardif, le comité de Bale adopte ces épreuves comme une base pour examiner les modèles internes des banques. Ces études ne fournissent pas des épreuves statistiques claires et manquent d'exactitude quant aux méthodes d'estimation. La plupart d'entre eux traitent l'exigence minimale du capital en utilisant plusieurs méthodes de calcul de la variance, et aussi par l'utilisation des données historiques de marché plutôt que des simulations.

Hendricks (1996), Pritsker (1997), Linsmeier et Pearson (1996), Jackson et al. (1997) et Aussenegg et Pichler (1997) comparent l'approche standard, présentée par le Comité Bale comme une alternative pour l'estimation du risque de marché, avec toutes les méthodes de calcul de la VaR. Ces études examinent les avantages et les inconvénients de chaque méthode en jouant sur les aspects suivants : le temps de calcul vis-à-vis de l'exactitude des évaluations (Pritsker, 1997) ; l'adaptation aux régions géographiques différentes (Powell et Balzarotti, 1996) ; l'effet des instruments financiers inclus dans le portefeuille d'investissement (Aussenegg et Pichler ,1997) .

Parmi les études qui examinent l'utilisation des modèles VaR, celle de Powell et Balzarotti (1996) qui fait une comparaison entre l'utilisation du modèle VaR et l'approche standard dans plusieurs pays latino américains. Powell et Balzarotti (1996) concluent que l'approche standard est préférable à plusieurs modèles VaR. Plusieurs modèles internes font des suppositions et des usages d'outils de mesures différentes qui peuvent produire des résultats variables pour le même ensemble de paramètres du marché et de position dans le portefeuille d'investissement. En outre, les modèles VaR sont très sensibles aux suppositions et aux données estimées, surtout dans le contexte d'actifs qui ne sont pas fondamentalement linéaires tels que les produits dérivés (Marshall et Seigel, 1997). Ces derniers notent que cette sensibilité, accompagnée de la liberté des banques dans le choix de leurs modèles internes, expose les systèmes bancaires et de surveillances au risque.

I-2 Les paramètres de la Value at Risk :

La VaR d'un portefeuille prend la forme d'un nombre unique par référence à une période de détention, un certain niveau de confiance et une distribution statistique du rendement du portefeuille. La prudence s'exprime par le choix intelligible de ces trois paramètres.

La période de détention :

C'est la période sur laquelle les pertes potentielles sont estimées. Son choix dépend de certains facteurs notamment de la fréquence de recomposition du portefeuille, de la liquidité des actifs financiers qui y sont contenues, de l'utilisation de la VaR. Selon Jorion (2001) la période de détention devrait correspondre à la plus longue période requise pour la liquidation normale du portefeuille.

En effet, pour que la mesure de risque soit significative, une hypothèse fondamentale est implicitement faite sur la stabilité des positions considérées ainsi que la composition du portefeuille jusqu'à l'échéance de détention. L'objectif est de ne pas trop s'écarter de la réalité. La validité de cette hypothèse est plus ou moins vérifiée selon les activités. Ainsi, pour les portefeuilles de commerce (constitués des crédits accordés et relèvent de la pure activité d'intermédiation financière par les banques) l'horizon de calcul doit être d'un jour étant donné le changement des positions et la liquidité élevée. Pour les portefeuilles de négociation, l'ajustement étant plus lent, une durée de détention d'un mois peut se justifier. En ce qui concerne la mesure des VaR pour les portefeuilles de négociation des institutions financières, la réglementation impose une période de 10 jours ouvrables soit deux semaines.

Notons que comme le but de calcul de la VaR est la mesure du risque de la baisse du cours de l'actif, l'horizon est préféré être court. Ceci mène à mieux cerner le champ de vision et à éviter les déviations significatives probables des variables de marché de leurs fourchettes normales.

Le niveau de confiance :

Le niveau de confiance est égal à un 1 moins la probabilité des évènements défavorables. Il reflète le niveau d'incertitude qu'on est prêt à accepter. Par exemple, si la mesure de la VaR se fait à un niveau de confiance de 95%, les pertes effectives devraient dépasser notre estimation seulement 5% du temps. Si cela paraît inconfortable pour l'investisseur, il peut utiliser une VaR de 99% et ne peut sous estimer alors que 1% des cas probables. Autrement, s'il craint les risques, il s'arrangera pour que la probabilité des évènements défavorables soit très petite.

Intuitivement, plus la mesure des pertes potentielles maximales est correcte, plus le niveau de confiance devra être large afin de saisir au mieux toutes les situations envisageables y compris les plus extrêmes. Notons dans ce même cadre que plus ce niveau est important, plus la VaR sera élevée. Le niveau de confiance est le paramètre sur lequel il est le plus facile de jouer, compte tenu de la dépendance des autres paramètres à d'autres considérations externes à l'investisseur.

T

( X _t X

- )

1

S

=

( 3 / 2 )

T

( )

ó ²

?

?

?

?

??

3

?=

t 1

La distribution des pertes et profits du portefeuille :

C'est le paramètre le plus important mais aussi le plus difficile à déterminer. Une question fondamentale se pose : comment peut-on choisir une distribution pour la variable de marché ? Idéalement, il faudrait un modèle qui soit simple et qui convienne le plus aux observations empiriques. La méthode de calcul est déterminée par la distribution choisie pour modéliser les pertes et profits du portefeuille. Empiriquement, trois principaux problèmes dans les séries temporelles financières sont détectés. Le premier est la non stationnarité des séries manifesté par la non stabilité des paramètres de la loi régissant les variables du processus temporel. Le deuxième problème est le caractère leptokurtique de la distribution des données qui consiste à des queues empiriques plus épaisses que celles considérés par la loi mise en hypothèse, ceci a pour conséquence la sous estimation de la Value at Risk et donc du risque assumé par l'investisseur. Le troisième problème est le phénomène de la dépendance de la volatilité appelé la persistance de la volatilité (clustering) issu du constat en pratique du fait que les volatilités élevées sont souvent suivies par des volatilités élevées et les volatilités faibles sont souvent suivis par des volatilités faibles. Ce phénomène peut être pris en compte par la famille des modèles ARCH-GARCH sur de courtes périodes d'estimation. La détection de l'effet ARCH dans la série des observations reste à vérifier pour justifier ce type de modélisation.

En théorie financière, une hypothèse de normalité des rendements est souvent adoptée comme réponse à la problématique de la distribution des rendements des actifs financiers. En effet, cette hypothèse accélère considérablement les calculs. Elle est bien adaptée dans l'application de la méthode RiskMetrics^TM (voir section suivante). Un test dit test de Jarque et Bera (JB) permet de valider ou non la normalité de la distribution. Il tient compte implicitement de deux paramètres essentiels : le coefficient d'asymétrie (Skewness) et le coefficient d'aplatissement (Kurtosis).

Le premier paramètre (Skewness) est le moment d'ordre 3 et mesure l'asymétrie du comportement des rendements autour de leur moyenne empirique. Son expression est la suivante :

Si S=0 la distribution est dite symétrique à l'instar de la loi normale. Si S>0 alors la densité de la distribution s'étale vers la droite et on a une asymétrie positive. Si S<0 alors la densité de la distribution s'étale vers la gauche et on est en présence d'une asymétrie négative.

Le deuxième paramètre, le kurtosis, est le moment d'ordre 4 et représente une mesure associée à l'épaisseur des queues de la distribution. Son expression est la suivante :

T

( X _t X

- )

1

K

=

2

T

( )

ó ²

? ? ? ? ??

4

?=

t 1

Si K=3 on dit que la distribution est mésokurtique comme c'est le cas pour la distribution normale qui sert de point de référence. Si K>3 la distribution présente des queues épaisses (fat tails). Elle est dite leptokurtique. Si K<3 la distribution présente des queues minces (thins tails). Elle est dite platikurtique.

En ce qui concerne le test de Jarque et Bera, il est basé sur la statistique suivante :

( / 6 ) [ ( 3 ) / 24 ] ( 2 )

2 2 ÷ ²

JB = TS + T K -

Cette statistique suit asymptotiquement la loi ÷² avec deux degré de liberté lorsque T (nombre des observations) est assez grande.

Le test d'hypothèse est le suivant :

H0 : la distribution est normale H1 : la distribution n'est pas normale

La règle consiste à rejeter H0 si la statistique JB est plus grande que ÷² avec deux degrés de liberté au seuil de signification choisie (1% par exemple).

Notons que la stationnarité des rendements du portefeuille d'actions est une condition nécessaire pour appliquer la méthode de simulation historique (voir section suivante). Le test de racine unitaire ADF (augmented Dickey-Fuller) consiste à tester l'hypothèse nulle:

H0 existence d'une racine unitaire série non stationnaire

Ce test consiste à rejeter H0 si la statistique obtenue est inférieure à une valeur critique dite valeur de MacKinnon.

I-3 Les principaux méthodes de mesure de la Value at Risk :

Mathématiquement, la notion de la Value-at-Risk se traduit ainsi:

Pr( Ä VpVaR)=1-c

Avec: ÄV = la variation de la valeur V du portefeuille sur la période de détention. c = le niveau de confiance

Plusieurs modèles ont été présentés pour l'estimation de la Value-at-Risk (Manganelli et Engle (2001)). L'élément clé qui distingue ces modèles est l'existence ou non d'une hypothèse de para métrisation de la distribution des pertes et des profits. Ainsi on classera ces méthodes en trois classes: les méthodes non paramétriques, les méthodes semi paramétriques et les méthodes paramétriques.

I-3-1 Les méthodes non paramétriques :

La méthode du quantile empirique :

La méthode du quantile empirique (ou Historical Simulation) est une méthode très simple d'estimation des mesures de risque fondée sur la distribution empirique des données historiques de rendements. Formellement, la VaR est estimée simplement par la lecture directe des fractiles empiriques des rendements passés. Si l'on considère par exemple un niveau de confiance de 95% et que l'on dispose d'un échantillon de 1000 observations historiques de rendements, la VaR est donnée par la valeur du rendement qui correspond à la 50ème forte perte.

La méthode du Bootstrap

Une amélioration simple de la méthode de la simulation historique consiste à estimer la VaR à partir de données simulées par Bootstrap. Le Bootstrap consiste à ré échantillonner les données historiques de rendements avec remise. Plus précisément, dans notre contexte, la procédure consiste à créer un grand nombre d'échantillons de rendements simulés, où chaque observation est obtenue par tirage au hasard à partir de l'échantillon original. Chaque nouvel échantillon constitué de la sorte permet d'obtenir une estimation de la VaR par la méthode HS standard, et l'on définit au final une estimation en faisant la moyenne de ces estimations basées sur les ré échantillonnages.

I-3-2 Les méthodes semi paramétriques :

La méthode basée sur la théorie des valeurs extrêmes :

Parmi les méthodes semi paramétriques figurent tout d'abord l'ensemble des méthodes et approches qui relèvent de la théorie des extrêmes (TVE) qui diffère de la théorie statistique habituelle fondée pour l'essentiel sur des raisonnements de type tendance centrale. Les extrêmes sont en effet gouvernés par des théorèmes spécifiques qui permettent d'établir sous différentes hypothèses la distribution suivie par ces extrêmes. Il existe deux principales branches de la théorie des valeurs extrêmes : la théorie des valeurs extrêmes généralisée et l'approche Peaks Over Threshold (POT) basée sur la loi de Pareto généralisée. L'approche POT permet l'étude de la distribution des pertes excessives au dessus d'un seuil (élevé), tandis que la théorie des valeurs extrêmes généralisée permet de modéliser la loi du maximum ou du minimum d'un très grand échantillon. Dans ce qui suit, on procèdera à l'application de cette approche. Pour cela, on définie la moyenne en excédent pour une distribution F par :

e ( u ) = E(X -uX >u)

C'est simplement une fonction de u qui s'exprime à l'aide de la fonction de survie de F. Plus les queues de distribution sont épaisses, plus cette fonction a tendance à tendre vite vers l'infini.

En pratique, si n est le nombre total de l'échantillon et si est le nombre d'observations au

N_u

dessus du seuil u, on a :

n

1

j=1

e( u) = ? ( x - u)1 { x>u }(x _j) , u > 0N _u

Le problème du choix de u reste entier. Usuellement, on trace cette fonction Mean Excess pour différents niveaux du seuil u. Le bon seuil est celui à partir duquel e(u) est approximativement linéaire. Graphiquement, cela se traduit par un changement de la pente de la courbe qui ensuite reste stable. Ce résultat provient de la remarque que pour la distribution de Pareto généralisée, e(u) est linéaire en u. Une fois le seuil optimal choisi, on construit une nouvelle série d'observations au dessus de ce seuil, et la distribution de ces données suit une distribution généralisée de Pareto, qui se définit comme suit :

1

? -

î î

? ?

1 1

- ? + x

? ? si 0

î ?

? â

G x

Sisib=0

( ) = ? ? ?

?
?

î â

,

?

- ?- x ?

1 exp ? ?

? â ?

est appelée l'indice de queue. Le paramètre â est un indicateur de la taille de la queue à une distance finie. L'estimation des paramètres î et â se fait par le maximum de

vraisemblance.

La densité de la distribution GPD s'écrit :

( x)

ⁱ_??ⁱ

?

â ^î( â + 4)

si

-

si 0

î =

? ⁰

â n

+ (( (1 - c))^-î-1)

VaR = u

?

î

? Nu

Et la log vraisemblance que nous maximisons est de la forme :

ln L( , â) =

n ?= [ { } ] ln , ( )1 0 ( ) g x t x t î â î > t 1

Une fois l'estimation terminée, on peut vérifier graphiquement la pertinence des estimations
en comparant la distribution GPD estimée avec la distribution empirique des observations au
dessus du seuil. La Value-at-Risk pour un niveau de confiance c est obtenue par la formule :

?

La simulation historique filtrée :

La méthode de la simulation historique filtrée est une forme de Bootstrap semiparamétrique qui vise à combiner les avantages de la simulation historique avec la puissance et la flexibilité des modèles à volatilité conditionnelle tel que le modèle GARCH. Elle consiste à faire un Bootstrap sur les rendements dans un cadre de volatilité conditionnelle, le Boostrap préservant la nature non paramétrique de la simulation historique, et le modèle à volatilité conditionnelle donnant un traitement sophistiqué de la volatilité.

I-3-3 Les méthodes paramétriques :

La méthode de Variance Covariance :

Cette méthode connu aussi sous le nom de méthode Riskmetrics. Les principales hypothèses simplificatrices consistent à supposer, d'une part, que les lois de probabilité qui régissent les distributions des variations des prix de marché sont normales et, d'autre part, que les instruments présentent un profil de risque linéaire. Sous ces hypothèses, la matrice de Variances Covariances peut être appliquée assez directement aux positions détenues pour calculer la VaR.

Ainsi, on aura: T

VaR = SCS

Avec:

S = le vecteur des VaR pour chaque position ou facteur de risque= [... q_i ó _i ù _i ...]

q i = le quantile de la loi normale

ó_i = la volatilité historique des facteurs de risque

ù i = la part de la richesse investie dans le facteur i

C = la matrice des corrélations entre les facteurs de risque.

Les calculs utilisés dans la méthode RiskMetrics sont rapides et simples, et requièrent uniquement la connaissance de la matrice des Variances Covariances des rendements du portefeuille. Néanmoins, cette méthode s'avère être inadaptée aux portefeuilles non linéaires (instruments optionnels), et théoriquement peu adaptée aux queues de distribution épaisses et aux distributions non normales des rendements.

La Simulation Monte Carlo :

La méthode de Monte Carlo consiste à simuler un grand nombre de fois les comportements futurs possibles des facteurs de risque selon un certain nombre d'hypothèses, et d'en déduire une distribution des pertes et profits à partir de laquelle on estime finalement un fractile. Plus précisément, on peut considérer l'exemple de l'hypothèse de normalité. La méthode Monte Carlo s'applique en trois étapes:

· La première étape consiste à simuler N scénario de l'évolution des facteurs de risque. Un scénario est obtenu à travers la formule suivante:

ÄS = tZ

Avec :

S = le vecteur des facteurs de risque

t = la matrice résultant de la décomposition de Cholesky de la matrice des Variances Covariances des facteurs de risque ( ? S = tt' )

Z = un vecteur de variables aléatoires indépendantes de loi normale centrée et réduite. On obtient suite à cette étape la série ( Ä S ,...., Ä S

1 ^N ).

· La deuxième étape consiste à déterminer les N variations respectives du

N

portefeuille. On obtient donc la suite ( Ä L ,...., Ä L

¹ ) des évolutions de la valeur

de la position initiale.

· La troisième étape consiste à déterminer le quantile de la même façon que pour la simulation historique à partir de la distribution simulée.

Si cette approche peut s'appliquer, en théorie, quelles que soient les lois de probabilité suivies par les facteurs de risque, elle est couramment utilisée en pratique, pour des raisons techniques, en supposant que les variations relatives des paramètres de marché suivent des lois normales. Cette méthode convient également à tous les types d'instruments, y compris optionnels, et permet de tester de nombreux scénarios et d'y inclure explicitement des queues de distribution épaisses (événements extrêmes pris en compte dans une certaine mesure) (voir Glasserman et al. (2001))

Méthodes basées sur les modèles GARCH

La méthodologie d'estimation de la VaR en se basant sur la modélisation GARCH est largement étudiée en littérature (voir par exemple Christoffersen et al. (2001), Engle (2001)). En ce qui concerne la détection de l'effet ARCH dans la série des observations, deux principaux tests complémentaires peuvent être effectué. Le premier s'intéresse au phénomène d'auto corrélation entre les termes d'erreur au carré du modèle : Test Q (p) de Ljung-Box (1978). Si le processus est ARCH, les résidus au carré doivent être corrélés. L'hypothèse nulle est l'absence d'auto corrélation d'ordre p. La statistique du test est supposée suivre une loi ÷2 avec p degrés de liberté. Le deuxième test d'intéresse plutôt au phénomène d'homoscédasticité (constance de la volatilité des termes d'erreur): Test ARCH (p) d'Engle (1982). Ce test vérifie l'absence d'hétéroscédasticité autorégressive conditionnelle d'ordre p. Si le processus est ARCH, les résidus au carré doivent être hétéroscédastiques. L'hypothèse nulle est celle de l'homoscédasticité. La statistique du test est supposée aussi suivre une loi ÷2 avec p degré de liberté. La règle de décision est la même pour les deux tests: accepter H0 si la statistique du test est inférieure à la valeur critique de la loi ÷² avec p degrés de liberté à un niveau de confiance donné. Notons que pour tester l'effet GARCH (p, q), il suffit de procéder à un test d'effet ARCH (p+q).

La prévision de la Value-at-Risk à partir d'un modèle GARCH est effectué selon une démarche indirecte: dans un premier temps, on fait une hypothèse sur la distribution conditionnelle des rendements de l'actif, puis l'on estime les paramètres du modèle GARCH sur les observations de la période 1 à T, généralement par une procédure de type maximum de vraisemblance. Dans une seconde étape, on déduit du modèle GARCH estimé une prévision de la variance conditionnelle, qui couplée à l'hypothèse retenue sur la distribution des rendements, permet de construire une prévision sur le fractile de la distribution de pertes et profits valable pour T+1.

Considérons l'exemple d'un modèle GARCH sous hypothèse d'une distribution quelconque (normale, student...) de paramètre v.

On suppose ainsi que les rendements d'un actif, notés r_t , satisfont le modèle suivant :

r_t = c+ å_t

å_t = ztó t

2 2 2

1

-

ó_t = á0 + á1 å t- 1 +â1ó t

Les sont indépendantes identiquement distribués selon la loi mise en hypothèse. Les

z_t

paramètres á₀ , á₁ , â₁ ,c sont des réels à estimer vérifiant les contraintes suivantes: á0 >- 0 , á1 = 0 , â1 = 0 (v peut aussi faire partir des paramètres à estimer comme dans le cas de la distribution de student).

Le terme ( \ t -1 ) désigne la variance conditionnelle du résidu

ó t 2 = E å _t å å_t et donc des

rendements . Une fois les variables sont estimées (par la méthode de maximum de

r_t

vraissemblance par exemple), on obtient l'expression suivante:

? 2 ?		? ?
ó	2 2 t +1 = á0 + á1 åt + â1ó t

Avec 2

ó₁ donné et donc :

?

2

? ?

? ?

ó t 1 á á ( r t c ) â ó t 2

= + - +

2

+ 0 1 1

Soit ( , ) la fonction de répartition de la loi de . La Value-at-Risk pour t+1 et pour un

G ¹ á v

- zt

niveau de confiance 1-a obtenue par la formule suivante:

? ? ? ?

VaR t + 1 = ó t+1 G-1 (á , v) + c

I-4 La VaR dans la littérature de la gestion de portefeuille

Depuis longtemps, les chercheurs dans le domaine de la finance reconnaissent l'importance cruciale de la mesure du risque d'un portefeuille d'actifs financiers dans le processus d'optimisation de l'allocation d'actifs. Ce souci remonte à quatre décennies lorsque Harry Markowitz (1952) initiant les recherches sur la sélection de portefeuille explore la définition et la mesure de risque. Depuis la mesure de risque devient une composante bien intégré dans l'activité financière. Dans le modèle proposé par Markowitz, les investisseurs maximisent l'espérance de rendement pour un niveau de risque donné, ce dernier est mesuré par la variance. Markowitz fait remarquer que les individus cherchent en fait à réaliser le meilleur compromis possible entre le gain espéré et son risque associé. Reste à formaliser ce

compromis. Puisqu'on est dans une économie risqué, le gain espéré sera l'espérance du revenu, le risque sera simplement mesuré par la variance ou l'écart type du revenu aléatoire. La variance est une mesure de fluctuation. Faire ce choix comme mesure de risque de marché implique donc que l'on considère comme risqué tout ce qui bouge par rapport à la moyenne aussi bien les mouvements à la hausse que les mouvements à la baisse.

De façon plus formalisée, le critère de Markowitz s'écrit :

X Y E X E Y Var X VaR Y

> ( ) ( ) et ( ) ( )

= p

ou bien

E X E Y Var X VaR Y ( ) ( ) et ( ) ( )

=

Le critère choisit par Markowitz est visualisé dans un plan appelé plan de Markowitz, où l'on représente en ordonnée le revenu (ou le rendement) attendu et en abscisse le risque. Chaque couple possible d'actifs peut être représenté dans ce plan. Pour chaque rendement, il existe un portefeuille qui minimise le risque. À l'inverse, pour chaque niveau de risque, on peut trouver un portefeuille maximisant le rendement attendu. L'ensemble de ces portefeuilles est appelé frontière d'efficience ou frontière de Markowitz. Cette frontière est convexe par construction : le risque n'augmente pas linéairement en fonction des poids des actifs dans le portefeuille.

Dans le même cadre d'étude, Tobin (1958) résume le processus de décision d'investissement en deux étapes: la première est similaire pour tous les investisseurs et au cours de laquelle ils choisissent le même "meilleur" portefeuille d'actifs risqués sur la frontière efficiente (appelée le portefeuille de marché), la deuxième étape est spécifique à chacun d'entre eux. Elle dépend de leur attitude vis à vis du risque. En effet, chaque investisseur combine le portefeuille de marché avec un emprunt ou un prêt de façon à obtenir le niveau de risque qu'il désire supporter. Chaque investisseur ne doit donc placer son argent que dans deux actifs : d'une part un portefeuille risqué commun et d'autre part un actif sans risque ayant le caractère d'un prêt ou d'un emprunt. Il est utile de remarquer que le critère de Markowitz ne permet pas de comparer tous les projets de point de vue domination de l'un sur l'autre.

Black et Litterman (1992) ont élargi le champ d'application possible de cette approche classique. L'extension du cadre classique pour tenir compte du skewness et du kurtosis ainsi que l'étude des mesures de risque alternative est aussi largement traitée en littérature (Kaplanski et Kroll (2002)). Fleming, Kirby et Ostdiek (2001) étudient la valeur économique de l'indexation temporelle de la volatilité et De Roon, Nijman et Werker (2003) montrent son utilité dans la couverture des risques de change pour les portefeuilles d'actifs internationaux.

Certains désavantages de cette méthode, tel que l'incertitude au niveau de la matrice des covariances ou dans les espérances de rendement, sont évalués (Jorion (1985), Bouchaud et Potters (2000)). En effet, face aux inconvénient majeures du modèle de Markowitz, principalement l'hypothèse de normalité de la distribution des rendements et l'hypothèse de l'indifférence de l'investisseur vis-à-vis des pertes et des profits, d'autres critères de mesure du risque ont apparu comme mesure alternative capable d'éviter ces inconvénients. La plus importante de ces critères est la Value-at-Risk (ou valeur à risque). Cette notion est traitée depuis longtemps dans la littérature de sélection de portefeuille sous un autre concept qui est la notion de perte potentielle. En effet, présente dans les travaux de Roy (1952) sur la sélection de portefeuille sous les contraintes de perte de valeur potentielle, l'idée de mesurer le risque par ce phénomène revient évidemment à la notion de valeur à risque. Roy définit cette contrainte en terme de probabilité limite de la dévaluation de la valeur du portefeuille au dessous d'un niveau préfixé. Depuis, la littérature d'allocation d'actifs sous cette contrainte est élargit (voir par exemple Leibowitz et Kogelman (1991)). Lucas et Klaassen (1998) ont constitué des portefeuilles en maximisant l'espérance de rendement sous la contrainte d'un rendement positif minimal sur un horizon de temps donnée et pour un niveau de confiance prédéterminé.

Alexander et Baptista (2001) comparent l'utilisation de la VaR et de la variance afin de construire la frontière d'efficience. Ils montrent que pour un investisseur averse au risque l'utilisation de la VaR peut conduire à la sélection de portefeuille avec des variances de rendement plus élevées comparées aux analyses Moyenne Variance. Le principal inconvénient de la VaR est qu'elle ne vérifie pas la condition de sous additivité, condition nécessaire pour considérer la mesure comme étant cohérente au sens de Artzner, Delbaen, Eber et Heath (2000). Pour cela certaines études se sont orientées vers des mesures alternatives cohérentes, dérivées de la notion de VaR, tel que l'expected shotfall appelé aussi VaR conditionnelle (CVaR) ( Pflug(2000), Acerbi et Tasche (2001, 2002), Rockafellar et

Uryasev (2002)), la déviation absolue étudiée par Denneberg (1990) ou la semi variance mesurant le risque de base (Fischer (2001)). Certaines de ces études se sont focalisées sur l'étude l'utilisation des mesures alternatives de risque en gestion de portefeuille. Krokhmal, Uryasev et Zrazhevsky (2002) cherchent l'optimisation de portefeuille pour les fonds de couvertures sous différentes mesures de risque tel que le CVaR, la déviation absolue moyenne, la perte maximale. Ils montent que les résultats pour la frontière d'efficience coïncidente pour ces différentes mesures et que leurs combinaisons permettent d'obtenir une gestion de risque meilleure.

Rockafellar et Uryasev (2000) présentent une approche de programmation linéaire permettant la construction de la frontière efficiente sous la contrainte d'expected shortfall empirique. Ils contribuent aussi à la résolution du problème d'optimisation dans le plan Moyenne-CVaR. De même, Konno et al (2003) fournissent des algorithmes d'optimisation sous la contrainte de semi variance qui sont facile à implémenter.

Dans le cadre d'optimisation dans le plan Moyenne-VaR, Gaivoronski et Pflug (1999) traite d'une façon générale le cadre mathématique du processus d'allocation de la richesse. Campbell et al. (2001) analysent le problème d'optimisation dans le même plan en présence de rendements distribués sous différentes hypothèses (empirique, normale, student) et ça en présence de deux classes d'actifs. Rengifo et Rombouts (2004) procèdent à l'extension du cadre statique de cette étude de Campbell et al. (2001) vers un cadre dynamique d'allocation d'actifs en procédant à la comparaison des performances de deux modèles d'estimation de la VaR à savoir le modèle GARCH (1,1) et le modèle APARCH (1,1) sous différentes hypothèses de distribution. ). Chabaane et al. (2003) optimisent l'espérance de rendement sous différentes contraintes de risque : l'écart type, la semi-variance, la VaR et l'Expected Shortfall. Différentes méthodes d'estimation de la VaR sont utilisées. Ils concluent que l'optimisation sous la contrainte de la VaR est plus délicate au niveau des algorithmes et de l'implémentation que l'optimisation sous les autres contraintes. De même, le choix de la méthode d'estimation de la VaR a moins d'influence que le choix de la contrainte de risque sur les portefeuilles optimaux. Ils remarquent aussi que le portefeuille optimal sous la contrainte de la VaR se rapproche de celui obtenu sous la contrainte de l'Expected Shortfall.

II-1 La modélisation du problème d'optimisation du portefeuille :

Dans un cadre statique d'étude, notre objectif sera principalement de déterminer deux éléments de la gestion de portefeuille. Dans un premier temps, on cherchera les proportions optimales de chaque actif risqué dans le portefeuille. Dans un deuxième temps, on déterminera le montant B de liquidité à prêter ou à emprunter de façon à constituer un portefeuille avec une VaR qui correspond à la VaR préfixé par l'investisseur. Ce niveau de VaR* reflètera le degré de l'aversion au risque de l'investisseur. Bien évidemment, le portefeuille constitué maximise l'espérance de rendement que peut obtenir l'investisseur sous la contrainte d'une VaR recherché. Dans ce qui suit, l'objectif est de présenter un modèle traduisant la problématique.

On suppose que l'on dispose d'un montant W(0) à investir sur un horizon de temps T. On rappelle qu'on cherche à investir de manière à avoir un niveau de VaR bien définie de notre portefeuille. Ce niveau peut être fixé par le gestionnaire de risque dans les institutions financières de sorte qu'il correspond aux exigences des autorités règlementaires, ou fixé par un investisseur particulier relativement à son degré d'aversion au risque. Ce montant peut être

investie avec un autre montant B qui représente un prêt si B<0 et un emprunt si B>0. est le

r_f

taux d'intérêt sans risque pour lequel l'investisseur peut prêter ou emprunter pendant la période T. On a n actifs disponibles sur le marché. ã (i) indique la fraction investie dans l'actif risqué i ainsi la somme des ã (i) doit être égale à 1. Soit aussi P(i, t) le prix de l'actif i au temps t (le présent correspond à t=0).

La valeur initiale du portefeuille représente la contrainte budgétaire:

n

W(0) + = B ?= ã ( ) ( , i P i i 1

0) (1)

Le problème fondamental sera ainsi de déterminer les fractions ã (i) ainsi que le montant initial B à emprunter ou à prêter.

En choisissant le niveau désiré de la VaR comme VaR * (exprimé en valeur absolue), on peut formuler la contrainte de perte potentielle de valeur comme suit:

Pr( (0) ( ) *) 1 (2)

W - W T = VaR = - c

Avec W(T) est la richesse final de l'investisseur compte tenu de son remboursement de l'emprunt ou le cas éventuel de son recouvrement du prêt avec les intérêts y associés, c est le niveau de confiance. Ceci donne:

Pr( ( ) (0) *) 1 W T = W - VaR = - c

(3)

Du fait que la VaR est la perte maximale, sur l'horizon de temps T, qui peut avoir lieu avec un niveau de confiance c, on constate que le degré d'aversion au risque de l'investisseur est reflété à la fois par le niveau de VaR désiré et par le niveau de confiance associé. L'investisseur est intéressé par la maximisation de la richesse à la fin de la période T. Soit r(p) le rendement total espéré sur le portefeuille p sur cette période. La richesse finale espérée de l'investissement dans le portefeuille p peut s'écrire:

) (4)

E W T

0 ( ( )) ( (0) )(1 ) (1

= W + B r p B r 1

+ - +

Résolution du problème d'optimisation du portefeuille

A partir de l'équation (1), on détermine l'expression de B:

n

B

= ?= ã ( ) ( i P i 1

i W ,0) -

(0)

Si on remplace cette expression dans l'équation (4), on obtient:

n

E W T W

( ( )) (0)(1 ) ( ) ( , 0)( )

= r 1 ã i P i r r

-

0 p 1

+ + ?=

i 1

?= i 1

(i) P( i,

0)

VaR * +W (0

) rf

=

q

(⁵)

rf

n

(c , p)

On suppose pour simplifier que E0 ( W( T )) = W(T ) , la valeur de r_p est ainsi donné par:

)) -W (0 )rf + r_f

(W( T ) W(0
? ã(i) P ( i , 0 )

i =1

A partir de la contrainte de la perte de la valeur de l'équation (2), on essayera d'introduire r_p dans l'inéquation. On a ainsi :

Pr( W (0) - W(T ) VaR*)1- c

Donc:

Pr( W (T ) - W(0) =- VaR*)1- c

Pr( r_p = rf

VaR * +W (0

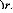
Donc:

=1-

) r

c

f

n

?= 1

ã (i) P ( i, 0)

i

Introduisons maintenant le terme q(c,p) qui représente le quantile correspondant à un niveau de confiance c dans la distribution des rendements du portefeuille. En effet, à partir de la dernière équation on peut obtenir les deux résultats souhaitées: d'une part l'expression de la valeur espéré de la richesse finale en fonction du quantile q(c,p) et d'autre part l'expression de B.

Ceci passe par les étapes suivantes :

ce qui donne:

n VaR W r

* (0)

+ 1

?= ã( ) ( , 0)

i P i =

r q c p

- ( , )

i 1 1

Une fois remplacé dans la dernière équation exprimant E0 ( W( T , p )) , on obtient:

r r

p 1

-

E W T W

0 ( ( )) (0)(1 )

= + +

r ( * (0) )

VaR W r

+

1 1

r 1

-

q

( , )
c p

En divisant par W(0) on obtient:

(6)

W T

( ) r r

p 1

-

E ₀ ( ) (1 )

= + +

r ( * (0) )

VaR W r

+

1 1

W(0) W r W q c p

(0) (0) ( , )

-

1

Cette dernière équation implique que la maximisation de l'espérance de rendement de l'investisseur passe à travers la maximisation de l'expression M (p) suivante:

M ( )

p

r p - r 1

=

0) r W q c p

- (0) ( , )

1

W (

(7)

On constate que la richesse initiale W(0) n'affecte pas le choix du portefeuille optimal puisque elle est considérée comme une constante dans l'expression M (p) à maximiser. Le processus d'allocation d'actif est ainsi indépendant de la richesse. Cependant, l'avantage d'avoir la richesse initiale dans le dénominateur est son interprétation. En effet, M (p) est égale au ratio de prime de risque espéré du portefeuille par rapport au risque assumé. Ce dernier est reflété à travers une perte potentielle maximale relativement à une référence (le rendement au taux sans risque). Vu que le produit du quantile négatif par la richesse initiale constitue la VaR du portefeuille pour un niveau donné de confiance, on pourra trouver une nouvelle expression ö(c, p) pour le risque.

En notons VaR(c, p) la VaR du portefeuille (avec un signe négatif vu que q(c,p) est un quantile négatif), le dénominateur devient:

? ( c , p ) = W(0) r _f -VaR(c, p ) (8)

Cette mesure du risque correspond au profil des investisseurs considérant le taux de rendement sans risque comme un benchmark pour le rendement de leur portefeuille et souhaitant en même temps que l'expression du risque soit en terme de perte potentielle. M (p) est ainsi une mesure de performance comme l'indice de Sharpe et peut être utilisé pour évaluer l'efficience de portefeuille (voir Sharpe (1994)). En plus sous l'hypothèse que l'espérance de rendement du portefeuille est normalement distribuée et que le taux sans risque est nul, M (p) converge vers un multiple de l'indice de Sharpe. Dans ce cas, les portefeuilles pour lesquelles ces deux indices sont maximisés sont les mêmes.

On constate aussi que le portefeuille optimal qui maximise M (p) est choisi indépendamment du niveau de la richesse initial ainsi que du niveau de VaR désiré (VaR *). En effet, la mesure de risque ö(c, p) pour les différents portefeuilles dépend de la VaR estimé du portefeuille et non de celui désiré. Les investisseurs débutent par la détermination de l'allocation optimale entre les actifs risqués, l'intervention ensuite du montant B vient pour montrer la différence entre la VaR estimé du portefeuille et la VaR désiré. Deux étapes séparées caractérisent le processus de décision comme dans le cas de l'approche de Moyenne Variance.

Afin de déterminer la valeur de B on combine l'équation (1) et l'équation (5). Ceci donne enfin :

=

W * ( VaR

* (

+ VaR c p '

B

))

(0)

,

?

(

c ,

p

'

)

(9)

On note que dans cette dernière expression, la est exprimé en valeur absolue et

VaR *

que la VaR est de signe négative. On remarque aussi le fait que ce modèle est indépendant des hypothèses de distribution de sorte que le modèle est dérivé dans le cadre de la maximisation de l'espérance de rendement sous la contrainte de perte de valeur désiré.

II-2 Le cadre de l'étude empirique :

Afin de déterminer l'effet de la déviation de l'hypothèse de normalité et de la variation de l'horizon d'estimation sur les portefeuilles optimaux à construire, nous avons choisit de se référer à deux indices du marché des capitaux des Etats-Unis : le Nasdaq 100 et le S&P500. Ces deux actifs représentent dans notre travail les actifs risqués. Rappelons que l'indice NASDAQ 100 contient 100 compagnies américaines de haute technologie cotées sur le marché du Nasdaq. La valeur des actions de ce type de sociétés est plus volatile que la valeur des actions des compagnies de l'économie traditionnelle. Le S&P 500 est un indice boursier basé sur 500 grandes sociétés cotées sur les bourses américaines. L'indice est possédé et géré par Standard & Poor's, l'une des trois principales sociétés de notation financière. Il représente sûrement un niveau de volatilité moins élevé que le Nasdaq 100. En fait, il contient plus de société ce qui implique un effet de diversification surtout que sa composition couvre des secteurs différents plus ou moins corrélés. Le logiciel utilisé pour l'analyse des données relatives à ces deux indices et l'implémentation du modèle sera le Matlab version 6.5. On suppose que les coûts de transactions sont négligeables et que les actifs financiers sont divisibles.

La période d'étude sera à partir du 01/04 /1997 jusqu'au 31/03/2007 et donc s'étale sur dix ans. Le nombre des observations des rendements journaliers est de 2515 (Figure 2). Le rendement journalier de l'indice est obtenu par la formule suivante :

C C

-

j j

^j Cj

R

1

1

Avec :

C_j = valeur de l'indice pour le jour j

Cj- 1 = valeur de l'indice pour le jour j-1

Le taux de rendement sans risque est considéré comme celui des Bons de trésor américains sur trois mois (US Treasury Bill). Il est de l'ordre de 4,97% annuellement fin du mois de mars 2007. La richesse initiale de l'investisseur est supposée égale à 1000$ (dollar américain). Les horizons de détention considérés sont trois : un jour, une semaine et dix jours. Ceci correspond aux périodes les plus pratiquées par les agents financiers avant la liquidation

du portefeuille. On se réfère à la moyenne géométrique pour calculer les moyennes de rendement des indices sur les différents horizons. L'expression générale pour l'obtenir est la suivante :

n

- 1

R

= ? + ( ) [ (1 )] ( 1 / ) n R i h m i=1

Avec :

h = durée de la sous période de détention (soit le jour, la semaine ou dix jours) n=nombre de sous période de durée h dans la période totale m

R_i = rendement de la i^ème sous période de durée h

( h )

R_m =rendement sur la période totale m

Par exemple, le rendement journalier moyen de l'indice du Nasdaq 100 sur la période d'étude est de 0,032%. Celui de l'indice S&P 500 est moins élevé et il est égal à 0,025%. L'écart type journalier du rendement du Nasdaq est aussi supérieur à celui de l'indice S&P 500. La volatilité est presque doublée puisque celle du premier indice atteint 2,22% alors que celle du deuxième est de 1,15%. La nouvelle mesure de risque présentée dans la section précédente est calculée pour les différentes séries de rendement selon une approche empirique d'estimation de la VaR et à un niveau de confiance de 99%. Rappelons qu'elle est obtenue par la formule suivante :

? = W₀ rf - VaR estimé

Les valeurs obtenues de cette mesure dans la table 1, montre bien sa croissance avec le temps. Plus l'horizon de détention est loin plus cette mesure est élevé. De même, la VaR relative du Nasdaq 100 reste toujours supérieure à celle du S&P 500 pour la même période de détention. Ceci est en conformité avec le fait que le premier indice offre un rendement espéré plus élevé et donc c'est évident qu'il fait supporter l'investisseur plus de risque.

En se référant à la table 1, on constate que le rendement moyen sur dix jours est supérieur à celui sur un jour, ceci est bien évident. L'écart type est lui aussi plus élevé mais il

dépasse les attentes données par la règle de la racine du temps (c'est-à-dire ó 10 j = 10ó 1 j ). Ceci indique l'existence du phénomène d'auto corrélation.

On constate aussi que pour les trois fréquences de données, les valeurs du coefficient d'asymétrie (skewness) et du coefficient d'aplatissement (kurtosis) sont différentes de celles données par une distribution normale. Pour le skewness, la seule valeur positive est celle du cas de rendement journalier du Nasdaq 100 ce qui indique une distribution asymétrique à droite. Dans tous les autres cas, la distribution est asymétrique à gauche. Pour le kurtosis les valeurs s'éloignent de 3. Ils sont plus élevés que cette valeur ce qui signifie de l'existence des queues épaisses pour les différentes cas. Ceci témoigne à priori de la non normalité des distributions. Le recours au test de Jarque et Bera à un niveau de confiance de 99% confirme ce constat puisque les statistiques JB calculées dépassent de loin la statistique de khi deux (2). On pourra penser dans ce cas à modéliser les distributions par la loi de student. Cette dernière a l'intérêt de tenir compte de phénomène leptokurtique. On sait qu'en s'appuyant sur la théorie des valeurs extrêmes, la mesure î de l'indice de queue peut être utiliser pour tester différents modèles de distribution. Cet indice prend la valeur 0 dans le cas normal. Il prend des valeurs entre 0 et 0.5 dans le cas de student. Le calcul de cet indice pour les rendements journaliers du Nasdaq 100 donne la valeur 0,186. Lorsqu'il est calculé pour les rendements journaliers du S&P 500 on le trouve proche de zéro. Les résultats sont similaires pour les autres horizons de détentions. Ceci témoigne du fait que la distribution du deuxième indice s'approche plutôt de la normalité que de la loi de student. Pour le cas de la distribution de student, le problème qui se pose est celui du choix du degré de liberté. Devant cette nuance provenant essentiellement de l'existence de queue épaisse, nous avons choisie dans les sections suivantes d'étudier le modèle d'allocation d'actifs en se référant à trois méthodes d'estimation de la VaR : la méthode empirique, la méthode normale (issu du modèle RiskMetrics) et la méthode TVE ( issu de la Théorie des Valeurs Extrêmes).

Notons enfin que l'estimation de la Value-at-Risk à partir des méthodes historiques requière théoriquement la stationnarité des séries des rendements. Pour cela on peut se référer au test de racine unitaire ADF (augmented Dickey-Fuller). A titre illustratif, l'application de ce test sur la série de rendement journalier sur la période d'étude du Nasdaq 100 donne une statistique égale à -20.50381 (le logiciel utilisé est Eviews 4.0). Cette dernière est inférieure à la valeur critique au seuil de signification de 1% qui est égale à -3,4575 ce qui indique la non stationnarité de la série. On suppose dans ce qui suit la stationnarité des séries de rendement des portefeuilles constitués par les deux indices.

II-3 L'application des méthodes de mesure de la Value at Risk :

Un élément fondamental du modèle d'allocation optimale d'actifs présenté dans cette étude est l'estimation de la Value-at-Risk. Pour cela, nous avons choisies d'appliquer et de comparer les résultats de certaines méthodes les plus traitées en littérature. Par hypothèse, on suppose que notre portefeuille est composé de 50% de l'indice Nasdaq 100 et de 50% de l'indice S&P 500. On se place dans le cas de rendement journalier. La période d'étude est celle mentionné ci-dessus, allant du 01/04/1997 jusqu'au 31/03/2007. Les résultats obtenus pour les différentes méthodes et pour les différents niveaux de confiance sont données dans la table 2 et représentée dans la Figure 3.

On constate que la méthode issue de la Théorie des Valeurs Extrêmes (EVT), que l'on appellera aussi méthode GPD (Generalised Pareto Distribution), a tendance à donner les valeurs de la VaR les plus élevées (en valeurs absolues) pour les différents niveaux de confiance. Le seuil (threshold) utilisé dans la méthode GPD est celui dépassé par 10% des observations de notre échantillon. On constate aussi qu'à un niveau faible de confiance, les différentes méthodes se rapprochent au niveau de l'estimation de la VaR. A un niveau élevé, on remarque que les deux méthodes non paramétriques (empirique et Bootstrap) convergent vers la même valeur estimée (-39,5). Dans le même cas de niveau élevé, les méthodes paramétriques basées sur l'hypothèse de normalité (Monte Carlo et Risk Metrics) donnent les valeurs les moins élevées de la VaR. Ceci est du à ce que l'hypothèse de normalité sous estime la VaR. Notons qu'on a procédé à 10 000 opérations de ré échantillonnage pour la méthode de Bootstrap et à 10 000 simulation de la loi normale centrée réduite pour la méthode MonteCarlo.

Comme mentionné précédemment, dans ce qui suit on choisi de comparer les résultats des modèles basées sur l'estimation de la VaR par la méthode empirique, la méthode normale (ou RiskMetrics) et la méthode GPD. Ceci est justifié par le caractère déterministe des estimations obtenues par ces méthodes. Il s'agit d'une condition nécessaire pour effectuer les opérations de maximisation. Les autres méthodes se basent plutôt sur la simulation et ont ainsi un caractère plus ou moins aléatoire.

II-4 La construction des frontières d'efficience :

Afin de construire la nouvelle frontière d'efficience dans le plan Moyenne-VaR relative, nous estimons simultanément l'espérance de rendement et la VaR relative des portefeuilles à différentes combinaisons de l'indice Nasdaq 100 et de l'indice S&P 500. En fait, en se basant sur ce nouveau plan, on arrive à construire la frontière d'efficience ,pour un niveau donné de confiance, en allant d'un portefeuille contenant 100% de l'indice Nasdaq 100 à celui contenant 100% de l'indice S&P 500. On garde la même période d'étude allant du 01/04/1997 jusqu'au 31/03/2007. Ainsi, l'estimation de la VaR est effectué selon les trois méthodes empiriques, normale et GPD sur trois horizons de détention possibles : le jour, la semaine et dix jours. A chaque horizon correspond, on établit les frontières d'efficiences pour trois niveaux de confiance : 95%, 97% et 99%. La nouvelle frontière d'efficience ressemble à celle du plan MoyenneVariance. Ce qui diffère est la définition du concept du risque : ici on fait recours à la VaR relative à un benchmark de rendement (qui est le taux sans risque) au lieu de l'écart type des rendements.

D'après les graphiques 4 à 6, on constate que les frontières d'efficiences obtenues par les trois méthodes tendent à se rapprocher pour des niveaux de confiance faibles et ce pour différents horizons de détention. A un niveau plus élevé (99%), la frontière d'efficience obtenue par la méthode normale se décale à gauche sur le graphique se situant ainsi au dessus des deux autres frontières d'efficience. Cela indique que les portefeuilles de cette frontière représentent pour un même niveau de rendement espéré, un niveau de risque moins élevé. Cela confirme une autrefois le caractère de sous estimation de la méthode normale. La frontière d'efficience de la méthode GPD s'éloigne parfois des deux autres d'une façon significative surtout dans le cas de niveau de confiance élevé (99%). Elle paraît plus proche de la frontière d'efficience empirique que de celle de la méthode normale dans les différents cas étudiés.

II-5 L'allocation optimale dans le cadre statique :

Dans cette section, on présente les résultats obtenus concernant les allocations optimales entre les deux actifs risqués pour différents niveaux de confiance et différents horizons de détention. De même le montant de prêt emprunt nécessaire au respect de la contrainte de la VaR est déterminé. Ceci étant effectué dans un cadre statique c'est-à-dire en se plaçant à un instant donné dans l'axe du temps (le 31/03/2007) et en effectuant les prévisions pour la période suivante (jour, semaine ou dix jours).

En ce qui concerne les allocations optimales, les tables 3,5 et 7 représentent les proportions retrouvés ainsi que la VaR estimé et la VaR relative du portefeuille optimal pour les différentes hypothèses de distribution. Ces résultats s'interprètent comme suit: Par exemple pour un investisseur qui cherche a constituer un portefeuille maximisant le rendement espéré sous la contrainte d'une VaR limite journalière a un niveau de confiance de 95% et en se basant sur une estimation empirique de la VaR, il aura intérêt a constituer un portefeuille dont la part de l'indice Nasdaq 100 est 48,18% et la part de l'indice S&P 500 est de 51,82%. La VaR a 95% de ce portefeuille calculé sur la base de la richesse initiale de l'investisseur sans recourir aux opérations de prêt-emprunt est égale a -19,856. D'une façon générale, le recours a ces opérations prend place si, pour un niveau de confiance donné, la VaR limite souhaité est différente de la VaR estimé du portefeuille optimal pour le même niveau de confiance (la VaR est retenu en signe négatif). Rappelons que le montant de liquidité B a prêter ou a emprunter est obtenu par la formule suivante :

B =

(0)

W * ( VaR

* (

))

,

+ VaR c p '

?

(

c ,

p

'

)

Avec :

W(0) = la richesse initiale de l'investisseur.

VaR * = la VaR limite choisit par l'investisseur (retenu en valeur absolue)

VaR ( c, p ' ) = la VaR estimé du portefeuille optimal pour le niveau de confiance considéré

?( c , p ' ) = la VaR relative du portefeuille optimal pour le niveau de confiance considéré.

En effet, dans le cadre du modèle d'allocation optimale de cette étude, le profil de risque de l'investisseur est supposé être reflété par le niveau de la VaR limite y inclut bien évidemment le niveau de confiance recherché. Ainsi, nous avons pris le cas des investisseurs qui ont différents profils de risque ,allant de celui de 95% a celui de 99%, et qui cherchent tous a constituer un portefeuille optimal avec une VaR limite égale a la VaR estimé du portefeuille optimale a 95%. Ceci est effectué pour les différents horizons de détentions et pour les différentes méthodes d'estimation de la VaR. A titre d'exemple, si on choisit d'estimer la VaR par la méthode empirique et qu'on cherche a avoir un portefeuille avec une VaR journalière a 99% égale a -19,856 (ce montant de VaR limite correspond a la VaR du

portefeuille optimal journalier à 95%), l'investisseur devra prêter un montant de 295,552 dollars. Toutefois, l'allocation de la richesse restante sera à la hauteur de 40,86% dans le Nasdaq 100 et de 59,15% dans le S&P 500, ce qui correspond à la répartition optimale du niveau de confiance 99%. Ceci lui permet de diminuer la VaR du portefeuille initialement égal à -28,268 tout en gardant le même niveau de confiance. C'est cela qui constitue la richesse de ce modèle générale d'allocation d'actifs. D'une façon générale, si la VaR limite pour un niveau de confiance donné est inférieur en valeur absolue à la VaR du portefeuille optimal pour ce même niveau de confiance, l'investisseur sera invité à prêter un montant B (négatif) au taux sans risque. Ceci était le cas général des recommandations obtenues dans nos calculs. Le seul cas d'emprunt était dans le cadre de l'hypothèse empirique, un horizon de dix jours et un niveau de confiance de 96% (Table 4) : l'investisseur devra emprunter 76,03 dollar pour faire passer la VaR du portefeuille optimale pour ce niveau de confiance de -43,546 à -46,959.

L'interprétation reste identique pour le cas des rendements hebdomadaires ou sur dix jours ainsi que pour le cas d'estimation de la VaR par les deux autres méthodes : normale et GPD. Cependant, on remarque que dans le cas de l'hypothèse de distribution normale des rendements (Table 5), l'allocation optimale entre les deux actifs est indépendante des niveaux de confiance. A chaque horizon de détention, correspond une combinaison optimale qui reste inchangé même si on change le niveau de confiance. L'attitude de l'investisseur vis-à-vis du risque exprimé au niveau de ce paramètre de la VaR est ainsi négligée dans le cas de la normalité. Ce qui reste déterminant dans son profil est le montant de la VaR limite choisit. Ceci s'explique par le fait que les quantiles q(c,p) dans le cas de normalité sont des constantes quelque soit la composition du portefeuille. La maximisation de l'expression M (p) sera ainsi indépendante du niveau de confiance. Elle dépend uniquement du couple Espérance/Ecart type du rendement du portefeuille. Cela n'est pas le cas pour les allocations déterminées dans le cas empirique ou dans le cas de la méthode GPD où les combinaisons optimales varient en fonction du niveau de confiance.

On constate aussi que le niveau de risque pour ces portefeuilles optimaux, mesuré par la VaR relative, est généralement plus élevé dans le cas empirique que dans le cas normal. Le quantile issu de la distribution empirique est plus élevé en valeur absolue que le quantile de la distribution normale pour n'importe quel niveau de confiance. Le caractère leptokurtique de la distribution effective des rendements du portefeuille optimal explique donc ce constat.

II-6 L'allocation optimale dans le cadre dynamique :

Dans ce qui suit, l'objectif est de comparer et de valider les méthodes d'estimation de la VaR dans le modèle d'allocation proposé à savoir : la méthode Empirique, la méthode normale et la méthode GPD. Ceci est effectué en passant à un cadre dynamique d'étude. Chaque méthode permet d'avoir un modèle de gestion dynamique issu du modèle général proposé. Nous nous intéressons à la gestion optimale quotidienne sur une période appelée période de prévision (outof-sample). L'hypothèse de normalité sera donc présenté à travers le modèle dynamique de prévision de la variance conditionnelle : GARCH avec des innovations de loi normale.

Présentation des données :

On se réfère aux mêmes données journalières des sections précédentes sur l'indice Nasdaq 100 et sur l'indice S&P 500. La période totale de l'étude s'étale donc du 01/04/1997 jusqu'au 31/03/07 (2515 observations). Cette période initiale est séparée en deux sous périodes : une période d'estimation (in-sample) et une période de prévision (out-of-sample). Cela permet d'obtenir une séquence de prévision de la VaR et de comparer ensuite les pertes effectives historiques des portefeuilles optimaux avec les VaR limites prédéfinies pour les mêmes jours. Dans notre cas, on a choisit la période d'estimation comme celle allant du 01/04/1997 jusqu'au 24/05/2005 (2050 observations) et la période de prévision comme celle allant du 25/05/2005 jusqu'au 31/03/2007 (465 observations). La figure 7 représente l'évolution du rendement des deux indices sur la période de prévision. La table 9 indique certaines statistiques descriptives des deux séries de rendements sur cette même période ainsi que leur VaR relative. La table 10 présente les résultats des deux tests de détection de l'effet ARCH (2) à un niveau de confiance de 99% : test Q (2) et le test ARCH (2) d'Engle. Ils sont appliqués sur les deux séries de rendement des deux indices NASDAQ 100 et S&P 500 durant toute la période d'étude. Rappelons que pour tester l'effet GARCH (p, q) il suffit de procéder à un test d'effet ARCH (p+q) et à un test de LjungBox. Les résultats pour la série des observations du Nasdaq 100 affirment l'existence d'une auto corrélation entre les termes d'erreur au carré ainsi que l'hétéroscédascticité de ces derniers : une modélisation GARCH (1,1) est donc justifiable. Pour la série du S&P 500, on constate une absence d'auto corrélation entre les termes d'erreurs au carré vu que la statistique

calculée est inférieure à la valeur critique de (2). On peut conclure que la modélisation par un

÷ ²

processus GARCH (1,1) est invalide dans ce cas malgré que le test d'effet ARCH (2) affirme
l'hétéroscédasticité. La richesse initiale de l'investisseur est supposée égale à 1000 dollars

américains. Le taux sans risque sur la période de gestion sera proche de la moyenne des taux des Bons de trésor américains sur trois mois (US Treasury Bill) pour la date du 24/05/2005 et du 31 /03/2007. Il est de l'ordre de 2,86% annuellement à la première date et de 4,97% dans la deuxième. Le taux sans risque journalier retenu sur la période de gestion sera ainsi de 0,016% (supposition de 250 jours ouvrables par an). Rappelons que les coûts de transactions sont supposés négligeables dans notre modèle. De même, on suppose que les actifs financiers sont divisibles. Dans le modèle GPD, on retient 9% des données (seuil u) pour estimer l'indice de queue.

Principe du modèle dynamique :

On suppose que la VaR limite recherchée par l'investisseur pour le jour j ( *

VaR_j ) est égale

à 2% de sa richesse cumulée jusqu'à la fin du jour j-1. Avec l'information disponible jusqu'au jour j-1, chaque méthode permet de prévoir pour le jour j le montant qui doit être emprunter (Bj > 0) ou prêter (Bj < 0) compte tenu de l'aversion au risque de l'investisseur. Celle-ci étant exprimée par le montant de la VaR limite choisi et le degré de confiance souhaité. Chaque méthode permet aussi de prévoir le poids optimal de chaque actif risqué dans le portefeuille durant le jour j. Ensuite, avec les recommandations établit en j-1, on détermine l'évolution effective de la richesse de l'investisseur durant j pour après reprendre la même procédure en incluant les données du jour j dans la période d'estimation afin d'établir les recommandations de j+1.

L'idée est ainsi de déterminer les recommandations d'investissement journalière en terme de poids optimaux des actifs risqués dans le portefeuille et en terme de montant prêt-emprunt. Ensuite, on détermine le taux d'échec résultant du dépassement de la perte journalière effective à la VaR limite prévu pour le même jour (supposé égale à 2% de la richesse finale du jour précédent). Il s'agit du test de Kupiec-LR (1995). La perte journalière effective du jour j est obtenue à partir du rendement effectif du portefeuille optimal constitué pour le même jour déduction faite des charges financières si Bj > 0 (il s'agit d'un emprunt) ou en ajoutant les produits financiers si BjB < 0 (il s'agit de prêt). Le taux d'échec multiplié par 465 représente le nombre de fois où le rendement effectif dépasse cette VaR limite pendant la période de prévision. La méthode qui présente le taux d'échec le moins élevé sera considérée la plus fiable parmi les trois. Un deuxième critère peut être utilisé : la richesse finale à l'issu de la période de prévision. Si l'investisseur adopte ce point de vue, le modèle le plus adéquat pour lui sera celui qui procure la richesse finale la plus élevée.

Résultats empiriques :

On s'intéresse à la performance des trois modèles : Empirique, GARCH et GPD pour trois niveaux de confiance de la VaR : 95%, 97% et 99%. Ces derniers correspondent à une aversion au risque croissante. Les résultats obtenus par l'application des trois modèles sur une période de gestion de 465 jours (out-of-sample) sont présentés dans les tableaux 11 et 12.

Le premier tableau présente le taux d'échec des trois modèles pour les différents niveaux de confiance cités ci-dessus. On constate que pour les différents modèles, le taux de dépassement de la perte effective du portefeuille à la VaR limite respecte le seuil d'erreur prévu. Cela affirme le respect de la contrainte de notre modèle de base. De même, ce taux décroît avec le niveau de confiance souhaité ce qui est en parfaite conformité avec le fait qu'à un niveau de confiance plus élevé (et donc dans le cas d'un investisseur averse au risque) la marge d'erreur devra être plus faible. Autrement, les recommandations d'investissement issu d'un niveau de confiance de 95% implique plus d'erreur de prévision que les recommandations d'investissement issu d'un niveau de confiance de 99%. En se référant au raisonnement de Kupiec LR (1995), le modèle le plus adéquat pour l'investisseur sera le modèle GPD. Il présente le taux d'échec le moins élevé pour les différents niveaux de confiance. Ainsi, ce modèle sera recommandé pour un investisseur qui juge la prédominance du critère de taux d'échec sur les autres critères. Cependant, les taux d'échec de ce modèle apparaissent relativement faible ce qui reflète une aversion assez grande. Le graphique 18 montre l'écart important entre les VaR limites et les pertes effectives dans le cadre de ce modèle pour un niveau de confiance de 99%. Cela s'explique par des recommandations qui favorisent l'opération de prêt allant jusqu'à 800 $ (voir figure 16). Ainsi, la perte effective réalisée sur les 200 $ investi en actif risqué devienne assez faible devant une VaR limite de l'ordre de 2% de la richesse initiale investi (soit à peu prés 20 $ par jour). Cette perte effective est en plus atténuée par une stratégie recommandant l'investissement dans l'actif le moins risqué (S&P 500) ce qui a pour conséquence de diminuer l'exposition du portefeuille risqué au risque (voir figure 17). Le modèle GPD apparaît donc comme un modèle conservatif. Il recommande l'opération d'emprunt seulement sur la deuxième dizaine de jour sur les 465 jours de prévision. Pendant ces jours, la VaR limite est donc supérieur à la VaR du portefeuille optimal constitué pour le même jour.

Le modèle Empirique se place dans le deuxième rang selon le critère statistique de taux d'échec . On constate comme même un taux faible d'échec pour les différents niveaux de confiance. Les recommandations de ce modèle, pour un niveau de confiance de 99%, en terme de part de chacun des deux indices dans l'actif risqué sont moins sensibles à l'augmentation de la série de données historique (voir figure 9). Ainsi, w1 reste constante sur plusieurs jours consécutifs. Cela convient mieux dans le cadre de l'existence de coûts de transactions. Tout au long de la période out-of-sample, ce modèle suggère de recourir au prêt pour respecter la contrainte de VaR limite. En fait, ces deux premiers modèles reflètent implicitement par leur recommandation de prêter une tendance négative des rendements des deux indices ce qui conduit à une VaR du portefeuille optimale supérieur à la VaR limite et ainsi à Bj < 0 (prêt).

Le modèle GARCH respecte le taux d'échec maximal autorisé. Cependant, à un niveau de confiance de 99%, les stratégies recommandées par ce modèle tendent à favoriser l'investissement dans l'indice le plus risqué, le Nasdaq 100, tout au long de la période de prévision (voir figure 13). Les opérations sur l'actif sans risque oscillent entre opération de prêt et celle d'emprunt.

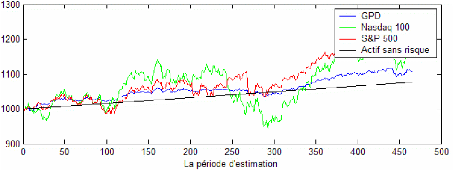
Le tableau 12 présente les résultats concernant le deuxième critère : la richesse finale. Dans c e cadre, l'investisseur aura intérêt à suivre les recommandations du modèle Empirique. Ce dernier permet d'avoir la richesse la plus élevée à l'issu de la période de gestion et ce pour les différents niveaux de confiance. Le modèle GPD arrive dans la deuxième position pour les niveaux de confiance de 95% et 97% et en troisième position pour un niveau de confiance plus élevé. Dans les graphiques 11,15 et 19 on a présenté l'évolution de la richesse durant la période de prévision avec les différents modèles ,à 99% de confiance, comparé à l'évolution de la richesse obtenu par l'investissement exclusif en Nasdaq 100, S&P 500 et l'actif sans risque.

Les limites de la variance comme mesure de risque ont mené les financiers à chercher d'autres mesures plus précises et plus pratiques. Parmi ces mesures, la Value-at-Risk s'est imposé comme un standard et une référence règlementaire incontournable aussi bien dans les milieux financiers que dans les milieux d'assurance. Dans ce travail, on a montré comment on peut intégrer cette notion dans le processus de sélection optimale de portefeuille dans une logique de contrôle de risque. Ainsi, à partir d'une Value-at-Risk souhaitée (et ainsi d'un niveau de risque assumé) on présente un modèle général permettant l'allocation optimale de la richesse entre les actifs risqués et les actifs non risqués. Ceci passe par la maximisation de l'espérance de rendement du portefeuille sous la contrainte de la VaR limite. Ce processus d'optimisation tient compte de l'estimation de la VaR. Ainsi, trois modèles sont choisis : le modèle empirique, le modèle GARCH et le modèle GPD. L'étude empirique se base sur deux actifs risqués : le Nasdaq 100 et le S&P 500 et ce pour une période de dix ans (1997-2007). La validation du processus d'optimisation sous chacun des trois modèles est effectuée à travers deux critères calculés sur une période de prévision s'étalant sur 465 jours. Le premier critère choisi est d'ordre statistique : le taux d'échec du modèle au niveau des stratégies d'allocations respectant la contrainte de la VaR limite. Le deuxième critère de performance est d'ordre économique : la richesse finale procuré par chaque modèle à la fin de la période de prévision. Les résultats montrent la supériorité du modèle GPD pour le premier critère et la dominance du modèle Empirique pour le deuxième critère. Cependant, on pourra se demander sur l'influence d'autres paramètres bien présents dans le cadre dynamique, tel que les coûts de transactions, sur les résultats obtenus. De même, inclure les produits dérivés dans le portefeuille risqué apparaît intéressant vu l'importance du volume de transaction de ces actifs à l'échelle mondiale. On sera ainsi mené à utiliser d'autres modèles d'estimation de la VaR tel que la méthode delta normal.

Figure 2 : Les rendements journaliers des deux indices sur la période d'étude du 01/04/1997 au 31/03/2007

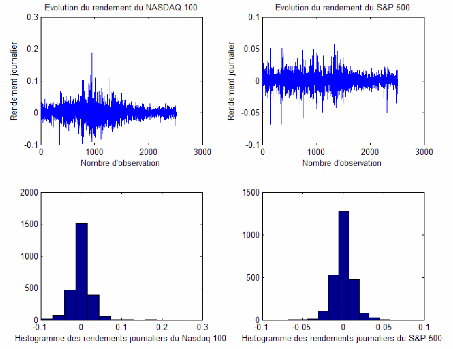
Table 1- Les statistiques descriptives des rendements des deux indices

NASDAQ 100	Journalier	Hebdomadaire	10 jours
Moyenne	0,000317681	0,001458065	0,002223235
Erreur-type	0,000443461	0,001903747	0,002839718
Médiane	0,001248879	0,0034419	0,007728195
Mode	0	0	#N/A
Écart-type	0,022239447	0,043703332	0,053879862
Variance de l'échantillon	0,000494593	0,001909981	0,00290304
VaR relative (cas empirique 99%)	57,17	105,83	134,42
Kurstosis (Coefficient d'aplatissement)	7,353	6,7125	4,8481
			-
Skewness (Coefficient d'asymétrie)	0,362181238	-0,225398467	0,283755071
Plage	0,286287108	0,463434319	0,466605164
	-		-
Minimum	0,098573958	-0,252490371	0,256512979
Maximum	0,18771315	0,210943949	0,210092185
Somme	1,418628296	1,275944057	1,328294549
Nombre d'échantillons	2515	527	360
Jarque et Bera (JB)	2,04E+03	302,9204	54,5011
S&P 500
Moyenne	0,000248808	0,001193247	0,001740883
Erreur-type	0,000229436	0,001021361	0,001419755
Médiane	0,000522287	0,001588924	0,004996629
	-
Mode	0,009116768	0	#N/A
Écart-type	0,011506178	0,023446856	0,026937964
Variance de l'échantillon	0,000132392	0,000549755	0,000725654
VaR relative (cas empirique 99%)	29,7677	67,2569	80,9452
Kurstosis (Coefficient d'applatissement)	6,0947	5,1243	4,7567
	-		-
Skewness (Coefficient d'assymétrie)	0,023422279	-0,302961499	0,281109516
Plage	0,125984128	0,188301993	0,218018302
	-		-
Minimum	0,068656812	-0,110501207	0,098852216
Maximum	0,057327316	0,077800787	0,119166086
Somme	0,792707206	0,774083881	0,757551233
Nombre d'échantillons	2515	527	360
Jarque et Bera (B)	1,00E+03	105,2544	49,5744
Khi deux (2) à 99%	0,0201	0,0201	0,0201
Taux sans risque	0,000194036	0,000933212	0,001348253

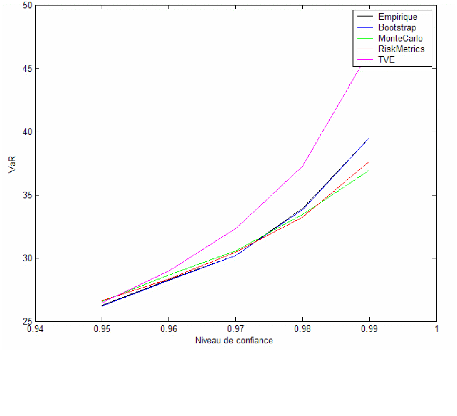
Table 2- Le montant de la Value at Risk journalière pour un portefeuille composé à 50% de l'indice NASDAQ 100 et à 50% de l'indice S&P 500

	Empirique	Bootstrap*	MonteCarlo**	RiskMetrics	TVE(GPD)***
95%	-26,228	-26,203	-26,574	-26,621	-26,466
96%	-28,298	-28,219	-28,622	-28,334	-28,970
97%	-30,161	-30,205	-30,563	-30,440	-32,311
98%	-33,936	-33,786	-33,427	-33,239	-37,242
99%	-39,513	-39,484	-36,926	-37,651	-46,316

* Pour la méthode de Bootstrap, on se base sur 10 000 réechantillonage

** Pour ces méthodes, on suppose la distribution normale des rendements du portefeuille (10 000 simulations pour la méthode Monte Carlo)

***Le seuil u pris en compte est celui dépassé par 10% des observations

Figure 3 : L'estimation de la VaR journalière (portefeuille à parts égaux de l'indice Nasdaq 100 et de l'indice S&P 500

Figure 4 : Les frontières d'efficience dans le cas de rendement journalier

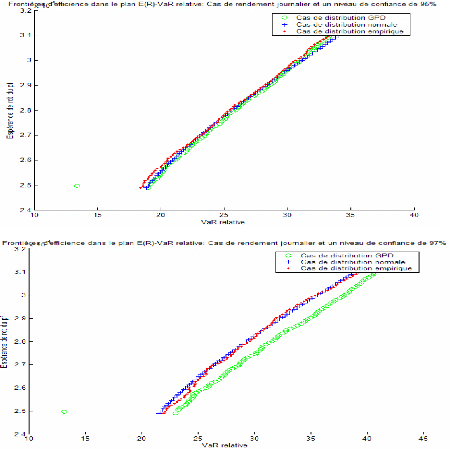
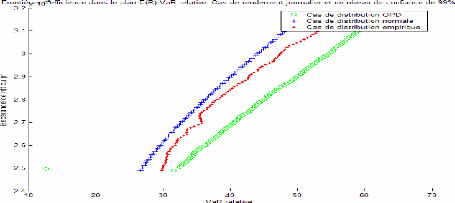
Figure 5 : Les frontières d'efficience dans le cas de rendements hebdomadaires

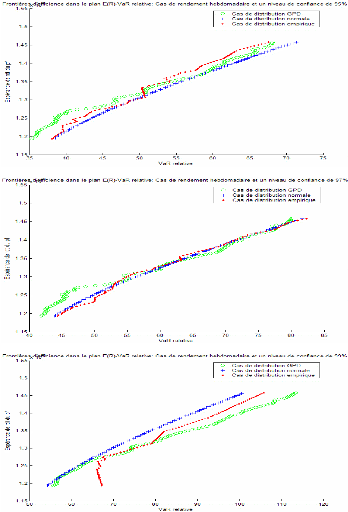
Figure 6: Les frontières d'efficience dans le cas de rendement sur dix jours

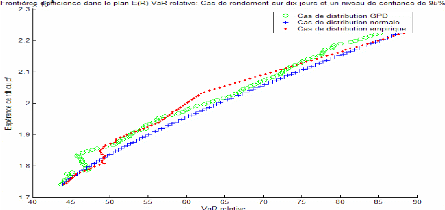
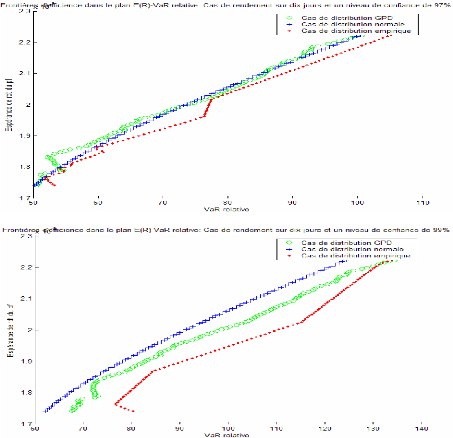
Table 3- L'allocation statique optimale et VaR (estimé et relative) dans le cas empirique

Rendement journalier	NASDAQ 100	S&P 500	VaR estimé	VaR relative
95%	48,18%	51,82%	-19,856	20,050
96%	40,03%	59,97%	-20,187	20,381
97%	51,63%	48,37%	-23,664	23,858
98%	47,71%	52,29%	-25,573	25,767
99%	40,86%	59,14%	-28,268	28,462
Rendement hebdomadaire
95%	53,04%	46,96%	-39,457	40,390
96%	60,09%	39,91%	-45,305	46,239
97%	44,11%	55,89%	-43,508	44,442
98%	53,64%	46,36%	-49,995	50,928
99%	30,46%	69,54%	-53,019	53,952
Rendement sur dix jours
95%	56,18%	43,82%	-46,959	48,307
96%	39,27%	60,73%	-43,546	44,894
97%	57,38%	42,62%	-60,487	61,835
98%	35,93%	64,07%	-57,513	58,861
99%	31,74%	68,26%	-68,839	70,187

Table 4- Le montant de prêt-emprunt nécessaire pour obtenir une VaR du portefeuille
égale à celle du portefeuille optimal à 95% de confiance (cas empirique)

	B journalier	B hebdomadaire	B sur dix jours
95%	0	0	0
96%	-16,2359	-126,478	76,0299
97%	-159,5901	-91,1558	-218,7659
98%	-221,8802	-206,9115	-179,2992
99%	-295,5525	-251,3644	-311,7281
VaR limite	19,856	39,457	46,959

Table 5- L'allocation statique optimale et VaR (estimé et relative) dans le cas de n ormalité

Rendement journalier	NASDAQ 100	S&P 500	VaR estimé	VaR relative
95%	45,55%	54,45%	-19,674	19,868
96%	45,55%	54,45%	-20,958	21,152
97%	45,55%	54,45%	-22,536	22,730
98%	45,55%	54,45%	-24,634	24,828
99%	45,55%	54,45%	-27,941	28,135
Rendement hebdomadaire
95%	43,80%	56,20%	-38,974	39,906
96%	43,80%	56,20%	-41,566	42,498
97%	43,80%	56,20%	-44,752	45,684
98%	43,80%	56,20%	-48,988	49,920
99%	43,80%	56,20%	-55,664	56,596
Rendement sur dix jours
95%	43,37%	56,63%	-44,948	46,296
96%	43,37%	56,63%	-47,965	49,313
97%	43,37%	56,63%	-51,675	53,023
98%	43,37%	56,63%	-56,606	57,954
99%	43,37%	56,63%	-64,378	65,726

Table 6- Le montant de prêt-emprunt nécessaire pour obtenir une VaR du portefeuille égale à celle du portefeuille optimal à 95% de confiance (cas de normalité)

	B journalier	B hebdomadaire	B sur dix jours
95%	0	0	0
96%	-60,6988	-60,9886	-61,19
97%	-125,9237	-126,4829	-126,8715
98%	-199,7895	-200,6016	-201,1654
99%	-293,845	-294,8986	-295,6294
VaR limite	19,6737	38,974	44,948

Table 7- L'allocation statique optimale et VaR (estimé et relative) dans le cas GPD

Rendement journalier	NASDAQ 100	S&P 500	VaR estimé	VaR relative
95%	48,57%	51,43%	-26,1317	20,430
96%	48,57%	51,43%	-28,587	22,336
97%	48,58%	51,42%	-31,871	24,884
98%	48,58%	51,42%	-36,735	28,659
99%	48,57%	51,43%	-45,731	35,640
Rendement hebdomadaire
95%	28,48%	71,52%	-39,190	32,318
96%	28,48%	71,52%	-42,029	34,604
97%	28,48%	71,52%	-45,972	37,781
98%	28,48%	71,52%	-52,117	42,730
99%	28,84%	71,16%	-64,670	52,793
Rendement sur dix jours
95%	38,68%	61,32%	-53,092	42,420
96%	38,68%	61,32%	-57,061	45,512
97%	38,68%	61,32%	-62,346	49,631
98%	38,68%	61,32%	-70,129	55,695
99%	38,68%	61,32%	-84,389	66,807

Table 8- Le montant de prêt-emprunt nécssaire pour obtenir une VaR du portefeuille
égale à celle du portefeuille optimal à 95% de confiance (cas de GPD)

	B journalier	B hebdomadaire	B sur dix jours
95%	0	0	0
96%	-109,9456	-82,0205	-87,1954
97%	-230,6458	-179,5135	-186,4525
98%	-369,9973	-302,5267	-305,8919
99%	-549,934	-482,6289	-468,466
VaR limite	26,1317	39,190	53,092

Figure 7 : Les rendements des deux indices sur la période de prévision (out-of-sample)

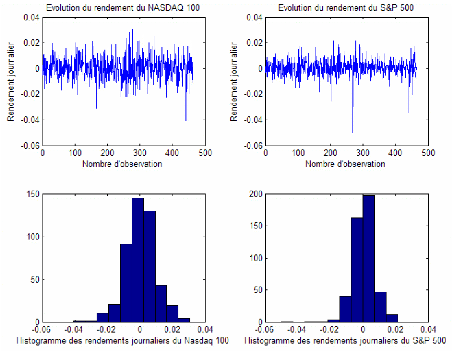
Table 9- Les statistiques descriptives de l'échantillon de prévision Nasdaq 100		S&P 500
Moyenne	0,000316	0,000374
Ecart-type	0,0093	0,0068
Skewness	-0,0677	-1,0852
Kurtosis	4,0605	11,0183
VaR relative (cas empirique à 99%)	22,098	18,476

Table 10- Les résultats des tests de détection de l'effet GARCH(1,1) pour un niveau de confiance de 99%

NASDAQ 100 S&P 500

	Q(2)	E(2)	Q(2)	E(2)
Statistique du test	19,543	197,764	4,584	136,733
Valeur critique ( ÷(2))	9,210	9,210	9,210	9,210
Décision	C *	C	NC **	C

* Confirmation de l'existence de l'effet ARCH

** Non Confirmation de l'existence de l'effet ARCH

Table 11- Le taux d'échec des trois méthodes (empirique, GARCH et GPD) pour différents niveaux de confiance

	Empirique	GARCH	GPD
95%	0,86%	3,66%	0,43%
97%	0,43%	2,58%	0,22%
99%	0,43%	0,86%	0,00%

Table 12- La richesse finale de l'investisseur en procédant à la gestion dynamique

	Empirique	GARCH	GPD
95%	1161,900	1112,400	1130,4
97%	1139,200	1111,800	1130,2
99%	1144,700	1108,200	1107,8

Figure 8: Le montant de prêt-emprunt quotidien durant la période de prévision dans le cas de la méthode Empirique à un niveau de 99% de confiance

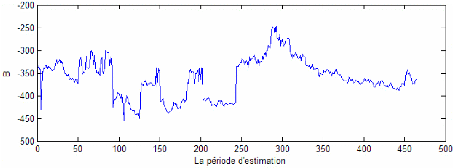
Figure 9: La part quotidienne de l'indice Nasdaq 100 durant la période de prévision dans le cas de la méthode Empirique à un niveau de 99% de confiance

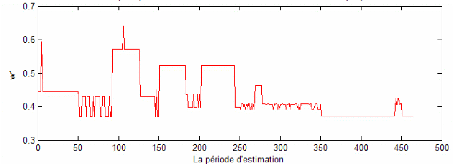
Figure 10: L'évolution de la VaR limite et des pertes effectives des portefeuilles optimaux quotidiens durant la période de prévision dans le cas de la méthode Empirique à un niveau de 99% de confiance

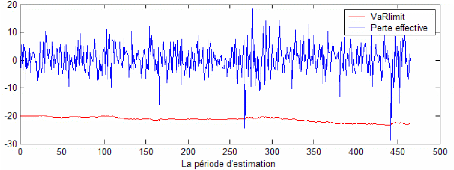
Figure 11: L'évolution de la richesse durant la période de prévision avec le modèle Empirique (99% de confiance) comparé à l'évolution de la richesse obtenu par l'investissement en Nasdaq 100, S&P 500 et l'actif sans risque d'une façon individuelle.

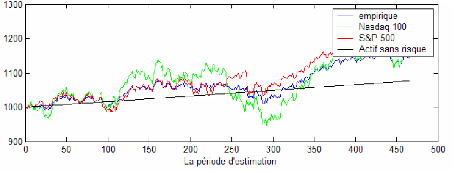
Figure 12: Le montant de prêt-emprunt quotidien durant la période de prévision dans le cas de la méthode GARCH à un niveau de 99% de confiance

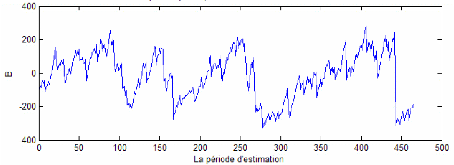
Figure 13: La part quotidienne de l'indice Nasdaq 100 durant la période de prévision dans le cas de la méthode GARCH à un niveau de 99% de confiance

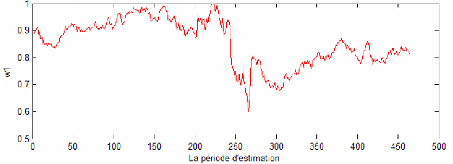
Figure 14: L'évolution de la VaR limite et des pertes effectives des portefeuilles optimaux quotidiens durant la période de prévision dans le cas de la méthode GARCH à un niveau de 99% de confiance

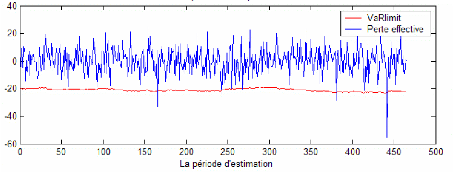
Figure 15: L'évolution de la richesse durant la période de prévision avec le modèle GARCH (99% de confiance) comparé à l'évolution de la richesse obtenu par l'investissement en Nasdaq 100, S&P 500 et l'actif sans risque d'une façon individuelle.

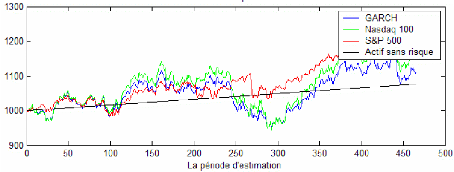
Figure 16: Le montant de prêt-emprunt quotidien durant la période de prévision dans le cas de la méthode GPD à un niveau de 99% de confiance

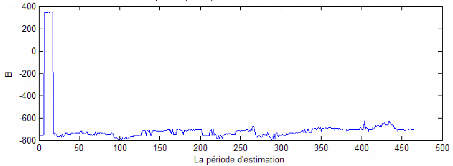
Figure 17: La part quotidienne de l'indice Nasdaq 100 durant la période de prévision dans le cas de la méthode GPD à un niveau de 99% de confiance

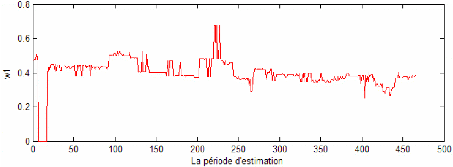
Figure 18: L'évolution de la VaR limite et des pertes effectives des portefeuilles optimaux quotidiens durant la période de prévision dans le cas de la méthode GPD à un niveau de 99% de confiance

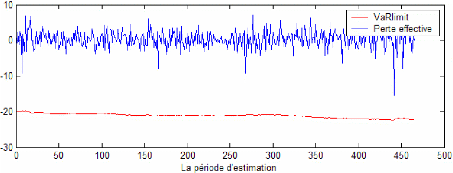
Figure 19: L'évolution de la richesse durant la période de prévision avec le modèle GPD (99% de confiance) comparé à l'évolution de la richesse obtenu par l'investissement en Nasdaq 100, S&P 500 et l'actif sans risque d'une façon individuelle.

Acerbi C., Tasche D. (2001) Expected Shortfall: a Natural Coherent Alternative to Value at Risk. Working Paper.

Acerbi C., Tasche D. (2002) On the Coherence of Expected Shortfall. Journal of Banking and Finance, vol. 26(7), 1487-1503.

Alexander G., Baptista A. (2001) A VaR-Constrained Mean-Variance Model: implications for Portfolio Selection and the Basle Capital Accord. Working Paper, University of Minnesota.

Artzner P., Delbaen F., Eber J.M., Heath D. (2000) Coherent measures of risk, Mathematical Finance, Vol 9 (3), 203-228.

Aussenegg W., Pichler S. (1997) Empirical Evaluation of Simple Models to Calculate Valueat-Risk of Fixed Income Instruments. Working Paper, Technische Universität Wien.

Black F., Litterman R. (1992) Global Portfolio Optimization. Financial Analysts Journal, vol. 48(5) 28-43.

Bouchaud J.P., Potters M. (2000) Theory of Financial Risks. Cambridge University Press.

Bredin D., Hyde S., (2001) FOREX Risk: Measurement and Evaluation using Value-at-Risk. Central Bank of Ireland, November.

Calvet A. L. (2000) La gestion globale des risques du marché : de la Value at Risk à Corporate Metrics^TM. Revue Internationale de Gestion, volume 25, numéro 3, automne.

Campbell R., Huisman R., Koedijk K. (2001) Optimal Portfolio Selection in a Value-at-Risk Framework. Journal of Banking and Finance, 25, 1789-1804.

Chabaane A., Laurent J.P., Malevergne Y., Turpin F. (2006) Alternative Risk Measures for alternative Investments. Journal of Risk 8, n°4, 1-32.

Christoffersen P., Hahn J., Inoue A. (2001) Testing and comparing Value-at-Risk measures. Journal of Empirical Finance, 8, Number 3, July, pp. 325-342(18).

Crnkovic C., Drachman J. (1996) A Universal Tool to Discriminate Among Risk Measurement Techniques. Working Paper, J. P. Morgan, corporation.

Denneberg D. (1990) Premium Calculation: Why Standard Deviation Should Be Replaced By Absolute Deviation. ASTIN Bulletin, vol. 20, 181-190.

De Roon F., Nijman T., Werker B. (2003) Currency Hedging for International Stock Portfolios: the Usefulness of Mean-Variance Analysis. Journal of Banking and Finance, 27, 327-349.

Engle R. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, p 987-1007, 1982.

Engle R. (2000) The Use of ARCH/GARCH Models in Applied Econometrics. Journal of Economic Perspectives, 15(4), 157-168.

Fischer T. (2001) Coherent Risk Measures Depending on Higher Moments, Working Paper.

Fleming J., Kirby C., Ostdiek B. (2001) The Economic Value of Volatility Timing. Journal of Finance, (1), 329-352.

Gaivoronski A., Pflug G. (1999) Finding Optimal Portfolios with Constraints on Value at Risk. Working paper, University of Vienna.

Glasserman P., Heidelberger P., Shahabuddin P. (2001) Efficient Monte Carlo Methods for Value-at-Risk. Mastering Risk, Vol 2, published by Financial Times-Prentice Hall.

Glasserman P., Shahabuddin P., Heidelberger P. (2000) Variance Reduction Technics for Estimating Value at Risk. Management Sciences, Vol.46 No.10, October.

Hendricks D. (1996) Evaluation of Value at Risk Models Using Historical data. Federal Reserve Bank of New York. Economic Policy Review 2, pp 39-70, Avril.

Jackson P., Maude D., Perraudin W. (1997) Bank Capital and Value-at-Risk. Journal of Derivatives 4, pp73-90, spring.

Jorion P. (1985) International Portfolio Diversification with Estimation Risk. Journal of Busines. vol. 58,no. 3.

Jorion P. (2001) Value at Risk: The New Benchmark for Managing Financial Risk. second edition, McGraw- Hill, New York.

Kahneman D., Knetsch J.L., Thaler R.H. (1990) Experimental tests of the endowment effect and the coax theorem. Journal of public Economics, 98, 1325-1350.

Kaplanski G., Kroll Y. (2002) VaR risk measure vs. traditional risk measures: An analysis and survey . Journal of Risk, 4, Printemps , 1-27.

Konno H., Waki H., Yuuki A. (2002) Portfolio Optimization under Lower Partial Risk Measures. Working paper, Kyoto University.

Krokhmal P., Uryasev S., Zrazhevsky G. (2002) Risk Management for Hedge Fund Portfolios. The Journal of Alternative Investments, vol. 5(1), 10-29.

Kupiec P.H. (1995) Techniques for verifying the Accuracy of Risk Measurement Models. Board of Governors of the Federal Reserve System. Finance and Economics Discussion Series, 95/24 May.

Leibowitz M.L., Kogelman S. (1991) Asset Allocation under Shortfall Constraints. Journal of Portfolio Management, Winter, 18-23.

Linsmeier T. J., Neil D. P. (1996) Risk Measurement: An Introduction to Value at Risk. ACE OFOR 9604, University of Illinois at Urbana-Champaign Juillet.

Ljung G.M., Box G.E.P. (1978) On a measure of a lack of fit in Time Series Models. Biometrika, 65, p 297-303, 1978.

Lopez J. A. (1996) Regulatory Evaluation of Value at Risk Models. Working Paper, Federal Reserve Bank of New York.

Lucas A., Klaassen P. (1998) Extreme Returns, Downside Risk, and Optimal Asset Allocation. Journal of Portfolio Management, Fall, 71-79.

Manganelli,S., Engel R.F. (2001) Value at Risk models in finance. Working Paper n°75. Markowitz H. (1952) Portfolio Selection. Journal of Finance, vol. 7(1), 77-91.

Marshall C., Siegel M. (1997) Value at Risk: Implementing a Risk Management Standard. Journal of Derivatives 4, .p73-84, spring.

Pflug G. (2000) Some remarks on the Value-at-Risk and the conditional Value-at-Risk in Probabilistic Constrained Optimization: Methodology and Applications, Kluwer Academic Publishers. S. Uryasev (Ed.), Dordrecht.

Powell A., Balzarotti V. (1996) Capital requirement for Latin American Banks in Relation to their Market Risks: The Relevance of the Basle 1996 Amendment to Latin America. Working Paper, series 347, Washington, D.C.

Pritsker M. (1997) Evaluating Value at Risk Methodologies: Accuracy versus Computational Time. Journal of Financial Services Research, 12 (2/3), October/ December, 201-242.

Rengifo E.W., Rombouts J.V.K. (2004) Optimal portfolio selection in a VaR framework. Working Paper.

Rockafellar R.T., Uryasev S. (2002) Conditional Value-at-Risk for General Loss Distributions. Journal of Banking and Finance, vol. 26(7), 1443-1471.

Roy A.D. (1952) Safety-First and the Holding of Assets. Econometrica, 20, 431-449. Rockafellar R.T., Uryasev S. (2000) Optimization of Conditional Value-at-Risk. The Journal of Risk, vol 2(3), 21-41.

Sharpe W. (1994) The Sharpe Ratio. Journal of Portfolio Management, 21, 49-58.

Tobin J. (1958) Liquidity Preference as Behavior Towards Risk. Review of Economic Studies, vol. 67, pp 65-86.

Référence en ligne :

http://www.gloriamundi.org/

http://193.49.79.89/esa prof/index.php