|
RÉPUBLIQUE DU CAMEROUN REPUBLIC OF
CAMEROON

UNIVERSITÉ DE DOUALA THE UNIVERSITY
OF DOUALA
°~-~°~-~°~-~°~-~°
°~-~°~-~°~-~°~-~°
Matricule : 05A2045
FACULTÉ DES SCIENCES FACULTY OF
SCIENCE
DÉPARTEMENT DE PHYSIQUE DEPARTMENT OF
PHYSICS
Etude des Phénomènes
Critiques
par les Méthodes de Monte
Carlo :
Cas du modèle d'Ising à 2D
pour
la transition de phase Ferro ? Para
Mémoire présenté en vue
de l'obtention du
DIPLÔME DE MAÎTRISE DE PHYSIQUE
OPTION : MATIÈRE
CONDENSÉE
par
TCHUENTE Rostand Choisy
Licencié ès Sciences
Physiques
Sous
et
LA DIRECTION DE : LA SUPERVISION DE :
Dr FOUEJIO David Dr NJEUGNA Ebenezer
CHARGÉ DE COURS MAÎTRE DE
CONFÉRENCES


Année académique
2005 ~ 2006
DEDICACES
A
toi papa ; Feu Roger Dupont TCHUENTE
vous ; mes futurs ...
qui représentez mon passé qui a attendu en vain,
mon espoir qui suivra je l'espère ces pas
REMERCIEMENTS
Alors qu'il m'est offert la possibilité de manifester
toute ma gratitude envers tous, qui ont participé à la
finalisation de ce travail, conscient de ne pouvoir être exhaustif, je
prierai les uns et les autres (ici cités ou non) de reconnaître en
ces petites paroles, la grandeur de la reconnaissance que je leurs accorde.
Au TOUT PUISSANT Seigneur de l'univers, qui sous ses ailles
m'a protégé et guidé à travers tous les
pièges de cette jungle, que ce travail puisse positivement inspirer ton
royaume.
Au staff administratif de l'Université de Douala, du
Département de Physique par le Dr OUSMANOU Motapon pour la constance des
efforts menés pour la bonne marche de notre formation.
Au Dr David FOUEJIO qui a proposé et accepté de
diriger ce travail. Malgré vos multiples charges, vous avez
présenté une disponibilité, un soutient multiforme, une
rigueur constante dans le travail, un esprit de collaboration qui ont fait
tâche d'huile. Recevez mes sincères remerciements.
A tous le corps enseignant du Département de Physique
de notre Faculté, mes enseignants et aînés ; les
Docteurs J. P. NGUENANG, E. WEMBE, C. NOUPA, S.G. NANA ENGO, G.E. NTAMACK,
et les Professeurs Oumarou BOUBA, KWATO NDJOCK, Norbert NOUTCHEGUEME, Pr.
Josué KOM MOGTO. C'est par vous que j'ai d'avantage pris goût
à la chose scientifique. Les modèles se trouvent t'ils à
l'infini ?
A ma famille ;
ma très chère maman Mme TCHUENTE Marthe Viviane
pour qui je n'aurai jamais assez de mots ...
mes grands frères Serge Jr., Christian Hervé,
Stephan Fleury, Henry Patrick TCHUENTE, André KAYO
ma petite soeur Sandrine Gaëlle TCHUENTE.
Votre soutien n'aura jamais d'égal et aucune tribune ne
sera suffisamment haute, aucun mot plus complet, pour vous dire MERCI au regard
de votre désir de me voir réussir.
A mes oncles et tantes, mon tuteur ;
M. KAYO Elie, Mme KOM MOGTO Elisabeth, M. & Mme GOUAMPE
Philippe, TCHATCHOUANG C, WONGTCHOUANG E, KOUONANG J.P. pour votre soutien des
plus remarquables.
M. & Mme KOM Samuel si seulement je savais m'exprimer,
j'aurai su vous dire MERCI...!
A mes cousins et cousines Perrault, Stéphane,
Dieudonné, Moselly, Favière, Marcelline, ... , Guy Alain
KAYO et Pélagie M. & Irène N. TCHUENTE, ...
A tous mes camarades et amis de promotion :
des baccalauréats E et F1, Hermine Jésus,
Lazare, Ghislain Martial, Honoré de Paul, Alban, J. Médard
de maîtrise de Physique, en particulier les
Maîtres Armand HYEUDIP, Nasser MBA T., Thierry NJASSAP, Roger T. MABOU,
C. FANKAM, ... nos échanges ont déterminés les tournures
de ce travail.
de Douala ; Hugues Joël, Christian, Justine
Valérie, Flore Josiane, Odilia, ...
de l'Université de Ngaoundéré ;
Valery Hervé, Ghislain Bérenger, Yves Mathurin, Jean Pierre,
Reine Grâce, Christelle, Linda, Edwige Patricia, Valérie, Emilie
Josyane. Vous avez été pour moi une 3ième
famille.
A tous qui ont été plus près de moi,
rêvés et crus en ce que je fais, encouragé et
supporté ;
Mon AMIE, ... Tave quaviero
A tous, nous avons combattus le bon combat, fraction de ce
qui reste à faire. Le meilleur est à venir
...
TABLE DES
MATIERES
SOMMAIRE
DEDICACE
.......................................................................................................
i
REMERCIEMENTS
...........................................................................................
ii
TABLES DES MATIERES
Sommaire
iii
Tables des Figures & Tableaux
v
Figures
v
Tableaux
vi
QUINTESSENCE
RESUME
vii
ABSTRACT
vii
INTRODUCTION GENERALE
.............................................................................
1
1ERE PARTIE: ETUDE THEORIQUE
Chapitre 1
Bases des simulations par les méthodes de
Monte Carlo pour les transitions de phase magnétiques
3
1.A. Introduction.
3
1.A.2. L'état d'équilibre
5
1.B. Les méthodes probabilistes de
Monte Carlo
6
1.B.1. Expressions théoriques des
grandeurs physiques
6
1.B.2. Fluctuation, Corrélations et
Réponse
7
1.B.3. Cas du modèle d'ISING.
10
1.B.4. Méthodes numériques
11
1.C. Principes de la simulation de Monte
Carlo à l'équilibre thermique
13
1.C.2. Echantillonnage important
14
1.C.2.1. Processus de Markov
14
1.C.2.2. Ergodicité
15
1.C.2.3. Balance spécifique
15
1.C.3. Rapport d'acceptation
17
Chapitre: 2
Etude des phénomènes critiques
À l'aide du modèle d'ISING à 2 D.
19
2.1. Les phénomènes
critiques
19
2.1.1. Les transitions de phase
19
2.1.2. L'exposant critique (sa mesure) et
les classes d'universalités
21
2.1.2.1. Notion d'universalité
22
2.1.2.2. Fluctuations critiques et
ralentissement critique
23
2.1.2.3. Fonction d'auto corrélation
de l'aimantation
24
2.1.2.4. Temps de corrélation et
exposant dynamique.
25
2.1.2.5. Mesure de l'exposant critique
25
2.2. Applications :
27
2.2.1. L'algorithme de construction de la
chaîne du processus de Markov.
27
2.2.2. Algorithme détaillé de
Métropolis.
27
2.2.2.1. Insuffisances de l'algorithme de
Métropolis. Le pas vers Wolff
28
2.2.3. L'algorithme de Wolff
29
2.2.3.1. Rapport d'acceptation pour les
algorithmes de cluster
29
2.2.3.2. Algorithme détaillé
de Wolff et avantages
31
2NDE PARTIE: ETUDE PRATIQUE
Chapitre 3
Les résultats des simulations
32
3.1. Introduction
32
3.2. Détermination de
l'équilibre thermique.
33
3.3. Détermination du temps de
corrélation.
38
3.4. Etude de la transition de phase.
39
3.4.1. Transition de phase Ferro?Para.
41
3.5. Résultats comparés des
algorithmes de Métropolis et de Wolff
45
3.6. Présentation du programme de
simulation : ISampling
48
CONCLUSION GENERALE
...............................................................................
49
REFERENCES BIBLIOGRAPHIQUES
...................................................................
I
ANNEXES
ANNEXE 1 :
II
Organigramme du processus de Markov.
II
ANNEXE 2 :
III
Organigramme de l'algorithme de
Métropolis.
III
ANNEXE 3 :
IV
Programme en C++ de l'algorithme de
Métropolis
IV
ANNEXE 4 :
V
Organigramme de l'algorithme de Wolff
V
ANNEXE 5 :
VI
Programme en C++ de l'algorithme de Wolff
VI
ANNEXE 6 :
VII
Algorithme de génération des nombres
aléatoires par congruence lineaire avec `shuffling'.
VII
ANNEXE 7 :
IX
Classification des transitions de phase
IX
!TABLES DES FIGURES &
TABLEAUX
Figures
Figure 2.1 :
schématisation des regroupements de spin en fonction de la
température
21
Figure 3.1 :
Aimantation du système de 100 x 100 spins du modèle d'Ising
à 2 D en fonction du temps (en MCS/Site) pour trois types de graine
simulé avec l'algorithme de Métropolis. Les nombres
aléatoires sont générés par congruence
linéaire simple et l'équilibre thermique est atteint au voisinage
de t = 600 MCS/Site à T = 2.4K
34
Figure 3.2 :
Aimantation du système de 100 x 100 spins du modèle d'Ising
à 2 D en fonction du temps (en MCS/Site simulé avec l'algorithme
de Métropolis. Les nombres aléatoires sont
générés par congruence linéaire simple ou suivie
d'un shuffling et l'équilibre thermique est atteint au voisinage de t =
800 MCS/Site à T = 2K
35
Figure 3.3 : Douze
états de 100 x 100 spins du modèle d'Ising à 2 D
amenés à l'équilibre thermique à T=2.4K au bout de
t = 400 MCS/Site avec l'algorithme de Métropolis. Les spins Up (+1) sont
représentés en noir et les spins Down (-1) sont en blanc.
36
Figure 3.4 :
Aimantation du système de 100 x 100 spins du modèle d'Ising
à 2 D en fonction du temps (en MCS/Site) simulé avec l'algorithme
de Métropolis. L'équilibre thermique est atteint au bout de t =
200 MCS/Sites à T = 2.2K. La simulation a débutée avec des
spins complètement aléatoires, puis « refroidie'
jusqu'à l'équilibre à T = 2.2K.
37
Figure 3.5 : Fonction
d'auto corrélation de l'aimantation pour le modèle d'Ising
à 2D sur un système de 100x100 spins à la
température T=2.2K par Métropolis. Le temps de corrélation
est de ô = 725 MCS/Site
38
Figure 3.6 : Temps de
corrélation pour 100x100 spins du modèle d'Ising à 2D en
fonction de la température simulé avec l'algorithme de
Métropolis.
39
Figure 3.7 :
Aimantation (carrés) et susceptibilité magnétique
(cercles) du système 5x5 spins du modèle d'Ising à 2D en
fonction de la température simulé avec l'algorithme de
Métropolis. Les points (carrés et cercles) sont les
résultats de la simulation et les traits, le calcul exacte à
l'aide de la fonction de partition.
40
Figure 3.8 :
Aimantation moyenne par spin du système 100x100 spins du modèle
d'Ising à 2D en fonction de la température, simulé avec
l'algorithme de Métropolis. Le tracé représente la
Transition Ferro ? Para. Le tracé représente la Transition Para?
Ferro
42
Figure 3.9 : Chaleur
spécifique moyenne à volume constant par spin du système
100x100 spins du modèle d'Ising à 2D en fonction de la
température, simulé avec l'algorithme de Métropolis. Le
tracé représente la Transition Ferro ? Para. Le tracé
représente la Transition Para? Ferro
43
Figure 3.10 :
Susceptibilité magnétique moyenne par spin du système
100x100 spins du modèle d'Ising à 2D en fonction de la
température, simulé avec l'algorithme de Métropolis. Le
tracé représente la Transition Ferro ? Para. Le tracé
représente la Transition Para? Ferro
44
Figure 3.11 :
Aimantation moyenne par spin du système de 100x100 spins du
modèle d'Ising à 2D en fonction de la température.
Carrés : algorithme de Métropolis ; Cercles :
algorithme de Wolff.
46
Figure 3.12 : :
Chaleur spécifique moyenne par spin du système de 100x100 spins
du modèle d'Ising à 2D en fonction de la température.
Carrés : algorithme de Métropolis ; Cercles :
algorithme de Wolff.
46
Figure 3.12 : :
Susceptibilité magnétique moyenne par spin du système de
100x100 spins du modèle d'Ising à 2D en fonction de la
température. Carrés : algorithme de Métropolis ;
Cercles : algorithme de Wolff.
47
Figure 3.14 :
Fenêtres de paramétrage de simulation (gauche) et d'options
graphiques (droite)
49
Figure 3.15 :
Fenêtre du choix de visualisation d'une grandeur
49
Figure 3.16 :
Fenêtre principale du programme ISampling
49
Figure A1 :
Organigramme du processus de Markov
II
Figure A2 :
Organigramme du processus de Métropolis
III
Figure A4 :
Organigramme du processus de Wolff
V
Tableaux
Tableau 2.1 :
Expressions de quelques grandeurs physiques en fonction de leurs exposants
critiques
22
Tableau 2.2 : Classe
d'universalité et modèles associés
23
Tableau 2.3 : Valeurs
des exposants critiques pour d = 2
26
Tableau A7 :
Classification des transitions
III
QUINTESCENCE.
RESUME
L'objectif initial de notre travail était la
comparaison de deux algorithmes de simulation des phénomènes
critiques par les méthodes de Monte Carlo, - l'algorithme de
Métropolis et l'algorithme de Wolff -. Nous devions par ailleurs
étudier les phénomènes critiques qui s'établissent
à la transition de phase. A cet effet, nous avons
déterminé, les courbes d'évolution des paramètres
du système (énergie, aimantation, susceptibilité, chaleur
spécifique) et celles des propriétés des différents
algorithmes étudiés (temps et longueur de corrélation)
toutes en fonction de la température et / ou de la taille du
système. Pour ce faire, nous avons étudié et simulé
un modèle d'Ising à 2 dimensions. Nous avons
indifféremment travaillé sur les transitions Ferro vers Para ou
Para vers Ferro (Ferro ? Para).
ABSTRACT
The aims of our work was the comparison of two algorithms of
critical phenomena simulation by methods of Monte Carlo, - the algorithm of
Métropolis and the algorithm of Wolff -. We had to study the critical
phenomena that settle to the phase transition of otherwise. Therefore, we have
determine curves of evolution of parameters of the system (energy,
magnetization, susceptibility, specific heat) and those of different studied
algorithm properties (correlation time and length) all according to the
temperature and / or of the size of the system. Thus we have studied and
simulated the two dimensional Ising model. We have worked indifferently on
transitions Ferro towards Para or Para towards Ferro (Ferro ? Para).
... de la même façon, on peut
apprécier les progrès scientifiques et y prendre plaisir,
même si l'on n'a personnellement aucune disposition pour la
créativité scientifique.
Mais demandera - t - on, à quoi
servirait-il ?
La 1ère réponse est que personne
ne peut se sentir chez soit dans le monde moderne, juger la nature de ses
problèmes et les solutions possibles, à moins d'avoir une
idée intelligente de ce que nous réserve la science. De plus
l'initiative au monde magnifique de la science apporte une intense satisfaction
esthétique, inspire la jeunesse, comble le désir de savoir et
permet d'apprécier plus profondément les merveilles
déjà réalisées par l'esprit humain, et celles dont
il est capable.
C'est pour permettre une telle initiative que j'ai
entrepris d'écrire ...
Isaac ASIMOV, L'univers de la science, InterEdition, 1986,
page 15
INTRODUCTION GENERALE
A la base de toute observation des objets de la nature, l'on
aperçoit l'aspect du système (ou objet) observé. Sous
l'influence de l'environnement dans lequel il beigne, cet aspect peut prendre
diverses configurations ou états ; on parle aussi de phase. Ce
à quoi nous nous intéressons dans notre présent travail,
c'est la description du système à l'instant précis
où il change de phase. Il s'agit d'un instant critique où se
produisent des phénomènes dits critiques, c'est à dire de
transition de phase.
Notre travail trouve ses applications sur les ordinateurs qui
permettent de simuler les systèmes physiques pour la résolution
des problèmes en physique statistique. Nous utiliserons à cet
effet comme méthodes numériques, celles de Monte Carlo qui
s'appuient sur un jeu d'échantillon d'une représentation d'un
système physique pris dans un état donné. Elles visent
ainsi à la détermination de manière efficace et rapide
des grandeurs physiques liées au système considéré,
par des procédés probabilistes.
En considérant la configuration granulaire (spin,
atome, molécule, ...) de la matière (système physique) et
sachant que ces éléments composites interagissent mutuellement,
les phénomènes critiques s'étudient avec les
théories de la physique statistique et plus particulièrement de
la mécanique statistique.
Ainsi donc, cumulés aux résultats
théoriques de la mécanique statistique, les simulations par les
méthodes numériques nous apportent des outils
complémentaires pour mieux comprendre les systèmes. Elles sont
essentielles pour des systèmes complexes, à l'approche de
l'instant critique où s'établi la transition. C'est ce qui fit
développer ces méthodes et plus particulièrement celle de
Monte Carlo, très utilisée et adaptée à cet effet.
La technique de Monte Carlo à été assez
développée à la suite de plusieurs travaux, introduisant
ainsi divers algorithmes de simulation, tous intéressants et
présentant des spécificités particulières
liées au système qu'ils étudient. La
1ère simulation de Monte Carlo remonte en 1953 suite aux
travaux de Métropolis & al. [1]. Bien d'autres suivirent, apportant
successivement des corrections remarquables, c'est le cas de [2] l'algorithme
de Wolff (proposé par Ulli Wolff en 1989) à l'encontre du
précédent qui traite sur les spins, celui-ci manipule des blocs
de spins ; l'algorithme de Swendsen - Wang (proposé par ces 2
chercheurs en 1987 et calqué sur le modèle de Wolff) ;
l'algorithme de Niedermayer (adapté à toutes sortes de
modèles, proposé individuellement par Ferenc Niedermayer en
1988), et bien d'autres ...
Le but principal de notre travail est celui de
présenter l'algorithme de Métropolis afin de dégager ses
défaillances et les corrections apportées par Wolff. Pour y
parvenir, nous introduirons :
Dans un premier temps, une partie dite
d' « étude théorique », tout d'abord par
une présentation à travers la mécanique statistique, des
expressions théoriques des grandeurs physiques qui nous
intéressent ; puis nous aborderons les méthodes
probabilistes de Monte Carlo où il s'agira pour nous de présenter
les différents éléments qui permettent d'établir
des résultats numériques proches de ceux déterminés
par les probabilités de Boltzmann. Ce qui nous permettra d'aborder en
fin, l'étude des phénomènes critiques appliqués au
modèle d'Ising à deux dimensions pour la transition de phase
Ferro ? Para, où nous comparerons l'algorithme de Métropolis
à celui de Wolff à travers leurs différentes
propriétés.
Dans un second temps, une partie dite
d' « étude pratique » nous permettra de
visualiser ces grandeurs par les simulations faites sur différents
systèmes, afin de vérifier les conclusions apportées par
la partie précédente.
1ère Partie : Etude théorique
Chapitre 1
Bases des simulations par les méthodes de Monte
Carlo pour les transitions de phase magnétiques
1.A.
Introduction.
Il nous paraît utile de présenter d'entrée
de jeu de cette partie, une vue sur la mécanique statistique qui nous
permet notamment de retrouver les expressions réelles des grandeurs
physiques - que nous déterminerons avant de retrouver l'état
optimal auquel tout système physique à tendance à
basculer (l'état d'équilibre)-, pour mieux étudier
les phénomènes critiques.
1.A.1. La mécanique statistique
La difficulté cruciale rencontrée dans les
systèmes que nous étudions est qu'ils sont composés de
plusieurs blocs (atomes ou molécules) généralement
identiques, pouvant avoir en très petit nombre des différences
mais obéissants tous néanmoins à de simples
équations du mouvement. De ce fait, tout le système peut
être mathématiquement modélisé de différentes
façons. Cependant, le nombre d'équations (obtenu par
l'étendu du problème) rend impossible la résolution
mathématique exacte. Par ailleurs, les conditions macroscopiques
observables dans lequel est plongé le système nous permettent de
prédire et simplifier d'avantage certaines de ces équations. La
mécanique statistique essaye donc de trouver les solutions de ces
équations par des procédés et propriétés
probabilistes définis sur plusieurs états.
Le vrai paradigme que nous étudierons ici, est que le
système est gouverné par un Hamiltonien H qui donne
l'énergie totale du système dans n'importe quel état
particulier. Ces énergies pouvant êtres discrètes ou
continues. L'état d'énergie stationnaire étant celui pour
lequel l'énergie reste constante au cours du temps, on observe des
échanges entre les différents états
dégénérés. Un autre obstacle que nous rencontrons
est celui de l'influence du réservoir thermique. C'est un très
grand système qui peut être pris comme une source (de
température par exemple), échangeant constamment de
l'énergie avec notre système dans la mesure où nous
impulserons toujours de la température au système comme
définie en thermodynamique. Nous pouvons incorporer l'effet de notre
réservoir dans nos calculs en donnant au système la dynamique de
la règle par laquelle il change périodiquement d'état. La
nature exacte de cette dynamique est dictée par la forme de la
perturbation de l'Hamiltonien que le réservoir produit dans le
système. A cet effet, considérons le cas suivant:
Soit 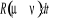 la probabilité au système de passer d'un état
ì à autre état õ. la probabilité au système de passer d'un état
ì à autre état õ. 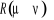 est le taux de transition et doit être normalement
indépendant du temps. En supposant cette hypothèse
réalisée l'on peut définir est le taux de transition et doit être normalement
indépendant du temps. En supposant cette hypothèse
réalisée l'on peut définir 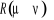 pour tout état possible õ que le système peut
avoir. Ces transitions de phases sont généralement tout ce que
nous pouvons avoir sur la dynamique. D'où, connaissant un état u
du système, nous n'avons besoin que d'un court instant
« dt » pour que le système évolue vers
n'importe quel autre état í. Nous appliquons ce raisonnement
lorsque le traitement probabiliste entre en jeu. Définissons pour tout état possible õ que le système peut
avoir. Ces transitions de phases sont généralement tout ce que
nous pouvons avoir sur la dynamique. D'où, connaissant un état u
du système, nous n'avons besoin que d'un court instant
« dt » pour que le système évolue vers
n'importe quel autre état í. Nous appliquons ce raisonnement
lorsque le traitement probabiliste entre en jeu. Définissons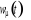 1(*), la
probabilité du système d'être à l'état u
à l'instant t. La mécanique statistique propose que ces poids
nous informe entièrement sur l'état du système. Nous
pourrons donc écrire la grande équation de l'évolution de 1(*), la
probabilité du système d'être à l'état u
à l'instant t. La mécanique statistique propose que ces poids
nous informe entièrement sur l'état du système. Nous
pourrons donc écrire la grande équation de l'évolution de
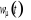 avec les termes de avec les termes de 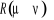 tel que : tel que :
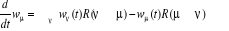 (1.1) (1.1)
Le premier terme de droite représente le taux de
probabilité du système d'être à
l'état u, tandis que le second est le taux de probabilité du
système d'être juste au dessus de cet état mais avant le
suivant. Toutefois, nous devons avoir la condition
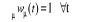 (1.2) (1.2)
Tant que le système sera dans cet intervalle
d'état. La solution de l'équation (1.1) nous donne la variation
temporelle du taux 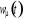 qui peut nous permettre de retrouver les propriétés
macroscopiques de notre système. Mais comment donc? qui peut nous permettre de retrouver les propriétés
macroscopiques de notre système. Mais comment donc?
Si nous désirons par exemple déterminer la
quantité Q qui prend à l'état u la valeur Qu,
nous définirons la valeur moyenne de Q à l'instant t pour tout le
système par
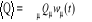 (1.3) (1.3)
Il est claire que cette quantité contient d'importantes
informations que nous sommes sensé avoir expérimentalement. Par
ailleurs la valeur précise Q de son observable 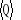 n'est peut-être pas assez claire. n'est peut-être pas assez claire.
En effet, imaginons que nous avons un grand nombre de
complexions (copies) de notre système qui interagissent chacun avec son
réservoir thermique passant d'un état à un autre durant
toute la durée de l'observation. L'on croirait que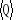 sera dès lors à sa meilleure estimation si nous faisions
une moyenne pondérale des valeurs de Q obtenues séparément
pour chaque système. Pourtant, il en existe bien plus que ce que l'on
considère! En réalité nous n'avons sur la main
expérimentalement qu'un seul système sur lequel nous
opérons toutes nos mesures de Q, d'où il ne s'agit pas d'une
simple mesure instantanée, mais d'une intégration de la mesure
sur une période de temps T. C'est ainsi que l'on détermine
l'espérance sur une moyenne de temps, de la quantité Q. sera dès lors à sa meilleure estimation si nous faisions
une moyenne pondérale des valeurs de Q obtenues séparément
pour chaque système. Pourtant, il en existe bien plus que ce que l'on
considère! En réalité nous n'avons sur la main
expérimentalement qu'un seul système sur lequel nous
opérons toutes nos mesures de Q, d'où il ne s'agit pas d'une
simple mesure instantanée, mais d'une intégration de la mesure
sur une période de temps T. C'est ainsi que l'on détermine
l'espérance sur une moyenne de temps, de la quantité Q.
Le calcul de l'espérance est un des buts principaux de
la mécanique statistique, et des simulations par Monte Carlo en Physique
statistique. Cependant, pour y arriver le système doit être
préparé à nous fournir des valeurs assez
représentatives de sa configuration. [3] Boltzmann nous renseigne que
c'est à un état dit d'équilibre que nous pouvons avoir ces
grandeurs là.
1.A.2.
L'état d'équilibre
Reconsidérons la grande équation (1.1); si
jamais notre système atteint l'état où les 2 termes de
gauche deviennent équivalents au point de s'annuler ou de donner un
autre terme constant, alors la variation du taux 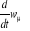 sera nulle et le poids statistique sera constant pour tout le reste du
temps : c'est l'état d'équilibre. C'est à ces
instants que l'on observe les interactions entres les éléments du
système. Tout système gouverné par l'équation (1.1)
atteint forcement l'équilibre. Il s'agira donc pour nous de simuler ces
systèmes par la technique de Monte Carlo. Le taux de transition sera nulle et le poids statistique sera constant pour tout le reste du
temps : c'est l'état d'équilibre. C'est à ces
instants que l'on observe les interactions entres les éléments du
système. Tout système gouverné par l'équation (1.1)
atteint forcement l'équilibre. Il s'agira donc pour nous de simuler ces
systèmes par la technique de Monte Carlo. Le taux de transition 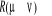 apparaissant dans (1.1) ne doit juste prendre que quelques valeurs. Le
point important est que nous connaissons à priori les valeurs de apparaissant dans (1.1) ne doit juste prendre que quelques valeurs. Le
point important est que nous connaissons à priori les valeurs de 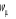 à l'équilibre. Elle nous permet d'avoir ce que l'on
appellera « probabilité d'occupation à
l'équilibre », notée à l'équilibre. Elle nous permet d'avoir ce que l'on
appellera « probabilité d'occupation à
l'équilibre », notée
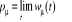 (1.4) (1.4)
Gibbs (1902) [3] montra que pour un système à
l'équilibre thermique tel un réservoir à la
température T, on a 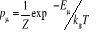 (1.5) (1.5)
Où Eu est l'énergie à
l'état u et Z la fonction de partition telle que
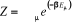 (1.6) (1.6)
Avec l'énergie d'agitation thermique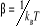 (1.6') (1.6')
A présent que l'équilibre thermique est atteint
dans les conditions sus-citées, nous pouvons déterminer les
expressions des différentes grandeurs recherchées afin de pouvoir
les simuler pour obtenir les configurations du système.
1.B.
Les méthodes probabilistes de Monte Carlo
1.B.1.
Expressions théoriques des grandeurs physiques
Nous avons pu établir précédemment les
conditions de l'état d'équilibre, en considérant cet
état atteint, nous déterminerons à présent les
grandeurs physiques caractéristiques du système.
Nous remarquons que la fonction de partition Z apparaît
dans beaucoup de développement mathématique en mécanique
statistique; la connaissance de Z nous permet d'évaluer virtuellement
tout ce que nous voulons savoir sur l'environnement macroscopique du
système [3]. Nous prendrons ainsi l'expression (1.6) comme
point de départ pour nos prochains développements.
Par généralisation, partant des équations
(1.3), (1.4), (1.5), l'espérance
mathématique d'une quantité Q pour notre système Physique
sera
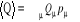 (1.7). (1.7).
Qu'il en soit pour l'énergie (Q = E) on aura
l'espérance
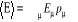 = U (1.8) = U (1.8)
De l'équation (1.6), nous aurions pu
écrire
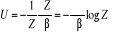 (1.9) (1.9)
La chaleur spécifique (massique) aura pour
expression :
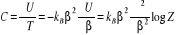 (1.10) (1.10)
Introduisant l'entropie S l'on obtient
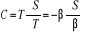 (1.11) (1.11)
En égalant (1.10) & (1.11) et en tenant compte des
conditions d'intégration, de la 3eme loi de la
thermodynamique fixant arbitrairement l'origine de l'entropie, on trouve
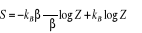 (1.12). (1.12).
Par ailleurs, des expressions (1.9,), (1.12)
Helmholtz [3] tire l'énergie libre 2(*)
F = U - TS = kBT logZ
(1.13)
Nous avons ainsi pu définir les grandeurs
thermodynamiques U, F, C, S à partir de Z. D'autres grandeurs dites
conjuguées ont des variables conjuguées qui sont les
réponses du système à ces sollicitations ou en d'autres
termes aux perturbations correspondantes. Par exemple, la réponse
à un système de gaz dans une boite par le changement de volume V
est la pression P. la pression `P' est donc la variable conjuguée de
`V' ; de même l'aimantation M est la réponse à la
variation du champ magnétique B. M et B sont variables
conjuguées.
F étant une différentielle totale par
l'équation (1.13) c'est-à-dire [3] :
dF = dU - TdS - SdT = - PdV - SdT (négligeant le
monôme lié au nombre N de particule du système) et sachant
que dU = TdS - PdV et 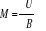 , l'on aura , l'on aura
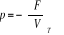 (1.14) (1.14)
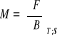 (1.15) (1.15)
Donc si nous pouvons avoir l'énergie libre F, nous
obtiendrons l'effet des autres paramètres variants. Tout ceci nous
ramène toujours à la fonction de partition Z. Cette fonction est
très utilisée dans les calculs évolués par la
méthode de Monte Carlo pour les propriétés du
système à l'équilibre.
1.B.2. Fluctuation3(*), Corrélations4(*) et Réponse
La mécanique statistique peut nous informer sur
d'autres propriétés du système telles l'entropie et la
pression. Une des plus importantes classes de ces propriétés est
la fluctuation des quantités observables. Il a été
décrit plus haut comment le calcul des espérances tient compte de
la moyenne temporelle sur plusieurs mesures de la même
propriété pour un système simple. En plus, pour calculer
la vraie valeur de ces différentes mesures, il serait
préférable de calculer leurs variations spécifiques qui
nous donne la mesure de la variation de la quantité que nous observons
sur le temps et nous donne aussi quantitativement (avec approximation) le
nombre d'essais effectués pour avoir la bonne valeur (valeur propre) de
l'espérance (observable).
Par exemple, considérons l'énergie interne U, la
moyenne du carré de la déviation individuelle instantanée
de la mesure de l'énergie est
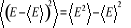 (1.16) (1.16)
Des formules (1.7), (1.8) et (1.9), nous
obtenons aisément 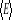 et / ou par dérivation de la fonction de partition Z on a
aussi et / ou par dérivation de la fonction de partition Z on a
aussi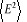 , ce qui nous donne , ce qui nous donne
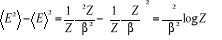 (1.17) (1.17)
Utilisant (1.10) pour éliminer la 2nde
dérivation on écrira alors
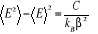 (1.19) (1.19)
D'où, l'écart type5(*) de E sera 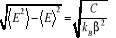 . (1.20) . (1.20)
Ce résultat nous est intéressant pour plusieurs
raisons :
Primo, il nous donne la magnitude (l'étalement) de la
fluctuation en terme de chaleur spécifique `C'6(*). Nous pouvons ainsi trouver
toutes les fluctuations des quantités que nous avons en thermodynamique
classique en sachant que nous devons absolument tenir compte de l'approche
microscopique que la thermodynamique n'a pas accès !
Segundo, hors de la limite de spectre d'énergie, les
fluctuations sont élevées.
Ceci nous prête à croire à nos premiers
arguments, que le traitement statistique peut nous offrir une véritable
estimation exacte de l'environnement de notre système tel que nous
l'espérions. La plus part des questions (le comportement) qui nous
intéresse en matière condensée se trouvent autour de la
limite thermodynamique, où l'on ignore la fluctuation pour de large
systèmes. Ainsi les algorithmes informatiques s'exercent à
simuler le comportement à cette limite pour d'aussi larges
systèmes que possible en un temps appréciable.
Qu'en est il donc à présent de la fluctuation
pour d'autres variables thermodynamiques? D'après les
équations (1.5) à (1.7) ainsi que la
définition de variable conjuguée vu plus haut, nous pouvons
réécrire de manière générale, pour une
grandeur quelconque X
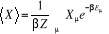 = = 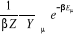 (1.21) (1.21)
Où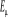 contiennent les termes en contiennent les termes en 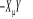 contenus dans l'Hamiltonien du système. La technique
utilisée pour le calcul de la température moyenne d'une
quantité est de réécrire contenus dans l'Hamiltonien du système. La technique
utilisée pour le calcul de la température moyenne d'une
quantité est de réécrire
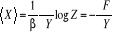 (1.22) (1.22)
Il est évident qu'aucun champ de couplage de cette
quantité ne se trouve dans l'Hamiltonien. Dans le cas contraire, nous
utiliserons un champ fictif que nous introduirons dans l'Hamiltonien pour y
assurer le couplage, utiliser (1.22) et le réduire enfin en un
champ nul après dérivation. Méthode communément
utilisée en mécanique statistique. Une autre
dérivée de logZ qui respecte Y produit un autre facteur de 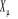 dans la somme sur tous les états u. Nous chercherons alors dans la somme sur tous les états u. Nous chercherons alors
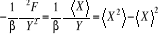 (1.23) (1.23)
Où nous reconnaissons les résultats tels
trouvés plus haut à l'équation (1.17). Nous
pouvons ainsi avoir la variance de n'importe quelle quantité X à
partir de la dérivée seconde de l'énergie interne F sur sa
variable conjuguée respective. On défini la
susceptibilité de X sur Y par le rapport
mesurant la force de X par le changement en Y contenu dans l'équation
précédente et usuellement notée ÷ : 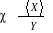 (1.24) (1.24)
D'où la valeur moyenne d'une variable X et sa variable
conjuguée Y sont proportionnelles. Ce résultat est connu depuis
le théorème de la réponse linéaire7(*), qui nous donne un moyen de
calculer (1.24) par la méthode de Monte Carlo en mesurant la taille
d'une fluctuation sur une variable.
En étendant l'idée de la susceptibilité
et par là le changement d'état de la thermodynamique classique,
nous pourrons apprécier ce qui arrive lorsque nous changeons
d'état (position sur l'espace de configuration) d'un paramètre.
Pour aborder ce type de problème, nous utiliserons un modèle
planétaire représenté par une matrice. C'est un
modèle plus réaliste où i,j représentent
coordonnées abscisses et ordonnées d'un point k. Une variable
Xk aura un champ conjugué Yk que nous retrouvons
dans l'Hamiltonien par les termes 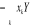 avec avec 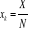 pour tous les N sites k. On réécrira donc (1.21)
et (1.22) pour tous les N sites k. On réécrira donc (1.21)
et (1.22)
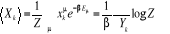 (1.25) (1.25)
Où 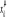 est la valeur de est la valeur de 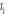 en un état u nous donnant donc une généralisation
de ÷ par en un état u nous donnant donc une généralisation
de ÷ par
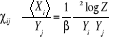 (1.26) (1.26)
En introduisant le résultat de (1.6) on
obtient
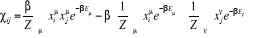 = =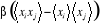
Plus simplement 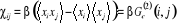 (1.27) (1.27)
Où 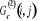 est la fonction de corrélation8(*) de x pour 2 points i et j connectés, que
nous présenterons plus tard. L'exposant (2) représente l'ordre de
la corrélation (ou le nombre de points). est la fonction de corrélation8(*) de x pour 2 points i et j connectés, que
nous présenterons plus tard. L'exposant (2) représente l'ordre de
la corrélation (ou le nombre de points).
1.B.3. Cas du modèle
d'ISING.
Pour essayer de rendre toutes ces relations un peu plus
concrètes, nous introduisons à présent un concept
nouveau : le modèle d'ISING. Certainement l'un des plus
recherché ou étudié en physique statistique. C'est un
modèle d'aimant. Les principes essentiels rodant autour de l'aimantation
et des models magnétiques sont que l'aimantation d'un matériau se
compose de moments magnétiques de plusieurs dipôles
magnétiques conjugués de spin. Le modèle postule qu'une
matrice (de dimension définie en fonction de la géométrie
du problème) peut représenter tous les états possibles de
spin d'un système. L'évaluation des propriétés se
fait donc en manipulant directement la matrice à travers les
différents états du système définis par les
coefficients de la matrice. Par soucis de simplification, ces coefficients
(valeurs des spins) prennent les valeurs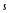 9(*). Dans le
modèle magnétique réel, les spins interagissent entre eux
(entre voisins), l'on tient donc compte de cette autre contrainte en
introduisant dans l'Hamiltonien les énergies d'interaction notées
J (pour les 1ers voisins) et J1 (pour les 2nds
voisins) facteurs des termes d'interactions. On aura [11] 9(*). Dans le
modèle magnétique réel, les spins interagissent entre eux
(entre voisins), l'on tient donc compte de cette autre contrainte en
introduisant dans l'Hamiltonien les énergies d'interaction notées
J (pour les 1ers voisins) et J1 (pour les 2nds
voisins) facteurs des termes d'interactions. On aura [11]
(au 1er ordre) 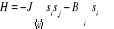 (1.28) (1.28)
(au 2nd ordre) 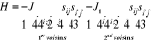 (1.28') (1.28')
Où i et j sont les coordonnées du spin de la
matrice ; dans la mesure où l'énergie d'interaction
dipolaire varie en 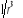 on aura on aura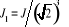 . En plus, le signe (-) en J est conventionnel et indique le sens de
l'interaction sur les paramètres J, lorsque J>0, tous les spins sont
Up et nous avons le modèle ferromagnétique. Dans le cas
contraire, nous obtenons un modèle dit
anti-ferromagnétique. . En plus, le signe (-) en J est conventionnel et indique le sens de
l'interaction sur les paramètres J, lorsque J>0, tous les spins sont
Up et nous avons le modèle ferromagnétique. Dans le cas
contraire, nous obtenons un modèle dit
anti-ferromagnétique.
Autant que chaque site (coefficient) peut prendre deux
valeurs, notre matrice de dimension N (nombre de spin) peut décrire donc
2N états possibles. Ce qui nous permettra de redéfinir
la fonction de partition décrite plus haut à
l'équation (1.16) par :
(au 1er ordre) 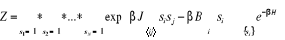 (1.29) (1.29)
(au 2nd ordre) 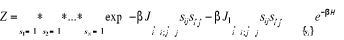 (1.29') (1.29')
Comme dit précédemment, nous pourrions ainsi
avoir avec Z toutes les propriétés thermodynamiques du
système et même leurs variables conjuguées. Comme
définies plus haut ;
La susceptibilité magnétique par spin
d'après (1.23) est :
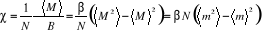 (1.30) (1.30)
La chaleur spécifique par spin se
référant à (1.19) sera :
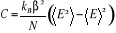 (1.31). (1.31).
De l'expression de l'Hamiltonien donnée en
(1.28), si nous considérons à présent une
variation partielle du champ J1 = B, l'on fera donc intervenir
Bi dans la sommation. La moyenne de l'aimantation sera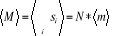 . Où . Où 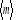 (simplement notée m) représente la moyenne par spin, elle
est plus généralement utilisée: (simplement notée m) représente la moyenne par spin, elle
est plus généralement utilisée:
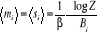 (1.32) (1.32)
La fonction de corrélation connectée sera
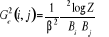 (1.33). (1.33).
Toutes ces grandeurs sont encore plus intéressantes par
visualisation à l'équilibre thermique lorsque nous l'atteignons,
par les méthodes numériques.
1.B.4. Méthodes
numériques
Les méthodes numériques nous permettent
d'obtenir avec plus de justesse et de rapidité, les comportements des
propriétés physiques précédemment définies.
Nous avons la fonction Z qui est (nous l'avons montré) un
élément pivot. Le problème actuel sera d'améliorer
la somme de celle-ci sur un grand nombre d'états. Plus encore, il faudra
considérer qu'à la limite thermodynamique, le nombre
d'états doit être considéré infini. Ce travail
à été réalisé sur un modèle plus
simple d'énergie discret, le modèle d'ISING à deux
dimensions [2]. Par ailleurs, la majorité des modèles
s'intéressent, autant qu'il n'est pas encore possible, d'obtenir
l'expression analytique exacte de Z.
La méthode la plus simple pour résoudre les
problèmes en physique statistique est de convertir notre système
en représentation matricielle (de dimension fonction de la
géométrie du problème considéré) et de
l'appliquer dès lors au modèle choisi. De ce fait, la fonction de
partition Z deviendra une somme de nombre finie de terme (pour un espace
discret) ou une intégrale sur l'espace considéré pour un
spectre continu d'énergie), nous pourrions dès lors utiliser un
ordinateur pour évaluer ces expressions. Regardons à
présent ce qui se passe pour le modèle d'ISING.
Considérons un cas à deux dimensions, un
système de 25 spins modélisables en une matrice carrée 5 x
5. En champ nul (B = 0), limitons les effets de bord en utilisant les
conditions aux limites cycliques de BVK10(*) (Born Von Karmer). Chaque spin pouvant prendre 2
valeurs (suivant qu'il soit Up ou Down), l'on aura alors 225 =
33554432 valeurs possibles (états possibles du système) !
Cependant, la matrice n'est jamais assez grande pour inclure toute la physique
importante. Ceci ne veut pourtant pas dire qu'un développement matriciel
est moins utile. Il existe des méthodes rendant le problème est
moins difficile où le calcul numérique et les solutions exactes
sont très appréciables. La technique des tailles d'échelle
d'intervalle fini (pas de divergence), nous entraîne à extrapoler
les résultats par des matrices de dimension finie aux systèmes de
taille finie ou infinie et donne de bons résultats aux limites
thermodynamiques [7].
Néanmoins, toutes ces techniques peuvent nous donner de
bons résultats pour les propriétés critiques. La
précision et l expression desdits résultats dépendent
de la taille du système. Dès lors, il est judicieux pour nous de
travailler avec d'aussi grand système que possible. Ce qui prendra
nécessairement du temps car il faudra tenir non seulement compte de la
géométrie du système mais aussi des
caractéristiques techniques du calculateur utilisé. La partie sur
les résultats obtenus nous en dira plus.
1.C. Principes de la simulation de
Monte Carlo à l'équilibre thermique
Il est à présent question pour nous de
présenter les éléments de base de la simulations par Monte
Carlo, à travers les trois idées maîtresses :
« l'échantillonnage important», « la balance
détaillé » et le « rapport
d'acceptation ». Maîtriser le sens de ces termes nous offrira
d'avantage informations sur la simulation de Monte Carlo à
l'équilibre thermique développée ces trente
dernières années.
1.C.1. L'estimateur
Nous avons dit plus haut que la recherche des valeurs
moyennes représente les principaux objectifs des simulations Monte
Carlo, mais pour accélérer le processus il serait plus facile
d'orienter nos résultats vers des valeurs probables.
Nous avons obtenu de (1.3), l'expression de la
moyenne de Q, par sommation sur tous les états ì du
système et sur leurs probabilités respectives
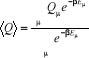 (1.31) (1.31)
Pour de grands systèmes, le mieux que nous pouvons
avoir est la moyenne sur une somme restreinte d'états. Il est donc
nécessaire d'introduire une quantité dans le calcul. La technique
de Monte Carlo s'exerce à choisir ce champ restreint d'état avec
une probabilité de distribution öì. En supposant
que nous choisissons M états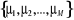 , l'on aura une meilleure estimation de Q par , l'on aura une meilleure estimation de Q par
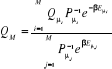 (1.32) (1.32)
Cette expression est l'estimateur de
Q, nous donnant une estimation de Q sur un model réduit et
avec la propriété que lorsque le nombre M d'états dans
l'échantillon grandit, l'on se rapproche de la vraie valeur 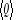 par Q. C'est-à-dire : par Q. C'est-à-dire :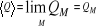
Reste alors à déterminer M pour une meilleure
expression de Q. Pour ce faire, il suffit de considérer une
équiprobabilité entre les états du système (c'est
à dire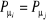 ), d'où : ), d'où :
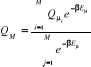 (1.33) (1.33)
1.C.2. Echantillonnage
important
Tel qu'il a été abordé dans un
précédent paragraphe, il est utile d'observer un temps moyen afin
de se rassurer que nous parcourrons au moins une période, durant le
temps de l'expérience, d'où il se pose le problème de la
longueur de la chaîne. A titre d'exemple, un litre de gaz, contient
1022 molécules, soient 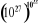 états possibles qui est un nombre spectaculairement grand
d'où l'importance de prendre une matrice de dimension assez grande sinon
l'on risquera de ne pas parcourir tous les états. On parle dans ce cas
d'échantillonnage important. états possibles qui est un nombre spectaculairement grand
d'où l'importance de prendre une matrice de dimension assez grande sinon
l'on risquera de ne pas parcourir tous les états. On parle dans ce cas
d'échantillonnage important.
1.C.2.1. Processus11(*) de Markov
Dans une simulation par Monte Carlo l'étape difficile
est la détermination de l'estimateur approprié. Au départ,
nous ne pouvons pas simplement choisir au hasard certains états et les
accepter ou rejeter en les prenant équiprobables à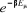 . Le résultat ne sera pas meilleur que celui issu d'un
échantillonnage hasardeux. L'on court le risque de
répéter virtuellement certains états autant que leurs
probabilités sont exponentiellement petites. Les algorithmes des
méthodes de Monte Carlo utilisent le processus de Markov pour choisir
les états utilisés (considérées). . Le résultat ne sera pas meilleur que celui issu d'un
échantillonnage hasardeux. L'on court le risque de
répéter virtuellement certains états autant que leurs
probabilités sont exponentiellement petites. Les algorithmes des
méthodes de Monte Carlo utilisent le processus de Markov pour choisir
les états utilisés (considérées).
Le processus de Markov est le mécanisme qui
génère un état í du système à partir
d'un autre 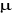 connu. L'état généré n'est pas toujours le
même, il parcourt le système à la recherche de nouveaux
états avec une probabilité de transition P connu. L'état généré n'est pas toujours le
même, il parcourt le système à la recherche de nouveaux
états avec une probabilité de transition P sur lesquels il impose deux conditions: sur lesquels il impose deux conditions:
i) elles ne varient pas avec le temps.
2i) elles dépendent uniquement des
propriétés du système sur les états u et
í.
Ceci traduit le fait que la probabilité de transition
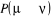 d'un état u à un autre í du processus de Markov
est toujours constante et devra satisfaire la relation de fermeture d'un état u à un autre í du processus de Markov
est toujours constante et devra satisfaire la relation de fermeture
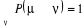 (1.34) (1.34)
Dans la simulation de Monte Carlo, nous utiliserons à
répétition le processus de Markov pour générer la
chaîne de Markov de nouveaux états. Il est
généralement utilisé spécialement lorsqu'on veut
partir de n'importe quel état du système et générer
une suite de configurations de certains états précis (final) par
exemple.
Pour parachever cette étude, il est utile d'imposer
deux nouvelles conditions : « Ergodicité » et
« balance détaillée ou spécifique »
sur le processus de Markov.
1.C.2.2. Ergodicité
La condition d'Ergodicité est le fait qu'il sera
possible par notre processus de Markov d'atteindre n'importe quel état
du système à partir d'un autre si nous évoluons durant un
temps suffisamment grand. Ceci est nécessaire pour atteindre notre
initial, celui de généraliser des états à partir
d'une probabilité correcte dite de Boltzmann. Chaque état 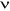 apparaît avec une certaine probabilité non nulle
Pí dans la distribution de Boltzmann. Et si cet état
ne peut-être accessible à partir d'un autre état u ce ne
sera pas un problème, nous continuerons notre processus et dans ce cas
l'on reprendra le schéma à partir de ce nouvel état. apparaît avec une certaine probabilité non nulle
Pí dans la distribution de Boltzmann. Et si cet état
ne peut-être accessible à partir d'un autre état u ce ne
sera pas un problème, nous continuerons notre processus et dans ce cas
l'on reprendra le schéma à partir de ce nouvel état.
La condition d'Ergodicité nous informe que nous pouvons
prendre certaines probabilités de transition nulle dans le processus de
Markov mais ceci ne sera pas le cas pour deux états distincts que nous
prenons dans un espace restreint. En pratique, la plupart des algorithmes de
Monte Carlo configurent toutes les probabilité de transition à
zéro, et il faudra faire attention dans ce cas à ne pas
créer un algorithme qui viole la condition d'Ergodicité.
1.C.2.3. Balance
spécifique12(*)
Cette autre condition du processus de Markov est l'une de
celles qui assurent que la probabilité de distribution de Boltzmann que
nous générerons après que notre système ait atteint
l'équilibre est la plus grande de toutes les autres distributions. La
déviation de cette balance est assez subtile. Comme défini en
introduction, le sens réel de « système à
l'équilibre » : l'équivalence entre les
différents états lors des transitions à
l'équilibre, peut s'exprimer mathématiquement par :
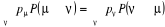 (1.35) (1.35)
Introduite, la relation de fermeture (1.34) sur
l'équation (1.35) conduit à :
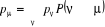 (1.36) (1.36)
Si cette équation est satisfaite, la probabilité
pí sera à l'équilibre dans le processus
dynamique de Markov. Mais il peut arriver que la satisfaction de cette
équation ne soit pas totalement efficiente pour garantir que la
probabilité de distribution puisse atteindre pu de n'importe
quel état du système si nous faisons tourner le système
pendant un long temps.
En effet, la probabilité de transition 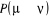 peut être déterminée comme un élément
de la matrice P13(*). En
considérant peut être déterminée comme un élément
de la matrice P13(*). En
considérant , si nous mesurons le temps mis dans chaque état durant la
chaîne de Markov, alors la probabilité à un instant t + 1
suivant (où sera le système à l'état í)
sera : , si nous mesurons le temps mis dans chaque état durant la
chaîne de Markov, alors la probabilité à un instant t + 1
suivant (où sera le système à l'état í)
sera :
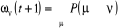 (1.37) (1.37)
Sous forme matricielle, on obtient 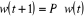 (1.38) (1.38)
Où w(t) est le vecteur dont les coordonnées sont
les différents poids statistiques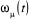 .A l'équilibre ( .A l'équilibre ( à à  ), le processus de Markov satisfera ), le processus de Markov satisfera 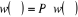 (1.39) (1.39)
Toutefois, il est possible au processus d'atteindre
l'équilibre dynamique par rotation de w sur toute la chaîne. En
notant « n » la taille limite du cycle parcouru, on
aura :
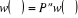 (1.40) (1.40)
Si nous choisissons une probabilité de transition (ou
de manière équivalente une matrice de Markov) pour satisfaire la
relation (1.36). Nous garantirons ainsi que la chaîne aura une
simple probabilité d'équilibre de distribution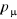 , quelque soit la valeur de « n ». , quelque soit la valeur de « n ».
De ce qui précède nous pouvons dire que nous
sommes informé que rien ne garantie que l'état d'équilibre
généré aura la probabilité de distribution
attendue.
Pour contourner ce problème l'on applique donc une
autre condition à notre probabilité de transition. la condition
de balance spécifique ou
détaillée énoncée telle que:
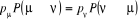 (1.41) (1.41)
Il est donc alors clair que chaque état qui satisfera
cette condition (1 .41) satisfera alors absolument
(1.35) qui n'est qu'une sommation de (1.41) sur les
différents états concernés. En remarquant la forme
bidirectionnelle équivalente de (1.41), l'on constate bien que la
condition de balance spécifique élimine la notion de cycle qui
incluait la limite « n ». En effet, la balance
détaillée nous informe qu'en moyenne, le système peut
quitter d'un état u vers un autre í indifféremment du
chemin choisi et après un temps infini, l'on aura une probabilité
de distribution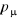 . (A . (A  , , 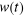 devra tendre exponentiellement comme les vecteurs propres correspondant
aux fortes valeurs propres de P). devra tendre exponentiellement comme les vecteurs propres correspondant
aux fortes valeurs propres de P).
Observons à nouveau l'équation (1.40), l'on
remarque que les grandes valeurs propres des matrices de Markov P pourront
être équivalentes. Si la limite du cycle de la forme (1.41)
était présente, nous pourrions ainsi avoir des valeurs propres
qui seront des racines complexes, mais la condition de balance
détaillée nous prévient de cette possibilité.
1.C.3. Rapport d'acceptation
De tous ce que nous avons jusqu'ici mentionné comme
élément important pour l'obtention rapide et efficace d'un
système à l'état d'équilibre, nous avons pu
généré un processus de Markov et avec ce dernier, nous
avons pu retrouver de nouveaux états avec une probabilité. Mais
cependant, il est difficile pour nous de prévoir le processus de Markov
approprié si nous nous trouvons dans un état donnée,
à sa bonne probabilité, et recherchons l'état suivant.
Bien qu'il soit encore possible d'utiliser les conditions suscitées,
nous pourrions ainsi suggérer plusieurs processus mais jusque là
sans pouvoir avoir la bonne probabilité de déclenchement, c'est
à dire celle nous permettant de transiter vers un état suivant
tout en respectant les équations (1.34) et
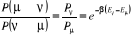 (1.42). (1.42).
La bonne nouvelle cependant est que nous n'aurions pas
à faire cela ! En réalité, il y'a dégât
lorsque nous nous laissons le choix de n'importe quel algorithme pour
générer de nouveaux états et de ce fait il est
nécessaire d'avoir une probabilité de transition souhaitée
par introduction d'une condition d'acceptation du taux de transition.
L'idée cachée derrière cette acceptabilité est la
suivante :
Nous mentionnions précédemment que nous
prévoyons introduire une probabilité de transition de base 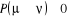 si nous le voulions. En posant í = u dans l'équation
(1.42), nous obtenons une tautologie (1 = 1). Ceci voudrait souligner que la
condition de balance détaillée est toujours
vérifiée pour si nous le voulions. En posant í = u dans l'équation
(1.42), nous obtenons une tautologie (1 = 1). Ceci voudrait souligner que la
condition de balance détaillée est toujours
vérifiée pour 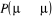 quelque soit la valeur de cette probabilité. Nous avons encore
une certaine flexibilité sur comment nous choisirons les autres valeurs
de quelque soit la valeur de cette probabilité. Nous avons encore
une certaine flexibilité sur comment nous choisirons les autres valeurs
de 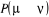 pour pour . Nous pouvons donc ajuster la valeur de n'importe quelle . Nous pouvons donc ajuster la valeur de n'importe quelle 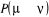 telle que la règle de fermeture (1.34) soit
vérifiée par simplement compensation de cet ajustement avec un
autre ajustement équivalent mais opposé telle que la règle de fermeture (1.34) soit
vérifiée par simplement compensation de cet ajustement avec un
autre ajustement équivalent mais opposé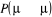 . La seule dont nous avons à observer est que . La seule dont nous avons à observer est que 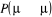 ne passe jamais hors de ses limites (soit ne passe jamais hors de ses limites (soit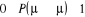 ). Si nous faisons cet ajustement, nous pourrions ainsi nous arranger
pour que l'équation (1.42) soit satisfaite en faisant un changement
simultané aussi sur ). Si nous faisons cet ajustement, nous pourrions ainsi nous arranger
pour que l'équation (1.42) soit satisfaite en faisant un changement
simultané aussi sur 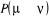 et alors l'on aura conservé leurs rapports. et alors l'on aura conservé leurs rapports.
Autrement dit, ces conditions nous donnent assez de
liberté sur les possibilités d'opérer des transitions sur
chaque site aux probabilités que nous souhaitons. Pour voir cela,
décomposons le rapport de transition en deux parties, soit 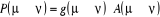 où où 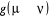 est la probabilité sélective (ou la probabilité
d'un état initial u de donner en fin d'étape un autre état
í) et est la probabilité sélective (ou la probabilité
d'un état initial u de donner en fin d'étape un autre état
í) et 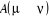 étant le rapport d'acceptation. étant le rapport d'acceptation. 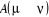 (Tel que (Tel que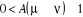 ), nous indique si nous devons commencer sur un état donné
u. Le choix de sa valeur nous est aussi libre. Choisir ), nous indique si nous devons commencer sur un état donné
u. Le choix de sa valeur nous est aussi libre. Choisir 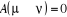 est équivalent à dire la certitude est équivalent à dire la certitude 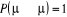 qui n'est cependant pas un cas que nous rechercherons. Il est donc
à proscrire ! De ce qui précède, nous avons aussi une
totale liberté sur le choix de qui n'est cependant pas un cas que nous rechercherons. Il est donc
à proscrire ! De ce qui précède, nous avons aussi une
totale liberté sur le choix de 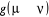 depuis la contrainte (1.42) qui fixe le ratio depuis la contrainte (1.42) qui fixe le ratio
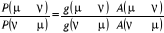 (1.43). (1.43).
Remarquons que 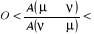 ? ? et et peuvent prendre n'importe qu'elle valeur souhaitée. peuvent prendre n'importe qu'elle valeur souhaitée.
Notre contrainte supplémentaire donnée par la
relation de fermeture (1.34) sera aussi satisfaite étant donnée
que la somme limitera à l'état de la chaîne de Markov
où nous avons commencé la sommation. Le cycle peut donc
être déterminé à n'importe quelle niveau !
Ainsi, dans le but de créer notre algorithme de Monte
Carlo, nous créerons un algorithme qui générera les
états successifs simplement avec les données de 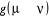 et nous sélectionnerons ensuite les états qui nous sont
utiles par la condition d'acceptation et nous sélectionnerons ensuite les états qui nous sont
utiles par la condition d'acceptation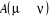 que nous choisirons telle qu'elle satisfera à l'équation
(1.43). Ceci devra satisfaire toutes les requêtes des probabilités
de transition tel que lorsque l'algorithme atteindra l'équilibre, l'on
tirera la vraie probabilité de Boltzmann. que nous choisirons telle qu'elle satisfera à l'équation
(1.43). Ceci devra satisfaire toutes les requêtes des probabilités
de transition tel que lorsque l'algorithme atteindra l'équilibre, l'on
tirera la vraie probabilité de Boltzmann.
Tout ceci paraît plaisant, mais il faudra tenir compte
de ce que si le taux d'acceptation est faible, notre algorithme paraîtra
immobile, ce qui bloquera naturellement l'évolution du système.
Il faut donc trouver un algorithme qui évoluera entres les états
pour un large échantillonnage. Il est impératif à veiller
à raccourcir le temps de traitement de notre matrice. Rechercher donc un
algorithme qui respectera un temps convenable par rapport à
l'échantillonnage qu'on dispose. Il suffit pour cela de remarquer que
l'équation (1.43) ne fixe que le taux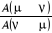 d'acceptation entre deux états distinct dans n'importe quelle
direction avec la contrainte que ce taux est compris entre 0 et 1 bien qu'on
puisse mathématiquement le multiplier proportionnellement par un
coefficient réel. d'acceptation entre deux états distinct dans n'importe quelle
direction avec la contrainte que ce taux est compris entre 0 et 1 bien qu'on
puisse mathématiquement le multiplier proportionnellement par un
coefficient réel.
La meilleure chose que nous puissions faire toutefois est de
le garder, mais de tenir compte des caractéristiques des
différents états en présence dans la probabilité de
sélection  et d'introduire aussi faiblement que nous pouvons le rapport
d'acceptation idéal (c'est à dire celui qui génère
de nouveaux états avec la vraie probabilité de transition). et d'introduire aussi faiblement que nous pouvons le rapport
d'acceptation idéal (c'est à dire celui qui génère
de nouveaux états avec la vraie probabilité de transition).
Le bon algorithme est celui qui conserve le rapport
d'acceptation (c'est à dire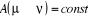 ) ! ) !
Chapitre: 2
Etude
des phénomènes critiques À l'aide du modèle d'ISING
à 2 D.
2.1. Les phénomènes
critiques
Les phénomènes critiques découlent des
transitions de phases qui peuvent s'établir dans un système
quelconque. Il s'agit en effet de la configuration du système à
l'instant précis de la transition qui est une phase critique. Le
système obéit à cet instant à des lois et
propriétés difficilement appréciables et qui
présentent un intérêt particulier à l'étude.
Lequel intérêt nous allons aborder dans ces prochaines lignes
où nous étudierons plus partiellement les configurations du
système à cette zone critique pour enfin déterminer les
paramètres physiques qui nous intéressent. Tout d'abord nous nous
éclairerons sur les notions de transitions de phases.
2.1.1. Les transitions de
phase
L'exemple fondamental, bien connu que l'on peut
présenter pour exprimer la notion de phase, est celui de l'eau dans ses
différents états. Nous savons que l'eau possède 3
différents états ou aspects: Solide (glace), Liquide (eau),
Gazeux (vapeur). Le passage d'une phase à une autre quotidiennement
observé, peut se décrire par le gel, l'ébullition ou la
sublimation qui, (ces différentes phases) sont
caractérisées par leurs propriétés qualitatives ou
quantitatives, qui sont des modifications de certains paramètres tels
(la pression, le volume, la température). La physique de la
matière condensée est notamment très riche en ces
exemples, qu'on parle du ferromagnétisme, de la
ferroélectricité, des liquides superfluides, de la
supraconductivité, des transitions ordre - désordre dans les
alliages ou encore de la transition de localisation d'Anderson ...etc.
De manière générale, toutes ces
transitions de phase ne sont pas identiques, il en ressort
schématiquement deux classes de transitions dépendamment de la
présence de la chaleur latente. C'est P. Ehrenfest, en 1933 [5] qui
proposa une classification14(*) des différentes transitions à partir du
comportement du potentiel thermodynamique associé (enthalpie libre,
énergie libre ...) :
i) Les transitions de phase du premier ordre
s'accompagnent de discontinuités des grandeurs
thermodynamiques, comme l'entropie et la densité, associées
à des dérivées premières de potentiels
thermodynamiques. (C'est le cas de transitions normales subit par l'eau.)
ii) Les transitions de phase du second ordre
pour lesquelles les potentiels thermodynamiques et leurs
dérivées premières sont continus et qui s'accompagnent de
certaines discontinuités des dérivées secondes de
potentiels thermodynamiques (comme la capacité calorifique). Pour ces
transitions, on passe de façon continue d'une phase à l'autre
sans que l'on puisse parler de coexistence des deux phases. (C'est le cas les
matériaux ferromagnétique.)
On peut généraliser la classification de
Ehrenfest et définir des transitions d'ordre supérieur15(*). Cependant, bien que la
classification d'Ehrenfest a le mérite de mettre en évidence des
différences et des similitudes entre diverses transitions, elle se
limite à des concepts thermodynamiques insuffisants pour bien comprendre
la physique d'une transition.
Par ailleurs, c'est aux travaux du physicien L. LANDAU (1937)
qu'on doit l'interprétation de plusieurs notions observées telles
celle de « brisure de symétrie », de
« paramètre d'ordre », et la classification suivante
:
i) Les transitions sans paramètres d'ordre
qui sont toujours de premier ordre au sens de Ehrenfest.
ii) Les transitions avec paramètres d'ordre.
Si le paramètre d'ordre est discontinu à la transition
celle ci est de premier ordre au sens de Ehrenfest. Elle est d'ordre
supérieur si le paramètre d'ordre est continu à la
transition.
Rappelons d'une part qu'une transition de phase sans Chaleur
latente s'accompagne d'un changement de la symétrie du système.
(Ainsi, si l'on prend l'exemple d'un matériau
ferromagnétique, on sait que celui ci ne possède pas
d'aimantation spontanée à haute température. Par contre,
en dessous de la température de Curie, il apparaît une aimantation
permanente orientée dans une direction bien précise. On dit alors
que la symétrie du matériau a été brisée
à basse température car le milieu n'est plus qu'invariant par une
rotation autour d'un axe parallèle à l'aimantation)[5]. D'autres
part, le paramètre d'ordre est une grandeur physique qui
caractérise une transition. Il est nul dans la phase la plus
symétrique (généralement la phase haute
température) et qui devient non nulle dans la phase la moins
symétrique (la phase ordonnée à basse température).
Le paramètre d'ordre des transitions de phase magnétique est
l'aimantation M
Pour l'exemple de l'eau, [8], l'on peut de ce qui
précède dire qu'il existe un point particulier dans son diagramme
de phase. Ce point dit critique, caractérisé par une
température de 647 K et une pression de 217 atmosphères.
Au-delà de ce point, il n'y a plus de distinction entre liquide et
vapeur. Il ne reste qu'une seule phase fluide et l'on ne peut plus faire
bouillir de l'eau. Près du point critique, il existe des variations de
densité sur toutes les échelles de longueurs. Elles apparaissent
sous la forme de gouttes de liquide intimement mélangées à
des bulles de gaz. La taille de ces gouttes et celle des bulles varient de la
taille d'une molécule à celle du récipient. Plus
précisément, au point critique, la longueur
caractéristique des fluctuations les plus grandes devient infinie, mais
les fluctuations les plus petites n'en disparaissent pas pour autant.
Cette attitude observée sur cet exemple fondamental
(l'eau) nous induit alors d'autres notions que nous étudierons plus
bas.
2.1.2. L'exposant critique (sa
mesure) et les classes d'universalités
T >>  T > T >  T = T = 
î
î et très petits î et augmentent
î et très grands
Les spins dans le modèle d'ISING se regroupent en
cluster (Région localement ordonnée de taille îd
)16(*), î
appelée « longueur de corrélation » (c'est la
dimension du cluster c'est à dire du bloc de spins parallèles);
les fluctuations en générale gouvernent le comportement du
système près de la transition [5], à l'approche de la
température critique (notée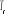 ), il peut exister un laps de temps ô appelé
« temps de corrélation »17(*) qui diverge avec î. Ce
phénomène peut être schématisé tel à
la figure ci-contre : ), il peut exister un laps de temps ô appelé
« temps de corrélation »17(*) qui diverge avec î. Ce
phénomène peut être schématisé tel à
la figure ci-contre :
Figure 2.1 :
schématisation des regroupements de spin en fonction de la
température
Pour l'étude des phénomènes critiques, il
est approprié de travailler avec une nouvelle variable appelée
« température réduite ». Les grandeurs :
le paramètre d'ordre, la chaleur spécifique, la longueur de
corrélation etc. ... peuvent être décrites par une loi en
puissance `t'.
Où 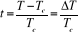 (2.1). (2.1).
À l'approche de la transition de phase (t ? 0 quand
ô > 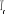 ), la divergence de la longueur de corrélation est
proportionnelle à la température réduite par la relation. ), la divergence de la longueur de corrélation est
proportionnelle à la température réduite par la relation.
 (2.2). (2.2).
La quantité positive non entière í
appelée « exposant critique » est définie par
[5] :
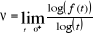 (2.3). (2.3).
Remarquons que la température t peut être prise
des deux côtés de 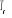 (à gauche ou à droite du nombre réel (à gauche ou à droite du nombre réel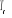 ) pour obtenir une même valeur de î d'où la valeur
absolue sur l'équation (2.2). ) pour obtenir une même valeur de î d'où la valeur
absolue sur l'équation (2.2).
Dans les simulations de Monte Carlo, í est
indépendant de l'algorithme utilisé, mais dépend de la
matrice utilisée : í a différentes valeurs qu'on soit
en dimension 2 ou 3 [5].
Par ailleurs, il existe d'autres exposants critiques, plus
particulièrement ceux qui nous intéressent proviennent de la
susceptibilité et de la chaleur spécifique qui découlent
directement de la divergence de la longueur de corrélation. De
même que (2.2), l'on a :
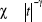 et et  (2.4) (2.4)
2.1.2.1. Notion
d'universalité
L'universalité d'une quantité repose sur son
invariance par rapport aux diverses transformations dans lesquelles elle
intervient. Ainsi, [5] l'hypothèse d'universalité proposée
en 1971 par L. Kadanoff et confirmée par la méthode du groupe de
renormalisation stipule qu'une quantité est dite
« universelle » si elle ne dépend que de certains
caractéristiques qualitatives essentielles du système qui
sont :
La dimension de l'espace physique (d),
La dimensionnalité du paramètre d'ordre
(n),
La portée d'interaction et leurs
anisotropies,
La symétrie du système.
Ces facteurs définissent ainsi une classe
d'universalité, chacune caractérisée par un ensemble
d'exposant critique. En l'absence d'un champ extérieur, nous pouvons
exprimer le comportement critique des grandeurs que nous manipulons dans le
tableau ci-dessous [5]:
Tableau 2.1 : Expressions
de quelques grandeurs physiques en fonction de leurs exposants
critiques
|
Grandeur physique
|
Exposant
|
Définitions
|
Conditions
|
|
Chaleur spécifique
|
á
á'
|
C t-á
C (-t-á)
|
t > 0
t > 0
|
|
Paramètre d'ordre
|
â
|
(-t-â)
|
t < 0
|
|
Susceptibilité isotherme
|
ã
ã
|
÷T t-ã
÷T (-t-ã)
|
t > 0
t < 0
|
|
Longueur de corrélation
|
í
í'
|
î t-í
î (-t-í)
|
t > 0
t < 0
|
|
Fonction de corrélation
|
|
g(R) R-(d-2+)
|
t = 0
|
Pour un système en dimension 2 (d =2), on peut citer
dans les cas des interactions à courtes portées les 3 classes
fondamentales représentées par les modèles d'Ising (n =
1), XY (n = 2) et Heisemberg (n= 3). En généralisation, le
tableau (2.2) suivant regroupe l'essentiel des classes d'universalité
avec des exemples à l'appui lorsqu'ils existent [12].
Tableau 2.2 : Classe
d'universalité et modèles associés
|
Classe d'universalité
|
Modèle théorique
|
Système physique
|
Paramètre d'ordre
|
|
d = 2
|
n = 1
|
Modèle d'Ising à deux dimensions
|
Films absorbés
|
Densité de surface
|
|
n = 2
|
Modèle XY à deux dimensions
|
Films d'Hélium 4
|
Concentration de la phase superfluide
|
|
n = 3
|
Modèle d'Heisenberg à deux dimensions
|
|
Aimantation
|
|
d > 2
|
n = 
|
Modèles sphériques
|
Aucun
|
|
|
d = 3
|
n = 0
|
Marche aléatoire sans croisement
|
Configuration des polymères à longue
chaîne
|
Densité des extrémités des chaînes
|
|
n = 1
|
Modèle d'Ising à trois dimensions
|
Aimant uni-axial
|
Aimantation
|
|
Fluide aux voisinages d'un point critique
|
Différence de densité entre phase
|
|
Liquide au voisinage du point de mélange
|
Différence de concentration
|
|
Alliage d'une transition ordre - désordre
|
Différence de concentration
|
|
n = 2
|
Modèle XY à trois dimensions
|
Aimant plan
|
Aimantation
|
|
|
Hélium 4 près de la transition super fluide
|
Concentration de la phase superfluide
|
|
n = 3
|
Modèle d'Heisenberg à trois dimensions.
|
Aimant isotrope
|
Aimantation
|
|
d 4
|
n = -2
|
|
Aucun
|
|
|
n = 32
|
Chromodynamique quantité
|
Quarks liés dans les protons, les neutrons, etc ...
|
|
2.1.2.2. Fluctuations critiques et
ralentissement critique
Lorsque nous approchons le point critique, ils se
présentent des fluctuations plus grandes, observées sur nos
grandeurs habituelles, c'est le fait des phénomènes critiques.
Reprenons l'exemple de l'eau présenté au paragraphe sur les
transitions de phases ; au cours d'une transition critique, les
fluctuations spatiales de certaines grandeurs thermodynamiques possèdent
toutes les échelles de longueurs possibles. Ce phénomène
est relativement inhabituel pour le physicien qui généralement se
concentre sur une échelle de longueur donnée pour résoudre
un problème.
Ces fluctuations ralentissent la marche du processus Markovien
et par là induisent un ralentissement du processus. Il est dit critique
à ces températures environnent . Le temps de corrélation grandi dangereusement, nous le
retrouverons par les corrélations existant entre états. . Le temps de corrélation grandi dangereusement, nous le
retrouverons par les corrélations existant entre états.
2.1.2.3. Fonction d'auto
corrélation de l'aimantation
Dans une simulation, il est en général beaucoup
plus facile de calculer la fonction de corrélation telle définie
au 1er chapitre (équations 1.26 et 1.27 du §A.1.2)
dès lors que l'on se place à l'état d'équilibre.
Lorsqu'on opère des mesures d'aimantation ou d'énergie sur divers
systèmes de même dimension, l'on constate qu'ils arrivent presque
simultanément à la transition. Ce qui nous permet de penser qu'il
existe effectivement des corrélations qui s'établissent entre les
états du système. La fonction d'auto corrélation nous
permettra notamment de déterminer le temps de corrélation.
Considérons le modèle d'Ising avec lequel l'on détermine
l'aimantation m, nous avons présenté l'expression de la
susceptibilité (1.26) & (1.27) puis la fonction de
corrélation (1.33), ce qui nous permet en posant que m(t) est
l'aimantation instantanée au temps t, de décrire une fonction
d'auto corrélation de l'aimantation par l'équation (2.5)
et sous sa forme discrète, l'équation (2.6)
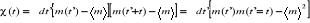 (2.5) (2.5)
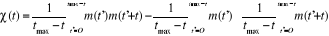 (2.6) (2.6)
La fonction d'auto corrélation donne la
corrélation entres deux instants distincts. Si nous intégrons
l'équation (2.5) précédente, 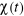 sera non nulle si en moyenne les fluctuations sont
corrélées et nulle dans le cas contraire. Globalement, l'on
obtient une échelle typique de mesure de la fonction d'auto
corrélation. Après un temps long, elle tendra vers une valeur
exponentielle définie par : sera non nulle si en moyenne les fluctuations sont
corrélées et nulle dans le cas contraire. Globalement, l'on
obtient une échelle typique de mesure de la fonction d'auto
corrélation. Après un temps long, elle tendra vers une valeur
exponentielle définie par : 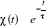 (2.7) (2.7)
On constate que le temps de corrélation noté
ô diminue de 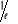 de sa valeur maximale à t = 0. de sa valeur maximale à t = 0.
Par ailleurs sur l'expression discrète (qu'on peut
compiler sur un ordinateur), lorsque t = tmax, la limite
supérieure devient petite et nous intégrerons donc sur un temps
vraiment court pour avoir le résultat escompté. Ceci nous informe
donc qu'à cause du hasard des fluctuations, l'erreur commise sur le
temps de corrélation devient grande. Il faudra donc simuler pendant un
temps grand pour réduire cet inconvénient.
2.1.2.4. Temps de
corrélation et exposant dynamique.
Comme introduit ci-dessus, le temps de corrélation est
un paramètre important pour les simulations autant que pratiquement il
nous guide sur la durée d'une simulation. Toutefois, à la
transition, ce dernier croît dangereusement. Pour décrire la
divergence du temps de corrélation ô, nous définissons
plutôt un autre exposant noté z, qui donne une
légère différence
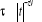 (2.8) (2.8)
où ô est mesurée dans les
différentes étapes de chaque site de la matrice de Monte Carlo.
On a
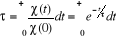 (2.8') (2.8')
L'exposant z est appelé exposant dynamique. z
diffère des autres exposants à cause de í 18(*).
Le temps de corrélation est le temps
élémentaire que prend le système pour se regrouper en
domaine, c'est à dire former des clusters. Il peut aussi être
considéré comme étant la durée moyenné de
vie des cluster. Comme nous le verrons au chapitre suivant, au voisinage de la
transition, la méthode de Monte Carlo avec un algorithme de type de
Métropolis ne nous offre malheureusement pas la possibilité
d'apprécier le système. Les échelles sur lesquelles
s'étendent les fluctuations à l'approche de 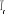 grandissent, impliquant le temps de relaxation correspondant car ils
sont liés par la relation grandissent, impliquant le temps de relaxation correspondant car ils
sont liés par la relation 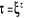 (2.9) (2.9)
En considérant l'équation (2.2) pour un
système infini ô diverge comme dit en (2.8), tandis que pour un
système fini î étant bornée par la taille du
réseau (échantillon), il obéira à la loi
 (2.10) (2.10)
Le temps de simulation devient extrêmement long !
Justifiant le ralentissement critique.
2.1.2.5. Mesure de l'exposant
critique
L'exposant dynamique nous donne le moyen de quantifier l'effet
de ralentissement critique. La valeur de ce ralentissement qui varie
typiquement entre 2 et 5 [5. Remarquons que la largeur du spectre des valeurs
de z entraîne celui de ô à  , ralentissant ainsi la simulation. D'où inversement, de petites
valeurs de z impliquent un algorithme plus rapide à l'approche de , ralentissant ainsi la simulation. D'où inversement, de petites
valeurs de z impliquent un algorithme plus rapide à l'approche de  , si z = 0, il n'y aura donc pas de ralentissement et l'algorithme
pourra tourner même lorsque la température est très proche
de , si z = 0, il n'y aura donc pas de ralentissement et l'algorithme
pourra tourner même lorsque la température est très proche
de  . .
La mesure de l'exposant critique dynamique z peut donc se
déduire de la relation (2.10). Dans le cas du modèle en 2D, [4]
Onsager (1944) à obtenu en champ externe nul  . .
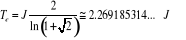 (2.11) (2.11)
Il a été possible d'améliorer les
séquences de la simulation à T= . Par l'algorithme de Métropolis, le modèle d'ISING
à 2D donne une droite de pente z = 2,09 #177; 0,06 [2]. La meilleure
valeur de l'heure fut déterminée par Nightingale et Blote en 1996
z = 2,1665 #177; 0,002 [2]. . Par l'algorithme de Métropolis, le modèle d'ISING
à 2D donne une droite de pente z = 2,09 #177; 0,06 [2]. La meilleure
valeur de l'heure fut déterminée par Nightingale et Blote en 1996
z = 2,1665 #177; 0,002 [2].
Comme dit plus haut z connu, l'on peut directement avoir les
autres exposants critiques. Ils ont été plus facilement
calculés grâce à la Théorie du Groupe de
Renormalisation (TGR)19(*), récapitulés dans le tableau suivant
[5]:
Tableau 2.3 : Valeurs des
exposants critiques pour d = 2
|
Exposant critique
Dimension du paramètre d'ordre.
á
|
â
|
ã
|
|
í
|
|
0
|
|
0,065 #177; 0,015
|
1,39 #177; 0,04
|
0,21 #177; 0,050,05
|
0,76 #177; 0,03
|
|
1
|
0(log)
|
0,125
0,120 #177; 0,015
|
1,75
1,73 #177; 0,06
|
0,25
0,26 #177; 0,05
|
1
0,99 #177; 0,04
|
|
2
|
|
|
|
|
|
|
3
|
|
|
2,5 #177; 0,1
|
|
|
La mesure de l'exposant critique remonte à très
longtemps, autant que beaucoup d'efforts ont été mené
à cet effet par de nombreux physiciens tout d'abord pour les transitions
de phases. Mais à présent l'on s'intéresse plus à
la mesure de l'exposant dynamique z, tout comme celle du ralentissement
critique de nos algorithmes.
2.2. Applications :
2.2.1. L'algorithme de
construction de la chaîne du processus de Markov.
Rappelons le ce processus permet de générer
n'importe quel état í à partir d'un autre état
ì.
Soit un espace à N dimension, f(ì,í) une
fonction de transition symétrique20(*) et ð(x) une densité de probabilité.
L'on construit une chaîne de Markov de la manière
suivante :
1. On se place au nième pas de la
chaîne Xn = ì et on génère un état
í candidat de Xn+1 à partir de
f(ì,í).
2. La probabilité de transition est alors 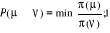
3. S'il y a transition (c'est à dire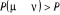 , P étant une variable aléatoire uniforme sur [0 ;1])
alors Xn+1 = í sinon Xn+1 = ì et on passe
au pas suivant. , P étant une variable aléatoire uniforme sur [0 ;1])
alors Xn+1 = í sinon Xn+1 = ì et on passe
au pas suivant.
NB. L'écriture sous forme d'organigramme de cet
algorithme est présentée en annexe 1
2.2.2. Algorithme
détaillé de Métropolis.
L'algorithme de Métropolis est une des plus efficace et
simple solution pour les problèmes de simulation en transition de phase.
Il est d'ailleurs conseillé de commencer tout traitement du genre par ce
type d'algorithme avant de mettre en oeuvre des algorithmes plus
compliqués car on y obtient une référence utile [9]. En
effet, les principes de cette méthode [8], exposés dès
1953 (Métropolis et al., 1953) suivent les considérations
décrit par la chaîne de Markov comme détaillés
ci-dessus, ce qui renvoie ainsi une série de valeurs
interdépendantes de ì dont on peut montrer que la distribution
statistiques à l'équilibre à pour densité ð(x),
la séquence itérative de la dynamique Métropolis pour un
système de N x N spins sera alors:
1. On sélectionne un site, en tirant au hasard un
nombre entier i tel que 1 = i = (N x N)
2. On calcule la différence d'énergie entre
la nouvelle configuration dans laquelle le spin sélectionné a
été retourné et l'ancienne. Pour une interaction à
courte portée, cette différence est en quelque sorte locale car
ne fait intervenir que le site du spin sélectionné et ses
voisins.
3. Si la nouvelle configuration est d'énergie plus
basse, la nouvelle configuration est acceptée. Si la nouvelle
configuration est d'énergie plus haute, on tire au hasard un nombre P,
tel que 0 < P < 1, si P < e[â(Ei-Ej], cette configuration est
acceptée, sinon on garde l'ancienne.
NB. L'écriture sous forme d'organigramme de cet
algorithme est présentée en annexe 2
La vitesse de convergence de l'algorithme de Métropolis
dépend de la fonction de transition f(ì,í). Le processus
de Markov étant introduit (pour atteindre l'état
d'équilibre), l'on devra donc respecter les conditions
d'Ergodicité, de balance spécifique et de normalisation (1.34).
En pratique, on choisi : 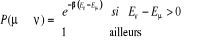 (2.12) (2.12)
Cependant, l'algorithme de Métropolis présente
des insuffisances aux phénomènes critiques.
2.2.2.1. Insuffisances de
l'algorithme de Métropolis. Le pas vers Wolff
Nous avons obtenu dans un paragraphe précédent
un exposant dynamique pour des modèles d'ISING à 2 D
simulés par l'algorithme de Métropolis, une valeur autour de z =
2,09 #177; 0,06 (pratiquement on prend z = 2,17), puis l'équation (2.10)
nous a permis de retrouver autrement la température critique . Ceci nous indique alors que l'algorithme de Métropolis est
meilleur pour investiguer l'environnement pour ces modèles à
l'approche du point critique. Cependant, il ne restera valable qu'à la
limite du type de modèle utilisé. . Ceci nous indique alors que l'algorithme de Métropolis est
meilleur pour investiguer l'environnement pour ces modèles à
l'approche du point critique. Cependant, il ne restera valable qu'à la
limite du type de modèle utilisé.
Le chronomètre guidé par l'horloge du processeur
de notre ordinateur indiquera une durée, « CPU
time » notée comme étant la durée mise entre un certain nombre
d'étapes d'exécution de l'algorithme. Ainsi comme étant la durée mise entre un certain nombre
d'étapes d'exécution de l'algorithme. Ainsi  grandira avec le nombre de site de Monte Carlo (c'est à dire
comme Ld). Il simulera une des valeurs du temps de simulation
grandissant avec le système comme grandira avec le nombre de site de Monte Carlo (c'est à dire
comme Ld). Il simulera une des valeurs du temps de simulation
grandissant avec le système comme 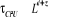 (21(*)). Ce
résultat nous conduit à une mesure difficile pour de grands
systèmes (L >>) aux régions critiques. A titre d'exemple,
lorsque L = 100 on peut compter environ 150.109 (21(*)). Ce
résultat nous conduit à une mesure difficile pour de grands
systèmes (L >>) aux régions critiques. A titre d'exemple,
lorsque L = 100 on peut compter environ 150.109 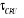 (plusieurs semaines avec un processeur moyen) afin d'avoir une valeur
raisonnable de ô. (plusieurs semaines avec un processeur moyen) afin d'avoir une valeur
raisonnable de ô.
La raison fondamentale des grandes valeurs de z dans
l'algorithme de Métropolis est la divergence que présente la
longueur de corrélation à l'approche de la transition. A  , plusieurs régions forment des spins parallèles
« domaines ou clusters» et il est difficile pour les
algorithmes de parcourir ces domaines étant donné qu'ils
opèrent spin par spin mettant ainsi assez de temps. De plus chaque
marche prenant une grande probabilité, le site considéré
sera rejeté à cause des interactions ferromagnétiques
entre proches voisins. La possibilité d'arriver au spin central est donc
faible à cause de l'action vers lui de ses plus proches voisins22(*). , plusieurs régions forment des spins parallèles
« domaines ou clusters» et il est difficile pour les
algorithmes de parcourir ces domaines étant donné qu'ils
opèrent spin par spin mettant ainsi assez de temps. De plus chaque
marche prenant une grande probabilité, le site considéré
sera rejeté à cause des interactions ferromagnétiques
entre proches voisins. La possibilité d'arriver au spin central est donc
faible à cause de l'action vers lui de ses plus proches voisins22(*).
L'algorithme de Métropolis est donc moins adapté
pour une étude sur un système quelconque, il apprécie mal
la divergence observée au point critique, quand l'exposant dynamique est
faible. Pour une généralisation, ces inconvénients seront
contournés par un nouvel algorithme, utilisant un exposant dynamique
plus petit et pouvant ainsi agir dans certaines complexités :
l'algorithme de Wolff.
2.2.3. L'algorithme de Wolff
La solution aux problèmes présentés au
dernier paragraphe fut apportée par l'algorithme de Wolff en 1987. Son
idée de base étant donc d'observer le système plutôt
sous l'angle des clusters que sur celui des spins comme les autres algorithmes.
Ce type d'algorithme se référencie dans la catégorie des
algorithmes à marche sur cluster ou plus simplement
« algorithme de domaine », qui devinrent très
célèbre ces dernière années.
Comment allons nous donc repérer ces clusters sur
lesquels nous marcherons ? La stratégie la plus simple
(utilisée par Wolff) se suggère d'elle-même. Il s'agit de
prendre au hasard un spin de la matrice et de regarder si ses proches voisins
sont parallèlement orientés. Dans ce cas, l'on évoluera de
proche en proche jusqu'à construire itérativement un cluster
entier. Cependant, l'on ne peut considérer au premier regard sur une
matrice des spins parallèles. Combien de retournements dépendront
en effet de la température ? Nous savons par exemple qu'à
haute températures23(*), les spins dans le modèle d'ISING tendent
à ne pas se corréler. Par ailleurs, à l'approche de  la taille des clusters est grande et le ferromagnétisme
s'installe orientant préférentiellement plusieurs spins, à
la limite de la couverture totale de la matrice. En d'autres termes, la taille
des clusters que nous retournons pourrait augmenter lorsque T
décroît. Tout ceci est physiquement réalisable si l'on
choisi au préalable un bon exemple de cluster. Mais nous n'ajouterons
pas tous les spins voisins parallèles, nous avons la probabilité
dite d'addition la taille des clusters est grande et le ferromagnétisme
s'installe orientant préférentiellement plusieurs spins, à
la limite de la couverture totale de la matrice. En d'autres termes, la taille
des clusters que nous retournons pourrait augmenter lorsque T
décroît. Tout ceci est physiquement réalisable si l'on
choisi au préalable un bon exemple de cluster. Mais nous n'ajouterons
pas tous les spins voisins parallèles, nous avons la probabilité
dite d'addition  [2] qui grandit lorsque T décroît. D'où plus
simplement, nous observons les voisins des spins que nous retournons et en
fonction de [2] qui grandit lorsque T décroît. D'où plus
simplement, nous observons les voisins des spins que nous retournons et en
fonction de  nous les ajouterons. Lorsque nous aurions rodé en refaisant
à chaque fois les mêmes tests, sur toute la zone des spins
similairement orientés, nous retournerons le cluster avec un taux
d'acceptation dépendant de l'énergie du retournement. La question
est alors posée sur la détermination du rapport d'acceptation
correct pour notre algorithme satisfaisant la balance spécifique, et
dans ce cas quel sera le meilleur choix du nous les ajouterons. Lorsque nous aurions rodé en refaisant
à chaque fois les mêmes tests, sur toute la zone des spins
similairement orientés, nous retournerons le cluster avec un taux
d'acceptation dépendant de l'énergie du retournement. La question
est alors posée sur la détermination du rapport d'acceptation
correct pour notre algorithme satisfaisant la balance spécifique, et
dans ce cas quel sera le meilleur choix du  pour faire tendre ce rapport le plus proche possible de 1 ? pour faire tendre ce rapport le plus proche possible de 1 ?
2.2.3.1. Rapport d'acceptation
pour les algorithmes de cluster
Nous regarderons à présent ce que le rapport
d'acceptation sera pour cette marche entre cluster, nécessairement la
condition de balance détaillée sera vérifiée. Ce
rapport, nous l'avons dit au chapitre précédent, défini la
possibilité que l'entité considérée (ici le
cluster) soit tenu en compte dans le processus sachant que la marche entre deux
états ì et í ici peut être sur une direction
préférentielle considérée dans les deux sens. L'on
adjoint à la probabilité d'addition , celle de non addition (1 - , celle de non addition (1 -  ) représentant la probabilité de brisure des sauts
à la frontière du cluster, la condition de balance
spécifique pour obtenir ) représentant la probabilité de brisure des sauts
à la frontière du cluster, la condition de balance
spécifique pour obtenir
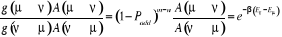 (2.13) (2.13)
Où `m' et `n' sont les nombres de sauts brisées
respectivement dans les marches allés et retours, nous retrouvons les
rapports d'acceptation des deux sens du mouvement A(ì?í) et
A(í?ì). La différence d'énergie entre les deux
états, Eí - Eì dépend du saut
qui à été brisé. Nous obtiendrons ainsi pour les
`m' bonds brisés à l'allé une variation d'énergie
de +2J et pour les n saut retours, elle sera -2J, d'où
Eí - Eì = 2J(m - n)
(2.14).
Introduit convenablement dans l'équation (2.13) nous
ressortons la condition du rapport d'acceptation
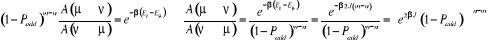
D'où si l'on prend
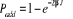 (2.15) (2.15)
On aura
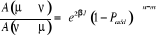 = 1 (2.16). = 1 (2.16).
Nous aurions de ce fait imposé au rapport de droite
d'être maximal indépendamment des propriétés des
états ì ou í, de la température ou de tout autre
quantité observable. Avec ce choix nous pouvons faire un rapport
d'acceptation égale à 1, pour les prochains ou
précédents mouvements, qui est ainsi la meilleure valeur que nous
pouvons prendre. Chaque mouvement que nous proposerons sera dès lors
accepté et l'algorithme satisfera la condition de balance
détaillée.
2.2.3.2. Algorithme
détaillé de Wolff et avantages
Le choix de l'équation (2.15) défini donc
l'algorithme des clusters et en particulier celui de l'algorithme de Wolff pour
le modèle d'ISING à 2 D. l'algorithme de Wolff peut donc se
détailler comme suit :
1. Choix au hasard du spin de départ (spin
idéal) dans la matrice
2. Observer ses voisins par retournement de chacun. S'il
est pointé vers la même direction, alors l'ajouter au cluster avec
la probabilité d'addition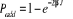 . .
3. Pour chacun des spins ajoutés dans les
conditions de la 2ième étape, examiner chacun de leurs
voisins respectifs, cherchant ceux des spins ayant la même orientation
afin de les ajouter aussi dans le cluster avec la même probabilité
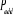 (il faut noter qu'autant que notre cluster grandira, nous devons
examiner de proche en proche tous les voisins et veiller à rejeter un
spin déjà considéré précédemment).
Cette étape devra être répétée autant que
cela sera nécessaire tant qu'il y'aura des spins qui n'ont pas
été considérés. (il faut noter qu'autant que notre cluster grandira, nous devons
examiner de proche en proche tous les voisins et veiller à rejeter un
spin déjà considéré précédemment).
Cette étape devra être répétée autant que
cela sera nécessaire tant qu'il y'aura des spins qui n'ont pas
été considérés.
4. Retourner le cluster
NB. L'écriture sous forme d'organigramme de cet
algorithme est présentée en annexe 4
Autant que nous aurions la condition de balance
détaillée, cet algorithme satisfait clairement les
critères d'Ergodicité vus au chapitre précédent.
Pour le constater, on remarque que l'on est sure avec cet algorithme que tous
les spins seront considérés et introduit autant que possible dans
un cluster durant un temps fini. Chaque mouvement générera
automatiquement et précisément un autre dans un temps fini tel
que le précise l'Ergodicité. D'après la condition de
balance détaillée, notre algorithme nous garanti que les
états de notre matrice qui apparaîtrons après
l'équilibre le seront avec leurs probabilités de Boltzmann
correct.
L'on remarque en effet aussi que 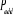 augmente lorsque la température décroît,
d'où la taille du cluster grandira lorsqu'il y'aura
refroidissement24(*) ! Le retournement de ces clusters est plus
facile ici qu'avec l'algorithme de Métropolis. Donc nous souhaitons
qu'à chaque instant l'algorithme prenne un faible exposant dynamique,
aussi petit que possible. augmente lorsque la température décroît,
d'où la taille du cluster grandira lorsqu'il y'aura
refroidissement24(*) ! Le retournement de ces clusters est plus
facile ici qu'avec l'algorithme de Métropolis. Donc nous souhaitons
qu'à chaque instant l'algorithme prenne un faible exposant dynamique,
aussi petit que possible.
2ième Partie : Etude pratique
Chapitre 3
Les résultats des
simulations
3.1. Introduction
Nous avons précédemment présenté
la méthode de Monte Carlo et les différents algorithmes qui
l'utilisent - en particulier l'algorithme de Métropolis et l'algorithme
de Wolff -, les notions liées à la transition de phase. Tous ces
éléments devaient nous permettre de déterminer les
grandeurs physiques liées à un système donné. Pour
y arriver, nous présentions les expressions théoriques de ces
grandeurs et à présent, à travers les conditions
imposées aux chapitres précédents, nous exposerons dans ce
chapitre les résultats des simulations numériques pour
l'étude des transitions de phases Ferromagnétique vers
Paramagnétique et vis-versa à l'aide du modèle d'Ising
à 2 D. Ainsi donc nous utiliserons l'échantillonnage important
appliqué dans un premier temps à l'algorithme de
Métropolis et dans un second temps à l'algorithme de Wolff au
voisinage de la transition de phase.
Afin de simplifier le problème, nous avons
considéré un réseau carré de paramètre de
maille ?a? dans lequel les spins sont placés sur les sites (i , j) du
réseau, chaque spin pouvant prendre les valeurs +1 (Up) ou -1 (Down).
Nous avons opéré nos simulations en champ magnétique nul
(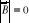 ), l'Hamiltonien de spin du système s'écrit donc ), l'Hamiltonien de spin du système s'écrit donc
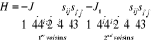
Sij étant le spin d'abscisse i et
d'ordonnée j, les J étant les intégrales d'échange
entres voisins.
Pour l'étude de la transition de phase, nous avons
considéré la plage d'intervalle des températures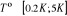 . Quant aux valeurs d'échange d'énergie, nous sommes
partis de la valeur théorique exacte déterminée par
Onsager [4] . Quant aux valeurs d'échange d'énergie, nous sommes
partis de la valeur théorique exacte déterminée par
Onsager [4]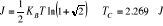 où J est donnée en °K. où J est donnée en °K.
Nous avons étudié le comportement en
température :
o du temps de corrélation,
ô
o de l'énergie interne du système de spins
E
o de l'aimantation du système, M
o de la chaleur spécifique à volume constant
C
o de la susceptibilité magnétique du
système, ÷
ainsi que les fluctuations critiques.
Pour toutes les simulations, nous avons
considéré 
Mais avant d'effectuer la mesure de ces grandeurs, nous devons
nous assurer que notre système de spins se trouve à l'état
d'équilibre thermodynamique (cf. chapitre 1 § 1.A.2).
C'est la configuration dans laquelle l'on peut appliquer la statistique de
Maxwell Boltzmann pour le calcul de la probabilité d'un état et
par ailleurs, que les corrélations entres deux mesures
consécutives sont faibles.
3.2. Détermination de
l'équilibre thermique.
D'après les grandes lignes de l'algorithme de
Métropolis présenté au précédent chapitre,
pour passer d'un état à un autre, il suffit de choisir de
manière aléatoire un spin et de le retourner si ce nouvel
état est plus stable ou dans le cas contraire s'il est plus probable.
Les mesures étant réalisées sur des systèmes ayant
un grand nombre de spins (échantillonnage important), les configurations
ainsi obtenues seront fortement corrélées.
Par contre, si dans une assemblée de N x N spins, on
considère comme état, la configuration obtenue après avoir
répété l'algorithme de base sur les N x N spins, les
configurations successives obtenues seront cette fois ci moins
corrélées.
Le temps nécessaire qu'il faut pour parcourir une
assemblée de N x N spins et de tirer à chaque fois de
manière aléatoire (ou pas), le spin à retourner à
une température donnée est appelé « Pas de Monte
Carlo » (MCS)25(*).
Nous devons donc exécuter notre simulation durant un
temps suffisamment long pour que le système de spins atteigne
l'équilibre à la température donnée. Cette
durée est appelée temps d'équilibre ôeq.
A l'équilibre thermique, la probabilité moyenne d'avoir notre
système dans un état particulier ì est proportionnelle au
poids de Boltzmann  de cet état. de cet état.
Les méthodes de Monte Carlo étant
essentiellement probabilistes, il est important de s'assurer que les
probabilité générées sont effectivement
aléatoires : pour cela, nous avons utilisé l'algorithme de
génération des nombres aléatoires par congruence
linéaire (voir annexe 2) avec éventuellement un mélange
(shuffling) et en utilisant différentes
« graines »26(*).
Nous avons représenté sur la figure 3.1
ci-dessous, les résultats de notre simulation pour trois27(*) types de
« graine » sur un réseau carré de 100 x 100
spins à la température T = 2.4K. Nous sommes parti d'un
état où tous les spins sont alignés (T = 0K) et
`réchauffé', jusqu'à l'équilibre thermique à
T = 2.4K. Nous constatons sur cette figure que les meilleurs résultats
s'obtiennent avec une « graine » égale à
3001. L'équilibre thermique est atteint au voisinage de t = 600
MCS/Site.
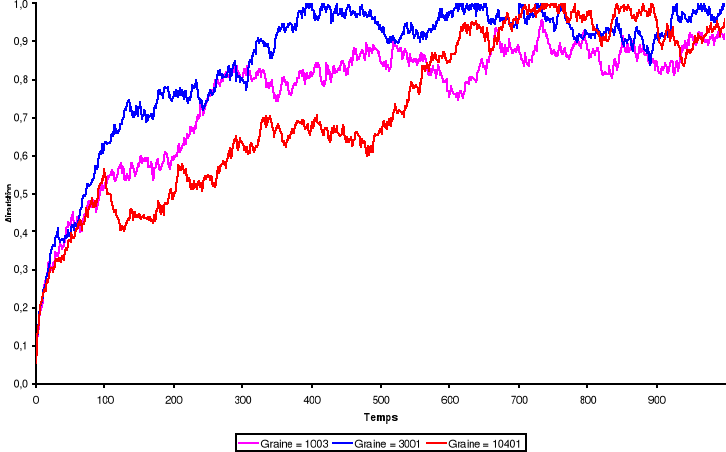
Figure
3.1 : Aimantation du système de 100 x 100
spins du modèle d'Ising à 2 D en fonction du temps (en MCS/Site)
pour trois types de graine simulé avec l'algorithme de
Métropolis. Les nombres aléatoires sont
générés par congruence linéaire simple et
l'équilibre thermique est atteint au voisinage de t = 600 MCS/Site
à T = 2.4K
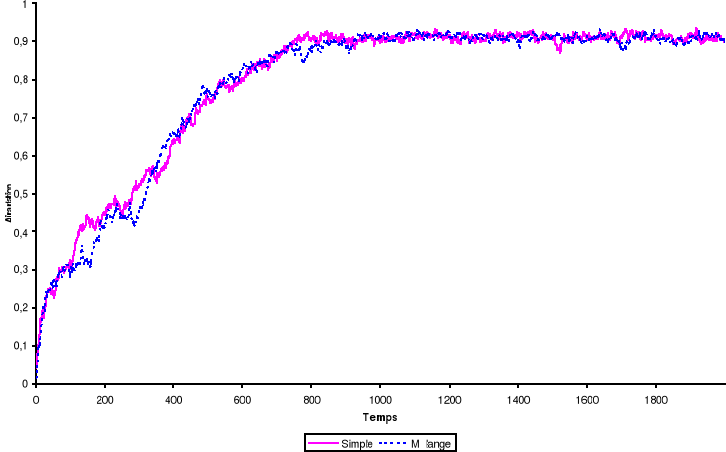
Figure
3.2 : Aimantation du système de 100 x 100
spins du modèle d'Ising à 2 D en fonction du temps (en MCS/Site
simulé avec l'algorithme de Métropolis. Les nombres
aléatoires sont générés par congruence
linéaire simple ou suivie d'un shuffling et l'équilibre thermique
est atteint au voisinage de t = 800 MCS/Site à T = 2K
Nous avons refait les simulations avec la graine
déterminée précédemment mais à T = 2°K
et en générant les nombres aléatoires par congruence
linéaire simple ou suivie d'un mélange (shuffling). La simulation
à débutée à T = 8, - état où tous les
spins ont des directions complètement aléatoires et M = 0- et
« refroidi » jusqu'à l'équilibre thermique
à T = 2°K. le temps étant mesuré en MCS/Site,
l'équilibre est atteint au bout de 800 pas par site. Les
résultats sont représentés sur la figure 3.2 ci-dessus, et
on peut remarquer que la congruence linéaire simple donne les
résultats meilleurs que celle suivie d'un mélange.
Nous allons donc, de ce qui précède à
poursuivre nos simulations avec une graine de 3001 et une congruence
linéaire simple pour générer nos nombres
aléatoires.
Nous avons pensé qu'il serait intéressent de
visualiser l'équilibre thermique directement en représentant le
système de spins en fonction du temps d'observation. La figure 3.3 nous
montre une succession d'état du modèle d'Ising à 2 D, sur
un réseau carré de 100 x 100 spins à la température
T = 2.4K, partant d'un état où tous les spins sont alignés
sont alignés (T = 0 K) et « réchauffer »,
jusqu'à l'équilibre thermique à T = 2.4K. Le temps
étant mesuré en Monte Carlo Step
|
 t = 0 t = 0
|
 t = 1 t = 1
|
 t = 2 t = 2
|
|
 t = 4 t = 4
|
 t = 6 t = 6
|
 t = 10 t = 10
|
|
 t = 20 t = 20
|
 t = 40 t = 40
|
 t = 100 t = 100
|
|
 t = 200 t = 200
|
 t = 500 t = 500
|
 t= 800 t= 800
|
Figure
3.3 : Douze états de 100 x 100 spins du
modèle d'Ising à 2 D amenés à l'équilibre
thermique à T=2.4K au bout de t = 400 MCS/Site avec l'algorithme de
Métropolis. Les spins Up (+1) sont représentés en noir et
les spins Down (-1) sont en blanc.
Cependant, la détermination de l'équilibre
thermique par cette procédure n'est pas précise. Il est vivement
conseillé de représenté plutôt l'aimantation moyenne
« m » du système en fonction du temps d'observation
et d'identifier le temps au bout duquel l'aimantation atteint la saturation.
Nous avons donc effectué nos simulations pour plusieurs
autres températures et nous avons constaté que hors mis les
températures proches de la transition (T=2.2°K et T=2.3°K)
pour lesquelles l'équilibre thermique intervient au bout de 2000
MCS/Site, il est en dessous de 1000 MCS/Site pour les autres
températures. La figure 3.4 ci-dessous représente les
résultats pour T=2.2°K, partant d'un état initial
désordonné (abaissement de température). On y remarque que
la saturation a lieu pour une aimantation bien en dessous de un (1), ce qui est
normal puisque nous quittons d'une phase à une autre.
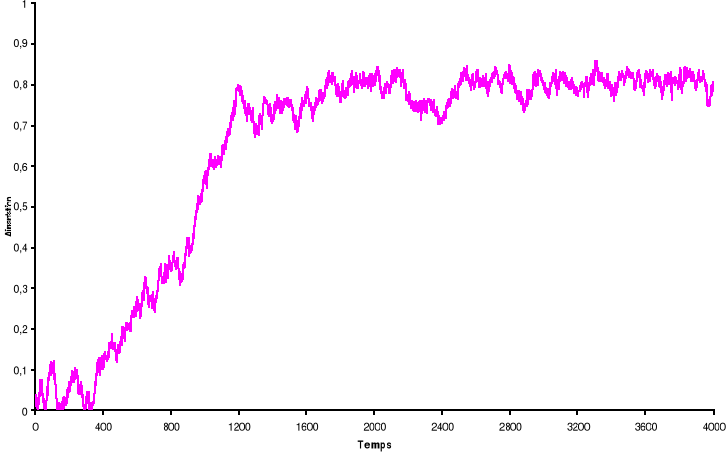
Figure
3.4 : Aimantation du système de 100 x 100
spins du modèle d'Ising à 2 D en fonction du temps (en
MCS/Site) simulé avec l'algorithme de Métropolis.
L'équilibre thermique est atteint au bout de t = 200
MCS/Sites à T = 2.2K. La simulation a débutée avec des
spins complètement aléatoires, puis « refroidie'
jusqu'à l'équilibre à T = 2.2K.
Remarquer que l'on parle de
« refroidir »28 ou de
« réchauffer »28 pour un système
qui a l'air de subir une trempe28(*). Il faut en effet considérer que nos
températures varient progressivement.
3.3. Détermination du temps
de corrélation.
Une fois l'équilibre thermique atteint, nous avons
effectué la mesure des grandeurs physiques qui nous intéressent
en l'occurrence, l'énergie « E », l'aimantation
« M », la chaleur spécifique à volume
constant « C », la susceptibilité magnétique
du système « ÷ » ... . Mais combien de mesures
indépendantes (non corrélées) ces données
représentent ? Autrement dit, quel est le temps de
corrélation ? Pour répondre à cette question, nous
devons déterminer le temps de corrélation à chaque
température. Pour ce faire, nous calculons la fonction d'auto
corrélation de l'aimantation à chaque température
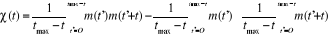
Nous représentons ci-dessous en figure 3.5 un exemple
de cette fonction à T= 2.2K.
Afin de déterminer le comportement en
température du temps de corrélation, nous avons mesuré
l'aimantation du système pour un temps d'observation en MCS/Site allant
de 2000 exceptées les températures T=2.2K et T=2.3K pour
lesquelles t variait de 0 à 4000 MCS/Site. Nous avons
déterminé ensuite à chaque température le temps de
corrélation ô qui est le temps au bout duquel la fonction d'auto
corrélation diminue de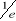 de sa valeur maximale à t = 0. de sa valeur maximale à t = 0.
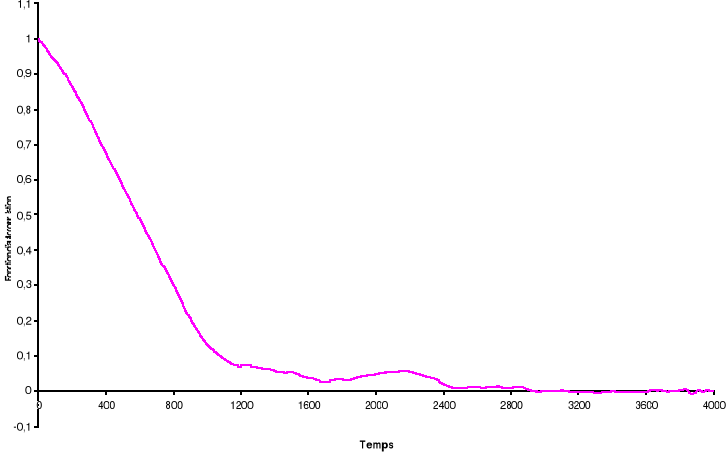
Figure
3.5 : Fonction d'auto corrélation de
l'aimantation pour le modèle d'Ising à 2D sur un système
de 100x100 spins à la température T=2.2K par Métropolis.
Le temps de corrélation est de ô = 725 MCS/Site
Pour T=2.2°K par exemple, nous avons obtenu un temps de
corrélation de ô = 725MCS/Site. Nous avons
représenté sur la figure 3.6 ci-dessous, les résultats
obtenus pour une gamme de températures allant de 0.2K à 5K et par
pas de 0.1K. Nous observons sur la figure une divergence à T=2.3K. Ce
phénomène est appelé ralentissement critique. Ce qui
signifie que dans la zone critique le système prend
énormément de temps pour atteindre l'équilibre d'une part
et d'autre part pour passer d'une configuration stable vers une autre :

Figure
3.6 : Temps de corrélation pour 100x100 spins
du modèle d'Ising à 2D en fonction de la température
simulé avec l'algorithme de Métropolis.
NB. Le trait continu est juste un guide pour l'oeil
Nous remarquons également qu'en dehors de la zone
critique , le temps de corrélation est inférieur à 40
MCS/Site (ô?35), condition que nous utiliserons par la suite dans nos
simulations. , le temps de corrélation est inférieur à 40
MCS/Site (ô?35), condition que nous utiliserons par la suite dans nos
simulations.
Disposant de toutes ces informations liées à la
bonne marche de nos processus de calcul, nous pouvons à présent
nous intéresser à la transition de phase et aux
phénomènes au voisinage de la transition.
3.4. Etude de la transition de
phase.
Afin de nous assurer que notre programme fonctionne bien, nous
l'avons au préalable testé sur un petit réseau de 5x5
spins (soit 25 spins ou 225 états possibles) dans la gamme de
températures allant de 0.2K à 5K. Dans ces conditions, toutes les
simulations à une température donnée ne prenaient que
quelques 2 à 3 secondes.
L'objectif étant de tester la validité de notre
programme, nous n'avons ni déterminé la configuration à
l'équilibre, ni le temps de corrélation entre 2 mesures
consécutives. Pour chaque température, nous avons simplement fait
tourné le programme pendant un temps de 20000 MCS/Site et
effectué les mesures à partir de t = 2000 MCS/Site et par
intervalle de Ät= 5 MCS/Site.
Les figures 3.7 et 3.8 ci-dessous montrent les
résultats normalisés à l'unité ( 1 ) (carrés
et cercles) de notre simulation et ceux (traits pleins) obtenus par un calcul
exact à l'aide de la fonction de partition
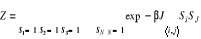
où  est la somme sur les premiers voisins. est la somme sur les premiers voisins.
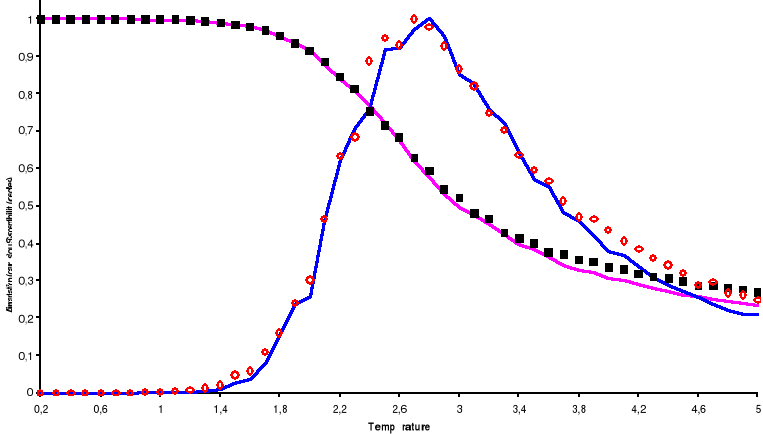
Figure
3.7 : Aimantation (carrés) et
susceptibilité magnétique (cercles) du système 5x5 spins
du modèle d'Ising à 2D en fonction de la température
simulé avec l'algorithme de Métropolis. Les points
(carrés et cercles) sont les résultats de la simulation et les
traits, le calcul exacte à l'aide de la fonction de partition.
Au vu de ces résultats, nous pouvons conclure sans
ambiguïté que notre programme fait bien son travail, et commencer
dès lors l'étude de la transition de phase Ferro ? Para.
3.4.1. Transition de phase
Ferro?Para.
Une transition de phase rappelons le, est un processus qui
fait passer le système d'une phase (de symétrie ou de
configuration donnée) vers une autre phase (de symétrie ou de
configuration différente de la phase de départ). Ce processus est
gouverné par une grandeur appelée paramètre d'ordre
noté ç. Ce paramètre d'ordre est non nul dans la
phase ordonnée et nul dans la phase désordonnée.
Pour les transitions de phase magnétique, le paramètre d'ordre
est l'aimantation du système noté â. A la transition, la
susceptibilité magnétique du système et la chaleur
spécifique à volume constant ont des comportements singuliers.
Elles divergent à la transition. Alors que l'aimantation passera
continûment d'une phase à une autre (transition du 2nd
ordre) ou bien passera directement d'une phase à une autre (transition
du 1er ordre).
Pour étudier cette transition, nous avons
considéré un système de 100 x 100 spins à J = 1 et
nous avons effectué nos mesures dans la gamme de température
allant de 0,2K à 5K et par pas de 0,1. Pour chaque température,
le système est d'abord amené à l'équilibre et les
mesures sont effectuées par intervalle de temps Ät = ô
déterminé précédemment.
Afin d'éviter des mesures dans les zones de saturation
où les variations des grandeurs physiques sont faibles et conduisent
à des résultats peu précis, Newman et Bakerna [2]
proposent de commencer les mesures dès que 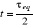 où où 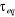 est le temps
d'équilibre en MCS/Site. est le temps
d'équilibre en MCS/Site.
Nous avons considéré pour nos simulations deux
configurations initiales de notre système de spins :
o Une configuration dans laquelle tous les spins sont
alignés.
(C'est à dire à la température T =
0K) : Transitions Ferro?Para,
o Une configuration dans laquelle tous les spins sont
aléatoirement orientés Up ou Down.
(C'est à dire la température est infinie) :
Transition Para?Ferro.
A chaque température et pour toute les mesures, nous
avons alors pris le temps d'équilibre  = 1000 MCS/Site et le temps de corrélation ô = 10 MCS/Site,
avec un temps d'observation global de 2000 MCS/Site. C'est à dire = 1000 MCS/Site et le temps de corrélation ô = 10 MCS/Site,
avec un temps d'observation global de 2000 MCS/Site. C'est à dire  =100 mesures indépendantes. =100 mesures indépendantes.
Les résultats normalisés à l'unité
( 1 ) sont représentés sur la figure 3.8 pour l'aimantation
moyenne par spin du système, sur la figure 3.9 pour la chaleur
spécifique moyenne à volume constant et sur la figure 3.10 pour
la susceptibilité magnétique moyenne du système.
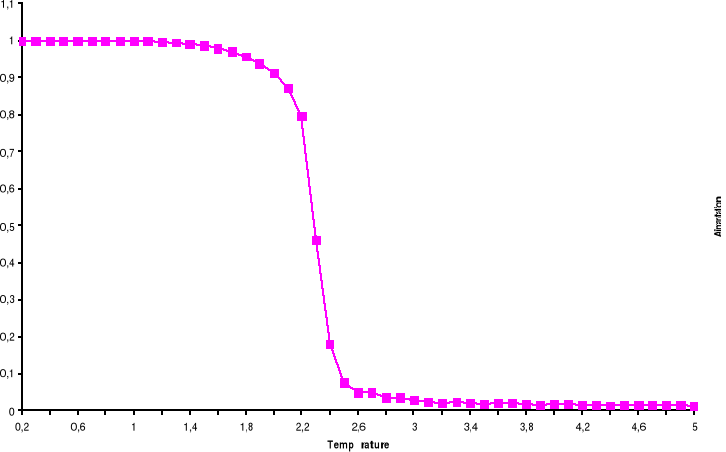
Figure
3.8 : Aimantation moyenne par spin du système
100x100 spins du modèle d'Ising à 2D en fonction de la
température, simulé avec l'algorithme de Métropolis. Le
tracé représente la Transition Ferro ? Para. Le tracé
représente la Transition Para? Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
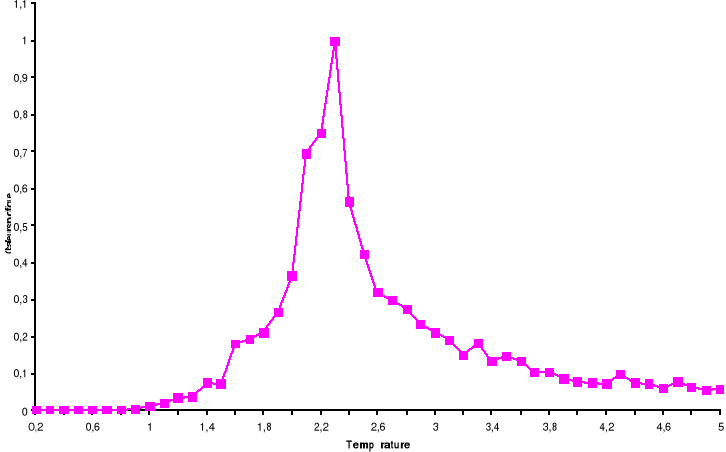
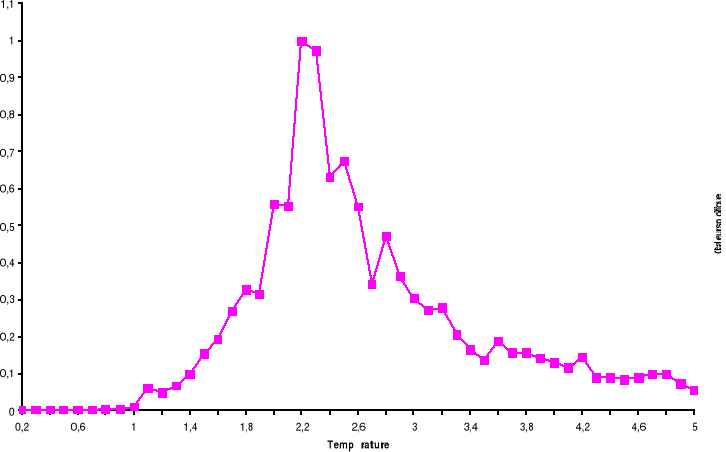
Figure
3.9 : Chaleur spécifique moyenne à
volume constant par spin du système 100x100 spins du modèle
d'Ising à 2D en fonction de la température, simulé avec
l'algorithme de Métropolis. Le tracé représente la
Transition Ferro ? Para. Le tracé représente la Transition Para?
Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
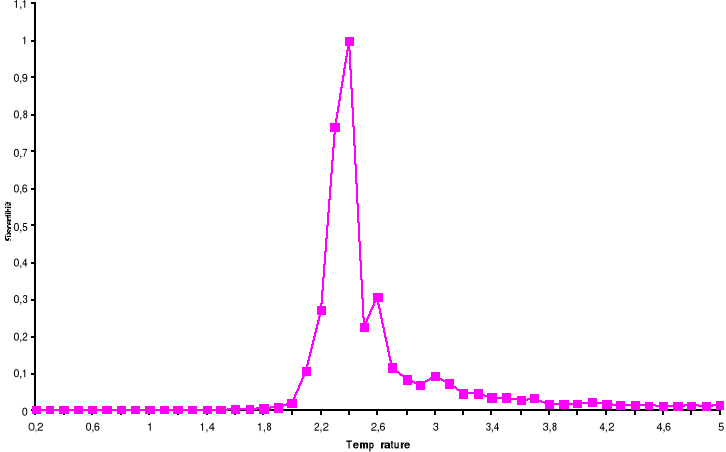
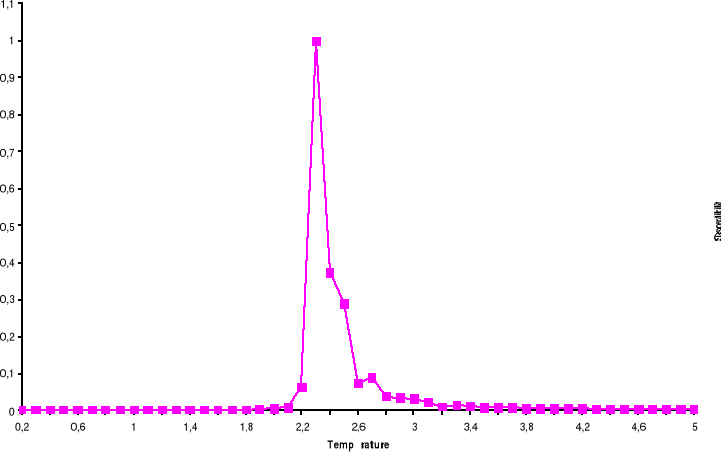
Figure
3.10 : Susceptibilité magnétique
moyenne par spin du système 100x100 spins du modèle d'Ising
à 2D en fonction de la température, simulé avec
l'algorithme de Métropolis. Le tracé représente la
Transition Ferro ? Para. Le tracé représente la Transition Para?
Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
Nous faisons le constat direct que les résultats sont
meilleurs pour la transition Para ? Ferro. Par ailleurs, aucune
hystérésis thermique n'a été observée durant
les deux cycles, et la transition de phase se produit à  =2.3K appelée température critique -la chaleur
spécifique et la susceptibilité magnétique divergent
toutes les deux à =2.3K appelée température critique -la chaleur
spécifique et la susceptibilité magnétique divergent
toutes les deux à  =2.3K, caractéristique d'un changement de phase- très
proche de la valeur théorique exacte =2.3K, caractéristique d'un changement de phase- très
proche de la valeur théorique exacte  =2.2692K déterminée par Onsager's. De même, les
résultats de la figure 3.8 montrent clairement qu'au dessus de la zone
critique, l'aimantation moyenne par spin devient petite et tend vers
zéro (0) aux grandes températures alors quelle tend vers un (1)
en dessous de cette zone, ce qui est caractéristique du paramètre
d'ordre d'une transition de phase. =2.2692K déterminée par Onsager's. De même, les
résultats de la figure 3.8 montrent clairement qu'au dessus de la zone
critique, l'aimantation moyenne par spin devient petite et tend vers
zéro (0) aux grandes températures alors quelle tend vers un (1)
en dessous de cette zone, ce qui est caractéristique du paramètre
d'ordre d'une transition de phase.
Ces résultats permettent également de conclure
en l'occurrence pour ce qui est de la chaleur spécifique et de la
susceptibilité que les fluctuations critiques ne sont pas
maîtrisées, problème lié à l'algorithme de
Métropolis et résolu par l'algorithme de Wolff.
En effet, lorsqu'on se rapproche de la transition de phase
(à partir des hautes températures), les spins initialement
désordonnés et non corrélés auront tendance
(grâce aux interactions entre eux) à se regrouper en blocs de
même orientation, formant ainsi des clusters dont la taille î
croît lorsque T? et diverge même à la transition. et diverge même à la transition.
3.5. Résultats
comparés des algorithmes de Métropolis et de Wolff
Contrairement à l'algorithme de Métropolis qui
traite individuellement chaque spin du cluster, l'algorithme de Wolff
considère le cluster comme un seul spin et le traite ainsi
globalement ; ce qui peut considérablement améliorer les
résultats. Afin de comparer les deux algorithmes, nous avons
considéré la transition de la phase Paramagnétique vers la
phase ferromagnétique (des hautes températures vers les basses
températures « refroidissement ») et nous avons
représenté sur la figure 3.11 l'aimantation moyenne par spin, sur
la figure 3.12 la chaleur spécifique moyenne à volume constant et
sur la figure 3.13 la susceptibilité magnétique moyenne du
système.
Ces courbes ainsi superposées, nous permettrons de
comparer facilement l'efficacité de chaque algorithme vis-à-vis
de l'autre pour les différentes étapes de la simulation.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
5
4,6
4,2
3,8
3,4
3
2,6
2,2
1,8
1,4
1
0,6
0,2
Température
Aimantation
Figure
3.11 : Aimantation moyenne par spin du
système de 100x100 spins du modèle d'Ising à 2D en
fonction de la température. Carrés : algorithme de
Métropolis ; Cercles : algorithme de Wolff.
Les traits continus ne sont justes qu'un guide pour l'oeil.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
5
4,6
4,2
3,8
3,4
3
2,6
2,2
1,8
1,4
1
0,6
0,2
Température
Chaleur spécifique
Figure
3.12 : : Chaleur spécifique moyenne par spin
du système de 100x100 spins du modèle d'Ising à 2D en
fonction de la température. Carrés : algorithme de
Métropolis ; Cercles : algorithme de Wolff.
Les traits continus ne sont justes qu'un guide pour l'oeil.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
5
4,6
4,2
3,8
3,4
3
2,6
2,2
1,8
1,4
1
0,6
0,2
Température
Susceptibilité
Figure 3.12 : :
Susceptibilité magnétique moyenne par spin du système de
100x100 spins du modèle d'Ising à 2D en fonction de la
température. Carrés : algorithme de Métropolis ;
Cercles : algorithme de Wolff.
Les traits continus ne sont justes qu'un guide pour l'oeil.
On remarque effectivement que l'algorithme de Wolff
améliore considérablement les résultats dans la zone
critique, et que les deux algorithmes sont équivalents à hautes
et basses températures (c'est à dire hors de la zone de
transition).
Cependant, contrairement à l'algorithme de
Métropolis dont les simulations ne prenaient que quelques heures (2
à 3 heures) sur un ordinateur Pentium III, l'algorithme de Wolff a pris
plus d'une semaine sur un ordinateur Pentium IV29(*). Rappelons que la fréquence de l'horloge du
processeur d'un ordinateur défini le nombre d'opérations que ce
calculateur peut traiter en une unité de temps (seconde), ce qui nous
permet de juger de la complexité des algorithmes que nous disposons.
Un programme de simulation a été écrit
sous Visual C++ 6.0 et baptisé ISampling, nous présentons
ci-dessous quelques écrans principaux, notamment ceux permettant de
modifier les paramètres de simulation.
3.6. Présentation du programme de
simulation : ISampling
Afin de rendre plus pratique l'étude que nous avons
mené, calculer les valeurs des propriétés, un programme de
simulation a été mis sur pieds. Lequel programme écrit
sous Visual C++ 6.0, exécute principalement les instructions des
algorithmes de base, de calcul que nous avons décrit plus haut. Faisant
référence à la donnée d'un échantillonnage
important, `ISampling' permet non seulement de calculer les grandeurs physiques
d'un système, mais aussi de représenter sont réseau de
spin, tel à la figure 3.3 précédente
A travers ISampling, il est possible d'obtenir une simulation
fidèle du comportement de l'énergie, l'aimantation, la chaleur
spécifique moyenne, la susceptibilité magnétique,
l'entropie, de l'équilibre thermique, de la fonction d'auto
corrélation sous les algorithmes de Métropolis ou Wolff. (les
versions futures, V3 et plus prendrons en compte d'autres algorithmes de
simulation ainsi que d'autres modèles : Ising à 3D, XY,
Heisemberg à 2D ou 3D).
Nous ne ferons pas dans ce mémoire une
présentation détaillée du programme ISampling. A cet
effet, le lecteur devra se référer au document d'utilisation du
programme.
La fenêtre principale de ISampling contient :
une barre de menus { Fichier ; Affichage ;
Simulation ; Options, Aide}
une barre d'outils {  } permettant respectivement d'exécuter } permettant respectivement d'exécuter  une simulation précédemment paramétrée, de
faire un choix de visualisation une simulation précédemment paramétrée, de
faire un choix de visualisation  d'une grandeur quelconque, d'ouvrir un nouveau fichier, d'enregistrer,
d'imprimer, d'établir les options de simulation d'une grandeur quelconque, d'ouvrir un nouveau fichier, d'enregistrer,
d'imprimer, d'établir les options de simulation  et du graphique et du graphique . .
une zone de résultat où s'affichent les
résultats (graphes) de notre simulation telle que nous l'avons
paramétré, exécuté et sous l'échelle que
nous avons spécifiée
une barre d'état donnant à gauche les
états d'exécution du programme et à droite la date du
système.
Pour opérer une simulation, ISampling a besoin des
paramètres de la simulation (Ctrl + P). Elles sont introduites dans la
fenêtre d'option de simulation, puis il a besoins des paramètres
graphique (Ctrl + G) permettant de configurer le repère sur lequel les
données devront êtres représentées et enfin
l'utilisateur lance la simulation (Ctrl + E).
La fenêtre d'option de simulation du sous menu
`Simulation' du menu `Option' demande :
les informations sur le type de simulation que l'on
souhaite effectuer ou d'algorithme que l'on désire utiliser.
les information sur l'échantillon : Le
paramètre de maille `a' et la taille de l'échantillon,
l'énergie d'interaction J entre voisins et de l'état du
système (para ou ferro)
les informations de simulation : les temps
d'observation, d'équilibre et de corrélation du système en
MCS/Site, les températures initiales et finales ainsi que son pas de
variation, le type de perturbation et de générateur de nombres
aléatoires appliqué.
Il offre par ailleurs aussi la possibilité de faire ces
calculs à partir de la fonction de partition.
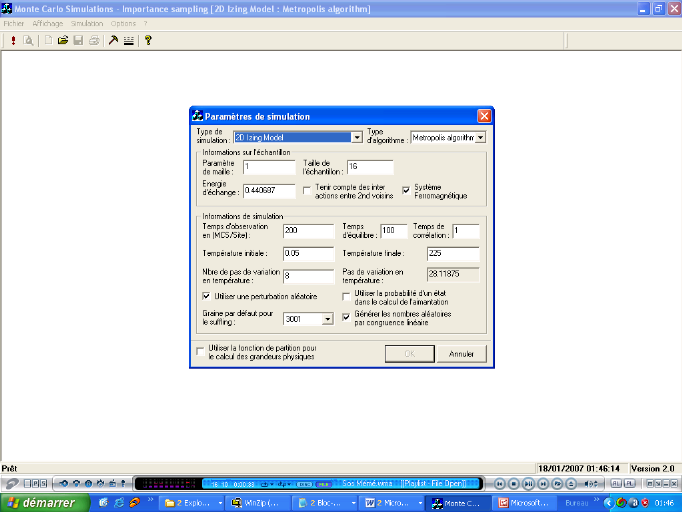
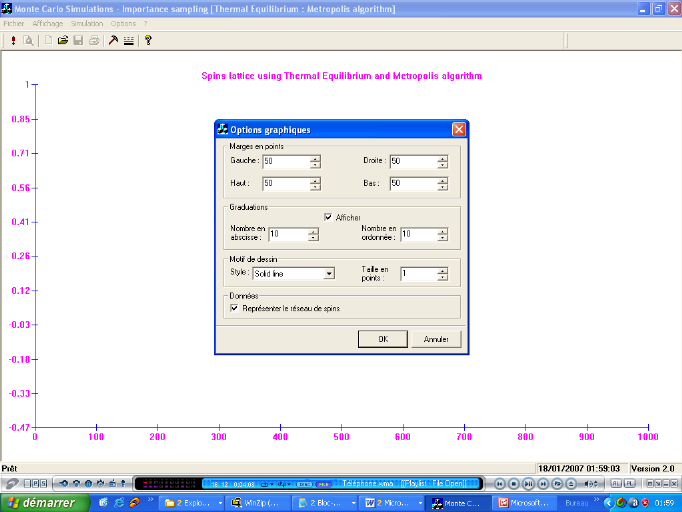
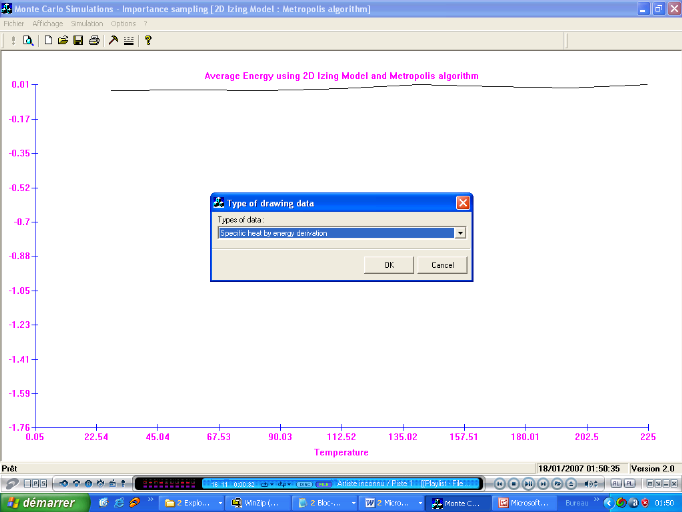
Figure 3.14 :
Fenêtres de paramétrage de simulation (gauche) et d'options
graphiques (droite)
Figure 3.15 : Fenêtre du choix
de visualisation d'une grandeur
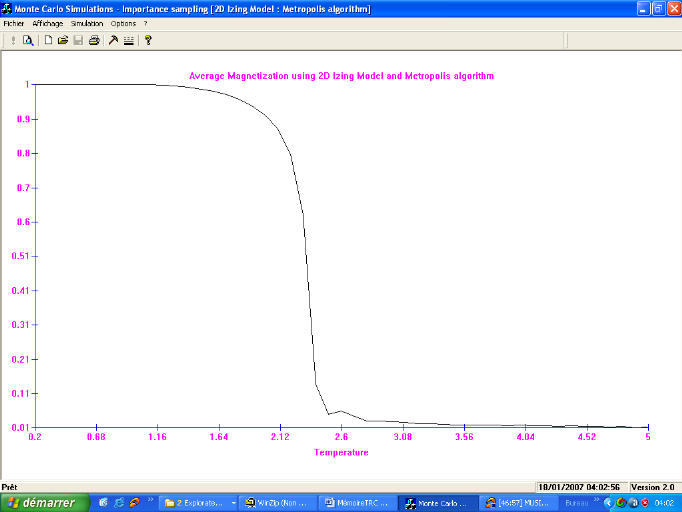
Figure 3.16 : Fenêtre
principale du programme ISampling
CONCLUSION GENERALE
L'étude du comportement de la matière
vis-à-vis des variations qu'elle peut subir face à l'influence
des attaques extérieures reste un point intéressant de la
recherche en physique. Pour y arriver, nous avons simulé à petite
échelle un modèle d'aimant à deux orientations possibles
(modèle d'Ising) par les techniques probabilistes et
d'échantillonnage important (méthode de Monte Carlo). Il
était question pour nous d'étudier les phénomènes
critiques observables pour les transitions de phase magnétiques
« Ferro ? Para ».
Pour ce faire, après avoir brièvement
présenté les expressions théoriques des grandeurs
physiques caractéristiques du système sous leurs formes
sommables, puis les méthodes de Monte Carlo et par là - dans un
but de comparaison- décrit les algorithmes de Métropolis et
Wolff, nous sommes arrivé à l'obtention des courbes
d'évolution des caractéristiques thermodynamiques du
système. Dans cet élan d'esprit nous avons dégagé
les avantages et insuffisances de l'algorithme de Métropolis puis les
corrections apportées par Ulli Wolff dans l'algorithme de Wolff.
Pour évaluer les paramètres physiques
thermodynamiques du système tel l'énergie, l'aimantation, la
chaleur spécifique à volume constant, la susceptibilité
magnétique, l'entropie, nous avons laissé tourné nos
programmes durant un certain temps afin d'atteindre l'état
d'équilibre, ce après quoi nous avons appliqué
successivement les algorithmes de Métropolis et Wolff. Nous avons au
cours de nos simulations plus insisté sur les systèmes pris
à haute températures, où les spins sont
aléatoirement disposés, et effectué un
« refroidissement » en passant par la température
critique 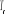 jusqu' à zéro degré. Nous constatons que les
résultats présentés par les deux algorithmes sont
identiques lorsque nous nous éloignons de jusqu' à zéro degré. Nous constatons que les
résultats présentés par les deux algorithmes sont
identiques lorsque nous nous éloignons de 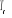 mais ils sont meilleurs au voisinage de mais ils sont meilleurs au voisinage de 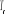 avec l'algorithme de Wolff. Ce constat provient de ce que l'algorithme
de Wolff au lieu de traiter les spins individuellement comme son homologue
Métropolis, noie les petites fluctuations observables dans un bloc de
spins qu'il considère au titre d'un seul. Ce bloc de spin (cluster) a la
qualité de présenter une configuration uniforme. Cette attitude
est donc fort appréciable à la zone critique où les
fluctuations sont généralement élevées, mais moins
utile aux températures extrêmes. Cependant, les étapes
d'exécution de l'algorithme de Wolff offrent la contrainte
matérielle qu'elles demandent beaucoup de mémoire pour stocker
les données qu'il réutilise, ce qui entraîne la
nécessité de disposer d'un calculateur d'excellente
qualité. avec l'algorithme de Wolff. Ce constat provient de ce que l'algorithme
de Wolff au lieu de traiter les spins individuellement comme son homologue
Métropolis, noie les petites fluctuations observables dans un bloc de
spins qu'il considère au titre d'un seul. Ce bloc de spin (cluster) a la
qualité de présenter une configuration uniforme. Cette attitude
est donc fort appréciable à la zone critique où les
fluctuations sont généralement élevées, mais moins
utile aux températures extrêmes. Cependant, les étapes
d'exécution de l'algorithme de Wolff offrent la contrainte
matérielle qu'elles demandent beaucoup de mémoire pour stocker
les données qu'il réutilise, ce qui entraîne la
nécessité de disposer d'un calculateur d'excellente
qualité.
Nous pouvons dire de ce qui précède que les
simulations numériques sont un excellent moyen de calcul des
données statistiques des systèmes physiques au vu des
résultats obtenus vis-à-vis des valeurs théoriques connus
depuis la statistique de Boltzmann.
Au terme de notre travail, nous pouvons dire que les
comparaisons que nous avons réalisées sur le plan pratique nous
ont donnés des résultats favorables nonobstant la limite de nos
moyens matériels. Par ailleurs, nous sommes désormais capable de
comprendre les principes des simulations par les méthodes de Monte
Carlo, mieux encore les algorithmes de Métropolis et Wolff et surtout de
pouvoir retrouver les courbes d'évolution des grandeurs thermodynamiques
d'après leurs expressions théoriques.
Toutefois notons que la détermination exacte de
l'exposant dynamique z, l'étude de la dynamique moléculaire sur
un système de spins ainsi que l'extension de ce travail en 3D nous
offriraient plus d'éléments d'appréciation. Par ailleurs,
le modèle d'Ising par son caractère discret, ne nous offre pas la
réalité physique de la matière lorsqu'elle est
considérée comme étant un système continu. Il
serait ainsi judicieux d'explorer des modèles continus tels XY et
Heisemberg.
REFERENCES BIBLIOGRAPHIQUES
[1] K. Binder, D.W. Heermann: Monte Carlo
Simulation in Statiscal Physics, and introduction, 3rt edition,
(springer serie in Solid-State Sciences)
[2] M.E.J. NEWMAN &
G.T.BARKERMAN, « Monte Carlo Methods in Statical
Physics », Oxford University press, 2002
[3] Oumarou BOUBA, Notes de cours
«Thermodynamique statistique» de licence, Université
de Ngaoundéré, 2nd semestre 2004
[4] L. Onsager. Phys. Rev. 65, 117 (1944)
[5] David FOUEJIO, Thèse de Doctorat
(NR) de l'Université du Maine (France), ½Etude par RPE et
Diffraction de rayon X des transitions de phase de KGaF4½, 1995
[6] Philippe NDONFACK, Mémoire de
maîtrise de Physique « Simulation des
phénomènes physiques par les méthodes de Monte
Carlo : Cas du modèle d'Ising pour l'étude des transitions
de phase» ; 2006
[7] Dominique BAKRY, Notes de cours DEA.
[8] Eric GAUME, INRS-EAU, Programme Doctoral,
TD application de l'algorithme METROPOLIS pour analyse de
sensibilité d'un modèle stochastique de pluie, 29 Avril
1999.
[9] Pascal VIOT, Notes de Cours de Master
[10] Vincent POUTHIER, INTRODUCTION AUX
PHENOMENES CRITIQUES, Notes de cours DEA
[11] David FOUEJIO, TP3 de maîtrise de
Physique, Etude du comportement en température d'un système
de spins à deux orientations possibles : Modèle d'Ising
à 2 D ; Université du Maine (France) ; 1995 -
1996
[12] K.G. WILSON, Pour la SCIENCE, Vol 10,
N° 24, p16 (1979)
ANNEXES
ANNEXE 1 :
ORGANIGRAMME DU PROCESSUS DE MARKOV.
Xn = ì
P [0;1]
P(ì?í)>P
n?n + 1
Oui
Xn = í
P est une variable uniforme aléatoire
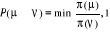
non
Figure
A1 : Organigramme du processus de Markov
ANNEXE
2 :
ORGANIGRAMME DE L'ALGORITHME DE
MÉTROPOLIS.
Les différents états sont
générés par le processus Markovien
Pf > P
oui
Perturbation
(retournement de spin)
Ef < Ei
non
Sf ; Ef ; P(Ef)
P est une variable uniforme aléatoire
0 < P < 1
Si ; Ei
Sf ; Ef
Sf ; Ef
oui
non
Figure
A2 : Organigramme du processus de
Métropolis
ANNEXE
3 :
PROGRAMME EN C++ DE L'ALGORITHME DE MÉTROPOLIS
Version simplifiée
/*beta = température inverse
*prob[] = tableau des probabilités d'acceptation
* s[] = matrice de spins avec les conditions de bord
* l = constante de longueur de la matrice
*/
# define N (l*l)
# define XNN 1
# define YNN l
int s[n];
double prob[5];
double beta;
void initialisation ()
{
int i;
for (i=2; i<5; i+=2)
prob[i]=exp(-2*beta*i);
}
void balayage ()
{
int i,k;
int nn,sum,delta;
for (k=0; k<N; k++)
{i=n*drandom(); /* choix aléatoire du site i*/
if ((nn=i+XNN)>=N) /* calcul de la somme sur les voisins
*/
nn -= N ;
sum = s[nn];
if ((nn=i-XNN)< 0)
nn += N ;
sum += s[nn];
if ((nn=i+YNN)>=N)
nn -= N ;
sum = s[nn];
if ((nn=i-YNN)< 0)
nn -= n ;
sum += s[nn];
delta = sum*s[i]; /* calcul de l'énergie lors du
retournement de spin*/
if (delta<=0) /* vérification de la
nécessité de retournement de spin*/
{
s[i]=-s[i] ;
} else if (drandom()<prob[delta])
{
S[i]=-s[i];
}
}
}
ANNEXE
4 :
ORGANIGRAMME DE L'ALGORITHME DE WOLFF
Les différents états sont
générés par le processus Markovien
Génération des clusters
Calcul des propriétés
Si
Si = [Sn+ ou Sn-] et tous
les voisins
Sk+1 ? Si
i = i +1
Algorithme de Métropolis
n+ = (i+1; j+1)
n- = (i-1;j-1)
Sk ? Si ; i =i+1
Parcours des 1ers voisins n+ et n-
oui
non
non
Figure
A4 : Organigramme du processus de Wolff
ANNEXE
5 :
PROGRAMME EN C++ DE L'ALGORITHME DE
WOLFF
/*padd = 1-exp(-2*beta*J)
*s[] = matrice de spin avec les conditions de bord
considérées
*s[] = matrice de spins avec les conditions de bord
*l = constante de longueur de la matrice
*/
# define N (l*l)
# define XNN 1
# define YNN l
int s[N];
double padd;
void etape ()
{
int i;
int sp ;
int oldspin, newspin ;
int current, nn;
int stack[N];
/* choix du spin central pour le cluster, */
i=n*drandom() ; /* Le mettre dans le tas et le
retourner */
stack[0]=i ;
sp = 1;
oldspin = s[i];
newspin = -s[i];
s[i] = newspin;
while (sp)
{ /*pousser le spin du tas par la méthode
LIFO*/
current = stack[--sp];
if ((nn =current+XNN)>=N) /* recherché des
voisins*/
nn -= N;
if (s[nn]==oldspin)
if (drandom()<padd)
{
Stack[sp++]=nn;
S[nn]=newspin;
}
if ((nn =current-XNN)<0) /* recherché des
voisins*/
nn += N;
if (s[nn]==oldspin)
if (drandom()<padd)
{
stack[sp++]=nn;
s[nn]=newspin;
}
if ((nn =current+YNN)>=N) /* recherché des
voisins*/
nn -= N;
if (s[nn]==oldspin)
if (drandom()<padd)
{
Stack[sp++]=nn;
S[nn]=newspin;
}
if ((nn =current-YNN)<0) /* recherché des
voisins*/
nn += N;
if (s[nn]==oldspin)
if (drandom()<padd)
{
Stack[sp++]=nn;
S[nn]=newspin;
}
}
}
ANNEXE
6 :
ALGORITHME DE GÉNÉRATION DES NOMBRES
ALÉATOIRES PAR CONGRUENCE LINEAIRE AVEC `SHUFFLING'.
Version simplifiée
# include <math.h>
# define a 1680
# define m 2147483647
# define q 127773
# define r 2836
# define conv (1.0/(m-1))
# define N 64
long i ;
long y ;
long j[N];
double drandom()
{
long L;
long k;
L = i/q;
i = a*(i-q*L)-r*L;
if (i<0)
I += m;
/* début du shuffling (mélange)*/
k = floor ((double) y*N/m);
y = j[k];
j[k] = i;
/* fin du mélange*/
return conv*(y-1);
}L'algorithme de génération des nombres
aléatoires par congruence linéaire proposé par lewis et
al. en 1969 [2] propose des nombres aléatoires « non
corrélés » compris entre 0 et 1. En 1976 Bays et Durham
introduisirent dans cet algorithme un reclassement désordonné des
nombres aléatoires proposés, rendant plus libres deux nombres
consécutivement générés : c'est le shuffling.
Il se défini ici par le vecteur j[k] introduit à la
dernière boucle de l'algorithme initial de Lewis.
Version complète, extraite de
ISampling
/* RandomNumber.cpp: implementation of the CRandomNumber
class.*/ ///////
#include "stdafx.h"
#include "ISampling.h"
#define _MAX_SUFFLING_NUMBER_ 64//97
#ifdef _DEBUG
#undef THIS_FILE
static char THIS_FILE[]=__FILE__;
#define new DEBUG_NEW
#endif
////////////////////////////// CRandomNumber
CRandomNumber::CRandomNumber()
{
m_psn = NULL;
/* Seed the random-number generator with current time so that the
numbers will be different every time we run. */
srand((unsigned)time(NULL));
}
CRandomNumber::~CRandomNumber()
{
if (m_psn != NULL)
delete[] m_psn;
m_psn = NULL;
}
/* Standard random support returns a pseudorandom integer in the
range 0 to n - 1 */
unsigned int CRandomNumber::GetNumber(unsigned int n)
{
return (rand() % n);
}
/*returns a floating point pseudorandom number in the range 0 to
1 */
double CRandomNumber::GetNumber()
{
double dblRet = rand();
dblRet = dblRet / RAND_MAX;
return dblRet;
}
/* Initialise le générateur de nombre
aléatoires permettant d'effectuer le "shuffling" (mélange) des
nombres générés par le système.*/
void CRandomNumber::InitShuffling()
{
if (m_psn == NULL)
m_psn = new double[_MAX_SUFFLING_NUMBER_];
for (int nIndex = 0; nIndex < _MAX_SUFFLING_NUMBER_;
nIndex++)
m_psn[nIndex] = GetNumber();
}
/* Renvoie un nombre aléatoire par congruence
linéaire tout en utilisant le "shuffling". Le nombre aléatoire
renvoyé est situé dans l'intervalle [0, 1[.La graine ou germe et
générée par le système.*/
double CRandomNumber::GetSysShuffledNumber()
{
VERIFY(m_psn != NULL);
double dblSeed = GetNumber();
int nIndex = int(dblSeed*_MAX_SUFFLING_NUMBER_);
if (nIndex >= _MAX_SUFFLING_NUMBER_)
nIndex = _MAX_SUFFLING_NUMBER_ - 1;
double dblRet = m_psn[nIndex];
m_psn[nIndex] = dblSeed;
return dblRet;
}
/* Renvoie un nombre aléatoire par congruence
linéaire tout en utilisant le "shuffling". Le nombre aléatoire
renvoyé est situé dans l'intervalle [0, n-1]. La graine ou germe
et générée par le système.*/
unsigned int CRandomNumber::GetSysShuffledNumber(unsigned int
n)
{
unsigned int nRet = unsigned int(GetSysShuffledNumber() *
RAND_MAX);
return (nRet % n);
}
#define _a_ 16807
#define _m_ INT_MAX
#define _q_ 127773
#define _r_ 2836
#define _conv_ 1.0/_m_
// static function CRandomNumber::IsValidSeed(int nSeed)
{
switch (nSeed)
{
case Default_Seed :
case Default_Seed_Ex :
case Default_Seed1 :
return true;
}
return false;
}
/* Renvoie un nombre aléatoire par congruence
linéaire. Le nombre aléatoire renvoyé est situé
dans l'intervalle [0, n-1].nSeed est la graine.*/
unsigned int CRandomNumber::GetLinearNumber(unsigned int&
nSeed, unsigned int n)
{
unsigned int nRet = unsigned int(GetLinearNumber(nSeed) *
_m_);
return (nRet % n);
}
/* Renvoie un nombre aléatoire par congruence
linéaire. Le nombre aléatoire renvoyé est situé
dans l'intervalle [0, 1[. nSeed est la graine.*/
double CRandomNumber::GetLinearNumber(unsigned int& nSeed)
{
unsigned int nValue = nSeed / _q_;
nSeed = _a_*(nSeed - _q_*nValue) - _r_*nValue;
if (nSeed < 0)
nSeed += _m_;
else if (nSeed >= _m_)
nSeed -= _m_;
return nSeed*_conv_;
}
/* Initialise le générateur de nombre
aléatoires permettant d'effectuer le "shuffling" (mélange) :
nSeed est la graine.*/
void CRandomNumber::InitShuffling(unsigned int& nSeed)
{
if (m_psn == NULL)
m_psn = new double[_MAX_SUFFLING_NUMBER_];
nSeed = 2*nSeed + 1;
for (int nIndex = 0; nIndex < _MAX_SUFFLING_NUMBER_;
nIndex++)
m_psn[nIndex] = GetLinearNumber(nSeed);
}
/* Renvoie un nombre aléatoire par congruence
linéaire tout en utilisant le "shuffling". Le nombre aléatoire
renvoyé est situé dans l'intervalle [0, 1[. nSeed est la
graine.*/
double CRandomNumber::GetShuffledNumber(unsigned int&
nSeed)
{
VERIFY(m_psn != NULL);
int nSize = _MAX_SUFFLING_NUMBER_ - 1;
double dblSeed = GetLinearNumber(nSeed);
int nIndex = int(dblSeed*nSize + 1);
if (nIndex < 0)
nIndex = 0;
else if (nIndex > nSize)
nIndex = nSize;
double dblRet = m_psn[nIndex];
m_psn[nIndex] = _conv_*(nSeed - 1); //dblSeed
return dblRet;
}
/* Renvoie un nombre aléatoire par congruence
linéaire tout en utilisant le "shuffling". Le nombre aléatoire
renvoyé est situé dans l'intervalle [0, n-1]. nSeed est la
graine.*/
unsigned int CRandomNumber::GetShuffledNumber(unsigned int&
nSeed, unsigned int n)
{
unsigned int nRet = unsigned int(GetShuffledNumber(nSeed) *
_m_);
return (nRet % n);
}
const unsigned int _m1_ = 259200, _m2_ = 134456, _m3_ =
243000;
const unsigned int _ia1_ = 7141, _ia2_ = 8121, _ia3_ = 4561;
const double _rm1_ = 1.0/_m1_, _rm2_ = 1.0/_m2_;
const unsigned int _ic1_ = 54773, _ic2_ = 28411, _ic3_ =
51349;
/* Initialise le générateur de nombre
aléatoires permettant d'effectuer le "shuffling" (mélange):
nSeed1, nSeed2, nSeed3 sont les graines.*/
void CRandomNumber::InitShuffling(unsigned int& nSeed1,
unsigned int& nSeed2, unsigned int& nSeed3)
{
if (m_psn == NULL)
m_psn = new double[_MAX_SUFFLING_NUMBER_];
nSeed1 = -abs(1 + 2*nSeed1);
nSeed1 = (_ic1_ - nSeed1) % _m1_;
nSeed1 = (_ia1_*nSeed1 + _ic1_) % _m1_;
nSeed2 = nSeed1 % _m2_;
nSeed1 = (_ia1_*nSeed1 + _ic1_) % _m1_;
nSeed3 = nSeed1 % _m3_;
for (int nIndex = 0; nIndex < _MAX_SUFFLING_NUMBER_;
nIndex++)
{
nSeed1 = (_ia1_*nSeed1 + _ic1_) % _m1_;
nSeed2 = (_ia1_*nSeed2 + _ic2_) % _m2_;
m_psn[nIndex] = (nSeed1 + nSeed2)*_rm1_*_rm2_;
}
}
/* Renvoie un nombre aléatoire par congruence
linéaire tout en utilisant le "shuffling". Le nombre aléatoire
renvoyé est situé dans l'intervalle [0, 1[. nSeed1, nSeed2,
nSeed3 sont les graines.*/
double CRandomNumber::GetShuffledNumber(unsigned int& nSeed1,
unsigned int& nSeed2,
unsigned int& nSeed3)
{
VERIFY(m_psn != NULL);
nSeed1 = (_ia1_*nSeed1 + _ic1_) % _m1_;
nSeed2 = (_ia1_*nSeed2 + _ic2_) % _m2_;
nSeed3 = (_ia1_*nSeed3 + _ic3_) % _m3_;
int nSize = _MAX_SUFFLING_NUMBER_ - 1;
int nIndex = nSize*nSeed3 / _m3_;
if (nIndex < 0)
nIndex = 0;
else if (nIndex > nSize)
nIndex = nSize;
double dblRet = m_psn[nIndex];
m_psn[nIndex] = (nSeed1 + nSeed2)*_rm1_*_rm2_;
return dblRet;
}
Vu la longueur d'un tel programme, nous nous réservons
de présenter ici les programmes complets issus de ISampling pour les
autres algorithmes. Leurs écritures simplifiées sont largement
suffisantes pour guider le lecteur.
ANNEXE 7 :
CLASSIFICATION DES TRANSITIONS DE
PHASE
Tableau A7 : Classification
des transitions
|
Transitions de phase
|
|
Classification d'Erhenfest
|
Propriétés
|
Exemple
|
Classification
de Landau
|
|
Transition du 1er ordre
|
Discontinuité sur les grandeurs thermodynamiques
Fonctions en escalier
|
l'eau
|
Transition sans paramètres d'ordre
|
|
Transition avec paramètres d'ordre
|
Si le paramètre est discontinu
|
|
Transition du 2nd ordre
|
Continuité sur les courbes des grandeurs
|
Matériaux ferromagnétiques
|
Si le paramètre est continu
|
|
Transition d'ordre > 2
|

... et si seulement vous avez retenu l'infiniment
petit qui peut être tiré de ce document ;
... et si seulement ce travail pouvait permettre de mieux
cerner, par un plus large public les mystères de la
science ;
... et si seulement vous pensez qu'il faut encore en dire
plus, après avoir parcouru ces textes ;
... et si seulement ...
Alors là, nous aurions la fierté d'avoir
été un temps soit peu utile ;
Tchueroschoy, Recueils , 1996, page 77
* 1 Cette probabilité
peut aussi être appelée `poids statistique' étant
donné quelle définie la force de présence du
système à l'état ì.
* 2 « F »
est en d'autre terme l'énergie totale du système
ôtée de l'énergie du désordre dérivant de
l'agitation thermique.
* 3Linguistique : la
fluctuation est une variation ou dénivellation d'une entité
mesurée.
* 4Linguistique : la
corrélation est le lien entre des éléments en relation
(dits corrélés)
* 5 L'écart type peut
mieux se comprendre comme étant une déviation standard.
* 6 La chaleur massique
C ; est une grandeur extensible car dépendant de E (voir
éq.(1.20))
* 7 La réponse d'une
grandeur suite à une excitation a une expression linéaire de
celle-ci.
* 8 Mesure du lien entre les
points d'une variable x, son signe va avec la fluctuation.
* 9 s = #177;1 (unité
de longueur de spin) suivant qu'il soit ? ou ?(voir physique atomique)
* 10 [5], [6] Chaque spin a
8 voisins. Dans la matrice, Les spins d'extrémité Si?N
sont voisins. D'un point de vue algorithmique, on imposera dans le cas d'une
chaîne de longueur N, SN+i = SN. Ces effets peuvent
influencer en raison de la petitesse du réseau !
* 11 Le processus est une
famille 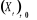 de variable aléatoires à valeurs dans un espace mesurable
E quelconque, indexée par de variable aléatoires à valeurs dans un espace mesurable
E quelconque, indexée par 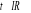 ; il est dit continu si ; il est dit continu si  . [10] . [10]
* 12 On parle aussi de
Balance détaillée provenant de l'anglais « Detailed
balance »
* 13 P étant la
matrice de Markov ou la matrice stochastique du processus de Markov.
* 14 Un tableau
récapitulant les différentes classifications est proposé
en annexe 7.
* 15 Transition d'ordre
supérieur ou transitions multi critiques
* 16 d est la dimension de
l'espace. Il est 3 dans ce cas.
* 17 ô est la
durée de vie moyenne des clusters.
* 18 En
réalité, l'exposant critique est plutôt zí et non z.
C'est pour cela qu'il n'est pas un exposant universel comme í,á,
ã. (ne pas le confondre à la fonction de partition !).
* 19 La TGR reconfigure le
système considéré en bloc d'éléments. Il est
donc semblable à une vision par domaine de spin (cluster) que par spin.
Les algorithmes de domaine sont calqués sur les modèles de la
TGR
* 20 La fonction est
symétrique, c'est à dire f(ì,í) =
f(í,ì)). ì et í étant les points (sites ou
états) quelconques de l'espace (matrice)
* 21 Pour le modèle
d'Ising à 2 dimensions on a (d + z = 4) soit L4
* 22 Un spin central
à 4 proches voisins de 1er ordre et 8 proches voisins au
2nd ordre.
* 23 Phase
para-magnétique.
* 24 Phase
ferro-magnétique
* 25 MCS vient de l'anglais
« Monte Carlo Step »
* 26 La graine est un nombre
caractéristique des algorithmes de génération de nombres
aléatoires
* 27 Nous avons
essayé avec les graines 1003, 10401, 3001 d'après la
documentation [2]
* 28 La trempe est une
opération de traitement thermique qu'on opère sur des alliages,
pour leurs conférer des propriétés mécaniques
spéciales. Elle consiste à une chute brutale de
température par trempage dans un liquide. Pour nos simulations, nous
nous plaçons directement à une température
déterminée partant d'une autre. Ce qui ressemble à une
trempe. Dans la réalité, nos matériaux se trouent dans un
four à température contrôlée et variable. De ce fait
les variations de températures sont douces.
* 29 Nous avons
utilisé des ordinateurs Pentium III dont la fréquence de
l'horloge du processeur était de 1.2 GHz et Pentium IV tournant à
2.2 GHz pour 512 Mo de RAM chacun.
| 


