2ième Partie : Etude pratique
Chapitre 3
Les résultats des
simulations
3.1. Introduction
Nous avons précédemment présenté
la méthode de Monte Carlo et les différents algorithmes qui
l'utilisent - en particulier l'algorithme de Métropolis et l'algorithme
de Wolff -, les notions liées à la transition de phase. Tous ces
éléments devaient nous permettre de déterminer les
grandeurs physiques liées à un système donné. Pour
y arriver, nous présentions les expressions théoriques de ces
grandeurs et à présent, à travers les conditions
imposées aux chapitres précédents, nous exposerons dans ce
chapitre les résultats des simulations numériques pour
l'étude des transitions de phases Ferromagnétique vers
Paramagnétique et vis-versa à l'aide du modèle d'Ising
à 2 D. Ainsi donc nous utiliserons l'échantillonnage important
appliqué dans un premier temps à l'algorithme de
Métropolis et dans un second temps à l'algorithme de Wolff au
voisinage de la transition de phase.
Afin de simplifier le problème, nous avons
considéré un réseau carré de paramètre de
maille ?a? dans lequel les spins sont placés sur les sites (i , j) du
réseau, chaque spin pouvant prendre les valeurs +1 (Up) ou -1 (Down).
Nous avons opéré nos simulations en champ magnétique nul
(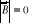 ), l'Hamiltonien de spin du système s'écrit donc ), l'Hamiltonien de spin du système s'écrit donc
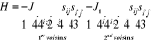
Sij étant le spin d'abscisse i et
d'ordonnée j, les J étant les intégrales d'échange
entres voisins.
Pour l'étude de la transition de phase, nous avons
considéré la plage d'intervalle des températures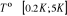 . Quant aux valeurs d'échange d'énergie, nous sommes
partis de la valeur théorique exacte déterminée par
Onsager [4] . Quant aux valeurs d'échange d'énergie, nous sommes
partis de la valeur théorique exacte déterminée par
Onsager [4]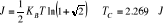 où J est donnée en °K. où J est donnée en °K.
Nous avons étudié le comportement en
température :
o du temps de corrélation,
ô
o de l'énergie interne du système de spins
E
o de l'aimantation du système, M
o de la chaleur spécifique à volume constant
C
o de la susceptibilité magnétique du
système, ÷
ainsi que les fluctuations critiques.
Pour toutes les simulations, nous avons
considéré 
Mais avant d'effectuer la mesure de ces grandeurs, nous devons
nous assurer que notre système de spins se trouve à l'état
d'équilibre thermodynamique (cf. chapitre 1 § 1.A.2).
C'est la configuration dans laquelle l'on peut appliquer la statistique de
Maxwell Boltzmann pour le calcul de la probabilité d'un état et
par ailleurs, que les corrélations entres deux mesures
consécutives sont faibles.
| 


