CONCLUSION GENERALE
L'étude du comportement de la matière
vis-à-vis des variations qu'elle peut subir face à l'influence
des attaques extérieures reste un point intéressant de la
recherche en physique. Pour y arriver, nous avons simulé à petite
échelle un modèle d'aimant à deux orientations possibles
(modèle d'Ising) par les techniques probabilistes et
d'échantillonnage important (méthode de Monte Carlo). Il
était question pour nous d'étudier les phénomènes
critiques observables pour les transitions de phase magnétiques
« Ferro ? Para ».
Pour ce faire, après avoir brièvement
présenté les expressions théoriques des grandeurs
physiques caractéristiques du système sous leurs formes
sommables, puis les méthodes de Monte Carlo et par là - dans un
but de comparaison- décrit les algorithmes de Métropolis et
Wolff, nous sommes arrivé à l'obtention des courbes
d'évolution des caractéristiques thermodynamiques du
système. Dans cet élan d'esprit nous avons dégagé
les avantages et insuffisances de l'algorithme de Métropolis puis les
corrections apportées par Ulli Wolff dans l'algorithme de Wolff.
Pour évaluer les paramètres physiques
thermodynamiques du système tel l'énergie, l'aimantation, la
chaleur spécifique à volume constant, la susceptibilité
magnétique, l'entropie, nous avons laissé tourné nos
programmes durant un certain temps afin d'atteindre l'état
d'équilibre, ce après quoi nous avons appliqué
successivement les algorithmes de Métropolis et Wolff. Nous avons au
cours de nos simulations plus insisté sur les systèmes pris
à haute températures, où les spins sont
aléatoirement disposés, et effectué un
« refroidissement » en passant par la température
critique 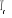 jusqu' à zéro degré. Nous constatons que les
résultats présentés par les deux algorithmes sont
identiques lorsque nous nous éloignons de jusqu' à zéro degré. Nous constatons que les
résultats présentés par les deux algorithmes sont
identiques lorsque nous nous éloignons de 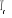 mais ils sont meilleurs au voisinage de mais ils sont meilleurs au voisinage de 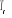 avec l'algorithme de Wolff. Ce constat provient de ce que l'algorithme
de Wolff au lieu de traiter les spins individuellement comme son homologue
Métropolis, noie les petites fluctuations observables dans un bloc de
spins qu'il considère au titre d'un seul. Ce bloc de spin (cluster) a la
qualité de présenter une configuration uniforme. Cette attitude
est donc fort appréciable à la zone critique où les
fluctuations sont généralement élevées, mais moins
utile aux températures extrêmes. Cependant, les étapes
d'exécution de l'algorithme de Wolff offrent la contrainte
matérielle qu'elles demandent beaucoup de mémoire pour stocker
les données qu'il réutilise, ce qui entraîne la
nécessité de disposer d'un calculateur d'excellente
qualité. avec l'algorithme de Wolff. Ce constat provient de ce que l'algorithme
de Wolff au lieu de traiter les spins individuellement comme son homologue
Métropolis, noie les petites fluctuations observables dans un bloc de
spins qu'il considère au titre d'un seul. Ce bloc de spin (cluster) a la
qualité de présenter une configuration uniforme. Cette attitude
est donc fort appréciable à la zone critique où les
fluctuations sont généralement élevées, mais moins
utile aux températures extrêmes. Cependant, les étapes
d'exécution de l'algorithme de Wolff offrent la contrainte
matérielle qu'elles demandent beaucoup de mémoire pour stocker
les données qu'il réutilise, ce qui entraîne la
nécessité de disposer d'un calculateur d'excellente
qualité.
Nous pouvons dire de ce qui précède que les
simulations numériques sont un excellent moyen de calcul des
données statistiques des systèmes physiques au vu des
résultats obtenus vis-à-vis des valeurs théoriques connus
depuis la statistique de Boltzmann.
Au terme de notre travail, nous pouvons dire que les
comparaisons que nous avons réalisées sur le plan pratique nous
ont donnés des résultats favorables nonobstant la limite de nos
moyens matériels. Par ailleurs, nous sommes désormais capable de
comprendre les principes des simulations par les méthodes de Monte
Carlo, mieux encore les algorithmes de Métropolis et Wolff et surtout de
pouvoir retrouver les courbes d'évolution des grandeurs thermodynamiques
d'après leurs expressions théoriques.
Toutefois notons que la détermination exacte de
l'exposant dynamique z, l'étude de la dynamique moléculaire sur
un système de spins ainsi que l'extension de ce travail en 3D nous
offriraient plus d'éléments d'appréciation. Par ailleurs,
le modèle d'Ising par son caractère discret, ne nous offre pas la
réalité physique de la matière lorsqu'elle est
considérée comme étant un système continu. Il
serait ainsi judicieux d'explorer des modèles continus tels XY et
Heisemberg.
| 


