|
THESE
Présentée à
L' UNIVERSITE D'
ORLEANS
Pour obtenir le grade de
DOCTEUR DE L'UNIVERSITE
D'ORLEANS
Discipline : Physique et physico-chimie de la
matière et des matériaux
Par
Gérald LEL ONG
ETUDE STRUCTURALE ET DYNAMIQUE DE SOLUTIONS DE
SUCRE
CONFINEES
Soutenue le 02 Février 2007, devant le jury composé
de :
- M. Clément Sanchez, Directeur de
Recherche - LCMC Jussieu Président
- M. Attilio Cesàro, Professeur -
Université de Trieste Rapporteur
- M. José Teixeira, Directeur de
Recherche - LLB - CEA Saclay Rapporteur
- M. John W. Brady, Professeur -
Université de Cornell Examinateur
- M. David L. Price, Directeur de Recherche -
CRMHT Orléans Examinateur
- M. Thomas Zemb, Professeur - INSTN - CEA
Saclay Examinateur
- Mme Marie-Louise Saboungi, Professeur -
Université d'Orléans Directeur de thèse
Remerciements
Avant toute chose, j'aimerais remercier très
chaleureusement les membres de mon jury pour l'honneur qu'ils m'ont fait en
acceptant de juger ce travail : Monsieur Clément Sanchez, directeur de
recherche au Laboratoire de Chimie de la Matière Condensée, pour
avoir accepté de présider ce jury; Messieurs Attilio
Césaro et José Teixeira, respectivement professeur à
l'Université de Trieste et directeur de recherche au Laboratoire
Léon Brillouin, en acceptant d'être les rapporteurs de cette
thèse ; Monsieur John W. Brady, professeur à l'Université
de Cornell, Monsieur David L. Price, directeur de recherche au Centre de
Recherche sur les Matériaux à Haute Température et
Monsieur Thomas Zemb, professeur à l'Institut National des Sciences et
Techniques Nucléaires pour leurs questions pertinentes.
J'aimerais adresser ici mes plus sincères et chaleureux
remerciements à ma directrice de thèse, Marie-Louise Saboungi,
qui a su, par sa très grande disponibilité et les nombreuses
discussions autour d'un thé ou ailleurs, m'inculquer l'envie et la
manière de mener des travaux de recherche. Je souhaiterais
également associer à ces remerciements David L. Price, qui a
toujours été présent et disponible durant ces 3
années. Merci à vous deux...
Je remercie également toutes les personnes quej 'ai eu
la chance de croiser ici ou là et avec qui j 'ai eu le plaisir
d'apprendre et de collaborer. Je pense notamment à André Douy,
Dominique Massiot, et Valérie Montouillout du CRMHT; Astrid Brandt et
Heloisa N. Bordallo du HMI; Miguel A. Gonzales, Isabelle Grillo, Claudia
Mondelli, Marie Plazanet, et Daniella Russo de l 'ILL; Spencer W. Howells et
Felix Fernandez-Alonso d 'ISIS; José Teixeira et Jean-Marc Zanotti du
LLB; Theodore Steriotis et Georgia Charalambopoulou de Demokritos ; Arnaud
Desmedt du LPCM; Adrien Lerbret du LSPES; Craig Brown, John Copley, Vicky
Garcia-Sakai, Eugene Mamontov, Inma Peral, Steve Kline, et Lionel Porcar du
NCNR. Merci à vous tous.
Et puis il y a toutes celles et ceux que j 'ai
côtoyés au quotidien durant ces trois années, et qui ont
contribué à ce travail. Pour leur soutien, leurs conseils et leur
bonne humeur, j'aimerais adresser ma plus grande sympathie et mes remerciements
à Sanjib Bhattacharyya, Thomas Cacciaguerra, Fabienne Méducin,
Christiane Pipeau, Jean-Paul Salvetat et Fabienne Warmont.
Mais, je n 'en oublie pas pour autant mes amis et
collègues post-doc et doctorants du CRMD sans qui ces trois
années n'auraient pas été ce qu'elles sont. C'est donc
avec nostalgie que je salue et remercie chaleureusement Hinda, Julien, Kevin,
Nathalie, Romain et Vincent pour leur bonne humeur communicative et leur
culture hétéroclite. Merci donc pour ces soirées
endiablées et inoubliables.
Merci également à nos dignes
prédécesseurs Alex, Conchi, Jérôme, Philippe,
Yannick, mais également à la relève prometteuse que sont
Haytham, Irena, José, Mathieu, Mathieu, Serigne, Tri et Yasin, sans
oublier Nani, Nicole, Roland, Samuel et Xavier, et mes amis de toujours
Fabrice, Florent, Marine, Marion, Pascal, et Stéphane.
Et puis enfin, j'aimerais remercier du plus profond de mon coeur
mes parents et mon frère sans qui rien de tout cela n'aurait
été possible. Merci.
Table des matières
CHAPITRE 1
1.1. LA BIOPROTECTION: LE PHENOMENE D'ANHYDROBIOSE - 17 -
1.2. LES SUCRES OU HYDRATES DE CARBONE - 18 -
1.2.1. Les monosaccharides
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 18 - 1.2.1.1.
Stéréochimie : le système D/L
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 19 - 1.2.1.2. Cyclisation et
nomenclature a43
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 19 - 1.2.1.3. Le
glucose et le fructose - 20 -
1.2.2. Les oligo- et poly-saccharides
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 20 -
1.3. INTERACTIONS SOLUTE - EAU - 21 -
1.3.1. L'eau et son réseau tétraédrique - 22
-
1.3.2. ffet des solutés sur la structure de l'eau - 23
-
1.4. LE ROLE DES SUCRES DANS LES PHENOMENES BIOPROTECTEURS - 24
-
1.4.1. Cas d'une déshydratation modérée
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 24 -
1.4.1.1. L'effet déstructurant - 24 -
1.4.1.2. L'exclusion préférentielle - 27 -
1.4.2. Cas d'une déshydratation sévère
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 28 - 1.4.2.1. Substitution de l'eau
d'hydratation ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 29 -
1.4.2.2. Vitrification - 30 -
1.5. DYNAMIQUE MOLECULAIRE DES SUCRES EN SOLUTION AQUEUSE - 30
-
1.5.1. Dynamique d'un disaccharide:
l'-tréhalose~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 31 - 1.5.2. Dynamique de
deux monosaccharides: le D-glucose et le D-fructose ~~~~~~~~~~~~~- 32 - 1.6.
CONCLUSION GENERALE DU CHAPITRE 1 - 32 -
|
CHAPITRE 2
2.1. LES NEUTRONS ET LA DIFFUSION NEUTRONIQUE
|
|
- 35 -
|
|
|
|
2.1.1. Le neutron et les interactions
rayonnement-matière ~~~~~~~~~~~~~~~~~~~~~~~~~~- 35 -
2.1.2. Principe
de la diffusion neutronique ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 37 -
2.1.3. Diffusion cohérente et incohérente -38 -
2.1.4. L'étude de la dynamique moléculaire par
diffusion quasi-élastique______________ - 40 -
|
2.2. DYNAMIQUE MOLECULAIRE DE SUCRES EN SOLUTIONAQUEUSE
|
-41-
|
|
2.2.1. Dynamique moléculaire du D-glucose
______________________________________
|
- 42 -
|
|
2.2.1.1. Préparation des solutions de
D-glucose/échange isotopique _________________
|
-42 -
|
|
2.2.1.2. Conditions expérimentales
____________________________________________
|
-43-
|
2.2.1.3. Traitement des données expérimentales
__________________________________
|
-44-
|
|
2.2.1.3.1. Normalisation au
moniteur_______________________________________ - 45 -
|
2.2.1.3.2. Soustraction de la cellule vide
____________________________________
|
- 45 -
|
|
2.2.1.3.3. Normalisation au vanadium
______________________________________
|
- 46 -
|
|
2.2.1.3.4. Regroupement
_________________________________________________
|
- 46 -
|
|
2.2.1.4. Modélisation des spectres
_____________________________________________
|
-47-
|
|
2.2.1.5. Résultats
__________________________________________________________
|
-51 -
|
|
2.2.1.5.1. DCS
__________________________________________________________
|
- 51 -
|
|
2.2.1.5.2. HFBS
________________________________________________________
|
- 55 -
|
|
2.2.1.6. Discussion
_________________________________________________________
|
- 57 -
|
|
2.2.1.6.1. Dynamique translationnelle
______________________________________
|
- 57 -
|
|
2.2.1.6.2. Dynamique rotationnelle
________________________________________
|
- 60 -
|
|
2.2.1.7. Conclusion
________________________________________________________
|
-61 -
|
2.2.2. Dynamique moléculaire du
D-fructose______________________________________ - 61 -
2.2.2.1. Préparation des solutions
deD-fructose/échange isotopique ________________ -61 - 2.2.2.2.
Conditions expérimentales ____________________________________________
-62- 2.2.2.3. Résultats
___________________________________________________________ -62 - 2.2.2.4.
Discussion _________________________________________________________ -63 -
2.2.2.5. Conclusion _________________________________________________________
-69-
2.2.3. Comparatif D-glucose /
D-fructose_________________________________________ -69 -
2.3. CONCLUSION GENERALE DU CHAPITRE 2 - 70-
CHAPITRE 3
3.1. CHOIX DE LA MATRICE DE CONFINEMENT
- 75 -
3.2. TAILLE DU CONFINEMENT - 76 -
3.3. SYNTHESE DE GELS DE SILICE AQUEUX (HYDROGELS) - 77-
3.3.1. Principes généraux
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 77 -
3.3.2.
Synthèse des hydrogels en présence de monosaccharides - 79
-
3.3.3. Caractérisation Raman
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 81 -
3.4. ETUDE STRUCTURALE PRELIMINAIRE DES GELS DE SILICE AQUEUX
CONTENANT DU D- GLUCOSE PAR DIFFUSION DES NEUTRONS AUX PETITS ANGLES - 84 -
3.4.1. Le formalisme de la diffusion aux petits angles - 84 -
3.4.2. Interprétation qualitative des différents
domaines de Q ~~~~~~~~~~~~~~~~~~~~~~~- 86 -
3.4.3. Paramètres
expérimentaux ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 89 -
3.4.4. Résultats et discussion - 89 -
3.5. CONCLUSION GENERALE DU CHAPITRE 3 - 93 -
CHAPITRE 4
4.1. ETUDE STRUCTURALE PAR LA METHODE DE VARIATION DE CONTRASTE -
97 -
4.1.1. Principe de la méthode - 97 -
4.1.2. Paramètres expérimentaux
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 99 -
4.1.3. Mesures
préliminaires pour la détermination des différents
contrastes - 99 -
4.1.3.1. Détermination du point de contraste moyen nul du
gel de silice ~~~~~~~~~~~~~- 99 -
4.1.3.2. Calcul des différentes fractions volumiques
~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 101 - 4.1.4. Résultats et discussion
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 102 - 4.1.5. Conclusions
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 103 -
4.2. EVOLUTION DE LA STRUCTURE DES GELS EN FONCTION DU TAUX
D'HYDRATATION -
|
EFFET PROTECTEUR DES SUCRES
|
|
- 103 -
|
|
|
|
4.2.1. Description du montage - 103 -
4.2.2. Préparation des échantillons
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 104 -
4.2.3. Conditions
expérimentales ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- 104 -
4.2.4. Résultats
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 105
-
4.2.4.1. Avant déshydratation
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 105 -
4.2.4.2. Après
déshydratation ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 107
-
4.2.5. Remarques générales
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 111 -
4.3. CONCLUSION GENERALE DU CHAPITRE 4 -111-
CHAPITRE 5
5.1. DYNAMIQUE DU D-GLUCOSE DANS LES GELS DE SILICE -115-
5.1.1. Conditions expérimentales
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 115 -
5.1.2. Traitement des
données ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 115
-
5.1.3. Résultats
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -
117-
5.1.3.1. DCS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -117-
5.1.3.2.
HFBS ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -119-
5.1.4.
Discussion ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 121
-
5.1.4.1. Dynamique translationnelle
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 121 -
5.1.4.2. Dynamique
rotationelle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 122 -
5.1.5.
Conclusion partielle sur la dynamique du D-glucose sous confinement ~~~~~~~~~~
- 122 -
|
5.2. DYNAMIQUE DU TREHALOSE DANS LES GELS DE SILICE
|
|
-122-
|
|
|
|
5.2.1. Conditions expérimentales
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 123 - 5.2.2. Traitement des
données _~~~~~~~~~~~~~~~~~~~~__~~~~~~~~~~~~~~~~~~~~__~~~~ - 123 - 5.2.3.
Mesures ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 124 -
5.2.4. Résultats et discussions
_~~~~~~~~~~~~~~~~~~~~__~~~~~~~~~~~~~~~~~~~~__~~~~ - 126 - 5.2.5. Conclusion
partielle pour la dynamique du tréhalose confiné
~~~~~~~~~~~~~~~~~~ - 128 -
5.3. CONCLUSION GENERALE DU CHAPITRE 5 -128-
CHAPITRE 6
6.1. ETATDE L'ART - 133 -
6.1.1. Historique
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 133-
6.1.2.
La famille M41S - 134 -
6.1.3. Principes de la synthèse
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 134 -
6.1.4.
Mécanismes de formation ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
- 135 -
6.1.4.1. Liquid crystal templating
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 135 -
6.1.4.2. Auto-assemblage
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 136 -
6.1.4.3.
Auto-assemblage coopératif ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -
136 -
|
6.2. SPHERES MESOPOREUSES
|
|
-137-
|
|
|
|
6.2.1. Synthèse
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 138
-
6.2.2. Caractérisations
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 139 -
6.2.2.1.
Microscopie électronique en transmission ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ -
139 -
6.2.2.2. Microscopie électronique à balayage
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 142 -
6.2.2.3. Diffraction des rayons X
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 142 -
6.2.2.4. Diffusion des
neutrons aux petits angles ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 143 -
|
6.2.2.5. Adsorption/désorption deN2 (BET)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 147 -
|
|
6.2.2.6. Accessibilité des solutions aqueuses
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 150 -
|
|
6.3. DISCUSSION SUR LE MECANISME DE FORMATION
|
-151-
|
6.4. CONCLUSION GENERALE DU CHAPITRE 6
|
-152-
|
|
|
CHAPITRE 7
|
|
|
7.1. REMPLISSAGE DES PORES
|
-157-
|
7.2. MESURES ELASTIQUES
|
-158-
|
|
7.2.1. Confinement de solutions d'tréhalose
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 158 -
7.2.2. Confinement de solutions de
D-glucose ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ - 163 -
7.2.3. Conclusion -
167 -
|
7.3. RESULTA TS PRELIMINAIRES DE DYNAMIQUE
|
|
-167-
|
|
7.4. CONCLUSION GENERALE DU CHAPITRE 7
|
|
-169-
|
|
|
|
|
CONCLUSION -171-
ANNEXE : LES SPECTROMETRES -175-
BIBLIOGRAPHIE - 181 -
Introduction
Le sucre, un nom bien familier...
Connu dès la plus haute Antiquité, le «roseau
sucré », originaire de Papouasie, fournit une
*
substance blanchâtre d'un goût suave et doux
à l'origine du sucre.Considéré alors comme un miel produit
sans le secours des abeilles, le sucre était utilisé en tant
qu'épice mais également comme médicament puisqu'on lui
reconnaissait une origine divine et de nombreuses vertus
thérapeutiques... Même si ces vertus ont longtemps
été surestimées, il n'en reste pas moins que les sucres,
en raison de leur très forte abondance dans les organismes vivants,
forment une classe de molécules biologiques tout à fait
particulière. Le fructose, la chitine, la cellulose, l'amidon, le
lactose, le glucose, le saccharose, le ribose, ..., toutes ces molécules
familières font partie de la très grande famille des sucres, et
sont les constituants de coenzymes, d'antibiotiques, de cartilages, de parois
cellulaires, du sang et même du matériel génétique!
Ils interviennent également dans de nombreux processus biologiques comme
le stockage énergétique, la reconnaissance moléculaire, ou
encore dans les phénomènes de biopréservation des tissus
...
Cette propriété de protection des structures
biologiques (cellules, protéines, tissus, ...) soumises à des
conditions de froid ou de chaud extrêmes est d'un intérêt
grandissant dans une problématique de conservation des organes, des
greffons ou des vaccins en médecine d'une part, ou encore pour
l'amélioration des procédés de stockage par
cryogénie ou par lyophilisation dans l'industrie agroalimentaire d'autre
part.
* C'est en Inde, que le terme sanskrit « sarkara » qui
signifie sable a donné naissance au mot sucre utilisé aujourd'hui
dans toutes les langues indo-européennes.
Mais la stabilité des édifices biologiques est
très dépendante des conditions environnementales comme le pH, la
température, le taux d'hydratation... ; et la congélation ou la
déshydratation, par exemple, causent des dommages irréversibles
voire fatals aux cellules. La présence de certains solutés
compatibles, comme le tréhalose ou le sucrose, dans les liquides
cellulaires permet de stabiliser les membranes en conservant l'espace
intermembranaire en l'état, mais également en évitant la
formation de glace intracellulaire. Les mécanismes moléculaires
à l'origine de ces phénomènes de bioprotection sont encore
assez débattus et différentes théories ont vu le jour
selon le niveau de déshydratation cellulaire considéré :
l'effet déstructurant des sucres, l'effet d'exclusion
préférentielle, la substitution de l'eau d'hydratation, et la
vitrification. Mais toutes ces hypothèses, prises individuellement, ne
permettent pas d'expliquer de manière satisfaisante les processus mis en
jeu sur une grande gamme de température et/ou de concentration.
Néanmoins, derrière toutes ces théories, basées sur
les propriétés exceptionnelles de l'eau et du sucre, se cachent
des problèmes d'interaction entre les molécules d'eau et de
sucre, et donc de dynamique moléculaire... (Chapitre 1)
Les systèmes biologiques en question sont assez
complexes et il est absolument nécessaire d'étudier des
modèles simplifiés. Des mélanges binaires eau/sucre sont
donc une première étape et l'étude de la dynamique des
molécules de solvant et des molécules de soluté en
fonction de la concentration et/ou de la température sera une aide
précieuse à la compréhension des processus de bases.
(Chapitre 2) Pour ce faire, des systèmes eau/monosaccharide seront
étudiés et comparés afin d'apprécier les effets de
la concentration, mais également de la stéréochimie, sur
la dynamique du solvant et du soluté. Mais toutes ces études
présentent un point faible non négligeable: aucune ne prend en
considération les échelles des structures cellulaires. D'une
manière générale, les échelles en question, bien
que variables d'une cellule à l'autre, se rapprochent plus volontiers de
la dizaine de nanomètre que du monde macroscopique... Et à la vue
de tous les changements de propriétés engendrés par la
réduction de taille, ces systèmes binaires gagneront à
être étudiés dans des environnements restreints
stériquement. Parmi la très grande variété de
matrices hôtes, les gels de silice aqueux ont été
sélectionnés pour confiner des solutions de sucre à des
concentrations données. (Chapitre 3) Une étude approfondie de la
structure de ces gels en fonction du taux d'hydratation sera
réalisée par diffusion des neutrons aux petits angles, et le
pouvoir bioprotecteur des sucres sera testé. (Chapitre 4) L'étude
de la dynamique d'un mono- et d'un disaccharide placés sous confinement
dans ces hydrogels sera également entreprise et l'effet de la taille des
molécules sur la dynamique translationnelle discutée. (Chapitre
5) Afin de regarder les effets de l'architecture des pores sur la dynamique,
des silices mésostructurées de type MCM-4 1 ont été
spécialement développées afin de répondre au mieux
aux impératifs de concentration liés au confinement des solutions
de sucre. Une caractérisation structurale complète a
été menée sur cette matrice mésoporeuse. (Chapitre
6) Enfin, les variations thermodynamiques liées au confinement et la
dynamique des molécules de sucre confinées dans ces silices
ordonnées seront étudiées. (Chapitre 7)
Chapitre 1
ETAT DE L'ART
1.1. La bioprotection:Le phénomène d 'anhydrobiose
17
1.2. Les sucres ou hydrates de carbone 18
1.3. Interactions soluté-eau 21
1.4. Le rôle des sucres dans les phénomènes
bioprotecteurs 24
1.5. Dynamique moléculaire des sucres en solution aqueuse
30
1.6. Conclusion générale du chapitre 1 32
CHAPITRE 1
ETAT DE L'ART
1.1. LA BIOPROTECTION: LE PHENOMENE D'ANHYDROBIOS
Une variété particulière de plantes
appelée Selaginella lepidophylla ou plus communément
dénommée « Rose de Jéricho » est
extraordinairement résistante à la sécheresse. Ces plantes
florifères apparaissent comme mortes après de longues
périodes sans hydratation, et recouvrent comme par miracle toute leur
splendeur à la moindre trace d'humidité. C'est pour cette raison
qu'elles ont été baptisées plantes de
résurrection.1 La Rose de Jéricho est loin
d'être le seul organisme vivant à présenter un tel
comportement vis-à-vis de la déshydratation. De nombreux autres
spécimens présentant cette même caractéristique ont
été découverts, des plus simples comme les organismes
unicellulaires, à des organismes beaucoup plus complexes comme des
plantes ou des invertébrés (Figure 1). Tous montrent cette
incroyable aptitude à tolérer de très
sévères niveaux de déshydratation* sur de
longues périodes pouvant aller de quelques mois à quelques
dizaines d'années2, le record revenant à un petit
tardigrade qui a recouvré la vie après plus de 120 ans
passés dans un musée italien ! De manière
générale, les organismes capables de résister à de
tels niveaux de déshydratation sont nommés des organismes
anhydrobiotiques (du grec anhydro qui signifie sans eau et biotique qui
qualifie un milieu dans lequel la vie peut se développer).

Figure 1: Deux exemples d'organismes anhydrobiotiques: le
tardigrade (à gauche) et la Borya septentrionalis une plante de
résurrection (à droite).
La déshydratation est l'un des stress environnementaux
les plus difficiles à gérer pour les organismes aussi bien
terrestres qu'aquatiques, car elle cause de nombreux dommages
irréversibles dans les structures biologiques. Les organismes
anhydrobiotiques sont donc, par leur résistance, d'un
intérêt majeur pour les biologistes, un intérêt qui a
débuté il y a maintenant plus de 300 ans.3
L'étude des masses sèches de ces organismes a mis en exergue une
grande quantité de solutés comme la proline, la sérine, la
glycine-bétaine, le mannitol, le sorbitol, les polyols, le
tréhalose, le sucrose et des
* La perte en eau dans ces organismes atteint
régulièrement des valeurs proches des 95 à 99%.
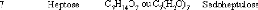
oligosaccharides comme le glucose ou le fructose. En
réponse à la déshydratation cellulaire, qu'elle soit
provoquée par une sécheresse, un froid extrême ou un choc
osmotique, les microorganismes ou les plantes accumulent ces solutés
dits compatibles dans leurs cellules. La plupart sont dans l'incapacité
de protéger activement les protéines et les membranes dans des
cas de déshydratations majeures. Seuls les sucres peuvent
répondre et structuralement et par leurs groupements fonctionnels
à la préservation des édifices biologiques dans de telles
situations.4 Le tréhalose et le sucrose par exemple sont
connus pour protéger la structure des macromolécules et
évitent la fusion des membranes durant les phénomènes
d'hydratation / déshydratation.5,6,7 Ces dernières
années, de nombreuses études ont été
réalisées sur ces systèmes et toutes les théories
invoquées convergent sur le fait que les sucres jouent un rôle
prépondérant sur la conservation des structures biologiques.
1.2. LES SUCRES OU HYDRATES DE CARBONE
Les sucres se composent, comme la plupart des corps
organiques, d'atomes de carbone, d'hydrogène et d'oxygène, et ont
pour formule brute Cx(H2O)y, formule à l'origine de leur
dénomination d'hydrates de carbone ou « carbones hydratés
». La famille des hydrates de carbone peut être divisée en
trois sous-groupes : les monosaccharides, les oligosaccharides et les
polysaccharides.
1.2.1. Les monosaccharides
Les monosaccharides, également appelés sucres
simples ou oses, sont les structures élémentaires constitutives
des oligo- ou polysaccharides. Possédant de 3 à 7 carbones, ils
sont caractérisés par la présence d'un groupe carbonyle et
de fonctions alcool sur les autres carbones. Les monosaccharides sont
classés selon leur nombre d'atomes de carbone et suivant leur groupement
fonctionnel aldéhyde ou cétone. Selon cette nomenclature, un
sucre à six carbones comportant un groupement aldéhyde sera
appelé aldohexose, alors qu'un cétohexose sera un hexose portant
un groupement cétonique.8 (Tableau 1)
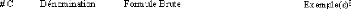

Tableau 1: Différents monosaccharides classés selon
leur nombre de carbone et selon leur groupement fonctionnel dans le cas des
hexoses.
1.2.1.1. Stéréochimie: le système
D/L
Un sucre simple typique est composé d'un certain nombre
de carbones asymétriques ou centres chiraux. Une méthode efficace
pour désigner les différentes configurations engendrées
par ces carbones asymétriques consiste à utiliser les deux
énantiomères du glycéraldehyde comme composés de
référence. Les monosaccharides sont alors vus comme
dérivant du D-glycéraldehyde ou du Lglycéraldehyde (Figure
2). Les désignations D- (pour dextrogyre) et L- (pour lévogyre)
des oses donnent donc une information sur la stéréochimie de la
molécule mais en aucun cas sur leur activité optique (sauf dans
le cas du glycéraldehyde bien évidemment).
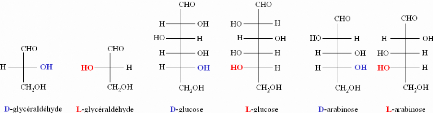
Figure 2: Les deux éniantomères du
glycéraldehyde sont utilisés comme composés de
référence dans les désignations D- et L- des hydrates de
carbone.
1.2.1.2. Cyclisation et nomenclature
Les monosaccharides de 5 à 6 carbones se cyclisent en
solution aqueuse et font ainsi apparaître un carbone asymétrique
supplémentaire, le carbone anomérique C1. La cyclisation des
hexoses ou pentoses conduit à la formation de deux structures
anomériques cycliqueset. La réaction de mutarotation permet
l'interconversion des formeset. Notons que, à l'équilibre
tautomère, une solution de D-glucose contient 35% d'-D-glucopyranose,
65% de-D-glucopyranose, et enfin 0,5% de D-Glucose dans sa forme
linéaire (Figure 3). Si la prédominance de la formen'a rien de
général, en revanche, la forme linéaire est toujours
présente sous forme de traces.

Figure 3: La molécule de D-Glucose sous forme cyclique
dessinée dans différentes représentations (projections de
Fisher, d'Harworth et conformation chaise-bateau)
1.2.1.3. Le glucose et le fructose
Parmi les huit diastéréoisomères des
aldohéxoses, seulement trois se trouvent de manière courante dans
la nature : le D-glucose, le D-mannose et le D-galactose. Le glucose est de
loin le plus important des monosaccharides naturels, il a une fonction de
transport via le sang entre les organes de stockage (le foie) et les organes
dits « consommateurs » tels que les muscles, le cerveau ou les tissus
nerveux. Parmi tous les oses, il est l'unique hexose à posséder
dans sa forme fi tous les groupements hydroxyles en position
équatoriale. Le fructose, qui est un isomère du glucose, fait
partie des héxocétoses, on le trouve abondamment dans les fruits
et le miel.
1.2.2. Les oligo- et polysaccharides
La plupart des hydrates de carbone ne se présentent pas
à l'état naturel sous la forme monomérique, mais
plutôt sous forme de polymères à plus ou moins longue
chaîne. Dans la famille des oligosaccharides, c'est-à-dire des
polymères possédant de 2 à 20 carbones, les disaccharides
y tiennent une place importante. Ils sont composés de deux oses
reliés l'un à l'autre par une liaison glycosidique. Les
propriétés des sucres sont très dépendantes de la
stéréochimie des molécules et la simple combinaison de
deux monosaccharides peut entraîner des comportements et des
propriétés tout à fait différents selon qu'ils
soient de même nature ou de nature différente. Comme nous avons pu
le voir en discutant l'anhydrobiose, le tréhalose et le sucrose sont
deux disaccharides non-réducteurs présents en grande
quantité dans les organismes anhydrobiotiques. Le tréhalose ou
plus exactement l' a--a tréhalose est un di-glucose
composé de deux molécules de glucose dans leur conformation a
reliées par un oxygène glycosidique. Il intervient dans la nature
en tant que réserve énergétique, mais l'industrie
agroalimentaire l'utilise également pour protéger les aliments
des différentes dégradations inhérentes au froid. Ses
principales particularités2,8 sont d'être: (1)
très soluble, (2) peu réactif, (3) de piéger les radicaux
libres et (4) de présenter une température de transition vitreuse
plus élevée que tous les autres mono- et disaccharides (Tg ~
393K9,10). Le sucrose ou saccharose combine pour sa part un cycle
glucose et un cycle fructose et intervient principalement dans le transport des
sucres dans les plantes.2
Dans la famille des polysaccharides, c'est-à-dire des
polymères contenant plus de 20 carbones, nous pouvons citer entres
autres exemples la cellulose [Glc(1-4)Glc]n qui est un composant
essentiel de la paroi cellulaire des plantes ainsi que de certains champignons,
la chitine [GlcNAc(1- 4)GlcNAc]n qui est un polysaccharide
constitutif de l'exosquelette des arthropodes (crustacés, insectes,
mille-pattes, araignées), ou encore l'amidon [Glc(1-4)Glc]n
très répandu chez les plantes et très utilisé dans
la fabrication du papier.
Les sucres, glucides ou hydrates de carbone forment donc une
classe très importante de molécules biologiques. Ils sont les
constituants, entre autres exemples, de coenzymes, d'antibiotiques, de
cartilages, de parois cellulaires, du sang et même du matériel
génétique avec le D-ribose et le 2- désoxyribose qui sont
des composants essentiels de l'ARN et de l'ADN. Ils interviennent
également dans de nombreux processus comme le stockage
énergétique, la reconnaissance moléculaire, ou dans les
phénomènes d'anhydrobiose.11 Mais comment une telle
famille de molécules peut-elle être mise en jeu dans des domaines
et des processus aussi variés ? La réponse à cette
question se trouve dans l'eau, ou plus exactement, dans les interactions sucre
/ eau.
1.3. INTERACTIONS SOLUTE -- EAU
L'eau est omniprésente sur Terre, et sans elle, la vie
serait semble-t-il impossible. Il n'est pas difficile de constater que l'eau
est partout : (1) elle constitue un milieu de vie pour bons nombres de
végétaux et d'animaux à travers les océans, les
mers, les rivières,... qui recouvrent 70% du globe terrestre ; (2) elle
est également la principale substance constitutive des cellules
vivantes. A titre d'exemple, notre sang est composé à 83% d'eau
et la teneur en eau de notre corps avoisine les 65% en masse.
L'eau est si familière qu'elle est souvent vue comme un
liquide « typique ». En réalité, l'eau n'a rien de
typique: déjà en étant la seule substance naturelle
à exister sous ses trois états: liquide, solide (la glace) et gaz
(la vapeur d'eau). L'eau présente un nombre important de
propriétés singulières, dites propriétés
anomales, qui sont fortement corrélées à l'existence
même de la vie. Certaines de ses propriétés comme sa grande
capacité thermique, son importante conductivité thermique et sa
présence en grande quantité dans les cellules contribueraient
à la régulation thermique et éviteraient les fluctuations
locales de température dans les organismes. Parmi les autres
propriétés anomales notables12,*, notons que l'eau
présente des points de fusion (0°C) et d'ébullition
(+100°C) anormalement élevés en comparaison à
d'autres solvants comme le benzène ou l'éthanol par exemple
(C6H6: TF = 5,5°C, TEb = 80,1°C ; C2H6O: TF = -
114,3°C, TEb = 78,4°C 13), et qu'elle présente, ce
qui est tout à fait unique, une forte expansion volumique lors de sa
cristallisation (environ 9% à pression
atmosphérique14).
Les propriétés physico-chimiques des liquides
sont directement liées à leurs propriétés
structurales, et plus particulièrement à la capacité plus
ou moins importante des molécules à former des liaisons
hydrogène entre-elles. La faible dimensionnalité des
molécules d'eau et leur grande aptitude à se lier entre elles par
l'intermédiaire de très nombreuses liaisons hydrogène sont
à l'origine même de ses propriétés
singulières.
* Selon les critères utilisés et la
définition apportée au terme d'anomalie, le nombre de
propriétés anomales de l'eau peut atteindre le chiffre
impressionnant de 41.
1.3.1. L'eau et son réseau
tétraédrique
La molécule d'eau H2O est une molécule qui
possède un important moment dipolaire lié à la
présence de liaisons O-H fortement polarisées. Lorsqu'il est
lié à un hétéroatome fortement
électronégatif comme l'oxygène, l'atome d'hydrogène
présente une déficience électronique suffisante pour lui
permettre d'accepter partiellement un doublet. En d'autres termes, la
polarisation des liaisons O-H fait apparaître une charge négative
partielle (-) sur l'atome d'oxygène et une charge positive partielle (+)
sur chacun des atomes d'hydrogène. Les moments électriques
d'ordre supérieur (quadripolaire, octupolaire, ....) sont non
négligeables ce qui explique l'inhomogénéité du
champ électrique autour de la molécule. A ces importantes
propriétés de polarité s'ajoute le fait que les atomes
d'hydrogène avec leur faible rayon atomique peuvent s'approcher
étroitement des atomes d'oxygène, ce qui génère des
forces d'attraction relativement fortes. C'est ce que l'on appellera un pont
hydrogène ou une liaison hydrogène (Figure 4).
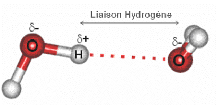
Figure 4 : Représentation d'une liaison hydrogène
entre deux molécules d'eau.
En phase condensée, chaque molécule d'eau va
former deux liaisons hydrogène avec ses propres atomes
d'hydrogène, plus deux liaisons hydrogène supplémentaires
mettant en jeu cette fois-ci les atomes d'hydrogène des molécules
d'eau voisines (Figure 5). Dans le premier cas, l'atome d'oxygène est
dit donneur, dans le deuxième il est dit accepteur. Les liaisons
hydrogène sont très sensibles aux transferts de charges d'un
donneur vers un accepteur dans une séquence qui produit un effet
appelé « coopérativité ».15,16
Là où d'autres liquides comme les alcools forment des
chaînes de liaisons hydrogène à cause de leur unique
groupement hydroxyle, l'eau forme des agrégats
tétraédriques, témoignant d'une plus grande
coopérativité. Dans la phase solide, l'arrangement
tétraédrique des molécules, qui s'étend à
longue distance, va constituer la forme cristalline. A température
ambiante, l'eau liquide présente une structure fortement
organisée, dont l'arrangement « moyen » est très voisin
de la structure tétraédrique de la glace hexagonale.
L'énergie des liaisons hydrogène est suffisamment faible (E ~
25kJ/mol de l'ordre de l'agitation thermique) pour que le réseau
tridimensionnel soit dynamique c'est-à-dire pour que les liaisons
hydrogène se fassent et se défassent en permanence.
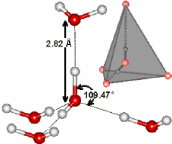
Figure 5 : Arrangement tétraédrique des
molécules d'eau dans la glace hexagonale.
Comme nous venons de le voir, l'eau présente des
particularités structurales tout à fait uniques. Mais
l'étude de la structure de l'eau « pure » ne peut-être
qu'une étude préliminaire, qui servira de base à la
compréhension de systèmes aqueux plus complexes.
1.3.2. Effet des solutés sur la structure de
l'eau
Les organismes vivants, qui sont composés pour une
grande part de solutions aqueuses, recèlent une myriade de
solutés biologiques de plus ou moins grandes tailles et de formes plus
ou moins diverses : des macromolécules comme les protéines ou
l'ADN, des virus, des cellules, des sucres, des sels, des ions, . Quand
un soluté se trouve dans un environnement aqueux, ses groupements
fonctionnels sont confrontés aux impératifs structuraux
inhérents au solvant, mais sa seule présence peut engendrer des
modifications locales de la structure du solvant dans son
voisinage.17,18,19,20 Franck et al.21 ont mis en
évidence la déformation plus ou moins importante du réseau
tétraédrique de l'eau sous l'effet de petits ions et ont
proposé une classification en fonction de la modification
apportée à la structure du solvant. Ainsi les cations de petites
tailles ou plus chargés que K+ sont appelés des
«faiseurs de structure », alors que K+, Rb+ et
Cs+ sont appelés des « briseurs de structure ».
Parmi les ions briseurs de structure, citons IY, ClO4Y, MnO4Y, Br-,
ClY, et parmi les ions faiseurs de structure Li+, Cu+,
Al3+, Mg2+, OH-.9 D'une
manière plus générale, cette appellation s'applique aux
autres solutés, qui seront classés briseurs ou faiseurs de
structure par rapport à leur influence sur le réseau de liaisons
hydrogène.
L'addition de petites molécules organiques non-ioniques
va également perturber les agrégats de molécules d'eau en
brisant certaines liaisons hydrogène. Comme la différence de
taille entre le soluté et le solvant est importante, l'introduction
même du soluté dans le réseau aqueux va engendrer, par
effet stérique, des ruptures des liaisons hydrogène entre les
molécules d'eau. De nouvelles liaisons hydrogène vont être
créées non seulement entre les molécules d'eau
elles-mêmes, mais également entre les molécules d'eau et le
soluté. Le solvant, fortement déstabilisé, va tendre
à se restructurer en
agrégats plus stables au voisinage du soluté
pour minimiser l'énergie libre de la solution. Le bilan final de
liaisons hydrogène du système, qui peut être positif ou
négatif, servira d'indicateur pour connaître le caractère
stabilisateur ou déstabilisateur de tel ou tel soluté.
Une analogie avec l'effet que peut avoir la température
ou la pression sur la connectivité en liaisons hydrogène du
réseau aqueux est quelquefois faite.22,23 Ainsi, les faiseurs
de structure sont alors des solutés qui ont un effet sur l'eau
comparable à une diminution en température, alors que les
briseurs de structure ont eux un effet comparable à une augmentation en
température.24
1.4. LE ROLE DES SUCRES DANS LES PHENOMENES
BIOPROTECTEURS
Les membranes constitutives des cellules sont des
édifices biologiques extrêmement sensibles aux variations de
composition de leurs liquides cellulaires et notamment à la
présence de solutés compatibles. Si ces liquides étaient
composés exclusivement d'eau, les couches phospholipidiques risqueraient
de fusionner lors de très fortes déshydratations ou pourraient
être soumises à de très fortes pressions internes
liées à la cristallisation de l'eau. Les dommages
engendrés par de tels stress sont irréversibles voire fatals pour
la cellule. La présence de certains solutés dans ces solutions
permet de stabiliser les membranes en gardant intact l'espace intermembranaire,
mais également en évitant la formation de glace intracellulaire.
Le rôle de certains sucres comme le tréhalose ou le glucose dans
la conservation des structures biologiques chez les organismes anhydrobiotiques
est maintenant reconnu de manière unanime. En revanche, les
mécanismes moléculaires à l'origine de ces
phénomènes de bioprotection sont encore débattus et
différentes théories ont été évoquées
selon le niveau de déshydratation cellulaire considéré :
l'effet déstructurant24,27,28,29,30,31 et l'exclusion
préférentielle4,50
pour des pertes en eau modérées ; la substitution
de l'eau d'hydratation51 et la vitrification11 dans le
cas de très importantes pertes en eau.
1.4.1. Cas d'une déshydratation
modérée :
1.4.1.1. L'effet déstructurant
Les hydrates de carbone ont une architecture chimique
très spécifique qui mêle étroitement des groupements
polaires et apolaires, des liaisons hydrogène inter- et
intramoléculaire, et de très nombreux groupements hydroxyles, qui
leur confèrent un fort caractère hydrophile. Les sucres
présentent donc naturellement une grande affinité avec l'eau
comme en témoigne leur très grande solubilité. Les
perturbations générées par la présence des sucres,
même en très faible quantité, résultent: (i) de
contraintes stériques imposées par les sucres25, et
(ii) de leur aptitude à former des liaisons hydrogène plus
nombreuses et plus stables avec l'eau, que les molécules d'eau
entre-elles.26 Des études de mélanges binaire
eau-sucre ont mis en évidence l'effet déstructurant que peuvent
avoir les hydrates de carbone sur l'arrangement tétraédrique
de l'eau.24,27,28,29,30,31 Autrement dit, la présence
des sucres dans l'eau génère de nombreuses
cassures dans le réseau de liaisons hydrogène de l'eau, et
l'arrangement tétraédrique du solvant va ainsi perdre de sa
coopérativité. Il est bien évident que cette tendance va
s'accentuer avec l'augmentation en concentration du soluté. (Figure 6)
Simultanément, le nombre de liaisons hydogène va augmenter avec
la teneur en sucre par l'intermédiaire de leurs groupements
hydroxyles.
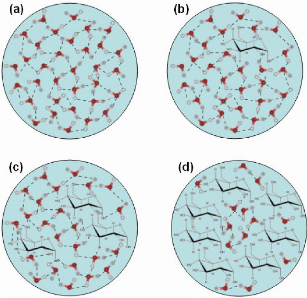
Figure 6: Schéma descriptif de l'effet d'un
soluté compatible (ici, le D-glucose) sur la structure de l'eau. (a) Cas
de l'eau «pure ». Les molécules d'eau forment de très
nombreuses liaisons hydrogène entre-elles et s'organisent en
réseau tétraédrique. Les schémas (b), (c) et (d)
présentent l'évolution de la structure de l'eau en fonction de la
concentration en D-glucose. Le D-glucose forme de très nombreuses
liaisons hydrogène avec les molécules d'eau, brisant ainsi la
structure tétraédrique de l'eau. Plus le ratio sucre/eau est
important, plus la taille des agrégats de molécules d'eau est
réduite et plus le volume d'eau susceptible de pouvoir cristalliser
diminue.
Si l'on regarde en détail, l'évolution des
interactions en fonction de la concentration, on remarque que les interactions
par formation de liaisons hydrogène entre molécules de solvant
sont majoritaires en milieu fortement dilué. Avec l'accroissement du
nombre de molécules de soluté dans le mélange, s'ensuit un
état intermédiaire qui mêle à la fois des
interactions eau-eau et sucre-eau. Enfin, lorsque la proportion en sucre est
nettement majoritaire, on peut observer un net appauvrissement du nombre de
liaisons hydrogène entre molécules d'eau au profit de nouvelles
et très nombreuses liaisons hydrogène inter-sucres et eau-sucre.
Pour des concentrations Cs supérieures à
60% en masse (seuil de percolation), un
phénomène d'encapsulation des agrégats d'eau dans une
matrice d'hydrates de carbone est observé lié à la
présence écrasante des molécules de sucre dans le
mélange (Figure 6). Donc, pour des solutions concentrées, le
volume des agrégats d'eau n'est plus suffisant pour permettre la
formation de centres de nucléation.32,* Une étude
récente, qui démontre que le tréhalose est beaucoup plus
efficace que le sucrose pour réduire la vitesse de
cristallisation33, vient corroborer cette hypothèse. La
déstructuration du réseau tétraédrique de l'eau par
les molécules de soluté conduit donc à la réduction
de la quantité d'eau susceptible de pouvoir cristalliser (Figure 6).
Mais tous les sucres ne présentent pas la même efficacité
et certains comme le glucose, le tréhalose, le sucrose ou le mannose se
voient être d'excellents briseurs de
structure.34,35,36,37,38,39,40
Comme nous venons de le voir, les molécules de sucre
ont donc plutôt tendance à déstructurer le réseau
tétraédrique de l'eau. Mais ceci est une vue simplifiée
des choses, et si d'un côté les sucres
«déstructurent» l'eau, dans le même temps, ils peuvent
la stabiliser ou la déstabiliser suivant le bilan final de liaisons
hydrogène, et suivant le sucre utilisé. Des simulations de
dynamique moléculaire49,41 réalisées sur des
solutions de D-glucose, D-mannose, D-fructose et sucrose ont pu montré
l'évolution des interactions agissant au sein même du
mélange selon la concentration en sucre (Cs).
(1) Cas dilué (Cs>> 20 molécules
d'eau par molécule de sucre)
Les sucres, très largement minoritaires,
s'insèrent dans la matrice d'eau. Des liaisons hydrogène se
brisent inévitablement par effet stérique. Selon le
positionnement des groupements hydroxyles du sucre considéré,
celui-ci s'insèrera de manière plus ou moins aisée dans le
réseau aqueux. Si la topologie du sucre est adaptée à
l'environnement aqueux, sans trop le déstabiliser, alors les
interactions soluté-solvant seront plus fortes, plus étendues et
incluront un nombre croissant de sphères d'hydratation. Des
résultats de simulations moléculaires ont ainsi montré la
compatibilité du D-glucose avec l'arrangement tétraédrique
de l'eau.42,43,44,45 Le D-glucopyranose présente toutes les
caractéristiques pour que sa sphère d'hydratation perturbe le
moins possible son environnement. De ce fait, les sucres s'insèrent
préférentiellement dans les agrégats d'eau, ce qui conduit
à une solution « stable» présentant de fortes
interactions. Des résultats comparables ont été
trouvés pour d'autres hydrates de carbone comme les
pentoses-D-xylopyranose et-D-arabinopyranose,30,46 ou comme le
disaccharidetréhalose.47,48 Dans le cas contraire,
c-à-d si la topologie des groupements hydroxyles ne s'ajuste pas avec
son environnement, alors les agrégats de molécules d'eau doivent
se réorganiser de manière plus importante afin de retrouver le
bon écartement entre l'atome d'oxygène de l'eau et les -OH des
sucres.
* La probabilité de nucléation est directement
reliée au volume de l'échantillon, au sous-refroidissement et
à la viscosité du liquide. Autrement dit le volume de
l'échantillon doit être supérieur à un volume
critique pour espérer observer la formation d'un centre de
nucléation.32
En résumé, l'insertion des molécules
d'hydrate de carbone dépend de la topologie des sucres, par le nombre de
groupements hydroxyle disponibles (plus important chez les disaccharides que
chez les monosaccharides) et par l'orientation de ces groupements hydroxyle,
qui permettront la formation de nouvelles liaisons. Ces deux derniers points
expliquent en partie pourquoi des isomères n'ont pas le même effet
sur la protection membranaire.
(2) Cas intermédiaire (Cs ~ 20
molécules d'eau par molécule de sucre)
Une étude par spectrométrie
infrarouge27 réalisée sur des solutions de D-glucose,
D-fructose et sucrose a permis de mettre en évidence un changement dans
les interactions aux alentours des 30% en masse. A l'apparition des
premières interactions sucre-sucre (~ 30%), les molécules de
soluté ne peuvent plus s'insérer dans le réseau aqueux
sans le déstabiliser. En d'autres termes, les agrégats de sucres
étant plus gros et plus rigides que ces mêmes molécules
seules, leur insertion dans l'environnement hydrique ne peut plus se faire sans
perturbation. Par conséquent, des ruptures majeures dans la
structuration en liaisons hydrogène du réseau commencent à
apparaître, ce qui conduit à la multiplication des petits
agrégats d'eau, agrégats qui font diminuer la
coopérativité et la stabilité de
l'ensemble.27
(3) Cas relativement concentré (Cs < 20
molécules d'eau par molécule de sucre)
Pour des concentrations relativement élevées,
au-delà de 30% en masse, les interactions sucre-sucre deviennent
importantes, et deux sous-réseaux imbriqués l'un dans l'autre
coexistent: un premier formé par les molécules de solvant et un
deuxième formé par les molécules de sucre. Avec
l'augmentation en concentration, la structure aqueuse devient chaotique,
c'est-à-dire que l'on ne trouve plus de grands domaines d'eau sans
défauts et de nombreux agrégats isolés sont
désormais répertoriés. La cristallisation de la solution
devient donc impossible.49
1.4.1.2. L'exclusion préférentielle
Des solutés, comme les polyols ou les oligosaccharides,
sont présents en quantité importante dans les liquides
membranaires. Bien que ces composés diffèrent de manière
importante du point de vue chimique, toutes ces molécules
présentent la particularité d'être exclues de la surface
des protéines: ce phénomène est appelé l'exclusion
préférentielle.4,50 Cette interaction étant
thermodynamiquement défavorable, la surface de la protéine en
contact avec les solutés va donc tendre à être minimale
afin de réduire l'énergie totale du système. En d'autres
termes, le phénomène de déshydratation va d'abord
«toucher» les sphères d'hydratation des solutés avant
de «toucher» celles de la protéine. Par voie de
conséquence, la protéine, dans sa forme repliée ou native,
restera hydratée malgré la perte en eau. En revanche, si les
solutés présentaient un effet d'hydratation
préférentielle, les molécules de soluté iraient
préférentiellement se lier aux protéines. Ce
phénomène étant favorisé thermodynamiquement, les
protéines tendraient à se déployer pour augmenter leur
surface en interaction avec le soluté. Ce
déploiement a pour conséquence de dénaturer les
protéines. Il faut garder en tête que ces deux
phénomènes peuvent se dérouler simultanément et que
leurs effets s'additionnent, créant ainsi un équilibre dynamique
exclusion préférentielle / hydratation
préférentielle en compétition permanente (Figure 7).
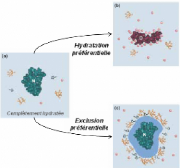
Figure 7 : Mécanismes de stabilisation des
protéines à différents niveaux de déshydratation.
(a) La cellule est complètement hydratée, la forme native de la
protéine (N) est thermodynamiquement favorable. (b) l'absence de
solutés compatibles (comme les sucres par exemple) fait que
l'hydratation préférentielle domine le phénomène
d'exclusion préférentielle, entraînant la formation de
liaisons entre les composés dénaturants et la protéine. La
protéine se déploie et finit par se dénaturer (D). (c)
L'exclusion prédomine sur l'hydratation, les solutés sont exclus
de la surface de la protéine, entraînant sa stabilisation dans son
état natif. 4
Le phénomène d'exclusion
préférentielle reste le principal mécanisme de protection
des macromolécules dans le cas d'une perte en eau d'hydratation
modérée. Cependant, ce mécanisme ne peut expliquer
à lui seul les mécanismes à l'origine de la protection
membranaire obtenue pour de plus importantes déshydratations, et
d'autres théories doivent rentrer en considération.
1.4.2. Cas d'une déshydratation sévère
:
Les dommages émanant d'un séchage à l'air
ou d'une lyophilisation peuvent être attribuées à deux
causes primaires: une modification de l'état physique des membranes
lipidiques et à une dénaturation des protéines. Quand la
déshydratation devient majeure, c'est-à-dire quand la
quantité d'eau atteint des niveaux inférieurs à 0,3 g
d'eau par gramme de matière sèche, parmi tous les solutés,
seuls les sucres peuvent répondre par leurs groupements fonctionnels et
par leurs structures aux impératifs liés à la
préservation des édifices biologiques. Afin d'expliquer comment
les membranes cellulaires peuvent résister à de telles
contraintes et quelle peut être l'action des hydrates de carbone,
différentes hypothèses ont été
élaborées autour des propriétés singulières
des sucres présents dans les liquides membranaires: (i) la substitution
de l'eau d'hydratation51, et (ii) le phénomène de
vitrification.11
1.4.2. 1.Substitution de l'eau d'hydratation
Quand la quantité d'eau devient critique dans les
cellules, c'est-à-dire quand l'eau qui constitue les sphères
d'hydratation commence à être atteinte par le dessèchement,
le phénomène d'exclusion préférentielle ne peut
plus avoir lieu. Tous les équilibres physiologiques sont brisés
et de nombreux dommages irréversibles apparaissent sur les bicouches
phospholipidiques52 comme par exemple la fusion des vésicules
ou encore l'apparition de «fuites» dans la membrane lors de sa
réhydratation (Figure 8).9,32 Les sucres, et plus
particulièrement les disaccharides non-réducteurs comme le
tréhalose, prendraient la place laissée libre par les
molécules d'eau lors de leur dissipation. Crowe et al. ont fait
l'hypothèse d'une substitution de l'eau d'hydratation51 par
certains mono- ou oligosaccharides après avoir observé que les
sucres interagissaient avec les têtes polaires des lipides constituant la
membrane.53,54,55,56,57 Lorsque les dernières
molécules d'eau quittent les têtes polaires, la température
de transition cristal liquide / gel (Tm) des membranes augmente
d'une manière significative, de l'ordre de 70°C. Cette augmentation
est liée en partie à la réduction importante de l'espace
entre les groupements polaires ainsi qu'à une densification des
chaînes acyles des lipides.
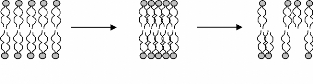
(a) (b) (c)
Figure 8: Représentation schématique d'une
membrane biologique en phase lamellaire (a). A cause du séchage, la
phase cristal liquide lamellaire se transforme en phase gel (b) puis
après réhydratation, la phase lamellaire présente des
défauts qui génèrent des fuites.
Cette augmentation de Tm peut être
empêchée par l'ajout de sucres5, qui par
l'intermédiaire de leurs groupements hydroxyles vont interagir, via la
formation de liaisons hydrogène, avec les têtes polaires des
molécules biologiques. Ces liaisons permettent de conserver
l'intégrité de la membrane en maintenant intact l'espace
intermembranaire et l'écartement entre les groupements
polaires.32 Certains sucres comme le tréhalose ou le sucrose
se sont révélés être de très bons
lyoprotecteurs, le premier ayant un meilleur pouvoir bioprotecteur. Le
tréhalose est en effet le seul disaccharide à ne pas
présenter de liaisons hydrogène intramoléculaires lui
permettant ainsi de se lier à un nombre plus important de
molécules d'eau que ces congénères.40,58 De
plus, des simulations numériques ont démontré que le
tréhalose était suffisamment flexible pour pouvoir étendre
ou contracter ses cycles glucose pour s'ajuster à l'espace
intermembranaire existant entre les têtes polaires des
lipides.59
1.4.2.2. Vitrification
L'autre interprétation, proposée par Green et
Angell11, se base sur le fait que les sucres présentent une
température de transition vitreuse anormalement élevée et
qu'ils sont de très bons formateurs de verre. Il est ainsi
postulé que, dans des cas quasi-anhydres, la grande viscosité du
liquide membranaire et son impossibilité à cristalliser
joueraient un rôle important dans le maintien de
l'intégrité fonctionnelle et structurale des organismes
plongés dans un état d'anhydrobiose.
Lorsqu'un liquide est refroidi, sa viscosité augmente.
S'il est refroidi suffisamment rapidement, comme dans le cas d'une trempe, la
viscosité va devenir si importante que l'arrangement moléculaire
dans le liquide en sera d'autant plus ralenti. Les dynamiques de
nucléation et de croissance du cristal sont devenues tellement lentes,
que la cristallisation n'a pas le temps de s'établir. Le liquide se fige
alors dans un état métastable sous la forme d'une phase vitreuse
selon un processus appelé vitrification. Une solution est dite
vitrifiée lorsque sa viscosité est supérieure à
1014 Pa.s.* Avec l'augmentation en concentration du
soluté, la diminution du stress imposé aux membranes ne peut se
produire que si les solutés ne cristallisent pas, autrement dit si le
liquide membranaire est vitrifié. Les sucres connus pour être de
très bons formateurs de verre, vitrifient dans l'espace intermembranaire
et évitent ainsi la fusion des couches
phospholipidiques.60,61
Toutes les hypothèses citées
précédemment ne sont valides que dans des gammes d'hydratation ou
de température données, et les théories invoquées
pour de faibles déshydratations4,24,27,28,29,30,31,50 ne permettent pas
d'expliquer à elles seules les phénomènes agissant pour
des pertes en eau beaucoup plus importantes et inversement. Vu sous cet angle,
aucune de ces théories prises individuellement ne permet d'expliquer de
manière globale et satisfaisante les processus à l'origine du
phénomène d'anhydrobiose. Néanmoins, il est facilement
imaginable que plusieurs de ces hypothèses se déroulent
simultanément, générant ainsi des couplages multiples dans
les systèmes macromolécules-sucres-ionseau, des
couplages/interactions qui sont étudiées à ce jour
séparément à travers des mélanges binaires ou
ternaires. Mais toutes ces études sont une première pierre
à l'édifice, et la compréhension de systèmes aussi
complexes nécessite, au préalable, des études
détaillées de modèles simplifiés, sans tenir
compte, à ce stade, de tous les constituants et de toutes les
interactions.
1.5. DYNAMIQUE MOLECULAIRE DES SUCRES EN SOLUTION
AQUEUS
Toutes ces théories sont principalement basées
sur les propriétés tout à fait uniques de l'eau et des
sucres. Et derrière ces changements de viscosité, de
déstructuration du réseau tétraédrique de l'eau et
de vitrification se cache des questions fondamentales sur la dynamique des
molécules et donc sur les
* A titre de comparaison, la viscosité de l'eau à
20°C est de 1mPa.s.
interactions solvant-soluté. Un certains nombres de
travaux théoriques et expérimentaux réalisés sur
des systèmes binaires (soluté-solvant), voire plus
récemment ternaires (soluté-solvant-protéine), sont
disponibles dans la littérature .40 Nous nous limiterons ici
aux mélanges binaires eau-sucre.
1.5.1. Dynamique d'un disaccharide:
l'-tréhalose.
Affouard et al. 62, Branca et al.63,64,
Ekdawi et al.65, Faraone et al.66, Köper et
al.67 et Magazù et al.68,69,70 ont étudié
expérimentalement la dynamique de l'-tréhalose et de l'eau en
fonction de la concentration en sucre et de la température. Grâce
à l'apport de la résonance magnétique nucléaire
(RMN) et à la diffusion neutronique, il leur a été
possible de découpler les dynamiques des molécules de solvant de
celles du soluté avec des échelles temporelles
complémentaires. Ainsi, la dynamique des molécules d'eau s'est
avérée être fortement affectée par la
présence du disaccharide. A titre d'exemple, le coefficient de diffusion
translationnelle des molécules d'eau diminue d'un facteur 30, pour des
concentrations en sucre allant de 0wt.%* à 7 1
wt.%.65 (Figure 9)

10-4
10-5
10-6
10-7
10-8
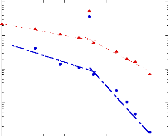
Dynamique de l'eau Dynamique du tréhalose
0 10 20 30 40 50 60 70 80
Concentration en tréhalose (wt.%)
Figure 9: Mesures RMN à 300K du coefficient de diffusion
translationnelle de l'eau (triangles) et du tréhalose (cercles) dans une
solution de tréhalose en fonction de la concentration.65
La dynamique des molécules d'eau en milieu dilué
diminue de manière faible mais régulière, puis le
ralentissement s'accélère au-delà des 40wt.% comme en
témoigne le changement de pente. Une rupture marquée dans la
dynamique moléculaire est notable vers 30-40wt.%. Cette forte diminution
de la dynamique est à rapprocher de l'augmentation importante de
viscosité observée lorsque la concentration en sucre
croît.71,72 Sachant que la viscosité est directement
liée aux interactions intermoléculaires, si la viscosité
augmente, alors les interactions eau-eau, eau-sucre et sucre-sucre sont plus
nombreuses et plus prononcées. Le tréhalose, à la
différence des autres disaccharides, présente
*L'abbréviation wt.% fait
référence aux pourcentages massique en sucre. Il se calcule selon
la formule suivante:
wt .% msucre .
msucre meau
une mobilité réduite à cause de sa plus
grande hydratation. Ainsi à 80wt.%, l'eau diffuse deux fois plus vite
dans une solution de sucrose que dans une solution de
tréhalose.65,73,74
Pour ce qui est du soluté, un net ralentissement de sa
dynamique est observé. Là où la dynamique de l'eau est
divisée par 30, la dynamique des molécules de tréhalose
est elle divisée par 300 pour des concentrations allant de 16wt.%
à 71wt.%.65 (Figure 9) Une nouvelle fois, une cassure dans la
dynamique est observée pour les mêmes raisons que celles
invoquées précédemment (viscosité, interactions,
...).
1.5.2. Dynamique de deux monosaccharides: le D-glucose et
le D-fructose.
Si la dynamique moléculaire du tréhalose en
solution aqueuse a été étudiée
expérimentalement et théoriquement de manière exhaustive,
il n'en est pas de même pour la dynamique du
Dglucose49,75,76,77 et du D-fructose49,78,79, dont les
premiers résultats ne sont que très récents... Ces travaux
expérimentaux ont mis en évidence une nette diminution des
dynamiques translationelle et rotationelle. L'eau voit ainsi son coefficient de
diffusion translationelle diminuer d'un facteur 10, et celui des
molécules de D-glucose d'un facteur 5 pour des concentrations allant de
15wt.% à 48wt.%.
Les dynamiques rotationnelle et translationnelle de ces
monosaccharides et disaccharides seront développées de
manière plus détaillée dans les prochains chapitres et un
accent tout particulier sera porté sur la dynamique moléculaire
du D-glucose, qui est au coeur même de ce travail de recherche.
1.6. CONCLUSION GENERALE DU CHAPITRE 1
L'anhydrobiose est un phénomène d'une incroyable
complexité et les processus mis en jeu ne sont à ce jour pas
encore compris de manière précise comme nous venons de le voir.
Néanmoins, toutes ces hypothèses convergent sur deux points : (1)
l'implication et le rôle essentiel de certains mono- et disaccharides
comme le tréhalose, et (2) par les interactions eau-sucre via la
formation de nombreuses liaisons hydrogène. Les liaisons
hydrogène sont à l'origine de la coopérativité du
réseau aqueux, du phénomène de cristallisation, de la
vitrification, des variations de viscosité ; en résumé,
elles sont à l'origine de toutes les propriétés
remarquables évoquées dans ces systèmes biologiques
complexes. Il apparaît donc comme essentiel d'étudier la dynamique
moléculaire de ces mélanges binaires eau-sucre, et donc à
travers leur dynamique, leurs interactions.
Chapitre 2
LA DIFFUSION NEUTRONIQUE APPLIQUEE A LA DYNAMIQUE
MOLECULAIRE
2.1. Les neutrons et la diffusion neutronique 35
2.2. Dynamique moléculaire du sucre en solution aqueuse
par QENS 41
2.2.1 Dynamique moléculaire du D-glucose
2.2.2 Dynamique moléculaire du D-fructose
2.3. Conclusion générale du chapitre 2 70
CHAPITRE 2
LA DIFFUSION NEUTRONIQUE APPLIQUEE A LA DYNAMIQUE MOLECULAIRE
2.1. LES NEUTRONS ET LA DIFFUSION NEUTRONIQUE
2.1.1. Le neutron et les interactions
rayonnement-matière
Le neutron, découvert en 1932 par James Chadwick, est
une particule subatomique qui présente une charge électrique
nulle, une masse m = 1,675.10-27 kg (~ 1836 fois celle de
l'électron), un spin 1/2 et un moment magnétique X =
-1,9132 41n* .80,81,82,83 L'énergie d'un neutron E est
reliée à sa vitesse v

par la relation E = 1/2 m.v2. A cette
particule est associée une onde plane de vecteur d'onde k , de longueur
d'onde 2 et d'énergie E :
|
Longueur d'onde :
|
h
|
Energie :
|
E
|
h2 h2.k2
|
|
m.v
|
2m22 2m
|

2 h.k

k
Vecteur d'onde : k = Moment : » = =
h .
2
où h est la constante de Planck, et h = h / 2= 1,
055× 10-34J.s est la constante de Dirac.
A cause de leur charge électrique nulle, les neutrons
n'ont pas d'interactions électrostatiques avec le nuage
électronique de l'atome à la différence d'autres
particules comme les rayons X ou les électrons. En revanche, ils sont
sensibles aux nucléons du noyau et c'est avec eux qu'ils interagissent
par des forces « nucléaires » de courte portée (~
10-12 cm). Et comme les neutrons sont 100 000 fois plus petits que
la distance noyau-noyau, leur probabilité d'interaction est de fait
relativement faible, ce qui leur permet de pénétrer la
matière en profondeur. (Figure 10) Les longueurs d'onde associées
aux neutrons froids et thermiques sont de l'ordre de grandeur des distances
interatomiques présentes dans les solides ou les liquides denses (1 <
l < 800 Å), et leurs énergies sont comparables à celles
des mouvements moléculaires (10-13 < t <
10-7 s). (Tableau 2) Les neutrons sont donc un outil de choix pour
sonder la structure et la dynamique atomique de la matière
condensée.
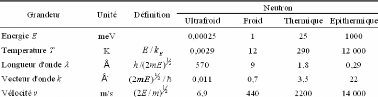
Tableau 2 : Caractéristiques des neutrons à
différentes énergies sélectionnées.80
* in est une constante physique appelée
magnéton nucléaire 1 un= 5,050 783 43×
10-27 A.m2.
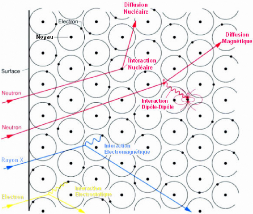
Figure 10: Interactions matière-rayonnem ent pour des
neutrons, des rayons X et des électrons.
La force d'interaction nucléaire entre un neutron lent
et un noyau est caractérisée par une grandeur appelée
longueur de diffusion b. Cette grandeur définit la zone autour de
l'atome dans laquelle le neutron va pouvoir interagir avec le noyau: il y a
interaction lorsque le neutron pénètre dans la sphère de
rayon b centrée sur l'atome. A la différence des rayons X, le
signe* et la valeur de b varient de manière
irrégulière en fonction du numéro atomique Z et de la
masse atomique A, ce qui rend les neutrons particulièrement sensibles
à la présence d'atomes légers comme l'hydrogène par
exemple.
Mais la situation est en réalité bien plus
complexe car les interactions ne sont pas uniquement
d'origine
nucléaire, mais également magnétique. Comme le neutron
présente un spin 1/2, il est sensible
au spin nucléaire du
noyau I. Dès lors que le noyau du centre diffusant possède un
spin I, la longueur
de diffusion b peut prendre les valeurs b ou b correspondant
aux états I + 1/2 ou I - 1/2 du système
respectivement. Dans
la pratique, les neutrons sont diffusés au hasard soit avec une longueur
b soit
avec une longueur b et il est donc nécessaire de
définir une longueur de diffusion moyenne. Pour
un
élément donné, constitué de différents
isotopes a, d'abondance ca et de spin nucléaire
Ia, la longueur
de diffusion moyenne b vaut alors:
c
b I b I b
a ( 1)
a a a a
a a
2 1
I
Il est intéressant de constater que les longueurs de
diffusion de deux isotopes sont généralement très
différentes. (Cf. Tableau 3) Ainsi une simple substitution isotopique
permet de moduler les
* Pour certains éléments ou isotopes, b peut
prendre des valeurs négatives: b(Ti) = -3,370×1012 cm,
b(46Ti) = 4,72×1012 cm.
intensités de diffusion en augmentant
l'intensité relative des zones d'intérêts et en diminuant
celle des zones moins intéressantes. Il est alors possible de
caractériser de manière très sélective les
constituants d'un système sans en modifier de manière importante
leurs propriétés physico-chimiques.
2.1.2. Principe de la diffusion neutronique
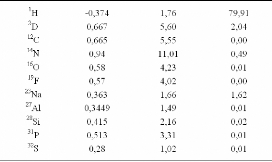
Une expérience de diffusion neutronique, comme celle
schématisée sur la figure 11, consiste à
|
~
envoyer sur l'échantillon un faisceau de neutrons de
vecteur d'onde ki
|
et d'énergie Ei . La majorité
|
des neutrons est transmise sans interaction, tandis qu'une
infime partie est diffusée et mesurée par un
détecteur.
A suffisamment grande distance du détecteur, l'onde diffusée peut
être considérée comme
|
~
plane avec un vecteur d'onde kf
|
~ ~
tel que ki; kf
|
, et une énergie Ef . Lors du
phénomène de
|
diffusion, le neutron et le système diffusant
échangent simultanément un moment et une énergie. Les lois
de conservation de l'énergie et du moment nous permettent d'exprimer
littéralement ces transferts :
? 2
Pour le transfert d'énergie* E = E --
Ef = h Am = h(coi --
w) = 2 - 2)
2m
~ ~ ~
Pour le transfert de moment** Q = k i-- k
f
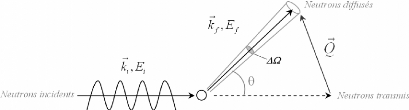
Figure 11 : Représentation schématique d'une
expérience de diffusion.
Dès lors que l'on envoie un courant de particules sur
une surface, il est possible de définir une section efficace a, dont
l'unité est le barn***. Durant une expérience de
diffusion, l'état du neutron incident est susceptible d'être
modifié en énergie, en direction et en spin. Trois types de
sections efficaces peuvent alors être distinguées :
· La section efficace totale de diffusion aS qui
prend en compte tous les neutrons diffusés.
· La section efficace différentielle de diffusion
d/d qui comptabilise tous les neutrons diffusés dans l'angle solide d et
quelle que soit leur variation d'énergie.
* Par convention, E est choisi positif lorsque le neutron
cède de l'énergie au système.
|
~~
** Le vecteur Q
|
caractérisant le transfert de moment est également
dénommé vecteur de diffusion.
|
*** L'unité de section efficace est le barn (b) : 1b =
10-28 m2.
La section efficace double différentielle de diffusion
d2/ddE qui comptabilise tous les neutrons diffusés dans
l'angle solide d et avec une variation d'énergie dE.
2
Ces différentes sections efficaces sont liées par
l'identité suivante:
S
dadn =rr
d 6 ddE dddE
De façon générale, le spectre
d'énergie de l'intensité diffusée par unité d'angle
solide n et pour un transfert en énergie E #177; dE s'écrit :
~~
d2a(Q,E)
If(Q,E)-- I0 dû.dE
où I0 est l'intensité incidente et
If(Q,E) est une quantité qui reflète à la fois
la structure et la dynamique d'un système.
2.1.3. Diffusion cohérente et incohérente
La section efficace double différentielle de diffusion
d'un système peut être décomposée en deux termes qui
représentent la diffusion cohérente et la diffusion
incohérente :
d2o- k 0-
dn2E kfi 4 Scoh k
(Q,E)+ f
ainc S (Q E)
ciroh
i
|
où
|
~~
coh , Cr inc , Scoh(Q, )
|
~~*
et S inc(Q, E)
|
sont les sections efficaces et les fonctions de diffusion ou
|
facteur de structure dynamique cohérent et
incohérent respectivement.
La diffusion cohérente (1er terme)
dépend de la corrélation entre la position de l'atome i au temps
0 et celle de l'atome i' au temps t. Ce terme contient tous les termes
d'interférence. La diffusion incohérente (2nd terme)
dépend de la corrélation entre la position de l'atome i au temps
0 et celle du même atome au temps t. Autrement dit, la partie
cohérente représente l'interaction entre paires d'atomes
différents, et la partie incohérente représente
l'interaction de chaque atome avec lui-même.
* Les expressions de Scoh(Q,E) et Sinc(Q,E)
sont données ici à titre indicatif:


1 ~~\\ \\
Scoh(Q, E) 2n?
= exp(--iot)E
expLQR! 0)) exp iQ
· Rjt)) dt
N jj


\ 1 r 1 \\ ~~~ ~~
(t)) Sinc (Q, E) =
expHCOOE exp/--QR j
0))exp/iQ. Rj
It)) dt
2?N j
Les fonctions de diffusion sont les transformées de
Fourier en énergie des fonctions intermédiaires de diffusion
cohérente Icoh(Q,t) et incohérente
Iinc(Q,t).
Dans le cas d'un système polyatomique, la double
différentielle de diffusion prend alors l'expression suivante:
d
2 k
c c b b S Q E
1/ 2 1/ 2 * '
dd k f
f ( , ) ( , )
c S Q E
d
d d d d coh
' ' d inc
d dE k i d
k
dd ' i
où cdNd N est la concentration de
l'élément d.
Les sections efficaces cohérente et incohérente,
dont leurs expressions littérales sont données ci- dessous, sont
fonction de la longueur de diffusion b qui est propre à chaque atome:
2
4 b 2 *
b
inc [ ?
2
coh 4 b

La section efficace totale de diffusion est la somme des sections
efficaces cohérente et incohérenteinc . Le tableau 3
présente les sections efficaces cohérente et
incohérente
total coh
de quelques éléments communs de la
classification périodique. Au vue de la section efficace
incohérente de l'hydrogène, qui est très largement
supérieure à celle des autres noyaux mais également
à sa propre section efficace cohérente, la diffusion des neutrons
sera donc par nature essentiellement incohérente à petits Q pour
des systèmes hydrogénés.

Tableau 3: Longueurs de diffusion b et les sections efficaces
cohérente et incohérente pour quelques éléments du
tableau périodique.84
* b est la longueur de diffusion moyenne pour un
élément donné. (Cf. le paragraphe
précédent).
2
b best la déviation quadratique moyenne, où
ca 2 2
b I b I b
2 ( 1)
a a a a
a Ia
2 1
2
. Physiquement,
la diffusion incohérente provient de la distribution
aléatoire des écarts à la moyenne des longueurs de
diffusion.
Le tableau 3 montre clairement que deux isotopes peuvent
présenter des valeurs de acoh et ainc
très
différentes. Ainsi, par exemple, on remarquera le grand
écart existant entre les sections efficaces incohérentes de
l'hydrogène (1H) et du deutérium (2H).
Cette propriété, très marquée dans le cas de
l'hydrogène, se retrouve chez d'autres atomes, comme l'ytterbium ou le
gadolinium, ou chez certains isotopes comme le titane. Le mélange des
isotopes nous permettra donc de jouer sur les densités de longueurs de
diffusion, ce qui nous permettra de caractériser les mouvements
individuels des atomes d'hydrogène dans le cadre d'études de
dynamique moléculaire.
2.1.4. L'étude de la dynamique moléculaire
par diffusion quasi-élastique
La diffusion quasi-élastique des neutrons (QENS) est
une technique très performante pour étudier les mouvements
diffusifs qui présentent des temps caractéristiques allant de la
nano- à la picoseconde, correspondant à des transferts en
énergie E allant de 1 ?eV à 1 meV. Il s'agit de mouvements
individuels tels que les mouvements de translation et de rotation des
molécules dans les liquides, la rotation de groupements chimiques ou de
molécules dans des phases solides désordonnées....
L'apparition des sources de neutrons froids a permis de
concevoir des spectromètres spécialement adaptés à
l'étude des mouvements diffusifs : les spectromètres à
temps de vol (TOF), à rétrodiffusion (BS) et à écho
de spin (NSE). Les spectromètres TOF et BS mesurent essentiellement la
diffusion incohérente dans les systèmes hydrogénés,
et donc les déplacements individuels des atomes, c'est-à-dire
leur diffusion et/ou leur rotation. Le spectromètre NSE, en revanche,
permet de mesurer la diffusion cohérente, qui donne accès
à la dynamique collective des molécules.* Le
schéma ci-dessous présente les échelles de longueur et de
temps accessibles par le TOF, le BS et le NSE. La bonne
complémentarité de ces trois instruments permet ainsi une
étude complète d'un système sur différentes
échelles de temps allant de la picoseconde à la nanoseconde.
(Figure 12) Dans le cadre de cette étude, nous nous limiterons aux
spectromètres à temps de vol (TOF) et à
rétrodiffusion (BS) qui correspondent aux échelles de temps
caractéristiques de nos systèmes eau/sucre.
* Le spectromètre NSE mesure en réalité
la différence entre la diffusion cohérente de spin et la
diffusion incohérente de spin pondérée d'un
facteur -1/3. Il est alors possible, pour des systèmes ne
présentant pas un taux d'incohérent trop
élevé de mesurer la diffusion cohérente de spin.
Figure 12 : Représentation schématique des
échelles de longueur et des échelles de temps accessibles avec
les techniques de diffusion de la lumière ou de neutrons (TOF, BS et
NSE) et les techniques spectroscopiques (RMN et diélectrique).
2.2. DYNAMIQUE MOLECULAIRE DE SUCRES EN SOLUTION
AQUEUS
La dynamique moléculaire de monosaccharides en solution
aqueuse avait commencée au sein de notre équipe par les travaux
sur le D-glucose de César Talón76 et Luis
Smith75. Ils avaient pour but d'étudier la dynamique de l'eau
et du sucre en une seule et même expérience. Cependant, ces
travaux ont été réalisés en deux temps, par des
expérimentateurs différents et sur deux types de
spectromètres présentant des résolutions assez
différentes: un spectromètre à temps-de-vol et un
spectromètre à rétrodiffusion. Notre intention est donc
d'asseoir ces résultats en réalisant dans les mêmes
conditions ces échantillons une deuxième fois et en les mesurant
cette fois-ci sur les deux types de spectromètres. Si les
résultats concordent, ces valeurs seront alors utilisées comme
des références pour l'étude de la dynamique des solutions
confinées qui est au coeur de cette étude.
2.2.1. Dynamique moléculaire du D-glucose
2.2.1.1. Préparation des solutions de D-glucose /
échange isotopique
Les solutions aqueuses de sucre sont des systèmes
fortement hydrogénés, et leur étude conduirait à
étudier la dynamique simultanée du solvant et du soluté.
En milieu dilué, comme c'est le cas ici, la proportion en eau est
écrasante, et la contribution du solvant est donc de fait très
largement majoritaire. Afin de découpler la dynamique moléculaire
du solvant de celle des molécules de sucre elles-mêmes, une
substitution isotopique ciblée est nécessaire. Cependant, les
hydrates de carbone sont des composés qui présentent des atomes
d'hydrogène dits échangeables liés aux atomes
d'oxygène, et des atomes d'hydrogène dits non-échangeables
liés eux à des atomes de carbone. Cette terminologie
échangeable/non-échangeable témoigne de l'aspect dynamique
des échanges atomiques qui prennent place en solution. Les
hydrogènes échangeables sont ceux qui peuvent «
s'échanger » avec les atomes d'hydrogène des
molécules de solvant voisines, à la différence des atomes
d'hydrogène dits non- échangeables qui eux restent
attachés à leur atome de carbone. Les sucres participeront donc
inévitablement à la diffusion. Cependant, si le « masquage
» intégral des molécules de sucre est infaisable
pratiquement, il est cependant possible de s'en prémunir le plus
possible en réalisant des prétraitements ciblés à
l'aide de la substitution isotopique H/D adaptée à la dynamique
que l'on veut observer, celle du solvant ou du soluté:
(1) Si l'on étudie la dynamique moléculaire du
solvant.
L'objectif principal est d'étudier la diffusion du
solvant, il est donc impératif de masquer celle du sucre. Lorsque l'on
dissout des molécules complètement deutérées de
D-glucose (C6D12O6) dans de l'eau légère (H2O), 5 des 12 atomes
d'hydrogène du sucre s'échangent inévitablement avec les
hydrogènes du solvant. Il n'est donc pas judicieux de deutérer
intégralement le D-glucose, seul une deutération des
hydrogènes non-échangeables des sucres (C6D7H5O6)
suffisent à abaisser au maximum la diffusion incohérente
émanant des hydrates de carbone.
(2) Si l'on étudie la dynamique moléculaire du
soluté.
L'idée désormais est de masquer le signal du
solvant pour ne s'intéresser plus qu'à celui du sucre.
L'utilisation de l'eau lourde (D2O) permettra de minimiser la diffusion
incohérente provenant du solvant. De plus, afin de s'affranchir des
échanges probables entre le soluté et le solvant, le D-glucose a
été tout d'abord mélangé avec de l'eau lourde pour
remplacer les 5 atomes d'hydrogène échangeables par des atomes de
deutérium.* Ce sucre partiellement deutéré
(C6D5H7O6) est ensuite dissout, dans des proportions adéquates,
dans du D2O pour la préparation des échantillons.
* Le D-glucose (Sigma-Aldrich) a été dissout
dans un large excès de D2O et agité pendant plusieurs heures en
boîte à gants. Cette solution de sucre partiellement
deutérée a ensuite été placée en
étuve à vide afin d'évaporer l'excédent de solvant.
La poudre blanche obtenue a été utilisée dans la
réalisation des solutions.
Trois concentrations molaires en sucre ont été
sélectionnées pour cette étude: 1:20, 1:55 et 0:100
C6H12O6: H2O; ces concentrations correspondent à des concentrations
massiques en sucre de 33,3, 15,4 et 0 wt.% respectivement, dans le cas de
solutions complètement hydrogénées.
2.2.1.2. Conditions expérimentales
Les expériences de QENS ont été
réalisées au NIST National Center for Neutron Research (NCNR) sur
deux spectromètres: le spectromètre à temps-de-vol
appelé disk chopper time-of-flight spectrometer85 (DCS) et
sur le high-flux backscattering spectrometer86 (HFBS), qui est un
spectromètre à rétrodiffusion. Dans les deux cas, les
solutions ont été placées dans des porte-
échantillons cylindriques en aluminium présentant un espace
annulaire de 0,1 ou 0,44mm, scellés, et placés dans un cryostat
dans lequel la température est régulée à #177;
1K.
Les expériences sur le DCS ont été
réalisées à 280 K avec une longueur d'onde incidente de 6
Å (0,25 < Q < 1,93 Å-1). La résolution en
énergie et la normalisation en intensité ont été
déterminées à partir de la mesure d'un cylindre creux de
vanadium réalisée dans les mêmes conditions que celles
utilisées pour les échantillons. La résolution
instrumentale a été estimée à 55j.teV à
partir de la largeur à mi-hauteur du pic élastique du
vanadium.
Les expériences sur le HFBS ont été
réalisées à 280 K avec une longueur d'onde incidente de
6,27 Å (0,36 < Q < 1,52 Å-1) pour une
résolution instrumentale de 1,2j.teV. La fenêtre de transfert
énergétique est de #177;36j.teV.
Nous avons mesuré sur ces deux spectromètres:
Un spectre de diffusion du vanadium,
Un spectre pour chaque porte échantillon en aluminium vide
(0,1 et 0,44mm), Les échantillons à 280K (Tableau 4).
La durée d'acquisition moyenne de chaque spectre
était de 12 heures pour le DCS et de 24 heures pour le HFBS. La
dénomination d-glc correspond à un D-glucose sur lequel les
hydrogènes non- échangeables ont été
substitués par des atomes de deutérium (C6D7H5O6). De
la même manière, h-glc correspond à un D-glucose sur lequel
les hydrogènes échangeables ont été
échangés par des deutériums (C6D5H7O6).
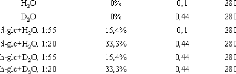
Tableau 4: Tableau récapitulatif des conditions
expérimentales pour les échantillons mesurés sur le DCS et
le HFBS. (d-glc: C6D7H5O6; h-glc: C6D5H7O6)
2.2.1.3. Traitement des données
expérimentales
Durant une expérience de diffusion, et plus
particulièrement dans le cas des spectromètres TOF et BS, nous
mesurons le nombre de neutronsn(t) diffusés pendant le temps T par
l'échantillon, détectés dans le canal correspondant au
temps de vol t et de largeurt, par un détecteur placé à un
angle B et couvrant un angle solide A
d t
2 B ( , )
n t T A t
( ) .
= i
0 d dt
où:
= 0 est le flux de neutrons incidents,
i est l'efficacité du détecteur,
A est un facteur qui prend en compte l'absorption de
l'échantillon,
est la section efficace de diffusion en échelle de
temps-de-vol.
d t
2 ( , )
B
d dt
.
La section efficace de diffusion en échelle de
temps-de-vol d2B(, t) ddt donne accès à la
section efficace de diffusion en énergie d2B(,) ddt
*, qui est proportionnelle au facteur de structure S(Q, E) qui nous
intéresse.

* La section efficace de diffusion en échelle de
temps-de-vol d2B(, t) d.dt et la section efficace de
diffusion
d d t dt
2 2
B ( , ) 1 ( , )
B
.
d dE d dt dE
. .
?
en énergie d2B(,) d.dE sont
liés par la relation suivante:

2
m nD
2
t
2 ( )
? E E
0
détecteur par l'expression
oùmn est la masse du neutron.
dt dE peut être déduite de la relation qui lie le
temps de vol t à la distance D séparant l'échantillon
du
L'objectif est donc d'obtenir le facteur de structure dynamique
S(Q,E), qui contient toute
l'information du système, à partir des
données brutes mesurées expérimentalement,
c'est-à-dire à partir de n(t). Pour ce faire, un traitement en
plusieurs étapes des données expérimentales a
été réalisé à l'aide de la série de
programmes DAVE développée à NIST.87
2.2.1.3.1. Normalisation au moniteur
Le flux 00 pouvant être fluctuant, et les
durées de mesures T plus ou moins longues, il est
indispensable de rapporter les spectres au même nombre de
neutrons incidents pour pouvoir les
comparer. Tous les spectres sont donc
normalisés par la grandeur 00.T , qui représente le
nombre de
neutrons effectivement reçus par l'échantillon.
2.2.1.3.2. Soustraction de la cellule vide
L'aluminium est utilisé de manière courante dans
la fabrication des instruments de neutronique
parce qu'il ne donne pas ou très peu de diffusion
incohérente (inc= 0,0082 barn). C'est la raison pour
laquelle, la plupart des porte-échantillons pour ces
types de spectromètre sont en aluminium. Néanmoins, bien que le
signal du porte-échantillon soit purement élastique, de la
diffusion incohérente « parasite » provenant
d'impuretés peut apparaître et fausser nos mesures. Afin de
s'affranchir de tels problèmes et d'extraire le signal de la solution
(DS), on soustrait au signal de diffusion (DS+EC) le signal de la
cellule vide (DEC) accompagné d'un coefficient A qui prend en compte la
transmission de l'échantillon:
DS = D S+EC --
A.DEC (Eq. 1)
La transmission des échantillons a été
calculée à partir des sections efficaces cohérentes et
incohérentes du solvant et du soluté. Les transmissions
étant toutes supérieures à 0,9, nous avons
considéré comme négligeable les diffusions multiples.
(Tableau 5)
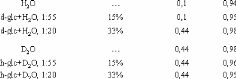
Tableau 5: Tableau récapitulatif des épaisseurs et
des valeurs des transmissions pour les différents échantillons
utilisés
2.2.1.3.3. Normalisation au vanadium
Les détecteurs ne présentent pas tous la
même efficacité et afin de rétablir une bonne
homogénéité, il convient de normaliser les spectres par le
signal obtenu par un échantillon de vanadium, qui est un diffuseur
purement incohérent. De cette manière, tous les détecteurs
présenteront la même efficacité après correction.
2.2.1.3.4. Regroupement
Les spectres de diffusion obtenus au niveau de chaque
détecteur ne présentent pas toujours une statistique suffisante
pour être exploitable, et il est courant de sommer les spectres sur des
groupes de détecteurs situés dans une même région de
l'espace. Dans notre cas, le nombre de groupes s'élève à
16, et ce sont ces spectres regroupés que l'on analysera par la
suite.
Toutes ces étapes nous ont donc conduit à
déterminer le facteur de structure dynamique S(Q,E). Les
représentations tridimensionnelles des fonctions de diffusion S(Q,E)
pour les échantillons dglc+H2O, 1:20 et d-glc+H2O, 1:55 mesurés
sur le DCS sont présentés en figure 13.
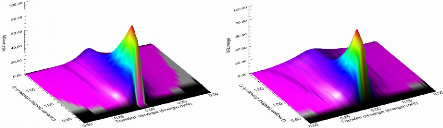
Figure 13 : S(Q,E) en fonction du transfert d'énergie E et
du transfert de moment Q pour les échantillons dglc+H2O, 1:20 (gauche)
et d-glc+H2O, 1:55 (droite) obtenus sur le spectromètre à
temps-de-vol DCS.
La figure 14, quant à elle, présente une coupe
de ces mêmes fonctions de diffusion pour une valeur de Q donnée,
ici pour Q= 0,97Å-1. Une coupe similaire a été
réalisée sur les fonctions de diffusion des échantillons
h-glc+D2O, 1:20 et h-glc+D2O, 1:55, obtenues sur le HFBS pour
Q=0,36Å-1.
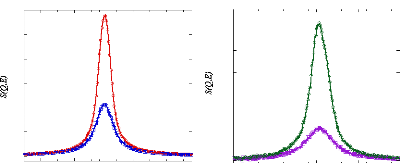
H
0
2
T = 280 K Q = 0,97 Å-1
0,05
(b)
D
0
2
T = 280 K Q = 0,36 Å-1
1:20
0,04
1:20
20
0,03
15
0,02
10
0,02
5
1:55
0,01
1:55
0
0
(a)
25
-0,4 -0,2 0 0,2 0,4
|
E (meV)
|
-0,01 -0,005 0 0,005 0,01
E (meV)
|
Figure 14 : (a) Spectres obtenus sur le DCS pour le d-glc+H2O,
1:20 (rouge) et d-glc+H2O, 1:55 (bleu). (b) Spectres
obtenus sur le HFBS pour le h-glc+D2O, 1:20 (vert) et h-glc+D2O, 1:55
(violet).
Une première analyse visuelle de ces coupes nous montre
un effet significatif de la concentration en sucre sur l'intensité et la
largeur à mi-hauteur des spectres, et ce aussi bien sur le
spectromètre à temps de vol (DCS) que sur le spectromètre
à rétrodiffusion (HFBS), qui présentent pourtant des
résolutions très différentes.
2.2.1.4.Modélisation des spectres
Une manière courante d'analyser des spectres de
diffusion de neutrons est de postuler que les différents types de
mouvements : vibrationnels, rotationnels et translationnels sont
découplés. Ceci n'a de validité que si les dynamiques
respectives présentent au moins un ou plusieurs ordre(s) de grandeur
~~
d'écart. Dans le cadre de cette approximation, la
fonction de diffusion Sinc (Q, E) s'exprime alors
comme le produit de convolution des facteurs de structure
correspondant aux différents types de mouvements :
~~ ~~ ~~ ~~
Sinc(Q,E) SV(Q,E)? SR(Q,E)?
ST(Q,E) (Eq. 2)
~~ ~~ ~~
où SV(Q,E) ,SR(Q,E) et ST(Q,E)
sont les fonctions de diffusion vibrationnelle, rotationnelle et
translationnelle respectivement.
Dans la région quasi-élastique qui nous
intéresse (c'est-à-dire pour des énergies E < 1meV),
la
fonction de diffusion vibrationnelle se limite à un facteur
Debye-Waller (DW)*. Le DW est

*Le facteur Debye-Waller (DW) s'exprime en fonction
du déplacement quadratique moyen u2 et du transfert
u2 Q2 /3
de moment Q : DW = e .
indépendant de l'énergie et prend en compte la
diminution de l'intensité quasi-élastique en fonction de Q, une
diminution qui est liée à des mouvements rapides se produisant en
dehors de la région quasiélastique.88 La fonction de
diffusion peut alors être exprimée uniquement en fonction des
facteurs de structure dynamique de rotation et de translation dans le domaine
quasi-élastique considéré:
2 2
~~ u Q
. ~~ ~~
S inc
(Eq. 3)
( , ) exp ( , ) ( , ) ( )
Q E S Q E S Q E R E
. R T
? ?
3 [ ?
La fonction de diffusion totale n'est désormais
composée que de deux termes correspondant à des mouvements de
type diffusifs. Deux modèles sont couramment utilisés pour
décrire ces type de mouvements: (i) le modèle dit de diffusion
par sauts, et (ii) le modèle de l'exponentielle étirée.
Dans notre cas, le modèle de l'exponentielle étirée ne
nous a pas permis d'obtenir un ajustement satisfaisant et par conséquent
n'a pas donné de résultats probants. C'est pour cette raison que
nous ne décrirons ici que le modèle de diffusion par sauts. Ce
modèle comporte deux composantes, une gaussienne, qui prend en compte la
diffusion élastique, et une composante Lorentzienne, qui prend en compte
tous les autres types de mouvements présents dans le système.
La deuxième loi de Fick, également baptisée
équation de diffusion, gouverne les mouvements de diffusion continue:
2 ( , )
( , ) C r t
0
D C r t V(Eq. 4)
0t
dans laquelle C(r,t)est la probabilité pour une particule
d'être à la position r à l'instant t et D est le
coefficient de diffusion de cette particule.
Sachant que les conditions aux limites sont C(r, 0)N(r) (N est
le nombre total de particules) et C(r, t - oc)0, la solution de cette
équation est une gaussienne*. Sa double transformée de
Fourier dans l'espace et le temps permet d'accéder au facteur de
structure dynamique incohérent:
1 ( )
[' Q
S Q E Q E
( , ) ( , )
.J7(Eq.5)
inc ( )
Q E
2 2
['
Le spectre de neutrons correspondant est une Lorentzienne avec
une demi-largeur à mi-hauteur
['(Q) /2. La théorie
d'Einstein89 sur le mouvement Brownien permet de faire le lien
entre
N
* L'équation de la fonction gaussienne solution de
l'équation est: C r t r Dt
2
( , ) 3/2 exp 4
(4 )
Dt
l'élargissement de la fonction de diffusion et le
coefficient de diffusion. Le modèle de diffusion continue prédit
pour ['(Q) la forme suivante:
2 ? DQ 2
[' ( Q )(Eq. 6)
où D est le coefficient de diffusion.
Cependant, ce modèle n'est valide que pour des forces
d'interaction intermoléculaires relativement faibles, et dans le cas
d'interactions plus fortes, comme dans les liquides structurés par
exemple, il est remplacé par le modèle de diffusion par sauts. Ce
modèle décrit des systèmes dans lesquels les
molécules présentent des mouvements oscillants localisés
présentant occasionnellement des mouvements de translation, durant
lesquels les molécules peuvent diffuser sur des distances
supérieures à leur amplitude de vibration. Le modèle de
diffusion par sauts définit deux nouveaux temps caractéristiques:
(i) le temps de saut r J durant lequel la particule
diffuse, et (ii) le temps de
résidence r0 durant lequel la
particule oscille sans translation.90 Dans la partie
quasi-élastique, ce
modèle donne lieu à des lois de diffusion qui
dévient du régime continu pour de grandes valeurs de Q. La
largeur à mi-hauteur s'exprime alors de la manière suivante:
2
? **
DQ 2
[' ( )
Q (Eq. 7)
1 J
Q Dr
2
Le temps de saut r J et la longueur de saut
caractéristique l0 sont reliés au coefficient de
diffusion D par la relation:

La fonction de diffusion translationnelle ST (Q, E)
utilisée ici est donc extraite de ces travaux classiques et de travaux
plus récents sur l'eau91,92 dans lesquels ST (Q,
E) est modélisée par la fonction Lorentzienne.t?(Wt,E)
suivante:
1 2
W t
S Q E W E
( , ) ( , )
.t?(Eq. 9) T t ( 2)
W E

2 2
t
2
2
W t
?DQ
avec
1 6
l Q
2 2
** Notons que pour des petites valeurs de Q, la loi de diffusion
par saut se réduit au modèle continu. (Eq. 6)
La diffusion rotationnelle, quant à elle, a
été modélisée à l'aide des premiers termes
du développement limité développé par
Sears93 pour la diffusion rotationelle d'une molécule
libre:
|
8
S Q E A
R i
( , ) ( ) ( ) ( , )
E A Q W E
~
0 i r
i1
|
(Eq. 10)
|
? i i
( 1)
2
avec A i ( Q ) (2 i 1) j i
(amQ), où am est le rayon moléculaire
effectif, W, et ôR est le
ri 3 ô R
temps de relaxation rotationnel.
Dans la gamme de Q utilisée ici, c'est-à-dire pour
Q < 2Å-1, le coefficient amQ présente
une
décroissance rapide avec i, et au-delà de i=3,
les termes deviennent négligeables. Ici, seuls les deux premiers termes
de ce développement, qui contribuent de manière significative,
ont été considérés dans cette étude.
Dans l'approximation d'une diffusion cohérente
négligeable devant le signal incohérent, et à partir des
équations précédentes, nous pouvons exprimer
littéralement le facteur de structure dynamique total
incohérent:

u Q
S
inc total
2 2 ? 8 ?
(Eq. 11)
( , ) exp ( , ) ( ) ( ) ( , ) ( )
Q E W E A
? ?
~ E A Q W E R E
~ ? ?
t 0 i r Ò
3 ? ?
i
[ i 1 ?
dans lequel R(E) est la résolution de l'instrument,
obtenue en mesurant un spectre élastique de l'échantillon
complètement gelé ou un échantillon de vanadium.
A partir de l'ajustement, pour chaque valeur de transfert de
moment Q, du facteur de structure dynamique total incohérent (Eq. 11) au
signal quasi-élastique incohérent expérimental, il est
possible d'extraire les paramètres suivants:
1. la largeur à mi-hauteur W t
2
2 ? DQ
de la Lorentzienne «étroite» qui décrit
les

1 6
l Q
2 2
mouvements de translations des molécules,
2. la largeur à mi-hauteurWr de la Lorentzienne
«large » qui décrit les mouvements de rotation des
molécules.
2.2.1.5. Résultats
2.2.1.5.1. DCS
inc
La fonction de diffusion théorique S Q E
( , ) a été ajustée aux données
expérimentales pour
total
chaque valeur de transfert de moment Q. Le meilleur ajustement
a été obtenu en combinant une fonction gaussienne étroite
(fonction delta), deux fonctions Lorentziennes (une large et une plus
étroite) et une ligne de base à pente non nulle afin d'autoriser
une légère déviation du signal de diffusion
inélastique (Figure 15). L'expression complète est donnée
ci-dessous:
Sinc
(Q,E)[(E)c1(Q).L(W1,E)c2(Q).L( W 2
,E)a?bE]R(E) (Eq. 12)
où R(E) est la résolution instrumentale et L(Wi,E)
une fonction Lorentzienne avec une largeur à mi- hauteur Wi, et(E) une
fonction delta.
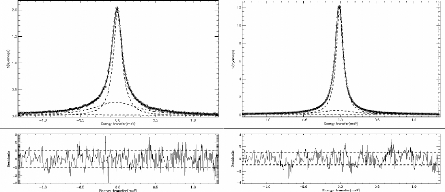
Figure 15: Deux exemples d'ajustements des données du
DCS composés de deux fonctions Lorentziennes et d'une ligne de base. Il
s'agit ici de l'eau (H2O) à gauche et du d-glc+H2O, 1:55 à droite
à 280K et à Q = 0,97Î1. Les résidus sont
présentés en dessous de chaque courbe.
Deux fonctions Lorentziennes sont ici nécessaires dans
l'ajustement: (i) une large pour les mouvements de rotation de la
molécule, et (ii) une que l'on qualifiera d'étroite pour les
mouvements d'ensemble des molécules.
Les expressions théoriques de W t (Eq. 9 et
10) montrent une dépendance en Q2 de la largeur à mi-
hauteur pour les deux types de mouvements diffusifs. Le tracé de ces
largeurs à mi-hauteur W1 et W2 en fonction de Q2 est
présenté dans la figure 16 pour les trois échantillons
dont le solvant est l'eau (H2O, d-glc+H2O, 1/20 et d-glc+H2O, 1/55) ainsi que
pour l'échantillon contenant de l'eau lourde uniquement (D2O).
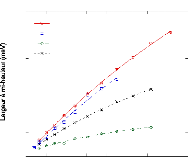
Lorentzienne "étroite" L1(W~~E)
(a)
H2O
T = 280 K
0,5
D2
O
0,4
d~glc+H2O, 1/20
d-glc+H2O, 1/55
0,3
0,2
0,1
0
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å2) (b) Lorentzienne "large"
L2(W~~E)
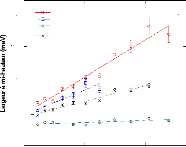
T = 280 K
H2O D2O d-glc+H2O, 1/20
d-glc+H2O, 1/55
0
2
1,5
1
0,5
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å2)
Figure 16: Largeur à mi-hauteur de la Lorentzienne
étroite W1 (a) et de la Lorentzienne large W2 (b) ajustées aux
données de l'eau et des solutions de glucose. Les courbes
représentent les ajustements effectués à partir des
équations 9 et 10.
Le tracé de W1 en fonction de Q2 montre une
première région linéaire qui tend à s'aplanir pour
atteindre une valeur constante théoriquement égale à 1 /
ô0. Cette dépendance non-linéaire en
Q2 de W1
renforce l'utilisation du modèle de diffusion par
sauts. Nous remarquons que le plateau n'est atteint que pour
l'échantillon le plus concentré en sucre en raison de la gamme de
Q sondée ici. Le tracé de W2 en fonction de Q2 montre
une dépendance linéaire à pente non nulle.
Théoriquement, W2 est indépendante de Q2 dans le cas
de mouvements parfaitement découplés. Cependant, pour pouvoir
découpler complètement les deux types de mouvements, il aurait
fallu pouvoir utiliser plus de deux fonctions Lorentziennes convoluées
avec la résolution durant l'ajustement, ce qui n'a pas été
possible dans notre cas. Nous estimerons donc W2 à sa valeur pour Q =
0.
La dépendance en Q2 des W n a
été ajustée par la méthode des moindres
carrés à l'aide des expressions suivantes:
Q 2
1
W(Eq. 13)
1 1 2
1 ã 1 Q
2 Q 2
W 2 (Eq. 14)
2
L'expression de l'équation 13 a bien évidemment
été choisie en rapport avec l'expression théorique de W
t déterminée précédemment. En revanche,
celle de l'équation 14 a été choisie de manière
purement empirique. Les ajustements sont présentés sur la figure
16 sous forme de lignes continues et les valeurs des paramètreset
1 1 ã 1 sont regroupées dans le tableau 6. Nous
pouvons remarquer
2 2
le très bon accord qui existe entre les courbes
expérimentales et théoriques, témoignant de la
validité du modèle utilisé.

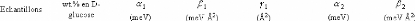

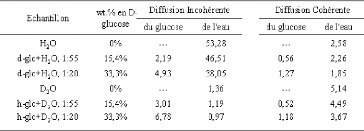
Tableau 6: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite W1 et pour la Lorentzienne large W2 à partir
des mesures réalisées sur le DCS à 280K.
Les valeurs des paramètres pour les échantillons
h-glc+D2O, 1:55 et h-glc+D2O, 1:20 doivent être manipulées avec
précaution. Le traitement direct de ces échantillons n'a pas
permis de les ajuster de manière complètement satisfaisante. Il
nous a fallu en effet soustraire le signal du solvant (D2O) afin de n'obtenir
plus que celui du sucre. Ce traitement supplémentaire ne peut être
considéré qu'approximatif en raison de la différence de
dynamique moléculaire existante dans un solvant pur et dans un solvant
contenant un soluté. Malgré cette soustraction,
l'échantillon h-glc+D2O, 1:20 ne nous a pas permis d'obtenir de
résultats valides. Cette difficulté de traitement a
vraisemblablement deux origines:
(i) les contributions relatives de la diffusion cohérente
et incohérente (Tableau 7) présentent un faible écart
relatif qui invalident l'approximation d'une diffusion cohérente
négligeable. Ce postulat inc
n'étant plus vérifié, notre expression
théorique de S Q E
( , ) n'est donc plus utilisable.
total
(ii) La diffusion incohérente du solvant et celle du
sucre s'équilibrent dans ces mélanges, rendant difficile la
séparation des signaux, et ce, malgré les deutérations
sélectives effectuées. Ainsi, au lieu de ne regarder que la
dynamique du D-glucose comme initialement prévu, c'est la dynamique
globale du mélange qui est sondée. (Tableau 7)
Tableau 7: Contributions relatives de la diffusion
cohérente et incohérente émanant du D-glucose et de l'eau
lourde ou légère.
Pour les échantillons préparés avec de
l'eau légère, l'approximation d'une diffusion cohérente
négligeable reste valable en raison du fort écart relatif
existant entre le signal cohérent et incohérent. De plus, les
contributions relatives de l'incohérent du sucre et de l'eau sont
suffisamment différentes pour permettre uniquement l'extraction du
signal provenant du sucre.
En rapprochant l'équation 9 de l'équation 13,
nous pouvons en déduire l'expression des paramètres
et ã1 :
1 1
0 (Eq. 15)
1
2 ? D (Eq. 16)
1
2
l
ã (Eq. 17)
1 6
De la même manière, en identifiant l'équation
10 à l'équation 14, il est possible de déterminer
l'expression analytique de2:
2

2
3 R
ô
(Eq. 18)
Les paramètresnous
1 1 ã 1 et permettent donc d'accéder aux
constantes physiques qui nous
2
intéressent, c-à-d le coefficient de diffusion D,
le temps de relaxation rotationel ôR ainsi que la
longueur de saut effective l. Les valeurs de ces constantes sont
répertoriées dans le tableau 8 suivant.
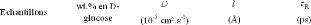

Tableau 8: Constantes physiques calculées à partir
des ajustements de W1 et W2 en fonction de Q.
2.2.1.5.2. HFBS
La figure 17 présente les fonctions de structure
dynamique S(Q, E) des échantillons H2O, D2O,
h-glc+D2O, 1:20 et h-glc+D2O, 1:55. Nous remarquons une nette
influence de l'effet de la concentration sur le profil de diffusion. Ainsi,
lorsque la concentration en D-glucose s'accroît, l'intensité du
pic augmente et sa largeur diminue, témoignant d'un ralentissement
général de la dynamique moléculaire du système.
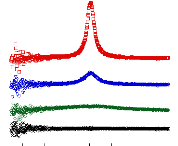
h-glc+D20,
1:20
h-glc+D20, 1:55
H 2
D 2
o
o
-40 -30 -20 -10 0 10 20 30 40
E (geV)
Figure 17 : Spectres mesurés sur le HFBS pour les
échantillons D2O (croix), H20 (losanges), h-glc+D2O, 1:20
(cercles) et h-glc+D2O, 1:55 (carrés) à 280K pour
un vecteur de diffusion Q= 0,47Å-1.
Les mesures réalisées sur le DCS sur ces
mêmes échantillons nous ont donné des temps de relaxation
de l'ordre de la picoseconde et des constantes de diffusion proches de
10-5 cm2s-1 pour les molécules d'eau
à 280K. Dans la gamme des valeurs de Q utilisées ici, ces valeurs
correspondent à des largeurs à mi-hauteur maximales de l'ordre de
~ 200-1500 geV pour la partie rotationnelle et de ~ 300 geV pour la partie
translationnelle.* La part de l'eau dans la diffusion totale se
résume donc à un signal très large de faible
intensité qui ne contribue pas significativement au profil de diffusion,
comme en témoigne les profils de l'eau de la figure 17. Il en est de
même pour les mouvements de rotation des molécules de sucre qui
présentent des temps de relaxation de l'ordre de la picoseconde, et les
énergies mises en jeu (0,3 < E < 2meV) sont bien en dehors de la
fenêtre énergétique considérée ici. De ce
fait, l'ajustement n'a nécessité l'utilisation que d'une unique
fonction Lorentzienne. Les dynamiques respectives des six échantillons
et la sensibilité instrumentale n'ont permis d'exploiter que les
échantillons h-glc+D2O, 1:20 et h-glc+D2O, 1:55, les quatre autres
présentant des dynamiques beaucoup trop rapides. Néanmoins,
l'ajustement aux données expérimentales, composé dans ce
cas d'une fonction delta, d'une fonction Lorentzienne et d'une ligne de base
à pente non nulle, a donné des résultats concluants.
*La fenêtre énergétique du
spectromètre à rétrodiffusion HFBS ( #177;36?eV)
est nettement plus étroite que celle du spectromètre
à temps-de-vol DCS (~15meV).
Le tracé de la largeur à mi-hauteur de l'unique
fonction Lorentzienne considérée en fonction de Q2 est
présenté sur la figure 18. Cette figure montre de manière
non équivoque l'effet de la concentration en D-glucose sur la dynamique
moléculaire de ce même monosaccharide. Comme en témoignent
les barres d'erreur de l'échantillon contenant 15% de D-glucose, la
dynamique des molécules de sucre sort rapidement de la fenêtre
énergétique de l'instrument, confirmant nos hypothèses
précédentes pour les échantillons
hydrogénés.



|
|
|
|
T = 280 K
|
|
h-glc+D2O, 1:20
h-glc+D2O, 1:55
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
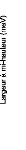
0,035
0,03
0,025
0,02
0,015
0,01
0,005
0

0 0,5 1 1,5 2
Q2 (A2)
Figure 18: Largeur à mi-hauteur, W1, de la fonction
Lorentzienne étroite ajustée aux mesures expérimentales
des solutions de glucose mesurées sur le HFBS.
Les valeurs des paramètres d'ajustement sont
présentées dans le tableau 9 et les constantes physiques qui en
découlent sont présentées dans le tableau 10.
Tableau 9: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite à partir des mesures réalisées
sur le HFBS à 280K.
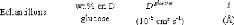

Tableau 10 : Constantes physiques calculées à
partir des ajustements de W en fonction de Q réalisés sur les
données du HFBS : Dglucose (Coefficient de diffusion) et l (distance de
saut effective).
2.2.1.6. Discussion
2.2.1.6.1. Dynamique translationnelle
Dynamique translationnelle du sucre
Les coefficients de diffusion du sucre pour les deux
séries de mesures précédentes sont regroupés pour
plus de clarté dans la figure 19 et sont accompagnés d'autres
résultats expérimentaux parus dans la
littérature.75,77
Dynamique moléculaire du D-glucose à 280K
Notre étude (HFBS) Smith et al. (QENS)75
Moran et al. (RMN)77 Notre étude (DCS)



0,6
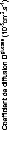
0,5
0,3
0,2
0
0 10 20 30 40 50
wt.% en D-glucose
Figure 19 : Coefficients de diffusion des molécules de
D-glucose (Dglue,
se) à 280K déterminés
expérimentalement dans cette étude. Les autres résultats
sont tirés de travaux expérimentaux75,77
présents dans la littérature.
La figure ci-dessus présente la variation du
coefficient de diffusion Dglucose en fonction de la concentration massique en
sucre de la solution. Cette figure montre une diminution d'un facteur
2-3* du coefficient de diffusion alors que la concentration est
multipliée par 2. Un tel résultat est à rapprocher de
différents travaux expérimentaux et théoriques
présents dans la littérature49,75,76,77. Les travaux
par diffusion neutronique (QENS) de Smith et al.75 notamment font
état de coefficients de
*En prenant en considération les barres
d'erreur, et notamment celle de l'échantillon h-glc+D2O, 1:55.
diffusion égaux à
0,252×10-5cm2 s-1,
0,123×10-5cm2.s-1 et 0,045×10-5cm2
s-1 pour des concentrations de
15,4, 33,3 et 48 wt.% à
280K respectivement. Moran et al.77 ont observé par RMN
à gradient de
Dglucose
champs pulsés des coefficients de diffusion très
similaires à ceux cités précédemment := 6×
10-7cm2 s-1 à 280 K pour une solution de glucose de 40 wt.%.
Toutes ces valeurs sont répertoriées dans le tableau 11.
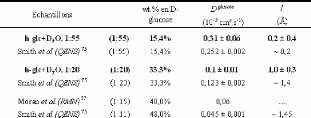
(Dglucose)
Tableau 11 : Comparaison des valeurs des coefficients de
diffusion du glucose et des longueurs de
saut effectives en solution de cette étude110
(en gras) avec les valeurs trouvées dans la littérature.
Une augmentation assez significative de la longueur de saut
effective est également à noter, l passe
ainsi de 0,2Å
pour une solution à 1 5,4wt.% en sucre à 1Å à
33,3wt.%. Cette augmentation de la
longueur de sauts est à rapprocher
de l'augmentation conséquente du temps entre les sauts ou temps de
rétentionô J l2 6D, qui passe de 0,21ps
à 16ps pour des concentrations allant de 15,4 à 33,3wt.%.
Une variation similaire de l avait été
observée par Smith et al.75. En augmentant la concentration
en
D-glucose dans le milieu, le coefficient de diffusion diminue certes,
mais les fortes augmentations de
la longueur de saut l et du temps entre les sauts
ôJ témoignent d'une modification plus profonde
de la
dynamique moléculaire. Des simulations
numériques menées par Roberts et Debenedetti49 sur des
systèmes eau-sucre ont montré que la concentration critique
au-delà de laquelle il y avait formation d'agrégats de
molécules de sucre se situait aux alentours de 30wt.%. Cette
interprétation a été corroborée par leur analyse
structurale du réseau de liaisons hydrogène, dans laquelle les
contributions sucre-sucre commençaient à dominer à cette
concentration. (Cf. Chapitre 1) Si l'on considère cette
interprétation, c'est-à-dire le passage d'une molécule
seule à une forme d'agrégats avec l'ajout de glucose,
l'augmentation de la taille de l'objet sondé expliquerait
l'élongation de la longueur de saut l, l'augmentation du temps de
résidence ôJ , mais également la
diminution de la dynamique
translationnelle observée.
Dynamique translationnelle de l'eau
Les coefficients de diffusion de l'eau pour les mesures
réalisées sur le DCS et le HFBS sont regroupés
dans la figure 20 ainsi que d'autres résultats
expérimentaux et théoriques parus ou à paraître dans
la littérature.49,76,77,94
Dynamique moléculaire de l'eau à 280K
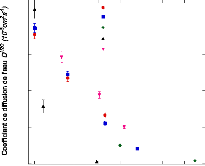
0,8
0,4
1,6
1,2
0
Notre étude (DCS)
Talon et al. (QENS)76
Moran et al. (RMN)77 Roberts et al.
(Simulations)49 Brady et al. (Simulations)94
0 10 20 30 40 50 60 70 80
wt.% en D-glucose
Figure 20 : Coefficients de diffusion des molécules d'eau
(DH2O) à 280K déterminés également dans
cette étude. Les autres résultats sont tirés de travaux
expérimentaux76,77 et théorique49,94.
La figure 20 présente l'évolution du coefficient
de diffusion de l'eau en fonction de la concentration en sucre. Nous pouvons
tout d'abord remarquer que, comme pour les molécules de D-glucose, la
dynamique translationnelle de l'eau est fortement ralentie par la
présence du soluté, en moyenne d'un facteur 3. Il apparaît
aussi que DH2O suit une loi linéaire entre 0 et 40 wt.%, une
linéarité qui a déjà pu être observée
dans les systèmes eau-tréhalose (Cf. Chapitre 1). Ces
mélanges eau-tréhalose présentent deux régimes
linéaires, la rupture se produisant vers 40 wt.% (Figure 9). Dans notre
cas, le peu de points expérimentaux au-delà de 40 wt.% ne nous
permet pas de conclure sur le comportement de DH2 O. Toutefois, les
travaux de Moran et al.77 par RMN à gradient de champ
pulsé (DH2O(7.-w
J t.%)=0,03×10-5cm2 s-1)
laissent penser qu'il existe un changement de régime dans cette gamme de
concentration. Hormis les travaux de simulation de Roberts et al.49
(T = 270 K) pour lesquels la concordance avec nos résultats n'est pas
réalisée, toutes les autres valeurs de DH2O(280K)
mesurées par QENS ou par RMN disponibles à ce jour corroborent
nos résultats expérimentaux. (Tableau 12) La longueur de saut
effective l varie avec la concentration, passant de l= (0,72 #177; 0,05)Å
pour l'eau pure à (0,92 #177; 0,05)Å pour une solution à
15,4 wt.% en sucre pour enfin terminer à (1,2 #177; 0,2)Å pour une
solution à 33,3 wt.%. Cet accroissement montre une certaine
évolution dans les interactions au sein de la solution. L'ajout du sucre
fait augmenter la longueur des sauts, c-à-d que la distance la plus
courte entre la molécule et un emplacement énergétiquement
favorable s'allonge.
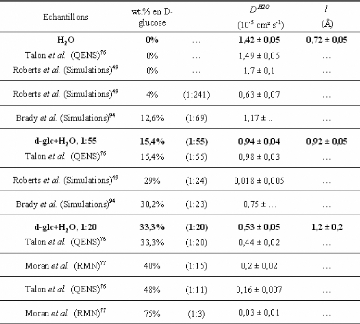
Tableau 12: Comparaison des valeurs des coefficients de
diffusion de l'eau et des longueurs de saut effectives en solution à 280
K tirés de cette étude (en gras) avec les valeurs trouvées
dans la littérature49,76,77,94. (Roberts et al. ont
réalisés des calculs pour T = 270 K)
2.2.1.6.2. Dynamique rotationnelle
Dynamique rotationnelle du D-glucose
En raison des difficultés de traitement avec le DCS et
de la fenêtre énergétique beaucoup trop étroite du
HFBS pour ce genre de mouvements, aucune information satisfaisante sur la
dynamique rotationnelle du D-glucose ne peut être extraite des mesures
précédentes.
Dynamique rotationnelle de l'eau
Comme nous avons pu le voir précédemment, le
temps de relaxation rotationnel nous donne une
information sur les rotations
de la molécule d'eau avec la concentration. Dans la gamme
de
concentration utilisée ici, les temps de relaxation rotationnels
zR calculés varient assez peu passant de
0,9ps à 1,38ps pour des concentrations comprises entre 0
et 33,3 wt.%. Ainsi, la dynamique
rotationnelle est diminuée d'un
facteur 1,5, ce qui est faible en comparaison de la baisse observée
dans
le cas de la dynamique translationnelle. Talon et al.76 ont
déterminé des temps de relaxation
rotationnelle par QENS, et ont trouvé des valeurs de
zR égales à 0,685, 0,769, 1,154 et 2,088ps pour
des concentrations de 0, 15,4, 33,3 et 48 wt.% respectivement.
Donc, pour une concentration entre de
15,4 et 33,3 wt.%, le temps
ô R est multiplié par un facteur 1,5, ce qui est
en parfait accord avec nos
résultats précédents.
2.2.1.7. Conclusion
L'étude des solutions de D-glucose en solution aqueuse
par diffusion quasi-élastique des neutrons, nous a permis de
déterminer l'impact des molécules de sucre tant sur la dynamique
moléculaire du solvant que sur celle du soluté. Nous avons pu
mettre en évidence qu'avec l'ajout de D-glucose, la dynamique
translationnelle de l'eau est réduite d'un facteur ~3-4, alors que la
dynamique rotationnelle n'est réduite que d'un facteur ~ 1,5. Quant
à la dynamique translationnelle du D-glucose, elle a diminuée
d'un facteur 3.
Notre méthode et les modèles appliqués
donnant des résultats plutôt encourageants, et avant de s'attaquer
à des systèmes beaucoup plus complexes, intéressons-nous
avant à des solutions aqueuses de D-fructose, un autre monosaccharide
d'intérêt. De même formule empirique que le D-glucose, il
est intéressant à double titre : il a tendance tout d'abord
à se cycliser sous la forme furanose, c'est-à-dire un cycle
à cinq, plutôt que sous la forme pyranose (cycle à six), ce
qui le différentie fortement de son confrère. De plus, il se
différentie du D-glucose par ses groupements fonctionnels et plus
particulièrement ses deux groupements -CH2OH, qui lui confèrent
un léger caractère hydrophobe.
2.2.2. Dynamique moléculaire du D-fructose
2.2.2.1. Préparation des solutions de D-fructose /
échange isotopique
Le D-fructose présente exactement les mêmes
difficultés que le D-glucose liées à la présence
d'hydrogènes échangeables et non-échangeables. Une
pré-deutération du D-fructose a donc été
effectuée pour se prémunir des échanges de proton avec le
solvant durant la préparation. Deux échantillons ont
été préparés afin de sonder sélectivement la
dynamique du solvant (d-fruc+H2O, 1:24,5) ou celle du sucre (h-fruc+D2O,
1:24,5). La dénomination d-fruc correspond à un D-fructose sur
lequel les hydrogènes non-échangeables ont été
substitués par des atomes de deutérium (C6D7H5O6). De la
même manière, h-glc correspond à un D-fructose sur lequel
les hydrogènes échangeables ont été
échangés par des deutériums (C6D5H7O6). Une
unique concentration molaire en sucre de 1:24,5 (C6H12O6:H2O)* a
été sélectionnée en raison de la durée
limitée en temps de faisceaux. La méthode préparatoire
ressemblant en tous points à celle réalisée pour le
D-glucose, je vous propose de vous référer, pour de plus amples
informations, au paragraphe (Chapitre 2 : Préparation des
échantillons).
*
Cette concentration molaire en sucre de 1:24,5
(C6H12O6:H2O)correspond à une concentration massique en sucre
de 29 wt. % dans une solution entièrement hydrogénée.
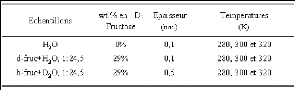
2.2.2.2. Conditions expérimentales
Les expériences de QENS ont été
réalisées sur le spectromètre à
rétrodiffusion IRIS sur la source de spallation ISIS du Rutherford
Appleton Laboratory.95 Les solutions ont été
placées dans des porte-échantillons annulaires en aluminium
présentant un espace annulaire de 0,1 ou de 0,5mm selon
l'échantillon. Après avoir été scellés
à l'indium, ils sont positionnés dans un cryostat dans lequel la
température est régulée à #177; 1 K.
Les expériences sur le spectromètre IRIS ont
été réalisées avec une longueur d'onde incidente de
6,7 Å. Le transfert de vecteur d'onde Q (pour la diffusion
élastique) couvre une gamme allant de 0,46 à 1,84
Å-1. Tous les échantillons ont été
mesurés à trois températures T = 280, 300 et 320 K, avec
des temps de comptage avoisinant 4 heures. (Tableau 13) La résolution en
énergie et la normalisation en intensité ont été
déterminées à partir de la mesure d'un cylindre creux de
vanadium réalisée dans les mêmes conditions que celles
utilisées pour les échantillons. La résolution
instrumentale a été trouvée égale à 17,5
jteV à partir de la largeur à mi-hauteur du pic élastique
du vanadium (Les cristaux analyseurs étaient dans la configuration
PG002, c'est-à-dire dans le plan de réflexion 002 du graphite
pyrolitique).
Tableau 13: Tableau récapitulatif des conditions
expérimentales pour les échantillons mesurés sur le
spectromètre IRIS. (d$fruc: C6D7H5O6; h$fruc:
C6D5H7O6).
Les spectres obtenus ont été corrigés de
la diffusion du porte-échantillon et du bruit de fond. Les
différentes séries de données ont été
réduites et analysées avec le logiciel d'analyse
MODES.96 Les modèles utilisés sont les mêmes que
ceux décrits précédemment pour le D-glucose.
2.2.2.3. Résultats
Les ajustements ont été réalisés
sur les trois échantillons (H2O, h-fruc+D2O, 1:24,5 et dfruc+H2O,
1:24,5) pour les trois températures considérées T = 280,
300 et 320 K. Le meilleur ajustement s'est avéré être
composé, comme dans le cas du D-glucose, d'une fonction delta, de deux
fonctions Lorentziennes (.L?~(W1,E) et.L?~(W2,E)) et
d'une ligne de base à pente non nulle. IRIS étant un
spectromètre à rétrodiffusion avec une
fenêtre énergétique assez étroite de #177; 400?eV,
toutes les fonctions de diffusion n'ont pas pu être ajustées avec
deux fonctions Lorentziennes, c'est entre autres le cas des échantillons
d'eau légère et de l'échantillon d-fruc+H2O, 1:24,5
à 320 K.

Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 (Figures 22, 23
et 24). Comme pour son diastéréoisomère, W1
présente une dépendance quadratique en Q non-linéaire et
W2 une dépendance linéaire en Q2. Ces
dépendances ont été ajustées à l'aide des
expressions 13 et 14. Tous les paramètres d'ajustement sont
présentés dans le tableau 14.
Tableau 14 : Valeurs des différents paramètres
d'ajustements obtenus pour la Lorentzienne
étroite2~(W1,E) et pour la Lorentzienne large
2,(W2,E) à 280K.
2.2.2.4. Discussion
Les valeurs du paramètre de diffusion
translationnelle 1 et du paramètre de diffusion
rotationnelle a2 tracées dans la figure 21 en fonction de
1000/T(K) dévoilent une dépendance en température qui suit
une loi de type Arrhénienne k = A
·
e-Ea RT .
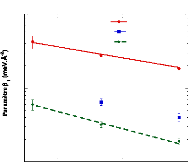
(a)
1
H 2
o
d-fruc+H20, 1:24,5
h-fruc+D20,
1:24,5
0,1
0,01
|
0,2
0,1 0,09 0,08
0,07
0,06
|
3,1 3,2 3,3 3,4 3,5 3,6
1000/1"(K) (b)
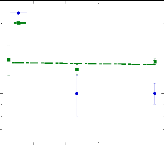
d-fruc+H20, 1:24,5
h-fruc+D20,
1:24,5
3,1 3,2 3,3 3,4 3,5 3,6
1000/1"(K)
Figure 21 : Valeurs de fi1 (a)
et de a2 (b) pour les échantillons H2O,
h-fruc+D2O, 1:24,5 et d-fruc+H2O, 1:24,5 en fonction de 1000/T(K). Les lignes
représentent les ajustements de la loi d'Arrhenius aux
données.
Les énergies d'activation Ea correspondant
aux deux types de mouvements tirées des ajustements de la loi
d'Arrhenius sont présentées et comparées aux
résultat disponibles dans la
littérature49,76,77,78,92. (Tableau 15)
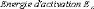
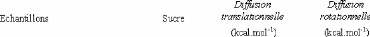


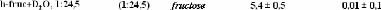
Tableau 15: Comparatif des énergies d'activation
Ea déterminées pour l'eau et les solutions de fructose
avec celles trouvées dans la littérature pour des solutions de
D-fructose et de D-glucose.
Ce qui ressort tout d'abord du tableau ci-dessus, c'est
l'accroissement de l'énergie d'activation de la diffusion
translationnelle de l'eau avec l'ajout du sucre : Ea passe ainsi de
(3,5 #177; 0,4) kcal mol-1 pour l'eau pure à (4,0 #177; 0,4)
kcal mol-1 pour une solution de fructose à 29 wt.%. Cet
excédent d'énergie témoigne du gain en stabilité de
la solution, une stabilité énergétique liée au
caractère stabilisateur de réseau du fructose. En d'autres
termes, le nombre de liaisons hydrogène (eau-eau, eau-sucre, sucre-
sucre) est supérieur au nombre de liaisons hydrogène
présentes dans l'eau pure (eau-eau), ce qui stabilise la solution et la
rend plus apte à résister aux contraintes extérieures.
Notons également l'évolution de Ea suivante:
Ea (h-fruc+D2O, 1:24,5) > Ea
(d-fruc+H2O, 1:24,5) > E a (H2O)
(Dfructose)
ou Ea > E a (Deau en
présence de fructose) > Ea (Deau)
Ces trois échantillons vont être traités
maintenant de manière séparée et nous reviendrons bien
sûr sur ces énergies d'activation que nous commenterons.

Dynamique de l'eau H20
La mesure de l'eau va jouer un double rôle: (i) d'abord
comme échantillon de référence afin de comparer les
valeurs des coefficients de diffusion déterminées dans ce travail
à des valeurs connues présentes dans la littérature, (ii)
mais également comme valeur à concentration nulle (0 wt.%) pour
l'étude de l'évolution de la dynamique du solvant en fonction de
la concentration en sucre.
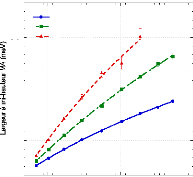
1
0.8
H2O 280K
H2O 300K
H2O 320K
0.6
0.4
0.2
0
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
Figure 22: Variations de W1 en fonction de Q2 pour
l'eau légère à 280K (cercles), 300K (carrés) et
320K (triangles). Les lignes représentent les ajustements.
La figure 22 présente les variations de W1 en fonction
de Q2 pour les trois températures. Cette figure montre bien
le resserrement de la largeur à mi-hauteur de la Lorentzienne avec
l'abaissement en température, ce qui se traduit physiquement par un
ralentissement de la dynamique, qui est parfaitement corroboré par les
valeurs de DH2O. Un comportement somme toute logique en raison de la
diminution de l'agitation thermique, mais également de l'augmentation
progressive des interactions eau-eau en se rapprochant du point de
solidification situé à TS = 273 K.
Les différents ajustements présentés sur la
figure précédente ont permis de calculer les coefficients de
diffusion DH2O et les longueurs de sauts effectives l. (Tableau
16)
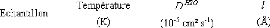
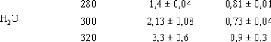
Tableau 16: Constantes physiques calculées à partir
des ajustements de W1 en fonction de Q.
Des travaux antérieurs sur l'eau donnent des valeurs
de DH2O = 1,34×10-5 cm2 s-1 à 280
K92, 2,67× 10-5 cm2 s-1
à 300 K79 et 3,43× 10-5 cm2 s-1
à 320 K92,*, des valeurs qui sont en très bon accord
avec nos résultats expérimentaux. Si l'on regarde maintenant
d'une manière plus qualitative ces résultats, nous remarquons que
DH2O augmente de manière significative entre 280 et 320 K,
passant de 1,4×10-5 à 3,3×10-5
cm2 s-1, c-à-d une augmentation d'un facteur ~
2,5. La dépendance en température de 1, autrement dit du
coefficient de diffusion DH2O, donne une énergie d'activation
moyenne pour la diffusion translationnelle de (3,5 #177; 0,4) kcal
mol-1, une valeur qui est très proche de 3,6 kcal
mol-1 déterminée dans l'étude classique de
l'eau réalisée par Teixeira et al.92 Notons
également que la longueur l n'évolue que très faiblement,
ne montrant pas de variation significative entre 280 et 320 K. Ainsi, la
longueur de saut reste quasi-constante dans la gamme en température
considérée, ce qui témoigne de
l'homogénéité de la structure du solvant avec la
température.
L'échantillon d-fruc+H20, 1:24,5 -- Dynamique du
solvant
Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 sur la figure
23.
0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
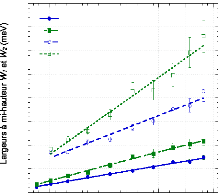
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Wi--T=280K Wi--T=300K W2 -- T = 280K W2 -- T = 300K
Figure 23: Largeurs à mi-hauteur W1 et W2 ajustées
aux mesures expérimentales de l'échantillon dfruc+H2O, 1:24,5
à 280 et 300K.
Cette figure montre de manière très claire la
différence énergétique qui existe entre les mouvements
de
rotation (partie supérieure) et les mouvements de translation
(partie inférieure). Comme dans le cas de
*Cette valeur est une valeur extrapolée
à partir des données de Teixeira et al.92
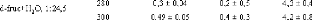
l'eau, W1 et W2 se rétrécissent avec
l'abaissement en température. Les paramètres a1 1, y,,
a2 et 2 tirés des ajustements de ces largeurs à
mi-hauteur, sont listés dans le tableau 14. Les constantes physiques qui
en découlent sont elles présentées dans le tableau
ci-dessous :
Tableau 17 : Constantes physiques calculées à
partir des ajustements de W1 : DH2O (Coefficient de
diffusion de l'eau) et l (distance de saut
effective).
Il faut remarquer tout d'abord que le coefficient de diffusion
de l'eau augmente de manière importante entre 280 et 300 K, passant de
DH2O = 0,3× 10-5 cm2 s-1 à 280 K
à DH 2O = 0,49×10-5 cm2
s-1 à 300K. La dynamique est ainsi divisée en moyenne
par un facteur ~ 4-5 par comparaison avec l'eau volumique. Cette diminution
reflète principalement l'effet du D-fructose sur la dynamique
moléculaire de l'eau, alors que le D-fructose ne contribue qu'à
hauteur de 12% dans la diffusion totale. Le coefficient f1 et donc
DH2O montrent une dépendance en température avec une
énergie d'activation Ea = (4,0 #177; 0,4) kcal
mol-1, valeur confirmée par Rampp et al. à partir de
la RMN à champs pulsés (Ea = 4,1 kcal
mol-1).78 A cela s'ajoute la faible augmentation de la
longueur de saut effective l qui passe de 0,2? à 0,4Å,
augmentation qui n'est pas réellement significative. A la
différence de la diffusion translationnelle, la diffusion rotationnelle
(ôR) ne varie pas avec la température,
observation corroborée par la faible
valeur de l'énergie d'activation correspondante
Ea = (0,3 #177; 0,2) kcal mol-1. Il faut toutefois
manipuler avec précaution les énergies d'activation
calculées dans le cas de l'échantillon d-fruc+H2O, 1:24,5 en
raison du faible nombre de points expérimentaux, en l'occurrence deux !
Si dans le cas de la diffusion translationnelle, le calcul de Ea
conduit à une valeur cohérente avec la littérature, il
n'en est pas de même pour la diffusion rotationnelle. En effet, les
valeurs connues de Ea pour l'eau pure et dans des solutions de
D-glucose sont très largement supérieures à cette valeur
(~ 6 fois), et aucune réelle justification ne peut expliquer un tel
écart si ce ne sont les incertitudes expérimentale et de
traitement.
L'échantillon h-fruc+D20, 1:24,5 -- Dynamique du
D-fructose
Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 sur la figure
24.
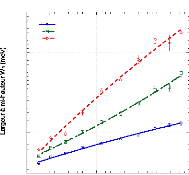
Lorentzienne "étroite"21(W1,E)
(a)
T = 280K
T = 300K
T = 320K
0.15
0.1
0.05
0
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
0.5 1 1.5 2 2.5 3 3.5
(b) Lorentzienne "large"22(W2,E)
0.6
0.5
0.3
0.2
0
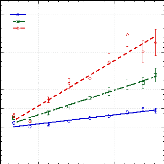
T = 280K
T = 300K
T = 320K
Q2 (Å2)

Figure 24 : Largeurs à mi-hauteur étroite, W1 (a)
et large W1 (b) ajustées aux données de l'échantillon
hfruc+D2O, 1:24,5 à 280, 300et 320 K.
Il apparaît que comme pour l'eau, la température
induit un ralentissement de la dynamique moléculaire du D-fructose. Les
valeurs des coefficients de diffusion Dfructose nous montrent une diminution
d'un facteur ~ 3 pour une baisse en température de 40K. (Tableau 18) De
la même manière, la dynamique du sucre est en moyenne deux fois
plus lente que celle de l'eau pour une concentration de 29wt.% en
D-fructose.
Tableau 18 : Constantes physiques calculées à
partir des ajustements de W1 en fonction de la température T : Dfructose
(Coefficient de diffusion), l (distance de saut effective) et
DR (temps de relaxation orientationnel).
La dépendance en température de la dynamique
translationnelle conduit à une énergie
d'activation
Ea = (5,4 #177; 0,5) kcal mol-1, une
énergie légèrement supérieure à celle
déterminée dans le cas d'une
solution de D-glucose
(Ea = (3,8 #177; 0,4) kcal mol-1).76 La
longueur de saut l ainsi que le temps de
relaxation DR ne dépendent pas
particulièrement de la température. l varie entre 0,4Å et
0,6 Å, une
valeur légèrement supérieure à celle
de l'eau(<leau> = 0,3 Å). Cette conservation de l avec
la température reflète une certaine conservation de la
structuration de la solution avec la température.
La viscosité et la dynamique étant
étroitement liées, il est intéressant de comparer leur
évolution en fonction de la température. Rampp et
al.78 ont étudié la viscosité dynamique d'une
solution aqueuse de D-fructose (33 wt.%) et ont montré que la
viscosité diminuait d'un facteur ~ 2,5 entre 280 et 300 K passant de
17,2 à 6,77 Pa.s. Pour la même gamme de température, nous
avons observé une accélération de la dynamique
translationnelle du fructose (×1,7). La viscosité et la dynamique
témoignent de la structuration en liaisons hydrogène du
mélange, c-à-d de la stabilité de la solution. Lorsque la
température diminue, le bilan total de liaisons hydrogène devient
largement positif, et la solution devient de plus en plus visqueuse. La
solution perd de sa mobilité comme en témoigne la diminution des
coefficients de diffusion de l'eau et du fructose.
2.2.2.5. Conclusion
De cette étude sur les solutions de D-fructose, il en
ressort que la dynamique de l'eau est fortement affectée par la
présence du monosaccharide. Les dynamiques rotationnelle et
translationnelle présentent une dépendance en température
qui suit une loi d'Arrhenius. Notons également que la dynamique de l'eau
est deux fois plus rapide que celle du D-fructose à 280 K pour une
concentration en sucre de 29 wt.%.
2.2.3. Comparatif D-glucose / D-fructose
Malgré une même formule brute C6H12O6,
le D-fructose et D-glucose présentent des stéréochimies
différentes entraînant un caractère
légèrement plus hydrophobe du D-fructose. La comparaison de la
dynamique de ces deux monosaccharides présente des dissemblances qui
peuvent s'expliquer par leurs différences stéréochimiques
:
Dynamique du sucre
A 280 K, le coefficient de diffusion du D-glucose à 33
wt.% (Dglucose= (0,1 #177; 0,01) ×10-5
cm2 s-1) et du D-fructose à 29 wt.% (Dfuctose =
(0,14 #177; 0,01) ×10-5 cm2 s-1) sont
différents et nous remarquons que Dglucose < Dfructose Etant
donné la différence d'hydrophilie entre ces deux sucres, il
s'ensuit que le fructose aura moins tendance à se lier aux
molécules d'eau environnantes que son congénère. En
conséquence, le D-fructose va présenter une plus grande
mobilité.
Dynamique du solvant
A 280 K, le coefficient de diffusion de l'eau en
présence de D-glucose (33 wt.%) (Deau(gluc)= (0,53 #177;
0,05) ×10-5 cm2 s-1) est inférieur
à celui de l'eau en présence de D-fructose (29 wt.%) (
Deau(fruc)= (0,3 #177; 0,04) ×10-5 cm2
s-1). En contraste, la dynamique de l'eau pure donne un coefficient
Deau = (1,5 #177; 0,05) ×10-5 cm2
s-1, valeur ~ 3 fois supérieure à celle de l'eau dans
une solution de D-glucose, et ~ 5 fois supérieure à celle de
l'eau dans une solution de D-fructose. A concentration égale, le
D-fructose réduit donc davantage la dynamique de l'eau que ne le fait le
D-glucose.
La légère hydrophobicité du fructose va
l'entraîner à moins se lier aux molécules d'eau
environnantes, qui vont par conséquent s'organiser en agrégats
plus stables, et réduire la dynamique de l'eau. Au contraire, le
glucose, qui a plus d'affinité avec les molécules d'eau, va
présenter plusieurs couches d'hydratation. Les molécules d'eau
libres, c-à-d non liées au sucre, vont donc être plus
nombreuses, et la dynamique du solvant plus rapide.
Comparatif Dynamique du soluté / Dynamique du solvant
A 280 K et pour une solution de D-glucose à 33 wt.%, la
différence relative de dynamique entre l'eau et le soluté est de
5. (Deau(gluc)= (0,53 #177; 0,05) ×10-5 cm2
s-1 et Dglucose = (0,1 #177; 0,01) ×10-5
cm2 s-1). En revanche, pour une solution de D-fructose
à 29 wt.% à 280 K, la différence relative entre la
dynamique de l'eau et celle du soluté n'est que de 2
(DeauOEruc)= (0,3 #177; 0,04) ×10-5 cm2
s-1 et Dfructose = (0,14 #177; 0,01) ×10-5
cm2 s-1).
2.3. CONCLUSION GENERALE DU CHAPITRE 2
Nous pouvons résumer les résultats et les
principales conclusions obtenus pour des solutions volumiques non
confinées d'eau, de D-glucose et de D-fructose par diffusion
quasi-élastique des neutrons :
Les dynamiques rotationnelle et translationnelle de l'eau sont
affectées par la présence des deux monosaccharides : le D-glucose
et le D-fructose.
Pour des solutions de D-glucose allant de 15wt. % à
33wt.%
- la dynamique translationnelle de l'eau est divisée par
~ 3-4
- la dynamique rotationnelle de l'eau est divisée par ~
1,5
- la dynamique translationnelle du D-glucose est divisée
par ~ 3
Pour des solutions de D-fructose entre 280 et 320K
- la dynamique translationnelle de l'eau volumique est
multipliée par ~ 2-3 et suit une loi de type Arrhenius
- la dynamique translationnelle de l'eau dans des solutions de
D-fructose est multipliée par ~ 1,7 entre 280 et 300K et suit
également une loi d'Arrhenius.
- la dynamique translationnelle du D-fructose est
multipliée par ~ 3,2
- la dynamique rotationelle reste quasiment stable dans la gamme
de températures.
Les différentes dynamiques obtenues entre le D-glucose et
le D-fructose proviennent vraisemblablement de leurs différences
stéréochimiques.
Le tableau ci-dessous récapitule les valeurs
numériques des constantes physiques obtenues pour l'eau, le D-glucose et
le D-fructose :


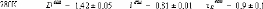
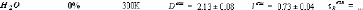

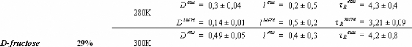
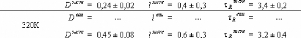
Tableau 19: Récapitulatif des différentes
constantes déterminées dans ce chapitre pour l'eau
légère, l'eau lourde, le D-glucose et le D-fructose.
Les résultats décrits précédemment
valident donc les choix de traitement effectués et nous donnent une
bonne assise pour l'étude de systèmes plus complexes que sont les
solutions de monosaccharide confinées.
Chapitre 3
POURQUOI CONFINER ET COMMENT? LES GELS DE SILICE
AQUEUX
3.1. Choix de la matrice de confinement 75
3.2. Taille du confinement 76
3.3. Synthèse de gels de silice aqueux 77
3.4. Etude structurale préliminaire des gels de silice
aqueux contenant du
D-glucose par diffusion des neutrons aux petits angles 84
3.5. Conclusion générale du chapitre 3 93
CHAPITRE 3
POURQUOI CONFINER ET COMMENT ? LES GELS DE SILICE AQUEUX
Les solutions de mono- et disaccharides volumiques permettent
de sonder les interactions sucre-eau, dans lesquelles la
stéréochimie s'avère être un paramètre majeur
à l'origine des diverses propriétés physico-chimiques du
mélange. Ces mesures nous permettent ainsi de comprendre pourquoi
certains sucres, comme le tréhalose, sont présents en
quantité importante dans les végétaux anhydrobiotiques.
Mais dans ce contexte biologique, un détail d'importance n'a jamais
été pris en considération dans toutes ces études
expérimentales : les échelles cellulaire et membranaire. Ces
échelles, bien qu'assez variables d'une cellule à l'autre, se
rapprochent plus du nano- ou du micromètre que du monde macroscopique.
Et à la vue de tous les changements de propriétés
engendrés par la réduction de taille, tout laisse à penser
que ces solutions de sucre pourraient présenter une dynamique tout autre
dans un milieu restreint stériquement. D'ailleurs, les récentes
études de l'eau confinée montrent que la taille de
l'environnement est un paramètre non négligeable, qui conduit
à une forte diminution des dynamiques translationnelle et
rotationnelle.97,98,99,100 Tous ces travaux sur les solutions
d'hydrates de carbone volumiques, bien que d'un grand intérêt
fondamental, gagneront donc à être explorées à
l'échelle nanométrique à l'exemple des nombreuses
investigations réalisées sur l'eau. Le confinement des solutions
de sucre présente donc un intérêt majeur pour la
compréhension des phénomènes en présence.
Cependant, de telles études, aussi bien expérimentales que
théoriques, sont pour l'heure manquantes. Le champ d'investigation est
par conséquent complètement ouvert et gigantesque, laissant libre
cours à toutes les voies de confinement possibles. Par
conséquent, il nous faut déterminer, en premier lieu, une matrice
de confinement appropriée qui réponde à tous nos
impératifs expérimentaux et techniques. C'est ce que nous allons
chercher à faire dans ce chapitre.
3.1. CHOIX DE LA MATRICE DE CONFINEMENT
L'utilité du confinement ne présente plus de
doute, mais il nous reste à déterminer quelle matrice de
confinement utiliser. A priori, la liste des matériaux susceptibles de
pouvoir servir de matrice hôte est vaste, mais de très nombreuses
contraintes techniques nous limitent dans le choix des matériaux poreux.
Les principales difficultés que nous avons à surmonter sont :
(i) de confiner une solution à une concentration en sucre
donnée en évitant les gradients,
(ii) d'avoir des échantillons compatibles avec les
mesures de diffusion de neutrons.
Revenons un peu plus en détail sur ces deux points.
(i) La concentration de la solution confinée doit
à tout prix présenter le plus faible gradient
en
concentration. En effet, la dynamique moléculaire étant
très sensible à la concentration, confiner une
solution de concentration « inconnue » ne nous
permettrait pas de conclure sur l'effet du confinement. (ii) Les mesures de
diffusion de neutrons ne nous permettent pas d'utiliser des matrices
organiques, telles que les gels de polyacrilamide par exemple, qui
présentent un nombre beaucoup trop important d'atomes
d'hydrogène. Le seul moyen de s'en prémunir serait d'utiliser des
précurseurs intégralement deutérés. Mais pour des
raisons de coût principalement, cette solution a été
abandonnée au profit de matrices inorganiques, nettement moins
coûteuses, mais qui présentent le double avantage d'être
relativement « transparentes » aux neutrons, mais aussi d'être
très modulables durant la synthèse. Parmi les matériaux
poreux inorganiques disponibles et susceptibles de pouvoir nous
intéresser, nous pouvons citer l'alumine Al2O3 et la silice
SiO2. Cependant, la chimie de l'alumine est difficile à mettre en oeuvre
en raison de la très grande réactivité de ses
précurseurs, limitant ainsi les formes et les tailles de pores
accessibles. Un défaut que ne partage pas la silice, dont les
méthodes de synthèse ont permis d'accéder à une
très grande variété de matériaux
mésoporeux.
3.2. TAILLE DU CONFINEMENT
Le choix de la taille du confinement est d'une très
grande importance, et la gamme de pores que nous allons choisir doit être
déterminée en relation avec les échelles existantes dans
le monde du vivant. L'idée n'est pas de reproduire à l'identique
une membrane, qui serait beaucoup trop complexe voire impossible à
étudier par QENS, mais plutôt d'extraire dans un premier temps les
dimensions caractéristiques afin de réaliser un modèle
simple qui « imiterait » une membrane.
Une membrane cellulaire se compose d'une bicouche de
phospholipides dans laquelle des protéines membranaires, dites
protéines de transport spécifiques, permettent le transport des
ions ou des molécules à travers les couches lipidiques. En
moyenne, l'épaisseur d'une membrane cellulaire classique mesure environ
5 à 10 nm. (Figure 25)
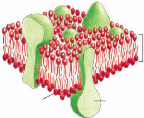
-- 5-10nm membrane
protéine
lipide
Figure 25 : Représentation schématique d'une
membrane cellulaire.
Afin d'élargir le choix dans les matrices de
confinement, nous chercherons à obtenir des diamètres de
pores
compris entre 2 et 20nm, des tailles qui sont du même ordre de grandeur
que l'espace
intermembranaire. Parmi les différents types de silices
poreuses, nous nous sommes dirigés vers des gels de silice aqueux
(hydrogels), et une silice mésoporeuse de type MCM-41, que nous avons
adapté à cette étude. Ces deux silices sont
complémentaires : la première présente des pores
interconnectés, non-organisés avec un diamètre de pore
moyen ; la deuxième, quant à elle, est composée de pores
calibrés et organisés. Ainsi, ces deux types de silice nous
permettront de juger de l'impact de la forme des pores sur la dynamique. Les
synthèses des hydrogels et des MCM-41 sont assez différentes,
d'autant que la synthèse de la silice mésoporeuse a
été spécialement développée pour
répondre à nos contraintes. De ce fait, nous allons
développer la synthèse des hydrogels dans la suite de ce chapitre
alors que celle des MCM-41 sera traitée dans le chapitre 6.
3.3. SYNTHESE DE GELS DE SILICE AQUEUX (HYDROGELS)
Les gels de silice aqueux ont été
synthétisés à l'aide du procédé «
sol-gel », qui permet par simple polymérisation de
précurseurs moléculaire en solution, d'obtenir des
matériaux vitreux sans passer par l'étape de fusion. Très
utilisé dans la fabrication des verres, des films et des fibres, il
permet également de synthétiser des particules de taille et de
forme contrôlées.101,102,103,104,105,106,107,108
3.3.1. Principes généraux
La méthode « sol-gel » a pour principe la
gélification d'un sol, qui est une dispersion stable de particules
solides dans un liquide. Le gel, qui en résulte, est moins
évident à définir puisqu'il s'agit d'un état
intermédiaire de la matière situé entre l'état
solide et l'état liquide. Un gel peut être vu comme un
réseau tridimensionnel solide qui s'est expansé au travers d'un
liquide.
La synthèse par voie « sol-gel » se fait
généralement à partir de précurseurs alcoxydes (ou
alcoolates) de formule brute M(OR)m où M est un atome
métalique et R un groupement alkyl CnH2n+1. (Nous nous limiterons ici au
cas du silicium, c-à-d M = Si). Les réactions chimiques à
la base du procédé se déclenchent lorsque les
précurseurs sont mis en présence d'eau : l'hydrolyse des
groupements alkoxy intervient alors, suivie par la condensation des produits
hydrolysés qui conduit au phénomène de
gélification.
- L'hydrolyse est une réaction de substitution
nucléophile, qui peut se répéter sur tous les groupements
-OR de l'alcoolate. Elle conduit à la formation de l'acide silicique
(Si-(OH)4) et libère des molécules d'alcool (ROH) (Eq. 19). Son
mécanisme, qui présente une vitesse minimale à pH ~ 7, est
activé par catalyse acide ou basique :
Si-(OR)4 +
4H2O?-*
Si-(OH)4 + 4ROH
(Eq. 19)
- La condensation est également une réaction de
substitution nucléophile. Elle se traduit soit par une expulsion d'eau
par réaction entre deux groupements silanols (Eq. 20), soit par le
départ d'alcool par réaction entre un groupe silanol et un groupe
alkoxy (Eq. 21). Cette étape de condensation conduit à la
formation de ponts siloxanes (-Si-O-Si-) qui constituent l'unité de base
du polymère inorganique.
HO -Si-O-H H-O-Si- OH ? HO -Si-O-Si- OH H O (Eq. 20)
3 3 3 3 2
Si- OR +2H O ? SiO +4ROH (Eq. 21)
4 2 2
La chimie des alcoolates du silicium conduit à des gels
polymériques ou colloïdaux selon que les conditions de pH soient
en-dessous ou au-dessus du point isoélectrique (pH ~ 2,5)*
et/ou la proportion d'eau utilisée pendant la réaction.
Gels polymériques:
Dans des conditions de catalyse acide (pH < 2,5) et
pour de petites quantités d'eau (H2O:Si < 5), la cinétique
d'hydrolyse est prépondérante devant celle de la condensation, et
les effets stériques confèrent à cette attaque une
difficulté croissante quand l'oxygène appartient successivement
à un monomère, une extrémité de chaîne ou un
milieu de chaîne. De ce fait, la condensation se fera
préférentiellement en bout de chaîne. Il y a alors
apparition de polymères linéaires ou faiblement ramifiés
(Figure 26(a)), qui s'enchevêtrent (b), et forment de nouvelles
ramifications donnant lieu au phénomène de gélification
(c).
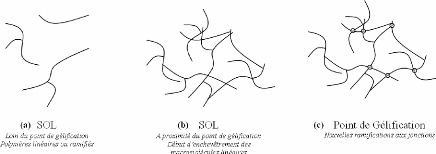
Figure 26: Croissance du polymère et formation d'un gel
dans les systèmes à catalyse acide, en fonction de l'avancement
de la réaction.103
* Le point isoélectrique est également
appelé point de charge nulle, et correspond à une charge
électrostatique nulle à la surface de la particule.
Gels colloïdaux :
Dans des conditions de catalyse basique (pH > 2,5)
et/ou en présence d'une grande quantité d'eau, les
réactions d'hydrolyse et de condensation se produisent
simultanément. La rapidité de la réaction conduit à
la formation d'agrégats très fortement ramifiés qui ne
peuvent s'interpénétrer et vont donc exister en tant
qu'entités discrètes (Figure 27(a)). Cependant, les clusters vont
se lier les uns aux autres pour former un gel colloïdal. Les
agrégats, en se liant les uns aux autres (b), vont former un
réseau tridimensionnel de particules enchevêtrées à
l'origine de la gélification (c).
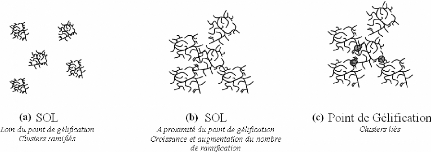
Figure 27 : Croissance du polymère et formation d'un gel
dans les systèmes à catalyse basique en fonction de
l'avancement de la réaction.103
3.3.2. Synthèse des hydrogels en présence de
monosaccharides
Les gels aqueux de silice contenant des solutions de D-glucose
ont donc été synthétisés à l'aide de ce
procédé « sol-gel ». La synthèse, en
collaboration avec Dr A. Douy du CRMHT, s'est fortement inspirée d'un
protocole expérimental décrit dans la
littérature.109 Cette synthèse110
nécessite les réactifs suivants : du D-glucose (C6H12O6), du
tetraéthoxysilane (Si-(OC2H5)4 (TEOS), = 98%), de l'urée
(CO(NH2)2, = 99%) de l'acide nitrique (HNO3, 67%) et de l'eau lourde
(D2O)*.
Pour cette nouvelle étude, nous nous sommes
limité à l'étude de la dynamique moléculaire du D-
glucose, et comme dans le cas des solutions volumiques, nous avons
utilisé du D2O et du D-glucose partiellement deutéré
(C6D5H7O6). Pour ce faire, le sucre (10 g) a été dissout en
boîte à gants (He) avec 30 mL d'eau lourde.** La
solution obtenue est agitée pendant quelques heures, avant d'être
placée dans une étuve à vide à 30°C pour
évaporer le solvant. Après complet séchage, le D-glucose
partiellement deutéré (C6D5H7O6) se présente
sous forme d'une poudre blanche prête à l'emploi.
* Tous ces produits chimiques proviennent de chez Sigma Aldrich,
exceptée l'eau lourde qui provient de chez Cambridge Isotope
Laboratory.
** Si l'on calcule le nombre d'atomes de deutérium par
molécule de D-glucose, nous trouvons 60:1, correspondant
à 60 D pour 5 H (en ne considérant que les hydrogènes
échangeables).
Le protocole expérimental pour la synthèse des
gels est le suivant. Dans un premier temps, le TEOS (1,5 g) est ajouté,
en boîte à gants, à une solution de D2O (20 mL)
acidifiée à l'acide nitrique (2- 3 gouttes). Puis, lorsque
l'hydrolyse du TEOS est terminée, c'est-à-dire lorsque la
solution est redevenue translucide, l'urée (0,1 g) et une
quantité donnée de D-glucose C6D5H7O6 (x g) sont ajoutées
à la solution. Après agitation, le sol est placé dans un
porte échantillon scellé à l'indium, puis vieilli entre 15
et 20 heures à 70-80 °C. La thermolyse de l'urée va
générer de l'ammoniac de manière homogène, qui, par
un processus catalytique et en augmentant le pH du sol, va faire polycondenser
l'acide silicique. Avec l'avancement de la réaction de polycondensation,
un réseau tridimensionnel de ponts siloxanes va s'étendre dans
tout le volume de la solution pour finalement former un gel. La solution de
sucre se retrouve alors confinée dans un squelette siliceux. (Figure
28)
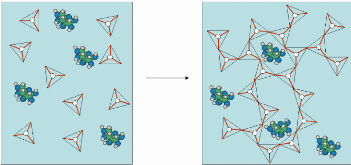
Figure 28 : Schéma représentatif de l'expansion du
réseau tridimensionnel siliceux dans tout le volume de la solution de
D-glucose.
Nous avons préparé des gels présentant
des fractions molaires glucose:eau = 0, 1:55 et 1:20. Il s'agit des ratios que
nous avons utilisés dans l'étude des solutions volumiques de
D-glucose (Cf. Chapitre 2). Elles correspondent à des concentrations
massiques de:
- 0, 13,4 et 30 wt.% dans des solutions intégralement
hydrogénées*,
**
- 0, 14,2 et 31,6 wt.% si l'on ne prend en compte que l'eau et le
sucre.
Le récapitulatif des échantillons est
présenté dans le tableau 20, dans lequel les ratios glucose:eau
sont donnés entre parenthèses.


*Lespourcentages massiques en sucre ont
été calculés de la manière suivante: wt.%msucre
mtotal ** Dans ce cas, wt.%msucre msucremeau

Tableau 20 : Tableau récapitulatif des gels de silice
synthétisés.
Le gel obtenu maintient parfaitement le liquide en son sein
(Figure 29), mais une fois sa surface brisée, le gel ne présente
plus aucune rigidité macroscopique et des écoulements de solution
apparaissent. C'est pour cette raison qu'il est absolument nécessaire de
synthétiser ces gels directement dans les porte-échantillons.

Figure 29 : Photographie d'un gel de silice aqueux.
3.3.3. Caractérisation Raman
Comme nous venons de le voir, le protocole expérimental
nécessite une montée en température de la solution pour
activer la thermolyse de l'urée. Ce chauffage, bien que
modéré (~ 80 °C), pourrait dégrader le
monosaccharide. Afin de s'assurer de l'intégrité des
molécules de D-glucose après gélification, des mesures de
spectrométrie Raman ont été réalisées en
collaboration avec Dr A. Desmedt du LPCM (Université Bordeaux 1).
La spectroscopie Raman permet de sonder les transitions
vibrationnelles, qui sont caractéristiques d'une molécule dans un
environnement donné. Les mesures en Raman confocal ont été
réalisées sur un spectromètre Labram II (Jobin-Yvon), dont
la source excitatrice est un laser Ar/Kr opérant à 514,5 nm et
avec une résolution spectrale de 6 cm-1. Un microscope
équipé d'un objectif 50× avec une ouverture numérique
de 0,75 et un trou confocal de 700 um ont été utilisés
pour faire converger le faisceau sur l'échantillon. Un filtre Notch a
également été utilisé pour filtrer la diffusion
Rayleigh. Les gels A1, A2 et A3, et une solution de D-glucose à 14 wt.%
ont été mesurés entre 100 et 4200 cm-1 à
la température ambiante. Les spectres sont présentés dans
la figure 30.
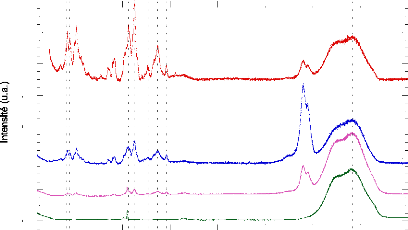
12
10
Solution 14 wt.%
8
6
4
2
A3
A2
Al
0
500 1000 1500 2000 2500 3000 3500 4000
Déplacement Raman (cm~1)
Figure 30: Spectres Raman pour les gels A1, A2 et A3, et pour une
solution de D-glucose à 14 wt. %. Les lignes en pointillés
marquent la position des pics Raman du D-glucose.
Les gels A2 et A3 présentent un nombre important de
pics dans la région spectrale comprise entre 250 et 1500
cm-1. Ces raies, que l'on observe très clairement dans la
solution, correspondent aux différents types de vibrations existantes
dans la molécule de D-glucose. Les attributions des différentes
raies sont listées dans le tableau 21. La coïncidence des raies,
sans décalage en fréquence, témoigne de la présence
du monosaccharide dans son intégrité structurale. Notons
également que l'on retrouve des pics de déformation pour les deux
variétés allotropiquesetdu D-glucose, ce qui confirme qu'il n'y a
pas eu de discrimination d'une variété par rapport à
l'autre durant la synthèse.
Un autre point est également à noter:
l'évolution de la bande des -OH entre 2700 et 3800 cm-1.
Lorsque l'on augmente la concentration en sucre, la bande des -OH diminue de
manière importante. Cette observation traduit l'augmentation du nombre
de liaisons hydrogène entre le monosaccharide et l'eau et donc, par voie
de conséquence, la diminution des liaisons hydrogène entre
molécules d'eau. Donc lorsque la concentration augmente, le sucre
«déstructure » le réseau aqueux.
On pourrait se demander, pourquoi n'observe t'on pas de
déplacement en fréquence, puisque nos solutions sont
confinées? En fait, la résolution instrumentale (6
cm-1) ne nous permet pas de déconvoluer deux pics
séparés de quelques cm-1. De plus, dans le cas
où les molécules de sucre interagissent avec la matrice
hôte, la proportion de molécules interagissant est si faible, que
le décalage en fréquence est masqué par les autres
vibrations plus nombreuses et donc plus intenses.
|
Espèce
concernée
|
Déplacement
Raman (cm-1) Type Attribution
|
170 vh2) élongation de la liaison
hydrogène
450 vL1) libration (inter)
780 vL2) libration (inter)
Eau 1650 v2a1 déformation symétrique
(intra)
3240 v, élongation symétrique
3400 v3 élongation asymétrique
3600 - groupements OH non interagissant
|
D-glucose
|
425 CCC) déformation -C-C-C-
450 CCO)endo déformation -C-C-O-
518 C2-C1-O1) déformation -C2-C1-O1- de la forme
540 C2-C1-O1) déformation -C2-C1-O1- de la forme
585 C6-C5-O5) déformation -C6-C5-O5-
710 O5-C1-O1) déformation -O6-C1-O1- de la forme
770 O5-C1-O1) déformation -O6-C1-O1- de la forme
842 vCC) élongation -C-C- de la forme
860 vCH) élongation -C-H- de la forme
893 vCC) élongation -C-C- de la forme
910 vCH) élongation -C-H- de la forme
1018 C-O-H) déformation -C-O-H-
1060 C-O-H) déformation -C-O-H-
1124 vCO) élongation -C-O-
1260 zCH2) twisting du groupement -CH2
1336 zCH2) twisting du groupement -CH2
1372 wCH2) wagging du groupement -CH2
1445 CH2) déformation du groupement -CH2
2900 vCH) élongation
2946 vCH) élongation
|
Tableau 21 : Affectation des fréquences observées
dans le spectre du D-glucose en solution aqueuse et dans
les gels A1, A2 et A3.111,112,113,114,115
La synthèse semble donc répondre à toutes
nos attentes : confinement, concentration, conservation de la structure
moléculaire de sucre, mais il nous reste une inconnue à
déterminer : le diamètre moyen des pores ... Afin de
répondre à cette question, nous avons étudié ces
trois mêmes gels à l'aide de la diffusion des neutrons aux petits
angles (SANS).
3.4. ETUDE STRUCTURALE PRELIMINAIRE DES GELS DE SILICE
AQUEUX CONTENANT DU D-GLUCOSE PAR DIFFUSION DES NEUTRONS AUX PETITS ANGLES
La diffusion des neutrons aux petits angles (SANS) est une
technique non-destructrice, qui, en mesurant la diffusion pour les faibles
valeurs de transfert de Q, permet d'étudier la géométrie
et la morphologie d'inhomogénéités de taille relativement
importante, généralement comprises entre 5 et 500 nm,
c-à-d pour 10-3 < Q < 0,5 Å-1. (Figure
31) Grâce à la gamme de tailles explorée et aux
particularités liées à la nature même des neutrons,
le SANS se révèle être un outil de choix pour sonder la
microstructure des matériaux et se voit être un très bon
complément des microscopies électroniques (MEB, MET) et optique,
mais également de la diffraction.
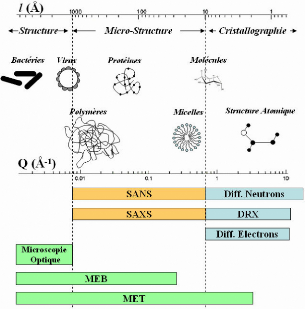
Figure 31 : Exemples de quelques objets dont les tailles sont
comprises entre 1 nm et 1 ,um. En dessous sont
présentées quelques techniques qui devraient
être utilisées dans cette gamme de taille.
3.4.1. Le formalisme de la diffusion aux petits angles
Dans le cas de la diffraction de Bragg classique, une intense
diffusion élastique cohérente est observée à chaque
fois que la loi de Bragg est satisfaite, c-à-d lorsque 2 = 2d
sinè 2, où d est une
0
distance caractéristique du réseau. Dans le cas
d'inhomogénéités « périodiques »,
séparées d'une
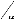
distance d, la diffusion se produit alors seulement aux angles de
Bragg où Q= 2ff 80,116
'
d

Il est alors possible de définir le vecteur d'onde
à la résonance de Bragg Q:
Q=4 sin sin
2
Durant une expérience de diffusion, l'intensité
diffusée I(Q) est mesurée en fonction de l'angle de diffusion, et
s'exprime sous la forme suivante :
I(Q) = 00.M.2.77.T.d.
d
d
où
= 0 est le flux de neutrons incidents, OSZ est l'angle solide
considéré,
est l'efficacité du détecteur,
T est la transmission de l'échantillon, d est
l'épaisseur de l'échantillon,
d est la section efficace différentielle de diffusion.
d
L'objectif de la mesure est donc de déterminer la
section efficace différentielle de diffusion, qui contient toute
l'information sur la forme, la taille et les interactions régnant dans
le système entre les entités diffusantes.
Dans des milieux isotropes contenant des particules relativement
lourdes comparée à la masse
du neutron, les diffusions élastique et
quasi-élastique, pour lesquelles

prédominent.117,118, 119 Dans ces
conditions, l'approximation statique peut-être utilisée pour
exprimer la section différentielle de diffusion par unité de
volume du matériau dE dQ . Pour un échantillon
composé de N atomes l, de longueur de diffusion bl, nous avons :

2
dE
bl
eie
N
1
V
L'angle de diffusion est habituellement appelé
20.
En général, la longueur de diffusion bl
dépend de la nature du noyau et de son état de spin. Il est alors
plus commode de séparer la section différentielle de diffusion
par unité de volume cohérente de celle incohérente :
dE dE lcoh dE linc
d l d J l d
où
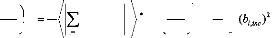
2
coh
N
1
dE
E
eiQRl
**
bl,coh
l
1
d
et = E
V
inc1N
d V
La diffusion cohérente a une distribution spatiale
caractéristique de la distribution des atomes dans l'échantillon
et donne des informations sur la structure d'un composé. Il est alors
possible de déterminer la structure et la taille d'un objet à
basse résolution. La diffusion incohérente, quant à elle,
ne donne qu'un bruit de fond indépendant de Q qui est proportionnel
à la section efficace de diffusion incohérente inc.
Il est alors possible de réécrire la section
efficace sous une forme plus simple :
d dE (A4)2 C pVpP(Q)S(Q)+
Binc
dans laquelle Cp est la fraction volumique des
diffuseurs, Vp le volume d'un diffuseur, (4)2 le
facteur de contraste, P(Q) le facteur de forme, S(Q) le facteur de structure et
Binc le bruit de fond incohérent. Nous reviendrons en
détail sur ces notions dans le chapitre 4.
3.4.2. Interprétation qualitative des
différents domaines de Q
Comme nous avons pu le voir, Q et d sont inversement
proportionnels, en d'autres termes, lorsque Q croît, d diminue et vice
versa. Ainsi, plus on augmente la valeur de Q, plus les détails de
petite taille sont mis à jour. D'une manière plus imagée,
jouer avec la valeur de Q, revient à jouer avec le grossissement d'un
microscope. La figure 32 schématise cette idée et présente
les différents domaines suivant les valeurs de Q
considérées.
* Nous rappelons que : bl,coh bl ** et que : bl2inc
bl2 -- b l 2
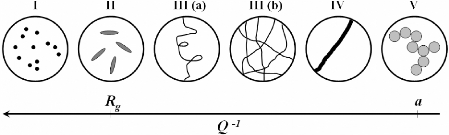
Figure 32 : Représentation schématique des
différents domaines de Q dans le cas d'une solution
diluée.118
Pour des valeurs de Q proche de 0 (Cas I), chaque
molécule est vue pratiquement comme un point, et il est impossible
d'obtenir une quelconque information sur sa structure. Maintenant, augmentons
la valeur de Q pour avoir Qf1 de l'ordre du rayon de giration
Rg (II). Si l'observation de la forme des molécules n'est
maintenant plus possible, leur forme générale apparaît et
c'est dans ce domaine, appelé domaine de Guinier, que l'on
mesurera leur rayon de giration Rg. Si l'on augmente encore un peu
plus la valeur de Q, nous atteignons les domaines III(a) et III(b). Pour une
solution diluée (Cas III(a)), seule une partie de la chaîne est
visible et il est alors possible de déterminer sa longueur de
persistance. Dans le cas d'une solution semi-diluée cette fois (Cas
III(b)), ce n'est pas un, mais plusieurs bouts appartenant à des
chaînes différentes que l'on observe. Il existe alors de nombreux
points de contacts entre les différentes chaînes, et la longueur
d'une chaîne entre deux ramifications devient une distance
caractéristique de l'échantillon appelée longueur de
corrélationî. En augmentant encore un peu plus la valeur de Q (Cas
IV), le polymère apparaît comme une chaîne gaussienne si la
longueur de persistance est plus petite que Q1, ou comme un
bâton si la longueur de persistance est plus grande que Q1.
Ces domaines III et IV vont constituer ce que l'on appelle le régime
de Porod. Enfin, pour des valeurs de Q, telles que
Qf1 soit de l'ordre de grandeur des liaisons chimiques (Cas
V), la structure locale de la chaîne pourra alors
être déduite. Au-delà, c-à-d pour des valeurs
correspondant aux grands angles, il est possible d'obtenir des informations sur
les distances interatomiques par des méthodes telles que l'analyse de
Rietveld. Cette région est désignée comme le domaine de
Bragg.
La figure 33 représente schématiquement une
courbe de diffusion aux petits angles dans le cas d'une solution diluée
de macromolécules. Le tracé log-log de l'intensité de
diffusion en fonction de Q a été découpé en suivant
les domaines de Guinier, de Porod et de Bragg définis
précédemment.
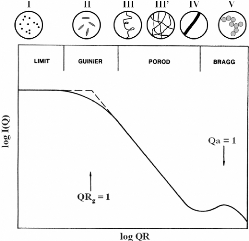
Figure 33 : Représentation schématique d'une
courbe de diffusion aux petits angles pour une solution
diluée de macromolécules (Rg
est le rayon de giration du polymère considéré, et a est
une longueur de liaison
interatomique).101
Revenons un peu plus en détail sur les régimes de
Guinier et de Porod :
Dans le régime de Guinier, correspondant à des
petits angles de diffusion (QRg rs, 1),
l'intensité diffusée est reliée au rayon de giration
Rg par l'expression suivante :
I(Q) ~ eQ2Rg2 3 .
Le tracé du logarithme de la section efficace en fonction
de Q2 doit donc donner une droite, dont la pente pour Q -->
0 permet de déterminer Rg . Ce tracé est
appelé représentation de Guinier.
Enfin, le régime de Porod, qui correspond à des
valeurs d'angles de diffusion intermédiaires (Rg »
Q-1 » a), présente une décroissance de
l'intensité diffusée qui suit une loi de puissance :
I (Q) ~ Q- X
avec -X = -2df+ dS= P dans laquelle P est la pente de Porod, df
la dimension du fractal de masse (0 = df= 3) et dS la dimension du fractal de
surface (2 = df= 3).
Dans le cas d'objets uniformes mais non-fractal, df = 3, dS =
2, et P vaut donc - 4. Dans le cas d'objets présentant un fractal de
masse, alors df = dS et donc P = - df. Dans ce cas, la dimension fractale est
obtenue directement en mesurant la pente. Dans le cas d'un fractal de surface,
df= 3 et P = dS - 6.

Le tableau 22 présente quelques valeurs de la pente de
Porod pour différents types de structure polymériques. Il
apparaît donc qu'à partir de l'analyse de la pente de Porod, on
peut en déduire une quantité importante d'information concernant
les dimensions fractales.
Tableau 22 : Quelques exemples de pentes de Porod pour
différentes structures.101
3.4.3. Paramètres expérimentaux
Les gels ont été synthétisés
directement dans des cellules en titane démontables mises à notre
disposition. Les échantillons, de 2 mm d'épaisseur, sont pris en
sandwich entre deux fenêtres en quartz, des joints et serre-joints
réalisant l'étanchéité. Les mesures ont
été réalisées sur l'instrument de diffusion aux
petits angles NG-3 30m120 en collaboration avec Dr S. Kline du
National Center for Neutron Research (NCNR). Une longueur d'onde incidente de 6
Å et trois distances détecteur- échantillon de 1,3, 4 et 13
m ont été utilisées alternativement pour permettre de
couvrir une grande gamme de Q (0,0035-0,47 Å-1).
3.4.4. Résultats et discussion
Les spectres ont été corrigés de la
cellule vide et de l'efficacité des détecteurs, puis
normalisés et enfin moyennés sur tous les angles pour chaque
position du détecteur. Les trois parties ont ensuite été
mises bout à bout pour recréer le spectre complet qui
s'étale sur toute la gamme de Q considérée. La figure 34
présente les spectres corrigés des gels A1, A2 et A3. Les
intensités de diffusion en fonction de Q présentent des
changements importants en fonction de la concentration en D-glucose et plus
particulièrement pour les plus faibles valeurs de Q. Dès lors que
l'on ajoute du sucre, le spectre présente une remontée en
intensité à petits Q, qui s'intensifie avec la concentration.
Dans le cas de A3, le plus concentré, cette remontée
présente même une pente en Q-4, qui indique la
présence d'une interface marquée, et donc
d'inhomogénéités plus larges.
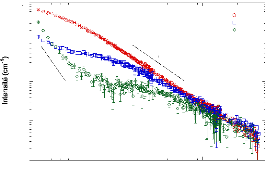
10
Al
A2
A3
1
Q-2
Q-4
0,1
0,01
0,001
0,01 0,1
Q(Å-1)
Figure 34 : Spectres SANS des gels A1 (rouge), A2 (bleu) et A3
(vert).
Ces spectres, dans la représentation de Guinier,
montrent de manière non équivoque qu'il n'existe pas de longueur
d'échelles caractéristiques dans ces échantillons. La
seule grandeur possiblement accessible est le rayon de Guinier R0 correspondant
à de petites particules formant la structure de base du gel. Ce rayon se
détermine à partir de la pente pour Q ? 0 du profil de diffusion.
(Figure 35)
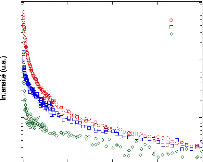
10
Al
A2
A3
1
0,1
0 0,002 0,004 0,006 0,008
Q2 (Å2)
Figure 35: Représentation de Guinier pour les trois gels
A1, A2 etA3.
Une estimation rapide de la pente de Porod donne une valeur
assez proche de 2. Afin de définir avec précision la dimension
fractale de nos gels et le rayon de Guinier, nous avons ajusté ces
spectres de diffusion à l'aide d'un modèle
fractal121,122 souvent utilisé dans le cas des gels de silice
de la forme:
I Q
( )( ) ( ) te
P Q S Q C
où P(Q) est le facteur de forme des particules
monomériques sphériques formant la structure fractale
Cte
et la est le bruit de fond incohérent indépendant
de Q. Le facteur de structure fractal S(Q) est
121,122
donné par :
sin ( 1) tan ( ) ( 1)
1
[ D Q D D
î ]
S Q
( ) 1 (Eq. 22)
( ) D 1 1 D
( 1) 2
QR Q 2 2
0 [ ]
î
dans laquelle D est la dimension fractale, R0 le rayon des
particules de silice formant la structure primaire, et î la
longueur de corrélation interprétée ici comme le
diamètre moyen des pores présents dans le gel de silice.
Les spectres des trois gels ont été
ajustés afin d'extraire les informations sur le gel (Figure 36). Ce
modèle ajuste parfaitement les données du gel A1. En ce qui
concerne les gels A2 et A3, l'accord est bon sur la majeure partie des spectres
excepté à petits Q où une déviation apparaît
et s'intensifie avec la concentration. Cette déviation peut être
due : (i) à la présence de large
inhomogénéités dans l'échantillon, ou (ii) à
des zones «riches en sucre », qui pourraient correspondre à
une séparation de phase par exemple, ou (iii) à une autre origine
qu'il reste à déterminer.
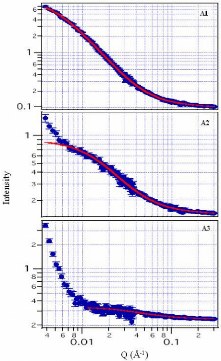
Figure 36: Spectres SANS pour les échantillons A1, A2 et
A3. Les courbes rouges représentent les ajustements du modèle
fractal décrit précédemment dans le texte.
Ainsi, nous avons déterminé que la dimension
fractale est D = 1,9 #177; 0,1. Cette valeur est tout à fait typique
d'un gel polymérique ramifié présentant un fractal de
masse (Tableau 22). De plus, le diamètre de Guinier, c-à-d la
taille des particules primaires, a été trouvée
égale à R0 = 6 #177; 1 Å. Notons que D et R0
présentent des valeurs quasi-identiques pour les trois gels. En revanche
la longueur de corrélation î diminue avec la
concentration, passant de 188 #177; 4 Å pour A1, à 70 #177; 3
Å et 25 #177; 7 Å pour les gels A2 et A3 respectivement.
Parmi tous les travaux existants sur le sujet, l'étude
de Schaefer et al.123 portant sur l'évolution du profil de
diffusion SAXS d'un sol en fonction du temps de gélation nous
apparaît très adéquate pour interpréter nos
résultats. La figure 37 présente le régime de Porod d'un
sol en fonction du temps normalisé par rapport à la
gélation. Il est clair que le spectre de diffusion dépend
fortement du temps de gélification. Ainsi le sol présentera un
profil très irrégulier, alors qu'à la fin de la
gélification, le régime de Porod est atteint et permet de mesurer
la dimension fractale du gel final.
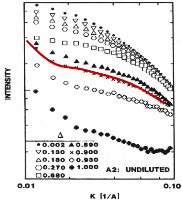
GEL
SOL
,123
Figure 37 : Evolution du profil de diffusion SAXS en fonction du
temps de gélation.101La courbe en rouge n'est qu'une aide
visuelle.
Les spectres intermédiaires entre le sol et le gel
laissent apparaître des profils présentant une remontée
à petits Q très similaire à celle observée pour nos
gels A2 et A3 contenant du sucre. L'origine de cette remontée serait
donc à rapprocher d'une gélification incomplète. Afin de
répondre à cette question, le gel contenant 30% de glucose a
été placé quelques heures supplémentaires en
vieillissement, avant d'être mesuré de nouveau. (Figure 38) Le
spectre ainsi obtenu a fortement évolué et présente
maintenant un profil typique d'un gel dans le régime de Porod. Cette
hypothèse est de plus corroborée par les valeurs
décroissantes de la longueur de corrélation î lorsque la
concentration en sucre augmente. Il est également intéressant de
constater, que pour une même durée de vieillissement, les gels A1,
A2 et A3, présentent des temps de gélifications
différents. Il y a donc un effet de la
concentration en sucre sur la cinétique de
gélification, qui se traduit par une diminution de la cinétique
de polymérisation avec l'ajout de sucre.
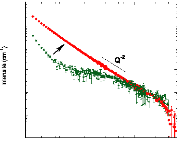
100
10
1
0,1
0,01
0,001
0,0001
0,01 0,1
Q (Å1)
Figure 38 : Evolution du profil de diffusion du gel contenant 30%
de glucose avec le temps de gélification. La courbe verte a
été mesurée après 15h de vieillissement, la courbe
rouge après 20h.
Nous avons donc estimé le diamètre moyen des
pores à 18,8 nm. Il est de plus important de noter que ces trois gels
ont été préparés spécialement pour les
mesures de diffusion quasi-élastique des neutrons, et qu'ils
n'étaient donc pas optimisés pour observer la structure du
réseau de silice par SANS. En effet, l'ajout du sucre dans le gel va
modifier le contraste de la solution. Cette première série de
mesure nous permet donc d'apprécier l'importance du temps de
gélification sur le profil de diffusion mesuré, mais elle
nécessite néanmoins une étude complémentaire afin
d'asseoir de manière définitive cette interprétation d'une
gélification incomplète. C'est pour cette raison qu'une nouvelle
série de mesures SANS utilisant la technique de variation de contraste a
été réalisée sur ces gels. (Chapitre 4)
3.5. CONCLUSION GENERALE DU CHAPITRE 3
Nous pouvons résumer ici les principales conclusions
obtenues dans ce chapitre sur la synthèse des gels de silice par voie
sol-gel :
Le confinement des solutions de sucre s'est faite dans des gels
de silice aqueux, qui présentent les avantages suivants :
- le sucre est conservé dans son intégrité
structurale,
- ils permettent le confinement d'une solution de sucre à
une concentration donnée,
- cette matrice répond à tous les
impératifs inhérents à la diffusion de neutrons,
c-àd, au point de vue de la « transparence » vis-à-vis
des neutrons et de la relativement faible quantité de proton
comparée à une matrice organique.
A partir des mesures SANS:
- la taille moyenne des pores est estimée à 18$20
nm,
- une remontée de l'intensité à petits Q
avec l'augmentation de la concentration en sucre est observée et
attribuée à une gélification incomplète
- un effet de la concentration en sucre sur la cinétique
de polymérisation est également observé.
Chapitre 4
ETUDE STRUCTURALE DES GELS DE SILICE CONTENANT DU
D-GLUCOSE A DIFFERENTS NIVEAUX D'HYDRATATION
4.1. Etude structurale par la méthode de variation de
contraste 97
4.2. Evolution de la structure des gels en fonction du taux
d'hydratation - Effet protecteur des sucres 103
4.3. Conclusion générale du chapitre 4 111
CHAPITRE 4
ETUDE STRUCTURALE DES GELS DE SILICE CONTENANT DU D-GLUCOSE SOUS
CONDITIONS « NORMALES » ET A DIFFERENTS NIVEAUX D'HYDRATATION
Comme nous avons pu le voir, certains sucres permettent la
conservation en l'état des édifices biologiques, et plus
particulièrement des membranes. La première étape de notre
étude était de déterminer une matrice de confinement
susceptible de pouvoir recevoir des solutions de sucre. De ce point de vue, les
gels de silice aqueux répondaient parfaitement aux impératifs de
concentration d'une part, mais également au mimétisme
d'échelle d'autre part. La matrice siliceuse de ces systèmes
modèles a également l'avantage de pouvoir se déformer sous
l'effet de la déshydratation. Il est alors possible d'utiliser ces gels
pour étudier de manière théorique les effets de la
biopréservation des sucres. Pour ce faire, nous allons dans un premier
temps étudier de manière beaucoup plus détaillée la
structure de ces gels, puis, dans un deuxième temps, nous regarderons
les effets de la déshydratation sur leur réseau de silice ...
4.1. ETUDE STRUCTURALE PAR LA METHODE DE VARIATION DE
CONTRAST
Comme nous avons pu le voir dans le chapitre
précédent, les mesures de diffusion aux petits angles nous ont
permis de déduire des informations structurales importantes sur ces
gels, mais ont également soulevé un certain nombre
d'interrogations, comme notamment la remontée en intensité SANS
des gels contenant les solutions de sucre. Quelques hypothèses ont
été évoquées pour expliquer ce comportement
à petits Q :
(i) la présence de larges
inhomogénéités dans l'échantillon,
(ii) des zones « riches en sucre », qui pourraient
correspondre à une démixtion,
(iii) une gélification incomplète
Afin de répondre de manière définitive
à ces questions, nous avons réalisé une nouvelle
série d'expériences de diffusion de neutrons aux petits angles,
une technique qui est particulièrement bien adaptée à nos
systèmes hydrogénés. Pour ce faire, nous avons
utilisé la technique de variation de contraste, qui est tout à
fait unique aux neutrons, et employée fréquemment dans les
systèmes bicouches/eau/sucre.124,125,126 Mais avant toute
chose, commençons par décrire brièvement le principe de la
méthode.
4.1.1. Principe de la méthode
Les neutrons voient un mélange de diffuseurs ayant des
longueurs de diffusion différentes et dont les positions dans l'espace
fluctuent de manière aléatoire. Ces fluctuations de
densité de longueur
de diffusion (SLD) contribuent à l'intensité
diffusée.118,119,127,128
La section efficace différentielle de
s'écrit alors de façon identique à celle
d'un gaz :
n(b2 --b2 )+
b EEeie71-rj)
n n
i=1 j=1

d
d

nndo- diffusion = EEbbeiQ(ri ej)
i j
di=1 j=1
Nous retrouvons bien ici les sections efficaces
cohérente
b2coh b et incohérente
b2inc b2 -- b 2
2
définies précédemment.
La diffusion incohérente correspond à toutes les
contributions dues à des fluctuations de longueur de corrélation
d'une taille très inférieure aux longueurs Q~1,comme
des fluctuations de composition isotopique ou de densité de solvant. La
soustraction de ces contributions incohérentes conduit à la
section efficace de diffusion cohérente :
do-coh 2 n n
iQ(r-rj)
b E
d i=1 j=1
Si l'on considère une solution dont le soluté
occupe une fraction volumique x, et le solvant une fraction x0. La
densité moyenne de longueur de diffusion s'écrit p
px + p0x0 avec p b v .
Pour un élément de volume i de
l'échantillon, l'écart à cette densité moyenne
devient :

p i(pxi p0x0i) -- p
pAxi + p0Ax0i ,
où xi représente l'écart à
la concentration moyenne en soluté.
Si le milieu est incompressible alors xi 1 et il s'en
suit que x0 = 1 -- x et Ax0i = --L xi
, d'où
Api = (p --
p0)Axi . La fonction de corrélation des
fluctuations de SLD est alors :
p

iApj = (p -- p0)2 xixj
Il est alors possible de d'exprimer la section efficace de
diffusion cohérente de la manière suivante :
coh
d
d
)
2 (p p0)2 L L
Ax Ax eiQ
i j
v

(ri -rj)
Il faut retenir de cette expression que l'intensité
diffusée est directement proportionnelle au facteur de contraste entre
le solvant et le soluté v2 (p -- p0 )2
.
De manière plus imagée, une particule sera d'autant
mieux observée que son facteur de contraste est
important. En diffusion de neutrons, il est possible de
modifier ce facteur en jouant avec le ratio H/D.* Prenons deux
objets en solution qui présentent des SLD différentes. En jouant
sur la SLD du solvant, via différents ratios H2O/D2O, il est possible de
masquer l'un des deux objets. (Figure 39)

Figure 39 : Schéma de principe de la technique de
variation de contraste. Les cercles sont des particules de
densités différentes. En jouant avec la
densité du solvant, il est alors possible de regarder l'une ou l'autre
des particules.
4.1.2. Paramètres expérimentaux
Les gels ont été synthétisés
directement dans des cellules en titane démontables, dans lequel les
échantillons, de 1 ou 2 mm d'épaisseur, sont pris en sandwich
entre deux fenêtres en quartz. Les mesures ont été
réalisées sur l'instrument de diffusion aux petits angles NG-7
30m129 en collaboration avec Drs S. Kline et L. Porcar du NIST
Center for Neutron Research (NCNR, Etats-Unis). Une longueur d'onde incidente
de 6 Å et trois distances détecteur-échantillon de 1, 4 et
13 m ont été utilisées alternativement pour permettre de
couvrir une grande gamme de Q comprise entre 0,0035- 0,47
Å-1.
4.1.3. Mesures préliminaires pour la
détermination des différents contrastes Cette étude va
donc se décomposer en deux parties :
(i) par la détermination du ratio « nul »
H2O/D2O pour atteindre le point de contraste moyen nul, pour lequel le signal
de la silice sera « éteint »,
(ii) par la synthèse de gels pour ce ratio H2O/D2O
particulier afin d'extraire uniquement l'information sur le sucre.
4.1.3.1. Détermination du point de contraste moyen
nul du gel de silice
Les SLD de l'eau légère H2O (SLD (H2O) =
-5×10-7Å-2) et de l'eau lourde D2O (SLD (D2O)
= 6,36×10-6 Å-2) permettent, en
réalisant des mélanges H2O/D2O dans des proportions
définies, d'atteindre la majeure partie des SLD caractéristiques
d'un échantillon. Afin de déterminer la valeur
* Les valeurs des SLD de H2O et de D2O sont très
différentes, ainsi ñ0 peut prendre toutes les valeurs
comprises entre -5× 10-7Å- 2 et 6,36×
10-6Å-2.
de la SLD de la matrice de silice, nous avons
synthétisé six gels de type A1, c-à-d sans sucre, pour les
fractions volumiques H2O/D2O suivantes: 100/0, 80/20, 60/40, 40/60, 20/80 et
0/100. Ainsi, en mesurant ces six échantillons, il nous sera possible de
déterminer avec précision le point de contraste nul pour lequel
le signal de la silice «s'éteint ». Les spectres,
mesurés lorsque le détecteur est à 13 m, sont
présentés sur la figure 40.
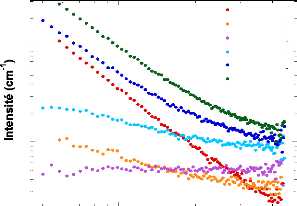
1
10
100% H2
40% H
2
20% H2
60% H2
80% H
2
0%H2
O
O
O
O
O
O
0,007 0,01 0,04
Q (+1)
Figure 40: Représentation log-log des spectres SANS des
gels de type A1 synthétisés pour différentes fractions
volumiques H2O/D2O.
Cette série de spectres montre une évolution de
la pente et de la valeur du bruit de fond incohérent pour les plus
grandes valeurs de Q lorsque l'on augmente la proportion d'eau
légère dans le solvant. L'ajout de l'eau légère
fait augmenter la quantité d'atomes d'hydrogène dans le milieu,
et par conséquent le signal incohérent. L'ordre des spectres,
pour Q = 0,04 Å-1, suit bien l'augmentation en proportion de
H2O. La pente, en revanche, évolue de manière non
linéaire: partant d'une pente décroissante (A1 - 0% H2O), elle
passe par une valeur proche de 0 (A1 - 40% H2O) pour enfin redevenir
décroissante (A1 - 100% H2O). Cette variation traduit l'évolution
du contraste du solvant par rapport à celui de la matrice siliceuse. On
en déduit donc que pour un mélange de solvant proche de 40% H2O -
60% D2O, le gel présente une SLD homogène sur l'ensemble de
l'échantillon, ce qui se traduit par un signal plat.
Rappelons ici que l'intensité diffusée est le
carré du module de l'amplitude de diffusion I(Q)A(Q) 2 , et que
l'amplitude A(Q) dépend de la SLD.
Ainsi en traçant la racine carrée de
l'intensité en fonction de la fraction volumique en H2O, il est alors
possible de déterminer le point de contraste nul de la silice. (Figure
41) Nous avons ainsi pu déterminé qu'une fraction volumique
H2O/D2O = 38/62 permet d'éteindre le signal de diffusion de la
silice.
0 20 40 60 80 100
Fraction volumique en H20 (x100)
Figure 41 : Racine carrée de l'intensité
diffusée par le gel A1 en fonction de la fraction volumique en H2O
La densité de longueur de diffusion de la silice peut
donc être calculée avec précision à partir de cette
valeur particulière du pourcentage volumique (%(H2O) = 38), et des
densités de longueurs de diffusion de l'eau légère et
l'eau lourde. Ce calcul conduit à une densité de longueur de
diffusion du réseau de silice égale à SLD (SiO2) = 3,8
Å-2.
4.1.3.2. Calcul des différentes fractions
volumiques
Nos gels sont des systèmes complexes, multicomposants,
qui sont formés de trois constituants : le gel, le sucre et le solvant.
Maintenant que la SLD du gel est déterminée avec
précision, il nous faut définir les points de contraste nul pour
les autres combinaisons de constituants, afin de pouvoir réaliser un
masquage sélectif. Trois cas peuvent être considérés
:
(1) si SLD (H2O/D2O) = SLD (sucre) --> on observera alors la
silice,
(2) si SLD (H2O/D2O) = SLD (SiO2) --> on observera alors le
sucre,
(3) si SLD (H2O/D2O/sucre) = SLD (SiO2) --> le milieu est
homogène et il n'y a pas de diffusion.
La détermination des fractions volumiques H2O/D2O
correspondantes s'est faite théoriquement, pour des raisons de temps de
faisceaux principalement, et sont présentées dans le tableau
23.

Tableau 23 : Conditions expérimentales utilisées
pour regarder sélectivement la silice et le monosaccharide. (SLD(sucre)
= 4,15×10-6 Å- 2, SLD(H2O) = -
5×10-7Å-2, SLD(D2O) =
6,36×10-6 Å-2)
Ainsi, si on s'intéresse à la structure de la
silice, on utilisera un mélange H2O/D2O dans les proportions 32/68, et
si on s'intéresse au sucre, nous utiliserons plutôt un
mélange 38/62.
4.1.4. Résultats et discussion
Les trois ratios H2O/D2O, cités
précédemment, ont été utilisés dans la
synthèse du gel A3, et ont donné lieux aux trois spectres
présentés sur la figure 42. Seul le spectre de
l'échantillon A3 32% H2O a été corrigé du bruit de
fond incohérent.
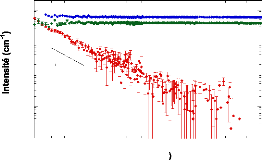
1
0
A3 38% H
2
0
0,1
Q-2
0,01
A3 32% H
2
0
0,001
0,0001
0,01 0,1
Q (A-1
A3 43% H
2
Figure 42 : Spectres SANS avec variation de contraste pour le gel
A3. (A3 - 32% H2O : SiO2 ; A3 - 43% H2O : nul ; A3 - 38% H2O : D-glucose)
Examinons ces trois spectres séparément :

A3 - 43% H20
Dans cette configuration, l'idée est de vérifier
que nos calculs de densités de longueur de diffusion (SLD) sont valides
et qu'il est possible de rendre l'échantillon complètement
homogène vis à vis des SLD. La courbe bleue montre de
manière évidente que pour ce ratio H2O/D2O, le signal est
parfaitement plat comme prévu. Ce résultat laisse donc à
penser que l'échantillon ne présente pas
d'inhomogénéités majeures en SLD.

A3 - 38% H2O
Cette fois-ci, nous regardons la diffusion de la solution de
sucre ... Dans le cas d'inhomogénéités de taille
importante, nous devrions observer un signal décroissant. Or, lorsque
l'on se place au point de contraste nul de la silice, comme c'est le cas ici,
le signal est parfaitement plat, ce qui indique que la solution de sucre est
totalement homogène dans le domaine de Q sondé. Notons aussi que
ce résultat se conserve après traitement du bruit de fond
incohérent. Nous pouvons donc en conclure que les molécules de
sucre ne forment pas d'agrégats et qu'il n'y a pas de
phénomènes de démixtion.
A3 - 32% H2O
Pour ce ratio particulier, nous n'observons que le signal
provenant du réseau de la silice. Le spectre présente une pente
de Porod voisine de 2, typique d'une structure fractale. Ainsi, il
apparaît qu'un gel parfaitement gélifié ne présente
pas de remontées pour les plus petites valeurs de Q. Il apparaît
donc de manière définitive maintenant, que les augmentations en
intensité observées pour les échantillons A2 et A3 ne sont
liées qu'à une gélification incomplète. Tous ces
résultats corroborent donc nos conclusions du chapitre
précédent.
4.1.5. Conclusions
Nous pouvons donc en déduire que l'ajout du sucre n'a
pas atteint la structure fractale du gel, et que les remontées
d'intensité observées précédemment ne sont dues
qu'à une gélification incomplète des échantillons.
Nous pouvons donc affirmer que nos échantillons sont homogènes et
qu'il y a une absence totale de gradients de concentration.
4.2. EVOLUTION DE LA STRUCTURE DES GELS EN FONCTION DU
TAUX D'HYDRATATION -- FFET PROTECTEUR DES SUCRES
Toutes ces études sur la structure des gels nous ont
permis de mieux connaître notre système et nous amènent
maintenant à tester les capacités du D-glucose dans la
conservation des édifices structuraux. L'idée est donc de simuler
des cycles de déshydratation sur ces gels qui ont la
particularité de pouvoir se déformer avec la perte en eau. Afin
d'étudier les évolutions de la structure du réseau
siliceux, nous avons réalisé des déshydratations in-situ
dans un spectromètre de diffusion aux petits angles en collaboration
avec Drs G. Charalambopoulou, T. Stériotis de Demokritos
(Athènes, Grèce) et A. Brandt du Hahn Meitner Institute (Berlin,
Allemagne).
4.2.1. Description du montage
Ce montage, tout à fait particulier, est unique parmi
toutes les sources neutroniques. Il est composé d'un banc de pompage,
équipé d'un système de vannes permettant de
réaliser des cycles de
déshydratation/hydratation. Les
portes-échantillons en verre, conçus spécialement pour
cette manipulation, sont composés d'une cellule en quartz
d'épaisseur 1mm et d'une valve en verre. La valve est constituée
d'un tube pour se raccorder au système de pompage, d'un robinet, et
d'une partie ovoïde permettant le raccordement avec la cellule. Les deux
parties sont scellées à l'aide d'une résine époxy,
qui, après séchage, assure la tenue de l'ensemble, mais
également l'étanchéité. (Figure 43)
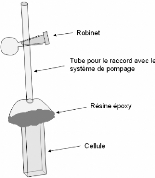
Figure 43: Schéma descriptif du montage
expérimental composé d'une cellule et d'une valve pour le pompage
et les mesures SANS in-situ.
4.2.2. Préparation des échantillons
Pour cette série de mesures, nous avons
synthétisé 6 gels avec des concentrations de 0, 10, 15, 20, 30 et
40 wt.%. La préparation des sols s'est réalisée comme
précédemment avec du D-glucose deutéré
(C6H7D5O6), de l'eau lourde, du TEOS et de l'urée. Une fois le
mélange effectuée, les sols ont été placés
dans les cellules scellées pour l'occasion par du scotch en aluminium,
afin de se prémunir de l'évaporation du solvant, mais
également des échanges possibles H/D entre le solvant et
l'humidité ambiante. Les cellules ont ensuite été
placées à l'étuve pour gélification (~ 15-16 h).
Dès que les sols sont devenus des gels, nous avons
réalisés le montage de la cellule avec la valve en utilisant une
résine époxy.
4.2.3. Conditions expérimentales
Les mesures ont été réalisées sur
l'instrument de diffusion aux petits angles V4130 en collaboration
avec Dr A. Brandt du Berlin Neutron Scattering Center (BENSC-HMI, Berlin,
Allemagne). Une longueur d'onde incidente de 6,05 Å et trois distances
détecteur-échantillon de 1,1, 4 et 16 m ont été
utilisées alternativement pour permettre de couvrir une gamme de Q
comprise entre 0,0035-0,33 Å-1. Les données
expérimentales ont été réduites à l'aide du
logiciel BerSANS.131 Tous les spectres présentés dans
cette partie ont été corrigés de la cellule vide, de
l'efficacité des détecteurs et du bruit de fond
électronique.
4.2.4. Résultats
4.2.4.1. Avant déshydratation
La figure 44 présente les spectres de ces six gels avant
déshydratation. Ces spectres n'ont pas été corrigés
du bruit de fond incohérent.
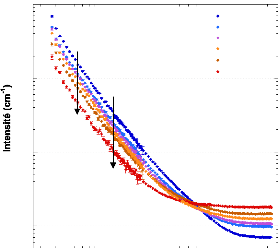
100
0.1
1
10
Gel 20%
Gel 0% Gel 10% Gel 15%
Gel 30%
Gel 40%
0.01 0.1
Q (k1)
Figure 44: Spectres SANS des six gels avant
déshydratation. Les pourcentages correspondent à la concentration
en sucre dans le gel.
Ces six gels, réalisés dans les mêmes
conditions, nous permettent d'étudier l'évolution de la structure
du réseau de silice avec l'augmentation en concentration du
D-glucose.
Pour les plus grandes valeurs de Q, c'est-à-dire vers
0,2-0,3 Å-1 , nous observons une augmentation de
l'intensité en fonction de la concentration. Ces plateaux sont dus
à la diffusion incohérente. En effet, l'échantillon, bien
que partiellement deutéré, présente une quantité de
protons qui augmente avec la concentration en sucre. Ainsi, plus la
quantité de D-glucose augmente, plus le nombre de protons est grand, et
plus le bruit de fond incohérent est important.
Pour les plus petites valeurs de Q, tous les spectres
présentent un comportement linéaire et sont tous
parallèles entre eux. Une décroissance en intensité est
observée et est liée à la différence de contraste
existante entre les échantillons. Afin de vérifier cette
hypothèse, nous avons tracé la racine carrée de
l'intensité I(Q) moins l'incohérent en fonction de la
concentration pour une valeur de Q donnée. (Figure 45)
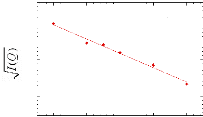
8
7
6
5
4
3
2
Q= 0,004 e1
0 10 20 30 40
Concentration (%)
Figure 45 : Tracé de I (Q) en fonction de la
concentration en glucose.
L'intensité s'exprime de la manière suivante :
I (Q) = (Añ(c))2 P(Q)
où (Añ(c))2 est le
facteur de contraste dépendant de la concentration, et P(Q) le facteur
de forme. Si l'on prend la racine carrée de l'intensité à
un Q donné, l'expression devient alors :

I (Q) = A.ñ (c)

Il apparaît alors que si le contraste est
dépendant de la concentration, le tracé de I (Q) en
fonction
de la concentration est une droite de pente A = P(Q) . La
figure 45 montre cette dépendance linéaire
de l'intensité montrant le rôle du contraste dans
le décalage. Afin de corroborer ce résultat, nous avons
tracé l'intensité corrigée du bruit de fond
incohérent et divisée par la SLD du mélange D2O/glucose.
(Figure 46) Nous observons alors que tous les spectres sont identiques, aux
erreurs expérimentales, de mesures et de traitement près. Les
barres d'erreur ne sont pas présentées sur cette figure pour une
question de visibilité, mais avec les barres, toutes les courbes se
recoupent. Nous pouvons alors observer deux régimes, un avec une pente
de Porod en Q-2, typique d'un fractal de masse ; et un second avec
une pente en Q-4 qui décrit les monomères constitutifs
du réseau.
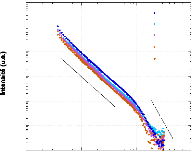
100
0%
10
10%
15%
1
20%
30%
0.1
Q-2
0.01
Q-4
0.001
0.0001
0.001 0.01 0.1 1
Q (+-1)
Figure 46 : Spectres des gels corrigés du bruit de fond et
normalisés à la densité de longueur de diffusion.
Nous pouvons donc en conclure que tous nos spectres
présentent le même profil en intensité et que les
décalages sont liés à une différence de contraste.
Ainsi, ces premiers spectres, tous équivalents, vont nous permettre
d'étudier les variations de la structure avec la
déshydratation.
4.2.4.2. Après déshydratation
La déshydratation des différents gels a
été réalisée par pompage sous vide. Le pompage de
l'eau va ainsi augmenter artificiellement la concentration en sucre du gel.
Notre idée est donc de simuler une déshydratation en milieu
confiné, et d'observer l'évolution de la structure du gel avec la
perte en eau.
La déshydratation s'est réalisée par des
petites évaporations successives afin de ne pas détériorer
prématurément les gels. Une première observation doit
être mentionnée ici: le temps de pompage pour extraire une
quantité d'eau équivalente augmente de manière importante
avec la concentration. En effet, le gel 0% perd une importante quantité
d'eau dès les premières minutes de pompage, et sa structure
macroscopique s'est retrouvée très rapidement affectée, le
rendant inutilisable. Dès lors que l'on ajoute du sucre dans le gel,
l'eau devient beaucoup plus difficile à extraire, et le gel semble plus
résistant. Néanmoins, il semble y avoir une limite entre les gels
30% et 40%. Pour le gel à 30%, le ménisque met un certain temps
à descendre, mais le délai de pompage reste raisonnable. Pour le
gel à 40% en revanche, le ménisque met un temps très long
pour descendre, et il est difficile d'atteindre des niveaux de
déshydratation important. Cette observation pratique peut s'expliquer
par les interactions eau-sucre présentes en solution. Lorsque la
concentration en sucre augmente, le nombre de molécules d'eau par
molécule de glucose diminue jusqu'à devenir critique lorsque deux
molécules de sucre adjacentes partagent une même sphère
d'hydratation. Les interactions sucre-eau deviennent alors
prépondérantes, et il ne reste que peu de molécules d'eau
isolées susceptibles de pouvoir être évaporées. Les
difficultés de pompage sont donc un bon indicateur de l'augmentation du
nombre d'interactions au sein de la solution. Aucune quantification du
phénomène n'a été réalisée pour le
moment, mais ce phénomène reste néanmoins important
à noter pour la suite.
Tous les échantillons ont été
déshydratés avec les mêmes précautions. Cependant,
tous les gels avec des défauts au niveau du ménisque ont
immédiatement présentés une rupture dès les
premiers pompages: c'est le cas, entre autre, des gels 10% et 20%. Le gel 0%,
quant à lui, ne présentait pas de défauts visuels
particuliers, mais a subi des dommages majeurs dans sa structure à cause
de sa faible tolérance à la déshydratation, comme nous
l'avons évoqué juste avant. Après quelques minutes de
*
pompage, le gel présentait des fractures importantes qui
rendaient toute mesure impossible.Seuls les
* Cet échantillon (gel 0%) a été
synthétisé deux fois. A chaque fois, le gel ne résistait
pas à la déshydratation.

gels 15% et 30% ont pu être déshydratés
correctement. Les spectres de ces gels après déshydratation sont
présentés sur la figure 47. La forme de ces spectres sera
discutée en détail dans les paragraphes suivants.
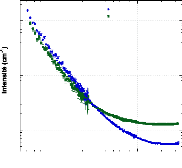
Gel 15% déshydraté
10
1
0.1
0.01 0.1
Q (A1
Gel 30% déshydraté
Figure 47 : Représentation log-log des spectres SANS des
gels 15 et 30% déshydratés par pompage.
Il est bien évident que lorsque l'on évapore une
partie du solvant, les concentrations de la solution confinée seront
complètement modifiées. Afin de calculer un pourcentage massique
virtuel de la solution confinée après pompage, nous devons
connaître la quantité d'eau extraite. Chaque cellule a donc
été pesée avant et après déshydratation, et
les concentrations finales sont listées dans le tableau 24.
Tableau 24: Tableau récapitulatif des pertes d'eau
liées au pompage et des pourcentages massiques correspondants.
Après déshydratation, les concentrations
atteintes sont très élevées et avoisinent les 75-80 wt.%,
dans l'hypothèse bien sûr où seule l'eau lourde est
extraite et de manière homogène dans tout l'échantillon.
Notons également que ces gels, qui emplissaient toute la cuvette en
quartz, ne forment plus maintenant que deux films assez épais qui
recouvrent les deux parois de la cellule. Les spectres SANS de ces gels
déshydratés sont présentés dans la figure 48 et
sont accompagnés des mesures réalisées avant
déshydratation pour comparaison.
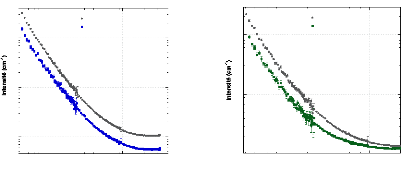
10
1
0.01 0.1
Q (A-1)
0.1
(a)
10
1
Gel 15%
Gel 15% déshydraté
0.01 0.1
Q (A-1)
(b)
Gel 30%
Gel 30% déshydraté
Figure 48 : Spectres SANS des gels 15% (a) et 30% (b)
déshydratés par pompage dans la représentation log- log.
Les spectres des gels 15% et 30% sont présentés ici à
titre comparatif.
Gel 15% déshydraté
Si l'on superpose le spectre du gel 15%
déshydraté à celui du gel 15%, nous pouvons voir que leurs
profils en intensité sont identiques (Figure 49 (a)), ce qui signifie
que la structure du gel de silice n'a pas été modifiée par
la déshydratation, alors que la perte en eau est conséquente. Les
molécules de D- glucose semblent donc protéger de manière
active la structure du gel.
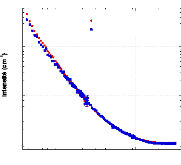
Gel 15%
Gel 15% déshydraté
10
1
0.1
0.01 0.1
Q (A-1)
(a)
(b)
0.01 0.1
Q (A-1)
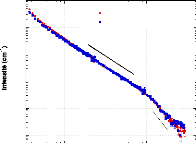
0.001
0.01
0.1
10
1
Gel 15%
Gel 15% déshydraté
Q-2,08
Q-4
Figure 49 : (a) Superposition des spectres SANS des gels 15% et
15% déshydraté, et (b) après soustraction du bruit de fond
incohérent.
La seule différence notable est que le gel 15%
déshydraté est décalé vers des intensités
plus basses. Ceci peut s'expliquer par le fait que le gel ne recouvre plus
l'intégralité de la cuvette, et qu'il forme maintenant un film
sur chaque face de la cuvette, laissant ainsi un espace libre entre les deux.
Par conséquent, le faisceau de neutrons traverse une zone « sans
échantillon » qui conduit inéluctablement à une
baisse en intensité. A cela s'ajoute l'évolution du contraste
lié au pompage du D2O.
Maintenant, si l'on soustrait le bruit de fond incohérent
(Figure 49(b)), nous trouvons deux régimes distincts :
- un premier, à grands Q, avec une pente en
Q-4, qui traduit la présence d'objets uniformes et
non-fractals. Il s'agit du signal des monomères qui constituent la
structure de base du réseau siliceux.
- Un deuxième, compris entre 0,003 et 0,8
Å-1, présente une pente en Q-2, qui indique
que nos particules élémentaires s'organisent pour former une
structure auto-similaire typique d'un réseau de polymères.
Que ce soit avant ou après soustraction du signal
incohérent, les diffusions des gels 15% et 15% déshydratés
se superposent parfaitement confirmant ainsi la conservation structurale de la
silice par le sucre.
Gel 30% déshydraté
Le gel 30% déshydraté et le gel 30%
présentent des profils de diffusion légèrement
différents. (Figure 48 (b)) La superposition de ces deux spectres
après correction du signal incohérent ne montre pas une
modification majeure de la structure. (Figure 50)
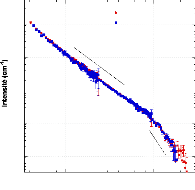
10
Gel 30%
Gel 30% déshydraté
1
Q-2,04
0.1
0.01
Q-3,9
0.001
0.010.1
Q (+-~)
Figure 50 : Superposition des spectres SANS des gels 30% et 30%
déshydraté après soustraction du bruit de fond
incohérent.
En fait, cette différence d'appréciation
provient du fait que les bruits de fonds incohérents des deux gels
génèrent une déformation du signal qu'il convient de
corriger. Cette fois encore, une légère différence
d'intensité est visible pour les plus grandes valeurs de Q, entre les
gels 30% et 30% déshydratés, mais cette différence est
malgré tout moins marquée. Après correction, nous
retrouvons bien les deux régimes en Q-2 et Q-4
déjà repérés dans le cas du gel 15%. Cette fois
encore, bien que les pertes en eau soient importantes, la structure du gel
semble résister à cette déshydratation forcée
grâce à la présence du monosaccharide.
4.2.5. Remarques générales
Cette étude pionnière, bien que qualitative pour
l'instant, apporte néanmoins des réponses sur les effets du sucre
sur la conservation de la matrice hôte. Il ressort donc que la structure
du gel aqueux sans sucre aura une résistance macroscopique
limitée, alors qu'un gel contenant du D-glucose résistera de
manière beaucoup plus importante à une déshydratation
sévère. Cette conclusion est en bon accord avec les études
de simulation moléculaire réalisées qui prédisent
que les sucres, en plus de se lier aux phospholipides, jouent un rôle
« d'espaceur de membrane » lorsque l'eau se retire. La
quantité de sucre présente initialement ne semble pas être
un facteur décisif dans la conservation des édifices structuraux
comme en témoignent les deux gels à 15% et 30% qui ne
présentent pas de modification majeures.
4.3. CONCLUSION GENERALE DU CHAPITRE 4
Ce chapitre apporte des éléments
supplémentaires dans notre compréhension de la structure des gels
de silice aqueux en présence ou non de sucre. L'étude de
diffusion des neutrons aux petits angles a donc permis de répondre
à nos interrogations sur la présence ou non d'un gradient de
concentration en sucre. Résumons ici les principaux résultats
obtenus sur la structure des gels.
(i) A partir des mesures de diffusion aux petits angles avec
variation de contraste :
· Les gels A1, A2 et A3 présentent une
géométrie fractale de dimension proche de 2,
· Le diamètre moyen des pores, estimé
à 18-20nm reste valide dans les gels contenant du sucre (A2 et A3)
· Les molécules de D-glucose ne forment pas
d'agrégats dans la gamme de Q considérée, il n'y a pas de
démixtion ou de forts gradients de concentration.
· Une gélification incomplète est à
l'origine de la remontée observée à petits Q
(ii) Pour différents niveaux de déshydratation
:
· Obtention d'une courbe universelle valide pour tous les
échantillons
· Les gels sans sucre (Gel 0% ou A1) ne présentent
qu'une résistance très limitée à la
déshydratation,
· La présence du monosaccharide permet la
conservation de la structure du réseau de silice,
· La rétention d'eau est plus importante dans les
gels contenant du sucre,
· La concentration initiale en sucre, au-delà de
10%, ne semble pas être un facteur capital pour la conservation des
édifices structuraux.
(iii) Une quantification des phénomènes de
rétention d'eau et de stabilité mécanique reste manquante
et il serait souhaitable que ces mesures in-situ soient poursuivies pour
élucider entièrement les processus de protection mis en jeu.
Chapitre 5
DYNAMIQUE MOLECULAIRE DU SUCRE CONFINE DANS UN GEL DE
SILICE AQUEUX
5.1. Dynamique du D-glucose confiné dans des gels de
silice 115
5.2. Dynamique du tréhalose confiné dans des gels
de silice 122
5.3. Conclusion générale du chapitre 5 128
CHAPITRE 5
DYNAMIQUE MOLECULAIRE DU SUCRE CONFINE DANS UN GEL DE SILICE
AQUEUX
D'après le chapitre précédent, il
émerge que les sucres présentent une forte aptitude à
conserver les édifices dans leur intégrité structurale.
Cette conclusion confirme donc les hypothèses avancées pour
expliquer la résistance des organismes anhydrobiotiques. Si cette
étude structurale nous apporte une confirmation supplémentaire du
rôle crucial des sucres, il reste néanmoins qu'elle ne fournit pas
à elle seule quelles en peuvent être les causes ? Parmi les
hypothèses évoquées pour de si grandes pertes en eau, la
substitution de l'eau d'hydratation et la vitrification sont les deux
phénomènes les plus probables. (Cf. Chapitre 1) Or ces deux
hypothèses sont basées sur des questions d'interaction eau-
soluté principalement. Ainsi, pour comprendre les origines mêmes
de cette protection, il est absolument nécessaire d'étudier les
aspects dynamiques des molécules de sucre, qui peuvent donner un
aperçu des interactions au sein de ces solutions. Dans ce chapitre, nous
allons donc étudier la dynamique des molécules de D-glucose d'une
part, puis celle des molécules d' tréhalose d'autre part,
confinées dans ces mêmes gels de silice. Nous pourrons donc
regarder les effets de la taille de l'environnement sur leurs dynamiques
respectives.
5.1. DYNAMIQUE DU D-GLUCOSE DANS LES GELS DE SILIC
5.1.1. Conditions expérimentales
Les mesures de dynamique moléculaire du D-glucose
confiné, par diffusion quasi-élastique des neutrons, ont
été réalisées au National Center for Neutron
Research (NCNR) sur les spectromètres DCS85 et
HFBS.86 La gélification des sols s'est faite directement dans
des porte-échantillons cylindriques d'espace annulaire 0,4 mm. Une fois
scellés, ils ont été placés dans un cryostat dans
lequel la température est régulée à #177; 1 K.
Les trois échantillons A1, A2 et A3 ont
été mesurés sur le DCS à 300 K, avec une longueur
d'onde incidente de 6 Å (0,25 < Q < 1,93 Å-1), et
pour une résolution instrumentale de 57p,eV. Pour les mesures
effectuées sur le HFBS, les paramètres expérimentaux
étaient les suivants : T = 300 K, 2%, = 6,27 Å, 0,36 < Q <
1,52 Å-1 avec une résolution de #177; 1,2 geV.
5.1.2. Traitement des données
Les spectres de chaque échantillon ont
été normalisés au moniteur, corrigés de la cellule
vide, normalisés au vanadium, puis regroupés afin
d'améliorer la statistique. Cette partie du traitement est en tout point
identique à celle décrite précédemment (Cf.
Chapitre 2 : p. 40).
Afin d'extraire la dynamique des molécules de
D-glucose, nous avons soustrait le gel sans sucre A1 des gels contenant du
sucre (A2 et A3), les spectres résultants s'appelleront respectivement
A2-A1 et A3-A1. Afin de prendre en compte les différents facteurs
d'atténuation du gel pur (A1) et des gels contenant du sucre (A2 et A3),
la diffusion de A1 a été multipliée par le facteur
d'atténuation du D- glucose avant la soustraction. Le coefficient
d'atténuation d'une espèce se calcule à partir du nombre
d'atomes i par unité de volume ñi, de la section efficace de
diffusion totale i, de la section efficace
S
i
d'absorption, et enfin du chemin optique x :
A
i i
A exp ( )
ñ x
espèce i S A
i?espèce
Si l'on suppose que la densité partielle du gel n'est
pas affectée par la présence du sucre, alors le
coefficient
d'atténuation d'un gel contenant du sucre est le produit des
coefficients d'atténuations du
gel et du sucre : A gel A gel × A glucose .
glucose
A titre d'exemple, la soustraction pour le gel A2 s'est
effectuée de la manière suivante:
A2 - A1A2AgelglucoseCVA × glucoseA1 × AgelCV
où Agel+glucose est le coefficient d'atténuation du
gel A2, Aglucose celui du D-glucose, et CV le signal de la cellule vide.
La validité de la procédure repose bien
évidemment sur l'hypothèse que la présence du sucre
n'affecte pas la dynamique du gel hôte. Cette hypothèse est
supportée par le fait que le gel est deutéré et qu'il
contribue donc relativement peu à la diffusion totale. (Tableau 25)

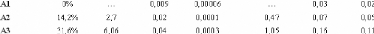
Tableau 25: Contributions relatives de la diffusion
cohérente et incohérente émanant du D-glucose, de l'eau
lourde et du gel.
Les fonctions de diffusion des échantillons A1 et A3,
et de la soustraction A3-A1, sont présentées sur la figure 51(a)
pour le DCS pour Q = 0,7Å-1 et sur la figure 51(b) pour le
HFBS pour Q = 0,36Å-1. Celles-ci montrent de manière
claire que la contribution solvant/matrice est faible en comparaison de celle
du D-glucose.
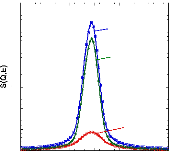
35
30
(a)
Q = 0.744
T = 300 K
A3
25
A3-Al
20
1 5
10
5
0
Al
-0.3 -0.2 -0.1 0 0.1 0.2 0.3
E (meV)
-40 -30 -20 -10 0 10 20 30 40
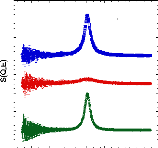
(3)
T = 300 K Q = 0,3644
A3-Al
A3
Al
E (peV)
Figure 51: Fonctions de diffusion pour les échantillons A1
(rouge), A3 (bleu) et A3-A1 (vert) tirées des mesures
réalisées sur le DCS (a) et sur le HFBS (b) à 300 K.
5.1.3. Résultats
5.1.3.1. DCS
Les fonctions de diffusion S(Q,E) corrigées ont
été ajustées à l'aide de la combinaison de
fonctions théoriques suivantes : une fonction delta,
deux fonctions Lorentziennes L(Wt, E) et une ligne de base qui prend en compte
le bruit de fond et autorise une légère déviation du
signal incohérent. (Figure 52)
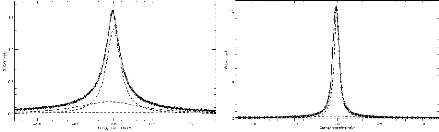

Figure 52 : Deux exemples d'ajustements des données du
DCS composés de deux fonctions Lorentziennes et d'une ligne de base. Il
s'agit ici du gel A1 à gauche et de la soustraction A3-A1 à
droite à Q = 1,1 Å$1. Les résidus sont
présentés en dessous de chaque courbe.
Les résidus précédents témoignent
du très bon accord existant entre nos données
expérimentales et la fonction de diffusion théorique
Sinc(Q,E) déterminée dans le chapitre 2. Les largeurs
à mi-hauteur W1 et W2 ainsi obtenues sont tracées en fonction de
Q2. (Figure 53).
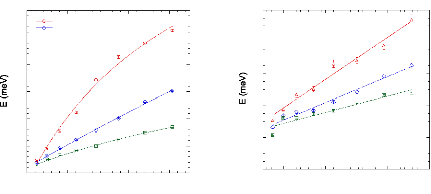
Lorentzienne "étroite" L1(W1,E)
(a)
0
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å1)
0,5
0,4
A1
A2
A3
0,3
0,2
0,1
(b) Lorentzienne "large" L2(W2,E)
A1
1,6
A2
1,2
A3
0,8
0,4
0
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å-1)
Figure 53 : Largeur à mi-hauteur de la Lorentzienne
étroite W1(a) et de la Lorentzienne large W2 (b) ajustées aux
données des gels A1, A2 et A3. Les courbes représentent les
ajustements effectués à partir des équations 13 et 14.
Il devient alors évident que la largeur des deux
Lorentziennes rétrécit lorsque la concentration augmente, ce qui
se traduit physiquement par un ralentissement général de la
dynamique des espèces présentes en solution. Afin de voir l'effet
de la concentration sur la dynamique des molécules de sucre, nous avons
tracé W1 et W2 en fonction de Q2 pour le gel A1 et pour les
soustractions A2-A1 et A3-A1.
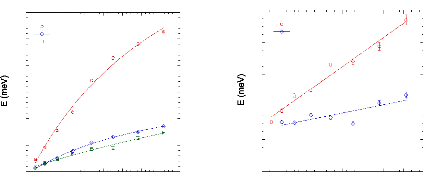
(a)
Lorentzienne "étroite" L1(W1,E)
1,2
0,8
(b)
Lorentzienne "large" L2(W2,E)
1,6
0,4
0
0,5
0,4
0,3
0,2
0,1
0
A1 A2-A1 A3-A1
A1
A3-A1
0 0,5 1 1,5 2 2,5 3 3,5 4 0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å1) Q2
(Å1)
Figure 54 : Largeur à mi-hauteur de la Lorentzienne
étroite W1(a) et de la Lorentzienne large W2 (b) ajustées aux
données des gels A1, A2 -A1 et A3 -A1. Les courbes représentent
les ajustements.

*Nous rappelons ici les expressions
paramétré es de W1 et W2:
1 ã 1 Q
W22 Q
2
2
2
1 Q
W112
Les ajustements présentés sur les figures 53 et 54
ont permis de déterminer les valeurs des paramètres
* regroupées
1 1 ã 1 et dans le tableau 26.
2 2

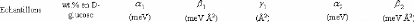
Tableau 26: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite W1 et pour la Lorentzienne large W2 à partir
des mesures réalisées sur le DCS à 300 K.
Comme pour les solutions massiques, les paramètres
d'ajustement nous permettent de calculer les constantes physiques qui
décrivent la dynamique des molécules de D-glucose. (Tableau
27)

Tableau 27: Constantes physiques calculées à
partir des ajustements de W1 et W2.
5.1.3.2. HFBS
En raison de la fenêtre spectrale plus réduite
(#177; 36 ?eV) dans le cas du HFBS, le meilleur ajustement des fonctions de
diffusion a été obtenu avec une fonction delta, une unique
fonction Lorentzienne et une ligne de base. Les largeurs à mi-hauteur de
la Lorentzienne pour les gels A2-A1 et A3-A1 sont présentées dans
la figure 55.
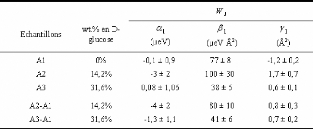
0,06
0,05
0,04
0,03
0,02
0,01
0
A2-A1
A3-A1
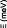
0 0,5 1 1,5 2 2,5 3
Q2 (ÅT2)
Figure 55: Largeur à mi-hauteur de la Lorentzienne
étroite W1pour les gels A2-A1 et A3-A1. Les courbes représentent
les ajustements.
Les paramètres des ajustements et les constantes physiques
qui en découlent sont répertoriés dans les tableaux 28 et
29.
Tableau 28: Valeurs des paramètres1,W1.
1 et ã1 pour la Lorentzienne étroite

Tableau 29: Constantes physiques calculées à
partir des ajustements de W1.
5.1.4. Discussion
5.1.4.1. Dynamique translationnelle
Ce qui frappe tout d'abord, c'est l'écart
d'intensité, qui existe entre les données du DCS et du HFBS, qui
est due aux grandes différences de résolution et de gammes
énergétiques des deux instruments. Néanmoins, dans les
deux cas, la valeur du coefficient de diffusion D est divisée par ~ 2
lorsque l'on passe d'une solution contenant 14wt.% de D-glucose (A2-A1)
à une solution à 30wt.% (A3-A1). Cette diminution ressemble
à celle observée dans le cas des solutions
volumiques.75 (Cf. chapitre 2)
Considérons maintenant l'effet du confinement,
c'est-à-dire les variations de la valeur du coefficient de diffusion D
engendrées par la réduction d'espace. Pour ce faire, il nous faut
comparer ces valeurs à celles trouvées
précédemment. Malheureusement, les mesures
précédentes, réalisées sur des solutions volumiques
de D-glucose ont toutes été menées à 280 K, au lieu
de 300 K. Cependant, il est possible d'estimer l'effet de ces 20 K sur la
dynamique moléculaire de trois manières:
(1) Dans leurs travaux par RMN sur une solution de glucose
à 40wt.%, Moran et al.77 trouvent une énergie
d'activation pour la diffusion des molécules de glucose de 27,8
kJ.mol-1, ce qui correspond à une augmentation d'un facteur
2,2 lorsque l'on passe de 280 à 300 K.
(2) Moran et al. ont également montré que les
énergies d'activation pour la diffusion des molécules d'eau et
des molécules de glucose sont très voisines. Il est alors
possible d'estimer la variation de D en utilisant l'énergie d'activation
pour la diffusion des molécules d'eau Ea = 15,5
kJ.mol-1 déterminée précédemment par
Talon et al.76 Ainsi, pour les solutions à 15 et 33wt.% en
sucre, nous trouvons une hausse proche de 1,6 lorsque la température
passe de 280 à 300 K.
(3) Nos mesures sur les solutions de D-fructose nous donnent
également une augmentation voisine de 1,6 - 1,7 entre 280 et 300 K selon
que l'on regarde la dynamique du solvant ou celle du soluté.
Tous ces résultats pris ensemble nous permettent
d'estimer à une valeur proche de 2 l'augmentation de la dynamique
moléculaire du D-glucose liée à la hausse en
température. Si l'on applique ce coefficient aux solutions volumiques
à 14wt.% et 33wt.% mesurées sur HFBS, nous trouvons que les
coefficients de diffusion de ces solutions valent respectivement 0,62 et
0,2× 10-5cm2.s-1 à T = 300 K. En
comparant ces valeurs à celles trouvées dans les gels (Tableau
29), nous trouvons qu'il n'y a pas de changements significatifs du coefficient
de diffusion des molécules de glucose.
De la même manière, la distance de saut effective
l, qui n'est pas ou peu dépendante de la concentration, présente
des valeurs de l'ordre de 1 à 2 Å, valeurs très similaires
à celles obtenues dans les travaux précédents.
5.1.4.2. Dynamique rotationelle
Pour l'échantillon A2-A1 sur le DCS, seul
échantillon pour lequel il a été possible de placer une
seconde fonction Lorentzienne durant l'ajustement, un temps de relaxation
rotationnel DR = 8,2 ps a été
obtenu. Si l'on compare cette valeur à DR ~ 9 ps
trouvée dans le cas d'une solution volumique à
33wt.%75, nous trouvons que la dynamique
rotationnelle, à son tour, n'est pas significativement affectée
par le confinement dans le gel.
5.1.5. Conclusion partielle sur la dynamique du D-glucose
sous confinement
L'étude des solutions aqueuses de D-glucose
confinées dans un gel de silice par diffusion quasi- élastique
des neutrons, nous a permis de démontrer que les dynamiques, aussi bien
translationnelle que rotationelle, du sucre présentent un comportement
similaire aux dynamiques observées en solution volumique. Cette
observation nous conduit à la conclusion que les dynamiques du sucre ne
sont pas significativement affectées par un confinement de 18 nm. Ce
résultat n'est cependant pas si surprenant si l'on considère la
taille du confinement. En effet, une molécule de D-glucose mesure en
moyenne un peu moins de 1 nm, il apparaît donc, que même avec
plusieurs couches de solvatation, la taille d'une molécule de ce
monosaccharide reste bien en deçà du diamètre moyen des
pores. C'est pour cette raison, et à la vue de ces résultats, que
nous nous sommes tournés vers un sucre de taille supérieure et
qui présente un fort intérêt dans le domaine de la
biopréservation : l'- tréhalose. (Figure 56)
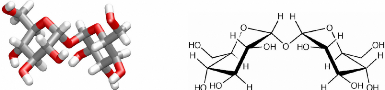
Figure 56: Molécule d' tréhalose et sa
représentation chaise-bateau. (les atomes de carbone,
d'hydrogène et d'oxygène sont respectivement
représentés en gris, rouge et blanc)
5.2. DYNAMIQUE DU TREHALOSE DANS LES GELS DE SILIC
Des gels de silice contenant des solutions d'- tréhalose
ont été préparés avec le même
protocole
expérimental que pour les gels précédents.
Nous avons choisi de n'étudier que la dynamique des
molécules
de tréhalose. Pour ce faire, nous avons procédé à
titre préventif à une deutération partielle

du tréhalose avec le même protocole que pour le
D-glucose. Le gel de silice renfermera donc une solution de tréhalose
partiellement deutéré (C12H14D8O11). Trois
concentrations ont été sélectionnées : 0, 14,2 et
31,6 wt.% en ne prenant en compte que l'eau et le tréhalose. Les trois
gels correspondants seront dénommés AT1 (Gel sans sucre), AT2
(gel + solution 1:55)* et enfin AT3 (gel + solution 1
:20)*.
5.2.1. Conditions expérimentales
Les expériences de QENS ont été
réalisées sur le spectromètre à
rétrodiffusion IRIS sur la source de spallation ISIS du
RAL.95 Les sols ont été placés dans des
porte-échantillons annulaires en aluminium présentant un espace
annulaire de 0,4mm. Après avoir été scellés
à l'indium, ils ont été positionnés dans un
cryostat dans lequel la température est régulée à
#177; 1 K.
Les mesures sur le spectromètre IRIS ont
été réalisées avec une longueur d'onde incidente de
6,7 ?, correspondant à un transfert de vecteur d'onde Q de 0,46 à
1,84 ?-1. Tous les échantillons ont été
mesurés à 300 K, à l'exception de l'échantillon
AT2, qui a été mesuré à 270, 300 et 330 K. Les
temps de comptage avoisinaient les 4 heures. (Tableau 30) La résolution
instrumentale a été trouvée égale à 17,5p,eV
à partir de la largeur à mi-hauteur du pic élastique du
vanadium (Les cristaux analyseurs étaient dans la configuration PG002,
c'est-à-dire dans le plan de réflexion 002 du graphite
pyrolitique).
Tableau 30 : Tableau récapitulatif des conditions
expérimentales pour les gels contenant des solutions de
tréhalose mesurés sur le spectromètre
IRIS.
5.2.2. Traitement des données
Le logiciel MODES96 a été
utilisé pour traiter les spectres obtenus. (normalisations, correction
de la cellule vide, regroupement). Pour de plus amples détails, nous
vous amenons à consulter le chapitre 2 à la page 40.
Comme dans le cas précédent, et afin d'extraire le
signal provenant des molécules de tréhalose, le gel sans sucre
AT1 a été soustrait des gels contenant du sucre (A2 et A3). Les
spectres résultants
* Le ratio correspond au nombre de molécules d'eau par
molécule de sucre - sucre: eau.
s'appelleront respectivement AT2-AT 1 et AT3-AT 1. Afin de
prendre en compte les différents facteurs d'atténuation du gel
pur (AT1) et des gels contenant du sucre (AT2 et AT3), la diffusion de AT1 a
été multipliée par le facteur d'atténuation du
tréhalose avant la soustraction. Encore une fois, cette démarche
repose sur l'hypothèse que l'effet du tréhalose sur la dynamique
de la matrice hôte est négligeable. (Tableau 31)
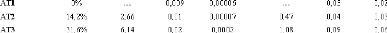
Tableau 31: Contributions relatives de la diffusion
cohérente et incohérente émanant du tréhalose, de
l'eau lourde et du gel.
5.2.3. Mesures
Les fonctions de diffusion des échantillons AT 1, AT2 et
AT3 à 300 K sont présentées sur la figure 57 pour une
valeur de Q = 0,71Å1.
Å1
Q = 0,71
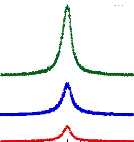
T = 300 K
AT3
AT2
ATI
-150 -100 -50 0 50 100 150
E (peV)
Figure 57: Fonctions de diffusion pour les échantillons
AT1 (rouge), AT2 (bleu) et AT3 (vert) tirées des mesures
réalisées sur le spectromètre IRIS à 300 K.
Les fonctions de diffusion S(Q, E) ont été
ajustées à l'aide de la combinaison de fonctions
théoriques suivantes convoluées avec la
résolution de l'instrument: une fonction delta, une ou deux fonctions
Lorentziennes .L?(Wn,E) suivant la concentration et la
température utilisée, et enfin une ligne de base. Les
informations sur la dynamique translationnelle ont été extraites
de la dépendance quadratique des Wn. Les valeurs des
paramètreset ã1 sont présentées dans le tableau
32.
1 1



Tableau 32: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite W1.
0.15
0.1
0.05
0
Les ajustements de la fonction Lorentzienne étroite
sont présentés sur la figure 58. L'effet de la concentration en
tréhalose sur la largeur à mi-hauteur W n est
clairement mis en évidence, et montre ainsi le ralentissement des
mouvements diffusifs des molécules de tréhalose.
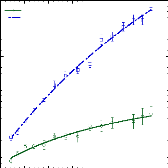
AT3 - AT1 - 30wt.% of trehalose
AT2 -AT1 - 14wt.% of
trehalose
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
Figure 58: Largeur à mi-hauteur de la Lorentzienne
étroite W1 ajustée aux données des soustractions A T2- AT1
etAT3-AT1. Les courbes représentent les ajustements.
Comme nous avons pu le voir dans les paragraphes et chapitres
précédents, les paramètres d'ajustement nous permettent de
remonter aux valeurs des différentes constantes physiques qui
caractérisent le système : le coefficient de diffusion D et la
longueur de saut effective l. Toutes ces constantes sont
répertoriées dans le tableau 33.
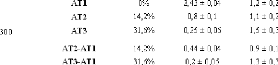

Tableau 33 : Constantes physiques calculées à
partir des ajustements de W1
5.2.4. Résultats et discussions
Tout d'abord, avant de passer à l'interprétation
des constantes physiques proprement dites, il est intéressant de jeter
un oeil sur les valeurs du paramètre d'ajustement 1
de l'échantillon AT2. Il apparaît que 1
présente une dépendance en température qui suit une loi
d'Arrhénius, comme en témoigne la figure 59. L'énergie
d'activation correspondante pour la diffusion translationnelle est de (17,5
#177; 1,7) kJ.mol-1, soit (4,2 #177; 0,4) kcal.mol-1.
Cette énergie est relativement proche de celles trouvées pour des
solutions de D-fructose ((4,0 #177; 0,4) kcal.mol-1) ou pour les
solutions de D-glucose ((3,6 #177; 0,2) kcal.mol-1).76 Ce
paramètre nous donne ainsi un aperçu de l'évolution de la
dynamique du tréhalose en fonction de la température, sans pour
autant être suffisant pour conclure de manière définitive
sur la molécule de sucre. En effet, les gels étant des
systèmes multicomposants, leur étude sans soustraction du gel AT1
ne peut être considérée que comme une approximation. Cette
valeur de l'énergie d'activation doit donc être maniée avec
précaution si l'on parle de la dynamique moléculaire du
tréhalose.
1
0,01
0,1
0,001
3 3,2 3,4 3,6 3,8
1000/T(K)
Figure 59 : Valeurs de 131
pour l'échantillon AT2 en fonction de 1000/T(K). La droite
représente l'ajustement de la loi d'Arrhénius aux
données.

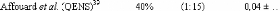
Dtrehalose.
Considérons les valeurs des coefficients de diffusion des
molécules de tréhalose A 300
K, le coefficient de diffusion translationnel diminue d'un
facteur 2 lorsque la concentration passe de
Dtrehalose
14,2 à 31,6wt.%. passe ainsi de 0,42×10-5
à 0,2×10-5 cm2.s-1. Cet
abaissement d'un facteur 2
coïncide avec des travaux réalisés sur des
solutions volumiques de tréhalose.40,62-70,132 Le tableau 34
répertorie tous ces résultats.

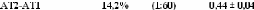
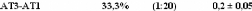
Tableau 34: Comparatif des coefficients de diffusion du
tréhalose confiné (en gras) avec ceux trouvés dans la
littérature.
Si l'on compare nos valeurs avec celles dans la
littérature, nous trouvons qu'il n'existe pas de changements
marqués du coefficient de diffusion translationnelle pour un confinement
estimé à une vingtaine de nanomètres. Ces résultats
viennent d'être très récemment corroborés par des
simulations de dynamique moléculaire réalisées par Drs A.
Lerbret et J.W. Brady de l'Université de Cornell.133
Ce résultat montre qu'un confinement de 20 nm ne semble
pas être suffisant pour affecter de manière significative la
dynamique du tréhalose. Le diamètre moyen des pores est
vraisemblablement trop important. En effet, si l'on ajoute à une
molécule de tréhalose une sphère d'hydratation, son
diamètre moyen atteindra 12-13 Å, une valeur quinze fois
inférieure à la porosité moyenne. Sachant que
l'épaisseur d'une sphère d'hydratation n'est en moyenne que de
5-8 Å, et qu'en milieu dilué, le nombre de sphères atteint
facilement le nombre de 3, une molécule de tréhalose
hydratée mesurera donc au maximum entre 2 et 3 nm, une valeur bien
inférieure au diamètre des pores. Par voie de conséquence,
la dynamique du sucre ne sera que très faiblement affectée par un
tel confinement. Il est intéressant de noter également que cette
conservation de la dynamique implique donc des interactions silice-sucre
relativement faibles, voire négligeables.
5.2.5. Conclusion partielle pour la dynamique du
tréhalose confiné
L'étude des solutions aqueuses d' tréhalose
confinées dans un gel de silice par diffusion
quasi-élastique des neutrons, nous a permis de
démontrer que la dynamique translationnelle du disaccharide
présente un comportement similaire aux dynamiques observées en
solution volumique. Cette observation nous conduit à la conclusion que
les dynamiques du tréhalose, bien que de taille supérieure au
glucose, ne sont pas significativement affectées par un confinement de
18 nm.
5.3. CONCLUSION GENERALE DU CHAPITRE 5
Nous pouvons résumer ci-dessous les résultats et
les principales conclusions obtenus pour des solutions confinées de
D-glucose et d' tréhalose par diffusion quasi-élastique des
neutrons :
La dynamique translationnelle du monosaccharide et du
disaccharide est ralentie par l'augmentation en concentration du sucre
Pour les gels de silice aqueux contenant une solution D-glucose
allant de 14 à 33 wt.% :
- la dynamique translationnelle du sucre est divisée par 2
comme dans les solutions volumiques
- la dynamique du sucre n'est pas significativement
différente de celle existante dans une solution volumique de même
concentration
Pour les gels de silice aqueux contenant une
solution a--a tréhalose allant de 14 à
33 wt. % :
- la dynamique translationnelle du sucre est divisée par
~ 2,2
- la dynamique du sucre n'est pas significativement
différente de celle existante dans une solution volumique de même
concentration
- la dynamique translationnelle du gel AT2 présente une
dépendance en température qui suit une loi de type
Arrhénius
Le tableau 35 liste toutes les valeurs numériques des
constantes physiques obtenues pour le D-glucose et l' tréhalose
confinés dans un gel de silice aqueux.

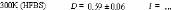
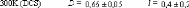

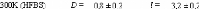
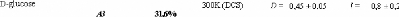
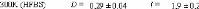
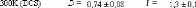

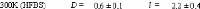
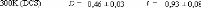

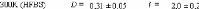
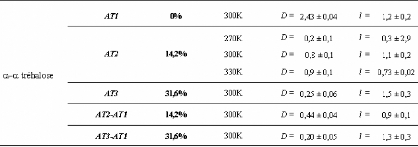
Tableau 35: Récapitulatif des différentes
constantes déterminées dans ce chapitre pour les gels de silice
contenant des solutions de D-glucose ou de l'tréhalose
Ces valeurs du coefficient de diffusion des molécules
de sucre sous confinement sont les toutes premières en la
matière, et bien que surprenantes, ces valeurs de D fournissent des
informations essentielles pour l'étude des systèmes
protéine-eau-sucre, pour lesquels les molécules de sucre à
la surface des protéines sont considérées comme
confinées. Ces premiers résultats donnent donc une limite
supérieure en deçà de laquelle nous pouvons espérer
observer un quelconque effet de confinement. Mais pour ce faire, il est
absolument nécessaire de réduire la taille des pores de la
matrice hôte vers l'échelle moléculaire. C'est ce que nous
allons chercher à faire dans les chapitres suivants, qui traiteront de
la synthèse de la matrice hôte, et des premiers résultats
émanant des mesures de QENS réalisées sur ces
systèmes.
-130-
Chapitre 6
SYNTHESE DE NANOSPHERES DE SILICE DE TYPE MCM-41
6.1. Etatde l'art 133
6.2. Sphères mésoporeuses 137
6.2.1.
Synthèse
6.2.2. Caractérisations
6.3. Discussion sur le mécanisme de formation 151
6.4. Conclusion générale du chapitre 6 152
CHAPITRE 6
SYNTHESE DE NANOSPHERES DE SILICE DE TYPE MCM-41
Les gels de silice sont une matrice hôte tout à
fait bien adaptée au confinement des solutions de sucre. Cependant, il
reste que le diamètre moyen des pores proposé par ces gels ne
permet pas de réduire de manière significative la dynamique
moléculaire des sucres. En modifiant les conditions de synthèse,
il est possible de réduire la taille des pores, mais en contrepartie la
diminution du ratio H2O/TEOS génère une quantité beaucoup
trop importante d'alcool, rendant difficile la dissolution du sucre. C'est pour
toutes ces raisons, que nous avons du abandonner ces gels au profit des
matériaux inorganiques organisés, qui présentent
l'énorme avantage de proposer une grande variété de
diamètres de pores. Il nous faut donc synthétiser un
matériau mésoporeux adapté à nos contraintes
instrumentales et qui permet de répondre à nos impératifs
de concentration. La famille des M41S, et plus particulièrement le
sous-groupe des MCM-41, répond à nos attentes par les tailles de
pore accessibles d'une part, et aux impératifs liés aux mesures
de diffusion de neutrons d'autre part (transparence, volume
d'échantillon, nombre limité de protons, ...). La silice
mésoporeuse conventionnelle s'étend sur de grands domaines et
présente par conséquent des longueurs de pores beaucoup trop
importantes pour espérer confiner une solution de sucre sans gradient de
concentration. C'est en partie pour cette raison, que nous avons
synthétisé des nanosphères de silice avec une
mésoporosité de type MCM-41, mais présentant une longueur
de pore acceptable. Ce chapitre traitera donc de la synthèse et de la
caractérisation de ces nanosphères de silice mésoporeuse,
précédé d'un court état de l'art sur les
matériaux mésoporeux de type MCM-41.
6.1. ETAT DE L'ART
Ce petit état de l'art non exhaustif sur la
synthèse des matériaux mésoporeux et plus
particulièrement sur celle des sphères de silice
mésoporeuses nous donnera un aperçu des techniques de
synthèse utilisées et des mécanismes mis en jeu.
6.1.1. Historique
Au début des années 90 au Japon, Kuroda et son
équipe ont développé des complexes d'intercalation
argile-alkylammonium, qui ont été soumis à
différents traitements hydrothermaux, puis calcinés. Le
matériau final, dit FSM 16, se présente sous la forme d'une
poudre très poreuse et avec une organisation des pores en nid
d'abeille.134,135 En parallèle de ces recherches, le groupe
Mobil a développé toute une série de nouveaux
matériaux poreux, regroupés sous le nom générique
de M41 S,136,137 et dont les méthodes de synthèse ont
fait l'objet de différents brevets publiés en 1991 et
1992.138,139,140 Il est assez intéressant de constater que ces deux
matériaux, japonais et américain, présentent de fortes
ressemblances. De manière assez surprenante, Chiola et al.141
ont décrit, dans un
brevet américain de 1971, la synthèse d'une
silice de faible densité basée sur l'hydrolyse et la condensation
d'un précurseur de silice en présence d'un tensio-actif
cationique. Les propriétés mésoporeuses tout à fait
uniques de ce matériau sont restées méconnues jusqu'en
1997 lorsque Di Renzo et al.,142 en reproduisant les
expériences décrites dans le brevet, ont démontré
que le produit final présente toutes les caractéristiques et
propriétés des MCM-41. Même si la paternité de cette
découverte semble être remise en cause par ces travaux
récents, il apparaît néanmoins que les nombreuses
découvertes de Mobil ont donné un remarquable essor à
cette branche de la chimie des
matériaux.143,144,145,146,147,148
6.1.2. La famille M41S
La famille des M41S est divisée en 4 sous-groupes
représentés schématiquement dans la figure 60. Le premier
d'entre eux se rapporte à des bâtonnets
désordonnés*, tandis que les trois autres
correspondent à des mésostructures bien définies : (i) les
MCM-41 avec leur arrangement hexagonal de pores unidirectionnels et
non-interconnectés, (ii) les MCM-48 avec une structure cubique
tridimensionnelle, (iii) les MCM-50 avec leur structure lamellaire instable.
Les MCM-41 sont très utilisés en raison de leur unique
architecture qui fait d'eux un matériau mésoporeux modèle
pour l'étude de molécules ou de fluides confinés.
Bâtonnets désordonnés MCM-41 MCM-48 MCM-50
Figure 60 : Les quatres phases principales formées
à partir du C16TMA/SiO2/H2O149
6.1.3. Principes de la synthèse
Une synthèse typique de MCM-41 requiert au minimum
quatre réactifs principaux : un solvant (eau et/ou éthanol), un
précurseur de silice, une molécule « template » et un
catalyseur. Une méthode générale de synthèse
consiste à dissoudre la molécule « template » dans le
solvant, puis à ajouter le précurseur de silice. Après une
période d'agitation à une température
déterminée pour permettre l'hydrolyse et la
précondensation, la température est ensuite remontée pour
favoriser le processus de condensation. Le produit est ensuite lavé,
séché, et les molécules organiques éliminées
par une méthode d'extraction ou par calcination.
* En anglais, « rod »
Les méthodes de synthèse sont, pour la plupart,
basées sur l'ajout de molécules organiques dites «template
». Le précurseur inorganique ajouté au mélange
viendra alors s'organiser autour des structures formées par ces
molécules, générant ainsi la mésostructure du
matériau.150 Ces molécules « template » sont
des molécules organiques amphiphiles composées d'une tête
hydrophile (ionique ou non-ionique) et d'une queue hydrophobe, et ont la
particularité de s'agréger entre elles pour former des structures
tridimensionnelles organisées. Prenons l'exemple des
alkyltrimethylammonium bromides ((CnH2n+1)(CH3)3NBr, CTMABr), qui
sont utilisées de manière très fréquente dans la
synthèse des matériaux de la famille des M41S. (Figure 61)
Au-delà de la concentration micellaire critique (CMC 1), les
molécules de CTMABr s'assemblent pour former des phases micellaires
isotropes. Lorsque la concentration augmente, les structures hexagonales
apparaissent (CMC 2), puis, avec la coalescence des cylindres, il y a formation
d'une phase lamellaire, et dans certaines conditions, d'une phase cubique
intermédiaire. L'ordre et les structures formées par les
molécules dépendent des interactions au sein de la
molécule, mais également avec le solvant.
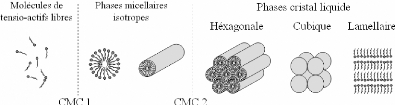
Figure 61: Evolution de l'organisation des molécules de
tensioactifpour des concentrations croissantes.151
D'une manière générale, une bonne
connaissance des paramètres ajustables (tensioactif, pH, concentration,
précurseur de silice, solvant, température, ...) et des chemins
réactionnels permettent de contrôler assez finement la forme
globale, mais également la structure interne et la taille des
pores.152,153,154
6.1.4. Mécanismes de formation
Différents mécanismes de formation permettent
d'accéder à des matériaux mésoporeux de type MCM-41
: le liquid crystal templating (LCT), l'auto-assemblage et l'auto-assemblage
coopératif.
6.1.4.1. Liquid crystal templating
La formation de la structure est basée sur le
mécanisme LCT proposé par Kresge et al.136 , dans
lequel une espèce organique s'organise pour former une structure
centrale entourée d'une ou plusieurs couches d'oxydes
inorganiques.155,156 Comme l'illustre la figure 62, les
molécules de tensioactif s'organisent en micelles pour former une phase
cristal-liquide (1), la tête hydrophile du tensioactif se
placant à la surface externe des micelles. Les produits
de l'hydrolyse du précurseur vont alors interagir avec les têtes
polaires des micelles et se condenser autour du cristal-liquide (2). Le
matériau obtenu après calcination est la réplique inverse
du cristal-liquide (3).

Figure 62 : Mécanisme LCTproposé par Kresge et
al.136
6.1.4.2. Auto-assemblage
Le phénomène d'auto-assemblage, quant à
lui, se produit lorsque les concentrations en tensioactifs présents dans
le mélange sont inférieures à celles utilisées dans
le mécanisme LCT, et notamment à la concentration micellaire
critique (CMC 2). Ainsi, seules des micelles isolées et
dispersées sont présentes dans le milieu réactionnel (1).
Quelques couches de silice vont alors se déposer sur ces micelles
isolées après l'ajout du précurseur inorganique (2). La
condensation de la phase siliceuse résultera de l'agrégation de
ces cylindres (3), et donnera naissance à un matériau
mésoporeux présentant une taille de pore régulière
(4). (Figure 63)
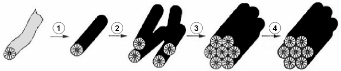
Figure 63 : Représentation schématique du
processus d'auto-assemblage.
6.1.4.3. Auto-assemblage coopératif
Ce mécanisme se met en place lorsque la concentration
en tensioactif est faible comparée aux deux mécanismes
précédents (< CMC 1). Dans ce cas, aucune micelle cylindrique
n'est présente dans le milieu. La condensation de la phase
silicatée induit alors la formation et l'agrégation des micelles.
Le processus d'assemblage des molécules de tensioactif est piloté
par la densité de charge présente à l'interface entre la
phase organique et la phase inorganique. Les ions silicatés
chargés se compensent alors avec les têtes chargées des
molécules de tensioactif. Avec la condensation de la silice, la
densité de charge diminue, et fait augmenter la surface par tête
polaire, conduisant à un réarrangement des charges pour respecter
l'électroneutralité. Ces changements entraînent une
augmentation de la courbure de la phase organique, produisant ainsi une
mésostructure similaire à celle obtenue avec le mécanisme
d'auto-assemblage.
6.2. SPHERES MESOPOREUSES
A la suite de la découverte des matériaux
mésoporeux, la synthèse d'objets présentant une structure
hiérarchiquement ordonnée et une forme choisie a
nécessité de gros efforts fondamentaux et expérimentaux.
Le contrôle simultané de la morphologie et de la texture est un
véritable défi dans la synthèse des particules
mésoporeuses de type M41S.157158 "159 "160 161 ,162
Grün et al., en adaptant la non moins fameuse
synthèse de Stöber163, ont démontré la
faisabilité de synthétiser des particules sphériques de
type MCM-41 en milieu basique.164 Le TEOS*,
fraîchement distillé est ajouté à une solution
alcoolique de tensioactif dilué et d'ammoniaque. Le solide obtenu est
calciné à 550°C à l'air pour produire le
matériau mésoporeux, et présente les pics de diffraction
caractéristiques des MCM-41, et un isotherme d'absorption de type
IV.165 Depuis lors, différentes voies, basées sur une
procédure où le TEOS est utilisé comme précurseur
de silice, le CTMABr comme tensioactif, l'alcool comme solvant et l'ammoniaque
comme catalyseur, ont été utilisées pour produire des
sphères de silice mésoporeuses.166 ,167 ,168 ,169
,170Notons que des sphères de silice peuvent également
être obtenues en milieu acide en remplaçant l'ammoniaque par
l'acide chlorhydrique.171
Différentes morphologies et textures peuvent être
obtenues en faisant varier la quantité de tensioactif et de solvant. Huo
et al. 172 ont ainsi fabriqué des sphères d'un
diamètre de 1 mm en utilisant la chimie des émulsions
biphasiques. En milieu basique, le butyl alcool (BuOH), qui est le produit de
l'hydrolyse du TBOS**, est immiscible dans l'eau. L'émulsion
de type huile dans l'eau, qui s'est formée dès les
premières étapes de la réaction, contient du BuOH (phase
aqueuse) et les résidus partiellement hydrolysés du TBOS (phase
huile). Le tensioactif joue un rôle très important dans la
stabilisation de l'émulsion. Les liaisons hydrogène entre le BuOH
et les molécules d'eau fournissent un chemin de diffusion aux
molécules d'eau et de tensioactif pour pénétrer dans les
goutellettes de TBOS/BuOH, et permettent l'hydrolyse du TBOS. Le silicate
polymérise alors sous l'influence du tensioactif qui dirige l'assemblage
et le transforme en sphères solides. Très récemment, les
processus de formation de ces sphères ont été
étudiés173 : les goutelettes d'eau dans le TBOS ont
été trouvées connectées les unes aux autres,
formant une nanostructure organisée grâce à
l'auto-assemblage du tensioactif.
L'effet de l'alcool sur la morphologie des sphères a
également été examiné en
détail.174,175,176 L'augmentation de la concentration en
éthanol dans le système TEOS-CTMABr-ammonique-eau à la
température ambiante conduit à la formation d'une succession de
mésophases dans l'ordre MCM-41
* TEOS = tétraéthylorthosilicate ** TBOS =
tétrabutylorthosilicate
(hexagonal), MCM-48 (cubique) et MCM-50 (lamellaire). Pour
expliquer une telle succession de phases, il a été postulé
que l'éthanol jouait le rôle d'un co-tensioactif. A faible
concentration en alcool, les structures ne sont pas ou que très
faiblement sphériques. Quand la concentration augmente, l'éthanol
va alors agir comme un co-solvant et former des particules sphériques.
Il a alors été suggéré que l'augmentation de la
quantité d'alcool modifie le paramètre d'arrangement du
tensioactif g177,178 donné par :
V
g a0l
où V est le volume total des chaînes de
tensioactif plus les molécules de co-solvant entre les chaînes, a0
la surface effective du groupement de tête à l'interface
organique-inorganique, et l la longueur de la chaîne du tensioactif.
Le paramètre g dirige la configuration de la phase
pendant la synthèse. Des petites valeurs de g stabilisent des surfaces
plutôt courbées tels que les MCM-41 (1/3 < g < 1/2), tandis
que les plus grandes valeurs stabilisent des structures présentant moins
de courbure comme les MCM-48 (1/2 <g < 2/3).
Une autre méthode pour synthétiser des
sphères mésoporeuses est d'utiliser la technique de
pulvérisation-séchage.* Après que Lu et
al.179 aient démontré la faisabilité de la
méthode, de récents travaux180,181,182,183 montrent que le
procédé d'auto-assemblage induit par évaporation
(EISA)184,185 peut donner naissance à des sphères de
silice mésoporeuses. Un sol, composé généralement
d'un précurseur de silice (TEOS), d'un tensioactif cationique (CTMABr)
et/ou d'un copolymère à blocs (PEO-PPO-PEO), un solvant
(iPrOH, éthanol) et de l'eau en milieu acide est
atomisé dans une chambre de séchage. Récemment, Alonso et
al.186 ont proposé un schéma pour la formation de ces
sphères à partir de l'atomisation d'un sol alcoolique. En
utilisant la RMN du solide du 29Si et du 1H, ils ont
ainsi pu déterminer que le mécanisme de formation se compose tout
d'abord d'une fragmentation des gouttelettes causé par
l'évaporation rapide du solvant, suivi des processus d'agrégation
et d'auto-assemblage des molécules de tensioactif avec les
oxo-oligomères. La mésophase résultante se propage alors
dans la particule pour former une texture ordonnée.
6.2.1. Synthèse
Réactifs utilisés
Cette synthèse, inspirée des travaux de
Grün et al.167 , a nécessité les produits
chimiques suivants : du tétraethylorthosilicate Si(OC2H5)4 (TEOS, 99%)
comme source de silice, le cethyltrimethylammonium bromide (CTMABr, 99%) comme
tensioactif cationique et du NH3 aqueux (reagent grade, 30wt.%) comme
catalyseur. Tous ces produits ont été utilisés sans
purification supplémentaire.
*
pulvérisation-séchage = spray-drying
-I-
m
eau
mC16TMABr
chantillons
Cinq échantillons ont été
préparés avec des concentrations en CTMABr allant de 0,1%
à 5% massique.* Les différents ratios molaires sont
présentés dans le tableau 36.

Tableau 36 : Conditions de synthèse des
différents MCM-41. (Ratios molaires)
Procédure
Tous les échantillons répertoriés
ci-dessus ont été synthétisés dans les mêmes
conditions, seule la concentration en tensioactif variait. Nous ne
détaillerons donc qu'une seule de ces synthèses.
L'échantillon MCM-0,1% a été préparé de la
manière suivante : 0,025 g de CTMABr a été dissout dans 25
mL d'eau distillée sous agitation (~ 400 rpm) à 60°C. Une
fois que la solution est redevenue transparente, c-à-d quasi
immédiatement pour cette concentration, 1,56 g de NH4OH sont
ajoutés. Après quelques minutes, la température est alors
remontée à 80-90°C, et 2,08 g de TEOS sont alors
ajoutés goutte à goutte. La solution prend alors un aspect
laiteux. Après 1h d'agitation, le produit est alors placé en
autoclave statique pendant une nuit, filtré, rincé à
l'eau, séché à 100°C et enfin calciné à
550°C pendant 3 heures à l'air.
6.2.2. Caractérisations
6.2.2.1. Microscopie électronique en
transmission
Les différents échantillons de silice
mésoporeuse ont été caractérisés par
microscopie électronique en transmission (MET), sur un microscope
Philips CM20 à une tension de 200 kV. Les poudres placées dans
l'éthanol absolu ont été déposées sur des
grilles en cuivre recouvertes d'une membrane à lacets de carbone.
* Les pourcentages massiques ont été
calculés à partir de la masse d'eau et de la masse de CTMABr
utilisés:
Les clichés MET de la figure 65, pris à
différents grandissements, montrent l'évolution de la morphologie
et de la texture en fonction de la concentration en CTMABr.
Pour une concentration massique en CTMABr de 5%, la silice
présente une forte porosité de type «worm»
non-organisée. En abaissant la concentration à 2,3%, nous
retombons alors sur des grands domaines constitués de pores cylindriques
(Ø ~ 3 nm) organisés en nid d'abeille tout à fait typiques
des échantillons de MCM-41.167 Pour des concentrations plus
faibles encore, les grands domaines disparaissent au profit de particules au
diamètre plus petit et aux formes beaucoup plus arrondies. Les pores,
qui ont conservé leurs dimensions, présentent une
légère courbure dans leur longueur. Vers 0,5%, les particules
prennent alors une forme sphérique avec des diamètres plus ou
moins variables pouvant aller de 80 à 200 nm. Un comptage statistique
sur plusieurs dizaines de particules a été réalisé
sur ces clichés MET, et la distribution en taille obtenue a
été ajustée à l'aide d'une fonction gaussienne
centrée sur 139 nm avec une largeur à mi-hauteur de 35 nm.
(Figure 64) Lorsque l'on diminue la concentration à 0,1%, c-à-d
pour une valeur proche de la CMC 1 du CTMABr, les sphères
présentent alors un diamètre moyen plus petit (~ 125 nm), et une
dispersion en taille de type gaussienne relativement faible (largeur à
mi-hauteur ~ 20 nm). (Figure 64) L'échantillon devient donc beaucoup
plus homogène du point de vue de la morphologie. La structure interne,
quant à elle, est composée de pores cylindriques
non-courbés, dont l'organisation en nid d'abeille est tout à fait
remarquable. Notons également qu'une gangue de silice amorphe semble
recouvrir la surface de ces billes.
D/nm D/nm
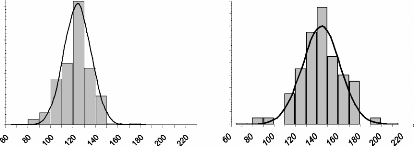
MCM-O,1 %
MCM-O,5 %
Figure 64: Dispersion en taille des échantillons MCM-0,1 %
et MCM-0,5%. Les lignes noires représentent les ajustements.
Dans la suite de cette étude, nous nous
intéresserons principalement aux particules présentant une
géométrie sphérique.
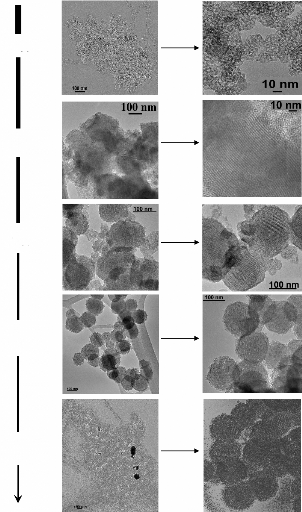
5%
2,3%
1%
0,5%
0,1%
Figure 65: Clichés MET de la silice montrant
l'évolution de la morphologie et de la structure en fonction de la
concentration en CTMABr.
6.2.2.2. Microscopie électronique à
balayage
La microscopie électronique à balayage (MEB) a
été réalisée sur un microscope Hitachi S4500
à effet de champ. Les échantillons ont été
déposés sur un adhésif en carbone, puis recouverts d'un
film d'or ou de carbone d'épaisseur 5 nm. Le MEB nous permet de
caractériser, à une tout autre échelle et en volume, la
forme et la taille des particules. Les micrographies présentées
dans la figure 66 présentent des particules sphériques d'un
diamètre moyen inférieur à 150 nm dans le cas des MCM0,1%
et inférieur à 200 nm dans le cas des MCM-0,5%. Le
diamètre des sphères est assez homodisperse en taille, ce qui
corrobore ainsi nos observations effectuées par MET. Nous pouvons
remarquer également, que les micrographies MEB, qui sondent une plus
grande quantité de matière que le MET, sont composées dans
leur grande majorité de sphères.
MCM-0,1% MCM-0,5%

Figure 66: Clichés MEB représentatifs des
échantillons MCM-0,1% (Echelle 200 nm) et MCM-0,5% (Echelle 1um).
6.2.2.3. Diffraction des rayons X
Afin de déterminer la structure interne de nos silices,
nous avons mesurés ces poudres sur un diffractomètre de poudres
Philips, Cu K, = 0,154 nm, permettant des mesures entre 1° et 30° (en
2è) avec un pas de 0,02° et un temps de comptage par point
de 20 s. Les diffractogrammes des échantillons MCM-0,1% et MCM-0,5% sont
montrés dans la figure 67. Les deux échantillons
présentent trois pics de Bragg distincts dans la région des
petits angles, correspondant aux plans (100), (110) et (200) d'un arrangement
hexagonal des pores. Nos deux silices présentent donc une structure de
type MCM-41, ce qui corrobore parfaitement nos observations par MET. La seule
différence notable se situe dans la position des pics de Bragg qui
diffèrent légèrement. En effet, les pics de
l'échantillon MCM-0,5% sont décalés vers les plus grands
angles de 0,06° par rapport à MCM-0,1%, ce qui traduit un
resserrement des pores. Nous pouvons noter également que
l'intensité du pic (100) diminue avec la concentration, ce qui implique
une plus grande cristallinité de MCM-0,1%.
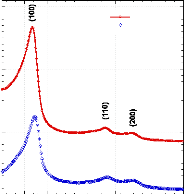
M CM-0,1%
MCM -0,5%
1500
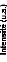
1000
500
0
1.5 2 2.5 3 3.5 4 4.5 5 5.5
2è (°)
Figure 67: Diffractogrammes sur poudre des échantillons
MCM-0,1% (cercles) et MCM-0,5% (carrés). Les valeurs entre
parenthèses correspondent aux indexations des pics.
La longueur de corrélation a0 entre deux milieux de pores
successifs dans les MCM-41 peut être calculée à partir de
l'équation suivante:
a0(2 3)d100
La position des pics en 2è, les distances d
équivalentes calculées à partir de la relation de Bragg
ainsi que les valeurs de a0 sont présentées dans le tableau
37.



Tableau 37: Récapitulatif des positions des pics de Bragg
et des distances interréticulaires d correspondantes pour les
échantillons MCM-0,1 % et MCM-0,5%.
6.2.2.4. Diffusion des neutrons aux petits angles
La diffusion des neutrons aux petits angles a également
été utilisée afin de déterminer la microstructure
interne, ainsi que la morphologie des particules.187,188,189 Les
expériences ont été menées sur les
spectromètres NG-3 et NG-7129 au NIST Center for Neutron
Research à une longueur
d'onde incidente de 6 Å. Afin de couvrir une grande
gamme de Q comprise entre 0,0035 et 0,47 Å-1, trois distances
échantillon-détecteur de 1,3, 4 et 13 m ont été
utilisées séquentiellement. Cette technique présente le
grand avantage d'être non-destructrice, mais surtout de sonder une
très importante quantité de matière, donnant ainsi une
vraie image de l'échantillon dans sa globalité. La fonction de
diffusion de l'échantillon MCM-0,1% est présentée dans la
figure 68.
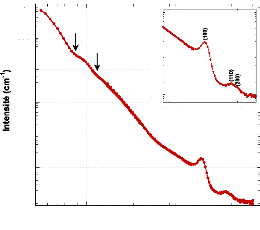
1 04
1
1000
0.1
100
0.01
10
0.06 0.08 0.1 0.3
1
0.1
0.01
0.01 0.1
Q(A~1)
Figure 68: Spectre SANS de l'échantillon MCM-0,1 %.
L'encart représente un agrandissement de la zone des pics de Bragg
à grands Q correspondant à un arrangement hexagonal des pores.
Une étude minutieuse du spectre montre des
détails qui corroborent nos clichés MET et nos mesures de DRX.
Dans la région des petites valeurs de Q, c-à-d jusqu'à
0,08 Å-1, la fonction de diffusion présente deux minima
indiqués par des flèches à Q = 0,0075 Å-1
et à Q = 0,0 12 Å-1. La présence même de
ces oscillations, qui est liée à la présence d'objets
sphériques, témoigne de la faible dispersion en taille de nos
particules. Dans la région des relativement grandes valeurs de Q, trois
pics sont clairement visibles à Q = 0,15, 0,26 et 0,3
Å-1. A titre de comparaison, les pics de Bragg, obtenus en
DRX, apparaissaient pour des angles de 2,17°, 3,77° et 4,35°, ce
qui correspond à des valeurs de Q de 0,154, 0,268 et 0,309
Å-1 respectivement. Ces pics sont donc attribuables aux plans
(100), (110) et (200) d'un arrangement hexagonal des pores.190,191
Le SANS, qui présente une résolution plus limitée que les
rayons X pour ce type d'échantillon, ne permet pas de définir
avec précision les positions des pics de Bragg, et il est alors
difficile de conclure sur le déplacement du pic (100) avec la
concentration. Signalons, que la fonction de diffusion de l'échantillon
MCM-0,5%, qui n'est pas montrée ici, présente également
trois pics de Bragg, mais les oscillations à petits Q n'apparaissent pas
ou que très faiblement, prouvant ainsi la moins bonne dispersion en
taille de l'échantillon.
A la vue des différentes formes (billes, cylindres), du
nombre de longueurs de corrélation différentes mises en jeu, et
de l'organisation tridimensionnelle des pores (Figure 69), un ajustement global
de la fonction de diffusion sur une grande gamme de Q est assez
compliqué à réaliser. Néanmoins en superposant les
facteurs de forme des différents objets formant la structure, il est
possible d'en déduire de nombreuses informations structurales.

Figure 69: Cliché MET des nanosphères (MCM-0,1%).
Ces deux sphères montrent la longueur des pores cylindriques (~ 120 nm)
et leur arrangement hexagonal.
Les facteurs de forme ont été calculés de la
manière la plus simple qu'il soit, c'est-à-dire dans le cas de
sphères et de cylindres «idéaux », homodisperses en
taille et non-interagissant.
- Le facteur de forme d'une sphère de rayon r est
donné par l'équation suivante118,192:
2
sin( ) cos( )
Qr Qr Qr
P Q v
( ) 9( ) 2 2
ñ C te
sphères sphère ( ) 3
Qr

2
- Le facteur de forme des cylindres de rayon r et de longueur 2H
est donné par la relation192:
2
te
1 ( sin )
J Qr
( ) 2( ) ( cos ) sin
1
P Q v j QH
ñ d C
cylindres cyl 0
v ( sin )
Qr
cyl 0
dans lesquelles vsphere et vcyl sont les volumes
des particules sphériques et cylindriques,
(ñ)2 le contraste, J1(x) la fonction de Bessel au
premier ordre,l'angle entre l'axe du cylindre et le vecteur de diffusion
Q*, et Cte le background incohérent.
Les clichés MET nous permettent donc de calculer
effectivement ces facteurs pour des sphères d'un
rayon de 60nm, et
pour des cylindres d'un rayon de 1,7 nm et de longueur 120 nm. Les pics de
Bragg
ont été simulés grâce à des
fonctions gaussiennes G(Q,) centrées sur 0,15 Å-1, 0,26
Å-1 et 0,3 Å-1, et
* L'intégrale surmoyenne ainsi le facteur de forme sur
toutes les orientations du cylindre.
ce d'après les mesures de DRX. La fonction de diffusion
de l'échantillon MCM-0,1%, les facteurs de forme des cylindres et des
sphères, ainsi que les trois pics de Bragg correspondant à la
structure tridimensionnelle des pores sont présentés sur la
figure 70(a).
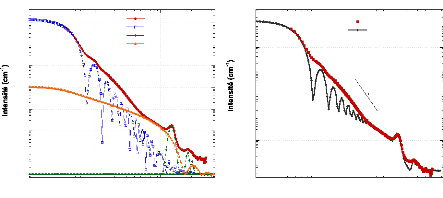
(a)
(b)
0.001
0.001 0.01 0.1
CI (A-1)
0.001 0.01 0.1
CI (A-1)
MCM-0,1%
FF Sphères
FS (Pics de Bragg) FF Cylindres
1000
104
Ajustement (Total)
MCM-0,1%
100
100
10
10
CI-4
1
1
0.1
0.1
0.01
0.01
104
1000
Figure 70 : Ajustement des différents facteurs de forme
des sphères, des cylindres et des pics de Bragg au spectre
expérimental (a). La figure (b) présente l'intensité
totale de toutes ces contributions comparée à celle de
l'échantillon MCM-0,1%.
Facteur de forme des sphères
Il apparaît très clairement que la
première partie du spectre (Q < 0,03 Å1) concerne
principalement les plus gros objets, en l'occurrence les sphères dans
leur globalité. Nous remarquons que les deux premiers minima
coïncident avec les oscillations visibles du spectre expérimental.
Le fait que ces oscillations ne soient pas plus marquées provient du
fait que les particules, bien que très régulières, ne
présentent pas une dispersion en taille idéale. Ainsi, la
dispersion en taille va se traduire par un lissage du spectre.
Néanmoins, cette valeur du diamètre (120 nm) est bien plus
représentative de l'échantillon que les images MET puisqu'elle
constitue une moyenne sur plusieurs centaines de milliards de particules,
prouvant ainsi la validité et la grande qualité de la
synthèse.
Facteur de forme des cylindres
Le facteur de forme des cylindres semble influencer le spectre
dans la région des moyennes et grandes valeurs de Q (0,03 < Q <
0,3 Å1). Il faut noter que l'utilisation de cylindres
identiques n'est pas tout à fait exacte. En fait, les cylindres ont des
longueurs variables pour pouvoir former un objet sphérique.
Néanmoins, l'approximation d'une longueur de cylindre fixe n'est
cependant pas si fausse à la vue du peu d'influence que peut avoir la
longueur L sur le facteur de forme P(Q).
Pics de Bragg
Les pics de Bragg, déterminés par rayons X,
coïncident parfaitement avec ceux présents sur le spectre SANS. Les
deux techniques nous donnent donc des résultats en bonne
adéquation.
Résultante
L'intensité résultante I(Q) est le produit du
facteur de forme P(Q) par le facteur de structure S(Q) :
I(Q) = P(Q)S(Q)
Or, les différentes formes en présence dans
l'échantillon, c-à-d des sphères et des cylindres, se
situent dans des échelles de longueur assez différentes. Le
facteur de forme des cylindres n'intervient vraiment que dans le Porod du
facteur de forme des sphères. Ce décalage nous permet alors
d'approximer le produit des facteurs de forme à une addition.
L'équation totale de I(Q), tenant compte de cette approximation, prend
alors la forme suivante :
I(Q) LPSphères(Q)#177; PCylindres(Q)1[1+
G(Q1,1) G(Q2, 2) +
G(Q3,3)]
dans laquelle le premier terme correspond au facteurs de forme,
et le deuxième au facteur de structure, qui correspond ici aux pics de
Bragg provenant de l'organisation hexagonale.
L'intensité résultante I(Q) est
présentée et comparée au spectre expérimental dans
la figure 70(b). L'ajustement réalisé par I(Q) est plutôt
correct sur toute la gamme de Q considérée. Pour 0,1 < Q <
0,3 Å-1, l'intensité simulée est plus faible,
indiquant que l'on sous-estime légèrement la surface des
sphères. Cette différence peut s'expliquer par le fait que notre
facteur de forme des sphères ne prend pas en compte une
légère polydispersité en taille. Par conséquent,
une petite variation du diamètre des sphères va alors avoir une
influence non-négligeable sur la surface totale.
Cette tentative d'ajustement, bien que sommaire, permet de
valider les grandeurs caractéristiques que nous avons
déterminées par microscopie et par diffraction. Un ajustement
global permettrait notamment de conclure avec beaucoup plus de précision
sur les valeurs numériques, mais la complexité du système
ne nous permet pas, à l'heure actuelle, de réaliser un ajustement
de la sorte.
6.2.2.5. Adsorption / désorption de N2 (BET)
Les isothermes d'adsorption/désorption de N2 ont
été mesurées à 77 K en utilisant un appareil de
physisorption ASAP 2010 M (Micromeritics). Les échantillons ont
été dégazés à 250 °C pendant 12 h avant
la mesure. Les surfaces spécifiques et les diamètres des pores
ont été calculés à l'aide du modèle DFT. Les
isothermes d'adsorption des échantillons MCM-0,1% et MCM-0,5% et leurs
distributions porales respectives sont montrées dans la figure 71.
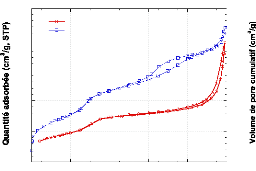
(a)
MCM-0,1 %
MCM-0,5%
400
300
200
100
0
0 0.2 0.4 0.6 0.8 1
(b)
0.07
0.06
0.05
0.04
0.03
0.02
0.01
0
1
10
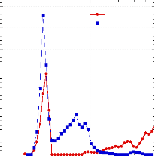
MCM-0,1%
MCM-0,5%
Pression relative P/P0
Taille de pore (nm)
Figure 71: Isothermes de sorption de N2 (a) et distributions des
pores d'après la méthode DFT (b) pour les échantillons
MCM-0,1% et MCM-0,5% obtenus à 77K.
Les isothermes ci-dessus, qui présentent des
hystérèses d'adsorption-desorption, peuvent donc être
classifiés comme étant des isothermes de type IV en accord avec
la classification BDDT193 et la nomenclature de
l'IUPAC194, ce qui est caractéristique des matériaux
mésoporeux. Les deux échantillons présentent une
première condensation capillaire pour une pression relative voisine de
0,3 liée à la présence des mésopores. Dans notre
cas, cette marche est totalement réversible. Cette gamme de pression
relative est reliée à la taille des mésopores. Si l'on
compare nos deux échantillons, nous remarquons que cette condensation ne
se produit pas exactement dans la même gamme de pression relative,
indiquant une légère différence dans le diamètre
des pores. Pour des pressions relatives élevées (P/P0 > 0,9),
une autre condensation capillaire, plus prononcée cette fois,
apparaît. Cette nouvelle marche est habituellement attribuée
à l'espace vide entre les particules sphériques. Entre ces deux
régimes (0,4 < P/P0 < 0,9), les deux échantillons
présentent chacun un comportement particulier :
- Echantillon MCM-0,1% : la pente de l'isotherme ne
présente pas d'accroissement réel dans cette région des
pressions relatives, et reste quasiment parallèle à l'axe des
abscisses jusqu'à P/P0 ~ 0,7. Ceci signifie que la distribution en
taille des pores est étroite et unimodale. La distribution porale
présentée dans la figure 71(b) corrobore cette
interprétation. La seconde condensation capillaire pour P/P0 > 0,9
est due à l'adsorption de N2 dans l'espace vide entre les particules
sphériques. Par conséquent, ce type de pore ne peut pas
être considéré comme une porosité intrinsèque
au matériau.
- Echantillon MCM-0,5% : dans ce cas, une
légère augmentation graduelle de la pente de l'isotherme est
visible après la marche de la première condensation capillaire.
Cet accroissement indique que la distribution en taille des mésopores
n'est pas uniforme. Bien que la plupart des mésopores se situent dans la
même gamme de pression relative (P/P0 ~

0,4), de plus grands mésopores coexistent dans la gamme
0,6 < P/P0 < 0,8. La boucle d'adsorption - désorption
présente même une hystérèse. Tout ceci indique donc
la présence d'une distribution bimodale des pores, distribution
corroborée par la figure 71(b). Cette seconde porosité, à
la différence de l'échantillon précédent,
apparaît comme étant une porosité intrinsèque du
matériau.
Le tableau 38 présente le récapitulatif des
surfaces BET, des volumes des pores et le diamètre moyen des pores
calculés à partir de la méthode DFT. Les surfaces BET sont
de l'ordre de 400-500 m2/g ce qui est relativement faible en
comparaison des MCM-41 conventionnels, pour lesquels une valeur de 1000
m2/g est courante.195,196 Il faut tout de même
signaler ici que l'isotherme de l'échantillon MCM0,1% commence à
des valeurs de P/P0 relativement élevées (P/P0 ~ 4×
10-2), ce qui ne permet pas de calculer avec précision le
volume des micropores d'une part, et la surface BET d'autre part qui se
retrouve par conséquent sous-estimée.
Tableau 38: Caractéristiques porales et surfaces
spécifiques des échantillons MCM-0,1% et MCM-0,5%. (micropores =
pores d'un diamètre <2 nm, mesopores = pores d'un diamètre
compris entre 2 et 50 nm)
Ces calculs montrent également qu'il existe une petite
différence de diamètre de pores entre ces deux
échantillons. Les MCM-0,1% présentent un diamètre moyen de
pore de 3,2 nm contre 2,9 nm pour les MCM-0,5%. Cette différence de
diamètre corrobore les mesures DRX qui montraient un déplacement
des pics de Bragg vers les plus grands angles lorsque la concentration
augmente.
Ces valeurs du diamètre moyen des pores,
accompagnées des longueurs de corrélation a0 obtenues par
*
DRX, nous permettent de calculer l'épaisseur des parois de
silice entre deux pores adjacents.
Nous obtenons des épaisseurs de parois de 1,49 et de
1,67 nm pour les échantillons MCM-0, 1% et MCM-0,5% respectivement. Les
murs de silice sont donc plus épais que la moyenne habituellement
estimée à 1 nm, expliquant en partie la faible valeur de surface
BET. En effet, en plus de présenter une densité
générale moins élevée, nos silices sont
également composées de murs plus épais, ce qui se traduit
par une densité de pores cylindriques par unité de volume
beaucoup moins importante que dans les MCM conventionnels.
* L'épaisseur de la paroi se déduit en
réalisant la soustraction suivante: Epaisseura02r.
6.2.2.6. Accessibilité des solutions aqueuses
Comme nous venons de le voir, cette silice mésoproreuse
de morphologie sphérique présente une texture
contrôlée de type MCM-41 tout à fait
régulière. Cependant, les clichés MET ont également
mis en évidence la présence d'une gangue de silice amorphe autour
de ces sphères, une gangue qui pourrait obstruer l'accès aux
pores. Les mesures d'adsorption/désorption de N2 nous ont permis de
déterminer la taille des mésoporosités, prouvant du
même coup l'accessibilité des pores aux gaz. Néanmoins,
pour s'assurer de la complète accessibilité de la
porosité, les pores de ces silices ont été
imprégnées d'eau, puis étudiées par diffusion des
neutrons afin d'observer les transitions de phase de l'eau.
Des scans en énergie à fenêtre
fixe* ont été réalisés en collaboration
avec Dr M. Gonzalez de l'Institut Laue-Langevin (Grenoble) sur le
spectromètre à rétrodiffusion IN16. Les
échantillons ont été mesurés à une longueur
d'onde = 6,27 Å, pour une résolution en énergieE = 0,9 jteV
(largeur à mi-hauteur) et une gamme de Q comprise entre 0,4 et 2
Å-1. L'intensité élastique, mesurée en
fonction de la température, est proportionnelle au nombre de diffuseurs
qui ne bougent pas ou qui apparaissent immobiles dans la fenêtre
temporelle correspondante à la résolution du spectromètre
(ô < ~ 2 ns).
L'échantillon MCM-0,5% a été
imprégné par de l'eau lourde tout de suite après
étuvage et a été placé dans un porte
échantillon plat en aluminium. Le scan élastique complet,
intégré sur la totalité de la gamme de Q, est
présenté sur la figure 72.
|
0,4 0,35 0,3 0,25 0,2 0,15 0,1 0,05
0
|
|
0 50 100 150 200 250 300
Température (K)
Figure 72: Scan élastique obtenu pour l'échantillon
MCM-0,5% imprégné de D2O. Deux transitions sont clairement
observées à 235 et 276 K.
* Scans en énergie à fenêtre fixe = Elastic
Scans
L'échantillon a été préalablement
refroidi à 10 K et stabilisé à cette température
pendant 30 minutes. La remontée en température s'est ensuite
réalisée en utilisant une rampe de 1,4 K/min. entre 10 et 180 K,
suivie d'une rampe beaucoup plus lente (0,4 K/min.) entre 180 et 300 K, pour
laisser le temps au système de s'équilibrer.
Lorsque l'on augmente la température,
l'intensité élastique décroît lentement
jusqu'à 230 K témoignant ainsi de l'augmentation de la
mobilité des diffuseurs dans l'échantillon. Au-delà de 230
K, deux transitions bien marquées apparaissent : une vers 235 K, et une
seconde, très abrupte, vers 276 K. La transition à 276 K peut
immédiatement être reliée à la température de
fusion de la glace deutérée. La transition aux alentours de 235 K
correspond, quant à elle, à une transition vitreuse d'eau lourde
amorphe confinée dans les pores. De fait, le confinement de l'eau induit
une diminution de 40 K de la température de fusion. Un comportement
similaire a déjà été décrit dans la
littérature,197,198,199 ce qui confirme
l'accessibilité des pores. Notons que les espaces interparticulaires,
qui pourraient également être responsables de cette Tf,
présentent des diamètres trop important (~ 10-20 nm) et une
distribution trop inhomogène pour pouvoir être à l'origine
de cette transition. Au-delà de 280 K, le signal élastique finit
ensuite par disparaître quasi-totalement. Seuls subsistent les signaux
élastiques du bruit de fond et de la matrice de silice.
Cette mesure permet de conclure que l'eau, et a fortiori les
solutions aqueuses, peuvent pénétrer à l'intérieur
même des pores cylindriques qui composent ces sphères.
6.3. DISCUSSION SUR LE MECANISME DE FORMATION
Toutes ces caractérisations nous ont donc permis de
connaître de manière beaucoup plus précise le produit final
et ses propriétés physico-chimiques. Intéressons nous
maintenant à la manière dont ont pu se former ces
sphères.
Dans les cas des silicates préparés à
partir de la plus faible concentration en tensioactif (0,1%), l'arrangement
hexagonal des pores et la morphologie sont beaucoup mieux définis que
ceux des échantillons contenant des teneurs en surfactant plus
élevées. Lorsque la concentration se rapproche de la
concentration micellaire critique (CMC), les molécules de tensioactif
sont libres ou très faiblement organisées en micelles
sphériques ou cylindriques. Dans un système biphasique, comme
c'est le cas ici, l'hydrolyse du TEOS se produit à l'interface. A cause
des interactions de type électrostatiques entre les oligomères
silicatés et la tête chargée du CTMABr, les micelles
faiblement assemblées se brisent alors en libérant leurs
molécules. Les molécules libres de tensioactif chargées
positivement présentes dans la phase aqueuse sont
électrostatiquement adsorbées par les oligomères
silicatés chargés négativement et présents dans la
phase du TEOS. (Figure 73(a)) Une microémulsion de type eau-dans-l'huile
se forme alors. Les premières agrégations de composites
organique-inorganiques
apparaissent à l'interface, où un
mécanisme d'auto-assemblage coopératif se produit .200
La petite quantité d'éthanol générée par
l'hydrolyse du TEOS va alors agir comme un co-surfactant, amenant les
agrégats de micelles à s'organiser sous forme sphérique
afin de minimiser leur énergie de surface. (Figure 73(b)) La croissance
des particules conduit à une forme sphérique qui présente
la plus haute symétrie et la plus basse énergie de surface. Ceci
est corroboré par la variété des longueurs des pores
cylindriques, qui sont assez courts à la périphérie et
plus longs au centre de la sphère.
(a) Système biphasique (b) A l'interface Si(OR)4
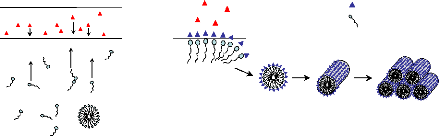
Si(OH)x(OR)4_x
Tensioactif
TEOS
Phase aqueuse
Figure 73: Représentations schématiques du
système biphasique Phase TEOS/Phase aqueuse (a), et du mécanisme
d'auto-assemblage coopératif (b).
6.4. CONCLUSION GENERALE DU CHAPITRE 6
Dans ce chapitre sur la synthèse de silice
mésoporeuse, nous avons évalué les effets de la
concentration en tensioactif sur la morphologie et la texture du produit final.
Cette étude nous a permis d'optimiser nos technique de synthèse
afin d'obtenir des nanosphères de silice présentant une
mésoporosité contrôlée. Parmi toutes les
méthodes d'élaboration répertoriées jusqu'alors,
aucune synthèse ne présente un tel résultat dans un milieu
100% aqueux, avec des concentrations en tensioactif aussi faibles, et en milieu
ammoniacal.164,172,201,202
Résumons ici les principaux résultats obtenus :
Morphologie :
o La diminution en concentration nous
a conduit à la formation d'objets sphériques,
o Des nanosphères de silice
mésoporeuse homodisperses en taille (Ø ~ 125 nm) ont
été synthétisées pour la plus faible concentration
en tensioactif.
Texture:
o La mésoporosité est de type MCM-41 (Ø ~ 3
nm, L ~ 100-120 nm),
o Les murs de silice entre les pores (Ep. ~ 1,5 nm) sont plus
épais que dans les MCM conventionnels,
o L'accessibilité des pores aux gaz et aux solutions
aqueuses a été démontrée.
Chapitre 7
DYNAMIQUE MOLECULAIRE DU SUCRE DANS DES PORES DE
TAILLE ET DE MORPHOLOGIE CONTROLEES
7.1. Remplissage des pores 157
7.2. Mesures élastiques 158
7.3. Résultats préliminaires de dynamique
moléculaire 167
7.4. Conclusion générale du chapitre 7 169
Chapitre 7
DYNAMIQUE MOLECULAIRE DU SUCRE DANS DES PORES DE TAILLE ET DE
MORPHOLOGIE CONTROLEES
Les matériaux mésoporeux et leurs pores
réguliers ont ouvert la voie à de nouveaux et nombreux champs
d'investigation pour l'étude des solutions sous confinement. Les silices
de la famille des M41S, les SBA-15 ou encore le Vycor ont contribué
grandement à la compréhension des modifications des
propriétés physico-chimiques liées à la
réduction d'échelle, comme en témoigne la très
grande activité scientifique depuis cinq ans autour de l'eau
confinée dans des nanopores.97,98,99,100,203,204,205,206,207,208 Si des
longueurs de pores de plusieurs centaines de nanomètres ne
présentent pas un problème majeur dans l'étude de l'eau,
il n'en est pas de même avec les systèmes binaires eau-sucre. De
tels pores augmentent de manière importante les risques de gradients de
concentration ou de démixtion. Les nanosphères, grâce
à leurs pores cylindriques de longueur relativement faible, sont de bien
meilleurs candidats. Dans ce chapitre, il sera donc question de confiner des
solutions de sucres dans les mésopores cylindriques de ces
sphères, puis d'étudier la dynamique de ces molécules sous
confinement par diffusion quasi-élastique des neutrons comme nous avons
pu le faire dans les chapitres précédents.
7.1. REMPLISSAGE DES PORES
Afin de confiner des solutions dans les MCM-41, plusieurs
techniques de remplissage sont habituellement utilisées :
(i) l'évaporation de la solution, puis condensation dans
la matrice hôte :
Cette technique, très performante dans le cas de l'eau ou
de certains alcools, est irréalisable dans notre cas en raison de la
trop grande pression de vapeur du sucre. Par conséquent, seule l'eau
s'évaporerait.
(ii) l'imprégnation de la matrice par une solution :
La matrice, préalablement déshydratée par
étuvage, est ensuite plongée dans une solution de sucre à
une concentration donnée. La solution va alors pénétrer
dans les pores et les remplir.
Cette dernière solution, c-à-d
l'imprégnation, a été retenue pour sa simplicité de
mise en oeuvre et pour sa faisabilité. Il faut tout de même garder
en tête, que l'imprégnation ne garantie pas totalement une
homogénéité en concentration de la solution et un
remplissage intégral des pores. Néanmoins, nos résultats
d'imprégnation de l'eau lourde dans cette même silice (Cf.
Chapitre 6) sont plutôt encourageants et la transition plutôt
abrupte de l'eau confinée témoigne de
l'homogénéité de l'imprégnation.
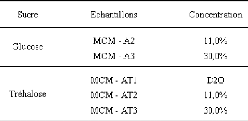
Du glucose ou du tréhalose partiellement
deutérés ont été dissous dans de l'eau lourde dans
des proportions adéquates pour atteindre des concentrations de 11% et
30% massiques en sucre. Les sphères de silice, calcinées et
préalablement déshydratées à 100°C dans une
étuve à vide, ont ensuite été placées dans
la solution en boîte à gants. Après une imprégnation
de plusieurs heures, le mélange a été filtré et
rincé au D2O afin de ne recueillir que la silice mésoporeuse. La
liste des différents échantillons est présentée
dans le tableau 39.
Tableau 39 : Liste des échantillons sur lesquels des scans
élastiques ont été réalisés.
7.2. MESURES ELASTIQUES
7.2.1. Confinement de solutions d' tréhalose
Des scans en énergie à fenêtre fixe ont
été réalisés sur le spectromètre à
rétrodiffusion IN16 de l'Institut Laue-Langevin. Les échantillons
ont été mesurés à une longueur d'onde 2%, = 6,27
Å, pour une résolution en énergie E = 1,2 peV (largeur
à mi-hauteur) et une gamme de Q comprise entre 0,36 et 1,52
Å-1. L'intensité élastique, mesurée en
fonction de la température, est proportionnelle au nombre de diffuseurs
qui ne bougent pas ou qui apparaissent immobiles dans la fenêtre
temporelle correspondante à la résolution du spectromètre
(t < ~ 2 ns).
Les différents échantillons ont
été préalablement refroidis à 10 K et
stabilisés à cette température pendant 30 minutes. La
remontée en température s'est faite ensuite en utilisant une
rampe de 1,4 K/min. entre 10 et 180 K, suivie d'une rampe beaucoup plus lente
(0,4 K/min.) entre 180 et 300 K, pour laisser le temps au système de
s'équilibrer. Les scans élastiques des échantillons
MCM-AT1, MCM-AT2 et MCM-AT3 mesurés entre 10 et 300K sont
présentés dans la figure 74.
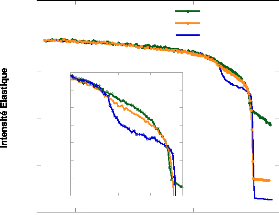
0,4
0,3
0,2
0,1
0
0,34
0,32
0,28
0,26
0,24
0,22
0,3
0,2
210 230 250 270
MCM-AT3 (30%)
MCM-AT2 (11%)
MCM-AT1 (D20)
0 50 100 150 200 250 300
T (K)
Figure 74 : Scans élastiques des échantillons
MCM-AT1, MCM-AT2 et MCM-AT3 mesurés entre 10 et 300K. L'encart
présente un grossissement de la transition située vers 230 K.
Le spectre de l'échantillon MCM-AT1, déjà
présenté dans le paragraphe précédent, permet de
mieux apprécier les différents régimes thermodynamiques.
(1) A température ambiante, les trois échantillons
présentent un plateau correspondant à l'intensité
élastique du bruit de fond et de la matrice de silice. Les
différences en intensité proviennent des quantités
d'échantillons utilisées, auxquelles s'ajoute l'augmentation du
signal cohérent qui augmente avec la concentration. (2) Vers 270-275 K,
une transition relativement abrupte, liée vraisemblablement à la
fusion du solide non confiné, apparaît. Elle conduit à un
second plateau dans le cas de l'eau lourde ou à une augmentation de
l'intensité élastique dans le cas des solutions de sucre. (3) Aux
alentours de 230-235 K, une seconde transition intervient. Dans le cas de
l'eau, cette transition est bien marquée et assez abrupte. Dans le cas
des solutions de tréhalose, cette transition est beaucoup moins
marquée, et il apparaît que pour des concentrations en sucre
croissantes, cette transition devient de plus en plus graduelle.
Afin de mettre en valeur les différentes transitions et
de déterminer avec plus de précisions leurs positions, nous avons
procédé à un ajustement succinct de ces données par
des fonctions sigmoïdales pour ces trois échantillons. (Figure
75)
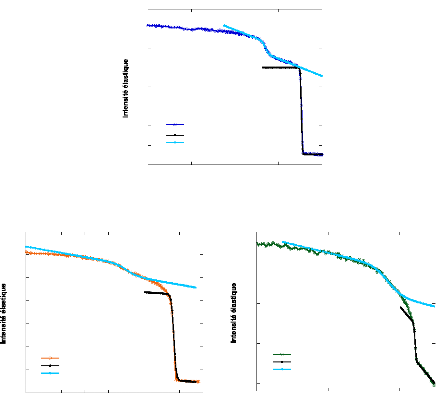
(b)
(c)
0,3
(a)
0,35
0,3
0,25
0,2
0,15
MCM-AT1 (D20)
Sigmoide 1
Sigmoide 2
0
0,1
0,05
100 150 200 250 300
T (K)
0,4
0,25
0,2
0,35
0,15
0,1
0,3
0,05
MCM-AT2 (11%) Sigmoide 1 Sigmoide 2
MCM-AT3 (30%) Sigmoide 1 Sigmoide 2
0,25
0
160 180 200 220 240 260 280 300
T (K)
50 100 150 200 250 300
T(K)
Figure 75: Ajustements des transitions observées dans les
scans élastiques des échantillons MCM-A T1(a), MCM-AT2 (b) et
MCM-AT3 (c). Les fonctions d'ajustements utilisées ici sont des
sigmoïdes.
La fonction sigmoïdale utilisée pour ces ajustements
est donnée ci-dessous :
|
f (x) = A1
|
1+ e-B(x--x0) )
1 )#177; (C --
Dx)
|
dans laquelle les paramètres A, B et x0 ajustent
respectivement la hauteur de la marche, l'aspect plus ou moins abrupte de la
transition, et la position de la transition (au niveau du point d'inflexion).
Le deuxième terme est l'équation d'une droite utilisée ici
pour positionner la sigmoïde en hauteur mais également pour jouer
sur son inclinaison. Les valeurs des paramètres B et x0 sont
présentées dans le tableau 40.

Tableau 40 : Récapitulatif des valeurs des
paramètres x0 et B tirées des ajustements réalisés
sur les transitions observées sur les scans élastiques.

MCM-AT1 (D20)
Deux transitions ont été clairement mises en
évidence par les ajustements présentés sur la figure
75(a). La première, située à T = 277 K, correspond
à la fusion de la glace deutérée volumique,209
alors que la deuxième, aux environs de 235 K, est due à la fusion
de la glace confinée dans les nanopores des
MCM_41.197,198,199,208 (Cf. Chapitre 6) Le paramètre B est
très intéressant, car il donne une information sur le
caractère plus ou moins abrupte de la transition, ainsi, plus B est
grand, plus la transition est abrupte, et inversement, plus B se rapproche de
0, plus elle est graduelle. Ce paramètre témoigne donc de la
coopérativité du système, et donc de son pouvoir à
plus ou moins cristalliser. Il apparaît ici très nettement, que ce
caractère change nettement avec le confinement, puisque B passe de 1,8
à 0,5 lorsque l'on confine la solution dans des pores de 3
nanomètres. Cette chute témoigne donc de la perte de
coopérativité du système, qui passe donc d'un état
cristallisé (T = 275 K) à un état que l'on pourrait
qualifier de vitreux lorsque l'on place la solution dans un état de
confinement (T = 235 K).
MCM-AT2 (11%)
L'ajustement de cet échantillon montre deux transitions
positionnées à 275 et 235 K. (Figure 75(b)) Comme
précédemment, la première est à relier à la
fusion du solide volumique. La transition vers 235 K correspond, quant à
elle, à une température de fusion ou de transition vitreuse,
similaire à celle observée pour l'eau lourde confinée. Le
type de la transition est assez difficile à déterminer pour
l'instant, et des mesures thermiques complémentaires (DSC, ATD) sont
nécessaires. Cependant, l'importante chute de B tend à indiquer
une perte de coopérativité générale par rapport
à la solution volumique, mais également par rapport au D2O
confiné. Ainsi, cette valeur semble montrer que, confinée, la
solution de tréhalose présente plutôt une structure assez
peu structurée, du type verre.
MCM-AT3 (30%)
La figure 75(c) montre une transition à T = 272 K, qui
correspond à la Tfus du mélange D2O/tréhalose
non-confiné. La diminution de 3 K de Tfus, par rapport
à MCM-AT2, est corroborée par le diagramme de phase. (Figure 76)
La seconde transition (234 K), mis en exergue par la sigmoïde, correspond
à la fusion de la glace contenue dans les pores de la silice. Cette
valeur de Tfus est cohérente avec les valeurs
précédentes. Notons également que la
coopérativité du solide confiné semble disparaître
à la vue de la valeur de B dans le cas confiné.
Comparatif de MCM-AT1, MCM-AT2 et MCM-AT3
Si l'on compare les différents échantillons
volumiques, nous remarquons une légère diminution de
Tfus avec la concentration. Maintenant, si l'on regarde le diagramme
de phase du système binaire H2Otréhalose210
présenté en figure 76, nous pouvons remarquer que nos valeurs de
Tfus sont en parfait accord*, dans l'approximation
où le diagramme de phase du mélange D2O/tréhalose
diffère assez peu de celui du mélange H2O/tréhalose.
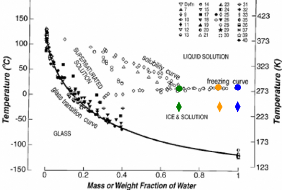
Figure 76 : Diagramme de phase du système binaire
H2O/tréhalose. (? : Tfus des solutions volumiques, : Tfus des solutions
confinées).210
En comparant les différentes valeurs de Tsol
des solutions confinées avec celles des solutions volumiques, nous
trouvons donc une diminution de ~ 40 K dans les trois cas. Il apparaît
donc que le confinement est responsable du décalage en
température de Tsol. Notons également, que la position
du liquidus est décalé vers les plus basses températures
et que sa forme n'est pas modifiée par le confinement. (Figure 76)
Le paramètre B montre une évolution certaine de
la coopérativité du réseau. Pour les solutions
* Nous avons tenu compte du décalage des valeurs de la
température de fusion entre l'eau légère et l'eau lourde.
Le diagramme est utilisé ici uniquement pour connaître
l'évolution générale du liquidus.
volumiques, il présente des valeurs
élevées, attestant de la cristallisation de la solution, alors
que les solutions confinées présentent elles des valeurs beaucoup
plus proches de 0, témoignant de l'aspect plus vitreux du solide
obtenu.
7.2.2. Confinement de solutions de D-glucose
Des scans en énergie à fenêtre fixe ont
été réalisés au NCNR sur le spectromètre
à rétrodiffusion HFBS86. Les échantillons ont
été mesurés à une longueur d'onde 2%, = 6,27
Å, pour une résolution en énergie E = 1,2 peV (largeur
à mi-hauteur) et une gamme de Q comprise entre 0,36 et 1,52
Å-1. L'intensité élastique, mesurée en
fonction de la température, est proportionnelle au nombre de diffuseurs
qui ne bougent pas ou qui apparaissent immobiles dans la fenêtre
temporelle correspondante à la résolution du spectromètre
(t < ~ 2 ns).
Comme précédemment, les échantillons ont
été préalablement refroidis à 10 K, puis
stabilisés à cette température. La remontée en
température s'est faite selon deux rampes : une première de 1,4
K/min entre 10 et 180 K, suivie d'une seconde de 0,22 ou 0,33 K/min pour les
échantillons MCM-A2 et MCM-A3 respectivement. Seule la solution de
glucose (30%) a été mesurée pendant la descente en
température. Les spectres de la solution à 30 % et de MCM-A2 et
MCM-A3 sont présentés dans la figure 77.
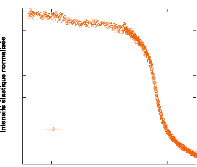
(a)
0,9
0,8
0,7
0,6
0,5
MCM-A2
0,4
0,3
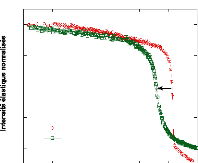
(b)
1
0,8
0,6
0,4
Solution 30% MCM-A3
0,2
0 50 100 150 200 250 300
T (K) 0 50 100 150 200 250 300
T (K)
Figure 77: Scans élastiques des échantillons MCM-A2
(a), MCM-A3 et d'une solution à 30% (b) mesurés entre 10 et 300
K.
A la différence des échantillons contenant du
tréhalose, la préparation a permis cette fois d'éliminer
la transition vers 275 K provenant de la fusion de la glace contenue entre les
particules. Seule persiste désormais la transition liée à
la fusion du solide confiné. Comme le signal provient, dans ce cas,
à 100% de la solution confinée, les transitions nous apparaissent
alors plus marquées. A titre comparatif, pour l'échantillon
MCM-AT1, la solution confinée n'était responsable que de 25% de
l'intensité
élastique totale. La figure 77(a) présente
l'évolution de l'échantillon MCM-A2 avec la température.
Une première transition (~ 220-230 K), bien marquée, correspond
à la température de fusion de la glace confinée. Notons
qu'il apparaît entre 50 et 100 K, une deuxième petite chute, dont
l'origine nous est, pour l'instant, inconnue. La figure 77(b) présente
un comparatif de l'échantillon MCM-A3 avec une solution volumique de
même concentration (30%). Il apparaît ici très nettement,
que la réduction d'échelle conduit à un abaissement de la
température de fusion d'au moins de ~ 30-40 K. Pour plus de
précision, nous avons utilisé une nouvelle fois des fonctions
sigmoïdes pour ajuster les transitions. Les ajustements sont
présentés dans la figure 78.
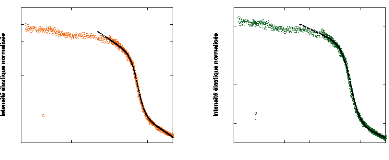
300 0 50 100 150 200 250
300
0 50 100 150 200 250
T (K)
T (K)
0,9
0,8
0,7
0,6
0,5
0,4
0,3
(a)
1
MCM-A2 (11%) Sigmoide
(b)
0,9
0,8
0,7
0,6
0,5
MCM-A3 (30%) Sigmoide
0,4
0,3
Figure 78 : Ajustements des transitions observées dans les
scans élastiques des échantillons MCM-A2 (a), et MCM-A3 (b). Les
fonctions d'ajustements utilisées ici sont des sigmoïdes.
MCM-A2 (11%)
La sigmoïde s'ajuste parfaitement à la courbe
expérimentale. (Figure 78(a)) La transition a ainsi été
trouvée à T = 231 K. Le paramètre B est égal
à 0,11, une valeur assez proche de celles déterminées pour
le tréhalose, et qui indique une faible coopérativité du
système.
MCM-A3 (30%)
De la même manière, l'échantillon MCM-A3 a
été ajusté à l'aide d'une fonction sigmoïdale
centrée à T = 231 K, et avec un paramètre de
coopérativité B ~ 0,14.
Comparatif MCM-A2 / MCM-A3
Les valeurs de la température de fusion
déterminées pour les deux solutions confinées sont
égales (~ 231 K). A la vue du diagramme de phase
H2O/glucose211 présenté dans la figure 79, nous
pouvons dire que ces résultats suivent la forme du liquidus. Il
apparaît ici, que comme pour les solutions de tréhalose
confinées, la réduction stérique conduit à un
abaissement de la branche du liquidus d'une quarantaine de degré.
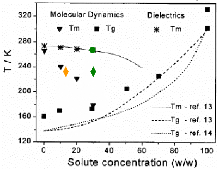
Figure 79: Diagramme de phase du mélange binaire
H2O/D-glucose en fonction de la concentration en monosaccharide. (? : Tfusdes
solutions volumiques, : Tfusdes solutions confinées).211
Comme nous avons pu le voir, dans les différents
chapitres précédents traitant des neutrons, durant
une
expérience de diffusion de neutrons incohérente, la fonction
mesurée est le facteur de structure
dynamique incohérent S inc (Q,), qui
présente deux contributions:
él
- une élastique: S inc Q
( )( , 0)
S inc Q
- une quasi-élastique, qui prend en compte des
énergies ?> 0.
Le déplacement carré moyen, u ,
2 qui prend en compte les fluctuations de toutes les particules
du
système étudié, est donné par:
d S Q
él
{ ln ( ) }
inc
dQ 2
Q 0
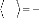
2
3
u
Une autre manière donc de déterminer l'existence
de transitions dans un scan élastique est de tracer
les
différentes valeurs du déplacement carré moyen
u2 en fonction de la température.212,213 La figure
80
présente ces tracés pour les échantillons
MCM-A2 et MCM-A3.
0,4
MCM-A2
0,3
0,2
T1
= 96 K
0,1
0
T 2
= 220 K
-0,1
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
MCM-A3
T1
= 86 K
T2
= 223 K
0 50 100 150 200 250
T(K)
0 50 100 150 200 250
T (K)
Figure 80 : Tracé du déplacement quadratique moyen
<u2> en fonction de T pour les échantillons MCM-A2 et
MCM-A3.
Les tracés ci-dessus montrent l'augmentation des
fluctuations dans le système avec la montée en
température. A basse température, entre 0 et 80 K, les vibrations
sont quasiment nulles, tout le système est figé. Vers 90 K, les
fluctuations atomiques augmentent alors brusquement, indiquant l'apparition
d'une transition. L'augmentation des fluctuations dans cette gamme de
température peut provenir du gain de mobilité de certains
groupements chimiques ou encore d'une transition vitreuse, qui paraît
malgré tout peu probable à ces températures... Si l'on
augmente encore la température, nous trouvons alors une deuxième
cassure assez nette dans les variations de <u2>.
L'augmentation brutale de la pente suggère que les molécules ont
une grande mobilité, comme dans un liquide... Beaucoup plus
marquée que la première, cette transition est due à la
fusion du solide présent dans les pores des sphères de silice. La
différence de température observée avec celles
déterminées avec les ajustements provient du fait que la
température de transition n'a pas été mesurée au
même endroit. Dans le cas précédent, Tfus
était pris au niveau du point d'inflexion, dans ce cas ci, elle a
été mesurée au début de la chute de
l'intensité élastique.

Si l'on regarde maintenant le tracé de u2 en
fonction de la température dans le cas de la solution
volumique à 30% (Figure 81), il est intéressant
de constater qu'une seule et unique transition n'est visible (~ 240 K). Cet
échantillon témoin montre donc que la première transition
n'est observée que dans le cas confiné, et que par
conséquent son origine est vraisemblablement à rapprocher de la
réduction d'échelle. Mais ces seuls résultats, sans
mesures complémentaires, ne nous permettent pas de conclure sur le type
de transition mis en jeu.
0,28
0,24
0,2
0,16
0,12
0,08
0,04
0
Solution 30%
0 50 100 150 200 250 300
T (K)
Figure 81: Tracé du déplacement quadratique moyen
<u2> en fonction de T pour la solution de glucose à
30%. Une unique transition est visible.
7.2.3. Conclusion
L'étude de la variation de l'intensité
élastique en fonction de la température de ces solutions
confinées a permis de mettre en évidence la présence de 2
ou 3 transitions selon l'échantillon :
- la première vers 270 K correspond à la fusion du
solide non-confiné,
- la seconde vers 230 K correspond à la fusion du solide
confiné,
- la troisième vers 90 K n'a pas encore été
déterminée.
Des mesures thermiques complémentaires (DSC, ATG, ...)
restent malgré tout nécessaires afin d'asseoir nos conclusions
sur les deux premières transitions et de définir l'origine de la
troisième.
Les variations de la dynamique des molécules d'eau et
de sucre en fonction de la température sont directement responsables de
ces transitions. Et une étude complète de la dynamique
moléculaire de ces systèmes par diffusion quasi-élastique
des neutrons va nous permettre d'obtenir quelques indications sur les
changements de propriétés liés à la
réduction de l'espace....
7.3. RESULTATS PRELIMINAIRES DE DYNAMIQUE
Les mesures de dynamique moléculaire du D-glucose
confiné dans des MCM-41, par QENS, ont été
réalisées au NCNR sur les spectromètres DCS85
et HFBS86. Les poudres, introduites dans des porte-
échantillons cylindriques d'espace annulaire 0,4 mm, ont
été scellées, puis placées dans un cryostat dans
lequel la température est régulée à #177; 1 K.
Les trois échantillons MCM-A1, MCM-A2 et MCM-A3 ont
été mesurés sur le DCS à 270 et 300 K avec une
longueur d'onde incidente de 6 Å, correspondant à une gamme de Q
comprise entre 0,25 et 1,93 Å-1, et pour une résolution
de 57p,eV.
Ces mesures, que nous avons réalisées
récemment, sont encore en cours de traitement, mais nous avons fait le
choix de présenter ici quelques résultats préliminaires
tirés des mesures réalisées sur l'échantillon
MCM-A2.
Les fonctions de diffusion S(Q,E) de l'échantillon
MCM-A2 à 270 et 300 K ont été ajustées à
l'aide de la combinaison de fonctions théoriques suivantes : une
fonction delta, deux fonctions Lorentziennes L(Wt, E) et une ligne de base. La
largeur à mi-hauteur de la Lorentzienne étroite W1 tirées
de ces ajustements sont tracées en fonction de Q2. (Figure
82)
0,15
0,05
0,1
0
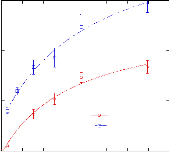
270 K (MCM-A2)
300 K (MCM-A2)
0 0,5 1 1,5 2 2,5 3 3,5 4
C-2 (+-2)
Figure 82 : Largeur à mi-hauteur de la Lorentzienne
étroite W1 en fonction de Q2.
Ce qui ressort ici avant tout, c'est un
rétrécissement de la largeur à mi-hauteur de la
Lorentzienne étroite lorsque la température diminue, ce qui se
traduit physiquement par un ralentissement général de la
dynamique des espèces présentes en solution. Les coefficients de
diffusion du D-glucose à 270 et 300 K ont été
trouvés égaux à (0,6 #177; 0,3)×10-5
cm2s-1 et (0,46 #177; 0,99)×10-5
cm2s-1 respectivement. Si l'on compare ces valeurs
à celles déterminées dans le cas des solutions à
280 K, Dsolutk'n = (0,31 #177; 0,06)×10-5
cm2s-1, ou dans le cas des gels à 300 K,
Dgel = (0,6 #177; 0,1)× 10-5
cm2s-1, nous pouvons alors remarquer une diminution de la
dynamique translationnelle d'au moins 20%. Ces valeurs
déterminées pour l'échantillon le moins concentré
(14,2%), sont les toutes premières présentes dans la
littérature. Cette diminution marque ainsi une première
étape intéressante puisqu'elle définit une limite minimale
de taille de pore en dessous de laquelle un effet sur la dynamique est
observé. Il faut tout de même garder en tête qu'il ne s'agit
là que de résultats préliminaires, et que ces valeurs du
coefficient de diffusion doivent être affinées.
7.4. CONCLUSION GENERALE DU CHAPITRE 7
Nous pouvons résumer ci-dessous les résultats
principaux obtenus dans ce chapitre pour des solutions confinées de
D-glucose et d' tréhalose :
Les scans en énergie ont mis en évidence trois
transitions distinctes :
o vers 270 K: fusion du solide non-confiné,
o vers 230 K : fusion du solide confiné,
o vers 90 K: origine à déterminer.
L'aspect coopératif des transitions a pu être
estimé et a mis en évidence un caractère plus vitreux des
solides confinés dans les MCM-41.
L'étude préliminaire de dynamique
moléculaire du D-glucose confiné dans ces mésoporeux a
montré une chute de la diffusion translationnelle d'au moins 20%.
-170-
Conclusion
Comme toute chose a une fin ...
L'anhydrobiose est un phénomène d'une incroyable
complexité et les processus mis en jeu ne sont à ce jour pas
encore compris de manière précise comme nous l'avons vu.
Néanmoins, toutes les hypothèses évoquées
permettent de comprendre le rôle crucial des interactions entre l'eau et
le sucre, via la formation de liaisons hydrogène. A l'origine du
phénomène de cristallisation, de la vitrification, des variations
de viscosité..., les liaisons hydrogène sont responsables de
toutes les propriétés remarquables évoquées dans
ces systèmes biologiques complexes. Les études de dynamique
moléculaire réalisées sur des mélanges binaires
eau/sucre permettent donc de suivre indirectement l'évolution du
réseau de liaisons hydrogène et par conséquent d'en
apprécier la coopérativité.
La diffusion quasi-élastique des neutrons s'est
avérée être un outil particulièrement bien
adapté à nos systèmes hydrogénés puisqu'ils
nous ont permis de sonder sélectivement la dynamique du solvant et du
soluté. L'étude de solutions de glucose et de fructose a conduit
à la détermination des constantes physiques
caractéristiques du mélange, comme le coefficient de diffusion,
le temps de relaxation, ou encore la longueur de saut effective. Un effet de la
concentration en sucre sur les dynamiques du D-glucose, comme celles du
D-fructose, a clairement été mis en évidence. Une
réduction significative de la dynamique translationnelle de l'eau (~ 3)
est notée lorsque l'on augmente la concentration en sucre. Un
comportement complètement similaire a été constaté
pour la dynamique translationnelle du D-glucose, qui subit une diminution d'un
facteur comparable (~ 3). La température
s'est avérée jouer un rôle crucial,
puisqu'elle abaisse les dynamiques du fructose d'un facteur 3 lorsque la
température diminue de 40 K. Ces effets de la concentration ou de la
température relatent donc les interactions qui se produisent dans le
mélange entre l'eau et le monosaccharide. Mais de tels résultats
montrent bien qu'une augmentation en concentration du sucre est
équivalente à une baisse en température en terme
d'interactions et de dynamiques moléculaires. Notons également
que les différences stéréochimiques de ces deux
monosaccharides, qui influent sur leur hydrophobicité et donc sur leurs
interactions avec l'eau, sont à l'origine des différences de
dynamique observées.
Cette étude, qui n'a pas l'ambition de copier le vivant
mais seulement de l'imiter d'une certaine manière, tente
néanmoins d'apporter quelques réponses aux questions liées
au confinement de solutions aqueuses de sucres. Cette problématique,
tout à fait nouvelle d'un point de vue expérimental, était
assez difficile à mettre en oeuvre en raison des très nombreuses
contraintes inhérentes au système: concentration,
évaporation, matrice,... Le choix de la matrice a d'ailleurs
été l'une des plus grandes difficultés. Malgré
cela, deux matrices ont été sélectionnées et
synthétisées par nos soins: un gel de silice aqueux (ou hydrogel)
et une silice mésoporeuse de type MCM-41 présentant une
morphologie sphérique. L'originalité, dans le premier cas, a
été d'intégrer le sucre dès la synthèse,
permettant ainsi un confinement de la solution en une seule et même
étape. L'étude structurale des gels par diffusion des neutrons
aux petits angles a permis d'estimer la taille moyenne des pores à ~ 18-
20 nm, et l'étude de la dynamique moléculaire du D-glucose
confiné dans ces gels a montré un ralentissement des mouvements
de rotation et de translation lié à l'augmentation en
concentration. Il est apparu également que le confinement ne modifiait
que très faiblement la dynamique comparée à celle d'une
solution non confinée de même concentration. La même
observation a également été faite sur des solutions de
tréhalose confinées dans les mêmes conditions. Des
simulations de dynamique moléculaire très récentes sont
même venues corroborer ces résultats. Cette conclusion, qui
pourrait paraître assez surprenante au premier abord, indique finalement
que les solutions de sucre confinées se comportent comme dans une
solution «normale », permettant ainsi une protection active des
tissus. Ce résultat, tout à fait nouveau, apporte une information
importante, utilisable notamment par la communauté des
théoriciens qui considèrent les molécules de sucre comme
confinées à la surface des protéines...
Mais, le gel s'est également
révélé être une excellente matrice pour
étudier la déformation de la structure siliceuse sous l'effet de
la perte en eau. Les déshydratations réalisées in-situ sur
ces gels ont été suivies par diffusion des neutrons aux petits
angles. Alors que les gels sans sucre présentaient des fissurations
importantes dans leur structuration, les gels contenant du glucose conservaient
leur structure interne alors même que le taux d'hydratation était
extrêmement faible. Cette étude expérimentale a donc
montré une résistance accrue des gels contenant du sucre. L'effet
protecteur du sucre a alors été clairement mis en
évidence.
L'étude s'est ensuite tournée vers le
confinement de solutions de sucre dans des pores de taille et de morphologie
contrôlées. Pour ce faire, il a fallu synthétiser des
silices mésoporeuses adaptées à nos besoins et nos
contraintes. La diminution de la concentration en tensioactif a ainsi permis de
former des particules sphériques mésoporeuses pour des
concentrations en CTMABr jamais utilisées jusqu'alors. L'optimisation
des conditions de synthèse a notamment permis d'obtenir des
sphères de silice mésoporeuses de type MCM-41 homodisperses en
taille. Les multiples caractérisations (MET, MEB, DRX, SANS, BET) ont
permis de déterminer le diamètre moyen des particules (Ø ~
125 nm), mais également le diamètre des pores (Ø ~ 3 nm),
et l'épaisseur des parois (1,5 nm). Nous avons pu mettre en
évidence un élargissement des pores lorsque la concentration du
tensioactif diminue. Le très bon accord des différentes
techniques de caractérisation est également à noter.
L'accessibilité des pores aux solutions aqueuses a également
été démontrée.
L'étude de la variation de l'intensité
élastique en fonction de la température des solutions de sucre
confinées a permis de mettre en évidence la présence de
plusieurs transitions selon l'échantillon : une première vers 270
K correspondant à la fusion du solide non confiné, une seconde
vers 230 K pour la fusion du solide confiné, et enfin une
troisième vers 90 K qui n'a pas encore été
déterminée. Dans le même temps, une perte de la
coopérativité a été observée lorsque l'on
passe d'une solution à une solution confinée. Une diminution de
la dynamique translationnelle des molécules de sucre confinées
dans la silice mésoporeuse a également pu être mise en
évidence.
Perspectives
Avant toute chose, il convient de finaliser le traitement des
mesures de dynamique moléculaire des solutions de D-glucose
confinées dans des MCM-4 1. Les résultats obtenus seront ensuite
comparés avec ceux obtenus pour les solutions et pour les gels. Les
expériences portant sur l'évolution de la structure en fonction
de la déshydratation nous semblent assez prometteuses, et il serait donc
intéressant de poursuivre ces expériences en élargissant
l'étude à des systèmes biologiques comme des membranes par
exemple. Une étude, qui pourrait être complétée par
des expériences de dynamique moléculaire mais également
par des mesures thermiques.
De nombreuses pistes sont envisagées pour
étendre les recherches sur le sujet, comme l'étude de la
dynamique dans un autre milieu confinant comme des structures carbonées
par exemple. Les carbones présentant des interfaces plutôt
hydrophobes, les interactions de l'eau ou du sucre avec la surface en seront
profondément modifiées. D'autres pistes sont également
envisageables, comme l'étude de solutions confinées dans une
matrice lamellaire comme des argiles ou des membranes. Ce confinement
bidimensionnel pourrait ainsi induire des effets inattendus ou rendre
anisotrope les mouvements diffusifs si l'épaisseur atteinte est
suffisamment faible. L'utilisation d'autres techniques
expérimentales est également envisagée
pour étudier les effets du confinement. La RMN à gradient de
champ pulsé, par exemple, serait particulièrement
intéressante car tout comme la diffusion de neutrons, elle permet de
sonder les dynamiques moléculaires, et permet également
d'accéder à des échelles temporelles différentes.
Des mesures Raman sont également envisagées. L'étude de
films minces de mono- ou de disaccharides nous paraît également
intéressante en raison de l'aspect bidimensionnel, mais également
en raison du très faible taux d'hydratation. Des mesures thermiques
(DSC, ATD) ou de diffusion de neutrons (scans élastiques) nous
permettraient de déterminer la température de transition vitreuse
de ces films en fonction de l'épaisseur.
Enfin, les nanosphères de silice méritent encore
de nombreuses investigations pour caractériser pleinement leur
structure. Des mesures de RMN du solide pourraient nous aider à
comprendre de manière plus détaillée les mécanismes
de formation lors de la synthèse. Une continuation des mesures de DRX et
de BET sur les échantillons non sphériques serait
également intéressante. Nous envisageons maintenant de
réduire la taille des sphères (< 100 nm), mais
également de modifier le diamètre des pores.
Annexe
Annexe: Les spectromètres
Les spectromètres à temps de vol
Le temps-de-vol (TOF) est une méthode
générale pour déterminer l'énergie d'un neutron en
mesurant
le temps qu'il met pour « voler » entre deux points. Des
neutrons de différentes énergies, et donc
de
différentes longueurs d'onde, se déplacent à
différentes vitesses : 2 = h mv où m est la masse du

neutron et v sa vitesse.
Ainsi, les neutrons de plus haute énergie se
déplacent plus rapidement et arrivent par conséquent dans un
temps plus court sur le détecteur que ceux d'énergie
inférieure. En mesurant le temps mis par un neutron pour atteindre le
détecteur, et en connaissant la distance
échantillon-détecteur, il est alors possible de calculer sa
vitesse et sa longueur d'onde (énergie). Ce calcul simple est à
la base même du TOF.
Deux types de spectromètres existent :
- les spectromètres en géométrie
directe dans lesquels l'énergie des neutrons incidents est
définie par un dispositif tel qu'un cristal ou un chopper, et
l'énergie finale est déterminée par le temps-de-vol.
- les spectromètres à
géométrie indirecte dans lesquels l'échantillon est
éclairé par un faisceau incident blanc. L'énergie des
neutrons incidents est déterminée par le temps-de-vol et celle
finale par un cristal ou un filtre.
(1) les spectromètres en géométrie
directe
Dans ce type d'instrument, les neutrons provenant de la
source sont envoyés sur l'échantillon, non pas de manière
continue, mais pulsés. Le faisceau incident est « haché
» à l'aide d'un ou plusieurs chopper(s). Des pulses de neutrons
monocinétiques atteignent l'échantillon à un temps
ts. Parmi l'infime partie des neutrons diffusés, la
majorité est diffusée élastiquement c'est-à-dire
sans échange d'énergie, et une minorité est
diffusée inélastiquement, c'est-à-dire avec une perte ou
un gain en énergie. Les neutrons arrivent au niveau des
détecteurs au temps tD où ils sont accumulés. Comme chaque
neutron présente un temps de parcours différent selon son
historique, une distribution de temps de vol est observée en fonction de
l'angle. Les temps de vol sont utilisés pour déterminer
l'énergie des neutrons en mesurant le temps qu'ils mettent, à
chaque pulse, pour parcourir la distance échantillon - détecteur.
La vitesse des neutrons froids, de l'ordre de 1000 à 2000
m.s-1, autorise la mesure de leur temps de parcours sur des
distances de quelques mètres avec une précision suffisante pour
en déduire
un spectre en énergie présentant trois domaines
distincts (Figure 83) :
Entre 0 et 1000gs/m : diffusion inélastique
(vibrations),
Entre 1000 et 2000 us/m : diffusion quasi-élastique
(réorientations, translations), Au niveau du pic : diffusion
élastique.
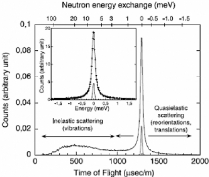
Figure 83 : Spectre typique obtenu sur un spectromètre
à temps de vol. L'encart présente le pic élastique.
Pour de plus amples détails concernant le
spectromètre à géométrie directe DCS (NIST)
utilisé dans cette thèse, nous vous invitons à consulter
le site suivant :
http://www.ncnr.nist.gov/instruments/dcs/
(2) les spectromètres à géométrie
indirecte ou à rétrodiffusion
Les spectromètres à rétrodiffusion sont
des instruments à géométrie indirecte dans lesquels seuls
les neutrons d'une énergie finale donnée sont
détectés. Les mouvements dans l'échantillon sont
sondés en modifiant l'énergie des neutrons incidents et en
mesurant le gain ou la perte en énergie qu'ils subissent lorsqu'ils
entrent en interaction avec la matière. Ces spectromètres
comportent un analyseur et un monochromateur, qui sont des cristaux parfaits
fonctionnant en rétrodiffusion. (Figure 84)
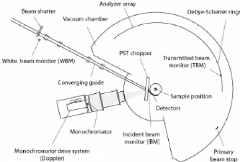
Figure 84 : Schéma d'un spectromètre à
rétrodiffusion
La spectroscopie de rétrodiffusion est basée
sur le fait que la dispersion en longueur d'onde d'un faisceau de neutrons
diffractés diminue lorsque l'angle de diffusion 20 avoisine 180°.
Ceci apparaît clairement lorsque l'on différencie la loi de Bragg
et si l'on divise le résultat par 2%, :
Lorsque 0 --> 00, le terme angulaire
disparaît. Ainsi, pour cette valeur la dispersion est minimale et ne
dépend plus que de d et de la valeur moyenne d correspondant à
l'espacement entre deux plans cristallins.
Pour de plus amples détails concernant les
spectromètres à rétrodiffusion utilisés dans cette
thèse, nous vous amenons à consulter les pages web suivantes :
- IN16 (ILL):
http://www.ill.fr/YellowBook/IN16/
- IRIS (ISIS) :
http://www.isis.rl.ac.uk/molecularspectroscopy/iris/
- HFBS (NCNR) :
http://www.ncnr.nist.gov/instruments/hfbs/HFBS
detailsNew.html
Les spectromètres de diffusion de neutrons aux petits
angles
Dans un spectromètre de diffusion, le faisceau incident
est focalisé par deux diaphragmes espacés d'une distance D. A la
sortie du collimateur, le faisceau est diffusé par l'échantillon,
puis traverse un tube à vide (non-représenté sur le
schéma), avant d'arriver au détecteur. Le détecteur
comptabilise le nombre de neutrons détectés pour chaque angle de
diffusion correspondant à chaque anneau.
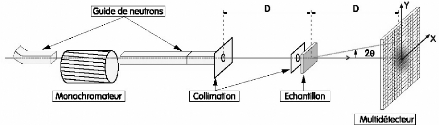
Figure 85 : Schéma d'un spectromètre pour
diffusion aux petits angles.214
Pour de plus amples détails concernant les
spectromètres SANS utilisés dans cette thèse, nous vous
invitons à consulter les pages web suivantes:
- NG-3 (NIST) :
http://www.ncnr.nist.gov/instruments/ng3sans/
- NG-7 (NIST) :
http://www.ncnr.nist.gov/instruments/ng7sans/
- PAXE (LLB) :
http://www-llb.cea.fr/spectros/spectro/g5-4.html
Bibliographie
1 P. Scott. Resurrection plants and the Secrets of
Eternal Leaf. Annals of Botany 85, 159, (2000).
2 M. Watanabe. Anhydrobiosis in invertebrates. Appl.
Entomol. Zool. 41 (1), 15, (2006).
3 J.C. Wright. Crytobiosis 300 years on from van
Leuwenhoek: what have we learned about Tardigrades ? Zool. Anz. 240, 563,
(2001).
4 F.A. Hoekstra, E.A. Golovina, J. Buitink. Mechanisms
of plant desiccation tolerance. Trends in Plant Science 6 (9), 431, (2001).
5 D.K. Hincha, M. Hagemann. Stabilization of model
membranes during drying by compatible solutes involved in the stress tolerance
of plants and microorganisms. Biochem. J. 383, 277, (2004).
6 L.M. Crowe. Lessons from nature: the role of sugars
in anhydrobiosis. Comparative Biochemistry and Physiology Part A 131, 505,
(2002).
7 A. Cesaro. All dried up. Nature Materials «News
& Views » 5, 593, (2006).
8 J. Lehmann. Carbohydrates: Structure and Biology,
p.8, Thieme, (1998).
9 A. Patist, H. Zoerb. Preservation mechanisms of
trehalose in food and biosystems. Colloids and Surfaces B: Biointerfaces 40,
107, (2005).
10 D.P. Miller, J.J. de Pablo. Calorimetric
Solution Properties of Simple Saccharides and Their Significance for the
Stabilization of Biological Structure and Function. J. Phys. Chem. B 104, 8876,
(2000).
11 J.L. Green, C.A. Angell. Phase relations and
vitrification in saccharide-water solutions and the trehalose anomaly. J. Phys.
Chem. 93, 2880, (1989).
12 Cf. le site Web de la London South Bank University
dédié à l'eau et ses propriétés à
l'adresse suivante:
http://www.lsbu.ac.uk/water/anmlies.html
13 D.R. Lide, CRC Handbook of Chemistry and Physics,
Internet Version 2005,
http://www.hbcpnetbase.com,
CRC Press, Boca Raton, FL, 2005.
14 P. G. Debenedetti. Supercooled and glassy water. J.
Phys.: Condens. Matter 15, R1669, (2003).
15 H.S. Frank, W.A.P. Luck (Ed.). Structure of water
and aqueous solutions. p. 10-47, Veinheim: Verlag Chemie, (1974).
16 M. Mathlouthi. Water content, water activity, water
structure and the stability of foodstuffs. Food Control 12, 409, (2001).
17 J. Israelachvili, H. Wennerstrom. Role of hydration
and water structure in biological and colloidal interactions. Nature 379
(6562), 219, (1996).
18 A. Tongraar, B.M. Rode. Ab Initio QM/MM dynamics of
anion-water hydrogen bonds in aqueous solution. Chem. Phys. Lett. 403, 314,
(2005).
19 R. Chitra, P.E. Smith. Molecular Association in
Solution : A Kirkwood-Buff Analysis of Sodium Chloride, Ammonium, Sulfate,
Guanidium Chloride, Urea and 2,2,2-Trifluoroethanol in Water. J. Phys. Chem. B
106, 1491, (2002).
20 C.W. Bock, G.D. Markham, A.K. Katz, J.P. Glusker.
The arrangement of first- and second-shell water molecules around metal ions:
effects of charge and size. Theor. Chem.Acc. 115, 100, (2006).
21 H.S. Frank, W.Y. Wen. Structural aspects of
ion-solvent interactions in aqueous solutions: a suggested picture of water
structure. Disc. Farad. Soc. 24, 133, (1957).
22 G. Barone, V. Crescenzi, V. Vitagliano. Potassium
Chloride Conductancein Aqueous Solution of a Structure-Forming Nonionic Solute,
Hexamethylenetramine. J. Phys. Chem. 72, 2588, (1968).
23 K. Buijs, G.R. Choppin. Near-Infrared Studies of
the Structure of Water. I. Pure Water. J. Chem. Phys. 39 (8), 2035, (1963).
24 C. Branca, S. Maccarrone, S. Magazù, G.
Maisano, S.M. Bennington, J. Taylor. Tetrahedral order in homologous
disaccharide-water mixtures. J. Chem. Phys. 122, 174513, (2005).
25 S.L. Lee, P.G. Debenedetti, J.R. Errington. A
computational study of hydration, solution structure, and dynamics in dilute
carbohydrate solutions. J. Chem. Phys. 122, 204511, (2005).
26 S. Lawrence, P.G. Debenedetti, J.R. Errington. A
computational study of hydration, solution structure, and dynamics in dilute
carbohydrate solutions. J. Chem. Phys. 122, 204511, (2005).
27 R. Giangiacomo. Study of water-sugar interactions
at increasing sugar concentration by NIR spectroscopy. Food Chemistry 96, 371,
(2006).
28 M.E. Gallina, P. Sassi, M. Paolantoni, A.
Morresi, R.S. Cataliotti. Vibrational Analysis of Molecular Interactions in
Aqueous Glucose Solutions. Temperature and Concentration Effects. J. Phys.
Chem. B 110, 8856, (2006).
29 J.L. Dashnau, K.A. Sharp, J.M. Vanderkooi.
Carbohydrate Intramolecular Hydrogen Bonding Cooperativity and its Effects on
Water Structure. J. Phys. Chem. B 109, 24152, (2005).
30 Q. Liu, J.W. Brady. Anisotropic Solvent Structuring
in Aqueous Sugar Solutions. J. Am. Chem. Soc. 118, 12276, (1996).
31 C. Branca, S. Magazù, F. Migliardo, P.
Migliardo. Destructuring effect of trehalose on the tetraedral network of
water: a Raman and neutron diffraction comparison. Physica A. 304, 314,
(2002).
32 J. Wolfe, G. Bryant. Freezing, Drying, and/or
Vitrification of Membrane-Solute-Water Systems. Cryobiology 39, 103, (1999).
33 T. Sei, T. Gonda, Y. Arima. Growth rate and
morphology of ice crystals growing in a solution of trehalose and water. J.
Crystal Growth 240, 218, (2002).
34 A. Lerbret, P. Bordat, F. Affouard, Y. Guinet,
A. Hédoux, L. Paccou, D. Prévost, M. Descamps. Influence of
homologous disaccharides on the hydrogen-bond network of water: complementary
Raman scattering experiments and molecular dynamics simulations. Carbohydrate
Research 340, 881, (2005).
35 C. Branca, S. Magazù, G. Maisano, P.
Migliardo. Anomalous cryoprotective effectiveness of trehalose: Raman
scattering evidences. J. Chem. Phys. 111 (1), 281, (1999).
36 C. Branca, S. Magazù, G. Maisano, P.
Migliardo, A.K. Söper. Study on Destructuring effect of
trehalose on water by neutron diffraction. Appl. Phys. A 74,
S450, (2002).
37 P. Bordat, A. Lerbret, J.-P. Demaret, F. Affouard,
M. Descamps. Comparative study of trehalose, sucrose and maltose in water
solutions by molecular modelling. Europhys. Lett. 65 (1), 41, (2004).
38 Y. H. Yoon, J.M. Pope, J. Wolfe. The Effects of
Solutes on the Freezing Properties and Hydration Forces in Lipid Lamellar
Phases. Biophys. J. 74, 1949, (1998).
39 F. Affouard, P. Bordat, M. Descamps, A. Lerbret,
S. Magazù, F. Migliardo, A.J. Ramirez-Cuesta, M.F.T. Telling. A combined
neutron scattering and simulation study on bioprotectant systems. Chem. Phys.
317, 258, (2005).
40 A. Lerbret. Etude de l'action bioprotectrice des
sucres: une investigation par dynamique moléculaire et spectroscopie
Raman. Thèse de Doctorat, Université des Sciences et Technologies
de Lille, 2005.
41 V. Molinero, T. Cagin, W.A. Goddard III. Sugar,
water and free volume networks in concentrated sucrose solutions. Chem. Phys.
Lett. 377, 469, (2003).
42 B. Leroux, H. Bizot, J.W. Brady, V. Tran. Water
structuring around complex solutes: theoretical modeling of -D-glucopyranose.
Chem. Phys. 216, 349, (1997).
43 K.S. Sidhu, J.M. Goodfellow, J.Z. Turner. Effect of
molecular shape and electrostatic interactions on the water layer around polar
and apolar groups in solution. J. Chem. Phys. 110 (16), 7943, (1999).
44 P.E. Mason, G.W. Neilson, A.C. Barnes, J.E.
Enderby, J.W. Brady, M.-L. Saboungi. Neutron diffraction studies on aqueous
solutions of glucose. J. Chem. Phys. 119 (6), 3347, (2003).
45 K. Fuchs, U. Kaatze. Molecular Dynamics of
Carbohydrate Aqueous Solutions. Dielectric Relaxation as a Function of Glucose
and Fructose Concentration. J. Phys. Chem. B 105, 2036, (2001).
46 R.K. Schmidt, M. Karplus, J.W. Brady. The Anomeric
Equilibrium in D-Xylose: Free Energy and the Role of Solvent Structuring. J.
Am. Chem. Soc. 118, 541, (1996).
47 M.C. Donnamaria, E.I. Howard, J.R. Grigera.
Interaction of Water with -Trehalose in Solution:
Molecular Dynamics Simulation Approach. J. Chem. Soc. Faraday
Trans. 90 (18), 2731, (1994).
48 Y. Choi, K.W. Cho, K. Jeong, S. Jung. Molecular
dynamics of trehalose as a »dynamic reducer» for solvent water
molecules in the hydration shell. Carbohydr. Res. 341, 1020, (2006).
49 C.J. Roberts, P.G. Debenedetti. Structure and
Dynamics in Concentrated, Amorphous CarbohydrateWater Systems by Molecular
Dynamics Simulation. J. Phys. Chem. B 103, 7308, (1999).
50 S.N. Timasheff. Protein Hydration, Thermodynamic
Binding, and Preferential Hydration. Biochemistry 41 (6), 13474, (2002).
51 J.H. Crowe, F.A. Hoekstra, L.M. Crowe.
Anhydrobiosis. Ann. Rev. Physiol. 54, 579, (1992).
52 S. Chianta, N. Kahya, P. Schwille. Dehydration
Damage of Domain-Exhibiting Supported Bilayers: An AFM Study on the Protective
Effects of Disaccharides and Other Stabilizing Substances. Langmuir 21, 6317,
(2005).
53 L.M. Crowe, J.H. Crowe, A. Rudolph, C. Wormersley,
L. Appel. Preservation of freeze-dried liposomes by trehalose. Arch. Biochem.
Biophys. 242, 240, (1985).
54 M.A. Villareal, S.B. Diaz, E. Anibal Disalvo, G.G.
Montich. Molecular Dynamics Simulation of the Interaction of Trehalose with
Lipid Membranes. Langmuir 20, 7844, (2004).
55 C. Lambruschini, A. Relini, A. Ridi, L. Cordone,
A. Gliozzi. Trehalose Interacts with Phospholipid Polar Heads in Langmuir
Monolayers. Langmuir 16, 5467, (2000).
56 B.W. Lee, R. Faller, A.K. Sum, I. Vattulainen,
M. Patra, M. Karttunen. Structural effects of small molecules on phospholipid
bilayers investigated by molecular simulations. Fluid Phase Equilibria 228-229,
135, (2005).
57 C.S. Pereira, P.H. Hünenberger. Interaction
of the Sugars Trehalose, Maltose and Glucose with a Phospholipid Bilayer: A
Comparative Molecular Dynamics Study. J. Phys. Chem. B 110, 15572, (2006).
58 T. Matsuoka, T. Okada, K. Murai, S. Koda, H.
Nomura. Dynamics and hydration of trehalose and maltose in concentrated
solutions. J. Molecular Liquids 98-99, 317, (2002).
59 A.K. Sum, R. Faller, J.J. de Pablo. Molecular
Simulation Study of Phospholipid Bilayers and Insights of the Interactions with
Disaccharides. Biophys. J. 85, 2830, (2003).
60 J.H. Crowe, J.F. Carpenter, L.M. Crowe. The role
of vitrification in anhydrobiosis. Annu. Rev. Physiol. 60, 73, (1998).
61 J.H. Crowe, A.E. Oliver, F.A. Hoekstra, L.W.
Crowe. Stabilization of Dry Membranes by Mixtures of Hydroxyethyl Starch and
Glucose: The role of vitrification. Cryobiology 35, 20, (1997).
62 F. Affouard, P. Bordat, M. Descamps, A. Lerbret,
S. Magazù, F. Migliardo, A.J. Ramirez-Cuesta, M.F.T. Telling. A combined
neutron scattering and simulation study on bioprotectant systems. Chem. Phys.
317, 258, (2005).
63 C. Branca, S. Magazù, G. Maisano, P.
Migliardo, E. Tettamanti. On the bioprotective effectiveness of trehalose:
ultrasonic technique, Raman scattering and NMR investigations. J. Molecular
Structure 480-481, 133, (1999).
64 C. Branca, S. Magazù, G. Maisano, P.
Migliardo, M.T.F. Telling. Temperature Evolution of the Diffusive Dynamics of
Disaccharide Aqueous Solutions by Quasielastic Neutron Scattering. J. Phys.
Chem. B 108, 17069, (2004).
65 N. Ekdawi-Sever, J.J. de Pablo, E. Feick, E. von
Meerwall. Diffusion of Sucrose and -Trehalose
in Aqueous Solutions. J. Phys. Chem. A 107, 936, (2003).
66 A. Faraone, S. Magazà, R.E. Lechner, S.
Longeville, G. Maisano, D. Majolino, P. Migliardo, U. Wanderlingh. Quasielastic
neutron scattering from trehalose aqueous solutions. J. Chem. Phys. 115 (7),
3281, (2001).
67 I. Köper, M.-C. Bellissent, W. Petry.
Dynamics from picoseconds to nanoseconds of trehalose in aqueous solutions as
seen by quasielastic neutron scattering. J. Chem. Phys. 122, 014514, (2005).
68 S. Magazù, R.E. Lechner, S. Longeville, G.
Maisano, D. Majolino, P. Migliardo, U. Wanderlingh. Diffusive dynamics in
trehalose aqueous solutions by QENS. Physica B 276-278, 475, (2000).
69 S. Magazù, P. Migliardo, M.T.F. Telling.
-Trehalose-Water Solutions. VIII. Study of the
Diffusive Dynamics of Water by High-Resolution Quasi Elastic
Neutron Scattering. J. Phys. Chem. B 110, 1020, (2006).
70 S. Magazù, V. Villari, P. Migliardo, G.
Maisano, M.T.F. Telling. Diffusive Dynamics of Water in the Presence of
Homologous Disaccharides: A Comparative Study by Quasi Elastic Neutron
Scattering. IV. J. Phys. Chem. B 105, 1851, (2001).
71 D.P. Miller, J.J. de Pablo, H. Corti.
Thermophysical Properties of Trehalose and Its Concentrated Aqueous Solutions.
Pharmaceutical Research 14 (5), 578, (1997).
72 C. Branca, S. Magazù, G. Maisano, F.
Migliardo, P. Migliardo, G. Romeo. -Trehalose/Water
Solutions. 5. Hydration and Viscosity in Dilute and Semidilute
Disaccharide Solutions. J. Phys. Chem. B 105, 10140, (2001).
73 N.C. Ekdawi-Sever, P.B. Conrad, J.J. de Pablo.
Molecular Simulation of Sucrose Solutions near the Glass Transition
Temperature. J. Phys. Chem. A 105, 734, (2001).
74 P.B. Conrad, J.J. de Pablo. Computer Simulation of
the Cryoprotectant Disaccharide -Trehalose
in Aqueous Solution. J. Phys. Chem. A 103, 4049, (1999).
75 L.J. Smith, D.L. Price, Z. Chowdhuri, J.W. Brady,
M.-L. Saboungi. Molecular dynamics of glucose in solution: A quasielastic
neutron scattering study. J. Chem. Phys. 120 (8), 3527, (2004).
76 C. Talon, L.J. Smith, J.W. Brady, B.A. Lewis,
J.R.D. Copley, D.L. Price, M.-L. Saboungi. Dynamics of Water Molecules in
Glucose Solutions. J. Phys. Chem. B 108, 5120, (2004).
77 G.R. Moran, K.R. Jeffrey. A study of the molecular
motion in glucose/water mixtures using deuterium nuclear magnetic resonance. J.
Chem. Phys. 110 (7), 3472, (1999).
78 M. Rampp, C. Buttersack, H.-D. Lüdemann.
c,T-Dependence of the viscosity and the self-diffusion coefficients in some
aqueous carbohydrate solutions. Carb. Res. 328, 561, (2000).
79 M. Feeney, C. Brown, A. Tsai, D. Neumann, P.G.
Debenedetti. Incoherent Quasi-elastic Neutron Scattering from Fructose/Water
Solutions. J. Phys. Chem. B 105, 7799, (2001).
80 K. Sköld, D.L. Price (Eds.) dans Methods of
Experimental Physics Volume 23 - Part A Neutron Scattering. Chapitre 1:
Introduction to Neutron Scattering. Academic Press, (1986).
81 G.L. Squires (Eds.) dans Introduction to the Theory
of Thermal Neutron Scattering. Chapitre 1: Introduction & Chapitre 2:
Nuclear scattering - basic theory, Cambridge University Press, (1978).
82 D.L. Price. Inelastic and quasielastic neutron
scattering. Curr. Opinion in Solid State & Material Science 2, 477,
(1997).
83 J.-P. Cotton. Diffraction et spectrométrie
des neutrons. Techniques de l'ingénieur. PE 1 095, (1996).
84 A.-J. Dianoux, G. Lander (Eds.). dans Neutron Data
Booklet. Institut Laue-Langevin, (2002).
85 J.R. Copley, J.C. Cook. The Disk Chopper
Spectrometer at NIST: a new instrument for quasielastic neutron scattering
studies. Chem. Phys. 292, 477, (2003).
86 A. Meyer, R.M. Dimeo, P.M. Gehring, D.A. Neumann.
The high-flux backscattering spectrometer
at the NIST Center for Neutron Research. Rev. Sci. Instrum. 74,
2759, (2003).
87 La série de programmes DAVE a
été utilisée pour déterminer la fonction de
diffusion S(Q,E). DAVE est téléchargeable gratuitement à
l'adresse
http://www.ncnr.nist.gov/dave/
.
88 M. Bée dans Quasielastic Neutron Scattering:
Principles and applications in Solid State Chemistry, Biology, and Materials
Science. Adam Hilger, Bristol (1998).
89 A. Einstein. Uber die von der molekularkinetischen
Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten
suspendierten Teilchen von A. Einstein. Ann. Phys. Leipzig 17, 549, (1905).
90 C.T. Chudley, R.J. Elliott. Neutron Scattering from
a Liquid on a Jump Diffusion Model. Proc. Phys. Soc. 77, 353, (1961).
91 K.S. Singwi, A. Sjölander. Diffusive Motions
in Water and Cold Neutron Scattering. Phys. Rev. 119 (3), 863, (1960).
92 J. Teixeira, M.-C. Bellissent-Funel, S.-H. Chen,
A.J. Dianoux. Experimental determination of the nature of diffusive motions of
water molecules at low temperature. Phys. Rev. A 31 (3), 1913, (1985).
93 V.F. Sears. Theory of cold neutron scattering by
homonuclear diatomic liquids. 2. Hindered rotation. Can. J. Phys. 44 (6), 1299,
(1966).
94 J.W. Brady, C. Talon, M.-L. Saboungi. Dynamics of
D-glucose-Water Systems by Molecular Dynamics Simulations. Communication
interne.
95 M.A. Adams, W.S. Howells, M.T.F. Telling. The IRIS
User Guide, 2nd edition, Rutherford Appleton Laboratory Technical Report
(RAL-TR-2001-002, 2001).
96 M.T.F. Telling, W.S. Howells. GUIDE - IRIS data
analysis, ISIS Facility, Rutherford Appleton Laboratory (2000), & W. S.
Howells, MODES manual, ISIS Facility, Rutherford Appleton Laboratory (2003).
97 L. Liu, A. Faraone, C.-Y. Mou, C.-W. Yen, S.-H.
Chen. Slow dynamics of supercooled water confined in nanoporous silica
materials. J. Phys.: Condens. Matter 16, S5403, (2004).
98 M.-C. Bellissent-Funel. Status of experiments
probing the dynamics of water in confinement. Eur. Phys. J. E 12, 83,
(2003).
99 A. Faraone, L. Liu, C.-Y. Mou, P.-C. Shih,
J.R.D. Copley, S.-H. Chen. Translational and rotational dynamics of water in
mesoporous silica materials: MCM-41-S and MCM-48-S. J. Chem. Phys. 119(7),
3963, (2003).
100 F. Mansour, R.M. Dimeo, H. Peemoeller.
High-resolution inelastic neutron scattering from water in mesoporous silica.
Phys. Rev. E 66, 041307, (2002).
101 C. J. Brinker, G.W. Scherer, Sol-Gel Science: The
Physics and Chemistry of Sol-Gel Processing, Academic Press, (1990).
102 J. Livage. Sol-Gel Processes. Current Opinion in
Solid State & Materials Science. 2, 132, (1997).
103 C.J. Brinker, G.W. Scherer. Sol Gel Glass: I.
Gelation and Gel Structure. J. Non-Cryst. Solids 70, 301, (1985).
104 R.K. Iler. The Chemistry of Silica : Solubility,
Polymerization, Colloid and Surface Properties, and Biochemistry. Wiley
Interscience, (1979).
105 J. Livage, M. Henry, C. Sanchez. Sol-Gel Chemistry
of Transition Metal Oxides. Progress in Solid State Chemistry 18 (4), 259,
(1988).
106 A.C. Pierre. Introduction aux
Procédés Sol-Gel. Editions Septima, Paris, (1992).
107 J. Philippou, L. Kocon. Elaboration des gels et
des aérogels. Techniques de l'ingénieur. J2, 230, (2004).
108 P. Audebert, F. Miomandre. Procédé
sol-gel de polymérisation. AM 3, 048, (2005).
109 I. Jaymes, A. Douy, D. Massiot. Synthesis of a
Mullite Precursor from Aluminium Nitrate and Tetraethoxysilane via Aqueous
Homogeneous Precipitation: An 27Al and 29Si Liquid- and
Solid-State NMR Spectroscopic Study. J. Am. Ceram. Soc. 78 (10), 2648,
(1995).
110 G. Lelong, D.L. Price, A. Douy, S. Kline, J.W.
Brady, M.-L. Saboungi. Molecular dynamics of confined glucose solutions. J.
Chem. Phys. 122, 164504, (2005).
111 M. Kaèuráková, M. Mathlouthi.
FTIR and laser-Raman spectra of oligosaccharides in water : characterization of
the glycosidic bond. Carbohydrate Research 284, 145, (1996).
112 M. Mathlouthi, C. Luu, A.M. Meffroy-Biget, D.V.
Luu. Laser-Raman Study of Solute-Solvent Interactions in Aqueous Solutions of
D-Fructose, D-glucose and Sucrose. Carbohydrate Research 81, 213, (1980).
113 M. Mathlouthi, D.V. Luu. Laser-Raman Spectra of
D-glucose and sucrose in Aqueous Solution. Carbohydrate Research 81, 203,
(1980).
114 G.E. Walrafen. Raman Spectral Studies of Water
Structure. J. Chem. Phys. 40 (11), 3249, (1964).
115 R.L. Frost, J. Kristof, L. Rintoul, J.T.
Kloprogge. Raman spectroscopy of urea-intercalated kaolinites at 77K.
Spectrochimica Acta Part A 56, 1681, (2000).
116 C.G. Windsor. An Introduction to Small-Angle
Neutron Scattering. J. Appl. Cryst. 21, 582, (1988).
117 S.-H. Chen, T.-S. Lang dans Methods of
Experimental Physics Volume 23 - Part B Neutron Scattering. Chapitre 16:
Colloidal Solutions. Academic Press, (1986).
118
J.S. Higgins, H.C. Benoit dans Polymers and Neutron Scattering.
Chapitre 4: Theoretical Basis of Scattering et Chapitre 6: Form Factors.
Clarendon Press - Oxford, (1994).
119 P. Lidnen, T. Zemb dans Neutron, X-ray and Light
Scattering. North-Holland, (1991).
120 C.J. Glinka, J. Barker, B. Hammouda, S.
Krueger, J. Moyer, W. Orts. The 30 m Small-Angle Neutron Scattering Instruments
at the National Institute of Standards and Technology. J. Appl. Cryst. 31 (3),
430, (1998).
121 T. Freltoft, J.K. Kjems, S.K. Sinha. Power-law
correlations and finite-size effects in silica particleaggregates studied by
small-angle neutron scattering. Phys. Rev. B 33 (1), 269, (1986).
122 J. Teixeira. Small-angle scattering by fractals
systems. J. Appl. Crystallogr. 21, 781, (1988).
123 D.W. Schaefer, K.D. Keefer dans Better Ceramics
Through Chemistry. C.J. Brinker (Eds), D.E.
Clark (Eds), D.R. Ulrich (Eds) . Elsevier North-Holland,
New-York, (1984).
124 F. Ricoul, M. Dubois, T. Zemb. Adsorption Study on
DDAB Bilayers Using Contrast Variation with SANS. J. Phys. II France 7, 69,
(1997).
125 B. Demé, T. Zemb. Measurement of sugar
depletion from uncharged lamellar phases by SANS contrast variation. J. Appl.
Cryst. 33, 569, (2000).
126 B. Demé, M. Dubois, T. Zemb, B. Cabane.
Effect of Carbohydrates on the Swelling of a Lyotropic Lamellar Phase. 100,
3828, (1996).
127 D. Lairez, J. Pelta. Diffusion de neutrons aux
petits angles : application à l'étude des macromolécules
biologiques en solution. J. Phys. IV France 1, 1, (2004).
128 J.P. Cotton. Variations on contrast in SANS:
determination of self and distinct correlations functions. Advances in Colloid
and Interface Science 69, 1, (1996).
129 C.J. Glinka, J. Barker, B. Hammouda, S.
Krueger, J. Moyer, W. Orts. The 30 m Small-Angle Neutron Scattering Instruments
at the National Institute of Standards and Technology. J. Appl. Cryst. 31 (3),
430, (1998).
130 U. Keiderling. A. Wiedenmann. New SANS Instrument
at the BER II Reactor in Berlin, Germany. Physica B 213-214, 895, (1995).
131 Le logiciel BerSANS peut être
téléchargé sur le site du BENSC à l'adresse
suivante :
http://www.hmi.de/bensc/instrumentation/instrumente/v4/v4
en.htm
132 S.B. Engelsen, C. Monteiro, C. Hervé de
Penhoat, S. Pérez. The diluted aqueous solvation of carbohydrates as
inferred from molecular dynamics simulations and NMR spectroscopy. Biophys. J.
93, 103, (2001).
133 A. Lerbret, J.W. Brady. Simulations de dynamique
moléculaire du tréhalose dans des gels de silice. Communication
Interne.
134 T. Yanagisawa, T. Shimizu, K. Kuroda, C. Kato.
The Preparation of AlkyltrimethylammoniumKanemite Complexes and Their
Conversion to Mesoporous Materials. Bull. Chem. Soc. Jpn. 63, 988, (1990).
135 S. Inagaki, Y. Fukushima, K. Kuroda. Synthesis of
Highly Ordered Mesoporous Materials From a Layered Polysilicate. J. Chem. Soc.,
Chem. Commun. 1993, 680, (1993).
136 C.T. Kresge, M.E. Leonowicz, W.J. Roth, J.C.
Vartuli, J.S. Beck. Ordered Mesoporous Molecular Sieves synthesized by a
Liquid-Crystal Template Mechanism. Nature. 359, 710, (1992).
137J. S. Beck, J.C. Vartuli, W.J. Roth, M.E.
Leonowicz, C.T. Kresge, K.D. Schmitt, C.T.W. Chu, D.H. Olsen, E.W. Sheppard,
S.B. McCullen, J.B. Higgins, J.L. Schlenker. A New Family of Mesoporous
Molecular Sieves Prepared with Liquid Crystal Templates. J. Am. Chem. Soc. 114,
10835, (1992 ).
138 J.S. Beck. US Patent 5,057,296, (1991).
139 C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C.
Vartuli. US Patent 5,102,643, (1992).
140 C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C.
Vartuli. US Patent 5,102,643, (1992).
141 V. Chiola, J.E. Ritsko, C.D. Vanderpool. US Patent
3 556 725, (1971).
142 F. Di Renzo, H. Cambon, R. Dutartre. A 28-year-old
synthesis of micelle-templated mesoporous silica. Microporous Materials 10,
283, (1997).
143 D. Zhao, J. Feng, Q. Huo, N. Melosh, G.H.
Fredrickson, B.F. Chmelka, G.D. Stucky. Triblock Copolymer Syntheses of
Mesoporous Silica with Periodic 50 to 300 Å Pores. Science. 279, 548,
(1998).
144 Q. Huo, D.I. Margolese, U. Ciesla, P. Feng,
T.E. Gier, P. Sieger, R. Leon, P.M. Petroff, F. Schüth, G.D. Stucky.
Generalized Synthesis of Periodic Surfactant/Inorganic Composite Materials.
Nature. 368, 317, (1994).
145 P. Feng, X. Bu, G.D. Stucky, D.J. Pine. Monolithic
Mesoporous Silica Templated by Microemulsion Liquid Crystals. J. Am. Chem. Soc.
122, 994, (2000).
146 C.Y. Chen, S.Q. Xiao, M.E. Davis. Studies on
Ordered Mesoporous Materials III. Comparison of MCM-41 to Mesoporous Materials
Derived from Kanemite. Microp. Mater. 4, 1, (1995).
147 C.S. Cundy, P.A. Cox. The Hydrothermal Synthesis
of Zeolites: History and Development from the Earliest Days to the Present
Time. Chem. Rev. 103, 663, (2003).
148 T. Linssen, K. Cassiers, P. Cool, E.F. Vansant.
Mesoporous templated silicates: an overview of their synthesis, catalytic
activation and evaluation of the stability. Advances in Colloid and Interface
Science 103, 121, (2003).
149 P. Selvam, S.K. Bhatia, C.G. Sonwane. Recent
Advances in Processing and Characterization of Periodic Mesoporous MCM-41
Silicate molecular Sieves. Ind. Eng. Chem. Res. 40, 3237, (2001).
150 G.J. de A.A. Soler-Illia, C. Sanchez, B.
Lebeau, J. Patanin. Chemical Strategies to Design Textured Materials: from
Microporous and Mesoporous Oxides to Nanonetworks and Hierarchical Structures.
Chem. Rev. 102, 4093, (2002).
151 D. Myers dans Surfactant Science and Technology,
VCH, New York, (1992).
152 J.Y. Ying, C.P. Mehnert, M.S. Wong. Synthesis and
Applications of Supramolecular-Templated Mesoporous Materials. Angew. Chem.,
Int. Ed. 38, 56, (1999).
153 X.S. Zhao, G.Q.M. Lu, G.J. Miller. Advances in
Mesoporous Molecular Sieve MCM-41. Ind. Eng. Chem. Res. 35, 2075,(1996).
154 V. Meynen. Synthesis and characterization of a new
generation of materials with bimodal porosity. Thèse de Doctorat,
Faculté des Sciences, Université d'Anvers, 2006.
155 N.K. Raman, M.T. Anderson, C.J. Brinker.
Template-Based Approaches to the Preparation of Amorphous, Nanoporous Silicas.
Chem. Mater. 8, 1682, (1996).
156 I. Soten, G.A.Ozin. Supramolecular Organization
and Materials Design. W. Jones, C.N.R. Rao, eds., Cambridge University Press:
Cambridge, UK, p. 34, (2002).
157 S. Han, W. Hou, J. Xu, Z. Li. Synthesis of hollow
spherical silica with MCM-41 mesoporous structure. Colloid Polym. Sci. 282
(11), 1286, (2004).
158 Y. Zhu, J. Shi, H. Chen, W. Shen, X. Dong. A
facile method to synthesize novel hollow mesoporous silica spheres and advanced
storage property. Microporous Mesoporous Mater. 84, 218, (2005).
159 E. Van Bavel, P. Cool, K. Aerts, E.F. Vansant.
Morphology variations of Plugged Hexagonal Templated Silica. J. Porous. Mater.
12, 65-69, (2005).
160 D. Zhao, J. Sun, Q. Li, G.D. Stucky. Morphological
Control of Highly Ordered Mesoporous Silica SBA-15. Chem. Mater. 12, 275,
(2000).
161 S. Huh, J.W. Wiench, J.-C. Yoo, M. Pruski, V.
S.-Y. Lin. Organic Functionalization and Morphology Control of Mesoporous
Silicas via a Co-Condensation Synthesis Method. Chem. Mater. 15, 4247,
(2003).
162 S. Bhattacharyya, G. Lelong, M.-L. Saboungi.
Recent progress in the synthesis and selected applications of MCM-41 : a short
review. Journal ofExperimental Nanoscience 1 (3), 375, (2006).
163 W. Stöber, A. Funk, E. Bohn. Controlled
growth of monodisperse silica spheres in the micron size range. Journal of
Colloid and Interface Science. 26 (1), 62 (1968).
164 M. Grün, I. Lauer, K.K. Unger. The synthesis
of micrometer- and submicrometer-size spheres of ordered mesoporous oxide
MCM-41. Adv. Mater. 9 (3), 254, (1997).
165 M. Kruk, M. Jaroniec. Accurate Method for Calculating
Mesopore Size Distributions from Argon Adsorption Data at 87 K Developed Using
Model MCM-41 Materials. Chem. Mater. 12, 222, (2000).
166 C.-Y. Mou, H.-P. Lin. Control of morphology in
synthesizing mesoporous silica. Pure Appl. Chem. 72, 137, (2000).
167 K.K. Unger, D. Kumar, M. Grün, G.
Bückel, S. Lüdtke, T. Adam, K. Schumacher,S.J. Renker. Synthesis of
spherical porous silicas in the micron and submicron size range: challenges and
opportunities for miniaturized high-resolution chromatographic and
electrokinetic separations. Journal of Chromatography A. 892 (1-2), 47,
(2000).
168 R.I. Nooney, D. Thirunavukkarasu, Y. Chen, R.
Josephs, A.E. Ostafin. Synthesis of Nanoscale Mesoporous Silica Spheres with
Controlled Particle Size. Chem.Mater. 14, 4721, (2002).
169 Y. Ma, -* .
L Qi, J. Ma, Y. Wu, O. Liu, H. Cheng. Large-pore mesoporous
silica spheres: synthesis and application in HPLC. Colloids and Surfaces A. 229
(1-3), 1, (2003).
170 K. Yano, Y.J. Fukushima. Particle size control of
mono-dispersed super-microporous silica spheres. J. Mater. Chem. 13 (10), 2577,
(2003).
171 H. Yang, G. Vovk, N. Coombs, I. Sokolov, G.A.
Ozin. Synthesis of mesoporous silica spheres under quiescent aqueous acidic
conditions. J. Mater. Chem. 8 (3), 743, (1998).
172 Q. Huo, J. Feng, F. Schüth, G.D. Stucky.
Preparation of Hard Mesoporous Silica Spheres. Chem. Mater. 9, 14, (1997).
173 Y. Miyake, T. Kato. The formation process of
spherical mesoporous silica with reverse nanostructure of MCM-41 in a two-phase
system. J. Chem. Eng. Japan, 38 (1), 60, (2005).
174 S. Liu, P. Cool, O. Collart, P. Van Der Voort,
E.F. Vansant, O.I. Lebedev, G. Van Tendeloo, M. Jiang. The influence of the
alcohol concentration on the structural ordering of mesoporous silica:
Cosurfactant versus cosolvent. J. Phys. Chem. B. 107, 10405, (2003).
175 G. Van Tendeloo, O.I. Lebedev, O. Collart, P. Cool
and E.F. Vansant. Structure of nanoscale mesoporous silica spheres? J. Phys.
Condens. Matter. 15, S3037, (2003).
176 O.I. Lebedev, G. Van Tendeloo, O. Collart, P.
Cool, E.F. Vansant. Structure and microstructure of nanoscale mesoporous silica
spheres. Solid State Sciences. 6, 489, (2004).
177 N. Israelachivi, D.J. Mitchell, B.W. Niham. Theory
of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J.
Chem. Soc., Faraday Trans. 72(2), 1525, (1976).
178 .-..
y Huo, D.I. Margolese, G.D. Stucky. Surfactant Control of Phases
in the Synthesis of Mesoporous
Silica-Based Materials. Chem. Mater. 8, 1147, (1996).
179 Y. Lu, H. Fan, A. Stump, T.L. Ward, T. Rieker,
C.J. Brinker. Aerosol-assisted self-assembly of mesostructured spherical
nanoparticles. Nature 398, 223, (1999).
180 B. Alonso, C. Clinard, D. Durand, E.
Vérona, D. Massiot. New routes to mesoporous silica-based spheres with
functionalised surfaces. Chem. Commun. 13, 1746, (2005).
181 N. Baccile, D. Grosso, C. Sanchez. Aerosol
generated mesoporous silica particles. J. Mater. Chem. 13, 3011, (2003).
182 M.T. Bore, S.B. Rathod, T.L. Ward, A.K. Datye.
Hexagonal Mesostructure in Powders Produced by Evaporation-Induced
Self-Assembly of Aerosols from Aqueous Tetraethoxysilane Solutions. Langmuir
19, 256, (2003).
183 B. Alonso, A. Douy, E. Véron, J. Perez,
M.-N. Rager, D. Massiot. Morphological and textural control of spray-dried
mesoporous silica-based spheres. J. Mater. Chem. 14, 1, (2004).
184 Y. -* , u
L R. Ganguli, C.A. Drewien, M.T. Anderson, C.J. Brinker, W.
Gong, Y. Guo, H. Soyez, B.
Dunn, M.H. Huang, J.I. Zink. Continuous formation of supported
cubic and hexagonal mesoporous films by sol-gel dip-coating. Nature 389, 364,
(1997).
185 C.J. Brinker, Y. Lu, A. Sellinger, H. Fan.
Evaporation-Induced Self-Assembly: Nanostructures Made Easy. Adv. Mater. 11,
579, (1999).
186 B. Alonso, A. Douy, E. Véron, J. Perez,
M.-N. Rager, D. Massiot. Morphological and textural control of spray-dried
mesoporous silica-based spheres. J. Mater. Chem. 14, 1, (2004).
187 S. Förster, A. Timmann, M. Konrad, C.
Schellbach, A. Meyer, S.S. Funari, P. Mulvaney, R. Knott. Scattering Curves of
Ordered Mesoscopic Materials. J. Phys. Chem. B 109, 1347, (2005).
188 K.J. Edler, P.A. Reynolds, J.W. White. Small-Angle
Neutron Scattering Studies on the Mesoporous Molecular Sieve MCM-41. J. Phys.
Chem. B 102, 3676, (1998).
189 J.D.F. Ramsay. Surface and pore structure
characterisation by neutron scattering techniques. Advances In Colloids and
Interface Science 76-77, 13, (1998).
190 .-..
y Cai, W.-Y. Lin, F.-S. Xiao, W.-Q. Pang, X.-H. Chen, B.-S. Zou.
The preparation of highly
ordered MCM-41 with extremely low surfactant concentration.
Microp. Mesop. Mat. 32, 1, (1999).
191 K.J. Edler, P.A. Reynolds, J.W. White. Small-Angle
Neutron Scattering Studies on the Mesoporous Molecular Sieves MCM-41. J. Phys.
Chem. B 102, 3676, (1998).
192 Les facteurs de formes utilisés ici ont
été calculés à partir des macros mises à la
disposition par le NCNR sur le site :
http://www.ncnr.nist.gov/programs/sans/data/available
SANS.html
193 S. Brunauer, S. Deming, L. Deming, E. Teller. On a
theory of the van der Walls Adsorption of Gases. J. Am. Chem. Soc. 62, 1723,
(1940).
194 IUPAC. Reporting Physisorption Data for Gas/Solid
Systems. Pure Appl. Chem. 87, 603, (1957).
195 C.G. Sonwane, S.K. Bhatia. Structural
Characterization of MCM-41 over a Wide Range of Length Scales. Langmuir 15,
2809, (1999).
196 U. Ciesla, F. Schüth. Ordered Mesoporous
Materials. Microporous Mesoporous Mater. 27, 131, (1999).
197 N. Floquet, J. Coulomb, N. Dufau, G. Andre, R.
Kahn. Confined Water in Mesoporous MCM-41 and Nanoporous AlPO4-5: Structure and
Dynamics. Adsorption 11, 139, (2005).
198 G.T. Gao, X.C. Zeng, H. Tanaka. The melting
temperature of proton-disordered hexagonal ice : A computer simulation of
4-site transferable intermolecular potential model of water. J. Chem. Phys. 112
(19), 8534, (2000).
199 A. Schreiber, I. Ketelsen, G.H. Findenegg. Melting
and freezing of water in ordered mesoporous silica materials. Phys. Chem. Chem.
Phys. 3, 1185, (2001).
200 A. Firouzi, D. Kumar, L.M. Bull, T. Besier, P.
Sieger, Q. Huo, S.A. Walker, J.A. Zasadzinski, C. Glinka, J. Nicol, D.
Margolese, G.D. Stucky, B.F. Chmelka, Cooperative organization of
inorganicsurfactant and biomimetic assemblies. Science 267, 1138, (1995).
201 Q.
Cai, Z.-S. Luo, W.Q. Pang, Y.-W. Fan, X.-H. Chen, F.-Z. Cui.
Dilute Solutions Routes to Various Controllable Morphologies of MCM-41 Silica
with a Basi Medium. Chem. Mater. 13, 258, (2001).
202 G. Büchel, K.K. Unger, A. Matsumoto, K.
Tsutsumi. A Novel Pathway for Synthesis of Submicrometer-Size Solid
Core/Mesoporous Shell Silica Spheres. Adv. Mater. 10 (13), 1036, (1998).
203 S. Mitra, R. Mukhopadhyay, I. Tsukushi, S. Ikeda.
Dynamics of water in confined space (porous alumina): QENS study. J. Phys.:
Condens. Matter. 13, 8455, (2001).
204 M.-C. Bellissent-Funel, S.H. Chen, J.-M. Zanotti.
Single-particle dynamics of water molecules in confined space. Phys. Rev. B 51
(5), 4558, (1995).
205 J. Banys, M. Kinka, J. Macutkevic, G.
Völkel, W. Böhlmann, V. Umamaheswari, M. Hartmann, A. Pöppl.
Broadband dielectric spectroscopy of water confined in MCM-41 molecular sieve
materials - low-temperature freezing phenomena. J. Phys.: Condens. Matter. 17,
2843, (2005).
206 B. Grünberg, T. Emmler, E. Gedat, I.
Shenderovitch; G.H. Findenegg, H.-H. Limbach, G.
Buntkowsky. Hydrogen
Bonding of Water Confined in Mesoporous Silica MCM-41 and SBA-15
Studied by 1H Solid-State NMR. Chem. Eur. J. 10, 5689,
(2004).
207 S. Takahara, S. Kittaka, T. Mori, Y. Kuroda, T. Yamaguchi,
M.-C. Bellissent-Funel. Neutron Scattering Study of Water Molecules Confined in
MCM-4 1. Adsorption 11,479, (2005).
208 K. Morishige, K. Kawano. Freezing and melting of water in a
single cylindrical pore: The poresize dependence of freezing and melting
behavior. J. Chem. Phys. 110 (10), 4867, (1999).
209 D'après le site de sigma-Aldrich à l'adresse
suivante:
http://www.sigmaaldrich.com/catalog/search/ProductDetail/ALDRICH/364312
210 T. Chen, A. Fowler, M. Toner. Literature Review: Supplemented
Phase Diagram of the TrehaloseWater Binary Mixture. Cryobiology, 40, 277,
(2000).
211 E.R. Caffarena, J.R. Grigera. Glass transition in aqueous
solutions of glucose. Molecular dynamics simulation. Carbhydrate Research 300,
51, (1997).
212 D.J. Bicout, G. Zaccai. Protein Flexibility from the
Dynamical Transition: A force Constant Analysis.Biophys. J. 80, 1115,
(2001).
213 S. Magazu, F. Migliardo, C. Mondelli, G. Romeo.
Temperature dependence of mean square displacement by IN13: a comparison
between trehalose and sucrose water mixtures. Chem. Phys. 292, 247, (2003).
214 Laboratoire Léon Brillouin. Brochure du laboratoire.
(1999)
ETUDE STRUCTURALE ET DYNAMIQUE DE SOLUTIONS DE SUCRE CONFINEES
Bien que le rôle actif des sucres soit connu dans la
stabilisation des membranes cellulaires lors de fortes déshydratations,
il s'avère que les processus à l'origine de cette protection ne
sont pas encore bien compris. Néanmoins, la très grande
affinité de l'eau pour le sucre, comme en témoigne la formation
de très nombreuses liaisons hydrogène, est semble-t-il
responsable en partie de cette propriété exceptionnelle.
L'étude expérimentale de la dynamique des molécules de
sucre et d'eau permettra ainsi de quantifier l'importance de ces
interactions.
Dans ce travail, nous nous sommes principalement
intéressés à des solutions de mono- et disaccharides
(glucose, fructose et tréhalose). La diffusion quasi-élastique
des neutrons a permis de mesurer, à l'échelle de la picoseconde,
la dynamique de l'eau et du sucre en solution et sous confinement dans des
matériaux poreux présentant un mimétisme d'échelle
avec le vivant. Les deux matrices sélectionnées,
c'est-à-dire un gel de silice aqueux et des nanosphères de silice
mésoporeuse de type MCM-41, qui présentent des diamètres
de pores de 18 et 3 nm respectivement, ont été
caractérisées grâce à un large panel de techniques
expérimentales (SANS, MET, MEB, Spectroscopie Raman, BET, DRX). L'effet
du confinement sur la dynamique et sur les transitions de phase solide-liquide
a ainsi pu être exploré, ainsi que l'effet protecteur des sucres
grâce à une étude de déshydratation in-situ suivie
par diffusion des neutrons aux petits angles.
MOTS-CLES : Sucres, mono- et disaccharides, solution
aqueuse, synthèse, silice, gel, sphères mésoporeuses,
MCM-41, confinement, dynamique moléculaire, transition de phase, QENS,
SANS.
STRUCTURAL AND DYNAMICAL STUDY OF CONFINED SUGAR
SOLUTIONS
Even though the active role of sugar molecules is well known
as stabilizer agent for cell membranes upon dehydration, the responsible
process is still unidentified. Nevertheless, the great affinity existing
between sugar and water molecules -- evidenced by the important number of
hydrogen bondings between these two species -- seems to be the main agent at
the origin of this exceptional property. An experimental study of sugar and
water molecules should allow to determine accurately the interactions causing
this remarkable resistance.
In this work, we focused on solutions of mono- and
disaccharides (glucose, fructose and trehalose). The quasi-elastic neutron
scattering is an appropriate tool to probe, at the picosecond timescale, the
dynamics of water and sugar in solution and under confinement in porous
materials presenting a scale mimicking the living world. Two matrices have been
chosen : silica gel and mesoporous silica spheres presenting pores of 18 and 3
nm respectively. Both have been characterized with a large set of experiments
(SANS, SEM, TEM, Raman Spectroscopy, BET, XRD). The effect of the confinement
on the dynamics and solid-liquid transitions have been explored, thus an
in-situ dehydration study monitored by small-angle neutron scattering allowed
us to better understand the bioprotective effect of theses sugars.
KEYWORDS : Sugars, mono- and disaccharides, aqueous
solution, synthesis, silica, gel, mesoporous spheres, MCM-41, confinement,
molecular dynamics, phase transition, QENS, SANS.
DISCIPLINE : Physique, mention Physique et Physico-chimie
de la matière et des matériaux
LABORATOIRE : Centre de Recherche sur la Matière
Divisée
1b, Rue de la Férollerie 45071 Orléans Cedex 2
France
| 


