Summary
We present in this memory the study of the effect of
the variation of geometry on the turbulent flow of air in a cyclone use of them
two digital models, the first model based on the dissipation of the kinetic
energy by viscosity (K å), as well as the second model based on the
resolution of the stress equations of Reynolds (RSM), for that one has to
divide this research with three parts:
Study of the effect of variation of the exit
inferior of the cyclone, one fixed a conical body in front of the exit of the
geometry (B), after one has to replace the body the preceding one by a
cylindrical tube (C), after one made a comparison in the differences in
pressure one has to note that the geometry (C) is better output point of view
of flow of air.
Study of the effect length of the higher outflow
tube of exit of the cleaning air, by the use three different lengths, one found
that the original length (A) is the best.
Study of the turbulent flow of the air in the
geometry (A) using the two preceding models one has to note that the model (K
å) gives good results in term of the time computing for the reduced
numbers of the variables.
Nomenclature
Nomenclature
Re nombre de Reynolds
Ui (i=1,2,3) vitesse instantanée, (m/s)
Ui (i=1,2,3) Vitesse moyenne, (m/s)
u 'i(i= 1,2,3) vitesse de fluctuation, (m/s)
P Pression, (N /m2 )
p' fluctuation de pression, (N/m2)
k énergie cinétique de turbulence,
(m2/s2)
uiu j tensions de Reynolds,
(m2/s2)
' '
L échelle de longueur des grosses structures de
turbulence, (m)
R rayon du cyclone
ds diamètre du conduit de sortie, (mm)
D : diamètre du cyclone, (mm)
H hauteur du cyclone, (mm)
S hauteur d'enfoncement du conduit de sortie du cyclone, (mm)
a,b longueur et largeur respectivement de la section
d'entrée, (mm)
yp,xk distances des noeuds prés de la paroi
Pk taux de dissipation de l'énergie cinétique de
turbulence
rt rayon limite entre les deux vortex
r rayon ( mm)
Ur vitesse de frottement ( égale à rp
p)
Sij tenseur de déformation
S norme du tendeur Sij
ij,k,l,m,n : indication des composantes
Cu, CE1 , CE2 , CE3 : constante du modèle standard et le
modèle RNG k- E
Symboles Grecs :
E taux de dissipation de la turbulence,
(m2/s3)
u viscosité dynamique, (kg/ms)
y viscosité cinématique, (m2/s)
p masse volumique, (kg/m3)
ut viscosité turbulente, (kg/ms)
ít viscosité cinématique,
(m2/s)
Cu, å1,å2, constantes du modèle de
turbulence
ók nombre de Prandtl associé à
l'énergie cinétique de turbulence
óå nombre de Prandtl associé au taux de
dissipation
äij symbole de kronecker
constante du vortex libre
ôp contrainte la paroi
â constante du modèle RNG k- å
ç0 constante du modèle RNG k- å
1-1) Introduction :
Le principe de fonctionnement d'un cyclone est basé sur
l'effet de la force centrifuge engendrée par un mouvement tangentiel
d'un fluide à l'entrée du cyclone. Les particules
emportées par le fluide se retrouvent éjectées vers les
parois extérieures puis collectées dans la partie conique
inférieure. Le fluide lui s'échappe dans le cylindre
intérieur appelé aussi conduit de sortie en haut de l'appareil.
Ce dispositif séparateur est simple par sa géométrie et sa
construction, peu coûteux et sans éléments en mouvement et
qui ne nécessite pas beaucoup de maintenance.
Beaucoup de produits industriels et naturels gazeux ou solides
se trouvent mélangés, et pour les séparer on a besoin d'un
mécanisme de séparation. Le premier appareil destiné
à cette opération fût le cyclone depuis la fin du
siècle dernier. L'idée est simple, on impose au fluide une
entrée tangentielle ou axiale (aidé par un organe) lui permettant
de projeter et de séparer les particules polluantes solides ou gazeuses
vers la paroi extérieure, où elle glissent vers le bas de
l'appareil, tandis que le gaz purifié est éjecté à
travers le conduit de sortie en haut de l'appareil. Les diverses contraintes
environnementales, l'évolution des moyens de productions et l'obligation
des résultats en matière d'hygiène, de santé
publique et de protection du travail imposent aujourd'hui à l'industrie
de maîtriser en terme de pollution aussi bien les effluents gazeux qu'il
rejette que l'air ambiant dans l'atelier. Ces contraintes ont poussé les
scientifiques et les industriels à s'investir dans ce domaine, ce qui a
élargi le domaine des cyclones dans plusieurs secteurs d'applications.
On peut citer par exemple :
- l'industrie alimentaire
- l'industrie mécanique (cimenterie, hydrocarbures,...)
- l'industrie chimique
- la fonderie (filtration de l'air, piégeage du fer,
...)
- l'industrie de traitement des déchets
- la Dépollution des sols.
- la Biotechnologie et la biomasse
Les cyclones par leur simplicité de fabrication ont des a
touts :
*) La mise en oeuvre est simple et les coûts
d'investissement et de maintenance réduits.
*) La gamme des débits traités est grande : des
cyclones échantillonneurs aux cyclones industriels, le débit
volumique peut varier de moins d'1 m3/h jusqu'à 30.000
m3/h.
*) des fluides très chargés peuvent être
traités, jusqu'à plusieurs kilogrammes de poussière par
mètre cube d'air dans des cyclones destinés au cimenterie, de
diamètre allant de 4 à 6 mètres.
*) les cyclones peuvent travailler à température
élevée (jusqu'au 2000 K) et à haute pression
(jusqu'à 100 bars)
Le principal facteur du cyclone est de prévoir ses
performances (perte de charge, efficacité, nature de
l'écoulement,...) et de le dimensionner. Pour résoudre ce
problème, de nombreuses études proposent des modèles de
turbulence pour bien comprendre la nature de l'écoulement
aérodynamique qui est très complexe. Ceci a conduit à
offrir une grande variété de formes de cyclones, qui sont autant
d'essais d'optimisation aux réponses à une application
spécifique. Nous donnerons un exemple d'un cyclone conventionnel
à entrée tangentielle, schématisé sur la figure
(1-1,1-2).
Figure-(1-1) Cyclone classique et Figure- (1-2) Schéma de
principe de la
notations associées séparation des particules
|
Géométries
|
A
|
B
|
C
|
A1
|
A2
|
|
H
|
950
|
950
|
950
|
950
|
950
|
|
h
|
500
|
500
|
500
|
500
|
500
|
|
D
|
400
|
400
|
400
|
400
|
400
|
|
ds
|
150
|
150
|
150
|
150
|
150
|
|
A
|
175
|
175
|
175
|
175
|
175
|
|
B
|
100
|
100
|
100
|
100
|
100
|
|
Dch
|
296
|
296
|
296
|
296
|
296
|
|
Hch
|
296
|
296
|
296
|
296
|
296
|
|
ö
|
180
|
180
|
180
|
180
|
180
|
|
L*
|
*****
|
*****
|
500
|
*****
|
*****
|
* La longueur de prolongement de la conduite cylindrique (C).
Tableau 1-1 : Dimensions des cyclones.
Plusieurs méthodes numériques sont alors
nées et ont contribuées à l'étude de plusieurs
phénomènes physiques que se soit industriel ou théorique.
Parmi, l'outil numérique le plus utilisé actuellement qui trouve
beaucoup d'applications dans le domaine industriel quelques soit la
complexité, on trouve le code commercial « FLUENT ». En effet,
les codes actuels de simulation s'adaptent très bien avec les
géométries complexes en utilisant un maillage non
structuré quelconque pour remédier aux problèmes de
frontières irrégulières ou aux formes un peu
particulières. Cette opportunité a permit l'élaboration de
plusieurs contributions récentes s'intéressants au champs
tridimensionnel complet de l'aérodynamique dans les cyclones. Parmi ces
travaux, certains s'intéressent aux trajectoires des particules pour
déterminer ce qu'on appel le diamètre de coupure pour lequel le
cyclone devient inefficace H.Yochida (1996). D'autres donnent plus d'importance
à l'aérodynamique du fluide sans injections de particules pour
étudier les phénomènes complexes qui ont lieu dans
différentes parties d'un cyclone pouvant, ainsi, remédier au
problème essentiel des cyclones qui est la perte de charge très
importante M. Slack (2003), comme la forme géométrique a son
influence sur l'efficacité de séparation des particules. Nous
sommes aller vers l'étude suivante.
1-2) Domaine d'étude
Dans ce travail, on va présenter trois configurations
géométriques différentes. Ces trois
géométries (A, B et C) sont constituées par un même
corps cylindrique dans lequel est monté le conduit de sortie et une
partie conique similaire. Les deux cyclones (A et B) sont identiques la
différence se trouvent seulement dans la partie
récupérateur où on implante un élément
parallèle à l'axe du cyclone qui piège les particules dans
ce dernier (voir figure-(1-4b).
On remarque, dans la première que le fond est une
cuvette de forme cylindrique. Cette figure
présente la forme la plus
courante des cyclones utilisées dans l'industrie. L'entrée
tangentielle
imprime au fluide chargé un mouvement de
révolution autour de l'axe. Le fluide, en écoulement de type
tourbillonnaire non entretenu, descend dans l'espace annulaire puis dans le
cône où se fait le retournement et, toujours en rotation, remonte
dans le conduit de sortie. Le cylindre est prolongé par un cône
(ou partie appelé aussi par un terme technique le trémie) vers le
bas duquel sont évacués les poussières captées. Le
conduit de sortie de l'air et les poussières fines est un conduit
coaxial au cylindre. L'écoulement après le parcourt de l'espace
libre trouve une zone de séparation qui peut-être
schématisé par deux vortex comme l'indique la figure (1-2). Nous
verrons plus loin que l'écoulement est très complexe, est peut
être gérer par:
- un vortex annulaire descendant (appelé aussi par
d'autres auteurs mouvement irrotationnel)
- un vortex central ascendant (mouvement rotationnel)
Du fait de la rotation, les particules présentes dans
le gaz sont soumises à une force centrifuge. Elles sont projetées
vers les parois du cyclone le long duquel elles descendent vers le
récupérateur. Dans la partie conique (ou trémie), le
mouvement de rotation est accéléré et la distance des
particules à la paroi est réduite.
Par contre, le cyclone B son fond est identique au cyclone A,
la seule différence se situe dans la cuvette du fond du cyclone,
où on rajoute dans cette partie un élément en plus (voir
figure-(1-4a et 1-4b)) qui sert pour le piégeage des particules dans
cette zone. Par la suite la conception du cyclone C est bien différente
aux deux autres, par sa partie inférieur à partir du cône,
on prolonge ce dernier par un tube cylindre pour canaliser l'écoulement
jusqu'à la cuvette.
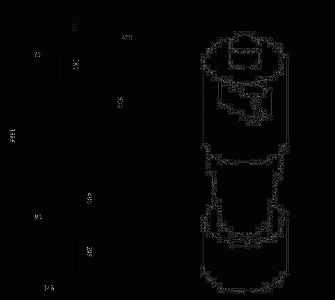
Figure-(1-3) définie le cyclone A

Figure-(1-4) définie le cyclone B, présentant un
obstacle de piégeage
Figure-(1-5) cyclone C avec une rallonge
cylindrique
1-3) Recherches bibliographies :
Yoshida. H (1996) a mené des
études expérimentales et numériques sur
l'efficacité de filtration d'un cyclone conventionnel et d'un cyclone
modifié. Ce dernier comporte dans la partie basse de
récupération des particules un cône
déplaçable verticalement qui empêche le retour vers le haut
des particules. Il est aussi caractérisé par une entrée en
spirale (virole) dans le plan perpendiculaire à l'axe. L'étude
numérique tridimensionnelle confirme le résultat
expérimental que l'efficacité de filtration obtenue par le
modèle proposé est meilleure que celle du cyclone conventionnel.
Le modèle de turbulence k-å appliqué à
l'écoulement en question qui a été utilisé en
conjonction avec le schéma numérique Quick s'est
avéré performant.
Slack et al. (2003) ont
présenté un développement d'une interface pour
améliorer l'utilisation du logiciel Fluent par des utilisateurs non
experts. L'article décrit un outil automatisé qui permet à
l'ingénieur d'effectuer des simulations sur les cyclones permettant
ainsi des conceptions plus rapides et moins coûteuses.
Bruno Reinhardt et al (1997)
Parallèlement à l'étude expérimentale faite par fil
à chaud, une étude numérique a été
menée à travers le développement de calcul, nommé
CYCLOP « fruit d'une collaboration européenne »qui
dérive du code FLUENT. Ce code développé se base
essentiellement sur la méthode des volumes finis, qui permet d
étudier des écoulements turbulents, visqueux, incompressibles,
bidimensionnels et axisymétrique grâce à l'utilisation
d'une condition de symétrie. L'Algorithme SIMPLE est utilisé pour
la résolution du système composé des équations de
Navier-Stokes et de fermeture K-å ou RSM. La simulation a
été testée sur des cyclones de 400 et 800 mm de
diamètre. Par la suite, l'auteur a utilisé une modification du
modèle de turbulence pour prendre correctement en compte l'effet
d'échelle sur le développement du vortex. Dans son travail, il
conclu que les profils de la vitesse tangentielle, adimensionnée par la
vitesse moyenne d'entrée, et du taux de turbulence, en fonction du
rayon, adimensionné par le rayon du cyclone, sont pratiquement confondus
et indépendants de la vitesse moyenne d'entrée pour les deux
configurations. Dans la région du vortex forcé, la simulation est
conforme avec l'expérimental, par contre dans le noyau du vortex (lieu
de rencontre des deux vortex), en utilisant les équations de N-S avec
les deux équations de fermetures K et å, les écoulements
dans les deux cyclones homothétiques, sont
en parfaite similitude, expérimentalement, les conclusions
sont totalement différentes. Le modèle de turbulence pour ce cas
doit-être changé d'après l'auteur.
Romualdo L et al (1999) Parmi les
différentes théories existantes pour prédire
l'efficacité de collection des cyclones, on montre que la théorie
de diffusivité de Mothes et Loffler (1988) donne le meilleur calage des
courbes d'efficacité observées. Toutefois, le manque de
connaissances sur la dépendance du coefficient de dispersion turbulente
des particules en fonction de la géométrie du cyclone, des
conditions de fonctionnement et de la taille des particules a
empêché jusqu'à présent l'application de cette
théorie à des fins de prédiction ou d'amélioration
de la conception des cyclones. Dans ce travail, on applique cette
théorie à des fins de prédiction, en recourant à
une relation empirique pour le coefficient de dispersion turbulente des
particules. La relation proposée s'appuie sur une analogie avec la
dispersion turbulente en lits garnis et s'exprime sous forme d'une
corrélation faisant intervenir les nombres de Peclet et de Reynolds,
radiaux de particules. Des cyclones à écoulement inverse à
l'échelle de laboratoire ayant des géométries non
encore publiées ont été construits afin de tester
l'applicabilité de la relation proposée. La théorie de
Mothes et Loffler (1988), lorsqu'elle est couplée aux estimations de
coefficients de dispersion turbulente proposées, est un outil puissant
pour prédire l'efficacité de collection des cyclones, sauf si on
recourt à des outils de simulation de la dynamique des fluides.
Li Xiaodong et al (2003) Du point de vue de
l'influence de la structure de turbulence, cet article présente une
analyse élémentaire de l'interaction entre une particule et une
phase gazeuses. Les effets de la structure de turbulence et l'épaisseur
de la couche limite sur l'efficacité de séparation dans un
séparateur cyclonique ont été étudiés. Les
effets de la force de Saffman sur la trajectoire de particules sont
également analysés. Les résultats indiquent que
l'efficacité de séparation diminue avec une augmentation de
l'intensité de turbulence et augmente avec une diminution de
l'épaisseur de la couche limite. La force de Saffman peut augmenter la
séparation de petites particules et peut également raccourcir
leur temps de séjour dans le cyclone.
L'incrément de la turbulence laisse les particules entrer
dans la zone où la vitesse axiale de
la phase gazeuse est ascendante qui donne une bonne explication
pourquoi l'efficacité de séparation des petites particules est
diminue relativement avec l'augmentation de l'intensité de
turbulence. Les résultats prouvent que l'efficacité
augmente avec une diminution de l'épaisseur de la couche limite pour les
particules de diamètre <30 micm.
Brennan. M.S (2003) Dans cet article
l'écoulement turbulent dans un séparateur cyclonique est
étudié avec la simulation des grand échelles (LES)
basée sur une méthode d'élément spectral (de
Fourier) on coordonnés cylindriques (SEM) En utilisant le modèle
de sous maille de smagorinsky dans sa formulation standard et dynamique. Dans
cette étude la partie inférieure est fermée car l'objectif
principal de cette étude est d'étudier l'écoulement
monophasé, qui est censé à partir du haut du cyclone. La
grande vitesse d'agitation produit des difficultés pour les
modèles statistiques simples de turbulence utilisés dans les
équations de Navier stocks (RSM) comme Le modèle K-e qui encore
est largement répandu pour la conception dans l'industrie. Pour le
tenseur linéaire des contraintes les corrélations dans ces
modèles échouent souvent en présence de la courbure des
lignes de courant accompagnée d'agitation. Cet échec de ces
modèles provoque souvent des profils de vitesse d'agitation typiques de
la rotation d'un solide. RANS d'autre part utilise des modèles de paroi
à pour dévier la couche limite, mais ne peut pas distinguer la
phase de transition ver la turbulence. Ceci a encouragé le
développement des approches hybrides telles que la simulation des
échelles détacher-(DES, spalart et al, (1997), pour les
résultats obtenus par RANS indiquent des faits de traction. Est d'abord
que ce modèle simple échoue à Capturer la distribution
correcte de vitesse de swirl et prévoit la vitesse axiale totalement
incorrecte La distribution qui semblent ne pas être influencés par
les conditions d'entré jusqu'à un degré semblable comme
les résultats de DES. Les résultats du cyclone par LES indiquent
le succès dans la prévision.
Richard Caetano et al (2003) Ce travail
consiste à modéliser l'efficacité de filtration du
système d'épuration Aireco. Cet échangeur épurateur
se compose d'un corps cyclonique et de nappes de serpentins
réfrigérés provoquant la condensation de la vapeur d'eau
contenue dans le gaz pollué traité. Dans ce modèle, il se
base sur deux cas de prédictions différents qui sont : *
L'impaction inertielle qui intervient quant les particules transportées
par l'air sont piégée
sur les serpentins en aval de l'entrée du fait de leur
inertie. Les particules sont incapables de suivre la courbure des lignes de
courant du fluide contournant le serpentin,
* Le piégeage des particules résiduelles par
centrifugation comme dans un cyclone classique.
Ces dernières
provoquent la condensation de la vapeur d'eau contenu dans le gaz pollué
traité.
Pour augmenter l'efficacité du système, au lieu
de considérer la pulvérisation de brouillards
d'eau dans l'écoulement gazeux comme il est parfois
pratiqué, les auteurs proposent la condensation de l'air humide dans le
corps même du cyclone. L'intérêt est de diminuer l'effluent
liquide en grande quantité produit sur la pulvérisation qu'il
faut ensuite traiter. Malgré, la complexité de la
géométrie originale, les propriétés
d'épuration du système sont décrites d'une manière
simple et satisfaisante avec une incertitude relative de l'ordre de 5%.
Cependant, cette approche globale est spécifique à cette
configuration et donc manque d'universalité. En plus, elle
nécessite la connaissance a priori de l'aérodynamique dans le
cyclone.
Stefan Schmidt (2003) Dans cet article
l'écoulement turbulent dans le cyclone est étudié en
utilisant la simulation des grandes échelles (LES) basée sur les
coordonnés cylindriques en utilisant la méthode des
éléments spectrales de Fourier (SEM) avec le modèle de
sous mailles de Smagorinesky dans sa forme standard et la formulation
dynamique. Les résultats montrent qu'il y a une différence dans
le modèle numérique et les résultats expérimentaux.
Le système de coordonnées cylindriques utilisé dans le
calcul par la méthode de Fourier (SMM) requises une
périodicité dans la direction azimutal et il n'est pas capable de
modéliser l'écoulement de paroi sur laquelle les profiles de
vitesses sont interpolés.
Souzaa. F. J, et al (2004) La contribution
actuelle vise à simuler un écoulement par le modèle LES
(Large Eddy Simulation) pour prévoir son comportement dans un
hydrocyclone fonctionnant sans noyau d'air (absence du core d'un cyclone
où zone centrale de dépression). Des équations
mathématiques régissantes l'écoulement ont
été résolues par une méthode « pas
fractionnement ou step method ». Cette approche exige que les grands
tourbillons anisotropes résolus directement tandis que les plus petits
tourbillons soient modelés. Le modèle de Smagorinsky est
employé principalement dans ce travail pour appuyer la consistance du
travail en question. Le grand avantage de ce modèle se situe dans sa
simplicité et la dépendance à l'égard d'une
constante seulement. L'auteur conclu que le résultat
numériquement obtenu est en bon accord avec les caractéristiques
principales du modèle de l'écoulement et conviennent
raisonnablement bien avec l`expérience, en suggérant que le
modèle LES représente une alternative numériquement
intéressante aux modèles classiques de turbulence lorsqu'ils sont
appliqués à la solution numérique des écoulements
dans les hydrocyclone.
L'accord entre les valeurs simulées et
expérimentales de la chute de pression est satisfaisant, l'auteur
espère que cette méthodologie actuelle sera employée dans
le proche futur comme outil pour l'étude, conception et optimisation des
hydrocyclones.
Obermain S. et al. (2001) ont effectué
des mesures par LDA de l'écoulement à l'intérieur de
différentes configurations de cyclone. Ils ont montré qu'en
changeant la géométrie du fond du cyclone, l'aérodynamique
résultante peut mener à une amélioration
appréciable de l'efficacité de filtration. En effet, pour le
cyclone conique classique les mesures montrent un vortex descendant le long des
parois et un deuxième vortex remontant au centre transportant les
particules vers le haut. Par contre, dans le cyclone qu'ils proposent où
on prolonge la conduite de sortie à section constante (tube cylindrique)
le piégeage de particules est bien capté dans cette
configuration. En effet, dans le tube cylindrique rajouté le vortex
ascendant traverse une région caractérisée par une grande
vitesse tangentielle et une faible intensité de turbulence. Les auteurs
concluent que cette dernière configuration améliore
l'efficacité de filtration par rapport à celle des cyclones
classiques.
Schmidt. St (2004) dans cet article l'auteur
étudie l'influence du tube de sortie avec ses différentes
configurations en longueur:
-a) tube de sortie : court, moyen, long et long centré
-b) tube de sortie : court courbé, long courbé et
long avec sortie horizontale vers l'atmosphère sur les
propriétés d'écoulement dans les cyclones en utilisant la
méthode de simulation DES (Detached Eddy Simulation). Les
résultats numériques obtenus à partir de
différentes formes employés du tube de sortie montrent bien qu'il
existe une influence importante sur le comportement d'écoulement dans le
cyclone. Ceci, par la présence des tourbillons oscillatoires dans la
région centrale de différents cyclones pour chaque cas (core, axe
du cyclone) réduisant sensiblement l'efficacité du cyclone comme
dispositif de séparation des particules. Il apparaît clairement
que pour le cas du tube court l'oscillation du noyau de vortex peut-être
clairement identifié en tant que région foncé serpentant
autour de la ligne centrale du cyclone. La ligne centrale de
l'écoulement pour le cas du tube court devient perturbée et non
axial. Par contre, pour les trois autres, elles ne le sont pas. En comparant
les résultats, il apparaît qu'à partir d'une certaine
longueur de tube, la forme de la géométrie n'a pas un impact fort
sur le comportement de l'écoulement dans le cyclone.
-a)
Jolius Gimbun et al (2001), Le présent
travail présente un calcul de simulation numérique par le
modèle RSM (Reynolds stress model) en utilisant un code commercial
FLUENT 6.1 d'un fluide dynamique pour prévoir et évaluer les
effets de la température et la vitesse d'admission sur la chute de
pression des cyclones de gaz. Dans cet article on examine aussi, la comparaison
de quatre modèles empiriques proposés par des hauteurs
cités dans sa bibliographie travaillants dans le domaine pour
prédire la chute de pression de la géométrie
considérée. L'auteur conclu que toutes les prévisions
avérées être satisfaisant une fois comparé avec les
données expérimentales présentées. Les simulations
de CFD prévoient d'une façon excellente la chute de pression de
cyclone sous différentes températures et vitesses à
l'admission avec un modèle empirique de déviation maximum de 3%
des données expérimentales. Le code Fluent rapporte aussi avec le
modèle RNG-K-å prévoit des prévisions raisonnables.
La chute de pression de cyclone peut-être récrite comme fonction
de la vitesse à l'entrée du cyclone. En conclusion, le
modèle RSM s'adapte parfaitement avec le modèle empiriques de
Lapple (1951) par contre le modèle de Dirgo (1985) est un peut
dévié par rapport au modèle numérique RSM.
Talbi. K (2004), Pour bien comprendre le
phénomène d'écoulement de séparation des particules
du fluide d'entraînement sous le conduit de sortie de l'air, une
étude expérimentale de l'écoulement turbulent
tridimensionnel dans un cyclone est présentée. Des mesures des
vitesses moyennes et des intensités de la turbulence axiales et
tangentielles ont été effectuées par LDA. Le dispositif
expérimental LDA a été monté de sorte que des
traversées radiales puissent être faites en différents
angles de la géométrie cylindrique du cyclone et en
différentes stations axiales. Un phénomène très
important est remarqué sous le conduit, est que, les courants descendant
et ascendant sont séparés par une surface qui se situe
pratiquement sur le prolongement du conduit central. L'existence d'un vortex
quasi-forcé au centre et d'un vortex quasi-libre l'entourant est
confirmée. Puis l'auteur de l'article confirme encore qu'il existe une
la surface fictive entre les deux types de vortex peut être clairement
définie comme l'ensemble de points d'intersection de la droite de pente
+1 (LnUt en fonction de Lnr) dans le vortex quasi-forcé et de la droite
de pente - 1 ( LnUt en fonction de Lnr) dans le vortex quasi -libre.
Kharoua. N (2005), la présente
contribution concerne l'étude de l'influence du maillage et des
schémas de discrétisation sur la solution numérique de
l'écoulement tridimensionnel turbulent dans un cyclone
dépoussiéreur (séparateur par effet
cyclone).
L'intérêt de l'étude de
l'aérodynamique dans les cyclones est d'optimiser leur fonctionnement,
c'est-à-dire d'augmenter leur efficacité de filtration, tout en
minimisant l'énergie consommée pour générer
l'écoulement de l'air qui est due à la chute de pression
importante entre l'entrée et la sortie du séparateur.
Des résultats, concernant la caractérisation du
champ aérodynamique dans un cyclone dépoussiéreur, ont
été obtenus par l'intermédiaire du code FLUENT.
Pour vérifier la consistance de son travail il a pris
comme références les résultats publiés par Slack
(2003) obtenus par le même code. Ce travail représente une
modélisation d'un cyclone avec un maillage hexaédrique et
plusieurs modèles de turbulence. Les résultats ont
été validés par des résultats expérimentaux
publiés par Boysan et al (1986).
Zhao et al (1999) ont étudiés
l'écoulement dans un cyclone par deux méthodes. La
première utilise le code commercial Fluent 3.03. L'écoulement est
considéré tridimensionnel donc non axisymétrique. Il est
tenu compte de l'effet de la turbulence par le modèle ASM. La
deuxième approche, développée par les auteurs, est
analytique. Une solution exacte a été donnée de
l'équation de la fonction de courant pour l'écoulement permanent
axisymétrique non- visqueux dans la zone conique du cyclone. Les
résultats du cyclone ont été comparés avec les
données expérimentales de Boysan et al (1982) et de Kelsall D.F.
(1992). Les résultats numériques, analytiques et
expérimentaux sont en bon accord. Cependant, il a été
trouvé que les conditions à l'entrée notamment la vitesse
moyenne et les contraintes de Reynolds ont une forte influence sur le
comportement de l'écoulement à l'intérieur du cyclone.
Noriler. D et al (2004). Dans ce travail, un
nouvel appareil mécanique pour améliorer l'écoulement du
gaz dans les cyclones, en réduisant la perte de charge, est
présenté et discuté. Ce comportement a lieu à cause
des effets d'introduction du phénomène de cassage du «
swirling » à l'entrée d'un tube qui canalise
l'écoulement vers le centre, l'appareil se compose d'un tube ayant deux
entrées de gaz, dans un « flux spiral » qui produit une
réduction brusque importante de la vitesse tangentielle, responsable
pour pratiquement de 80% de la perte de charge dans les cyclones. A son tour,
Cette réduction de perte de charge casse le « swirling », et
à cause de ça, les particules solides tendent à se
déplacer plus rapidement vers la paroi, ce qui augmente le rendement de
dépôts. Comme résultat de ce
phénomène, la performance globale des cyclones
est augmentée. Les simulations numériques faites à 3-D,
transitoire, asymétrique et anisotrope de turbulence à l'aide des
équations différentielles des contraintes pour les
géométries standards de 0.3 m de diamètre de Lapple (1951)
et Stairmand (1951), montre une réduction des pertes de charge de 20% et
un décalage du maximum de la vitesse tangentielle vers la paroi. Toutes
les expériences numériques ont été menées
à l'aide d'un code CFD commercial 3D montrant une stabilité
numérique et de bons taux de convergence à l'aide des
schémas d'interpolation d'ordre élevé, SIMPLEC pour le
couplage pression-vitesse et d'autres propriétés
numériques.
Fuping Qian et al (2006). L'article à
pour but d'étudier la partie de l'écoulement des gaz dans le
récupérateur ( casier) pour différents formes de cyclones,
cyclone conventionnel et une variante de cyclones avec des tubes
prolongés rattachés. Le modèle des contraintes de Reynolds
a été utilisé pour prédire les champs
d'écoulement des cyclones conventionnels et modifiés, de la
vitesse axiale et de l'énergie cinétique turbulente ont
été présentés ; et les débits
d'écoulement descendant au récupérateur des trois cyclones
sont comparés. Les performances de séparation de ces cyclones
sont testées. Le résultat indique que la vitesse tangentielle, la
vitesse axiale et l'énergie cinétique turbulente dans le
récupérateur subissent une grande diminution lorsque le tube
vertical a une longueur de 0.5 m. Par ailleurs, le tube vertical
prolongé augmente l'espace de séparation des poussières.
Le débit descendant vers le récupérateur du cyclone
prolongé diminue par rapport au cyclone conventionnel. Les
résultats expérimentaux montrent que le tube vertical
prolongé peut améliorer le rendement de séparation par un
accroissement léger de la perte de charge.
Cependant, pour un tube encore plus long, le rendement de
séparation est légèrement diminué. Ainsi, il y'a
une longueur optimale du tube pour un cyclone donné.
| 


