Méthodes géostatistique pour l'interpolation et la modélisation en 2d/3d des données spatiales

2/ Ajustement à un modèle

Le variogrammme expérimental calculé et ses propriétés étudiées, il faut ajuster une courbe théorique. Elle doit être définie pour toutes les distances et toutes les directions de l'espace. Cependant toute fonction mathématique ne peut être utilisée comme modèle. Un modèle variographique doit être une fonction de type négatif conditionnel (Cressie, 1993 p.86) c'est-àdire que :

n n

0

? ? ù ù 2ã ( )

i j s _i s j

- =

i = =

1 1

j

n

quel que soit {si : i=1,...,n} et {ùi : i=1,...,n / ?= ù = i i 1

0}

C'est pourquoi le modèle de variogramme est choisi parmi un ensemble de fonction dont on sait qu'elles sont de type négatif conditionnel (cf. partie II, chap.3.3).

Remarque : quel que soit le mode d'ajustement retenu, la modélisation du variogramme aux courtes distances est particulièrement importante.

2.1/ Cas monovariable

Des anisotropies dans les directions -35° et 55° ont été détectées dans le paragraphe 1.3. Il convient d'ajuster le variogramme dans ces directions. D'autre le palier dans les directions principales est égal à la variance de la variable régionalisée, soit 38,6. N'ayant pas observé d'effet pépite, le comportement à l'origine de la variable aléatoire régionalisée est linéaire.

Ces observations amènent à choisir entre un modèle sphérique et un modèle exponentiel. Le modèle sphérique est préférable, d'une part parce qu'il s'ajuste mieux sur les points de petite distance du variogramme expérimental et d'autre part parce qu'après plusieurs essais il donne de meilleurs résultats.

M. Arnaud et X. Emery montrent que la variance d'estimation (variance de krigeage) est plus élevée dans le cas du modèle exponentiel ; l'explication vient du fait que ce dernier croît plus rapidement que le modèle sphérique, ce qui traduit un phénomène qui se déstructure plus vite, d'où une moins grande précision dans l'estimation.

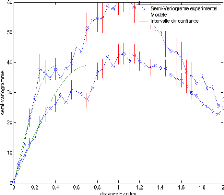
Direction -35°

Direction 55°

Figure 4.6

Le modèle choisi pour les deux directions s'écrit :

? 3

3 h h ?

h ?? 3 8,6 × ? -

? ?

( ) = 3

a

? 2 2 a ?

??

ã

3 8,6

0

a h

= =

pour

>a

pour h

a identifie la portée ;

a= 0.399 km dans la direction -35° a= 0.699 km dans la direction 55°

Remarque : L'estimation du paramètre de la portée se fait en résolvant le problème :

L à min n = ? ? ?= ù ? ? i 1

i

2 ? ( ã h i ã h i à ( ) ( ) - ) ? ? ?

n : longueur du vecteur h

ãà ( h_i ) : valeur estimée du variogramme pour la distance hi

_ã(hi) : valeur de la fonction variographique pour la distance hi

ùi : poids accordé à la distance hi ( les poids sont inversement proportionnels à la distance).

D'autres fonctions variographiques ou paramètres d'ajustement auraient pu être choisis. C'est pour cela qu'il est nécessaire de contrôler la qualité du modèle d'ajustement. On effectue à cette fin une validation croisée.

Pour tester les résultats de la validation croisée, nous comparons ceux obtenus pour le modèle précédent et ceux obtenus pour le modèle variographique qui ne tient pas en compte l'anisotropie (cf. figure 4.7).

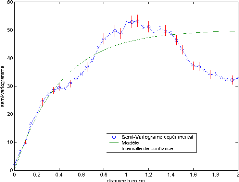
Figure 4.7

ã ( ) 50 1 exp( h h ? - = × - ) ?? 0.412

? ??

2.2/ Validation croisée

D'après le rapport INERIS (2003), la validation croisée doit être réalisée avant d'entreprendre le krigeage. Elle fournit des critères statistiques de sélection dans le choix d'un modèle de variogramme.

La validation croisée consiste à éliminer temporairement un point de l'ensemble des données puis à estimer sa valeur par krigeage à l'aide des données restantes et du modèle de variogramme qui a été ajusté. Cette opération est répétée pour tous les points.

Ainsi en tout point d'observation si, est calculé par krigeage, avec le modèle variographique

à

retenu, une valeur estimée Z ( s_i ) et un écart-type de krigeage óok(si). Le rapport INERIS

recommande alors de calculer :

à

- la moyenne et la variance de l'erreur d'estimation (Z(si)- Z ( s_i ) ),

n 2

- l'erreur quadratique moyenne (EQM= ?= [

1 Z s _i Z s i

( ) à ( )

- ] )

n 1

i

à

- la moyenne de l'erreur relative (100*[Z(si)- Z ( s_i ) ]/ Z(si)),

à

- la moyenne et la variance de l'erreur standardisée ([Z(si)- Z ( s_i ) ]/ óok(si)),

à

- le coefficient de corrélation entre Z(si) et Z ( s_i ) .

La qualité du modèle est d'autant meilleure que :

- la moyenne des erreurs d'estimation et des erreurs réduites (standardisées) est plus proche de 0, ce critère assure l'absence de biais,

- la variance des erreurs d'estimation est plus faible, ce critère traduit la robustesse de l'estimateur et renseigne sur la précision de l'estimation,

- la variance des erreurs standardisées est plus proche de 1, ce critère indique que

l'écart-type de krigeage reflète correctement la précision de l'estimation,

- la moyenne des erreurs relatives est plus proche de 0, ce critère traduit la bonne

précision de l'estimateur,

à

- la corrélation entre Z(si) et Z ( s_i ) est plus proche de 1 et le nuage de corrélation

plus resserré.

L'application aux données :

N=441	Modèle avec anisotropie	Modèle isotrope
Erreur Quadratique Moyenne	3,34	3,18
Moyenne des erreurs d'estimation	-0,01	-0,001
Ecart-type des erreurs d'estimation	1,83	1,78
Moyenne des erreurs relatives	-22,16 %	-21,18%
Moyenne des erreurs standardisées	0,003	0,0007
Ecart-Type des erreurs standardisées	0,66	0,63
Coefficient de corrélation	0,95	0,96
% de données dont l'erreur standardisée est inférieure à 2,5	99	96

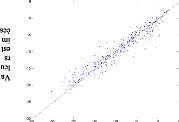
Modèle anisotrope

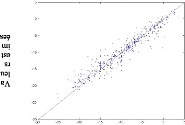
Modèle isotrope

Vraies valeurs Vraies valeurs

Nuage de corrélation entre valeurs vraies et estimées

Figure 4.7

Les nuages sont concentrés le long de la première bissectrice, ce qui indique une bonne précision des estimations. Les deux modèles rendent une estimation globalement sans biais, les erreurs d'estimation ne s'écartent pas fortement de 0. D'après Arnaud et Emery (200, p.156), pour valider un modèle on espère au moins 95% de données dont l'erreur standardisée est inférieure à 2,5. C'est le cas pour les deux modèles. Les écarts-types sont proches de 1, les erreurs relatives n'excèdent pas 23%. En revanche quelques fortes profondeurs sont sous estimées.

Il est également intéressant de localiser les erreurs d'estimation. La figure 4.8 nous les montre.

Embouchure Pointe de l'île

Erreur d'estimation du modèle anisotrope	Figure 4.8	Erreur d'estimation du modèle isotrope

Les cartes montrent que l'on estime mal aux endroits à fort dénivelés (à l'embouchure au nord) et certains points au sud-est. Ces erreurs sont dues à des incohérences entre sources de données différentes (MNT et Sismique, cf. chap. III § 2.1.2).

Après application des deux modèles, le géologue a préféré les résultats obtenus par le modèle à anisotropie.