Méthodes géostatistique pour l'interpolation et la modélisation en 2d/3d des données spatiales

3.5/ Cas multivarié : calcul des variogrammes croisés

Nous avons vu qu'un des avantages des méthodes géostatistique (chap. I § 1.2) était de pouvoir inclure dans le modèle d'interpolation des variables auxiliaires qui apportent de l'information sur la variable cible. Pour décrire la structure de dépendance entre la variable cible et les covariables il convient de calculer le variogramme croisé.

Soit Z_p la variable principale et Zq la variable secondaire, alors

à ã

( h) 1 2N( h)

N(h ) ?= [ i 1

Z p (s i ) - Z p ( s +h) ][ Z q (s i ) - Zq ( s +h)] i

L'analyse du variogramme croisé se fait de la même façon que celle du variogramme simple. C'est-à-dire que l'on relève ses propriétés (effet de pépite, palier, porté, amplitude) et on y ajuste une fonction.

4/ Krigeage

Cette section expose l'une des techniques de géostatistique d'estimation locale, connue sous le nom de krigeage et cokrigeage ordinaire.

Nous cherchons à estimer la valeur d'une variable régionalisée z (profondeur au substratum) en un point s0 quelconque du champ à partir des mesures observées z(si), i=1,..,n (n : nombre de points observés). Le krigeage est un interpolateur exact (la valeur estimée sur un point de mesure est égale à la valeur du point de mesure) et optimal (il minimise la variance sur l'erreur d'estimation).

Il existe trois types de krigeage : le krigeage simple, le krigeage ordinaire et le krigeage universel. Le krigeage ordinaire est le plus fréquemment utilisé en pratique car les hypothèses de départ sont moins contraignantes que celle du krigeage simple. Seul le krigeage ordinaire sera développé ici car il répond aux besoins de notre problématique.

4.1/ Hypothèses et contraintes

Le krigeage ordinaire ne requiert pas la connaissance de l'espérance de la variable régionalisée. Autrement dit, on se place dans l'hypothèse d'une stationnarité intrinsèque. Il n'en reste pas moins que la moyenne doit rester constante à l'échelle du voisinage de krigeage.

Définition du voisinage de krigeage : Domaine du champ qui contient le site à estimer et les données utilisées dans l'estimation.

Comme pour les méthodes barycentriques (chap. I § 1.1.3), le voisinage de krigeage se résume à un cercle ou à une ellipse autour du point à estimer.

Le modèle de base de cette méthode s'énonce comme suit :

Z ( s ) = ì (s) + ä (s)

avec s D (le champ), _ì(s)=E(Z(s)) quasi-constante inconnue et ä(s) fonction aléatoire stationnaire intrinsèque d'espérance nulle (E(ä(s))=0) et de structure de dépendance connue (ã(|si-sj|) connu). Dans son mémoire (2005, p.31), S. Baillargeon explique que le caractère quasi-constant de _ì(s) signifie que l'espérance n'est pas contrainte à demeurer la même partout dans le champ D. Elle doit par contre rester constante à l'intérieur de chaque voisinage de krigeage.

En outre, l'estimateur du krigeage ordinaire doit vérifier les propriétés suivantes :

à

La linéarité : Z ( s₀ ) est une combinaison linéaire des données Z(si) i=1,..,n.

n n

1

Z s a

à ( ₀ ) = + ? ù ( ) avec ?

i Z s i ù =

i

i =1 i=1

Le non-biais : Z^à ( s₀ ) est sans biais : E[ Z à ( s ₀ ) - Z(s ₀) ] = 0

Démonstration

à

E(Z ( s ₀) -Z (s 0 ))

E(a + ? ù_i Z(s _i) -Z(s₀))

i

E ( a + ? ùZ(s _i)) -E(Z ( s ₀))

i

or E( Z (s _i ) ) = E( Z (s₀)) ì (stationarité)

= a + ? ù _iE(Z ( s_i))-ì i

= a+

? ??

? i

ù

1

? ??

×

ì

x 1- a=ì =

n ? ù ?i ? i = 1 ?

Or _ì étant inconnue, le seul moyen de garantir le non-biais de l'erreur est de poser :

n

a= 0 et ?ù= 1

i 1

Optimalité : c'est-à-dire que Var ( Z^à ( s₀ ) - Z(s ₀)) est minimale.

Var Z(s ₀ ) ) = (2( s ₀ ) - Z(s₀ )) 1 = E( 2( s₀ ) ²) - 2E[ 2( s ₀ ) Z ( s ₀ )] + E( Z (s0) ²⁾

ì 2

2

n n n n n

E( Z ( s ₀ ) ²⁾ =E0),Z(s_i) ? E w _iw_iE(Z (s_i)Z (s _j)) =? ? ùiùj cov(Z(s _i ), Z ( s _j))+

i=1 i= 1 i==

1 1

j

car dans le cas d'une variable aléatoire stationnaire, E(Z(si))=E(Z(sj))=_ì, d'où E(Z(si))E(Z(sj))=_ì2

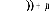
2

E( Z (s ₀ ) ²) = Var

(Z( s

+ ì

E[

n n n

2( s ₀ ) Z ( s ₀ ) ] = i Z(s _i ) Z ( s₀ ) -?1 = _iE( Z (s )Z ( s ₀ ) ) = i cov( Z(s _i), Z ( s ₀)) + ì2

i = 1i=1 i = 1

donc

Var ( 2( s ₀ ) - Z(s ₀ )) = Var( Z(s₀ ) ) - ù _i cov(Z(s _i ), Z ( s ₀ )) + ? ? ùiù j cov(Z(s ), Z ( s ))

n n n

i= 1 i= 1 j= 1

n

Le but est de trouver le vecteur ù qui minimise cette variance sous la contrainte ?=ù =

i 1 i 1

Pour y parvenir, on peut utiliser la méthode de Lagrange. La fonction de Lagrange :

n n n n ?

L = Var Z s

( ) ? (

( ) 2

- ) ? = ? = (

+ ù ù Z s Z s ) ?

? -

( , ,..., )

ë ù ù cov ( ), ( )

ù Z s Z s cov ( ) , ( ) + ë ù 1

1 n 0 i i 0 i j i j ?? i ??

i = 1 i 1 1

j i = 1

ë est le multiplicateur de Lagrange

Minimiser cette fonction revient à trouver la solution du système :

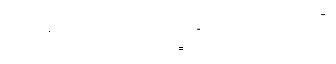
1

j

1

ù i

ë

0

+

n

Z s Z s

( ), ( ) ) + ? ù ( )

i j cov ( ) , ( )

Z s Z s

0 i j

n

?

1

i

=

ⁿ ) = - cov(

? L

(ë , ù₁,...,ù

?

ù_i

?

Ce système peut se réécrire à l'aide du variogramme ã(h)=C(0)-C(h)

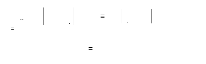
n

-

-

-

ù

ë

(s_i

ã

)

)

(s_i

s₀

_jã

1

? i = 1, ... , n

1

ù i

?

=

i

?

j

s_j

n

?

1

La variance minimum est atteinte au point :

n

ó 2 (ok 0 ) = ?ùiã ( s_i - s₀)- ë

i= 1

Cette fonction est appelée variance de krigeage. C'est la valeur minimale de la variance de l'erreur de prévision.

4.2/ Estimateur de krigeage

Le krigeage est un interpolateur linéaire sans biais. Il prend en compte la géométrie des données, les caractéristiques de la régionalisation et de la variance. Son but est de lisser les données.

Ayant calculé les poids ùi par la résolution du système précédent, nous pouvons écrire l'estimateur de la manière suivante :

n

à

1

?=

i

Z₁ ( s₀ ) = ù _i Z(s _i)

4.3/ Cas multivariable : Cokrigeage

Il est possible d'améliorer les estimations obtenues par krigeage en ajoutant à la variable à estimer, l'information fournie par d'autres variables (variables secondaires). La démarche à suivre est la suivante.

Pour estimer la variable Z1 au point s0, on utilise une combinaison linéaire pondérée des mesures concernant toutes les autres variables (Z2, ..., Zp).

p n i

Z( s₀ ) = ? ? ù j i i j i

Z s

( , )

,

i= 1 j=1

Les poids ùj,i sont solution du système :

j i

,

ù

?

?
?
?

?

?

?

? ?

?

i = =

1 j

?

j

j

p

n_i

n1

1

1

ù

n_i

1

j

ù ã - - = - =

j i i q i q j q

s s

( ) ë ã

q q i q

( s s q p

) 1 . . .

, , , , , 0

,

1

=

0 i=2...

1

p

Les ë_q sont des multiplicateurs de Lagrange.

Remarques :

- La variance d'estimation (ou de krigeage) obtenue par cokrigeage est toujours inférieure à celle obtenue par krigeage.

- En pratique, on observe que le gain est moindre lorsque les variables sont peu corrélées entre elles (Arnaud et Emery, 2000, p.195).

- L'estimation ponctuelle par (co)krigeage en un site d'observation est égale à la

valeur mesurée. D'autre part, la variance d'estimation associée est nulle.