Compression d'image animmée par le codage EZW 3D

2.4.2 Transformation discrète en ondelettes

Cette approche [2.7] peut être utilisée pour traiter des images. Nous supposons que les

données { ( 0 ) }

f_i sont les produits scalaires en un pixel 'i' de la fonction f(x) et d'une fonction

d'échelle donnée Ö(x) :

fi ( 0) f x x i 2.6

=< ( ) ; Ö ( - ) >

Où Ö(x) doit satisfaire l'équation de dilatation :

Ö ? Ö ?

( ^x ) ( ) ( )

h n x n

2

1

2

n

Où h (n) est la valeur de l'échantillon n. 2.7

Le premier processus effectué entre deux échelles conduit à l'ensemble de { ( 1 ) }

f_i La

différence { ( 0) }

f_i - { ( 1 ) }

f_icontient l'information entre ces deux échelles i

Fet i + 1

F .

22 -

Compression d'images animée par codage EZW 3D

Chapitre 2 Transformée en ondelettes

C'est l'ensemble discret associé a la transformation en ondelettes correspondant à Ö(x)L'ondelette associée ø (x) est : 1 / 2 ( / 2) ( ) 1 / 2 ( / 2)

ø x = Ö x ? Ö x

F ? ? ? ? ?

0

F ? ? ? ? ?

1

F ? ? ? ? ?

2

Figure 2.3 : Filtrage avec un facteur décroissant de distance deux entre les échantillons La distance entre deux échantillons croit par un facteur de deux de l'échelle (n-1) à la

suivante, ( k )

f_i est donné par (voir la figure 2.3) :

f h n f k 2.8

( )

k = ? + - k

( ) 1 -

( 1 )

i i n 2

n

Et la transformation discrète en ondelettes w (i, j) par :

w i k = f i - - f

( , ) k

( 1 ) ( )

k

i

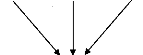
h ( - 1 )

h (1)

h (0)

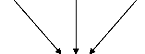
h ( - 1 )

h (1)

h (0)

2.9

23 -

Compression d'images animée par codage EZW 3D

Chapitre 2 Transformée en ondelettes

2.4.3 Familles d'ondelettes

2.4.3.1 Ondelettes orthogonales

Soit {V_n ; n ? Z} une analyse multirésolution, engendrée par une fonctionÖ , et soit ø une ondelette associée, qui engendre les sous espaces complémentaires W _n , n ? Z.

L'ondelette ø est orthogonale si et seulement si: pourn ? k, et pour tout j,l? Z :

øk,j^-øn,l (<øk,j;øn,l >= 0) 2.10

Dans ce cas W _n , n ? Z sont des espaces complémentaires orthogonaux. Cependant, en général nous n'avons pas øk , j orthogonal àøl , j.

2.4.3.2. Ondelettes biorthogonales

~

Il existe une fonction d'échelle duale Ö

et une ondelette dualeø^~ , qui génèrent une

~		~
analyse multirésolution duale avec les sous espaces V j	, et W j		, tels que :

V^~_j - W_j et V^~_j - W^~_j 2.11

W^~j -

W ~ et pour j '

j?j ' 2.12

Ce qui est équivalent à :

< Ö ? >=< Ö ? >=

ø x l ø x l

~

, ( ) , ( ) 0 2.13

En plus, les fonctions duales aussi doivent satisfaire :

~

~ <Ö , Ö (

x-l) >= ä l

et < ø , ø ( x - l ) >= ä l ~ 2.14

24 -

Compression d'images animée par codage EZW 3D

Chapitre 2 Transformée en ondelettes

Par l'utilisation d'un argument d'échelle, nous avons des propriétés plus générales telles que :

< Ö Ö >= ä l , l ' , j ? Z 2.15

~

'

j l -

, , ' l l

j l

,

Et

<øø >= ä ä l l j j ? Z

~ '

, , ' . , , , ' 2.16

' '

j l ' j j l l

- -

j l

,

~

Les définitions de Ö et ø ~ sont semblables a celles de Ö etø . Le rôle de la base

j , l j , l j , l j , l

~ (Ö etø) et de la base duale ( Ö

etø~ ) peuvent être interchangées. [2.8]