DEDICACES
Remerciements
Résumé/Abstract
Listes des figures
Introduction Générale
CHAPITRE I : METHODES DE CALCUL
1.1 Introduction
1.2 Méthode de structure électronique
1.2.1 Approximation orbitale
1.2.2 Approximation de Hartree-Fock
1.2.2.1 Les équations de Hartree-Fock
1.2.2.2 Les équations de Roothaan-Haal
1.3 Méthodes « post Hartree-Fock »
1.3.1 Interaction de configuration
1.3.1.1 Principe de la méthode
1.3.2 La méthode du champ autocohérent
multiconfigurationnelle(MCSCF)
1.3.3 Interaction de configuration multireférence(MRCI)
1.4 Choix de la base d'orbitales moléculaires
1.4.1 Quelques critères de choix d'une base
1.4.2 Approximation LCAO
1.5 Conclusion
CHAPITRE II : MISE EN OEUVRE POUR LA MOLECULE
DE NO
2.1 Introduction
2.2 Présentation de la molécule de NO
2.2.1 Etats électroniques de NO
2.3 Diagramme de corrélation
2.4 Choix de la base
2.5 Résultats et discussion
2.6 Conclusion
CONCLUSION GENERALE ET PERSPECTIVES
REFERENCES
ANNEXES
LISTE DES FIGURES
1.1 Diagramme des déterminants de slater excités
à partir de la référence HF
2.1 Configuration électronique de NO
2.2 Courbe de potentiel MCSCF l'état fondamental
2.3 Courbes de potentiel MCSCF des trois premiers états
excités 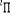
2.4 Courbes de potentiel MCSCF des quatre premiers états
excités 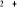
2.5 Courbes de potentiel MCSCF des trois premiers états
excités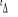
2.6 Synthèse des courbes de potentiel MCSCF de NO
INTRODUCTION GENERALE
La pollution étant un fait marquant de la
société actuelle, on se propose d'étudier l'interaction
entre les molécules responsables de cette pollution avec notre
environnement. Comme molécules polluantes nous pouvons citer le CO, le
NO, le CN, ...
Mais le NO a retenu notre attention pour plus d'un titre
déjà parce qu'il joue un rôle assez important dans le cycle
de l'azote, il est également produit par toutes les cellules du corps
humain.
Dans la seconde édition du Spectra of Diatomic
Molecules Herzberg, Gaylon et co-auteurs ont obtenu par diffraction aux rayons
X les spectres des molécules diatomiques connues. De ces spectres, on a
pu déterminer les constantes spectroscopiques de l'état
fondamental et de quelques états excités du monoxyde d'azote
NO.
Il nous a semblé important de faire une étude
d'ensemble de cette molécule. En commençant par la structure
électronique nous poursuivrons plus tard par la spectroscopie et la
photodissociation.
Nous utilisons les méthodes de calculs ab
initio ou méthodes de base de la Chimie quantique pour
déterminer les courbes de potentiel et quelques constantes
spectroscopiques à l'instar de la distance internucléaire
à l'équilibre, l'énergie de dissociation et la
fréquence de vibration. Données qui nous permettra de
déterminer plusieurs propriétés relatives à cette
molécule notamment les moments de transition, les sections efficaces et
bien d'autres utiles dans l'étude de la photodissociation.
Dans le chapitre I sont décrites les différentes
méthodes de calcul de structure moléculaire. Au chapitre II nous
appliquons la méthode MCSCF à la molécule de NO pour
déterminer les courbes de potentiel et les constantes spectroscopiques
citées plus haut. La conclusion résume ce travail et en
dégage les perspectives.
CHAPITRE I :
METHODES DE CALCUL
1.1 Introduction
Les méthodes de calcul ab initio des
structures électroniques ont atteintes un degré de
précision important pour avoir un impact considérable dans
plusieurs domaines des sciences c'est le cas de l'astrophysique, la chimie
atmosphérique pour ne citer que ceux-là. Ce succès est
dû au développement des nouveaux algorithmes et aux ordinateurs de
plus en plus puissants. Cependant, certaines ne servent qu'à des fins
qualitatives, car ignorant la corrélation électronique. Pourtant
pour obtenir des résultats précis, il faut inclure cette
corrélation dans le traitement. Dans ce chapitre, nous présentons
les méthodes CI (Interaction de Configuration), MRCI (Multi
référence, Interaction de Configuration) MCSCF
(Multiconfigurationnel Self Consistent Field). Mais dans ce travail nous
utiliserons la MCSCF.
1.2 Méthode de structure
électronique
Toute l'information que l'on peut obtenir sur un
système constitué d'un ensemble de particules est contenue dans
la fonction d'onde 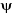 du système. La fonction d'onde d'un système
composé de N atomes et n électrons est obtenue en
résolvant l'équation de Schrödinger indépendante du
temps suivante : du système. La fonction d'onde d'un système
composé de N atomes et n électrons est obtenue en
résolvant l'équation de Schrödinger indépendante du
temps suivante :
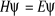 (1.1)
(1.1)
où E est l'énergie du système et H
l'hamiltonien du système. 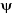 sera fonction des coordonnées des noyaux et des
électrons. Il n'est cependant pas possible de résoudre
rigoureusement une telle équation mise à part des systèmes
à un électron. C'est pour cela que des approximations ont
été introduites dans la théorie quantique proposée
dès les années 20 afin de pouvoir résoudre cette
équation de façon approchée.(2) sera fonction des coordonnées des noyaux et des
électrons. Il n'est cependant pas possible de résoudre
rigoureusement une telle équation mise à part des systèmes
à un électron. C'est pour cela que des approximations ont
été introduites dans la théorie quantique proposée
dès les années 20 afin de pouvoir résoudre cette
équation de façon approchée.(2)
Pour un système traité comme étant
composé de charges ponctuelles (n électrons et N noyaux) sans
traitement relativistes, l'hamiltonien pour un système à couches
fermées est donnée par :
(1.2)
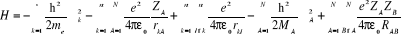
Energie de répulsion électrostatique
électrons /électrons
Energie cinétique des électrons
Energie de répulsion électrostatique entre noyaux
Energie potentielle
des électrons dans le champ des noyaux
Energie cinétique
des noyaux
 est la constance de Planck divisée par est la constance de Planck divisée par  , me est la masse de l'électron, e est la charge de
l'électron. , me est la masse de l'électron, e est la charge de
l'électron. 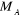 est la masse du noyaux A, est la masse du noyaux A, 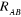 est la distance entre les noyaux de l'atome A et de l'atome B dont les
charges nucléaires sont respectivement est la distance entre les noyaux de l'atome A et de l'atome B dont les
charges nucléaires sont respectivement 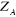 et et 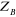 . . 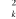 est le laplacien du kième électron. est le laplacien du kième électron.
Cet hamiltonien ne prend pas en considération les
interactions entre les électrons et les champs extérieurs au
système.
On utilisera par la suite les notations en unités
atomiques. Dans ce système d'unité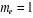 , , 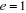 , , 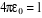 soit : soit :
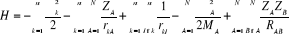 (1.3) (1.3)
La première des approximations à être
introduite est celle de Born-Oppenheimer
1.2.1 Approximation de Born-Oppenheimer
En 1927, Born et Oppenheimer(3) ont proposé
de simplifier la résolution de l'équation (1.1) en
séparant la partie électronique de la partie nucléaire
dans la fonction d'onde 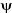 . Cette approximation est basée sur le fait que les
électrons ont une vitesse beaucoup plus grande que celle des noyaux,
ceci étant dû à la masse beaucoup plus faible des
électrons (environ 1836 fois plus petite que la masse du proton). La
fonction d'onde du système solution de l'équation de
Schrödinger dans l'approximation de Born et Oppenheimer peut donc
s'écrire sous la forme d'un produit de deux fonctions : . Cette approximation est basée sur le fait que les
électrons ont une vitesse beaucoup plus grande que celle des noyaux,
ceci étant dû à la masse beaucoup plus faible des
électrons (environ 1836 fois plus petite que la masse du proton). La
fonction d'onde du système solution de l'équation de
Schrödinger dans l'approximation de Born et Oppenheimer peut donc
s'écrire sous la forme d'un produit de deux fonctions :
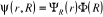 (1.4)
(1.4)
où  est la fonction d'onde nucléaire, est la fonction d'onde nucléaire, 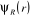 est la fonction d'onde électronique correspondant à un jeu
de position R des noyaux figées, r et R étant respectivement les
positions des électrons et des noyaux. est la fonction d'onde électronique correspondant à un jeu
de position R des noyaux figées, r et R étant respectivement les
positions des électrons et des noyaux.
En négligeant la contribution de l'opérateur
énergie cinétique des noyaux vu que leur vitesse est très
négligeable devant celle des électrons, la fonction d'onde
électronique 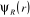 sera alors solution de l'équation de Schrödinger
électronique suivante : sera alors solution de l'équation de Schrödinger
électronique suivante :
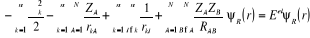 (1.5) (1.5)
Cette équation décrit donc le mouvement
électronique dans le champ des noyaux fixes, la fonction d'onde 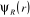 et l'énergie électronique et l'énergie électronique 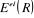 dépendent des coordonnées nucléaires et l'ensemble
des dépendent des coordonnées nucléaires et l'ensemble
des  constitue ce qu'on appelle une courbe de potentiel (pour une
molécule diatomique) et intervient comme paramètre dans
l'équation d'onde nucléaire(4). constitue ce qu'on appelle une courbe de potentiel (pour une
molécule diatomique) et intervient comme paramètre dans
l'équation d'onde nucléaire(4).
L'équation (1.5) peut encore s'écrire :
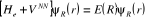 (1.6) (1.6)
Où 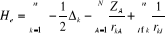 (1.7) (1.7)
Et 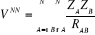 (1.8)
(1.8)
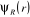 est la fonction propre et est la fonction propre et 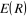 est l'énergie incluant les interactions électrostatiques
nucléaires solutions de l'opérateur est l'énergie incluant les interactions électrostatiques
nucléaires solutions de l'opérateur 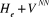 les indices l, k sont relatifs aux électrons et A, B sont
relatifs aux noyaux. les indices l, k sont relatifs aux électrons et A, B sont
relatifs aux noyaux.
Comme 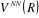 ne dépend que des coordonnées nucléaires, ne dépend que des coordonnées nucléaires, 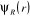 vérifie aussi l'équation suivante : vérifie aussi l'équation suivante :
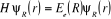 (1.9)
(1.9)
où 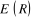 est l'énergie électronique du système, et on
a : est l'énergie électronique du système, et on
a :
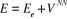 (1.10).
(1.10).
Dans le cas d'une molécule diatomique, la
géométrie ne dépend que de la distance entre les noyaux.
La fonction 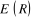 est appelée courbe de potentiel. est appelée courbe de potentiel.
Notons que cette approximation est erronée lorsque deux
ou plusieurs solutions de l'équation (1.9) ont des énergies
voisines. Dans la majeure partie des systèmes moléculaires, cette
approximation introduit une erreur. Son utilisation permet de ramener le
problème à la résolution de l'équation de
Schrödinger électronique pour un ensemble de
géométrie des noyaux(5).
1.2.2 Approximation de Hartree-Fock
Encore appelée approximation du "champ self consistant"
SCF, Hartree (1928), Fock (1930) elle fût proposée en 1928 par
Hartree. Le problème électronique est un problème multi
corps et du fait de la présence des termes d'interaction entre les
électrons, il est impossible de traiter séparément les
différents électrons.
Toutefois, on peut séparer les variables en supposant
que chaque électron se meut dans le champ moyen des autres
électrons(4).
L'Hamiltonien électronique pour un système
à n électrons donné par l'équation (1.9) peut se
mettre sous la forme suivante :
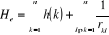 (1.11)
(1.11)
où
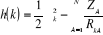 (1.12)
(1.12)
et h est l'opérateur monoélectronique, on
a :
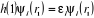 (1.13)
(1.13)
Les 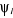 sont les fonctions propres de l'Hamiltonien monoélectronique h
vérifiant les conditions d'orthonormalités et sont les fonctions propres de l'Hamiltonien monoélectronique h
vérifiant les conditions d'orthonormalités et 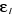 sont les énergies propres de h. sont les énergies propres de h.
En l'absence de couplage spin-orbite, on définit une
spinorbitale 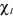 comme le produit d'une fonction d'espace comme le produit d'une fonction d'espace 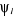 appelée orbitale moléculaire d'espace et d'une fonction
de Spin appelée orbitale moléculaire d'espace et d'une fonction
de Spin 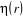 que l'on écrit : que l'on écrit :
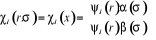 (1.14)
Où (1.14)
Où 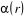 , , 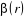 correspond aux spins pointés vers le haut et vers le bas
respectivement. correspond aux spins pointés vers le haut et vers le bas
respectivement.
La fonction d'onde totale pour tenir compte du principe
d'exclusion de Pauli, s'écrira sous la forme d'un déterminant de
Slater construit à partir des K spinorbitales 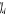 (rivail (1989)) : (rivail (1989)) :
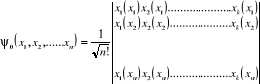 (1.15) (1.15)
L'énergie électronique dans cette approximation
s'écrit :
 (1.16) (1.16)
Pour un système à n électrons à
couches fermées, l'énergie électronique dans
l'approximation de Hartree-Fock s'écrit : (Schaefer (1977)).
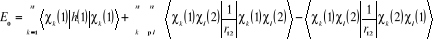
(1.17)
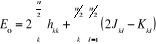 (1.18) (1.18)
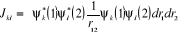 (1.19) (1.19)
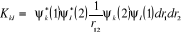 (1.20) (1.20)
1.2.2.1 Les équations de
Hartree-Fock
Il s`agit ici de déterminer les orbitales
moléculaires qui minimisent l'énergie donnée par
l'expression (1.17) et ceci est possible grâce à la méthode
utilisant le principe variationnnel. Si on fait l'hypothèse que les
spinorbitales 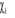 correspondent à un extremum de correspondent à un extremum de 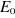 , on doit pouvoir vérifier qu'une petite modification
apportée à l'une des spinorbitales donnant un autre jeu
d'orbitales , on doit pouvoir vérifier qu'une petite modification
apportée à l'une des spinorbitales donnant un autre jeu
d'orbitales 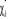 n'entraîne pas de variation de n'entraîne pas de variation de 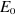 et impose aux spinorbitales d'être orthonormées. et impose aux spinorbitales d'être orthonormées.
Une façon de construire la spinorbitale 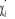 à partir de à partir de 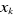 est de poser : est de poser :
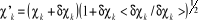 (1.21) (1.21)
Les intégrales 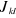 et et 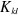 sont respectivement appelées intégrales de Coulomb et
intégrales d'échanges ; l'intégrale de Coulomb a un
équivalent en mécanique classique, alors que l'intégrale
d'échange provient de la nécessité d'antisymétriser
la fonction d'onde. Les intégrales de Coulomb et d'échange
d'écrivent les interactions entre électron. On ne tient pas
compte du spin dans sont respectivement appelées intégrales de Coulomb et
intégrales d'échanges ; l'intégrale de Coulomb a un
équivalent en mécanique classique, alors que l'intégrale
d'échange provient de la nécessité d'antisymétriser
la fonction d'onde. Les intégrales de Coulomb et d'échange
d'écrivent les interactions entre électron. On ne tient pas
compte du spin dans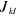 . . 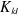 réduit l'interaction Coulombienne entre deux électrons
situés dans les orbitales réduit l'interaction Coulombienne entre deux électrons
situés dans les orbitales 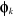 et et 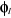 ayant des spins parallèles(2). ayant des spins parallèles(2).
Où 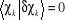 et et 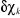 est la variation apportée à est la variation apportée à 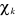 . La variation de l'énergie au premier ordre pour un
système à couches fermées s'écrit : . La variation de l'énergie au premier ordre pour un
système à couches fermées s'écrit :
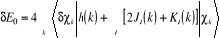 (1.22) (1.22)
On définira donc l'opération de Hartree-Fock
pour un électron par :
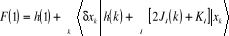 (1.23) (1.23)
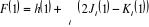 (1.24) (1.24)
Les opérations de Coulomb et d'échange sont
définies par leur action sur les spinorbitales de la manière
suivante :
 (1.25) (1.25)
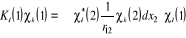 (1.26) (1.26)
Les équations de Hartree-Fock prennent alors la
forme : 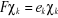 (1.27) (1.27)
En toute rigueur, ces équations ne permettent pas le
calcul de ces orbitales puisque l'opérateur F contient les
opérateurs J et K qui pour être définis supposent que l'on
connaisse ces spinorbitales solutions de l'équation (1.13) ; dans
la pratique, on fait des approximations successives où, à partir
des fonctions calculées à la nième, itération, on
définit un opérateur F permettant de calculer un nouvel ensemble
de fonctions propres correspondant à la (n+1)ième
itération.
La procédure est poursuivie jusqu'à ce que le
champs ressenti par un électron devienne stationnaire ;
c'est-à-dire que la différence entre deux itérations 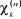 et et 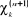 soit inférieur à la précision
fixée.(3) soit inférieur à la précision
fixée.(3)
L'équation de Hartree-Fock (1.27) peut se
résoudre numériquement de façon à obtenir les
orbitales atomiques des atomes en utilisant la symétrie
sphérique. Pour les molécules de symétrie plus basse, on
utilise une méthode proposée par Roothaan et Hall.
1.2.2.2 Equations de Roothaan - Hall
Hall et indépendamment Roothaan ont
démontrés qu'en introduisant un jeu de fonction spatiales
connues, les équations intégro-différantielles peuvent
être transformées en un système d'équations
algébriques et être résolu en utilisant la méthode
des matrices.
Les équations de Hartree-Fock peuvent s'écrire
en fonction des 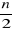 orbitales moléculaires d'espace orbitales moléculaires d'espace 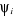 et on a : et on a : 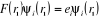 (1.28) (1.28)
Une bonne méthode pour résoudre les
équations de Hartree-Fock est l'approximation LCAO (Linear Combination
of Atomic, Orbitals) dans laquelle les orbitales moléculaires d'espace
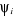 sont développés sur une base de M orbitales atomiques sont développés sur une base de M orbitales atomiques
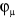 , et pour un système à couchers fermées comportant
n électrons, l'orbitale moléculaire a pour expression : , et pour un système à couchers fermées comportant
n électrons, l'orbitale moléculaire a pour expression : 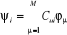 (1.29) (1.29)
Où les coefficients 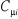 sont réels. Les orbitales moléculaires doivent, en outre,
respecter les combinaisons de normation et d'orthogonalité mutuelle que
l'on écrit : sont réels. Les orbitales moléculaires doivent, en outre,
respecter les combinaisons de normation et d'orthogonalité mutuelle que
l'on écrit : 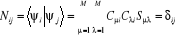 (1.30) (1.30)
Où 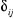 est le symbole de Kronecker et est le symbole de Kronecker et 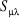 est l'intégrale de recouvrement des orbitales est l'intégrale de recouvrement des orbitales 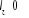 et . et . 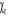 . .
En combinant (1.28) et (1.29) et en multipliant de chaque
côté par 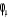 puis en intégrant, on obtient les équations de
Hall-Roothaan(3). puis en intégrant, on obtient les équations de
Hall-Roothaan(3).
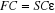 (1.31)
(1.31)
Où F est la matrice de Fock dont les
éléments sont :
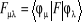 (1.32)
(1.32)
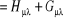 (1.33)
(1.33)
avec 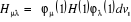 (1.34)
(1.34)
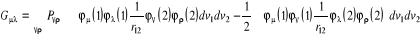 (1.35)
(1.35)
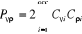 (1.36)
(1.36)
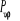 matrice des populations des couches fermées matrice des populations des couches fermées
C est la matrice carrée des coefficients du
développement et 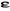 le vecteur des énergies d'orbitales. le vecteur des énergies d'orbitales.
Les équations de Roothaan-Hall (1.31) sont
résolues d'une manière identique à celle des
équations de Hartree-Fock et ne sont valable que pour des
systèmes à couches fermées avec un nombre pair
d'électrons. Les électrons sont appariés et l'un d'entre
eux à un spin 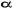 et l'autre un spin et l'autre un spin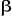 . La fonction d'onde correspondante est du type restricted Hartree-Fock
(RHF). . La fonction d'onde correspondante est du type restricted Hartree-Fock
(RHF).
Les systèmes à couches ouvertes peuvent aussi
être décrits par les fonctions d'onde limitées, mais dans
lesquelles la partie spatiale des orbitales doublement occupées est la
même que précédemment. La fonction d'onde dans ce cas est
du type restricted open-shell Hartree-Fock (ROHF), mais une telle restriction
n'est pas justifiée dès lors que l'électron non
apparié avec un spin 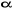 interagit différemment avec un autre électron interagit différemment avec un autre électron  et un électron et un électron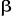 . Par conséquent, les orbitales optimales . Par conséquent, les orbitales optimales  et et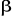 devraient être différentes. On fait alors recours à
la fonction d'onde du type Unrestricted Hartree-Fock (UHF) qui tient compte des
orbitales avec des spins différents. Il faut toutefois faire attention
du fait que la fonction d'onde UHF n'est pas une fonction propre de
l'opérateur devraient être différentes. On fait alors recours à
la fonction d'onde du type Unrestricted Hartree-Fock (UHF) qui tient compte des
orbitales avec des spins différents. Il faut toutefois faire attention
du fait que la fonction d'onde UHF n'est pas une fonction propre de
l'opérateur 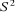 qui évalue le carré du spin total de
l'électron ; mais demeure la fonction de qui évalue le carré du spin total de
l'électron ; mais demeure la fonction de 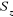 dès lors qu'on utilise des spin orbitales pures dès lors qu'on utilise des spin orbitales pures  et et 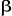 . D'autre part, la fonction d'onde UHF est très flexible et donne
les énergies beaucoup plus basses que celles données par la
ROHF. . D'autre part, la fonction d'onde UHF est très flexible et donne
les énergies beaucoup plus basses que celles données par la
ROHF.
Une erreur systématique sur l'énergie SCF est
due à l'approximation orbitale, qui ne tient pas compte du fait que les
mouvements des électrons sont corrélés. D'une façon
générale, on dit que deux événements 1 et 2 sont
corrélés si la probabilité de l'un est modifiée par
la survenue de l'autre. Or les électrons sont corrélés
à un double titre :
- En tant que corpuscules chargés négativement,
ils se repoussent.
- En tant que fermions, ils se repoussent quand ils sont de
même spin.
Ainsi, la présence d'un électron en un point
diminue-t-elle la probabilité de présence d'un second à
proximité, à fortiori d'un autre électron de même
spin. On donne parfois de ce phénomène une représentation
imagée selon laquelle un électron est entouré d'un
« trou de Coulomb » et d'un « trou de
fermi » qui annihilent plus ou moins, respectivement, l'apparition
dans son voisinage d'une particule négative et d'une particule de
même spin(4).
1.3 Méthodes « post
Hartree-Fock »
L'approximation de Hartree-Fock donne la meilleure
représentation d'une fonction d'onde décrite par un seul
déterminant de Slater. Cependant étant donné que les
électrons interagissent relativement à un champs moyen alors
l'énergie calculée n'est pas très précise, elle ne
représente qu'environ 99% de l'énergie totale. La
différence c'est-à-dire environ 1% restant, porte le nom de
l'énergie de corrélation(3).
 (1.37)
(1.37)
Pour récupérer cette énergie de
corrélation, on a recours aux méthodes dites de post-HF. Il
existe deux types de méthodes de corrélation
électronique :
- Les méthodes variationnelles telles que l'interaction
de configuration (CI), l'interaction de configuration multi
référence (MRCI) et la méthode du champ auto
cohérent multiconfigurationnelle (MCSCF).
- Les méthodes de perturbation telles que la
théorie des perturbations multi corps (MBPT) et la méthode de
clusters couplés (CC).
Dans le cadre de ce travail, nous utiliserons la
première classe de ces méthodes qui offre l'avantage de pouvoir
traiter les états excités. Il est cependant important de rappeler
que le point de départ de toutes ces méthodes de
corrélation est par principe la fonction d'onde de HF. Donc pour tout
traitement de la corrélation, la fonction d'onde
s'écrira :
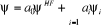 (1.38)
(1.38)
Avec 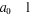 . Ces méthodes de corrélation diffèrent dans la
manière de calculer les coefficients . Ces méthodes de corrélation diffèrent dans la
manière de calculer les coefficients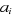 . Les déterminants additionnels . Les déterminants additionnels 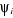 sont obtenus par excitations des électrons des orbitales
occupées de la fonction d'onde HF. Vers les orbitales initialement
vacantes suivant le diagramme de la figure (1.1). sont obtenus par excitations des électrons des orbitales
occupées de la fonction d'onde HF. Vers les orbitales initialement
vacantes suivant le diagramme de la figure (1.1).
---- ---- ----
---- ---- ----
---- ---- ----
---- ---- ----
HF S. Type D. Type
fig.1.1 diagramme des déterminants de slater
excités à partir de la référence
HF
1.3.1 Interaction de
configuration
1.3.1.1 Principe de la méthode
Elle consiste à optimiser une fonction d'onde
formée d'une combinaison linéaire de plusieurs
déterminants de Slater c'est probablement la meilleure des
méthodes qui prend en compte la corrélation dynamique. Relevons
qu'il existe deux types de corrélation. La corrélation de Coulomb
qui correspond à des spins antiparallèles et la
corrélation de Fermi qui correspond à des spins
parallèles.
La fonction d'onde s'écrira donc :
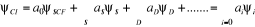 (1.39) (1.39)
Les 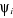 permettent de décrire l'état fondamental et les
états excités du système. permettent de décrire l'état fondamental et les
états excités du système.
Introduisons la fonction de Lagrange
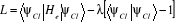 (1.40) (1.40)
En appliquant le principe variationnel, on obtient
l'équation matricielle
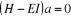 (1.41)
(1.41)
où a est la matrice des coefficients 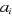 , I la matrice identité et H la matrice dont les
éléments sont , I la matrice identité et H la matrice dont les
éléments sont 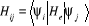 . L'énergie d'IC est la plus petite valeur propre de la matrice
d'IC. . L'énergie d'IC est la plus petite valeur propre de la matrice
d'IC.
1.3.2 La méthode de champ auto cohérent
multiconfigurationnelle (MCSCF)
En effet, la méthode d'IC est valide lorsque la
configuration de HF est largement prédominante. Cependant, lorsque
l'énergie des orbitales moléculaires vacantes se rapproche de
celles des OM occupées, le système devient de moins en moins
monoconfigurationnel. Il est donc préférable d'effectuer un
calcul SCF optimisant l'énergie d'une combinaison de plusieurs
déterminants, impliquant donc plusieurs configurations de
référence : c'est un calcul SCF optimisant l'énergie
d'une combinaison de plusieurs déterminants, impliquant donc plusieurs
configurations de référence : c'est un calcul MCSCF (Multi
Configuration SCF). Elle a l'avantage de prendre en compte une partie de la
corrélation électronique . La fonction d'onde s'écrit.
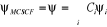 (1.42)
(1.42)
Où 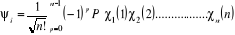 (1.43) (1.43)
Et 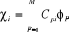 (1.44)
(1.44)
Avec 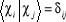 (1.45)
(1.45)
Et 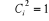 (1.46)
(1.46)
P est l'opérateur de permutation et M est la
dimension de La base des orbitales atomiques en général est
caractérisée par :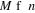 . .
L'énergie électronique correspondante à
la fonction d'onde 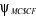 est donnée par : est donnée par :
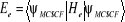 (1.47)
(1.47)
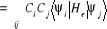 (1.48)
(1.48)
Dans la mise en oeuvre de la théorie MCSCF, les
coefficients Ci ainsi que les OM, utilisées pour construire
les déterminants 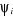 sont optimisées. La procédure de minimisation de
l'énergie consiste à résoudre les équations : sont optimisées. La procédure de minimisation de
l'énergie consiste à résoudre les équations :
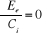 (1.49)
(1.49)
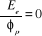 (1.50)
(1.50)
Un tel calcul peut se réaliser sous la forme CASSCF
(Complete Active Space SCF). Elle consiste à partitionner les
OMs en deux espaces actif et inactif. L'espace actif correspond aux
orbitales moléculaires HOMO (Highest Occuped Molecular Orbitals)
auxquels on ajoute quelques OMs LUMO (Lowest Unocupied Molecular
Orbitals).
1.3.3 Interaction de configuration
multiréférence (MRCI)
La méthode MRCI est une approximation dans laquelle la
fonction d'onde est encore une combinaison linéaire des
déterminants de Slater. Elle utilise comme référence la
fonction d'onde MCSCF et n'autorise que les simples et doubles excitations
à partir de cette dernière on a :
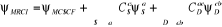 (1.51) (1.51)
Les 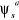 et et 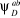 sont les fonctions de configurations générées
à partir de la fonction multiconfigurationnelle MCSCF. sont les fonctions de configurations générées
à partir de la fonction multiconfigurationnelle MCSCF.
L'un des avantages majeurs de la méthode MRCI est que
la fonction d'onde correspondante permet une meilleure prise en compte de la
corrélation. Cependant, le nombre de configurations
générées est souvent trop élevé ce qui a
pour effet d'alourdir les calculs.
Pour rendre les calculs faisables, on a souvent recours
à de nouvelles approximations. En général, on ne choisit
que les configurations s dont le poids statistique dans la définition de
la fonction d'onde est important. On peut aussi à cela associer la
contraction des configurations dans le but d'en diminuer le nombre
Ces différentes approximations diminuent la
quantité d'énergie que l'on peut récupérer par
corrélation. Par ailleurs, le fait de ne pas inclure les excitations
quadruples diminue également la flexibilité de la fonction
d'onde. Pour remédier à ces inconvénients, Davidson
propose la correction qui porte son nom et qui consiste à prendre en
compte les excitations quadrupolaires à l'aide de l'approximation.
 (1.52) (1.52)
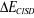 est la correction en énergie due aux simples et doubles
excitations. est la correction en énergie due aux simples et doubles
excitations.
1.4 Choix de la base d'orbitales moléculaires
L'un des aspects important aux méthodes de calcul ab
initio est le choix de la base d'OM. En effet, une base d'orbitales
moléculaire de dimension infinie permettrait d'obtenir l'énergie
la plus exacte possible par rapport à une méthode donnée.
Cependant, une base de taille infinie rendrait les calculs impossibles compte
tenu de la taille de la matrice d'IC.
En général, la base doit avoir une dimension
raisonnable.
1.4.1 Quelques critères de choix d'une
base(4)
Pour avoir une bonne base, il faudrait que :
a) La base soit étendue pour faire des calculs
précis.
b) Par contre pour décrire les orbitales de coeur, qui
ne sont pas déformées par la formation de la molécule, on
peut utiliser une base plus restreinte (fonctions contractées)
c) Pour décrire un état moléculaire de
type Rydberg, il est nécessaire d'ajouter dans la base atomique des
fonctions dites de types diffus c'est-à-dire ayant une grande amplitude
à grande distance
d) Afin de déduire la déformation du nuage
électronique due à la formation de la liaison (c'est à
dire la perte de la symétrie sphérique), on doit introduire dans
la base, des fonctions dites de polarisation. Ce sont des orbitales ayant un
nombre quantique azimutal  supérieur à ceux des orbitales atomiques de la base qui
est utilisées pour décrire la configuration de l'état
fondamental. Ainsi pour les atomes de la deuxième et troisième
ligne de Mendeleïev, les fonctions de polarisation correspondantes sont
les orbitales d,f,g,... supérieur à ceux des orbitales atomiques de la base qui
est utilisées pour décrire la configuration de l'état
fondamental. Ainsi pour les atomes de la deuxième et troisième
ligne de Mendeleïev, les fonctions de polarisation correspondantes sont
les orbitales d,f,g,...
1.4.2 Approximation LCAO
Dans cette approximation LCAO (Linear Combination of Atomic
Orbitales), les 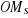 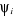 sont choisies comme combinaison linéaire des orbitales atomiques sont choisies comme combinaison linéaire des orbitales atomiques
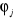
 (1.53)
(1.53)
Il existe deux types d'AOs : les orbitales
slatériennes et les orbitales gaussiennes.
Les orbitales slatériennes (Slater type orbitales STO)
sont des fonctions de la forme :
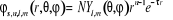 (1.54)
(1.54)
t est un paramètre qui décrit la taille
de l'orbitale, N la constante de normalisation tandis que les 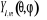 sont les harmoniques sphériques. sont les harmoniques sphériques.
Les orbitales gaussiennes (Gaussien type orbitals GTO)
s'écrivent en coordonnées polaires et cartésiennes.
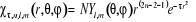 (1.55) (1.55)
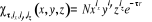 (1.56) (1.56)
Respectivement la somme 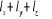 ( ( 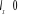 , , 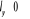 et et 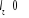 ) détermine le type d'orbitale. Bien que de qualité
inférieure aux STO, les GTOs ou l'avantage de donner dans
l'approximation LCAO une bonne représentation des Oms. Par ailleurs, les
orbitales gaussiennes sont commodes pour le calcul des intégrales
à plusieurs centres qui peuvent être déterminées
analytiquement ou numériquement à l'aide d'un schéma
unidimensionnel s'appuyant sur la règle du produit des gaussiennes. ) détermine le type d'orbitale. Bien que de qualité
inférieure aux STO, les GTOs ou l'avantage de donner dans
l'approximation LCAO une bonne représentation des Oms. Par ailleurs, les
orbitales gaussiennes sont commodes pour le calcul des intégrales
à plusieurs centres qui peuvent être déterminées
analytiquement ou numériquement à l'aide d'un schéma
unidimensionnel s'appuyant sur la règle du produit des gaussiennes.
Les divers types de bases utilisées appartiennent aux
catégories suivantes :
- Les « bases minimales» où l'on ne
considère que les orbitales atomiques occupées dans la
configuration électronique de l'atome libre ; ce sont des bases
simple zéta.
-Les « bases étendues » où
chaque OA occupées est représentée par plusieurs OA de
même type. On obtient des bases double zéta (vdz),si celles-ci
sont représentées par deux OA. Triple zéta (vtz) pour
trois OA etc...
-Les « bases étendues
polarisées » où l'on introduit en plus des orbitales de
polarisation correspondant aux OA non occupées dans l'atome libre.
1.5 Conclusion
Après avoir exposé toutes ces méthodes de
calcul, on constate qu'aucune de ces méthodes n'est parfaite car chacune
d'elles présente des insuffisances. Cependant au fur et à mesure
qu'on corrige ces insuffisances, on obtient de résultats meilleurs.
| 


