

Faculté des Sciences appliquées
Conception et calcul des structures
en verre
Promoteur: Y. Rammer Mémoire
de fin d'étude présenté par
Co-Promoteur : M. Provost
STUDER Mathieu
Lecteur : C. Pimpurniaux en vue de
l'obtention du grade
d'Ingénieur Civil Architecte
Année Académique 2007-2008
«The most powerful way that an enginner can
contribute to the work of architects is by exploring the nature of the
materials and using that knowledge to produce a special quality (...).
Exploration and innovation are the keys.»
Peter Rice
An Engineer Imagines, Paris, Artemis, 1994
«What the engineer perceives as a structure the
architect sees at a sculpture - of course it's both»
Ove Arup
Stacking of glass- Structures and Sculptures, GPD, 200
Résumé
Le verre est un matériau connu depuis plus de 5000 ans.
Cependant, son usage en tant que vitrage ne remonte qu'à quelques
siècles. Depuis une dizaine d'années, des progrès
importants tant du point de vue de la production que des différents
procédés de modifications ont permis d'augmenter les
capacités de résistance du verre.
Actuellement, il existe quelques réalisations de
structure en verre, qui répondent à un besoin de l'architecture
contemporaine d'utiliser des éléments de construction de plus en
plus minces comme l'acier ou de plus en plus transparents comme le verre. Les
structures en acier ont déjà été largement
étudiées dans le passé et le comportement des
différents éléments est aujourd'hui bien
maîtrisé. Le comportement fragile du verre a souvent
été un frein à son utilisation comme élément
de structure. Le verre reste un matériau de construction encore mal
connu et mal maîtrisé du point de vue de ses
propriétés, de sa résistance, de son dimensionnement et de
ses différents moyens d'assemblage.
Ce travail donne une méthodologie d'un point de vue de
la conception du calcul des colonnes et des poutres chargées dans le
plan des feuilles. La méthode pour déterminer la
résistance du verre tient compte de l'état de surface et de la
durée de chargement. Le dimensionnement tient compte des
différents phénomènes d'instabilité car les
éléments en verre sont souvent très élancés.
Il donne également une vision sur les différents moyens
d'assemblages sans pour autant développer des méthodes de
calcul.
Remerciements
Je tiens tout d'abord à remercier le professeur Y.
Rammer qui m'a accordé sa confiance pour la mise en oeuvre de ce sujet
et pour m'avoir prodigué quantité de conseils pratiques
importants.
Ensuite, j'aimerais remercier Monsieur M. Provost pour m'avoir
aiguillé tout au long de ce travail et pour son aide dans la
compréhension de certains concepts.
Je tiens également à remercier toutes les
personnes qui de près ou de loin m'ont aidées dans la quête
d'informations et de compréhension et tout particulièrement
Monsieur C. Pimpurniaux (SECO), Monsieur G. Zamarti (CSTC), Monsieur M.
Crisinel (EPFL, CH), Monsieur A. Luible (Josef-Gartner, CH), Monsieur M.
Haldimann (Emch + Berger, CH), Monsieur F.P. Bos (T.U. Delft, NL), Monsieur R.
Speelman (AGC flat glass), Monsieur L. Daudeville (UJF Grenoble, FR) et
Monsieur B. Espion (ULB).
J'aimerais également remercier ma famille de Bruxelles
à Giseny et tout particulièrement mes parents pour m'avoir
donné le goût d'apprendre et cela dès le plus jeune
âge.
Je tiens également à remercier mes amis qui ont
toujours été là pour moi, qui m'ont aidé à
décompresser et qui ont toujours cru en moi durant toutes ces
années d'études.
Tables des matières
Résumé iiRemerciements iiiTables des
matières iv
Symboles viiSymbole latin viiSymbole grec
viii1 Introduction 1
2 Le verre dans l'architecture 3
2.1 Les origines 3
2.2 L'architecture antique 3
2.3 L'architecture romane 4
2.4 L'architecture gothique 4
2.5 L'architecture Baroque 5
2.6 Le 18ème siècle 5
2.7 L'architecture moderne 6
2.8 L'architecture contemporaine 7
3 Les caractéristiques du verre et les principes de
construction du verre plat 8
3.1 Information générale 8
3.1.1 Définition 8
3.1.2 Le processus de fabrication (voir figure 3.1.1) 8
3.2 Composition 9
3.3 Caractéristiques mécaniques 10
3.3.1 Résistance théorique 11
3.3.2 Défauts de volume (inclusions de Nickel) 11
3.3.3 Défauts de surface 12
3.4 Mécanique de rupture 12
3.4.1 Fissuration sous critique (fatigue statique) 12
3.5 Les différents types de verre 14
3.5.1 Le verre trempé 14
3.5.2 Le verre durci 18
3.5.3 Le verre feuilleté ou laminé 18
3.5.4 Le verre armé 20
3.5.5 Les autres types de verre 20
4 Détermination de la résistance du verre 21
4.1 Résistance à la compression du verre recuit
21
4.1.1 Valeur de la résistance en compression du verre
recuit 21
4.2 Résistance à la traction du verre recuit 22
4.2.1 Principe général 22
4.2.2 Les différentes méthodes 22
4.3 Résistance due à la trempe 26
4.3.1 Formule analytique 26
4.3.2 Valeur des fournisseurs ou des normes 27
4.4 Principes de superposition 29
4.5 Résumé des formules de la résistance du
verre 30
5 Dimensionnement d'une structure en verre 31
5.1 Combinaison d'actions 31
5.1.1 Etat Limite Ultime (E.L.U.) 31
5.1.2 Etat Limite de Service (E.L.S.) 32
5.2 Classifications des structures 33
5.2.1 Généralité 33
5.2.2 Les paramètres 34
5.2.3 Axes de démarcations 35
5.3 Elément comprimé 37
5.3.1 Design 37
5.3.2 Etat limite ultime 39
5.3.3 Etat limite de service 45
5.4 Elément fléchis 45
5.4.1 Design 46
5.4.2 Etat limite ultime 46
5.4.3 Etat limite de service 48
5.5 Elément comprimé et fléchis 49
5.6 Actions accidentelles 49
5.6.1 Résistance aux chocs 50
5.6.2 Résistance au feu et gradient thermique 51
6 Les assemblages 53
6.1 Assemblage métallique 53
6.2 Assemblage collé 54
6.3 Assemblage par connecteur 55
6.3.1 La géométrie 55
6.3.2 La résistance 56
7 Avantages et inconvénients 58
7.1 Inconvénients 58
7.1.1 Connaissances limitées, l'obligation de faire des
essais 58
7.1.2 Matériau fragile 59
7.1.3 Sensible à l'état de surface 60
7.1.4 Effet psychologique 60
7.1.5 Vandalisme 61
7.2 Avantages 61
7.2.1 Capacité portante théorique importante 61
7.2.2 Durabilité, inerte 61
7.2.3 Effet sur l'environnement et recyclage 61
7.2.4 Matériau novateur et nouvelles perspectives
architecturales 62
7.3 Tableau comparatif avec le béton, l'acier et le bois
63
8 Exemples de réalisation 64
8.1 Tableau des différents exemples 64
8.2 Centre administratif, Saint-Germain-en-Laye, FR. 65
8.3 Centre de Recherches et de Restauration des musées de
France, Paris, FR. 67
8.4 Passerelles en verre, Rotterdam, NL. 68
8.5 Apple Store 5th avenue, New York, USA 69
8.6 Pavillon en verre, Rheinbach,ALL 71
8.7 Autres exemples 72
9 Le projet 74
9.1 Programme 74
9.2 Esquisses et plans 75
9.3 Dimensionnement de colonnes et poutres en verre 76
9.3.1 Dalle de toiture 76
9.3.2 Poutre de toiture P.Sec.1 79
9.3.3 Poutre de toiture P.princ.1 82
9.3.4 Colonne C 2.1 85
Conclusion 88
Bibliographie 91
Annexes 97
Annexe A (copie de l'annexe F de l'Eurocode 3) 97
Annexe B 103
Annexe C 104
Symboles
Symbole latin
a Longueur de la fissure
a0 Distance inter atomique
c Capacité thermique
e Épaisseur nominale
e Excentricité
ei Épaisseur des différents
éléments
f Flèche
fb ; k Résistance caractéristique
des contraintes de trempe
fg ; c Résistance caractéristique
du verre à la compression
fg ; c ; d Résistance de calcul
du verre à la compression
fg ; t Résistance caractéristique
du verre à la traction
fg ; t ; d Résistance de calcul
du verre à la traction
fg ; t ; k Valeur
caractéristique du verre recuit en traction
h Hauteur
i0 Rayon de giration de la section par
rapport au centre de torsion
kmod Le facteur pour la durée de chargement
ksp Le facteur pour le profil de la surface du verre
kv Le facteur pour le procédé
de trempe
l Épaisseur de la plaque
m Paramètre de forme dans la loi de Weibull
n Nombre de feuilles de verre
t Temps
tref Temps de référence
teff Epaisseur efficace
v Vitesse
w0 Flèche initiale
A Aire
Aeff Aire effective
Afr , c Aire frontale fissurée
Atot Aire totale
Dglass Dommage
E Module de Young
G Valeur des actions permanentes
G Module de glissement
I Inertie
Is Inertie d'un verre feuilleté
Iw Inertie sectorielle principale
K Inertie de torsion
KÉ Facteur d'intensité de
contrainte
L Longueur de l'élément de la structure
Li Longueur des différents
éléments
Lk Longueur caractéristique
Mcr , D Moment critique au
déversement
Mrd , y Moment résistant
MD , Rd Moment ultime au déversement
Ncr , e Charge critique d'Euler
Nc ; rd Valeur de l'effort normal
N rd , f Résistance au flambement
Qk ,1 Valeur caractéristique de la principale
charge variable
Qk , i Valeur caractéristique des
charges variables secondaires
Smom Contrainte égale à un chargement
momentané
Srep Contrainte égale à la rupture du
verre
Ssls Contrainte égale à l'état
limite de service
Ssw Contrainte égale au poids propre de
l'élément
Suls Contrainte égale à l'état
limite ultime
VRd Valeur de calcul de la résistance au
cisaillement
W Module de section élastique
Symbole grec
á Coefficient de dilatation
linéique moyen entre 20°C et 300°C
â Coefficient de dilatation thermique
ã Energie de création d'une
unité de surface
ãG Coefficient partiel pour l'action
permanente
ãM ; A Coefficient de
sécurité sur le verre recuit
ãM ; v Coefficient de
sécurité sur les contraintes de trempe
ãQ Coefficient partiel pour l'action
variable
å Emissivité
ë Conductibilité thermique
ë Elancement réduit
í Coefficient de Poisson
ñ Masse volumique
ók Contrainte dans la section pour
une charge en compression d'Euler
ónf Contrainte de base dans la loi de Weibull
óth Contrainte théorique
ø Diamètre nominal
÷b Coefficient de réduction au
flambement
÷D Coefficient de réduction au
déversement
ø0 ;i Coefficients pour les actions
variables
ø1 Coefficients pour les actions
variables
ø2 ,i Coefficients pour les
actions variables
Les objets en verre sont présents en abondance et de
manière très diversifiée dans notre vie quotidienne :
récipients pour les aliments, boissons et produits de beauté,
matériel scientifique, oeuvres d'art décoratives ou enfin comme
vitrage tout simplement.
Mais qu'en est-il en tant que matériau de structure ?
La découverte du verre remonte à près de
5000 ans, on pourrait donc s'attendre à avoir une parfaite
maîtrise de ce matériau, cependant, la réalité est
toute autre. Pendant longtemps, l'utilisation du verre en construction se
limitait à la fonction de vitrage. Depuis une dizaine d'années,
les architectes et les ingénieurs ont commencé à
l'utiliser à des fins structurelles mais de manière
occasionnelle.
Quelles ont été les motivations des concepteurs
? Le verre sera-t-il autant utilisé que les autres matériaux
comme le béton ou l'acier ? Comment déterminer sa
résistance ? Comment le dimensionner ? autant de questions auxquelles
j'essaierai de répondre au travers de ce mémoire.
Des choix ont été faits afin d'axer ma recherche
sur des éléments précis. Le travail développera les
éléments structurels en verre chargés dans leur plan et
issu du procédé de fabrication « float ».
Dans ce travail, j'expliquerai tout d'abord l'évolution
de la place du verre dans l'architecture et la tendance actuelle de
l'architecture qui pousse à l'utilisation du verre comme matériau
de structure.
Ensuite, une explication sera donnée sur le
matériau en tant que tel, le procédé de fabrication et les
divers types de verre qui existent. Une bonne connaissance du matériau
est indispensable pour comprendre les différents mécanismes qui
influencent sa résistance.
Par après, je m'attarderai sur le développement
de la résistance du verre et sur les méthodes de dimensionnent
dans le cas d'une colonne et d'une poutre. Le développement et la
généralisation des structures en verre passeront par la mise au
point de normes et d'un véritable code de calcul. A travers ces deux
chapitres, je proposerai une méthode de calcul pour le dimensionnement
des colonnes et des poutres.
Par la suite, les différents systèmes
d'assemblage une structure en verre seront mis en
évidence car ils
sont des éléments importants qui permettent la transmission
d'efforts et de
Chapitre 1 : Introduction
sollicitations d'un élément à un autre. Ce
chapitre s'attachera à l'explication des différents types
d'assemblages, leurs calculs sortant du cadre de ce travail.
Il m'a également semblé important de mettre en
évidence l'ensemble des qualités et des inconvénients de
ce type de structure afin de savoir quelle utilisation serait la plus
appropriée.
Mon travail s'achèvera par la présentation de
plusieurs exemples de réalisation et par l'application à mon
projet d'architecture.
La conclusion apportera des éléments de
réponses aux différentes questions posées.
|
Chapitre
|
|
|
2
|
|
|
|
Le verre dans l'architecture
|
2.1 Les origines
Des fragments de verre existent à l'état naturel,
ils proviennent soit d'une météorite, soit du monde animal (le
squelette de certaines éponges), soit d'origines volcaniques.
Les origines du verre élaboré par l'homme se
situent probablement en Phénicie vers 3000 av. J-C. Plusieurs
légendes existent sur l'apparition du verre, la plus connue, celle de
Pline l'ancien raconte que le verre aurait été découvert
par hasard par des marchands phéniciens qui, sur la plage, auraient
introduit du nitre (carbonate de soude, employé pour la conservation des
momies) dans leur brasier, celui-ci se mêlant au sable aurait
formé des perles de verre retrouvées le lendemain dans les
cendres. Cette légende peut paraître cohérente puisque les
ingrédients essentiels à la fabrication du verre sont
présents. Cependant, vu la température importante pour faire
fondre du verre, cette légende semble peu probable.
Au début, le verre était considéré
comme un matériau noble grâce à sa transparence et à
sa difficulté de fabrication car il n'était pas facile d'obtenir
une température suffisamment élevée. Son usage
était limité à des bijoux (perles, colliers, ...) ou des
objets de décorations (vases,...).
Le soufflage du verre qui a permis l'essor de verre creux est
une étape important dans l'histoire de la fabrication du verre et dans
son développement. Ce procédé a été
découvert en Syrie, durant le 1er siècle av. J-C.
Durant le 1er siècle, les Romains avaient
mis au point un procédé de fabrication de verre plat qu'ils
utilisaient comme vitrage essentiellement dans les maisons bourgeoises et les
bâtiments militaires. Cependant, son développement a
été très limité et ce procédé a
même complètement disparu pour ne réapparaître qu'au
15ème siècle dans l'architecture civile. A
l'époque, on se prémunissait des intempéries au moyen de
volets en bois, de toiles ou encore des peaux de bêtes.
2.2 L'architecture antique
Il ne nous reste peu de vestiges de l'architecture domestique
antique. Seuls des pyramides,
des mausolées et des temples ont
traversés les siècles. Ces bâtiments sont des espaces
clos,
totalement hermétique à la lumière. Il ne faut
pas perdre de vue que les pyramides étaient
des tombeaux propres à chaque pharaon. Il fallait donc
les protéger des éventuels pillards et surtout de
l'atmosphère et de la lumière qui ne sont pas des
éléments propices à la conservation.
Cependant, les archéologues ont trouvés des
traces d'ouverture dans les murs de maisons domestiques, ce qui conforte
l'idée que l'homme a toujours voulu laisser pénétrer la
lumière à l'intérieur de son habitat.
Les vestiges égyptiens ont jeté les bases de
l'architecture, essentiellement d'un point de vue formel. L'ensemble des
bâtiments est régi selon deux axes perpendiculaires
orientés nord-sud et est-ouest. Ces axes représentent
premièrement la vallée du Nil et deuxièmement la course du
soleil.
L'architecture grecque est une architecture où les
cultes sont célébrés dans des temples. Ceux-ci sont
construits selon des ordres. Les traces d'orthogonalité de
l'architecture égyptienne sont toujours présentes mais une notion
anthropomorphe apparaît.
Avec le développement de l'architecture romaine, on
voit apparaître de véritables espaces intérieurs où
il y a une recherche d'ornementations et de représentations. Cependant,
les percements sont encore peu présents dans les édifices
religieux et publics mais on en voit déjà les prémices.
2.3 L'architecture romane
L'architecture romane voit apparaître l'utilisation des
vitraux et de la transparence unilatérale : on voit la lumière de
l'intérieure mais on ne voit pas ce qu'il se passe à
l'extérieure.
Le développement de l'architecture romane se fait dans
une période de troubles et d'invasions barbares. Cette architecture
d'appel au culte est représentative du développement et de
l'épanouissement du christianisme. Les églises servaient de lieux
de rassemblement lors de chaque invasion, il est donc normal que ces
constructions ressemblent plus à des châteaux que des lieux
consacrés à la religion.
Les vitraux de part leurs motifs et leurs couleurs donnent un
effet de lumière céleste voir même divine. Ces
éléments constituent le seul apport de lumière dans ces
édifices.
Dans le plan des églises romanes, La neffe centrale
représente la vie sur terre assez sombre au bout du quel on peut voir
l'autel illuminé par des vitraux qui symbolise le but de la vie à
savoir le salut divin.
2.4 L'architecture gothique
L'architecture gothique est l'évolution logique de
l'architecture romane. En effet, elle tente de dématérialiser la
structure et celle-ci apparaît comme une dentelle.
Toute la maçonnerie qui disparaît est
remplacée par des éléments vitrés, qui comme dans
l'architecture romane, mais de manière encore plus importante offrent
une transparence et un apport de lumière non négligeable. Cela
est rendu possible grâce à l'utilisation de nouvelles techniques
structurales (arc boutant). L'arc boutant rejette une partie des efforts sur
des éléments structurels se trouvant à l'extérieur
du lieu de culte (culées, contreforts,...). Grâce à ce
procédé, une place importante se libère, les hauteurs sous
plafond sont plus importantes et il y a donc plus de place pour les vitraux et
des ouvertures, la lumière peut donc mieux pénétrer. De
plus, une partie des sollicitations étant rejetées à
l'extérieure de l'ouvrage, la structure intérieure paraît
beaucoup plus fine et moins imposante. L'espace intérieur commence
à se dégager petit à petit.
2.5 L'architecture Baroque
L'évolution de la technique verrière a permis un
développement important durant cette époque. Le
développement des vitrages transparents de plus grandes tailles a permis
l'apparition de la transparence bilatérale : on peut voir dans les deux
sens, de l'intérieur vers l'extérieur et inversement. C'est
à partir de ce moment que le contexte et l'environnement ont
commencé à avoir une place certaine dans l'architecture. Le
château de Versailles, plus particulièrement, le rapport entre la
galerie des glace et les jardins en est un parfait exemple.
Alors que l'architecture gothique est un espace beaucoup plus
mystique, notamment dû à l'utilisation des vitraux et de la
lumière céleste qui en découle, l'architecture baroque est
quant à elle un espace beaucoup plus dynamique et plus orienté
sur le mouvement. Ce désir de mouvement se ressent dans l'utilisation de
certaines formes ; du cercle de l'architecture de la renaissance on passe
à l'ellipse.
Cette évolution est aussi perceptible du point de vue
de la lumière ; on passe d'une lumière mystique à une
lumière naturelle, beaucoup plus vive qui provient directement du
soleil. Cette lumière naturelle semble agrandir les pièces et
également effacer les limites. Le développement des vitres
transparentes de grandes tailles a également permis l'essor des miroirs.
L'utilisation de ceux-ci dans l'architecture a permis d'accentuer l'effet
d'immatérialité et d'infinité de la pièce.
L'importance de la lumière naturelle se fait ressentir
et le début des jeux de lumière et de reflets apparaît.
L'interaction entre le monde extérieur et l'architecture, entre le
dedans et le dehors commence à exister.
2.6 Le 18ème siècle
Jusqu'au 18ème siècle, l'architecture est assez
limitée car elle était dépendante de certains
matériaux naturellement disponibles et dans une relative
proximité. C'est la raison pour laquelle l'ensemble des bâtiments
de nos régions était fabriqué à base d'argile,
pierre et bois. Même d'un point de vue structurel, les
possibilités étaient limitées. L'argile et la pierre sont
deux matériaux qui ne fonctionnent qu'en compression.
Vers la fin du 18ème siècle, le
charbon à coke a été utilisé dans la
sidérurgie ce qui a permis la fabrication de fer en grande
quantité et surtout de meilleure qualité. De plus, le fer
possède une importante capacité de chargement et une
résistance à la traction sans précédent.
Grâce à toutes ces qualités, une nouvelle ère
architecturale commence à apparaître, pas seulement d'un point de
vue structurel mais aussi de l'expression architectonique. En effet, là
où on avait besoin d'un mur épais pour reprendre les forces, seul
une mince structure de fer suffit. L'espace a donc pu commencer à
être libéré.
Si la structure devient plus fine, le mur s'estompe lui aussi et
laisse la place au vitrage. On obtient ainsi d'importantes façades
presque entièrement vitrées.
Le bâtiment qui représente le mieux et montre
l'apologie de cette époque est sans aucun doute le Cristal Palace de
Joseph Paxston à Londres.
2.7 L'architecture moderne
L'essor industriel devient de plus en plus présent en
architecture. La transparence y paraît de plus en plus inévitable.
L'ouvrage de Paul von Scheerbart écrit en 1914 « Glasarchitecktur
» (Architecture de verre) servira d'inspiration à cette nouvelle
génération d'architectes. Il y fait une analogie entre
l'ouverture de l'espace et l'ouverture de l'esprit. Cette comparaison va de
pair avec l'évolution de l'industrie et les prémices de
mondialisation de l'époque. Il y prône également une
architecture entièrement vitrée où il n'y aurait plus de
fenêtres mais des murs de verre.
Pendant ce temps, Le Corbusier propose sa structure dom-ino.
Le concept de cette structure composée de colonnes et de dalles permet
de libérer les espaces des murs porteurs, d'avoir des étages dont
les murs sont disposés différemment les uns par rapport aux
autres et permet également d'avoir des espaces totalement ouverts. De
plus, les façades ne jouent plus qu'un rôle secondaire de peau et
peuvent donc se libérer totalement de l'utilisation de la
maçonnerie et créer ainsi une importante
perméabilité avec le monde extérieur.
Mies Van Der Rohe applique, lui aussi, un concept analogue
à celui de Le Corbusier dans son pavillon d'exposition de Barcelone.
L'espace intérieur y est totalement dégagé, plus aucune
porte n'est présente ce qui montre bien la disparition progressive des
murs. L'ensemble de l'ouvrage repose sur 8 colonnes disposées de
manière régulière. Le bâtiment semble encore assez
hermétique vis-à-vis du regard extérieur mais cela
évoluera dans les différents projets de Mies Van Der Rohe
jusqu'à atteindre l'ouvrage de référence du minimalisme
à savoir la maison Farmsworth. Cette réalisation
entièrement vitrée possède une fine structure
métallique qui est encore perceptible en façade. L'espace
intérieur est quant à lui totalement dégagé. La
perméabilité y est quasi absolue avec le monde
extérieur.
2.8 L'architecture contemporaine
L'architecture d'aujourd'hui se base sur les principes
constructifs du mouvement moderne même si les techniques de construction
ont évoluées et que le critère de confort a fortement
changé.
On a pu voir qu'au fils du temps la lumière naturelle et
les vitrages ont pris une place de plus en plus importante dans
l'architecture.
Aujourd'hui, des espaces totalement vitrés sont
créés de manière régulière où des
jeux de lumière sont monnaie courante. Aujourd'hui les façades
sont utilisées comme supports publicitaires, que ce soit par
sérigraphie ou bien par bandes lumineuses. De plus, il existe des
façades en double peau où les reflets des vitres changent de
couleurs en fonction de la luminosité.
Conclusion du chapitre
Tout au long de ce chapitre, on a pu voir l'évolution
de l'architecture de ces débuts à aujourd'hui. La lumière,
les vitrages et les jeux de lumière qui en découlent ont pris une
place de plus en plus importante. Cependant, leurs effets restent pour le
moment limités aux seuls éléments de façades car
même s'il existe des effets de lumière à l'intérieur
des bâtiments ceux-ci restent tout de fois minimes. La raison principale
est la place et surtout l'opacité des structures actuelles quelles soit
en béton, en acier ou encore en bois. Une structure transparente, comme
le verre, permettrait, de faire pénétrer ces effets de
lumière à l'intérieur des bâtiments et donnerait un
nouvel élan à l'architecture contemporaine. C'est pour toutes ces
raisons que le monde architectural est demandeur de ce nouveau type de
structure.
|
Chapitre
|
|
|
3
|
|
|
|
Les caractéristiques du verre et les principes de construction du
verre plat
|
3.1 Information générale
3.1.1 Définition
Le verre est un matériau homogène de type
silico-sodo-calcique (voir Tableau 3.2.1 pour la composition
détaillée). Le nombre de compositions du verre est
illimité, ce qui permet d'avoir des propriétés
également très diverses et spécifique en fonction du
domaine d'utilisation. Il n'y a donc pas de formule chimique unique du verre.
Les molécules ne forment pas un réseau cristallins mais sont
disposées de manière désordonnée : c'est
grâce à cette particularité que le verre est
transparent.
Lors de sa fabrication, l'ensemble des composants du verre est
porté à une température si élevée que ce
mélange devienne visqueux, puis on les laisse refroidir. Le verre n'a
pas de température de fusion spécifique, mais suite à
l'ajout de chaleur, il passe d'un état solide à un état
viscoplastique et puis liquide. Ce procédé ne permet pas à
l'importante masse visqueuse de s'ordonner lors du refroidissement : «
le silicate et l'oxygène ne forment aucune structure ordonnée
mais présentent une disposition moléculaire qui est gelée.
Le verre est ainsi constitué d'un réseau tridimensionnel de
tétraèdre d'oxyde de silice (SiO4) avec des vides et des cations
dans les interstices » [24]. C'est pour
cette raison que l'on dit que le verre est un liquide surfondu figé.
3.1.2 Le processus de fabrication (voir figure 3.1.1)
Aujourd'hui, la majorité des verres sont issus de la
méthode dite du << verre flotté >> ou << float
>> (en anglais). L'ensemble des composants du verre, quelques adjuvants
et les débris de verre sont dosés, mélangés et
amenés dans un four où le tout est chauffé à la
température de fusion de 1500°C. La silice seule a une
température de fusion plus importante (environ 1700°C) mais
grâce à l'ajout de fondant, essentiellement de la soude et des
débris de verre on peut donc diminuer la température de fusion.
La soude entre en fusion à une température de 1200°C et
crée donc un bain dans lequel trempe la silice. Les atomes de silices
sont donc chauffés sur toute leur surface, ce qui diminue le besoin de
chaleur. A la sortie du four la température n'est plus que de
1100°C, le liquide visqueux est versé sur de l'étain en
fusion plus dense que le verre. Cette particularité permet au verre de
flotter sur l'étain et d'avoir une surface parfaitement plane et aussi
une épaisseur constante. Le bain d'étain est placé sous
une atmosphère d'azote et d'hydrogène afin d'éviter tout
risque d'oxygénation. Le verre est entraîné par rouleaux
qui fixent par leur vitesse,
l'épaisseur du vitrage. Le vitrage passe par un four de
recuisson, c'est lors de cette étape que l'on découpe le verre
aux dimensions choisies. On obtient à la fin de ce processus ce qu'on
appelle le verre recuit. D'autres traitements de finitions sont possibles afin
d'améliorer l'une ou l'autre propriété du verre. Quelques
unes des possibilités seront développées
ultérieurement. Ce procédé de fabrication en continu fait
que les industries produisent du verre 24 heures par jour et ce, tous les jours
de l'année.
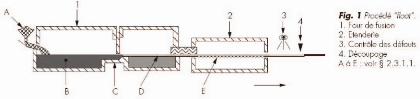
Figure 3.1.1 Processus de fabrication du verre flotté
[53]
Le verre qui sort de la chaîne de fabrication peut avoir
une épaisseur variant de 2mm à 25mm. Les dimensions maximales
d'une feuille de verre standard sont de 6000mm x 3210mm (dimension maximale
chez AGC flat glass) en verre recuit avec une tolérance de 5mm. Il est
possible au niveau technique de fabriquer des feuilles avec des dimensions plus
grandes mais cela pose des problèmes au niveau du transport, l'ensemble
des chevalets a été conçu pour des feuilles de maximum 6m.
Comme pour tous les matériaux fabriqués en usine, il y a une
certaine tolérance permise sur ces mesures. De plus, il y a
également une vérification à faire vis-à-vis de
l'équerrage : il faut vérifier que les angles soient
|
suffisamment proche de 90°.
Epaisseur nominale `e' (mm)
|
Tolérance sur l'épaisseur Verre float
(mm)
|
|
3
|
#177; 0.2
|
|
4
|
#177; 0.2
|
|
5
|
#177; 0.2
|
|
6
|
#177; 0.2
|
|
8
|
#177; 0.3
|
|
10
|
#177; 0.3
|
|
12
|
#177; 0.3
|
|
15
|
#177; 0.5
|
|
19
|
#177; 1
|
|
25
|
#177; 1
|
Tableau 3.1 1 : Tolérance sur l'épaisseur nominale
du verre float valeurs [53]
3.2 Composition
Comme cela a été dit au point
précédent, il n'y a pas de formule chimique du verre, et donc pas
de composition unique. Cependant, dans les normes européennes, des
fourchettes de quantité ont été déterminé.
Voici un tableau récapitulatif des différents types de verre et
de leur composition. Lors de ce travail, l'intérêt sera
porté sur le verre silicio-sodo-calcique qui constitue la majeure partie
des vitrages. La composition de deux autres types de verre
est indiquée en guise d'information. Ce sont les
pourcentages massiques qui sont utilisés dans le tableau.
|
|
Verre silicio-
sodo-calcique EN 572-1
|
Verres borosilicates EN 1748-1
|
Vitrocéramiques EN 1748-2
|
|
Dioxyde de silicium
|
SiO2
|
69 à 74%
|
70 à 87%
|
50 à 80%
|
|
Oxyde de calcium
|
CaO
|
5 à 12%
|
-
|
0 à 8%
|
|
Oxyde borique
|
B2O3
|
-
|
7 à 15%
|
-
|
|
Oxyde de sodium blanc
|
Na2O
|
12 à 16%
|
0 à 8%
|
0 à 2%
|
|
Oxyde de magnésium
|
MgO
|
0 à 6%
|
0 à 8%
|
0 à 8%
|
|
Oxydes d'aluminium
|
Al2O3
|
0 à 3%
|
0 à 8%
|
15 à 27%
|
|
Oxydes de lithium
|
Li2O
|
-
|
-
|
0 à 5%
|
|
Oxydes de zinc
|
ZnO
|
-
|
-
|
1 à 5%
|
|
Dioxyde de titane
|
TiO2
|
-
|
-
|
0 à 5%
|
|
Dioxyde de zirconium
|
ZrO2
|
-
|
-
|
0 à 5%
|
|
Oxyde de baryum
|
BaO
|
-
|
-
|
0 à 8%
|
|
Oxyde de potassium
|
K2O
|
-
|
-
|
0 à 2%
|
|
Autres
|
|
0 à 5%
|
0 à 8%
|
0 à 5%
|
Tableau 3.2.1 : Composition, pourcentages massiques des
différents types de verre selon l'Eurocode
Certains adjuvants peuvent encore être ajoutés
pour modifier la couleur par exemple, mais leurs concentrations sont tellement
faibles qu'ils n'altèrent en rien les propriétés
mécaniques du verre.
3.3 Caractéristiques mécaniques
Malgré l'existence de fourchettes dans la composition
du verre, les propriétés mécaniques de celui-ci varient
peu. Le tableau 3.3.1 met en avant les principales valeurs du verre. On fera
particulièrement attention à la valeur du module de Young qui est
une donnée importante dans le cas du dimensionnement des
éléments et qui interviendra tout au long de ce travail. Pour une
masse volumique identique à celle du béton, le verre
possède un module de Young bien supérieur, qui est identique
à celui de l'aluminium. Cependant, vu ces qualités
indéniables, le verre doit faire face un défaut important qui
jusque ici, l'a rendu très peu populaire auprès des
ingénieurs : il possède une rupture fragile.
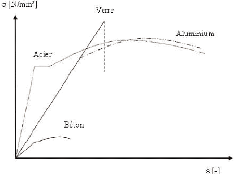
Figure 3.1.1 Graphique contrainte- déplacement pour le
verre, l'acier, le béton, l'aluminium [25]
Quand on le compare à l'acier, on peut remarquer le
palier plastique de l'acier et toute la réserve de déformation
qu'il possède encore avant la rupture. Le verre ne possède pas
cette réserve et sa rupture est donc brutale. Les déformations
importantes en acier permettent d'anticiper la rupture. C'est pour cette raison
qu'il faut prendre des valeurs plus importantes pour les coefficients de
sécurité des éléments fragiles.
|
Verre silicio-
sodo-calcique EN 572-1
|
Verres borosilicates EN 1748-1
|
|
ñ kg/m3
|
2500
|
2200-2500
|
|
HK0,1/20Gpa
|
6
|
4,5-6
|
|
E Mpa
|
70000
|
60000-7000
|
|
í -
|
0,2
|
0,2
|
|
|
class 1: 3,1-4,0
|
|
|
class 2:4,1-5,0
|
|
á 10^-6 K-1
|
9
|
class 3: 5,1-6,0
|
|
c J/(kg*K)
|
750
|
800
|
|
ë W/(m*K)
|
1
|
1
|
|
å -
|
0,837
|
0,837
|
masse volumique à 18°C Dureté
module de Young
coefficient de Poisson
Coefficient de dilatation
linéique moyen entre 20°C et 300°C
capacité thermique spécifique Conductibilité
thermique Emissivité
Tableau 3.3.1 : Propriétés physiques et
caractéristiques mécaniques du verre selon l'Eurocode
3.3.1 Résistance théorique
Orowan, en 1949, a établi une formule [16] pour
déterminer la valeur théorique de la résistance des
matériaux fragile. Cette valeur dépend directement du module de
Young (E), de la distance inter-atomique ( a0 ) et
l'énergie de création d'une unité de surface (ã)
:

Eã
ó = (3.1)
th
a0
Si on prend comme valeur pour a0 = 0.2 nm et
pour ã = 3.5 J/m2. On obtient comme
valeur
théorique 35GPa. Cette valeur n'est en réalité
jamais atteinte mais permet de voir le grand
potentiel qu'il y a dans le
domaine du verre. Les prochaines parties du chapitre essaieront
d'expliquer
pourquoi cette résistance théorique n'est jamais atteinte.
3.3.2 Défauts de volume (inclusions de Nickel)
Il existe des risques de défauts de volume suite
à la fabrication du verre. En effet, des inclusions de Nickel peuvent
exister. En service, ces imperfections sous l'effet de la chaleur solaire
grossissent en volume et créent donc des contraintes pouvant mener
à la rupture du verre. Cependant, aujourd'hui, les fabricants de verre
ont mis au point un test "heat soak test" afin de s'assurer qu'il n'y a pas de
danger de rupture en service à cause de ces inclusions. Ce test consiste
à chauffer l'ensemble des verres pendant 8 heures à une
température de 290°C. A cette température, les inclusions,
si elles sont présentes changent
d'état et il y a rupture du vitrage. Ces
éléments sont donc simplement retirés du processus de
fabrication et il n'y a donc plus aucun risque de voir apparaître ces
défauts de volume.
3.3.3 Défauts de surface
Lors de la fabrication du verre et des différentes
manipulations de celui-ci, des micro ou macro fissures peuvent
apparaître. Le contact avec des autres éléments ainsi qu'un
environnement poussiéreux altèrent la qualité de surface
du verre. Plus ces défauts sont profonds, plus la résistance du
verre sera faible. La géométrie de la fissure joue
également un rôle important dans la résistance. En effet,
plus la fissure est allongée et de faible épaisseur, plus il y
aura une concentration de contrainte et donc une faible résistance.
3.4 Mécanique de rupture
La mécanique de rupture traite de l'évolution
d'une fissure au sein d'un élément et suppose l'existence d'une
fissure initiale. Comme cela a été expliqué au point
précédent, le verre est un matériau naturellement
fissuré à sa surface, il est donc primordial de s'attarder
à la mécanique de rupture d'un tel élément. Ce
phénomène est à la base de la détermination de la
résistance de calcul du verre.
3.4.1 Fissuration sous critique (fatigue statique)
Les défauts de surfaces induisent des concentrations de
contraintes en pointe de fissures qui sont souvent plus importantes que la
résistance élastique de l'élément. Dans le cas
d'éléments en acier, ce dépassement local a peu
d'influence car le matériau plastifie, continuant à offrir une
résistance égale et empêchant la propagation de la fissure.
Pour le verre, la situation est différente. Le caractère fragile
du verre influence la résistance de l'élément et sa
mécanique de rupture : le matériau ne possédant pas les
mêmes qualités que l'acier ne peut pas plastifier en pointe de
fissure, laissant ainsi cette dernière se propager.
Ce phénomène, appelé aussi « fatigue
statique », a été découvert en 1899 par Grenet qui
avait mis en évidence une relation entre la résistance du verre,
la vitesse et la durée de chargement. Evidemment, le sens du mot fatigue
est différent de son utilisation traditionnelle en mécanique.
Dans ce cas-ci, il n'y a pas de charges cycliques même une charge
constante peut amener à la rupture.
L'accroissement continu d'une fissure joue un rôle
important dans la détermination de la résistance du verre. Les
formules de résistance du verre actuelles prennent en compte ce
phénomène lié à la durée de chargement,
elles seront développées au chapitre 4.
La propagation de la fissure peut avoir deux causes
différentes ou résulter de la combinaison des deux.
3.4.1.1 Sous chargement constant
Lorsque le verre est sollicité sous un chargement
constant, certaines zones peuvent être en traction. Ces zones sont
propices à la propagation de fissures car elles augmentent les
concentrations de contraintes en pointe de fissure. Il existe trois modes de
propagation de fissures (traction ; cisaillement dans le plan,
déchirement ou cisaillement hors du plan). Dans le cas du verre, seul la
propagation de fissures par traction est importante car elle est
prépondérante par rapport aux deux autres modes. Dans une zone en
compression, il n'y a pas de risques de propagation de fissure.
3.4.1.2 Sous l'effet de l'eau et de l'humidité
En présence de particules d'eau, il se passe une
réaction d'hydrolyse (Formule (3.2)) entre l'humidité ambiante et
le verre. Cette réaction est favorisée par les
déformations en fond de fissures, par la chaleur et par le PH de
l'environnement, plus celui-ci est important, un milieu basique, plus la
réaction est importante. D'après Michalske et Frieman [16], cette
réaction s'effectue en trois étapes (voir Figure 3.4.1).
Si-O-Si+H2O -> Si-OH+HO-Si (3.2)
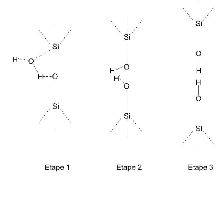
Figure 3.4. 1 Etapes de la rupture du verre en présence
d'eau
Etape 1 : Une particule d'eau (H20) est absorbée en
fond de fissure. Une réaction de Van der Waals se crée entre
l'atome d'hydrogène de l'eau et l'atome d'oxygène du verre
Etape2 : Les liaisons Si-O et H-O sont cassées par le
transfert d'un électron et d'un proton. Les deux silanols apparaissent
liés par une liaison d'hydrogène.
Etape 3 : La liaison d'hydrogène se rompt et la surface
de rupture est couverte par les deux silanols.
3.4.1.3 Conclusion
Le mécanisme de rupture du verre dépend de
plusieurs éléments certains propres au matériau
(défauts de surface et de volume) et d'autres relatifs à
l'environnement (humidité, température, vitesse de chargement).
Les fissures sont à l'origine du mécanisme de rupture et, comme
le verre est un matériau naturellement fissuré, la théorie
de la mécanique de rupture revêt une importance capitale.
Cependant, la détermination du nombre de fissures, de leurs orientations
étant totalement aléatoire, les formules qui régissent la
mécanique de rupture sont issues de la théorie de la
probabilité et sont également à la base de la
détermination de la résistance du verre. Les différentes
méthodes pour déterminer la résistance du verre recuit
seront développées dans le chapitre 4.
3.5 Les différents types de verre
A la sortie du four de recuisson, il est possible d'effectuer
plusieurs opérations sur le verre pour améliorer certaines
propriétés comme la résistance mécanique ou pour
assembler plusieurs feuilles entre elles. Il s'agit notamment du verre
trempé et du verre feuilleté.
3.5.1 Le verre trempé
Le verre peut être trempé de deux manières
différentes, soit de manière thermique, soit de manière
chimique. Dans le cas des applications structurales du verre, il est
conseillé d'utiliser la méthode thermique. Le processus de trempe
permet d'obtenir un matériau précontraint.
3.5.1.1 Le verre trempé thermiquement
Le verre trempé est obtenu grâce à un
traitement thermique dont le but est d'augmenter les capacités
mécaniques. Le verre est amené dans un four où il est
chauffé à une température d'environ 600°C-650°C
et ensuite, il est brusquement refroidi par des jets d'air. Cette
opération crée l'apparition de contraintes internes (voir Figure
3.5.1). En effet, en propulsant de l'air froid sur la surface du verre,
celle-ci se refroidi plus rapidement. Comme elle est libre de se raccourcir car
le coeur de la vitre est également encore chaud, il n'y a pas d'efforts
internes. Lorsque le centre de la vitre se refroidit à son tour, le
raccourcissement est empêché car les extrémités sont
déjà froides. Ce raccourcissement provoque des efforts de
compression aux extrémités du verre et un effort de traction au
centre.
Les dimensions maximales des feuilles de verre trempé
varient d'un fournisseur à un autre mais ils sont limités par les
dimensions du four de trempe chez AGC flatt glass les dimensions maximales sont
2500mm x 4800mm.
Grâce à l'utilisation de la trempe, la
résistance du verre qui dépend de son état de surface et
des zones en traction se trouve amélioré car la surface est en
compression. Il faut donc d'abord compenser les contraintes résiduelles
de compression avant que ne puisse apparaître un effort de tension dans
le verre susceptible d'amener la rupture. Le verre trempé est un
matériau précontraint, il possède donc une réserve
de résistance. La détermination des contraintes de trempes se
fera au chapitre 4.

Figure 3.5 1 Schéma des différentes étapes
lors du refroidissement des contraintes de trempe
Il existe deux procédés de fabrication du verre
trempé thermiquement (voir Figure 3.5.2) :
|
- la trempe horizontale : le verre repose sur des rouleaux
horizontaux pendant l'opération de trempe.
- la trempe verticale : le verre est suspendu à des
pinces pendant l'opération de trempe.
|
Figure 3.5 2 les deux procédés de trempes
thermiques [53]
Le verre trempé possède un faciès de
rupture caractéristique (voir Figure 3.5.3). Lors d'un choc,
étant donné la quantité d'énergie
emmagasinée par les contraintes résiduelles, celuici se rompt en
petits morceaux non tranchants. Cette propriété le classe parmi
les verres dits de sécurité.
Si une ouverture atteint la zone tendue, toute
l'énergie est libérée et la pièce se rompt. Il
n'est donc plus possible d'effectuer des découpes ou des trous sur du
verre trempé car ce dernier se romprait. Il faut donc s'assurer de la
bonne découpe et de la position des trous avant la trempe.
Lors de la trempe verticale, des déformations et une
diminution de la précision des trous apparaissent dans la pièce.
Ce problème se révèle important si on désire
réaliser des verres feuilletés à partir
d'éléments trempés percés, les différences
relatives entre les trous de chaque feuille peuvent être non
négligeable. Cependant, aujourd'hui, les producteurs réalise
l'ensemble des verres trempés par le procédé de trempe
horizontale avec lequel il n'y a pas de risques de déformation de
l'emplacement des trous.

Figure 3.5 3 Type de fragmentation du verre de gauche à
droite : verre recuit, verre durci et verre trempé [40]
De par la nature du procédé, le verre
trempé n'est pas aussi plan que le verre recuit. Cette différence
est encore augmentée lors de la trempe verticale par les pinces qui
provoquent des déformations appelées « points de trempe
». Il existe des limites de tolérances pour les déformations
du verre trempé.
|
Longueur ou Largeur (mm)
|
Épaisseur <12 mm
|
Épaisseur >12 mm
|
|
<2000
|
#177;2.5 (trempe horizontale) #177;3 (trempe verticale)
|
#177;3
|
|
Entre 2000 et 3000
|
#177;3
|
#177;4
|
|
>3000
|
#177;4
|
#177;5
|
Type de
verre
Flèche générale
(mm/mm)
Flèche locale (mm/300mm)
Float
0.003
0.5
Autres
0.004
0.5
Tous types
0.005
1
Tableau 3.5 1 : Tolérance maximale sur
l'épaisseur d'un verre trempé [53]
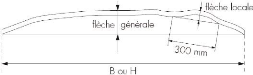
Figure 3.5 4 Flèche
générale et flèche locale du verre trempé
verticalement [53]
Tableau 3.5 2 : Valeurs de flèches maximales et
locales pour le verre trempé [53]
Procédé de trempe
- L'effet de bord
Jusqu'à présent, l'effet de trempe était
considéré au milieu de la feuille de verre. Au bord de la feuille
toute la surface est à l'air libre et peut donc se refroidir
entièrement lors du processus. Les contraintes ne varient que faiblement
par rapport au reste de la feuille. Le bord des feuilles n'est donc pas un
point faible et ne mérite pas de mesures particulières. La figure
suivante montre comment se répartissent les contraintes de trempes aux
différents endroits d'une même feuille de verre trempé.
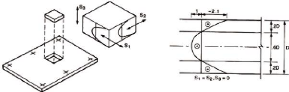
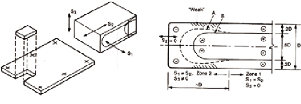
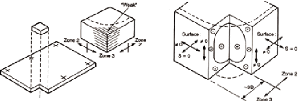
Figure 3.5 5 Allure des contraintes de trempe à
différents endroits d'une feuille de verre [78]
3.5.1.2 Le verre trempé chimiquement
Le but est évidement le même que le verre
trempé thermiquement. Cependant, le procédé utilisé
est différent. Le verre est trempé dans un bain de sels fondus
à 400°C. Il y a échange d'électrons entre les K+ du
sel fondu KNO du bain et les Na+ présents dans le verre. Comme la taille
d'un atome de potassium K+ est plus importante que celle d'un atome de Sodium
Na+, il résulte une compression à la surface du verre qui le rend
plus résistant. L'allure des contraintes de trempe des deux
procédés n'est pas la même (voir Figure 3.5.6). Le verre
trempé chimiquement est un procédé qui agit
essentiellement à la surface et pénètre peu dans
l'épaisseur du verre. Le verre trempé thermiquement lui
s'imprègne plus en profondeur. La résistance mécanique du
verre trempé chimiquement est beaucoup plus importante de l'ordre de 350
N/mm2. Il est cependant peu, voir pas du tout utilisé dans le
domaine de la construction. Son prix important et son faciès de rupture
semblable à celui du verre recuit empêchent son
développement. Grâce à son importance résistance, ce
type de verre est utilisé lors de très fortes sollicitations.
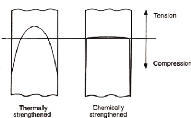
Figure 3.5 6 Différence d'allure de contrainte entre le
verre trempé thermiquement et chimiquement [41]
3.5.2 Le verre durci
Le verre durci, tout comme le verre trempé
thermiquement, résulte d'une opération thermique. Cependant, le
niveau de contrainte du verre durci est inférieur à celui du
verre trempé car le refroidissement a été
réalisé de manière plus lente.
Le verre durci ne peut plus subir de découpes ou de
poinçonnages. Il possède une résistance au gradient de
température de l'ordre de 100°C alors que pour un verre recuit
cette résistance n'est que d'une trentaine de degrés. La rupture
du verre durci s'assimile plus à celle du verre recuit que du verre
trempé. En effet, lors d'un choc, il y a apparition de grands morceaux
de verre qui sont coupants. On ne peut donc pas considérer le verre
durci comme un verre de sécurité. Contrairement au verre
trempé, et grâce au refroidissement plus lent, il ne faut pas
effectuer d'opérations supplémentaires (« heat soak test
») pour se prévenir des risques d'inclusions de Nickel.
3.5.3 Le verre feuilleté ou laminé
Le verre est feuilleté est un élément
composé d'au moins deux feuilles de verre assemblées à
l'aide d'un intercalaire qui sert à coller les différentes
feuilles entre elles à conférer des performances
supplémentaires. On peut utiliser n'importe quels types de feuilles de
verre pour la réalisation de verre feuilleté. Il existe deux
types d'intercalaire, ceux à base de plastique et ceux à base de
résine.
Ce type de verre est utilisé comme verre de
sécurité car lorsque qu'il reçoit un choc les
différents bouts de verre restent en place. Cette
propriété permet de l'utiliser pour la résistance à
l'effraction, protection contre les armes à feu, les explosions,
l'isolation acoustique, ....
Ce procédé est également
intéressant d'un point de vue structurel car il permet d'augmenter la
section et la portée en disposant les feuilles en quinconce (voir Figure
3.5.7). Ce procédé a été utilisé dans
l'Apple Store de New York pour pouvoir disposer d'éléments
d'environ 10m de long, cet exemple sera traité plus en détail au
chapitre 8. Actuellement, la seule limite de longueur de cette méthode
est la taille des autoclaves nécessaires pour fixer les intercalaires
plastiques.
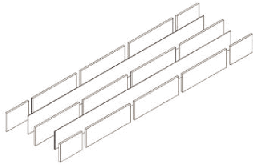
Figure 3.5 7 Exemple de disposition des feuilles de verre [46]
3.5.3.1 Intercalaire plastique
Différents types d'intercalaires plastiques existent
notamment le polyvinylbutyral (P.V.B.) qui reste le plus utilisé, et
l'Ionoplaste SentryGlass®Plus (S.G.P.) qui possède des
caractéristiques plus intéressantes dans la plupart des
applications structurales, surtout car il possède une plus grande
raideur. Malheureusement, son coût encore très important et les
difficultés de mise en oeuvre limitent son développement.
Lors de la fabrication d'un verre feuilleté avec des
feuilles en P.V.B., il faut d'abord s'assurer du découpage et du
façonnage des différentes feuilles de verre. Ensuite, celles-ci
sont lavées à l'eau ionisée. Dans une enceinte
fermée, on place les films de P.V.B. entre les différentes
feuilles de verre en fonction de la composition désirée. Il faut
encore enlever les bulles d'air éventuelles par calandrage et sceller
les bords de l'ensemble afin de prévenir tout risque de
pénétration d'air lors de la dernière étape. Le
traitement en autoclave est l'opération finale qui consiste à
coller le verre de manière définitive en portant l'ensemble
à une pression de 12 bars et à une température de
135°C-145°C. Cette opération permet de ramollir suffisamment
le P.V.B. afin que celui-ci puisse parfaitement épouser la surface du
verre.
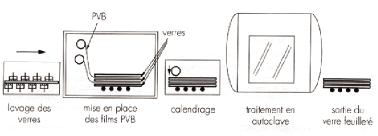
Figure 3.5 8 Procédé de fabrication du verre
feuilleté avec P.V.B. [53]
La convention de nomenclature des verres feuilletés
est la suivante : xx.y où les premiers chiffres indiquent le nombre et
l'épaisseur des feuilles de verres utilisées. Le chiffre
après le point indique le nombre total (mais pas l'épaisseur) des
feuilles de PVB. Ainsi un vitrage 101010.2 consiste en trois feuilles de verres
de 10 mm séparées chacune par deux couches de PVB. Il existe des
films de 0.38, 0.76, 1.14 ou 1.52 d'épaisseur mais on mentionne toujours
dans la nomenclature xx.y la valeur y en multiple de 0.38. [25]
3.5.3.2 Intercalaire résineux
Les verres feuilletés composés d'intercalaires
résineux peuvent être utilisés à des fins
structurelles que dans de très rares cas. Leur faible rigidité et
leurs faibles caractéristiques de sécurité empêchent
leurs usages à des fins structuraux. Les résines sont
composées de polymères d'acryle qui se solidifient sous U.V
(ultras violet).
Pour réaliser, ce type de verre feuilleté, on
utilise des écarteurs afin d'obtenir l'entre distance
désirée, on rempli l'espace de résine. La solidification
se fait sous lampes à U.V.
3.5.4 Le verre armé
Le verre armé est de moins en moins utilisé
depuis l'apparition du verre feuilleté. Celui-ci servait de verre de
sécurité car il permettait de maintenir les bris de verre
ensemble lors d'un choc. De plus, la présence d'un treillis
métallique diminue la résistance mécanique au lieu de
l'augmenter. Enfin, l'armature, ajoutée lors de la phase de fabrication,
est un élément opaque qui nuit au caractère transparent du
verre.
3.5.5 Les autres types de verre
Il existe actuellement énormément de
variétés de verre qui dépendent du type d'adjuvant ou des
procédés de modifications. Il est impossible de tous les
énumérer ici. Dans le cadre d'un travail sur le caractère
structurel du verre, seuls les éléments verriers qui peuvent
avoir ou qui ont eu une importance ont été
développés.
Conclusion du chapitre
Le verre possède des qualités
intéressantes d'un point de vue mécanique. Cependant, à
cause de son caractère fragile, le mécanisme de rupture est
différent des autres matériaux : dans le cas de contraintes trop
importantes en pointe de fissure, les matériaux élasto-plastiques
peuvent plastifier tandis que le verre par son caractère fragile propage
la fissure. Ce mécanisme est responsable du phénomène de
« fatigue statique » qui consiste en une diminution de la
résistance du verre en fonction du temps sous chargement constant.
Heureusement, certains traitements et/ou opérations existent qui
permettent d'améliorer la résistance mécanique du verre
(verre trempé thermiquement) et la section d'un élément
(le verre feuilleté). Ces deux modifications complémentaires
constituent l'ensemble des éléments structurels en verre.
|
Chapitre
|
|
|
4
|
|
|
|
Détermination de la résistance mécanique du verre
|
Il existe différents types de produits verriers qui
possèdent chacun une résistance mécanique propre. Dans ce
chapitre, seule la résistance du produit verrier de base (verre recuit)
et des produits possédant la résistance la plus importante (verre
trempé) seront traités car ces produits uniquement sont
utilisés pour des applications structurelles.
4.1 Résistance à la compression du verre
recuit
La résistance à la compression du verre est
beaucoup plus importante que sa résistance en traction. Un
élément en verre soumis à un effort axial de compression
ne subit pas le phénomène de fissure sous-critique (voir 3.4) et
sa résistance ne varie pas avec le temps.
4.1.1 Valeur de la résistance en compression du
verre recuit
Dans la littérature, il existe plusieurs valeurs
différentes pour la résistance en compression du verre. Aucune de
ces valeurs ne semble vraiment sortir du lot, cependant dans le cadre de ce
travail, il a fallu faire un choix concernant cette valeur. Le choix s'est
porté sur la valeur la plus faible pour se trouver du coté de la
sécurité. La valeur de la résistance en compression du
verre n'a que très peu d'importance, à cause du mode de rupture
de ce matériau. Cette valeur est donnée de manière
indicative, la résistance en compression du verre n'a jamais
été le frein à son utilisation.
f g ; c = 600N/mm2
De même, il n'existe aucune valeur concernant les
coefficients de sécurité à prendre pour cette valeur. Dans
une prénorme européenne [60] (cette prénorme sera
développée plus loin), un coefficient de sécurité
est utilisé pour le verre recuit.
ã M ; A = 1.8
fg c d ; ;
fg c ;
La valeur de la résistance de calcul à la
compression d'un verre recuit est donc de
= = 600/1.8 =333.33 N/mm2 (4.1)
ã M A
;
Dans le cas de la détermination de la résistance
en compression du verre, on ne considère pas l'effet de trempe. Tout
comme dans le cas du béton précontraint, la précontrainte
à un effet positif sur les efforts en traction mais n'a aucune influence
sur la résistance en compression du béton.
4.2 Résistance à la traction du verre
recuit
La détermination de la résistance à la
traction du verre recuit est importante car c'est l'élément
verrier de base. Celui qui sort de la chaîne de fabrication sans avoir
subi le moindre traitement particulier. La connaissance mécanique de cet
élément est utile pour la détermination de la
résistance de n'importe quels autres éléments verriers.
4.2.1 Principe général
Dans le chapitre 3, le principe de la mécanique de
rupture du verre et le phénomène de fatigue statique ont
été développés. Il a été
expliqué que la résistance du verre recuit dépendait de
plusieurs éléments dont les plus importants sont le
caractère aléatoire de son état de surface et la
durée de chargement. Suite à la manutention des
différentes feuilles de verre, la quantité et la profondeur des
fissures de surface sont difficilement quantifiables. A cause du
phénomène de fatigue statique, plus le temps de charge sera
important, plus la résistance sera faible.
4.2.2 Les différentes méthodes
Il existe plusieurs méthodes de déterminations
de la résistance mécanique du verre. Cependant, aujourd'hui, une
d'entre elles semblent se détacher des autres. D'autres méthodes
plus anciennes qui mettent en évidences les différents
problèmes liés à la résistance du verre seront
également exposées.
4.2.2.1 Loi de Weibull
La loi de Weibull a été mise au point pour
déterminer de la répartition des défauts de surface des
matériaux fragiles. Elle se base sur la théorie du maillon
faible, la résistance maximum de l'élément est
donnée par la résistance la plus défavorable. De plus,
cette loi est fonction de la taille de l'élément car il semble
logique que plus l'élément est grand, plus il y a de chance
d'avoir des défauts de surface.
|
Ff
|
? ? - ? ?
m
( )
ó ó
= - ? - ? nf
1 exp ? ?
? ? è ? ?
? ? ? ?
|
(4.2)
|
Les deux paramètres de Weibull sont m et
ónf . Le premier est un paramètre de forme et
le deuxième est une contrainte de base.
La loi de Weibull a cependant une portée limitée et
ceci est dû à différents paramètres que voici [24]
:
· Les paramètres doivent être
indépendants de la durée de chargement, de la surface et de la
géométrie de verre.
· Les valeurs de m ne sont pas
adimensionnelles.
· Chaque essai donne une autre valeur de m.
· La valeur de m n'est pas directement
mesurable.
· Pour des données identiques, deux auteurs
peuvent obtenir des valeurs de m différents selon la méthode
suivie.
· Si on utilise une certaine valeur pour m, alors la
méthode devient déterministe et non plus statistique.
Cette loi ne présente que peu d'intérêt.
Elle permet essentiellement de mettre en évidence le caractère
aléatoire de la répartition des défauts de surface. Pour
le lecteur intéressé, l'explication et la méthode de
détermination des deux paramètres ont été
développées par Hélène Carré dans le cadre
de sa thèse de doctorat [16].
4.2.2.2. Loi d'Evans
La loi d'Evans se base sur le phénomène de
fissuration sous critique du verre ou le phénomène de fatigue
statique. Elle établit donc une relation entre la vitesse de fissuration
et la valeur de la contrainte
da n
v = = É (4.3)
AK
dt
a = longueur du défaut
1
KÉ = óYa 2 = le
facteur d'intensité de contrainte A, n = paramètres de la loi
d'Evans
Tout comme la loi de Weibull, la loi d'Evans ne
présente que peu d'intérêt actuellement pour la
détermination de la résistance mécanique du verre, mais
elle permet de mettre en évidence une relation entre la vitesse de
fissuration et le facteur de contrainte. Grâce à cette loi, on
voit l'importance de connaître la durée de chargement afin de
pouvoir déterminer la résistance du verre. Ce paramètre
n'est d'habitude pas pris en compte dans le dimensionnement des
éléments structurels construits à base d'autres
matériaux que le verre.
D'autres théories existent pour déterminer la
résistance mécanique du verre dont la liste se trouve ci-dessous
:
- Shen - Wörner
- Güsgen - Sedlacek - Siebert
- Porter - Houlsby
Actuellement, une prénorme européenne est
à l'étude dans ce domaine. Cette prénorme a
été déterminée par plusieurs professionnels
européens du domaine verrier. Il semble donc logique de la
considérer comme la plus représentative et la plus proche de la
réalité.
4.2.2.3. La prénorme européenne prEN
13474-3
Durant ce chapitre, il est question de la détermination
de la résistance mécanique du verre. Plusieurs théories
ont été exposées pour le calcul. Cependant, aucune
information n'a été donnée sur les coefficients de
sécurité à prendre en considération car il y a
très peu d'informations concernant les coefficients de
sécurité pour des matériaux fragiles dans la
littérature.
La valeur 3,5 est apparue dans un travail de L. Daudeville, F.
Bernard et H. Carré [8]. Cette valeur pour les matériaux fragiles
prend en compte également les incertitudes liées aux chargements
et au matériau. Cette valeur doit être multiplié par un
coefficient 2 qui représente la perte de résistance du verre dans
le temps suite au phénomène de fatigue statique. Ce qui
correspond, selon cette source, à une valeur de 7 comme coefficient de
sécurité pour les éléments en verre structurel.
Dans le cadre de la prénorme européenne, la
valeur de 1.8 a été choisie comme coefficient de
sécurité pour le verre. Cela suppose une incertitude plus faible
concernant la contrainte dans le verre. L'effet de fissures sous-critiques est
pris en compte, dans la formule de la prénorme, dans le coefficient
kmod . Dans le cas d'un chargement permanent à long
terme
(voir tableau 4.2.1), la valeur de ce coefficient vaut 0.29.
D'après la prénorme, le coefficient de sécurité
à long terme vaut donc (1,8/0,29) 6,2. Ce coefficient comprend
l'incertitude sur le verre et l'effet de fatigue statique.
Voici la formule proposée par la prénorme
européenne prEN 13474-3 [60] afin de déterminer la
résistance de calcul en traction d'une feuille de verre recuit :
k (4.4)
|
fg t d ; ;
|
k k f
mod sp g t
; ;
ãM A
;
|
kmod = est le facteur pour la durée de chargement
(voir tableau 4.2.1)
ksp = est le facteur pour le profil de la surface du
verre (voir tableau 4.2.3) fg ; t ; k = la
résistance caractéristique du verre recuit à la flexion
(45 N/mm2) ãM ; A = le coefficient de
sécurité pour le verre recuit (=1.8)
Le facteur pour la durée de chargement
kmod
Le coefficient réducteur kmod
permet de tenir compte du phénomène de fatigue statique pour la
détermination de la résistance du verre recuit. La formule pour
calculer le kmod en fonction du temps est la suivante :
1
16
k mod 0.663 t
= (4.5)
t = temps de chargement en heure
La valeur maximum de kmod est de 1, la valeur
minimum est de 0.25. Dans le tableau suivant (Tableau 4.2.1), certaines valeurs
typiques de kmod seront données.
|
Action
|
Durée de chargement
|
kmod
|
|
charge de personnes
|
court et unique
|
1,0
|
|
Vent
|
court et multiple
|
0,74
|
|
Neige
|
intermédiaire
|
0,43
|
|
poids propre
|
permanent
|
0,29
|
|
variation quotidienne de température durée de 11h
valeur maximal extrême
|
intermédiaire
|
0,57
|
|
variation annuelle de température durée de 6 mois
valeur moyenne extrême
|
intermédiaire
|
0,39
|
|
variation de pression barométrique
|
intermédiaire
|
0,5
|
Tableau 4.2. 1 Quelques valeurs caractéristiques pour
kmod adapté de l'anglais de la
référence [60]
La valeur 0.43 est une valeur obtenue en faisant une moyenne
de la valeur de kmod à une durée de
chargement de une semaine ( kmod =0.48) et celle d'une
durée de chargement de trois mois ( kmod =0.41).
Actuellement, quand il y a plusieurs sollicitations à
prendre en considération, on détermine un
kmod combiné en fonction des différents types
de sollicitations d'après la formule cidessous :
ã " "
+ ã ? ã ø
,1 " "
G G k Q Q k + i Q ki i k i
, 0, Q ,
(4.6)
i
k =
mod, combi G Q Q
k k ,1 k ,
ã " "
+ ã " "
+ ? ã ø
G Q ,1 i Q ki i
, 0,
k k k
mod, G mod, Q mod, Q
k k ,1 k i
,
L'ensemble des termes présent dans cette équation
est expliqué dans l'Eurocode 0 excepté les différents
kmod qui sont obtenus d'après la formule
donnée plus haut.
Selon l'Eurocode 1, il existe quatre types de classes
différentes de bâtiment, chacun ayant une durée
d'utilisation minimale. Ces durées d'utilisation peuvent servir de
référence pour la détermination de la valeur de
kmod (voir tableau 4.2.2).
|
Classe
|
Durée d'utilisation de projet prescrite
[années] (heures)
|
Exemple
|
kmod
|
|
1
2
3
4
|
[1-5]
(8760-43800)
[25]
(219000)
[50]
(438000)
[100]
(876000)
|
Structures temporaires
Eléments structuraux remplaçables par ex. poutres
de roulement, appareils d'appui
Structures de bâtiments et autres structures courantes
Structures monumentales, de ponts et d'autres ouvrages de
génie civil
|
0.34 0.30 0.295 0.281
|
Tableau 4.2.2 Classification de la durée d'utilisation de
projet [29]
Le facteur pour le profil de la surface du verre
ksp
Ce coefficient réducteur prend en compte la forme et le
type de surface du verre. Dans le cas le plus courrant du verre flotté,
la valeur vaut 1 sauf dans de rares cas (Tableau 4.2.3).
|
Verre (n'importe quelle
composition)
|
Le facteur pour le profil de la
surface du
verre
|
|
verre flotté
|
1.0
|
|
feuille de verre tirée
|
1.0
|
|
verre flotté émaillé
|
1.0
|
|
verre sérigraphié
|
0,75
|
|
verre sérigraphié émaillé
|
0,75
|
|
verre armé poli
|
0,75
|
|
verre armé sérigraphié
|
0,6
|
Tableau 4.2.3 Les valeurs du facteur pour le profil de la surface
du verre ksp , adapté en français [60]
4.3 Résistance due à la trempe
L'utilisation de la trempe permet d'augmenter la
résistance mécanique du verre en mettant l'ensemble de sa surface
en compression (voir 3.5.1). Dans ce chapitre-ci, les différentes
méthodes pour la détermination des contraintes de trempes seront
développées.
La trempe induit une contrainte de compression aux bords de la
plaque qui est deux fois plus importante en valeur absolue que la contrainte de
traction au coeur.
4.3.1 Formule analytique
La formulation analytique qui existe pour déterminer
les contraintes de trempes se limite aux contraintes dans une plaque
considérée comme infinie [16] : au coeur de la plaque.
Actuellement, il n'existe aucune formulation analytique qui prend en compte les
effets de bords. Cependant, la différence de contrainte entre les effets
de bords et le centre de la plaque est négligeable (voir 3.5.1).
E c l v
â
ó = 2 (4.7)
m 24(1 )
- í ë
E = module de Young
â = coefficient de dilatation thermique
c = chaleur spécifique volumique l =
épaisseur de la plaque
v = vitesse de refroidissement í =
coefficient de poisson
ë = conductivité thermique
Cette formule met en évidence les différents
paramètres influençant les contraintes de trempe. On remarque que
la contrainte augmente si la vitesse de refroidissement augmente
également.
Quatre paramètres influencent de manière importante
les contraintes de trempe :
- la température de base (température à
laquelle les paramètres viscoélastiques sont connus)
- le module de Young
- le coefficient de dilatation thermique
- la conductivité thermique du verre
Parmi ces quatre paramètres, deux (la
température de base et le module de Young) peuvent être facilement
et précisément déterminés. La conductivité
thermique est assez bien connu mais a une influence moindre par rapport aux
autres. Malheureusement, le coefficient de dilatation thermique du verre
liquide est connu avec une incertitude assez importante. Il est dès lors
très difficile d'utiliser cette formule de manière optimale. Dans
la vie pratique, cette formule n'est jamais utilisée.
4.3.2 Valeur des fournisseurs ou des normes
La formule analytique qui détermine les contraintes de
trempe est fonction de l'épaisseur de la plaque. Malheureusement,
à l'heure actuelle, les fournisseurs de verre ne proposent pas de
valeurs de trempe qui est fonction de l'épaisseur. Sur demande
seulement, ils garantissent une certaine valeur pour la contrainte de trempe.
Cette garantie est la même quelque soit l'épaisseur de la feuille
demandée. Pour déterminer les contraintes de trempes, les
producteurs procèdent de la manière suivante : ils effectuent
d'abord le processus de trempe et ils vérifient grâce à
différentes méthodes que le verre possède bien la
contrainte de trempe souhaitée. Dans le cas contraire, la feuille est
retirée de la production.
4.3.2.1 Méthodes de
vérification
Il existe deux types de méthodes pour la mesure des
contraintes de trempe : les méthodes destructives et les méthodes
non-destructives. Différentes méthodes seront
développées dans ce paragraphe. La méthode utilisée
par les fournisseurs est la méthode de mesure optique car c'est une
méthode non destructive et qui n'endommage pas le matériau.
- Méthodes destructives
- Mesure par comptage de fragment : un verre
trempé doit se rompre en un nombre minimal de morceau par unité
de surface
- Mesure par relaxation de contrainte : On dispose
une jauge sur le verre, on découpe la feuille tout autour de la jauge
pour relaxer les contraintes et on obtient ainsi la valeur opposée de la
trempe.
- Mesure par pelage : Une petite épaisseur est
enlevée de la feuille de verre. Les contraintes se relaxent mais
connaissant la déformation, la courbure de l'élément et
son épaisseur on peut déterminer les contraintes.
- Méthodes non-destructives
Les méthodes non destructives utilisent la technique de
photoélasticimétrie (méthode optique) pour
déterminer les contraintes de trempe dans le verre. Cette technique de
mesure est possible grâce à la transformation de la transparence
du verre recuit en un matériau biréfringent suite au processus de
trempe
Plusieurs appareillages différents existent afin de
calculer la contrainte de trempe. Cependant, la polarimétrie reste
l'appareillage le plus utilisé.
Le rayon lumineux émit par la source traverse un
polariseur et se polarise. Ensuite, le rayon passe par l'élément
en verre à analyser et enfin par un analyseur qui mesure la
différence de phase du rayon lumineux par rapport au polariseur. Cette
différence de phase permet de déterminer les contraintes de
trempe grâce à diverses équations.
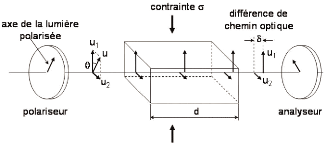
Figure 4.3. 1 Schéma explicatif de la polarimétrie
[38]
Dans les normes, ils existent des valeurs pour les contraintes de
trempe qui varient en fonction du type de trempe et du type de feuille de verre
(voir Tableau 4.3.1).
|
Verre (n'importe quelle composition)
|
Valeurs caractéristiques de la contrainte en
flexion pour différents procédés de
précontrainte
|
|
trempe thermique
|
verre durci
|
trempe chimique
|
|
Verre flotté ou feuille de verre étiré
|
120 N/mm2
|
70 N/mm2
|
150 N/mm2
|
|
Verre sérigraphié
|
90 N/mm2
|
55 N/mm2
|
150 N/mm2
|
|
Verre émaillé
|
75 N/mm2
|
45 N/mm2
|
|
|
Verre sérigraphié émaillé
|
75 N/mm2
|
45 N/mm2
|
Tableau 4.3 1 Valeurs des contraints de trempe [60]
Coefficient de sécurité sur les contraintes
de trempe
Les valeurs des contraintes de trempe sont difficiles à
déterminer car on ne maîtrise pas
tous les paramètres du
processus de manière précise. Heureusement, les méthodes
de
vérifications sont précises et se contentent de
vérifier le résultat final. Tout comme dans la
sidérurgie, les valeurs des contraintes de trempe dans
le verre sont des valeurs assurées par le fournisseur. On pourrait se
demander dès lors pourquoi le coefficient de sécurité
préconisé dans les normes est de seulement 1.2 [60] alors qu'il
pourrait encore être diminué. Cette valeur sécuritaire
résulte de l'erreur relative sur les instruments de mesure optique et
aussi sur le manque d'applications et d'essais en la matière.
Coefficient de sécurité pour les surfaces
pré sollicitées ãM ; v = 1.2 Le
facteur pour le procédé de trempe du verre
kv
Il existe deux méthodes pour réaliser un
trempage thermique du verre (voir 3.5.1.1). Le procédé de trempe
vertical induit des déformations supplémentaires au niveau des
pinces. Cet effet a pour conséquence l'utilisation d'un coefficient
minorateur (voir Tableau 4.3.2). Actuellement, les verres sont trempés
majoritairement par un procédé de trempe horizontale sauf dans
des applications très rares.
|
procédé de fabrication
|
Le facteur pour le procédé
de trempe
kv
|
|
trempe horizontale
(tout procédé n'utilisant pas des pinces pour
pendre le verre)
|
1
|
|
trempe verticale
(tout procédé utilisant des pinces pour pendre le
verre)
|
0,6
|
Tableau 4.3 2 Valeurs pour le facteur du procédé
de trempe [60]
4.4 Principes de superposition
Les différents paragraphes précédents ont
montrés comment on pouvait déterminer les contraintes du verre
recuit et les contraintes de trempe. Cependant, le verre trempé ne se
limite pas à la contrainte de trempe. Lorsque la contrainte de trempe
est atteinte, le verre trempé possède un comportement analogue
à celui de verre recuit, à l'instar du béton
précontraint. Il faut d'abord décompresser la surface mais
après le verre possède encore toute la résistance du verre
recuit. Ce phénomène nous permet d'écrire la relation de
superposition suivante qui permet de déterminer la résistance du
verre trempé :
Résistance du verre trempé =
Résistance
du verre recuit + Contrainte de trempe
Selon la prénorme européenne, la mise en
équation du principe précédent donne la relation suivante
pour la détermination de la résistance de calcul en traction du
verre trempé :
|
fg t d ; ;
|
k k f k f f
v ( b k - g t
k )
mod sp g t k
; ; ; ; ;
+ (4.8)
ã ã
M A
; M v
;
|
kmod , ksp , ãM ;
A , fg ; k : Ces coefficients ont déjà
été expliqués précédemment
kv = le facteur pour le procédé de trempe du
verre (voir Tableau 4.3.2)
fb ; k = la valeur de la contrainte de trempe
(voir Tableau 4.3.1)
Dans le cas du verre trempé, il est
préférable de travailler avec la résistance de calcul au
lieu de la résistance caractéristique car les coefficients de
sécurité ne sont pas les mêmes pour la résistance du
verre recuit et pour les contraintes de trempe.
4.5 Résumé des formules de la
résistance du verre
Résistance caractéristique du verre à la
compression :
fg ; c = 600N/mm2
fg ;c ;d
f g ;c
Résistance de calcul du verre à la compression :
= (4.1)
ãM ;A
Résistance caractéristique du verre recuit à
la traction à long terme :
fg ; t = kmod ksp fg
;k (4.9)
Résistance de calcul du verre recuit à la traction
:
|
fg ;t ;d
|
k modk sp fg
;
ãM ;A
|
k
|
(4.4)
|
Résistance caractéristique du verre trempé
à la traction à long terme:
fg ; t = kmod ksp fg
; k + kv ( fb ; k - fg
;k) (4.10)
Résistance de calcul du verre trempé à la
traction :
fg; t ;d
(4.8)
k mod k sp f
g;k g;k k v (
fb; k -fg
;k)
= +
ã M ; A ãM ;v
Conclusion du chapitre
Ce chapitre a expliqué comment déterminer la
résistance du verre recuit et du verre trempé. Tous les
problèmes du verre qui ont été expliqués au
chapitre 3 influencent la résistance par la présence de nombreux
coefficients réducteurs. La détermination de la résistance
du verre trempé résulte des propriétés de ce
dernier, la présence de contrainte en compression qu'il faut d'abord
annuler avant de solliciter le verre recuit permet d'augmenter
considérablement la résistance du verre, grâce au principe
de superposition. La résistance du verre peut donc être
déterminée. Ceci représente la première
étape du dimensionnement des structures en verre. Il représente
le terme de droite dans la relation de base suivante.
Ed < Rd
|
Chapitre
|
|
|
5
|
|
|
|
Dimensionnement d'une structure en verre
|
Les formules utilisées lors du dimensionnement d'une
structure sont indépendantes du matériau de construction. Les
structures en verre ne dérogent pas à cette règle.
Cependant, il y a quelques modifications lors de la détermination de
certains paramètres. A cause de la géométrie des feuilles
de verre, certaines formules pour le dimensionnement des structures en verre se
basent sur la théorie des parois minces. Dans ce chapitre, les formules
seront développées dans le cas d'une feuille de verre simple et
dans le cas du verre feuilleté. Dans la pratique, on ne rencontra jamais
une structure en verre composée d'une seule feuille. Cependant, le
développement de certaines formules d'une seule feuille met en
évidence plusieurs comportements.
La valeur de la résistance de calcul en traction du
verre à long terme fg ; t ; d sera
utilisé (voir
chapitre 4). Cette valeur comprend déjà les
coefficients de sécurité, son utilisation est plus facile que la
valeur de la résistance caractéristique à cause de la
présence de deux coefficients de sécurité
différents. Cependant, la résistance caractéristique en
traction du verre à long terme fg ; t ; k est
également utilisée dans ce chapitre.
5.1 Combinaison d'actions
5.1.1 Etat Limite Ultime (E.L.U.)
Voici ce que renseigne l'Eurocode 1, la norme ENV 1991-1 : 1994
p. 28, concernant l'étatlimite ultime.
« 3.2 Etats-limites ultimes
1)P Les états-limites ultimes sont ceux qui
associés à un effondrement ou à d'autres formes similaires
de défaillance structurale.
2) Les états précédant un
effondrement structural et qui, pour des raisons de simplification, sont pris
en compte à la place de l'effondrement luimême, sont aussi
traités comme des états-limites ultimes.
3)P Les états-limites ultimes susceptibles de devoir
être pris en compte comprennent :
- la perte d'équilibre du tout ou d'une partie de la
structure, considéré comme un corps rigide ;
- une défaillance due à une
déformation excessive, à la transformation de tout ou partie de
la structure en un mécanisme, à une rupture, à une perte
de stabilité de tout ou partie de la structure, y compris ses appuis et
fondations ;
- une défaillance provoquée par la fatigue ou
d'autres effets liés à la durée. »
Dans le cas de l'état limite ultime, il n'existe qu'une
seule combinaison d'actions qui s'écrit comme ceci :
F = ã G + ã Q + ?
ã ø Q (5.1) G " " Q k ,1 " " Q o
, i k , i
d
i
G = Valeur des actions permanentes
Qk , 1 = Valeur caractéristique de la principale
charge variable
Qk , i = Valeur caractéristique des
charges variables secondaires
ãG = Coefficient partiel pour l'action
permanente
ãQ = Coefficient partiel pour l'action
variable
ø0 ;i = Coefficients pour les actions
variables, la valeur de ces coefficients est indiqué dans la norme ENV
1991-1 : 1994 p. 51
Il s'agit donc de déterminer la limite au-delà de
laquelle il y a un risque de défaillance, de rupture de la structure ou
d'une partie de celle-ci.
5.1.2 Etat Limite de Service (E.L.S.)
Voici ce que renseigne l'Eurocode 1, la norme ENV 1991-1 : 1994
p. 29, concernant l'étatlimite de service.
« 3.3 Etats-limites de service
1)P Les états-limites de service correspondent
à des conditions au-delà desquelles les exigences d'aptitude au
service spécifiées pour une structure ou un élément
structural ne sont plus satisfaites.
2)P Les exigences en matière d'aptitude au service
concernent : - le fonctionnement de tout ou partie des constructions ;
- le confort des personnes ;
- l'aspect
3)P Une distinction doit être faite, le cas
échéant, entre les états-limites de services
réversibles et irréversibles.
4) Sauf indication contraire, il convient que les exigences
en matière d'aptitude au service soient déterminées dans
les contrats et/ou dans le projet.
5) Les états-limites de service susceptibles de
devoir être pris en compte comprennent :
- les déformations et déplacements qui
affectent l'apparence ou l'utilisation effective de la structure (y compris le
fonctionnement des machines ou des services) ou endommagent des finitions ou
des éléments non structuraux ;
- les vibrations qui nuisent au confort des personnes,
endommagent la structure ou les matériels qu'elle supporte, ou qui
limitent son efficacité ;
- les dommages (y compris les fissures) susceptibles de nuire
à l'aspect, à la durabilité ou à la fonction de la
structure ;
- les dommages visibles causés par la fatigue et
d'autres effets liés à la durée »
Selon l'Eurocode 1, il y a trois types de combinaisons d'actions
possibles pour le calcul à l'état limite de service :
- Combinaison rare
- Combinaison fréquente
- Combinaison quasi-permanente
La combinaison fréquente est celle le plus souvent
utilisé pour le dimensionnement de structure. Dans le cas de structure
sans effet de précontrainte, la formule s'écrit comme ceci :
F = G + ø Q + ? ø Q
(5.2) d " " 1 k ,1 " " 2, i k , i
i
G , Qk ,1 , Qk , i
: ces termes ont été expliqués
précédemment
ø 1 ;ø2 , i =
Coefficients pour les actions variables, la valeur de ces coefficients est
indiqué dans la norme ENV 1991-1 : 1994 p. 51
Il s'agit donc de déterminer la limite au-delà
de laquelle, une structure n'est plus apte à assurer l'ensemble des
fonctions auxquelles elles étaient destinées ou bien de limiter
l'aspect négatif de la structure, sa déformée ou des
éventuelles fissures, qui influe sur l'effet psychologique des
utilisateurs.
5.2 Classifications des structures 5.2.1
Généralité
Des chercheurs néerlandais de l'université de
Delf (TU Delf), on mit au point une nouvelle approche de classification de
structure pour le verre. Dans les normes européennes actuelles, on
limite le risque avec une approche probabiliste. Pour ces chercheurs, la
question à se poser ne devrait pas juste être « Quand le
verre se cassera » (approche probabiliste) mais « Que se passera-t-il
quand il sera casser » (approche basé-
conséquence) (Phrase traduite de l'anglais :
`when will the glass break ?' ( probalistic approach) but also `what will
happen when is does' (consequence-based approach)[13] . En
réalité, les concepteurs se soucient déjà de ce
problème en utilisant certaines méthodes comme par exemple le
verre feuilleté. Cependant, ces différentes méthodes ne
sont pas réglementées et elles dépendent de
l'expérience et de l'opinion de l'ingénieur, la localisation, le
type de structure et encore d'autres paramètres.
Dans les normes actuelles, la notion de risque a
été introduite qui est un produit entre la probabilité
qu'un élément se fissure et la conséquence de cette
fissure. Pour une approche probabiliste complète, il est important de
connaître toutes les données relatives aux
propriétés structurales du matériau et des actions sur la
structure. En réalité, on utilise des approximations et des
estimations basées sur l'expérience et les recherches. Dans le
cas du verre, le manque de connaissance et de formulations claires concernant
le comportement après fissuration rend difficile l'approche
traditionnelle.
Les chercheurs de l'université de Delf ont donc
décidé de mettre au point une méthode. Ils ont introduit
un nouveau concept MCC (Member Consequence Classes). C'est un
classement des éléments fissurés qui se base sur les
contraintes résiduelles de ces éléments pour une certaine
période en fonction d'un niveau de dommage. Cette nouvelle approche
permet de créer un outil de comparaison entre les différentes
structures. Ce nouveau classement des éléments de structure se
base sur le rôle et la fonction des différents
éléments au sein de la structure et l'accessibilité de la
structure.
5.2.2 Les paramètres
Deux paramètres ont déjà
été cités plus haut, il s'agit de la résistance des
contraintes résiduelles et le temps durant lequel la structure va
résister après que la fissure soit entamée.
La fissure d'un élément en verre peut avoir
plusieurs formes. Un verre feuilleté est considéré comme
fissuré quand l'ensemble de ces feuilles sont fissurées mais
aussi quand seulement une de ces feuilles l'est (voir Figure 5.2.1).
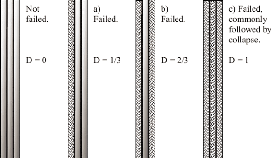
Figure 5.2 1 Schéma représentatif du niveau de
dommage d'un élément en verre [13]
Il est normal de considérer plusieurs cas
différents de post-fissures en fonction des
différents types
de dommages. Afin de faire la distinction, le concept de dommage
Dglass a
été introduit comme étant le
troisième paramètre de cette approche de sécurité.
5.2.3 Axes de démarcations
5.2.3.1 Le dommage
Quand une feuille se rompt, la fissure se propage le long de
toute la feuille. Cette
caractéristique permet de considérer
le dommage comme une fonction du nombre de
feuilles de verre. Le
paramètre Afr, c (la surface fissurée) peut
être affinée en ne considérant
que la partie réellement fissurée et non pas comme
si toute la feuille de verre l'était (voir Figure 5.2.2)
Dglass
A fr , c
Figure 5.2 2 Représente l'aire frontale en
hachuré
Atot
= (5.3)
A fr ,c = Aire frontale fissurée
Atot = Aire totale
5.2.3.2 La contrainte
La contrainte au sein d'un élément est
différente en fonction des combinaisons d'actions et des usages. Le
niveau de contrainte exigé pour un élément peut être
le même que celui-ci soit endommagée ou bien qu'il ne le soit
pas.
Ssw = Contrainte égale au poids propre de
l'élément Smom = Contrainte égale
à un chargement momentané Ssls = Contrainte égale
à l'état limite de service
Suls = Contrainte égale à l'état
limite ultime Srep = Contrainte égale à la rupture du
verre 5.2.3.3 Le temps
Peu d'informations existent pour déterminer le temps
pendant lequel la contrainte recommandée peut être maintenue.
Voici les temps de référence proposés :
30 sec : Temps nécessaire pour fuir immédiatement
d'un dommage d'un élément structurel
2h : Temps nécessaire pour évacuer et fermer un
espace autour d'un membre endommagé 24h : Temps pour prendre des mesures
structurelles (étançonnement)
72h : Temps pour prendre des mesures structurelles
complémentaires
tref : Temps de référence pour la vie du
bâtiment
5.2.3.4 Member Consequence Classes (MCC)
Il est maintenant possible de déterminer un tableau en
fonction du rôle de la structure dans le bâtiment et son
accessibilité. Contrairement à l'eurocode qui classe les
structures en fonctions seulement de leur importance, de leur rôle dans
le bâtiment. 6 classes différentes ont été
proposées.
Rôle au sein de la structure Accessibilité
de la structure MCC
Structure clé Élevé - Espace Publique 6
Structure clé Moyen - Espace semi publique/ bureau 6
Structure clé Bas - privé 5
Structure principale Élevé - Espace Publique 4
Structure principale Moyen - Espace semi publique/ bureau 3
Structure principale Bas - privé 2
Structure secondaire Élevé - Espace Publique 3
Structure secondaire Moyen - Espace semi publique/ bureau 2
Structure secondaire Bas - privé 1
Tableau 5.2
1 : Tableau de classification des structures [13]
|
MCC
|
d<1 (pré fissuré) contrainte temps
|
d=1 (extérieur)
Contrainte temps
|
d=m (toutes les feuilles
extérieures)
contrainte temps
|
d= n (toutes les
feuilles)
contrainte temps
|
|
1
2
3
4
5
6
|
Suls Suls Suls
Suls
Suls
Suls
|
tref tref tref
tref
tref
tref
|
Suls
Ssls
Suls
Ssls Suls
Suls Suls
Srep
|
2h
24h
24h
72h
72h tref tref
tref
|
Smom
Suls
Ssls
Suls
Ssls
Suls
Ssls Suls
Srep
|
30sec
2h
24h
24h
72h
72h tref
tref tref
|
0
Smom
Smom
Ssls Smom
Suls Ssls
Srep
|
0
30sec
2h
24h
72h
24h
72h
tref
|
Tableau 5.2 2 Temps et contraintes recommandées pour une
certaine valeur de dommage [13]
Cette classification est pour l'instant difficile à
établir car la résistance de calcul d'une feuille de verre
endommagée n'a jamais été véritablement
étudiée.
5.3 Elément comprimé
Les éléments comprimés occupent une place
importante dans le domaine de la construction car ils transmettent l'ensemble
des charges gravitaires jusqu'aux fondations. Les efforts transmis sont
généralement dans l'axe de la colonne sauf dans les treillis.
Dans certains cas, il se peut que l'effort de compression soit couplé
avec un moment de flexion significatif, l'élément de structure
est considéré comme comprimé fléchi.
Dans la classification MCC, les colonnes se rangent
dans la classe 2, 3 ou 4 en fonction de l'accessibilité. Le remplacement
de ce type d'élément est donc permis cependant, même
fissurés ces éléments doivent pouvoir reprendre un
certaine quantité de charge.
L'ensemble des éléments comprimés peut
être victime d'une instabilité. Ce phénomène est
appelé flambement. L'élément a alors tendance à
fléchir dans la direction perpendiculaire à la charge.
5.3.1 Design
Il est intéressant de réfléchir aux
différents types de sections possibles pour les structures en verre
sollicitées en compression. Contrairement à l'acier où ils
existent des moules de différentes formes ou au béton où
l'on peut réaliser presque n'importe quelle forme de coffrage, les
structures en verre doivent être issues d'une composition de feuilles de
verre. De ce fait, plusieurs contraintes existent et limitent l'utilisation de
certains types de profile. Après réflexion, deux types de profile
sortent du lot dans le cas de structure soumise à une compression, celle
de forme circulaire et celle en forme de croix.
L'ensemble des profils creux n'est pas propice à
l'utilisation du verre car ceux-ci doivent être construit sous vide et
fermer de manière hermétique afin de prévenir toutes
infiltrations qui pourraient salir l'intérieur de la structure. Une fois
le tube fermé, il n'est plus possible d'y accéder afin de
l'entretenir. Cependant, des expériences ont déjà
été réalisées sur des profils circulaires creux.
De part la nature de la sollicitation et les risques de
flambement, il est plus intéressant d'avoir une structure doublement
symétrique afin d'optimiser l'utilisation de matière. De cette
manière on possède la même raideur (inertie) dans les deux
sens. Ceci est particulièrement intéressant s'il le type d'appui
est le même dans tous les orientations.
Enfin, l'assemblage de deux feuilles de verre perpendiculaires
se fait à l'aide de colles qui sont des points faibles de ce type des
profilés. Il semble donc utile et préférable de limiter
leurs utilisations au minimum.
5.3.1.1 La section circulaire
Même si les sections circulaires sont des profils creux
et que leur utilisation ne me semble pas être la plus appropriée
dans le cas de matériau transparent. Ils existent certains exemples de
réalisation et des recherches ont été effectuées
sur ce type de section. Il est vrai que la section circulaire est la plus
efficace dans le cas d'un effort de compression car elle dispose d'une plus
grande inertie pour une même quantité de matière. L'inertie
intervenant dans la résistance au flambement est donc importante. Dans
le tube, la matière est concentrée là où la section
en a le plus besoin, c'est-à-dire loin du centre de gravité.
Il est possible d'augmenter l'épaisseur de la section
circulaire. Il suffit de prendre deux tubes de verre de diamètres
différents et de compléter le vide entre les deux par de la
résine. La résine se solidifie grâce aux ultraviolets. On
obtient ainsi une colonne en verre feuilleté. Ces intercalaires
possèdent une faible rigidité et des faibles
caractéristiques de sécurité et d'habitude, ils ne sont
pas utilisés à des fins structurelles. Cependant, dans ce cas-ci
et à cause de la manière de procédé, il est
impossible d'utiliser une feuille plastique afin d'obtenir un verre
feuilleté.
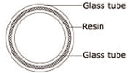
Figure 5.3 1 Section d'une colonne feuilletée [56]
5.3.1.2. La section cruciforme
Cette section est obtenue en prenant une feuille ou plusieurs
feuille de verre qui possèdent la longueur voulue. Après cela on
vient coller au milieu de ce premier élément, une ou des autres
feuilles de verre à 90° et cela de chaque coté afin
d'obtenir une croix.
Cette forme de section permet de limiter à deux le
nombre de joint de colle nécessaire. De plus, sa double symétrie
permet de s'affranchir d'une vérification supplémentaire et les
questions d'entretiens qui se posent dans le cas de structures creuses ne se
posent pas.
L'inertie d'une telle forme est intéressante même
si elle n'est pas optimale comme dans le cas d'un cylindre. Une partie de la
matière de la section se retrouve vite éloignée du centre
de la section.
L'inconvénient de ce type de section est la
présence de joint de colle supplémentaire qui sont obligatoire la
réalisation de cette section. L'utilisation de ce liant crée un
matériau non homogène. La rupture et l'instabilité de ce
genre de section n'a pas encore été étudiée en
profondeur ni les risques de flambements locaux (le risque qu'une des parties
collées ne flambe d'abord au lieu que l'ensemble de la section ne
subisse l'instabilité).
Figure 5.3. 2 Section transversale en croix
5.3.2 Etat limite ultime
D'après l'extrait repris au point 5.1.1, le calcul aux
états-limites ultimes d'une section en verre soumise à une
compression doit comprendre deux vérifications. La première est
la résistance de la section transversale et la deuxième est la
résistance au flambement.
5.3.2.1 Résistance des sections
transversales
Dans le cas d'une section soumise à une compression pure,
sans tenir compte des instabilités, la formule pour déterminer la
charge maximale que peut reprendre une feuille de verre est la suivante :
Nc , rd = fg , c , d
. A (5.4)
Nc , rd = Valeur de l'effort normal
fg , c , d = Résistance de
calcul en compression A = Aire de la section
Dans le cas du verre laminé composé de n feuilles
de verre, la formule devient :
Nc , rd = fg , c , d
. Aeff (5.5)
Nc , rd ; fg , c , d
ont déjà été expliqués
Aeff = Aire effective, aire qui participe à la
résistance
Le verre feuilleté est un mélange entre des
feuilles de verre et un film plastic adhésif. Ce film comme tous les
éléments possède une épaisseur, il est
préférable de négliger cette quantité de
matière car cette approximation nous met du côté de la
sécurité. L'aire totale d'un verre feuilleté est donc
l'aire de chacune des feuilles de verre.
A = ? A (5.6)
eff i
i
Ai = Aire de la feuille de verre i
5.3.2.2 Résistance au flambement et
résistance à la traction transversale
Le flambement est un phénomène
d'instabilité qui existe lorsqu'un élément est soumis
à un
effort de compression. Sous un effort axial,
l'élément se met à fléchir dans la direction
perpendiculaire à celle de la charge, ceci explique sa
dénomination complète «flambement par flexion ». Ce
phénomène apparaît avant la ruine du matériau, il
est donc important de déterminer la charge critique maximale par rapport
à ce phénomène.
La détermination de la résistance au flambement
d'une structure soumise à un effort de compression fait partie de la
vérification aux états-limites ultimes d'une structure. Dans le
cas du verre, les formules du flambement eulérien ne comprennent pas
seulement un terme en compression mais également un moment dû
à l'excentricité des efforts. Les parties sollicitées en
traction sont les parties dimensionnantes de la structure. En pratique, la
réalisation d'assemblage permettant une transmission des efforts par
compression pure est totalement illusoire. Cependant, cette formule est bien
celle que l'on utilise en général pour avoir une idée de
la valeur maximale de la charge critique. On se permet de négliger les
efforts du second ordre car les autres matériaux peuvent plastifier et
ainsi limiter voir empêcher la propagation des fissures. Dans le cas du
verre, le phénomène de propagation sous-critique (voir chapitre
3) amène à la ruine même sous chargement constant car c'est
un matériau fragile. De plus, on sait également qu'il existe
certaines tolérances vis-à-vis de la construction d'une feuille
de verre. Les feuilles de verre trempé possèdent toujours une
légère flèche qui contribue à augmenter l'effet de
second ordre existant.
Dans le cas du verre, la formulation de la charge critique
d'Euler donne une valeur maximale de la charge admissible. La loi d'Euler se
base sur deux hypothèses :
- utilisation d'un matériau parfaitement
élastique
- On admet qu'il n'y a aucune tension ne dépassant la
limite proportionnelle
Pour une feuille de verre simple, la première
hypothèse est vérifiée mais la deuxième n'est
jamais vérifiée, peu importe le matériau. La formule
d'Euler est valable pour un matériau possédant une
résistance infini. L'instabilité interviendrait de manière
instantanée. La réalité est différente, lors d'un
essai en compression, la charge augmente petit à petit et l'on peut voir
une flexion apparaître dans l'élément. Quand la charge
critique est presque atteinte, il y a une bifurcation soudaine de
l'élément.
Dans le cas d'une feuille de verre simple et grâce
à son caractère élastique, la charge critique d'Euler
donne une valeur satisfaisante pour la charge critique de flambement sans pour
autant prendre des coefficients de réduction.
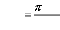
2
EI
N
cr , e 2
L k
(5.7)
E = Module de Young
I = Inertie de la section
Lk = Longueur caractéristique
La formule a été établie pour des
éléments comprimés bi articulés. Cependant, il est
possible de fixer les colonnes de plusieurs manières différentes.
Il est donc important de connaître les longueurs de flambement dans ces
autres cas. Il existe des abaques avec différents types d'appuis et la
longueur de flambement relative, la figure 5.3.3 reprend la valeur de la
longueur de flambement de différents cas simples.
La détermination de la charge critique d'Euler n'est
pas suffisante dans le cas d'une structure en verre. Un élément
n'est jamais en compression parfaite, il y a toujours des excentricités
des charges. Ces excentricités induisent des efforts de second ordre et
des zones en traction peuvent apparaître qui sont
déterminantes.
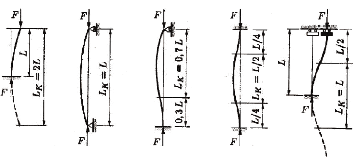
Figure 5.3. 3 : Valeurs de la longueur caractéristique de
flambement dans différents cas [35]
Le dimensionnement des structures en verre soumises à un
effort de compression peut se faire selon deux principes :
- par un calcul au deuxième ordre (résistance
à la traction transversale) - par la détermination de la
résistance au flambement
Voici donc les formules préconisées pour la
vérification de la contrainte [49] pour le calcul au état limite
ultime en compression.
Dans le cas d'une feuille de verre simple Dimensionnement
par un calcul au deuxième ordre :
N N ? e w ?
ó = #177;
0
? + ? = f (5.8)
g t d
, ,
A W ? cos / 2 /
L N EI 1 / ,
- N N
? k cr e ? ?
A = Aire de la section
W = Module de section élastique e =
excentricité
w0 = flèche initiale
Ncr , e = charge critique d'Euler
La valeur de la flèche initiale w0 est
donnée dans le chapitre 3, l'usage conseillerait de
prendre la valeur de tolérance de construction la plus
grande de la flèche globale dans le cas du verre trempé
thermiquement et horizontalement.
L'excentricité dépend de plusieurs
paramètres tels que le type d'assemblage, le type d'appui ou bien encore
la position de l'élément au sein de la structure. On ne peut pas
généraliser la valeur e. C'est l'ingénieur qui doit
déterminer cette valeur en fonction de la condition de fixation des
extrémités de la colonne. Comme il n'y a pas des détails
types elle peut être différente pour chaque application.
Dimensionnement par l'utilisation d'un coefficient de
réduction :
D'après la référence [49], le coefficient
de réduction ne peut pas être déterminé à
partir des courbes de flambement. L'auteur propose une autre méthode
pour la détermination de la résistance de calcul au flambement en
se basant sur l'utilisation d'un coefficient de réduction.
Nrd , b = ÷b . A
. fg , t ,d (5.9)
Nrd , f = La résistance de calcul au
flambement ÷b = Coefficient de réduction
A = Aire de la section
fg ; t , d = Résistance de
calcul de traction d'une feuille de verre
La valeur du coefficient de réduction est obtenue à
partir du graphe (voir Figure 5.3.4) et de l'élancement réduit
ë
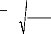
fg , t , d
ók
ë
(5.10)
ók = Contrainte dans la section pour
une charge en compression d'Euler
Dans la formule du flambement, il peut paraître
étonnant de voir apparaître la résistance
caractéristique en traction du verre. Comme la résistance en
compression est très élevée pour le verre, la
capacité portante d'une colonne en verre en compression est toujours
limité par la résistance en traction due à la flexion de
l'effet du second ordre.
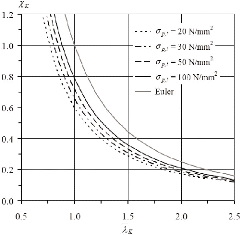
Figure 5.3 2 Courbes pour la détermination du coefficient
de réduction en fonction du flambement [49]
( ó p , t = fg ; t ,
d )
Contrainte maximale en compression pour une feuille de
verre
La valeur de contrainte maximale que peut supporter un
élément en verre soumis à une charge de compression est la
plus petite des valeurs obtenues par les différents
procédés de dimensionnement de la charge critique de flambage.
Tous les termes de cette formule ont déjà été
expliqués précédemment.
|
ómax,b
|
? ? N N ? e w ? N
?
0 rd b ?
,
= min ? #177; ? + ? ; ? (5.11)
cos / 2 / 1 /
? ? A W ? L N EI - N N A
? k cr e
, ? ? ? ?
|
Dans le cas d'un verre feuilleté composé de
n feuilles
A cause de la présence de feuilles plastiques dans le
verre feuilleté, le comportement mécanique est
légèrement différent de celui d'une feuille en verre
simple. Le caractère plastique du film adhésif donne au
matériau un caractère plastique. Il faut utiliser la
théorie élastique des éléments « sandwich
» afin de représenter le plus correctement le comportement des
verres feuilletés.
ð á ð áâ
2(1 + + 2 ) EI s
N = (5.12)
cr K
, 1 2
+ ð â Lk2

2
=
i
2
i n
=
Lk
G b
PVB
( )2
? z i
i n
=
? (5.13) ;
I
i 2 i
=
I s
t EI
PVB s
i n
=
I b t z
s = ? i i
á =
â =
(5.14) ;
2(5.15)
i = 2
Figure 5.3 3 Verre feuilleté avec 2 intercalaires et 3
intercalaires [49]
b = longueur
z = distance entre le milieu de l'intercalaire et le
milieu de la feuille de verre
Une autre approche a été
développée qui tend à généraliser le
comportement mécanique des éléments soumis à une
charge de compression. Dans le cas de verre feuilleté, la section
sandwich pourrait être remplacé par une section monolithique avec
une épaisseur effective donnée par la formule suivante [49].
« Pour des charges de longue durée comme le poids propre ou
pour des températures supérieures à 30°C, la
contribution du PVB peut être
négligée. Le comportement
visco-élastique peut être simplifié par l'utilisation d'un
module de glissement élastique équivalent, ce qui permet un
calcul élastique du système. »[23J :

( 1 + +
á ð áâ
2 )
b ( )
1 2
+ ð â
12 I s
3
=
teff
(5.16)
teff = largeur efficace
á , â , Is
,b ont été expliqués au point
précédent
L'utilisation de cette valeur efficace permet de se rapporter
aux formules relatives à une
seule feuille de verre simple. Il faut
juste remplacer la valeur de b par la valeur de teff et
de
changer tous les termes où la largeur intervient.
5.3.2.3 Résistance à la torsion flexion de
la section cruciforme
De part la géométrie et le mode de fabrication
des éléments vitrés, il semble important et indispensable
d'appliquer la théorie relative aux parois minces à ces
éléments. Il faut donc ajouter cette vérification pour
s'assurer du bon dimensionnement de la structure. Les formules proposées
ici seront celles relatives à la section cruciforme (voir 5.3.1). C'est
la section qui convient le mieux pour ce type de matériau et ce type de
sollicitation. La formule de la capacité portante maximale d'une section
possédant une double symétrie et soumise au flambement en
torsion-flexion est la suivante [33] :
|
N=
cr K
,
|
1 ( ð 2 )
EI w
GK +
i L
0 2 k 2
|
(5.17)
|
i0 = le rayon de giration de la section par
rapport au centre de torsion
K = Inertie de torsion
Iw = Inertie sectorielle principale G
= Module de glissement
Dans le cas d'une section cruciforme, le terme
Iw = 0, ceci permet donc de supprimer toute
la deuxième partie de la formule.
L'inertie de torsion d'une section ouverte est donnée par
la formule suivante :
1
K = ? L e (5.18) 3 i i 3
i
Li = longueur des différents
éléments
ei = épaisseur des
différents éléments
Le module de glissement est une donnée relative de
chaque matériau présent. Dans le cas du verre feuilleté,
le comportement visco-élastique peut être simplifié par
l'utilisation d'un module de glissement élastique équivalent, ce
qui permet un calcul élastique du système.
La rigidité de torsion de Saint-Venant peut donc
être calculée de la manière suivante :
GK = ? GK (5.19)
eff i
i
Dans cette formule, i représente l'ensemble des couches
présentes indépendamment de la nature de leur matériau
(verre et film plastique).
5.3.3 Etat limite de service
Dans le cas de structure en verre soumise à
compression, la seule vérification à faire est une
vérification de la déformée. Ils n'existent pas d'autres
risques ou contraintes concernant l'aspect ou la sécurité des
personnes. Le risque de fissuration ne doit pas être pris en compte dans
le calcul à l'état limite de service car dès qu'une
fissure apparaît, celà mène directement à la
ruine.
5.3.3.1 Deformation
Comme pour l'état-limite ultime, les effets du second
ordre ont un effet important sur la déformé, il faut donc les
prendre en considération.
Concernant la valeur admissible de la flèche, selon la
norme belge NBN B 03-003 [50], la flèche la plus contrainte est celle
relatif au confort visuel. C'est la valeur de la flèche en sommet de
colonne.
h
f = (5.20)
250
h = Hauteur de l'élément
Dans la norme belge, il n'y a pas de dispositions concernant la
flèche maximale au milieu de la colonne. Il faudrait donc prendre les
mêmes dispositions que pour une poutre :
h
f = (5.21)
300
La formule pour déterminer la flèche au milieu de
la colonne si on ne considère qu'une force axiale et tenant compte
également des effets du second ordre est :
e
w = +
cos( k / 2 / cr ) 1 / cr
L N N - N N
w0
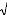
(5.22)
Cette formule est la même que ce soit une feuille de verre
simple ou bien un verre feuilleté. La différence entre les deux
se fait au niveau de la détermination de la charge critique
Ncr .
5.4 Elément fléchis
Dans les structures de bâtiments, la poutre est avec la
colonne l'élément structural le plus
courrant. Sa fonction
principale est de recevoir les charges transversales et de les
transmettre aux colonnes. Même dans le cas d'une flexion
simple d'une poutre, l'élément structurel est également
soumis à un effort tranchant. Dans le cas oü il existe un effort de
compression additionnel, la poutre sera soumise à une flexion
composée.
Dans la classification MCC, les poutres se rangent
dans la classe 2, 3 ou 4 en fonction de l'accessibilité. Le remplacement
de ce type d'élément est donc permis cependant, même
fissurés ces éléments doivent pouvoir reprendre un
certaine quantité de charge.
La flexion induit un effort de compression et de traction au
sein de la section transversale. Lorsqu'il existe des efforts même
partiels de compression, il y a des risques d'instabilités qui peuvent
mener à la ruine. Dans le cas d'une poutre, ce phénomène
qui associe flambement d'axe faible et torsion s'appelle le déversement.
La présence de zones en traction dans un élément
fléchi oblige à tenir compte de la résistance de calcul en
traction du verre pour le dimensionnement car celle-ci est plus faible que la
résistance de calcul en compression.
5.4.1 Design
Les éléments vitrés sont conçus
à partir de feuilles de verre. De plus, l'utilisation de colle n'est pas
recommandée. Ces dispositions constructives limitent donc le choix de
possibilités des sections transversales. La section la plus
adéquate est une poutre en verre feuilleté. Il est vrai que la
matière n'est pas utilisée de manière optimum mais la
facilité de construction du verre feuilleté compense ce surplus
de matière. La matière serait beaucoup mieux utilisée si
elle était concentrée loin du centre de gravité (profil en
I). Cependant, l'utilisation de colle, moins efficace que le verre
feuilleté, pour la réalisation de ces profils limite leur
utilisation.
5.4.2 Etat limite ultime
Dans le cas d'un élément fléchis, plusieurs
vérifications doivent avoir lieur pour s'assurer de la stabilité
de la structure :
- la résistance de la section transversale -
résistance au déversement
- résistance à l'effort tranchant
5.4.2.1 Résistance des sections
transversales
Dans le cas d'une section soumise à une flexion pure, la
formule pour déterminer la charge admissible d'une feuille de verre est
la suivante :
Mrd , y = fg ; t ; d
. W (5.22)
Mrd , y = Moment résistant
W = Module de section élastique du verre
fg ; t ; d = Résistance de
calcul en traction d'une feuille de verre
La résistance à la compression du verre
étant beaucoup plus élevée que celle en traction. La
vérification de la section se fait uniquement au niveau de la section en
traction.
Dans le cas du verre laminé composé de n
feuilles de verre, la formule est identique. La seule différence entre
les deux formules se trouve dans le calcul du module de section
élastique du verreW . En effet, le calcul de l'inertie change
que l'on ait une feuille ou plusieurs. Dans le cas d'une feuille rectangulaire,
l'inertie est égale à bh3/12. Par contre, pour un
verre feuilleté composé de n feuilles identiques, l'inertie est
égale à n.bh2/12. De manière
générale, cette formule s'écrit :
I = ? I (5.23)
tot i
i
En utilisant cette formule, on néglige l'effet du film
plastique entre les feuilles de verre. Cette approximation nous met du
côté de la sécurité.
Au chapitre 3, le mode d'assemblage des feuilles de verre
feuilleté a été expliqué. Des feuilles peuvent
être mis en quinconce afin d'augmenter la portée. Dans ce cas, il
faut vérifier le moment pour chaque section critique et s'assurer de la
résistance tout le long de la poutre.
5.4.2.2 Résistance au
déversement
Le phénomène de déversement se manifeste
lorsqu'un élément fléchis selon son axe fort n'est pas
tenu latéralement, la partie comprimée de sa section peut alors
éventuellement se dérober. Si la section est tenue sur toute sa
longueur, le déversement ne peut pas se produire et il ne faut donc pas
vérifier la résistance au déversement de
l'élément.
De manière générale, la formule de
résistance au déversement s'écrit :
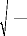
ð 2 EI ? ? ?
? k I kl GK ?
y ( ) (
2 ?
ù
M = C 2 + - + ) (
2 + + )
cr D
, 1 ? ? ? C z C z C z C z
2 g 3 j 2 g 3 j ? (5.24)
( )
kL 2 k I 2
EI
? ? ? ð
? ù y y ? ?
Mcr , D = Moment critique au
déversement
Les termes sont expliqués dans l'annexe A qui est une
copie de l'annexe F de l'eurocode 3. Cette formule donne la valeur du
déversement critique. Cette valeur n'est jamais atteinte pour les
mêmes raisons évoquées pour la charge critique d'Euler en
compression.
Le calcul du moment ultime au déversement d'une poutre en
verre est analogue à celui d'une poutre en acier.
M D , Rd = ÷D .
W . fg ; t ;d (5.25)
MD , Rd = Moment ultime au déversement
W = Module de section élastique du verre
fg ; t ; d = La résistance de
calcul en traction d'une feuille de verre
÷D = Coefficient de réduction
pour le déversement
Les valeurs du coefficient de réduction
÷D sont obtenues, pour une valeur
d'élancement
réduitë , en regardant dans le tableau des
courbes de flambement (voir annexe B). Dans le cas du verre, A. Luible [21]
préconise l'utilisation de la courbe c.
f I
g t d y
, ,
ë = (5.26)
M h
cr D
,
Les termes ont déjà été
expliqués précédemment. L'explication de l'utilisation de
la résistance de calcul en traction du verre est la même que dans
le cas de la compression.
5.4.2.3 Résistance à l'effort
tranchant
Une structure fléchie est toujours soumise à un
moment fléchissant et à un effort tranchant. Il est donc normal
de vérifier la structure à ce type de sollicitation
également. La formule proposée se base sur la formulation des
Eurocode :
V Rd = Anette ( fg ; t ;
d/ 3) (5.27)
VRd = La valeur de calcul de la résistance au
cisaillement
Anette = Aire totale de la section diminuée de la
dimension des trous éventuels
5.4.3 Etat limite de service
Dans le cas de structure en verre soumise à flexion, la
seule vérification à faire est une vérification de la
déformée. Ils n'existent pas d'autres risques ou contraintes
concernant l'aspect ou la sécurité des personnes.
5.4.3.1 Détermination de la
flèche
Concernant la valeur admissible de la flèche, selon la
norme belge NBN B 03-003 [50], la flèche la plus contrainte est celle
relatif au confort visuel. Il existe deux configurations, si la structure est
bi appuyée ou bien si elle est en prote à faux.
L
- Structure bi appuyée f = (5.28)
300
L
- Structure en porte à faux : f = (5.29)
150
L = Longueur de l'élément de la
structure
Ces valeurs sont des limites supérieures de
flèches prescrites par la norme belge et peuvent être plus
contraignantes s'il existe un accord entre le client, le concepteur et
l'autorité compétente.
Cependant, dans un premier temps, augmenter les exigences de
la flèche pourrait être bénéfique. Le verre
possède une image négative (voir chapitre 7.1.4). C'est un
matériau fragile et cassant et il inspire donc peu à la
confiance. Afin de ne pas augmenter ce caractère
d'insécurité, limiter la flèche de manière plus
contraignante peu sembler un choix judicieux.
5.5 Elément comprimé et
fléchis
Dans le cas d'un élément soumis à une
flexion et à un effort axial, le principe est de s'assurer que la
contrainte maximale dans la fibre la plus sollicitée soit
inférieure à la résistance de calcul du verre. Deux
vérifications s'impose la première pour les zones en traction et
la deuxième pour les zones en compression car la résistance de
calcul n'est pas la même dans les deux cas. Ces inégalités
peuvent être modifiées afin de contenir les influences de la
compression et des moments.
Pour les zones en traction :
ómax = fg ; t ; d
(5.30)
Pour les zones en compression :
ómax = fg ; c ; d
(5.31)
Pour les zones en traction :
N N ? e w ? M M
0 ,
+ ? + ? + + = 1 (5.32)
sd y sd z
,
A f W f
. . cos / 2 / 1 /
; ; ; ; , ? . .
g t d g t d ? ? L N EI - N N W f W
f
k cr e ? y g t d
; ; z g t d
; ;
Pour les zones en compression :
N N ? e w ? M M
0 sd y
, sd z
,
+ ? + ? + + =1 (5.33)
A f W f
. . cos / 2 / 1 /
; ; ; ; , ? . .
g c d g c d ? ? L N EI - N N W f W
f
k cr e ? y g c d
; ; z g c d
; ;
Les deux premiers termes prennent en compte l'effort normal
ainsi que le moment secondaire dû à l'excentricité des
charges, les deux suivants prennent en compte la flexion dans les deux
directions principales.
5.6 Actions accidentelles
Les actions énumérées et
développées au-dessus sont les sollicitations principales des
structures. Ils existent d'autres actions qui doivent être
vérifiées dans le cas d'un calcul de structure complet.
Aujourd'hui, vu le caractère novateur des structures en verre, ces
sollicitations exceptionnelles sont encore très peu
étudiées. Les éléments principaux qu'on peut en
retirer sont développés dans ce paragraphe.
5.6.1 Résistance aux chocs
Encore plus que les autres structures, les
éléments en verre peuvent subir des chocs. De part son image
fragile et cassant, le verre est souvent soumis à des actes de
vandalisme (voir chapitre 7.15). Il faut donc s'assurer que la structure puisse
résister suffisamment aux chocs.
Il existe deux types d'essais afin de vérifier la
résistance aux chocs d'un élément en verre. Il s'agit de
l'essai de chocs de corps mous et de l'essai de chocs de corps durs.
L'essai aux chocs de corps mous permet de mettre en
évidence le type de rupture du verre. Il existe trois types
différents de modes de cassures en fonction du type de verre.
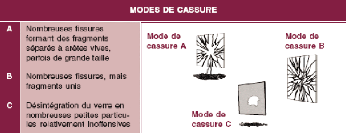
Figure 5.6 1Modes de cassures du verre selon la norme NBN EN
12600 [52]
Dans le cas d'une application structurel du verre, il est
important que le verre possède un mode de rupture au moins de type de B
(caractéristique du verre feuilleté) ou de type C
(caractéristique du verre trempé thermiquement). Afin
d'empêcher des morceaux de verre de se détacher de la structure,
il est bon de prévoir un film plastique sur la face extérieur de
la feuille de verre.
Deux niveaux de classements existent pour la
détermination de la résistance aux chocs de corps durs. Le
premier niveau correspond à l'aptitude des vitrages à
résister aux jets d'objets. L'essai à la chute de bille de 4,1 kg
est satisfait si 3 éprouvettes résistent à la
pénétration (3 impacts en triangle). Le deuxième niveau
correspond aux tentatives d'effraction à l'aide d'une masse ou d'une
hache pour réaliser une ouverture de 40 cm x 40 cm, appelée
"passage d'homme". Le nombre d'impacts nécessaires à sa
réalisation détermine la classe du vitrage.
Dans le tableau suivant (Tableau 5.6.1), une relation a
été établie entre les classes de la norme EN 356 et le
classement MCC. Lors d'une utilisation structurelle du verre, le choix
de la classe du verre est importante, mais celui-ci est déterminé
par deux critères (les mêmes que pour le classement MCC,
voir paragraphe 5.2), l'accessibilité de la structure et le rôle
de l'élément au sein de la structure. Dans le cas de
bâtiments publics, il est possible d'obtenir des verres résistants
à l'onde de choc d'une explosion.
Le classement de la structure, selon le MCC permet
d'avoir une information sur la résistance aux chocs nécessaire
pour ce type d'élément.
Classe MCC
EN356
Niveau 1 :
hauteur de chute (m) de 3
billes
P1 A 1,5 m
P2 A 3 m
P3 A 6 m
P4 A 9 m 1
P5 A 9 m (chute de 9 billes) 2-3
Niveau 2 :
Masse + hache (coups min.)
P6 B 30 coups 4
P7 B 51 coups 5
P8 B 71 coups 6
Tableau 5.6 1 Classement des éléments en verre aux
chocs de corps durs d'après la EN 356
5.6.2 Résistance au feu et gradient thermique
De par sa nature, le verre est un matériau
incombustible. Cependant, des bris par choc thermique peuvent apparaître
s'il existe entre deux zones d'une feuille de verre une différence
importante de température. Si l'élément vitré est
chauffé de matière constante, il y a une dilatation
générale de la pièce. Cependant, si une seule partie de la
pièce est soumise à un changement de température et que
l'autre reste froide alors celle-ci empêchera la libre dilatation et il
se crée alors des contraintes de traction qui peuvent être plus
important que la résistance du verre. Dans ce cas-là, il y a donc
un bris par choc thermique. L'existence et l'apparition de ces gradients
thermiques sont multiples. La résistance à ces bris varie en
fonction du type de verre et logiquement, celui possédant la
résistance la plus grande est le verre trempé car il
possède une meilleure résistance en traction. Voici les valeurs
des gradients thermiques maximales pour les différents types de
verre.
- Le verre trempé : 200°K (EN 12150-1) - Le verre
durci : 100°K (EN 1863-1)
- Le verre recuit : 40°K (EN 572-1)
Il existe des feuilles de verre pouvant résister
à la chaleur comme les verres borosilicatés ou bien les
vitrocéramiques. Ceux-ci ont des coefficients de dilatation proche de
zéro ce qui leur permet de résister au feu pendant près de
4 heures.
A l'heure actuelle, ceci est la seule information sur la
résistance du verre sous l'effet de la température. Aucune
information sur l'évolution du module de Young ou de l'inertie en
fonction de la température n'existe comme c'est le cas dans l'acier ou
bien encore le béton. Il est donc impossible aujourd'hui de dimensionner
un ouvrage, un bâtiment aux normes incendies. Ceci est donc un champ
d'investigation possible pour de futures recherches dans le domaine verrier.
Conclusion du chapitre
Ce chapitre a permis d'expliquer comment on pouvait
déterminer la résistance des différents
éléments en verre comme les colonnes et les poutres. Bien que les
formules utilisées se basent sur la résistance des
matériaux et que l'utilisation de ces formules est courante dans le
monde de la construction, on a pu voir que certaines de ces formules ne
pouvaient pas s'appliquer telle que dans le cas du verre. Des inconnues
subsistent encore dans plusieurs domaines notamment la résistance au
feu. Cependant, ce chapitre donne une bonne vision des formules à
utiliser pour dimensionner une structure en verre à l'état actuel
des connaissances. Ce chapitre permettait donc de déterminer le
deuxième de terme de l'équation de base de la résistance
des matériaux
Ed < Rd
|
Chapitre
|
|
|
6
|
|
|
|
Les assemblages
|
Les assemblages sont des éléments importants
d'une structure, car ils permettent la transmission d'efforts et de
sollicitations d'un élément à un autre. Il existe une
multitude d'assemblages différents que l'on peut regrouper en fonction
du type de matériau et du type de connection.
Dans le cas du verre, les assemblages constituent un
problème important car ils sont le lieu de concentration de contrainte
importante et vu le caractère purement élastique de ce
matériau, des contraintes trop importantes ne peuvent pas être
reprises par une plastification partielle du matériau.
Les différents types d'assemblages seront
expliqués dans ce chapitre afin de donner un aperçu des
différentes méthodes existantes. Cependant, aucune formule ne
sera développée ici car le calcul des assemblages utilise soit
des matériaux différents que le verre, comme l'acier ou bien ils
utilisent des produits (colle par exemple) dont seul le fabricant garanti les
valeurs.
6.1 Assemblage métallique
Dans l'ensemble des solutions qui existe pour les assemblages
de structure en verre, celui des assemblages métalliques occupe une
place de choix. La grande connaissance de ce type de connections permet de
diminuer la charge de travail car ils font référence à des
calculs déjà normalisés dans les eurocodes et
déjà amplement expérimentés.
La particularité de ce type de connections
réside dans l'utilisation d'une couche en caoutchouc entre les feuilles
de verre et le dispositif de connection. La présence de ce
matériau permet de mieux répartir l'ensemble de la charge et
ainsi limiter les concentrations de contraintes.
Tous les calculs des assemblages métalliques d'une
structures en verre sont donc les mêmes que ceux relatifs à la
connection d'éléments métalliques. Il faut juste
prévoir de l'espace pour pouvoir disposer l'élément en
caoutchouc et aussi permettre un jeu entre les différents
éléments en fonction de la tolérance de fabrication.
Cette technique est particulièrement utilisée
pour des poutres en verre (voir exemple chapitre 8). On dispose des sabots
métalliques sur les murs. Entre l'élément
métallique et le verre, on dispose un joint souple afin d'éviter
les concentrations de contrainte.
6.2 Assemblage collé
Contrairement à l'acier, il est impossible de faire des
soudures avec du verre. Une solution alternative est possible avec le collage.
Aujourd'hui, le comportement à court terme des colles est assez bien
maîtrisé, contrairement au long terme. Les assemblages
collés permettent de transférer l'ensemble des efforts de
manière beaucoup plus continue et sur une surface plus grande. Il y a
donc moins de risques de concentration de contrainte dans les
éléments vitrés. Cependant, les colles sont
fabriquées avec des produits toxiques et l'utilisation de ce liant lors
de la fabrication sur chantier implique des mesures de sécurité
encore plus strictes que pour les autres types d'assemblage.
Il existe deux inconvénients majeurs lors de
l'utilisation de colle. Le premier est l'absence de normalisation dans le
domaine, les concepteurs doivent effectuer les essais eux-mêmes. Ce qui
engendre des coûts d'études supplémentaires, ceci est
d'autant plus vrai que les essais doivent tenir compte de l'effet à long
terme et durent donc plus longtemps.
Deuxièmement, une structure collée ne peut pas
être remplacée. Si un élément possède des
bris ou est cassé, il est impossible de le changer sans risquer une
ruine complète.
Actuellement, la conception des éléments
adhésifs est assez complexe, la modélisation de leur comportement
implique l'utilisation de modèles de calcul relativement lourds qui
doivent toujours être validés par des essais en laboratoire.
L'environnement dans lequel se situe la zone d'assemblage
possède également un effet sur le comportement de ce dernier. La
température est un facteur important. Lorsque la température
diminue, les éléments en verre se rétractent et les joints
se rigidifient. Par contre, sous la chaleur, les adhésifs peuvent se
décoller si le coefficient de dilatation thermique est trop
différent de celui des matériaux en place. La présence
d'humidité est aussi néfaste car l'eau par capillarité
peut s'immiscer entre le verre et l'adhésif et rendre ce dernier
totalement inutilisable.
Les assemblages à base de colle permettent un gain de
poids pour la structure. Ils sont aussi intéressant quand il s'agit
d'assembler des éléments relativement minces entre eux.
L'utilisation de colle permet une épuration visuelle, les assemblages
n'existants plus seul la transparence reste.
Le mode d'assemblage par << tenon et mortaise » est
appliqué pour des assemblages de poutres et de colonnes. Cependant cette
technique est seulement réalisable avec du verre feuilleté.
Généralement, les deux feuilles extérieures de la poutre
sont interrompues, tandis que les deux feuilles de verre extérieures de
la colonne sont quant à elles prolongées. Il est donc possible
d'effectuer un emboîtement entre les deux éléments
structurels. L'espace entre les deux éléments est rempli de
résine dont la polymérisation est activée par des lampes
à UV.
Voici une idée des résistances données dans
la fiche technique du << NOVABOND 2 » de la firme Novatio [79], ceci
est une valeur indicative d'un produit particulier:
Résistance à la traction : 210 N/cm2
Résistance au cisaillement : 73 N/cm
L'ensemble des efforts doit donc être
décomposé selon deux axes. Le premier dans le sens du joint de
colle (résistance à la traction) et le second dans le sens
perpendiculaire au joint de colle (résistance au cisaillement).
6.3 Assemblage par connecteur
Des trous sont effectués dans les feuilles de verre et
des connecteurs métalliques relient ces différentes feuilles
entre elles. La résistance de ces éléments
métalliques étant connue et déjà normée, ce
paragraphe se focalisera sur la détermination de la
géométrie des trous et de la charge maximale que le verre peut
reprendre par trou. Les trous sont effectués sur des feuilles de verre
recuit qui sont trempées par après car il n'est pas possible de
découper une feuille de verre trempé.
6.3.1 La géométrie
Il est conseillé de ne pas effectuer des trous dont le
diamètre est plus petit que l'épaisseur d'une feuille de verre
[53]. Les distances admises entre le bord d'un trou et le bord de la feuille,
ou entre deux bords de trous dépendent de l'épaisseur du verre e.
Voici trois figures (Figures 6.3.1) qui indiquent quelles sont les dispositions
géométriques à prendre en considération lors du
façonnage des trous.
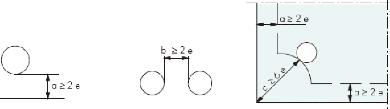
Figure 6.3 1Disposition géométriques à
prendre à considération [53]
Il existe une tolérance par rapport au façonnage
des trous dans une feuille de verre recuit qui est repris dans le tableau
ci-dessous.
Diamètre nominale ø (mm)
Tolérances (mm)
4<ø<20 1
20< ø<100 2
100< ø Consulter le fabricant
Tableau 6.3 1 Tolérance de construction du
diamètre nominale [53]
Lors de la trempe verticale, le verre est
réchauffé puis refroidi rapidement, ce processus crée des
petits déplacements au niveau des pinces par rapport à la
position initiale des trous. Il n'existe pas à l'heure actuelle de
tolérance sur les changements de positions des trous après ce
processus de trempe. Cependant, si on préconise, la trempe horizontale
qui est le procédé utilisé aujourd'hui par les
entreprises, il n'y a pas de déplacements des trous.
6.3.2 La résistance
Une étude a été menée en France
[8] afin de déterminer la résistance du verre dans les zones
d'assemblage. Les auteurs ont décidé lors de cette étude
d'empêcher la décompression du verre dans ces zones, c'est cette
valeur qui est dimensionnante. Ils ont testé différents types de
sections. Pour les trois sections les plus résistantes (voir tableau
6.3.2), ils ont déterminé la valeur de décompression
maximale du verre en fonction de différents couples de serrage (voir
tableau 6.3.3).
|
Désignation
|
Öint (mm)
|
Öext (mm)
|
|
A
|
24
|
40
|
|
B
|
40
|
56
|
|
C
|
30
|
40
|
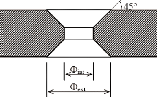
|
Figure 6.3 2 Coupe d'une plaque de verre au niveau d'un trou
[8]
|
Tableau 6.3 2 Géométrie des trous les plus
résistants [8]
|
|
Couple de pré serrage
(daN.m)
|
0
|
1
|
2
|
2.5
|
3
|
|
A
|
69,3
|
69,8
|
71,0
|
-
|
-
|
|
B
|
77,5
|
78,3
|
79,5
|
80,1
|
80,9
|
|
C
|
57,5
|
59,6
|
60,9
|
62,0
|
62,3
|
Tableau 6.3 3 Charges de décompression de la surface (kN)
pour les trois types de trous les plus résistants [8]
Les résultats obtenus dans le tableau sont des valeurs
expérimentales et elles correspondent à une résistance
caractéristique du verre. Il serait prudent de prendre un coefficient de
sécurité sur ces valeurs.
Les valeurs mesurées sont des charges de
décompression du verre trempé elles ne tiennent pas compte de la
résistance du verre recuit. Dans les zones d'assemblages qui sont le
lieu de concentrations de contraintes, ce choix est sécuritaire. Les
valeurs obtenues ont été mesurées par polarimétrie.
C'est la même méthode utilisée par les producteurs pour
garantir les valeurs des contraintes de trempe (voir chapitre 4). Selon la
prénorme européenne pr EN 13474 [60], le coefficient de
sécurité pour les surfaces pré sollicitées
estãM ; v = 1.2.
Conclusion du chapitre
Dans ce chapitre, on a pu voir qu'il existait
différents modes d'assemblage. Actuellement, le mode d'assemblage le
plus souvent utilisée est celui constitué
d'éléments métallique car il existe des normes pour ce
type d'assemblage. Les assemblages collés permettent d'augmenter la
perméabilité de ne plus avoir d'éléments opaque au
sein de la structure. Cependant, ce mode d'assemblage ne nous permet de
remplacer une partie de structure si celle-ci est endommagée. Les
connecteurs métalliques sont utile car ils allient à la fois les
connaissances des connecteurs métalliques mais ils limitent les
connections à quelques éléments ponctuels, la transparence
n'est que très légèrement altéré par la
présence de ces connecteurs. Cependant, les déplacements des
trous lors du processus de trempe pose des problèmes de superpositions
de feuilles de verre trouées. Chaque assemblage possède ses
qualités et ses défauts et le choix du mode d'assemblage doit
faire partie intégrante de la conception de la structure en verre.
|
Chapitre
|
|
|
7
|
|
|
|
Avantages et inconvénients
|
7.1 Inconvénients
7.1.1 Connaissances limitées, l'obligation de faire des
essais
L'utilisation du verre comme élément de
structure est assez très récente. Les réalisations sont
encore assez rares et peu développées. Bien qu'il existe
plusieurs références sur les structures en verre et que les
différentes méthodes de calcul se basent sur la résistance
des matériaux, les essais sont encore très importants. Il existe
énormément de type d'essais pour le verre ayant chacun leurs
propres caractéristiques.
A l'heure actuelle, il n'existe pas de normes ni de code de
calcul pour le dimensionnement des éléments porteurs en verre.
Cette carence, le manque de connaissance du comportement structurel du verre et
le peu de réalisations ne permettent pas encore de valider la conception
d'une structure en verre sans essais. La résistance du verre qui se base
sur des principes probabilistes et le phénomène de fissuration
sous critique sont des valeurs variables. Une prénorme européenne
[60] existe actuellement pour déterminer la résistance de calcul
du verre. Cependant, la résistance du verre diminue avec le temps car il
n'y a pas de plastification dans les zones en traction et les fissures peuvent
donc continuer à se propager même sous un chargement constant
(phénomène de fatigue statique). Ce phénomène est
pris en compte dans la prénorme par le biais d'un coefficient
minorateur.
Dans le paragraphe 5.6, il a été expliqué
que la résistance aux chocs d'une structure en verre n'est
validée qu'après une série d'essais en fonction de la
classe que l'on désire obtenir. Actuellement, c'est la seule
manière d'offrir une garantie suffisante pour la résistance aux
chocs sur une structure en verre.
C'est pour toutes ces raisons qu'il est fortement
recommandé de faire des essais grandeur nature sur une partie de la
structure lors de la construction d'une structure totalement en verre. Ceux-ci
permettent de s'assurer du bon dimensionnement et de la résistance de la
structure. L'effet à long terme n'est pas encore maîtrisé
mais le coefficient de sécurité de 1,8 dans la résistance
de calcul assure une sécurité sur cette valeur.
7.1.2 Matériau fragile
Le verre est un matériau fragile. Cette
caractéristique est très contraignante pour les structures car on
préfère les matériaux ductiles. Ceux-ci se
déforment considérablement avant de se rompre, on a donc le temps
de se rendre compte d'une surcharge éventuelle et surtout d'un
début de rupture. Dans le cas du verre, les grands déplacements
ne sont pas possibles, la rupture du verre survient bien avant car il n'y a pas
de redistribution ni de plastification dans le matériau. Une fois le
mécanisme de rupture atteint, la ruine est quasi instantanée.
Cependant, des chercheurs de l'université de Delft
(P-B) ont mis au point un verre « armé » en analogie au
béton armé. La présence d'armature n'altère presque
pas la transparence de la poutre (Figure 7.1.1). Le béton possède
une faible résistance à la traction et s'il n'est pas
précontraint peut se fissurer très vite. L'apparition de ces
fissures fait chuter considérablement sa résistance, heureusement
dans le cas du béton armé la présente d'armature permet de
reprendre les efforts de traction dès l'ouverture de fissures.

Figure 7.1 1 et Figure 7.1 2 Photographie et coupe d'une poutre
en verre renforcée [47]
Dans le cas du verre « armé », la
présence d'armature permet de reprendre un effort de traction et laisser
le verre travailler en compression. Cependant, tout comme dans le cas du
béton, l'armature intervient dès que le verre est fissuré.
La présence de cette armature augmente la sécurité des
occupants lors de la fissuration du verre et confère au matériau
une certaine ductilité. Cependant, l'aspect visuel de la structure est
altéré par les fissures et ne correspond plus aux attentes de
l'état limite de service (ELS).
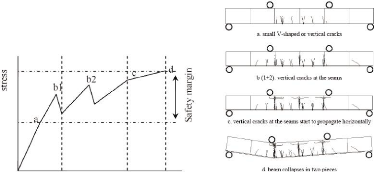
Figure 7.1 3 et Figure 7.1.4 Evolution de la résistance et
des fissures lors d'un chargement d'une poutre renforcée [47]
Il existe différentes solutions d'éléments
composites pour offrir une certaine ductilité aux structures en verre
qui ont été développées par d'autres instituts :
- Fibre de carbone (Palumbo)
- béton-verre (développé par TU Graz)
- bois-verre (dévelopé par l'EPFL)
- Acier-verre (RWTH Aachen et l'université de Dortmund)
L'intérêt d'une structure en verre est la
transparence des éléments porteurs. Si le maître d'oeuvre
désire utilisé ce matériau c'est pour utiliser cette
caractéristique et la mettre en avant. La proposition de
l'université de Delft (TU Delft) a très bien compris l'aspect
architecturale de la structure car l'ajout des éléments en acier
n'altère pas la transparence de la poutre et sa présence n'est
quasi pas remarquée (voir Figure 7.1.1).
7.1.3 Sensible à l'état de surface
La résistance du verre se base sur une théorie
probabiliste qui est fonction du type de microfissures de la surface. Le nombre
de micro fissures et aussi leur géométrie altèrent la
résistance du verre. Il est donc important de protéger au maximum
la surface des feuilles de verre lors des différentes manutentions. Si
on utilise du verre feuilleté pour la réalisation
d'éléments structurel en verre. Il est préférable
de déposer un film plastique sur les feuilles extérieures afin de
les prémunir contre toutes dégradations supplémentaires
liées aux divers frottements.
7.1.4 Effet psychologique
Les structures en verre ne sont pas répandues à
cause de l'image que dégage ce matériau. Tout le monde a
déjà laissé tombé un verre et celui-ci s'est
brisé par contre si on laisse tomber un élément en
métal ou en béton ce dernier ne se rompra pas. Le verre ne
supporte pas les concentrations de contrainte car il ne peut pas redistribuer
les efforts. Quand un verre tombe, il y a une concentration de contrainte au
point de contact entre le verre et le sol qui peut dépasser la
résistance du verre et il y a donc rupture.
L'inquiétude est également présente
dès que l'on utilise un nouveau matériau dans la construction.
Cela a été le même problème pour le métal,
lors de l'inauguration du Crystal Palace à Londres, les responsables ont
demandé de couvrir la structure afin que les invités ne
remarquent pas la finesse de la structure.
De plus, un élément opaque (béton, acier,
bois, ...) offre une impression de matérialité plus importante
qu'un élément transparent où la structure semble
être dématérialisée voir inexistante. Plus un
élément est massif et visible plus il dégage une image de
sécurité.
Les matériaux traditionnels de structure ont
déjà fait leur preuve et montrer qu'ils pouvaient résister
dans le temps aux surcharges. Les structures en verre doivent se
généraliser et résister afin de dégager la
même confiance.
7.1.5 Vandalisme
Les éléments en verre sont victimes d'actes de
vandalisme. C'est à cause de l'image cassante, et de la faible
résistance aux chocs qu'il est facile de faire des dégâts
et de le briser sans trop de difficulté. Les premières
applications de structures en verre sont à l'intérieur de
bâtiments et dans des zones privées afin de limiter l'accès
à des personnes extérieures. Des structures en verre existent
dans des lieux publics, cependant, l'accès aux différents
éléments de la structure par les passants est quasi impossible.
Si la généralisation des structures en verre est possible, il
faut cependant penser à la conception générale du
bâtiment et à la facilité d'atteindre oui ou non un
élément de structure en verre.
L'utilisation de structure dans des lieux publics où il
n'existe pas de véritable contrôle semble être difficile.
Son usage sera limité à des fonctions où son accès
sera difficile voir impossible comme des poutres par exemple.
7.2 Avantages
7.2.1 Capacité portante théorique importante
La résistance théorique du verre est très
important (voir 3.3.1). Cependant, à cause de l'état de surface
celle-ci n'est jamais atteinte. Des études se poursuivent encore
aujourd'hui pour savoir comment on pourrait améliorer cet état de
surface afin de se rapprocher de la résistance théorique du
verre.
De plus, le phénomène de fissuration
sous-critique oblige à utiliser un coefficient réducteur
important en fonction du temps de chargement. Toutes ces mesures bien
qu'obligatoire diminuent fortement la résistance du verre, si on pouvait
trouver des solutions à ces problèmes la résistance du
verre serait considérablement augmentée.
7.2.2 Durabilité, inerte
Le verre est un matériau totalement inerte qui ne
s'altère pas avec le temps, on a retrouvé des morceaux de verre
datant de plusieurs siècles dans un très bon état.
Ils possèdent de très bonnes
caractéristiques face aux agents agressifs. En effet, le verre est
pratiquement insensible à l'eau salée, aux acides forts, aux
solvants organiques, aux rayonnements ultraviolets et à l'eau
oxygénée. Il peut uniquement être sensible aux substances
très alcalines et ce dans des conditions de température et de
pressions très particulières. C'est pour toutes ces raisons que
le verre est utilisé dans l'industrie chimique comme
récipient.
7.2.3 Effet sur l'environnement et recyclage
L'environnement est une question primordiale dans notre
société et les matériaux de construction n'y
échappent pas. Il faut donc tenir compte de l'impact de la fabrication
du verre, de sa durée de vie et de son recyclage.
Si nous considérons tout d'abord la consommation de
matières premières et d'énergie, le verre apparaît
comme un matériau très intéressant. En effet, le verre
peut être recyclé presque infiniment. Les déchets de verre
utilisés sont d'ailleurs devenus indispensables, aujourd'hui, pour la
production du verre flotté, puisqu'ils permettent d'atteindre la fusion
des constituants à une température plus faible. Cela permet donc
une économie d'énergie et donc, aussi, une économie
financière. Cela explique pourquoi le verre est recyclé avec tant
d'efficacité.
Le verre est un matériau transparent qui laisse donc
pénétrer la lumière et les rayons du soleil. Si celui-ci
est bien utilisé, cette particularité permettrait de faire des
économies non négligeables d'éclairage et de chauffage
dans certains locaux.
Contrairement aux autres matériaux de structure, le
verre est inerte et donc reste insensible face aux attaques
atmosphériques et il ne nécessite donc pas de renouvellement
d'une quelconque couche protectrice.
Son entretien se limite à un nettoyage annuel ou
semestriel à l'eau clair. De ce point de vue là, plusieurs firmes
ont mis au point des vitrages autonettoyants en utilisant une couche
transparente pour permettre à l'eau de former un film qui glisse sur la
vitre, ce procédé permet d'éliminer les salissures
minérales. La lumière du jour est elle utilisée pour
décomposer les saletés organiques grâce à une couche
d'oxyde de titane, une fois brûlées, les particules sont
entraînées par la pluie. Dans un environnement intérieur,
l'humidité ambiante peut jouer le rôle de pluie dans une moindre
mesure.
7.2.4 Matériau novateur et nouvelles perspectives
architecturales
Il existe déjà plusieurs matériaux de
construction dont le comportement est bien connu et dont il existe des normes
(béton, acier, maçonnerie, bois, aluminium). Historiquement, ces
matériaux ont été trouvés et mis au point car on
désirait augmenter la résistance des différents
éléments ou bien diminuer le volume de matière à
mettre en oeuvre.
Aujourd'hui, le verre est au centre de plusieurs recherches en
tant que matériau de construction. Il est vrai que sa résistance
théorique est très élevée mais il possède
une rupture fragile.
Cependant, le verre contrairement à tous ces
matériaux possède une caractéristique, une
propriété indéniable : il est
transparent. Cette caractéristique permet d'offrir ce
qu'aucun autre matériau de construction n'a su apporter jusqu'ici.
Depuis plusieurs années, les architectes commencent à demander
qu'on utilise le verre comme matériau de structure. Ceux-ci voient dans
ce matériau et sa principale caractéristique des nouvelles
perspectives pour les bâtiments de demain.
7.3 Tableau comparatif avec le béton, l'acier et
le bois

verre
(trempé)
caractéristiques verre
(recuit)
acier 355 béton
c40/45 bois aluminium
excellente
excellente
moyen mauvais mauvais bon
moyen mauvais mauvais bon
résistance à l'eau salée excellente
aux acides forts excellente
E module de young (N/mm2) 70000
résistance caractéristique à la
compression 600
résistance caractéristique à la traction
court terme (N/mm2) 45
long terme 13,05
masse volumique (kg/m3) 2500
Prix ($)/ tonnes (à titre indicatif) 2000
énergie grise (Gj/m3) 35
énergie grise (Gj/tonne) 14
|
70000
|
210000
|
27000
|
9000
|
70000
|
|
600
|
355
|
40
|
22
|
275
|
|
120
|
355
|
8
|
22
|
275
|
|
90
|
355
|
8
|
22
|
275
|
|
2500
|
7950
|
2500
|
900
|
800
|
|
2000
|
500
|
|
|
|
|
35
|
300
|
5
|
1
|
500
|
|
14
|
50
|
2
|
2
|
184
|
Tableau 7.3. 1 Tableau comparatif avec les autres
matériaux de constructions
Conclusion du chapitre
Le verre comme tous les matériaux possède des
qualités et des défauts. Sa rupture fragile et sa
résistance variable en fonction du temps sont des défauts qui
condamnerait n'importe quel autre matériau de construction. Mais la
principale qualité du verre est son caractère transparent dont le
monde architecturel est friand. Grâce à cette demande de plus en
plus importante, des études sont menées afin de réduire
les effets négatifs du verre. Cependant, un des inconvénients
reste l'effet psychologique du verre et sa faible résistance aux chocs.
Ce matériau inspire peu à la confiance en tant que
élément de structure. Mais, cette image changera, avec la
généralisation de ce type de structure. De plus, son impact pour
l'environnement est limité, son recyclage est maîtrisé
depuis longtemps et connaît une très grande efficacité.
Comparé aux autres matériaux, sa résistance à la
compression est très élevée, elle n'a jamais
été une limite à son utilisation. La résistance en
traction dépend elle du temps de chargement, il faut faire attention aux
hypothèses de départ que l'on prend pour ce type de structure. Le
verre laisse donc entrevoir de belles perspectives d'utilisations grâce
à ces qualités mécaniques et surtout à sa
qualité visuelle mais si ce matériau possède des
défauts non négligeables, cependant les chercheurs mettent au
point des méthodes afin d'en diminuer les effets négatifs.
|
Chapitre
|
|
|
8
|
|
|
|
Exemples de réalisation
|
8.1 Tableau des différents exemples
Le tableau ci-dessous donne une idée synthétique
des différents éléments en verre et types de connections
présents dans les exemples expliqués afin de donner une vision
d'ensemble. Les exemples ont été choisis afin de mettre en
évidence les différentes possibilités du verre comme
élément de structure. Ils existent des exemples de prototype de
structure en verre comme des treillis ou des dômes entièrement en
verre mais ces différents éléments ne sont pas mis dans
des situations d'utilisation quotidienne. La quête d'information sur les
différents exemples s'est avérée être très
difficile car les structures en verre constituent un nouveau défi et
chacun veut garder ses secrets de construction. Il est donc pas étonnant
de voir que le bureau d'architecte et le bureau d'étude soit les
mêmes pour les deux ouvrages en France. A l'heure actuelle, il n'existe
que quelques bureaux spécialisés dans ce type de structure.
|
Exemple Colonne
en verre
|
Poutre
en verre
|
Assemblage par élément métallique
|
Assemblage
par collage
|
Assemblage
par
connecteur
|
Saint-Germain-
en-Laye X X
Centre de
recherche du X X
Louvre
Passerelle
Rotterdam X X X X
Apple store
(New York) X X X X
Pavillon X (murs
Rheinbach en verre) X X
Tableau 8.1 1 Composition des différents
éléments structurels en verre dans les différents exemples
traités
8.2 Centre administratif, Saint-Germain-en-Laye, FR
.
Il s'agit d'un centre administratif situé dans la ville
de Saint-Germain-en-Laye, près de Paris (France). La pièce dans
laquelle se trouvent les colonnes en verre est un bureau paysager. Les colonnes
sont en forme de croix. Ces éléments sont reliés au reste
de la structure par des assemblages en métal pourvu d'une couche de
caoutchouc. Ce bâtiment a été conçu par le bureau
d'architecture « BRUNET & SAUNIER ARCHITECTES »[15]. Le bureau
d'étude qui s'est occupé du dimensionnement s'appelle OTH, il
s'agit d'un bureau français. Les colonnes ont une hauteur de 3,4m et de
250 mm de large. Les charges peuvent atteindre 3.9t sans neige (valeurs
données sur le site du bureau d'architecture). Les concepteurs ont
prévu une feuille de verre supplémentaire de contour afin de
prévenir tout risque lors d'un choc sur une des feuilles.

Figure 8.2 1 [15]
Figure 8.2 2 [15]
Les assemblages sont réalisés par des
éléments en acier recouverts d'une feuille de caoutchouc qui
relient la colonne en verre au reste de la structure métallique.

Figure 8.2 3 [15] Figure 8.2 4 [15]
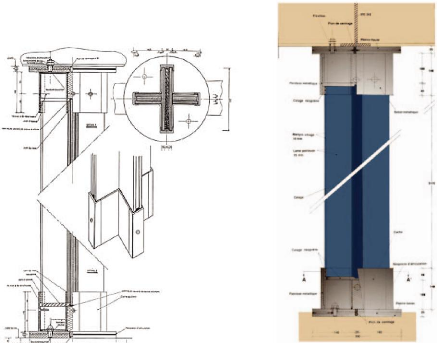
Figure 8.2 5 [15] Figure 8.2 6 [15]
8.3 Centre de Recherches et de Restauration des
musées de France, Paris, FR.
Les poutres de la toiture en verre du Centre de Recherche et
de Restauration des Musées de France sont en verre. Ce bâtiment
est situé au Louvres à Paris. Le bureau d'architecture et le
bureau d'étude sont les même que celui du bâtiment de
Saint-Germain-en-Laye, il s'agit du bureau « BRUNET & SAUNIER
ARCHITECTES » et de OTH. Le bâtiment a été
réalisé en 1994. Le projet comporte 11 poutres en verre pouvant
supporter chacune 14 tonnes (valeurs données sur le site du bureau
d'architecture [15]). L'utilisation de ces poutres a permis la création
d'une dalle de verre de 64m2. Les poutres sont reliées au
reste de la structure à l'aide de sabots métalliques. Les poutres
sont composées de 4 feuilles de verre de 15mm et possède une
portée de 4m de long.

Figure 8.3 1 [15] Figure 8.3 2[15]
On peut voir la vue de l'intérieur du bâtiment
grâce à l'utilisation d'une structure en verre (Figure 8.3.2), la
quantité de lumière qui pénètre est plus
importante. Sur la photographie de droite (Figure 8.3.2), on peut voir
l'utilisation des sabots métalliques.

Figure 8.3 3 [15] Figure 8.3 4 [15]
Ces deux images sont intéressantes. Celles de gauche
(Figure 8.3.3), on voit le préjugé d'un passant qui n'ose pas
s'aventurer sur les éléments en verre sûrement à
cause de l'image cassante de celui-ci. Sur l'autre image (Figure 8.3.4), les
deux architectes profitent de leur création. Sur l'image ci-dessous
(Figure 8.3.5), il s'agit de deux détails de la poutre en verre et du
sabot métallique.
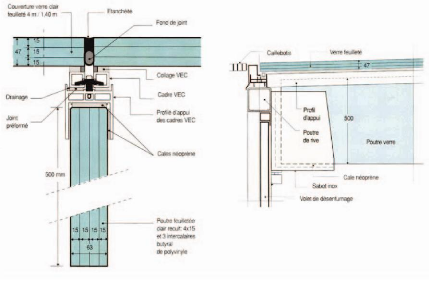
Figure 8.3 5 [15]
8.4 Passerelles en verre, Rotterdam, NL .
Il s'agit d'une passerelle en verre situé à
Rotterdam. Lors de leur expansion, le bureau d'architecture a acheté un
immeuble voisin au sien. Cependant, il n'y avait pas de façade commune.
Afin de permettre un passage entre les deux ailes du bureau sans devoir sortir,
les dirigeants ont décidé de créer une passerelle en
verre. La passerelle est composée de deux parties. La première
qui comprend les éléments de reprise de charge. La structure
comprend deux poutres à inertie variable correspondant au diagramme des
moments et d'un tablier en verre. La deuxième partie comprend les
protections par rapport au vent et à la neige. Il s'agit de trois
feuilles de verre refermant la boîte.
La portée de cet ouvrage est de 3.5m. Les deux poutres
sont composées de 3 feuilles de verre de 10mm chacune. Les panneaux de
verre possèdent une épaisseur de 15mm. Cet ouvrage a
été réalisé en 1994 par le bureau d'architecture
propriétaire des deux immeubles à savoir « KRAAIJVANGER
URBIS » [43], le bureau d'étude était ABT. Les assemblages
des différentes feuilles ont été réalisés
à l'aide de connecteurs en acier, un joint de silicone permet
d'éviter les pénétrations d'eau.
Figure 8.4. 1[78] Figure 8.4. 2 [43]
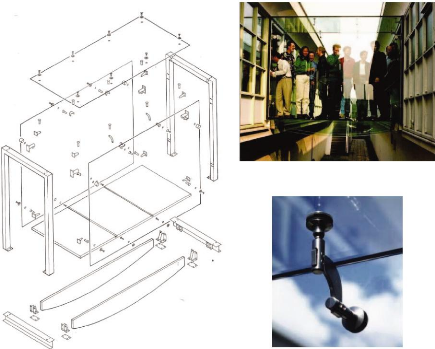
Figure 8.4.2 [43]
Sur la photographie en haut à droite (Figure 8.4.2), il
s'agit de l'inauguration de la passerelle entre les deux bâtiments. Les
personnes n'ont pas l'air rassurées sur cette photographie, ceci est
encore dû à l'image cassante du verre. L'image de gauche (Figure
8.4.1) donne une vue éclatée des différents
éléments qui constitue la structure, on peut notamment voir les
deux sabots métalliques de chaque coté qui sont utilisés
pour assembler les deux poutres principales à la structure des deux
bâtiments. Sinon comme on peut le voir sur la troisième image
(Figure 8.4.3), les assemblages se font à l'aide de connecteurs
métalliques.
8.5 Apple Store 5th avenue, New York, USA
La firme Apple spécialisé dans l'informatique
joue un rôle important dans le développement des structures en
verre. Plusieurs de ces magasins possèdent des éléments en
verre. Le bureau d'architecture est « BOHLIN CYWINSKI JACKSON >> et
le bureau d'étude est « Eckersley O'Callaghan >>. Le plus
récent, l'Apple store de New York situé sur la
5ème avenue, est un bâtiment dont l'entrée est
entièrement en verre. C'est ce partenariat qui a conçu l'ensemble
des différents magasins Apple. Il s'agit d'un cube de 10m de
côté, la portée des éléments a
été obtenue en disposant les feuilles de verre en quinconce. Pour
obtenir cette longueur, il a fallu travailler avec des autoclaves de longueurs
plus importantes qui ne sont pas utilisés par l'industrie
verrière.
L'escalier en colimaçon qui permet de descendre
à l'étage inférieur est également en verre.
L'assemblage entre les marches et le garde-corps se fait à l'aide de
connecteurs métalliques disposés entre les feuilles
extérieures des marches (voir Figure 8.5.3).
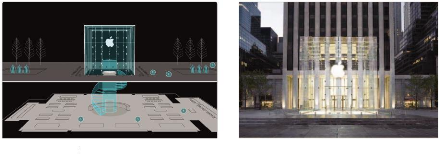
Figure 8.5. 1 [27] Figure 8.5. 2 [27]

Figure 8.5. 3 [27] Figure 8.5. 4 [27]
Sur la photographie de gauche (Figure 8.5.3), on peut voir que
les connecteurs qui relient l'escalier à la paroi en verre sont
intégrés à l'intérieur des marches en verre.
L'ensemble des feuilles de verre intérieur aux marches est plus court
afin d'y disposer les connecteurs.

Figure 8.5. 5 [27]
Cette photographie (Figure 8.5.5) permet de se rendre compte
de l'effet et des perspectives des structures en verre. L'ensemble de la
toiture a d'abord été monté sur le sol afin de faciliter
les manipulations (Figure 8.5.6).

Figure 8.5. 6 [27] Figure 8.5. 7 [27]
8.6 Pavillon en verre, Rheinbach,ALL .
Cet ouvrage se situe en Allemagne à Rheinbach. Cet
ouvrage a été construit par l'institut de construction
métallique de l'université d'Aix la chapelle et par le bureau
d'architecture « Marquardt & Hieber ». Le pavillon mesure 32.5m
de long et 15 m de large. Les charges verticales et horizontales sont reprises
par des éléments en verre. L'ensemble des
éléments
vitrés verticaux est composé de boîtes de
verre d'une dimension de 3.8m sur 1.5m. Les panneaux de ces boites sont
composés de 3 feuilles de verre 2 de 10mm à l'extérieure
et une feuille de 19 mm eu centre. Les colonnes en verre sont fixées au
sol par des éléments en acier.

Figure 8.6 1[64] Figure 8.6 2 [64]
Figure 8.6 3 [64] Figure 8.6 4 [64]
8.7 Autres exemples
Différents photographies seront montrées dans ce
paragraphe afin de donner un aperçu des autres possibilités
(prototypes et structures déjà réalisées) des
structures en verre. Les exemples ne seront pas détaillés. Pour
le lecteur intéressé, la référence sera à
chaque fois indiquée.
Ce projet est situé en Australie à Brisbane plus
particulièrement. Ce projet a été dessiné par un
bureau new-yorkais Front- INC [36].

Figure 8.7. 1 Vue d'ensemble du projet [36] Figure 8.7. 2 Arc de
la structure en verre [36]
L'université de Delft a réalisé deux
prototypes en verre, un dôme et un pavillon en taille réduite.

Figure 8.7. 3 Prototype de dôme en verre [14] Figure 8.7.4
Prototype de pavillon tout en verre [14]
|
Chapitre
|
|
|
9
|
|
|
|
Le projet d'architecture
|
9.1 Programme
Le projet d'architecture de cette année
académique 2007-2008 s'inscrit dans un programme plus vaste qui
s'étend sur l'ensemble du cursus universitaire. Il constitue un travail
de synthèse des différentes thématiques architecturales
rencontrées au fil des années.
- la forme
- la fonctionnalité - la spatialité
- la visibilité
- la contextualité ...
En plus de toutes ces contraintes, une demande a
été faite pour introduire ce projet au sein du travail de fin
d'étude. Dans mon cas, il s'agissait d'utiliser le verre comme
matériau de structure.
Le programme du projet concerne la rénovation de la
station de métro et de futur R.E.R Schuman à Bruxelles. Ce projet
s'inscrit dans une logique de la S.T.I.B. (société de transport
intercommunale bruxellois) de vouloir rénover l'ensemble de ces stations
les plus vétustes.
Le cas de la station Schuman est légèrement
différent des autres et cela pour deux raisons essentielles. Tout
d'abord, plusieurs lignes de chemins de fer du nouveau R.E.R. (réseau
express régional) passeront par cette gare. Il y a un désir de
fusionner les deux entités à savoir la gare ferroviaire et la
station de métro de Schuman afin de créer un véritable
pôle multimodal. Cette volonté se voit également dans les
projets en surface de la STIB et le parcours prévu et modifié de
certaines lignes de trams et de bus. De plus, la station Schuman est au centre
des différents bâtiments de la communauté
européenne. Celle-ci se doit d'offrir un nouveau visage de
modernité aux usagés. Cette nouvelle station représentera
l'Europe au près des bruxellois, et Bruxelles auprès des
institutions européennes.
La contextualité
Bruxelles a depuis plusieurs années connu un nouvel
essor. La venue de institutions européennes lui a conféré
un statut de ville mondiale de premier plan et de capital de l'Europe.
L'ensemble de ces institutions s'est regroupé au sein d'un même
quartier, au rond point Schuman. La station de métro Schuman a
été mise en service en 1969 et depuis elle n'a jamais subi de
rénovation. Aujourd'hui, cette station se situe au centre du quartier
européen et est l'une des stations les plus utilisées. Cependant,
son caractère vétuste ne renvoie pas l'image d'une ville capitale
de l'Europe. C'est une station en souterrain qui manque de
visibilité.
Cette station est bordée par plusieurs artères
importantes comme la rue de loi par exemple. Une majorité des voiries
environnantes a été restauré afin de redorer l'image de
Bruxelles auprès des institutions européennes, la prochaine
étape est celle de la restauration de la station de métro qui
s'inscrit dans une logique de restauration - construction du quartier.
Le programme
Le projet comprend la rénovation du 1er sous-sol de la
gare Schuman, au niveau des guichets. La conception au niveau de cet
étage d'un ensemble de commerces. La rénovation des
différentes circulations verticales, l'installation de systèmes
accès pour les personnes à mobilité réduite. Un
nouveau portail d'entrée pour la station. L'objectif principal du projet
est d'offrir une importante visibilité à la station. La nouvelle
station ne sera pas seulement un lieu de passage, grâce à
l'implantation de zones de commerces. Il doit être possible d'envisager
des postes de contrôle d'accès et de sortie du métro. La
STIB envisage de mettre des dispositifs de contrôle d'accès aux
rames de métro sur l'ensemble de son réseau afin de lutter contre
la fraude.
9.2 Esquisses et plans
L'idée générale du projet était de
créer un véritable puit de lumière afin d'apporter de la
lumière naturelle au sein de ce premier niveau de sous-sol de la station
Schuman. Le volume souterrain de la station se trouve au milieu de la place
entre le rond point et le début de la sortie du tunnel rue de la Loi.
Cependant, actuellement les principaux accès à cette station se
trouvent éloignés de cet espace central.
En créant un nouvel élément au dessus de
cet espace central, on répond à deux objectifs. Tout d'abord, on
offre un volume supplémentaire qui permet d'apporter la lumière
au niveau du sous-sol. Ensuite, ce nouveau bâtiment offre une nouvelle
visibilité à la station. Cependant, ce nouveau volume oblige
à le munir de circulations verticales supplémentaires.
Les façades du projet seront également en verre.
Celles-ci seront tenues à l'aide de feuilles de verre mise
perpendiculairement qui agiront comme une poutre face à l'effet du vent
sur les façades.
Sur le plan de structure (Figure 9.2.1), il y a trois
éléments plus foncés, ce sont ces
éléments-là qui feront l'objet du dimensionnement.

Figure 9.2. 1 Structure du projet en 3d
9.3 Dimensionnement de colonnes et poutres en verre
Les calculs de résistance se porteront exclusivement
sur les éléments porteurs en verre (colonne et poutre). Le calcul
d'assemblage aborde d'autres aspects et ceux-ci ne seront donc pas
abordés dans ce travail de pré dimensionnement. Les
éléments porteurs en verre sont tous des verres trempés
thermiquement et feuilletés, si l'épaisseur l'exige.
Dans le chapitre 4, sur la résistance du verre, il a
été expliqué que la résistance du verre variait en
fonction du temps, il est donc important de savoir pour quelle durée de
vie la bâtiment est prédestinée. Il s'agit d'un
bâtiment de classe 3 selon l'Eurocode 1 [29]
« Structures de bâtiments et autres structures
courantes ». Sa durée de vie est donc de 50 ans.
Les calculs relatifs aux colonnes et aux poutres seront
précédés du numéro de l'équation auxquels
ils se réfèrent.
9.3.1 Dalle de toiture
La toiture est composée d'éléments de
vitrage de 3m x 2m qui sont portés par des poutres secondaires qui
elles-mêmes rejoignent les poutres principales
.
Le dimensionnement des éléments en verre
chargé hors de leur plan n'est pas le travail de ce mémoire. Afin
d'obtenir une épaisseur de vitrage indicative pour pouvoir effectuer la
descente de charge, les calculs seront faits de manière analogue
à celui d'un calcul de dalle. Les calculs ne tiendront compte que du
moment et de la flèche de la dalle.
9.3.1.1 Les actions
La toiture du projet est classée d'après l'Eurocode
1 en catégorie H :
« Toitures inaccessibles sauf pour l'entretien normal,
les réparations, la peinture et les réparations mineures »
[29]
La neige
D'après l'eurocode 1, la charge de neige dépend de
l'altitude. A Schuman, on se trouve en dessous de 100m d'altitude. La norme
prévoit de prendre une surcharge :
sk = 0.5 kN/m2
Le vent
Pour le vent, j'ai choisi une valeur de : wk
=0.7 kN/m2 Le poids propre de dalle de verre
L'épaisseur de la dalle de verre est de 0.03 m. Il s'agit
d'un verre feuilleté et trempé de 3 couches de 1 cm. Sachant que
le verre a une masse volumique de 2500 kg/m3 = 25
kN/m3
gdalle = 0.03 25 = 0.75 kN/m2 Les
surcharges d'exploitation
La toiture doit pouvoir est classée en catégorie H,
elle doit donc pouvoir soutenir des surcharges d'exploitation
qk = 0.75 kN/m2 charges
réparties Qk = 1.5 kN charge ponctuelle
9.3.1.2 Le système statique
Les dalles reposent sur des deux poutres secondaires
espacées de 2m. Il s'agit d'un système isostatique pour chaque
dalle.
Figure 9.3 1 Schéma statique et chargement de la dalle
de toiture
9.3.1.3 Dimensionnement Etat Limite Ultime :
- Sollicitations
|
Les actions réparties variables
|
Coefficient
partiel
|
Larg. de
bande (m)
|
Valeur par mètre
courrant kN/m
|
|
Neige
|
sk = 0,5 kN/m2
|
1,5
|
1
|
0,75
|
|
vent
|
wk = 0,7 kN/m2
|
1,5
|
1
|
1,05
|
|
Charges
d'exploitation
|
qk = 0,75kN/m2
|
1,5
|
1
|
1,125
|
|
Les charges réparties permanente
|
|
|
|
|
Poids propre
|
gdalle = 0,75kN/m2
|
1,35
|
1
|
1,0125
|
|
Total
|
|
|
|
3,93
|
Les actions ponctuelles variables Coefficient partiel
Valeur kN
Charges d'exploitation
variables Qk = 1,5 kN 1,5 2,25
Total 2 ,25
Le moment sollicitant vaut donc : Msd = 3,93
22/8 + 2,25 2/4 = 3,09 kNm -
Résistance de calcul du verre (voir chapitre 4)
kmod, combi
1,35 0,75 1,5
× +
( 0,75 0,7 0,5
+ + )
La présence des plusieurs actions avec des durées
de chargement différentes oblige calculer un k
mod,combi expliqué à la formule (4.6).
= =0,325
0,75 0,75 0,7 0,5
1,35 + 1,5 + 1,5 + 1,5
0,29 0,74 0,74 0,43
La formule (4.8) donne la valeur de la résistance de
calcul à long terme en traction du verre.
|
fg t d = ; ;
|
0,325 1 45 1 120 45 70,625 /
× × × ( )
-
+ = kN
1,8 1,2
|
mm
|
2
|
- Résistance de la section :
Mrd = fg ; t ; d . W
= 70,625.0,032.1/6 = 10,59 kNm
Msd = 3,09 kNm <
Mrd = 10,59 kNm ok !
Etat limite de Service : - Sollicitations
|
Les actions réparties variables
|
Coefficient
partiel
|
Larg. de
bande (m)
|
Valeur par mètre
courrant kN/m
|
|
Neige
|
sk = 0,5 kN/m2
|
1
|
1
|
0,5
|
|
vent
|
wk = 0,7 kN/m2
|
1
|
1
|
0,7
|
|
Charges
d'exploitation
|
qk = 0,75kN/m2
|
1
|
1
|
0,75
|
|
Les charges réparties permanente
|
|
|
|
|
Poids propre
|
gdalle = 0,75kN/m2
|
1
|
1
|
0,75
|
|
Total
|
|
|
|
2,7
|
Les actions ponctuelles variables Coefficient partiel
Valeur kN
Charges d'exploitation
variables Qk = 1,5 kN 1 1,5
Total 1,5
- Flèche
4 3 4 3
f =
mm
5 pl 1 2,7 2
Pl 5 × 1 1,5 2
×
+ = + = 5,15
3 3
384 EI 48 EI 384 1 0,03 48
× 1 0,03
×
70000 × 70000×
12 12
- Flèche admissible
L
f =
max
= 2000 6,66
= mm
300 300
- Vérification
f = 5,15 mm = f max =
6,66mm ok !
9.3.2 Poutre de toiture P.Sec.1
Lors du dimensionnement des poutres, celles-ci sont
supposées être tenues latéralement. Cette condition permet
de s'affranchir de la vérification au déversement. La poutre
secondaire de toiture est de classe 2 d'après le MCC (chapitre
5.2).
9.3.2.1 Les actions Actions de dalle :
Charges réparties variables (voir détails dalle) :
0,5 + 0,7 + 0,75 kN/m2 Charges réparties permanentes (voir
détails dalle) : 0.75 kN/m2
Charge ponctuelle variable (voir détails dalle) : 1.5
kN/m2
|
Poids propre de la poutre et section
La poutre secondaire a une section efficace de 6cm de large
pour une hauteur de 25cm. La poutre est composée de 6 feuilles de verre
trempé de 1cm et de 5 intercalaires plastiques de 0,38 mm. Entres les
feuilles, un intercalaire d'une épaisseur de 0,38 mm sera
placé.
gpou ,sec = 0,06 m.0,25m.25 kN/m3 = 0,375
kN/m
|
|
Figure 9.3. 2 Section de la poutre
secondaire
9.3.2.2 Le système statique
Les poutres secondaires entre distantes de 2m relient les
poutres principales entre distantes de 6m. C'est un système isostatique.
La charge ponctuelle est une charge d'entretient, elle doit donc se trouver
à l'endroit le plus défavorable de la poutre, dans ce cas-ci, il
s'agit du milieu de la poutre.
Figure 9.3 3 Schéma statique de la poutre secondaire
9.3.2.3 Dimensionnement Etat Limite Ultime :
- Sollicitations
|
Les actions réparties variables
|
Coefficient
partiel
|
Larg. de
bande (m)
|
Valeur par mètre
courrant kN/m
|
|
Neige
|
sk = 0,5 kN/m2
|
1,5
|
2
|
1,5
|
|
vent
|
wk = 0,7 kN/m2
|
1,5
|
2
|
2,1
|
|
Charges
d'exploitation
|
qk = 0,75kN/m2
|
1,5
|
2
|
2,25
|
|
Les actions réparties permanente
|
|
|
|
|
Poids propre
|
gdalle = 0,75kN/m2
|
1,35
|
2
|
2,025
|
|
Poids propre
poutre secondaire
|
gpou ,sec = 0,375 kN/m
|
1,35
|
|
0,506
|
|
Total
|
|
|
|
8,38
|
Les actions ponctuelles variables Coefficient de
sécurité Valeur kN
Charges d'exploitation
variables Qk = 1,5 kN 1,5 2,25
Total 2 ,25
Le moment sollicitant vaut donc : Msd = 8,38
62/8 + 2,25 6/4 = 41,09 kNm -
Résistance de calcul du verre
La détermination du
kmod,combi est la même que pour le cas de la
dalle : kmod,combi = 0.325
La formule (4.8) donne la valeur de la résistance de
calcul à long terme en traction du verre.
0,325 × 1 × 45 1 ×
= 70, 625 kN /
1,8 1,2
f=
g ; t ;d
(
120 -45
)
2
mm
- Résistance de la section (d'après la
formule (5.22)):
Mrd = fg ; t ; d .
W = 70,625.0,06.0,252.1/6 = 44,14
kNm
Msd = 41,09 kNm <
Mrd = 44,14 kNm ok !
La poutre a une portée de plus de 4m. Il faut donc
vérifier s'il est possible d'avoir des feuilles de verre trempé
de plus de 4m ou bien, il faut vérifier les sections critiques. La
juxtaposition de deux feuilles est une section critique car on ne peut pas
considérer que l'ensemble de la section travaille en flexion à
cet endroit.
- Résistance à l'effort tranchant
(d'après la formule (5.27)) :
VRd = Anette ( fg ; t
; d / 3 ) = 0,06.0,25.70625/ 3 = 611,
63kN
Vsd = 26,26kN
Vérification : sd 26,26
V = kN < Vrd =
611,63kN ok !
Etat limite de Service :
- Sollicitations
Les actions réparties variables Coefficient Larg.
de Valeur par mètre
partiel bande (m) courrant kN/m
Neige sk = 0,5 kN/m2 1 2 1,0
vent wk = 0,7 kN/m2 1 2 1,4
Charges
qk = 0,75kN/m2 1 2 1,5
d'exploitation
Les actions réparties permanente
Poids propre gdalle = 0,75kN/m2 1 2 1,5
poutre secondaire gpou ,sec = 0,375 kN/m
Poids propre 1 0,375
Total 5,775
Les actions ponctuelles variables Coefficient partiel
Valeur kN
Charges d'exploitation
variables Qk = 1,5 kN 1 1,5
Total 1,5
- Flèche
|
f =
|
4 3 4 3
5 pl 1 5,775 2
Pl 5 × 1 1,5 2
×
+ = + = 19,05
3 3
384 EI 48 EI 384 0,06 0,25 48
× 0,06 0,25
×
70000 × 70000 ×
12 12
|
mm
|
- Flèche admissible (d'après la formule
(5.28))
L = 6000 20
f = = mm
max 300 300
- Vérification
f = 19,05 mm = f max = 20mm
ok !
La vérification de la résistance aux chocs est
validée par différents essais. Comme la poutre est de classe 3,
elle devra être au moins classée P5 A selon la EN 356.
9.3.3 Poutre de toiture P.princ.1
Les poutres principales sont soutenues par deux colonnes.
L'ensemble des surcharges de toitures est ramené sur la poutre
principale par l'intermédiaire des poutres de secondaire. Les forces
à prendre à considération sont donc le poids propre et
l'ensemble des charges dû aux poutres secondaire. La poutre principale de
toiture est de classe 3 d'après le MCC (chapitre 5.2).
9.3.3.1 Les actions
Effort des poutres secondaires :
- Surcharge permanente (p.p dalle + poutre secondaire) : 1,5 +
0,375= 1,875 kN/m - Surcharge variable (neige + vent + exploitation): 1 + 1,4
+1,5 = 3,9 kN/m
|
Poids propre de la poutre
La poutre a une section efficace de 10 cm de large et une hauteur
de 65
cm pour une portée de 12m.La section est composée
de 4 feuilles de 25 mm chacune.
g pou , princ = 0,1 m.0,65 m.25
kN/m3 = 1,625 kN/m
|
|
|
Figure 9.3.4 section de la poutre
principale
|
9.3.3.2 Le système statique
La poutre principale mesure 16m de long. La distance entre
appuis est de 12m, il y a un porte-à-faux de 2m de chaque coté.
C'est un système isostatique. Les poutres principales sont entre
distantes de 6m. Le cas de charge le plus défavorable est celui
où il n'y a que les charges permanentes en bout de porte-à-faux
et l'ensemble des surcharges entre les appuis dues aux poutres secondaires. Il
y a 7 poutres secondaires centrales dont deux qui arrivent directement sur les
appuis et deux poutres secondaires de rives, sur le schéma, il n'est pas
représenté la charge répartie due au poids propre. (Figure
9.3.3).
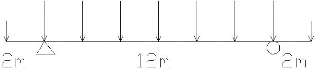
Figure 9.3 4 Schéma statique de la poutre principale
9.3.3.3 Dimensionnement
Etat Limite Ultime :
- Sollicitation
Poutre secondaire de rive seulement chargée avec
les charges permanentes :
0,75 kN/m (2 fois une demie dalle) + 0,375 kN/m (p.p. de la
poutre sec) = 1,125 kN/m La force ponctuelle agissant en bout de
porte-à-faux = 1,125 kN/m.6m.1,35 = 9,11 kN Poutres secondaires
centrales chargées avec l'ensemble des surcharges :
[1,5 kN/m (dalle) + 0,375 kN/m].1,35.6 + [1 + 1,4 +1,5].1,5.6=
50,29 kN Poids propre:
g pou , princ = 1,625 kN/m . 1,35 = 2,19
kN/m
Le moment sollicitant vaut donc :
Le moment sollicitant est décomposé en deux parties
:
Premièrement, le moment dû au poids propre : M
sd , G pou , princ = 2,19
(122-4.22)/8 = 35,04 kNm Deuxièmement le moment
dû aux autres charges :
Msd = 8. 9,11 + 2. 50,29 + 4. 50,29 - 6. 134.835 =
434,39 kNm
= 469,43 kNm
Msd , tot
- Résistance de calcul du verre (d'après la
formule (4.8)):
La détermination du
kmod,combi est la même que pour le cas de la dalle :
kmod,combi = 0.325
|
f =
g ,t,d
|
0,325 × 1 × 45 + 1 × ( 120 -45 ) = 70,625
kN/
1,8 1,2
|
mm
|
2
|
- Résistance de la section (d'après la
formule (5.22)):
Mrd = fg ; t ; d . W
= 70625.0,1.0,652.1/6 = 497,31 kNm
Msd = 469,43 kNm <
Mrd = 497,31 ok ! -
Résistance à l'effort tranchant (d'après la formule
(5.27)):
VRd = Anette ( f g; t ;
d / 3 ) = 0,1.0,65.70625/ 3 = 2650,39kN
Vsd =
93,375kN
Vérification : sd 93,375
V = kN < Vrd =
2650,39kN ok !
Etat Limite de Service :
- Sollicitation
Poutre secondaire de rive seulement chargée avec
les charges permanentes :
0,75 kN/m (2 fois une demie dalle) + 0,375 kN/m (p.p. de la
poutre sec) = 1,125 kN/m La force ponctuelle agissant en bout de
porte-à-faux = 1,125 kN/m.6m. = 6,75 kN
Poutres secondaires centrales chargées avec
l'ensemble des surcharges : [1,5 kN/m (dalle) + 0,375 kN/m].6 + [1 +
1,4 +1,5].6= 34.65 kN
Poids propre :
gpou , princ = 1,625
kN/m
- Flèche :
Le calcul des flèches est séparé en deux.
Premièrement, le calcul sera effectué pour l'ensemble des charges
ponctuelles. Deuxièmement, le calcul sera effectué pour le poids
propre. Les deux flèches seront additionnées et comparées
à la valeur admissible.
Pour l'ensemble des charges ponctuelles (effectué par
intégrale de Mohr voir Annexe C pour le détail du calcul):
4349,92
Flèche des charges ponctuelles : fponct = = 27,15
mm
0,1 0,65 3
×
70000 ×
12
qL L
2 ( 5 24
2 - c 2 2 2 2
) 1,625.12 5.12 24.2
( - )
=
Flèche charge répartie : f =
rep
= 2,37mm
3
384 EI 0,1.0,65
384.70000.
12
- Flèche admissible (d'après la formule
(5.28)) :
L
f =
max
12000 40
= = mm
300 300
- Vérification
f = 29,52 mm = fmax =
40mm ok !
La vérification de la résistance aux chocs est
validée par différents essais. Comme la poutre est de classe 3,
elle devra être au moins classée P5 A selon la EN 356.
9.3.4 Colonne C 2.1
La colonne a une hauteur de 2,5 m. La colonne principale est de
classe 4 d'après le MCC (chapitre 5.2).
9.3.4.1 Les surcharges
Le poids propre et section de la colonne
|
Comme tout élément structurel le poids propre de
la structure est à prendre en compte en considération lors du
dimensionnement. Il s'agit d'une colonne en croix composée de 6 feuilles
de 25mm
Gcol = (0, 4.0,15 (0, 4 0,15).0,15).2,5.25 =6,09kN
|
|
|
|
|
|
Figure 9.3.4 Section de la colonne
Les surcharges verticales
Surcharges variables : [0,5+0,7+0,75].6.2 + [(1 + 1,4 +1,5).6
.7]= 187,2 kN
Surcharges permanentes :
[1,125 kN/m.6m.2 (nombre de poutre de rive) ] +
[(1,5 kN/m + 0,375 kN/m).6.7(nombre de poutres centrales)] = 92,25
kN
9.3.4.2 Le système statique
Il s'agit d'un élément en compression,
encastré en pied et en tête. Ceci afin de limiter la longueur
caractéristique de flambement. La colonne a une hauteur de 2,5m
9.3.4.3 Dimensionnement Etat Limite Ultime
- Sollicitation :
|
Nsd = 280,8 +24,54 + 8,22 = 214,8kN 2
|
Gcol =6,09.1,35= 8,22 kN Qvar = 187,2.1,5=
280,8kN Qperm = 92,25.1,35=124,54kN
|
|
|
- Résistance de calcul du verre (d'après la
formule (4.8)) :
|
fgt d = ; ;
|
0,29 × 1 × 45 + 1 × ( 120 - 45 ) = 69820
kN/
1,8 1,2
|
mm
|
2
|
- Résistance au flambement (voir chapitre
5.3)
Il faut déterminer la largeur de verre équivalente
grâce à la formule (5.16). Avant cela, il faut déterminer
les 3 paramètres présents dans cette formules (5.13) ;(5.14) et
(5.15)
Is =5.0,4.0,025.0,025382 =
3,220722 .10^-5 m4 á = 6.0,35.0,0253/12.1/
Is =0,097
2
i
=
t PVB EI s
0,00038 70000.0,0000322 = 0, 000016
â=
2 29160.0,35.5.0,025382 1,25
2
12 Is ( 1 + á +
ð2áâ)
b( 1 + ð2â)
=0,102m
i =n
Lk
G PVBb
( ? zi)2
3
=
teff
On peut donc considérer une section monolithique en verre
dont l'épaisseur est de 0,102m Valeurs caractéristiques pour la
section efficace (d'après les formules (5.6) et (5.7)):
Aeff =(0, 4.0,102 (0, 4 0,102).0,102)= 0,0712
m2
Ieff = (0,4.0,1023/12 +
0,102.0,43/12) = 5,79 10^-4 m4 N euler
, eff =3,142.70000.(5,79.10^4) /(2,5/2)2=
255,75 kN
ó euler,eff = 255,75/(0, 4.0,102+(0,
4-0,102).0,102)= 3,6 MPa
- Par la méthode du coefficient de réduction
(d'après les formules (5.10)):
K=
N cr K =
,
1 ( )
GK
2 = 880,6 kN
i0
1
3
69,820 4,4
ë = =
3,6
La valeur du coefficient de réduction doit être
déterminée sur la Figure 5.3.4 d'après l'élancement
réduit. La valeur de l'effort normal résistant réduit est
calculé d'après la formule (5.9).
Nrd = 0,075.0,0712.69850 = 372,99 kN -
Par l'effet du second ordre (d'après la formule (5.8))
:
La flèche initiale est de 0,003mm/mm, il s'agit d'une
colonne de hauteur 2,5m, la flèche initiale vaut donc 7,5mm.
Concernant l'excentricité, comme cela a
été expliqué dans le travail, cette valeur est choisie par
l'ingénieur. Pour cet exercice, l'excentricité vaudra 1/10 de la
plus grande des dimensions de la section.
214,8 214,8 ? 0,04 0,0075 ?
ó = #177; ? + ?
4
0,0712 5,79.10 - cos(2,5/ 2 214,8/ 70000.5,79.10 ) 1 214,8/
255,75
- 4
? -
? ? ?
0,2
ó = 9,46MPa = 69,85MPa
- Parois minces (d'après les formules (5.17) et (5.18))
:
5,79.10
-4
i = = 0,09
0 0,0712
G = 29160MPa
3 -
( 0,4.0,102 2. 0,149.0,102 3 2,46.10 4
+ ( ) ) =
Vérification :
214,8 kN < min{372,99 kN ;880,6kN }
La vérification de la résistance aux chocs est
validée par différents essais. Comme la colonne est de classe 4,
elle devra être au moins classée P6 B selon la EN 356.
Conclusion
Le verre est un matériau présent en abondance
dans notre environnement. Cependant, son application en tant que
matériau de structure est tout récente. Ce travail a
été axé sur la création d'un manuel et sur la
recherche d'éléments de réponse pour la conception et la
réalisation de cette nouvelle utilisation du verre.
L'évolution de l'architecture a montré
l'intérêt de l'utilisation de vitrage, toujours grandissant, chez
les professionnels de la construction. Auparavant, les fenêtres
permettaient seulement de faire pénétrer la lumière.
Aujourd'hui, celles-ci intègrent des jeux de lumière et de reflet
limités aux seules façades. Malgré des résistances
de plus en plus élevées, les matériaux traditionnels sont
opaques et empêchent donc la lumière de pénétrer
pleinement dans le bâtiment. Une structure transparente offrirait donc un
nouvel élan à l'architecture contemporaine en permettant de
créer des effets de lumière au sein même des
bâtiments et de dématérialiser totalement les
structures.
Le verre possède des qualités
intéressantes d'un point de vue mécanique. Cependant, son
caractère fragile a longtemps empêché son utilisation. Lors
de concentration de contrainte importante, les matériaux
élasto-plastique peuvent plastifier tandis que le verre à cause
de son caractère fragile laisse les fissures se propager. Ce
phénomène appelé « fatigue statique » engendre
une diminution de la résistance en traction du verre en fonction du
temps sous un chargement constant. De par son mode de fabrication, la section
des feuilles de verre est assez limitée. Des traitements existent
aujourd'hui pour améliorer la résistance mécanique du
verre et pour augmenter l'épaisseur des éléments en
verre.
Son caractère fragile empêche d'utiliser le
maximum de la capacité de résistance. La durée de
chargement et l'état de surface sont deux caractéristiques qui
interviennent dans la détermination de la résistance du verre
recuit par l'intermédiaire de coefficients minorateur. Le verre
trempé est un matériau précontraint, il possède une
réserve de résistance équivalente aux contraintes de
trempes qui permet d'augmenter considérablement la résistance
grâce au principe de superposition.
Les formules de résistance des poutres et colonnes se
basent sur la résistance des matériaux. Cependant, des
ajustements doivent être faits pour pouvoir utiliser ces formules dans le
cas du verre.
Les assemblages sont le lieu de concentration de contrainte.
Dès lors, les concepteurs préfèrent utiliser des autres
matériaux que le verre (colle et éléments
métalliques) pour réaliser les différentes connections.
L'effet psychologique est un élément important
d'une structure. Il y a une certaine appréhension vis-à-vis de ce
matériau à des fins structurel. Ceci est dû à
l'image que possède le verre à savoir celle d'un matériau
cassant et peu résistant. Mais au fil des utilisations de plus en plus
importantes et diverses, cette image changera. A cause de cette idée et
de sa faible résistance aux chocs, le verre est souvent victime d'actes
de vandalisme. L'utilisation du verre est plus propice pour des structures
secondaires où les sollicitations sont moindres ou dans des espaces plus
privés. L'impact du verre sur l'environnement est assez limité,
son recyclage est maîtrisé depuis longtemps et connaît une
très grande efficacité. Sa principale qualité et raison
d'utilisation reste sa transparence.
Organigramme pour le dimensionnement d'une
poutre
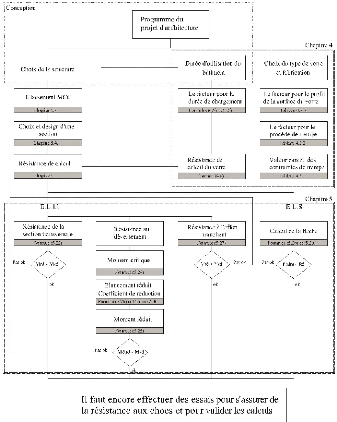
Deux organigrammes qui montrent la démarche à
suivre pour le dimensionnement des éléments structurels en verre
ponctuent ce travail. Ces deux figurent synthétisent les
différentes étapes à effectuer pour le calcul de
structure. Seuls les colonnes et les poutres ont été
analysées car ce mémoire ne traitait que ces deux types
d'éléments. Dans ces organigrammes, les différentes
instructions sont indiquées dans les rectangles. Ceux-ci sont
complétés avec la référence de la
formule, du tableau et/ou de la figure correspondant. Les tests sont quant
à eux mis dans des losanges. Certaines cellules sont regroupées
ont sein d'un même cadre. Ces cadres généraux font
référence à des chapitres du travail ou à la phase
d'avant projet.
Organigramme pour le dimensionnement d'une
colonne
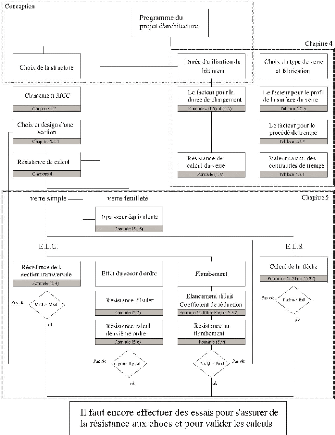
Le verre laisse donc entrevoir de belles perspectives
d'utilisations grâce à ces qualités mécaniques et
surtout à sa qualité visuelle. Les domaines de recherchent sont
multiples. La résistance au feu, la résistance des
éléments fissurés, des assemblages transparents ou la
viabilité de ce type de structure sont autant de questions qui restent
à l'heure actuelle encore sans réponses.
[1]
[2]
[4]
[6]
[8]
[9]
[11]
[13]
[15]
Bibliographie
ADDIS, Bill <<The art of the
structural Engineer », Londres : Artemis, 1994
AUCH-SCHWELK, Hegger et ROSENKRANZ, Fuchs
<'Construction Materials Manual», Munich : Birkhäuser,
2006
BALKOW, D. SCHITTICH, C., SCHULER, M., SOBEK, W. et
STAIB, G. <' Construire en verre », Lausanne :
Presses Polytechniques et universitaires romandes, 2001
BALKOW, D. SCHITTICH, C., SCHULER, M., SOBEK, W. et
STAIB, G. <' Glass Construction Manual 2nd revised
and expanded edition», Basel : Birkhäuser, 2007
BALTHASART, Claude << Conception d'une
véranda en verre
structurel », mémoire de fin d'étude,
Liège : Université de Liège, 2003
BEER, B. <'Innovative glass
structures-A focus on specialist coatings and interlayers » issu du
rapport Glass Processing Days 2007, p50 - p56 , 2007
BELIS, J. <'Kipsterkte van monolithische
en gelamineerde glazen liggers » thèse de doctorat, Gand,
Université de Gand, 2005
BERNARD, F., CARRE, H. et DAUDEVILLE, L.
<' Le verre structural maîtrise du comportement pour une
conception optimal» Rapport final, 2005
BERNARD, F., DAUDEVILLE, L. et GY, R. <'
Calcul des contraintes résiduelles dans les zones d'assemblages de
plaques en verre trempé » issu de Mécanique et
Industries 6(1) : p.55-p.64, 2005
[10] BERNARD, F., DAUDEVILLE, L. et GY, R.
<'Une mesure des contraintes pour le contrôle en service
des structures en verre» issu de Instrumentation Mesures
Métrologie. 4(3-4) : p.89-p.104, 2004
[11] BERNARD, F., DAUDEVILLE, L. et GY, R.
<' Sur le dimensionnement des structures en verre trempé
» issu de la Revue française de génie civil, volume X -
n°X, 2001
[12] BERNARD, F., DAUDEVILLE, L. et GY, R.
«Vers une procédure de contrôle des structures
en verre trempé» issu de Mécanique et Industries. 5(3)
: p.265-p.273, 2004
[13] BOS, F. « Towards a combined
probalistic/consequence-based safety approach of structural glass members»
issu de la revue HERON, vol. 52 (1/2) p 59- p 86, TU Delft, Delft, 2007
[14] BOS, F., NIJSE, R., ROMEIN, T. et VEER, F.
«The evaluation of the all transparent pavilion project»
issu du rapport Glass Processing Days 2005, p1 - p5 , 2005
[15] BRUNET SAUNIER, bureau d'architecture
http://www.brunetsaunier.com/
[16] CARRE, Hélène <<
Etude du comportement à la rupture d'un matériau fragile
précontraint : le verre trempé », thèse de
doctorat, Paris, Ecole nationale des ponts et chaussées, 1996
[17] CRISINEL, M. « Stabilité
des éléments porteurs en verre» Rapport Scientifique,
2004
[18] CRISINEL, M. « Structures en
verre recherches en cours à l'ICOMEPFL » Tracès
n°17, p14-p19, 2004
[19] CRISINEL, M., LAUFS, W. et LUIBLE, A.
« Introduction à l'utilisation du verre comme élément
porteur dans les bâtiments modernes » Lausanne : Ecole
Polytechnique fédérale de Lausanne, 2003
[20] CRISINEL, M. et LUIBLE, A. «
Buckling design of glass element under compression » issu du rapport
International Symposium on the Application of Architectural Glass 2004, 2004
[21] CRISINEL, M. et LUIBLE, A. «
Design of glass beams subjected to lateral torsional buckling»
Proceedings of the IABSE Symposium "Responding to Tomorrow's Challenges in
Structural Engineering", Budapest, Hungary, September 2006, published by IABSE,
Zurich, p. 42-43 + CD-Rom.
[22] CRISINEL, M. et LUIBLE, A. «
Plate buckling of glass panels » issu du rapport Glass Processing
Days 2005, p1 - p4, 2005
[23] CRISINEL, M et LUIBLE, A. «
Rapport scientifique : Stabilité des éléments porteurs en
verre » Lausanne : Ecole polytechnique fédérale de
Lausanne, 2004
[24] DELINCE, Didier, ZARMATI, Gauthier et BELIS,
Jan << Utilisation du verre feuilleté dans les
applications structurales rapport final » Bruxelles : Centre
scientifique et technique de la construction, C.S.T.C., 2007
[25] DELMEE, Robert et MENGEOT, Pierre
« Vers une application structurale du verre feuilleté Etude et
modélisation du comportement composite en flexion simple »,
mémoire de fin d'étude, Louvain-laNeuve : Université
Catholique de Louvain, 2005
[26] DUFFAURE-GALLAIS, I. « La
spectaculaire évolution du vitrage multifonction » Le Moniteur
n°5184- 4 avril p58-p62 2003
[27] ECKERSLEY O'CALLAGHAN, structural design
http://www.eckersleyocallaghan.com
[28] EN 12600 :2003 « Verre dans la
construction - Essai au pendule - Méthode d'essai d'impact et
classification du verre plat » CEN, 2003
[29] EN 1991-1 : 1994 « Eurocode 1 :
Bases de calcul et actions sur les structures », CEN, 1994
[30] EN 1991-1 : 1994 « Eurocode 3 :
Calcul des structures en acier », CEN, 1994
[31] EN 356 : 2000 « Verre dans la
construction - Vitrage de sécurité - Mise à essai et
classification de la résistance à l'attaque manuelle »
CEN, 2000
[32] EN 572-1:2004 « Verre
dans la construction - Produits de base : verre de silicate sodo-calcique -
Partie 1 : Définitions et propriétés physiques et
mécaniques générales » CEN, 2004
[33] ESPION, B. « Parois Minces »
syllabus de cours, Université Libre de Bruxelles, Bruxelles,
année académique 2007-2008
[34] FELDMANN,M., KASPER, R. et SEDLACEK,
G. « Das biegedrillknickverhalten von Glasträgern aus
Verbundglas» Berlin, Stahblau n°3, mars 2007
[35] FREY, François «Analyses
des structures et milieux continus» Lausanne : Presses Polytechniques
et universitaires romandes, 2000
[36] FRONT Inc., specialist façade
consulting practice http://www.frontinc.com/
[37] GUILLEMET, Claude « Evolution des
méthodes photoélastiques verrières » Verre, vol.
8, n°4, juillet août 1994 p 292-297
[38] GUILLEMET, Claude «
Photoélasticité du verre» Power point issu de la
conférence de Berlin : Springer-Verlag, 1993.
[39] HALDIMANN, M. « Flexible,
Consistent and Safe Design of Structural Glass Element » issu du
rapport Glass Processing Days 2005, p 1 - p 5 , 2005
[40] HALDIMANN, M. « Fracture strength
of structural glass elements- Analytical and numerical modelling, testing and
design » thèse de doctorat, Lausanne : Ecole Polytechnique
fédérale de Lausanne, 2006
[41] HAULOT, Valentin « Le verre en
tant que matériau structurel : le point de vue de l'ingénieur
architecte », mémoire de fin d'étude, Liège :
Université de Liège, 2001
[42] HOBBELMAN, G.J., VEER, F.A. et WURM,
J. «The design, construction and validation of a structural
glass dome» issu du rapport Glass Processing Days 2003, p1 - p3 ,
2003
[43] KRAAIJVANGER URBIS, architecture,
intérieur, urbanisme http://www.kraaijvangerurbis.nl/
[44] LAUFS, W., LUIBLE, A. et MOHREM, R.
« Etude préliminaire sur le verre comme
élément de construction dans le bâtiment »
Lausanne : Ecole polytechnique de Lausanne, 2001
[45] LOUTER, P.C. « Adhesively bonded
reinforced glass beams » issu de la revue HERON, vol. 52 (1/2), p
31-p 58 TU Delft, Delft, 2007
[46] LOUTER, P.C., RIJGERSBERG, H., RUYTENBEEK, D.,
VEER, F.A. et ZUIDEMA, J. «Composite glass beams, the third
chapter» issu du rapport Glass Processing Days 2003, p307 - p310 ,
2003
[47] LOUTER, P.C., ROMEIN, T., SCETTERS, L., van
HERWIJNEN, F. et VEER, F.A. «Experimental research on scale
1:8 models of an 18m reinforced glass beam » issu du rapport
International Symposium on the Application of Architectural Glass (ISAAG)
2006
[48] LUDWIG & WEILER, ingénieur
conseil http://www.ludwig-weiler.de/
[49] LUIBLE, A. « Stabilität von
tragelementen aus glas » thèse de doctorat, Lausanne : Ecole
Polytechnique fédérale de Lausanne, 2004
[50] NBN B 03 -003 :2003 «
Déformation des structures - Valeurs limites de déformation -
Bâtiments », 2003
[51] NIJSSE, Rob « Glass in structure
» Basel : Birkhäuser, 2003
[52] NIT 206 « Protection
mécanique de la menuiserie et des vitrages contre l'effraction »
CSTC (Centre scientifique et technique de la construction),
décembre 1997
[53] NIT 214 « Le verre et les
produits verriers -Les fonctions des vitrage» CSTC (Centre
scientifique et technique de la construction), décembre 1999
[54] O'CALLAGHAN, J. « A case study
of the Apple computer stores - Glass structures 2001-2005» issu du
rapport Glass Processing Days 2005, p 1 - p 4 , 2005
[55] O'CALLAGHAN, J. «Structural
bearings in holes in glass» issu du rapport Glass Processing Days
2005, p469 - p472 , 2005
[56] O'CALLAGHAN, J. et COULT, G. « An
all glass cube in New York city» issu du rapport Glass Processing
Days 2007, p98 - p 101 , 2007
[57] PASTUNINK, J.R. et VEER, F.A. «
Developing a transparent tubular laminated coulmn» issu du rapport
Glass Processing Days 1999, p 277 - p 280 , 1999
[58] PIMPURNIAUX, Claude « Le verre en
tant qu'élément de construction » paru dans A+
p109-p114
[59] PIMPURNIAUX, Claude « Le verre
structurel » note d'une conférence donnée à
l'Institut Supérieur d'Architecture Victor Horta
[60] prEN 13474-1:1999. « Glass in
building - Design of glass panes - Part 1: General basis of design. »
CEN, 1999.
[61] RICE, Peter et DUTTON, Hugh « le
verre structurel, 2ème éd mise à jour et
augmentée. » Paris : Le Moniteur, 1995
[62] SAGOT, F. « Des vitrages
multifonctions » Le Moniteur n°4957 -18 septembre p57-60,
1998
[63] SAGOT, F. et MIGUET, L. « Des
vitrages multifonctions » Le Moniteur n°5184- 4 avril p62-p74
2003
[64] SEDLACEK, G. et WELLERSHOFF, F. «
Glass pavilion Rheinbach- Stability of glass columns » issu du
rapport Glass Processing Days 2003, p 316 - p 318 , 2003
[65] SCHOLZE, H. « Le verre : nature,
structure et propriétés 2ème éd. »
Paris : Institut du verre, 1980
[66] TAVERNIER, M. et ZARMATI, G. «
Etude de l'influence de la température sur le comportement
structurel du verre feuilleté », mémoire de fin
d'étude, Louvain-la-Neuve : Université Catholique de Louvain,
2006
[67] TIMOSHENKO, S. « Théorie
de la stabilité élastique » Paris et Liège,
Librairie Polytechnique CH. Béranger, 1943
[68] TU DELF, université de Delft, Glass
& Transparency, http://www.bk.tudelft.nl/
[69] VAN WETTER, Anne « Etude de
comportement de poutres mixtes en bois et verre liées statiquement
», mémoire de fin d'étude, Bruxelles :
Université Libre de Bruxelles, 2002
[70] VEER, F.A. « Developing a
Transparent Tubular Column Laminated » issu du rapport Glass
Processing Days 1999, p 277 - p 280, 1999
[71] VEER, F.A. « The strength of
glass, a nontransparent value » issu de la revue HERON, vol. 52
(1/2), p87-104 TU Delft, Delft, 2007
[72] «Avis Technique 2/05-1172 Raidisseurs et poutres
en verre: STRUCTURA SUPPORT » Centre Scientifique et Technique du
Bâtiment CSTB, 2007
[73] « Les différents types de verre de
sécurité et leurs applications dans le bâtiment»
Fédération de l'industrie du verre, juillet 2003
[74] « Rapport d'activités 2005 : centre
scientifique et technique de la construction » C.S.T.C.
[75] « Rapport d'activités 2006 : centre
scientifique et technique de la construction » C.S.T.C.
[76] « Renseignement sur le matériau «
verre » » Fédération de l'industrie du verre
[77] « To make the world a brighter place »
brochure d'information de Glaverbel
[78] « Structural use of glass in buildings »
, The Institution of structural Engineers, publié par SETO, Londres
1999.
[79] «Novabond 2 » Fiche technique du produit
Novabond 2 de la firme Novatio®
Annexe A (copie de l'annexe F de l'Eurocode
3)


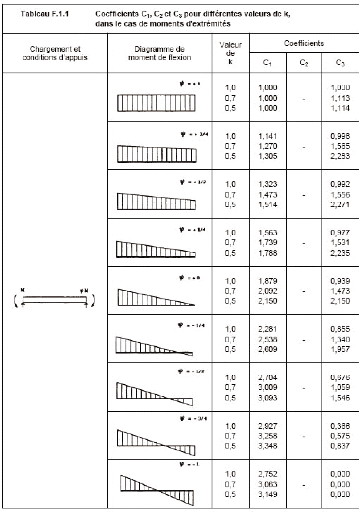
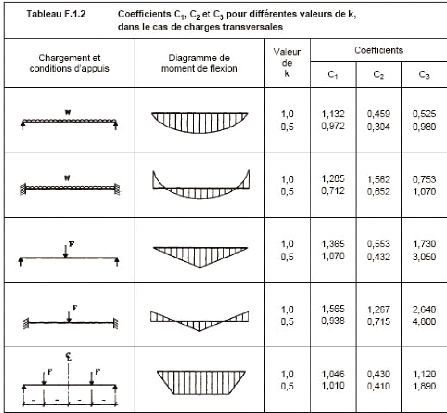
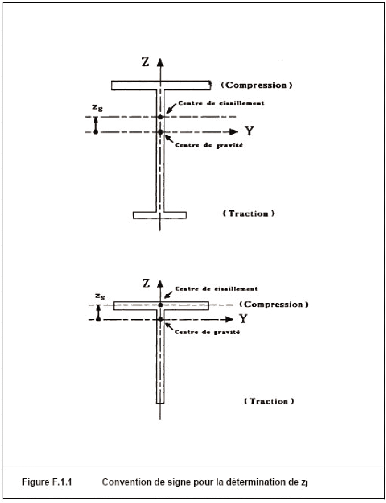

Annexe B
Tableau A.B donnant les valeurs du coefficient de
réduction en fonctions de l'élancement réduit. Dans le cas
du verre, il faut regarder la courbe c. Ce tableau est issu de l'Eurocode 3 :
Calcul des structures en acier. ENV 1993-1-1 : 1992 p.98
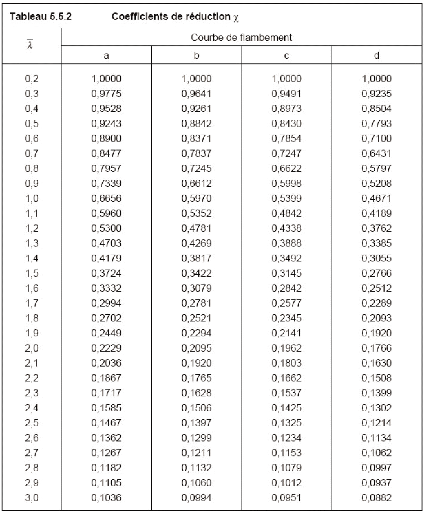
Annexe C
Détermination de la flèche de la poutre principale
du projet pour les charges ponctuelles. La flèche a été
calculée par intégrale de Mohr.
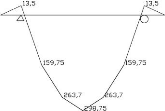
Figure A.C 1 Allure du moment dû aux charges
ponctuelles

Figure A.C 2 Allure du moment pour une charge ponctuelle de 1
centré au milieu de la poutre
J'ai décidé d'effectuer une simplification pour
alléger les calculs. Dans le premier diagramme (Figure A.C 1), le moment
ne coupe pas à l'appui mais près de celui-ci a une distance de
0.15 m afin de d'alléger les calculs j'ai considéré que le
moment passait par l'appui.
intervalle Calcul Résultats
[0-2] 0 0
|
[2-4]
|
2.159,75.1
|
106,5
|
|
3
|
|
[4-6] 2.1. ( 2.159,75 263,7 ) 2.2. ( 159,75 2.263,7 )
+ + +
6
[6-8] 2.2. ( 2.263,7 298,75 ) 2.3. ( 263,7 2.298,7 )
+ + +
6
[8-10] 2.2. ( 2.263,7 298,75 ) 2.3. ( 263,7 2.298,7 )
+ + +
6
[10-12] 2.1. ( 2.159,75 263,7 ) 2.2. ( 159,75 2.263,7 )
+ + +
6
|
652,5 1415,96 1415,96 652,5
|
|
[12-14]
|
2.159,75.1
|
106,5
|
|
3
|
[14-16] 0 0
Total 4349,92



