EM-OCL : une extension mathématique d'OCL

Table des figures

1.1	Modèle UML de la structure de données Pile	13
1.2	Modèle UML d'une compagnie	14
1.3	Le package Types représentant le méta-modèle des types supportés par OCL . .	14
1.4	Les types collectifs en OCL	16
2.1	Le méta-modèle des types EM-OCL	26
2.2	Graphe de classes de la bibliothèque EM ajoutée à OCL	34
3.1	Modèle initial tiré à partir de la spécification initiale	46
3.2	Second modèle après premier raffinement	47
3.3	Troisième modèle après deuxième raffinement	49
3.4	Quatrième modèle après troisième raffinement	52
3.5	Cinquième modèle après quatrième raffinement	54
3.6	Accès Personne/Bâtiment	57
3.7	Deux diagrammes d'objets rspectant l'invariant global	58
3.8	Système bancaire simple	60

Liste des tableaux

3.1 Modèle mathématique correspondant à une association UML 59

Table des matières

Table de figures Liste de tables Introduction Générale			1 3 8
1	La conception par contrats en UML/OCL		9
	1.1	Généralités sur la conception par contrats	9
	1.2	Le langage OCL	10
		1.2.1 OCL langage sans effet de bord	10
		1.2.2 OCL est un langage basé sur la logique des prédicats du 1er ordre . . .	10
		1.2.3 L'approche fonctionnelle du langage OCL	11
		1.2.4 Exemples	12
	1.3	Mécanisme de typage dans le langage OCL	14
		1.3.1 Les types collectifs en OCL	15
	1.4	Travaux liés à OCL	21
2	Une extension d'OCL : EM-OCL		25
	2.1	Augmentations liées au package Types	25
		2.1.1 Description de nouveaux types	26
		2.1.2 Conformité des types	28
		2.1.3 Règles de bonnes utilisations des nouveaux types	30
	2.2	Augmentations liées à la bibliothèque standard d'OCL	32
		2.2.1 Conception d'une bibliothèque mathématique	32
		2.2.2 Opérations offertes par la bibliothèque EM	34

3 Quelques utilisations potentielles d'EM-OCL 43

3.1 Notion de raffinement 43

3.2 Le raffinement en EM-OCL 44

3.2.1 Spécification initiale 44

3.2.2 Premier raffinement 47

3.2.3 Deuxième raffinement : Introduction des portes 48

3.2.4 Troisième Raffinement : Introduction des voyants lumineux 51

3.2.5 Quatrième raffinement : Introduction des lecteurs de cartes 53

3.2.6 Discussion 56

3.3 Validation d'un diagramme de classes 56

3.3.1 Approche de validation proposée 56

3.3.2 Exemple 56

3.4 EM-OCL en tant que langage de requêtes 59

3.4.1 Formulation en OCL 60

3.4.2 Formulation en utilisant EM-OCL 60

3.4.3 Comparaison 60

Conclusion et Perspectives 62

A Annexe mathématique 63

A.1 Logique fondamentale 63

A.2 Ensemble 64

A.3 Tuple 64

A.4 Relations 64

A.4.1 Opérations sur les relations 65

A.4.2 Itérations 65

A.4.3 Restrictions 66

A.5 Fonctions 66

B Annexe de la bibliothèque EM 67

B.1 Pair 67

B.2 SetRef 67

B.3 SequenceRef 67

B.4 BinaryRelation 68

Introduction Générale

OCL [10] [11](Object Constraint Language), est un langage déclaratif basé sur la logique du premier ordre. Il est de plus en plus utilisé pour décrire des contraintes formelles des modèles UML en s'inspirant de la conception par contrat [1] [2] (précondition, postcondition et invariant). En outre, OCL est utilisé au niveau méta-modélisation afin de décrire d'une façon formelle les règles de bonne utilisation (Well-formedness rules) des langages de modélisation comme UML et les profils UML.

Mais OCL présente des insuffisances vis-à-vis de son utilisation dans les domaines suivants : développement incrémental des diagrammes de classes basé sur la technique de raffinement, à l'instar des méthodes formelles comme B [3] [7] et Event-B [21], validation des diagrammes de classes en se basant sur des scénarios plausibles décrits en utilisant les diagrammes d'objets et utilisation d'OCL en tant que langage de requêtes. Ces applications nécessitent des propriétés invariantes globales liées aux modèles UML et a fortiori à des diagrammes de classes.

La description des propriétés invariantes globales nécessitent des objets mathématiques non supportés par OCL tels que relations et fonctions. Pour y parvenir, nous apportons une extension à OCL -intitulée EM-OCL (Extension Mathématique pour le langage OCL)- en révisitant sa bibliothèque de classes afin d'y intégrer de nouvelles classes modélisant les relations et fonctions mathématiques.

Ce mémoire se compose de trois chapitres et de deux annexes. Le premier chapitre comporte une présentation de la conception par contrats en UML. En effet, nous présentons successivement la conception par contrats issue du langage Eiffel [6] [4] [5], le langage OCL notamment son mécanisme de typage et ses types collectifs (Collection, Set, Bag, OrderdSet et Sequence). En outre, ce chapitre donne un aperçu sur les travaux de recherche récents liés au langage OCL. Le deuxième chapitre, présente notre extension mathématique d'OCL : EM-OCL. Ce chapitre comporte deux sections importantes : la première section propose des augmentations liées au

package Types d'OCL, quant à la deuxième section, elle propose des augmentations liées à la bibliothèque standard d'OCL. Le dernier chapitre, est consacré à des utilisations potentielles de notre bibliothèque EM-OCL. La première utilisation concerne le développement incrémental des diagrammes de classes UML basé sur la technique de raffinement. La deuxième utilisation concerne la validation des diagrammes de classes, et la dernière utilisation permet d'exhiber les facilités offertes par EM-OCL en tant que langage de requêtes. Enfin, l'annexe A regroupe les définitions des notions mathématiques utilisées pour étendre OCL, et l'annexe B récapitule les nouvelles possibilités offertes par EM-OCL.

Chapitre 1

La conception par contrats en UML/OCL

Introduction

En général, les langages graphiques (comme UML [?]), ne décrivent qu'un aspect partiel du système. Les contraintes sur le modèle sont décrites sous la forme de notes en langage naturel, ce qui induit une ambiguïté de ce dernier et pénalise sa vérification automatique.

Le langage OCL [10](Object Constraint Language) vient remédier àces insuffisances proposant la possibilité à un Classifier donné d'établir ses responsabilités d'une façon précise moyennant un ensemble de propriétés. Dans ce chapitre, nous étudions d'une façon approfondie les aspects généraux d'OCL et donnons un aperçu sur les travaux de recherche récents liés à OCL.

1.1 Généralités sur la conception par contrats

Le fondateur de la conception par contrats (Design by contracts) est Bertrand Meyer auteur du langage de programmation orienté objet pur : Eiffel [6]. Un contrat exige deux partenaires. Dans l'approche par objets, on distingue :

- contrat client basé sur la relation Fournisseur-client (association en UML) entre deux classes; - contrat d'héritage basé sur la relation d'héritage simple (généralisation-spécialisation en UML) entre deux classes.

Afin de définir d'une façon formelle un contrat, on distingue les clauses suivantes : - Précondition : doit être vérifiée avant l'exécution d'une opération ou méthode.

- Postcondition : doit être vérifiée après l'exécution d'une opération ou méthode.

- Invariant: doit être vérifiée en permanence (au moment stable) durant la vie d'un objet (après

sa création).

Pour le contrat client, le protocole à respecter est le suivant :

- précondition est une obligation pour le client et un droit pour le fournisseur. - postcondition est un droit pour le client et une obligation pour le fournisseur. - invariant est un droit pour le client et une obligation pour le fournisseur.

Pour le contrat d'héritage, le protocole à respecter par la classe descendante est : - on peut affaiblir la précondition d'une méthode ou opération héritée.

- on peut renforcer la postcondition d'une méthode ou opération héritée. - on peut renforcer l'invariant venant de la classe ascendante.

1.2 Le langage OCL

OCL est un langage sans effet de bord, fortement typé, s'applique sur les objets et les liens d'un diagramme de classes. C'est un langage fonctionnel, basé sur la logique du premier ordre, navigationnel et déclaratif. OCL est un langage de spécification pas de programmation : haut niveau d'abstraction, pas forcément exécutable. Il permet de trouver des erreurs beaucoup plus tôt dans le cycle de vie. Deux utilisations possibles d'OCL pourront être envisagées :

- OCL pour la conception de contrats;

- OCL en tant que langage de requêtes à l'instar de SQL [17].

1.2.1 OCL langage sans effet de bord

OCL n'a aucune action de modification sur un diagramme d'objets (contrairement au langage SQL qui utilise les constructions insert, update et delete). De même, il n'a aucune action sur le diagramme de classes (contrairement au langage SQL qui peut créer et mettre à jour un schéma relationnel). Toute expression OCL est censée décrire une contrainte ou bien une requête.

1.2.2 OCL est un langage basé sur la logique des prédicats du 1er ordre

OCL utilise deux types de formules. Les formules ouvertes, qui font référence à des objets ou données, sont utilisées à travers les itérateurs (select, reject, ..). Les formules fermées, qui font appel à des quantificateurs et dont le résultat est booléen, sont utilisées à travers les deux opérateurs exists ? et forAll ?.

1.2.3 L'approche fonctionnelle du langage OCL

OCL est un langage fonctionnel

Toute expression OCL retourne un résultat de type : une donnée de base (Boolean, String, Integer,...), ou un objet de l'une des classes du diagramme de classes, ou une collection. Tout interprète retourne deux informations après évaluation d'une expression OCL : le résultat et le type du résultat.

Enchaînement des opérations sur les collections

Toute expression retourne un résultat typé, donc on peut appliquer une opération à ce résultat. Ceci évite l'utilisation des variables intermédiaires.

Syntaxe générale des expressions OCL

Une expression OCL est toujours écrite dans un contexte qui peut être soit un type soit une opération. Si le contexte est un type, le mot-clé self dans une expression se rapporte à un objet de ce type. Sinon, self désigne le type qui possède cette opération.

context Type

stéréotype : expression-ocl

Plusieurs stéréotypes peuvent précéder une expression OCL : - inv : permettant d'exprimer un invariant d'un type donné.

context Type

- Ceci permet de spécifier un invariant d'un type inv : expression-ocl

- pre : permettant de spécifier le comportement d'une opération par une précondition.

context Typename::operationName(param1 : Type1,... ) : ReturnType - Ceci permet de spécifier une précondition d'une opération

pre: expression-ocl

- post : permettant de spécifier le comportement d'une opération par une postcondition.

context Typename::operationName(param1 : Type1,... ) : ReturnType - Ceci permet de spécifier une postcondition d'une opération

post: expression-ocl

Le mot-clé result ne peut figurer que dans une postcondition , où il désigne le résultat de l'évaluation d'une opération.

- body : une expression OCL peut être utilisée pour exprimer le résultat d'une requête.

context Typename::operationName(param1 : Type1,... ) : ReturnType - Ceci permet de spécifier le corps lors de la création d'une opération body: expression-ocl

- init : spécifie la valeur d'un attribut ou d'une association.

context Typename::attributeName(param1 : Type1, ... ) : Type

- - Ceci permet de spécifier la valeur initiale d'un attribut ou d'une association init : expression-ocl

- derive: spécifie les règles de dérivation d'un attribut ou d'une association.

context Typename::assocRoleName(param1 : Type1,... ) : Type

- - Ceci permet de spécifier une dérivation d'un attribut ou d'une association derive: expression-ocl

- def : permet de définir des opérations (ou des variables) qui pourront être (ré)utilisées dans

une expression OCL. Ceci permet de définir des fonctions utilitaires en OCL.

- let : permet de déclarer et de définir la valeur d'un attribut qui pourra être utilisé dans l'ex-

pression qui suit in.

Navigation dans le modèle

En partant d'un objet spécifique, on peut naviguer une association dont le but est de se référer aux objets et leurs propriétés. Pour cela on peut naviguer une association, en utilisant le nom du rôle opposé ou par défaut le nom de la classe opposée en minuscule. object.associationEndName

La valeur de cette expression est un ensemble d'objets de type de la classe de l'association opposée. Cet ensemble dépend de la multiplicité et des qualificatifs associés à l'association.

1.2.4 Exemples

Spécification de la structure de données Pile

La figure 1.1 donne le modèle UML permettant de spécifier la structure de données Pile non générique mémorisant des entiers.



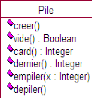
FIGURE 1.1 - Modèle UML de la structure de données Pile

La sémantique de la classe Pile est définie par les contraintes OCL données ci-dessous :

context Pile

inv A1 : vide() implies card()=0
inv A2 : card()=0 implies vide()

Dans le contexte Pile, la notation vide() est équivalente à self.vide().

context Pile ::empiler(x :Integer) post card()= card@pre() +1

post dernier()=x

post not vide()

context Pile ::depiler() pre not vide()

post card()=card@pre()-1

context Pile ::creer() post card()=0

post vide()

context Pile ::dernier() :Integer pre not vide()

L'opérateur @pre donne l'état avant l'exécution. Il est autorisé uniquement au sein d'une post-condition.

Spécification d'une compagnie

La figure 1.2 donne un modèle UML permettant de spécifier une compagnie. Une compagnie est dirigée par une personne. Une personne peut diriger plusieurs compagnies.



FIGURE 1.2 - Modèle UML d'une compagnie

A ce modèle vient s'attacher la contrainte suivante : Le directeur d'une compagnie ne peut pas être considéré comme un employé.

context Compagnie

inv A1 : not(self.dirigée_par.embauchée)

1.3 Mécanisme de typage dans le langage OCL

OCL est un langage typé, voire fortement typé. Chaque expression possède un type qui est explicitement déclaré ou qui peut être dérivé statiquement. L'évaluation de chaque expression OCL doit avoir toujours une valeur dans ce type. La figure 1.3 présente le méta-modèle des types supportés par OCL [10].



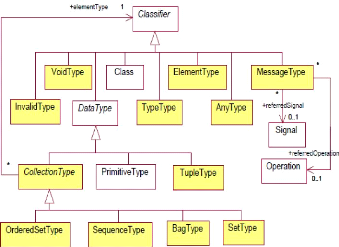
FIGURE 1.3 - Le package Types représentant le méta-modèle des types supportés par OCL

Dans la suite, nous expliquons les principales métaclasses qui nous intéressent directement.

TupleType

Le type TupleType permet de regrouper plusieurs champs de divers type à l'instar des types
structurés des langages de programmation commue type struct de C et record de Pascal et d'Ada.

CollectionType

La méta-classe CollectionType modélise la notion d'une collection (Collection) offerte par OCL (voir 1.3.1). Il s'agit d'une méta-classe abstraite ayant quatre descendantes : SetType, OrdredSetType, BagType et SequenceType.

SetType

La méta-classe SetType modélise la notion d'un ensemble (construction Set) offerte par OCL (voir 1.3.1) : pas de doublons et l'ordre n'est pas significatif.

OrdredSetType

La méta-classe OrderdSetType modélise la notion d'un ensemble ordonné (construction OrderdSet) offerte par OCL (voir 1.3.1) : pas de doublons mais l'ordre est significatif.

SequenceType

La méta-classe SequenceType modélise la notion de séquence (construction Sequence) offerte par OCL (voir 1.3.1) : les doublons sont autorisés et l'ordre des éléments est significatif.

BagType

La méta-classe BagType modélise la notion de sur-ensemble (construction Bag) offerte par OCL (voir 1.3.1) : les doublons sont autorisés et l'ordre n'est pas significatif sur les éléments.

1.3.1 Les types collectifs en OCL

Le langage OCL offre des types de base tels que Boolean, Integer, Real, String et enum. Ces types sont dotés de divers opérateurs. En outre, le langage OCL supporte des types collectifs permettant de stocker une collection d'éléments. Ces types collectifs sont modélisés par le diagramme de classes donnée par la figure 1.4.



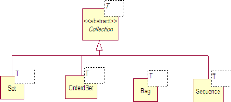
FIGURE 1.4 - Les types collectifs en OCL

La classe Collection est une classe abstraite et générique. Elle modélise la notion d'une collection d'éléments au sens général. Elle est paramétrée sur le type d'éléments. Elle admet quatre classes descendantes :

- classe Set représente un ensemble mathématique non ordonné ne contenant pas d'éléments dupliqués.

- classe Bag représente un ensemble mathématique non ordonné pouvant contenir d'éléments redondants.

- classe Sequence représente un ensemble mathématique ordonné pouvant contenir d'éléments redondants.

- classe OrdredSet représente un ensemble mathématique ordonné ne contenant pas d'éléments dupliqués.

Opérations de calcul sur les collections

Ces opérations sont :

- select : permet de construire une nouvelle collection à partir d'une collection donnée en sélectionnant des éléments selon un critère donné par un prédicat.

- reject: de manière analogue, construit une nouvelle collection formée des éléments ne vérifiant pas un critère.

- collect : construit une nouvelle collection en évaluant une expression portant sur chaque élément d'une collection donnée. Ceci permet par exemple de réaliser une projection d'une collection par rapport à un attribut de chaque élément.

- forAll : renvoie vrai si un prédicat est vrai pour tous les éléments d'une collection. C'est le quantificateur universel quelque soit ?.

- exists : renvoie vrai si au moins un élément d'une collection vérifie un prédicat. C'est le

quantificateur existentiel il existe ?.

- iterate : permet de balayer les éléments d'une collection d'éléments élément par élément. Sur chaque élément visité, elle effectue une action donnée.

La classe Collection

La classe Collection regroupe plusieurs opérations de consultation (<<query>>). Elles sont au nombre de 10. La sémantique de ces opérations est définie formellement en OCL. Dans la suite, nous donnons les spécifications pré/post des opérations : size, count, includes et excludes. size() : Integer

-Le nombre d'éléments de la collection self

post :result = self ?iterate(elem ;acc :Integer=0|acc+1)

Sachant que elem joue le rôle d'une variable de parcours, acc est l'accumulateur et acc+1 est l'action à effectuer à chaque itération.

count(object : T) : Integer

-Le nombre d'apparitions d'object dans la collection self

post :result = self ?iterate(elem ;acc :Integer=0|

if elem=object then acc+1 else acc endif) includes(object : T) : Boolean

-True sit appartient à self

post :result = self ?count(object)>0 excludes(object : T) : Boolean

-True si object n'appartient pas à self, sinon False

post :result = self ?count(object)=0

Notons au passage, l'utilisation de l'opération count afin de spécifier les deux opérations includes et excludes . Ceci caractérise les spécifications pré/post des types de données abstraits matérialisés par des classes.

La classe Set

La classe Set regroupe plusieurs opérations de consultation (<<query>>). Elles sont au nombre
de 15. La sémantique de ces opérations est définie formellement en OCL. La classe Set est
une classe descendante de la classe Collection. De ce fait, plusieurs opérations sont héritées

de la super classe sans être redéfinies qui sont : size(), includes(), excludes(), includesAll(), excludesAll(), isEmpty(), notEmpty() et sum(). L'opération count() est une opération héritée de la classe ascendante, qui a subi une redéfinition. Les autres opérations, appartenant à la classe Set, constituent l'apport de cette classe. Dans la suite, nous donnons les spécifications pré/post des opérations : count, intersection, including et union.

count(object : T) : Integer

-Le nombre d'apparitions d'object dans la collection self post :result<=1 -pas de redondance dans un ensemble Set

intersection(s :Set(T)) : Set(T)

-permet de calculer l'intersection de self et s

post :result?forAll(elem|self?includes(elem) and s?includes(elem)) post :self?forAll(elem|s?includes(elem)=result?includes(elem)) post :s?forAll(elem|self?includes(elem)=result?includes(elem))

union(s :Set(T)) : Set(T)

-permet de calculer l'union de self et s

post :result?forAll(elem | self?includes(elem) or s?includes(elem)) post :self?forAll(elem | result?includes(elem))

post :s?forAll(elem | result?includes(elem))

including(object :T) : Set(T)

-permet d'inserer un élément object dans self

post :result?forAll(elem|self?includes(elem) or (elem=object)) post :self?forAll(elem|result?includes(elem))

post :result?includes(object)

La classe OrderdSet

La classe Set regroupe plusieurs opérations de consultation ( «query»). Elles sont au nombre de 8. La sémantique de ces opérations est définie formellement en OCL. La classe OrdredSet est une classe descendante de la classe Collection. De ce fait, plusieurs opérations sont héritées de la classe ascendante sans être redéfinies qui sont : size(), includes(), excludes(), count(), includesAll(), excludesAll(), isEmpty(), notEmpty() et sum(). Les autres opérations, appartenant à

la classe OrderdSet, constituent l'apport de cette classe. Dans la suite, nous donnons les spécifications pré/post des opérations : insertAt, first et last.

insertAt(index : Integer, object: T) :OrderdSet(T)

- permet d'insérer un élément object à une postion index dans self post :result?size()=self?size()+1

post :result?at(index)=object

post :Sequence{1..(index-1)}?forAll(i :Integer| self?at(i)=result?at(i))

post :Sequence{(index+1)..self?size()}?forAll(i :Integer| self?at(i)=result?at(i+1))

first() : T

-retourne le premier élément de self
post :result=self?at(1)

last() : T

-retourne le dernier élément de self post :result=self?at(self?size())

La classe Bag

La classe Bag regroupe plusieurs opérations de consultation ( «query»). Elles sont au nombre de 13. La sémantique de ces opérations est définie formellement en OCL. La classe Bag est une classe descendante de la classe Collection. De ce fait, plusieurs opérations sont héritées de la super classe sans être redéfinies qui sont : size(), includes(), excludes(), includesAll(), excludesAll(), isEmpty(), notEmpty() et sum(). L'opération count() est une opération héritée de la classe ascendante, qui a été redéfinie. Les autres opérations, appartenant à la classe Bag, constituent l'apport de cette classe. Dans la suite, nous donnons les spécifications pré/post des opérations: intersection, et including.

intersection(bag :Bag(T)) : Bag(T)

-permet de calculer l'intersection de self et s

post :result?forAll(elem|

result?count(elem)= self?count(elem).min(bag?count(elem)))

post :self?forAll(elem|

result?count(elem)= self?count(elem).min(bag?count(elem)))

post :bag?forAll(elem|

result?count(elem)= self?count(elem).min(bag?count(elem)))

including(object :T) : Bag(T)

-permet d'inserer un élément object dans self

post: result?forAll(elem|

if elem=object then

result?count(elem)=self?count(elem)+1 else

result?count(elem)=self?count(elem) endif)

post: self?forAll(elem|

if elem=object then

result?count(elem)=self?count(elem)+1 else

result?count(elem)=self?count(elem) endif)

La classe Sequence

La classe Sequence regroupe plusieurs opérations de consultation ( «query» ). Elles sont au nombre de 18. La sémantique de ces opérations est définie formellement en OCL. La classe OrdredSet est une classe descendante de la classe Collection. De ce fait, plusieurs opérations sont héritées de la classe ascendante sans être redéfinies qui sont : size(), includes(), excludes(), includesAll(), excludesAll(), isEmpty(), notEmpty() et sum(). L'opération count() est une opération héritée de la classe ascendante, qui a été redéfinie. Les autres opérations, appartenant à la classe Sequence, constituent l'apport de cette classe. Dans la suite, nous donnons les spécifications pré/post des opérations : count, union, insertAt et at.

count(object : T) : Integer

-Le nombre d'apparitions d'object dans la collection self union(s :Sequence(T)) : Sequence(T)

-permet de calculer l'union de self et s

post :result?size()=self?size()+s?size()

post :Sequence{1..self?size()}?forAll(index :Integer| self?at(index)=result?at(index))

post :Sequence{1..s?size()}?forAll(index :Integer|
s?at(index)=result?at(index+self?size()))

insertAt(index : Integer, object: T) :OrderdSet(T)

- permet d'insérer un élément object à une postion index dans self post :result?size()=result?size()+1

post :result?at(index)=object

post :Sequence{1..(index-1)}?forAll(i :Integer|

self?at(i)=result?at(i))

post :Sequence{(index+1)..self?size()}?forAll(i :Integer| self?at(i)=result?at(i+1))

at(i :Integer) : T

-retourne le i-ème élément de self pre :i>=1 and i<=self?size()

1.4 Travaux lies à OCL

Il est utilisé pour décrire la sémantique statique des langages de modélisation comme UML et les profils UML et des langages de méta-modélisation comme MOF. Également, OCL permet d'attacher des propriétés sémantiques aux modèles UML en utilisant avec profit le paradigme conception par contrat (voir 1.1). En outre, OCL peut être utilisé comme langage de requêtes. Enfin, il est de plus en plus utilisé dans le cadre de l'approche MDA préconisée par l'OMG. Dans la suite, nous donnons un aperçu sur les travaux récents liés au langage OCL au sens strict.

Le travail décrit dans [?] préconise l'utilisation de la technique de refactoring afin d'améliorer la compréhension Le langage OCL joue un rôle de plus en plus important aussi bien dans l'activité de modélisation que de méta-modélisation.et la maintenance des spécifications OCL. Les auteurs de ce travail identifient les mauvaises utilisations d'OCL (OCL smells) et proposent une collection de refactorings permettant d'écarter ces OCL smells. Parmi les OCL smells identifiés

(une douzaine) par ces auteurs, nous citons : Implies Chain, Redundancy, Non-atomic rule, And Chain, ForAll Chain, etc.

Le travail décrit dans [?] critique la hiérarchie des types collectifs (voir Figure 1.3) proposée par OCL. Les auteurs de ce travail se démarquent de l'approche orientée opération (spécification pré/post) suivie par l'OMG lors de la définition d'OCL et préconisent une nouvelle approche orientée invariant de classe. Ainsi, ils proposent une nouvelle hiérarchie des types collectifs : Bag et Sequence descendant de Collection et Set et OrderedSet descendent respectivement de Bag et Sequence.

Le travail décrit dans [?] propose une méthode basée sur une approche IDM (Ingénierie Dirigée par les Modèles) permettant de spécifier des opérations de raffinement en utilisant des contrats de transformation exprimés en OCL attachés au niveau méta (M2).

Lors de la manipulation des expressions OCL, deux exceptions peuvent apparaître : invalid et null. La première exception traduit une valeur indéfinie (par exemple division par zéro) et la deuxième traduit une référence nulle à l'instar des langages de programmation orientés objet. Le travail décrit dans [?] propose une formulation des éléments nuls dans le cadre d'OCL basée sur l'environnemnt HOL-OCL [14].

Plusieurs travaux permettent de traduire des contraintes OCL vers des formalismes logiques du premier ordre [?] [?] et d'ordre supérieur [14] [?] existent. De tels traducteurs entraînent la possibilité de raisonner sur des modèles UML équipés des contraintes OCL.

Afin d'ouvrir OCL sur le développement incrémental basé sue la technique de raffinement à l'instar des méthodes formelles comme B [3] et Event-B, nous apportons une extension d'OCL appelée EM-OCL permettant la représentation et la manipulation des objets mathématiques tels que : couple, relation et fonction.

Conclusion

Dans ce chapitre, nous avons présenté la conception par contrat permettant de formaliser les responsabilités d'une classe vis-à-vis des autres classes. Ensuite, nous avons présenté d'une façon approfondie le langage OCL. Enfin, nous avons passé en revue les principaux travaux récents liés à OCL. Dans le chapitre suivant, nous allons décrire notre extension à OCL : une extension mathématique d'OCL (EM-OCL).

Introduction

Dans ce chapitre, nous proposons une extension d'OCL appelée EM-OCL (Extension Mathématique pour le langage OCL) permettant de représenter et manipuler les concepts mathématiques couple, relation binaire, fonction partielle, fonction totale, fonction surjective et fonction bijective. Les utilisations potentielles de notre extension EM-OCL sont traitées dans le chapitre 3.

Ce chapitre comporte deux sections importantes. La première section propose des augmentations liées au package Types d'OCL afin de typer (ou métamodéliser) les concepts mathématiques cités ci-dessus. Sachant que le package Types d'OCL décrit le système de types d'OCL (voir chapitre 1). La deuxième section propose des augmentations liées à la bibliothèque standard d'OCL (OCL standard Library) afin de définir d'une façon formelle -en utilisant OCL lui-même- les opérations applicables sur les nouveaux concepts mathématiques introduits dans OCL.

2.1 Augmentations liées au package Types

OCL est un langage fortement typé. Le méta-modèle des types supportés par OCL a été présenté dans le chapitre 1. EM-OCL apporte des nouveaux types modélisant les concepts mathématiques couple, relation et fonction (voir Figure 2.1). Les méta-classes ajoutées au package Types d'OCL sont coloriées en rouge.



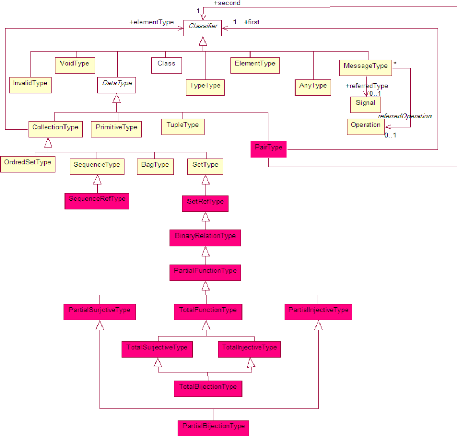
FIGURE 2.1 - Le méta-modèle des types EM-OCL

2.1.1 Description de nouveaux types

PairType

La méta-classe PairType modélise le concept d'une paire ordonnée offerte par EM-OCL. Elle descend de la méta-classe abstraite DataType. Elle se distingue de la méta-classe TupleType par le fait que celle-ci modélise le concept d'une structure comportant plusieurs champs dont l'ordre n'est pas significatif à l'instar de type struct de C ou record de Pascal ou Ada. Les deux

méta-associations first et second entre PairType et Classifier modélisent la nature de deux éléments formant la paire ordonnée.

SequenceRefType

Elle hérite de SequenceType en apportant des nouvelles opérations (voir 3.2).

SetRefType

Elle hérite de SetType en apportant des nouvelles opérations (voir 3.2).

Les liens entre les méta-classes données ci-dessous sont traduits par des relations d'héritage simples et multiples inspirées de [7].

BinaryRelationType

BinaryRelationType représente le concept relation binaire. Elle descend de SetRefType et par conséquent elle est assimilée à un ensemble de couples.

PartialFunctionType

PartialFunctionType représente le concept d'une fonction partielle dont chaque élément du domaine est relié à au plus un élément du co-domaine.

TotalFunctionType

TotalFunctionType représente le concept d'une fonction totale dont le domaine correspond à tous les éléments de l'ensemble de départ.

PartialInjectiveType

PartialInjectiveType représente le concept d'une fonction injective partielle.

TotalInjectiveType

TotalInjectiveType représente le concept d'une fonction injective totale.

PartialSurjectiveType

PartialSurjectiveType représente le concept d'une fonction surjective partielle.

TotalSurjectiveType

TotalSurjectiveType représente le concept d'une fonction surjective totale.

PartialBijectionType

PartialBijectionType représente le concept d'une fonction bijective partielle.

TotalBijectionType

TotalBijectionType représente le concept d'une fonction bijective totale.

2.1.2 Conformité des types

Le package des types d'OCL propose des règles de conformité des types supportés par OCL. Ces règles sont formalisées en OCL. Elles sont définies comme des propriétés invariantes (clause inv) établies au sein de contexte de la méta-classe inhérente au type concerné. Dans la suite, nous élaborons les déclarations EM-OCL relatives à la conformité de types des nouveaux types supportés par EM-OCL.

PairType

Les types Pair sont conformes si les types des éléments formant les couples ordonnées le sont.

context PairType

inv : PairType.allInstances()-+forAll(p|

self-+first().conformsTo(p -+ first()) and

self-+ second().conformsTo(p -+second())implies self.conformsTo(p))

BinaryRelationType

BinaryRelationType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context BinaryRelationType

inv : BinaryRelationType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

PartialFunctionType

PartialFunctionType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context PartialFunctionType

inv : PartialFunctionType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

TotalFunctionType

TotalFunctionType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context TotalFunctionType

inv : TotalFunctionType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

PartialInjectiveType

PartialInjectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context PartialInjectiveType

inv : PartialInjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

TotalInjectiveType

TotalInjectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context TotalInjectiveType

inv : TotalInjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

PartialSurjectiveType

PartialSurjectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context PartialSurjectiveType

inv : PartialSurjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

TotalSurjectiveType

TotalSurjectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context TotalSurjectiveType

inv : TotalSurjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

PartialBijectiveType

PartialBijectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context PartialBijectiveType

inv : PartialBijectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

TotalBijectiveType

TotalBijectiveType est conforme à tout autre type dont les types des éléments sont conformes entre eux.

context TotalBijectiveType

inv : TotalBijectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo( s.elementType) implies self.conformsTo(s))

2.1.3 Règles de bonnes utiisations des nouveaux types

A l'instar d'OCL, nous représentons les règles de bonnes utilisations (Well-formdness rules) des nouveaux types proposés par EM-OCL.

PairType

Le nom du typePair est 'Pair' suivi par les deux noms des types des éléments formant le couple ordonné.

context PairType

inv : name='Pair('+self.first.name+','+self.second.name+')'

SetRefType

Le nom du type SetRef est 'SetRef' suivi par le nom du type des éléments de l'ensemble.

context SetRefType

inv : name='SetRef('+self.elementType.name+')'

SequenceRefType

Le nom du type SequenceRef est 'SequenceRef' suivi par le nom du type des éléments de l'ensemble.

context SequenceRefType

inv : name='SequenceRef('+self.elementType.name+')'

BinaryRelationType

Le nom du type BinaryRelation est 'BinaryRelation' suivi par le nom du type pair des couples de la relation.

context BinaryRelationType

inv : name='BinaryRelation('+self.elementType.name+')'

PartialFunctionType

Le nom du type PartialFunction est 'PartialFunction' suivi par le nom du type pair des couples de la fonction.

context PartialFunctionType

inv : name='PartialFunction('+self.elementType.name+')'

TotalFunctionType

Le nom du type TotalFunction est 'TotalFunction' suivi par le nom du type pair des couples de la fonction.

context TotalFunctionType

inv : name='TotalFunction('+self.elementType.name+')'

PartialInjectiveType

Le nom du type PartialInjecive est 'PartialInjective' suivi par le nom du type pair des couples de la fonction.

context PartialInjectiveType

inv : name='PartialInjective('+self.elementType.name+')'

PartialSurjectiveType

Le nom du type PartialSurjective est 'PartialSurjective' suivi par le nom du type pair des couples de la fonction.

context TotalSurjectiveType

inv : name='TotalSurjective('+self.elementType.name+')'

TotalInjectiveType

Le nom du type TotalInjecive est 'TotalInjective' suivi par le nom du type pair des couples de la fonction.

context TotalInjectiveType

inv : name='TotalInjective('+self.elementType.name+')'

PartialSurjectiveType

Le nom du type PartialSurjective est 'PartialSurjective' suivi par le nom du type pair des couples de la fonction.

context PartialSurjectiveType

inv : name='PartialSurjective('+self.elementType.name+')'

TotalBijectiveType

Le nom du type TotalBijective est 'TotalBijective' suivi par le nom du type pair des couples de la fonction.

context TotalBijectiveType

inv : name='TotalBijective('+self.elementType.name+')'

PartialBijectiveType

Le nom du type PartialBijective est 'PartialBijective' suivi par le nom du type pair des couples de la fonction.

context PartialBijectiveType

inv : name='PartialBijective('+self.elementType.name+')'

2.2 Augmentations liées à la bibliothèque standard d'OCL

2.2.1 Conception d'une bibliothèque mathématique

La conception d'une bibliothèque mathématique [?]- représentant et manipulant des notions mathématiques telles que paire ordonnée, relation et fonction - en adoptant une approche orientée objet doit tenir compte de certains problèmes liés à des concepts mathématiques utilisés dans la théorie des ensembles tels que :

- problème d'héritage dans la hiéarchie : La hiérarchie d'héritage modélisant les relations entre les nouvelles collections ne correspond pas nécessairement à la taxonomie naturelle des structures mathématiques. Ceci est illustré par un exemple explicatif :

Considérons les deux classes BinaryRelation(Pair(G,H)) et PartialFunction(Pair(G,H)) correspondant respectivement à une relation binaire de couples d'éléments et une fonction partielle de couples d'éléments. D'un point de vue mathématique, il est évident qu'une fonction hérite d'une relation binaire. En effet, une fonction est une relation binaire dont chaque élément du domaine est relié à au plus à un élément du co-domaine. D'un point de vue orientée objet, l'utilisation d'une relation d'héritage entre ces deux classes entraîne un mécanisme de polymorphisme : plusieurs opérations valides pour une relation binaire, ne le seront pas pour une fonction. En effet, il faut tenir compte de certaines contraintes pour l'opération d'intersection (l'intersection d'une fonction doit être nécessairement une fonction), ainsi que l'inverse d'une fonction injective (l'inverse d'une fonction injective doit être une fonction injective).

- Extension de la classe Set : certaines opérations qui s'appliquent sur les ensembles doivent être ajoutées à l'ensemble des opérations applicables sur la classe Set. Pour cela, on définit SetRefType descendant du type Set.

Ces opérations sont les suivantes : identity, firstProj, secondProj.

- Extension de la classe Sequence certaines opérations qui s'appliquent sur les ensembles doivent être ajoutées aux opérations applicables sur la classe Set. Pour cela ,nous avons introduit le nouveau type SequenceRefType descendant du type Sequence. Ces opérations sont les suivantes : insertRight, reverse, tail et front.

La figure 2.2 propose une taxonomie des notions mathématiques intégrées dans EMOCL. Nous notons que toutes les classes sont génériques. Elles admettent un seul paramètre générique ayant la forme suivante : T=Pair(G,H), où :

G : le type des éléments de l'ensemble de départ.

H : le type des éléments de l'ensemble d'arrivée.



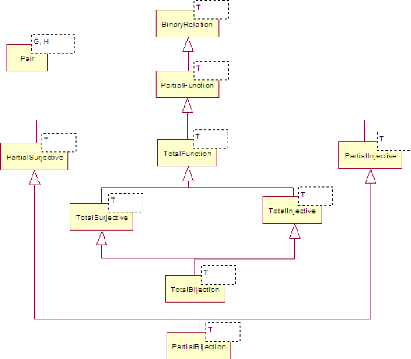
FIGURE 2.2 - Graphe de classes de la bibliothèque EM ajoutée à OCL

2.2.2 Opérations offertes par la bibliothèque EM

Ici, nous présentons les opérations applicables sur les classes offertes par la bibliothèque EM. La sémantique de ces opérations est soigneusement définie en EM-OCL.

La classe Pair

make(f :G, s :H) :Pair(G,H) Permet de créer une paire ordonnée.

post :result.first()=f post :result.second()=s

first() : G

Permet d'extraire le premier élément d'une paire ordonnée.

second() : H

Permet d'extraire le second élément d'une paire ordonnée.

=(p :Pair(G,H) :Boolean

Rend True si les deux éléments de self et p coincident.

post :result implies self.first()= p.first() and self.second()=p.first()

reverse() :Pair(H,G)

Permet d'inverser une paire ordonnée.

post :result.second()=self.first() post :result.first()=self.second() post :result.reverse()=self - - l'opération = de Pair

La classe SetRef

On suppose que la classe SetRef a comme paramètre générique de type G.

identity() :BinaryRelation(Pair(G,G)) Retourne l'identité d'un ensemble.

post: let c : Pair(G,G)=Pair[] in

result=self-+iterate(e :G|accu :BinaryRelation(Pair(G,G))=BinaryRelation{}| accu-+including(c.make(e,e)))

firstProj(ens :Set(H)) :BinaryRelation(Pair(Pair(G,H),G)) Permet de calculer la première projection d'un ensemble.

post: let c2 : Pair(G,H)=Pair[], c1 :Pair(Pair(G,H),G)=Pair[] in

result=self-+iterate(e1 :G|accu :BinaryRelation(Pair(Pair(G,H),G))=BinaryRelation{}| ens-+iterate(e2 :H|accu.including(c1.make(c2.make(e1,e2),e1))))

secondProj(ens :Set(H) :BinaryRelation(Pair(Pair(G,H),H) Permet de calculer la deuxième projection d'un ensemble.

post: let: c2 : Pair(G,H)=Pair[], c1 :Pair(Pair(G,H),H)=Pair[] in

result=self-+iterate(e1 :G|accu :BinaryRelation(Pair(Pair(G,H),H))=BinaryRelation{}| ens-+iterate(e2 :H|accu.including(c1.make(c2.make(e1,e2),e2))))

La classe SequenceRef

On suppose que la classe SequenceRef a comme paramètre générique de type G.

insertRight(o :G) :SequenceRef(G)

Permet d'insérer un élément o à la fin de la séquence.

post :result=self?insertAt(self?size()+1,o) post :result?size()=self?size()+1

reverse() :SequenceRef(G) Permet d'inverser self.

post :result=Sequence{1..self?size()}?iterate(pn;

acc :SequenceRef(G)=SequenceRef{}| acc?insertAt(self?size()+1-pn ;self?at(pn))) post: result?size()=self?size()

tail() :SequenceRef(G)

Permet d'écarter le premier élément de la séquence.

pre :self?size()>0

post :result=self?subSequence(2,self?size()) post : result?size()=self?size()-1

front() :SequenceRef(G)

Permet d'écarter le dernier élément de la séquence.

pre: self?size()>0

post :result=self?subSequence(1,self?size()-1) post : result?size()=self?size()-1

La classe BinaryRelation

domaine() : SetRef(G)

Retourne les éléments du premier ensemble G qui sont effectivement en relation avec des éléments du second ensemble H.

post: result = self?iterate(e : Pair(G,H);

accu : SetRef(G)=SetRef{}|accu?including(e.first()))

range() :SetRef(H)

Retourne des éléments de l'ensemble H qui sont en relation avec des éléments du premier ensemble G.

post: result = self-+iterate(e : Pair(G,H);

accu : SetRef(G)=SetRef{}|accu-+including(e.second()))

imageSet(F : SetRef(G)) : SetRef(H) Retourne l'image de l'ensemble F.

pre: G-+includesAll(F)

post: result = self-+iterate(e : Pair(G,H); accu : SetRef(H) =SetRef{}| if ( F-+includes(e.first()))

then accu-+including(e.second()) endif) )

imageElt(e :G) : SetRef(H)

Retourne l'ensemble des éléments de H qui sont en relation avec e.

pre: G-+includes(e)

post: result = self-+iterate(x : Pair(G,H); accu : SetRef(H) =SetRef{}|
if(e.first()=x) then accu-+including(e.second()) endif) )

inverse() :BinaryRelation(Pair(H,G)) Retourne l'inverse de la relation binaire self.

post: let couple : Pair(G,H)=Pair[] in

result = self-+iterate( e : Pair(G,H);

accu : BinaryRelation(Pair(H,G)) :BinaryRelation{} | accu-+including( couple.make(e.second(),e.first()))

post: result.inverse()=self post: result-+size()=self-+size()

seqComposition(r :BinaryRelation(Pair(H,K))) :BinaryRelation(Pair(G,K)) Retourne la composition séquentielle de deux relations binaires.

post: let couple : Pair(G,H)=Pair[] in

result = self-+iterate ( e : Pair(G,H); accu :BinaryRelation(Pair(G,K))=BinaryRelation{}| r-+iterate(e1 : Pair(H,K) |

if( e.second()=e1.first()) then accu-+including( couple.make(e.first(),e1.second())) endif ))

directProduct(r : BinaryRelation(Pair(G,K))) :BinaryRelation(Pair(G ,TupleType(H,H)))

retourne le produit direct de deux relations binaires.

post: let c1 : Pair(G,TupleType(H,K))=Pair[] in

result = self-+iterate(e1 :PairType(G,H);

accu :BinaryRelation(Pair(G,TupleType(H,K)))=BinaryRelation{}| r-+iterate( e2 : Pair(G,K)| if (e1.second() =e2.second()) then

accu-+including(c1.make(e1.first(), tuple(e1.second(),e2.second()))) endif))

ParallelProduct(r : BinaryRelation(Pair(K,M))) :BinaryRelation(Pair(Pair(G,K), Pair(H,M)))

retourne le produit parallèle de deux relations binaries.

post: let c1 : Pair(G,H)=Pair[] ,

c2 : Pair(K,M)=Pair[],

couple : Pair(Pair(G,H),Pair(K,M))=Pair[] in

result = self-+iterate(e1 :Pair(G,H);

accu :BinaryRelation(Pair(Pair(G,K),Pair(H,M)))=BinaryRelation{}| r-+iterate( e2 : PairType(K,M)| acc -+including(couple.make(c1.make(e1.first(),e2.first()), c2.make(c1.second(),c2.second())))))

-Iterations

Les itérations sur les relations permettent d'itérer une relation: c'est-à-dire la composer séquentiellement avec elle-même un certain nombre de fois.

iteration(n :Integer) :BinaryRelation(Pair(G,H))

pre: G.oclIsTypeOf(H)

post: if (n=0) then result=G-+identity() else

let acc :BinaryRelation(Pair(G,H))=self in Sequence{2..n}-+iterate(pn ;acc=self| acc-+seqComposition(self))

endif

closeTrans() :BinaryRelation(Pair(G,H))

pre: G.oclIsTypeOf(H)

-Restrictions

restrictionDomaine(E :Set(G)) :BinaryRelation(Pair(G,H)) Permet de restreindre une relation sur un sous-ensemble du domaine.

pre: G::allInstances()-+includesAll(E)

post: let couple : Pair(G,H)=Pair[] in

result= self-+iterate(e1 :Pair(G,H);

accu :BinaryRelation(Pair(G,H))=BinaryRelation{}|

if E-+includes(e1.first()) then accu-+including(couple.make(e1.first(),e1.second())) endif )

soustractionDomaine(E :Set(G)) : BinaryRelation(Pair(G,H)) Permet de soustraire une relation sur un sous-ensemble du codomaine.

pre: G::allInstances()-+includesAll(E)

post: let couple : Pair(G,H)=Pair[] in

result= self-+iterate(e1 : Pair(G,H); accu :BinaryRelation(Pair(G,H)))=BinaryRelation{}| if E-+excludes(e1.first()) then accu-+including(couple.make(e1.first(),e1.second())) endif )

restrictionRange(F :SetRef(H)) : BinaryRelation(Pair(G,H)) Permet de restreindre une relation sur un sous-ensemble du codomaine.

pre: H::allInstances()-+includesAll(F)

post: let couple: Pair(G,H)=Pair[] in

result= self-+iterate(e1 : Pair(G,H); accu :BinaryRelation(Pair(G,H)))=BinaryRelation{}|

if F-+includes(e1.second()) then accu-+including(couple.make(e1.first(),e1.second())) endif )

soustractionRange(F :SetRef(H)) : BinaryRelation(Pair(G,H))) Permet de soustraire une relation sur un sous-ensemble du codomaine.

pre: H::allInstances()->includesAll(F)

post: let couple : Pair(G,H)=Pair[] in

result= self-+iterate(e1 : PairType(G,H); accu :BinaryRelation(Pair(G,H))=BinaryRelation{}|
if F-+excludes(e1.second()) then accu-+including(couple.make(e1.first(),e1.second())) endif )

La classe PartialFunction

Nous préconisons une approche orientée invariant afin de modéliser l'abstraction PartialFunction.

invariant de classe

Une fonction est une relation dont chaque élément du domaine est associé à au plus à un élément du co-domaine et son domaine est inclus dans l'ensemble de départ.

context PartialFunction

inv : self?forAll(e1,e2 : Pair(G,H)| if e1.first()=e2.first() then e1.second()=e2.second()) inv : G:: allInstances()?includesAll(self?domain())

redéfinition des opérations

intersection(f :PartialFunction(Pair(G,H))) :PartialFunction(Pair(G,H)) L'intersection de deux fonctions doit être une fonction.

post: result?forAll(elem|self->includes(elem) and f?includes(elem)) post: self?forAll(elem|f?includes(elem)= result?includes(elem)) post: f?forAll(elem|self?includes(elem)=result?includes(elem))

imageElement(x :G) : H

Permet de retourner l'image d'un élément x appartenant au domaine par une fonction.

pre: self ?domaine()?includes(x)

post: let couple : Pair(G,H)=Pair[] in self?includes(couple.make(x,result))

La classe TotalFunction invariant de classe

Une fonction totale est une relation dont le domaine correspond à tous les éléments de l'ensemble de départ.

context TotalFunction

inv : self?domaine()=G::allInstances

La classe PartialInjective

Une fonction injective partielle est fonction partielle dont l'inverse doit être injective.

context PartialInjective

inv : self?inverse().oclIsTypeOf(PartialFunction)

La classe PartialSurjective

Une fonction surjective partielle est fonction partielle dont le codomaine correspond à l'ensemble d'arrivée.

context PartialSurjective

inv : self?range()=H::allInstances()

La classe TotalSurjective

Une fonction surjective totale est fonction totale dont le codomaine correspond à l'ensemble d'arrivée.

context TotalSurjective

inv : self?range()=H::allInstances()

Conclusion

Dans ce chapitre nous avons proposé une extension mathématique du langage OCL. Il était alors nécessaire d'examiner l'intégration des nouveaux concepts mathématiques (couples, relations et fonctions) dans le package Types afin de les métamodéliser. Ensuite, nous avons proposé des augmentations liées à la bibliothèque standard d'OCL en proposant les nouvelles classes génériques suivantes : Pair, BinaryRelation, PartialFunction, PartialSurjective, Total-Function, PartialInjective, TotalSurjective, TotalInjective, TotalBijection et PartialBijection.

Dans la suite de ce mémoire, nous proposons des utilisations potentielles de notre extension EM-OCL.

Introduction

Dans ce chapitre, nous proposons trois utilisations potentielles de notre extension mathématiques d'OCL : EM-OCL. La première utilisation concerne le développement incrémental de diagrammes de classes UML basé sur la technique de raffinement à l'instar des méthodes formelles comme B et Event-B. La deuxième utilisation concerne la validation des diagrammes de classes en se basant sur des scénarios plausibles décrits par des diagrammes d'objets. Enfin, la troisième utilisation permet d'exhiber les facilités offertes par EM-OCL en tant que langage de requêtes.

3.1 Notion de raffinement

D'une façon informelle, le raffinement est un processus de transformation d'une spécification abstraite en une spécification concrète vérifiant que chaque transformation de spécification préserve bien sa correction vis-à-vis de la spécification précédente. On peut distinguer principalement deux catégories de raffinement : Le raffinement algorithmique (encore appelé raffinement de données) et le raffinement de détails.

Le raffinement algorithmique consiste à choisir une autre représentation mémoire de l'état du système modélisé afin :

- de minimiser l'espace mémoire utilisé et/ou le temps de calcul. Ainsi, le raffinement favorise l'élaboration des solutions efficaces.

- d'aller progressivement, sans se précipiter, vers la représentation ultime. Ainsi, le

raffinement favorise l'identification des structures de données appropriées.

Le raffinement de conception ou de détails consiste à spécifier un système de manière plus détaillée.

Le raffinement constitue la pierre angulaire des méthodes formelles comme B, Event-B, Z[8] et Object-Z[9].

Le raffinage a été défini de manière intuitive par J.R. Abrial ainsi "une substitution (travaillant dans le contexte d'une certaine machine abstraite M) est dite raffinée par une substitution T, si T peut être utilisée à la place de S sans que l'utilisateur de la machine s'en rende compte. En pratique, cela signifie que toutes nos attentes au sujet de S seront remplies par T. Si c'est le cas, alors T est dit être un raffinage de S, et S une abstraction de T [3]".

Contrairement aux méthodes formelles comme B et Event-B où le concept raffinement est précisément défini, UML [?] propose la dépendance stéréotypé «refine» ayant une définition très floue et plutôt considérée comme une simple décoration graphique.

3.2 Le raffinement en EM-OCL

Dans cette section, nous exhibons les possibilités offertes par EM-OCL afin d'utiliser la technique de raffinement en UML. Pour y parvenir, nous développons d'une façon incrémentale pas-à-pas en UML/EM-OCL l'application accès aux bâtiments modélisée en Event-B par J.R. Abrial et décrite en [19].

3.2.1 Spécification initiale

Le premier modèle du système est un modèle très abstrait dans lequel, il n'y aura pas de distinction entre le logiciel et le matériel. L'objectif principal du système est de contrôler l'entrée, la sortie, ainsi que la situation dynamique de la présence des personnes dans les bâtiments. Une simplification du modèle consiste à identifier l'extérieur à un bâtiment (dans lequel toute personne a le droit de se trouver).

Plusieurs contraintes doivent être attachées au modèle initial:

- L'impossibilité pour une même personne de se trouver simultanément dans deux bâtiments distincts.(1)

- À un instant donné, une personne se trouve dans un bâtiment au plus.(2)

- Toute personne se trouvant dans un bâtiment est autorisée à y être.(3)

- À un instant donné, une personne se trouve dans un bâtiment au moins.(4)

- L'ensemble des personnes n'est pas vide.(5) - L'ensemble des bâtiments n'est pas vide.(6) - Chaque personne est autorisée à pénétrer dans un certain bâtiment (et pas dans d'autres).(7)

Modélisation

La modélisation de ce système est donnée par une seule classe, intitulée AccèsBâtiment, englobant les propriétés du système au fur et à mesure dans la phase de conception, contenant :

- deux attributs personne et bâtiment représentant respectivement l'ensemble des personnes et des bâtiments.

- une relation binaire autorisation représentant l'ensemble des couples "personne,bâtiment" dont chacun relie une personne à un bâtiment où elle est autorisée à se rendre. Une personne est autorisée à aller dans plusieurs bâtiments. De ce fait, il s'agit d'une relation binaire.

- une fonction totale situation représentant l'ensemble des couples "personne,bâtiment" dont chacun relie une personne au bâtiment auquel il se trouve, et représentant la dynamique des gens dans les bâtiments. Le fait qu'il s'agisse d'une fonction correspond à la formalisation de la propriété(2). Et le fait qu'elle soit totale correspond à la propriété(4).

- un attribut univers : l'extérieur est un bâtiment spécial. Dans la sémantique de l'opération de construction initialiser celle-ci se charge d'affecter toutes les personnes concernées au bâtiment univers.

La figure 3.1 représente la classe AccèsBâtiment dans l'étape de la spécification initiale .



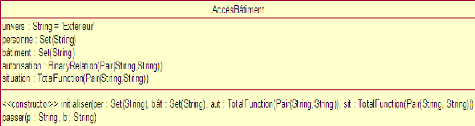
FIGURE 3.1 - Modèle initial tiré à partir de la spécification initiale

Formulation des contraintes attachées au modèle

Ce modèle doit être complété par la formalisation des contraintes décrites ci-dessus.

context AccèsBâtiment

inv CS : personne-+notEmpty() inv C6 : bâtiment-+ notEmpty() inv C7 : autorisation-+includesAll(situation)

Événement

Une opération de construction intitulée initialiser , jouant le rôle d'un constructeur permettant d'initialiser l'ensemble des propriétés du système.

context AccèsBâtiment::initialiser(per :Set(String),bât :Set(String),aut : BinaryRelation(Pair(String,String)), sit :TotalFunction(Pair(String,String)))

pre: per-+notEmpty() and bât-+notEmpty()and aut-+notEmpty() and sit-+notEmpty()

pre: aut-+forAll(couple :Pair(String,String) | per-+includes(couple.first())and bât-+includes(couple.second()))

pre: sit-+forAll(couple :Pair(String,String) | per-+includes(couple.first())and couple.second()=univers)

post: personne=per and bâtiment=bât and autorisation=aut and situation=sit post: autorisation-+notEmpty()

post: situation-+notEmpty()

A ce niveau d'abstraction, une seule transition est observée correspondant à l'entrée d'une personne p dans un bâtiment b. En effet, une personne p ne peut passer d'un bâtiment à un autre, que sip est bien autorisée de se trouver dans b, et si bien entendu, elle n'est pas déjà dans b.

context AccèsBâtiment::passer(p :String,b :String)

pre: personne?includes(p) and bâtiment?includes(b) pre: situation?imageElt(p)<>b

pre: let couple: Pair(String,String)=Pair[] in autorisation?includes(couple.make(p,b))

post: let couple : Pair(String,String)=Pair[] in situation?includes(couple.make(p,b))

Remarque : Pour des raisons de simplification, nous ignorons dans la suite l'opération initialiser.

3.2.2 Premier raffinement

Dans cette étape, nous introduisons la communication possible entre les bâtiments. Une contrainte supplémentaire, évidente à respecter qu'un bâtiment ne communique pas avec luimême.(8)

Modélisation

La classe AccèsBâtiment, sera augmentée par l'attribut communication représentant l'ensemble des couples "bâtiment,bâtiment" qui relie chaque bâtiment à un autre avec lequel sensé communiqué. La figure 4.2 représente la classe AccèsBâtiment après premier raffinement.



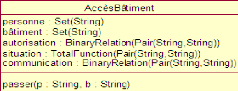
FIGURE 3.2 - Second modèle après premier raffinement

Formulation des contraintes attachées au modèle

Ce modèle doit être complété par la formalisation de la contrainte (8).

context AccèsBâtiment

inv C8 : communication?intersection(bâtiment?identity())?isEmpty()

Événement

À ce niveau d'abstraction, le seul événement intéressant est l'événement passer. En effet, les deux bâtiments concernés par le passage d'une personne doivent communiquer entre eux.

context AccèsBâtiment::passer(p :String,b :String)

pre: personne-+includes(p) and bâtiment-+includes(b)

pre: let couple: Pair(String,String)=Pair[] in communication-+includes(couple.make(situation-+imageElt(p),b))

pre: let couple: Pair(String,String)=Pair[] in autorisation-+includes(couple.make(p,b))

post: let couple : Pair(String,String)=Pair[] in situation-+includes(couple.make(p,b))

3.2.3 Deuxième raffinement : Introduction des portes

Au cours de deuxième raffinement, nous introduisons les portes à sens unique faisant communiquer les bâtiments entre eux. Une personne peut entrer dans un bâtiment en franchissant une porte que si elle est débloquée pour elle. Les portes peuvent être physiquement bloquées. Elles ne peuvent pas être débloquées que pour une seule personne à la fois autorisée à entrer dans le bâtiment. Ceci peut être exprimée par la propriété suivante : toute personne est admise à franchir une porte faisant communiquer le bâtiment oil elle se trouve à un bâtiment oil elle est autorisée à aller. De plus cette personne ne doit pas être déjà engagée avec une autre porte(P1).

Modélisation

La classe AccèsBâtiment sera augmentée par les attributs suivants :

- porte : représentant l'ensemble des portes présentes dans les bâtiments.

- origine : représentant une fonction totale, qui à chaque porte lui correspond son bâtiment origine.

- destination : représentant une fonction totale, qui à chaque porte lui correspond son bâtiment destination.

- acceptation : représentant une fonction injective partielle reliant chaque personne à la porte à laquelle elle est acceptée de franchir.

La figure 3.3 représente la classe AccèsBâtiment après second raffinement.



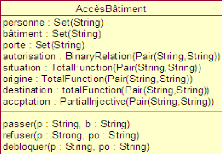
FIGURE 3.3 - Troisième modèle après deuxième raffinement

Formulation des contraintes attachées au modèle

À ce modèle vient s'ajouter plusieurs contraintes, qui sont décrites en utilisant B : - L'ensemble des portes n'est pas vide.(9)

- Pour toutes ces portes, les bâtiments origine et destination représentent exactement les couples de bâtiments impliquées dans la relation communication introduite au cours du raffinement précédent. Ceci, peut être formulé comme suit:

communication = (origine^-1; destination).(10)

- Lorsqu'une porte est débloquée pour une certaine personne, celle-ci se trouve dans le bâtiment d'origine de la porte en question. Ceci, peut être formulé en B par l'expression B suivante : (accepter; origine) ? situation.(11)

- Par ailleurs, la personne pour laquelle une porte est débloquée est bien autorisée à aller dans le bâtiment de destination de cette même porte .Ceci peut être formulé en B de la façon suivante : (accepter; destination) ? autorisation.(12)

context AccèsBâtiment

inv C9 : porte-+ notEmpty()

inv C10 : communication=(origine-+inverse()-+seqComposition(destination) inv C11 : situation -+includesAll(accepter-+seqComposition(origine))

inv C12 : autorisation-+includesAll(acceptation -+seqComposition(destination))

événements

La propriété (P1) exprimant la condition d'admission d'une personne à franchir une porte donnée , est donné par le prédicat admis, considéré comme un fonction utilitaire en utilisant la construction def.

context AccèsBâtiment

def admis(p :String,po :String) : Boolean =

let couple: Pair(String,String)=Pair[] in

situation ?imageElt(p)=origine?imageElt(po) and autorisation?includes(couple.make(p,b)) and acceptation ?dom()?(p))

débloquer.Une porte po est débloquée pour une personne pe que si cette dernière est admise à franchir po. Par conséquent, elle sera acceptée.

context AccèsBâtiment::débloquer(p :String , po :String)

pre: personne ? includes(p) and bâtiment ? includes(b) pre: admis(pe,po)

post: let couple : Pair(String,String)=Pair[] in acceptation ?includes(couple.make(p,po))

refuser.Une personne pe est refusée de franchir une porte po que si elle n'est pas admise à y franchir.

context AccèsBâtiment::débloquer(p :String,po :String) pre: personne?includes(p) and porte?includes(po) pre: vrt?union(rge)? excludes(po)

pre: not(admis(pe,po))

post: rge=rge@pre?union(po)

passer

L'événement passer est raffiné. Il peut se déclencher lorsqu'une personne est admis à entrer et que la porte est débloquée. Les actions associées sont le passage de la personne admise et la fermeture de cette porte. Ce raffinement s'accompagne d'un changement de paramètres de l'événement passer, le bâtiment est remplacé par une porte.

context AccèsBâtiment::passer(p :String , po :String)

pre: personne ? includes(p) and porte ? includes(po)

pre: acceptation?range()? includes(po)

post: acceptation?range()? excludes(po)

post: let couple :Pair(String,String)=Pair[] in situation?includes(couple.make(p,destination?imageElt(po)))

3.2.4 Troisième Raffinement : Introduction des voyants lumineux

Dans cette étape de raffinement, on introduit les voyants lumineux dans le système. Un voyant vert est associé à chaque porte. Il est allumé tant que celle-ci est débloquée(14). Dès qu'une personne est passée, la porte se rebloque. Si au bout de 30 secondes, aucune personne ne passe une porte débloquée, celle-ci se rebloque toute seule. Dans les deux conditions, le voyant vert s'éteint.

De même, un voyant rouge est associé à chaque porte. Il est allumé et éteint dans les conditions suivantes :"Le voyant rouge d'une porte dont l'accès vient d'être refusé s'allume pour une période de 2 secondes, la porte restant évidement bloquée".

Une propriété, évidente à respecter, correspond à l'exclusion mutuelle pour les deux voyants soient allumés simultanément (14).

Modélisation

La classe AccèsBâtiment sera augmentée par les attributs suivants :

- vrt : représentant l'ensemble des portes dont les voyants verts sont allumés.

- rge : représentant l'ensemble des portes dont les voyants rouges sont allumés.

La figure 3.4 représente la classe AccèsBâtiment après troisième raffinement.



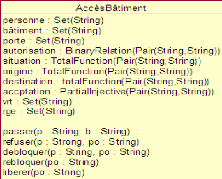
FIGURE 3.4 - Quatrième modèle après troisième raffinement

Formulation des contraintes attachées au modèle

A ce modèle viennent s'ajouter plusieurs contraintes :

- Le codomaine de la fonction acceptation, correspond à toutes les portes qui sont engagées dans le processus éventuel de passage d'une certaine personne qui, cependant, n'est pas encore passée. Ceci est formalisé, en utilisant la notation B par :vrt = ran(accepter). Cette définition correspond partiellement à la formulation de la propriété (14).

- Par simultanéité, on introduit l'ensemble des portes dont le voyant rouge est allumé.

Les voyants verts et rouges d'une même porte ne peuvent pas être allumés simultané-

ment. Ceci est formalisé, en utilisant la notation B par: rge ? porte (14).

- La formulation de la contrainte (14), en notation B, est donnée par: vrtnrge = .

context AccèsBâtiment

inv C13 : vrt= acceptation?range()

inv C14 : (vrt?excludesAll(rge))?isEmpty()

Èvénements

A ce niveau d'abstraction, deux nouveaux événements s'ajoutent au système. rebloquer.permet d'éteindre le feu vert d'une porte;

context AccèsBâtiment::rebloquer(po :String) pre: vrt? includes(po)

pre: admis(pe,po)

post: acceptation = acceptation@pre? soustractionDomaine(po)

liberer. permet d'éteindre le feu rouge d'une porte.

context AccèsBâtiment::liberer(po :String)

pre: rge? includes(po)

post: acceptation =acceptation@pre? excludes(po)

débloquer.

context AccèsBâtiment::débloquer(p :String,po :String) pre: personne ? includes(p) and porte? includes(po) pre: (vrt ? union(rge))?excludes(po)

pre: admis(pe,po)

post: let couple : Pair(String,String)=Pair[] in acceptation? includes(couple.make(p,po))

refuser.

context AccèsBâtiment::refuser(pe :String,po :String)

pre: personne ? includes(p) and porte? includes(po) pre: (vrt ? union(rge))?excludes(po)

pre: not(admis(pe,po))

post: rge= rge@pre? union(po)

passer.

context AccèsBâtiment::passer(po :String)

pre: porte? includes(po

pre: situation ? imageElt(acceptation?inverse(po))=destination ?imageElt(po) pre: not(admis(pe,po))

post: acceptation= @acceptation?soustractionRange(po)

3.2.5 Quatrième raffinement : Introduction des lecteurs de cartes

Chaque personne dispose d'une carte magnétique. Des lecteurs de cartes sont installés à chaque porte permettant de lire les informations contenues sur une carte. Ces informations seront par la suite transmise au micro-ordinateur de contrôle au moyen de message véhiculé par le réseau. De plus, chaque lecteur de carte est supposé resté bloqué entre le moment ou le contenu d'une carte est envoyé au système et la réception par ce lecteur de l'acquittement correspondant. Cet acquittement vient lorsque le protocole de passage est entièrement achevé(avec succès ou non).

Modélisation

La classe AccèsBâtiment sera augmentée par les attributs suivants :

- LBL : l'ensemble des lecteurs bloqués. Ceci est représenté par un ensemble des portes.
- mLe : l'ensemble des messages envoyés des lecteurs vers le système de contrôle,

représentée par les couples "portes,personnes" formant ainsi une fonction partielle

représentant l'information lue par le lecteur asocié à la porte sur la carte. - mLa : l'ensemble messages d'acquittement.

La figure 3.5 représente la classe AccèsBâtiment après troisième raffinement.



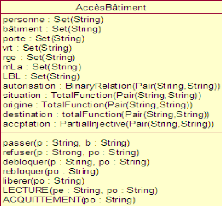
FIGURE 3.5 - Cinquième modèle après quatrième raffinement

Événements

débloquer.

context AccèsBâtiment::débloquer(pe : String,po String) pre: personne? includes(pe) and porte? includes(po)

pre: let couple: Pair(String,String)=Pair[] in mLe? includes(couple.make(po,pe))

pre: admis(pe,po)

post: let couple : Pair(String,String)=Pair[] in

mLe= mLe@pre?excludes(couple.make(po,pe))

refuser.

context AccèsBâtiment::refuser(pe : String,po String)

pre : let couple : Pair(String,String)=Pair[] in mLe-+ includes(couple.make(po,pe))

pre : not(admis(pe,po))

post : rge=rge@pre-+union(po)

post : let couple : Pair(String,String)=Pair[] in

mLe= mLe@pre-+excludes(couple.make(po,pe))

rebloquer.

context AccèsBâtiment::rebloquer(po :String)

pre : vrt-+includes(po)

pre : acceptation = acceptation@pre-+soustractionDomaine(po) post : mLa= mLa@pre-+ union(po)

liberer.

context AccèsBâtiment::liberer(po :String)

pre : rge-+ includes(po)

pre : acceptation = acceptation@pre-+ excludes(po) post : mLa= mLa@pre-+ union(po)

passer.

context AccèsBâtiment::passer(po :String)

pre : porte-+ includes(po)

pre : situation -+ imageElt(acceptation -+inverse(po))= destination -+imageElt(po) post : acceptation= acceptation@pre-+soustractionRange(po)

post : mLa= mLa@pre-+ union(po)

LECTURE.

context AccèsBâtiment::LECTURE(pe :String,po :String) pre : personne-+ includes(pe) and porte-+ includes(po) pre : LBL= @LBL-+union(po)

post : let couple : Pair(String,String)=Pair[] in mLe= @mLe-+union(couple.make(po,pe))

ACQUITTEMENT.

context AccèsBâtiment::ACQUITTEMENT(po :String) pre : LBL-+includes(po)

pre : LBL= LBL@pre-+ excludes(po)

post : mLa= mLa@pre-+ excludes(po)

3.2.6 Discussion

Nous avons développé d'une façon incrémentale pas-à-pas en UML-OCL l'application accès aux bâtiments en s'inspirant du processus de raffinement proposé par J.R. Abrial pour cette application [19]. Pour y parvenir, nous avons utilisé avec profit les nouvelles possibilités offertes par notre extension à OCL (EM-OCL) telles que : BinaryRelation, TotalFunction, PartialFunction et PartialInjective.

Le dernier modèle obtenu (voir figure 3.5) représente un modèle abstrait cohérent du futur système. Un tel modèle exhibe les propriétés formelles du futur système.

La classe AccèsBâtiment représentant le dernier modèle obtenu peut être raffinée davantage en prenant des décisions liées à l'identification des classes pertinentes au sens de l'approche par objets [4]. La vérification de la correction du raffinement peut être confiée à la plateforme Rodin d'Event-B moyennant des règles de transformation systématique d'UML/EM-OCL vers Event-B.

3.3 Validation d'un diagramme de classes

3.3.1 Approche de validation proposée

Un diagramme de classes comportant des classes d'analyse modélisant les concepts métier issus de l'application est censé traduire fidèlement des diagrammes d'objets supposés corrects. Autrement dit, nous commençons par la sélection des diagrammes d'objets représentatifs du monde réel à modéliser. Ensuite, nous vérifions si ces diagrammes respectent ou non les propriétés invariantes du diagramme de classes à valider. En cas d'échec, le coupable est le diagramme de classes. Nous préconisons l'idée d'un invariant global ( construction invariant proposée par EM-OCL ) afin de décrire les propriétés invariantes attachées à un diagrammes de classes.

3.3.2 Exemple

Le diagramme de classes proposée par la figure 3.6 comporte :

- deux classes Personne et Bâtiment qui représentent l'ensemble des personnes et des bâtiments,

- deux associations autorisation et situation qui relient les classes Personne et Bâtiment. La multiplicité de l'association situation exprime le fait qu'une personne se trouve dans au plus un bâtiment. Quant à l'association autorisation, elle modélise les autorisations d'entrer dans différents bâtiments accordées à chaque personne.



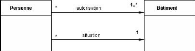
FIGURE 3.6 - Accès Personne/Bâtiment

Description informelle de l'invariant du système

Ce modèle doit être complété par les propriétés suivantes : - l'ensemble des personnes n'est pas vide,

- l'ensemble des bâtiments n'est pas vide,

- chaque personne est autorisée à entrer dans certains bâtiments,
- toute personne dans un bâtiment donné est autorisée à y entrer.

Description formelle en EM-OCL de l'invariant du système invariant - invariant global

persone_pas_vide : Personne::allInstances()?notEmpty() bâtiment_pas_vide : bâtiment::allInstances()?notEmpty() cardinalite : situation?size()=Personne::allInstances()?size() situation_autorisee : autorisation?includesAll(situation)

Afin d'écrire l'invariant donné ci-dessus, nous avons utilisé les conventions suivantes :

- le nom d'une association UML orientée désigne soit une relation binaire (BinaryRelation) soit une fonction (TotalFunction). Par exemple, l'association autorisation est de type BinaryRelation(Pair(Personne,Bâtiment)) et situation est de type TotalFunction(Pair(Personne,Bâtiment)). En outre, les deux multiplicités associées à l'association sont utilisées comme guides (voir TABLE 3.1) afin d'identifier avec précision la nature d'une fonction (totale, partielle, injective, surjective et bijective). Enfin, nous pouvons utiliser des contraintes associés au nom de l'association afin de préciser sa nature mathématique (voir 3^me colonne TABLE 3.1).

- la construction invariant offerte par notre extension EM-OCL comporte plusieurs prédicats étiquetés et reliés implicitement par and logique.

Par exemple, les deux diagrammes d'objets proposés par la figure 3.7 respectent l'invariant global du système.



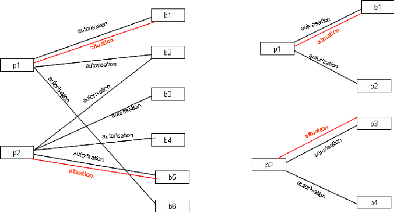
FIGURE 3.7 - Deux diagrammes d'objets rspectant l'invariant global

En injectant une erreur voulue dans l'invariant (autorisation? excludesAll(situation) au lieu de (autorisation?includesAll(situation)), les deux diagrammes d'objets concernés ne respectent plus l'invariant global du système. Ainsi, le diagramme de classes proposé est incorrect.

UML

classe générique offerte par EM-OCL

UML/EM-OCL

BinaryRelation(Pair(A,B))

PartialFunction(Pair(A,B))

TotalFunction(Pair(A,B))

PartialInjective(Pair(A,B))

TotalInjectivePair(A,B))

PartialSurjective(Pair(A,B))

PartialBijective(Pair(A,B))

TotalBijective(Pair(A,B))





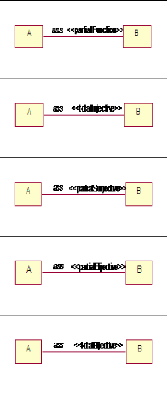
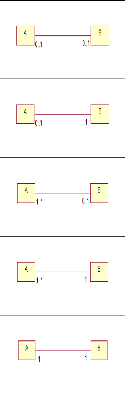
TABLE 3.1: Modèle mathématique correspondant à une association UML

3.4 EM-OCL en tant que langage de requêtes

Le langage OCL offre des possibilités favorisant son utilisation en tant que langage de requêtes telles que : collect, select et reject. Mais les requêtes écrites en OCL doivent être liées à un contexte local c'est-à-dire à l'objet courant self. Ceci entraîne des difficultés relatives à l'écriture de telles requêtes. La figure 3.8 modélise des liens potentiels entre des entités issues d'un système bancaire simple. On se propose de formaliser en OCL et EM-OCL la requête suivante : pour chaque banque, trouver l'ensemble des ses comptes, en utilisant la construction body permettant de spécifier des requêtes utilitaires dans un contexte donné.





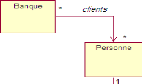
FIGURE 3.8 - Système bancaire simple

3.4.1 Formulation en OCL

context Banque::comptesBancaires() :Set(TupleType(b :Banque , c :Compte)) body: Banque::allInstances()?iterate(b :Banque;

accu :Set(TupleType(b :Banque,c :Compte))=Set{}|

b.personne?iterate(p :Personne|

p.compte?iterate(c :Compte|accu?including(tuple{b,c}))))

3.4.2 Formulation en utilisant EM-OCL

context Banque::comptesBancaires() :BinaryRelation(Pair(Banque,Compte)) body: cients?seqComposition(comptes)

3.4.3 Comparaison

La formulation en OCL utilise les constructions allInstances, TupleType et iterate. Elle a un aspect impératif : deux iterate imbriqués. Ainsi, elle est moins abstraite que celle d'EMOCL basée sur l'opération de composition séquentielle de deux relations (clients et comptes), offerte par la classe générique d'EM-OCL BinaryRelation.

Conclusion

Nous avons proposé trois utilisations potentielles de notre extension mathématique EMOCL : développement incrémental de diagrammes de classes UML basé sur la technique de raffinement, validation de diagrammes de classes et utilisation d'EM-OCL en tant que langage de requêtes.

Conclusion générale

Dans ce mémoire, nous avons proposé une extension mathématique au langage OCL appelée EM-OCL permettant de représenter et manipuler les concepts mathématiques suivants : couple, fonction totale, fonction partielle, fonction injective, fonction surjective, fonction bijective et relation binaire. Ces concepts sont modélisés par des classes génériques. Ces classes sont intégrées d'une façon judicieuse dans la bibliothèque de classes OCL. Les opérations offertes par ces classes sont définies formellement en utilisant une spécification pré/post supportée par OCL et par conséquent par EM-OCL. Des utilisations potentielles de notre langage EMOCL ont été exhibées sur des exemples bien ciblés, dans divers domaines : développement des diagrammes de classes en utilisant la technique de raffinement, validation de diagrammes de classes et utilisation d'OCL en tant que langage de requêtes.

Plusieurs outils sont associés au langage OCL. Ils sont de niveaux différents. Les modéleurs permettent une vérification syntaxique des contraintes OCL : exemple l'outil OCLE [15]. Les vérificateurs permettent la construction des diagrammes d'objets et la vérification de leurs conformités aux diagrammes OCL, exemple l'outil USE [12]. Les générateurs de code permettent la génération d'un squelette d'application à partir du modèle UML/OCL. Les contraintes OCL associées aux modèles seront surveillées à l'exécution et les expressions (type, initialisation, règle de dérivation) seront respectées, exemple l'outil Dresden OCL Toolkit [13]. L'outil HOL-OCL[14] représente un environnement de preuve interactif dédié au langage OCL implémenté à base de Isabelle/HOL permettant, d'analyser des systèmes des contraintes OCL, établir des raffinements formels entre des packages et de vérifier des programmes simples à base de contraintes OCL.

Quant aux perspectives de ce travail, nous pourrions envisager les prolongements sui-

vants :

- intégrer notre langage EM-OCL dans l'outil USE afin de vérifier des propriétés invariantes globales d'un diagramme de classes UML,

- intégrer notre langage EM-OCL dans l'environnement HOL-OCL afin d'utiliser le raffinement formel dans le cadre UML.

- proposer des règles de transformation systématique d'UML/OCL vers Event-B afin d'utiliser le raffinement formel dans le cadre d'un développement conjoint UML/EMOCL et Event-B.

Annexe A

Annexe mathématique

Cette annexe est inspirée de [7].

A.1 Logique fondamentale

Les expressions logiques dénotent des prédicats qui ont une interprétation dans le domaine des valeurs de vérité : true et false.

Symbole	Signification	Définition
?	et logique
#172;	négation
?	ou logique	a ? b = #172;(#172;a ? #172;b)
	implication	a b = #172;a ? #172;b
?	équivalence	a ? b = (a b) ? (b a)

On peut quantifier les prédicats par les quantificateurs universel et existentiel.

Symbole	Signification	Syntaxe	Définition
?	pour tout	?Id_liste.(Prdicat)
?	il existe	?Id_liste.(Prdicat)	?x.(P) = #172;?x.(#172;P )

Le non-terminal Id_liste représente une liste d'identificateurs séparés par des virgules. Le non-terminal Prdicat désigne un prédicat quelconque .

A.2 Ensemble

On désigne par s et t deux ensembles. x un élément de s. On dispose des prédicats suivants relatifs aux ensembles:

Symbole	Signification	Définition
?	appartient à
??	n'appartient pas	x ? s = #172;(x ? s)
?	est inclus dans	s ? t = s ? P(t)
??	n' est pas inclus dans	s ?? t = #172;(s ? t)
?	est strictement inclus dans	s ? t = (s ? t ? s =? t)
??	n'est pas strictement inclus dans	s ?? t = #172;(s ? t)

A.3 Tuple

Syntaxe		Nom
(a1,a2,	,an)	tuple d'éléments
(x,y)		paire ordonnées d'éléments
first		permet d'extraire le premier élément d'une paire ordonnée
second		permet d'extraire le second élément d'une paire ordonnée

A.4 Relations

Les relations sont un cas particulier de constructions d'ensembles.

Symbole	Siginification	Définition
E1 ? E2	relations entre deux ensembles	E1 ? E2 . = E1 × E2

On définit le domaine d'une relation comme les éléments du premier ensemble E1 qui sont effectivement en relation avec des éléments du second ensemble E2. Le codomaine est l'ensemble des points du second ensemble E2 qui sont en relation avec des éléments du premier ensemble E1. L'image d'un ensemble par une relation, notée r[F] est l'ensemble des éléments de E2 qui sont en relation avec les éléments de F par la relation r. Plus formellement :

Annexe A. Annexe mathématique

Condition	Expression	Définition
r ? E1×E2	dom(r)	{x|x ? E1 ? ?y.(y ? E2 ? (x ?? y) ? r)}
r ? E1×E2	ran(r)	{y|y ? E2 ? ?x.(x ? E1 ? (x ?? y) ? r)}
r ? E1×E2 et F ? E1	r[F]	{y|y ? E2 ? ?x.(x ? F ? (x ?? y) ? r)}

A.4.1 Opérations stir les relations

Il existe de nombreuses opérations sur les relations. Les opérations sur les ensembles s'appliquent évidemment aux relations (qui sont effectivement des ensembles de couples). En particulier, une relation vide est la même chose qu'un ensemble vide. Néanmoins, il y a quelques opérations spécifiques, dont la plupart sont très usuelles. On a la relation identité sur un ensemble, qui à chaque élément associe le même élément. La relation inverse d'une relation don-née. On distingue ensuite trois formes de composition de relations. Enfin, on a les opérations de projection qui construisent les relations entre les ensembles paramètres et les éléments projetées droite ou gauche.

Condition	Expression	Définition
	id(E)	{x,y|(x ?? y) ? E×E ? x = y}
r ? s ? t	r^-^1	{y,x|(y ?? x) ? t×s ? (x ?? y) ? r
r1 ? t ? u r2 ? u ? v	r1;r2	{x,z|x,z ? t×v? ?y.(y ? u ? (x ?? y) ? r1 ? (y ?? z) ? r2}
r1 ? t ? u r2 ? t ? v	r1?r2	{x, (y, z)|x, (y, z) ? t×(u×v)? (x ?? y) ? r1 ? (x ?? z) ? r2}
r1 ? t ? u r2 ? v ? w	r1 ? r2	{(x,z),(y,a)|(x,z),(y,a) ? (t×v)×(u×w)? (x ?? y) ? r1 ? (z ?? a) ? r2}
	prj1(E,F)	{x,y,z|x,y,z ? E×F×E ? z = x}
	prj2(E,F)	{x,y,z|x,y,z ? E×F×F ? z = y}

A.4.2 Itérations.

Une itération d'une relation est la composer séquentiellement avec elle même un certain nombre de fois. On note : r ? s ? s

Notation	Siginification	Définition
rn	itération n fois de r	rn . = r; r^n-^1sin > 0 r0 . = id(s)
r+	fermeture transitive de r	r+ . = ?n.(n ? N1|r^n)
r	fermeture transitive reflexive de r	r . = ?n.(n ? N|r^n)

A.4.3 Restrictions

Les opérateurs de restrictions sur les relations consistent à restreindre ces relations sur des sous-ensembles du domaine ou du codomaine. Dans le tableau des définitions, on a : R ?

s ? t, E ? s, F ? t, Q ? s ? t

Notation	Siginification	Définition
E < R	restriction sur le domaine	{x, y|(x ?? y) ? R ? x ? E} r0 . = id(s)
E < R	soustraction sur le domaine	{x, y|(x ?? y) ? R ? x ? E}
R > F	restriction sur le codomaine	{x, y|(x ?? y) ? R ? x ? E}
R F	sur le codomaine	{x, y|(x ?? y) ? R ? x ? E}

A.5 Fonctions

Symbole	Siginification	Définition
s ?? t	fonction partielle	{r|r ? s ? t? ?x,y,z.(x,y ? r ? x,z ? r y = z)}
s ? t	fonction totale	{f|f ? s ?? t ? dom(f) = s}
s >--? t	injective partielle	{f|f ? s ?? t ? f^-^1 ? t ?? s}
s >- t	injective totale	f ? s '--*? t n f ? s ? t
s -*? t	surjective partielle	{f|f ? s ?? t ? ran(f) = t}
s - t	surjective totale	f ? s -*? t n f ? s ? t
s ??? t	bijective partielle	f ? s '--*? t n f ? s -*? t
s ?? t	bijective totale	f ? s ? t n f ? s - t

Annexe B

Annexe de la bibliothèque EM

B.1 Pair

On suppose que la classe Pair est paramétrée par les deux types G et H.

Signature de l'opération	Description
Pair[]	constructeur par défaut de la classe Pair
make(f : G, s : H) : Pair(G, H)	permet de créer une paire ordonnée
first() : G	extraire le premier élément d'une paire ordonnée
second() : H	extraire le second élément d'une paire ordonnée
reverse() : Pair(H, G)	inverser une paire ordonnée d'élément
= (p : Pair(G, H) : Boolean	Rend True si les deux éléments de self et p coincident

B.2 SetRef

On suppose que la classe SetRef est paramétrée par le type G.

Signature de l'opération	Description
identity() : BinaryRelation(Pair(G, G))	identité d'un ensemble
firstProj(ens : Set(H)) : BinaryRelation(Pair(Pair(G, H), G))	calculer la première projection d'un ensemble
secondProj(ens : Set(H) : BinaryRelation(Pair(Pair(G, H), H)	calculer la seconde projection d'un ensemble

B.3 SequenceRef

On suppose que la classe SequenceRef est paramétrée par le type G.

Signature de l'opération	Description
insertRight(o : C) : SequenceRef(C)	insérer un élémnt o à la fin de la séquence
reverse() : SequenceRef(C)	permet d'inverser une séquence
tail() : SequenceRef(C)	écarter le premier élément de la séquence
front() : SequenceRef(C)	écarter le dernier élément de la séquence

B.4 BinaryRelation

Signature de l'opération	Description
domaine() : SetRef(C)	retourne le domaine d'une relation binaire
range() : SetRef(H)	retourne le codomaine d'une relation binaire
imageSet(F : SetRef(C)) : SetRef(H)	retourne l'image de l'ensemble F par une relation binaire
imageElt(e : C) : SetRef(H)	retourne l'image de l'élément e par une relation binaire
inverse() : BinaryRelation(Pair(H, C))	retourne l'inverse d'une relation binaire
seqComposition(r : BinaryRelation(Pair(H, K))) : BinaryRelation(Pair(C, K))	calculer la composition séquentielle de deux relations
directProduct(r : BinaryRelation(Pair(C, K))) : BinaryRelation(Pair(C, Pair(C, H)))	calculer le produit direct de deux relations binaires
ParallelProduct(r : BinaryRelation(Pair(K, L))) : BinaryRelation(Pair(Pair(C, K), Pair(H, L)))	calculer le produit parallèle de deux relations binaires
iteration(n : Integer) : BinaryRelation(Pair(C, H))	itérer une relation binaire n fois
closeTrans() : BinaryRelation(Pair(C, H))	calculer la fermeture reflexive transitive d'une relation
restrictionDomaine(E : Set(C)) : BinaryRelation(Pair(C, H))	restreindre une relation sur un sous-ensemble E du domaine
soustractionDomaine(E : Set(C)) : BinaryRelation(Pair(C, H))	soustraire une relation sur un sous-ensemble E du codomaine
restrictionRange(F : SetRef(H)) : BinaryRelation(Pair(C, H))	restreindre une relation sur un sous-ensemble F du codomaine
soustractionRange(F : SetRef(H)) : BinaryRelation(Pair(C, H)))	soustraire une relation sur un sous-ensemble F du codomaine

Bibliographie

[1] B. Meyer, Applying "Design by Contract",in Computer (IEEE), 25, 10, October 1992, pages 40-51.

[2] B. Meyer, Design by Contract, Technical Report TR-EI-12/CO, Interactive Software Engineering Inc., 1986.

[3] J.R. Abrial, The B-book: assigning programs to meanings, Cambridge University Press, 1996.

[4] B. Meyer, Conception et programmation orientées objets, Éditions Eyrolles, 2000.

[5] B. Meyer, Object Oriented Software Construction, 2nd edition, Prentice Hall, 1997.

[6] B. Meyer, Eiffel : the language, Prentice Hall, 1992.

[7] M.L Potet, and D. Bert, Spécification en B (support de cours), École des Jeunes Chercheurs en Programmation, 2007, http :// www-lsr.imag.fr/users/Didier.Bert/Exams/poly-B-2007.pdf.

[8] J.M. Spivey, The Z Notation : a reference Manual, Prentice-Hall, 1999.

[9] G. Smith, The Object-Z Specification Language, Kluwer Academic Publishers, 2000.

[10] OMG, UML 2.0 OCL Specification, Mai, 2006.

[11] E. Cario, Object Constraint Language, 2003, http ://www.lirmm.fr/ hu-
chard/Enseignement/IDM/coursOCL20.pdf.

[12] F. Büttner, M. Gogolla, and M. Richters, A Uml-based Specification Environnement, Science of Computer Programming, 2007, http :// www.db.informatik.uni-bremen.de/projects/USE/.

[13] B. Demuth, and C. Wilke, Dresden OCL Toolkit, http :// dresden-ocl.sourceforge.net/.

[14] A.D. Brucker, and B. Wolff, Isabelle/HOL-OCL, August 2006, http :// www.brucker.ch/research/hol-ocl/.

[15] M. Bortes, D. Corutiu, C. Botiza, and A.Cârcu,Object Constraint Language Environement, version 2.0, 1999, http :// lci.cs.ubbcluj.ro/ocle/index.htm.

[16] J. Melton, and A. R. Simon, Understanding the New SQL : A Complete Guide, Morgan Kaufmann Publishers, 1994.

[17] J.S. Bowman, S.L. Emerson, and M. Darnovsky, SQL L'Intro, CampusPress, 2002.

[18] J.B. Warmer, and A.G. Kleppe, The object constraint language : precise modeling with UML, Addison Wesley Longman, 1999.

[19] J.-R. Abrial, Étude de cas : Le contrôle d'accès aux bâtiments, http :// wwwlsr.imag.fr/B/Documents/ClearSy-CaseStudies/PORTES/SourcesFR/main.html, June 2000.

[20] G. Booch, J. Rumbaugh, and I. Jacobson, The Unified Modelling Language User Guide, Addison Wesley, 1999.

[21] C. Metayer, J-R Abrial, and L.Voisin, Event-B language, RODIN Project Deliverable D7, May 2005.