Conclusion
Dans ce chapitre, nous avons présenté la
conception par contrat permettant de formaliser les responsabilités
d'une classe vis-à-vis des autres classes. Ensuite, nous avons
présenté d'une façon approfondie le langage OCL. Enfin,
nous avons passé en revue les principaux travaux récents
liés à OCL. Dans le chapitre suivant, nous allons décrire
notre extension à OCL : une extension mathématique d'OCL
(EM-OCL).
Introduction
Dans ce chapitre, nous proposons une extension d'OCL
appelée EM-OCL (Extension Mathématique pour le langage OCL)
permettant de représenter et manipuler les concepts mathématiques
couple, relation binaire, fonction partielle, fonction totale, fonction
surjective et fonction bijective. Les utilisations potentielles de notre
extension EM-OCL sont traitées dans le chapitre 3.
Ce chapitre comporte deux sections importantes. La
première section propose des augmentations liées au package Types
d'OCL afin de typer (ou métamodéliser) les concepts
mathématiques cités ci-dessus. Sachant que le package Types d'OCL
décrit le système de types d'OCL (voir chapitre 1). La
deuxième section propose des augmentations liées à la
bibliothèque standard d'OCL (OCL standard Library) afin de
définir d'une façon formelle -en utilisant OCL lui-même-
les opérations applicables sur les nouveaux concepts
mathématiques introduits dans OCL.
2.1 Augmentations liées au package
Types
OCL est un langage fortement typé. Le
méta-modèle des types supportés par OCL a
été présenté dans le chapitre 1. EM-OCL apporte des
nouveaux types modélisant les concepts mathématiques couple,
relation et fonction (voir Figure 2.1). Les méta-classes ajoutées
au package Types d'OCL sont coloriées en rouge.
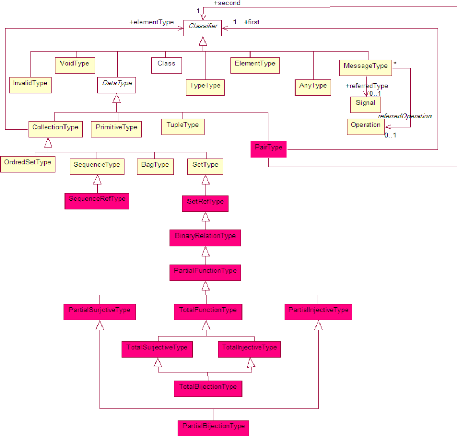
FIGURE 2.1 - Le méta-modèle des types EM-OCL
2.1.1 Description de nouveaux types
PairType
La méta-classe PairType modélise le concept
d'une paire ordonnée offerte par EM-OCL. Elle descend de la
méta-classe abstraite DataType. Elle se distingue de la
méta-classe TupleType par le fait que celle-ci modélise le
concept d'une structure comportant plusieurs champs dont l'ordre n'est pas
significatif à l'instar de type struct de C ou record de Pascal ou Ada.
Les deux
méta-associations first et second entre
PairType et Classifier modélisent la nature de deux
éléments formant la paire ordonnée.
SequenceRefType
Elle hérite de SequenceType en apportant des nouvelles
opérations (voir 3.2).
SetRefType
Elle hérite de SetType en apportant des nouvelles
opérations (voir 3.2).
Les liens entre les méta-classes données ci-dessous
sont traduits par des relations d'héritage simples et multiples
inspirées de [7].
BinaryRelationType
BinaryRelationType représente le concept relation binaire.
Elle descend de SetRefType et par conséquent elle est assimilée
à un ensemble de couples.
PartialFunctionType
PartialFunctionType représente le concept d'une fonction
partielle dont chaque élément du domaine est relié
à au plus un élément du co-domaine.
TotalFunctionType
TotalFunctionType représente le concept d'une fonction
totale dont le domaine correspond à tous les éléments de
l'ensemble de départ.
PartialInjectiveType
PartialInjectiveType représente le concept d'une fonction
injective partielle.
TotalInjectiveType
TotalInjectiveType représente le concept d'une fonction
injective totale.
PartialSurjectiveType
PartialSurjectiveType représente le concept d'une fonction
surjective partielle.
TotalSurjectiveType
TotalSurjectiveType représente le concept d'une fonction
surjective totale.
PartialBijectionType
PartialBijectionType représente le concept d'une fonction
bijective partielle.
TotalBijectionType
TotalBijectionType représente le concept d'une fonction
bijective totale.
2.1.2 Conformité des types
Le package des types d'OCL propose des règles de
conformité des types supportés par OCL. Ces règles sont
formalisées en OCL. Elles sont définies comme des
propriétés invariantes (clause inv)
établies au sein de contexte de la méta-classe inhérente
au type concerné. Dans la suite, nous élaborons les
déclarations EM-OCL relatives à la conformité de types des
nouveaux types supportés par EM-OCL.
PairType
Les types Pair sont conformes si les types des
éléments formant les couples ordonnées le sont.
context PairType
inv :
PairType.allInstances()-+forAll(p|
self-+first().conformsTo(p -+ first())
and
self-+ second().conformsTo(p
-+second())implies self.conformsTo(p))
BinaryRelationType
BinaryRelationType est conforme à tout autre type dont les
types des éléments sont conformes entre eux.
context BinaryRelationType
inv :
BinaryRelationType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
PartialFunctionType
PartialFunctionType est conforme à tout autre type dont
les types des éléments sont conformes entre eux.
context PartialFunctionType
inv :
PartialFunctionType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
TotalFunctionType
TotalFunctionType est conforme à tout autre type dont les
types des éléments sont conformes entre eux.
context TotalFunctionType
inv :
TotalFunctionType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
PartialInjectiveType
PartialInjectiveType est conforme à tout autre type dont
les types des éléments sont conformes entre eux.
context PartialInjectiveType
inv :
PartialInjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
TotalInjectiveType
TotalInjectiveType est conforme à tout autre type dont les
types des éléments sont conformes entre eux.
context TotalInjectiveType
inv :
TotalInjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
PartialSurjectiveType
PartialSurjectiveType est conforme à tout autre type dont
les types des éléments sont conformes entre eux.
context PartialSurjectiveType
inv :
PartialSurjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
TotalSurjectiveType
TotalSurjectiveType est conforme à tout autre type dont
les types des éléments sont conformes entre eux.
context TotalSurjectiveType
inv :
TotalSurjectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
PartialBijectiveType
PartialBijectiveType est conforme à tout autre type dont
les types des éléments sont conformes entre eux.
context PartialBijectiveType
inv :
PartialBijectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
TotalBijectiveType
TotalBijectiveType est conforme à tout autre type dont les
types des éléments sont conformes entre eux.
context TotalBijectiveType
inv :
TotalBijectiveType.allInstances()-+forAll(s|self-+elementType.conformsTo(
s.elementType) implies self.conformsTo(s))
2.1.3 Règles de bonnes utiisations des nouveaux
types
A l'instar d'OCL, nous représentons les règles de
bonnes utilisations (Well-formdness rules) des nouveaux types proposés
par EM-OCL.
PairType
Le nom du typePair est 'Pair' suivi par les deux noms
des types des éléments formant le couple ordonné.
context PairType
inv :
name='Pair('+self.first.name+','+self.second.name+')'
SetRefType
Le nom du type SetRef est 'SetRef' suivi par le nom du
type des éléments de l'ensemble.
context SetRefType
inv :
name='SetRef('+self.elementType.name+')'
SequenceRefType
Le nom du type SequenceRef est 'SequenceRef' suivi par le nom du
type des éléments de l'ensemble.
context SequenceRefType
inv :
name='SequenceRef('+self.elementType.name+')'
BinaryRelationType
Le nom du type BinaryRelation est 'BinaryRelation' suivi par le
nom du type pair des couples de la relation.
context BinaryRelationType
inv :
name='BinaryRelation('+self.elementType.name+')'
PartialFunctionType
Le nom du type PartialFunction est 'PartialFunction' suivi par le
nom du type pair des couples de la fonction.
context PartialFunctionType
inv :
name='PartialFunction('+self.elementType.name+')'
TotalFunctionType
Le nom du type TotalFunction est 'TotalFunction' suivi par le nom
du type pair des couples de la fonction.
context TotalFunctionType
inv :
name='TotalFunction('+self.elementType.name+')'
PartialInjectiveType
Le nom du type PartialInjecive est 'PartialInjective' suivi par
le nom du type pair des couples de la fonction.
context PartialInjectiveType
inv :
name='PartialInjective('+self.elementType.name+')'
PartialSurjectiveType
Le nom du type PartialSurjective est 'PartialSurjective' suivi
par le nom du type pair des couples de la fonction.
context TotalSurjectiveType
inv :
name='TotalSurjective('+self.elementType.name+')'
TotalInjectiveType
Le nom du type TotalInjecive est 'TotalInjective' suivi par le
nom du type pair des couples de la fonction.
context TotalInjectiveType
inv :
name='TotalInjective('+self.elementType.name+')'
PartialSurjectiveType
Le nom du type PartialSurjective est 'PartialSurjective' suivi
par le nom du type pair des couples de la fonction.
context PartialSurjectiveType
inv :
name='PartialSurjective('+self.elementType.name+')'
TotalBijectiveType
Le nom du type TotalBijective est 'TotalBijective' suivi par le
nom du type pair des couples de la fonction.
context TotalBijectiveType
inv :
name='TotalBijective('+self.elementType.name+')'
PartialBijectiveType
Le nom du type PartialBijective est 'PartialBijective' suivi par
le nom du type pair des couples de la fonction.
context PartialBijectiveType
inv :
name='PartialBijective('+self.elementType.name+')'
2.2 Augmentations liées à la
bibliothèque standard d'OCL
2.2.1 Conception d'une bibliothèque
mathématique
La conception d'une bibliothèque mathématique
[?]- représentant et manipulant des notions
mathématiques telles que paire ordonnée, relation et fonction -
en adoptant une approche orientée objet doit tenir compte de certains
problèmes liés à des concepts mathématiques
utilisés dans la théorie des ensembles tels que :
- problème d'héritage dans la
hiéarchie : La hiérarchie d'héritage
modélisant les relations entre les nouvelles collections ne correspond
pas nécessairement à la taxonomie naturelle des structures
mathématiques. Ceci est illustré par un exemple explicatif :
Considérons les deux classes
BinaryRelation(Pair(G,H)) et PartialFunction(Pair(G,H))
correspondant respectivement à une relation binaire de couples
d'éléments et une fonction partielle de couples
d'éléments. D'un point de vue mathématique, il est
évident qu'une fonction hérite d'une relation binaire. En effet,
une fonction est une relation binaire dont chaque élément du
domaine est relié à au plus à un élément du
co-domaine. D'un point de vue orientée objet, l'utilisation d'une
relation d'héritage entre ces deux classes entraîne un
mécanisme de polymorphisme : plusieurs opérations valides pour
une relation binaire, ne le seront pas pour une fonction. En effet, il faut
tenir compte de certaines contraintes pour l'opération d'intersection
(l'intersection d'une fonction doit être nécessairement une
fonction), ainsi que l'inverse d'une fonction injective (l'inverse d'une
fonction injective doit être une fonction injective).
- Extension de la classe Set : certaines
opérations qui s'appliquent sur les ensembles doivent être
ajoutées à l'ensemble des opérations applicables sur la
classe Set. Pour cela, on définit SetRefType descendant du type
Set.
Ces opérations sont les suivantes : identity,
firstProj, secondProj.
- Extension de la classe Sequence certaines
opérations qui s'appliquent sur les ensembles doivent être
ajoutées aux opérations applicables sur la classe Set.
Pour cela ,nous avons introduit le nouveau type SequenceRefType descendant du
type Sequence. Ces opérations sont les suivantes : insertRight,
reverse, tail et front.
La figure 2.2 propose une taxonomie des notions
mathématiques intégrées dans EMOCL. Nous notons que toutes
les classes sont génériques. Elles admettent un seul
paramètre générique ayant la forme suivante : T=Pair(G,H),
où :
G : le type des éléments de
l'ensemble de départ.
H : le type des éléments de
l'ensemble d'arrivée.
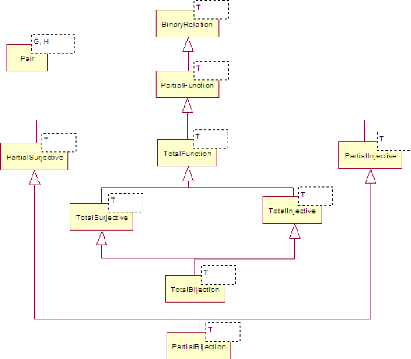
FIGURE 2.2 - Graphe de classes de la bibliothèque EM
ajoutée à OCL
2.2.2 Opérations offertes par la
bibliothèque EM
Ici, nous présentons les opérations applicables sur
les classes offertes par la bibliothèque EM. La sémantique de ces
opérations est soigneusement définie en EM-OCL.
La classe Pair
make(f :G, s :H) :Pair(G,H) Permet de
créer une paire ordonnée.
post :result.first()=f
post :result.second()=s
first() : G
Permet d'extraire le premier élément d'une paire
ordonnée.
second() : H
Permet d'extraire le second élément d'une paire
ordonnée.
=(p :Pair(G,H) :Boolean
Rend True si les deux éléments de self et
p coincident.
post :result implies
self.first()= p.first() and
self.second()=p.first()
reverse() :Pair(H,G)
Permet d'inverser une paire ordonnée.
post
:result.second()=self.first() post
:result.first()=self.second() post
:result.reverse()=self - - l'opération =
de Pair
La classe SetRef
On suppose que la classe SetRef a comme paramètre
générique de type G.
identity() :BinaryRelation(Pair(G,G)) Retourne
l'identité d'un ensemble.
post: let c : Pair(G,G)=Pair[]
in
result=self-+iterate(e :G|accu
:BinaryRelation(Pair(G,G))=BinaryRelation{}|
accu-+including(c.make(e,e)))
firstProj(ens :Set(H)) :BinaryRelation(Pair(Pair(G,H),G))
Permet de calculer la première projection d'un ensemble.
post: let c2 :
Pair(G,H)=Pair[], c1 :Pair(Pair(G,H),G)=Pair[] in
result=self-+iterate(e1 :G|accu
:BinaryRelation(Pair(Pair(G,H),G))=BinaryRelation{}| ens-+iterate(e2
:H|accu.including(c1.make(c2.make(e1,e2),e1))))
secondProj(ens :Set(H) :BinaryRelation(Pair(Pair(G,H),H)
Permet de calculer la deuxième projection d'un ensemble.
post: let: c2 :
Pair(G,H)=Pair[], c1 :Pair(Pair(G,H),H)=Pair[] in
result=self-+iterate(e1 :G|accu
:BinaryRelation(Pair(Pair(G,H),H))=BinaryRelation{}| ens-+iterate(e2
:H|accu.including(c1.make(c2.make(e1,e2),e2))))
La classe SequenceRef
On suppose que la classe SequenceRef a comme paramètre
générique de type G.
insertRight(o :G) :SequenceRef(G)
Permet d'insérer un élément o
à la fin de la séquence.
post
:result=self?insertAt(self?size()+1,o)
post
:result?size()=self?size()+1
reverse() :SequenceRef(G) Permet d'inverser
self.
post
:result=Sequence{1..self?size()}?iterate(pn;
acc :SequenceRef(G)=SequenceRef{}|
acc?insertAt(self?size()+1-pn ;self?at(pn)))
post:
result?size()=self?size()
tail() :SequenceRef(G)
Permet d'écarter le premier élément de la
séquence.
pre :self?size()>0
post
:result=self?subSequence(2,self?size()) post
: result?size()=self?size()-1
front() :SequenceRef(G)
Permet d'écarter le dernier élément de la
séquence.
pre: self?size()>0
post
:result=self?subSequence(1,self?size()-1)
post : result?size()=self?size()-1
La classe BinaryRelation
domaine() : SetRef(G)
Retourne les éléments du premier ensemble G qui
sont effectivement en relation avec des éléments du second
ensemble H.
post: result = self?iterate(e :
Pair(G,H);
accu : SetRef(G)=SetRef{}|accu?including(e.first()))
range() :SetRef(H)
Retourne des éléments de l'ensemble H qui sont en
relation avec des éléments du premier ensemble G.
post: result = self-+iterate(e :
Pair(G,H);
accu :
SetRef(G)=SetRef{}|accu-+including(e.second()))
imageSet(F : SetRef(G)) : SetRef(H) Retourne
l'image de l'ensemble F.
pre: G-+includesAll(F)
post: result = self-+iterate(e :
Pair(G,H); accu : SetRef(H) =SetRef{}| if (
F-+includes(e.first()))
then accu-+including(e.second())
endif) )
imageElt(e :G) : SetRef(H)
Retourne l'ensemble des éléments de H qui sont en
relation avec e.
pre: G-+includes(e)
post: result = self-+iterate(x :
Pair(G,H); accu : SetRef(H) =SetRef{}|
if(e.first()=x)
then accu-+including(e.second())
endif) )
inverse() :BinaryRelation(Pair(H,G)) Retourne
l'inverse de la relation binaire self.
post: let couple : Pair(G,H)=Pair[]
in
result = self-+iterate( e :
Pair(G,H);
accu : BinaryRelation(Pair(H,G)) :BinaryRelation{} |
accu-+including( couple.make(e.second(),e.first()))
post: result.inverse()=self post:
result-+size()=self-+size()
seqComposition(r :BinaryRelation(Pair(H,K)))
:BinaryRelation(Pair(G,K)) Retourne la composition séquentielle
de deux relations binaires.
post: let couple : Pair(G,H)=Pair[]
in
result = self-+iterate ( e : Pair(G,H);
accu :BinaryRelation(Pair(G,K))=BinaryRelation{}| r-+iterate(e1 :
Pair(H,K) |
if( e.second()=e1.first()) then
accu-+including( couple.make(e.first(),e1.second()))
endif ))
directProduct(r : BinaryRelation(Pair(G,K)))
:BinaryRelation(Pair(G ,TupleType(H,H)))
retourne le produit direct de deux relations binaires.
post: let c1 : Pair(G,TupleType(H,K))=Pair[]
in
result = self-+iterate(e1
:PairType(G,H);
accu :BinaryRelation(Pair(G,TupleType(H,K)))=BinaryRelation{}|
r-+iterate( e2 : Pair(G,K)| if (e1.second()
=e2.second()) then
accu-+including(c1.make(e1.first(),
tuple(e1.second(),e2.second()))) endif))
ParallelProduct(r : BinaryRelation(Pair(K,M)))
:BinaryRelation(Pair(Pair(G,K), Pair(H,M)))
retourne le produit parallèle de deux relations
binaries.
post: let c1 : Pair(G,H)=Pair[] ,
c2 : Pair(K,M)=Pair[],
couple : Pair(Pair(G,H),Pair(K,M))=Pair[] in
result = self-+iterate(e1
:Pair(G,H);
accu :BinaryRelation(Pair(Pair(G,K),Pair(H,M)))=BinaryRelation{}|
r-+iterate( e2 : PairType(K,M)| acc
-+including(couple.make(c1.make(e1.first(),e2.first()),
c2.make(c1.second(),c2.second())))))
-Iterations
Les itérations sur les relations permettent
d'itérer une relation: c'est-à-dire la composer
séquentiellement avec elle-même un certain nombre de fois.
iteration(n :Integer)
:BinaryRelation(Pair(G,H))
pre: G.oclIsTypeOf(H)
post: if (n=0) then
result=G-+identity() else
let acc :BinaryRelation(Pair(G,H))=self
in Sequence{2..n}-+iterate(pn ;acc=self|
acc-+seqComposition(self))
endif
closeTrans() :BinaryRelation(Pair(G,H))
pre: G.oclIsTypeOf(H)
-Restrictions
restrictionDomaine(E :Set(G)) :BinaryRelation(Pair(G,H))
Permet de restreindre une relation sur un sous-ensemble du domaine.
pre:
G::allInstances()-+includesAll(E)
post: let couple : Pair(G,H)=Pair[]
in
result= self-+iterate(e1 :Pair(G,H);
accu :BinaryRelation(Pair(G,H))=BinaryRelation{}|
if E-+includes(e1.first()) then
accu-+including(couple.make(e1.first(),e1.second()))
endif )
soustractionDomaine(E :Set(G)) :
BinaryRelation(Pair(G,H)) Permet de soustraire une relation sur un
sous-ensemble du codomaine.
pre:
G::allInstances()-+includesAll(E)
post: let couple : Pair(G,H)=Pair[]
in
result= self-+iterate(e1 : Pair(G,H);
accu :BinaryRelation(Pair(G,H)))=BinaryRelation{}| if
E-+excludes(e1.first()) then
accu-+including(couple.make(e1.first(),e1.second()))
endif )
restrictionRange(F :SetRef(H)) :
BinaryRelation(Pair(G,H)) Permet de restreindre une relation sur un
sous-ensemble du codomaine.
pre:
H::allInstances()-+includesAll(F)
post: let couple: Pair(G,H)=Pair[]
in
result= self-+iterate(e1 : Pair(G,H);
accu :BinaryRelation(Pair(G,H)))=BinaryRelation{}|
if F-+includes(e1.second())
then
accu-+including(couple.make(e1.first(),e1.second()))
endif )
soustractionRange(F :SetRef(H)) :
BinaryRelation(Pair(G,H))) Permet de soustraire une relation sur un
sous-ensemble du codomaine.
pre: H::allInstances()->includesAll(F)
post: let couple : Pair(G,H)=Pair[]
in
result= self-+iterate(e1 :
PairType(G,H); accu :BinaryRelation(Pair(G,H))=BinaryRelation{}|
if
F-+excludes(e1.second()) then
accu-+including(couple.make(e1.first(),e1.second()))
endif )
La classe PartialFunction
Nous préconisons une approche orientée invariant
afin de modéliser l'abstraction PartialFunction.
invariant de classe
Une fonction est une relation dont chaque élément
du domaine est associé à au plus à un
élément du co-domaine et son domaine est inclus dans l'ensemble
de départ.
context PartialFunction
inv : self?forAll(e1,e2 : Pair(G,H)|
if e1.first()=e2.first() then
e1.second()=e2.second()) inv : G::
allInstances()?includesAll(self?domain())
redéfinition des opérations
intersection(f :PartialFunction(Pair(G,H)))
:PartialFunction(Pair(G,H)) L'intersection de deux fonctions doit
être une fonction.
post:
result?forAll(elem|self->includes(elem) and
f?includes(elem)) post:
self?forAll(elem|f?includes(elem)=
result?includes(elem)) post:
f?forAll(elem|self?includes(elem)=result?includes(elem))
imageElement(x :G) : H
Permet de retourner l'image d'un élément x
appartenant au domaine par une fonction.
pre: self
?domaine()?includes(x)
post: let couple : Pair(G,H)=Pair[] in
self?includes(couple.make(x,result))
La classe TotalFunction invariant de
classe
Une fonction totale est une relation dont le domaine correspond
à tous les éléments de l'ensemble de départ.
context TotalFunction
inv : self?domaine()=G::allInstances
La classe PartialInjective
Une fonction injective partielle est fonction partielle dont
l'inverse doit être injective.
context PartialInjective
inv :
self?inverse().oclIsTypeOf(PartialFunction)
La classe PartialSurjective
Une fonction surjective partielle est fonction partielle dont le
codomaine correspond à l'ensemble d'arrivée.
context PartialSurjective
inv : self?range()=H::allInstances()
La classe TotalSurjective
Une fonction surjective totale est fonction totale dont le
codomaine correspond à l'ensemble d'arrivée.
context TotalSurjective
inv : self?range()=H::allInstances()
| 


