Chapitre 2
Introduction aux réseaux d'ondelettes
Introduction aux réseaux d'ondelettes
Introduction
En 1983, J. Morlet et Grossmann ont proposé un
procédé révolutionnaire, l'analyse par ondelettes, qui
permet d'analyser efficacement des signaux où se combinent des
phénomènes d'échelles très différentes.
L'analyse par ondelettes est reconnue comme un outil puissant d'analyse et de
reconstruction de signaux.
Dans ce chapitre, nous présentons, tout d'abord, les
limites des techniques classiques d'analyse des signaux. Ensuite, nous abordons
l'historique des ondelettes, puis nous détaillerons cette théorie
et ses avantages.
Dans la seconde partie, nous décrivons la notion des
réseaux de neurones, leurs principes de fonctionnement illustrés
par quelques exemples et leurs relations avec les ondelettes.
Enfin, nous montrons une nouvelle approche hybride
basée sur la combinaison entre les réseaux de neurones et les
ondelettes : les réseaux d'ondelettes. Différents
modèles de ces réseaux d'ondelettes sont
étudiés.
I. L'analyse de Fourier
L'analyse de Fourier a dominé l'analyse
mathématique pendant plus d'un siècle. Elle a même
influencé la théorie des nombres et les probabilités. En
dehors des mathématiques, son influence est incontestable. Que se soit
dans les domaines de la téléphonie, de l'imagerie médicale
ou des outils de communications radios, l'analyse de Fourier est
omniprésente. Très souvent, lorsque des scientifiques ou des
ingénieurs analysent des systèmes ou cherchent des solutions,
c'est l'analyse de Fourier qui est utilisée.
La décomposition en série de Fourier d'une
fonction périodique permet de représenter celle-ci comme une
somme infinie de sinus et de cosinus de fréquences différentes
(2.1). Ce qui permet une foule d'applications, notamment le traitement du
signal (les signaux carrés, triangulaires, ...). Mais, la
catégorie de fonctions auxquelles elle s'applique est restreinte.
Par conséquent, la décomposition en série
de Fourier est très limitée et peu de signaux naturels
remplissent la condition d'être périodique.
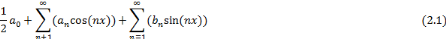
Si on veut représenter une fonction périodique
f par une série trigonométrique, il faut
déterminer les paramètres an et
bn.
La série de Fourier d'une fonction f
périodique tel que f(t+T) = f(t) se déduit donc de
l'expression (2.1) et on la définit comme une série
trigonométrique :
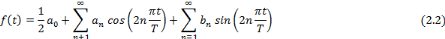
Où les coefficients de Fourier a0,
an et bn sont définis par :



Les séries de Fourier sont, dans certains cas,
limitées. Tout d'abord, la fonction f doit être
périodique. Elle est exprimée par une somme de sinusoïdes
qui sont des fonctions périodiques et on peut montrer qu'une somme
quelconque de fonctions périodiques est encore une fonction
périodique. En effet, pour représenter d'autres fonctions sur  , on aura besoin d'un nouvel outil : La transformée de
Fourier [45]. , on aura besoin d'un nouvel outil : La transformée de
Fourier [45].
La transformée de Fourier est un passage d'une
représentation d'un signal à une autre.

La reconstruction du signal peut être
réalisée par la transformée inverse :

En règle générale, tous les signaux
physiques remplissent les conditions nécessaires pour être
traités par transformée de Fourier. L'intérêt d'une
telle décomposition est alors de pouvoir analyser ces signaux en
fréquences et repérer ainsi leur contenu fréquentiel
[45].
L'analyse de Fourier, Malgré ses avantages, elle
représente quelques inconvénients, en particulier son manque de
localisation temporelle. En effet, elle permet de connaître les
différentes fréquences excitées dans un signal,
c'est-à-dire son spectre, mais ne permet pas de savoir à quels
instants ces fréquences ont été émises. Cette
analyse donne une information globale et non locale, car les fonctions
d'analyse utilisées sont des sinusoïdes qui oscillent
indéfiniment sans s'amortir. Cette perte de localité devient un
problème pour l'étude de signaux non stationnaires.
| 


