3.3 Profil de Pauvreté
L'analyse de profil de la pauvreté des ménages
est faite dans l'objectif de voir les caractéristiques des
ménages qui expliquent leur état de pauvreté.
L'idée est de caractériser ces ménages à travers
des facteurs comme le groupe socio-économique du chef de ménage,
son niveau d'instruction, son statut matrimonial, son milieu de
résidence, son âge, sa région d'habitation et la taille du
ménage.
3.3.1 Résultats de l'analyse discriminante
Dans notre étude, l'échantillon porte sur 7552
ménages. Dans notre exemple il n'y a pas de données manquantes,
toutes les unités ont été utilisées pour faire
l'analyse discriminante. Pour rappel toutes les analyses multidimensionnelles
ne tolèrent pas les données manquantes, dans de telles
conditions, deux options nous est offertes, soit corriger les données
manquantes, soit les exclure de l'analyse.
3.3.1.1 Vérification de l'existence de
différence entre les deux groupes
L'étude des profils des deux groupes à partir du
graphique 02 montre qu'il ya des différences notables entre scores
moyens sur les variables.
Graphique 02 : Profils des groupes
constitués
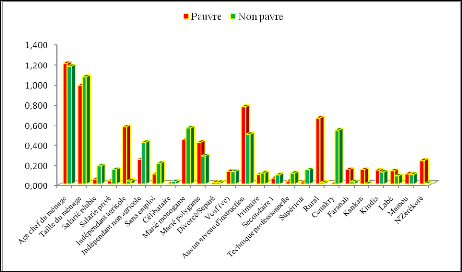
Source : Calcul de l'auteur sur les données de l'ELEP 2007
sous SPSS
34
Mémoire de fin d'études
La significativité de ces différences peut
être davantage mise en évidence grâce aux tests de
Fisher et au lambda de Wilks réalisés dans le cadre
de l'analyse discriminante.
Hypothèses du test
y' H0 : moyenne du groupe des pauvres = moyennes du groupe des
non pauvres
y' H1 : moyenne du groupe des pauvres ? moyennes du groupe des
non pauvres
Prise de décision
y' Si la valeur de alpha est supérieure à 0,05,
nous devons accepter l'hypothèse nulle et
conclure qu'il n'y a pas de différence significative entre
les groupes.
y' Si la valeur de alpha est inférieure ou égale
à 0,05, on rejette l'hypothèse nulle et
conclure qu'il y a une différence significative entre les
groupes.
Tableau 06 : Tests d'égalité des
moyennes des groupes
|
Lambda de
Wilks
|
Fisher
|
ddl1
|
ddl2
|
Signification
(á)
|
|
Âge chef du ménage
|
0,998
|
12,574
|
1
|
7550
|
0,000
|
|
Taille du ménage
|
0,993
|
51,225
|
1
|
7550
|
0,000
|
|
Salarié public
|
0,954
|
366,513
|
1
|
7550
|
0,000
|
|
Salarié privé
|
0,958
|
331,030
|
1
|
7550
|
0,000
|
|
Indépendant agricole
|
0,757
|
2418,149
|
1
|
7550
|
0,000
|
|
Indépendant non agricole
|
0,971
|
222,406
|
1
|
7550
|
0,000
|
|
Sans emploi
|
0,979
|
164,477
|
1
|
7550
|
0,000
|
|
Célibataire
|
0,992
|
61,192
|
1
|
7550
|
0,000
|
|
Marié monogame
|
0,989
|
84,208
|
1
|
7550
|
0,000
|
|
Marié polygame
|
0,984
|
124,166
|
1
|
7550
|
0,000
|
|
Divorcé/Séparé
|
1,000
|
0,084
|
1
|
7550
|
0,772
|
|
Veuf (ve)
|
1,000
|
0,011
|
1
|
7550
|
0,918
|
|
Aucun niveau d'instruction
|
0,928
|
589,733
|
1
|
7550
|
0,000
|
|
Primaire
|
1,000
|
2,739
|
1
|
7550
|
0,098
|
|
Secondaire 1
|
0,997
|
22,696
|
1
|
7550
|
0,000
|
|
Technique professionnelle
|
0,977
|
181,418
|
1
|
7550
|
0,000
|
|
Supérieur
|
0,946
|
431,416
|
1
|
7550
|
0,000
|
|
Rural
|
0,662
|
3856,593
|
1
|
7550
|
0,000
|
|
Conakry
|
0,558
|
5979,317
|
1
|
7550
|
0,000
|
|
Faranah
|
0,969
|
241,101
|
1
|
7550
|
0,000
|
|
Kankan
|
0,957
|
336,970
|
1
|
7550
|
0,000
|
|
Kindia
|
0,999
|
4,704
|
1
|
7550
|
0,030
|
|
Labé
|
0,995
|
37,956
|
1
|
7550
|
0,000
|
|
Mamou
|
1,000
|
0,473
|
1
|
7550
|
0,491
|
|
N'Zérékoré
|
0,926
|
606,704
|
1
|
7550
|
0,000
|
Source : Calcul de l'auteur sur les données de l'ELEP 2007
sous SPSS
35
Mémoire de fin d'études
Le tableau 06 présente les résultats d'analyse
de variance univarisée pour chacune des variables indépendantes.
Ces analyses vérifient s'il existe des différences entre les
moyennes des groupes sur chacune des variables prises isolément.
La comparaison des moyennes des groupes par le biais du test
de Fisher et le lambda de Wilks montre que pour un niveau de signification de
0,05 les moyennes des groupes diffèrent pour toutes les variables sauf
pour les quatre variables « Divorcé/Séparé »,
« Veuf », « Primaire » et « Mamou ».
Les variables « Divorcé/Séparé
», « Veuf », « Primaire » et « Mamou ».n'ont
aucun effet discriminant sur le niveau de vie, puisque leurs seuils de
signification sont supérieurs au seuil minimal de 0,05.
La valeur du lambda de Wilks univarié varie entre 0
(pouvoir discriminant absolu) et 1 (pouvoir discriminant nul). La valeur 1
signifie l'égalité des moyennes pour l'ensemble des groupes. Une
valeur quasi nulle signifie des différences fortes entre les groupes.
Les lambdas associés à ces quatre variables sont
très élevés puisque chacune d'elle a un lambda égal
à 1.
|
|



