1.2.9. Calcul de centralité [CH10]
Un réseau social est un ensemble
d'individus ou d'organisations reliés par des interactions
sociales régulières. Un domaine scientifique nommé
analyse des réseaux sociaux, les étudie en se basant sur la
théorie des graphes et l'analyse sociologique.Le calcul de
centralité est depuis plusieurs décennies une
problématique importante dans le domaine de l'analyse des réseaux
sociaux [WF94]. Le calcul de centralité est une notion qui a
été mise en oeuvre pour rendre compte de la popularité ou
la visibilité d'un acteur (noeud) au sein d'un groupe (graphe). Cette
notion représente l'une des contributions les plus importantes dans le
domaine de l'analyse de réseaux sociaux. Ces contributions sont
traitées dans l'article « Centrality in social networks:
Conceptual clarification [FR79]. Dans son article, Freeman propose trois
définitions formelles du concept de centralité que nous
présentons ci-dessous.
Dans le but de quantifier cette notion d'importance d'un noeud
dans un graphe, les chercheurs ont proposé plusieurs définitions
connues sous le nom de mesures de centralité. En effet, l'identification
des noeuds centraux dans un graphe représente un enjeu important dans
plusieurs domaines. Prenons le cas des réseaux de communication ;
le fait de connaitre les noeuds importants permet d'adopter des
stratégies afin de mieux protéger ces noeuds qui jouent un
rôle essentiel dans la communication au sein du réseau.
Considérons à titre d'exemple le réseau de communication
de la figure 1.16.
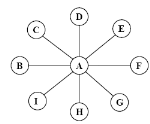
Figure 1.16 : Exemple d'un réseau de
communication
On remarque que si le noeud B tombe en panne, la communication
entre les différents noeuds ne sera pas affectée. Par contre, si
le noeud A (point d'articulation du graphe) tombe en panne, cela engendrerait
un grand problème de communication puisque tous les noeuds se
retrouveront isoles.
Lors de l'étude de la notion de centralité, il
est important de distinguer le cas des graphes orientés du cas des
graphes non-orientés. Dans les graphes orientés, les noeuds
possèdent deux types de liens, à savoir des liens entrants et des
liens sortants. Pour une définition donnée de la notion de
centralité, chaque noeud aura alors deux mesures d'importance : une
mesure relative à ses liens sortants, appelée mesure de
centralité, d'influence, d'hubité ou de centralité
sortante, et une autre mesure relative à ses liens entrants,
appelée mesure de prestige, de popularité, d'autorité ou
de centralité entrante. Dans un graphe non-orienté, chaque noeud
possède un seul type de liens ou de relations avec les autres noeuds.
Chaque noeud possède alors une seule mesure d'importance (correspondant
à une définition précise) appelée mesure de
centralité [WF94].
Dans la suite de ce chapitre, nous décrivons quelques
mesures de centralité dans les graphes orientés et
non-orientés. Nous commençons par rappeler les principales
mesures proposées dans le domaine de l'analyse des
réseaux sociaux (qui sont des applications très
rependue des bases de données graphe). Celles-ci incluent les
centralités de degré, d'intermédiarité ainsi que de
proximité.
a. Centralité de degré
La centralité de degré [FR79] représente
la forme la plus simple et la plus intuitive de la notion de centralité.
Elle est basée sur l'idée qu'un noeud (individu) occupe une place
importante dans un graphe (groupe) s'il est à plus des voisins (s'il a
plusieurs personnes qu'il connait ou interagit directement). Cela consiste
alors à calculer le nombre de ses sommets voisins, ou de manière
équivalente, à calculer le nombre de liens qui lui sont incidents
qu'on appelle évidemment degré du noeud, d'où
l'appellation de centralité de degré.
Soit G = (X, U) un graphe d'ordre n représente par sa
matrice d'incidence sommets-sommets de A. Dans le cas où le graphe G est
non-orienté, la centralité de degré d'un noeud
xi? X est définie par :
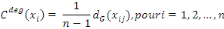
En notation matricielle, le vecteur de la centralité de
degré est donne par :
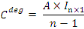
Où 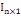 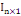 est un vecteur-colonne de dimension n necontenant des que 1. est un vecteur-colonne de dimension n necontenant des que 1.
Au lieu d'utiliser la matrice d'adjacence A (qu'on appelle
aussi matrice d'incidence sommet-sommet), on peut aussi utiliser la matrice de
degrés D.
Ce qui implique que le vecteur calcul de centralité de
degré en notation matricielle peut s'écrire :
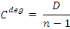
Dans le cas où le graphe G est orienté, chaque
noeud xi?X possède alors deux mesures de centralité de
degré : une par rapport aux arcs incidents extérieurement et une
par rapport aux arcs incidents extérieurement.
Elles sont définies respectivement par :
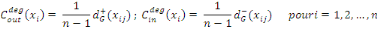
En termes de matrices, les vecteurs de centralité de
degré sortant et de degré entrant sont donnés
respectivement par :
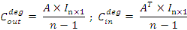
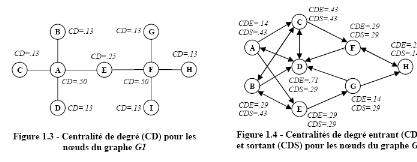
Les figures 1.17 et 1.18 indiquent respectivement la
centralité de degré pour les noeuds graphes G1 et
G2. Les résultats fournis par cette analyse de la
centralité de degré montrent que les noeuds A et F, ayant quatre
liens chacun, sont les plus importants dans le graphe G1. Pour le
graphe G2, les noeuds A, B et C possèdent la plus forte
centralité par rapport aux liens sortants, tandis que le noeud D
possède la plus forte centralité par rapport aux liens entrants.
La centralité de degré est aussi appelée
mesure de centralité locale car elle ne prend pas en compte la structure
globale du graphe et n'est calculée qu'à partir du voisinage
immédiat d'un sommet. Bien qu'elle soit pertinente dans certaines
situations, la centralité de degré s'avère être peu
informative dans d'autres cas, comme par exemple pour l'analyse des graphes de
pages web. Les mesures que nous présentons dans la suite sont toutes des
mesures de centralité globales.
|
Figure 1.17 : Centralité de degré (CD)
pour les noeuds du graphe G1
|
Figure 1.18 : Centralité de proximité
entrante (CDE) et sortante (CDS) pour les noeuds du graphe
G2
|
Source : [CH10]
b. Centralité de proximité
La centralité de proximité [FR79] est une mesure
de centralité globale basée sur l'intuition qu'un noeud occupe
une position stratégique (ou importante) dans un graphe s'il est
globalement proche des autres noeuds de ce graphe. Par exemple dans un
réseau social, cette mesure correspond à l'idée qu'un
acteur est important s'il est capable de contacter facilement un grand nombre
d'acteurs avec un minimum d'effort (l'effort ici est relatif à la taille
des chemins). En pratique, la centralité de proximité d'un noeud
est obtenue en calculant sa proximité moyenne vis-à-vis des
autres noeuds du graphe.
Soit G = (X, U) un graphe (orienté ou non) d'ordre n
représente par sa matrice d'adjacence A. Dans le cas où le graphe
G est non-orienté, la centralité de proximité d'un noeud
xi? X est définie par :
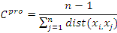
Où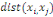 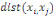 est la distance entre les deux sommets est la distance entre les deux sommets 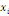 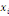 et et 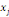 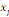
Dans le cas où le graphe G est orienté, chaque
noeud xi? X possède alors deux mesures de centralité
de proximité : une par rapport aux liens sortants et une par rapport aux
liens entrants. Elles sont définies respectivement par :
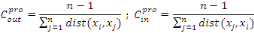
Où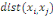 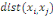 est la distance entre les deux sommets est la distance entre les deux sommets 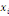  et et  
Pour le calcul des distances entre sommets, plusieurs
métriques peuvent être utilisées. Freeman propose par
exemple d'utiliser la distance géodésique entre les noeuds.
D'autres mesures de distance telle que la distance euclidienne peuvent
également être utilisées pour le calcul de la
centralité de proximité.
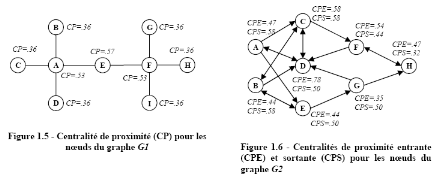
Les figures 1.19 et 1.20 indiquent respectivement la
centralité de proximité (de Freeman) pour les noeuds des graphes
G1 et G2.
|
Figure 1.19 : Centralité de proximité
(CP) pour les noeuds du graphe G1
|
Figure 1.20 : Centralité de proximité
entrante (CPE) et sortante (CPS) pour les noeuds du graphe
G2
|
Source : [CH10]
Remarque : La centralité
d'intermédiarité a pour inconvénients de ne pas fournir
des bons résultats lorsque le graphe n'est pas connexe. Il n'est par
conséquent pas possible de calculer la centralité de
proximité puisque les distances géodésiques entre certains
noeuds sont indéfinies, c'est-à-dire elles ont des valeurs   puisqu'il n'existe aucun chemin entre ces noeuds. puisqu'il n'existe aucun chemin entre ces noeuds.
c. Centralité d'intermédiarité
La centralité d'intermédiarité [FR79] est
une autre mesure de centralité globale proposée par Freeman.
L'intuition de cette mesure est que, dans un graphe, un noeud est d'autant plus
important qu'il est nécessaire de le traverser pour aller d'un noeud
quelconque à un autre. Plus précisément, un sommet ayant
une forte centralité d'intermédiarité est un sommet par
lequel passe un grand nombre de chemins géodésiques le graphe.
Dans un réseau social, un acteur ayant une forte centralité
d'intermédiarité est un sommet tel qu'un grand nombre
d'interactions entre des sommets non adjacents dépend de lui [BE06].
Dans un réseau de communication, la centralité
d'intermédiarité d'un noeud peut être
considérée comme la probabilité qu'une information
transmise entre deux noeuds, qui passe par ce noeud intermédiaire
[BE06].
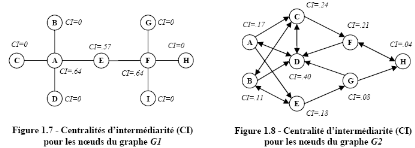
|
Figure 1.21 : Centralité
d'intermédiarité (CI) pour les noeuds du graphe
G1
|
Figure 1.22 : Centralité
d'intermédiarité entrante (CI) pour les noeuds du graphe
G2
|
Source : [CH10]
Soit G = (X, U) un graphe (orienté ou non) d'ordre n.
La centralité d'intermédiarité d'un noeud xi? X
est définie par :
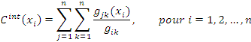
où 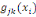 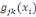 est le nombre total de chemins géodésiques entre les
noeuds est le nombre total de chemins géodésiques entre les
noeuds 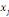 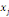 et et 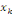 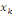 qui passent par le noeud qui passent par le noeud 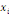 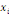 , et , et 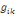 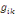 est le nombre total de chemins géodésiques entre les
noeuds est le nombre total de chemins géodésiques entre les
noeuds 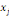 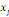 et et 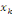 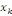 . .
Les figures 1.21 et 1.22 indiquent respectivement la
centralité d'intermédiarité pour les noeuds des graphes
G1 et G2. Nous remarquons que les noeuds A et F sont les
plus importants dans le graphe G1; ces deux noeuds sont en effet les
plus traverses par les chemins géodésiques entre les noeuds du
graphe. Pour le graphe G2, le noeud D est celui par lequel passe le
plus grand nombre de chemins géodésiques entre les noeuds du
graphe; il possède par conséquent la plus forte
centralité. Il est également intéressant de noter pour le
graphe G2, que les noeuds E et F possèdent des
centralités d'intermédiarité différentes bien
qu'ils aient le même nombre de liens entrants et de liens sortants.
La centralité d'intermédiarité est
basée sur l'hypothèse que les noeuds ne communiquent où
interagissent entre eux qu'à travers les chemins les plus courts.
Certains chercheurs ont alors proposé de modifier cette hypothèse
afin de prendre en compte le fait que les noeuds peuvent interagir en utilisant
des chemins autres que les chemins géodésiques. Par exemple,
Freeman [FR91] a proposé la centralité du flux
d'intermédiarité qui n'utilise pas que les chemins
géodésiques mais plutôt tous les chemins
indépendants entre deux noeuds c'est-à-dire les chemins dont les
ensembles d'arcs sont disjoints.
| 


