I.2.2. Graphe complet
Un graphe est dit complet si tous
ses sommets sont reliés et par conséquent ils sont tous de
même degré.
On parle aussi de clique pour un
graphe complet. Ainsi, un graphe complet d'ordre n est appelé
n-clique, on note généralement
Kn, c'est-à-dire un graphe complet d'ordre n
est appelé n-clique.
Quand un graphe n'est pas complet, et que l'ensemble de
sommets peut être partitionné en cliques :
On notera ù le nombre
maximal de sommets d'une clique sous-graphe.
On notera è le nombre
minimal de cliques nécessaires pour partitionner l'ensemble des sommets
du graphe.
Exemple 1.5 : Soit le graphe
K5
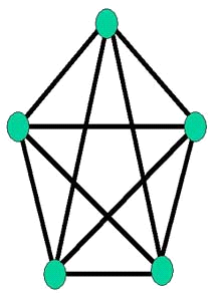
Figure 1.6 : Représentation sagittale d'un
graphe complet
I.2.3. Graphe biparti
Un graphe est dit biparti si
l'ensemble de sommets peut être partitionné en deux classes de
sorte que les sommets d'une même classe ne soient jamais adjacents.
Les graphes de fonctions, applications, bijections sont des
graphes bipartis
On définit aussi des graphes bipartis complets,
notés Km,n
a
b
c
d
e
f
Exemple 1.6 : Soit le graphe
K3,3
Figure 1.7 : Représentation sagittale d'un
graphe biparti
On
appelle sous-graphe engendré par A (partie de
X) le graphe obtenu en ne conservant que les sommets de A et les arcs les
reliant.
On appelle graphe partiel un graphe
obtenu en supprimant un nombre quelconque d'arcs au graphe initial.
On appelle chaîne une
succession d'arcs dont l'extrémité chaque arc
intermédiaire a une extrémité en commun avec l'arc
précédent l'autre extrémité en commun avec l'arc
suivant.
Une chaîne ne rencontrant pas deux fois le même
sommet est dite élémentaire.
Une chaîne ne rencontrant pas deux fois le même
arc est dite simple.
On appelle chemin une succession
d'arcs dont l'extrémité terminale coïncide avec
l'extrémité initiale de son suivant à l'exception du
dernier i.e. un chemin est une chaîne « bien
orientée », car tous les arcs de la chaîne sont
parcourus dans le bon sens.
On appelle cycle une chaîne
simple qui rentre dans son extrémité de départ.
On appelle circuit un cycle
« bien orienté », à la fois cycle et
chemin.
b
a
d
e
f
c
u6
u2
u5
u1
u4
u3
u7
Exemple 1.7 : Soit le graphe G
Figure 1.8 : Graphe ayant une chaine, un chemin, un
circuit et un cycle
· (u1, u4, u5) est une
chaîne dont les arcs 1 et 4 sont directs et 5 inverse
· (u7, u2, u1,
u4) est un chemin : tous les arcs sont parcourus dans le bon
sens.
· (u1, u4, u5,
u2) est un cycle, les extrémités
« libres » des arcs 1 et 2 sont égales; (a,b) puis
(b,f) puis (e,f) puis (e,a).
· (u6, u7, u2) est un
circuit.
On appelle
chaîne eulérienne une chaîne qui
passe une et une seule fois par toutes les arêtes du graphe.
On appelle
chaîne hamiltonnienne une chaîne qui
passe une et une seule fois par tous les sommets du graphe.
On peut bien évidemment étendre les deux notions
précédentes aux chemins, cycles, circuits.
Ainsi, en particulier,
· Le problème consistant à passer, d'une
manière minimale, par tous les sommets du graphe une et une seule fois
en revenant au sommet du départ s'appelle problème du
voyageur de commerce.
· Le problème consistant à parcourir, d'une
manière minimale, tous les arcs du graphe une et une seule fois en
revenant au sommet du départ s'appelle problème du
postier chinois.
| 


