3- Validation
économétrique du modèle de long terme
· Test d'autocorrélation
Le terme d'erreur à une période est dit
autocorrélé s'il est lié à toutes ou à
certaines de ses valeurs passées. Le test de Durbin Watson permet de
détecter l'autocorrélation d'ordre 1. Il n'est valable que si la
variable dépendante retardée n'est pas incluse dans les variables
explicatives. Pour ce qui est du test de Breusch-Godfrey, il s'agit d'un test
LM.
Nous avons utilisé la statistique de Durbin-Watson pour
le test de détection d'autocorrélation des résidus. Apres
la régression du modèle, nous obtenons cette statistique de
Durbin-Watson DW = d = 1.355332. Cette valeur nous indique qu'il y a doute
quant à l'absence d'autocorrélation entre les résidus.
Nous avons alors effectué le test de Breuch-Godfrey pour lever ce doute.
Le tableau suivant donne les résultats de ce test.
Tableau 19 : Test
d'autocorrélation des résidus de Breusch-Godfrey LM Test
|
F-statistic
|
1.279120
|
Prob F(2,15)
|
0.3070
|
|
Obs*R-squared
|
3.788207
|
Prob Chi-square(2)
|
0.1505
|
Source : auteur
La probabilité associée à la F-statistic
qui est de 0.3070 est largement supérieure à la valeur critique
à 5%. Par conséquent nous acceptons l'hypothèse nulle
d'absence d'autocorrélation entre les résidus.
· Test de normalité des
erreurs
Il s'agit de s'assurer que les erreurs suivent une loi
normale. Nous avons appliqué le test de Jarque et Bera. Ce test est
fondé sur la notion de Skewness (asymétrie) et de kurtosis
(aplatissement). La statistique de Jarque et Bera nous donne une valeur de
1.205821. Cette valeur est inférieure au chi-deux à deux
degré de liberté qui est de 5,99. L'hypothèse de
normalité des résidus est donc vérifiée. Nos
résidus suivent donc une loi normale.
· Test
d'hétéroscédasticité des erreurs.
Nous avons obtenu de la mise en oeuvre du test de White, la
statistique égale à 8.116841. Celle-ci se révèle
être inférieure à la valeur du chi-deux (p) à 18
degré de liberté qui est de 28.869, avec p = 2(k+1), k
étant le nombre de variables explicatives (huit dans notre cas). Ceci
entraine le rejet de l'hypothèse H1
d'hétéroscédasticité.
De plus la probabilité du F-statistic est égale
à 0.4939, ce qui est largement supérieur à 5%. Ainsi fort
de tous ces résultats nous rejetons l'hypothèse alternative
d'hétéroscédasticité et acceptons
l'hypothèse nulle d'homoscédasticité au seuil de 5%.
· Test de stabilité du
modèle
Pour tester la stabilité des paramètres de notre
modèle, nous avons utilisé le test de Cusum. Le graphique
ci-dessous est le résultat de ce test.
Figure 18 : test de stabilité de CUSUM
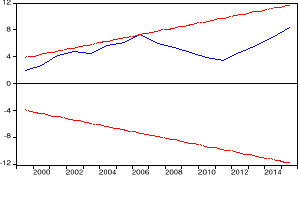
Source : auteur
Le test de Cusum révèle que la courbe
associée à ce test, même si elle le frôle, ne coupe
pas le corridor. Le modèle est donc stable au seuil de 5%.
| 


