II-3-2. Commande vectorielle indirecte par orientation du
flux rotorique
Dans le cas ou une régulation de vitesse est
envisagée, il suffit de prendre la commande indirecte déjà
présentée en ajoutant un régulateur PI pour la boucle de
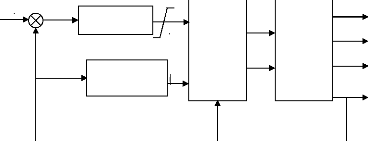
vitesse et contrôle du flux rotorique par réaction Fig. II-3
[2,9,16].

Ù ref
+
-
Régulateur
Bloc non Linéaire
Ör *
*
C
e
DE COU PLA GE
M A S
Fig II-3. Schéma fonctionnel de la commande
vectorielle indirecte de la MAS
alimentée en tension.
BNL : bloc non linéaire est défini par la relation
:
Ö r si Ù ref = Ùr
Ö r = (II-5)
Ù
Ö si Ùref > Ù r
ref
r. Ù r
II-3-3. Le découplage
Le flux réduit à sa seule composante `d' peut
être commandé par le courant Ids et le couple par le
courant Iqs. D'après les équations (I-21), (I-23),
(I-24) et en imposant à la variable ès d'avoir une
valeur telle que Öqr soit nulle, on obtient :

)i
ds
2
)i
qs
2
M
ù
s s
+ ù ó +
. L .i
s sds r
L
r
di
v L
= ó + +
ds (R
dss dt s
di
qs
v L
= ó+ +
(R
qs s s
dt
óL
(II-6)
2
M
-
ù
.
L
r
R
r
2
M
L
r
R
r
*
M
-
2
L
r
Ö
r
R
r
.i
qs
*
Ö
r
Dans ces équations les composantes des deux axes (d, q)
sont couplées.
Leur découplage est possible par l'introduction de deux
nouvelles variables vds1 et vqs1, telles que
vds1 n'agisse que sur ids et
vqs1 sur iqs.
D'après les conditions de l'orientation du flux rotorique
: ( Ö = Ö dr = Ö r et Ö qr = 0), nous pouvons
avoir les équations suivantes :
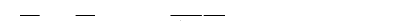
d Ö
(1
)
ó
-
r
(II-7)
dt
M
U
ó + = + ó ù -
ds ds
T i T i T
sdt dsR s s qs
dI
s
s
ó
di U (1 )
- ó
qs qs
T + = - ù ó +

i ( T .i T Ö
s dt qs R s s ds s r
M
s
Les équations montrent bien que les deux axes d, q sont
couplés. On défini les deux nouvelles variables comme suit :
di
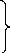
v R ( T ds
ds 1 = s ó s + (II-8)
ds i )
dt
di
v R
=
qs 1 s
i
qs )
ó s +
qs
( T
dt
Nous aurons :
)
I(p) ds
L .p + R s
s
/(
ds 1
= v ó
= v/(óL s .p + R s ) (II-9)
I(p)
qs
qs 1
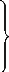
Nous obtenons les équations de découplage suivantes
:
=
v
ds1
1
(
+
1
+
ó T
s
.p
ù
s
v )
qs1
T (1 )
-ó
T
r
L (1)
-ó
s
M.T
r
v T
-ó
ds1 s
s
v
ds
Ö
r
(II-10)
.v +
qs1
v v
=
qs qs1
ó T
s
+ù .(
s ó +
T .p 1
s
L . (1 )
-ó
. Ö
r )
s
M
Le système d'équation (II-8) et (II-10) peut
être représenté par le schéma fonctionnel Fig. II-4
:
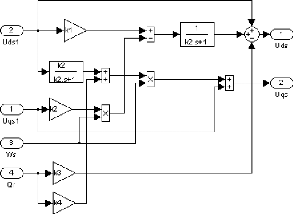
Fig II-4. Schéma fonctionnel du circuit de
découplage
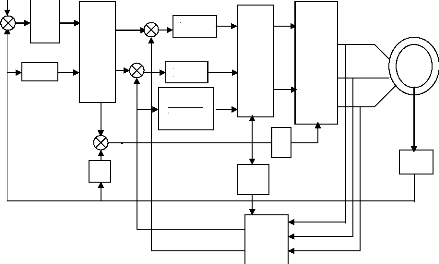
II-3-4. Structure de la commande vectorielle indirecte
Ù
-
+
Bnl
Rv
Ör *
Ce
ùsl ùs
ùr
O F R
p
+
-
+
Ids *
I qs *
+
-
M
T .p 1
r +
R.Ids
R.Iqs
Ids
Iqs
vds1
Ör
vqs1
Dé- cou pla- ge
?
.
Park abc / dq
vds
vqs
?
MLI
+ On -du -leur
Ia
Ib
Ic
Ua
Ub
Uc
GT
M A S
ref
Fig II-5. Schéma fonctionnel de la commande
vectorielle alimentée en tension par
orientation du flux
rotorique
Rv, R.Iqs, R.Ids : représentent
respectivement régulateurs de type PI, de vitesse du courant Iqs et du
courant Ids.
Dans cette commande nous avons trois régulateurs de type
PI (proportionnel intégral) et un bloc d'estimation du flux rotorique
à partir de Ids [16].
| 


