Systeme de transition sur les ordre Partiellement complet

S_ystèmes de transition sur les ordres partiels

complets

DONGHO Joseph

Janvier 2006

Dédicaces

Je dédie ce travail à :

· Mon père FOMDOCK Joseph _qui m'a toujours procuré ce dont j'avais besoin pour mon épanouissement. Que cette oeuvre soit une exhortation à ses voeux.

· Ma mère NGUIMMO Jeanne pour sa vitamine de croissance. Merci Maman.

· A mon tuteur REMBOU ZEUFACK Célestin _que je considère beaucoup.

· A ma défunte _grand-mère ZEMFACK Cecile. Que ceci soit un début d'accomplissement de tes rêves.

· A mon oncle et plus _que père TELEZEM Jean Marie pour toute sa débauche d'éner_gie à la réussite de ce travail. Que ce mémoire soit pour lui le fruit de ma promesse.

Remerciements

Mes remerciements vont tout droit :

· A l'endroit du Dr. NKUIMI JUGNIA Célestin pour avoir _guidé mes premiers pas dans la recherche. Que cette oeuvre soit pour lui le _ga_ge de toute ma reconnaissance, afin _que l'élève sache _qui est le maître et le vénère.

· A tous mes ensei_gnants du supérieur, pour les connaissances de toute nature dont ils m'ont fait _grâce. Particulièrement, je dit un _grand merci à mon ensei_gnant de lo_gi_que Dr. Marcel TONGA dont la ri_gueur et la flexibilité dans les principes m'ont donné un amour illimité de l'al_gèbre.

· Je remercie tous les membres de l'ERAL pour l'instruction _qu'ils m'ont donnée à travers les séminaires et Ateliers. Que Dieu prête lon_gue vie à cette modeste é_quipe. Plus particulièrement, je remercie mes aînés de l'option caté_gorie à savoir Kiampi, Mavou_ggou, Tchou_gon N_guefack, Ko_guep, Fokou, Tchoupo.

· A mon ami de toutes les peines et joies MBIAKOP Hilaire Geor_ges.

· A mes frères et soeurs FOUELEFACK Mitterine . MANETEUG Mitterine, NOUMOGNI Robert, M TENANGUE Gu_y, Mme TENANGUE Laure, DONKENG Pascal, TEMGOUA Solan_ge, LEMOGO David pour _qui je ne re_grette pas la fraternité.

· A ma modeste famille Annie Noel DONFACK, DONGHO Berkoff Junior, FUMDOCK TSAFACK Veudris U, MAGIMTSA Maïva

· A mon cousin et père Dr. TEMGOUA Abert Pascal, pour m'avoir accueilli à Yaoundé et pour m'avoir assisté dans toutes mes entreprises. Je lui exprime ici toute ma _gratitude ainsi _qu'à sa modeste famille _que je respecte beaucoup.

· A mes camarades de promotion en l'occurrence , TABET, PELAP, DIEKOUAM, TCHOUKOUEGNO, NGONDIEP, MENOUKEU, ONGADOA Christian à _qui j'exprime un _grand soula_gement. Qu'ils trouvent en ce mémoire le fruit des nuits blanches passées dans les amphis et laboratoires.

Que tous ceux _qui ont contribué de loin ou de près à la réussite de ce chef d'oeuvre acceptent mes sincères remerciements.

iii

Résumé

Considérons un ordre A dont toute partie diri_gée admet un supremum. Un tel ordre est appelé opc. La collection des parties de A filtrantes et inaccessibles par suprema diri_gés induit sur A une structure topolo_gi_que appelée topolo_gie de Scott. Les applications continues au sens topolo_gi_que entre opc^s sont essentiellement celles _qui préservent les supréma diri_gés. En informati_que théori_que, un s_ystème de transition est un couple ( ) formé d'un

S, S //

ensemble S et d'un sous ensemble S // de S X S. Jus_qu'à présent, cette théorie n'est

définie _que sur la caté_gorie ENS. Nous l'introduisons sur la caté_gorie CPO dont les objets
sont des ensembles enrichis d'une structure ordonnée. Par analo_gie au cas ensembliste, un

( )

s_ystème de transition sur la caté_gorie CPO est simplement un couple A, A // formé

d'un opc A et d'un sous opc A // de A X A.

Nous montrons _que bon nombre de propriétés des s_ystèmes de transition ensemblistes restent vraies dans le cas des s_ystèmes de transition sur les opc^s.

Table des matières

Dédicaces i

Remerciements ii

Résumé iii

Introduction 1

1 ETUDEDELA CATÉGORIE CPO 2

1.1 Construction de la caté_gorie CPO. 2

1.1.1 Quel_ques définitions de bases 2

1.1.2 Quel_ques exemples d'opc⁵ 3

1.1.3 Morphismes d'opc⁵ . 4

1.1.4 Topolo_gie de Scott 5

1.1.5 Caractérisation des monos et épis dans la caté_gorie CPO. 8

1.2 Produits d'opc⁵ . 10

1.3 Exponentiation dans CPO 16

1.3.1 Graphe d'un homomorphisme d'opc⁵ 18

1.4 Coproduit des opc⁵ 20

1.4.1 Exemples de coproduits 21

1.5 Complétion d'un ensemble ordonné en un opc 22

2 SYSTÈME DE TRANSITION SUR LA CATÉGORIE CPO 26

2.1 Construction de la caté_gorie des s_ystèmes de transition sur CPO. 26

2.1.1 Quel_ques définitions de base. 26

2.1.2 Quel_ques propriétés des s_ystèmes de transition. 27

2.1.3 Quel_ques exemples et contre exemples de s_ystèmes de transition. 29

2.1.4 Morphismes de s_ystèmes de transition. 29

2.1.5 Quel_ques propriétés des morphismes de s_ystèmes de transition. . 30

2.1.6 Quel_ques exemples de morphismes de s_ystèmes de transition. . . 31

2.2 Notion de bissimulation entre s_ystèmes de transition sur CPO 34

2.2.1 Quel_ques exemples de bissimulations 34

2.2.2 Construction de _quel_ques bissimulations . 36

2.3 S_ystème de transition et coal_gèbre d'un endofoncteur de CPO 37

2.3.1 Coal_gèbre 37

2.3.2 S_ystème de transition comme coal_gèbre d'un foncteur 38

Biblio_graphie 40

Introduction

D'une manière informelle, une transition est une relation entre deux états d'un s_ystème évolutif_; cette relation peut exprimer l'évolution du s_ystème. Par exemple, le passa_ge de l'eau de l'état solide à l'état li_quide est une transition. Dans la caté_gorie ENS, un s_ystème de transition est la donnée d'un couple ( ) formé d'un ensemble S et d'un sous

S, S //

ensemble S //de S x S. Par analo_gie, étant donné un opc S, une structure de transition

sur S est un sous opc S //de S x S. La maîtrise de la notion de s_ystème de transition

sur un opc nécessite une bonne connaissance des opc⁵.

-Au chapitre premier, nous construisons la caté_gorie CPO des opc⁵. Nous montrons _que tout opc est enrichi d'une structure topolo_gi_que, la topolo_gie de Scott. Nous montrons _que les morphismes de CPO sont exactement les applications continues au sens topolo_gi_que. Nous terminons par l'importante construction de la complétion d'un ensemble ordonné en un opc.. -Au chapitre deux, nous construisons la caté_gorie des s_ystèmes de transition sur la caté_gorie CPO et nous prouvons l'essentiel des résultats énoncés par J.J.J.M.Rutten dans son article intitulé Universal coal_gebra : a theor_y of s_ystems_{; q}ui traite des s_ystèmes de transition ensemblistes.

ChaPItre PremIer

ETUDE DE LA CATÉGORIE CPO

Nous donnons les définitions de base de la caté_gorie CPO. Nous introduisons les topolo_gies de Scott et nous montrons _que les morphismes de CPO sont exactement les applications continues au sens topolo_gi_que. Nous terminons en montrant _que CPO est cartésienne fermée.

1.1 Construction de la catégorie CPO .

1.1.1 Quelques définitions de bases.

Définition 1.1. On appelle ensemble ordonné ou simplement un ordre tout couple (A, A) formé d'un ensemble non vide A et d'une relation binaire A sur A _qui est réflexive, antisymétrique et transitive.

Etant donné un ordre (A, A), toute partie totalement ordonnée de A par l'ordre induit est appelée chaîne.

Une chaîne de la forme :

a0 _A a1 _A ...

est appelée une w-chaîne

Définition 1.2. Un ordre (A, ) est dit w-complet si toute w-chaîne de (A, ) possède une borne supérieure.

Une notion aussi couramment utilisée _que celle de l'ordre w-complet est celle de l'ordre diri_gé-complet.

Définition 1.3. Soit (A, ) un ordre. Une partie non vide D A est dite filtrante ou

diri_gée si pour tout x, y dans D, il existe z dans D tel _que x z et y z.

Un ordre (A, ) est dirigé-complet ou filtrant-complet si toute partie diri_gée de (A, ) admet. un supremum.

La proposition suivante dont la démonstration re_quiert l'axiome de choix, établit l'é_quivalence entre ces deux définitions. Nous l'admettons.

Proposition 1.1. Un ordre minoré est w - complet si et seulement s'il est diri_gé-complet. Nous pouvons à présent donner la définition d'un opc

Définition 1.4. Un opc est un ordre diri_gé-complet.

Lors_qu'en plus (A, ) possède un plus petit élément, l'on dit _qu'il est un opc minoré.

1.1.2 Quelques exemples d'opcs.

i) Soit X un ensemble. (P(X), Ç) possède l'ensemble vide comme plus petit élément.

Toute partie D Ç P(X) admet U X?D		X comme supremum arbitraire, à fortiori, pour D
dirigée, U X?D	X est le supremum de D.

Donc (P(X), Ç) est un opc minoré.

ii) (N, ) n'est pas diri_gé-complet car la w-chaîne : 0 1 2 ...

n'admet pas de supremum. Donc (N, ) n'est pas un opc.

iii) (N, )=(N U {+00}, ) où, est le prolon_gement de l'ordre naturel de N par la
relation pour tout n dans N, n +00, admet zéro comme plus petit élément et pour toute partie diri_gée D Ç N,

sup N

½ +00 si D est infini ou si +00 est dans D D = max{d, d E D} si D est fini.

Donc (N, ) est un opc minoré.

iv) (Q, )=(QU{+00}, )où est le prolon_gement de l'ordre naturel de Q par la relation pour tout x dans Q, x +00, n'est pas un opc car la suite croissante :

? ? ?	x0 = 1 xn+1 =	2xn + 2
		xn + 2

de points de Q conver_ge vers J2 E/ Q. Donc (Q, ) n'est pas un opc.

vi) Soit (A, ) un ordre majoré. Posons Filt(A) l'ensemble des filtres (pour l'ordre) sur A.

Nous rappelons _qu'une partie non vide F d'un ordre (A, ) est un filtre pour l'ordre sur A si pour tout x, y E A, si x E F et x y, alors y E F. Soit D une partie de (Filt(A), Ç). Posons

UF = X.

X?D

* Montrons _que F est un filtre sur A.

Soientx,yEFtels_quex y.IlexisteXEDtel_quexEXetx y.OrXED. Donc x E X et x y, impli_que_; y E X Ç F. Par suite, F est un filtre sur A.

* * Montrons _que si D est une partie diri_gée de (Filt(A), Ç), alors F est son supremum diri_gé .

Comme F est le supremum arbitraire de toute partie D de (P(A), Ç), à fortiori, pour D partie diri_gée de (Filt(A), Ç), il est le supremum diri_gé de D.

* * * Montrons à présent _que (Filt(A), Ç) admet un plus petit élément. Soit a0 le majorant de (A_; ).

Il est clair _que {a0} est un filtre sur A et _que {a0} est le plus petit élément de (Filt(A), Ç).

On conclut donc _que (Filt(A), Ç) est un opc minoré.

viii) Soit N un ensemble non vide. Posons Fonct(N, N) l'ensemble des fonctions de N vers N. Munissons Fonct(N, N) de l'ordre de prolon_gement défini par la relation :

f g si et seulement si domf Ç domg et g prolon_ge f

- Montrons _que (Fonct(N, N)_; ) est diri_gé-complet.

Soit D une partie diri_gée de (Fonct(N, N)_; ). Considérons la fonction

÷:U f?D

domf -? N

x i-?f(x) sixEdomf
- Montrons _que ÷ est bien définie.

Soit x E U f?D

dom f; si x est dans domf n domg alors, f et g étant dans la partie

diri_gée D de (Fonct(N, N) ; ), il existe h dans D tel _que f h et _g h, i.e, h prolon_ge f et g. Donc f(x) = h(x), g(x) = h(x) i.e_; f(x) = g(x). Ce _qui achève de montrer _que ÷ est bien définie. Il est clair _que ÷ est le supremum de D. Ainsi (Fonct(N, N)_; ) est un opc.

Notations

i) Dans la suite, un opc (A, ) sera noté A lors_qu'aucune ambi_guïté n'est possible.

ii) Etant donné un opc A, le supremum d'une partie diri_gée D Ç A sera noté ^VA D.

1.1.3 Morphismes d'opcs .

Définition 1.5. Une application f: A ? B entre deux opc^s A et B est dite continue, au sens de l'ordre, si elle préserve les suprema diri_gés, i.e pour toute partie diri_gée D de A, V8 f(D) f(V^A D).

Remar_que 1.1. i) Si f est croissante alors pour toute partie diri_gée D de A, f (D) est

une partie diri_gée de B. En effet, si f (x), f (x') E f (D) alors, comme D est diri_gée, il existe t E D tel _que x t et x' t. f étant croissante, f (x) f (t) et f (x') f (t). Donc f (D) est une partie diri_gée de B.

ii)

Si f préserve les suprema diri_gés, alors pour tout x x', x' étant le supremum diri_gé de {x, x'} Ç A, f(x') = V⁸{f(x), f(x')}, i.e, f(x) f(x'). Donc f est croissante.

Ainsi, toute application _qui préserve les suprema diri_gés est croissante. Cependant, l'on notera _qu'il existe des applications croissantes _qui ne préservent pas les suprema diri_gés. C'est le cas de l'application f définie de A vers A ci-dessous représentée où les flèches non éti_quettées représentent l'ordre et les flèches éti_quetées par f l'application f

f **

₇₇

§§

₇₇

z _gg

f

§§

z _gg

y·

""

y·

§§

x

x

y _gg

₇₇ y

_FF

::

f

Car A est une partie diri_gée de supremum z mais f (z) =6 z.

Ceci étant, pour montrer _qu'une application f est continue, nous montrerons simplement _qu'elle préserve les suprema diri_gés.

est continue.

n +1 si n +oo +oo si non

(N, <) (N, <)

s

n 7!

Exemple 1.1. 1) Les identités sont continues.

2) L'application suivante

Dans l'opti_que de construire une caté_gorie a_yant pour objets les opc^s, il convient pour nous de voir si la composée des applications continues est continue. Ceci est l'objet du résultat ci-dessous.

Proposition 1.2. La composée de deux applications continues est continue.

Preuve. Soient f : A --> B et g : B --> C deux applications continues. Soit D une partie diri_gée de A, alors f (D) et g (f (D)) sont diri_gées de B et C respectivement. De plus,

g 0 f (_VA _D) i_f (_V1

= V g (f (D)) , car g est continue

g VB f (D)

car f est continue

,

VC g 0 f (D)

Donc g f (VA D) VC g f (D). Par suite, g 0 f est continue.

Nous en déduisons le résultat ci-dessous.

Théorème 1.1. Les opc^s et les applications continues entre eux forment une caté_gorie notée, CP O.

1.1.4 Topologie de Scott.

Définition 1.6. Soit A un opc.

Une partie U de A est appelée ouvert de Scott si :

1) elle est ascendante (filtrante), i.e_; pour tout x, y dans A, si x < y et x E U alors y E U;

2) elle est inaccessible par suprema diri_gés i.e ; si D est une partie diri_gée de A et VA D EU alors D nU =6 ö.

Notations Soit A un opc, et x E A. On note : x #=fy E A : y < xl et x ify E A : x yl.

Proposition 1.3. Soit U C A; U est un ouvert de Scott ssi pour toute partie diri_gée D de

A, V^A D EU ssi D nU =6 ö

Preuve. Soit U une partie de A.

* Supposons U un ouvert de Scott.

Soit D une partie diri_gée de A. Supposons V^A D E U, d'après la définition(1.6.(2))

D nU =6 ç. Récipro_quement, si D nU =6 ç, il existe d0 E D nU.

d0 W^AD et d0 E U impli_quent, d'après la définition(1.6.(1)), que W^AD E U.

** Récipro_quement, Supposons _que pour toute partie diri_gée D de A, ^WA D E U ssi DnU=6 ç.

Montrons _que U est ouvert de Scott.

i) Si x y et x E U alors y est le supremum de la partie diri_gée {x, y} et x E {x, y} n U. Donc, par h_ypothèse, y=W^A{x, y} E U.

ii)

La deuxième propriété est immédiate.

Exemple 1.2. Dans (N? {+8}, ), les ouverts de Scott sont les sous ensembles n j de N pour n E N.

Proposition 1.4. Les ouverts de Scott d'un OPC A induisent sur A une Topolo_gie. Preuve.

i) Stabilité pour l'union arbitraire.

Soit(Ui) _i E I une famille d'ouverts de Scott de A. Posons U = S i?IUi.

* Soient x et y deux éléments de A tels _que x y et x E U. Il existe j0 E I tel _que_; x E Ui0. Ui0 étant un ouvert de Scott, x E _Ui0 et x y impli_que, y E Ui0 ? U. Donc U est filtrante.

** D

WA D Soit une partie diri_gée de A telle que ^WA D E U, alors il existe j0 E I tel _que

E Ui0. Ui0 étant inaccessible par suprema diri_gés, il existe d E D tel _que, d E Ui0 ? U. Donc U n D =6 ç. i.e, U est inaccessible par suprema diri_gés.

ii) Stabilité pour les intersections finies.

Soient U et V deux ouverts de Scott.

* Soient x et y deux éléments de A tels _que x y et x E U n V. Alors, l'ascendance de U et de V entraîne _que y E U n V.

** Soit D une partie diri_gée de A telle que ^WA D E U n V. U étant inaccessible par suprema diri_gés, il existe d1 dans U n D. De même, il existe d2 dans V n D. D étant diri_gée, il existe d E D tel _que_; d0 d et d1 d. U et V étant ascendants, d E U n V. Donc (UnV)nD=6 ç.

Définition 1.7. La topolo_gie définie par les ouverts de Scott est appelée topolo_gie de Scott

Lemme 1.1. Une partie F d'un ope A est fermée si et seulement si pour toute partie diri_gée D de A, D ? F si et seulement si W^AD E F

Preuve. La preuve découle de la définition (1.7) De ce lemme, il en découle _que :

Lemme 1.2. x ? est un fermé de Scott. Preuve. Soit D une partie diri_gée de A.

D?x? ssj pourtoutyED,yEx ? ssj pour tout y E D, y x ssj W^ADEx?

Exemple 1.3. (Quel_ques fermés de Scott)Donnons les fermés de Scott des opc⁸ A, B et C ci-dessous représentés :

i)

A= a

u

_``BB>>~
BB~
_B~
_B~
_B~
B ~ ~

v

₉₉

``AAee AAAAAA

x

_O

₉₉

_O

>}> }}}}}}}

t

dd __????????

z

₉₉

w ff

m ff

_ee

a pour fermés

{m}, {v}, {w}, {m, v}, {m, w}, {v, w}, {m, v, x}, {m, x, v, w},

{m, x, v, z}, {m, x, v, w, z}, {v, w, u}, {m, v, w, u}, {m, v, w, x, u}, {m, z, x, t, v, u, w}, {m, w, x}, {m, w, x, v}, {m, v, w}, A et ç!)

B= :: b c _dd

£ AA£

]]<<<<<<<< £ £

£ £

£ £

d

₉₉

ii)

apourfermés {d}, {b, d}, {c, d}, B, etç!)

iii)

C= x

_OO

_ee

??

z

₉₉

y

^{ee^^==}==₌₌₌₌

t _dd

a pour fermés {z}, {t}, {z, t, y}, {z, t}, C et ç!)

Etant donnée une application f: A ? B entre deux opc⁸, f peut être continue au sens de l'ordre ou au sens de la topolo_gie de Scott. L'on se demande si ces deux continuités sont é_quivalentes? Les résultats ci-dessous nous permettent de conclure.

Proposition 1.5. Soient A et B deux opc⁸. Si f: A -? B est continue au sens de l'ordre, alors f est continue au sens topolo_gi_que.

Preuve. Supposons f continue au sens de l'ordre.

Montrons _que f est continue au sens topolo_gi_que.

Soit U un ouvert de B. Nous allons montrer que f-¹ (U) est un ouvert de A.

Soient x et y dans A tels _que x y et x E f-¹ (U) alors f(x) E U. f étant monotone, x y et f(x) E U impli_que f(x) f(y) et f(x) E U. De plus U étant filtrant, f(y) E U. Donc
y E f-¹ (U). Soit D une partie diri_gée de A telle que W^AD E f-¹ (U). Alors f(V^AD) E U.

Comme f préserve les suprema dirigés, ^VB {f (d) , d E D}= f (V^A D) E U. D étant une partie diri_gée de A et f monotone, {f (d), d E D} est une partie diri_gée de B. U étant un ouvert de B et V^B {f (d), d E D} E U, il existe d0 dans D tel _que f (d0) E U.

Donc D n f-¹ (U) =6 ö.

Les résultats ci-dessous nous permettent d'établir la récipro_que de cette proposition.

Lemme 1.3. Soit A un opc, y un élément de A. l'ensembleU_y={x : x y} est un ouvert de Scott.

Preuve. Soit D une partie diri_gée de A

D n U_y = ö ssi pour tout d E D, d= y
ssi V^A D = y

ssi V^A D E/U_y

De la proposition (1.3), on conclut _que U_y est un ouvert de Scott.

Lemme 1.4. Si une application f : A ? B entre deux opc^s A et B est continue au sens topolo_gi_que, alors elle est monotone.

Preuve. Soient x et y deux éléments de A tels _que x = y. Il faut montrer _que f (x) = f (y). Supposons f(x) f(y) alors, d'après le lemme(1.3), Uf(y) est un ouvert. f étant continue au sens topologique, f-1 (Uf(y)) est un ouvert de A. Or x = y et x E f-1 (Uf(y)). Donc f-1 (Uf(y))est filtrant et x = y_; par suite, y E f-1 (Uf(y)). Ce _qui si_gnifie _que f (y) f (y). Absurde car A est un opc.

Donc f(x) = f(y).

A l'aide de ces lemmes, nous pouvons à présent démontrer la récipro_que de la proposition(1.5) suivante :

Proposition 1.6. Si f : A -? B est continue au sens topolo_gi_que, alors f est continue au sens de l'ordre.

Preuve. Soit D une partie diri_gée de A, alors f étant croissante, f (D) est une partie diri_gée de B. De plus,

1 (_VB f (D)) ?

V^B f (D) majore f (D) ssi pour tout d E D, d E f-

ssi D C f-1 (VB f (D)) ? ssi ^VB D E _f-1 (VB f (D))?carf-1 (V^B f (D)) ? est fermé . ssi f ^iVA D E ^(VA f (D))

ssifD=f(D)

La deuxième inégalité découle de la monotonie de f.

1.1.5 Caractérisation des monos et épis dans la catégorie CPO.

Proposition 1.7. Les monos de CPO sont exactement les injections continues_; alors _que ses épis sont les surjections continues.

Preuve.

i) Monos de CPO.

* Soit m : A -? B une injection continue entre deux opc^s A et B. Montrons _que m est un monomorphismes.

m étant continue, il suffit de montrer _que pour tout opc C et pour toutes applications continues f, g : C -? A, m o f = m o g impli_que f = g.

Supposons m o f = m o g. Pour tout c E C,

m o f (c) = m o g (c) par h_ypothèse m(f(c)) = m(g(c))

f (c) = g (c) car m est injective .

Donc f = g.

** Soit m: A -? B un mono.

Montrons _que m est une injection continue.

La continuité de m découle du fait _que m est un morphisme. Il suffit de montrer _que m est injective. Soient a et a' deux éléments de A tels _que m (a) = m (a'). Considérons l'opc trivial à un seul élément_; {*}, et définissons les applications continues suivantes : f: {*}-?Apar f(*) = aet g: {*} -? Apar f(*)= a'. On a

m (a) = m (f (*)) et m (a') = m (g (*)). De m (a) = m (a'), on a m (f (*)) = m (g (*)). m étant un mono, f (*) = g (*). i.e, a = a'.

ii) Épis de CPO.

* Soit e : A -? B une surjection continue.

Montrons _que e est un épimorphisme. e étant continue, il suffit de montrer _que pour tout opc C et pour toutes applications continues f, g : B -? C, f o e = g o e impli_que f =g.

Supposons f o e = g o e. Pour tout b E B, il existe a dans A tel _que b = e (a). (car e est surjectif. )

f(b) = f(e(a))

= g (e (a)) par h_ypothèse

= g(b) pour tout b E B.

D'où f = g.

Donc e est un épimorphisme.

** Soit e : A -? B un épimorphisme.

Montrons _que e est surjective en montrant _que Im (e) = B.

Pour cela, il suffit de montrer _que Xe(A) = X13. où XC dési_gne l'application caractéristi_que de C pour tout ensemble C. Il suffit de remar_quer _que {0, 1} muni de l'ordre ci-dessous représenté :

1 _ee

0 //

est un opc, pour le_quel la topolo_gie _grossière {{0, 1}, } est de Scott. Pour

Xe(A) : B :-? ({{0, 1}, {{0, 1}, }}) et X13 : B :-? ({{0, 1}, {{0, 1}, }}). On a pour tout a E A, _Xe(A) o e (a) = X13 o e (a) = 1.

Donc Xe(A) = X13 .

1.2 Produits d'opcs .

Soient A et B deux opc. Munissons A x B de l'ordre point par point" défini par (x, y) = (x', y') si et seulement si x = x' et y = y'.

Il est clair _que (A x B, =) est un ordre.

Nous nous proposons de montrer _que A x B muni de la première et de la seconde projection est l'opc produit de A et B.

Lemme 1.5. Soient A et B deux opc^s.

Soit D une partie diri_gée de A x B. On pose :

D1 = {x1 E A tel _qu' il existe x2 E B; (x1,x2) E D} et

D2 = {x2 E B tel _qu' il existe x1 E A; (x1, x2) E D}. Alors,

(i) D1 (respD2) est une partie diri_gée de A (resp B). (ii)V^A×B D=(V^A D1, VB D2)

Preuve.

(i) Soient x1 et y1 deux éléments de D1. Cherchons x E D1 tel _que x1 = x et y1 = x. Comme x1 E D1, il existe x2 E D2 tel _que (x1, x2) E D. De même il existe y2 E D2 tel _que (y1, y2) E D. D étant diri_gée de Ax B, il existe (x, y) E D tel _que (x1, x2) = (x, y) et (y1, y2) = (x, y). Donc x1 = x et y1 = x. Ce _qui montre _que D1 est une partie diri_gée de A.

De même, on montre _que D2 est une partie diri_gée de B.

(ii) * Montrons _que (V^A D1, ^VB D2) est un majorant de D. Soit (x, y) E D, alors x = V^A D1 et y = V^B D2. Donc (x, y) = (V^A D1, V^B D2). Ce _qui prouve _que _(V A D1, V^B D2) est un majorant de D.

** Montrons _que (V^A D1, VB D2) est le plus petit majorant de D.

Soit (a, b) un majorant de D. Pour tout x E D1 il existe y E D2 tel _que (x, y) E D. (a, b) étant un majorant de D, (x, y) = (a, b). Donc x = a pour tout x E D1. Partant, a est un majorant de D1 et, V^A D1 = a.

De même, on montre _que V^B D2 = b. Ce _qui montre _que (V^A D1, V^B D2) = (a, b). Donc (V^A D1, V^B D2) = VA×B D.

Lemme 1.6. Soient A et B deux opc^s (i) Les projections

ð1: A x B ----> A (a, b) 1----> a

et

ð2 : A x B ----> B (a, b) 1----> b

sont continues .

(ii) Pour tout opc C, une application f :C ---> A x B est continue si et seulement si r1 o f et r2 o f sont continues.

Preuve.

(i) Soit D une partie diri_gée de AxB. D'après le lemme(1.5), (V^A D1, V^B D2) = VAXB D. (VAXB D) = VA r1 (D).

Montrons _que r1
Nous savons _que

(_VAXB D) = (VA _D1, ^VB D2 )

_=VA

D1

=VA r1 ^(D) .

Donc r1 est continue.

(ii) ) Si f est continue, r1 o f et r2 o f sont continues comme composées d'applications continues.

?)Supposons r1 o f et r2 o f continues et montrons _que f est continue.

Soit D une partie diri_gée de C. Nous allons montrer _que f (VC ^D) VA X B f (D)

f (VC D) = ir1 o f ^(VC , r2 o f (VC _D) )

VA r1 o _{f (D)} , VB r2

o f (D)) car ri o f est continue pour i E {1, 2}

=

= VAXB f (D) d'après lemme (1.5)

On conclut _que f est continue.

Remar_que 1.2. Soit L un opc muni de deux applications continues q1 : L ---> A et q2 : L---> B , d'après la propriété universelle de A x B dans ENS, il existe une uni_que

application < q1,q2 >:L --> A x B

l 1---> (q1 (l), q2 (l))

rendant commutatif le dia_gramme suivant :.

Q2	//B
		.

A< L

CC_CC<Q1,Q2>
ð1_V ð2

AxB

D'après lemme (1.6), < q1, q2 > est continue

De cette remar_que et des lemmes (1.5) et (1.6), nous déduisons _que : Corollaire 1.1. La caté_gorie CPO admet des produits binaires.

Remar_que 1.3. L'opc trivial (réduit à un seul élément ) est un objet final de la caté_gorie CPO.

A présent, l'on désire montrer _que CPO admet des produits finis. Pour cela, nous avons besoin du résultat classi_que ci-après.

Théorème 1.2. (f4J)Si une caté_gorie C admet des produits binaires et un objet final alors elle admet des limites finies.

De ce résultat et des lemmes et corollaires ci-dessus, nous déduisons _que : Proposition 1.8. CPO est cartésienne.

Pour faciliter la compréhension de cette notion, construisons _quel_ques exemples de produits.

Exemple 1.4. 1) A la remar_que(1.1), nous avons défini sur A = {x, y, z} une structure

d'opc représentée par :

₇₇

z ^qq hh

%%

x

3₃ y

_ee

Le produit A x A est illustré par :

¼¼

(z,z)

_'t

_AA

]]

_R

¼¼

(y,x)

(x,y)

(y,y)

_jj

₇₇

_Lt

]]

_AA

(x,x)

_YY

¼¼

₇₇

_MM

_gg

(y,z)

(z,y)

_XX

¼¼

(z, x)

(x,z)

_JJ

Dans cette représentation, les flèches dési_gnent l'ordre composante par composante.

2) Le produit N x N est illustré par :

·

>
·

·

(0, 2)

₇₇

¼¼

··

·

·

//

₇₇

₇₇

(0,1)

(1,1) //

_JJ

(2, 2)

··

··

(1, 2)

//

(0, 0)

Ji

(1,0)

''

11

''

//

(2,1)

·

·

· >
·

J'

''

(2, 0)

4

Proposition 1.9. Soient A, B et C trois opc^s. Une application f: A x B ? C est continue si et seulement si ses applications partielles f (--, b) et f (a, -) sont continues pour tout a E A et b E B.

Preuve.

i) Supposons f (-, b) et f (a, -) continues pour tout a E A et b E B.

* Soient (x, y) et (x', y') deux éléments de A x B ; tels _que (x, y) = (x', y') alors, f (x, y) = f (x, y') car f est monotone en son deuxième ar_gument

= f (x', y') car f est monotone en son premier ar_gument

Ce _qui montre _que f est monotone.

** Soit D une partie diri_gée de A x B.

D'après le lemme (1.5), V^A×BD = (V^A D1, V^B D2). Où D1 et D2 sont définies comme au lemme(1.5). Par ailleurs,

f ^(V- D)f VAD1, VB D2)

( -,

f

V

BD2)(

V

A

= WC n (f-VB D2) (a), a E D1o , carf (-, y) est continue

= WC nf (a, --) (VB D2) , a E Do , carf (x, -) est continue = _WC nVC If (a, b) , a E D1, b E D2}o

= WC f (D1 x D2)

Comme D ? D1 x D2, WC f (D) = WC f (D1 x D2) .

Pour démontrer l'iné_galité inverse, notons _que tout élément (x, y) de D1 x D2 est inférieure ou é_gal à un élément de D.

D1)

= WC n f(a, VBD2) , a E Do

En effet, comme x E D1, il existe y^f E D2 tels _que (x; y^f) E D. De même, il existe x^f E
D1 tel _que (x^f, y) soit dans D. Comme D est une partie diri_gée, il existe (x^ff, y^ff) E D

(_xf _y) < (x» y") ; ff et y =

tel _que (x, y^f) = (x^ff , , y") et ) en particulier, x = x y^ff.

\

i.e, (x, y) = (xff, y^ff ) . Comme tout élément (x, y) de D1 x D2, est majoré par un élément de D, et comme f est monotone, tout majorant de f (D) est aussi majorant de f (D_oo x DE). On a donc ^We f (D1 x D2) = We f (D).

D'où ^We f (D) = f (y 'Ax8 D. Ce _qui montre _que f est continue.

ii) Récipro_quement, supposons f continue de A x B dans C. Pour toute partie diri_gée D de B, et pour tout x E A, la partie {x} x D de A x B est une partie diri_gée de A x B. Soit f (x, -) l'application _qui à tout y E B associe f (x, y). Comme f

est continue, f ^(\tAx8 {x} D) = We f ({x}

x D). Donc f (x, -) est continue. De

même, on montre, par un ar_gument similaire _que l'application f (-, y) _qui à tout x E A associe f (x, y) est continue.

observation 1.1. Ce résultat est un cas particulier car en topolo_gie _générale, il est démontré _que la continuité d'une application définie sur un produit impli_que celle de ses fonctions partielles. La récipro_que de ce résultat est fausse. L'exemple t_ype est le cas de la fonction f :118 xl -?R définie par :

½20)+y xy

f (x, y)=x 2 si (x, y) (0, 0)

(

0 les applications partielles f(0,--) et f(--, 0) sont des
, fonctions nulles et sont donc continues. En revanche, pour y = ax, a E IR et x =6 0, on a

f (x, ax) = 1%2 _qui ne tend pas vers 0 avec x. La fonction n'est donc pas continue en (0, 0). C'est ce _qu'illustre son _graphe ci-dessous.

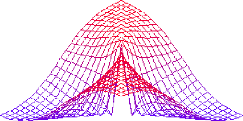
Nous allons à présent établir un lien entre la topolo_gie de Scott sur les produits et celle de T_ychonoff.

Théorème 1.3. La topolo_gie de Scott sur les produits est plus fine _que celle de T_ychonof.

Preuve. Soit A et B deux opc^s.

Soit U un ouvert de T_ychonoff de A x B, il existe U1 (resp U2) ouvert de A

(resp ouvert de B) tels _que U = 7r1^-1 (U1) n 7r2^-1 (U2)

Montrons _que U est un ouvert de Scott.

* Soient (a, b) et (á, â) deux éléments de A x B tels _que (a, b) = (á, â) et (a, b) E U. Nous devons montrer _que (á, â) E U. Comme U = 7r₁^-1 (U1) n 7r2¹ (U2), alors (a, b) EU impli_que (a, b) E 7ri¹ (U1) et (a, b) E 7r2¹ (U2) . Donc (á, â) E 7ri¹ (U1) n 7r2¹ (U2) car cha_que 7r_i^-1 (Ui) est filtrant pour i = 1, 2 . Partant, (á, â) E U.

.

** Montrons _que U est inaccessible par suprema diri_gés.

Soit D une partie diri_gée de A x B telle que _VA× B

D E U. Il faut montrer _que D n U =6 ç Cependant, il existe D1 et D2 définis comme au lemme (1.5) tels _que

.

VA×B (VA D1, ^VB D2) .

Ainsi

VA×B D E U é_quivaut à (V^A D1, V^B D2) E 7r₁^-1 (U1) n 7r2^-1 (U2)

implique ^(VA D1, ^VB D2) E-1(U1) ^(VA D1,V^B D2) E 7r₂ (U2) impli_que V^A D1 E U1 et V^B D2 E U2

impli_que D1 n U1 =6 ç et D2 n U2 =6 ç

impli_qu'ils existent d1 E D1 n U1 et d2 E D2 n D2

D'après la définition de Di, il existe a E D2 (resp b E D2) tel _que (d1, a) E D et (b, d2) E D. D étant une partie diri_gée de A x B, il existe (x, y) E D tel _que (d1, a) = (x, y) et (b, d2) = (x, y) . Donc d1 = x et d2 = y. Comme di EUi et Ui est filtrant, d1 = x et d2 = y impli_que x E U1 et y E U2. Partant, (x, y) E 7r^-1 (U1) n E 7r^-1 (U2) n D.

Ce _qui montre _que U est inaccessible par suprema diri_gés. Par consé_quent, tout ouvert de T_ychonoff est é_galement ouvert de Scott.

Ce résultat était prévisible car la topolo_gie de T_ychonoff est la moins fine des topolo_gies définies sur A x B rendant continues les projections 7r1 et 7r2. Or nous avons montré au lemme(1.6) _que A x B muni de la topolo_gie de Scott rendait continue ces projections. Donc par minimalité, la topolo_gie de Scott est plus fine _que celle de T_ychonoff.

Pour démontrer la récipro_que de ce théorème, nous allons utiliser la propriété universelle du produit A x B. C'est l'objet du théorème suivant.

Théorème 1.4. La topolo_gie de Scott est moins fine _que celle de T_ychonof.

Preuve. Posons S (resp T) la topolo_gie de Scott (resp T_ychonoff) sur AxB. Le théorème précédent montre _que T C S. Ce _qui si_gnifie _que l'identité

idA×B : (A x B, S) -? (A x B, T) (_que nous noterons idS?T) est continue. Il suffit de montrer _que l'identité idA×B : (A x B, T) -? (A x B, S) (_que nous noterons idT?S) est continue pour conclure _que S C T. D'après la P.0 de (A x B, S) (resp (A x B, T)), il existe une uni_que application continue ? (resp ) rendant commutatif le dia_gramme ci-dessous. i.e, 7rio ? = 7ri et 7ri o = 7ri pour i = 1, 2. Comme idS?T est continue, on déduit l'unicité de ? _que ? = idS?T. D'après la P.0 de (A x B, S) , idS?S est la seule application f continue de (A x B, S) vers (A x B, S) telle _que 7ri o f = 7ri pour i = 1, 2. Cependant, 7ri o?o = 7ri pour i = 1,2. On conclut d'après l'unicité de idS?S _que ? o = idS?S. Comme ? = idT ?S,

on déduit _que b = idS?S. Ce _qui montre _que S Ç T. (A, SA)(A x B, T )

ð2 // (B, SB)

oo ð1

ça

_OO

ø

²²

^eeJJJJJJJJ_JJJJJ

ð1 JJJJJJJJ

_9t9

_ttttttt^tttttttttttt

ð2

(AxB, S)

1.3 Exponentiation dans CPO

Soient A et B deux opc^s. Posons [A -* B] := { f: A -* B , continue }. Munissons [A -* B] de l'ordre point par point défini par

f g ssi f (x) g (x) pour tout x E A.

Nous nous demandons si ([A -* B], ) est un opc. Soit F une partie diri_gée de [A -* B]. On a :

Proposition 1.10. Pour tout x E A, I_x = {f (x), f E F} est une partie diri_gée de B.

Preuve. Soient f (x) et g (x) deux éléments de I. f, g E F impli_qu'il existe h E F tel _que f h et g h. i.e, pour tout x E A, f(x) h(x) et g(x) h(x). Donc I_x est une partie diri_gée de B.

De ce résultat, il ressort que ^VB I_x existe et _que la correspondance

V F : A -* B

_qui à tout x E A associe ^VB I_x ; est une application.

Nous nous proposons de montrer que ^V F est le supremum de la partie diri_gée F de [A -* B]. C'est l'objectif du lemme ci-dessous.

Lemme 1.7. ^V F = V[A?B] F.

Preuve. Soit f un élément de F.

Pour tout x E A, f(x) E {f(x), f EF} et f(x) VF(x) pour tout x E A. Donc VF

est un majorant de F. Soit W un majorant de F. Pour tout f E F, f W. i.e, pour tout x E A, f (x) W (x). Donc ^VB I_x W (x) pour rout x E A. Partant, ^V F W. Donc VF= ^V[A?B] F.

Ceci conduit au résultat suivant.

Corollaire 1.2. [A -* B] est un opc.

Nous allons à présent montrer _que CPO admet des exponentiels.
Lemme 1.8. Soient A et B deux opc^s. Pour tout a E A, l'application.

_åA

B

[A--*B]xA --* B (f, a) F--* f(a)

est continue.

Preuve. Soit D une partie diri_gée de [A * B] x A. D'après le lemme(1.5).

)V[A?B]×A D = (V[A?B] D1, ^VA D2

)[A?B] _D=VB åA B (D).

où les Di sont définis comme au lemme(1.5) pour i = 1, 2. (V Nous allons montrer que åA B

) )

_åA (V[A?B] D = _åA (V[A?B] D1 , ^VA D2

B B

= V[A?B] D1 ^(VA D2 ) par définition de åA B

= VBV[A?B] D1(D2)

= VB {V[A?B] D1 (a) , a E D2o, (car V[A?B] D1 est continue) = _VB (VB {f(a), a E D2, f E D1})

= V^B{f(a), a E D1} = VB åA B (D1)

Ce _qui traduit la continuité deåA _B .

Par ailleurs åA B est caractérisée par la propriété universelle suivante :

Lemme 1.9. Soient A, B et C trois opc^s. Pour toute application continue

h:CxA-*B

il existe une uni_que application continue

^bh: C -* [A*B]

rendant commutatif le dia_gramme ci-dessous.

[A * B] x A _;v;

_vvvvvvv^vvvvvvvvvvvv

h

_EA

73

// B

^bh×1A

CxA

Preuve. Soit ^bh: C -* [A * B] continue.

Montrons _que l'uni_que application donnée par la propriété universelle de l'exponentiation de B par A dans ENS, définie par

^bh:C -* [A*B]

c i-*

^bh(c): A-*B ai-*h(c, a)

est continue.

Soit D une partie diri_gée de C, pour tout a E A,

((WC D, a

= h(vC _D, WA { = h

)

a}₎

= h ^(VC×A D x {a}

bh (WC D (a) ) ))

= W B {h ( d , a) , d E D} , (car h est continue)

(WB bh (D) )
= (a) .

On conclut é_galement d'après la propriété universelle de åA B dans ENS que ^bh rend commutatif le dia_gramme ci-dessous.

EA 73	// B
		.

[A?B] xA_;v;

^bh×1A

_vvvvvvv^vvvvvvvvvvvv

h

CxA

De la proposition(1.10) et du lemme(1.9) nous pouvons conclure _que CPO est exponentiable. A_yant montré _que CPO est une sous caté_gorie de TOP et sachant _que TOP n'est pas exponentiable, nous avons là un exemple de sous caté_gorie de TOP sur la_quelle l'on peut définir des espaces fonctionnels.

1.3.1 Graphe d'un homomorphisme d'opc^s

Etant donnée une application f de A vers B, le _graphe de f est le sous ensemble G (f) de A x B défini par G (f) = {(x, f (x)), x E A}. La notion de _graphe d'un morphisme d'opc⁵ nécessite celle de sous opc.

Dans ce para_graphe, nous allons définir la notion de sous opc et montrer _que si f est une application continue de l'opc A vers l'opc B, G (f) = {(x, f (x)), x E A} est un sous opc de A x B. C'est le _graphe de f.

Définition 1.8. Soit A un opc. Un sous opc de A est une partie S de A _qui munie de l'ordre induit est un opc.

Exemple 1.5. i) Soit n0 un entier naturel. L'ensemble Xn0 = {n E N,n0 n}) est un

sous opc de N.

ii) Soit X un ensemble non vide. Soit x E X la collection < x > des sous ensembles de X contenant x est un sous opc de l'opc (P (X), Ç).

iii) L'ensemble des entiers naturels N n'est pas un sous opc de (N, =); car la partie diri_gée, P = {2n, n E N} n'admet pas de supremum dans N.

iv) Le sous ensemble P2 = {n², n E N} U {oc} de N est un sous opc de N.

En effet, si D est une partie diri_gée de P2, alors elle admet un plus _grand élément si elle est finie. Si non elle admet oc comme supremum.

Remar_quons _que pour tout opc A. Un sous ensemble S de A est un sous opc de A si et seulement si S est non vide et stable par suprema diri_gés. C'est-à-dire _que toute famille diri_gée D de S admet un supremum dans S.

Le résultat suivant montre _que le _graphe d'un morphisme d'opc f : A -? B est un sous opc de A x B :

Lemme 1.10. Soit f : A ? B une application continue entre deux opc^s. Le sous ensemble G (f) = {(x, f (x))x E A} de A x B est un sous opc de A x B.

Preuve. Il faut montrer _que toute partie diri_gée de G (f) = {(x, f (x)) ; x E A} admet un supremum. Soit D une famille diri_gée de G (f) = {(x, f (x)) ; x E A}. D'après le lemme (1.5), il existe D1 et D2 définies par :

D1 = {x E A tel _qu'il existe y E B, (x, y) E G (f)} et

D2 = {y E B tel _qu'il existe x E A, (x, y) E G (f)} tels que ^VG(f) D = (VA _D1, ^VB D2) . L'on remar_que _que tout couple (x, y) E A x B est élément de G (f) si et seulement si y= f (x)

Ceci étant, D2 = f (D1). D1 étant une partie diri_gée de A, V^A D1 existe. f étant continue, f (D1) = {f (d) ; d E D} est une partie diri_gée de B et f ^(VB D1) = VB _{f (D1) .D}'_où

(_VA D1, _VB f (D1)) 1A

V D1, f ^(VB D1)) _qui est bien un élément de G (f) . Donc G (f)

est un sous opc de A x B.

Exemple 1.6. * Sur l'opc N = N U {oc}, l'application s :N -? N définie par

½s (n) = n +1 si n oc

ocsin=oc

est continue et a pour _graphe G (s) = {(n, n +1); (oc, oc) ; n E N} .

** L'application ci-dessous schématisée est continue de l'opc P2 vers N

²²

22 >

f

· //

f

V

2n //

f

· //

f

· //

2

V

₂3

f

·

1₁ 01₁/_/1 1₁ // 2 // 11 3 1₁ //
· // 1₁
· // 22 n // 1₁
· 1₁-_/
·
·
·
·

oc

f

et a pour _graphe

G (f) = {(2ⁿ, n) ; et (oc, oc) ; n E N}

f

f

f

f

²²

²²

oc

²²

²²

·
·
·

* * *

v) Le _graphe du morphisme ci-dessous représenté :

_FF

₇₇y

y

f ;;

_gg

::

f

x

§§

§§

₇₇

z _gg

f

··

""

Ir

₇₇

z _gg

§§

est : G (f) = {(y, y), (x, z), (z, y)}.

1.4 Coproduit des opc s

Notre objectif est de déterminer le coproduit d'une famille d'opc^s. En s'inspirant de la construction des coproduits dans la caté_gorie ENS. Soit _(Ai)i?I une famille d'opc^s. Posons

_X A_i = {(a,i), a E A_i et i E I}

i?I

Munissons P i?I		Ai de la relation d'ordre définie par (a, i) (a', j) si et seulement si i = j et
a a'. Le lemme suivant permet de conclure que P i?I définies par : li (a) = (a, i), est le coproduit de la famille (Ai)i?I. Lemme 1.11. Soit (Ai)i?I une famille d'opc^s.			Ai, muni des injections li : Ai ? P i?I	Ai
i) P i?I	Ai muni de la relation ci-dessus définie est un opc.

ii) Les li sont continues

iii) Pour tout opc C et pour toute famille d'applications continues fi : A_i ? C, il existe

une unique application continue ? : P i?I

Ai ? C rendant commutatif le diagramme

suivant.

_P
i?I

ça

²²

C

A_i

~~}}}}}}}}}}}}}}}}}}

fi

li

A_i

Preuve. i) Montrons que P i?I

Ai est un opc. Soit D une partie dirigée de P i?I

Ai.

Pour tout (a, i) et (a', j) dans D, il existe (a», k) dans D tel _que (a, i) (a», k) et

(a', j) (a», k) d'après la définition de , i = k = j. Il s'en suit _que D est continue

dans une unique composante {i} x Ai de P i?I

Ai. D étant dirigé {a, (a, i) E D} est une

partie diri_gée de A_i.

i?I

On montre sans peine _que (V^Ai{a, (a, i) E D}, i) = VP Ai D.

ii) Montrons que les injections li : Ai ? P j?I

Aj sont continues.

Soit D une famille diri_gée de A_i. On a :

li (D) = {li (d), d E D}

= {(d, i), d E D}, donc

_P

VAj li (D) = VP

j?I j?I Aj {(d, i), d E D}

_P

= Vj?I Aj D x {i}

=V^AjDx {i}

VAi D )

= li

Donc li est continue.

iii) Montrons que P iEI

Ai possède la propriété universelle des coproduits. Soit C un opc. Soit

(fi) une famille d'applications continues de Ai dans C.

Considérons l'application ? : P jEI

A j ? C définie par ? ((a, j)) = fi (a). Les fi étant

continues, il en est de même pour ?. De plus cette application rend commutatif le dia_gramme suivant :

_P
iEI

ça

²²

C

A_i

~~}}}}}}}}}}}}}}}}}}

fi

_oo

li

A_i

.

Il reste à démontrer que ö est unique. Soit ø : P jEI

A j ? C rendant commutatif le

dia_gramme ci dessus. Pour tout (a, j) E P Aj

jEI

? ((a, j)) = ? o li (a)

= fi (a), par commutativité du dia_gramme

= øoli (a) = ø ((a, j))

donc ?= ø

Pour illustrer cette notion et faciliter sa compréhension, nous allons donner _quel_ques exemples.

_OO

_OO

(2,0)

(x,0)

1.4.1 Exemples de coproduits

i) Soient deux OPC^s R et T ci-dessous représentés

R = z qq

_{77 hh}

%%

x

3₃ y

_ee

Leur coproduit est représenté par :

R + T = (z,1)

₇₇

_gg

uu

<<

1₁ (y, 1)

(x,1)

zz

T= 2 qq x rr

^^>>>>>>>>

^ccGGGGG_GGGG

1 mm

_zmm

y _mm

uu

uu

_OO

(z, 0) LL

(y, 0) LL

(1,0) LL

ii) Posons A₂ = {2p, p = 8}. Munissons le de l'ordre <défini par 2ⁿ < 2^m si et seulement si n divise in. Il est clair _que A2 muni de cette relation est un opc. Munissons é_galement A2 de la structure d'opc définie par la relation d'ordre :

2n 4 2^m ssi n et in ont même parité et 2ⁿ = 2^m.

Le schéma de représentation du coproduit de ces deux opc est :

(2⁵, 0)

₇₇

(2⁴, 1)

(2⁶, 1)

₇₇

₇₇

_{OO :u:}

_uuuu^uuuu

_OO

(2⁷,0)

₇₇

(2⁸, 1)

_OO

₇₇ (2⁵, 1) ₇₇ (2⁷, 1)

_OO :u: 5j5

₇₇

(2², 1)

^ddIIIII_IIII

₇₇

(2³, 1)

₇₇

(2³,0)

₇₇

(2¹, 1)

₇₇

(2¹,0)

₇₇

(2⁴,0)

(2², 0)

₇₇

Pour tout x = y E S I_a ilexisteáEËtel_que(x = yEI_a)doncxEI_a ? S I_a

aEË aEË

1.5 Complétion d'un ensemble ordonné en un opc.

_OO

_OO

_OO

_OO

Lors_que l'on considère un opc et _que l'on oublie les opérations partielles de supremum filtrants l'on obtient simplement un ensemble ordonné. Nous voulons étudier le problème inverse i.e partir d'un ordre et construire un opc dont la structure soujacente est la plus proche possible de la structure de départ. Dans un sens _que nous allons préciser et _qui est techni_quement appelé propriété universelle.

Soit (A, =) un ordre. Une partie I de A est dite descendante si pour tout x, y E A, x = y E I impli_que x E I. Dans ce contexte, nous entendons par idéal de A toute partie descedante et diri_gée de A. L'exemple t_ype est le se_gment inférieure x ? défini par x. Notons Id(A) l'ensemble des idéaux de A. Id(A), muni de l'inclusion, est un ordre. La proposition ci-dessous montre _que Id(A) est un opc _qui est le complété de A.

Proposition 1.11. Soit (A, =) un ordre. Les propriétés suivantes sont vérifiées :

(i) Id(A) est un opc.

(ii) A se plon_ge dans Id(A) par çA : A -? Id(A)

x 7? x ?

(iii) Pour tout opc B, toute application continue f : A -? B croissante se factorise de manière universelle à travers çA. i.e, _qu'il existe une uni_que application continue f : Id(A) -? B au sens de Scott rendant commutatif le dia_gramme suivant.

A çA //

Id(A)

_Â

_Â

_Â

_Â f

_Â

²²Â

^CCCCCCCC_CCCC

f CCCCC!C!

B

Preuve.

(i) Il suffit de montrer _qu'une union filtrante d'idéaux de A est un idéal de A. Soit {Ia}aEË une famille filtrante d'idéaux de A.

· Montrons que S aEA

Ia est descendante.

· Montrons que U aEA

Ia est filtant. Soient x, y E U aEA

Ia. Il existe a, â E A tels que

x E I_a, y E Iâ. La famille _{Ia}aEA étant filtrante, il existe ä E A tel _que I_a, Iâ ç I8. On a donc x, y E I8 et il existe z E I8 tel _que x, y z.

(ii) Il est clair _que çA est un plon_gement.

(iii) Soit B un opc. Soit f : A -? B une application croissante. Cherchons l'uni_que application continue au sens de Scott f : Id(A) -? B telle _que f o çA = f.

Si f o çA = f, alors f o çA(x) = f(x) i.e f(x ?) = f(x) pour tout x E A. Or pour tout

idéal I de A, I = U aEI

x ?. Donc pour tout idéal I de A on doit avoir

f(I) =f(U x ?)

xEI

= V8 {f(x ?), x E I} = V⁸f(I)

donc f(I) = V8 f(I) pour tout idéal I de A. f est bien définie car I étant une partie diri_gée de Id(A) et f croissante, f(I) est une partie diri_gée de B. Il est clair _que f oçA = f.

Montrons _que f est continue au sens de Scott. Soit S une partie diri_gée de Id(A)

f(VId(A) S) = f( U I)

IES

= V8 _f( U I)

IES

=V8 U f(I)

IES

=

V^8f(S)

Ce _qui montre _que f est continue au sens de Scott.

Unicité de f. Soit g : Id(A) -? B une application continue telle _que g o çA = f. Alors pour x E A, g o çA(x) = f(x)_; i.e g(? x) = f(x). Donc Pour tout I E Id(A), g(I) = f(I).

La correspondance _qui à tout ordre (E; ) associe l'opc (Id(E), ç) des idéaux de (E, ) est fonctorielle_; elle se définie sur les flèches par :

(E, ): f // (F, ) Â // Id(f) : Id(E) // Id(F)

IÂ // f(I)

où f est l'uni_que application continue rendant contimutatif le dia_gramme suivant :

f

²²

E çE //

Id(E)

_Â

_Â

_Â

_Â f

_Â

²²Â

FçF // Id(F )

En notant Ord la caté_gorie des ordres et des applications croissantes, Id est un foncteur de Ord dans CPO. Ce foncteur est un adjoint à _gauche du foncteur d'oublie

U : CPO -? Ord. En effet, pour tout opc A et pour tout ensemble ordonné , pour toute application croissante h: (E', =') -? (E, =), le dia_gramme suivant est commutatif.

CPO (Id(E), A) ?E,A //			Ord (E, U(A))
Id(h)^*				h*
²		²

CPO (Id(E'), A) ?E',A // Ord (E', U(A))

car pour toute application continue

Id(E) u // A

on a :

h* (?E,A(u)) = h^* (u|E) = u o h

et

?E',A (Id(h)^*(u)) = ?E',A (u o h) = u o h|EF = u o h

Donc h^* o ?E,A = ?E⁰,Ao Id(h)^*.

De même, pour tout opc B, pour toute application continue h : A -? B, le dia_gramme suivant commute.

CPO (Id(E), A) ?E,A //			Ord (E, U(A)) U(h)^*
h*
²²		²

CPO (Id(E), B) ?E,B // Ord (E', U(B))

Donc, Id est un adjoint à droite de U. On note Id a U.

Exemple d'idéaux d'un ensemble ordonné.

Les idéaux de l'ordre (E, =) ci-dessous représenté sont : ö,{a}, {c}, {a, b, c}, {c, d} :

E= b d

_OO

_OO

__????????????????

a

c

nous en déduisons le dia_gramme des idéaux suivant :

Id(E) = {a, b, c} {c, d}

^{ddHHHHHHHHHHH}HH_HHHHHH

{a}

{c}

_[[77DD

_{77 7} 77

77

77
_7
7

7

ö

Qui est bien celui d'un opc. C'est même un opc minoré.

ChaPItre DeUx

SYSTÈME DE TRANSITION SUR

LA CATÉGORIE CPO

Dans ce chapitre, nous proposons une définition de s_ystème de transition à support un opc. Nous définissons les bissimulations entre ces s_ystèmes et nous démontrons _quel_ques unes de leurs propriétés.

2.1 Construction de la catégorie des systèmes de transition sur CPO.

Dans cette section, nous mettons sur pied les éléments de base de la caté_gorie des s_ystèmes de transition sur la caté_gorie CPO.

2.1.1 Quelques définitions de base.

Habituellement, un s_ystème de transition est un couple (S, -?) formé d'un ensemble S d'états et d'une confi_guration -? sur les états (formellement, -? est ensemble de S X S). Dans ce _qui nous concerne, S est déjà enrichi d'une structure d'ordre_; nous exi_geons de la confi_guration -? _qu'elle respecte cet enrichissement_; nous proposons donc la définition suivante :

Définition 2.1. Un s_ystème de transition est un couple ( ) formé d'un opc S et

S, S //

d'un sous opc S // de S X S.

S est appelé support ou objet d'états du s_ystème.

S // est appelé structure de transition du s_ystème. Les éléments de S sont appelés états

Notations

* Lors_que (s, s') E S // , on note s S // s' et on lit 's évolue vers s' sous la transition

"

S

** lors_qu'aucune confusion n'est possible, l'on note la structure de transition S //sim-

plement par -? et le système ( ) par S.

S, S //

* * * Pour s fixé dans S, s -?:= {s' E S, s -? s'}.

Définition 2.2. Un s_ystème de transition S est dit à branchements finis si pour tout état s, s -? est fini.

Lors_que s -? est de cardinal 1, le s_ystème de transition S est dit déterministe.

Remar_que 2.1. Etant donné un s_ystème de transition S, cha_que état s de S est caractérisé par deux structures :

* l'ordre de l'opc .

** la structure de transition du s_ystème S.

Pour différencier ces structures, nous représenterons les transitions par des flèches éti_quetées d'une lettre majuscule et l'ordre par des flèches simples.

2.1.2 Quelques propriétés des systèmes de transition.

Nous proposons _quel_ques propriétés caractéristi_ques des s_ystèmes de transition. Proposition 2.1. S = (S, S //) est un s_ystème de transition si et seulement si pour toutes familles dirigées _(xi)iEI et _(yi)iEI de S, telles _que pour tout i E I, (xi, yi) E S // ,

(VS xi, VSyi)E S //

Preuve. ) Supposons S //Structure de transition et posons

L = {(xi, yi), i E I}

* Montrons _que L est une partie diri_gée de S //.L est par définition une partie de S // .

Soient (xi, yi) et (x7, y7) E L . _(xi)iEI (respectivement _(yi)iEI) étant une partie diri_gée de S,

il existe xk (respectivement yk) tel _que xi xk et x7 xk (respectivement yi yk et y7 yk).

On déduit de la définition de l'ordre composante par composante _que (xi, yi) (xk, yk) et

(xi, yi) (xk, yk). Ce _qui prouve _que L est diri_gée de S // . Comme S // est un sous

opc, il est stable pour les suprema diri_gés. Donc VS L E S // . Et d'après le lemme (1.6)

VS xi S // VSyi

?) La réciproque découle de la définition de système de transition. De manière analogue, on démontre la proposition suivante.

Proposition 2.2. S = (S, S // ) est un s_ystème de transition si et seulement si pour

toutes w-chaînes

x0 x1 ... x_n ...

et

y0 y1 ... y_n ...,

si xi S // yi alors

_VS xi S // VSyi

Nous en déduisons le corollaire suivant

Corollaire 2.1. Pour toute famille filtrante _{xi}iEI, on a :

· s'il existe aES tel _que pourtouti E I, xi S // a alors V5xi S // a_;
· s'il existe aES tel _que

xi'

.
.
.

_F#177;F

#177;

#177;#177;#177;#177;#177;#177;#177;#177; (c) CC(c)

(c) (c)

(c) (c)

(c) (c) >}>

#177;#177;#177;#177;#177;#177;#177;#177; (c)
}}}}}}}}}}}}}}}}

(c) (c)

#177;#177;#177;#177;#177;#177;#177;#177; (c) (c)

(c) (c) _ooooooo^oooooo7o7 (c) (c)

(c) (c)

(c)

#177; (c) (c)

a _O// xii

.
.

₆ A6 AOAOO

_{6 AO}

6 ₆ AOOO

_AO_O

6 6 AO

6 AOO _A'O' _{6 A}

6 A

6 AA

_{6 A}

_{6 A}

_{6 A}

₆ A

6 6 6 6 6 6 ¾6¾

.

alorsa S // V5xi

Remar_que 2.2. Nous venons de montrer _que (S, S // ) s_ystème de transition é_quivaut d'une part à

i) Pour tout ensemble I et pour toutes familles dirigées _(xi)iEI et _(yi)iEI de S, si pour tout

// V5 yi et d'autre part à

i E I, xi S // yi implique ^V5 xi S

ii)Pourtoutesw-chaînesx0=x1=...=x_n =...ety0=y1=...=y_n =...,,xi _S//yi implique ^V5 xi S // V5yi.

De cette remar_que, nous déduisons le théorème suivant.

Théorème 2.1. Soit S un s_ystème de transition. Les assertions suivantes sont é_quivalentes :

i) Pour tout ensemble I et pour toutes familles dirigées _(xi)iEI et _(yi)iEI de S, si pour tout i E I, xi S // yi, alors

ii) Pour toutes w-chaînes

V5

xi S //

V5 yi

x0 = x1 = ... = x_n = ...

et

y0 = y1 = ... = y_n = ...,

si xi S // yi alors

V5

xi S //

V5 yi

2.1.3 Quelques exemples et contre exemples de systèmes de

transition.

1) Tout opc est un s_ystème de transition de structure de transition s S //s' si et seulement si s = s'.

2) Sur l'opc N, (N, N x N) n'est pas un s_ystème de transition.

3)

,

₇₇ z ^qq hh

%%

x 3₃ y

_ee

Sur A l'opc représenté par :

les dia_grammes ci-dessous sont des s_ystèmes de transition à support A :

// y

x

S

££

--

_FF°

° ° °

S °

° ° ° ° ° °

²² ° °

z

_XX00dd

⁰⁰0₀₀S

₀₀

S 000

ÁÁ 0

yy

S

%%

x _ll

²²

_{FF° OO}

°

° °

S ° °

° °

° ° S

° ° °

--

z

££

_{__}^????_??S

??????

S ???

S ?

// %%

,, y S

_ii

[[

S

yy

\\

S

[[

S

_BB

4) Soit A un opc. Soit a0 fixé dans A. On montre sans peine _que a0 ?= {x, a0 = x} est un sous opc de A et a0 ? xa0 ? est un s_ystème de transition sur a0 ?.

2.1.4 Morphismes de systèmes de transition.

Dans le cas des s_ystèmes de transition ensemblistes, J.J.J.Rutten appelle morphisme du s_ystème de transition S vers le s_ystème de transition U toute application f : S -? U vérifiant :

i) Pour tout s, s' E S, si s S //s' alors f (s, ) S // f (s', ) (l'on dit dans ce cas _que f
préserve les transitions de S).

ii) PourtoutsESetuEU,sif(s,) S//ualorsilexistes'EStelques S // s'et
f (s') = u. (l'on dit dans ce cas _que f réfléchit les transitions de U).

En nous inspirant de cette définition, nous proposons la définition suivante de morphisme de s_ystèmes de transition sur un opc.

Définition 2.3. Soient S et U deux s_ystèmes de transition. Un morphisme de S vers U est un morphisme d'ope^s f : S -? U vérifiant :

i) Pour tout s, s' E S, si s _S> s' alors f (s)

S > f (s') ;

ii)Pour tout s E S et u E U, si f (s) _S> u alors il existe s' E S tel _que s _S> s' et

f (s') = u.

Les morphismes de s_ystèmes de transition sur des opcⁿ sont donc les applications continues _qui préservent et réfléchissent les transitions

2.1.5 Quelques propriétés des morphismes de systèmes de tran-

sition.

Au chapitre précédent, nous avons montré _que les monos (respectivement épis) de la caté_gorie CPO sont exactement des injections (respectivement surjections) continues. De ces résultats, nous déduisons les caractérisations suivantes des morphismes de s_ystèmes de transition :

Lemme 2.1. Soient S et U deux s_ystèmes de transition déterministes. Une application continue f : S -? U est un morphisme de s_ystèmes de transition si et seulement si elle préserve les transitions.

Preuve. ?) Supposons f : S -? U continue et préservent les transitions. Pour montrer _que f est un morphisme, il suffit de montrer _que f réfléchit les transitions.

Supposons _que f (s ) _S> u, alors S étant déterministe, il existe un uni_que s' E S tel _que

s _S> s'. Comme f préserve les transitions, f (s) _S> f (s' ) . Comme U est déterministe,

f (s) _S> f (s' ) et f (s ) S //u impli_quent u = f (s') . Donc f réfléchit les transitions.
)La récipro_que est immédiate.

Proposition 2.3. Tout homomorphisme de s_ystèmes de transition _qui est un homéomorphisme est nécessairement un isomorphisme.

Preuve. Soit f : S -? U un homéomorphisme. Soit g : U-? S sa bijection récipro_que. Pour montrer _que f est un isomorphisme il suffit de montrer _que g est un morphisme de s_ystèmes de transition.

· Soient u, u' E U tels _que u _S> u', alors u = f o g (u) _S> u'. Comme f réfléchit les

transitions, il existe s dans S tel _que f (s) = u' et g (u) _S> s. Or f o g (u') = u' = f (s) .

Donc g (u') = s. Partant, g (u) _S> s = g (u') . ie ; g (u) _S> g (u') .

·
· Soient u E U et s E S tels _que g (u) _S> s'. Alors g (u) _S> g o f (s') . Donc il existe

u' := f (s') tel _que g (u) = s'. Comme f préserve les transitions g (u) _S> go f (s') impli_que

fog(u) _S> fogof(s'). i.e, u _S> f(s')etgof(s')=s'

Le résultat suivant nous permet de construire des morphismes de s_ystème de transition à partir des morphismes d'opcⁿ et d'autres morphismes de s_ystèmes de transition.

Lemme 2.2. Soient S, T et U trois s_ystèmes de transition. Soient f : S -? T, g : S -? U

et h :U-? T trois applications continues rendant commutatif le dia_gramme suivant :

S	f	> T

⁰⁰⁰0₀₀₀

g 00000»0»

_FF° ° ° ° ° ° °

h

° ° ° °

° °

U

1) Si g est un épi d'opc', f et g des homomorphismes de s_ystèmes de transition, alors h est un homomorphisme de s_ystèmes de transition.

2) Si h est un mono d'opc', f et h des homomorphismes de s_ystèmes de transition, alors g est homomorphisme de s_ystème de transition.

Preuve.

Cette preuve fait usa_ge exceptionnel des relations. Contrairement à celle de J.J.J.Rutten _qui est basée sur le point de vue fonctoriel des s_ystèmes de transition ensemblistes.

1) Supposons f = h o g et g épis d'opc', f et g des homomorphismes.

· Montrons _que h préserve les transitions.

Soit u, u' E U, tels _que u S > u'. Il faut montrer _que h (u) _S> h (u') . Comme g est

un épi d'opc', il est surjectif. Il existe donc s', s E S tels _que u = g (s) et u' = g (s') .
Donc u _S> u' impli_que g (s) _S> g (s') . Comme g réfléchit les transitions, il existe

s» E S tel _que g (s») = g (s') et s _S> s». Comme f préserve les transitions,

s _S //s» implique f (s) _S> f (s»)

implique h (g (s)) _S> h (g (s'))

implique h (u) _S> h (u') .

·
· Montrons _que h réfléchit les transitions. Soit u E U et t E T tels _que h (u) _S> t.

Il faut chercher u' E U tel _que h (u') = t. g étant surjective, il existe s E S tel _que
u = g (s) . Donc h (g (u)) _S> t c-à-d f (u) _S> t. Comme f réfléchit les transitions,

f (u) S > t impli_que _qu'il existe s' E S tel _que f (s') = t et s S > s'. Or f (s') = t

é_quivaut à h (g (s')) = t. On pose u' = g (s') et on obtient u = g (s) S > g (s') = u'.

2) De fa_çon analo_gue, on montre le 2).

2.1.6 Quelques exemples de morphismes de systèmes de transi-

tion.

1) Pour tout s_ystème de transition S, l'application identitité 1S : S -? S est un morphisme de s_ystèmes de transition.

2) Considérons l'application : N -? 2 ? définie par (n)={ n+2 sin=68 8 sinon

ç') est continue et pour tout n, m E N,n /> m impli_que 2 + n 2? /> m + 2.

N

Donc ç') préserve les transitions.

Par ailleurs, pour tout n E 2 ?, l'é_quation en x :

2+x =n
admet une uni_que solution dans N. D'où ç') est un morphisme de s_ystème de transition.

3) Soient S et T deux s_ystèmes de transition ci-dessous représentés.

Soit G (f) ={(x, v), (z, u), (y, o), (t, o)} le _graphe de f:S-?T.

Nous nous proposons de construire à partir de S et T des s_ystèmes de transition pour les_quels f est un morphisme de s_ystèmes de transition.

et

S=

S

££

S

z

_{99 FF OO}

§§

x \\

t \\

y

S

yy

u T

o

T

T

v \\

w \\

££

T=

;; _G²G UU ^^=======T

T ====

²²²²²²²²²²²²²=

T ==

T ====

%% {{

xx

L'application f est continue par construction. La transition x S />z est préservée par f car , f (x) = v T /> u = f (z). De même, la transition z _S />x, est préservée par f car f (z) = u T /> v = f (x). De fa_çon analo_gue, l'on montre _que f préserve les transitions x S />x et z _S />z. Partant, f est continue et préserve les transitions

de S. Pour _que f soit un morphisme de s_ystèmes de transition, il faudrait _qu'elle réfléchisse les transitions de T.

· Les transitions v T /> u et u T /> v sont naturellement réfléchies par f. La seule

transition _qui fait problème est u T /> w; _qui n'est pas réfléchie par f, car w n'est

ima_ge d'aucun état de S. Pour _que celle-ci soit réfléchie, nous devons affaiblir les transitions de T. Le plus simple serait de supprimer la transition u T /> w.

Ainsi, pour T' ci-dessous représenté, f est un morphisme de s_ystèmes de transition.

yy

u T

T

T

v \\

w \\

;; _G²G UU ^^<<<<<<<

T <<<

²²²²²²²²²²²²²²<

T <<

T <<<<

{{

T' =

%%

xx

££

o

·
· Nous pouvons aussi modifier S et G (f) de manière à obtenir un morphisme tout en conservant la transition u

_T> w. Si la transition u

_T> w est maintenue, pour _que l'on ait un morphisme, il faudrait simplement _que w soit ima_ge d'un état 0 de S où 0 est tel _que z _T> 0. Comme y et t ont la même ima_ge par f, nous pouvons chan_ger dans G (f) le couple (y, o) par (y, w) . Ceci étant, on imposerait simplement la transition z _S> y. La nouvelle application f' ainsi construite sur le nouveau s_ystème S' ci-dessous représenté est un morphisme.

S' =

S

S

S

z

££

S //

y .

_99FFJO

k

x \\

t \\

Ce morphisme a pour _graphe : G (f') = {(x, v), (z, u), (y, w), (t, o)}.

S

S

S' =

S

uu

k§

S

z

££

S/_/

y

.

_99FFA

x \\

t \\

·
·
· En conservant l'application f', l'on peut modifier le s_ystème S' en S» ci-dessous représenté

Remar_que 2.3. On démontre sans peine _que la composée des morphismes de s_ystèmes de transition est un morphisme de s_ystèmes de transition. Les identitités étant des morphismes de s_ystèmes de transition, l'on conclut _que les s_ystèmes de transition et les morphismes de s_ystèmes de transition forment une caté_gorie.

2.2 Notion de bissimulation entre systèmes de transition sur CPO

Une bissimulation entre deux s_ystèmes de transition ensemblistes A et B est un sous ensemble R de A X B tel _que pour tout (a, b) E R, on a :

i) Si a A // a', alors il existe b' E B tel _que b B //b' et (a', b') E R.

ii) Sib B // b', alorsilexiste a'EAtel_que a _S //a'et (a', b') ER.

En s'inspirant de cette définition, nous proposons la définition suivante de bissimulation entre s_ystèmes de transition à support un opc.

Définition 2.4. Soient S et T deux s_ystèmes de transition. On appelle bissimulation de S par T tout sous opc R de S X T tel _que, pour tout (s, t) E R, on a :

i) Sis S // s',alorsilexistet'ETtelquet T // t'et(s',t')ER.

ii) Si t T // t',alors il existe s' ES tel _que s S //s' et (s', t') E R.

2.2.1 Quelques exemples de bissimulations .

Soient S et U deux s_ystèmes de transition. Soit f : S -? U, un morphisme d'opc^s. Le résultat ci-dessous montre _que le _graphe de f est une bissimulation si et seulement si f est un morphisme de s_ystèmes de transition.

Proposition 2.4. Soient S et U deux s_ystèmes de transition. Une application continue

f : S -? U est un morphisme de s_ystèmes de transition si et seulement si son _graphe est une bissimulation.

Preuve. * Supposons _que f est un morphisme.

· Montrons _que son _graphe G (f) est une bissimulation.

* Soient (s, f (s)). Pour tout s E S et u E U, si f (s) _U //u, alors, comme f réfléchit les

transitions, il existe s' dans S tel _que f (s') = u et s _S //s'. Comme s' E S, et f est une

application, (s', f (s')) E G (f).

** Si s S // s', alors f étant un morphisme, préserve les transitions. Donc f (s) U //f (s')

*** Supposons _que G (f) soit une bissimulation et montrons _que f est un morphisme. et (s', f (s')) E G (f)

* Si s S // s', alors comme (s', f (s')) E G (f), il existe u E U tel _que f (s) U //u et

.

(s', u) E G (f) ie, u = f (s'). Donc f (s) U // f(s).

** si f (s) _U //u, alors compte tenu du fait _que (s, f (s)) E G (f), il existe s' dans S tel

_que s S />s' et (s', u) E G (f). Or (s', u) E G (f) impli_que u = f (s'). Ce _qui montre _que

f réfléchit les transitions de U. D'où le résultat.

De cette proposition, il s'en suit _que la dia_gonale du produit S X S de s_ystèmes de transition est une bissimulation de S par S car c'est le _graphe de l'identité de S. On démontre sans difficultés la proposition suivante.

Proposition 2.5. Soit R une bissimulation de S par U. R-¹ = {(u, s) telque (s, u) E R} est une bissimulation de U par S.

De cette proposition, il s'en suit _que la dia_gonale du produit S X S de s_ystèmes de transition est une bissimulation de S par S car c'est le _graphe de l'identité de S. On démontre sans difficultés la proposition suivante.

Proposition 2.6. Soit R une bissimulation de S par U. R-¹ = {(u, s) telque (s, u) E R} est une bissimulation de U par S.

Définition 2.5. Soient S et U deux s_ystèmes de transition un span est un couple d'homomorphismes de même domaine. Le dia_gramme ci-dessous illustre un span

T

ÄÄ~~^~~~~~

^@@@@@@Â@Â

S U

Tout span induit une bissimulation entre les codomaines de ses morphismes.

Le résultat suivant donne la construction d'une telle bissimulation. Dans le cas des s_ystèmes de transition ensemblistes, J.J.J.M.Rutten utilise le point de vue fonctoriel des s_ystèmes de transition pour le prouver. Nous utilisons ici le point de vue relationnel.

Proposition 2.7. Soient f : T -p S et g : T -p U deux morphismes de s_ystème de transition.

Soit K = {(f (t), g (t)) , t E T}. K est une bissimulation de S par U.

Preuve. Nous devons montrer _que K est un sous opc de S X U et satisfait les axiomes i) et ii) de la définition (2.4)

Considérons l'application ? : T -p S X U définie par ? (t) = (f (t), g (t)). f et g étant continues, ? est continue.

Donc K est un sous opc de S X U.

Il reste à montrer _que K vérifie les axiomes i) et ii).

· Soit (f (t), g (t)) E K. Si f (t) _S />s, alors comme f réfléchit les transitions, il existe t'

dans T tel _que t T /> t'; et ? (t') E K.

Par ailleurs, comme g préserve les transitions, t T /> t' impli_que g (t) T /> g (t') . Ce _qui

montre l'axiome i).

De manière analo_gue, on montre le deuxième axiome de la définition (2.4).

2.2.2 Construction de quelques bissimulations .

1) Les états des deux s_ystèmes ci-dessous représentés sont bissimulaires.

££

U= u

_ee

U

s1

s0//

S

''

? _GG

? ? ? ? ? ? ? ?

S = ? ? S

? ? ?

S ? ? ?

(( Â?Â

_CC

_gg

²²

··

S

S

s2 S

_gg

Posons R = {(s0, u) , (s1, u) , (s2, u)} et montrons _que R est une bissimulation de
S par U. Comme (s0, u) E R, s0 _S //s1 et s0 _S //s2, il faut chercher u1 et u2 dans

Utelsqueu U // u1etu U // u2.Commeu U // u,onprendu1=u2=u. Parailleursu U // u,s0 S // s1, s0 ^S// s2et(si,u)ERpouri=1;2.

De même, on montre _que s1 est simulaire à u et s2 est simulaire à u.

2) Chan_geons U en U' ci-dessous représenté et montrons _que S x U' n'est pas une bissimulation de S par U'. Il suffit de remar_quer _que (s0, u1) E S x U'. Mais u1 n'évolue pas.

_U,

U'= u0

_hh

_U,

u1 ²²

[[

3) En modifiant U' en U» de manière à ce_que S x U» soit une bissimulation de S par U». Dans l'exemple ci-dessus, la transition _qui fait problème est u0 _U, //u1. En la

supprimant, on obtient U'' représenté par :

_U,,

U'' = u0

_hh

¾¾

^²u1

L'axiome i) reste vérifié. L'axiome ii) découle du fait _que u0 _S //u0.

4)

Rappels 2.1. Un alphabet est un ensemble fini de s_ymboles .

Soit A un alphabet.

Un mot sur A est une suite finie (m) _i où miE A. Un mot est vide s'il n'est formé

d'aucun s_ymbole. Nous noterons le s_ymbole vide par c ou par un petit espace vide. Le premier s_ymbole d'un mot est appelé tête du mot. L'ordre d'un mot est le nombre de s_ymboles _qui le constituent. Concaténer deux mots c'est les juxtaposer. Nous notons A°° l'ensemble des mots sur A. La notion du mot nous permet de dire _que tous les mots ont même ordre_; ceci en les complètant par des s_ymboles vides. Sur A^°° l'ensemble des mots complètés avec une infinité de s_ymboles vides définissons l'ordre suivant :

u v si et seulement si il existe in E N tel _que pour tout i in, u = v et _u<vm où < dési_gne l'ordre des s_ymboles de l'alphabet. (A^°°, ) est un opc à plus petit élément. En effet, pour toute partie diri_gée D de (A^°°, ), le mot obtenu par concatenation de tous les mots de D est le supremum de D.

· Définissons sur A^°° la relation :

(u ) EN A // (v ) _EN ssi u = v 1 i.

L'on définit ainsi une structure de transition sur A^°°.

·
· La concatenation étant associative, R = {((u.v) .w), (u. (v.w))} est une bissimulation de A^°° par A^°°.

2.3 Système de transition et coalgèbre d'un endo-

foncteur de CPO.

Traditionnellement, un s_ystème de transition à support ensembliste est la coa_gèbre du foncteur puissance covariant P : ENS -? ENS . J.J.M.Rutten dans [51 pose les bases de la théorie des s_ystèmes de transition ensemblistes vus comme coal_gèbres d'un endofoncteur de ENS. Cette section, a pour objets :

· rappeler la notion de coal_gèbre_;

· prouver _que les s_ystèmes de transition ensemblistes sont les coal_gèbre du foncteur puissance covariant.

2.3.1 Coal_gèbre .

Dans cette sous section, nous présentons de prime à bord la notion de coal_gèbre et de morphismede coal_gèbres.

Définition 2.6. Soit F : C -? C un endofoncteur d'une caté_gorie C. Une F-coal_gèbre est un couple (S, aS) formé d'un objet S de C et d'un C-morphisme aS : S -? F (S) appelé F-costructure sur l'objet S de C.

Soit F : C -? C un endofoncteur d'une caté_gorie C. Soient S = (S, aS) et T = (T, aT) deux F-coal_gèbres. Un morphismes (ou plus précisément un F-morphisme) de S vers T est un C-morphisme f : S -? T rendant commutatif le dia_gramme suivant.

S f // T

aS		aT

²² ²²

F (S) F(f) // F (T)

i.e, aS o f = F (f) o aS.

Soient f: S -? T et g: T -? Z deux F-morphismes. Le C-morphisme go f :S -? Z rend commutatif le dia_gramme suivant.

_Sgo f // Z

as		az

²² ²²

F(go f)

F (S) F (Z)

En effet :

F (g o f) o aS = F (g) o F (f) o aS

= F (g) o F (f) aS = F (g) o aS o f

= aS o (g o f) .

De plus, les identités sont des morphismes de F-coal_gèbres. Ceci nous permet de conclure

_que les coal_gèbres et leurs morphismes forment une caté_gorie.

2.3.2 Système de transition comme coalgèbre d'un foncteur.

Sur le point de vue ensembliste les s_ystèmes de transition sont les coal_gèbres du foncteur puissance covariant.

En effet, pour tout s_ystème ensembliste (S, S > ), l'application : aS : S -? P (S) _qui à

tout s E S associe aS (s) = {s' tel que s S > s'} est une co-structure du foncteur puissance covariant P. Donc (S, aS) est une P-coal_gèbre.

Récipro_quement, à toute P-coal_gèbre (S, aS) correspond un s_ystème de transition (S, S >)

avec _S> = {(s, s') E S x S, s' E aS (s)} .

Bien évidemment, tout P-morphisme f : S -? U est un morphisme de s_ystèmes de transition et récipro_quement.

En effet, si f est un morphisme de s_ystème de transition, pour tout s E S, on a :

aU o f (s) = aU (f (s))

= {u E U, f (s) > u}

{=f (s^'), s^' E S; f (s)

> f (s')} car f réfléchit les transitions

S

= {f (s'), s' E aS (s)} =P (f) o a, (s)

Donc aU o f = P (f) o aS. Ce _qui montre bien _que f est un P-morphisme. D'où le résultat suivant :

v

Sur la caté_gorie CPO, considérons la correspondance F : CPO -? CPO définie : * Sur les objets par F (A) = (P (A), ?) pour tout opc A.

Résultat 2.1. Les s_ystèmes de transition supportés par un ensemble sont les coal_gèbres du foncteur puissance covariant

** sur les morphismes par

F (f) : (P (A), ç) -? (P (B),ç)

X 7-? f (X) pour toute application continue f : A -? B.

Cette correspondance définie un foncteur de CPO dans CPO. áS n'est pas continue car pour le s_ystème de transition ci-dessous représenté, s(a) = {a, b} {b} = s(b)_; pourtant, a = b.

_T

S :: b _{OO T}

%%

a

_BB

Remar_quons _que le foncteur F a été construit par analo_gie au foncteur puissance covariant P _qui se défini sur les objets par P(A) = 2 pour tout ensemble A_; ceci suppose donc l'existence d'un classifiant de sous objets (c'est le cas dans ENS où 2 = {0, 1} est un classifiant de sous objets). Or nous n'avons pas pu construire dans la caté_gorie CPO un classifiant de sous objets. nous _y reviendrons dans nos prochains travaux.

Bibliographie

[11 GOLDBLATT, R.(2004). A Comonadic Account ofBehavioural Covarieties of Coal_gebras, Centre for Lo_gic, Lan_gua_ge and computation, Victoria Universit_y, P.O Box 600, Wellin_gton, New Zealand. Rob.Goldblatt@.vuw.ac.nz

[21 Gumm, H.P (1999). Elements of the _general theor_y of coal_gebras. LUATCS'99, Rand Africans Universit_y, Johannesbour_g, South Africa, 60pp.

[31 Hu_gues, J.(2001b), A Stud_y of Caté_gories of Al_gebras and Coal_gebras, PhD thesis, Carne_gie Mellon Universit_y.

[41 Mac Lane, S.(1971), Cate_gories for the workin_g Mathematicien, Sprin_ger-Verla_g.

[5 Rutten, J.(2000), Universal coal_gebra : a theor_y of s_ystem, Theorical computer science,249(1) 3-80.

[61 Worrel, J.(1998), Toposes of coal_gebras and hidden al_gebras, coal_gebraic Methods in computer science,Vol 11, Elsevier Science. 1998, pp. 215-233.

[71 , Ordres partiels complets : une cate_gorie -complet Mémoire de maitrise, Fac.sciences, Université de Yaoundé 1989