5.1.6. Méthode d'inférence MAX-MIN
Cette méthode représente l'opérateur «
ET » par la fonction « Min », la conclusion
« ALORS » par la fonction « Max » et
l'opérateur « OU » par la fonction « Min ». La
représentation graphique de cette méthode
d'inférence est illustrée par la (Fig.41).


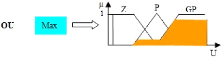
Figure 47: Méthode d'inférence MAX-MIN
1.2 8. INTERFACE DE DEFUZZIFICATION
Les méthodes d'inférence génèrent une
fonction d'appartenance, il faut
transformer cette grandeur floue en grandeur physique
réelle. L'opération de
défuzzification permet de calculer à partir des
degrés d'appartenance à tous les sous-
ensembles flous de la variable de sortie, la valeur de sortie
à appliquer au système. Il y a
plusieurs méthodes de défuzzification à
savoir la méthode du maximum, la méthode des
hauteurs pondérées et la méthode du centre
de gravité, cette dernière est la plus
utilisée L'expression de la sortie dans cette
méthode donnée par l'équation suivante.
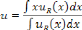
1.2 9. OPTIMISATION PAR COLONIES DE FOURMIS
5.1.7. Introduction
Les études éthologistes ont montré que dans
la nature, les petites créatures faibles
que sont les fourmis, arrivent à résoudre
collectivement des problèmes quotidiens
nombreux et trop complexes pour une seule fourmi tels que :
recherche de nourriture,
construction du nid, division du travail et allocation des
tâches entre les individus, avec
une organisation excrément structurée et sans
aucune supervision. Par les
comportements simples de chacune des fourmis, des interactions
limitées à travers une
coopération inconsciente, émergent des
comportements collectifs intelligents et des
modèles d'auto-organisation [42]. Les fourmis sont
devenues dés lors une nouvelle
source d'inspiration pour la conception de méthodes de
résolution de problèmes
complexes. De plus cette source d'inspiration n'est pas unique
étant donné que les
fourmis sont dotées d'une grande diversité de
caractéristiques disjointes et de
comportements collectifs variés. Une nouvelle classe
d'algorithmes est alors apparue
sous le nom « algorithmes de fourmis artificielles ».
Leur popularité est due d'une part à
la facilité de mise en oeuvre et d'autre part à
la complexité des fonctions réalisables
[43, 44, 45, 46, 47, 48,49]. Deux comportements collectifs ont
été principalement étudiés
chez les fourmis : l'optimisation de chemin et le tri des
cadavres. Le premier
comportement appelé aussi fourragement permettent aux
fourmis de retrouver le plus
court chemin entre leur nid et une source de nourriture
grâce à un système de marquage
de phéromones. Ce comportement naturel a
été modélisé et transposé à la
résolution de
nombreux problèmes d'optimisation combinatoires sous le
nom d'une nouvelle
métaheuristique « optimisation par les colonies de
fourmis ou OCF ». Le deuxième
comportement collectif des fourmis concerne la capacité
de certaines espèces de
fourmis à organiser collectivement des cimetières
composés de cadavres empilés les uns
sur les autres. Là aussi, les chercheurs ont
exploité ce comportement pour fournir des
algorithmes de classification pour lequel l'informatique
classique n'a pas donné de
solution satisfaisante. Dans la suite nous présentons
une brève introduction au monde
des fourmis, ensuite nous décrirons en détail
chacun des modèles de fourmis artificielles
ainsi que les différents algorithmes qui lui sont
associés [51, 52, 53, 54, 55, 56, 57,58].
| 


