|
Ces dernières années, les séries
financières sont caractérisées par des faits
stylisés tels que la non normalité des rendements des actifs
financiers et l'asymétrie négative à cause de
l'accroissement de la volatilité. De ce fait, la complexité du
marché financier et son comportement imprévisible amènent
les investisseurs à quitter la bourse pour investir sur d'autres
marchés plus stables. Afin de mettre des limites aux pertes
catastrophiques, des modèles récents de choix de portefeuille ont
été émis pour réintégrer ces agents dans le
marché boursier.
Le modèle Moyenne-Variance de Markowitz (1952) est la
base de théorie moderne de choix de portefeuille. L'idée
fondamentale de Markowitz étant que les investisseurs choisissent de
façon optimale les portefeuilles efficients en minimisant le risque,
mesuré par la variance, pour un niveau de rendement
espéré.
En pratique, ce modèle est intensivement utilisé
pour contrôler le risque et évaluer les portefeuilles. Cependant,
le champ d'application du critère Moyenne-Variance est limité
parce qu'elle est basée sur la variance comme mesure de risque. En
effet, cette dernière n'est pas constante au cours de temps puisqu'elle
est fondée sur les taux de rendement qui sont plus élevé
au moment des crises et faible lorsque le marché boursier est immobile.
Aussi, elle ne donne pas importance aux valeurs négatives des taux
rendement parce qu'elle analyse les pertes et les gains de la même
manière et n'est valable que dans un univers gaussien. Or comme la loi
normale est caractérisée par une queue fine, l'approche classique
ne tient pas compte des valeurs extrêmes situées au niveau des
queues.
Des études récentes ont montré que les
pertes sévères ne sont pas rares puisque les distributions des
taux de rendement d'actifs financiers sont asymétriques à queue
épaisse (l'hypothèse de normalité est rejetée). De
ce fait, des scénarios indésirables et des pertes catastrophiques
ne peuvent pas être prise en compte seulement par la variance. Ainsi, des
nouvelles mesures des risques sont prises en compte lors des choix des
portefeuilles. Du point de vue statistique, une innovation importante apparue
est l'attention prêtée à la partie du risque des queues.
Dès 1963, Mandelbrot a montré qu'il y a une
nécessité d'employer une mesure de risque de chute du cours
à la place de mesure classique pour le choix de portefeuille. Parmi ces
mesures, la Value-at-Risk (VaR) et l'Expected Shortfall (ES). La
propriété de ces concepts
étant de mesurer le comportement d'un processus pour des
niveaux exceptionnellement grands ou petits.
C'est à la fin des années quatre-vingt, que la
Value-at-Risk a marquée sa présence pour la première fois
sur le marché financier aux Etat Unis par la banque «Bankers
Trust», aussitôt, cette mesure devient de plus en plus populaire
notamment grâce à la banque Américaine «J P.
Morgan» en 1994 et son système « Riskmetrics ».
D'une manière générale, la VaR est une
mesure de la perte potentielle maximale que peut subir un portefeuille dont les
rendements suivent une loi spécifiée, pour une probabilité
donnée sur une période de détention fixée en cas
d'évolution défavorable des facteurs du marché.
Ainsi, Rockafellar et Uryasev (2000) ont proposé la
mesure ES de perte comme solution pour l'insuffisance du VaR lors de choix du
portefeuille. Comparée à la VaR, la CVaR est une mesure
cohérente plus générale puisqu'elle mesure les risques au
delà de la Value-at-Risk. A cet instar, on peut définir
l'Expected Shortfall comme le quantile correspondant à la perte
potentielle qui peut subir un titre ou un portefeuille suite à des
mouvements défavorables des prix de marché avec un seuil de
confiance á donné sachant que cette perte dépasse au moins
la VaR.
Nous essayerons dans notre mémoire de présenter
les critères de choix de portefeuille en ajoutant une contrainte de type
VaR ou CVaR au modèle classique de Markowitz afin de tenir compte des
asymétries des distributions des rendements. Le but de l'ajout de cette
contrainte est de limiter la perte à un niveau fixé par
l'investisseur lui-même. Contrairement aux études
antérieures, le risque de portefeuille est contrôlé par
deux mesures ; la variance et la VaR ou CVaR.
En conséquence l'objectif de ce travail est :
d'examiner l'impact d'ajouter une contrainte VaR ou CVaR au modèle
Moyenne-Variance de Markowitz, étudier l'effet d'augmenter le niveau de
confiance á et/ou l'intervalle de variation de
deuxième contraint (VaR ou CVaR) sur la réduction de perte ainsi
analyser la capacité de cette approche à réduire le risque
dans le choix des portefeuilles.
Pour atteindre ces objectifs, nous étudierons les
hypothèses suivantes ; tout d'abord, les concepts des mesures de
risque et de risque de perte, ainsi l'aversion au risque et
l'aversion aux pertes. Ensuite, nous concéderons la
généralisation de l'approche
Moyenne-Variance de Markowitz en incorporant une
deuxième contrainte Value-at-Risk ou Expected Shortfall.
De ce fait, nous commencerons l'étude théorique
par le premier chapitre où nous traiterons dans une première
cellule, la notion de la fonction d'utilité et la différence
entre l'aversion au risque et l'aversion aux pertes. La deuxième sera
consacrée au concept de la diversification et la théorie de choix
du portefeuille définie par Markowitz.
Dans Le deuxième chapitre, nous
analyserons les mesures de risque simples telles que les mesures de Downside et
les mesures de dispersion. Cependant, ces mesures restent une simple estimation
de risque et ne peuvent pas être une vraie représentation de
risque. Pour cela les investisseurs averses au risque ont recherché des
nouvelles stratégies pour assurer leurs portefeuilles. Parmi ces
approches, nous mentionnerons la théorie de Safety-First de Roy (1952).
À la fin de ce chapitre, nous citerons les mesures de risque de perte
telle que la Valueat-Risk et l'Expected Shortfall.
La partie empirique sert à étudier quatre
approches de choix des portefeuilles. Après avoir présenter
l'échantillon de l'étude, nous étudierons l'approche
classique. Puis, nous calculerons la VaR paramétrique et la VaR
historique. Ainsi, nous traiterons l'approche Moyenne-VaR. Dans la suite, nous
étudierons le troisième modèle de sélection de
portefeuille, l'approche Moyenne-Variance-VaR. A la fin de cette partie, nous
analyserons les implications de choix de portefeuille résultant
d'imposer une contrainte de type CVaR au modèle classique
Moyenne-Variance.
Introduction
«La théorie moderne du portefeuille»,
introduite par Markowitz en (1952) présente les concepts de
référence en matière du choix de portefeuille et constitue
le point de départ d'autre méthodes dites plus complet.
L'objectif de tout investisseur rationnel est de trouver la
combinaison optimale d'actifs financiers, composant son portefeuille, qui
procure le meilleur rendement possible pour une certaine quantité de
risque. Or la réalisation de cet objectif passe par un ensemble des
objectifs secondaires classés suivant une méthodologie logique
qu'on développera ci-après.
La théorie de l'utilité espérée a
dominé l'analyse de la prise de décision sous le risque. Elle a
été courante comme modèle normatif du choix raisonnable
(Keeney et Raiffa 1976) et largement appliquée comme modèle
descriptif du comportement économique (Friedman et Savage 1948). Ainsi,
on le suppose que toutes les personnes raisonnables souhaiteraient obéir
les axiomes de la théorie du Neumann et Morgenstern (1944) et que la
plupart des personnes font réellement, le plus souvent, autrement dit
tous les investisseurs sont averse au risque et agirent de tel sorte qu'ils
maximiseront leurs utilités espérés.
Ce chapitre s'organise de la façon suivante : la
première section nous amène à mieux comprendre certaines
notions fondamentales sur la rentabilité et ces différentes
classes. Une deuxième section sera consacrée sur le comportement
d'investisseur face au risque au sein du quelle nous développerons la
notion de la fonction d'utilité et l'aversion aux pertes. La
troisième section de ce chapitre se concentre sur le concept de la
diversification. Enfin dans la dernière section nous examinerons en
profondeur la théorie de choix du portefeuille définie par
Markowitz.
I.1 Notion du taux de rentabilité
De nombreux modèles financiers utilisent le taux de
rentabilité historique pour estimer les cours futures des actifs
financiers et par suite prendre la décision adéquate. On
distingue deux types de taux de rentabilité : d'une part, le taux de
rentabilité discret dont le flux monétaire procuré par le
titre est versé une seule fois à la fin du période, et
d'autre part, le taux de rentabilité continue où l'actif
financier pourvoit des flux monétaires en continue.
Ce deux taux permettent d'estimer les propriétés
stochastiques des rentabilités correspondantes telles que la
rentabilité moyenne et la variance.
Pour la rentabilité moyenne on peut mentionner la
moyenne arithmétique de taux de rentabilité où n'y a pas
une capitalisation des revenus intermédiaires et la moyenne
géométrique de taux de rentabilité dont lequel les revenus
intermédiaires réinvestissent après chaque versement.
Notation :
Ri, t : taux de rentabilité de l'actif financier i
à la date t.
Ci, t-1 : cours de l'actif à la date t-1.
Ci, t : cours de l'actif à la date t.
Di, t : les flux monétaires procuré l'actif sur la
période t-1 et t (comme le dividende, des intérêts...).
ri, t : taux de rendement de la titre i à la date t.
Q : nombre de fois de distribution de flux monétaire
pendant une période donnée. n : nombre des périodes.
Xi : proportion de l'actif i investie dans un portefeuille.
ói : Volatilité associé
au titre i.
I.1.1 Taux de rentabilité en temps discret
Le taux de rentabilité d'un actif financier i
donné en temps discret, est l'accroissement relatif de cours de cet
actif entre deux dates successives, toute en supposant qu'il n'y a pas de flux
monétaire distribué au cours de cette période.
En absence des revenus intermédiaires, ce Taux de
rentabilité s'écrit :
i, t (1)
(C - C )
i, t i, t - 1
R =
i, t-1
C
Dans ce cas, Ri, t est considéré comme la
plus/moins value relative de cours du l'actif i à la date t.
En présence de dividende, le taux de rentabilité
est égal à la somme du taux de rentabilité en absence de
dividende et le taux de rendement de cet actif.
(2)
(C - C D )
i, t i, t - 1 i, t
+ (C - C )
= +
i, t i, t - 1
R = r
i, t i, t
i, t -1
C C
, t -1
i
Également on peut définir le taux de rendement
comme le pourcentage de dividende versé à la date t de cours
passé de l'actif, c'est-à-dire le rapport entre le cours ancien
de l'actif et la dividende versée.
I.1.2 Taux de rentabilité en temps continue
Pour déterminer le taux de rentabilité au temps
discret, on suppose que les flux monétaires, procurant par l'actif, sont
versés une seule fois à la fin de période, or il est
possible d'avoir des titres pourvoyant des flux monétaire en continue,
c'est-à-dire durant la période de leur détention. A cet
instar, on définie le taux de rentabilité en temps continue comme
le taux de capitalisation des flux versés par l'actif.
En absence des revenus intermédiaires, la formule
mathématique est :
R
q
=
i,
t
1
i, t -
(C D
i, t i,
+
q (3)
- 1
1
)
t
C
I.1.3 Moyenne de taux de rentabilité
Afin de mesurer le taux d'accroissement d'un actif financier
sur une seule période, on calcule le taux de rentabilité, comme
on a cité dans le paragraphe précédent, par contre si on
souhaite d'évaluer cet actif sur plusieurs périodes successives,
on détermine la rentabilité moyenne. Cette nouvelle notion sert
à mesurer l'évaluation exacte du titre sur une maturation plus ou
mois longue.
En effet, on distingue deux types de moyenne : la moyenne
arithmétique et la moyenne géométrique. La première
est utilisée lorsque les revenues intermédiaires ne sont pas
réinvesties. Ainsi, son expression est :
n
MA (Ri) (1/n) (4)
= Ri
i=1
Lorsque la rentabilité des actifs est incertaine, on
opte le concept de rentabilité espéré qui consiste
à estimer la probabilité Pi, d'avoir un tel taux de
rentabilité c'est-à-dire la probabilité qu'une
rentabilité soit certainement réalisée.
N
MA
i (5)
= P R
(Ri) i
i = 1
Le deuxième type de moyenne tient compte de
capitalisation des flux intermédiaires supportant par l'actif. Cette
moyenne est mise en place si les revenus intermédiaires
réinvestissent à l'intérêt composé. Autrement
dit, lorsque le capital initial augmente, chaque fois, des revenues
intermédiaires. Ainsi, son expression est :
n 1
MG (i) = ? + rt
[ (1 ) n
t = 1
c
] 1
- avec 1
rt = -
t
c -
t1
(6)
Cependant, la moyenne arithmétique de taux de
rentabilité peut être égale à la moyenne
géométrique uniquement lorsque tous les taux de
rentabilité passé et actuel sont équivalents.
I.1.4 Rentabilité d'un portefeuille
La rentabilité d'un portefeuille constitué de n
actifs financiers sur un horizon de temps t, noté RPF, est la
moyenne pondérée des rentabilités procurées par ces
titres.
n
R PF X i R i, t (7)
=
i 1
=
Il est possible de calculer la rentabilité de ce
portefeuille à partir de ses valeurs historique.

- 1
=(v - v ) t t -1
vt
RPF
(8)
Où vt-1 : valeur de portefeuille à la date t-1. vt
: valeur de portefeuille à la date t.
Pour certains cas, un investisseur s'est dérangé
par deux ou plusieurs choix, comment cet investisseur se comportera devant ces
situations risquées ? et quelles sont les facteurs qui influenceraient
la manière du son choix ?
I.2 Comportement de l'investisseur face au risque
Depuis longtemps, la finance comportementale évolue et
connu une dilatation et un déploiement inévitable, toutefois ce
domaine incorpore les concepts de la psychologie dans l'analyse et la gestion
des portefeuilles. Pour cela, cette section se focalisera sur l'attitude des
investisseurs en vers les résultats aléatoires.
Von Neumann et Morgenstern (1944) entrevoient que tous les
investisseurs se comporte d'une manière rationnelle par le fait que
chaque investisseur peut targuer d'avoir calculer avec précision la
somme qu'il désirera recevoir étant donné un certain
risque. Toutefois sur le plan pratique, il a été
démontré que la rationalité reste un comportement
idéal et que le comportement des investisseurs oscille entre
l'appréhension d'une perte et l'espoir d'un gain.
En 1958, Tobin affirmait que le rendement espéré et
la variance du portefeuille sont indispensables pour représenter
l'utilité d'un investisseur, mais qu'est ce qu'une utilité ?
En fait, chaque investisseur possède une utilité
qui est en fonction de sa richesse
Bref, la fonction d'utilité décrit le comportement
des investisseurs et en particulier la qualité des décisions
prises dont les résultats sont aléatoires.
I.2.1 Les critères du choix en condition
d'incertitude
Il est intéressant de noter qu'en se basant sur la
distribution de probabilité, le rendement d'un actif dans un milieu
incertain (Camerer et Weber, 1992) peut prendre différentes valeurs,
donc on doit recours à une liste des critères de choix.
- Maximisation du rendement espéré :
pendant longtemps, utilisé comme le seul critère
disponible nonobstant qu'il n'est valable pour tous les investisseurs.
N
E (Ri) R i , j p i , j (9)
=
j 1
=
On rappel qu'une distribution du probabilité est
attribué à la relation entre une valeur possible et ses chance de
survenir.


- Maximisation de l'utilité de gain :
méthode cité par Von Neumann et Morgenstern en présentant
cinq axiomes de comportement d'un individu pour analyser sa rationalité.
C'est-àdire, un individu opte pour le titre qui présente
l'utilité espérée la plus élevé.
En fait, l'utilité d'un investisseur est une fonction
croissante de sa richesse si son comportement vérifie les axiomes
suivants :
i) Comparabilité : définir un ordre de
préférence complet.
ii) Transitivité : si X est
préféré à Y et Y est préféré
à Z donc fortement X est préféré à Z.
iii) Continuité : si X est
préféré à Y et Y est préféré
à Z donc il existe une probabilité P tel que l'investisseur soit
indifférent entre Y et (X, P, Z ,1-P).
iv) Indépendance forte : si X est
préféré à Y donc pour tout P on a(X, P, Z ,1-P) est
préféré à (Y, P, Z, 1-P).
v) Dominance : si X est préféré
à Y, pour tout P > Q ; (X, P, Z ,1-P) est
préféré à (X, Q, X, 1-Q).
I.2.2 Propriété des fonctions
d'utilité
Chaque investisseur possède sa propre fonction
d'utilité qui fait correspondre à chaque panier de biens, ou
chaque portefeuille, un nombre réel.
Schématisé par une courbe d'indifférence
sur un plan (rendement - risque), cette dernière représente
l'ensemble des portefeuilles avec différentes combinaisons du risque et
du rendement espéré pour les quelles tout investisseur conserve
la même préférence et le même niveau de satisfaction.
Par le biais de sa fonction d'utilité, on mesure la satisfaction d'un
investisseur associée à un niveau donné de la richesse.
Donc, la fonction d'utilité reflet le niveau de
préférence pour différents degrés de fortunes.
Un investisseur rationnel, qui opte à
sélectionner un portefeuille optimal, dispose une fonction qui
évolue dans le même sens avec la rentabilité et d'une
manière inverse avec le risque.
U»(x) : aversion U»(x) > 0 preneur de risque
(courbe convexe).
U»(x) = 0 attitude indifférente.
U»(x) < 0 aversion au risque (courbe concave).
Une fonction d'utilité croissante (U'(x) > 0) ayant
également une utilité marginale croissante décrit
l'attitude d'un individu averse au risque. Pour mesurer ce degré
d'aversion au risque on introduit :
-L'aversion absolue AA(R) = -U `'(R) / U'(R) avec R
désigne la richesse.
Dans ce contexte, il a été
démontré qu'une aversion absolue au risque croissante (constante,
décroissante) en R, amène à une valeur détenue de
titres risqués décroissante (constante, croissante) avec la
richesse.
-L'aversion relative AR(R) = -R. [U `'(R)/U'(R)] avec R
désigne la richesse.
De même, une aversion relative au risque est croissante
(constante, décroissante) en R, amène à un pourcentage
détenue de la valeur de titres risqués décroissante
(constante, croissante) avec la richesse.
I.2.3 La fonction d'utilité quadratique
b
Dans le cadre d'un modèle de Markowitz, un investisseur
choisit un certain panier désiré entre le risque et la
rentabilité. Cette relation de préférence peut
également être exprimée par la fonction d'utilité
suivante :
U(R) = R - Tel que b > 0 (10)
R 2
2
b
AA(R)= (11)
1 - bR

bR
AR(R) avec b
= R < 1 (12)
1 - bR
Chamberlain (1983) a démontré que dans le cas
des distributions elliptiques, la fonction d'utilité quadratique offre
des approximations exactes pour plusieurs fonctions d'utilité standard.
Cette approche suppose que tous les rendements des titres suivent une
distribution normale, ce qui rend simple le choix du portefeuille optimal.
A ce propos, il est intéressant de s'interroger si les
deux premiers moments ont l'aptitude de synthétiser de façon
adéquate l'information quantitative sur le rendement. Pour cela,
plusieurs fonctions d'utilité sont mises en place.
I.2.4 Autres fonctions d'utilité
4 Fonction d'utilité linaire : U(R) = a
+ b.R (13)
tel que AA(R)=AR(R)=0
Les aversions au risque sont explicitement nulles, pour cette
raison la fonction d'utilité linéaire est désigné
comme étend utilité à risque-neutre.
4 Fonction d'utilité logarithmique :
U(R) = ln(R) (14)
1
tel que AA(R)= et AR(R) = 1
R
Cette fonction d'utilité est caractérisée
par une aversion relative constante.
Ce type d'utilité est mis en place lors de la
résolution d'un problème d'optimisation non linéaire avec
contrainte dans un modèle multi périodique.
4 Fonction puissance d'utilité : U(R) R
á
= (15)
avec á désigne le paramètre
d'aversion au risque et y compris entre 0 et 1. AA(R) á
1 -
= et AR(R)=1-á
R
On remarque que l'aversion relative est indépendante de
la richesse, et si á =1, cet individu est neutre au risque.
4 Fonction d'utilité exponentielle :
U(R) ë
1 - . R
= - e (16)
ë
AA(R) =ë et AR(R) =ë.R
Cette fonction d'utilité est caractérisée
par une aversion absolue constante.
Pratiquement, le choix entre ces fonctions d'utilité
dépend à la fois de la situation particulière actuelle et
la méthodologie suivie dans les calculs.
La résolution de la maximisation d'utilité
espérée, devient aujourd'hui plus simple grâce à la
mise en place de l'une des fonctions d'utilité donnée.
Kallberag et Ziemiba (1983) ont prouvé par une
comparaison entre les différentes fonctions d'utilités que ces
fonctions affectent la composition du portefeuille optimal, et que tous les
investisseurs qui possèdent la même aversion au risque absolu vont
choisir les mêmes portefeuilles optimaux. On rappelle que le portefeuille
optimal est celui qui maximise l'espérance d'utilité sur une
durée de temps bien définie.
-1
-
2
0 0
2
3
1
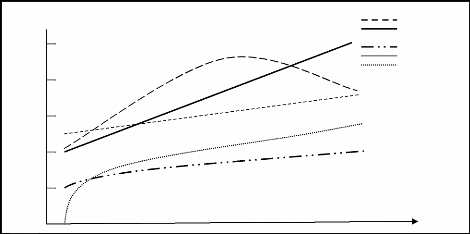
Utilité
Richesse
Quadratique Linéaire Exponentielle Puissance
Logarithmique
Figure (1) (1) : Les différentes fonctions
d'utilité.
I.3 Aversion aux pertes
Dans cette partie, nous allons essayer d'expliquer les
décisions des investisseurs à travers la notion d'aversion aux
pertes. Mais tous d'abord, il faut avoir en tête que le mot perte
désigne à la fois les pertes et les manques à gagner.
En effet, la théorie classique de l'utilité
prévue suppose que les investisseurs prennent des décisions d'une
manière objective et rationnel en s'appuyant seulement sur des
probabilités affectés en fonction des informations disponibles et
que leurs préférences sont stables. Néanmoins, plusieurs
psychologues comme Kahneman et Tversky (1979) ont donné la preuve que la
psychologie comportementale put être une cause de la divergence entre la
perte approximé théoriquement et la perte réellement
scruter.
Kahneman et Tversky (1979) expliquent l'aversion aux pertes
par l'habilité d'un investisseur de payer davantage pour éviter
l'augmentation d'un risque ce que permet de réduire un risque
déjà subi dans les mêmes proportions
Il est important de signaler que l'aversion aux pertes de
chaque gérant du portefeuille, ces sanctions ainsi que les erreurs
d'estimation effectuent directement ses décisions. En outre un
investisseur averse aux risques de perte, favorise une perte non certaine toute
en essayant d'éviter les pertes certaines.
(1): FABOZZI et al. (2006). Financial Modeling
of the equity Market: from CAPM to cointegration .Wiley Fiance. pp 45.
Daniel Kahneman obtint le Prix Nobel en 2002 sur ses recherches
concentrées sur le comportement des investisseurs dans les situations
incertaines.
En fait, Tversky et Kahneman (1991) dans leur théorie des
prospectives soulignent trois hypothèses fondamentales :
4 « losses loom larger than corresponding gains
» une perte est perçue de manière deux fois plus
déplaisant qu'un gain.
4 L'investisseur tend à surpondérer les
évènements rares dans sa décision, autrement dit payer une
prime d'assurance bien trop élevée par rapport au risque
réel encouru.
4 Chacun investisseur défini une référence
« statu quo » à partir du quelle il évalue les gains et
les pertes.
On peut déduire de ces trois hypothèses qu'il y a
souspondération pour les probabilités élevées et
surpondérées pour les probabilités faibles.
En outre, l'effet de surpondération est plus important que
l'effet de souspondération.
Tversky et Kahneman (1991) ont prolongé les notions des
points de référence et l'asymétrie de perte de gain aux
tâches bien choisies à plusieurs attributs ayant des solutions de
rechange qui ne peuvent pas être assignées des probabilités
explicites.
Tout changement significatif par rapport à la statue
référentielle met l'investisseur face à un risque de
perte. De ce fait, par rapport à un cours de référence,
cet investisseur opte comme stratégie de ne pas vendre les titres
perdants en se limitant à vendre les titres gagnants afin de ne pas le
regretter si le cours baissera.
« l'aggravation que celle-là éprouve en
perdant une somme de l'argent semble être plus grand que le plaisir
lié à gagner le même montant... d'ailleurs, le degré
d'aversion croit d'une manière symétrique avec la taille des
enjeux » (Kahneman and Tversky, 1979, p: 279).
C'est que signifie que l'aversion de perte se rapporte au
traitement asymétrique des profits et des pertes relativement à
un point de référence : résultats qui sont perçus
pendant que des pertes sont éprouvées plus profondément
que des résultats perçus comme gagne.

Valeur marginale des gains et des pertes

Gain
Perte
Figure (2): Valeur marginale des gains et des
pertes
Dans ce graphique, on montre que l'aversion aux pertes se
rapporte au traitement asymétrique des profits et des pertes
relativement à un point de référence fixé :
autrement dit, un investisseur se comporte d'une asymétrie dans la prise
de risque face à des perspectives de gains ou de pertes.
Bleichrodt et al. (2006) ont montré par une
expérimentation que la fonction d'utilité pour les gains est
concave et qu'elle est convexe pour les pertes. De plus, ils ont
dévoilé que les hommes sont moins averses aux pertes que les
femmes, de plus l'investisseur tend à prendre une quantité de
risque plus élevé en fin de journée dans l'espoir de
rééquilibrer son portefeuille.
Un investisseur averse aux pertes ne vendait jamais un titre
perdant, mais il attend une situation plus performant. Cependant dans quelle
ampleur serai le coût suite à la détention d'un titre
perdant un certain laps ?
Pour corriger cet aversion aux pertes, il faut effectuer des
modifications structurelles sur la manière d'appréhender le
portefeuille tel que le fait de concrétiser les gains d'une part et
à ne jamais concrétiser les pertes d'autre part, mais
également il faut être prudent quant à la notion du
référentielle, puisqu'un tel événement est
disparu.
Si on opte l'hypothèse que les anticipations de
rentabilité des investisseurs sont homogènes mais pas
nécessairement qu'ils possèdent les mêmes degrés
d'aversion pour le risque, dans ce contexte, tous les investisseurs choisissent
le portefeuille de marché qui regroupe tous les actifs disponibles sur
le marché, néanmoins cette pensée théorique reste
quasi impossible de l'épier sur un plan concret.
Peut-on réduire le risque global, dans un portefeuille,
pour un niveau optimal des titres ? La réponse est positive et c'est
à travers la construction d'une combinaison optimale entre le rendement
et le risque. Cette technique est connue sous le non de la diversification.
I.4 Le concept de la diversification
C'est une manière d'améliorer la rentabilité
d'un portefeuille et à la fois réduire considérablement
son risque.
L'adage populaire dit « on doit pas mettre tous ses oeufs
dans le même panier »
Pour cette raison, un investisseur opte pour un investissement
sur plusieurs actifs au lieu d'investir dans un seul actif, donc il doit
repartir son capital sur plusieurs titres.
Le principe de la diversification se traduit par la
sélection d'actifs qui ne soient pas, ou peu positivement
corrélés, cela permet d'obtenir la même espérance de
rendement en diminuant la volatilité d'un portefeuille.
Il faut avoir en tête que la qualité de la
diversification dépend de deux paramètres qui sont: - le nombre
de titre inclus dans le portefeuille.
- le niveau de corrélation entre les rendements des
titres.
Le graphique ci-dessous condense l'effet de l'augmentation du
nombre d'action dans le portefeuille sur la volatilité de la
rentabilité en fonction de la corrélation entre les actions.
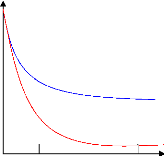
ó PF
Avec corrélation positive
Sans corrélation
10 100 Nombre des actions dans le
portefeuille
Figure (3) : Impact du nombre d'action sur la
volatilité en fonction de la corrélation.
Markowitz (1952) cite dans son fameux article « portfolio
selection » la formulation suivante:
« Pour tout investisseur, le portefeuille
d'utilité maximal, qu'il choisi s'il est rationnel, est un portefeuille
optimalement diversifié dans le sens ou il présente le rendement
attendu le plus élevé qu'il est possible d'obtenir pour le niveau
de risque qui est celui de portefeuille ».
Dans le paragraphe suivant, on essaye d'introduire l'effet de
la corrélation entre deux actifs financiers A et B sur le rendement d'un
portefeuille ainsi que sur sa volatilité, pour un niveau de
corrélation ?AB ;
- Si ?AB = 1
: Les rendements des titres sont parfaitement corrélés
entre eux, donc varient dans le même sens. Pas d'effet de diversification
autrement dit le niveau de risque reste invariant quelque soit la
manière de répartition des placements voir que les pertes
s'additionne.
- Si ?AB = -1
: Les évolutions des rendements des titres sont parfaitement et
négativement corrélés entre eux, donc les titres
évoluent en sens opposé donc la diversification élimine
tous les risques supportés par les investisseurs et les gains et les
pertes se compensent et l'effet sera maximal.
- Si ?AB = 0 :
Les rendements des deux titres sont indépendants, donc la
diversification réduit effectivement le risque.
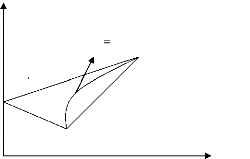
óPF
EPF
0
?
?
1
?=1
=
Figure (4) : Influence du coefficient de
corrélation sur les caractéristiques d'un
portefeuille
Les recherches statistiques ont affirmé que la prise en
considération des corrélations entre les
actifs financiers
améliore sensiblement les résultats. En effet, plusieurs
statisticiens ont conclu
une relation entre le nombre des titres et le gain
provenant de la diversification; Plus le
nombre de titres est grand, plus les covariances sont importantes
et donc plus faible sera le gain provenant de la diversification
supplémentaire.
I.5 Risque systématique
On rappel que le risque globale dans un portefeuille
composé d'actifs financiers, rejoint deux types de risques qui sont le
risque spécifique et le risque systématique liés aux
fluctuations des facteurs du marché.
En effet, le risque systématique en tant que la seule
source d'incertitude dans un portefeuille efficient résulte de la
corrélation entre la rentabilité des portefeuilles efficients
avec celle du portefeuille de marché. L'expression du risque
spécifique est donné par :
N
1
ó 2 ó
=
N 1
i=
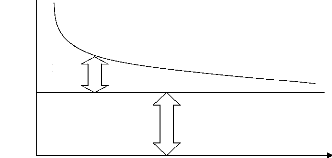
Il convient de noter qu'il existe une relation entre le risque et
le nombre des titres dans un portefeuille, à ce cotexte on avance le
schéma suivant :

5 10 20 50
óPF
R. div
R. systématique
Limite: COV
Nombre de titres
Figure (5) : L'effet de diversification sur le risque
d'un portefeuille
On observe que la réduction du risque est d'abord
très rapide, toutefois elle se freine assez vite. Ceci est due au faite
que le risque systématique est non éliminable par diversification
en raison d'effet de covariance des plus parts des titres.
Markowitz note que « le risque d'un portefeuille bien
diversifié tend vers la moyenne des
covariances des titres inclus dans le portefeuille
» C'est-à-dire ; si N ? 8 ,
ó2PF ?
COV
Il faut mentionner que le risque systématique,
mesuré par Bêta, ignore les risques diversifiables, les risques
asymétries ainsi que les risques spécifiques à chaque
institution financière.
I.6 Le modèle de Markowitz et
détermination de frontière efficiente
Markowitz affirme dans sa théorie que la moyenne et la
variance des taux de rentabilité sont les critères les plus
pertinents en matière d'évaluation des actifs.
Pour analyser cette approche, cette section, souligne la
technique du choix des portefeuilles.
I.6.1 Calcul des portefeuilles efficients
Il est très connu que tous les investisseurs
préfèrent une espérance de rentabilité
élevée ainsi qu'une variance faible. Toute fois, pour un niveau
de risque, on préfère une rentabilité élevée
à une autre moins élevée. Pour se faire, il est judicieux
de rappeler que les courbes d'indifférence représentent la mesure
la plus efficace des préférences des investisseurs,
c'està-dire déterminer le degré de risque qu'un individu
est prêt a accepter afin d'obtenir un certain taux de rentabilité
aléatoire.
Il est maintenant possible de choisir le meilleur portefeuille
dit portefeuille optimal qui correspond à la meilleur combinaison entre
le rendement et le risque en appliquant les concepts de probabilité.
A ce niveau là, Markowitz intervient, une fois encore,
en introduisant la notion du portefeuille dominant, connu encore sous le non du
portefeuille efficient, qui consiste à déterminer le taux de
rentabilité espère le plus élevé pour un niveau de
risque fixé.
A ce propos, Markowitz admet comme cible la détermination
des portefeuilles efficients en les traçant sur un plan (rendement
espéré, risque).

Frontière efficiente
Ensemble des couples (moyenne variance)
*
* *
**
* * * * * * * * * * * * * *
* * ** **
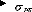
Courbes d'indifférences

EPF
Figure (6) : Le choix du portefeuille
efficient
D'après le graphique, on observe que pour chaque niveau
de risque, il existe un portefeuille qui maximise le rendement attendu ou
encore, pour chaque niveau de rendement, il existe un portefeuille qui minimise
le rendement. L'ensemble de ses portefeuilles construit la frontière
efficiente de Markowitz.
On remarque que par construction, la frontière est convexe
ce qui provoque que le risque n'augmente pas linéairement en fonction
des poids d'actifs dans le portefeuille.
Il est à noter que la région située au
dessus de la frontière implique qu'un tel portefeuille est impossible
à construire, alors que région située au dessous de la
frontière implique que ces portefeuilles sont sous-optimaux et
n'intéresseront pas un investisseur rationnel.
Le problème ici se manifeste par la
détermination du portefeuille optimal, en d'autre terme celui qui
coïncide avec la courbe d'indifférence. Pour se faire, le
problème se résoudre par une simple translation de la courbe
d'indifférence jusqu'au atteindre une tangente entre cette
dernière courbe et celle de la frontière efficiente, bien que
cette tangence représente un portefeuille efficient.
D'une manière plus précise, le portefeuille
optimal est celui qui correspond, pour un investisseur, le mieux aux
caractéristiques de sa fonction d'utilité particulière
c'est à dire en fonction de ces préférences en
matière de rendement ainsi que du risque.
Mais comment bâtir un tel portefeuille ? La réponse
fait l'objet de la suite.
En fait, le but de cette partie c'est de trouver les proportions
Xi à investir dans les différents titres à travers la
résolution de ce système.
Min X X X (18)
i j ij
ó
N
i = 1 N
1
Xi
i = 1
avec Ei : Rendement espéré du titre.
Xi : Proportion investie dans le titre i.
óij : Covariance des rendements des titres i et
j.
óii : Variance des rendements du titre i.
On fera appel à la méthode des multiplicateurs de
Lagrange qui consiste à minimiser
*
|
l'expression de Lagrange, pour chaque niveau de E
|
, qui est donner par :
|
|
N
|
N
|
N
|
N
|
|
Z = X i X j ó ij
|
+ ë ( E*)
Xi E i ë2
- +
1
|
( 1) (19)
Xi -
|
|
i
|
= 1 1
j =
|
i
|
=1
|
i
|
=
|
1
|
Résoudrons cette équation :
?X1
?Z = 2X1 ó11 +
2X2ó12 + .+
2XNó1N + ë 1 E1 +
ë2 = 0 (20)
.
.
?XN
?Z = 2 X1 óN1 +
2X2 óN2 + + 2 XNó
NN + ë 1 EN +
ë2 = 0 (21)
?Z
?ë1
?Z
?ë2
= X1E1 + X2E2 + +XNEN - E* = 0
(22)
= X1+ X2 + XN -1 = 0 (23)
On obtient un ensemble de (N+2) inconnus qui peuvent
s'écrire sous la forme matricielle : C.X= K (24)
|
2 2
ó ó
11
|
121 1
. . 2 1
ó E N
|
X 1
|
0
|
|
:
|
:
|
:
|
:
|
:
|
:
|
:
|
:
|
|
avec C=
|
2 2 . . 2 1
ó ó ó
N N NN N
E
1 2
|
,
|
X= XN
|
et K =
|
0
|
|
E1
|
E E
..
2 N
|
00
|
ë 1
|
E
|
*
|
|
1 1
|
..
|
1 00
|
ë2
|
1
|
Par un simple jeu mathématique, on arrive à trouver
que X = C-1 .K
Le vecteur X représente la structure du portefeuille
efficient pour le niveau de rendement
|
espéré E*
|
. On enregistre finalement une série des portefeuilles
efficients correspond chacun
|
par un niveau de rendement espéré donné.
L'ensemble de ces portefeuilles efficients constitue la frontière
efficiente.
Black (1972 P.448-449) a bien démontré que la
combinaison de deux portefeuilles efficients est un portefeuille efficient,
donc il légitime de conclure que toute combinaison linéaire de
deux portefeuilles est un portefeuille efficient.
I.6.2 L'introduction d'un actif sans risque
Jusqu'à présent, nous avons analysé des
portefeuilles composés d'actifs de nature risqués. Toute fois,
sur le marché réel il existe des actifs sans risque, et
l'introduction d'un tel actif permet à l'investisseur de prêter et
d'emprunter au même taux.
Puisqu'il ne soutient aucun risque, un actif sans risque est
caractérisé par un taux de rémunération
parfaitement certain, une variance nulle ainsi qu'une covariance nulle avec les
autres actifs risqués. Il est généralement associé
aux titres émis par l'Etat à court terme sous forme de Bon de
Trésor, donc son rendement est connu à l'avance.
De ce faite, on note que l'introduction d'un actif sans risque
n'a aucun effet sur l'expression de la variance des portefeuilles cependant, il
apportera des modifications sur ces deux contraintes.
N
(25)
* *
Xi Ri + X + R
= E
N 1 F
i 1
=
N 1
+
* X i 1 (26)
=
i 1
=
En effet, l'espérance de rentabilité est
formée de l'actif sans risque augmenté d'une prime de risque et
l'expression de Lagrangien devient :
|
N
|
N
|
N
|
N+
|
1
|
|
Z = X i X j ij
ó +
|
ë ( N F
X i E i X 1
R
+ +
1
|
- E*) + ë2 (
|
Xi -1) (27)
|
|
i 1 1
= =
j
|
i=1
|
i
|
=
|
1
|
Suivant une même démarche de résolution, on
déduit le vecteur Xi.
De ce fait, on déduit que le rendement
espéré de ce portefeuille est exprimé par une droite
quelque soit la proportion investie dans l'actif sans risque.
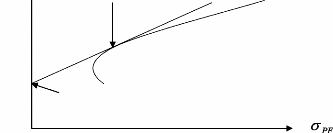
RF
A
Figure (7) : Frontière efficiente avec un actif
sans risque
On constate que l'introduction d'un actif sans risque
transforme la frontière efficiente en une droite partant par le niveau
de l'actif sans risque RF, de façon de toucher la pente la
plus élevé autrement dit la pente de la tangente avec la
frontière définie par Markowitz et cette droite représente
l'ensemble des combinaisons possibles entre l'actif sans risque et l'actif
risqué, autrement, elle offre de nouvelles opportunité
d'investissements donc augmenter son niveau de satisfaction. Cette droite est
connue sous le nom CML(1) « Capital Market
Line ».
Bref, un investisseur opte pour un portefeuille situé
sur le point A, déplie tout ses richesses dans l'actif sans risque.
Cependant, dans le point B l'investisseur place tout son argent dans l'actif
risqué. Un point situé entre A et B implique qu'un tel
investisseur reparti son capital entre l'actif sans risque et l'actif
risqué.
On peut déduire finalement que selon cette approche,
l'optimisation de portefeuille est faite en deux étapes ; la
première était de trouver la combinaison optimale des actifs
risqués en identifiant les poids optimaux pour chacun des titres
composant un portefeuille et la deuxième c'est d'ajouter à ce
portefeuille optimal une certaine proportion d'actif sans risque.
I.6.3 Théorème de
séparation
Dans ce contexte, il intervient à notre esprit une
question fondamentale qui est la suivante : Existe-il une relation entre
l'attitude de l'investisseur en face au risque d'une part, et d'autre part le
choix des combinaisons d'actif risqué ?
(1) on rappel que la droite du marché CML
exprime que le rendement espéré du portefeuille est égal
au taux sans risque plus une prime du risque spécifique à ce
portefeuille.
Markowitz a été principalement
intéressé par la diversification des titres risqués. Tobin
(1958) a ajouté le concept de combiner les actifs sans risque avec les
titres risqués lors de choix du portefeuille. Dans la même logique
de l'approche classique Moyenne-Variance on définie la
théorème de séparation comme suite ; la sélection
de portefeuille optimal pour un niveau donné de tolérance de
risque peut être séparé en deux étapes: d'abord
trouvant un mélange optimal des titres du marché invariant avec
le risque, et ensuite le combinant avec une quantité appropriée
d'actifs certains. C'est-à-dire, il y a une séparation entre les
choix des actifs risqués qui sont le même pour tous les
investisseurs et l'ajout des titres sans risques qui dépendent de
degré d'aversion au risque.
En effet, cette théorie évoque que la
sélection des proportions des actifs risqués des portefeuilles ne
dépend pas de degré d'aversion au risque de l'investisseur. Par
contre la répartition de sa richesse entre les actifs risqués et
les titres certains est basée sur son aversion au risque. Par
conséquent, le choix de portefeuille est fondé sur les
capacités de l'agent d'investir dans le marché financier et ne
plus de l'aversion au risque même dans le cas où il n'y a pas des
actifs certains.
I.6.4 Limites du modèle classique
Comme pour tout modèle, les limites sont
généralement focalisées autours de ces hypothèses
ainsi que sur l'estimation de ces paramètres.
En effet, en cas de défaut, ou encore en cas des pertes
exceptionnelles l'hypothèse de normalité n'est plus vigoureuse
à cause d'une part, l'excès de probabilité des
événements aérogares, et d'autre part l'asymétrie
des rendements c'est à dire que cette approche ne différencie pas
les variations positives (ampleur des variations au-dessous de la moyenne)
à celle négative (ampleur des variations au dessous de la
moyenne).
En outre, le modèle moyenne variance suppose que les
premiers moments sont explicitement suffisants afin de condenser toute
l'information englobée au tour des séries des rendements des
actifs financiers.
De plus, les indicateurs traditionnels préjugent que
les facteurs de marché reste sédentaire pendant la durée
d'investissement ce qui est loin d'être réelle. Par analogie,
l'approche traditionnelle suppose que la volatilité est durable dans le
temps nonobstant, dans la pratique, plusieurs facteurs associés à
la volatilité évoluent au cours de temps tel que le taux
d'intérêt, le bénéfice, les facteurs
macroéconomiques ainsi que l'importance du l'allocation des fonds.
La volatilité n'est plus valides en cas des
portefeuilles complexes c'est-à-dire ceux qui contiennent les produits
dérivés et souvent incapable d'estimer avec précision les
risques et surtout extrêmes.
Tous ces limites nous font douter sur la pertinence des
résultats quelles nos procurent.
Conclusion
Toutefois le taux de rentabilité est calculé
comme étant la différence entre deux cours, l'une initial et
l'autre finale rapporté au cours initial. La rentabilité d'un
investissement incertain exige des estimations probabilistes des états
de nature possibles ; c'est à dire que à chaque état de
nature on effectue une probabilité de réalisation d'un futur
incertain et par suite il faut choisir la distribution appropriée.
Ce chapitre décrit brièvement la théorie
du choix des portefeuilles, On a vu que les préférences d'un
investisseur peuvent être représentées par une fonction de
rendement espéré et la variance d'un portefeuille et que les
hypothèses de la théorie de l'utilité prévue
peuvent être violés systématiquement.
À la lumière de ces observations nous arguons du
fait que théorie de l'utilité, pendant qu'elle est
généralement interprétée et appliquée, n'est
pas à modèle descriptif proportionné.
Un investisseur averse au risque préfère un
rendement certain à n'importe quelle perspective risquée avec la
valeur prévue X. Dans la théorie de l'utilité
prévue, l'aversion de risque est équivalente à la
concavité de la fonction d'utilité, ce qui explique l'orientation
vers les actifs qui possèdent le risque le plus faible.
Or plusieurs études ont donné la preuve que dans
les choix risqué, les investisseurs tendent à surestimer la
probabilité des événements extrêmes et à
sous-estimer la probabilité des événements normaux.
On a cité que le concept d'aversion aux pertes se
repose sur deux résultats centrales, la première étant que
l'analyse des gains et des pertes est évalué relativement
à un point de référence neutre, et la deuxième,
porte sur les changements qui rendent une perte perçue de manière
deux fois plus déplaisant qu'un gain.
Markowitz condense l'optimisation de portefeuille en deux
stations ; dans un premier temps, on trouve la combinaison optimale d'actifs
risqués puis, on ajoute, à ce portefeuille optimal risqué,
une certaine proportion d'actif sans risque.
À travers une simple programmation quadratique
(minimiser la variance pour une rentabilité donnée), on
sélectionne les titres à mettre dans notre portefeuille sous deux
hypothèses, la première c'est la normalité des rendements
du portefeuille et la seconde c'est que la moyenne du rendement et sa
volatilité résument toute l'information nécessaire sur la
performance du portefeuille, mais aussi de son risque.
L'ensemble des solutions pour différents niveaux de
rentabilité constitue une série des portefeuilles dite efficients
et chaque investisseur, suivant son degré d'aversion au risque,
détermine le portefeuille optimal.
Introduction :
Le choix de portefeuille est basé sur un arbitrage
entre le rendement et le risque, à cet effet, plusieurs méthodes
de mesure de risque sont apparues depuis le début du
XXéme siècle dans le but d'évaluer le risque
simple et également le risque de perte: En effet, c'est Neumann et
Morgenstern qu'ont développé la première mesure de risque
fondamental qui est la volatilité. Mais, suite à des crashs
boursiers catastrophiques, d'autres mesures ont été
dévoilées. Toutefois, ces mesures ne donnent qu'une approximation
du risque. Pour cela les investisseurs ont recherché des nouvelles
stratégies pour assurer leurs portefeuilles. Parmi ces politiques, on
mentionne, la théorie de Safety-First de Roy (1952).
Néanmoins, l'utilisation des mesures de risque simples
est insuffisante dans certains cas, puisqu'elles ne tiennent pas compte des
pertes extrêmes qui peuvent conduire les investisseurs à des
pertes catastrophiques, voir même la banqueroute. A ce fait, et
après la crise boursière de 1987 qui a un effet négatif
sur l'accroissement de la volatilité, les gestionnaires de risque ont
élaboré un nouveau indicateur du risque financier qui est
à la fois globale et synthétique ; c'est la mesure de risque de
perte présenté en terme de la Value at Risk et la Value at Risk
conditionnelle.
De ce fait, nous déroulons ce chapitre en trois
sections : la première propose la notion de risque ainsi que la
définition d'une mesure cohérente. La seconde section est
consacrée à la présentation des mesures de risque simples
tel que les mesures de Downside et les mesures de dispersion. Dans la
troisième section, nous exposons la VaR et la CVaR comme mesure de
risque de perte dans la gestion de risque.
II.1 Mesure cohérente de risque
II.1.1 Notion de risque
En Tunisie tous comme à l'échelle
internationale, les institutions financières sont disciplinés par
une variété des risques qui sont généralement
classés sous quatre genres qui sont :
· Le risque de crédit : c'est
incapacité à respecter les engagements de régler les
dettes que se soient principale ou intérêt.
· Le risque de liquidité : ce type
de risque touche toute personne physique ou morale à cause de la
détention d'un actif peu liquide.
· Le risque de marché : ce type
de risque peut être résultat d'une évolution
défavorable des paramètres de marché, D'une manière
plus précise, c'est le risque de perte sur la position du bilan et du
hors bilan.
· Le risque opérationnel : c'est
l'ensemble des risques provenant d'erreurs dans le développement des
outils de valorisation ainsi que de défaillance de procédure, de
personne ou de système.
Se couvrir contre ces risques d'une part, et profiter d'une
situation propice d'autre part, sont les intérêts d'un
investisseur rationnel et l'accès à ces objectifs part par la
mesure de risque.
II.1.2 Notion de la mesure cohérente de
risque
Artzner et al (1997) ont définie une mesure
cohérente de risque en 1997 comme suite : une mesure ? : V
?R de risque s'appelle une mesure cohérente de risque si
elle satisfait les
quatre propriétés suivantes
- Invariance par translation : ?(X
+ á.r) =?(X) -
á
L'addition d'un montant sureá au portefeuille
initial réduit le risque globale d'un montantá.
- Homogénéité positive :
?(ëX) = ë? . ( X )
Le risque est proportionnel à la taille de la position X
pour tenir compte d'un éventuel risque de liquidation lorsque la taille
de X est grand.
- Sous-additive : ? Portefeuille X et Y,
?(X + Y) = ?(X)
+?(Y)
Cette propriété reflète le gain de la
diversification en matière de réduction de risque par le fait de
la corrélation entre les composantes de portefeuille.
- Monotonie : ? X et Y?V si X > Y donc
?(X)=?(Y)
Le risque a une fonction croissante avec la perte autrement dit
la position caractérisé par une perte plus élevé,
elle semble plus risqué.
II.2 Mesures de risque simples
Markowitz et Tobin (1959) ont montré qu'un investisseur
rationnel choisie un tel actif financier à partir deux épreuves ;
le rendement espéré et la variance de titre. Cependant, dans
certain cas ces deux critères sont insuffisants, à titre
d'exemple lorsque la variance et l'espérance rendent l'investisseur
indifférent entre deux titre ou plus.
Toutefois, Si on veut apprécier la performance d'un
actif financier et tenir compte de risque, l'investisseur doit calculer
correctement le risque de chaque titre de portefeuille qui veut construire.
À cet instar, il existe deux types des mesures de risque simples ; la
mesure de dispersion et la mesure de Downside.
II.2.1 Mesures de baisse ou de Downside
L'objectif de ces mesures est la maximisation de
probabilité pour que le rendement de portefeuille soit au-dessus d'un
certain niveau acceptable et minimal, souvent ce dernier est connu sous le nom
de Benchmark (1) ou le niveau de faillite.
II.2.1.1 Semi - Variance
Markowitz a proposé l'utilisation du semi - variance
dans le cas où l'investisseur est indifférent entre deux titres
ou plus après avoir calculer la variance, c'est-à-dire, la
variance est parfois insuffisante pour prendre la décision
adéquate.
À cet instar, la semi- variance, noté SV, est
défini comme l'espérance des carrés des écarts que
les valeurs d'un taux de rentabilité d'une action inférieure
à son espérance présentent par rapport à celle-ci
:
n
|
SV(R ) = p
i i
|
( ) 2
R i E R i
- ( )
|
|
avec Ri
|
i 1
=
< E(R )
i
|
(28)
|
Bien que cette mesure soit un remède dans le cas où
la variance est insuffisante pour choisir le portefeuille optimal, elle
néglige les rendements supérieurs à la moyenne E (Ri).
(1) Florin Aftalion « la nouvelle
finance et la gestion des portefeuilles»: « il existe des fonds qui
possèdent un Benchmark, c'est-à-dire un indice ou un portefeuille
dont la gestionnaire doit reproduire plus ou moins exactement la performance en
essayant de l'améliorer.... Les performances des fonds possèdent
un Benchmark doivent donc se mesure par rapport à celles de leurs
Benchmark et non dans l'absolu. «pp 165.
II.2.1.2 Probabilité d'une rentabilité
négative
C'est une généralisation de Semi - Variance,
elle consiste à calculer le pourcentage des taux de rentabilité
négatif pour un horizon de temps T spécifique de chaque titre
choisissant par l'actionnaire. Elle est définie comme suite :
T
i = 1
Avec pn,i est le pourcentage de taux de
rentabilité de iéme titre négatif.
L'inconvénient de cette mesure est qu'elle
néglige totalement les taux de rentabilité positif, de plus elle
ne tient pas compte des interrelations entre les taux de rendement des titres
considérés.
II.2.1.3 Le Downside Risk.
Afin de minimiser le risque, un investisseur, fixe souvent un
seuil minimal de taux de rentabilité qu'il ne faut pas dépasser
lors de sélection des actifs financiers. Pour cette raison, chaque fois
il doit calculer la probabilité d'avoir un taux inférieur
à un niveau fixé. Cet probabilité est appelé
Downside Risk, noté DN et donné par :
T
DN p R s i (30)
= ( )
,
Où p(Rs,i) est la probabilité d'avoir un
taux de rendement inférieur à une seuil donnée.
L'inconvénient de cette mesure est qu'elle néglige totalement les
taux de rentabilité supérieur au seuil fixé par
l'investisseur.
II.2.2 Mesure de dispersion
Les mesures de dispersion sont des mesures d'incertitude.
Néanmoins, cette incertitude ne mesure pas nécessairement le
risque contrairement aux mesures de Downsides. En effet, elles utilisent des
déviations positives et négatives au même temps et imposent
que ces déviations soient identiquement distribuées.
II.2.2.1 Mesure historiques de risque : La
variance
Le taux de rentabilité moyen est insuffisant pour
évaluer et mesurer la performance d'un actif financier pour un horizon
de temps donné. Il est plus favorable de tenir compte de la distribution
de taux de rentabilité autours de son moyen. Généralement,
on utilise la variance
des taux de rentabilité pour mesurer l'amplitude des
variations de ce dernier autour de sa moyenne.
À cet effet, on définie la variance de taux de
rentabilité d'un actif financier i et on la note
2
parói , la moyenne arithmétique des
carrés de la différence entre le taux de rentabilité et le
taux de rentabilité moyen pour une période T;
T
2 2
1 i
ó i R i t R
= ( )
- (31)
,
T t = 1
L'inconvénient de cette mesure est qu'elle s'infliance par
les taux de rendement élevés et faibles.
II.2.2.2 La volatilité
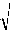
La volatilité d'un actif financier, noté
parói, est définie comme étant la
dispersion de la valeur du titre autour de sa moyenne.
ó (32)
2
= n -
1 i
n
i t i
( , )
R R
- 1
t = 1
Afin d'avoir une bonne approximation de la volatilité,
il est nécessaire de choisir un nombre d'observation très
important et d'utiliser des observations très récent (par exemple
données intraday...).
Bien qu'elle soit une mesure populaire du risque, la
volatilité ne donne pas importance à la valeur négative de
rendement, puisqu'elle traite les cours positifs et négatifs des actions
de la même façon. Un autre problème d'estimation de la
volatilité est qu'elle est instable au cours de temps : plus forte au
moment de crise et faible lorsque le marché boursier est immobile.
II.2.2.3 L'intervalle de variation
(Étendu)
Il consiste à calculer la différence entre le
taux de rentabilité le plus élevé et le taux de
rentabilité minimal de chaque titre i du portefeuille sur un horizon de
temps T. L'actif le plus risqué est celle dont son étendu est
plus élevé :
ETD= (taux de rentabilité maximal) - (taux de
rentabilité minimal) (33)
Cependant cette mesure néglige les taux de
rentabilité intermédiaire, autrement, elle ne prend pas en
considération les taux supérieurs au taux de rentabilité
minimal et inférieurs au taux de rentabilité maximal.
pi
EAM =
t =
II.2.2.4 L'écart absolu moyen
L'écart absolu moyen est la moyenne arithmétique
absolue des écarts qui existe entre le taux de rentabilité et le
taux de rentabilité moyenne, on le note par EAM et on le calcule comme
suite :
|
|
1
|
|
T
|
|
|
|
|
EAM
|
|
|
|
RitR
- i
,
|
(34)
|
|
=
|
T
|
|
|
1
|
|
|
t
|
=
|
|
|
Si les taux de rentabilité des actions, dans le
portefeuille, sont exprimés en pourcentage, autrement dit en fonction de
proportion de chaque titre, dans ce cas on utilise une autre formule pour
calculer l'écart absolu moyen :
T
(35)
RitR
- i
,
1
Où pi désigne la proportion de l'action i dans le
portefeuille.
L'inconvénient primordial de cette mesure est qu'elle
ne tient pas compte des taux de rentabilités négatifs, de plus
elle n'exprime pas le lien qui existe entre les fluctuations respectives de
taux de rentabilité entre les différents titres.
II.3 Assurance de portefeuille
A la suite de crise octobre 1987, les Risks Managers ont
recherché des nouvelles stratégies d'assurance des
portefeuilles.
La première procédure d'assurance, apparue au
début de vingtième siècle, est appelée
assurance Hedgers de portefeuille (1). A priori,
cette méthode a été rejetée par la plupart des
investisseurs parce qu'elle a crée une déviation importante au
prix des actions.
Plusieurs financiers ont tenté de construire des
modèles permettant la protection des portefeuilles contre les variations
brusques des cours d'actifs financiers, parmi ces financiers, on trouve Roy
(1952) qui a évoqué l'approche « Safety-First » dans
lequel un investisseur garantit qu'un certain montant du principal avant le
choix de portefeuille.
(1) L'assurance Hedgers de portefeuille est
une méthode d'assurance basé sur les prix historiques des titres
et le graphique d'évaluation des cours, elle consiste à vendre
les titres suite à une baisse de cours ou à acheter les actifs en
réaction à une hausse
II.3.1 L'approche Safety-First
Deux approches importantes de choix de portefeuille ont
été éditées en 1952. La première, est celle
de Markowitz qui est la théorie classique de choix de portefeuille et la
seconde, de Roy « Safety-First ». Cette dernière est la
théorie fondamentale pour le développement des mesures de risque
de chute du cours.
En effet, Roy a montré qu'un investisseur au lieu de
constituer son portefeuille en terme de fonctions d'utilité comme l'a
proposé Markowitz, il doit tout d'abord, s'assurer qu'un certain montant
du principal est préservé. Ensuite, il choisit le rendement
acceptable et minimal réalisant cette garantie obligatoire.
De même, Roy a précisé qu'un investisseur
préfère l'investissement intéressant avec la plus petite
probabilité d'investir au portefeuille plus rentable mais plus
risqué aussi.
Généralement, cet investisseur choisit ce
portefeuille en résolvant le système d'optimisation suivant ;
Min = (36)
p ( R p R 0 )
w
S/c w' I=1
avec I : vecteur unitaire.
p : est une fonction de probabilité.
Rp : taux de rentabilité du portefeuille. R0 :
niveau de rentabilité fixé.
Nonobstant, l'investisseur ne connaît pas, souvent, la
véritable fonction de probabilité. Pour cela, on fait recours
à l'inégalité des Tchebycheff (1) :
ó 2
p
) =
0
p R R
( =
p
( )
2
(37)
u R
-
p 0
Avec u p et ó p sont respectivement
l'espérance et l'écart type de portefeuille.
(1) Pour une série de variable
aléatoire x où son espérance égale à u et sa
variance égale à 2
ó i l'inégalité de
Tchebycheff
2
ó x
affirme que pour tout nombre positif c, on a
l'inégalité suivante p x u c
( )
- > =Dans notre cas
c 2
2
ó
p
0 ) 2
p R R 0 p u R u R 0
( ) ( )
p = = p - p = p -=
(u
p R - Connaissant la fonction de probabilité,
l'investisseur résout l'approximation comme suite :
S/c w'I=1
Si l'investisseur fixe un niveau de rendement R0 identique
à l'actif sans risque, ce problème d'optimisation est
équivalent à maximiser un portefeuille de ratio de Sharpe.
II.4 Mesure de risque de perte
Divers facteurs contribuent à l'apparition d'une
nouvelle mesure globale de risque, plus efficace, plus pertinent et surtout une
mesure dont tout investisseur a besoin d'en mettre confiance. Parmi ces
facteurs, on cite :
* La crise du dollar et premier choc pétrolier en 1973
* La krach de Wall-Street en octobre 1987
* La crise des monnaies européenne en 1992
* La faillite de la banque Barings en 1994
* La crise des pays asiatiques en 1997
Ainsi qu'un portefeuille diversifié reste
dépoitraillé en matière d'analyse du son risque ou encore
de le calibrer, surtout lorsqu'il renferme certains produits spécifiques
tels que les options, les devises, les obligations.
La succession de ces différentes crises a
renforcé les institutions financières à réviser
leur système de l'analyse du risque d'une part, et d'autre part de
moderniser leurs tactiques de faire face aux risques dans le but d'avoir qu'une
mesure de risque ne soit ni surestimé le risque ni le
sous-estimé.
Or puisque les mesures de risque simples sont insuffisantes
à estimer les risques des événements extrêmes, des
récentes mesures de perte sont mises en place tels que La Value-atRisk
(VaR) et l'Expected Shortfall (ES).
II.4.1 La Value at Risk (VaR)
La Value at Risk est une méthode d'évaluation des
risques fines, elle permet de quantifier les différentes nature du
risques en un seul chiffre appelé montant à risque.
D'une manière éclatante, la VaR peut être
définie comme étend la perte potentielle maximale d'un
investisseur sur la valeur d'un ou d'actifs financiers dont le rendement suit
une loi spécifiée en tenant compte d'un horizon de
détention et d'un intervalle de confiance bien
spécifié.
A partir du chiffre monétaire donné par la VaR, on
peut certifier sur le niveau du risque en fonction de la valeur du portefeuille
et de l'aversion au risque.
Selon Esch, Kieffer « la VaR d'un portefeuille ou
d'un actif pour une durée T et un niveau de probabilité
á, se définit comme le montant de perte attendu de
façon que ce montant, pendant la période [0, T], ne devrait pas
être plus important que la VaR et ceci avec une probabilité (1-
á) ».
On rappel que la VaR se focalise sur des observations
centrales, mais également elle reflète toute l'information
contenue dans la queue gauche adjoint aux pertes de la distribution des taux de
rendements d'un portefeuille d'actifs financiers. Mathématiquement on
définie la Value at Risk comme suit :
VaR (á) = F
-1(á) (39)
avec F (.) désigne la fonction de répartition
associé a la distribution des gains et des pertes.
VaRá (x) = inf {r \ P(x = r) =á }
(40)
Pr (r - VaR ) = Pr (r VaR ) =
= = á á (41)
Fréquence
Probabilité
des
événements
extrêmes
VaR
Figure 8 : Distribution des profits et des pertes d'un
portefeuille
Esch, Kieffer, , "Value at Risk - Vers un Risk Management
moderne", De Boeck université 1997.
Si on admet une VaR d'un portefeuille de 10 millions sur un
niveau de confiance de 95%. Ceci implique sous les conditions normales du
marché on a seulement 5% de chance pour que la perte soit
supérieure à 10 millions.
Cependant la VaR était qualifié comme un
standard en mesure du risque, pourtant il faut l'interpréter comme
étend un instrument de contrôle et de gestion ainsi qu'un signe
d'une bonne maîtrise des risques. En effet, la VaR est un outil
adhérent dans l'identification des sources du risque dans un
portefeuille globale.
II.4.1.1 Paramètres
Comme pour toute mesure de risque, avant d'accéder aux
méthodes de calcul, il faut bien définir quelques
éléments fondamentaux dans l'interprétation d'un chiffre
VaR.
Horizon: C'est la période de
détention du l'actif ou du portefeuille, il doit être le plus
proche possible de la réalité.
La littérature a montré un horizon bref est
préférable qu'un horizon long pour deux raisons, la
première c'est que la combinaison dans un portefeuille reste stable
durant cette période, et la second est que la rareté des
donnés disponible ne pose aucune difficulté sur la
détermination de la VaR donc pour un long horizon les pertes peuvent
être graves.
Il est autorisé d'effectuer une transformation
d'horizon.
Seuil de confiance: Il indique le degré
de couverture contre le risque, ainsi qu'il reflète le degré
d'aversion des investisseurs face au risque de perte. C'est la
probabilité pour que les pertes éventuelles d'un portefeuille ne
dépassent pas la VaR donc elle doive être située entre 0 et
1 pour être significative.
Distribution des profits et des pertes du portefeuille
visés en fin du période: Valeur en fin du période
du portefeuille déduite à partir des cours historiques des titres
dans un portefeuille, c'est donc une identification du niveau d'exposition du
portefeuille en actif risqué.
Bien qu'on arrive à concevoir les caractéristiques
du VaR, pourtant que son calcul nécessite certaines simplifications.
II.4.1.2 Méthodes de calcul du VaR
Afin d'estimer la VaR, il existe une liste de modèles.
Chaque modèle a ses propres prétentions. Mais la
prétention la plus commune qui rassemble ces modèles c'est
l'exploitation des données historiques du marché pour estimer les
changements futurs.
Il est intéressant de signaler que la mise en place
d'une telle méthode dépend essentiellement des titres
étudiés, pourtant dans un univers gaussien les différentes
méthodes convergent vers des résultats très proches.
II.4.1.2.1 La méthode historique ou non
paramétrique
« Le future est le prolongement du passé »
C'est sur cette hypothèse sous-jacente qu'on part l'identification de
cette méthode. En effet, elle est fondée sur un Record des
distributions passées des rendements des actifs, et a partir des quels
on reproduit une nouvelle distribution sous l'hypothèse que ces
rendements soient iid.
Le calcule de la VaR par une telle méthode se
déroule comme suit : Il faut tout d'abord déterminer la valeur
actuelle du portefeuille. Puis, identifier les N variations potentielles toute
en classant ces valeurs historiques par ordre croissant. Finalement, en
déterminant le quantile correspond au niveau de couverture, on
déduit la VaR.
Bien que cette méthode soit la plus simple puisqu'elle
n'impose aucune hypothèse sur la nature de distribution des rendements
ou des facteurs de risque donc elle puisse être utilisée pour des
portefeuilles contenant des options.
La rareté des donnés et des nombreux calculs
peuvent apporter des problèmes quant à l'application de cette
méthode, donc on déduit que la longueur de la série affect
la qualité des résultats. Ainsi la méthode historique
suppose que le marché est stationnaire
II.4.1.2.2 La méthode paramétrique ou
analytique
Afin d'estimer la matrice du
òVariance-Covariance des rendements du portefeuille pour le
calcul de la VaR, cette méthode convoque deux hypothèses, la
première est que les taux de rentabilité suivent une distribution
gaussienne et la seconde est qu'il existe une relation linéaire entre la
valeur du portefeuille et les facteurs de risque,
Pourtant, le recours à cette approche impose certes une
faible probabilité pour les événements extrêmes.
L'application de cette méthode se déploie en trois étapes
: dans un premier temps, il faut estimer la matrice du Variance-Covariance.
Ensuite, on détermine la variance de perte du portefeuille. Enfin, on
calcule la VaR en multipliant la volatilité du ce portefeuille par le
nombre d'Êcart-type associé à un niveau de confiance
donné.
C'est une méthode rapides et simple car elle suppose la
linéarité des facteurs, ce qui écarte les
difficultés pratiques et rend l'agrégation possible mais aussi
assure une perfection quant à la précision de la VaR.
Cependant, cette méthode suppose que la matrice du
Variance-Covariance est stable c'est à dire la composition de
portefeuille et les corrélations entre ces titres sont invariables
durant la période considérée, or dans la pratique la
volatilité influent positivement les corrélations entre les
actifs financiers.
II.4.1.2.3 La méthode de Monte-Carlo
C'est une méthode sophistiquée qui consiste
à effectuer une séquence de simulation dite aussi
réévaluation sur les comportements futurs possibles des facteurs
de risque. La méthode de Monte Carlo combine deux types d'estimation,
l'une des paramètres comme pour la méthode paramétrique et
l'autre d'estimer le quantile comme pour la méthode historique.
Tant que cette procédée peut être
appliqué quelque soit la distribution des facteurs de risque sur le plan
théorique, alors que sur le plan pragmatique cette approche appelle
l'hypothèse que les prix de marché sont distribués selon
une loi gaussienne.
Cette méthode se déroule comme suit : tout d'abord,
on effectue une simulation des trajectoires d'estimation des sources de risque.
Á partir de ces facteurs simulés, on détermine la valeur
du portefeuille. On calcule, finalement, la VaR correspondante.
Cette méthode accepte tous distribution des rendements
ce qui offre une flexibilité attirante dans la mesure ou elle autorise
la modification des modèles. De plus, cette méthode tient en
considération des portefeuilles contenant des produits
dérivés.
Nonobstant, puisque la méthode de Monte-Carlo est
basée sur des processus stochastiques, son application est assez
complexe et également coûteux en matière de temps de
calcul. Autant cette approche suppose une évolution nulle du risque dans
le temps.
II.4.1.3 Limites de la VaR
Malheureusement, la VaR n'est pas la panacée des
méthodologies de mesure de risque. Cependant, le choix du
Valeur-à-Risque comme mesure de risque a été
critiqué par plusieurs théoriciens tels que Szergö (1999),
Danielsson et al. (2001) pour plusieurs raisons : dans un premier temps la VaR
n'est pas une mesure cohérente au sens d'Artzner et al. (1997). Cette
insuffisance mène à plusieurs problèmes théoriques
et pratiques. En effet, pour des distributions non normales, la VaR n'est pas
sous-additive (Embrechts et al. 2002), et peut
mener aux politiques inefficaces de diversification de risque
et aux problèmes graves dans l'exécution pratique des algorithmes
d'optimisation de portefeuille (M. Chabaane et al 2002), autrement dit si on
introduit une action additionnelle dans la composition du portefeuille, le
risque augmente donc la diversification ne permet pas de réduire le
risque total, ce qui ne reflète pas la réalité.
Tandis que son calcul pour un portefeuille donné
indique que son rendement sera au- dessous de la VaR avec la probabilité
(1- á) × 100%, elle ne fournit aucune information sur
l'ampleur de la queue de la distribution ce qui peut
être tout à fait long; dans ces cas, le rendement du portefeuille
peut prendre sensiblement des valeurs inférieures que la VaR et avoir
comme conséquences des pertes graves.
De plus, la base des donnés historiques disponibles sur
le marché, le nombre des facteurs de risque pris en considération
lors de calcul ainsi que la taille de portefeuille posent des contraintes sur
l'application et la précision de la VaR .
Pour remédier ces défauts, On a proposé
l'alternative en termes de VaR Conditionnelle ou Expected Shortfall (Artzner et
al 1997, Acerbi et Tasche 2002, par exemple), qui apprécie la
propriété de la sous-additivité.
II.4.2 La CVaR: Expected Shortfall (ES)
Néanmoins que la VaR représente une mesure plus
générale et utilisée par les plus parts des investisseurs,
des banquiers et des teneurs de marché financier, elle a
été critiqué en tant qu'étant théoriquement
délicat, puisqu'elle ne vérifie pas la sous-additivité de
théorie d'Artezner et al, et numériquement sophistiqué,
à cause de la non convexité. De ce fait une autre mesure de
risque de perte a été introduite à la fin de
vingtième siècle qui est l'Expected Shortfall.
Dans la littérature, cette mesure de risque notée
également sous le nom du Conditional Value-at-Risk et Expected tail loss
(ETL).
En effet, l'Expected Shortfall est une mesure de risque plus
pertinente et aussi puissante que la Value-at-Risk puisqu'elle tient compte des
catastrophes des événements de grands dommages encourus.
Autrement dit, la CVaR, de plus qu'elle est une mesure de perte comme la VaR,
elle est aussi une mesure des événements rare.
A cet instar, on peut définir la CVaR comme le quantile
correspondant à la perte potentielle qui peut subir un titre ou un
portefeuille suite à des mouvements défavorables des prix de
marché avec un seuil de confiance á donné sachant que
cette perte dépasse au moins
la VaR. Donc elle permet de répondre à la
question suivante : combien un investisseur peut il perdre sur un portefeuille
sélectionné avec une probabilité á et pour un
horizon de temps donnée sachant que cette perte dépasse au moins
la VaR ?
Par conséquence, la CVaR est une mesure relative de
risque, elle est définie comme étant l'espérance
conditionnelle des pertes dépassant la VaR pour un niveau de confiance
donné. Pour un portefeuille, elle est équivalente à
l'espérance conditionnelle des rendements des titres au-dessous du
rendement de la VaR.
Comme présenté par Rockafellar et Uryasev (2000),
pour des distributions continues, CVaRá d'un titre p et de
taux de rendement égale à Rp est donnée par :
CVaR R E R R VaR R
á = - - = á
( ) ( / ( )) (42)
p p p p
En outre la VaR est le minimum de l'équation (16) pour
cela elle peut être une solution optimale de cette fonction et dans ce
cas la CVaR est égale à la VaR.
Une autre définition peut être
élaborée à l'Expected Shortfall est l'addition d'une Mean
Exess (moyenne de perte) à la VaR. En effet, la figure (9) montre que la
CVaR á d'un
portefeuille est plus élevée que la VaR
á. De ce fait, la VaR-conditionnelle est
donnée par l'équation suivante :
CVaR ( R p ) = VaR +
Moyenne de perte dépassant la VaR (43)
á á á
CVaR (R p ) = VaR + VaR
-
á á å ( á ì)
(44)
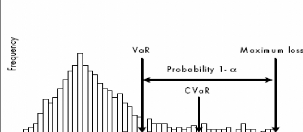
Figure 9 (1) : VaRá et
CVaRá d'un portefeuille
(1) On extrait cette figure de l'article «
VaR, CVaR and mean-downside Risk portfolio selection » des auteurs Paolo
Vanini et Luigi Vignola page 5.
Rockafellar et Uryasev (2002) ont montré que la CVaR
est une mesure cohérente de risque au sens d'Artezner et al et ils ont
exposé la justification dans leur article «Conditional
value-at-risk for general loss distributions«. De plus ils ont
dévoilé que cette mesure peut être estimée
même dans le cas où l'estimation de la VaR est
échouée.
D'autre part, pour des répartitions discrètes,
la formule (42) conduit à une fonction non convexe en position de
portefeuille, et aussi à une mesure non sous-additive de risque. Une
définition de CVaR pour des distributions générales
(répartitions discrètes y comprîmes) a été
présenté par Rockafellar et Uryasev:
1 1
CVaR ( 1
= - p) Z + p R (45)
á s s s
1 - á { } { }
1 - á
s / R Z
? Ù = s / R Z
? Ù =
s s
T
Avec Ps : la probabilité positive
associée au titre s tel que ps = 1 et Z =
VaR á
s = 1
Pflug (2000) a montré que l'Expected Shortfall est plus
significatif que la Value-at-Risk, particulièrement, quand les
données du marché suivent une distribution discrète et/ou
non normale.
En discutant quelques propriétés
mathématiques de la CVaR, elle est toujours plus petite ou bien
égale à la VaR. mais comme nous avons mentionné ci-dessus,
CVaR est une mesure cohérente tandis que le VaR ne l'est pas. On peut
également montrer que ES est une fonction concave
(1) et a, en conséquence, un minimum unique.
II.5 Comparaison entre la volatilité, VaR et
CVaR
Pendant longtemps, la volatilité était la mesure
des risques financiers la plus dominante, grâce à sa
simplicité. D'autre part, la VaR est imposée par les
régulateurs comme mesure plus pertinente, alors que la CVaR est
recommandé par plusieurs statisticiens comme mesure alternative au VaR.
A cet instar, le tableau (1) résume les caractéristiques
particulières de chaque mesure.
(1) La démonstration de convexité
de CVaR á a été élaborer par
Paolo Vanini et Luigi Vignola dans l'article «VaR, CVaR and mean-downside
Risk portfolio selection«
Tableau 1 : Comparaison entre la Volatilité, la
VaR et la CVaR.
|
Volatilité
|
|
La VaR
|
|
La CVaR
|
|
-Représentation commode et simple des risques (un seul
nombre)
- Mesure standard de risque et utilisé par les plus part
des investisseurs.
- Cohérente au sens d'Artzner et al.
- S'infliance par les rendements élevés et
faibles.
- Inapplicable aux distributions non linéaires, tels que
des options, avec des distributions non normales.
-On peut appliquer une procédure de validation de la
volatilité telle que test d'homoscédasticité et
d'autocorrélation.
|
|
-Représentation commode et simple des risques de perte (un
seul nombre)
- Mesure standard de risque de perte et utilisé par les
plus part des investisseurs
- Non cohérente au sens d'Artzner et al car elle ne
vérifie pas l'axiome de sousadditivité.
-Une mesure de risque de chute du cours.
- Applicable aux distributions non linéaires.
-On peut appliquer une procédure de validation de la VaR
tel que Backtesting
-Ne mesure pas des pertes dépassant la VaR.
|
|
- Représentation commode et simple des risques de perte
(un seul nombre)
-Mesure recommandé pour des pertes excédant la
VaR.
- Cohérente au sens d'Artzner et al.
-La meuilleure mesure de risque de chute du cours
-Applicable aux distributions non linéaires.
-Pas facilement d'appliquer les méthodes Backtesting
pour tester la validation de CVaR
-Plus conservatrice que la VaR: elle mesure les risques au
delà de la VaR.
|
Conclusion
Tout au long de ce chapitre, nous avons donc expliqué les
principales mesures de risque et celle de perte.
La rentabilité anticipée peut être
biaisé par le risque, c'est-à-dire, différente de la
rentabilité effectivement observé. Pour cette raison les
gérants de portefeuille doivent tenir copte de l'incertitude. Ce
principe va de soit depuis plusieurs années dés que Markowitz et
Tobin (1958) ont proposé la volatilité comme mesure du niveau de
risque mais seulement dans un univers gaussien.
Mais à cause de l'instabilité des facteurs de
marché et l'asymétrie de l'information d'une part, et de
l'existence des événements rares d'autre part, les investisseurs
sont appelé à moderniser leurs stratégies des mesures dans
un premier temps et de couverture contre ces risque dans un deuxième, et
donc s'orienter vers des nouvelles mesures de risque permettant
l'identification et la modélisation des risque d'une manière plus
élégante, on parle de la VaR et la CVaR qui permettent
d'éviter les pertes inacceptable; en effet la VaR est une mesure de
quantile d'une distribution donnée pour un degré de confiance
spécifié. Elle nous permet d'assimiler les
événements de faible probabilité mais possible et d'impact
dramatique sur la richesse et de quantifier cette perte potentielle en
unité monétaire. Donc rend l'influence des décisions plus
flexible. Toutefois, la VaR peut sous-estime le risque puisqu'elle n'est pas
une mesure cohérente au sens d'Artzner (1997) de fait qu'un portefeuille
diversifié peut s'avérer plus risqué. Une autre limite de
la VaR c'est qu'elle néglige toute l'information sur les pertes
excédant le seuil de confiance.
Pour ces raisons Rockafellar et Uryasev (2000), ont introduit
la CVaR au champ d'optimisation de portefeuille, comme mesure alternative au
VaR. Bref, la CVaR représente la moyenne de toutes les valeurs dans la
queue gauche dépassant la VaR. De plus, elle est une mesure
cohérente, en particulier elle encourage la diversification.
Pourtant, un portefeuille composé de plusieurs produits
exotiques rend l'application de la CVaR très compliqué
Introduction
Les gestionnaires des actifs financiers visent à
créer un portefeuille optimal qui rapporte en même temps, un taux
de rendement espéré plus élevé et un niveau de
risque acceptable. Pour cela, on va comparer dans ce chapitre, quatre approches
de choix de portefeuille.
En effet, après avoir présenté
l'échantillon de l'étude, nous rappelons dans la deuxième
sous-section, l'approche Moyenne-Variance de Markowitz, ainsi la Courbe
d'indifférence et l'effet d'introduire un actif sans risque sur la
frontière efficiente.
Ensuite, dans une troisième partie, nous
commençons par une comparaison entre deux méthodes d'estimation
du VaR. Ainsi, nous étudions, une deuxième approche
d'optimisation du portefeuille et qui est l'approche Moyenne-VaR.
Cependant, parce qu'un investisseur rationnel cherche toujours
à limiter sa perte maximale pour des niveaux de risque fixés par
lui-même, nous traitons dans une cinquième sous section l'impacte
d'ajouter une contrainte de type VaR au modèle classique
Moyenne-Variance, ainsi nous comparons cette approches aux autres vus
pré-avant.
Or, puisque la Value-at-Risk n'est pas une mesure
cohérente dans le sens d'Artzner, dans la dernière partie, nous
allons traiter l'impacte d'ajouter une contrainte de type CVaR au modèle
de Markowitz sur le choix de portefeuille optimal.
III.1 Présentation de l'échantillon du
l'étude
Les donnés de notre étude sont
constituées de vingt actions de CAC40 cotées à la bourse
française sur dix ans. Ces actions sont : Air France, Air Liquide,
Alcatel-Lucent, Axa, BNP, Bouygues, Carrefour, Danone, Essilor-Intl, Lafarge,
LVMH, Michelin, L'orial, Peugeot, Renault, Schneider Electrique,
Société Générale, Total, Vallourec et Vinci.
Les cotations journaliers de ces actions sont comptés
à partir des cours correspondant à une période qui
s'étale de 01 janvier 1997 jusqu'au 17 décembre 2007, la taille
de l'échantillon et donc de 2859 observations.
A partir de ces cotations, on a calculé les taux de
rentabilité journaliers de chaque action pour déterminer les
caractéristiques de chaque titre ; parmi ces caractéristiques on
citera dans
le tableau suivant, la moyenne de chaque actif financier, la
variance, l'étendu, ainsi les taux de rendement maximal et minimal sur
l'horizon de temps considéré :
Tableau 2 : caractéristiques des actions de
l'échantillon
|
Actions
|
Moyenne
10^- 3
|
Variance
10^- 3
|
Ecart
type
|
Rmin
|
Rmax
|
Etendu
|
|
Air France
|
0.7
|
1.07584
|
0.0328
|
-0,12022
|
0,8215
|
0,94172
|
|
Air Liquide
|
0.5
|
0,31329
|
0.0177
|
-0,1099
|
0,0836
|
0,1935
|
|
Alcatel-Lucent
|
0.3
|
1.14244
|
0.0338
|
-0,3839
|
0,4054
|
0,7893
|
|
Axa
|
0.5
|
0,53824
|
0.0232
|
-0,1707
|
0,1332
|
0,3039
|
|
BNP
|
0.8
|
0,46656
|
0.0216
|
-0,1178
|
0,1437
|
0,2615
|
|
Bouygues
|
1
|
0,56644
|
0.0238
|
-0,1504
|
0,1584
|
0,3088
|
|
Carrefour
|
0.2
|
0,37249
|
0.0193
|
-0,1037
|
0,1172
|
0,2209
|
|
Danone
|
0.6
|
0,256
|
0.0160
|
-0,1019
|
0,1019
|
0,2038
|
|
Essilor Intl
|
0.6
|
0,35721
|
0.0189
|
-0,1311
|
0,1251
|
0,2562
|
|
Lafarge
|
0.6
|
0,41209
|
0.0203
|
-0,169
|
0,1308
|
0,2998
|
|
LVMH
|
0.5
|
0,44944
|
0.0212
|
-0,1074
|
0,1226
|
0,23
|
|
Michelin
|
0.4
|
0,43264
|
0.0208
|
-0,097 1
|
0,1283
|
0,2254
|
|
L'orial
|
0.6
|
0,38416
|
0.0196
|
-0,1507
|
0,1112
|
0,2619
|
|
Peugeot
|
0.6
|
0,38809
|
0.0197
|
-0,1297
|
0,1102
|
0,2399
|
|
Renault
|
0.9
|
0,56644
|
0.0238
|
-0,1297
|
0,1294
|
0,2591
|
|
Schneider.Elec
|
0.6
|
0,47524
|
0.0218
|
-0,204
|
0,1126
|
0,3 166
|
|
Sté générale
|
0.8
|
0,49284
|
0.0222
|
-0,1334
|
0,1185
|
0,2519
|
|
Total
|
0.6
|
0,32761
|
0.0181
|
-0,1233
|
0,0921
|
0,2154
|
|
Vallourec
|
1.4
|
0,58564
|
0.0242
|
-0,2578
|
0,1012
|
0,359
|
|
Vinci
|
1.1
|
0,33856
|
0.0184
|
-0,096
|
0,0809
|
0,1769
|
Ce tableau, devanture que l'action Alcatel-Lucent est plus
risqué que les autres actifs : D'une part, il dispose, à peu
près, la plus petite moyenne et la variance aussi élevée.
D'autre part, il possède un étendu le plus grand par rapport aux
autres titres à cause de la faible valeur de Rmin.
Pareillement, à partir de la moyenne, on conclue que
l'action Vallourec est plus rentable, soit un taux de rendement moyen
égal à 1,4. Contrairement au titre Carrefour qui est le plus
risqué dans notre échantillon d'un taux équivalent
à 0,2.
Également, pour les investisseurs averses au risque,
l'actif Danone est préférable que les autres titres, car sa
variance est la moins élevée d`une valeur 0,256.
Cependant, Nicolas Bernoulli a montré dans la
première moitié du 18émme siècle que la
maximisation du rendement espéré est un critère de choix
très anciens. De plus, il a mentionné certains
inconvénients de cette approche telle que la négligence du risque
lors de sélection de portefeuille.
A cet effet, l'approche Moyenne-Variance de Markowitz, qu'on
va l'évoquer dans le paragraphe suivant, est plus
généralisé que le critère de maximisation du
rendement espéré, puisqu'elle regroupe la moyenne et le risque
lors de choix des titres optimaux.
III.2 L'approche Moyenne-Variance
Selon Markowitz, l'analyse de la sélection de
portefeuille peut être formalisée comme un système
d'optimisation composé par une fonction de minimisation de variance sous
une contrainte d'un taux de rendement fixé.
Pour résoudre ce système, Markowitz suppose que les
taux de rendements sont normalement distribués
(1).
Figure 10 : Histogramme de l'échantillon
sélectionné
La figure (10), représente l'histogramme des taux de
rendement de portefeuille des actions triés. En effet, cet histogramme
semble être symétrique par rapport à un axe
parallèle à l'axe des coordonnés passant par le point
d'abscisse 0. Cela est un indicateur d'une distribution normale et
centrée. De ce fait, on peut utiliser l'approche classique pour la
sélection de portefeuille optimal.
L'objectif d'investisseur rationnel, d'après la
théorie Moyenne-Variance, est la construction d'un portefeuille qui
offre le risque le plus faible possible pour un niveau de rendement
désiré. Dans ce cas, le risque est contrôlé par un
seul instrument, qu'est la variance
(1) : Une loi normale est
caractérisée par deux propriétés ; la
première est le coefficient de Kurtosis (d`aplatissement) qui est
égale à 3 et la deuxième le coefficient de Skewnes
(d'asymétrie) qui est équivalent à 0.
En choisissant les proportions de chaque titre dans le
portefeuille, un investisseur choisit parmi les paires disponibles de
Moyenne-Variance, les actions intéressées. Afin de calculer
les allocations pour une paire possible, nous fixons un taux de
rendement espéré R.
Pour se faire, le portefeuille optimal pour tous les
investisseurs averses au risque est celui qui résoudre ce système
:
Min X' i Ó X (46)
i
x
X
' . 1 i ô =
) = R
S/c
X' . E (R
i i
Avec Ó matrice Variance-Covariance de portefeuille (voir
annexe).
X1
Xi = : Vecteur des poids des titres dans le
portefeuille choisi.
X20
1
ô Vecteur unitaire de vingt colonnes et une
ligne.
1
= :
E R
( )
1
|
E R i
( ) =
|
: Vecteur des espérances des titres (voir tableau (1),
colonne
|
E R
( )
20
« Moyenne »).
À travers une programmation sur le logiciel de Matlab,
on détermine les proportions Xi à investir dans les
différentes actions. Or pour tracer la frontière d'efficience, on
fixe chaque fois un taux de rendement espéré et on
détermine la variance minimale de portefeuille. Ainsi, dans le tableau
(3), nous comptons les vecteurs d'allocation d'actifs ainsi la variance de
portefeuille pour des espérances équivaut à ; 0.02% ;
0.04%; 0.06%; 0.08% ; 0.09% et 0.1%.
Tableau 3 : Les proportions des actions dans les
portefeuilles optimaux
|
Xi R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
X1
|
0.0352
|
0.0434
|
0.0782
|
0.0385
|
0.0555
|
0.0567
|
|
X2
|
0.0000
|
-0.0000
|
0.0391
|
0.0186
|
0.0619
|
0.0393
|
|
X3
|
0.3637
|
0.3465
|
0.3163
|
0.0559
|
0.1471
|
0.1590
|
|
X4
|
0.0281
|
0.0002
|
0.0487
|
0.0361
|
0.0557
|
0.0316
|
|
X5
|
0.0486
|
0.0818
|
0.0131
|
0.0406
|
0.0427
|
0.0272
|
|
X6
|
-0.0000
|
0
|
0
|
0.0308
|
0.1007
|
0.0523
|
|
X7
|
0.1154
|
0.0944
|
0.1340
|
0.1071
|
0.0928
|
0.0555
|
|
X8
|
0
|
0.0193
|
0.0560
|
0.0726
|
0.0900
|
0.0637
|
|
X9
|
0
|
0.0186
|
-0.0000
|
0.0766
|
0
|
0.0276
|
|
X10
|
0.0014
|
0.0000
|
0.0031
|
0.0594
|
0.0017
|
0.0351
|
|
X11
|
0.1012
|
0.0540
|
0.0633
|
0.0739
|
0.1060
|
0.1054
|
|
X12
|
0.0000
|
-0.0000
|
0.0078
|
0.0694
|
0.0458
|
0
|
|
X13
|
0.0876
|
0.0638
|
0.0607
|
0.0225
|
0.0364
|
0.0820
|
|
X14
|
0.0948
|
0.0934
|
0.0732
|
0.0689
|
0.0183
|
0.0703
|
|
X15
|
0.0228
|
0.0186
|
0.0378
|
0.0885
|
0.0836
|
0.0105
|
|
X16
|
0
|
0.0259
|
0.0264
|
0.0174
|
0.0396
|
0.0568
|
|
X17
|
0.0940
|
0.0783
|
0.0338
|
0.0903
|
0.0054
|
0.0658
|
|
X18
|
0.0070
|
0.0618
|
0.0085
|
0.0118
|
0.0167
|
0.0612
|
|
X19
|
0
|
0
|
0
|
0.0101
|
0
|
0
|
|
X20
|
-0.0000
|
-0.0000
|
0
|
0.0110
|
0
|
0
|
|
Variance
|
0. 987
|
1.026
|
1.0607
|
1.3001
|
2.2677
|
2.335
|
|
10-4
|
|
|
|
|
|
|
|
VaR99%
|
0.0237
|
0.0243
|
0.0251
|
0.0358
|
0.0360
|
0.0365
|
En conséquence, on remarque que plus le niveau du
rendement espéré est élevé plus le risque, qui est
mesuré par la variance, est grande. Par exemple, pour une
espérance égale à 0,02%, on a une variance
équivalente à 0,987.10-4. Par contre, en augmentant le
taux de rendement espéré à une valeur 0, 1%, le risque
accroît également pour atteindre une valeur de 2,335.1
0-4. Pareillement, on peut mesurer le risque de portefeuille
à partir du VaR. A ce fait, nous avons calculé la VaR de
portefeuille pour un niveau de confiance égale à 99%. Comme la
variance, chaque fois l'espérance est augmentée, la
VaR99% amplifie.
Pour bien marquer la relation entre le taux de rendement
espéré et la variance d'un portefeuille, nous traçons dans
le graphique suivant, la frontière efficiente dont ainsi définie
:
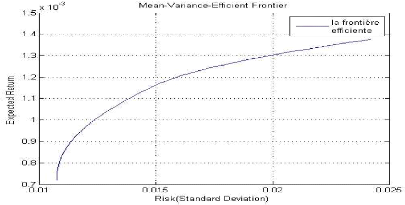
Figure 11 : La frontière efficiente de
l'approche Moyenne -Variance
Cette frontière contient les portefeuilles optimaux
pour chaque niveau de rentabilité espéré où le
risque est minimum. Ces portefeuilles forment une courbe concave et elliptique
dont les coordonnées sont le risque et la rentabilité
espérée.
Une question fondamentale s'interroge dans cette partie qu'est ;
comment un investisseur averse au risque choisit son portefeuille parmi ces
derniers ?
III.2.1 Courbe d'indifférence
Chaque investisseur sélectionne une fonction
d'utilité qui est spécifique à son niveau d'aversion au
risque. Or pour un investisseur averse au risque, construit son portefeuille en
maximisant l'espérance de rendement et en réduisant le risque. La
fonction qui satisfait ces deux conditions est la fonction quadratique. Or,
pour déterminer la courbe d'indifférence, on doit maximiser la
fonction d'utilité espérée :
'
(47)
Max = ë Ó
E(U(w)) E (R ) X - (1/2) X X
i i i i
x
20
S/c 1
X i
=
i
Où ë est le degré d'aversion au
risque.
Pour illustrer la courbe d'indifférence, on fixe, au
départ, ë à une valeur équivalente à
1.3 et on augmente chaque fois l'espérance pour déterminer la
variance. Ainsi on trouve les différentes valeurs dans le tableau 4.
Tableau 4 : Variances des portefeuilles optimums pour
un degré d'aversion ë= 1.3
|
E(Ri)
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
ó 2(10)-4
|
1.005
|
1.108
|
1.1214
|
1.068
|
1.0091
|
1.008474
|
À partir des valeurs trouvées, on trace la courbe
d'indifférence dans un plan des coordonnés variance et
espérance :
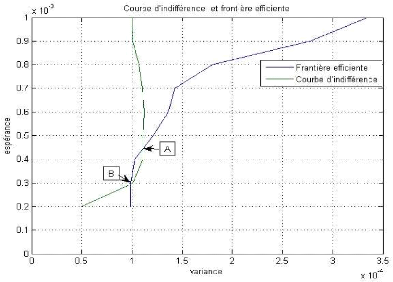
Figure 12 : Courbe d'indifférence et
frontière efficiente
Sur la figure (12), sont représentées deux
courbes ; la première, tracé en bleue, est la frontière
efficiente et la deuxième en verte, est la courbe d'indifférence.
On remarque que la courbe d'indifférence est convexe ce qui provoque que
le risque n'augmente pas linéairement en fonction du poids des actifs
dans le portefeuille. De plus elle coupe la frontière de Markowitz en
deux points A et B ; ces deux points représente deux portefeuilles
optimums.
Ainsi, selon sa tolérance au risque, l'investisseur
choisit son portefeuille parmi ces deux points. à titre d'exemple, s'il
est moins averse au risque, il sélectionne le portefeuille A, sinon, le
portefeuille B sera plus efficace.
Cependant, chaque investisseur dispose un degré
d'aversion au risque spécifique à sa position selon sa
préférence du risque. De ce fait, on va étudier par suite,
l'effet d'augmenter ë à une valeur 5, sur le choix de
portefeuille efficient.
Tableau 5 : Variances des portefeuilles optimums pour
un degré d'aversion ë= 5
|
E(Ri)
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
ó 210-4
|
3.9070
|
4.1922
|
4.3370
|
4.007
|
3.9377
|
3.8025
|
A partir des valeurs trouvées dans les tableaux 4 et 5, on
trace les courbes d'indifférence dans le plan des coordonnés
variance et espérance :
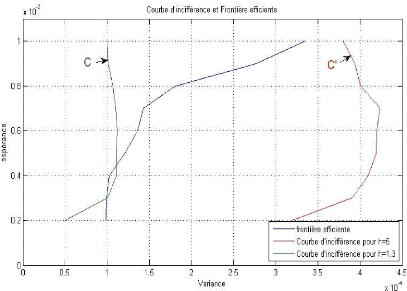
Figure 13 : Courbes d'indifférence et
frontière efficiente
Sur la figure 13, sont représentées deux courbes
d'indifférence C et C' pour deux
niveaux d'aversion successifs 1,3 et 5. La courbe C'
représente un niveau de risque plus élevé que
C, pour cela son intersection avec la frontière
d'efficience se réalise à deux points ; la première,
à un niveau d'espérance plus haut que le point A (Figure 12), par
contre la deuxième à un niveau plus faible que le point B (Figure
12). En conséquence, la courbe C' offre un niveau de
satisfaction plus faible que la courbe C. Mais ces deux
courbes ne produisent pas le niveau d'utilité le plus
élevé puisqu'elles ne sont pas tangentes à la
frontière efficiente.
III.2.2 Introduction d'un actif sans risque
Supposons maintenant qu'il existe un actif sans risque dont le
taux de rentabilité Rf est fixé à une valeur égale
à 6.10-4 sur l'horizon de temps considéré. Dans
ce cas, le risque de l'actif est nul (c'est-à-dire variance = 0) et son
espérance égale à 0.06%.
Dans ce cas le système d'optimisation de portefeuille
devient :
|
Min
x
|
20 20
i j
|
Xi Xj cov( , )
R R (48)
i j
|
20
|
Xi Ri
|
+
|
X f R f R
=
|
|
s/c
|
i
20
|
Xi X 1
+ =
f
i
Où Xf désigne la proportion prise par
l'investisseur dans l'actif sans risque.
A cet effet, dans le tableau 6, nous déterminons les
vecteurs d'allocation des actions ainsi la variance de portefeuille lorsqu'on
introduit un actif sans risque.
Tableau 6: Les proportions des actions dans les
portefeuilles optimaux suite à
l'introduction d'un actif sans
risque
|
Xi
|
R =0.6 10-3
|
|
X1
|
0
|
0
|
|
X2
|
0
|
0
|
|
X3
|
0
|
0
|
|
X4
|
0
|
0
|
|
X5
|
0
|
0
|
|
X6
|
0
|
0
|
|
X7
|
0
|
0
|
|
X8
|
0.1481
|
0.1020
|
|
X9
|
0
|
0
|
|
X10
|
0
|
0
|
|
X11
|
0
|
0
|
|
X12
|
0
|
0
|
|
X13
|
0.8199
|
0.8227
|
|
X14
|
0
|
0
|
|
X15
|
0
|
0
|
|
X16
|
0
|
0
|
|
X17
|
0
|
0
|
|
X18
|
0
|
0
|
|
X19
|
0
|
0
|
|
X20
|
0
|
0
|
|
Xf
|
0.0321
|
0.0752
|
|
Variance 10-4
|
1,0506
|
1,0432
|
Pour R égal à 0.06%, on remarque que
l'ajout d'un actif sans risque fait diminuer le risque, mesuré par la
variance, de 1,0607.10-4 à 1,0506.10-4. De plus
lorsqu'on augmente la proportion de l'actif sans risque dans le portefeuille de
3.21% à 7.52% la variance diminue de 1,0506.10-4 à
1,04320.10-4.
Suite à l'introduction d'un actif sans risque, la
frontière efficiente n'est plus elliptique, elle se transforme en une
droite linéaire passant par le taux de rentabilité Rf et tangente
à l'ancienne frontière. Donc on peut schématiser cette
frontière comme suite :
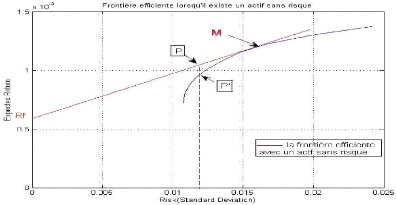
Figure 14 : Effet de l'actif sans risque sur la
frontière efficiente
Ainsi, l'investisseur place une fraction Xf dans l'action sans
risque et les restes dans le portefeuille risqué. La frontière
d'efficience prend alors la forme d'une demi droite qui est [Rf , M[. Le point
M qui correspond au point de tangence entre l'ancienne frontière et la
récente. On remarque aussi, que l'introduction d'un actif sans risque
fait augmenter le rendement espéré de p'
à p, pour un même niveau de risque
égale à 0,012.10-2.
Le portefeuille optimal est celui qui correspond au point de
tangence entre la demie droite [Rf , M[ et la courbe d'indifférence la
plus élevée qu'il peut l'atteindre.
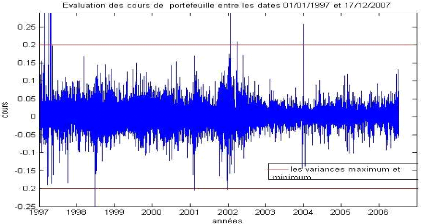
Figure 15 : évaluation des cours de
portefeuille
Bien que l'approche Moyenne-Variance est la plus
utilisé en pratique par la plupart des investisseurs, elle souffre de
certaines limites, telle qu'elle se base sur la variance comme mesure de
risque, qui analyse les pertes et le les gains de même façon et
n'est valable que dans un univers gaussien. Or puisque la loi normale
possède une queue fine, l'approche classique ne tient pas compte des
valeurs extrêmes situant au niveau des queues. Ainsi, dans la figure 15,
nous avons illustré les cours du portefeuille examiné sur
l'horizon de temps considéré. On enregistre, pendant les dix ans,
des valeurs qui dépassent les variances maximum et minimum #177; 0.2.
De ce fait, on va introduire dans la partie suivante une autre
mesure de perte dont elle tient compte des valeurs extrêmes, la
Value-at-Risk, et on étudiera son effet sur le choix de portefeuille
efficient.
III.3 Estimation de la VaR
Nous étudierons dans cette section deux méthodes
d'estimation du VaR : la méthode paramétrique et la
méthode empirique.
III.3.1 VaR paramétrique
Afin de calculer la VaR paramétrique, nous supposons
que les rendements des actions ainsi de portefeuille suivent une loi normale. A
partir, d'une programmation sur Matlab, on calcule la VaR pour trois niveau de
confiance 99%, 95% et 90%. Les résultats trouvés sont
enregistrés dans le tableau 7 :
Tableau 7 : Estimation de la VaR par la méthode
paramétrique
|
VaR(á)
Actions
|
VaR (0.99)
%
|
VaR (0.95)
%
|
VaR (0.90)
%
|
|
Air France
|
-7,56
|
-5,32
|
-4,13
|
|
Air Liquide
|
-4,07
|
-2,86
|
-2,22
|
|
Alcatel-Lucent
|
-7,84
|
-5,54
|
-4,31
|
|
Axa
|
-5,33
|
-3,75
|
-2,91
|
|
BNP
|
-4,94
|
-3,47
|
-2,68
|
|
Bouygues
|
-5,43
|
-3,81
|
-2,95
|
|
Carrefour
|
-4,46
|
-3,15
|
-2,45
|
|
Danone
|
-3,65
|
-2,56
|
-1,98
|
|
Essilor Intl
|
-4,34
|
-3,05
|
-2,36
|
|
Lafarge
|
-4,67
|
-3,28
|
-2,55
|
|
LVMH
|
-4,89
|
-3,45
|
-2,68
|
|
Michelin
|
-4,81
|
-3,39
|
-2,63
|
|
L'orial
|
-4,49
|
-3,16
|
-2,45
|
|
Peugeot
|
-4,51
|
-3,17
|
-2,46
|
|
Renault
|
-5,44
|
-3,82
|
-2,96
|
|
Schneider.E
|
-5,02
|
-3,53
|
-2,74
|
|
Sté générale
|
-5,08
|
-3,57
|
-2,76
|
|
Total
|
-4,14
|
-2,91
|
-2,26
|
|
Vallourec
|
-5,49
|
-3,84
|
-2,96
|
|
Vinci (EXSGE)
|
-4,19
|
-2,93
|
-2,26
|
Le Tableau 7, nous permet de constater que chaque fois le
niveau de confiance diminue, la VaR baisse. Par exemple la VaR (99%) de
l'action Air France équivalente à 7.56% en valeur absolu,
cependant, elle diminue lorsque le niveau de confiance devient 90% à une
valeur 4.13%. On peut expliquer cette résultat de la façon
suivante : la VaR (99%)=7.56% cela signifie qu'il y a 1% d'avoir une perte
maximale sur l'action Air France dépasse 7.56%. Mais
pour la VaR (90%) on a 10% de chance d'enregistrer une perte
maximale dépasse 4.13% ; C'est -à- dire qu'on est moins douteux
d'avoir un résultat parfait lorsque on estime la VaR à un niveau
de confiance de 99% que d'un niveau de confiance équivaut à
90%.
De plus, pour différent niveau de confiance, on voit
que l'action Alcatel-Lucent est plus risquée que les autres actifs. Par
contre l'action Danone est la plus efficace en terme de perte, puisqu'elle
possède la plus petite valeur de VaR.
III.3.2 VaR historique / empirique
Cette méthode présume que le futur est le
prolongement de passé. Autrement-dit, à partir des cours
passés, on estime les cours futurs. Selon une programmation sur Matlab,
on calcule la VaR pour trois niveaux de confiance 99%, 95% et 90%. Les
résultats trouvés sont enregistrés dans le tableau 8 :
Tableau 8 : Estimation de la VaR par la méthode
historique
|
VaR(á)
Actions
|
VaR (0.99)
%
|
VaR (0.95)
%
|
VaR (0.90)
%
|
|
Air France
|
-7,79
|
-3,63
|
-2,72
|
|
Air Liquide
|
-4,43
|
-2,80
|
-2,06
|
|
Alcatel-Lucent
|
-8,69
|
-5,07
|
-3,46
|
|
Axa
|
-6,50
|
-5,07
|
-2,42
|
|
BNP
|
-6,05
|
-3,24
|
-2,27
|
|
Bouygues
|
-6,50
|
-3,58
|
-2,51
|
|
Carrefour
|
-5,20
|
-3,05
|
-2,14
|
|
Danone
|
-3,87
|
-2,36
|
-1,63
|
|
Essilor Intl
|
-4,93
|
-2,81
|
-1,97
|
|
Lafarge
|
-5,54
|
-3,21
|
-2,30
|
|
LVMH
|
-5,27
|
-3,29
|
-2,30
|
|
Michelin
|
-5,54
|
-3,35
|
-2,29
|
|
L'orial
|
-4,96
|
-3,11
|
-2,18
|
|
Peugeot
|
-4,88
|
-3,09
|
-2,13
|
|
Renault
|
-5,92
|
-3,74
|
-2,61
|
|
Schneider.E
|
-5,58
|
-3,36
|
-2,40
|
|
Sté générale
|
-6,39
|
-3,47
|
-2,33
|
|
Total
|
-4,71
|
-2,90
|
-2,10
|
|
Vallourec
|
-6,12
|
-3,63
|
-2,52
|
|
Vinci (EXSGE)
|
-4,59
|
-2,77
|
-1,94
|
De même que la VaR paramétrique, on constate que,
plus le niveau de confiance est élevé, plus la perte subie par
l'investisseur est grande. Toutefois, pour toutes les actions on remarque
que la VaR(99%) empirique est inférieur à celle
paramétrique ; à titre d'exemple, pour l'action Air France, on a
une VaR paramétrique équivalente à 7.56% en valeur
absolue, par contre lorsque on l'estime par la méthode empirique, elle
augmente pour atteindre une valeur 7,79%. Nonobstant, pour des niveaux de
confiance inférieure à 99%, la VaR empirique devient
supérieure à celle paramétrique.
Une question fondamentale se pose ici; qu'elle est la meilleure
méthode d'estimation du VaR?
L'estimation de VaR par la méthode historique est plus
efficace, dans certain cas, que par la méthode paramétrique. En
effet, elle n'impose aucune hypothèse sur la nature de distribution des
rendements, contrairement à la méthode paramétrique que
suppose que les taux de rendement soient normalement distribués. Mais La
rareté des donnés peut apporter des problèmes quant
à l'application de cette méthode.
III.4 Approche Moyenne-VaR
Puisque l`approche de Markowitz est imparfaite pour le choix
de portefeuille à cause de la non considération des valeurs
extrêmes, dans cette partie, nous nous intéressons à
l'optimisation de portefeuille avec la VaR. Pour cette raison, et comme
l'approche Moyenne- Variance, nous examinons l'effet d'introduire la VaR au
lieu de la variance comme mesure de risque sur la sélection de
portefeuille. Pour ce faire on a procédé à une
programmation sur Matlab ; il s'agit de minimiser la fonction objective, la
VaR, sous contrainte un niveau désiré de taux de rendement
espéré. Le portefeuille optimal pour cette approche est celui qui
résoudre la programme suivante ;
X
' . 1 i ô =
) R
S/c
X'. E (R
i i
Pour faciliter les calcules, on utilise la méthode
paramétrique afin d'estimer la VaR des actions ainsi de portefeuille,
pour cela on peut récrit le système de manière suivante
;
Min X ' E ( R ) - Z
á X ' Ó X (50)
i i i i
x
X
' . 1 i ô =
S/c
X' . E (R)
i i R
avec Zá le quantile d'ordre
á de la loi normale N (0,1).
Par ailleurs, notre objectif est de déterminer les
proportions Xi représentant les poids des actions dans le portefeuille
optimum. A cet effet, dans le tableau (9) nous calculons les vecteurs
d'allocation des actifs ainsi la VaR de portefeuille pour un niveau de
confiance 99%.
Tableau 9 : Les proportions des actions dans les
portefeuilles optimaux (á =99%)
|
Xi R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
X1
|
0.0431
|
0.0032
|
0
|
0.0574
|
0.0158
|
0.1115
|
|
X2
|
0.0092
|
0.0622
|
0.0697
|
0.0636
|
0.1103
|
0.0418
|
|
X3
|
0
|
0
|
0
|
0.05 13
|
0.0205
|
0
|
|
X4
|
0.0091
|
0.0163
|
0
|
0.0698
|
0.0916
|
0.0786
|
|
X5
|
0.057 1
|
0
|
0
|
0.0899
|
0.0449
|
0.0962
|
|
X6
|
0.0263
|
0.1045
|
0.1501
|
0.0058
|
0.0637
|
0.0245
|
|
X7
|
0.0531
|
0.1079
|
0.1294
|
0.0278
|
0.0169
|
0
|
|
X8
|
0.0746
|
0.0724
|
0.0089
|
0.0809
|
0.0052
|
0.0523
|
|
X9
|
0.0871
|
0.0687
|
0.0589
|
0.0310
|
0.0303
|
0.0079
|
|
X10
|
0.0889
|
0.0602
|
0.0365
|
0.0968
|
0.0230
|
0.0719
|
|
X11
|
0.0101
|
0.0131
|
0.0098
|
0.0672
|
0.0919
|
0.1005
|
|
X12
|
0.0560
|
0.0652
|
0.0412
|
0.0073
|
0.0205
|
0.0491
|
|
X13
|
0.0730
|
0.0791
|
0.1745
|
0.0057
|
0
|
0.0568
|
|
X14
|
0.0467
|
0.0259
|
0.0665
|
0.0000
|
0.0300
|
0
|
|
X15
|
0.0224
|
0.0606
|
0.0654
|
0.0226
|
0.0795
|
0.0501
|
|
X16
|
0.0865
|
0.0882
|
0.0392
|
0.0536
|
0.0997
|
0.0459
|
|
X17
|
0.0567
|
0.0059
|
0
|
0.0455
|
0.0559
|
0.0272
|
|
X18
|
0.0840
|
0.0850
|
0.0341
|
0.0698
|
0.01 14
|
0.0248
|
|
X19
|
0.0423
|
0.0552
|
0
|
0.0943
|
0.1381
|
0.1401
|
|
X20
|
0.0738
|
0.0263
|
0.1157
|
0.0596
|
0.0508
|
0.0208
|
|
VaR(á)
|
-0.0264
|
-0.0267
|
-0.0269
|
-0.027 1
|
-0.0273
|
-0.0274
|
|
ó2(10)-4
|
1.4478
|
1.4838
|
1.5639
|
1.7390
|
1.8584
|
1.8743
|
De même que l'approche de Markowitz, on constate que le
niveau de risque, mesuré par la VaR, augmente chaque fois que le
rendement espéré accroît. En effet, pour une
espérance
égale à 0.02%, la VaR (99%) équivalente
à 2.64% en valeur absolu, par contre, lorsqu'on augmente le taux de
rendement espéré à une valeur 0.1%, le risque
accroît, également, pour atteindre une valeur égale
à 2.74%.
Le calcul de la variance de portefeuille nous amène
à déduire que, chaque fois l'espérance est
augmentée, la variance de portefeuille est amplifie. De plus, pour
différent niveau de taux de rendement espéré, on voit que
le poids de l'action Alcatel-Lucent (x3) dans la plupart des portefeuilles, est
nul. Cela est expliqué de faite que ce titre est plus risqué (on
a déjà montré ça dans le paragraphe «
estimation de VaR »).
III.4.1 Comparaison des approches Moyenne-Variance et
Moyenne-VaR
Pour faire cette comparaison, on illustre dans le tableau (10)
les caractéristiques des différents portefeuilles optimaux
sélectionnés par les deux approches :
Tableau 10 : Comparaison des approches Moyenne-Variance
et Moyenne-VaR
|
Approche
|
ó2
|
R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
M-Variance
|
ó2(10)-4
|
0. 987
|
1.026
|
1.0607
|
1.3001
|
2.2677
|
2.335
|
|
M-VaR(99%)
|
ó2(10)-4
|
1.4478
|
1.4838
|
1.563
|
1.7390
|
1.858
|
1.8743
|
En comparant, les deux approches antérieures, on
constate que les portefeuilles sélectionnés par l'approche
Moyenne-Variance pour les espérances qui s'étalent de 0.02%
à 0.08% sont les plus optimaux en terme de risque ; par exemple, pour un
même taux de rendement espéré 0.08%, on enregistre une
variance de 1,3001.1 0-4 pour l'approche classique, mais pour
l'approche Moyenne-VaR, la variance est de 1,739.10-4.
Cependant, lorsque le taux de rendement espéré
dépasse la valeur 0.08%, les portefeuilles choisis par l'approche
Moyenne-VaR, sont plus efficients en terme de risque. En effet, si
l'espérance est équivalente à 0,1%, on enregistre une
variance de 2,335.10-4 pour l'approche classique, mais pour
l'approche Moyenne-VaR, la variance est plus faible de valeur
1,8743.10-4.
Donc on peut schématiser dans un plan (variance,
espérance) les frontières efficientes de deux approches, comme
suite :
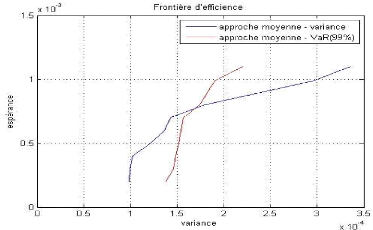
Figure 16: Frontières efficientes
On constate que la frontière de l'approche Moyenne-VaR
est sous forme d'un arc, Cette frontière contient les portefeuilles
optimaux pour chaque niveau d'espérance choisie et un minimum VaR. Par
ailleurs, pour un niveau de taux de rendement inférieur à 0.0825%
on observe que la courbe de l'approche Moyenne-VaR (99%) est situé au
dessous de la frontière efficiente de l'approche classique. Par contre,
lorsque l'espérance dépasse 0.0825%, la courbe de l'approche
classique devient au dessous de la courbe qui est en rouge. Les deux courbes
ont un point d'intersection de valeur 0.0825%. Mais comment choisir la
meilleure approche ?
Selon sa préférence au risque et le niveau
d'espérance désiré, l'investisseur choisit les
portefeuilles adéquats en utilisant l'un de deux approches
antérieures. Le tableau suivant classe ces deux approches en fonction de
niveau de taux de rendement espéré :
Tableau 11 : L'approche adaptée selon le niveau
d'espérance désiré
|
Niveau d'espérance
désiré par
l'investisseur
|
R < 0.0825%
|
R =0.0825%
|
R> 0.0825%
|
|
L'approche adaptée
|
l'approche Moyenne-Variance
|
Indifférent entre les deux approches
|
l'approche Moyenne-VaR
|
Cependant, quelle est l'approche adaptée lorsque le
niveau de confiance diminue à 90% ? Pour répondre à cette
question, nous calculons, dans le tableau 12, la variance des portefeuilles
optimaux pour deux niveaux de confiances á=99% ainsi á=90%. En
effet, les
portefeuilles optimaux sont construits en résolvant le
problème de l'optimisation MoyenneVaR ci-dessus, pour différents
niveaux de confiance. Ainsi, les résultats trouvés sont
enregistrés dans le tableau ci-dessous :
Tableau 12 : Variances des portefeuilles en fonction du
niveau de confiance
|
á
|
ó2
|
R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
99%
|
ó2(10)-4
|
1.4478
|
1.4838
|
1.563
|
1.7390
|
1.858
|
1.8743
|
|
90%
|
ó2(10)-4
|
1.9159
|
1.9686
|
2.014
|
2.0743
|
2.092
|
2.1695
|
En comparant, les deux approches Moyenne-VaR(99%) et
Moyenne-VaR(90%), on constate que les portefeuilles sélectionnés
par la première approche sont plus optimaux en terme de risque ; par
exemple, pour un même taux de rendement espéré 0.1%, on
enregistre une variance1.8743.10-4 pour l'approche dont á =
99%. Mais, pour la deuxième approche, la variance est de
2.1695.10-4.
On peut conclure donc, que plus le niveau de confiance á
est élevé, plus qu'on a une chance d'avoir un portefeuille plus
efficace dont le risque est minimum.
En d'autres termes, on peut certifier ce résultat à
partir la figure (17) où on trace les deux frontières efficientes
pour á=99% ainsi á=90%.
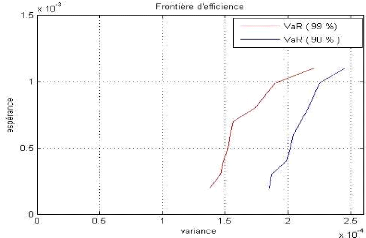
Figure 17 : Frontières efficientes selon
á
Sur cette figure, nous distinguons deux frontières
d'efficiences différentes correspondant à á = 99% et
á = 90%. Ainsi, On constate que la courbe de l'approche Moyenne-VaR
(99%) se situe au dessus de la frontière efficiente de l'approche
Moyenne-VaR (90%).
III.5 L'approche Moyenne-Variance-VaR (99%) :
Afin de limiter les pertes potentielles, nous explorons
maintenant une moderne approche édité par Rockafellar et Uryasev
(2002) connue sous le nom approche Moyenne-VarianceVaR. Cette approche est plus
générale que les deux approches vues précédemment
puisqu'elle combine deux mesures de risque au même temps : la Variance et
la VaR.
Il intervient à notre esprit une question fondamentale :
comment un investisseur sélectionne le portefeuille le plus optimal ?
Dans ce sens, un portefeuille efficient, d'après
Rockafellar et Uryasev, est le portefeuille qui minimise la
variance et se borne le VaR à une valeur absolue maximale égale
à V. D'où, on peut définir ce modèle sous la forme
suivante :
Min X' i Ó X (51)
i
x
|
X' .
i
|
ô
|
=
|
1
|
|
)
|
=
|
 R R
|
S/c i i
X' . E (R VaR á V
=
Afin de résoudre ce système et trouver les
justes proportions de chaque action dans le portefeuille optimal, et
pourá =99%, on fixe deux valeurs pour V et on compare chaque
fois les résultats trouvés avec les résultats vus
auparavant.
À cet instar, on choisit pou la première valeur V =
0.756%. Ainsi, dans le tableau 13, nous comptons les poids des actions dans les
portefeuilles efficaces et ces variances :
Tableau 13 : Les proportions des actions dans les
portefeuilles optimaux á =99%
et V=
0.756%.
|
Xi R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
X1
|
0.0065
|
0.0623
|
0.0697
|
0.0244
|
0.0786
|
0.1079
|
|
X2
|
0.0470
|
0.0583
|
0.0703
|
0.0218
|
0.0565
|
0.0512
|
|
X3
|
0.0044
|
0.0084
|
0.0039
|
0
|
0
|
0
|
|
X4
|
0.0891
|
0.0163
|
0.0348
|
0.0009
|
0.0615
|
0
|
|
X5
|
0.0183
|
0.0269
|
0
|
0.0281
|
0.0698
|
0.0067
|
|
X6
|
0.0371
|
0.0284
|
0.0810
|
0.0794
|
0.0173
|
0.1091
|
|
X7
|
0.0755
|
0
|
0.0023
|
0.0655
|
0.0419
|
0.0578
|
|
X8
|
0.0232
|
0.0051
|
0.0384
|
0
|
0.0223
|
0.0353
|
|
X9
|
0.0887
|
0.0784
|
0.0021
|
0.0654
|
0.0551
|
0.0018
|
|
X10
|
0.1018
|
0.0333
|
0.0298
|
0.0777
|
0.0406
|
0.0440
|
|
X11
|
0.0108
|
0.0282
|
0.0669
|
0.0555
|
0.0663
|
0.0748
|
|
X12
|
0.0341
|
0.0913
|
0.0812
|
0.0913
|
0.0260
|
0.0426
|
|
X13
|
0
|
0.0088
|
0.0204
|
0.0504
|
0.0454
|
0.0080
|
|
X14
|
0
|
0.0645
|
0.0674
|
0.0567
|
0.0150
|
0.0344
|
|
X15
|
0.0707
|
0.0605
|
0.0436
|
0.0301
|
0.0402
|
0.1052
|
|
X16
|
0.0198
|
0.0804
|
0.0496
|
0.0787
|
0.0382
|
0.0737
|
|
X17
|
0.0784
|
0.0309
|
0.0443
|
0.0207
|
0.0480
|
0
|
|
X18
|
0.0111
|
0.0830
|
0.0532
|
0
|
0.0126
|
0.0397
|
|
X19
|
0.1447
|
0.1572
|
0.1556
|
0.1474
|
0.1662
|
0.1612
|
|
X20
|
0.1388
|
0.0778
|
0.0854
|
0.1061
|
0.0986
|
0.0467
|
|
ó2(10)-4
|
1.0056
|
1.0397
|
1.0566
|
1.0904
|
1.0931
|
1.1031
|
Comme pour l'approche classique, on remarque que plus le
niveau du rendement espéré est élevé, plus le
risque est grand. Mais l'évolution de l'espérance et de variance
n'est pas de même proportion, puisque cette dernière évalue
avec proportion très faible. En outre, pour une espérance de
0.02%, on a un portefeuille optimal où la variance est minimum de valeur
1.0056.10-4. Cependant, lorsque on augmente le taux de rendement
espéré à 0.1%, la variance de portefeuille efficace
augmente aussi et prendre une valeur de 1.1031.1 0-4.
De plus, on constate que, pour différents niveaux des
taux de rendement espérés, le poids de l'action Alcatel-Lucent
(X3) dans les plus part des portefeuilles, est presque nul. Cela est
expliqué, de faite que ce titre est plus risqué (on a
déjà montré ça dans le paragraphe « estimation
de VaR »).
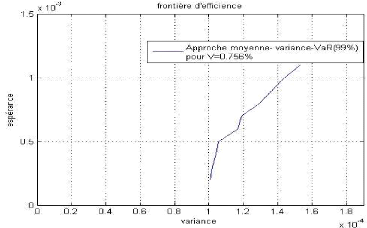
Figure 18 : Frontière efficiente de l'approche
Moyenne-Variance-VaR pour V= 0.756%
La figure 18 illustre la frontière efficiente de
l'approche Moyenne-Variance-VaR (99%) quand V = 0.756%. On constate que cette
frontière n'est plus sous forme elliptique, puisque la variance
évalue avec une proportion très faible. En effet, Cette
frontière contient
les portefeuilles optimaux pour chaque niveau d'espérance
choisie et un minimum de variance dont la valeur de VaR est limitée
à 0.756%.
III.5.1 Comparaison des approches Moyenne-Variance,
Moyenne-VaR(99%) et Moyenne-Variance-VaR(99%)
Pour faire cette comparaison, on illustre dans le Tableau 14 les
caractéristiques des différents portefeuilles optimaux
sélectionnés par les trois approches :
Tableau 14 : Comparaison entre les trois
approches
|
Approche
|
ó2
|
R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
M-Variance
|
ó2(10)-4
|
0. 987
|
1.026
|
1.0607
|
1.3001
|
2.2677
|
2.335
|
|
M-VaR(99%)
|
ó2(10)-4
|
1.4478
|
1.4838
|
1.563
|
1.7390
|
1.858
|
1.8743
|
|
M-V-V (99%)
|
ó2(10)-4
|
1.0056
|
1.0397
|
1.0566
|
1.0904
|
1.0931
|
1.1031
|
Il est donc visible, d'après ce tableau, que l'approche de
Markowitz reste encore plus performante que les deux autres approches, pour les
espérances qui s'étalent de 0.02% à
0.04% puisqu'elle permet de sélectionner les
portefeuilles les moins risqués. En effet, on constate que pour ces deux
taux de rendement espérés, les portefeuilles trouvés par
l'approche classique sont caractérisés par la variance la plus
faible.
Mais, lorsque l'espérance dépasse 0.05%,
l'approche Moyenne-Variance-VaR (99%) dévient l'approche la plus
adaptée par l'investisseur. En outre, elle permet d'avoir des
portefeuilles optimaux dont leurs variances sont les plus minimums.
En d'autres termes, on peut certifier ce résultat à
partir la figure 19 où on trace les trois frontières efficientes
dans un même plan :
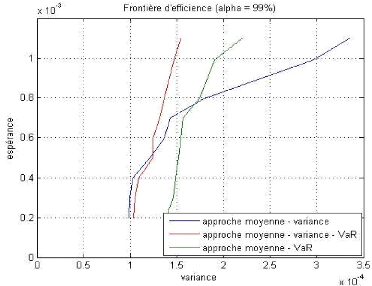
Figure 19 : Frontières efficientes des trois
approches
Par ailleurs, pour un niveau de taux de rendement
inférieur à 0.05%, on observe que la courbe de l'approche
Moyenne-VaR (99%) se situe au dessous de deux autres frontières, ce que
implique que pour un même espérance, cette approche donne des
portefeuilles très risqués contrairement à la courbe de
l'approche classique qui est plus rentable. Par contre, lorsque
l'espérance dépasse 0.05%, la courbe de l'approche
Moyenne-Variance-VaR(99%) est au dessus des autres courbes, de plus cette
courbe s'intersecte avec la frontière de Markotitz pour un
espérance de 0.05% .
Pour récapituler, on illustre un tableau où on
classe les trois approches selon la variance ainsi l'approche adaptée en
fonction de portefeuille sélectionné :
Tableau 15: L'approche adaptée selon le niveau
d'espérance désiré
|
Niveau d'espérance
désiré par
l'investisseur
|
R < 0.05%
|
R =0.05%
|
R> 0.05%
|
|
L'approche adaptée
|
Approche
Moyenne-Variance
|
Indifférent entre
M-V-V (99%)
et
Moyenne-Variance
|
Approche
M-V-V (99%)
|
Néanmoins, comment varie la variance des portefeuilles
optimaux sélectionnés par cette dernière approche, lorsque
on augmente la borne de VaR (99%) de 0.756% à 7,5% ?
Pour répondre à cette question, nous calculons
dans le tableau 16, la variance des portefeuilles optimaux pour deux niveaux de
V (0.756% et 7,5). Ainsi, le résultat trouvé est
enregistré dans le tableau ci-dessous ;
Tableau 16 : Effet d'augmenter V sur la variance du
portefeuille
|
V
|
ó2
|
R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
0.756%
|
ó2(10)-4
|
1.0056
|
1.0397
|
1.0566
|
1.0904
|
1.0931
|
1.1031
|
|
7.5%
|
ó2(10)-4
|
1.0354
|
1.0530
|
1.2438
|
1.3185
|
1.3651
|
1.4444
|
En conséquence, on constate que plus V est
élevé, c'est-à-dire plus on augmente l'intervalle de
variation de VaR, plus les portefeuilles efficients choisis par cette approche
sont risqués. Par exemple, pour un taux de rendement
espéré de 0.1%, le portefeuille optimal trouvé a une
variance de 1.103 1.10-4 lorsque V=0.756%. Par contre, en augmentant
V à une valeur 7.5%, la variance de portefeuille optimal accroît
à 1.444.10-4.
Ainsi, on peut certifier ce résultat à partir la
figure (20) où on trace les deux frontières des portefeuilles
efficients pour V=0.756% et V=7.5%.
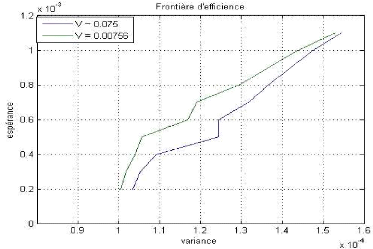
Figure 20 : Frontière efficiente en fonction de
V
La figure 20, montre que chaque fois on diminue V, on trouve
des portefeuilles plus optimaux, puisque la frontière d'efficience pour
V=0.756% est situé au dessus de courbe de V=7.5%.
III.6 Estimation paramétrique de la CVaR
Afin de calculer la CVaR paramétrique, nous supposons que
les rendements des actions ainsi de portefeuille suivent une loi normale. De ce
fait, la formule de CVaR est donnée par :
CVaR ( R p ) = VaR +
Moyenne de perte dépassant la VaR (52)
á á á
A partir, d'une programmation sur Matlab on calcule la CVaR pour
trois niveaux de confiance 99%, 95% et 90%. Les résultats trouvés
sont enregistrés dans le tableau suivant :
Tableau 17 : Estimation paramétrique de la
CVaR
|
Action
CVaR(á)
|
CVaR(0.99)%
|
CVaR(0.95)%
|
CVaR(0.90)%
|
|
Air France
|
-15.31
|
-1094
|
-866
|
|
Air Liquide
|
-8.26
|
-5.96
|
-4.8 1
|
|
Alcatel-Lucent
|
-15.87
|
-11.44
|
-9.15
|
|
Axa
|
-10.86
|
-7.81
|
-6.24
|
|
BNP
|
-10.07
|
-7.23
|
-5.77
|
|
Bouygues
|
-11.07
|
-7.96
|
-6.38
|
|
Carrefour
|
-9.04
|
-6.54
|
-5.24
|
|
Danone
|
-7.43
|
-5.35
|
-4.26
|
|
Essilor-Intl
|
-8.82
|
-6.35
|
-5.05
|
|
Lafarge
|
-9.5
|
-6.85
|
-5.51
|
|
LVMH
|
-9.92
|
-7.17
|
-5.74
|
|
Michelin
|
-9.76
|
-7.06
|
-5.65
|
|
L'orial
|
-9.13
|
-6.6
|
-5.27
|
|
Peugeot
|
-9.17
|
-6.63
|
-5.31
|
|
Renault
|
-11.08
|
-7.99
|
-6.41
|
|
Schneider.Elec
|
-10.2
|
-7.34
|
-5.9
|
|
Sté générale
|
-10.37
|
-7.48
|
-5.96
|
|
Total
|
-8.42
|
-6.09
|
-5.48
|
|
Vallourec
|
-11.22
|
-8.06
|
-6.43
|
|
Vinci (EXSGE)
|
-8.56
|
-6.15
|
-8.66
|
Le Tableau (17) nous permet de constater que chaque fois le
niveau de confiance diminue, la CVaR baisse. De plus, on remarque que la CVaR
est plus grande que la VaR pour toutes les actions, ceci est dû au fait
que l'Expected Shortfall est une mesure de risque plus générale
que la Value-at-Risk. En outre, pour différent niveau de confiance on
voit que l'action AlcatelLucent est plus risquée que les autres actifs.
Par contre l'action Danone est la plus efficace en terme de perte, puisqu'elle
possède la plus petite valeur de CVaR.
III.7 L'approche Moyenne-Variance-CVaR
Un investisseur rationnel cherche toujours à minimiser
le risque du portefeuille et par suite limité sa perte maximale pour des
niveaux de risque fixés par lui même. Or, puisque la Valueat-Risk
n'est pas une mesure cohérente dans le sens d'Artzner, dans cette partie
nous allons traiter l'impacte d'ajouter une contrainte de type CVaR au
modèle classique Moyenne- Variance. En outre, dans ce cas le risque de
portefeuille sélectionné est contrôlé par deux
mesures ; la variance et la CVaR.
Le portefeuille optimal pour cette approche est celui qui
minimise la variance et se borne le CVaR à une valeur absolu maximale
égale à C.
Ce portefeuille est trouvé à partir la
résolution de système suivante :
Min X' i Ó X (53)
i
x
) = R
S/c X' . E (R
i i
CVaR á C
=
Afin de résoudre ce système et trouver les
justes proportions de chaque action dans le portefeuille optimal, et
pourá =99%, on fixe deux valeurs pour C et on compare chaque
fois les résultats trouvés avec les résultats vues
auparavant.
À cet instar, on choisit pou la première valeur
C=0.756%. Ainsi, dans le tableau (18) nous déterminons les poids des
actions dans les portefeuilles efficaces et ces variances :
Tableau 18 : Les proportions des actions dans les
portefeuilles optimaux
pour á =99% et C=
0.756%.
|
Xi R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
X1
|
0.0150
|
0.0850
|
0.0172
|
0.0352
|
0.0796
|
0.0869
|
|
X2
|
0.0000
|
0.0295
|
0.0403
|
0.0395
|
0
|
0.0709
|
|
X3
|
0.2596
|
0.1049
|
0.0367
|
0.0423
|
0
|
0.0136
|
|
X4
|
0.0188
|
0.0863
|
0.0459
|
0.0789
|
0.0008
|
0.0540
|
|
X5
|
0.0224
|
0.0568
|
0.0869
|
0.0595
|
0.1090
|
0.0151
|
|
X6
|
0.0598
|
0.0701
|
0.0336
|
0.0358
|
0.0166
|
0.0308
|
|
X7
|
0.0637
|
0.0760
|
0.0311
|
0.0668
|
0.0963
|
0.0226
|
|
X8
|
0
|
0.0338
|
0.0344
|
0.0917
|
0.0188
|
0.0538
|
|
X9
|
0.0726
|
0.0619
|
0.0703
|
0.0295
|
0.095 1
|
0.0398
|
|
X10
|
0.0397
|
0.0123
|
0.0609
|
0.0974
|
0.0739
|
0.0738
|
|
X11
|
0.0610
|
0.0910
|
0.0948
|
0.0328
|
0.0673
|
0
|
|
X12
|
0
|
0.0118
|
0.0761
|
0.0063
|
0.0583
|
0.0718
|
|
X13
|
0.0 168
|
0.0740
|
0.0492
|
0.0202
|
0.0026
|
0.0595
|
|
X14
|
0.1454
|
0.0614
|
0.0653
|
0.0568
|
0.0276
|
0.0761
|
|
X15
|
0.0912
|
0.0133
|
0.0051
|
0.0479
|
0.0810
|
0.0367
|
|
X16
|
0.0124
|
0.0030
|
0.0518
|
0.0077
|
0.0196
|
0.0043
|
|
X17
|
0.0992
|
0.0329
|
0.0484
|
0.0098
|
0.0069
|
0.0227
|
|
X18
|
0.0223
|
0.0883
|
0.0850
|
0.0886
|
0.0711
|
0.0544
|
|
X19
|
0
|
0.0061
|
0.0336
|
0.1195
|
0.1371
|
0.1780
|
|
X20
|
- 0.0000
|
0.00 13
|
0.0334
|
0.0338
|
0.0383
|
0.0352
|
|
ó2(10)-4
|
0.87538
|
0.88911
|
0.90762
|
0.96580
|
0.98852
|
0.99122
|
De même que les autres approches, on constate que le
niveau de risque augmente chaque fois que le rendement espéré
accroît. En outre, pour une espérance 0.02%, on a un portefeuille
optimal où la variance est minimum de valeur 0.87538.10-4.
Cependant, lorsqu'on augmente le taux de rendement espéré
à 0.1%, la variance de portefeuille optimal aussi augmente pour prendre
une valeur de 0.99122.10-4.
Pour bien marquer la relation entre le taux de rendement
espéré et la variance d'un portefeuille, nous traçons dans
le graphique suivant la frontière efficiente dont ainsi définie
:
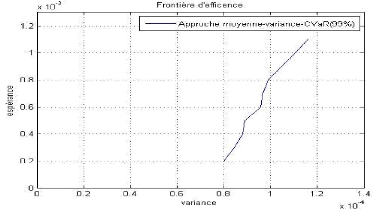
Figure 21 : La frontière efficiente de l'approche
Moyenne-Variance-C VaR
Cette figure illustre la frontière efficiente de
l'approche Moyenne-Variance-CVaR (99%) quand C = 0.756%. On constate que cette
frontière n'est plus sous forme elliptique, puisque la variance
évalue avec une proportion très faible par rapport à
l'espérance.
III.7.1 Comparaison des quatre approches
Pour faire une comparaison entre les quatre approches vues
auparavant, on illustre dans le tableau 19 les caractéristiques des
différents portefeuilles optimaux sélectionnés par ces
quatre approches :
Tableau 19 : Comparaison des quatre approches
|
Approche
|
ó2
|
R
|
0.02%
|
0.04%
|
0.06%
|
0.08%
|
0.09%
|
0.1%
|
|
M-Variance
|
ó2(10)-4
|
0. 987
|
1.026
|
1.0607
|
1.3001
|
2.2677
|
2.335
|
|
M-VaR (99%)
|
ó2(10)-4
|
1.4478
|
1.4838
|
1.563
|
1.7390
|
1.858
|
1.8743
|
|
M-V-V (99%)
|
ó2(10)-4
|
1.0056
|
1.0397
|
1.0566
|
1.0904
|
1.0931
|
1.1031
|
|
M-V-C (99%)
|
ó2(10)-4
|
0.87538
|
0.88911
|
0.90762
|
0.96580
|
0.98852
|
0.9912
|
On constate, d'après ce tableau, que l'approche
Moyenne-Variance-CVaR est la plus performante, puisqu'elle permet de
sélectionner les portefeuilles les moins risqués pour un
même taux de rendement espéré.
À l'aide des valeurs trouvées dans le tableau
précédant, on peut tracer les frontières efficientes des
quatre approches, dans un plan des coordonnés variance et
espérance :
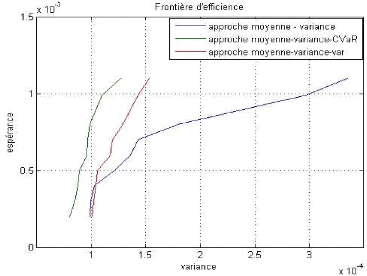
Figure 22 : les frontières efficientes des
différents approches
La figure 22 nous exprime que les portefeuilles
sélectionnés par l'approche MoyenneVariance-C VaR sont les plus
optimaux, puisque sa frontière efficiente est située au dessus
des autres courbes.
Mais, comment varie la variance des portefeuilles optimaux
sélectionnés par l'approche Moyenne-Variance-CVaR lorsque la
borne de CVaR (99%) passe de 0.756% à 7,5% ?
Pour répondre à cette question, nous calculons,
dans le tableau 19, les variances des portefeuilles optimaux pour deux niveaux
de C (0.756% et 7.5%). En effet, les portefeuilles optimaux sont construits en
résolvant le problème de l'optimisation Moyenne-Variance-CVaR
ci-dessus, pour différent niveau de C. Ainsi, les résultats
trouvés sont enregistrés dans le tableau ci-dessous :
Tableau 20 : Effet d'augmenter C sur la variance du
portefeuille
|
C
|
ó 2
|
R
|
0.02%
|
0.04%
|
0.0006
|
0.08%
|
0.09%
|
0.1%
|
|
0.756%
|
ó2(10)-4
|
0.87538
|
0.88911
|
0.90762
|
0.96580
|
0.98852
|
0.99122
|
|
7.5%
|
ó2(10)-4
|
0.98831
|
0.99294
|
1.0102
|
1.0117
|
1.0955
|
1.1622
|
En augmentant C à une valeur de 7.5%, on constate que
les portefeuilles sélectionnés sont les plus risqués,
puisque ils ont des variances plus élevées. À partir les
chiffres calculés dans le tableau ci-dessus, on trace les
frontières d'efficience pour différentes valeurs de C, dans un
plan des coordonnés variance et espérance :
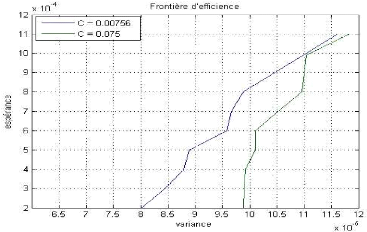
Figure 23 : Frontière efficiente en fonction de
C
Comme pour l'approche Moyenne-Mariance-VaR et d'après
la figure 23, on constate que chaque fois on diminue C, on trouve des
portefeuilles plus optimaux, puisque la frontière efficiente pour
C=0.756% est située au dessus de courbe de C=7.5%. Aussi on voit que les
deux frontières se convergent lorsque l'espérance augmente. On
peut expliquer cela par le fait que ; lorsque les risques des portefeuilles
efficients augmentent, les taux de rendements aussi augmentent mais de
manière très faible, parce que on ne peut pas avoir des
rentabilités qui tend vers l'infini contrairement aux variances.
Conclusion :
Un des objectifs principaux de la gestion de risque, est
d'évaluer et d'améliorer les modèles de sélection
des portefeuilles à la lumière des risques pris pour
réaliser des bénéfices. Ainsi, des nouvelles mesures des
risques sont prises en compte lors des choix des portefeuilles. Parmi ces
mesures on trouve, la Value-at-Risk et l'Expected Shortfall.
Dans ce chapitre, nous avons présenté quatre
approches de choix des portefeuilles. Après avoir spécifier
l'échantillon de l'étude et calculer les caractéristiques
des actions sélectionnées telle que les moments d'ordre un et
deux, nous avons exposé la première approche Moyenne- Variance de
Markowitz. En effet, nous avons démontré que, plus le niveau du
rendement espéré est élevé plus le risque,
mesuré par la variance, est grand. De ce fait, un investisseur averse au
risque construit son portefeuille en se basant sur la tangence entre la courbe
d'indifférence est la frontière efficiente. Or, nous avons
prouvé que, plus les niveaux d'aversions sont grands, plus les
portefeuilles sélectionnés sont risqués mais aussi plus
rentables. A la fin de cette partie, nous avons expliqué que l'ajout
d'un actif sans risque a un effet positif sur la réduction de risque de
portefeuille.
Il existe des nombreuses méthodes d'estimation de la
Value-at-Risk, nous avons calculé, dans la deuxième section la
VaR paramétrique ainsi la VaR historique. Dans la
suite, nous avons traité les choix des portefeuilles pour un taux de
rendement espéré fixé et une VaR minimale ; nous avons
constaté que plus le niveau de confiance á est
élevé, plus le portefeuille obtenu est optimum. En comparant
cette approche à l'approche classique nous avons remarqué que
lorsque l'investisseur accepte d'investir dans un portefeuille risqué
mais aussi plus rentable, la deuxième approche est admis.
Cependant, comme mesure de risque, la VaR a identifié
des limites telle que les manques de la sous-additivité et de
convexité (Artezner et al 1997), pour cela la CVaR, qui est une mesure
cohérente de risque, est fréquemment employée dans les
dernières années dans la gestion de risque.
A la fin de ce chapitre, nous avons analysé les
implications de choix de portefeuille résultant d'imposer une contrainte
de type VaR au modèle classique Moyenne-Variance et la comparée
à celle qui résulte de l'implication d'une contrainte CVaR. En
outre, nous avons démontré que l'approche Moyenne-Variance-CVaR
est plus performante que les autres approches, puisqu'elle permet de
sélectionner des portefeuilles moins risqués pour des
niveaux des espérances fixées. De plus nous
avons prouvé, pour les deux approches Moyenne-Variance-VaR et
Moyenne-Variance-C VaR, que chaque fois l'intervalle de variation de
deuxième contrainte (VaR ou CVaR) augmente, les niveaux de risque des
portefeuilles optimaux augmentent.
En récapitulant, pour avoir un portefeuille optimal,
l'investisseur doit baser sa sélection sur l'approche
Moyenne-Variance-CVaR où le niveau de confiance á est plus
élevé et l'intervalle de variation de deuxième contrainte
CVaR est minimum. Cependant ce type de modèle à un effet
défavorable parce qu'elle force les agents averses aux risques à
choisir des portefeuilles avec des plus grands écart type lorsqu'il
n'existe pas d'actifs sans risque.
Les gestionnaires des actifs financiers visent à
choisir les portefeuilles qui rapportent le rendement espéré le
plus élevé, tout en même temps, assurer un niveau
acceptable d'exposition au risque. Ainsi, ils peuvent utiliser ses
expériences pour combiner des techniques de modélisation
quantitatives dans le processus de sélection de portefeuille. Parmi ces
techniques, La théorie des valeurs extrêmes définie comme
étant la discipline statistique la plus utilisée dans le champ
des finances au cours des dernières années.
Plus de cinquante ans après, le critère de
sélection de portefeuille Moyenne-Variance, reste aujourd'hui l'un des
critères de base dans le champ pratique. Cependant, à cause de la
successivité des crashs boursiers dans les dernières
années, cette approche ne permet pas de couvrir tous les risques du
portefeuille lorsque les distributions des rendements sont asymétriques
et caractérisées par des queues épaisses. Pour ces
raisons, nous nous sommes intéressés à étudier
d'autres modèles de choix du portefeuille permettant de limiter les
risques et par conséquence les pertes catastrophiques.
C'est dans le cadre de détermination des proportions
des actions dans le portefeuille optimal et dans la minimisation des risques de
perte que se situent les objectifs de notre travail.
Nous avons examiné, tout d'abord, les concepts des
mesures de risque et de risque de perte, ainsi l'aversion au risque et
l'aversion aux pertes. Ensuite, nous avons étudié la
généralisation de l'approche Moyenne-Variance de Markowitz en
incorporant une deuxième contrainte Value-at-Risk ou Expected
Shortfall.
Pour mieux appréhender l'impact d'ajouter une
contrainte sur la minimisation de risque, nous avons procédé dans
la partie empirique par quatre approches de choix de portefeuille ;
après avoir exposer l'approche classique de Markowitz, nous avons
constaté que chaque fois qu'on augmente le degré d'aversion au
risque, le portefeuille sélectionné est plus rentable mais
également plus risqué. En second lieu, nous avons traité
l'approche Moyenne-VaR qui nous a amené à prouver que plus le
niveau de confiance á est élevé, plus on a une chance
d'avoir un portefeuille efficient.
Pour réduire le risque de portefeuille à un
niveau plus faible et afin de limiter aux pertes catastrophiques, nous avons
présenté une troisième approche d'optimisation plus
générale, Moyenne-Variance-VaR, qui combine deux mesure de
risque, la variance et la VaR Cependant, cette approche n'est valable que pour
des niveaux des variances assez élevés et
pour une limite de deuxième contrainte VaR très
petite. En dernier lieu, et dans la même logique que la troisième
approche, nous nous sommes intéressés à choisir un
portefeuille optimal selon l'approche Moyenne-Variance-C VaR. En outre, cette
approche est plus pertinente que les autres modèles dans le choix de
portefeuille et la minimisation de risque.
D'après notre étude, nous avons constaté
que la généralisation de l'approche Moyenne- Variance a
un impact favorable sur le choix de portefeuille optimal. En effet,
l'analyse des implications de choix de portefeuille résultant d'imposer
une contrainte (VaR) au modèle de Moyenne-Variance et la comparaison
à ceux qui résultent de l'imposition d'une contrainte
conditionnelle (CVaR), nous permet de constater que pour un niveau de confiance
donné, la contrainte CVaR est plus efficace comme outil de gestion
qu'une contrainte VaR.
De plus cette approche est plus adéquate lorsque
l'investisseur fixe un niveau de confiance á assez élevé
et un intervalle de variation de deuxième contrainte CVaR minimum. En
outre, ce modèle nous permet de mieux appréhender la forme de la
distribution et offre l'avantage à l'investisseur de tenir compte de
l'asymétrie des distributions et des valeurs extrêmes dans les
séries boursières, ainsi de limiter les pertes extrêmes.
En conclusion, notre étude aident les investisseurs
averses aux risques, intervenant sur les marchés boursiers, à
améliorer ses critères de choix de portefeuille en leur offrant
une meilleure prise en compte des nouvelles caractéristiques des
marchés financiers telles que l'asymétrie des distributions des
rendements et les risques des événements extrêmes.
Cependant, en pratique, l'application de l'approche
Moyenne-Variance-CVaR est compliquée à cause de la
difficulté de l'estimation de la CVaR. En fait, l'approximation de
l'Expected Shortfall est fondée sur une équation contenant les
paramètres de loi de Paréto généralisée qui
n'inclut pas une variable affectant les proportions des actions.
De plus, ce type de modèle à un effet
défavorable puisqu'il force les agents averses aux risques à
choisir des portefeuilles avec des écarts-types élevés
lorsqu'il n'existe pas d'actif sans risque. En outre, cette approche encourage
l'investisseur à accepter trop de risque lorsqu'il existe des actions
des rendements intéressants.
Tableau 2 : Les Means Excess de portefeuille
|
ME
|
Me(0.99)
|
Me (0.95)
|
Me (90)
|
|
Air France
|
-0.0775
|
-0.0562
|
-0.0453
|
|
Air Liquide
|
-0.0419
|
-0.0310
|
-0.0259
|
|
Alcatel-lucent
|
-0.0803
|
-0.0590
|
-0.0484
|
|
Axa
|
-0.0553
|
-0.0406
|
-0.0333
|
|
BNP
|
-0.05 13
|
-0.0376
|
-0.0309
|
|
Bouygues
|
-0.0564
|
-0.0415
|
-0.0343
|
|
Carrefour
|
-0.0458
|
-0.0339
|
-0.0279
|
|
Danone
|
-0.0378
|
-0.0279
|
-0.0228
|
|
Essilor Intl
|
-0.0448
|
-0.0330
|
-0.0269
|
|
Lafarge
|
-0.0483
|
-0.0357
|
-0.0296
|
|
LVMH
|
-0.0503
|
-0.0372
|
-0.0306
|
|
Michelin
|
-0 .0495
|
-0.0367
|
-0.0302
|
|
L'orial
|
-0.0464
|
-0.0344
|
-0.0282
|
|
Peugeot
|
-0 .0466
|
-0.0346
|
-0.0285
|
|
Renault
|
-0 .0564
|
-0.0417
|
-0.0345
|
|
Schneider
|
-0.0518
|
-0.0381
|
-0.0316
|
|
Sté générale
|
-0 .0529
|
-0.0391
|
-0.0320
|
|
Total
|
-0.0428
|
-0.03 18
|
-0.0322
|
|
Vallourec
|
-0.0573
|
-0.0422
|
-0.0347
|
|
Vinci
|
-0.0437
|
-0.0322
|
-0 .0265
|
Articles
[1] Artzner et al., 1997. Coherent measures of risk,
Mathematical Finance. Vol.9, pp 203-228.
[2] Acerbi, C. et Tasche, D., 2002. On the coherence of expected
shortfall. Journal of Banking and Finance, vol.26, pp 1487-1503.
[3] Black, F., 1972. Capital Market Equilibrium with Restricted
Borro-wing, Journal of Business. vol. 45, pp 444-454.
[4] Bleichrodt el al., 2006. Measuring Loss Aversion under
Prospect Theory: A ParameterFree Approach. Working Paper, GRID, ENSAMESTP,
Paris, France and Erasmus University, Rotterdam, The Netherlands.
[5] Camerer, C. et Weber, M., 1992. Recent Developments in
Modelling Preferences: Uncertainty and Ambiguity. Journal of Risk and
Uncertainty.vol.5, pp.325-70.
[6] Chabaane, M., et al., 2002 .Alternative risk measures for
alternative investments. Working Paper. pp.653.
[7] Chamberlain, G., 1983. A characterization of the
distributions that imply mean-variance utility functions. Journal of Economic
Theory, vol.29, pp 185-201.
[8] Danielsson, J. et al., 2001. An academic response to Basel
II. Working Paper. FMG and ESRC, London.
[9] Embrechts, P. et al., 2002. Correlation and Dependence in
risk management: properties and pitfalls, In: Risk Management: Value at Risk
and Beyond. Ed. M.A.H. Dempster, Cambridge University Press, pp. 176-223.
[10] Fabozzi, F. et al., 2006. Financial Modeling of the equity
Market: from CAPM to cointegration .Wiley Fiance, pp 45.
[11] Friedman, M., et Savage, L., 1948 .The utility analysis of
choices involving risks. Journal of Political Economy, vol. 56, pp279-304.
[12] Keeney, L. et Raiffa, H., 1976. Decisions with multiple
objectives, Preferences and value tradeoffs. New-York: Wiley.
[13] Kallberag, J. et Ziemiba, W., 1983. Comparison of
alternative utility functions in portfolio selection problems. Management
Science, vol.29, pp. 1257-1276.
[14] Markowitz, H., 1952. Portfolio selection. Journal of
Finance, vol.VII, pp77-91.
[15] Markowitz, H., 1956. The optimization of a quadratic
function subjet to linear constraints. Naval research logistics quarterly, vol.
III, pp111 -133.
[16] Markowitz, H., 1979. Approximating Expected Utility by a
Function of Mean and Variance. American Economic Review, vol.69, pp 308-318.
[17] Markowitz, H., 1984. Mean-variance versus direct utility
maximization. Journal of Finance, vol.39, pp 47-6 1.
[18] Markowitz, H., 1991. Foundations of Portfolio theory,
Journal of finance, vol. 2, pp 469- 477.
[19] Mandelbrot, B., 1963.The Variation of Certain Speculative
Prices. Journal of Business, vol.36.
[20] Pflug, 2000. Some Remarks on the Value-at-Risk and the
Conditional Value-at-Risk. In Probabilistic Constrained Optimization:
Methodology and Applications Ed. S.
[21] Rockafellar, R. et Uryasev, S., 2000. Optimization of
Conditional Value-at-Risk. The Journal of Risk, Vol.2, No. 3, pp 21-41.
[22] Rockafellar, R. et Uryasev, S., 2002.Conditional
value-at-risk for general loss distributions, Journal of Banking & Finance,
vol. 26.
[23] Roy, 1952. Safety-First and the Hoding of Assets.
Econometrica, vol.20, ppÀ3 1-449.
[24] Szerö, G., 1999. A critique to Basel regulation, or
how to enhance (im) moral hazards; Proceedings of the International Conference
on Risk Management and Regulation in Banking. Bank of Israel. Kluwer.
[25] Tobin, J., 1958. Liquidity Preference as Behavior towards
Risk. Review of Economic Studies, vol. 25, pp 65-86.
[26] Tversky, A. et Kahneman, D., 1979. Prospect theory: An
analysis of decisions under risk. Econometrica, vol. 47, pp. 279.
[27] Tversky, A. et Kahneman, D., 1991. Loss aversion in
riskless choice: a referencedependent model. Quarterly Journal of Economics,
vol. 106, pp103 9-1061.
[28] Uryasev, S., 2000. Conditional Value-at-Risk: Optimization
Algorithms and Applications. Financial Engineering, News, No.14.
[29] Von Neumann et Morgenstern, O., 1944. Theory of games and
economic behaviour. Princeton University press.
Ouvrages :
[1] Aftalion, F., 2003. La nouvelle fiance et la gestion des
portefeuilles. Paris, Economica. pp1 1-67.
[2] Esch, L. et Kieffer, R., 1997. Value at Risk - Vers un Risk
Management moderne, De Boeck Université.
[3] J. P. Morgan Co., Riskmetrics-Technical Document, 4th ed,
New York, 1996.
[4] Markowitz, H., 1959. Portfolio selection: efficient
diversification of investment, Yale University Press, New Haven, 2ème
edition, 1971.
| 


