Etude de l'influence des efferts d'echelle dans le modele de Dugdale

3.3 Démonstration de la convergence uniforme de l'intégrale I :

Le critère de convergence uniforme d'une intégrale impropre s'énonce comme suit : S'il

00

existe une fonction continue M(t) telle que

00

ff (x, t).dt est uniformément convergente.

0

Soit la fonction e^-2h :

f (x,t ) M(t) et fM (t).dt est convergente, donc

0

7.

_j C^{al 1} d2=-¹

0

h

r -2h-1-- 1

(3.30.52)

h

_Le 10 =

Cette intégrale est bien convergente. Allons prouver que :

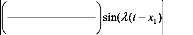
-_e 2 h

(h+x2)e-

+e

+e-(h-x2)

ah

<e

-2h

(3.31.53)

La fonction sinus est une fonction bornée dans l'intervalle[-1.1], (3.53) est donc vérifié si :

<e	-2h

e 2-2(h+x2) + e - (h-x2)

e ^-Âh + e.1h

)

1

<

2h

2

+

1

e

e2+ _e2-2,(h - (h-x2

(3.32.54)

-1 o

sin(2(t - x1)

Nous allons prouver que la fonction en valeur absolue est inférieur ou égale a 1. On considère 2 comme paramètre sachant que 2> 0 .

)

f (2, x 2

e

-2.1h +1

Notons par f et g respectivement le numérateur et le dénominateur de la fonction en valeur absolue définie précédemment.

f(2, x₂) = e-2(h+x2) + e-2(h-x2) (3.33.55)

g(2) = e-22

Nous avons comme données :

2>0,x₂e [-h,0],h> 0 (3.34.56)

Pour la fonction f (2, x₂) :

La dérivée par rapport a x₂ :

af (2, x2) = ile-2h (e^2x2 - e^-2.2) (3.35.57)

ax₂

La dérivée est strictement négative V (2 > 0, x₂ E [- h,0 ]) ,

La variation de la fonction f (2, x₂) est présentée sur le tableau suivant :

x2	-h 0

h

2e^-

Il est donc claire que :
f(^2,x2) g(x) Vx2
Et donc
	f (2, x2 )	£ 1	(3.36.58)
	g (2)
En conclusion, l'intégrale I est bien uniformément convergente.

3.4 Conclusion :

L'équation intégrale ainsi établie, nous allons procéder dans le chapitre suivant à la résolution de cette équation en utilisant une méthode numérique basée sur les polynômes de CHEBYSHEV.

CHAPITRE 4
RESOLUTION DE L'EQUATION INTEGRALE

4.1 Introduction :

Dans cette partie nous allons procéder à la résolution de l'équation intégrale établie dans le chapitre précédent. Pour alléger les écritures on note park le terme k^" de l'équation intégrale.

4.2 Résolution :

L'équation intégrale s'écrit :

)

(4.1)

1 1

+k(x₁,t)W(t).dt = ^2.11-1"(x1

t x

- m

-1 1

Avec la condition :

1

fv (t)dt = 0

- 1

Avec :

+

k

, (4.2)

.0_2.e-a.11

0

(x1,t)= f _{e +e}2.11.s^{in 2}.(t^- )⁴².

4.2.1 Introduction des quantités normalisées :

Tout d'abord, nous introduisons les quantités normalisées suivantes :

t

x₁

r= , s = ,

l_a

l_a

=

le Kt) = f (s), k (x ₁ , t) = L(r, s), 1-(x₁) = 1-(r) . (4.3)

l, _a

Ainsi l'équation (4.1) prend la forme suivante :

1

+

1

J[

s

1

71^-

-

r < 1. (4.4)

1 2

+ l _a .L(r , s)].f (s).ds = .r(r),

--r

Il

Avec la condition :

+1

Jf(t).dt = 0 (4.5)

-1

Dans (4.4), le chargement 1-(r) est donné par :

~ - 1- ,

~ ~--1-...+1-e,

77

(4.6)

1-(r)

si r <
si ¹7 <r

<1

On remarque que le chargement (4.6) présente des discontinuités. Pour ce type de chargement, la méthode de résolution de ce type d'équation intégrale ne donne pas de bons résultats. Par conséquent, et suivant une méthode développé par (IOAKIMIDIS, 1980 [32]), on remplace f (s) par une nouvelle fonction 0(s) telle que :

f (s) = h(s) + 0(s), (4.7)

Où h(s) est la solution de l'équation intégrale suivante :

1	+1 J -1	1	.h(s).	ds = 2 .r(r),	r <1. (4.8)
71^-		s -- r		Il

Avec la condition supplémentaire suivante :

+ 1

J h(s).ds = 0 (4.9)

-

1

<1

r

Où

+ l _aL(r, s

(4.10)

s ds

)]0 ( ). (r),

g

1

+

1

1

-

71-

1[_s

1

r

-

1

+

1

1

g (r) = -

71- fl _a .L(r ,s).h(s).ds

(4.11)

Avec la condition

+1

10(t).dt = 0 (4.12)

-1

Il est clair a partir de l'équation (4.11) que, puisque L(r ,s) a un comportement régulier, ceci
est également vrai pour g(r) , et les techniques numériques classiques pour la résolution de

l'équation intégrale singulière peut être directement appliqué pour résoudre l'équation (4.10) sans aucune modifications.

La solution de l'équation (4.8) et (4.9), est donnée par [28] :

2 (r)

h(s) =-.(1-s² ) ².1(1-r² ) 2. r dr

71-./.i_-1 r - s

1 +1 1

s <1, (4.13)

On obtient :

Où

h(s) = h₁ (s) + h₂ (s)(4.14)

2.s

h₁ = . (1-s² ) ^{- 2}.(-2 .71- + 2.r_c . arccosil), (4.15)

/ni./

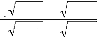
²

1

-

1

il

2

s -s

2

il

2

1

-

1

s

+s

il

il

h₂(s) = 2r c ln

71-_izi

(4.16)

On voit que h₂ (s) présents des singularités logarithmiques aux points s #177;il.

4.2.2 Application de la méthode de résolution standard des équations intégrales :

Il a été montré dans (ERDOGAN et al. 1973 [18]) que l'équation intégrale singulière (4.10) a l'indice 1 car la fonction inconnue 0(s) à des singularités intégrables aux points #177;1.

1

-

poids associé au polynôme de CHEBYSHEV de premier ordre

T _n(s) = cos(n.arccos(s)) et ço(s) est une fonction continue et bornée sur l'intervalle [-1, 1]

laquelle peut être exprimé comme une série tronquée des polynômes de CHEBYSHEV du premier ordre. A cause de la symétrie du position par rapport à x₂ on à ço(s) = --ç(s) . Donc, la solution de l'équation (4.10) s'exprime :

1 N

--

0(s) = (1-- s2) 2 EAn.T 2n--1(s) (4.17)

n=1

Substituons l'équation (4.17) dans l'équation (4.10) en utilisant les relations suivantes :

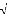
	1
Avec	-- 1 1T n(s)(1 -- s2) 2 CIs n> 0 = s -- r --1 0, n=0			(4.18)

U_n(r)= sin((n +1).arccos(r))/ 1-- r² (4.19)

L'équation (4.19) design les polynômes de CHEBYSHEV de second ordre. On trouve :

N

E An [U _2,2 0+ H _n(r)]= g(r), r <1. (4.20)

n=1

Ou:

1 1

(r) = ¹1(1-- s2) ²¹.¹(r, sg2n--1(s)CIs p

n

--1

(4.21)

L'équation (4.20) peut être résolue en sélectionnons les N points de collocation données par :

rj = cos

~(2 j --1)/z 2(2N--1) J , j,......,N. (4.22)

Utilisant les points de collocation donnés par l'équation (4.22) dans l'équation (4.20) on arrive a un système de N équations a N inconnus, nommés A₁,........, A_N laquelle peut être

exprimé ainsi :

N

E A ^n[U 2n--2(rj)+H n(rj)]= g(r ), j = 1,........., N (4.23)

n=1