Contribution à la détermination des paramètres ultrasonores des gondolements des fibres dans un matériau composite à matrice céramique renforcé des fibres du «rhectophyllum camerunense

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

V T V I C A C T

MEMOIRE DE MASTER II RECHERCHE		2008-2009

A

.

JvIes 4pouses

MEMOIRE DE MASTER II RECHERCHE		2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

R T .M T R C I T .M T J1 T' S

Ce travail de recherche est le fruit d'une collaboration entre le laboratoire de mécanique, matériaux ,structure et productique ( L2MSP ) de l'unité de formation doctorale de physique et sciences de l'ingénieur de l'université de Douala et la société HYDRAC S.A (HYDROCARBURES-ANALYSES-CONTROLES ),laboratoires certifiées ISO 9001 :2008 et ISO 14001 :2004.

J'adresse tous mes remerciements aux personnalités suivantes :

· Dr ATANGANA ATEBA Jean, responsable du Laboratoire de Mécanique, Matériaux, Structure et Productique (L2MSP) pour sa disponibilité, le suivi et l'encadrement de ce travail sans oublier les enseignements reçus de ce dernier.

· Dr NTENGA Richard, en tant qu'enseignant du L2MSP et surtout pour son encadrement.

· Mr MOUSSA BAKOURA, Expert CND niveau 3, HYDRAC S.A pour ses conseils dans la présentation des résultats.

· Mr NJENE EBONGO Hans, inspecteur certifié en ultrason, HYDRAC S.A pour son assistance dans l'acquisition des données en laboratoire d'ultrason.

· A tous les enseignants de l'unité de formation doctorale en physique et sciences de l'ingénieur.

· A tous les membres de jury qui ont bien voulu se prêter à l'évaluation de ce travail.

· A DJODA PAGORE, AYISSI Zacharie, NJOM Abel, NOAH (INSA-LYON) pour leur assistance dans les corrections et relecture.

· Aux enfants NGO MBEI SOUMEYYA FAOUZANNE, NGO MBEY AR-ROUBAI BALKIS, MBEI HABIBOU RAHMANE, ABOUBAKAR MBEI LISSOUCK pour leur soutien moral et leur patience de mon absence tout au long de ce travail.

· A ABDALLAH MOUYAKAM, Imam SOULEYMAN MBOUEMBOUO, IBRAHIM BIDIAS et NGO TIGYO FAIZA pour leur soutien moral.

MEMOIRE DE MASTER II RECHERCHE			2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

£ISrT DTS I~1JRTS

N° figure Intitulé Page

Fig1.1. Fig.1.2. Fig.1.3. Fig.2.1

Paramètres qui conditionnent les performances d'un composite Concept d'interphase et d'interface Rupture d'un composite à matrice céramique dans un test de traction selon la qualité de l'interface Surpression d'un gaz dans un piston en mouvement

6 7 8 10

Fig.2.2 Variation du volume d'une tranche de fluide 10

Fig.2.3 Mouvement d'une masse constante de gaz 11

Fig.2.4 Ondes progressives et régressives 13

Fig.2.5 Représentation d'un volume balayé lors du déplacement 15

Fig.2.6 Représentation de la variation totale de volume 15

Fig.2.7 Représentation de la direction de propagation des OPP en 3D 17

Fig.2.8 Schéma de propagation d'une OPP suivant les axes 18

Fig.2.9 Schéma d'illustration d'une déformation 19

Fig.2.10 Volume représentatif 20

Fig.2.11 Propagation des ondes 22

Fig.2.12 Propagation des ondes planes dans les milieux isotropes 22

Fig.2.13 Projection de la vitesse d'énergie sur la direction de propagation 24

Fig.2.14 Allure schématique du lieu de l'extrémité du vecteur vitesse de 24

propagation

Fig.2.15 Illustration du phénomène de réflexion / transmission 25

Fig.2.16 Interprétation géométrique 1 26

MEMOIRE DE MASTER II RECHERCHE iv 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

N° figure Intitulé Page

Fig.2.17 Interprétation géométrique 2 26

Fig.2.18 Présentation des vecteurs lenteurs sur la surface 27

Fig.2.19 Allure schématique des angles critiques et courbes des lenteurs 27

Fig.3.1 Principe de la mesure de vitesses en incidence oblique 32

Fig.4.1. Présentation des échantillons 34

Fig.4.2 Représentation A-scan des échos du bloc étalon normalisé 39

Fig.4.3 Représentation A-scan des échos de l'échantillon I 40

Fig.4.4 Représentation A-scan des échos de l'échantillon II 41

Fig.4.5 Représentation A-scan des échos de l'échantillon III 42

Fig.4.6 Représentation A-scan des échos IV de l'échantillon avec défauts 43



CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

LIS T DTS ARLTA'UX

N° Tableau Intitulé Page

Tableau 4.1 Caractéristiques des appareillages utilisés 35

Tableau 4.2. Résultats de l'étalonnage du bloc étalon normalisé 39

Tableau 4.3 Résultats de l'étalonnage sur échantillon de plâtre sain(I) 40

Tableau 4.4 Résultats de l'étalonnage sur échantillon de plâtre sain(II) 40

Tableau 4.5 Résultats de l'étalonnage sur échantillon de plâtre sain(III) 42

Tableau 4.7 Résultats du contrôle matériaux composites avec défauts 43

MEMOIRE DE MASTER II RECHERCHE

2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

£ISrT DTS ~~R~VLkTZO.NS

· u (x,t ) : champ scalaire de déplacement.

· O. . : onde plane progressive

· C.Jvt. : composite à matrice polymère

· C.Jvt.1i4 : composite à matrice métallique

· C.Jvt.0 : composite à matrice céramique

· o : pression de l'équilibre

· S : dilatation de la tranche de fluide

· 3I : force volumique

· 'VIT : vitesse onde longitudinale

· 'Vt : vitesse onde transversale

· 'Ve : vitesse d'énergie

· C.~~D : correction amplitude distance

· (x, t) : variation de pression

· dÙ : volume de la tranche

· ö (%Ù) : variation du de la tranche

· I : vecteur de poynting

MEMOIRE DE MASTER II RECHERCHE vii 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

rARLT DTS .MArZTRTS

INTRODUCTION GÉNÉRALE 1

PREMIERE PARTIE : REVUE DE LA LITTERATURE 3

CHAPITRE I : PRÉSENTATION DES MATÉRIAUX COMPOSITES 4

1.1. INTRODUCTION 4

1.2. DIFFERENTS TYPES DE COMPOSITES 4

I.3.COMPORTEMENT DE L'INTERFACE FIBRE / MATRICE DANS LES COMPOSITES A MATRICE

CERAMIQUE 6

I.3.1. Généralités 6

I.3.2. comportement d'un composite unidirectionnel (rôle de l'interface) 7

Chapitre II : PROPAGATION DES ONDES ULTRASONORES 10

2.1. INTRODUCTION 10

2.2. ÉQUATION DE PROPAGATION 10

2.2.1 Expression du champ de surpression 10

2.2.2 Équation fondamentale de la dynamique 11

2.2.3 Solutions progressives dans un milieu illimité 1D 12

2.2.4. Vitesse de propagation et propriétés du milieu 14

2.2.5. Notion d'impédance 14

2.3. RÉGIME D'ONDES PLANES DANS LES SOLIDES ANISOTROPES ILLIMITÉS 15

2.3.1. Modèle tridimensionnel 15

2.3.2. Flux de puissance - Vecteur de Poynting 16

2.4. PROPAGATION DES ONDES PLANES PROGRESSIVES EN 3D 17

2.4.1. Expression analytique des O. P. P. 18

2.5. PROPAGATION DES ONDES PLANES ET ÉTAT DES CONTRAINTES 19

2.5.1. Déformations 19

2.5.2. Contraintes 20

2.5.3. Équation du champ : équilibre statique - dynamique 20

2.5.4. Loi de comportement linéaire d'un solide élastique 21

2.5.5. Régime d'ondes planes dans les solides anisotropes illimités 21

2.6. PROPAGATION DES ONDES PLANES DANS LES MILIEUX ISOTROPES ILLIMITES 22

2.7. Vitesse d'énergie 23

2.8. Phénomènes de réflexion / transmission (régime d'ondes planes et milieux isotropes) 25

MEMOIRE DE MASTER II RECHERCHE viii 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

DEUXIEME PARTIE : APPLICATION A LA CARACTERISATION DES PARAMETRES ULTRASONORES DE

DETECION DES GONDOLEMENTS DES FIBRES DANS UN MATERIAU COMPOSITE 28

CHAPITRE 3 : PRESENTATION GENERALE DE LA METHODE ET DU DISPOSITIF EXPERIMENTAL 29

3.1. INTRODUCTION 29

3.2. LE CONTRÔLE PAR REFLEXION SUR ECHO D'ANOMALIE 29

3.2.1. Définition de la méthode 29

3.2.1.1. La détection 29

3.2.1.2. La caractérisation 30

3.2.2. Méthode de mésure de l'amplitude des échos d'anomalie (réflectivité) 30

3.2.2.1. Méthode d'écho de fond 30

3.2.2.2. Méthode de la courbe expérimentale C.A.D. 31

3.3. MISE EN OEUVRE DU CONTRÔLE ULTRASONORE 31

3.3.1. contrôle par contact - contrôle par immersion 31

3.3.1.1. Contrôle par contact 31

3.4.1.2. Contrôle par immersion 32

CHAPITRE 4 : REALISATION DES ESSAIS PRATIQUES ULTRASONORES SUR UN MATERIAU

COMPOSITE(ESSAI DE DETECTION DES GONDOLEMENTS ) 34

4.1. INTRODUCTION 34

4.2. PRESENTATION DES EPROUVETTES ET DISPOSITIF D'ESSAI 34

4.2.1. Des éprouvettes 34

4.2.2. Fabrication et mise en oeuvre des composites 35

4.2.3. Dispositif d'essai 35

4.3.PREPARATION DU CONTROLE MANUEL 36

4.3.1. Vérification de l'appareillage 36

4.3.2. Etalonnage de la base de temps 36

4.3.3. Réglage d'amplification 37

4.4. EXECUTION DES ESSAIS 37

4.4.1. Le plan de sondage 37

4.5. PRESENTATION DES RESULTATS DE L'ESSAI ET COMMENTAIRES 38

4.5.1. Etalonnage de l'appareil en utilisant un bloc étalon en acier au carbone 38

4.5.2. Étalonnage de l'appareil en utilisant un échantillon de composite sain 39

4.5.3. Contrôle du matériau composite comportant des défauts artificiels (gondolements) 42

CONCLUSION 43

MEMOIRE DE MASTER II RECHERCHE ix 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

RES'WMT

A mesure que le recours aux Matériaux Composites pousse aux limites de la science et de la technologie, certains défauts sur les fibres comme leurs distributions et géométrie qui leur sont traditionnellement associées prennent aussi de l'ampleur. Les techniques de détection et de quantification des gondolements des fibres (sinuosités) sont cependant limitées voire inexistantes. La méthode faisant appel aux rayons X est une possible voie d'exploration, mais reste hors de portée car elle est non portable et les couts de réalisation y relatifs sont encore élevés. Aussi, cette étude se propose de recourir aux techniques d'ultrasons pour dépasser ces limitations et parvenir ainsi à la détection et la quantification des défauts de gondolement des fibres en particulier.

Dans l'objectif de cette analyse micromécanique fine de l'interface fibre-matrice dans les composites, des échantillons de matériaux composites unifilamentaires à base du "Rhectophyllum Camerunense " et du plâtre ont été élaborés, en incorporant quelques défauts artificiels (gondolements).

La détermination des paramètres de détection de ces défauts artificiels et inter faciaux a impliqué des essais non destructifs aux ultrasons qui ont été effectués en utilisant une technique expérimentale de contrôle ultrasonore par contact.

L'absence des données sur les caractéristiques ultrasonores de ce type de matériau composite nous a conduit de prime abord à établir les paramètres de détection de ces défauts de gondolements. La détermination de ces paramètres a conduit à l'étalonnage successif de l'appareillage en utilisant comme matériau de référence notre échantillon sain de composites. Ceci a aboutit à établir un seuil de réflectivité des échos d'anomalies comme paramètres de détection ainsi qu'un préalable pour les essais ultrasonores sur un matériau composite à fibre naturelle / plâtre.

Mots-clés : Fibres naturelles-Gondolement-Materiaux Composites-Détection-QuantificationUltrason- plâtre

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN
MATÉRIAU COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

~RS~44Cr

As the recourse to Composite Materials leads to the limits of science and technology, certain defects on fibres like their distribution and geometry, which are traditionally associated for them, become also extensive. The techniques of detection and quantification of the gondolements of the fibres (sinuosity) are however limited even non-existent. The method calling upon x-rays is a possible way of exploration, but remains out of reach and it is not portable. The costs of realization relating to it are still high. In addition, this study proposes to resort to the techniques of ultrasounds to exceed these limitations and to thus arrive at detection and the quantification of the defects of gondolements of fibres in particular.

In the objective of this micromechanical analysis of the interface matrix / fibres in the composites, the unifilamental composite material samples at base of "Rhectophyllum Camerunense" fibres and the plaster was elaborate, by incorporating some artificial defects (gondolements).

The determination of the parameters of detection of these artificial defects and inters facial implied non-destructive tests with the ultrasounds, which were carried out by using an experimental technique of ultrasonic control per contact.

The absence of the data on the ultrasonic characteristics of such composite materials first led us to establish the parameters of detection of these defects of gondolements. The determination of these parameters led to the successive calibration of equipment by using like material of reference our healthy sample of composites. This leads to establish a threshold of reflectivity of the echoes of anomalies like parameters of detection as well as a precondition for the ultrasonic tests on a composite material to natural fiber/plaster.

Keys words: natural Fibres-Gondolements- Composites material-Detection-QuantificationUltrasound- plaster

MEMOIRE DE MASTER II RECHERCHE

2008-2009

MEMOIRE DE MASTER II RECHERCHE 1 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

INTRODUCTION GÉNÉRALE

Les matériaux composites sont de plus en plus utilisés pour la réalisation des pièces de structures. Les propriétés mécaniques spécifiques de ces matériaux permettent en effet un allègement des structures particulièrement recherchées dans des secteurs d'activités comme l'aéronautique et l'automobile. Ainsi les trois grandes classes de matériaux composites à matrice céramique, métallique et polymères connaissent un développement soutenu. Ces matériaux intéressent au plus haut point le Cameroun dans son avancé vers l'émergence.

L'utilisation des matériaux composites engendre toutefois de nombreuses difficultés relatives au dimensionnement et à la durabilité des structures ce qui limite encore la diffusion de ces structures composites a plus grande échelle. Les difficultés relatives au dimensionnement des pièces en composites proviennent principalement du caractère anisotrope de leurs propriétés mécaniques. Le calcul des structures en matériaux composites demande donc une connaissance plus précise du comportement mécanique anisotrope de ces matériaux. Ainsi, l'une des questions faisant actuellement l'objet d'actives recherches dans ce domaine, concerne la détermination expérimentale et le calcul théorique des propriétés mécaniques effectives des composites en relation avec la morphologie et les propriétés des phases qui les constituent.

Des études menées par Alexis BEAKOU, ATANGANA J.A & al. [1], ont démontré que les fibres issues du « Rhectophyllum Camerunense » plante d'origine du Sud Cameroun, présentent des propriétés mécaniques intéressantes. L'un des problèmes à résoudre afin que cette fibre puisse être utilisée avec efficacité comme renfort est la détection et la quantification des gondolements qui pourraient apparaitre lors de la fabrication du composite. D'ou le thème : « CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU COMPOSITE A MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU "RHECTOPHYLLUM CAMERUNENSE" ». Deux approches, l'une expérimentale et l'autre théorique, sont développées parallèlement. La méthode expérimentale est une méthode non destructive utilisant la propagation des ondes ultrasonores. La méthode théorique quant à elle, est une approche mathématique du modèle d'un fluide sur pression. Les résultats obtenus sont analysés en relation avec une connaissance précise de la morphologie du matériau.

Notre travail comporte deux parties regroupées en quatre chapitres et organisé tel qui suit :

MEMOIRE DE MASTER II RECHERCHE 2 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

La première partie fait une incursion dans la revue de la littérature et comprend deux chapitres : Le premier présente tout d'abord les principaux types des matériaux composites et leurs applications, ainsi que l'influence des défauts des fibres sur les interfaces. Tandis que le deuxième est essentiellement consacré à la physique qui gouverne la propagation des ondes ultrasonores et leur interaction avec les solides.

La deuxième partie portant sur la caractérisation des paramètres ultrasonores des gondolements des fibres dans notre matériau composite comprend également deux chapitres : le troisième donne la description générale de la méthode de contrôle par ultrasons utilisée et le quatrième parle de la réalisation des essais pratiques du contrôle ultrasonore et de la présentation des résultats.



PREMIERE PARTIE : REVUE DE LA
LITTERATURE

MEMOIRE DE MASTER II RECHERCHE 3 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

MEMOIRE DE MASTER II RECHERCHE 4 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

CHAPITRE I : PRÉSENTATION DES MATÉRIAUX COMPOSITES

1.1. INTRODUCTION

Un matériau composite peut être défini comme l'assemblage de plusieurs matériaux de natures différentes à l'échelle microstructurale. Les composites sont le plus souvent constitués d'une matrice dans laquelle on a dispersé de façon contrôlée ou non des renforts (fibres). La matrice maintient les renforts et assure les transferts de charge, tandis que les renforts apportent principalement leurs caractéristiques mécaniques élevées (modules et limites d'élasticité, résistance mécanique...) [2]. Cette association a pour but d'obtenir un matériau dont les propriétés spécifiques (propriétés mécaniques rapportées à la masse volumique) sont supérieures à celles de la matrice non renforcée. Le concept de matériau composite, par le choix des constituants et de leurs proportions respectives, ainsi que par le choix de la forme, des dimensions et de la disposition des renforts, permet donc de concevoir un matériau présentant les caractéristiques spécifiques recherchées.

1.2. DIFFERENTS TYPES DE COMPOSITES

La nature du matériau constituant la matrice permet de répertorier trois grandes classes de composites. Elles sont considérées ici par ordre croissant de tenue en température : les composites à matrice polymère (C.M.P.), les composites à matrice métalliques (C.M.M) et les composites à matrice céramique (C.M.C.), il est alors possible d'associer à ces trois types de matrices soit des renforts discontinus, dont toutes les dimensions sont très inférieures aux dimensions de la pièce, soit des renforts continus, dont au moins une dimension est du même ordre de grandeur qu'une dimension de la pièce. Les matériaux utilisés, comme renforts sont des fibres qui présentent de bonnes propriétés mécaniques intrinsèques (carbone, alumine, silice, kevlar, acier...). Selon l'application envisagée, l'assemblage de ces fibres peut être unidimensionnel (plis unidirectionnels), bidimensionnel (plis tissés, mats à fibres coupées de quelques centimètres ou à fibres continues) ou tridimensionnel (tissus multidimensionnels) [2].

1.2.1. Les Composites à Matrice Polymère (C.M.P)

La fabrication des C.M.P. emploie deux types de matrices : les résines thermodurcissables qui représentent 3/4 des C.M.P. actuels (époxyde, polyester, vinyles ter, polyuréthane...) et les résines thermoplastiques (polypropylène, polyamide...) qui sont moins utilisées mais en pleine progression du fait notamment d'une plus grande recyclabilité (réutilisation après broyage). Les matrices polymères renforcées par des fibres de verre, employées notamment dans les produits de

MEMOIRE DE MASTER II RECHERCHE 5 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

grande diffusion, sont d'une grande importance industrielle. Les fibres de carbone et de Kevlar sont utilisées dans une moindre mesure pour des applications hautes performances dans l'aéronautique et l'aérospatiale. D'autres types de renforts sont employés tels que des billes (verre, élastomère...) et des charges (fibres broyées, poudres...). Les pièces en composite à matrice polymère prennent des formes variées (coques, plaques, pièces de révolution...) grâce aux nombreux procédés de formage mis au point (moulage, pultrusion, estampage, enroulement filamentaire) [3]. Ces composites permettent un allègement des pièces de structure habituellement fabriquées en alliages métalliques. L'utilisation des C.M.P. reste limitée au domaine de températures inférieures à 200°C.

1.2.2. Les Composites à Matrice Métallique (C.M.M)

Pour des applications plus haute température, on fait appel aux composites à matrice métallique (C.M.M) jusqu'à 600°C. Les métaux ou alliages métalliques utilisés dans la fabrication des C.M.M., sont généralement choisis en fonction de leurs propriétés spécifiques dans l'état non renforcé [4]. Ainsi, l'aluminium, le titane et le magnésium sont les métaux les plus couramment utilisés. Les procédés de fabrication des C.M.M. diffèrent selon que la matrice se trouve lors de l'introduction des renforts à l'état liquide (forgeage liquide, fonderie moyenne pression), dans un état semi-solide ou dans l'état solide (métallurgie des poudres). Les C.M.M. présentent de bonnes caractéristiques mécaniques spécifiques, une bonne résistance en température et aux chocs thermiques ainsi qu'une bonne résistante à l'usure et à l'abrasion.

1.2.3. Les Composites à Matrice Céramique (C.M.C.)

Enfin, lorsque les températures d'utilisation sont supérieures à 1000°C on a recours aux composites à matrice céramique (céramiques industrielles). Leur renfort est généralement constitué de fibres longues en carbone, en silice ou en carbure de siliciums, assemblées par tissage multidimensionnel. Ces matériaux sont développés dans le domaine aérospatial. D'autres par contre sont utilisés pour l'ingénierie bâtiment. Aujourd'hui les recherches sont actives sur les possibilités de combinaison des fibres naturelles comme renfort dans les matériaux composites à matrice céramique.

MEMOIRE DE MASTER II RECHERCHE 6 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

I.3.COMPORTEMENT DE L'INTERFACE FIBRE / MATRICE DANS LES
COMPOSITES A MATRICE CERAMIQUE

I.3.1. Généralités

Les propriétés d'un composite dépendent fortement des caractéristiques physico-chimique des constituants primaires tels que renfort (fibres, particules... etc.) et matrice. Mais le comportement résultant du composite ne peut pas être représenté comme une combinaison simple des propriétés de chacun des constituants.

D'autres facteurs aussi importants que le choix des constituants sont liés directement à la performance du composites : le procédé de fabrication de ce composite et les propriétés de l'interface fibres et matrice.



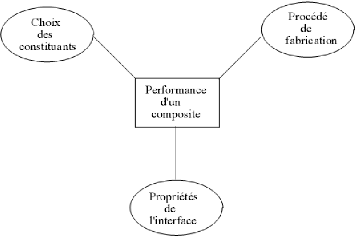
Fig.1.1.Paramètres qui conditionnent les performances d'un composite

En effet, il est reconnu que le comportement mécanique des composites à matrice céramique à renforts fibreux dépend fortement de la liaison fibre/matrice qui s'établit entre les constituants lors de l'élaboration du composite [27].Cette liaison est constituée d'une ou de plusieurs interphases et interfaces. Rappelons tout d'abord la distinction entre les termes interphase et interface :

L'interphase est un milieu continu qui peut être une zone de réaction chimiquement formée par les constituants du composite lors de son élaboration, ou une fine couche introduite volontairement dans le but de protéger la fibre ou de contrôler la liaison inter-faciale (Fig.1.2.a).

MEMOIRE DE MASTER II RECHERCHE 7 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

L'interface est un terme utilisé dans le domaine des matériaux composites, pour décrire la surface ou la zone qui sépare la fibre et la matrice (discontinuité macroscopique) (Fig.1.2.b).



Fig.1.2. Concepts d'interphase et d'interface [29]

C'est dans cette zone que s'effectue précisément le transfert de charge de la matrice vers le renfort (ou vice vers) et elle est également le siège de concentration de contraintes résiduelles lors de la préparation du composite.

Pour que le transfert de charge ait lieu, un certain contact ou adhérence à l'interface entre les constituants est nécessaire. Comme caractéristiques de cette adhérence (caractéristiques de l'interface) il ya : la contrainte de décohésion (Td), la contrainte de frottement (T ), le coefficient de frottement (j.t), la microstructure, l'énergie d'adhésion et d'autres grandeurs physico-chimiques. Suivant ces caractéristiques, le comportement du composite est déterminé.

I.3.2. comportement d'un composite unidirectionnel (rôle de l'interface)

Dans un composite céramique unidirectionnel sollicité parallèlement aux fibres, le comportement à rupture peut être imaginé comme étant constitué des séquences suivantes (Fig.1.3.) : d'abord, fibres et matrice subissent la même déformation ; le composite possède donc un comportement linéaire élastique (domaine OA) jusqu'à l'apparition d'une première fissure matricielle. Cette fissure se propage et s'approche d'une fibre, ensuite on peut distinguer les cas suivants

-Cas d'une interface très forte : si l'adhérence entre fibres et matrice est forte, la fissure continue
sa propagation comme si elle n'avait rencontré aucun obstacle (Fig.1.3.a).Cela entraine aussi des
concentrations de contraintes sur les fibres voisines et provoque la rupture catastrophique du

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

composite (domaine AE, Fig.1.3). Le comportement du composite est celui d'un matériau fragile et les fibres n'exercent aucun effet de renforcement sauf éventuellement par leur énergie de rupture.

Cas d'une interface très faible : si l'interface est trop faible, la fissure matricielle est bien déviée à l'interface, mais la décohésion entre fibres et matrice s'étend sur une très grande distance sur laquelle la matrice n'intervient donc plus. Dans ce cas, la résistance du composite est très faible. Cas d'une interface relativement faible et assez forte : si l'adhérence entre fibre et matrice est relativement faible, la fissure au contact d'une fibre se dévie dans un plan perpendiculaire (mode II de la rupture) en provoquant un décollement de la matrice au niveau de l'interface. La fissure continue à se propager en répétant le même scénario avec les autres fibres jusqu'à ce qu'elle traverse tout l'échantillon (Fig.1.3, b). Si la fraction volumique des fibres Vf est suffisamment élevée et l'interface assez forte, il peut s'opérer un transfert de charge matrice -fibres permettant à ces dernière de supporter la surcharge due à la fissuration matricielle ; celle- ci peut s'étendre jusqu'à saturation en accord avec le principe énergétique développé par AVESTON et al [29] (domaine AB, Fig.1.3).



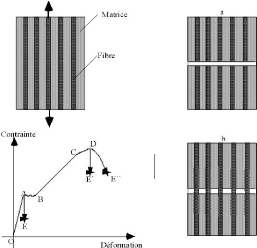
MEMOIRE DE MASTER II RECHERCHE 8 2008-2009

Fig.1.3 : Rupture d'un composite à matrice céramique dans un test de traction selon la qualitéde l'interface : interface forte (a) et interface relativement faible (b).

MEMOIRE DE MASTER II RECHERCHE 9 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Ensuite l'essai se poursuivant, les fibres portent la fissure et jouent leur rôle de renfort en supportant la sollicitation : elles se déforment élastiquement en frottant dans les gaines de matrice (domaine AC). Dans cette étape la décohésion se propage au long des fibres et une étape de glissement pour extraire les fibres, après leurs rupture.

Dans le domaine CD de la couche, outre le rôle de l'interface, les fibres commencent à se rompre progressivement en accord avec la statique de Weibull.

Enfin, suivant les caractéristiques de l'interface, il y a soit rupture brutale (DE) soit contrôlée (CD).

Les caractéristiques de l'interface sont fonction de plusieurs paramètres : les propriétés physico-chimiques des constituants (fibres et matrice). La microstructure de l'interface (interphase et rugosité). Les contraintes thermiques résiduelles, la méthode d'élaboration du composite.

MEMOIRE DE MASTER II RECHERCHE 10 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Chapitre II : PROPAGATION DES ONDES ULTRASONORES

2.1. INTRODUCTION

L'étude de la propagation des ondes ultrasonores dans les solides nécessite la connaissance de la structure de l'onde et des propriétés du milieu de propagation [5]. Dans la suite de cette étude, l'onde supposée plane, progressive et monochromatique, se propage dans un milieu élastique, anisotrope et homogène par rapport aux longueurs d'ondes considérées.

2.2. ÉQUATION DE PROPAGATION



Fig. 2.1 : Surpression d'un gaz dans un piston en mouvement

Hypothèses :

.Gaz traité comme un milieu continu : particule fluide grand nombre de particules

microscopiques

· Pression P0 à l'équilibre

· Problème unidirectionnel : la pression introduite par le mouvement du piston est de la forme 6p(x, t).

2.2.1 Expression du champ de surpression

La variation de 6(dfl) du volume dfl de la tranche est initialement comprise entre x et x + dx. u(x, t) est le déplacement à l'abscisse x.



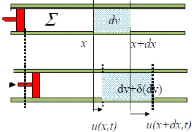
Fig.2.2 : variation du volume d'une tranche de fluide

MEMOIRE DE MASTER II RECHERCHE 11 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

S(d?) = ?[u(x + dx) -- u(x)1 (2.1)

Or u(x + dx) '' u(x) + ~~~

~~~ dx (2.2)

S(~?) ,,, ? (au

~~) _dx 8(c?) ~? ~ ~~ ~~~

~~~ (2.3)

Alors

8(c?) (2.4)

Et =

d?

S est la dilatation de la tranche fluide. C'est une des grandeurs propagée par l'onde.

_Sp = _k 8(d") ~" ~ ~~ ~~~

~~~ (2.5)

est l'équation de couplage entre les champs de surpression et de déplacement propagés par l'onde. 2.2.2 Équation fondamentale de la dynamique

On suit le mouvement d'une masse constante dm de gaz, initialement comprise entre deux sections d'abscisse x et x + dx.

Position à t de la tranche en x au repos : x + u(x, t).

Position à t de la tranche en x + dx au repos : x + dx + u(x + dx, t)



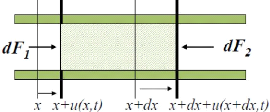
Fig. 2.3 : mouvement d'une masse constante de gaz

Force résultante sur la tranche :

dF = dF1 + dF2 = ?[P0 + Sp(x + u(x)) -- (1³0 + Sp(x + dx + u(x + dx)))] (2.6)

dF = ? .9x ^asP (1 + ~~

_ax) dx (2.7)

Approximation acoustique : ~~

~~ <<< 1 = amplitude de vibration des particules <<< 2.

~$ + ? ~~,

~~ ~~ ~ ~# 0

10 ~ 2(?~~ 0

10 on obtient par la suite, (2.8)

3⁴5

364 = 78₉ 3⁴5

3:4: Équation d'onde [5] (2.9)

Remarque :

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Soit u(x, t) le champ scalaire de déplacement d'une particule fluide.
· Cas d'un milieu parfait illimité :

{ AO -- k ^a25., 0
^P =

Po at^-

(2.10)

Po at²

k a2ri

= 0

Art --

Cette équation qui vérifie à la fois le champ de surpression, le champ de déplacement, la vitesse de particules et la dilatation est appelée Équation d'Alembert [6]

En prenant l'expression suivante :

a²sp

at²

= 0

k



A8p --

Po

On remarque que la constante k

s'exprime en (ms^--1)^-2 ; l'équation précédente s'écrit :

= 0 (2.11)



Po

1

A8p --

_C2



a²sp
at²

MEMOIRE DE MASTER II RECHERCHE 12 2008-2009

où la constante c a les dimensions d'une vitesse.

2.2.3 Solutions progressives dans un milieu illimité 1D

Recherchons s'il existe des solutions de l'équation d'Alembert sous forme d'ondes progressives, telles que nous les avons définies plus tôt. Pour le champ de surpression nous supposons une fonction telle que :

8p(x, t) = f(a(x, t)) + ^9(f3(x, t)) (2.12)

x Avec a(x, t) = t -- v

; f3(x, t) = t +^x v

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».



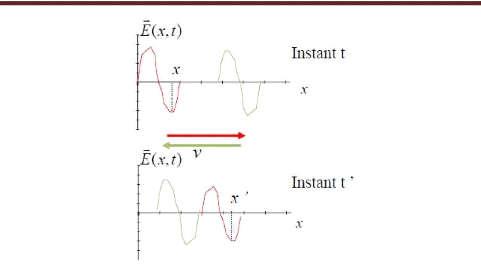
Fig. 2.4 : ondes progressives et régressives

Ici, V représente la vitesse de propagation des ondes progressives dans le milieu.



.

a²6p(x,t)

at²

a²6p(x,t) 1

ax^{2 ~}v²

= 0 (2.15)

aSp(x,t)

aa(x,t)

=

aSp(x,t)

ax

^df-I-

af3(x,t)

ax da ax

aSp(x,t)
ax

df1

-I-
da v

dg

(2.13)

df3

aa(x,t)

=

^df-I-

af3(x,t)

at da at

aSp(x,t)
ax

dg

-I- df3 (2.14)

dP

df

=

at

dg
df3

.

1
v

=

dg
df3

.

MEMOIRE DE MASTER II RECHERCHE 13 2008-2009

Les ondes progressives sont solution de l'équation d'Alembert, dans laquelle intervient la constante V.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.2.4. Vitesse de propagation et propriétés du milieu

La vitesse de propagation des ondes élastiques est directement liée aux propriétés du matériau.

v= .\I = Po

(2.16)

Cette relation peut être exploitée :

· Pour évaluer la distance dans un milieu connu par mesure d'un temps de propagation ;

· Pour évaluer les modules de compression par mesure de la vitesse de propagation.

2.2.5. Notion d'impédance

Soit une OPP se propageant dans le sens des x croissants (respectivement décroissants) :

a87(x, t) = f (t #177; x) (2.17)

a6p(x,t)

at

=f

O JZ[ . X ~,~

X ~ YO X ~,~

a6p(x,t)

ax

X (2.18)

~ Y 1

·

= W>? = ~ ^2( ~ 2(O

(2.22)

Z_C =

V

k

MEMOIRE DE MASTER II RECHERCHE 14 2008-2009

Équation d'état du fluide X ~, ~~ ~ ~~ ~~~,1

~~ . ~~,~,1

1 ~ ~~ ~~\ ~,1

~~ (2.19)

Donc : +a 6p(x, 0 V 36

= k35\ (x,t) (2.20) 36

Soit en intégrant, aop(x, t) = +:

it(x, t) = Zii(x, t) (2.21)

Avec Z = + k v

= +;

On note que Z_c ne dépend que des propriétés du milieu.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.3. RÉGIME D'ONDES PLANES DANS LES SOLIDES ANISOTROPES ILLIMITÉS

2.3.1. Modèle tridimensionnel

Le volume balayé par d? lors du déplacement :

d? = uA^B . d?

--) = u.1

d? (2.23)



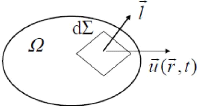
Fig. 2.5 : représentation d'un volume balayé lors du déplacement Variation totale de volume :

?(?) = I?it⁾ .`^B d? = i_?diV(11)d? = i_? (i^B)C? (2.24)

(i⁾-) = div (1)





MEMOIRE DE MASTER II RECHERCHE 15 2008-2009

	a^2.A^B		AAAAAAAAB			Po
			(op) (2.27)

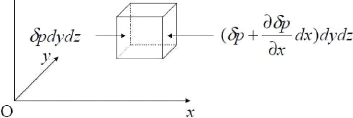
Fig. 2.6 : représentation de la variation totale de volume

sp a

F_x = Spdydz -- (Sp + _aax dx) dydz = _ax^e dxdydz (2.25)

aux asp 2(~e~f 10 ~ ~ ~~~e~f . 2( 0g

10 ~ ~ ~~,

~~ (2.26)

~~

Compte tenu des relations identiques sur les axes y et z, l'équation fondamentale de la dynamique devient :

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En prenant la divergence des deux membres,

Po	a2div(u) B		= --div (grci(Sp)) = --?(8P) (2.28)

Prenons en compte la relation de compressibilité du milieu qui s'écrit maintenant :

sp .k 5(c?) ~? ~ ~~ ~d^B ~ ~~~cO~~~^AB (2.29)

a20 _k

Il vient que : = ?(8p) (2.30)

a1 0 Po

2.3.2. Flux de puissance - Vecteur de Poynting

En présence d'une densité de force appliquée, la loi fondamentale de la dynamique s'écrit :

Po

a2ri a1^0 = Po

dit dt

AAAAAAAA^B = --grad

(^8p) +f

(2.31)

= (fu) = ^d_t (e_c + ep) + div(P) (2.39)

d

^B

dw

.

dt

=f

dil
dt

MEMOIRE DE MASTER II RECHERCHE 16 2008-2009

Et le travail des forces appliquées au cours du déplacement

-, dw = f

. dit (2.32)

AAAAAAAA^B dw = grad Avec A^B ~ \^AB

- (SP) . dil + Po^dd^ut^. d

. dif (2.33)

AAAAAAAA^B . dw = grad Or

(Sp) . dil + Poll

-) . dit

(2.34)

AAAAAAAA^B grad

(Sp) . &it = div(Sp . dif) -- Spdiv(dif) (2.35)

Et

div(dif) = d (i²) (2.36)

.dw = div(Sp ii) -- Sp. d ^B + d(¹₂ poiI²) (2.37)

d C port²) = de_c : Variation de la densité volumique d'énergie potentielle Sp. d ^B ~ de_p : Variation de la densité volumique d'énergie cinétique.

-) On définit le vecteur de Poynting par : P D'où :

-) = Spit

(2.38)

MEMOIRE DE MASTER II RECHERCHE 17 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En intégrant sur tout le volume ? ,on obtient :

dW
dt

mo (E' + E) + ff?p-) d?AAAAAA) (2.40)



m

Avec :

mn : Puissance fournie par les sources internes au volume

mo

mo (E + E_~):Puissance stockée sous forme d'énergie cinétique et potentielle

m

a?'^AB d?^AAAAAB: Puissance rayonnée vers l'extérieur.

Le vecteur de Poynting représente en direction et en amplitude la densité par unité de surface de puissance rayonnée vers l'extérieur d'un volume.

La puissance rayonnée est égale au flux du vecteur de Poynting à travers la surface limitant le volume ?.

On définit l'intensité comme la moyenne dans le temps du vecteur de Poynting, soit :

I =< P(t) >= limTxy w f 8p(t)~\ (t)

w

G dt [5] (2.41)

(

2.4. PROPAGATION DES ONDES PLANES PROGRESSIVES EN 3D

o Une onde plane progressive est une onde plane propage qui se dans une direction et un sens bien définis.

o L'onde plane est définie par la direction dans laquelle elle se propage.



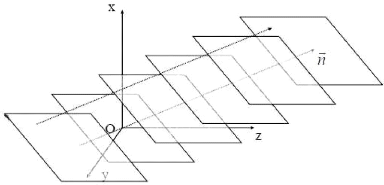
Fig. 2.7 : représentation de la direction de propagation des O.P.P. en 3D

= x .0(¹, t) = ⁸7³1 (t -- ^~_x) (2.47)

^B

-) -)

-)

.r

n = e_x; n

MEMOIRE DE MASTER II RECHERCHE 18 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.4.1. Expression analytique des O. P. P.

On peut facilement déduire l'expression d'une onde plane progressive du schéma ci-dessous :



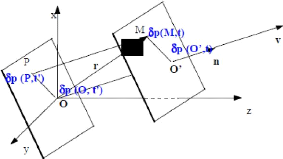
Fig. 2.8 : Schéma de propagation d'une O.P.P suivant les axes

613(I K, t) = 613(01,t) (2.42)

613(0, t^') = 613(', t^') = 6131(t') (2.43)

Avec

t = t' +^"1 v

t' = t ^PM v

ii . i-' = t i;

(2.44)

En posant : il' = OM B

81(M, t) = 81(P, C) = 0(⁰,0 (2.45)

.8W-, t') = Sp (0, t AB . ...B

" ~ = 8p1(t AB . ...B

" ~ (2.46)


· Cas particulier d'une onde se propageant suivant Ox

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.5. PROPAGATION DES ONDES PLANES ET ÉTAT DES CONTRAINTES

2.5.1. Déformations

Il ya déformation si le gradient des déplacements est non nul mais ne s'annule pas pour une rotation d'ensemble.



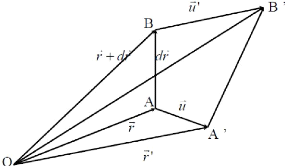
Fig. 2.9 : schéma d'illustration d'une déformation

~A^B}= A^B

(1^2 + di^)-) (2.48)

~^}i)~‡ ~~~‡* ~ ~i)~‡* ~ ~~à

~~%o UXi = Ui(Xj) + dui (2.49)

~d^B}= aldf=i -- dr = (al -- ~i‡*~d^B‡ (Rotation infinitésimale) (2.50)

1 yo 0 0 yo 0

Avec Ki ‡ ~ ~ 1 0 OE ~~à

~~%o ~ )Ki ‡ ~ ~i‡* ~ ~ 0 0 OE (2.51)

0 0 1 0 0 0

Èéè ~ F G '~~à

~~à ~ Èéè ~ i‡ ê

~~%o ~ ~~%o

~~à« ; h†~cDe#é~dcï~k

(2.52)

~~%o i‡ ~ F G '~~à

~~%o ~ ~~%o

~~à« ; De#é~dcï~k

MEMOIRE DE MASTER II RECHERCHE 19 2008-2009

Seule la partie symétrique s'annule pour tout mouvement d'ensemble. Donc seul ij (tenseur des déformations) représente une variable de déformation.

Pour résumer :u; = ui ~ ÈéèdXi + iidXi (2.53)

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

La dilatation s'exprime par :

A^B = div(u)

~

aui axi

= ii = 11 + 22 + 33 (2.54)

MEMOIRE DE MASTER II RECHERCHE 20 2008-2009

2.5.2. Contraintes

^AB)`^B* = (dFe-->i) mdE-> 0 dE

(2.55)



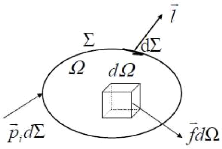
Fig. 2.10 : volume représentatif

Fi = i_ETAdÓ + 1?fid? = 0 (2.56)

Théorème de Green fi = ^aTik (2.57)

axk

Avec : Ti(t) = Tiklk

2.5.3. Équation du champ : équilibre statique - dynamique

aTik

+ = 0 (2.58)

oxk

En l'absence des forces volumiques, on a :

aTLi

~ 0 (2.59)

~~oe

Fi = iETKNÓ + i_?Ji~? = 1?~Xc~ _X~+ f₁)d? (2.60)

pù$ú at

²ⁱ 2 -- + f. (2.61)

at ₂- aT axk.k

Avec : Ti(t) = Tiklk

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.5.4. Loi de comportement linéaire d'un solide élastique Hypothèse des petites déformations :

raTo f a²Ti;

kI ,,, + ...(6) (2.62)

Tik(Skt) = Tik(Skt = 0) + ) kl

2 .
·9.SkiaS_nini Sia=⁰ --

Smn=⁰

ask' _sia=0

Soit Tik( ki) = Cijki ki (2.63)

Avec §i‡=· ~ ~~wà%o

~ oe~ oecents( (2.64)


· Équation de propagation

La prise en compte de la loi de Hooke dans la loi fondamentale de la dynamique conduit à : Hypothèse : les forces de pesanteur de densité volumique f sont négligeables.

2 X2~c

X2 ~ ~wà%o X2`

~~%o (c) 2 X2~c

X2 ~ §c·` X·X~ (2.65)

c· ~ §c·` <sup>X`</sup> axk

2.5.5. Régime d'ondes planes dans les solides anisotropes illimités

~i ~ i. $ ~~ ~ A^B . ...^B

« ~ ~ i. $ ~~ ~ %o . ...%o

« ~ (2.66)

a2u1 X2 ~ c. $

<=

®

I,

#172;

02111 = U`. ^njn2 ^k F ax.aXk

pUi. F

_njnk

= C ijklU I. 2 P (2.67)

~ nj

1. _v P

II_;

au,

ax.

MEMOIRE DE MASTER II RECHERCHE 21 2008-2009

pV²Ui = Cijki ?link U1 : Equation de Christoffel [7] (2.68)

Signification de l'Equation de Christoffel

PV²Ui = Ct_./id njnk U1

En posant : ll = Cum nink (2.67)

Il vient que : ll u1 = pV²Ui (2.68)

La polarisation U1 est un vecteur propre du tenseur ii avec pour valeur propre pV².

MEMOIRE DE MASTER II RECHERCHE 22 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

NB : Le tenseur de Christoffel étant symétrique, ses valeurs propres sont réelles et positives et ses vecteurs propres orthogonaux.



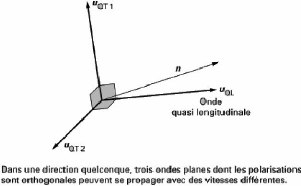
Fig 2.11 : Propagation des ondes [2]

2.6. PROPAGATION DES ONDES PLANES DANS LES MILIEUX ISOTROPES
ILLIMITES

Dans une direction donnée n d'un solide isotrope, peuvent se propager une onde plane longitudinale et une onde plane transversale.



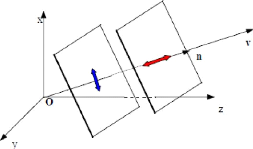
Fig 2.12 : Propagation des ondes planes dans les milieux isotropes

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Les vitesses de propagation respective de l'onde longitudinale 17_/, et de l'onde transversale VT sont données par :

VL ~ W'Fu

> (2.69)

VT = .\11.1 > (2.70)

2.7. Vitesse d'énergie

Par définition, le vecteur « vitesse d'énergie » est égal au quotient du vecteur de Poynting par la densité volumique d'énergie : [5]

~~à

1 ~ i J}

Si ~i ~ i J ~~ ~ %o ~%o

« ~ ; (2.71)

~~%o ~ %o

~~à « i J}

F

G 2 ~ ~0~à ~ F G 2 i FJ}F

10 ~

e_c =

(2.72)

MEMOIRE DE MASTER II RECHERCHE 23 2008-2009

e_P =

1 2

§i‡=· i‡ =· ~ F G §i‡=· ~~à ~~%o ~~ ~~oe ~ F G §i‡=· †‡†= à «0 J}F (2.73)

Christoffel donne :

Ciiki nink UL Ul = 2 V2Ui2 (2.74)

te e, =

G 2 i F J}F ~ kH (2.75) F

e = 2 Ui² f'² (2.76)

~~%o ~~ ~~%o

'i ~ ~i‡ ~ ~§i‡=· 'i ~ ~§i‡=· ‡ · oe « J}F (2.77)

1 ~~oe 1

_v Cijkl U j Ulnk ·

= ; en choisissant UL = 1 (2.78)

PV

La vitesse d'énergie indique (comme le vecteur de Poynting) la direction du transport de l'énergie c'est-à- dire la direction du « rayon acoustique ». [8]

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

On parle de mode de propagation pur quand le rayon est perpendiculaire au plan d'onde. Pour une direction de propagation donnée, formons le produit scalaire

O^B·. †A^B = vi ·. n = Ctjkl ^U) Ulnknt ; or _{CjjktfljflkUj} U1 = 2 V² Ui F (2.79)

> à 0 «

O^Be. †A^B _. V (2.80)



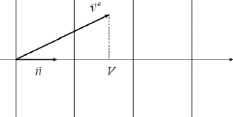
Fig 2.13 : projection de la vitesse d'énergie sur la direction de propagation

La projection de la vitesse d'énergie sur la direction de propagation est égale à la vitesse de

phase.


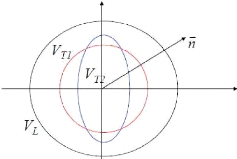
· Surfaces caractéristiques - Surface des vitesses

Lieu de l'extrémité du vecteur vitesse de propagation, tracé à partir d'une origine O, lorsque la direction de propagation varie.

Un solide anisotrope est alors décrit par une surface des vitesses constituée de trois nappes (une pour l'onde quasi-longitudinale et une pour chacune des ondes quasi-transversales.)



MEMOIRE DE MASTER II RECHERCHE 24 2008-2009

Fig. 2.14 : allure schématique du lieu de l'extrémité du vecteur vitesse de propagation [9]

MEMOIRE DE MASTER II RECHERCHE 25 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.8. Phénomènes de réflexion / transmission (régime d'ondes planes et milieux isotropes)



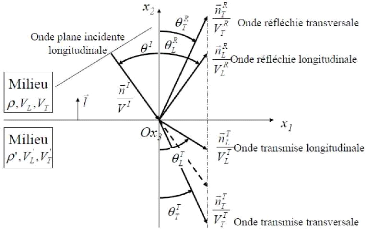
Fig. 2.15 : illustration du phénomène de réflexion/transmission [10]


· Conditions aux limites

fliⁱi (X2 = 0) + ? ~i ½ ~~F ~ 0 ~ ? ~i ^w ~~F ~ 0 ; c ~ 1,2,3

½ w

(2.81)

Ti (x2 = ⁰) + ? i ½ ~~F ~ 0 ~ ? i ^w ~~F ~ 0 ; c ~ 1,2,3

½ w

¼ J¼ ~~ ~ AB....B

~i ¼ ~ i « ~ (2.82)

Conséquences des conditions aux limites

En i= = 0A^B

,

Ui ¼ f^I(t) + ? R Ur fR = ? T ut f^T(0; t = 1,2,3 ; V t (2.83)

f^l(t) = f(t) = f^R(t) (2.84)

Toutes les ondes sont de même forme temporelle. Pour les ondes harmoniques, cela signifie que toutes les ondes en presence ont la même fréquence.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En r= i.>p,

w J '~ ~ ABÄ....ÂAB

i ¼ J '~ ~ AB....ÂAB

« « ~ ? i ½ J '~ ~ AB....ÂAB

« « ~ ? i 1,2,3 ; À ~ (2.85)

½ w «Ä « ; c ~

nA^Br.r_~A^B

nA^BÁ.d_~A^B

~

V^I

V^R

~ nAB.r~AB

(2.86)

V^T

~A^B

« ~ AB _vi) . r_p^-

= 0

; (2.87)

~A^BÄ

«Ä ~ AB

«~ . d^B, = 0

· Interprétation géométrique

_triR _fit

\

vR vI) . r_p = 0 (2.88)



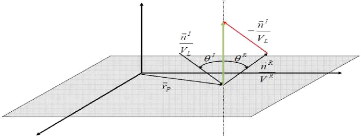
Fig 2.16 : interprétation géométrique 1

Fe est contenu dans le plan défini par la normale et 71.^1/4

₍._FiT .₇₁1₎ it 0

_vT _VI p = (2.89)



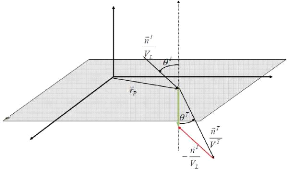
MEMOIRE DE MASTER II RECHERCHE 26 2008-2009

Fig 2.17 : interprétation géométrique 2

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

--)T --)I

n est contenu dans le plan défini par la normale et n

· Loi de Snell - Descartes : interprétation géométrique

~A^B

« ~ AB ÅéÆ Ç

« ~ ÅéÆ Ç

«~ . d^B, ~ 0 «

; ; (2.90)

~A^BÄ

«Ä ~ AB ÅéÆ ÇÄ

v¹

«Ä ~ ÅéÆ Ç

«~ . d^B, ~ 0



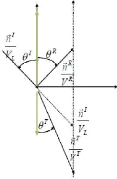
MEMOIRE DE MASTER II RECHERCHE 27 2008-2009

Fig 2.18 : présentation des vecteurs lenteurs sur la surface

'x fi_x ^x

Tous les vecteurs lenteurs = ont la même projection sur la surface.

v

· Angles critiques et courbes des lenteurs



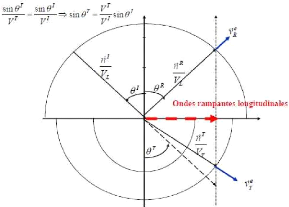
Fig 2.19 : allure schématique des angles critiques et courbes des lenteurs [11 ]



DEUXIEME PARTIE : APPLICATION A LA
CARACTERISATION DES PARAMETRES ULTRASONORES
DE DETECION DES GONDOLEMENTS DES FIBRES DANS
UN MATERIAU COMPOSITE

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

MEMOIRE DE MASTER II RECHERCHE 29 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

CHAPITRE 3 : PRESENTATION GENERALE DE LA METHODE ET DU
DISPOSITIF EXPERIMENTAL

3.1. INTRODUCTION

Le contrôle par ultrason est un procédé de contrôle non destructif semblable aux techniques RADAR ou SONAR. Il consiste à engendrer une impulsion ultrasonore dans le matériau et à observer les échos éventuels réfléchis par les discontinuités rencontrées. Les premières méthodes de contrôle étaient fondées sur la transmission d'ondes ultrasonores continues à travers des pièces contrôlées de formes simples (tôle, etc). la présence d'un défaut (manque des matières, discontinuité acoustique, etc) provoquait une dimunition ou une disparition de l'énergie ultrasonore transmise, mais il n'était pas possible de localiser en profondeur l'anomalie. L'évolution du matériel, avec en particulier l'utilisation d'impulsion brèves, a permis de faire évoluer le contrôle par ultrasons vers la technique par réflexion (écho d'anomalie) qui permet de localiser les défauts en profondeur. La méthode de contrôle par écho d'anomalie est la plus appropriée. Il s'agit de rechercher les signaux d'échos réfléchis par les anomalies ou défauts rencontrés lors de l'exploration de la pièce contrôlée.

3.2. LE CONTRÔLE PAR REFLEXION SUR ECHO D'ANOMALIE

3.2.1. Définition de la méthode

L'opérateur déplace le traducteur sur la surface de la pièce à contrôler, selon un mode opératoire appelé plan de sondage, qui permet d'assurer l'exploration de tout ou partie de la pièce à contrôler.

Pendant cette exploration, on peut distinguer deux phases essentielles : détection et caractérisation

3.2.1.1. La détection

Lors de l'explôration, l'opérateur doit surveiller l'apparition d'échos dont la position et l'amplitude sont révélatrice d'une anomalie.


· La position

La position de l'écho permet de localiser le réflecteur. A cette fin, il est nécessaire de faire précéder le contrôle d'un étallonage de la base des temps. Il s'agit de régler l'échelle horizontale pour garantir la parfaite correspondance entre la position de l'écho sur l'écran et la position du réflecteur dans la pièce contrôlée.

MEMOIRE DE MASTER II RECHERCHE 30 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».


· L'amplitude

L'amplitude de l'écho des anomalies permet d'estimer leur importance. Il n'a jamais été possible d'utiliser la mesure directe (en volt par exemple) en raison de la diversité des appareils utilisés. Il est, à cet égard fort difficile d'effectuer leur étallonage absolu. C'est pourquoi toutes les méthodes de contrôle par ultrasons sont actuellement fondées sur des mésures relatives à l'amplitude d'échos. On compare toujours l'amplitude d'un écho d'anomalie d'un réflecteur parfaitement défini.

Cette comparaison est définie comme la réflectivité de l'anomalie. Les différentes méthodes de mesures de la réflectivité utilisées sont les suivantes :

- écho de fond ;

- écho d'entaille ;

- courbe de correction amplitude distance (C.A.D.) ; - diagramme de reflectivité.

D'une façon générale, pendant le contrôle, il faut être attentif à l'apparition d'échos dont l'amplitude atteint le seuil dit de prise en compte. En effet, l'anomalie qui est l'origine de l'échos peut se revéler préjudiciable à la tenue mécanique de la pièce contrôlée (risque de rupture). Le seuil, qui dépend de la méthode de mésure choisie, est génélament définie dans les documents de contrôle.

3.2.1.2. La caractérisation

Lorsque le seuil de prise en compte est atteint, il est alors nécessaire de caractériser l'anomalie afin de permettre en aval de juger de l'acceptation ou du rebut. Les carctéristiques de base sont :

- Localisation,

- Mésure de l'amplitude de l'écho d'anomalie selon une méthode définie ci-dessus (appelée estimation de la réflectivité de l'anomalie).

3.2.2. Méthode de mésure de l'amplitude des échos d'anomalie (réflectivité)

3.2.2.1. Méthode d'écho de fond

Lorsqu'on contrôle une pièce qui possède deux faces parallèles (ou assimilable à deux faces parallèles), l'écho réfléchi par la face opposée est appélé écho de fond. Plusieurs échos de fond

MEMOIRE DE MASTER II RECHERCHE 31 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

peuvent être visualisés compte-tenu d'aller et retour successif de l'impulsion ultrasonore dans l'épaisseur de la pièce (voir fig. 3.1 annexe 4).

L'amplitude de l'écho d'anomalie est caractérisée par une grandeur K égale au rapport entre la hauteur de l'écho d'anomalie et la hauteur de l'écho de fond relevée dans une région saine de la pièce (au voisinage immédiat d'une anomalie).

3.2.2.2. Méthode de la courbe expérimentale C.A.D.

Pour remédier aux inconvénients de la méthode de l'échos de fond, il est d'usage d'établir une Correction Amplitude Distance (C.A.D.). Cette correction se traduit généralement par une courbe tracée sur l'écran de l'appareil de contrôle et reliant les amplitudes d'échos (relévé) de réflecteur de même type situé à des distances différentes (fig. 3.2 annexe 4).

L'allure et la pente de la courbe varient en fonction du traducteur utilisé et des déflecteurs choisis (dimensions, forme ). En pratique, l'amplitude de l'écho d'anomalie est définie par le rapport (exprimé en pourcentage) entre la hauteur de l'échos sur l'écran et la hauteur de la courbe C.A.D. pour la même profondeur.

Hauteur écho d'anomalie

A = 100

3.3. MISE EN OEUVRE DU CONTRÔLE ULTRASONORE

3.3.1. contrôle par contact - contrôle par immersion

Les ultrasons aux fréquences utiliséses ( 1 à 10 MHZ ),ne se propagent pas dans l'air.Pour assurer le passage des ultrasons entre le traducteur et la piece à contrôler, il faut placer entre les deux un milieu dit de couplage .Deux techniques existent pour assurer ce couplage : le contrôle par contact et le controle par immersion.

3.3.1.1. Contrôle par contact

Le traducteur est directement placé sur la piece à controler. La liaison acoustique est assurée par un film d'agent de couplage qui est généralement soit une graisse ou une huile,soit de la colle cellulosique,soit des gels spéciaux ( fig 3.3 annexe 4). L'épaisseur du film de couplage est de l'ordre du dixieme de millimetre.

MEMOIRE DE MASTER II RECHERCHE 2008-2009

32

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

3.4.1.2. Contrôle par immersion

La technique expérimentale, utilisée pour la mesure des vitesses de propagation des ondes ultrasonores de volume en incidence oblique, est une technique impulsionnelle en immersion. La première mise en oeuvre de cette méthode réalisée par Markham en 1970 a été, depuis, largement utilisée et améliorée par différentes équipes [10], [11], [12].

L'éprouvette, sous forme de lame à faces parallèles de surfaces régulières et d'épaisseur e est placée dans un liquide de couplage (dans notre cas de l'eau) entre un émetteur Å et un récepteur R dont les faces sont planes et parallèles. Cette configuration permet de faire varier l'angle d'incidence i de l'onde plane générée par l'émetteur E par rapport à la normale à la face de l'échantillon. Dans le cas le plus général, trois ondes de volume peuvent être générées au sein du matériau par conversion de mode à l'interface eau/matériau : une onde quasi longitudinale et deux ondes quasi transversales [5]. La figure 2.11 présente les différents parcours ultrasonores considérés par la suite.



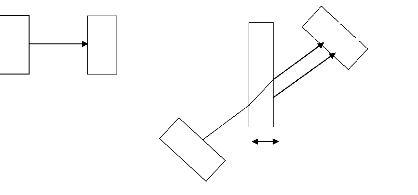
R'

R

D

Signaux de mesure

C

i_r

E

R

Signal de référence

B

i_m

e

Fig. 3.1.Principe de la mesure de vitesses en incidence oblique

E

La mesure de vitesse commence par l'acquisition d'un signal dit de référence qui correspond au trajet (ER) d'une impulsion entre l'émetteur E et le récepteur R dans l'eau. Une fois l'éprouvette placée entre l'émetteur E et le récepteur R, le signal dit de mesure, correspondant au trajet (EBDR') d'une impulsion ultrasonore, est à son tour enregistré. La vitesse de propagation, correspondant au trajet (BD) dans l'éprouvette, est alors déduite de l'écart ô₁ = t m - t_r des temps de

propagation des signaux de mesure et de référence :

EB DR

+ ' BD ER BD BC

ô₁ = - =

t t

+ - = - (3.1)

m ^r V V V V V

eau eau eau

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

V et _Veau sont respectivement la vitesse recherchée au sein du matériau et la vitesse dans l'eau. A partir de considérations géométriques simples l'expression de ô devient :

e e r

cos( 1)

-

ô = - (3.2)

¹ r r

cos V _eau cos r

L'angle de réfraction r est déduit de la loi de Snell-Descartes à l'interface eau/échantillon :

(3.3)

V

r= arcsin - i

sin

V eau

La substitution de l'expression (3.3) dans l'équation (3.2) conduit après simplification à la vitesse de propagation V de l'onde ultrasonore dans le matériau :

eV eau



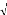
e 1 + 2 ô 1 cos

V e V i

eau eau

² + ô ²

V = (3.4)

Ainsi, la mesure de vitesse de propagation V d'une onde ultrasonore en incidence variable dans un matériau donné, fait intervenir la vitesse de propagation dans l'eau _(Veau). L'épaisseur e de l'éprouvette, l'angle d'incidence i du faisceau ultrasonore et la différence de temps de vol ô₁

obtenue, dans notre cas, par inter corrélation des signaux de mesure et de référence.

A partir de différents temps de vol et de la vitesse des ultrasons dans l'eau _Veau, il est possible de déterminer simultanément e et la vitesse longitudinale en incidence normale Vl [12]

Ce chapitre a permis de faire un tour d'horizon rapide des principes généraux de la méthode expérimentale, et de fournir les éléments éventuels concernant le contrôle de nos éprouvettes. La méthode retenue ici est la méthode de mesure de l'amplitude des échos d'anomalies(échos de fond) à l'aide d'une technique de contrôle ultrasonore dite contrôle par contact. Pour cela nous devrions, pour exécuter un contrôle de nos éprouvettes, se référer à une procédure particulière précise. Nous devons fixer dans le détail les méthodes choisies, les plans de sondage, les critères de prises en compte et la façon de caractériser les anomalies.

Le prochain chapitre nous permettra de présenter dans les détails la phase pratique de nos

essais

2008-2009

33

MEMOIRE DE MASTER II RECHERCHE

MEMOIRE DE MASTER II RECHERCHE 34 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

CHAPITRE 4 : REALISATION DES ESSAIS PRATIQUES
ULTRASONORES SUR UN MATERIAU COMPOSITE(ESSAI DE
DETECTION DES GONDOLEMENTS )

4.1. INTRODUCTION

Cette partie présente les informations pratiques éssentielles sur la façon dont les éssais ont été menés.Ces éssais se comportent en deux phases :

- exploration du volume de l'éprouvette controlée en vue de la détection des anomalies(gondolages) ;

- caracterisation des éventuelles anomalies décélées ( détermination des parmètres de détection ).

L'exploration est manuelle.Les principes de bases sont contenus dans les différentes opérations qu'il implique.Pour assurer la bonne transmission des ondes ultrasonores entre le traducteur et la pièce, de meme qu'un bon couplage acoustique ,un produit liquide de couplage a été nécessaire (ici la graisse ).

4.2. PRESENTATION DES EPROUVETTES ET DISPOSITIF D'ESSAI

4.2.1. Des éprouvettes

Nos éprouvettes sont des matériaux composites unidirectionnels fibre /platre, de dimensions 130 x 100 x 25 (mm ) (figure.4.1). Les fibres utilisées sont des fibres naturelles du "Rhectophyllum camerunense" de la region du Sud Cameroun. Ces fibres ont une couleur marron et d'une section circulaire avec un diamètre variant entre 0.20 et 0.70 mm. Le platre utilisé est un produit du gypse importé disponible dans le commerce.



Fig.4.0. Présentation des échantillons

MEMOIRE DE MASTER II RECHERCHE 35 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

4.2.2. Fabrication et mise en oeuvre des composites

Pour fabriquer notre composite, nous dévons préparer des moules. Il est nécessaire
d'enduire les surfaces d'un agent de démoulage.Nous emploierons ici une solution aqueuse de svon
de Marseille . Le savon est gras , celui-ci empechera l'adhérence du platre et il neutralisera aussi la
porosité des surfaces absorbante. Le savon de Marseille sera posé dans un récipient contenant de un
peu d'eau chaude car la detrempe du savon est assez rapide etproduit un gel blanchatre visqueux.
Prendre la solution visqueuse à l'aide d'un pinceau et enduire les surfaces devant recevoir le platre.

Le platre qui doit occuper environ un volume proche de 1.3 litres dans le coffrage, sera préparé dans les proportions de 1.5 Kg de platre pour 1 litre d'eau. La densité absolue du platre de Paris est d'environ 2.63. Gaché dans les proportions indiquées précédemment, onobtien donc un volume de 2075 litres de platre liquide ayant un poids de 4.38 Kg (1.75 Kg d'eau + 2.63 Kg de platre). Après battage avec un fouet de cuisine ,jusqu'à l'obtention d'un mélange homogène.On verse doucement le contenu dans les moules rectangulaires de 130x100x25 (mm) ou sont installées les fibres , puis on remue lentement par alternance avec la spatule pour faire remonter les bulles d'air en surface.

Nous avons fabriqué deux lots de type d'échantillons :

· Un lot de composite à base des fibres du R.C sans défauts artificiels.

· Un lot de composite à base de fibres avc défauts artificiels (Gondolements).

Le démoulage se fait 24 heures après la fabrication .Toutes les plaques sont conditionnés à l'air ambiant du laboratoire jusqu'à 10 jours.

4.2.3. Dispositif ^d'essaiL'appareillage comporte un ensemble électronique appelé « appareil ultrasonore » et un traducteur qui lui est relié electriquement( fig 3.5 annexe 4).

L'appareil ultrasonore comprend principalement :

· un émetteur : il fournit au traducteur l'énergie électrique nécessaire pour le mettre en vibration pendant un temps tres bref ;

· un récepteur :il recueille et met en forme le signal ;

· un écran de visualisation : il permet d'identifier les échos ultrasonores par leur amplitudes (verticale ) en fonction de leur instant d'apparition (horizontale )

MEMOIRE DE MASTER II RECHERCHE 36 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Le role du traducteur est d'émettre une impulsion ultrasonore dans le matériau et de recueillir les échos.

4.3.PREPARATION DU CONTROLE MANUEL

L'exécution du controle a été nécessairement réalisée en 4 étapes de préparation :

· vérification du bon fonctionnement de l'appareil ;

· règlage de la base de temps ;

· règlage de la sensibilité ;

· plan de sondage.

Au terme de cette 4eme étape, nous avons préparé également les documents nécessaires au dépouillement et à la rédaction du compte rendu.

4.3.1. Vérification de l'appareillage

Les opérations ici consistent à s'assurer visuellement du bon état des cables et des traducteurs (aucune dégradation ne doit apparaître ).nous avons vérifié les linéarités horizontales et verticales de l'écran ainsi que la justesse du réglage de gain ( atténuateur calibre ).

4.3.2. Etalonnage de la base de temps

L'étalonnage de la base de temps de l'apparail de contrôle par ultrasons a pour but d'établir une correspondance entre la position d'un écho,mesurée en nombre de carreaux,et le parcours ultrasonore. Nous avons donc fais deux réglages successifs pour étalonner la base de temps de cet appareil en prenant en compte les caractéristiques propres :

- aux matériaux ( vitesse de propagation ) et à l'échelle choisie ; - au traducteur et au couplage.

Le premier réglage ( échelle) nous a permi d'étalonner plus ou moins l'échelle horizontale pour aboutir à une échelle représentative en millimètre par carreau.

Le second réglage ( décalage ) nous a permi de compenser le temps de parcours préliminaire dans le transducteur afin que la position horizontale zéro corresponde à un parcours ultrasonore nul ( point d'entrée de l'onde dans le matériau ou point d'émergence en contrôle par contact ).

MEMOIRE DE MASTER II RECHERCHE 37 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

4.3.3. Réglage d'amplification

Il s'agit d'une étape essentielle dans la préparation des éssais.En effet ,une amplification insuffisante ne permet pas de détecter d'éventuels défauts.

A l'inverse, une amplification trop importante risque de noyer les informations dans un bruit (écho intempestif lié à la structure métallurgique de la pièce).

Pour s'assurer de la validité des mésures d'amplitude d'écho quelques vérifications rapides ont été réalisées.

En particulier il s'agit de :

· s'assurer de l'absence de seuil résiduel ;

· vérifier globalement le fonctionnement de l'atténuation calibrée ;

· vérifier rapidement la linéarité verticale.

4.4. EXECUTION DES ESSAIS

4.4.1. Le plan de sondage

Le plan de sondage est un mode opératoire qui définit les positions successives du traducteur
permettant d'explorer au mieux tout le volume de la zone à controler.Pour cela nous avons délimité
la surface de contrôle et préparé un référentiel de repérage des positions du traducteur.



4.1.chaine de mesure

MEMOIRE DE MASTER II RECHERCHE 38 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Le plan de sondage étant établi, il s'agit de passer aux éssais, c'est-à-dire de déplacer le traducteur sur la surface de l'éprouvette à controler.Il importe que l'opérateur s'éfforce de maintenir le couplage de façon constante.

En outre, il faut surveiller en permanence l'écran de l'appareil afin d'être informé de l'apparition d'échos d'anomalies. Nous faisons un recouvrement à 20 /100 du diamètre du transducteur,la distance entre 2 lignes successives de balayage est égale à 0,8 fois le diamètre du transducteur.

4.5. PRESENTATION DES RESULTATS DE L'ESSAI ET COMMENTAIRES

Les travaux se sont déroulés dans le laboratoire de contrôle par ultrasons de HYDRAC sis

au siège de Bassa à Douala.

Le contrôle par ultrasons étant en fait un contrôle de comparaison, pour détecter les éventuels défauts dans une pièce.

Le déroulement du contrôle est le suivant :

· Etalonnage de l'appareil en utilisant un bloc étalon en acier au carbone ;

· Etalonnage de l'appareil en utilisant un échantillon de composite sain (absence de défauts);

· Contrôle du matériau composite comportant des défauts artificiels et recueil des résultats. L'objectif est de rechercher et retrouver ces défauts artificiels matérialisés sous forme de gondolements (Sinuosités) ;

4.5.1. Etalonnage de l'appareil en utilisant un bloc étalon en acier au carbone Il s'agit d'une étape essentielle dans la préparation du contrôle.

Tableau.4.1 : Caractéristiques des appareillages utilisés

Item	Désignation	Nature	Marque	Type	Numéro de série	Fréquence	Dimension
1	Pièces de tests	Matériau composite Plâtre + fibre	-	-	-		130 x 100 x 25
		Acier au carbone	IIW (Institut international de soudure)	Bloc V2			Epaisseur 25mm
2	Appareil Ultrasons	Digital A-scan	SONATEST	Site scan 140	1401151C	15MHZ
3	Palpeur	Piézo- électrique	Krautkramer	BS4/Single	57746- 08169	Ø24 - 4MHZ
4	Couplant	Graisse	Eldon's	High quality	-	-	-

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».



5

Câble coaxiale

-

Krautkramer

Gros/single

-

1m

Tableau.4.2 : Résultats de l'étalonnage sur un bloc étalon normalisé (acier au carbone)

Item	Désignation	Résultats
		Vitesse de l'onde longitudinale (m/s)	Zéro du palpeur			Echelle (mm)	Gain (dB)	Amplitude du 1^er écho par rapport à l'origine 0	Amplitude du 2^ème écho par rapport à l'origine 0
1	Bloc étalon, type A	5895	2.081			50	47.0	87%	66%
				1er écho à 25 mm de l'origine 0 (ou 1^er écho de fond) 2ème écho à 50 mm de l'origine (ou 2^ème écho de fond)
					écho initial à l'origine (écho de surface)



Echo initial à l'origine ou Écho de surface

MEMOIRE DE MASTER II RECHERCHE

39

2008-2009

Figure.4.2.Représentation A-scan des échos du bloc étalon

4.5.2. Étalonnage de l'appareil en utilisant un échantillon de composite sain

Le but de l'étalonnage est d'établir une correspondance entre la position d'un écho mesurée et le parcours ultrasonore

Tableau.4.3 : Résultats de l'étalonnage sur un échantillon de composite sain

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeu r	Echelle (mm)	Gain (dB)	Amplitude du 1er écho par rapport à l'origine	Amplitude du 2^ème écho par rapport à l'origine
2	Matériau composite	5895	2.081	50	47.0	0%	0%

MEMOIRE DE MASTER II RECHERCHE 40 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Figure.4.3. Représentation A-scan de l'écho de l'échantillon I

Commentaires :

On remarque l'absence d'écho de fond lorsqu'on passe de l'acier au composite. Ceci est dû à la forte atténuation du matériau composite (plâtre), les vitesses de propagation des ondes n'étant pas les mêmes dans ces matériaux. Il faudra donc trouver la vitesse des ondes dans le composite.

Tableau.4.4 : Résultats de l'étalonnage sur un échantilon de composite sain

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeur	Echelle (mm)	Gain (dB)	Amplitude du 1^er écho de fond par rapport à l'origine	Amplitude du 2ème écho de fond par rapport à l'origine
1	Acier au carbone	6631	3.004	0 - 50	85.5	Plus de 100%	Plus de 100%
2	Matériau composite	6631	3.004	0 - 50	85.5	76%	Le % n'est pas appréciable



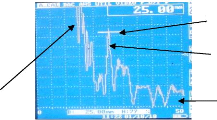
Amplitude du 2^ème écho de fond confondu avec le bruit de fond

Echo initial à l'origine ou écho de surface

Gate ou porte indiquant la position exacte de l'écho

1er écho à 25 mm de l'origine ou 1er écho de fond

Figure.4.4. Représentation A-scan des échos sur échantillon II

Commentaire :

L'étalonnage a été fait sur le matériau composite en utilisant une vitesse de propagation obtenue par approximation, ceci a permis d'obtenir au moins un premier écho de fond dont l'amplitude est à 76% de la hauteur de l'écran.

Le second n'est pas clairement visible car confondu avec le bruit de fond. Ceci peut s'expliquer par la composition du matériau qui comporte une structure à gros grain. Cette structure non seulement attenue les ondes mais aussi les disperse. On remarque également que si on applique

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

la même vitesse à l'acier au carbone, on obtient des échos dont l'amplitude dépasse largement la hauteur de l'écran.

Tableau.4.5 : Résultats de l'étalonnage sur un échantillon de composite sain

Désignation	Nature	Marque	Type	Numéro de série	Fréquence
Palpeur	Piézo- électrique	Krautkramer	Single	73433	Ø12-2MHZ

On reprend les mêmes paramètres, mais on change de palpeur et la vitesse est légèrement modifiée.

Tableau.4.6 : Résultat de l'étalonnage

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeur	Echelle (mm)	Gain (dB)	Amplitude du 1er écho par rapport à l'origine 0	Amplitude du 2^ème écho par rapport à l'origine 0
1	Acier au carbone	6217	1.583	0 - 50	62.6	Plus de 100%	Plus de 100%
2	Matériau composite (plâtre + fibre)	6217	1.583	0 - 50	62.6	72%	12%



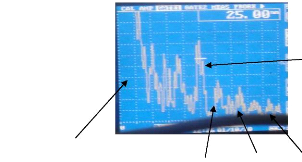
Echo initial à l'origine 0

1er écho de fond à 25 mm de
l'origine 0

MEMOIRE DE MASTER II RECHERCHE 41 2008-2009

Echos de fond dû à la nature du matériau

Figure 4.5 : Représentation A-scan des échos III

Commentaires :

On constate qu'en utilisant un palpeur de fréquence faible, on obtient au moins le 2^ème écho de fond. C'est avec ces paramètres que les contrôles des échantillons comportant des défauts

Commentaires :

MEMOIRE DE MASTER II RECHERCHE 42 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

artificiels ont été conduits. Cette expérience a été répétée avec d'autres palpeurs de faible fréquence et le résultat a été le même.

4.5.3. Contrôle du matériau composite comportant des défauts artificiels (gondolements)

La caractérisation d'une anomalie implique la détermination des différents paramètres parmi lesquels la réflectivité (amplitude de l'écho) est primordiale.

Tableau.4.7 : Résultats du Contrôle de notre matériau composite avec défauts

Désignatio n

Nature

Marque

Type

Numéro de série

Fréquence

Palpeur

Piézo- électrique

Krautkrame r

Single

73433

Ø12-2MHZ

Item

Désignation

Résultats

Vitesse de l'onde (m/s)

Zéro du palpeur

Echell e (mm)

Gain (dB)

Amplitude du 1er écho par rapport à l'origine 0

Amplitude du 2^ème écho par rapport à l'origine 0

1

Matériau composite (plâtre + fibre)

6217

1.583

0 - 50

62.6

37%

20%



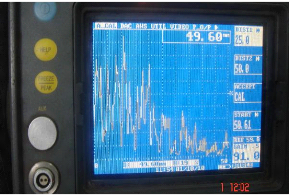
Fig.4.6. Représentation A. scan des échos IV

MEMOIRE DE MASTER II RECHERCHE 43 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Les échos obtenus nous ont permit de constater la nature hétérogène de notre matériau composite. Nous observons que le second écho de fond a pu être obtenu.

CONCLUSION

Devant l'utilisation croissante des matériaux composites, la connaissance précise des propriétés mécanique des constituants, ainsi que la mesure précise des propriétés effectives des matériaux composites, ont été pour nous, des conditions nécessaires à la résolution d'un grand nombre de problèmes reliant son comportement global à la microstructure.

Les approches, tant expérimentales que théoriques, que nous avons développées dans cette étude, rentrent dans le cadre général précité. Au cours de cette étude, nous avons d'une part procéder à l'étalonnage de l'appareil ultrasonore à l'aide d'un bloc étalon normalisé en acier au carbone, d'autre part nous sommes passé à l'étalonnage d'un échantillon sain à base des fibres /plâtre afin d'obtenir des signaux (échos) de références. La caractérisation des paramètres optimums d'étalonnage par la méthode de contrôle par contact nous a permis d'obtenir les résultats ci-après :

- Vitesse de l'onde longitudinale : 6217 m/s

- Gain : 62,6 dB ;

- Fréquence : 15 MHz

- Palpeur piézo-électrique KrautKramer de fréquence 2MHz et Ø 12mm.

Il ressort que les échos obtenus confirment le caractère hétérogène de notre matériau composite. Il serait intéressant d'utiliser lors des essais futurs des palpeurs focalisant pour la détection des gondolements dans un matériau composite à base de plâtre et renforcé de fibres de "Rhectophyllum Camerunense". Les résultats obtenus sont intéressants et constituent une étape majeure pour la suite des travaux. Les résultats pourront être incorporés dans les codes de calcul des structures sous forme d'un facteur de gondolement ou facteur de sinuosité.

MEMOIRE DE MASTER II RECHERCHE 44 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

BIBLIOGRAPHIE

[1]: BEAKOU A. ; ATANGANA J.A. ; NTENGA R. ; AYINA L.O. ; LEPETIT J., Physicochemical and micro structural characterization of "Rhectophyllum Camerunense" plant fiber. Composites. Part A, Applied science and manufacturing. 2008, vol.39, no 1, pp. 67-74.

[2]: GAY, D., Matériaux composites, 3ème édition. Paris : Hermès, 1991.569p. [3] : REYNE, M., Technologie des composites. 2ème édition. Paris : Hermès, 1995.190p.

[4]: ASKELAND, D., The science and Engineering of Materials, 3rd Ed., PWS Publishing Company, Boston, MA.1994.

[5] : ROYER, D. et DIEULESAINT, E. Ondes élastiques dans les solides. Tome1: propagation libre et guidée. Paris: Masson.1996.328p.

[6]: AULD, B.A. Acoustic fields and waves in solids. Vol.1.New-York: Wiley Interscience.1973.420p.

[7]: HUDSON, J.A., The excitation and propagation of elastic waves, Cambridge University Press, Cambridge, U.K., 1980.

[8]: KRAUTKRAMER, J. and KRAUTKRAMER, H., Ultrasonic Testing of Materials,3^rd Edition, Springer-Verlag ,Berlin,1983

[9]: HOSTEN, B. Anisotropic materials characterization by simple or double transmission ultrasonic method. Ultrasonic International 89. Madrid (Spain), Juillet 1989, p.31-36.

[10] : ROUX, J., HOSTEN, B., CASTAGNEDE, B.et DESCHAMPS, M. Caractérisation mécanique des solides par spectro-interférométrie ultrasonore. Revue Phys. Appl., 1985, No 6, p.351-358.

[11]: HOSTEN, B. Reflection and transmission of acoustic plane waves on an immersed orthotropic and viscoelastic solid layer. J. Acoustic. Soc. Am., 1991,Vol.89. No 6 , p. 2745-2752.

[12] : DUBUGET, M. Evaluation non destructive des matériaux par ultrasons : caractérisation de l'état initial et suivi sous charge des propriétés d'élasticité linéaire et non linéaire d'alliages d'aluminium. Thèse de doctorat : Institut National des Sciences Appliquées de Lyon, 1996.196p.

[13]: HSU, D.K. and HUGHES, M.S. Simultaneous ultrasonic velocity and sample thickness measurement and application in composites. J. Acoust. Soc. Am., 1992, Vol.92, No 2, p. 669-675.

[14] : LANDAU, L. et LIFCHITZ, E.M. Physique théorique. Tome 7 : Théorie de l'élasticité. Moscou : Mir, 1967. 207 p.

MEMOIRE DE MASTER II RECHERCHE 45 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

[15] : THEVENIN, P. Synthèse sur la durabilité des structures composites en fibres de verre / résine époxyde. Collection de notes internes de la direction des études et recherches. Clamart : EDF, 1997. 114p.

[16] : François, D., et ZAOUI, A. Comportement mécanique des matériaux. Volume 2. Paris : Hermès, 1993. 496 p.

[17] : BERTHAUD, Y. Mesure de l'endommagement du béton par une méthode ultrasonore. Thèse de doctorat : Université Paris VI, 1988. 89 p.

[18]: SEZAWA, K., Dispersion of elastic waves propagating on the surface of stratified bodies and on curved surfaces. Bulletin Earthquake Research Institute, Vol. 3, 1927, pp. 1-18.

[19]: BRADAEL, I., Characterization of Ultrasonic Transducers, Chapter 5. Research Techniques in Nondestructive Testing. Vol. III, R. S. Sharpe Ed., Academic Press, London, 1997.

[20]: SATTER, F. J. and PARK, D.Y., Beam Equations for Ultrasonic Examination of cylindrical and spherical shape. American society for Nondestructive Testing. Spring Conference, Orlando, FL, April 11-15, 1986.

[21]: NJEUGNA Ebenezer, Dynamique des fluides. Notes de cours, ENSET-DOUALA, 2006.

[22] : PERDIJON, J., Le contrôle non destructif par ultrasons. Traité des Nouvelles Technologies, série Mécanique, Hermès (1993).

[24] : ZAREMBOWITH, A., "Les ultrasons", Que sais-je ? No 21, Presses Universitaires de France, (2003)

[25]:P.D.EDMONS, Ultrasonic's Methods of Experimental Physics.Vol 19, Academic Press, (1981)

[26]: RUDENKO, O.V.and HEDBERG, Nonlinear response of a layer to pulse interaction in diagnostic of small inhomogenities. Report of the RUSSIAN Academy of Sciences.Vol.374, No2, pp 194-197 (2000).

[27]: GRAM, HE. Durability of material fibres in concrete.In: SWAMY, RN. (Ed.). Natural fibre reinforced cement and concrete.Glasgow: Blackie, 1988.

[28]: GUIMARAES, SS. Vegetable fiber-cement composites In: International Symposium on vegetable plants and their fibres as building materials; 1990; Salvador.London; CHAPMAN and HALL, 1990.P.98-107.

[29] : AVESTON and Al. Composites Interfaces. J.Materials Sciences ,29(1994).110.



ANNEXES

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

MEMOIRE DE MASTER II RECHERCHE 47 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

[Annexe 1]

II-1 DESCRIPTION DES FIBRES DU Rhectophyllum Camerunense (RC)

Le Rhectophyllum Camerunense est une plante des forêts équatoriales et tropicales, de la famille des aracées, qu'on retrouve dans la zone forestière du Cameroun, du Nigeria et du Gabon ainsi que dans les forêts de galerie des régions tropicales. Etudié pour la première fois par NTEPENYAME en 1981, le RC est une plante qui se fixe sur le tronc de l'arbre au dessus du sol, fait pousser ses longues racines jusque dans le sol d'où elle puise ses nutriments. Ayant une tige courte, elle est une plante grimpante qui peut qui peut s'élever jusqu'à plus de 30 mètres au dessus du sol et, est appelée localement "nkapgué" chez les bassa et "ayang yop" chez les béti (voir fig.2.1)



Fig. 2.1 : plante grimpante du RC accrochée sur le tronc d'un arbre
Le RC a de longues racines aériennes (pouvant atteindre 35 mètres) qui sont de deux types :

- Plates (1.5 à 4 cm de largeur), pubescentes et non verruqueuses ; - Crampon horizontales, plates et pubescentes.

MEMOIRE DE MASTER II RECHERCHE 48 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».



Fig. 2.2 : racines du RC recouvertes de la peiicule protectrice.

La fibre végétale du RC est extraite des racines aériennes de cette plante qui sont souvent recouvertes d'une pellicule protectrice rugueuse. Ces fibres dont l'utilité est indéniable sont déjà utilisées traditionnellement dans la confection des filets de pêche et des cordes.

II-2 - PROCEDES D'EXTRACTION DES FIBRES DU RC

Les fibres sont issues des longues racines aériennes ; leurs méthodes d'extraction sont encore traditionnelles. En général, la racine encore humide est débarrassée de sa coque protectrice par un battage manuel léger, ensuite plongée dans de l'eau pendant deux à trois jours (rouissage), afin de la débarrasser du tissus d'extractifs (pectine,...), puis rincée à l'eau pour obtenir des fibres qu'on peut faire sécher avant l'usage.

D'autres méthodes peuvent être utilisées telles que la méthode chimique (utilisation des solutions alcalines et des solutions d'acide doux), la méthode biologique ou enzymatique (utilisation des pectinases, des cellulases et hémi-cellulases), la méthode chimio-enzymatique qui est l'association des méthodes chimiques et biologique.

MEMOIRE DE MASTER II RECHERCHE 49 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».



Fig. 2.3 : Fibres de RC extraites par rouissage à l'eau II-3 QUELQUES PROPRIETES DE LA FIBRE DU RC

Suite aux travaux déjà effectués par Dr NTENGA, nous disposons de quelques propriétés chimiques, physiques et mécaniques de la fibre RC

II-3-1-COMPSITION CHIMIQUE EN %

Tableau 2.1 : Composition chimique du RC [13]

Cellulose	Lignine	Pentosanes
68.2	15.6	16.0

II-3-2-PROPIRETES PHYSIQUES ET MORPHOLOGIQUES

Quelques unes des propriétés physiques et morphologiques des fibres RC sont consignées dans le tableau ci-dessous :

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Tableau 2.2 : Propriétés physiques et morphologiques du RC [13]

Porosité %

Aire app. (mm^2)

0 fibre (m)

0 canal (jim)

0 lumens (jim)

Circularité %

l/0

Masse volumique (g/cm^3)

Taux d'humidité %

28 à 36

50e-4 962e-4

à

70 350

à

25 110

à

2 à 29

60.8 94.5

à

>2000

0.947

10 à 12

Le caractère poreux des fibres du RC lui confère une masse volumique très faible comparativement à celle des autres fibres. La micrographie de la fibre permet d'avoir les formes des cellules de base ou lumens ; celles-ci ont en général des formes polygonales et (ou) arrondies.

	Lumen

MEMOIRE DE MASTER II RECHERCHE 50 2008-2009

Fig. 2.4 : Microstructure des cellules (échelle= 10m) [13]

II- 3-3 PROPRIETES MECANIQUES

Les tableaux ci-après donnent le module d'Young et la résistance à la rupture en fonction du diamètre des fibres suivant les travaux réalisés en laboratoire.

MEMOIRE DE MASTER II RECHERCHE 51 2008- 2009

COMPOSITE Á MATRICE CERAMIQUE

RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Tableau .2.3.

Module d'Young et résistance à la rupture de quelques spécimens de RC en

fonction du diamètre ø des fibres



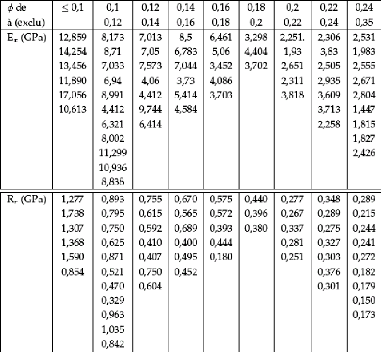
Les résultats de ces tableaux permettent de choisir :

* 1447MPa E_x 17056MPa

*150MPa R_r 1738 MPa

CONCLUSION

A la lumière de ce qui précède, nous constatons que la fibre du RC a des propriétés physiques,

; de plus

mécaniques et même morphologiques très intéressantes le RC est une plante disponible

dans nos forêts et dont l'exploitation n'est pas coûteuse. Bien que sa fibre ne soit pas encore exploitée industriellement, nous pensons que sa mise en valeur et son association dans les matériaux composites seraient les bienvenues tant pour les industriels, que pour des producteurs de cette fibre.

MEMOIRE DE MASTER II RECHERCHE 52 2008- 2009

COMPOSITE Á MATRICE CERAMIQUE

RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

[Annexe 2]

The flexural behaviour of fibrous plaster sheets

D.A. St. John, b and J.M. Kelly, b

^a Department of Scientific and Industrial Research, Lower Hutt, New Zealand

^bUniversity of California, Berkeley, California, U.S.A.

Received 3 March 1975;

Accepted 28 April 1975.

Refereed.

Available online 12 February 2003.

Abstract

Tests on fibrous plaster sheet, reinforced with sisal

and glass fibres in the bulk density range 56 to



72.5 lb/ft³

(W/P = 0.9 to 0.6), show that sisal

fibre decreases the strength of the gypsum

composite

by approximately 30 to 50% and glass fibre by approximately 0 to 30%. The effect on compressive stren

gth shown by the two fibres can be largely explained on the basis of differing volumes and stiffness. Variation of the fibre content in the plaster sheet increases the tensile strength with increasing fibre contents much as would be expected.

A theory based on a non-linear stress-

strain curve is proposed and the predictions of this theory are found to be in reasonable agreement with the test results. However, it is concluded that variations

sisal is used as the rei

in the ultimate flexural strength, where nforcing fibre, are of such

magnitude that it is impossible to predict flexural strengths with any degree of accuracy. Until the source of this variability can be found it is not possible to make any design improvements to the strength of the fibrous plast

er sheet. The outlook is more hopeful for the use of glass fibre as a reinforcing material but further work is required to confirm this.

MEMOIRE DE MASTER II RECHERCHE ₅₃ 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

[ANNEXE 3]



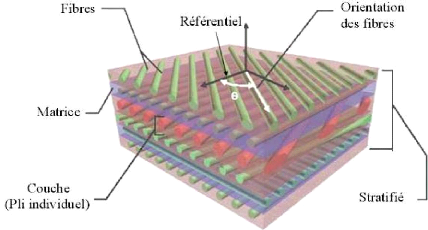
Figure.1. composite à fibres de carbone stratifié





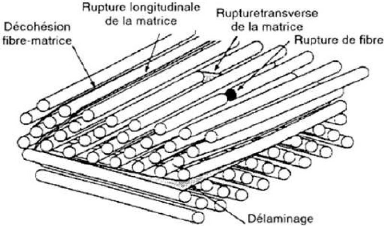
MEMOIRE DE MASTER II RECHERCHE 54 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Figure.2. Résumé des différents défauts des matériaux composites à fibres