|
REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE
MINISTERE DE
L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE
SCIENTIFIQUE
UNIVERSITE LARBI
BEN M'HIDI (OUM EL-BOUAGHI)
INSTITUT DES SCIENCES TECHNOLOGIQUES
SIMULATION NUMERIQUE D'UNE FLAMME
TURBULENTE
PREMELANGEE AXSYMETRIQUE
PAR FLUENT
Par
CHERAD IBRAHIM
OUBADI
ABDELGHANI
MEMOIRE PRESENTE AU DEPARTEMENT DE GENIE
MECANIQUE
POUR L'OBTENTION
DU DIPLOME D'INGENIEUR D'ETAT EN GENIE
MECANIQUE
OPTION : ENERGETIQUE
ENCADREUR :
MAMERI
ABDELBAKI
AIN-BEIDA, ALGERIE
JUIN 2010

Remerciements
Avant toute chose ,nous remercie
Dieu le tout
puissant de nous avoir aidé et éclairé le
chemin pour la
réalisation de ce modeste travail.
Puis, nous s'adressons notre
sincère remerciements à notre
monsieur «
DR.MAAMERI ABDELBAKI » qui nous avoir
fait
l'honneur de deriger notre travail, ainsi que
pour son
suivi, sa patience et ses conseils qui ont
grandement facilité
notre travail.
Nous tenons à remercier
aussi tout les membre de jury.
C'est avec un grand respect que
nous s'adressons
notre
remerciement s à tous nos enseignents pour leurs
conseils et
leurs remarques.
En fin ; nous ajoutons à nos
remerciements tout qui nous
ont encouragé et nous
aidé.
MERCI

SESICACE
A ma mère et mon
père, qui grâce à eux,
j'ai pu franchir
avec intrépidité toutes les
en traves
et un grand merci pour avoir apporté
le soleil dans
ma vie.
A mes soeurs, et toute la
famille.
A tous mes amis
specialement
:Abdellah,Fares,Aissa,Fattouh,Jimi,
Mouh,Fawzi,massi,
khaled,walid et toute la classe
de
géni__mécanique
N'oublier pas non plus Amina et Imane
Et
tous qui est proches
je dédie ce modeste travail.
4WciklAg

Dédicace
» C'est une grave erreur de croire que la joie de
l'observation et
de la recherche peut croître sous l'effet de la
contrainte ou du sens
du devoir. Au contraire, je pretends que l'on arriverait
même à
enlever sa voracité à une bête de proie,
si on la forçait à avaler
sans cesse, même quand ele n'a pas
faim, et si de plus on
choisissait la quantite d'aliments administres sous cette
torture de
façon inversement proportionnele
à son besoin ... » A Einstein
A ce petit monde formé du Groupe
des
Amis de longue date, l'amis de
l'horizon autres et bien entendu de
ma
mère Sirr el hoda, qui m'ont permis
de
garder le bon cap dans des eaux
parfois
peu clémentes.



Spécialement pour :
Mes frères Salah,Hakko et mes
soeurs
Samira et Naima

Mes proches amis
Fattouh, Abelghani et Abdelah

Brahim Cherad
SOMMAIRE
Introduction générale 1
CHAPITRE I :
Aérothermochimie et stoechiométrie
1) introduction 6
2) Choix des variables primitives 6
3) Notions sur la thermochimie 7
4) La stoechiométrie dans les flammes
prémélangées 9
5)Equation de conservation des espèces 10
6) Mécanismes réactionnels et taux de
réaction 14
7) Formulation générale pour le calcul du taux de
réaction 15
8) Approximation de la combustion par une seule réaction
globale 17
9)Approximation par un mécanisme réactionnel
formé par des réactions élémentaires 17
10) conclusion 19
CHAPITRE II : Notions sur la turbulence
1) Introduction 20
2) Où observe t on la turbulence 20
3) Les deux points de vue sur la turbulence 21
4) L'expérience de Reynolds (1883) 21
5) Caractéristiques d'un écoulement turbulent
22
6) La transition du laminaire au turbulent 23
7) La cascade de KOLMOGOROV 24
8) Quelques types de simulation numériques de la
turbulence 26
8.1) La simulation numérique directe (DNS) 27
8.2) La simulation des grandes échelles (LES) ) 27
8.3) La simulation des équations de Navier Stokes
moyennées
(RANS) 27
9) Les équations moyennées 28
9.1) Quelques propriétés de la moyenne 28
9.2)Equations de bilan moyennées au sens de Favre 29
10) Equation de la continuité 31
11) Equation de conservation de la quantité de mouvement
31
12) Equation de conservation de l'énergie 31
13) Quelques modèles de la turbulence 32
13.1) hypothèse de Boussinesq 32
13.2) Modèle à zéro équation 32
13.3) Modèle à une équation de transport :
Prandtl-Kolmogorov 33
13.4) Modèles à deux équations 33
13.4.1) Modèle k-å 33
13.4.2) Le modèle k-å RNG 34
14) Correction de Pope 35
15) La fermeture du second ordre 36
16) conclusion 37
CHAPITRE III : notion et modalisation de la
combustion
1) Introduction 38
2) Echelles caractéristique d'une flamme 41
3) Combustion laminaire 43
3.1) Flamme laminaire prémélangée 43
3.2) Flamme laminaire non prémélangée 45
4) La combustion turbulente 48
4.1) La combustion turbulente prémélangée
48
4.1.1) l'effet de la turbulence sur les flammes 49
4.1.2) L'effet inverse 49
4.2) Classification des flammes 49
6) Modélisation de la combustion turbulente 55
6.1) Modèle Eddy Break Up 55
6.2) Modèle EDM dans le code FLUENT 56
7) Variable d'avancement de la réaction 57
8) Conclusion 58
CHAPITRE VI : Résultats du calcul
numérique
1) Dispositif expérimental 60
1.1) La chambre de combustion 60
1.2) Le bruleur 61
2) Modélisation de la chambre de combustion 62
2.1) Géométrie de la chambre 62
3) Etude numérique du jet d'air turbulent dans la chambre
de combustion 62
3.1) Conditions aux limites 62
3.2) Maillage de calcul 63
3.3) Calcul de l'écoulement non réactif et
ajustement de la correction de POPE 64
3.3.1) Résultats du calcul 64
3.3.2) Coeur potentiel 66
4) Calcul de l'écoulement réactif du
méthane-ai 67
4.1) Les caractéristiques du mélange
(méthane/air) à l'entrée du bruleur 67
4.2) résultats de calcul 68
pour O = 0.6 68
Pour O=0.7 71
Pour O=0.8 72
5) Structure interne de la flamme 74
6) conclusion 77
Conclusion générale 78
Bibliographie 80

NOMENCLATURE
LETTRES LATINES :
m : Masse
: Masse molaire
R : Constante des gaz parfaits
n : Nombre de mole
p : Pression
Re : Nombre de Reynolds
t Nombre de Reynolds turbulent
Production d'énergie cinétique t :
Temps
: Tenseur des contraintes
|
:
|
:
:
|
Vitesse moyenne Vitesse instantanée
Vitesse fluctuante Vecteur vitesse
|
V* : Vitesse molaire
V : Vitesse massique
Y : Fraction massique
uL : Vitesse de la flamme laminaire
K : Coefficient d'équilibre
: Fraction de mélange
D : Diffusivité massique
lt : Echelle intégral
r : La taille de tourbillon
II
: Variable d'avancement
s : coefficient stoechiométrique
|
:
|
|
|
|
|
Énergie sensible
Enthalpie sensible
Enthalpie de formation
Variations entropie de réaction
Variations enthalpie de réaction
|
|
|
|
|
|
|
|
|
|
|
|
|
|
:
|
|
: Énergie d'activation
Kf j : Coefficient de taux élémentaire d'aller
Krj : Coefficient de taux élémentaire de retour
[Xk] : Concentration molaire
A, B : Constantes de modèle EDM
?
: Flux de diffusion moléculaire
a : Nombre de Damköhler
Ka : Nombre de Karlowitz
?
S : Nombre de Schmidt
? ?? ?
? 0 ? S
(x, y, z) : Coordonnées cartésiennes
LETTRES GRECQUES :
: Taux de dissipation
: Delta de Kronecker
: Viscosité dynamique
: Viscosité turbulente
: Viscosité cinématique
: Tenseur des taux de rotation
III
: Masse volumique
: Tenseur des contraintes visqueuses
Tenseur de Reynolds
? : Taux de production de réaction
: Épaisseur de la flamme
: Richesse
: Dissipation scalaire de Z
: Coefficient stoechiométrique
Q : Quantité de chaleur libérer par la
combustion
: Épaisseur de la flamme
: La conductivité thermique
Taux molaire de production

:
: Petite échelle de turbulence
, : Coefficients de diffusion
IV
LISTE DES FIGURES
Figure (1) Evolution de la demande mondiale en énergie en
mégatonnes
équivalents pétrole de 1860 à 2004
1
Figure (2) Emission de CO2 équivalent à demande de
l'énergie mondiale 2
Figure (1.1): débit axial a travers un volume de control
11
Figure (2.1) :Le passage d'écoulement laminaire vers
turbulent 22
Figure (2.2) : Dessin schématique de la cascade de
KOLMOGOROV 25
Figure (2.3) :Cascade de Richardson 26
Figure (2.4) : La comparaison graphique des
déférentes simulations 28
Figure (3.1) : schéma d'une flamme
prémélangée 39
Figure (3.2) : schéma d'une flamme
non-prémélangée 39
Figure (3.3) : Schéma de la structure d'une flamme
laminaire de prémélangée
bidimensionnelle (gauche), et
d'une flamme de diffusion (droite) 40
Figure (3.4) : Système pratiques de combustion
classée selon le type d'introduction des
réactifs(prémélangée ou non) et la nature laminaire
ou turbulente de l'écoulement 41
Figure(3.5) : structure interne d'une flamme laminaire
stationnaire de mét 42
Figure (3.6) : schéma d'une flamme laminaire
prémélangée 43
Figure (3.7) : Structure d'une flamme laminaire
prémélangée 44
Figure (3.8) Profile d'une flamme laminaire non
prémélangée 45

Figure(3.10) :régime 1 de combustion 52
Figure(3.11) :régime 2 de combustion 53
Figure(3.12) :régime 3 de combustion 53
Figure(3.13) :regime4 de combustion ..54
Figure (3.14) : Diagramme de régimes de la combustion
54
Figure(3.15) : Définition de la variable d'avancement
57
Figure (4.1) : installation de combustion haute pression 60
Figure (4.2) : bruleur de prémélangée
(gauche) et grille de tranquillisation de la turbulence
(droite) 61
Figure (4.3) : Géométrie détaillée de
la chambre de combustion 62
Figure (4.4.1): Profile de vitesse d'entré (U) 63
Figure (4.4.2) : profile de l'énergie cinétique
turbulente K 63
Figure (4.5) : Maillage près de la zone d'injection 64
Figure (4.6) : vitesse axial [m2/s2] 65
Figure (4.7) énergie cinétique de turbulence k
[m2/s2] 65
Figure (4.8) : Vitesse axial (u) 66
figure (4.9) : énergie k 66
Figure (4.10) : Résidus du calcul pour une richesse de 0.6
68
Figure(4.11) : Champs de vitesse (m/s) 69
Figure(4.12) : Ligne de courants 69
Figure(4.13) : Energie turbulent k(m2/s2)
69
Figure(4.14) : Taux de dissipation e
(m2/s3) 69
Figure(4.15) : Température (K) 70
VI
Figure(4.16) : Taux de réaction ~
~ ) 70
Figure(4.17) : Fraction massique du CH4 70
Figure(4.18) : Fraction massique du CO2 70
Figure (4.19) : Maillage pour le calcul dans le cas de 71
Figure (4.20) : Les résultats des calculs pour 71
Figure(4.21) :champs de Température 72
Figure(4.22) : Fraction massique du CO2 72
Figure(4.23) : les résultats des calculs pour 8 72
Figure(4.24) : Champs de Température (K) 73
Figure(4.25) : Fraction massique du CO2 73
Figure(4.26) :Conteur de la variable d'avancement c
calculée pour les trois richesses 73 Figure(4.27) : Contours de la
variable d'avancement c mesurée pour les trois
richesses 74
Figure(4.28) : Différentes stations représentation
sur la flamme 74
Figure (4.29) : Variable d'avancement le long de l'axe pour une
richesse de 0.6 75
Figure (4.30) : Variation de la Température (K) dans les
trois stations 75
Figure(4.31) : Variation d'énergie turbulente k
(m2/s2) dans les trois stations 75
Figure(4.32) : Variation de la vitesse (m/s) dans les trois
stations 76
Figure(4.33) : Variation de taux de réaction m
~ ) dans les trois stations 76
Figure(4.34) : Structure de la flamme pour une richesse de 0.6
76
Figure(4.35) : Fraction massique du CO2 sur l'axe pour les trois
richesses 77
VII
LISTE DES TABLEUX
Tableau(1.1) : Enthalpies de formations pour
quelques espèces 8
Tableau (1.2) :valeurs de S et Y pour quelque réactions
10
Tableau(3.1) : échelles temporelles et spatiales pour les
flammes turbulentes prémélangées 51
Tableau(4.1) : les fractions massiques obtenues pour chaque
richesse. 68
INTRODUCTION GENERALE
Le feu est l'un des premières sources d'énergie
que l'être humain a utilisée dans sa vie quotidienne pour se
réchauffer, pour cuire sa nourriture, dans les guerres...etc. Le
développement industriel actuel est basé sur l'énergie
produite en partie majeur par la combustion. Pour subvenir aux besoins de la
société moderne, la demande mondiale en énergie ne cesse
de croître, elle utilisa toutes les sources possibles à savoir le
charbon, le pétrole, le gaz, le nucléaire, etc. (figure1).
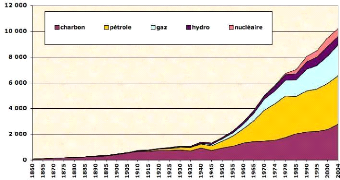
Figure (1) : Evolution de la demande mondiale en énergie
en mégatonnes équivalents pétrole de 1860 à
2004.
En plus du bienfait exothermique de la combustion, elle
dégage d'autres émissions très nocives pour notre
environnement, on peut citer les émissions les plus dangereuses pour
l'être humain:
v' Le CO2 qui est un gaz toxique à effet de serre
v' Le CO, gaz qui se forme dans des conditions de manque
d'oxygène, il peut se combiner rapidement avec l'hémoglobine
sanguine et provoquer l'asphyxie et la mort dans quelques minutes
v' Les gaz NOx qui sont aussi toxiques et qui altèrent les
bronchioles et provoquent des problèmes respiratoires
Donc le contexte contemporain de notre progrès est
défini par deux éléments contradictoires
qui régissent nos sociétés.
v' D'une part le désir de confort se traduisant par
l'accroissement de la demande mondiale en énergie, et de la consommation
d'énergies fossiles par des procédés industriels :
transports, manufacture, bâtiment, exploitation agricole, transformation
d'énergie... Comme illustré sur la figure (1)
v' D'autre part le souci écologique : exprimé
par la certitude d'un épuisement des ressources fossiles ainsi que la
dégradation irréversible des écosystèmes par la
pollution. En témoignent la figure (2)

Figure (2) Emission de CO2 équivalent à demande de
l'énergie mondiale
Certains pays, les signataires du protocole de Kyoto, ont
décidé de réduire leurs émissions de gaz à
effet de serre. Ces pays ne devraient pas augmenter leur consommation de
charbon, mais plutôt la réduire pour limiter leurs
émissions de CO2. Pour les autres, en raison du renchérissement
du prix du pétrole, il est probable que le charbon deviendra une source
d'énergie meilleure marchée, dans laquelle ils vont puiser encore
davantage. La part du charbon dans la consommation d'énergie primaire
(un tiers) devrait rester stable pendant encore une ou deux dizaines
d'années, puis aller en s'accroissant. Certains problèmes de
pollution liée au charbon peuvent être résolus en traitant
les fumées de combustion, mais il reste toujours le difficile
problème du CO2.
Peut-on remplacer la combustion ?
Pour éviter les problèmes de pollution, les
ingénieurs ont développés des nouvelles technologies pour
la production d'énergie renouvelable est non polluantes. On peut citer
par exemple l'énergie solaire et l'éolien.
1) L'énergie solaire
L'énergie solaire est transmise á la terre
á travers l'espace sous forme de particules d'énergie, des
photons et de rayonnement. Elle est captée et transformée en
chaleur ou en électricité grâce á des capteurs
adaptés. Le soleil produit ainsi une énergie inépuisable
et naturellement disponible en quantité. L'énergie solaire
reçue chaque année sur la terre équivaut á plus de
20 fois nos besoins énergétiques. Elle est disponible partout, il
suffit simplement de la capter pour bénéficier d'une
énergie gratuite et écologique.
Les inconvénients essentiels de cette source
d'énergie sont :
ü Le coût initial de l'installation d'un
système d'énergie solaire fabriquée en grande partie de
matières semi-conductrices très chères ainsi que les
accumulateurs et régulateurs. Cela fait que le coût de
l'électricité d'origine solaire est plus haut comparé
á l'électricité non renouvelable.
ü Les panneaux solaires exigent un grand espace pour
réaliser des installations efficaces.
ü La production de l'énergie solaire est
intermittente, elle est aussi influencée par la présence des
nuages ou de la pollution dans le ciel.
2) L'énergie éolienne
L'énergie éolienne (du mot grec Eole, le Dieu du
vent) est l'énergie produite par le vent. Cette énergie
mécanique est exploitée par des éoliennes, hélices
installées au sommet de pylônes et qui tournent sous l'action du
vent. La rotation des hélices actionne un système produisant de
l'électricité. C'est une énergie cinétique du vent
qui est durable et propre, en plus les éoliennes ne nécessitent
que cette énergie (le vent), et uniquement cette énergie. Une
éolienne n'a besoin que de très peu de places, ce qui n'engendre
qu'une perte d'environ 2% du sol agricole sur les exploitations où des
parcs éoliens ont été installés. La surface
restante étant disponible pour une exploitation agricole ou
d'élevage. La simplicité des éoliennes permet aux
particuliers de participer directement á la conservation de notre
environnement via l'installation de dispositifs personnels.
Concernant les inconvénients des éoliennes, on peut
dire que
v' L'énergie produite par les éoliennes est
intermittente et nécessite donc souvent l'utilisation
de centrales thermiques (qui tournent au ralenti) afin de
réguler les variations imprévisibles de la production
éolienne. Toutefois, plus le nombre d'éolienne est grand, et
moins les perturbations naturelles influent sur la production
d'électricité (cas des très grands parcs éoliens) :
l'énergie produite est donc plus régulière.
v' L'énergie éolienne est considérée
comme une énergie d'appoint car la construction de
centrales thermiques tournant au ralenti coûte cher.
v' Les riverains se plaignent de la destruction visuelle de leur
paysage (exemple notable en
Bretagne).
v' Enfin, l'éolienne est dépendante de la
météo, et dépendante de sa topographique (on ne
peut pas installer une éolienne sur n'importe quel
terrain).
On peut dire que le pétrole et le gaz naturel restent
les combustibles par excellence. L'alternative est non pas l'utilisation
massive imminente du solaire ou de l'éolienne mais l'amélioration
et le contrôle des émissions nocives issues de la combustion.
Parmi les techniques utilisées dans le contrôle des
émissions, la combustion pauvre qui consiste à brûler moins
de combustible avec plus d'air. Ce mode de combustion vise d'une part à
réduire les émissions en CO2 car on brûle moins de
combustible et d'autre part à réduire la température de la
combustion qui inhibe la formation des NOx.
Motivation du présent travail
L'énergie électrique en Algérie est
produite à 80% par les turbines à gaz, ces dernières
brûlent le gaz naturel composé en majorité du
méthane. L'Algérie est l'un des premiers pays qui ont
ratifiés le protocole de Kyoto, d'où vient la
nécessité de ce travail.
Ce travail s'inscrit dans la simulation des écoulements
réactifs turbulents, en particulier l'étude numérique des
flammes turbulente (prémélangées). Les bases
expérimentales de ce travail sont les mesures réalisées
par LACHAUX T. [1]et HALTER F.[2] à l'ICARE (Institut de Combustion,
Aérothermique, Réactivité et Environnement) du CNRS
d'Orléans en France.
Objectif du travail
Ce travail constitue une suite logique aux travaux
numériques des années précédentes, HAFID M.[3],
GHOUGAL A. et TRAD DJ. [4], TOUT M. et IKEN A. [5], ou on a
considéré l'injection de l'air dans les chambres de combustions
puis on a amélioré le modèle de turbulence k-å par
la correction de POPE et on a aussi étudiée différents
aspects des mélanges non réactifs de différentes
espèces dans une chambre de combustion. Le
présent travail va considérer la combustion
turbulente par un modèle assez simple (EDM Eddy Dissipation Model) dans
une chambre de combustion similaire à celle des turbines à gaz.
On va simuler la combustion pauvre pour les richesses 0.6, 0.7 et 0.8.
Le mémoire est réparti sur quatre chapitres
débuté par la présente introduction. Le premier chapitre
comprend la formulation mathématique du phénomène, il
détaille surtout les équations de conservation pour les
espèces chimiques. On a aussi démontré le calcul du taux
de réaction pour une réaction globale a un pas et pour un
mécanisme réactionnel détaillé. Le deuxième
chapitre est consacré au phénomène de la turbulence,
différentes approches de modélisations ont été
évoquées et enfin un listing des différents modèles
à été fait. Dans le troisième chapitre, on a
étudié les différentes échelles des flammes
laminaires et de la turbulence, l'interaction entre ces échelles donne
le diagramme de combustion turbulente qui nous a permis de choisir le
modèle de la combustion turbulente. Finalement, on a introduit le
modèle EDM ainsi que son intégration dans le code FLUENT. Dans le
dernier chapitre, on a exposé la chambre de combustion, sa
modélisation ainsi que les résultats des calculs par le code
FLUENT.
CHAPITRE I
AEROTHERMOCHIMIE ET STOECHIOMETRIE
1) Introduction
Un gaz en réaction est un mélange non isotherme
d'espèces multiples (hydrocarbures, oxygène, eau, dioxyde de
carbone, etc.) qui doivent être suivies individuellement et
instantanément. Les données thermodynamiques sont
également plus complexes que dans l'aérodynamique classique car
les chaleurs spécifiques changement dans le gaz réactif de
façon significative avec la température et la composition.
v' Les espèces réagissent chimiquement avec des
vitesses (taux de réactions) qui exigent des modélisations
spécifiques.
v' Etant donné que le gaz en réaction est un
mélange de plusieurs espèces, les coefficients de transport
(diffusivité thermique, diffusion des espèces, viscosité,
etc.) nécessitent une attention particulière.
La dérivation des équations de conservation de
la masse, des espèces ou des bilans d'énergie peut être
trouvé dans les ouvrages classiques tels que ceux de Williams, Kuo ou
M ?
Candel [6]. Dans ce chapitre on se limite à citer les
différentes formes utilisées dans les
M ?
codes de calcul et sur leurs implications pour des techniques
numériques 2) Choix des variables primitives
La combustion implique multiples espèces qui
réagissant dans diverses réactions chimiques. Ces espèces
sont caractérisées par leurs fractions massiques Yk pour k = 1
à N, où N est le nombre d'espèces dans le mélange
réactif. Les fractions de masse Yk sont définis par:
(1.1)
Où Mk et sont respectivement : la masse et la
densité de l'esSqFeINIprésente dans un
volume donné V, M est la masse totale de gaz dans ce
volume.
Les variables primitives pour le cas tridimensionnel
réactif sont:
·
(1.4)
(1.5)
(1.6)
La densité,
(1.2)
· Les vitesses dans les trois directions i
(i=1,2 et 3)
· Une seule variable pour l'énergie (enthalpie h ou
température T)
· Les fractions massiques Yk des espèces
Il faut donc calculer N+5 variables au lieu de 5 dans le cas
non réactif. Sachant que la combustion implique un grand nombre
d'espèces (N est supérieur à 50 pour la plupart des
hydrocarbures simples), l'effort de calcul est considérable dans la
simulation des
n M
k
X Y
écoulements réactifs (vu le nombre
d'équations de conservation à résoudre). n M
tot k
3) Notions sur la thermochimie
Il est nécessaire de définir quelques variables
usuelles ainsi que des notions de la thermochimie. Commençons par
l'équations d'état du gaz parfait qui relie la pression, la
température et la densité du gaz en question:

(1.3)
Pour un mélange gazeux la masse molaire du gaz est
calculée par :
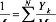
La fraction molaire Xk de l'espèce k s'écrit :
Où n est le nombre de molles.
La concentration [Xk] de l'espèce k est donnée par
:
T
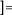
L'énergie sensible de l'espèce k est donnée
par :
(1.7)
I.'entIia1pie sensible J.e III 1 I 11111 II I I 1111111111 II
33 33 3
IE1.' LI Ll1IpLIL1I Lillilil I I I I I III I I III I I I I HI I I
I I I I I I I I I I liii I I I I I II I I II I 1IflJ JJ LII I III I I I Ii
IIIIIIIIIII!
33 3' 3
LIILLI] ' LLIientha1pie JLflhi1JI III HII 11111
IL II H
33 33 ' 3
I H IL Ij LiIIIJJLIJ_p H I I I H I H I H I ILl H H II I H HIll I
liii H I I1IJI I I I I I H 11111 LH I H Hi I' LI Hill
IWH'erithalpie
LLImJI1Lour former 1kg de l'i I I III ILIIIIIII III H ILLhIL1J p
I IIJJ' II
33 33 3 3
|
____ 1 i iii ii
|
3LJJ L1
|
|
Ahm
fk
3LJ fflLJ3L1
|
|
|
''''JLI1
|
|
|
|
'J'''LI1
|
'3''33L11
|
|
|
!33J!
|
'J' JLI1
|
|
|
|
''''JLI1
|
|
|
'3'''JLI1
|
'J'333LI1
|
|
3! !
|
!
|
!
|
|
3! !
|
!
|
!
|
|
'3'J3LI1
|
'LII
|
'LII
|

4) La stoechiométrie dans les flammes
prémélangées
Dans la combustion prémélangée le fuel et
l'oxydant sont mélangé avant d'entrer dans la chambre de
combustion.
Considérons la réaction globale suivante
Par exemple ( + o0. --> CO. + oll.0 ). Les constantes
sont les coefficients
stoechiométriques correspondants au fuel et à
l'oxydant.
m n défini le rapport stoechiométrique s par
(1.12
(1.13
(1.1
La richesse du mélange est définie p

Qui s'écrit aussi

vec et sont les débits massiques du fuel et de
l'oxydant
La richesse est un paramètre principal pour les gaz
prémélangé
· 0 > 1 combustion riche en fuel
· 0 < 1 combustion pauvre en fuel
Dans les flammes hydrocarbures/air, CIEIBFtiR(EP DAiqXe
EdXEIXeEEstATFKiRP pITiIXeE ( =1 ) est donnée par :
(1.15)
/ IiIEpta(tEFRP SRspEd'X(eEP RleEE'Rx\ Jq(eETIET.76 EP
ROEdIE(itARTq(1E3(EYRlXP Hi ELe tableau suivant donne quelques valeurs du
coefficient VATFKiRP pITiqXeEsEItElEEIrIFtiR(E P DAiqXIEstATFKiRP ptriqXe
EdXEIXel ( =1).
|
Réactions globale
|
s
|
Y:
|
|
CH4 +2(02 +3.76N2)
-*CO2 +2H20 +7.52N2
|
4.00
|
0.055
|
|
C3H8 +5(02 + 3.76N2)
-->3CO2 +4H20 +18.8N2
|
3.63
|
0.060
|
|
2C81/18 + 25(02 +
3.76N2) -->16CO2 +18H20 +
94N2
|
3.51
|
0.062
|
|
2H2 + (02 + 3.76N2) -->
2H20 + 3.76N2
|
8.00
|
0.028
|
Tableau (1.2) :valeurs de S et Y pour quelque réactions
&I EtIRDIXEP R(t11E1Xe ESRXrEaYRi1EX(e EFRP
FXstiR(EstATFKiRP pITiqXE, ENEqXE(titpEdXE combustible injectée est
très faible comparativement à l'air qui est composé en
grande partie par l'azote.
5) Equation de conservation des
espèces
Puisque notre travail consiste à étudier les
écoulements réactifs, on va détailler la procédure
de déduction de l'équation de conservation de la masse de
n'importe quelle espèce dans un mélange multi composants. Cette
déduction va se faire en prenant simultanément le taux de
réaction en g 3 et en 3 ce qui va permettre d'introduire le loi de
Fick.
Nous commençons par faire un bilan de masse sur un
élément fluide arbitraire dans un mélange binaire.
Appliquons la loi de conservation de la masse sur un élément de
volume
z fixe dans un espace à travers lequel un mélange
binaire des espèces A et B s'écoule et réagit.
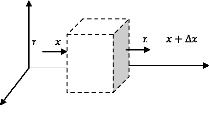
y
? I
? I
X
Figure(1.1)
Z
Dans ce volume de contrôle infinitésimal,
l'espèce A peut être produite ou consommée par
réaction chimique avec un taux ? g 3 . Si ? , l'espèce A est
consommée. Les différents thermes qui contribuent à
l'équilibre massique sont :
Le taux d'accumulation de la masse de l'espèce dans le
volume de contrôle
t z (1.16)
Les flux de A entrants et sortants dans le volume par la
direction x respectivement aux positions x et sont
?
/ z (1.17)
?
z (1.18)
Le taux de production de l'espèce A par la réaction
chimique ? z
?
est le taux de production spécifique de A.
Le même principe est appliqué aux autres directions,
on somme puis on divise par z ce qui donne :
( ?
?
? ~
~ ) ? (1.19)
~
|
C'est l'équation de continuité du composant A,
elle
|
aussi appelée l'équation de
|
|
?
|
?
|
?
|
|
conservation du masse d'espece A. Les quantités
|
|
|
|
|
z sont les composantes
|
|
|
|
z
|
scalaires du vecteur du flux de masse ? , dans le rectangle de
coordonné. Dans la notation
vectorielle, l'équation s'écrit :
t rh ci) (1.20)
D e la même façon, l'équation de la
continuité du composant B est
t B
rh ci) (1.21)
D ans un mélange binaire, une espèce peut se
convertir vers l'autre et vice versa. Le taux
de production d'une espèce et égal au taux de
destruction de la deuxième ce qui implique
que la somme des équations (1.20) et (1.21) donne
l'équation de conservation du mélange
t V (1.22)
Pour obtenir l'équation (1.22), on a utilisé ? ? l
et ? ?
Pour un fluide de densité massique constante
l'équation (1.22) devient : ~
G On va maintenant faire le développement en terme de 3 ,
Si ? est le
taux molaire de production de A par unité de volume, alors
l'analogue molaire de l'équation (1.20) est :
En remplaçant ? V -- ~ dans l'équation (1.20) on
obtient :
t V Y ? (1.24)
Avec l la vitesse massique de diffusion et dans B
En remplaçant aussi ? V -- dans l'équation (1.24)
on obtient :
Oil V est la vitesse molaire de diffusion [6]
Si on a pas de réaction chimique, les taux de
réactions massiques et molaires ? , ? , ? , et ? sont nuls. Si en plus,
V est nulle dans l'équation 5 ou ~ est nulle dans l'équation
|
6, on obtient :
|
c
t
|
(1.26)
|
Cette relation est dite "la deuxième loi de Fick de
diffusion" . Cette équation est généralement
utilisée pour la diffusion dans les solides, les liquides
stationnaires,... Cette équation est similaire à
l'équation de la conduction de la chaleur :

(1.27)
t
A l'aide de les relations ~ et v v V pour un système multi
composants,
l'équation 3 devient :
~ [~ ~ V ] ? (1.28)
t
L'équation ci-dessus dans sa forme de divergence peut
être réduite à la forme d'Euler. Par expansion des termes
à gauche on a :
Y
t
Y
t
~ ~ ~ ~ ~ ~ ? (1.29)
Alor on obtient :

t
Y v( ? Y ) -- v( ) ? (1.30)

Avec le flux de diffusion moléculaire. On adopte la loi de
Fick pour le transport diffusif de la masse :
?
_ Y (1.31)
Avec le coefficient de diffusion moléculaire de
l'espéce .
6) Mécanismes réactionnels et taux de
réaction
On a vu que chaque espèce dans le mélange gazeux
doit être représentée par une équation de
conservation. Cette dernière décrit l'évolution de
l'espèce donnée dans l'espace et dans le temps. Dans le milieu
réactif, plusieurs espèces entrent en compétition chacune
avec un taux de réaction bien déterminé.
Pour expliquer la méthode de calcul du taux de
réaction, prenons une partie d'un mécanisme réactionnel de
la combustion de l'hydrogène dans l'oxygène -- .
(1.33) (1.34) (1.35) (1.36) (1.37) (1.38)
Ou Kf et K sont les coefficients du taux
élémentaire de réaction dans le sens direct (gauche
à droite) et dans le sens inverse de la réaction j.
Par exemple, le taux net de production d'oxyg~ne est la somme
de tous les taux élémentaires des réactions qui produisent
l'oxyg~ne moins la somme de tous les taux élémentaires des
réactions qui consomment l'oxygqne.
|
[0 1
t
|
~ [ ][ ] K [ ][ ] K [ ][ ]
|
--Kf [ ][ ] -- Kf [ ][ ] -- Kf [ ] (1.39)
De la même façon, on peut écrire cette
expression pour chaque espèce qui participe dans le mécanisme.
Cela donne un ensemble d'équations différentielles ordinaires du
premier ordre qui représentent l'évolution du système
chimique à partir des conditions initiales :
|
[ ] t
t
|
{[ ] [ ] ... [ ] } (1.40)
|
Avec [ ] [ ~
Une fois qu'on a trouvé taux de réactions
élémentaires, on peut résoudre les équations de
conservations des espèces et finalement trouver toutes les variables
primitives.
7) Formulation générale pour le calcul du
taux de réaction
Un mécanisme réactionnel peut être
écrit sous une forme compacte, pour une réaction
élémentaire i, qui combine N (j=1,N) espèces chimiques, on
écrit
~ ~ì
? ~ ~ ~ìì
~ (1.41)
~
|
Où ~ì et ~ìì
produits.
|
sont les coefficients stoechiométriques respectivement
des réactifs et des
|
Pour expliquer cette notation, reprenons les réactions
(1.33)- (1.38), qui combinent six espèces à savoir :
On définit j comme espèce et i comme
réaction selon la table suivante:
|
j
|
Espèces
|
i
|
Réaction
|
|
1
|
|
1
|
(1.33)
|
|
2
|
|
2
|
(1.34)
|
|
3
|
|
3
|
(1.35)
|
|
4
|
|
4
|
(1.36)
|
|
5
|
|
5
|
(1.37)
|
|
6
|
|
6
|
(1.38)
|
D'autre part, on utilise j comme l'indexe des colonnes et i des
lignes, ce qui donne une matrice des coefficients stoechiométriques
et
On remarque que la réaction élémentaire
implique au maximum trois à quatre espèces réactives, ce
qui fait que la matrice des coefficients est presque nulle lorsque le nombre
d'espèce est grand.
Le taux de production de l'espèce j est calculé en
sommant sur toutes les réactions i, il est donné par
cb El1= t q j=1.2...N (1.42)
0
Oil
|
0Et
|
iì ~ìì ?? 1
|
-- ~ì (1.43)
|
q Kf ?i1= [ ] ì j -- K ?i1= [ ]
ììi
(1.44)
Le taux de production ? correspond au terme gauche des
équations (1.39) et (1.40), on a pour un mécanisme complet
?
[dt l (1.45)
L'équation (1.44) définit le taux de progression q
pour la réaction élémentaire, par
exemple pour la
réaction (1.33), on pose i=1ce qui donne
q Kf [ ] [ ] [ ] [ ~ [ ] [ ~
--K [ ] [ ] [ ] [ ] [ ] [ ] (1.46)
q Kf [ ] [ ] K [ ] [ ] (1.47)
De même façon on écrit les expressions pour
i=2.3...6, et on somme l'équation (1.42) pour obtenir le taux de
réaction ? .
Le calcul des constantes et constitue un problème central
dans la modélisation
de combustion. Souvent, elles sont modélisées en
par la loi empirique d'Arrhenius qui est basée sur l'observation
expérimentale.
8) Approximation de la combustion par une seule
réaction globale
Pour simplifier les calculs, on approxime la combustion par
une réaction globale d'une mole de fuel avec « á »
moles d'oxygène pour produire « â » moles d'un produit
de combustion P
F á â 1 (1.48)
D'une part on facilite les calculs, et d'autre part perd des
informations sur les espèces intermédiaires qui sont parfois
très importantes.
'apr~s l'expérience, le taux de réaction du fuel
est donné par
|
[ ]
t
|
KG [ ] [ O ] (1.49)
|
Avec [ ] concentration molaire 3 de l'esp~ce i dans le
mélange,
KG est le coefficient du taux global de réaction qui est
généralement fonction de la température,
Les exposants n, m sont reliés aux coefficients
stoechiométriques de la réaction, d'après
l'équation (1.49) le fuel est dit d'ordre n et le combustible d'ordre
m.
9) Approximation par un mécanisme
réactionnel formé par des réactions
élémentaires Dans le cas général, la
combustion est approximé par un mécanisme réactionnel
formé
par plusieurs réactions élémentaires. La
plus part des réactions élémentaires concernant la
combustion sont « bi moléculaires » c'est-à-dire deux
molécules réagissent pour donner deux molécules
différents :
Le taux de réaction s'écrit en fonction de la
concentration molaire de [A]
|
[ ]
t
|
3
K ano [ ] [ ] ( )
k o / (1.50)
|
Le coefficient K o est donné par [6]
(1.51)
*~ +
T
K o
Cette formule est donnée par l'expérience. Les
constantes A, c et (l'énergie
d'activation) sont tabulées et donnée pour chaque
mécanisme réactionnel.
Dans ce qui suit un exemple qui montre un mécanisme
réactionnel H2-O2 (9 espèces et 19 réactions)
écrit sous un format universel dit format : CHEMKIN [8] (les
commentaires entre parenthèses ne font pas partie du mécanisme,
elles sont données à titre explicatif)
ELEMENTS
H O N F (dans cette ligne on un les elements chimiques)
END SPECIES
H2 O2 OH O H H2O HO2 H2O2 N2 F (ici les espèces
chimiques)
END
REACTIONS F ( dans ce qui suit les reactions
élémentaires)
(Réaction const. A c Ea)
H2+O2=OH+OH 1.700E13 0.0 47780.0
H2+OH=H2O+H 1.170E09 1.30 3626.0
H+O2=OH+O 5.130E16 -0.816 16507.0
O+H2=OH+H 1.800E10 1.0 8826.0
H+O2+M=HO2+M 2.100E18 -1.0 0.0
H2/3.3/ O2/0./ N2/0./
H2O/21.0/
H+O2+O2=HO2+O2 6.700E19 -1.42 0.0
H+O2+N2=HO2+N2 6.700E19 -1.42 0.0
OH+HO2=H2O+O2 5.000E13 0.0 1000.0
H+HO2=OH+OH 2.500E14 0.0 1900.0
O+HO2=O2+OH 4.800E13 0.0 1000.0
|
Aérothermochimie et stoechiométrie
|
|
|
19
|
|
OH+OH=O+H2O
|
6.000E08
|
1.3
|
0.0
|
|
H2+M=H+H+M
|
2.230E12
|
0.5
|
92600.0
|
|
H2/3./ H/2./ H2O/6.0/
|
|
|
|
|
O2+M=O+O+M
|
1.850E11
|
0.5
|
95560.0
|
|
H+OH+M=H2O+M
|
7.500E23
|
-2.6
|
0.0
|
|
H2O/20.0/
|
|
|
|
|
HO2+H=H2+O2
|
2.500E13
|
0.0
|
700.0
|
|
HO2+HO2=H2O2+O2
|
2.000E12
|
0.0
|
0.0
|
|
H2O2+M=OH+OH+M
|
1.300E17
|
0.0
|
45500.0
|
|
H2O2+H=H2+HO2
|
1.600E12
|
0.0
|
3800.0
|
|
H2O2+OH=H2O+HO2
|
1.000E13
|
0.0
|
1800.0
|
|
END
|
|
|
|
|
10) Conclusion
|
|
|
|
Ce chapitre représente la formulation
mathématique du phénomène, les détails de calcul du
taux de production pour une réaction globale, la conservation des
espèces. Ainsi, que des notions sur la thermochimie et la \toeFKLRP
ptrLe.J
CHAPITRE II
NOTIONS SUR LA TURBULENCE
1) Introduction
Chacun est capable de citer des effets bien visibles de la
turbulence dans plusieurs cas dans la nature, elle est très proche de
nous, par exemple la fumée d'une cheminée ou le
développement d'un filet d'eau coulant d'un robinet.
Dans ces cas et d'autres, des structures tourbillonnaires
plus ou moins organisées rendent l'écoulement complexe et il
devient difficile d'en appréhender les détails, d'en
prédire précisément l'évolution instantanée
et locale, méme en mettant en oeuvre les moyens de calcul qui ne cessent
de voir leur puissance s'accroitre.
La prise en compte, plus ou moins raffinée, de
l'influence de ces structures est cependant indispensable dans une grande
partie des applications industrielle courantes.
2) Oü observe t on la turbulence?
La turbulence est un phénomène présent de
manière très facilement visible dans la nature :
v' Dans l'air : les rafales de vent, les mini-tornades dans le
désert, le panache de fumée des grandes cheminées,
turbulence atmosphérique : (tourbillons de taille > 1000 km).
v' Dans l'eau : le lait dans le café, les remous dans les
rivières.
v' Dans la mer : le Gulf Stream
v' Dans la terre : le mouvement des plaques continentales
v' Dans l'espace : l'atmosphère externe de Jupiter
Il est également très présent dans les
écoulements industriels :
v' Aérodynamique externe des voitures, des camions,
v' Sillage des avions
v' Aérodynamique interne dans les moteurs (combustion,
etc....)
3) Les deux points de vue sur la turbulence
Et pourtant, certaines grandeurs macroscopiques sont bien
reproductibles. Par exemple :
ü Traînée et portance d'une voiture dans une
soufflerie donnée
ü Débit d'une conduite á haut Reynolds
ü Puissance d'un moteur á combustion
ü Température maximale des disques de frein
ü Durée de persistance du sillage d'un avion de
ligne
ü Portance et traînée d'un avion
Les scientifiques ont alors deux points de vue possibles :
ü Soit chercher á moyenner directement la
turbulence, á lisser le phénomène : c'est le point de vue
statistique. On cherche uniquement les grandeurs moyennes, et l'énergie
cinétique turbulente moyenne. C'est une vision "figée" ou
"rationnelle" de la turbulence, souvent celle des numériciens.
ü Soit chercher á extraire la cohérence
dans la turbulence : c'est le point de vue des "structures cohérentes".
On cherche alors l'évolution des structures qui persistent au milieu du
chaos, celles qui vont déterminer la physique de l'écoulement.
C'est une vision instationnaire, fluctuante et plus expérimentaliste de
la turbulence.
4) LiHxSpUHQcHRSH 5 HyQIIdN EILEE3)
Cette expérience montre le phénomène de
la turbulence dans un écoulement turbulent, le colorant est rapidement
dispersé avec formation des structures sous forme de volutes,
appelées tourbillons. Dans cette situation, une mesure de la composante
axiale de la vitesse (par vélocimétrie, laser ou par fil chaud)
montre que celle-ci fluctue de façon aléatoire dans l'espace et
le temps [9].
La figure suivant montre les déférents
étapes de passage d'un écoulement laminaire à un
écoulement turbulent en passant par le profile de transitionnel
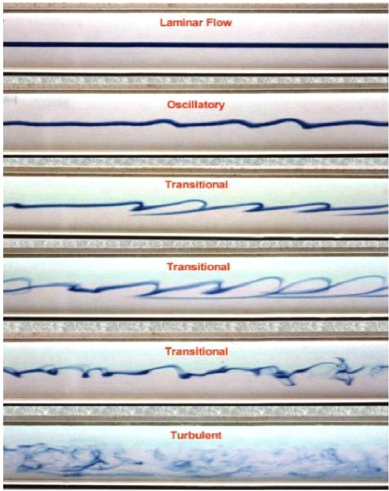
Figure (2.1) :Le passage d'écoulement laminaire vers
turbulent
5) Caractéristiques d'un écoulement
turbulent
En général, un écoulement turbulent peut
être caractérisé par les propriétés
suivantes: v' L'écoulement est instationnaire.
v' Incertitude (de mesure, de calcul).
v' Le vecteur de vitesse en un point varie de façon
aléatoire en direction et en module. v' L'écoulement contient un
grand nombre de tourbillons de taille très variée.
v' Augmentation du mélange : forte diffusion des
quantités transportées (exemple le lait et le café, la
fumée, etc.).
v' Le bruit : les écoulements turbulents sont bruyants
du fait des sources acoustiques créées par les fluctuations de
pression dans le fluide. Cela peut générer de l'inconfort dans
certains cas (exemple le bruit des rétroviseurs extérieurs des
véhicules),
v' Les effets de la turbulence sont parfois positifs, parfois
négatifs :
v' Effets positifs : l'augmentation du mélange permet
d'améliorer la combustion par exemple, d'améliorer la portance
des avions, de réduire la température. v' Effets négatifs
: diffusion de la pollution.
6) La transition du laminaire au turbulent
Le nombre de Reynolds a été introduit par Osborne
Reynolds en 1883. Il compare les termes de convection (non linéaires)
aux termes de dissipation visqueuse [10].
(2.1)
Au fur et à mesure que le nombre de Reynolds augmente,
on observe un changement de topologie de l'écoulement qui correspond
à la transition laminaire/ turbulent. Le nombre de Reynolds critique
correspond à ce passage, il est en général de l'ordre de
1000. Il prend
des valeurs différentes selon le type
d'écoulement. Quand Re << 1 les termes non linéaires (la
convection) sont masqués par la diffusion visqueuse, les
équations se rapprochent donc d'équations linéaires.
Quand Re >> 1, les termes non linéaires deviennent
prépondérants, et l'approximation linéaire n'est plus
possible.
· Pour un écoulement de Poiseuille
(écoulement dans un tube 1841), au delà de Re = 2000,
les quantités ne dépendent plus du nombre de Reynolds. Le
frottement est
proportionnel à ( ) au lieu de ( ) dans le cas
laminaire
ü Pour un écoulement de Couette (écoulement
entre deux plans infinis) :
ü Pour une couche limite sur plaque plane, on utilise le
nombre de Reynolds basé sur l'épaisseur de couche limite
ä
(2.2)
Pour Res = 5 20, la couche limite se développe suivant
un profil de Blasius en 8=- .
Pour 5 20 < Res < 2000 on a une zone de transition dans
laquelle se développent des ondes dites de Tollmien-Schlichting. Au
delà, des petites échelles apparaissent et on parle alors de
couche limite pleinement développée. Le nombre de Reynolds
correspondant basé sur la distance x depuis le démarrage de la
couche limite est d enviro n Rex = 106. Dans un
écoulement d'air à (10m/s) la couche limite devient pleinement
turbulente à environ (1m) du bord d'attaque.
ü Pour une couche de mélange (écoulement
qui résulte du mélange de deux fluides injectés à
deux vitesses différentes), le nombre de Reynolds critique basé
sur la vitesse moyenne; (U2 -- U1)/2 et sur l'épaisseur de couche de
mélange 8(x) et Rec = 25 00 environ
7) La cascade de KOLMOGOROV
La notion de Richardson (1881-1953) de la turbulence
était qu'un écoulement turbulent est composé de
tourbillons de différentes tailles. Les grands tourbillons sont
instables et meurent en se cassant en tourbillons plus petits, et
l'énergie cinétique du grand tourbillon initial est
divisée par les plus petits tourbillons qu`il a
généré. Ces petits tourbillons subissent le même
processus, provoquant encore de plus petits tourbillons qui héritent de
l'énergie de leurs tourbillons prédécesseurs, et ainsi de
suite [10]. De cette façon, l'énergie passe des grandes
échelles du mouvement aux plus petites échelles jusqu'à
atteindre une échelle suffisamment petite de longueur tels que la
viscosité du fluide peut efficacement absorber l'énergie
cinétique dans l'énergie interne, cette vision de cascade n'est
valable que d'un point de vu statistique.
Effectivement, la notion dynamique de cascade étape par
étape est dénuée de sens. Il existe une théorie qui
a contribué de façon majeure dans la compréhension de la
turbulence, la théorie de Kolmogorov (1941). Elle repose sur une vision
"statistique" de la turbulence, elle
dit que les tourbillons dans l'écoulement ont une
taille comprise entre les deux tailles limites suivantes [10] :
v' La plus grande échelle de l'écoulement L
(imposée par la géométrie de l'écoulement, par
exemple typiquement le diamètre d'un cylindre, le diamètre d'une
cheminée, ou encore la hauteur d'une voiture).
v' La plus petite échelle de l'écoulement :
imposée par la viscosité du fluide cette
échelle est appelée échelle de Kolmogorov,
ou échelle de dissipation visqueuse. L'ordre de grandeur entre et est le
suivant [25] :
4 (2.3)
La théorie de la "cascade" énergétique
prédit que les tourbillons ne reçoivent de l'énergie que
des échelles les plus grandes qu'eux, et la transmettent ensuite aux
échelles les plus petites qu'eux, et ainsi de suite jusqu'à la
plus petite échelle présente dans l'écoulement
`'l'échelle (ç)`'
On parle de production d'énergie lorsque les grosses
structures sont générées, par un décollement par
exemple, et de dissipation d'énergie lorsque les tourbillons
disparaissent complètement en aval de l'obstacle. Lorsque la production
d'énergie est égale à la dissipation d'énergie, on
parle de turbulence "en équilibre".
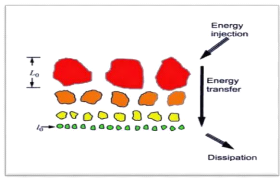
Figure (2.2) : Dessin schématique de la cascade de
KOLMOGOROV
Figure(2.3) :Cascade de Richardson
8) Quelques types de simulation numériques de la
turbulence
Le besoin de recourir aux simulations numériques en
Mécanique des Fluides est aujourd'hui omniprésent dans de
multiples domaines d'applications (automobile, aéronautique et thermique
par exemple) et ce pour plusieurs raisons. Tout d'abord, les simulations
numériques permettent de comprendre les phénomènes
impliqués dans un écoulement : l'accès à certaines
informations est rendu possible, l'écoulement peut être
calculé et donc visualisé en 3D.
De plus, les simulations numériques permettent de
tester- l'influence de plusieurs paramètres sans avoir à
reconstruire tout un banc expérimental. On conçoit
évidemment qu'il est plus aisé, par exemple, de modifier un
maillage de turbine à gaz plutôt que de faire construire de
nouvelles pièces. Les simulations numériques peuvent
également permettre d'observer les comportements d'un écoulement
dans une géométrie à plus grande échelle ("scaling
up") sans pour autant nécessiter la construction de pilotes encombrants
(par exemple en lit fluidisé).
Il existe trois types de simulation numérique en
Mécanique des fluides : DNS (Direct Numerical Simulation), LES (Large
Eddy Simulation) et RANS (Reynolds Average Navier Stokes). Dans ces
dernières années, on note le développement d'une nouvelle
approche dite DES (Direct Eddy Simulation) qu'on ne va pas citer dans ce qui
suit.
8.1) La simulation numérique directe
(DNS)
Dans les simulations DNS, les équations de
Navier-Stokes sont entièrement résolues : la turbulence est
calculée et non plus modélisée. Ces simulations sont donc
des plus précises mais ont un coût de calcul beaucoup trop
élevé pour qu'il soit envisageable (du moins à ce jour) de
simuler une configuration industrielle en DNS. En effet, le nombre de points
nécessaire pour réaliser une DNS est directement lié au
nombre de Reynolds de l'écoulement
( 4 )[10]. Les simulations de type DNS sont donc limitées
à des calculs "académiques"
de type boîte cubique de petit côté, ou
bien à des écoulements à faible nombre de Reynolds.
Méme s'il n'est pas exclu qu'un jour les moyens de calcul autoriseront
de telles simulations. 8.2) La simulation des grandes échelles
(LES)
Les simulations LES résolvent les équations de
Navier-Stokes filtrées spatialement, seules les petites structures sont
modélisées alors que toutes les autres sont calculées. En
pratique, le filtrage spatial est imposé par le maillage : seules les
structures plus grosses que le maillage seront résolues.
Par ailleurs, des modèles, dits modèles de
sous-maille, sont introduits pour simuler la turbulence des petites
échelles. Avec ce genre de simulation, il est possible d'obtenir des
grandeurs moyennes mais également des grandeurs fluctuantes, ce qui fait
l'intérêt de la LES en comparaison aux simulations RANS. Les
coûts de calcul, certes plus importants que pour des simulations RANS,
restent raisonnables et autorisent la simulation de géométries
complexes sur des maillages raffinés.
8.3) La simulation des équations de Navier Stokes
moyennées (RANS)
Les simulations RANS résolvent les équations de
Navier-Stokes moyennées. En d'autres termes, la turbulence est ici
entièrement modélisée. De ce fait, les résultats
obtenus ne sont pas toujours représentatifs de la réalité,
surtout si les configurations simulées sont complexes (en situation
réactive notamment). Toutefois ce type de simulation permet d'obtenir un
bon ordre de grandeur de l'écoulement moyen aussi bien en termes de
vitesse que de température ou de pression. C'est pour cela que beaucoup
des codes industriels actuellement sur le marché sont basés sur
ce principe. Le coût de calcul (en temps CPU) est en effet relativement
faible, ce qui permet de simuler des configurations très complexes sur
des maillages raffinés.
Le schéma suivant définit une comparaison graphique
approximative des principales simulations


Figure (2.4) : La comparaison graphique des
déférentes simulations
9) Les équations moyennées

On introduit dans les équations de Navier Stokes une
décomposition, en une moyenne et une fluctuation, d'une composante du
vecteur de vitesse ou, u ou. Celles ci peuvent
s'écrire sous la forme :
u u u (2.4)
Où u une valeur moyenne indépendante du temps et u
représente une partie fluctuante superposée à u.
Par définition, la moyenne temporelle de u est nulle, et
on peut donc écrire : u ? u
(2.5)
u ? u
(2.6)
Où représente un laps de temps suffisamment long
pour que les valeurs moyennes soient indépendantes du temps.
9.1) Quelques propriétés de la
moyenne
1' La moyenne d'une somme est égale à la somme des
moyennes :

g g
1' La moyenne d'un produit d'une fonction f par une
constante est :


Attention cela ne marche pas pour deux fonctions non
constantes:
9 g

v' La moyenne est invariant par elle-même : on tire de
cette relation et de la
précédente que : g g
v' La moyenne d'une fluctuation est nulle : u
v' Mais la moyenne du carré d'une fluctuation n'est pas
nulle: u u v' (Sauf si u )
v' On peut intervertir les opérations de moyenne et de
différentiations ~ mais
cela ne marche pas avec la dérivée
matérielle à cause du terme convectif (non linéaire). [10]
9.2) Equations de bilan moyennées au sens de Favre
Comme on souhaite obtenir des équations moyennées,
si on utilise la décomposition de Reynolds employée pour les
équations incompressibles :
|
Pour un terme comme
|
|
|
on aura :
)(
|
'~
|
|
(2.7)
(2.8)
(2.9)
(2.10)
(2.11)
|
|
|
)(
|
')
|
|
'
|
|
'
|
Et bien sur :
' = 0 ,
On constate que cette moyenne sera difficile à
utilisée en écoulement compressible en effet on souhaite que les
équations moyennées gardent la même forme. Favre donc a
définit un nouvel opérateur de moyenne (qui pondéré
par la masse) :
Þ
(2.13)
A partir de cette moyenne la partie fluctuante de sera
donnée par :
Comme la moyenne classique, l'opérateur de Favre est
linéaire, il est aussi idempotent dans le sens que :
|
Þ Þ
|
Þ
|
|
|
Þ
9
|
Þ
9
|
Þ
9
|
9
|
Þ
9
|
|
On remarque par ailleurs que
Þ
Þ
|
Þ
|
|
|
~ ~
Et
Þ
Donc
Þ
|
|
(2.15)
(2.16)
(2.17)
|
10) Equation de la continuité
L'introduction des valeurs instantanées au sens de Favre
donne,
·
·
·
(2.18)
On voit que donc que la moyenne de Favre permet de garder garde
la même forme à l'équation moyenne par rapport à
l'équation original instantanée.
11) Equation de conservation de la quantité de
mouvement
De la même façon, on introduit les valeurs
instantanée dans l'équation de la quantité de mouvement et
on obtient
~ ~ ~
Ou le tenseur de Reynolds s'écrit :
...
·
·
·
·
·
·
|
|
~ F (2.19)
|
|
|
|
(2.20)
|
U U
|
|
|
12) ( DUANOIEFIFIKAHAINFI
IEBTON111
Sa forme moyennée s'écrit :
~ Þ ~ Þ
Þ ~ ( ~ )
Ou
|
~
~ (2.21)
|
|
Þ ~ ~
|
v Þ
|
............ U U
|
(2.22)
|
|
Le terme u u
|
est dit énergie turbulente moyenne.
|
Pour l'équation d'état on aura :
(2.23)
13) Quelques modèles de la turbulence
Les équations moyennes résultantes comportent de
nouveaux termes qui traduisent la production des fluctuations des vitesses et
constituent le transfert d'un mouvement convectif dû aux fluctuations de
la vitesse. Ces nouveaux termes sont appelés les contraintes de Reynolds
( I ~ . ) . Celles-ci posent un problème de fermeture des
équations gouvernantes, dont la résolution doit passer par une
modélisation de la turbulence.
13.1) hypothèse de Boussinesq
Après qu'il fût établi
expérimentalement que les contraintes turbulentes augmentaient avec
l'augmentation de taux de déformation moyen des éléments
de fluide. Boussinesq proposa une relation entre les contraintes de Reynolds et
le taux de déformation, qui été donné par la
suite:
~ ~ ~ ~
~ ~ 3 (
) (2.24)
Où est le symbole de Kronecker et l'énergie
cinétique turbulente u u
Dans cette équation, le terme à modéliser
est la viscosité turbulente , elle est liée dans la plupart des
modèles aux structures turbulentes de l'écoulement à
l'aide d'une expression de la forme :
u l (2.25)
Ou u est la vitesse caractéristique de la turbulence et
I sa longueur caractéristique. Selon les modèles, la
viscosité peut être déterminée par une relation
algébrique, une ou deux équations différentielles.
13.2) Modèle à zéro
équation
Ce modèle de turbulence est le plus simple car celui-ci
ne fait appel à aucune équation de transport. Prandtl et
Kolmogorov ont proposé une viscosité turbulente
modélisée sur le produit d'une vitesse caractéristique U
et d'une longueur caractéristique de turbulence I :
u l (2.26)
Avec :
13.3) Modèle à une équation de
transport : Prandtl-Kolmogorov
La viscosité turbulente est déterminée comme
suite
v l (2.27)
L'énergie cinétique de la turbulence est
déterminée à l'aide d'une équation de transport, on
trouve :
1
(
) (2.28)
Donc on trouve:
v |
1 | (2.29)
13.4) Modèles à deux
équations
13.4.1) Modèle k-å
Ce modèle de turbulence est le plus utilisé en
pratique, dû à Launder et Spalding (1974). Il consiste à
introduire dans les équations de Navier-Stokes moyennées (ou
équations de Reynolds) une viscosité turbulente pour
modéliser les tensions de Reynolds et une diffusivité turbulente
pour représenter les flux turbulents de masse et de quantité de
chaleur. Cette viscosité est calculée à partir de deux
grandeurs : l'énergie turbulente par unité de masse k et la
dissipation par unité de masse. Ces deux grandeurs sont obtenues chacune
par résolution d'une équation de transport. La viscosité
turbulente :
e v ~
~ (
) (2.31)
e, sont données par les équations de transport
citées ci-dessous en n'import quel point du domaine
d'écoulement.
( )
~ ~ ~ ~
{ (2.32)
( E) ~
~ ~ ~ ~ ~ ~ ~ ~~
Et dans lesquelles le terme de production de l'énergie
cinétique turbulente , et les coefficients de diffusion et E
sont données par :
~
~
(2.33)
Et:
~~
{
(2.34)
E
~
Les coefficients du modèle sont déterminés
par l'expérience comme suit[26]:
9 E E 9 c o-E
13.4.2) Le modèle k-å RNG
Le modèle k-å RNG a été
dérivé utilisant une technique statistique appelle «
Renormalization », il contient les avantages suivants :
ü Un terme additionnel dans l'équation de (å)
qui améliore la précision des écoulements avec contraintes
rapide.
ü L'effet de tourbillonnement est amélioré
afin de croitre la précision des écoulements tourbillonnaires.
ü Prendre en compte l'effet des bas nombres de Reynolds.
ü Donc les équations de transport sont :
( )
~ ~~ ~ ~ ~
( E) ~ ~
~
~ ~ ~~ ~ ~ ~ ~~
{ (2.35)
Les coefficients et Esont les inverses du nombre de
Prandtl pour k et å
respectivement. Pour un nombre de Reynolds
élevé:
|
Þ E
E Þ E3
|
Þ ~
|
E ) ~Þ Þ (2.39)
|
( - )
E 9 , ff E E E
Avec:
~
(2.36)
{
ili = 0.012
Étant une mesure scalaire du tenseur de déformation
:
v (2.37)
Est le tenseur des taux de rotation :
((2.38) Les constantes de ce modèle sont standard [11]
:
9 E E 9 c ciE
Ces valeurs sont déterminées de l'expérience
pour étudie un écoulement cisaillées. 14)
Correction de Pope
Le modèle k-å prédit d'une manière
très correcte les configurations planes, cependant il sous estime
l'épanouissement des jets rond par environ 15%. Plusieurs auteurs on
essayés de corriger ce problème en agissant directement sur les
constantes du modèle. S. Pope a proposé une explication physique
du problème du modèle k-å, selon laquelle il remarque que
dans les écoulements axisymétriques, les tourbillons toriques qui
entourent le jet vont être étirés, ce
qui provoque un taux de dissipation plus important
comparativement au cas plan [11].
Mathématiquement, cette correction introduit un nouveau
terme source dans l'équation de qui s'écrit :
|
Þ
E
|
Þ
u ~Þ *(
Q ) ~Þ
+
|
|
Notions sur la turbulence
|
|
|
|
|
|
|
36
|
|
Avec :
Þ
Þ
Þ
|
Þ
|
Þ
~Þ
~
|
Þ
Þ
|
~
|
Þ
|
~
|
(2.40)
(2.41)
(2.42)
|
|
Þ
~Þ
~
|
Þ
|
Þ
|
~
|
|
Þ
|
|
|
|
Dans le cas d'un écoulement axisymétrique sans
prérotation, l'invariant Þ se réduit á :
~
( Þ ~Þ
Þ (~Þ Þ) ~ Þ
) (2.43)
L'étirement des tourbillons n'intervient pas dans les
écoulements plans, limitant ainsi la correction aux cas
axisymétriques seulement.
15) La fermeture du second ordre
Il est possible de dériver des équations exactes
pour les contraintes de Reynolds en prenant la moyenne temporelle (moment du
second ordre).
1 (i ) l u ) (2.44)
Où u ) est l'opérateur de Navier-Stokes c a d :
u )
au a
a a ~
~~
~
~
On utilisant la moyenne de l'équation (2.44) pour cette
dernière on obtient l'équation du transport des contraintes de
Reynolds pour un écoulement incompressible donnée par :
u E k (2.45)
k k
Avec : est la production de l'énergie cinétique de
turbulence, le terme des
contraintes de pression, e le terme du taux de dissipation et est
le terme de diffusion du
troisième ordre, ils sont donnés par
:
(2.46)
k k
|
Notions sur la turbulence
|
|
|
|
37
|
|
E
|
|
|
U
|
(2.47)
(2.48)
(2.49)
|
|
(
|
~
|
|
U
|
|
k k
|
|
U U U
|
La partie est la partie fluctuante du tenseur de contraintes. La
première partie de
est le terme de triple vitesse, il représente le
transport par la convection fluctuante. Les deux
autres termes sont de
transport de pression (la corrélation vitesse pression). On remarque
que
l'équation des contraintes de Reynolds contient une autre
inconnue d'ordre supérieur
( u ~ u ). L'équation (2.49) peut être fermée
par une formulation empirique, cela est du à la nature non
linéaire des équations de Navier-stokes.
16) Conclusion
Cette analyse du phénomène de la turbulence a
montrée les différentes approches de la simulation
numérique utilisée pour les écoulements turbulents. On a
mis en évidence les caractéristiques de l'approche RANS et le
modèle - ~~.
CHAPITRE III
NOTION ET MODALISATION DE LA COMBUSTION
1) Introduction
C'est quoi la combustion ?
Les Phénomènes de combustion se composent de
nombreux processus physiques et chimiques qui présentent un large
spectre d'échelles de longueurs et de temps à déterminer.
Une description mathématique de la combustion n'est toujours triviale,
bien que certaines solutions analytiques des situations simples des flammes
laminaires existent. Ces modèles analytiques sont
généralement limités à des problèmes de
zéro ou une dimension de l'espace.
La combustion est aujourd'hui un des principaux moyens de
conversion de l'énergie. Elle est utilisée dans de nombreux
systèmes pratiques aussi bien pour produire de l'énergie
thermique (chaudières ou fours domestiques et industriels) ou de
l'électricité (centrales thermiques), que pour le transport
(moteurs automobiles et aéronautiques, moteurs fusée, ...) ou
encore la destruction de déchets (incinérateurs). La combustion
peut être caractérisée comme une (ou des)
réaction(s) irréversible(s) fortement exothermique(s) entre un
combustible (ou réducteur) et un comburant (ou oxydant) selon le
schéma global :
Combustible + comburant ? produits de combustion +
énergie thermique
Plus précisément, cette réaction induit
un fort dégagement de chaleur dans une zone très mince (les
épaisseurs typiques de l'ordre de 0,1 à 1 mm) conduisant à
des gradients thermiques très élevés (le rapport des
températures entre réactifs et produits de combustion est
couramment de 6 à 8) et à de larges variations de la masse
volumique ñ. Le taux de réaction raide et fortement non
linéaire (Loi d'Arrhenius en laminaire).
Les combustibles les plus divers, qu'ils soient gazeux,
liquides ou solides peuvent être utilisés :bois, charbon,
hydrocarbures (méthane CH4, propane C3H8 , essence, gasoil,
kérosène, fuel, ...), l'hydrogène (H2)... Le comburant est
le plus souvent l'oxygène de l'air, plus exceptionnellement de
l'oxygène pur (moteur-fusée, certains
fours industriels) qui permet d'atteindre des
températures plus élevées et éviter le stockage
d'azote inerte mais pose des problèmes de sécurité. Plus
rarement, d'autres comburants sont utilisés (moteurs fusée
pyrotechniques) [12].
Deux situations génériques idéales,
schématisée ci-dessous, ont été identifiées,
selon la procédure utilisée pour introduire les réactifs
dans le foyer. Dans les flammes prémélangées
(figure 3.1), les réactifs, combustible et comburant, sont
mélangés avant la zone de réaction. Au contraire, dans les
flammes non- prémélangées ou de diffusion
(figure 3.2), les réactifs sont introduits
séparément, de part et d'autre de la flamme et sont alors
essentiellement entrainés l'un vers l'autre par diffusion
moléculaire.
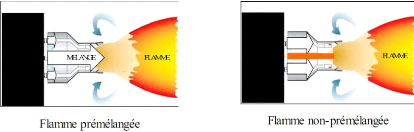
Figure( 3.1) Figure (3.2)

Figure (3.3) : Schéma de la structure d'une flamme
laminaire de prémélangée bidimensionnelle
(gauche)et
d'une flamme de diffusion (droite) [12].
La combustion prémélangée est, a priori,
plus efficace puisque les réactifs sont déjà en contact
avant la combustion. Mais, une telle flamme est susceptible de se propager dans
le mélange combustible/oxydant jusqu'à l'endroit où
s'effectue le mélange, ce qui pose de problèmes de
sécurité. En revanche, si la flamme de diffusion
moléculaire requiert l'apport de réactifs
à la zone de réaction par diffusion moléculaire, elle ne
peut en aucun cas remonter l'écoulement et est donc plus sure. Sa
réalisation pratique est aussi plus simple puisqu'elle ne
nécessite pas un mélange des réactifs dans des proportions
bien définies (c'est-à-dire dans les limites
d'inflammabilité du combustible). Un bruleur non
prémélangée est souvent simplement constitué, par
exemple, d'un injecteur de combustible dans le l'air ambiant ou d'un ou
plusieurs groupes d'injecteurs de comburant(moteur-fusée, fours,...).
Dans la combustion intervenant en milieu gazeux, quatre
situations génériques, résumées sue le figure(3.4),
sont identifiables, selon que l'écoulement est laminaire ou turbulent et
les réactifs prémélangée ou non. En pratique, la
combustion a le plus souvent lieu au sein d'écoulement turbulents
où les transferts sont plus intenses qu'en écoulement
laminaire.
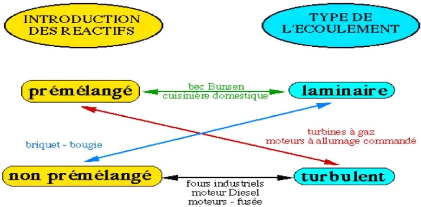
Figure(3.4) : Système pratiques de combustion
classée selon le type d'introduction
des
réactifs(prémélangée ou non) et la nature
laminaire ou turbulente de l'écoulement.
La principale difficulté réside alors dans
l'interaction entre l'écoulement turbulent et le dégagement de
chaleur qui met en jeu une large gamme d'échelles
caractéristiques : échelles spatiales et temporelles de la
turbulence et des réactions chimiques. Les rapports de ces
échelles dépendent d'ailleurs fortement des aspects
étudiés. Ainsi, le temps caractéristique de l'oxydation du
combustible est généralement court comparé aux
échelles des phénomènes turbulents. En revanche, la
formation des
espèces polluantes (oxydes d'azote en particulier) demande
des temps caractéristiques sensiblement plus longs.
L'objectif des recherches en combustion turbulente est
principalement de mieux comprendre les phénomènes complexes qui
entrent en jeu pour pouvoir les modéliser car l'objectif final est la
simulation numérique complète d'un système industriel. En
effet, les coûts de développement d'un prototype, qu'il s'agisse
d'un moteur automobile ou d'un réacteur d'aviation, sont
extrêmement chers. Ils pourraient être sensiblement réduits
en optimisant par simulation numérique un foyer avant de construire un
prototype aussi proche que possible du produit final. Cette optimisation peut
se faire selon différents critères suivant la destination finale
du produit : rendement maximal, moindres émission polluantes, etc....Ils
s'agit aussi d'éviter, ou de contrôler l'appariation
d'instabilités de combustion (couplage entre hydrodynamique de
l'écoulement, dégagement de chaleur et champ acoustique qui
conduit à de fortes oscillations des caractéristiques du
système, augmentant les bruits et les transferts de chaleur et pouvant
conduire à une destruction rapide de l'installation). A l'heure
actuelle, si certaines tendances sont bien reproduites par les calculs, des
simulations numériques vraiment prédictives sont encore loin
d'être disponible.
2) Echelles caractéristique d'une
flamme
Les écoulements prémélangés se
caractérisent par le fait que le combustible et l'oxydant sont
mélangés a une échelle moléculaire. Une
augmentation de la température locale, l'ignition, peut démarrer
le procédé de la combustion si l'écoulement
prémélangé est dans les limites
d'inflammabilité[13]. La combustion se fait sous la forme d'un front de
flamme se propageant dans l'écoulement.
Le temps caractéristique de la chimie et les
échelles de longueurs qui décrivent ces structures sont
déterminées par l'étude de la structure interne d'une
flamme laminaire de prémélangé. La figure 3
représente la structure interne d'une flamme laminaire stationnaire. Les
zones caractéristiques peuvent être identifiées par : la
zone de préchauffage, la couche interne et la couche d'oxydation.
La zone de préchauffage est d'épaisseur 0(1),
elle est chimiquement inerte avec un équilibre de la convection et la
diffusion. Dans cette zone les gaz frais qui s'approchent de la flamme avec une
vitesse sont initialement préchauffés.
La couche interne est une zone mince réactive
d'épaisseur 0( ) [14]. Le combustible est consommé dans cette
région avec un équilibre diffusif-réactif. La couche
interne est caractérisée par sa température , qui
correspond à la température de passage entre les réactions
en chaines de branchement et de rupture [15]. Le procédé de
combustion est maintenu si la couche interne demeure intacte. Les
réactions dans la zone interne peuvent s'interrompre si le transport de
chaleur et des radicaux vers l'extérieur dépasse leurs
productions dans la couche interne, ce qui provoque l'extinction de la
flamme.
Dans la couche d'oxydation de taille 0(e), le OO et l'H2
s'oxydent pour former le OO2 et l'H2O. Oes réactions sont d'une
importance mineure par rapport aux caractéristiques de la flamme.
Les échelles caractéristiques de longueur
peuvent être identifiées dans la structure de la flamme laminaire.
L'épaisseur de la flamme laminaire F est approximée
par la taille de la zone de préchauffage définie par [1] :
|
|
( p/ )
( ) (3.1)
|
|
F (O O / )
|
OU est la conductivité thermique, Op la chaleur
spécifique à pression constante, la densité et la vitesse
de la flamme laminaire qui décrit la vitesse à laquelle le front
de flamme prémélangée se propage dans la direction normale
dans le mélange frais(une propriété thermochimique).
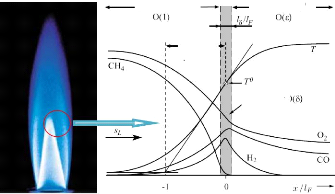
Zone de préchauffage Couche d'oxydation
Epaisseur de
Couche interne
Figure(3.5) : structure interne d'une flamme laminaire
stationnaire de méthane-air
3) Combustion laminaire
On considère les flammes en milieu laminaire, c'est
à dire en milieu où les échanges par diffusion turbulente
sont pratiquement inexistants. Si les flammes laminaires semblent n'intervenir
que dans quelques applications plutôt anecdotiques (bougies et flamme de
briquet) la compréhension de la structure de ces flammes est cependant
fondamentale pour la description et la modélisation de nombreuses
situations industrielles.
3.1) Flamme laminaire
prémélangée
Le combustible et le comburant sont mélangés
à l'avance, la propagation de la flamme est le résultat d'une
opération composée de deux phénomènes :
· Un préchauffage qui se fait sur une
épaisseur äp où les réactions chimiques sont
inexistantes et où les phénomènes convectifs et diffusion
de masse et de chaleur sont prépondérants.
(Gaz frais)
Préchauffage
Zone de
La zone de la réaction
är
Gazes brulés
Figure (3.6) : schéma d'une flamme laminaire
prémélangée
· Arrivant à un certain niveau de
température, les gaz réagissent en dégageant de la
chaleur, c'est la zone de réaction qui se déroule sur une
épaisseur är. Cet échauffement se fait sur une
épaisseur äL qu'on appelle épaisseur de la flamme laminaire
et qui peut être assimilée à la distance parcourue par la
chaleur libérée
par réaction pendant le temps ôc
que dure cette réaction. Ainsi, en faisant intervenir le coefficient de
diffusion thermique D.
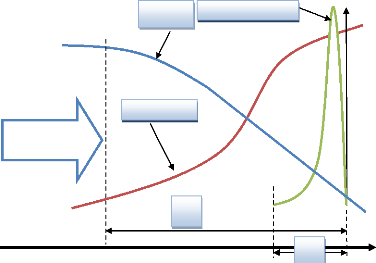
Vitesse des gazes
Température
Réactifs
äL
Taux de réaction
är
Figure (3.7) : Structure d'une flamme laminaire
prémélangée
L'épaisseur de la flamme est exprimée par [8] :
( ) (3.2)
Ces zones se déplacent dans le milieu à une
vitesse de propagation perpendiculaire au front de flamme que l'on appelle
vitesse de flamme laminaire et que l'on note UL. Cette vitesse
dépend de différents paramètres (nature des
réactifs, richesse des mélanges et température des gaz
frais) est de l'ordre de 0.1 à 1 m/s [17].On peut dire que le front de
la flamme progresse pendent le temp de combustion (reaction)
. Sa vitesse est de la forme :

( ..) (3.3)
~
La relation entre la température et le coefficient
d'équilibre est donnée comme suite :
(- ) (3.4)
Ou bien comme :
~
(- ) (3.5)
Tel que les coefficients A B C D E et F sont des constants
tabulés.[18]
3.2) Flamme laminaire non
prémélangée
La caractéristique principale de la flamme non
prémélangée, dite de diffusion, consiste en une zone de
réaction séparant les réactifs (combustible et oxydant).
Les profils des fractions massiques et de température sont
présentés sur la figure suivante :
COMBUSTIBLE
Combustible
La flamme
TEMPERATURE
OXYDANT
TAUX DE REACTION
Oxydant
Figure (3.8) Profile d'une flamme laminaire non
prémélangée
Comme les flammes de prémélangé, les
flammes de diffusion se développent grâce au concours des
phénomènes de réaction ainsi que des
phénomènes de diffusion de chaleur et de masse qui se produisent
de part et d'autre de la zone réactive.
Le phénomène de convection joue cependant un
rôle plus important en amenant les réactifs et en emportant les
produits de façon plus efficace que la diffusion seule. Pour que la
flamme reste laminaire, il faut que les vitesses d'écoulement ne soient
pas trop grandes. Le taux de réaction de ce type de flammes est
principalement contrôlé par diffusion moléculaire qui
gouverne l'apport des réactifs vers les flammes.
Considérons la réaction chimique entre le
combustible F et l'oxydant O : F s ( s)F (3.6)
Où s désigne le coefficient
stoechiométrique massique.
En terme de fraction massique cette réaction devient :
F F p (3.7)
YF,YO, YP désignent les fractions massiques et les
coefficients stoechiométriques
molaires de la réaction.
Les équations de transports des fractions massiques sont
;
a
a
a
a
a
a
_ p ( F F) ? F (3.8)
( ) ? (3.9)
( ~ ) F? ( ) (3.10)
p
Où la diffusion moléculaire des espèces est
décrite par la loi de Fick.
Q est la quantité de chaleur libérée par la
combustion d'une unité de masse de combustible.
Une nouvelle grandeur nommée fraction de mélange Z
(variable de Schwab-Zeldovich) est définit par :
(
) (
) (3.11)
F est la fraction massique de Fuel dans l'écoulement
(cette fraction massique peut être inférieure à
l'unité si le combustible est dilué) [18].
Et est celle de loxydant (typiquement dans l'air est égale
à 0.23).
Si on suppose que les coefficients de la diffusivité
massiques du combustible et
comburant sont égaux (DF = DO=D) alors la grandeur Z sera
un scalaire passif qui suit une équation de convection-diffusion sans
terme source :
a a a
a a a
( a
a ) (3.12)
Les propriétés de ce scalaire passif sont
très intéressantes sont ;
· Z=1 dans le combustible.
· Z=0 dans le comburant.
· Z(x,t) represente le degré du mélenge de
combustible dans le comburant. Sous l'hypothèse de la chimie infiniment
rapide (c à d l'oxydant et le combustible ne coexistent jamais sans
réagir), le front de la flamme est définit par la relation
~ correspondant à l'iso-surface
vi
T
Oxydant
Combustible
0 Zst 1
Figure(3.9) Fractions massiques réduites du
mélange en fonction de Z dans le cas de la chimie infiniment
rapide(
solution de Burke et Schumann)
On peut réécrire les équations des
fractions massiques et de la température dans un nouveau système,
où elles sont exprimées en fonction de la fraction de
mélange uniquement.
On supposant que les effets instationnaires sont
négligeables, ce qui donne :
2 ( ) (3.14)
Or est la dissipation scalaire de Z.
Dans le cas de la chimie infiniment rapide (hypothèse
de Bruke et Schumann) le taux de réaction ? est nul en dehors de la zone
de la reaction definie par Z=Zst . Dans ce cas les
fractions massiques et la température sont alors affines par morceaux.
(Voir la figure(3.9).
4) La combustion turbulente
Dans un foyer, l'écoulement est turbulent,
c'est-à-dire que la vitesse des gaz, mesurée en un point, fluctue
continument de façon apparemment aléatoire, même en
régime parfaitement établi; cela est vrai aussi pour la
température et toute autre caractéristique du milieu. Cette
turbulence est due à une forte vitesse de l'écoulement entrant ;
elle s'est développée dans le canal amont à cause des
gradients de vitesse aux parois et à partir d'obstacles tels que les
injecteurs. Le taux de dégagement de chaleur et la structure de la
flamme, varient selon des temps caractéristiques, qui sont souvent le
temps de la réaction chimique ôc et le temps
de fluctuation de l'écoulement ôt.
4.1) La combustion turbulente
prémélangée
Dans la combustion turbulente prémélangée
les structures de la turbulence influent le front de la flamme qui peut avoir
une vitesse d'ordre de (10 m/s) et d'une épaisseur de (1 mm) jusqu'au
(1m). Cette interaction peut produire une augmentation de la consommation de la
masse et une augmentation de l'épaisseur globale de la flamme.
4.1.1r1ll11f14EF la turbulence sur les
flammes
Damkohler en (1940) est le premier qui a décrit la
combustion turbulente et a introduit le principe de rides comme le principal
mécanisme qui contrôle les flammes turbulentes.
Dans une combustion turbulente, ST est la vitesse
à l'entrée du volume nécessaire pour maintenir la
combustion turbulente stationnaire, cette vitesse est dite vitesse de la flamme
turbulente.
4.1. Erif lgniViliM
On a vu que dans un écoulement turbulent
réactif, la combustion dépend de la turbulence, aussi la
combustion a une influence sur la turbulence. Quand la température passe
du front de flamme vers celle des gaz frais, la viscosité et le nombre
de Reynolds local sont modifiés en conséquence.
Par exemple, pour l'air la viscosité est proportionnelle
á T1.7, pour une flamme
avec taux de température de le nombre de Reynolds est 40
fois plus petit dans les
gaz brulés. C'est pourquoi on observe le
phénomène de relaminarisation (après l'allumage
l'écoulement turbulent peut devenir laminaire) [18].
4.2) Classification des flammes
La classification de la combustion turbulente
prémélangée peut être faite si on
observe
l'interaction entre le front de flamme (épaisseur et vitesse
SL) et l'ensemble des
tourbillons (échelles
intégrales lt jusqu'aux tourbillons de Kolmogorov avec la
taille
) où :
(
~ ~ ) (3.15)
Et de la vitesse de Kolmogorov á la
vitesse intégrale [8].
La relation entre le rapport de l'échelle intégrale
lt et la longueur de Kolmogorov est donné par
Si on suppose que la turbulence est homogène et isotrope
alors la vitesse u'(r) s'exprime par :
( ( ))
£ (3.17)
Ou r désigne la taille des tourbillons.
Le temps turbulent typique pour un tourbillon de taille
r
( )
( ) ~ (3.18)
On compare avec l'échelle de temps d'une flamme (chimique)
telque
/ (3.19)
On introduire le nombre de Damköhler Da qui
caractérise le temps de la turbulence par rapport au temps de la
chimie
Da(r) change lorsque r varie de la taille de
Kolmogorov vers l'échelle integralle lt.
A quelle valeur de r peut on contrôler la
structure de la flamme ?
Les approches classiques introduisent deux nombres correspondant
pour limiter la valeur de r :
. Le nombre de Damköler definit pour les
grands tourbillons et correpondantà
l'échelle integrale de temps t/ ( D et à
l'échelle de temps chimique ;
li
1
a
c
/ (/ ) (3.21)
/
Le nombre de Karlowitz Ka correspondant aux petits
tourbillons, donc c'est le rapport de l'échelle de temps chimique et du
temps de Kolmogorov ;
a c
~
a( ) m( )
( ) / (3.22)
/
Ce nombre peut s'exprimer comme suit

~
~ (~ ( v~ /
) ) ( ) / (3.23)
Le nombre de Reynolds turbulent basée sur l'échelle
intégrale s'écrit:
I ( ) (~ ) (3.24)
Ou bien :
a a (3.25)
5) Diagramme de la combustion turbulente
prémélangée
On peut distinguer plusieurs types de flammes turbulentes
prémélangées suivant la valeur des deux nombres
caractéristiques
et ~
, et sont la vitesse et longueur
caractéristiques de la turbulence qui règnent
dans la flamme au point considéré, et est la vitesse, est
l'épaisseur d'une flamme laminaire[19]. Trois droites divise le
diagramme de Borghi (Borghi 1984, Candel et Al 1994, Poinsot et Al 1991) en
quatre domaines chacun a un comportement spécial. La première
droite est pour le nombre de Reynolds turbulent égal a 1, la
deuxième correspond au critère de Kilmov-Wiliams KW, qui
égalise entre le temps global de la réaction et le temps de
Kolmogorov , et la troisième est pour un nombre de Damkohler
a=1. Pour bien éclairer cette opération, on va
définir les différents paramètres utilisés
au-dessus dans le tableau suivant :
|
Echelle de
|
Flamme
|
Turbulence
|
|
|
Nombre
|
|
Temps
|
Temps global de la
réaction
|
Temps de Kolmogorov Temps intégral
6
|
/
(V ~)
|
a
--
|
|
Longueur
|
L'épaisseur de la flamme laminaire
|
L'échelle intégrale L'échelle
intégrale de
Kolmogorov (v ~
|
|
/
|
|
|
4 /
)
|
6
|
Tableau(3.1) : échelles temporelles et spatiales pour les
flammes turbulentes prémélangées
D'après le diagramme de combustion on peut remarquer qu'on
a quatre régimes :
Régime1: , dit régime des
flammes plissées, les fluctuations turbulentes
sont
très petites devant la vitesse de propagation laminaire de
la flamme >> . C'est à
dire que les déformations du front de flamme à
cause des tourbillons sont détruites par la propagation du front de
flamme, donc la turbulence ne produit aucun effet sur la flamme qui reste
laminaire, seulement des petits plissements peuvent être observés.
Ce régime est nécessaire pour l'amélioration du
procédé de combustion.
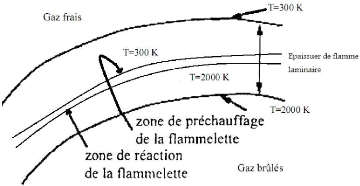
Figure(3.10) :regime1 de combustion
Régime 2 : Ce régime est
limité par et par , il est divisé aussi en deux
sous régimes, le première au-dessous de
~ , le front de flamme laminaire est
affecté par les contraintes de la turbulence dont
l'échelle spatial de Kolmogorov est
très grande devant , cela veut dire que la rotation des
tourbillons de grandes échelles est supérieure à la
vitesse de la flamme laminaire, ondulant aussi le front de la flamme. Seulement
le front de flamme est déformé sans être
déchiré, par contre le rapport U > , les plissements va se
déformer de plus en plus, c'est le régime des flammes
ondulées. Les deux régimes 1 et 2, sont dit les
régimes des flammelettes.
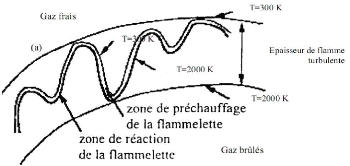
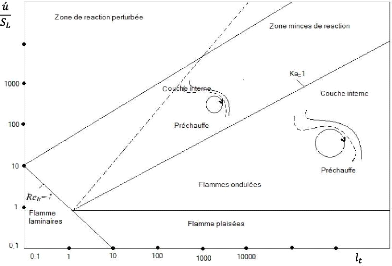
Figure(3.11) :regime2 de combustion
Régime3 : Ce régime est dit
régime de la zone de réaction,
limité par K - W = 1 et par la droite Da = 1,
l'échelle de Kolmogorov 11k est donc petite devant l'épaisseur de
la flamme laminaire SL et T > Tk.Dans ce cas les contraintes dues aux
petites structures de la turbulence peuvent influencer la structure interne du
front de flamme instantané et donner lieu a son étirement qui
peut modifier son épaisseur et sa vitesse de propagation laminaire.
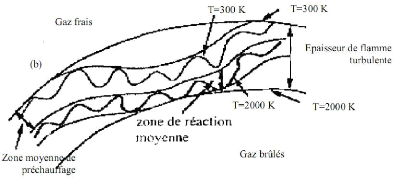
Figure(3.12) :regime3 de combustion
Régime4 : Ce régime est
appelé régime de la zone perturbée,
c'est l'expansion du régime précédent, il se
caractérise par un nombre de Damkohler inferieur à 1. Dans ce
régime aucun plissement de flamme ne peut exister, on parle seulement de
la zone de réaction que de flamme avec une épaisseur
définie. En d'autres termes, les plus petits
tourbillons pénètrent dans la couche interne,
provoquant des ruptures locales des réactions chimiques dues à la
perte de chaleur en direction de la zone de préchauffage et induisant
une diminution de la température et une perte des radicaux.
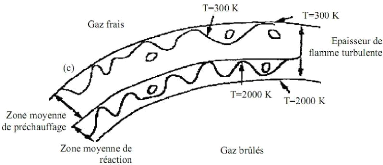
Figure(3.13) :regime4 de combustion

Figure (3.14) :Diagramme de régimes de la combustion
6) Modélisation de la combustion
turbulente
Pour maitriser et optimiser la combustion turbulente, il faut
comprendre les mécanises qui intervient dans ce phénomène
et les interactions entre la turbulence et les flammes. Pour cela deux voies
sont possibles, celle expérimente qui reste très couteuse, non
accessible et limitée surtout dans l'espace. L'autre alternative est le
calcul numérique par l'intermédiaire de la modélisation de
la combustion turbulente. Dans ce cas et suivant l'échelle de temps et
de l'espace de la combustion et de la turbulence, on peu se situer d'une
façon grossière sur le diagramme de combustion, cela va permettre
de connaitre le type de flamme qui va être modélisée.
Les mesures de l'expérience utilisée dans notre
travail [1],[2] montrent que l'échelle de temps de la réaction
est très court par rapport à celui de la turbulence, aussi les
fluctuations turbulentes et la vitesse de la flamme laminaire sont comparable.
Ceci dit, la combustion se passe dans le régime des flammelettes ou un
découplage de la chimie du champs dynamique turbulent est possible.
Parmi les modèles les plus simples et les plus utilisé dans ce
type de flammes, l' EDM (Eddy dissipation Model).
6.1) Modèle Eddy Break Up
Ce modèle est basé sur une analyse
phénoménologique de la combustion turbulente aux grands nombres
de Reynolds (Re>> 1) et de Damkhöler (Da >> 1). Suivant la
cascade de Kolmogorov, la turbulence provoque la cassure des tourbillons des
gaz frais. Une des premières approches modélisant le terme source
chimique moyen est proposé par Spalding[20]. Il suppose que le
mélange turbulent contrôle le taux de réaction chimique. En
prenant une reaction chimique irréversible à un pas:
R (réactifs) P (produits)
Le taux de réaction moyen est donné pour les
produits par :
~~ U Þ ~Þ ( Þ~ ) (3.26)
Avec Þ~ la variance de la fraction massique des produits et
U une constante libre de
modélisation.
Plus tard, ce modèle est amélioré par
Magnussen et Hjertager [11], donnant ainsi
le modèle EDM (Eddy
Dissipation Model). Dans ce dernier, la variance est
substituée par la fraction massique de l'espèce en
déficit. D'où, le terme source moyen est calculé par :
~ Þ~ Þ n ( Þ~ Þ' Þ~
) (3.27)
Où A et B sont des constantes de modèle et est le
coefficient stoechiométrique donné par :
M
M
íO est le coefficient stoechiométrique de
l'oxygène et íF est le coefficient
stoechiométrique du fuel.
En plus, les termes de transport turbulent pour les scalaires
réactifs sont modélisés par l'approximation en gradient.
Dans les deux modèles l'échelle de temps chimique est
remplacée par celle du temps turbulent, représentant la chimie
infiniment rapide seulement. Il faut noter que les constantes des deux
modèles sont libres. Elles sont déterminées par
optimisation pour chaque combustible et pour chaque géométrie.
Ces modèles sont largement utilisés dans les codes, surtout pour
démarrer d'autres modèles plus compliqués, à cause
de leurs implémentations très simples et leurs coûts en
calcul négligeable.
6.2) Modèle EDM dans le code FLUENT
Le modèle EDM est intégré dans le code
fluent, le taux de production d'une réaction élémentaire
k, est déterminé par le minimum des deux expressions
suivantes : Limiteur des réactifs
E
V
V
~ (
~ ~ ) (3.28)
V
Limiteur des produits
E ? p p (3.29)
? v
~! M
Avec , est la fraction massique des produits et la fraction
massique du réactif R, A et B sont des constantes qui prennent pour
valeurs 4 et 0.5.
7) Variable d'avancement de la
réaction
L'avancement de la réaction ou de la flamme est le
résultat d'un grand nombre de réactions chimiques
élémentaires. Pour l'hydrocarbure le plus simple, une dizaine
d'espèces intermédiaires et une centaine de réactions
chimiques sont nécessaires. Cependant, il faut noter que peu de
réactions influent le procédé général. Par
conséquent, l'avancement chimique peut être
représenté par peu de variables et dans le cas le plus simple par
une variable d'avancement de la réaction c. Cette variable doit
être normalisée et varie entre zéro (pour le mélange
frais) et un (pour le gaz brûlé) figure suivante :
Gaz frais Gaz brûlés
Font de flamme
Figure(3.15) : Définition de la variable d'avancement
Dans les systèmes adiabatiques fermés, la
température varie d'une manière monotone en fonction du
procédé chimique. Dans ce cas, une fonction de la
température normalisée peut définir la variable
d'avancement de la réaction c :
( ~ )
( ~ ) (3.30)
Où T représente la température
locale effective, Tf la température des gaz frais et
Tb la température adiabatique des gaz complètement
brûlés.
La variable d'avancement peut être également
basée sur une fraction normalisée d'une espèce des
réactifs ou de produit stable de la combustion. Par exemple, Ferreira
[11].utilisa la définition suivante :
( -- )
( -- ) (3.31)
Avec YF est la fraction massique réelle locale du
combustible, YF, f et YF, b représentent
respectivement les fractions massiques dans les conditions fraîches et
brûlées.
Conclusion
Dans ce chapitre on a vu les différents types de la
combustion et les régimes concernant la combustion turbulente
prémélangée, ainsi que l'influence de la turbulence sur la
flamme et l'effet inverse.
Le modèle utilisé est celle d'EDM qu'est simple et
est contrôlé par la turbulence pour l'hypothèse de la
chimie infiniment rapide.
CHAPITRE VI
RESULTATS DU CALCUL
NUMERIQUE
1) Dispositif expérimental
1.1) La chambre de combustion

Couvercle
Accès optique
Vérin de brûleur
Cylindre en acier
Matériel de mesure
Figure (4.1) : Installation de combustion haute pression
La chambre de combustion (figure 4.1) est composée de
deux cylindres en acier, chacun a une hauteur de 600 mm et un diamètre
intérieur de 300 mm. Les deux blocs ont quatre accès optiques
circulaires de diamètre 100 mm disposés à 90°. Les
deux parties sont superposées et coiffées par un couvercle qui
récupére les condensats issus de la combustion, qui sont ensuite
évacués par une pompe. La pression est réglée par
quatre soupapes de sécurité posées sur le couvercle. A la
base de la chambre de combustion de trouve un bruleur pouvant se
déplacer verticalement car les dispositifs de mesure sont fixes. Les
accès optiques sont chauffés par des résistances
électriques afin d'éviter la condensation d'eau.
1.1) Le bruleur
C'est un tube en laiton enveloppé par un autre en acier
inoxydable, sa longueur est de 230 mm. Ce tube est muni d'une grille de
turbulence (de solidité = rapport entre la surface bloquée et la
surface totale = 51%) placée à 50 mm en amont de la sortie, afin
d'éviter les détériorations causées par les
problèmes de rentrée de la flamme. La flamme pilote est annulaire
de largeur 2 mm, elle permet de stabiliser la flamme principale lorsque le
mélange est pauvre et de compenser les pertes thermiques à la
base du bruleur. L'allumage de la flamme pilote est fait par une
électrode en cuivre (haute tension 11kv). Cette électrode ne
perturbe que très peu la flamme pilote et aucunement la flamme
principale. L'allumage de la flamme principale est réaliser par la
flamme pilote.
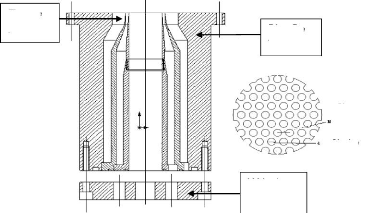
Flamme pilote
Distance entre 2 trous
Diamètre de trou
Vérin du brûleur
Disp. De fixation
Figure (4.2) : Bruleur de prémélangée
(gauche) et grille de tranquillisation de la turbulence (droite)
2) Modélisation de la chambre de combustion 2.1)
Géométrie de la chambre
La chambre de combustion est modélisée par un
cylindre de longueur 1.2 m. l'entrée d'air se fait par un injecteur de
diamètre de 25 mm et pénétrant dans la chambre d'une
distance de 150 mm. En raison de l'axisymétrie, on considère le
problème bidimensionnel.
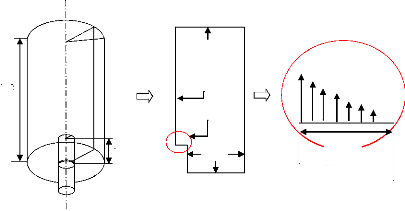
L=2
Sortie
Axe de
Zone
Linj=0.1 Paroi
U(m/s)
25 mm
Figure (4.3) : Géométrie détaillée de
la chambre de combustion
3) ( t7ISI-1H7X
prTq7I-1IS71jI-t1ISIBTr1t7rE7lI-Ht1ISBHT1lB1chambre de
combustion
Pour connaitre la structure de l'écoulement dans la
chambre de combustion, un premier test est fait avec un jet d'air non
réactif. Le mélange air-combustible est remplacé par la
même quantité d'air seul à température ambiante. En
effet, la proportion de méthane a richesse 0.6 ne représente que
0.4% en masse de la quantité d'air et ne change quasiment pas les
viscosités.
3.1) Conditions aux limites
Les conditions aux limites prises de l'expérience sont :
Entrée du jet principal
Vitesse u : (figure (4.4.1))
Energie de turbulence k : (figure (4.4.2))
Le taux de dissipation : son profile est calculé à
partir de celui de k par la relation 3/ ( P ), où P est le
diamètre hydraulique.
Sortie de la chambre
Pression de sortie : Celle de l'air ambiant, elle est prise
égale à 1 atm ou 101.3 kPa. Taux de turbulence :
L'écoulement à la sortie est établi, l'intensité de
turbulence est 1% Axe de symétrie de la chambre
On a choisis une limite de type axe de symétrie (tous les
gradients sont nuls avec vitesse v=0)
Parois solides
Les études expérimentales ont montrés que
l'effet des parois est négligeable.
|
Figure (4.4.1) : Profile de vitesse
d'entré (U)
|
Figure (4.4.2) : profile de
l'énergie
cinétique turbulente (K)
|
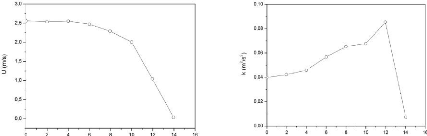
3.2) Maillage de calcul
La première étape du calcul réside dans
l'élaboration d'un maillage qui assure la convergence de la
procédure numérique, et qui est capable de capter toutes les
variations des paramètres dans le domaine de calcul. En plus, un
maillage doit assurer l'indépendance de la solution du raffinement
(augmentation du nombre de mailles), ce critère est dit «
indépendance maillage-solution ». Dans notre étude plusieurs
maillages ont été testés, on a choisis le maillage qui
assure ces critères avec un nombre minimal de cellules.
Le maillage de calcul élaboré est non uniforme,
il est fin dans la zone de forts gradients de vitesse (prés des parois
de l'injecteur, dans la couche cisaillée du jet). Les cellules les plus
petites sont placées sur les lèvres de l'injecteur. La figure
représente une partie du maillage à la proximité de sortie
d'injecteur. Le maillage est formé par 16291 noeuds.

Figure (4.5) : Maillage près de la zone d'injection
3.3) Calcul de l'écoulement non réactif et
ajustement de la correction de POPE L'introduction de la correction de
Pope (chapitre II) est faite par un programme externe, écrit en C++, qui
est compilé et exécuté avec FLUENT.
Mathématiquement, cette correction introduit un nouveau
terme source dans l'équation de Þ qui s'écrit (est
déjà vue dans le chapitre II) :
Þ t
Þ
~ Þ *( t
~ ) Þ
+ Þ
Þ
Þ

(4.1)
( 3 Þ -- )
Dans le cas du jet libre, le coefficient 3 9 . Dans notre cas,
et après plusieurs
calculs, on a trouvé que la valeur de 3 donne un meilleur
compromis entre les
variations axiales de l'énergie turbulence et la
vitesse.
3.3.1) Résultats du calcul
La figure (4.6) montre une comparaison entre les calculs et
l'expérience pour la vitesse u le long de l'axe. On peut dire que les
résultats sont très acceptables surtout lorsqu'on utilise la
correction de Pope. L'épanouissement du jet le long de l'axe est
très proche de l'expérimentale, la même constatation peut
être faite sur la figure (4.7) où on représente
l'énergie cinétique de la turbulence.
U
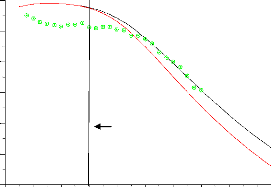
(X=0.2)
X
Calcul Exp. Calcul sans pope
Figure (4.6) : vitesse axial [m2/s2]
X
8 0.3 0.32 0
Calcul Exp. Calcul sans pope
Figure (4.7) énergie cinétique de turbulence k
[m2/s2]
3.3.2L[& Xr[SR,IQ,iIl
Une des caractéristiques les plus importantes des jets
est la longueur du coeur potentiel ou cône potentiel. Ce coeur est
crée par la décharge du jet dans la chambre de combustion ou la
vitesse est très faible (de l'ordre de 0.01 m/s). Le jet trouve la
couche de mélange et le phénomène d'entrainement qui le
font perdre sa quantité de mouvement au profit du fluide ambiant (figure
(4.8)). Cette perte se traduit par la diminution de la vitesse de jet à
sa périphérie et par une production de l'énergie de
turbulence k (figure(4.9)). A la sortie du bruleur, la zone du mélange
turbulent n'a pas d'épaisseur. Elle s'épaissit en
s'éloignant de l'injecteur et finit par atteindre l'axe ou la vitesse
axiale commence à décroitre. La zone limitée par la sortie
du brûleur et la position ou la vitesse axiale commence à
décroitre est appelée coeur potentiel.
La figure (4.6) montre le changement de pente (à x=
0.2m) indiquant la fin du coeur potentiel. Plus loin dans le jet, lorsque le
profil ne varie plus d'une section à l'autre, le jet est dit pleinement
développé.
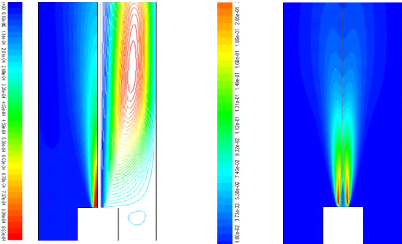
Figure (4.8) : Vitesse axiale (u) Figure (4.9) : Energie de
turbulence k
Les figures (4.8) et (4.9) montrent respectivement la
distribution de la vitesse et de l'énergie de turbulence. La vitesse est
maximale sur l'axe de symétrie, elle diminue pour
s'annuler sur les parois solides. La quantité du
mouvement introduite par le jet est transférée à
l'écoulement stagnant dans la chambre. Le mouvement tourbillonnaire dans
la chambre provoque une légère augmentation de la vitesse
à proximité des parois.
Pour l'énergie de turbulence, on remarque qu'elle est
produite essentiellement dans la zone de mélange entre le jet principal
et celui stagnant dans la chambre.
4) Calcul pour de l'écoulement réactif du
méthane-air
Après l'écoulement non réactif, on va
calculer la combustion turbulente pauvre du méthane avec valeurs
différentes de la richesse et nous conservons les autres conditions
telles que les profils de la vitesse (u) et l'énergie turbulente (k).
4.1) Les caractéristiques du mélange
(méthane/air) à l'entrée du bruleur
Nous avons comme données , la fraction massique du
combustible est donnée par :
(4.2)
Pour la réaction (méthane/air), on a
déjà calculé la valeur de s dans le chapitre I s = 4.00,
la mass molaire de N2 et O2 sont respectivement
MN2=28 (kg/mol) et MO2=32 (kg/mol).
Pour
YCH4=0.0337
Et comme
(4.3)
0
Alors
YO2=0.02243
Les fractions massiques obtenues pour les trois cas sont :
|
Richesse
|
0.6
|
0.7
|
0.8
|
|
YCH4
|
0.0337
|
0.0390
|
0.0444
|
|
YO2
|
0.2243
|
0.2231
|
0.2219
|
Tableau(4.1) : les fractions massiques obtenues pour chaque
richesse.
4.2) Résultats du calcul 4.2.1)
Richesse
Pour la richesse 0.6, on a gardé le même maillage du
cas froid. Vu l'optimisation
des constantes A et B du modèle EDM, le calcul a
convergé après 17097 itérations. L'évolution des
résidus est montrée par la figure (4.10).
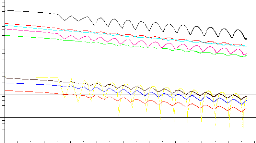
Figure (4.10) : Résidus du calcul pour une richesse de
0.6
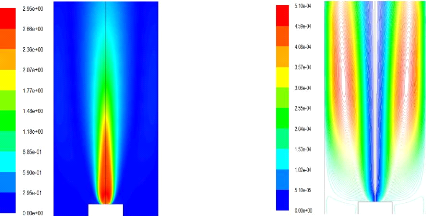
Figure(4.11) :Champs de vitesse (m/s) Figure(4.12) : Ligne de
courants
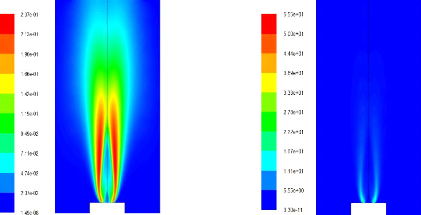
Figure (4.13) : Energie turbulent k(m2/s2)
Figure (4.14) : Taux de dissipation (m2/s3)
On montre le champ dynamique par les figures (4.11), (4.12),
(4.13) et (4.14). Les vitesses sont plus importantes que dans le cas froid,
ceci est du à l'expansion des gaz à cause de la combustion. Aussi
on remarque que l'énergie cinétique de turbulence et son
taux de dissipation qui sont plus importantes, ceci est logique
car les gradients de vitesses sont plus grands.
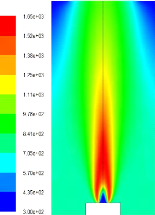

a ps e a e ac o
Figure (4.15) : Température (K) Figure (4.16) : Taux de
réaction ( m
m3 )
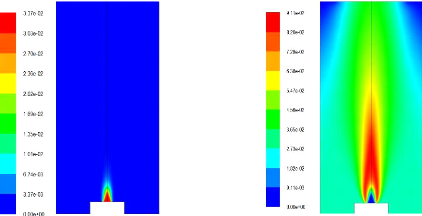
Figure(4.17) : Fraction massique du CH4 Figure(4.18) : Fraction
massique du CO2
Dans les figures (4.15, 16, 17 et 18), on montre les champs
thermiques et des espèces. La température adiabatique de la
combustion est bien reproduite par le modèle EDM, elle est de l'ordre de
1650 K (celle calculée par PREMIX [11] est 1664K). Le taux de
réaction
est principalement concentré dans la zone de
mélange car il dépend directement de l'énergie
cinétique de turbulence et son taux de dissipation. Pour les
espèces, on a présenté le combustible (CH4) et le CO2,
dès que le combustible est injecté il s'chauffe et s'enflamme
donnant le CO2 et l'H2O. La fraction massique maximale du CO2 est de l'ordre de
0.0091.
4.2.2) Pour / =0.7 :
Dans ce cas, et a cause des problèmes dans la convergence,
on a optimisé le maillage par le raffinement de la zone de
réaction.
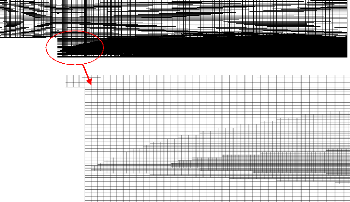
Figure (4.19) : Maillage pour le calcul dans le cas de
Le calcul prend 10 000 itérations pour converger, on
montre le cumule des résidus dans la figure (4.20).
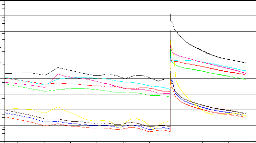
Figure (4.20) : Les résultats des calculs pour =0.7.
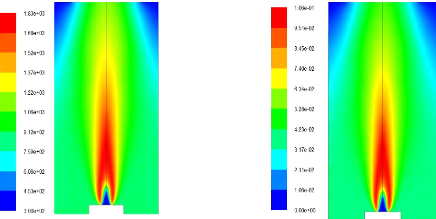
Figure(4.21) :Champs de Température Figure(4.22) :
Fraction massique du CO2
A cause de la ressemblance des résultats, sauf dans
l'aspect quantitatif, on se limite à la représentation des champs
de température et de CO2. La température atteint 1830 K, ce qui
favorise la formation des NOx thermique. La valeur maximale du CO2
est 0.1.
4.2.3) Pour ~
La convergence est obtenue après 1500 itérations
depuis de dernier calcul. Les figures (4.24 et 25) montrent le champ de la
température qui présente un maximum de 2000 K, la valeur
donnée par PREMIX est 1997K. Le CO2 atteint son maximum à une
fraction massique de 0.12.
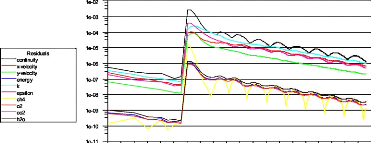
Figure (4.23) : les résultats des calculs pour
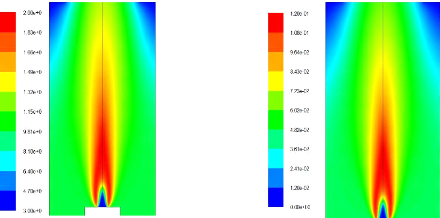
Figure(4.24) :Champs de Température (K) Figure(4.25) :
Fraction massique du CO2
Une comparaison de la variable d'avancement, calculée
en post traitement à partir de la température, est faite avec les
mesures pour les trois richesses (fig. 4.26 et 27). L'optimisation des
constantes A et B de l'EDM nous a permis d'obtenir une longueur de la flamme
très proche à celle expérimentale pour la richesse 0.6. On
a essayé de faire le même ajustement pour les autres richesses
(0.7 et 0.8) mais la température obtenue dépassait largement
celle adiabatique et la procédure numérique diverge. A notre avis
le modèle utilisé n'introduit pas les caractéristiques
physico chimiques du combustible, c'est pourquoi il ne donne pas une bonne
longueur de la flamme. Cette dernière est le résultat de la
compétition entre la vitesse d'injection et celle de la flamme
turbulente.

Figure (4.26) : Contours de la variable d'avancement c
calculée pour les trois richesses.

Figure (4.27) : Contours de la variable d'avancement c
mesurée pour les trois richesses.
5) Structure interne de la flamme
Pour représenter les propriétés
calculées on a pris trois stations ou coupes transversales et une
longitudinale le long de l'axe de symétrie dans le domaine de calcul. La
première station est à une hauteur h/3 de la hauteur de la
flamme, la deuxième est à 2h/3 et la troisième est
à h (figure 4.28).
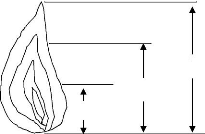
h
2h/3
h/3
Figure (4.28) : Différentes stations représentation
sur la flamme
On compare la variable d'avancement post traitée à
partir de la température avec cette mesurée sur l'axe de
symétrie. On voit le bon accord entre les deux courbes.
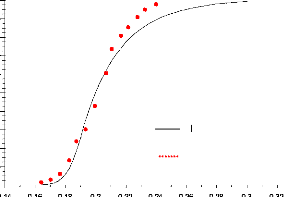
Numérique Expérimentale
X
Figure(4.29) : Variable d'avancement le long de l'axe pour une
richesse de 0.6.
On a comparé aussi les propriétés sur les
trois plans de coupe dans la flamme de richesse 0.6. On remarque la
distribution de la température sur ces stations qui est égale
à celle de l'injection (300K) sur le cône potentiel, elle augmente
au fur et à mesure qu'on monte dans la flamme et lorsqu'on se dirige
vers le front de la flamme ou le gaz se réchauffe et s'enflamme. Ceci
est traduit par les courbes des vitesses, de l'énergie cinétique
de turbulence et du taux de réactions qui présentent les
mêmes variations. En résumé dès qu'on s'approche du
front de flamme, on na expansion des gaz et par la suite augmentation de la
vitesse et production de l'énergie cinétique de turbulence.
h/3 2h/3 h
|
T
|
|
|
k
|
|
|
|
|
|
Y
|
|
Y
|
|
|
Figure(4.30) Variation de la Température (K) dans les
016 018 02 022 024 026 028
trois stations
Pit
|
2Figure(4.31) : Variation d'énergie turbulente
k
(m2/s2) dans les trois stations
|

|
U
|
|
|
|
|
Yi
Y
|
|
|
Y
|
|
Figure(4.32) : Variation de la vitesse (m/s) dans les
trois
stations
|
Figure(4.33) : Variation de taux de réaction
(
m
) dans les trois stations
m
|
|
( m ) O2/3 CH4 H2O CO2
|
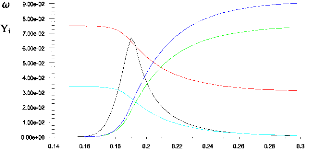
x
Figure (4.34) : Structure de la flamme pour une richesse de
0.6
Sur la figure (4.34), on montre la structure interne de la
flamme, on voit bien que le combustible et le comburant réagissent pour
donner les produits de réaction avec un taux de réaction maximal
au front de la flamme.
= 0.6 0.7 0.8

x
Figure (4.35) : Fraction massique du CO2 sur l'axe pour les trois
richesses
La figure (4.35) montre l'évolution axiale de la
fraction massique du CO2 pour les richesses 0.6, 0.7 et 0.8. On remarque que la
production de ce gaz à effet de serre augmente avec la richesse en
régime pauvre. Ce résultat est logique car on augmente la
quantité de combustible et par conséquent celle du carbone.
Conclusion :
Dans ce chapitre, on a commencé par le calcul du cas
non réactif pour ajuster le modèle de turbulence par la
correction de Pope. Ensuite, on a entamé une séries de calculs
pour les richesses 0.6, 0.7 et 0.8. Les résultats trouvés
concordent avec les expériences surtout la température
adiabatique de la combustion et la variable d'avancement, cependant la longueur
de la flamme n'est pas bien reproduite surtout dans les richesses 0.7 et 0.8.
On a trouvé que la production du CO2 augmente avec la richesse en
régime pauvre.
Ju 1, 200
CONCLUSION
La combustion turbulente est modélisée par EDM(
Eddy dissipation model). Ce model est très simple, il est totalement
géré par la turbulence, la chimie est supposée infiniment
rapide. La cinétique chimique est approximée par une
réaction globale irréversible.
Dans une première étape, on a calculé le
jet non réactif de l'air pour ajuster le model de combustion. Ceci est
fait par l'optimisation de la constante libre introduite par la correction de
Pope.
Deuxièmement, on a effectué des calculs pour le cas
de la combustion turbulente aux richesses 06, 0.7 et 0.8.
Les résultats trouvés sont comparés avec
les mesures expérimentales disponibles (figures (4.6), (4.7)). On a
trouvé un bon accord surtout pour la richesse 0.6. La longueur de la
flamme n'est pas bien reproduite pour les deux autres richesses malgré
les optimisations faites sur le model EDM. A notre avis ceci est due au
modèle qui ne tient pas compte des caractéristiques
thermophysiques du combustible, car la longueur de la flamme est
essentiellement basé sur ces propriétés.
L'Algérie est un pays qui produit son énergie
électrique à partir du gaz naturel et du pétrole, en plus
des moyens de transport, la combustion joue un rôle central dans toutes
ces commodités. Malgré les bien faits de la combustion, elle
produit des émissions nocives à notre environnement.
Notre travail s'inscrit dans la lutte antipollution, il
considère l'effet de la richesse sur la combustion pauvre du
méthane. En effet, la combustion pauvre est un outil très
efficace dans la minimisation des émissions nocives, essentiellement le
CO2, CO et NOx. Ce qui implique moins de O2 et une combustion quasi-
complète. Ainsi, le régime pauvre permet de contrôler la
température de la combustion et d'inhiber la formation de NOx
thermiques qui ne sont produites qu'aux températures supérieurs
à 1750 K.
Dans notre travail on a étudié la combustion
pauvre à trois richesses (0.6, 0.7 et 0.8) pour déterminer
l'effet d'ajout du méthane sur la formation du CO2. La solution est
faite par le code Fluent, on a adopté le model k-
corrigé par Pope pour tenir compte de la géométrie
axisymétrique.
Pour la production du CO2, qui est le but essentiel de ce
travail, on a obtenu des résultats très satisfaits. Le model EDM
prévoit une augmentation de CO2 avec l'augmentation de la richesse, ceci
est bien cohérant avec la littérature .
Les températures maximales de combustion sont bien
reproduites par le model utilisé, elles augmentent avec la richesse.
On estime que le but de ce travail est largement atteint et on
recommande de continuer ce travail par d'autres modèles de combustion
plus élaborés.
Résumé
Notre travail est consacré à la combustion
prémélangée pauvre et turbulente du méthane. On a
adopté le model k- corrigé par Pope pour la turbulence.
Pour le model de la combustion, on a pris un model très simple et qui
permet de donner une idée générale sur la formation du
CO2, model EDM. Le calcul est réalisé par le code Fluent, les
résultats trouvés montrent l'augmentation de la
température et du CO2 avec la richesse.
Mots clés :
Ecoulements turbulents, flamme laminaire, combustion turbulente,
combustion prémélangée pauvre.
BIBLIOGRAPHIE
[1] Lachaux .T, Etude des effets de la haute pression
sur la structure et la dynamique des flammes turbulentes de
prémélange pauvre de méthane-air, Thèse de
doctorat, univ. D'Orléans 2004.
[2] Haleter .F, Caractérisation des effets de
l'ajout d'hydrogène et de la haute pression dans les flammes turbulentes
de prémélange méthane/air, Thèse de
doctorat, univ. D'Orléans 2005.
[3] Hafid Mohamed, simulation numérique d'un jet
plan turbulent par fluent, mémoire ingéniorat juin
2008
[4] GHOUGAL A. et TRAD DJ. Simulation numérique
d'un jet rond turbulent par fluent. Juin2008
[5] Tout. M, Iken. A, simulation numérique d'un
jet rond turbulent a masse volumique variable par fluent. Juin2009
[6] Kenneth .K KUO, Principles of combustion,
2nd ed. John Wiley & Sons ed. 2005
[7] CHEMKIN, reaction design
www.reactiondesign.com
[8] Poinsot .T, Veynante D., Theoretical and numerical
combustion, Edwards ed. 2001.
[9] B.BENABES, cours de mécanique des
fluides, Institut de génie mécanique, C.U.LARBI BEN
M'HIDI (Oum El Bouaghi), ALGERIE, 2007/2008.
[10] LAETITIA DORIS, Introduction à la simulation
numérique des écoulements turbulents.
PSA Peugeot Citroën Direction de la Recherche et de
l'Innovation Automobile. 2005.
[11] MAAMERI A. Simulation Numérique de la
Stabilisation d'une Flamme Turbulente de Méthane en Régime Pauvre
Par Ajout d'Hydrogène, Centre Universitaire Larbi BEN M'HIDI,
Oum El Bouaghi Algérie 2007
[12] GRIEBEL P.et al, Flame characteristics
and turbulent flame speeds of turbulent, high pressure, lean premixed
methane/air flames, ASME GT 2005- 68565.
[13] GAUDUCHEAU. J.L. et al, A numerical study
of lean CH4/H2/Air premixed flames at high pressure, Combust. Sci.
& Tech. 1998, Vol. 137, pp. 81-99.
[14] G. S. Jackson et al, Influence of H2 on
the response of lean premixed CH4 flames to high strained flows,
Combustion & Flame 132 (2003) 503-511.
[15] E.R. Hawkes & J.H. Chen, Direct numerical
simulation of hydrogen enriched lean premixed methane-air flames,
Combustion & flame 138 (2004) 242-258.
[16] Suhas V. Patankar, numerical heat transfer and
fluid flow University of Minnesota
[17] NOUI SAMIRA. Mémoire magistère, etude
numérique de la combustion des gaz dans les fours industriel,
chapitre 2.2006
[18] FAWZY EL-MAHALLAWY. SAAD EL-DIN HABIK, fundamentals
and technology of combustion, tableau 2-2 page 97 Cairo Egypt 2002
[19] MOKHTARI L., étude numérique des
écoulements réactifs turbulentes dans un chambre de combustion
d'un moteur diesel, thèse de magister université de
Constantine.2003
[20] CHASSAING P., Turbulence en mécanique des
fluides, Cépaduès ed. 2000
[21] Frank M. White, Fluid Mechanics,
4eme edition University of Rhode Island [22]NOROBERT.P,
turbulent combustion, Institute de mécanique Aachen
GERMANY 2000
[23]EASTOP T.D. Macconkey, Applied
thermodynamics 5eme edition 2009 [24]STEPHEN.R, an
introduction to combustion, propulsion engineering research center and
department of mechanical and nuclear engineering Pennsylvania USA 2000
[25] PASCAL BLEUYARD, Génération de champs
de vecteurs turbulents, Blaise Pascal, 2002.
[26] TUNCER CEBECI, FASSI KAFYEKE, JIAN P. SHAO & ERIC
LAURENDEAU, « Computational Fluid Dynamics for Engineers (From
Panel to Nervier-Stokes Methods with Computer Programs), Horizons
Publishing Inc., Long Beach, California , 2005.
[28]Bigler R.W., The structure of turbulent non-premixed
flames, Proc. Combust. Inst., vol. 22, pp. 475 - 488. (1988)
[29] Spalding DB., Mixing and chemical reaction in
steady confined turbulent flames, 13th Int. Symposium on
Combustion. Pittsburgh: the combustion institute, 1971
[30] Magnusson B. F., Hjertager B. H., Proceeding of the
Combustion Institute,(1976)
[31] CANDEL.S, Cours & Problèmes
résolus de mécanique des fluides, 1999
[32]JEAN.Philipe.Boin, Turbulence, 2001/2002
[33] John B.Heywood, internal combustion engine
fundamentals, 1988
[34] CFD on line Combustion
www.cfd-online.com
[35] Bjorn F. Magnusson the eddy dissipation concept a
bridge between science and Technology, Trondheim, Norway 2005
[36]Barbra.P, caractérisation numériques
et expérimentale d'un bruleur a gaz swirl variable longuer de flamme et
transfert thermique, faculté polytechnique de Mons 2006
[37] Toporov. D Howard R. J. A. Full-length article:
The eddy dissipation combustion model developed for large eddy simulation,
University of Aveiro Portugal
[38]Peters. N, laminar diffusion flamelet models in
non-premixed turbulent combustion, Prog. Energy Combust. Sci.,
1984.
[39] Ferziger .J.H, Péric. M, Computational
methods for fluid dynamics, 3rd ed. Springer 2002.
[40] BOURAS FETHI, simulation de la combustion
turbulente non-prémélangée par le modèle
«LES» Université de BATNA 2006
[41]MARCEL Lesier, La turbulence, Presses
universitaires de Grenoble France 1994 [42]BORGHI.R, DESTRIAU.M, la
combustion et les flammes, Paris France 1995 [43] A.FAVRE &
P.VIGLIANO, Introduction à la mécanique statistique de la
turbulence, Institut de Mécanique de MARSEILLE, 2005.
| 


