à‰tude du phénomène d'infiltration de l'eau en fonction du débit dans un sol sablo-limoneux et essai de modélisation.

1

INTRODUCTION

Le manque d'eau et l'accroissement constant des besoins en eau en agriculture, conjugués aux conflits d'usage avec les autres secteurs tels que l'industrie et la consommation en eau potable, nous amènent à constamment réfléchir sur les économies d'eau et d'énergie. Ceci passera forcement par une gestion efficace de l'irrigation ainsi que par la maîtrise de l'utilisation et le choix des systèmes d'irrigation.

Les surfaces irriguées devenant de plus en plus importantes, il devient nécessaire de mieux choisir les espèces végétales adaptées et les systèmes d'irrigation pour mieux optimiser les rendements.

Malgré l'introduction des techniques d'irrigation telles que l'irrigation par aspersion et l'irrigation goutte à goutte, l'irrigation gravitaire demeure le mode majoritaire d'irrigation à l'ensemble des surfaces irriguées par les agriculteurs algériens.

Ces dernières années, nous sommes témoins de recherches intensives des questions d'irrigation par infiltration dans le but de minimiser les pertes d'eau et d'optimiser les rendements.

La présente contribution porte sur des essais réalisés sur deux raies bouchées de même longueur. L'objectif recherché est de déterminer les paramètres d'ajustement les plus appropriés « K » et « C » de l'équation de KOSTIAKOV modifiée, afin de reproduire les résultats conformes ou très proches de ceux issus de l'expérimentation.

Ce suivi de l'étude de l'infiltration en fonction du débit a permis d'aborder les aspects suivants :

- Dans une première partie,

1- l'eau dans le sol

2- l'irrigation à la raie

3- le phénomène de l'infiltration

4- le bilan du volume - Dans une seconde partie,

1- l'étude pratique de l'infiltration en fonction du débit

2- la modélisation

Ma

Me

Mt

Ms

Va

Vv

Ve

Vt

Vs

2

CHAPITRE I : L'EAU DANS LE SOL

On conçoit que l'étude des relations entre le sol, l'eau et même l'atmosphère a une extrême importance du point de vue agronomique. Cette étude est d'un intérêt capital lorsqu'il s'agit de comprendre le rôle de la terre comme réservoir d'alimentation en eau des plantes et de déterminer les conditions les meilleurs pour apporter à la terre, par l'irrigation, l'eau qui lui est nécessaire.

La technique de cette opération repose sur la connaissance de la constitution des sols et leurs propriétés physiques, notamment la porosité, le pouvoir de rétention des terres pour l'eau et la perméabilité.

Ces différents facteurs sont liés entre eux et également à d'autres propriétés du même ordre ; le tout constitue un ensemble solidaire qu'il nous paraît indispensable d'examiner au double point de vue : statique et quantitatif, puis dynamique, les mouvements de l'eau dans le sol, revêtant une importance capitale en déterminant les possibilités de stockage et d'alimentation de la plante.

1.1 : Les propriétés physiques du sol

Le sol joue essentiellement un rôle de réservoir. Ce sont les caractéristiques de ce réservoir et son mode de fonctionnement qu'il est utile de connaître dans un périmètre d'irrigation.

Le sol est un système à trois phases : solide, liquide, gazeux. Ses propriétés physiques résultent des rapports entre les éléments solides et les deux fluides air et eau. La phase solide (45 à 65%) est celle dont le volume est le plus constant, tandis que les volumes occupés par les phases liquides et gazeuses sont très variables.

AIR (25%)

EAU (25%)

SOLIDE (50%)

3

Figure 1 : Représentation schématique des trois phases du sol (D.HILLEL, 1988)

1.1.1 : La texture du sol

Elle caractérise la nature, la taille et la distribution des particules solides qui le constituent. Quantitativement, elle peut s'apprécier par le « toucher » du matériel du sol, qui décrit les proportions relatives des diverses tailles des particules solides.

Tableau 1 : Classification des particules solides du sol en fonction de leur diamètre.

Particules	Argile		Limon		Sable fin		Sable grossier	Gravier		Cailloux
Diamètre en mm			0,002	0,02		0,2		2	20

(DUCROCQ, 1987)

1.1.2 : La structure du sol

Elle traduit la manière dont les constituants élémentaires (sables, limons, argiles) et complexes (agglomérats, éléments structuraux) du sol sont disposés les uns par rapport aux autres.

La structure est le résultat d'interaction multiple entre ces constituants, d'une part et un ensemble de facteurs liés au climat, à l'activité de la faune et des racines et aux techniques culturales, d'autre part.

On distingue généralement trois types de structures du sol :

. Structure particulaire : pas de cohésion entre les éléments constitutifs. . Structure continue : type ciment, gris et poudings.

. Structure fragmentaire : les particules grossières englobées par un ciment argileux

1.1.3 : Les densités du sol

C'est le rapport du poids d'un mètre cube d'un corps par rapport à un mètre cube d'eau.

Deux types de densités revêtent une importance capitale en agronomie.

4

1.1.3.1 : La densité réelle (dr)

Elle correspond à la masse volumique des éléments constituant la phase solide. Constante pour un sol donné, elle varie avec les proportions de ces éléments. Elle est, en général comprise entre 2,4 et 2,8. Ce n'est qu'exceptionnellement qu'elle peut s'en écarter : dans le cas des sols humifères par exemple, elle peut descendre à des valeurs voisines de 2.

dr=

Ms (1)

Vs

Avec : dr = densité réelle, en g/cm³. Ms = masse du solide, en g ; Vs = volume du solide, en cm³.

1.1.3.2 : La densité apparente (da)

La densité apparente est le rapport de la masse de terre sèche d'un échantillon au volume en cm³ qu'occupait cet échantillon se sol non remanié à l'état humide.

da=

Ms (2) Vt

Avec : da = densité apparente, en g/cm³.

Vt = volume apparent du sol en place, en cm³.

La densité apparente est variable selon la nature et l'état structural (degré de compaction ou d'ameublement) du sol. Elle peut prendre des valeurs entre 0,8 et 2 ; mais sa valeur moyenne est de l'ordre de 1,45. Les résultats obtenus varient selon divers auteurs, entre les limites suivantes (Anonyme, 1977) :

-Sols sableux :	da = 1,50 à 1,80
-Sols limoneux :	da = 1,30 à 1,50
-Sols argileux :	da = 1,10 à 1,30

1.1.4 : La porosité du sol (P)

La porosité est représentée par l'ensemble des espaces libres entre les particules solides du sol occupés par l'eau et l'air. Elle peut se définir comme le rapport du volume de l'espace poral au volume du sol en place.

Vt Vs

P (%)= Vp -

= (3)

Vt Vt

Avec : Vp = volume de l'espace poral, en cm3 ;

Vt = volume apparent du sol en place, en cm³ ; Vs = volume des constituants solides, en cm³.

Sa valeur oscille généralement entre 0,3 et 0,6. Lorsque la porosité s'abaisse au-dessous de 30%, le milieu devient asphyxiant. Un bon sol agricole doit présenter une porosité comprise entre 45 et 50%.

Les résultas de nombreux travaux ont montré que les sols à texture grossière sont moins poreux que les sols à texture fine, alors que la taille des pores est plus grande dans les premiers que dans les derniers (Diehl, 1975).

-Sols sableux : P = 30 à 40%

-Sols argileux : P = 40 à 55%

Expérimentalement, la porosité peut être estimée par l'expression :

P = ×100

dr

dr - da (4)

5

Sa répartition adéquate est de 20% de macroporosité et de 30% de microporosité.

· La macroporosité comprend les pores supérieurs à 8 microns et loge normalement l'air (et l'eau tant que le sol n'est pas ressuyé) ;

· La microporosité regroupe les pores inférieurs à 8 microns et contient l'eau utilisable par les plantes.

30% 20%

SOLIDE

EAU

AIR

Macroporosité Microporosité

50% 50%

Porosité

Figure 2 : Répartition en volume des constituants du sol (Agronomie moderne, 1994)

6

1.2 : Les propriétés hydriques du sol

1.2.1 : Expression de l'humidité du sol

La phase liquide du sol étant sujette à une variabilité spatiale et temporelle, sa description quantitative s'avère très souvent nécessaire. Celle-ci repose sur la notion "d'humidité relative".

Ainsi, la teneur en eau d'un sol peut s'exprimer soit en masse, soit en volume.

1.2.1.1 : L'humidité pondérale (Hp)

D'une façon générale, il est normal d'exprimer l'humidité d'un sol par le rapport du poids d'eau qu'il convient (Me) au poids du sol sec (Ms).

Me Mh - Ms

Hp (%) = x100= x100 (5)

Ms Ms

Avec : Me = poids d'eau contenu dans un échantillon de sol, en g ; Ms = poids de l'échantillon sec, en g ;

Mh = poids de l'échantillon humide (frais), en g.

1.2.1.2 : L'humidité volumétrique (Hv)

Elle permet de rapporter l'humidité non plus au poids du sol, mais au volume du sol en place ; en agriculture, ce qui importe en effet, c'est le volume de sol exploré par les racines. La densité apparente est indispensable pour passer de l'humidité pondérale à l'humidité relative et inversement.

Hv=daxHp (6)

1.2.2 : Les humidités spécifiques du sol

Le sol constitue un milieu convenable pour les racines lorsqu'un équilibre est respecté : l'air est nécessaire à la respiration des racines et l'eau doit pouvoir leur être cédée sans difficulté. Ainsi, il existe différents niveaux d'humidité dans un sol lorsqu'il passe de l'humidité maximale à la sécheresse absolue.

1.2.2.1 : L'humidité à la saturation (Hs)

Elle correspond au sol gorgé d'eau lorsque toute la porosité est occupé et que le sol ne contient plus d'air, constituant ainsi un milieu impropre à toute végétation.

7

1.2.2.2 : L'humidité à la capacité au champ (Hcc)

Elle correspond à l'état de ressuyage d'un sol arrosé qui s'est drainé librement et traduit, théoriquement, le passage de l'état de saturation à l'état de capillarité de l'eau dans le sol , défini par la loi de JURIN. On peut la considérer comme équivalente aux conditions proches de l'optimum de croissance des cultures pour la plupart des sols. Correspondant au pF = 2,8, la capacité de rétention à une valeur sensiblement égale à « l'humidité équivalente » pour des valeurs comprises entre 14 et 30%.

1.2.2.3 : L'humidité équivalente (He)

C'est une valeur arbitraire du taux d'humidité atteint par un échantillon de sol dans les conditions expérimentales précises (centrifugation). Correspondant au pF = 3, l'humidité équivalente est souvent substituée à l'humidité à la capacité au champ de détermination délicate.

1.2.2.4 : L'humidité critique (Hc)

Elle correspond à l'humidité du sol en dessous de laquelle la plante commence à souffrir d'un déficit hydrique (ETR < ETM). Notion importante mais essentiellement fluctuante, elle ne dépend pas seulement du sol mais aussi du climat et des caractéristiques de la plante.

1.2.2.5 : L'humidité au point de flétrissement (Hpf)

C'est l'humidité au-dessous de laquelle la majorité des plantes flétrissent de façon irréversible subissant ainsi des dommages à cause de la sécheresse. Notion également variable selon la nature de la plante, on convient en général de la caractériser par une tension correspondant à peu près au pF = 4,2.

De façon qualitative, on conçoit que la plante n'ait de l'eau à sa disposition que si le sol se trouve entre le point de ressuyage (ou capacité au champ) et le point de flétrissement.

8

1.3 : Définition de bases

Tableau 2 : Définition de bases : Densité, porosité, Humidité.

Termes	Symboles	Définition	Ordre de grandeur		Observation	Densité réelle
dr	Masse des solides	Sol moyen : 2,6 à 2,7
da	Masse des solides	-Variable avec la texture -Sol sableux : 1,3 à 1,4 -Sol limoneux : 1,2 à 1,5 -Sol argileux : 1,1 à 1,3	Permet de calculer Hv
P	Volume des vides	Sol argileux : 50 à 70%	Exprime le volume maximum d'eau qu'un sol peut contenir
Hp	Masse de l'eau	Hv = da x Hp	Déterminée au laboratoire
Hv	Masse de l'eau

9

1.4 : Les réserves hydriques du sol

Les quantités d'eau disponibles dans le sol pour la plante sont fonction

des niveaux des réserves hydriques du sol.

Ces niveaux d'eau dépendent principalement :

- Des caractéristiques hydrodynamiques du sol ;

- De la profondeur d'enracinement.

On définit trois types de réserves hydriques à savoir : la réserve utile (RU), la

réserve facilement utilisable (RFU) et la réserve de suivie (RS).

1.4.1 : La réserve utile (RU)

C'est la quantité maximale utilisable par une plante pour un type de sol donné.

RU da(Hcc - Hpf)z 100

(7)

Avec : RU = réserve utile, en mm ;

da = densité apparente de la terre sèche ;

Hcc, Hpf = humidité pondérale à la capacité au champ et au point de

flétrissement, en % ;

z = profondeur d'enracinement, en mm.

1.4.2 : La réserve facilement utilisable (RFU)

C'est la fraction de la RU disponible à une tension suffisamment faible pour que la plante transpire à l'ETM.

da ( Hcc - Hc ) z

RFU = (8)

100

Avec : RFU = réserve facilement utilisable, en mm ; da = densité apparente de la terre sèche ; Hcc, Hc = humidité pondérale à la capacité au champ et critique, en % ; z = profondeur d'enracinement, en mm.

Dans la pratique, il est difficile d'avoir une estimation suffisante de Hc, et l'on se contente d'estimer la RFU à partir de la RU :

RFU= á'RU (9)

Avec : 0,5 ? á < 1 (la valeur 2/3 étant la plus couramment employée)

10

Tableau 3 : Variation de la RFU en fonction du type de sol

Types de sol		RFU	Sol argileux
30 à 40% de la RU		Sol limoneux
40 à 60% de la RU		Sol sableux
70% de la RU

(Didacticiel Bilhy, 1993)

1.4.3 : La réserve de survie (RS)

Les notions précédentes (RU et RFU) conduisent à considérer schématiquement le sol comme un réservoir dont une partie est disponible à volonté (RFU), et dont le reste (RS) est d'autant plus rationné que l'on proche de l'épuisement.

RS=RU-RFU (10)

Il est donc évident que pour obtenir un rendement optimum des cultures, il faut maintenir le taux d'humidité du sol à un niveau tel que la réserve de survie ne soit pas atteinte, c'est-à-dire proche de la capacité au champ.

1.5 : L'état de l'eau dans le sol

La connaissance de l'état relatif de l'eau dans le sol est d'une importance fondamentale car cet état et ses variations dans le profil déterminent la direction et influencent le régime du mouvement de l'humidité du sol et du prélèvement en eau par les plantes.

1.5.1 : L'état énergétique e l'eau dans le sol

L'eau est retenue dans le sol par des forces que l'on regroupe sous le terme de "force de succion" du sol. Cette force de succion est d'autant plus forte que l'humidité du sol est faible. On trouve, en effet, plusieurs états de l'eau dans le sol.

1.5.1.1 : L'eau de constitution

L'eau de constitution est celle qui se retrouve au sein même des cristaux et des molécules minérales et organiques du sol. Elle fait donc partir de la constitution chimique du sol et n'est pas utilisable par les végétaux. Elle ne disparaît pas non plus lors d'un séchage du sol à l'étuve à 105°C.

11

1.5.1.2 : L'eau hygroscopique

Elle est formée d'une fine pellicule d'eau, de quelques molécules d'épaisseur, qui est adsorbée à la surface des particules de sol. Cette eau n'est pas utilisable par les végétaux. En laboratoire, elle lors du séchage à l'étuve à 105°C mais elle se reconstitue presque instantanément à partir de l'humidité atmosphérique.

1.5.1.3 : L'eau capillaire non absorbable

L'eau capillaire non absorbable est l'eau qui est retenue par les particules de sol avec une force de succion qui dépassent celle que les plantes peuvent exercer. Elle occupe les pores les plus fins du sol et de ce fait sa quantité dépend de la granulométrie. Il y en a plus dans les sols argileux que dans les sols sableux. Elle peut cependant être limitée par évaporation dans les conditions de sécheresse. Elle se reconstitue par humectation du sol lors des précipitations.

1.5.1.4 : L'eau capillaire absorbable

C'est l'eau qui est la plus utile pour la croissance de la végétation, car elle est retenue par le sol à cause de la capillarité et elle est absorbable par les végétaux. Elle leur permet donc de survivre entre deux pluies et de résister aux périodes de sécheresse. On la mesure "in situ" en saturant le sol et en le laissant égoutter 24 heures (capacité au champ) ou en le saturant et en le plaçant sous une trompe à vide au laboratoire pendant une heure (humidité équivalente). L'eau capillaire est absorbable correspond à la réserve utilisable (RU) nécessaire aux calculs du bilan hydrique.

1.5.1.5 : L'eau de gravité

L'eau de gravité est celle que le sol ne peut pas retenir par capillarité et elle s'écoule verticalement dans le profil du sol. Alimentant l'écoulement hypodermique et souterrain et causant ce que les pédologues appellent le lessivage du sol, responsable de l'évolution pédologique et de l'apparition des horizons. Ce lessivage est, en effet, accompagné par la migration des éléments dissous avec l'eau de gravité, formant les horizons A d'où les éléments comme les oxydes de fer et les carbonates sont enlevés, et les horizons B, enrichis par la précipitation d'une partie d'entre eux.

12

1.5.2 : Expression du potentiel hydrique

Le potentiel hydrique est la résultante des différents phénomènes agissant sur l'eau, et dont les plus importants sont :

1.5.2.1 : La gravité : le potentiel gravitationnel (Wg)

Indépendant des propriétés du sol, de la plante ou même de l'atmosphère, le potentiel gravitationnel dépend en effet uniquement de la distance verticale entre la référence (établie à toute hauteur adéquate, telle que la surface du sol) et le point considéré. Son amplitude absolue est presque insignifiante.

g=zxg (11)

Avec : z = distance au-dessus du plan de référence ; g = accélérateur de la pesanteur.

1.5.2.2 : Le potentiel matriciel (Wm)

Sous le nom de potentiel matriciel on désigne la tension superficielle et les phénomènes de capillarité, auxquels s'ajoute l'adhésion superficielle sur certaines particules du sol.

Propriété dynamique du sol et de la plante, il est commode de considérer le potentiel matriciel comme une fonction continue de la teneur en eau de façon à ce qu'il soit possible quand on a un sol saturé sous une nappe d'eau (potentiel de submersion) et négatif quand le milieu poreux est insaturé (potentiel capillaire). En théorie, øm est nul si le sol est saturé.

m=Pxg=8exhxg (12)

Avec : P = pression d'eau ;

äe = masse volumique e l'eau.

Le potentiel matriciel peut se mesurer de manière directe au champ grâce au tensiomètre.

1.5.2.3 : Le potentiel osmotique (Wo)

Dû à la présence de substances dissoutes dans l'eau, il n'influence pas son mouvement dans le sol de façon notable vu que les solutés peuvent être entraînés par l'eau.

Il est cependant très important dans l'adsorption de l'eau par les plantes et dans la diffusion de la vapeur d'eau.

13

1.5.2.4 : Le potentiel osmotique (Wp)

Ce potentiel est négligé du fait que l'on considère généralement que la pression d'air est uniforme dans le profil du sol.

Øp=Pa×g (13)

Avec : Pa = pression d'air contenue dans le sol.

Le système est en équilibre lorsque le potentiel hydrique total (W) est le même en tout point.

Ø= Øm+Øo+Øg+Øp=cste (14)

L'avantage principal du concept de potentiel total réside en ce qu'il fournit une mesure unifiée par laquelle l'état de l'eau peut être évalué à n'importe quel moment et à n'importe quel endroit au sein du continuum sol-plante-atmosphère.

L'expression du potentiel total est généralement simplifiée et on ne tient compte que de la somme du potentiel de gravité (Wg) et du potentiel matriciel (Wm) dans le cas du sol.

Ø= Øg +Øm (15)

1.6 : Dynamique de l'eau dans le sol

L'eau se meut dans le sol suivant deux principaux cas :

· Le milieu est saturé avec, comme cas fondamental, le sol gorgé d'eau. L'eau subit alors des mouvements descendants essentiellement régis par la pesanteur : c'est la percolation ou drainage.

· Le milieu est insaturé comme c'est le cas en général du sol. L'eau subit des mouvements ascendants et latéraux régis par la diffusion capillaire et si la dessèchement se poursuit, à partir de pF = 3,7 correspondant sensiblement au point de flétrissement temporaire, par évaporation.

+ La percolation

Elle est fonction de la perméabilité du sol, elle-même dépendant de la texture et de la structure su sol.

Après une pluie ou une irrigation, l'eau se situe d'abord en surface où elle rempli tout l'espace poral ; puis elle se redistribue sur une profondeur plus importante jusqu'à un certain niveau appelé « front d'humectation ».

14

+ La remonté capillaire

L'eau retenue dans le sol, part progressivement en surface soit par évaporation au contact de l'air soit par absorption par la plante.

Ainsi, le sol se dessèche en surface, et des différentes de potentiel capillaire donc de pF apparaissent favorisant la remonté de l'eau de la profondeur vers la surface. Cette remonté qui se fait par diffusion entre les films capillaires reliant les agrégats, d'abord nulle, naît et par elle, l'humidité des couches inférieures remonte vers les couches supérieures.

1.6.1 : Comportement dynamique : loi de DARCY

La loi de comportement de la phase liquide d'un sol traduit l'existence d'une relation entre les forces auxquelles sont soumis le fluide et sa vitesse d'écoulement.

La plupart des ressources de l'écoulement de l'eau dans le sol se déroulent dans l'état de sol non saturé. Ces processus sont généralement compliqués et difficile à décrire quantitativement à cause de la variabilité spatiale de l'état de la teneur en eau du sol pendant l'écoulement.

En effet une équation du type DARCY semble être applicable dans le cas d'un sol saturé et non saturé.

Q

Ks × S × dH dZ

(16)

Le débit d'eau Q est proportionnel à la surface de la section de flux (S) et au gradient hydraulique dH/dZ.

Le signe (-) indique que le flux a lieu dans le sens des potentiels décroissants.

Le coefficient de proportionnalité (Ks) appelé coefficient de Darcy, coefficient de perméabilité ou conductivité hydraulique caractérise le sol.

1.6.1.1 : Cas d'un sol saturé

On peut définir le milieu saturé, comme un milieu dans lequel les forces de rétention sont supérieures à celles de gravité.

Dans ce cas, la force motrice est le gradient hydraulique.

La loi de Darcy s'écrit :

Q

Ks × dH dZ

(17)

15

Avec : Q = flux transitant, en mm.h^-1 ; dH = charge hydraulique totale, en m ;

Ks = conductivité hydraulique à la saturation, en mm.h^-1 dZ = énergie de position, en m.

1.6.1.2 : Cas d'un sol non saturé

C'est le cas le plus abondant, dans lequel le gradient hydraulique devient un gradient de succion et la conductivité n'est plus constante, mais fonction de la teneur en eau. La loi de DARCY s'écrit :

Q - × Ø

= (18)

K d t dZ

Avec : Q = flux transitant, en mm.h^-1 ; K = coefficient de Darcy, en mm.h^-1 ; dØt = énergie potentielle totale ; dZ = énergie de position, en m.

1.6.2 : La perméabilité du sol (K)

La perméabilité du sol est définie comme la plus ou moins grande facilité de descente de l'eau vers les couches inférieures du sol.

Elle s'exprime en cm.s^-1.

Tableau 4 : Limites des diverses classes de perméabilité

Vitesse d'infiltration K en cm.s^-1	Types de sol
K < 10^-5	Sols imperméables
10^-5 < K < 10^-4	Sols peu perméables
10^-4 < K < 10^-3	Sols moyennement perméables
10^-3 < K < 10^-2	Sols perméables
K > 10^-2	Sols très perméables

(C.T.G.R.E.F, 1979)

Pour les sols saturés en eau, après une forte pluie par exemple, K est comprise entre 1,4.10^-3 et 2,8.10^-3 cm.s^-1 pour les sols à texture sableuse ; il varie entre 0,5.10^-3 à 14.10^-3 cm.s^-1 dans un horizon A selon le type d'humus pour les sols

16

limoneux et, est de l'ordre de 0,03.10^-3 cm.s^-1 dans les horizons B enrichis en

argile.

Une couche est réputée imperméable pour des valeurs de K de l'ordre de 10^-9 cm.s^-1.

1.6.3 : La conductivité hydraulique (K(è))

La diffusion de l'eau dans le sol est régie par les différences de tension entre les différents points. Le flux d'eau est donc proportionnel au gradient de tension, ce qui s'exprime par l'équation suivante :

ö = (è) (19)

K d Ø

dz

Avec : Ø = flux d'eau, en cm.s^-1 ;

K(è) = conductivité hydraulique du sol en cm².s^-1.atm^-1 ; dz = profondeur, en cm ;

dØ = tension de l'eau du sol, en atm.

Le coefficient K(è) exprime la plus ou moins grande facilité avec laquelle l'eau capillaire se déplace sans le sol, pour un gradient de tension donné.

La conductivité hydraulique est plus élévé pour les sols légers que pour les sols lourds. Elle varie également avec l'état d'humidité du sol ; elle est d'autant plus forte que le sol est plus humide.

La conductivité hydraulique ne peut se mesurer que de manière indirecte, à partir de mesures de flux hydriques.

1.7 : Conclusion

Dans l'étude des rapports du sol et de l'eau, deux types d'informations sont généralement nécessaire : la quantité d'eau contenue dans le sol et son état énergétique. Quoique celles-ci peuvent être mesurées indépendamment, elles sont cependant fonction l'une de l'autre. Cette relation décrite par la courbe pF est d'une importance capitale car elle exprime l'influence de la structure, de la porosité, de la distribution des pores et de l'adsorption sur l'état de l'eau dans le sol. Cet état hydrique du sol, par sa dynamique, fournit au végétale les nutriments qui lui sont nécessaires à sa croissance.

Ainsi, lorsqu'un certain équilibre est respecté, le sol devient la source nutritionnelle et un réservoir d'alimentation en des plantes

17

CHAPITRE II : IRRIGATION A LA RAIE

Cette méthode d'irrigation consiste à laisser écouler l'eau dans les raies ou sillons tracés entre les lignes de plantation. Cette raie est préalablement aménagée dans le sens ou en travers de la plante. L'eau s'infiltre dans le fond et sur les cotés du sillon, pour humecter toute la zone racinaire.

Les raies ou sillons sont orientés suivant la plus faible pente de sol.

2.1 : Application

2.1.1 : La culture

L'irrigation à la raie convient à la plupart des cultures, excepté celles qui requièrent une submersion permanente, comme le riz. Elle convient particulièrement aux plantes craignant une submersion du collet ou de la tige, puisque les cultures peuvent être déposées sur des billons ou entre les raies.

2.1.2 : Le sol

Cette méthode convient le mieux aux sols de texture moyenne à modérément fine, ayant une réserve utile relativement élevée et une conductivité hydraulique suffisante qui assure une bonne mobilité de l'eau, aussi bien horizontalement que verticalement. Elle convient aux sols de texture fine et peu perméable, sur des parcelles horizontales ; ce qui augmente la durée de submersion.

Dans les sols de texture grossière, l'infiltration dans les raies est essentiellement verticale avec très peu de pénétration latérale. Pour de tels sols, l'irrigation à la raie est efficiente si les raies sont courtes, les durées d'application faibles, les raies relativement rapprochées et les doses d'arrosage réduites.

2.2 : Caractéristiques des raies

2.2.1 : La forme des raies

En irrigation à la raie, les formes des raies connues sont :

2.2.1.1 : Raies plates

Il existe deux types :

o Raies de forme rectangulaire dont la longueur est de 0,5 à 0,6 m et la hauteur, 0,2 à 0,25 m.

o Raies de forme trapézoïdale dont la largeur est de 0,5 à 0,6 m et le hauteur d'eau de 0,04 à 0,05 m.

2.2.1.2 : Raies de forme triangulaire en «V»

Leur largeur est comprise entre 0,25 et 0,30 m et leur hauteur, 0,2 à 0,5 m. La forme et la profondeur des raies sont fonction de la nature du sol et du débit apporté.

La forme des raies en sol sableux est moins large et profonde, alors qu'en sol argileux, elle est large et peu profonde.

Les raies plates sont plus avantageuses que les sillons en «V» ; on peut avoir des difficultés à humecter la partie supérieure.

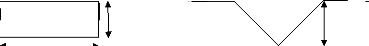
h

h

18

L

Sillon large et plat Sillon triangulaire

Le périmètre mouillé varie avec la hauteur, aussi bien dans le cas du sillon plat que du sillon triangulaire.

2.2.2 : La longueur des raies

La longueur d'un système d'irrigation à la raie est en fonction étroite avec le débit appliqué. La longueur maximale est généralement basée sur le débit maximal non érosif ou la capacité de la raie.

La longueur minimale d'une raie sur des sols filtrants et peu filtrant est généralement comprise respectivement entre 40 à 90 m et 100 à 200 m. Sa détermination est en fonction du coefficient de perméabilité «K» du sol et de la dose d'arrosage, il faut qu'il y ait équilibre entre le débit d'arrière d'eau et le débit d'infiltration de la surface mouillée (S) du canal.

Tableau 5 : Ordre de grandeur des longueurs maximales des raies (m) en fonction de la pente, du type de sol, du débit et de la dose d'arrosage.

19

Pente du sillon

	Débit par sillon (l/s)	Dose d'irrigation (mm)
		Argile		Limon		Sable
(%)		50	75	50	75	50	75
0,0	3,0	100	150	60	90	30	45
0,1	3,0	120	170	90	125	45	60
0,2	2,5	130	180	110	150	60	95
0,3	2,0	150	200	130	170	75	110
0,5	1,5	150	200	130	170	75	110

(FAO, 1990)

2.2.3 : La profondeur des raies

La profondeur de la raie varie en fonction de la nature du sol, de la pente du terrain et de la culture mise ne place. Elle est généralement comprise entre 0,07 à 0,125 m et il est important d'avoir une profondeur suffisante pour que l'eau ne déborde pas.

2.2.4 : L'écartement des raies

L'écartement des raies varie selon la nature du sol, la pente du terrain et la culture choisie.

Pour les sols sableux, l'écartement des raies varie entre 0,30 et 0,60 m (cela dépend de la taille des particules)

Pour un sol argileux, il varie entre 0,7 et 1,50 m.

Tableau 6 : Ecartement des raies ne fonction de la nature du sol

Nature du sol	Sillon en «V» (m)	Sillon plat (m)
Limono-sablonneux	0,6	1,50
Limono-argileux	1,10	2,00

(FAO, 1990)

2.2.5 : La pente

En règle générale, la pente doit être inférieure à 1% ; mais peut aller jusqu'à 3%, dans les zones rides et semi-arides. Dans les zones humides, la pente doit être inférieure à 0,3%.

D'après la FAO (1990), la pente ne doit jamais dépasser 0,5%. Il est d'usage courant que les sillons doivent avoir des pentes douces allant jusqu'à 0,05% pour assurer le drainage des eaux à la fin de l'irrigation, ou l'évacuation des eaux de pluies (méthode d'irrigation manuelle).

On peut calculer la pente par la formule suivante :

20

67

S (max) = (20)

(

30 ) 1 / 3 P

Avec : S (max) = pente maximale non érosif, en (m/m) et exprimé en % ; (P30) = précipitation biennale de durée 30 minutes.

2.2.6 : Les types de raies

Il existe quatre types de raies :

V' Les raies horizontales ;

V' Les raies rectilignes en pente ; V' Les raies en courbes de niveau ; V' Les sillons.

Chaque type nécessite une étude et un tracé spécifique.

L'adaptation de chaque type dépend de la culture, de la topographie du terrain, du type de sol, des façons culturales et des facteurs climatiques.

Les raies peuvent être classées également en fonction de la nature de leur extrémité aval en deux catégories.

2.2.6.1 : Raies à extrémité aval fermée

Ce type de raies où les pertes en colature sont nulles, pose un problème d'uniformité d'arrosage.

2.2.6.2 : Raies à extrémité aval ouvert

Pour ce type de raies, les pertes en colatures sont grandes ; mais l'uniformité de l'arrosage est bonne par rapport au premier type.

L'utilisation d'un réseau de colature afin de récupérer les eaux pour une éventuelle réutilisation est conseillée dans ce cas.

2.3 : Les différents modes d'alimentation

En irrigation à la raie, on distingue quatre modes d'alimentation dont la plus classique est l'alimentation à débit unique.

2.3.1 : Alimentation à débit unique sur terrain en pente

Le débit en tête est constant et continu durant toute la durée de la période d'apport. Les raies ouvertes à leurs extrémités débouchent sur un fossé permettant la récupération de l'écoulement en colature.

21

2.3.2 : Alimentation à deux débits sur terrain en pente

Ce mode d'alimentation permet de diminuer les pertes en colature d'un arrosage à débit unique et par conséquent amélioré le rendement hydraulique, en réduisant le débit d'apport pendant une partie de la durée d'apport. Ce mode consiste à apporter un débit élevé appelé débit d'attaque pendant une proportion de la durée d'application et de continuer l'arrosage avec un débit d'entretien plus faible pendant le reste de la duré d'apport.

2.3.3 : Alimentation par vagues

L'irrigation par vagues consiste à appliquer l'eau en gorgées c'est-à-dire que le débit reste constant mais il est apporté par intermittence. Ce mode d'alimentation nécessite obligatoirement une automatisation du système et permet une grande économie d'eau.

2.3.4 : Alimentation sur un terrain horizontal

Ce mode d'alimentation consiste à apporter de l'eau à la raie avec un débit constant durant un temps relativement court puis elle y stagne et s'infiltre sans qu'il y ait des pertes en colature.

2.4: Les quatre phases de l'arrosage en irrigation à la raie

La durée d'infiltration en irrigation à la raie est plus importante que la durée de l'alimentation. Cette durée d'infiltration est le temps que met l'eau pour s'infiltrer dans le sol même si l'alimentation est terminée.

2.4.1 : La phase d'avancement (TL)

Elle correspond à la durée entre le débit de l'arrosage (t0) et l'arrivée de l'eau à l'extrémité aval de la raie (tL).

TL = tL - t0 (21)

2.4.2 : La phase d'entretien (TEnt)

C'est le temps écoulé entre l'instant d'arrivée de l'eau à l'extrémité avale de la raie (tL) et l'instant d'arrêt de l'alimentation (tC0).

TEnt = tC0 - tL (22)

TEnt

tC0

tL

2.4.3 : La phase de Latence (TLat)

Elle correspond à la durée comprise entre l'arrêt de l'alimentation en tête (tC0) et la disparition de l'eau à l'extrémité amont de la raie (tR0).

TLat = tR0 - tC0 (23)

2.4.4 : La phase de récession (TR)

C'est le temps de la disparition complète de l'eau en chaque point de la raie. Sa durée commence à partir de la disparition de l'eau de l'extrémité amont de la raie et se termine avec la disparition totale de l'eau en tout point de la raie.

TR = tR(L) - tC0 (24)

La succession de ces quatre étapes de l'arrosage est illustrée par la figure suivante :

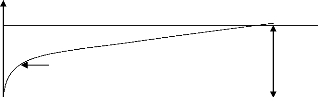
Courbe de récession Tr

Phase de récession

Temps (min)

tR(L)

tR(o)

TLat

Phase de latence

Phase d'entretien

Tapp

Courbe d'avancement

Phase d'avancement TL

22

t0

Longueur (m)

Figure 5 : Représentation schématique des différentes phases d'irrigation à la raie

23

2.5 : Les paramètres de l'irrigation à la raie

Deux paramètres principaux se distinguent en irrigation à la raie.

· Le débit en tête de la raie ;

· La durée d'apport ou temps d'alimentation.

2.5.1 : Le débit en tête de la raie

Il constitue un facteur fondamental, d'autant puisqu'il conditionne le déroulement et le résultat d'un arrosage. Le débit en tête doit être :

· Le même pour chaque raie ;

· Inférieur au débit érosif et supérieur à l'infiltration totale.

Les valeurs usuelles du débit par raie sont de 0,2 à 0,5 l/s pour 100 m de longueur.

Tableau 3 : Conséquences des différents débits en tête sur les paramètres de performance.

Débit		Conséquences	Trop faible
Importantes pertes par percolation, rendement hydraulique faible, mauvaise uniformité.		Trop fort
Importantes pertes par percolation, rendement hydraulique faible, bonne uniformité.		Débit unique bien adapté
Equilibre entre les pertes par percolation et colature, 60% et 70% respectivement pour le rendement hydraulique et le coefficient d'uniformité.		Double débit
Avancement rapide, perte par percolation, faible perte par colature, le coefficient d'uniformité et le rendement hydraulique peuvent dépasser les 80%.

(CEMAGREF, 1990)

24

2.5.2 : La durée d'apport

Elle est déterminée par la dose apportée et le débit au niveau de la tête de la raie. C'est la somme du temps d'entretien _(TEnt) et du temps d'avancement (TL). Il varie en sens inverse avec le débit.

Tapp = TL + TEnt (25)

2.6 : Les doses d'irrigation

2.6.1 : La dose brute (db)

C'est la quantité d'eau apportée au cours de l'irrigation le long de la raie par unité de surface. Elle est généralement exprimée en (mm) ou (m³/ha) et n'est pas totalement utilisable par la plante.

db = volume brut /surface arrosée (26)

La dose brute correspond à la dose théorique majorée des pertes. Elle est également donnée par la formule :

db

60x Qox Tapp (27) ExL

Avec : db = dose brute d'arrosage, en mm ;

Q0 = débit d'entrée en tête de la raie, en l/s ;

Tapp = durée d'apport, en mm ;

E = écartement entre les raies, en m ;

L = longueur de la raie, en m.

2.6.2 : La dose nette ou dose théorique (dn)

C'est la quantité d'eau apportée par unité de largeur pour un sol donné ; on peut l'exprimer en (mm) ou en (m³/ha).

dn= axdaxHexZ (28)

Avec : dn = dose nette d'arrosage, en mm ;

da = densité apparente du sol ;

He = humidité équivalente, en % ;

Z = profondeur des racines, en mm ;

á = coefficient qui est fonction de la sensibilité de la culture.

(Plante sensible : á = 0,3 ; plante résistante : á = 0,6)

25

2.6.3 : La dose infiltrée

L'infiltration cumulée exprimée en hauteur équivalente rapportée à une surface de longueur unitaire et de largeur égale à l'espacement entre les raies est donnée par l'expression suivante :

'(0-x) = [a (T^b _inf(0-x) + c]. P / E (29)

Avec : I(0-x) = hauteur d'eau infiltrée équivalente, en mm ;

T^binf(0-x) = temps moyen de séjour de l'eau à la surface du sol

entre l'amont et l'abscisse x, en min ;

a, b, c = constantes liées à la texture du sol ;

P = périmètre mouillé, en mm ;

E = écartement entre les raies, en m.

2.7 : Les pertes

C'est la somme des quantités d'eau perdues soit en colature soit par infiltration en profondeur.

2.7.1 : Les pertes en colature (Pc)

L'écoulement superficiel équivalent au ruissellement, c'est-à-dire les pertes en colature, est la différence entre la dose brute d'arrosage (db) et l'infiltration moyenne I(0-L).

Pc = db - '(0-L) (30)

Avec : Pc = pertes en colature, en mm ;

db = dose brute d'arrosage, en mm ;

I(0-L) = infiltration moyenne sur toute la longueur de la raie, en mm.

2.7.2 : Les pertes par infiltration en profondeur (Pp)

Elles sont aussi appelées pertes par percolation et sont obtenues en retranchant la dose nette d'arrosage de l'infiltration moyenne sur toute la longueur de la raie.

Pp = '(0-L) - dn (31)

Avec : Pp = pertes par percolation, en mm ; dn = dose nette d'arrosage, en mm.

2.8 : Les paramètres de performance

Ce sont des valeurs exprimées souvent en pourcentage, ils permettent de qualifier un arrosage. On distingue deux paramètres de performance :

> L'efficience de l'arrosage, estimée à partir du rendement hydraulique (Rh) ;

> L'uniformité de l'arrosage, estimée à travers le coefficient d'uniformité (Cu).

2.8.1 : Le rendement hydraulique (Rh)

Il indique la partie utile de volume d'eau apportée à la raie ; il est défini comme étant le rapport entre la dose nette et la dose brute d'arrosage.

dn

Rh = × 100 (32)

db

Avec : Rh = rendement hydraulique, en % ; dn = dose nette d'arrosage, en mm ; db = dose brute d'arrosage, en mm.

Si en un pont quelconque, la dose nette n'est pas atteinte, c'est-à-dire db inférieur à dn, le rendement hydraulique sera égal au rapport entre la dose minimale apportée (volume infiltré) et la dose brute appliquée.

Dose nette d'arrosage		Perte en colature

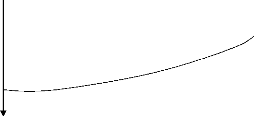
Perte par infiltration

Distance

Profondeur

26

Figure 6 : Répartition des volumes de la dose brute appliquée

27

2.8.2 : Le coefficient d'uniformité (Cu)

C'est un coefficient qui indique la qualité de la répartition de l'eau d'irrigation le long de la raie.

ë = ×

n

1

ⁿ Xi Xm (33)

Xm

Avec : Cu = coefficient d'uniformité, en % ; Xi = dose infiltrée au point i, en mm ;

Xm = dose infiltrée sur toute la longueur de la raie, en mm ;

N = nombre d'observations ou nombre de points.

2.9 : Avantages et inconvénients de l'irrigation à la raie

2.9.1 : Les avantages

Elle est applicable aux différents terrains ;

Frais d'aménagement du sol réduits ;

La terre reste sèche entre les sillons, ce qui facilite les travaux ;

Les parties aériennes des plantes sont à l'abri de l'eau, ce qui évite

les maladies cryptogamiques ;

La terre ne forme aucune croûte ;

Les débits employés dans les sillons sont faibles, ce qui limite les

érosions ;

On obtient un drainage superficiel excellent si la pente des raies est

suffisante et si la parcelle est équipée d'ouvrages de colature

adéquats ;

Technique moins coûteuse du point de vue matériel.

2.9.2 : Les inconvénients

Besoins en main d'oeuvre importants ;

Perte d'eau très importante ;

La concentration des solutions entre les rigoles peut présenter des

dangers ;

Rendement hydraulique global faible par rapport aux autres

systèmes ;

La gêne causée par les sillons pour les déplacements latéraux.

28

2.10 : Conclusion

Dans l'étude de l'irrigation à la raie, il convient de rappeler que seule une partie du sol reçoit directement l'eau qui s'infiltre verticalement et latéralement dans le creux de la raie. Son principe conduit à un excès d'eau, puisque la partie aval du sillon doit être aussi humide que la partie amont.

En pratique, il faut d'abord apporter un fort débit afin d'avoir une humectation aussi homogène que possible du fond de la raie, puis un débit réduit pendant un temps plus long, pour que la totalité de la dose pénètre en profondeur.

29

CHAPITRE III : L'INFILTRATION

L'infiltration est le nom donné au processus d'entrée de l'eau dans le sol, généralement à travers la surface du sol et verticalement vers le bas.

L'infiltration signifie le transfert de l'eau à travers les couches superficielles du sol, lorsque celui-ci reçoit des averses ou s'il est exposé à une submersion. L'eau infiltrée remplie en premier lieu les interstices du sol en surface et pénètre par la suite dans le sol sous l'action de la gravité et des forces de succion. Ce processus est d'une grande importance dans la pratique, car son régime détermine souvent le ruissellement qui se forme à la surface du sol.

3.1 : Les types d'infiltration

On distingue deux types d'infiltration 3.1.1 : L'infiltration horizontale

Dans ce cas, seules les forces de succion matricielle entraînent l'eau dans le sol. L'influence de la pesanteur est nulle ou négligeable. C'est le cas le plus simple d'infiltration.

3.1.2 : L'infiltration verticale

Elle est orientée vers le bas dans un sol initialement saturé. Elle est due généralement à l'influence combinée des gradients de succion et de la gravité. L'eau pénètre en profondeur et le gradient moyen de succion diminue. Cette tendance continue jusqu'à ce que le gradient de succion dans la partie supérieure du profil devienne négligeable avec un gradient gravitationnel constant.

3.2 : Capacité et taux d'infiltration

3.2.1 : La capacité d'infiltration

Désignée aussi sous le terme de capacité d'absorption, la capacité d'infiltration représente le flux d'eau maximale que le sol est capable d'absorber à travers sa surface lorsqu'il reçoit une pluie efficace ou lorsqu'il est recouvert d'eau. Par le biais de la conductivité hydraulique, elle dépend de la structure et de la texture du sol, mais également des conditions aux limites, c'est-à-dire la teneur en eau initiale du profil et de la teneur en eau imposé en surface.

3.2.2 : Le taux d'infiltration

Le taux d'infiltration est le rapport entre la quantité d'eau infiltrée et la durée d'infiltration. Il dépend avant tout du régime d'alimentation (irrigation, pluie), de l'état d'humidité et des propriétés physiques du sol.

i

I Tinf il

(mm) (34)

30

La variation spatiale et temporelle de la teneur en eau dans le sol est décrite par des profils d'infiltration ou généralement par des profils hydriques successifs représentant la distribution verticale des teneurs en eau dans le sol à différents instants donnés.

3.3 : Les différentes zones du profil d'infiltration

Ce profil est défini par trois zones liées entre elles ; mais en fonction de la nature du flux, elles présentent les caractéristiques suivantes :

- Zone de saturation : s'étend sur quelques centimètres proche de la surface du sol.

- Zone de transmission : joue le rôle de transmission de l'humidité entre la première et la troisième zone.

- Zone d'humectation : On observe une diminution de la teneur en eau jusqu'au front d'humectation, ce dernier es la limite entre le sol sec et humide.

Plan d'eau

Teneur en eau

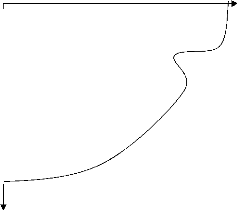
Zone de saturation

Zone de transmission

Zone d'humectation

Profondeur

31

Figure 7 : Les différentes zones du profil d'infiltration 3.4 : Les facteurs affectant l'infiltration

L'infiltration de l'eau dans le sol est influencée par certains facteurs. Les plus importants sont :

· La structure : lorsque la surface du sol est poreuse, l'infiltrabilité initiale est très élevée par rapport à celle d'un sol uniforme mais l'infiltrabilité finale reste inchangée.

· La texture : La vitesse d'infiltration est plus faible dans un sol à texture fine (argile), que dans un sol à texture grossière (sable).

· La teneur en eau initiale : la vitesse d'infiltration est beaucoup plus élevée pour un sol sec qu'un sol humide.

· La densité et la porosité : ces deux facteurs sont en relation avec la texture.

· La topographie et la morphologie du sol : la pente par exemple agit à l'opposé de la végétation. En effet, une forte pente favorise les écoulements au dépend de l'infiltration.

· La couverture du sol : la végétation ralentit l'écoulement de l'eau à la surface du sol.

3.5 : Les lois d'infiltration

Une loi d'infiltration est une équation de la courbe qui donne l'infiltration cumulée en fonction de la durée d'infiltration.

Plusieurs lois ont été proposées pour l'estimation de l'infiltration. On peut citer :

> Loi de KOSTIAKOV

> Loi de KOSTIAKOV modifiée

> Loi de GREEN et AMPT

> Loi de PHILIPP

> Loi de S.C.S

3.5.1 : Loi de KOSTIAKOV

L'estimation de l'infiltration par la loi de KOSTIAKOV est basée sur la méthode mesurée de MUNTZ. C'est une loi simple qui est donnée par :

I=a×t ^b (35)

32

Avec : I = volume infiltré cumulé, en mm/min ;

t = temps de séjour de l'eau à la surface du sol, en min ; a, b = constantes.

Cette loi n'est pas précise car elle ne tient pas compte de :

- La teneur en eau du sol,

- La structure du profil,

- L'utilisation du double anneau de MUNTZ, en l'enfonçant dans le sol, - L'espace poreux, ce qui influe sur les propriétés conductrices du sol.

Ayant constaté cette imprécision, KOSTIAKOV a proposé une autre loi. 3.5.2 : Loi de KOSTIAKOV modifiée

Elle est donné par :

I=a×t^b +c×t (36)

Avec : I = volume infiltré cumulé, en mm/min ; t = temps d'infiltration, en min ;

c = constante représentant l'infiltration stabilisée ; a, b = constantes empiriques.

3.5.3 : Loi de GREEN et AMPT

La méthode de GREEN et AMPT est une formule physique qui s'applique d'une manière assez satisfaisante dans certains cas d'infiltration dans les sols initiale secs.

I= Lf×Äè (37)

Avec : I = volume infiltré cumulé ;

?è = accroissement de la teneur en eau ; Lf = profondeur du front humidifiée.

Après quelques transformations, GREEn et AMPT arrivent à l'équation finale :

I=K×t (38)

Avec : I = volume infiltré cumulé, en l/m ; K = transmissivité, en l/t ;

t = temps d'infiltration, en min.

33

Cette méthode est essentiellement empirique puisqu'elle suppose que la succion reste constante, mais on sait que la teneur en eau d'un sol initiale sec varie avec le temps.

3.5.4 : Loi de PHILIPP

Philipp a proposé une méthode de résolution de l'équation de l'infiltration verticale dans certaines conditions initiales et limites. Cette loi introduit la notion de l'absorptivité qui représente la capacité d'un sol à absorber l'eau lorsque l'écoulement se produit uniquement sous l'action du gradient de pression.

I t = S × t 1 / 2 + K × t

( ) (39)

Avec : I (t) = volume infiltré cumulé, en l/m ;

S = absorptivité du sol, en L/T^1/2 ;

K = transmissivité, en L/T.

3.5.5 : Loi de S.C.S

Elle est donnée par la loi :

I = a × t +c

^b (40)

Avec : I = volume infiltré cumulé, en mm/min ;

t = temps d'infiltration, en mm ;

c = constante = 0,7 ;

a, b = coefficients d'ajustement fonction de la texture du sol.

3.6 : Conclusion

Les systèmes d'irrigation à la raie exigent une approche différente concernant la loi d'infiltration. En fait, sur la parcelle à irriguer seulement une partie de cette surface est humectée donc en contact avec l'eau ; donc la surface d'infiltration n'est pas la même que dans les autres techniques d'irrigation (par submersion ou par ruissellement) où la surface totale de la parcelle ou de l'unité d'arrosage est en contact avec l'eau.

34

CHAPITRE IV : BILAN DU VOLUME

La détermination de la quantité d'eau infiltrée dans un sol est l'obstacle le plus important dans le suivi d'un projet en irrigation de surface.

Le principal problème des chercheurs en irrigation de surface est l'évolution du comportement de l'infiltration. Pour cela, un modèle est proposé pour l'évolution du comportement de l'infiltration, ce modèle est régit par le principe de la conservation de la masse.

La relation du bilan de volume est utilisé dans le but de :

- L'estimation de la vitesse si les caractéristiques d'infiltration du sol sont connues.

- L'estimation des caractéristiques d'infiltration si le temps d'avancement est connu.

4.1 : Relation du bilan de volume

Les modèles du bilan du volume sont fondés sur l'équation de continuité et quelques hypothèses. Le plus connu de ces modèles est celui de LEWIS et MILNE (1938).

Dans ce modèle, l'écoulement de surface est supposé de type piston (le tirant d'eau est considéré constant dans l'espace et dans le temps), et l'écoulement souterrain est souvent décrite par une équation empirique à 2 ou 3 paramètres de types KOSTIAKOV (1932), PHILIPP (1957).

Leur première équation décrite pour le cas de l'irrigation par planche est donnée par la formule :

k

(41)

Q tx y x Z t t ds x = x + ? ( K _ S ) x

0

Avec : Q = débit de longueur de la planche ;

tx = temps d'avancement à la distance x ;

y = hauteur moyenne de la nappe en surface ;

x = distance d'avancement (L);

Z(tk - t_s) = hauteur infiltrée (L) au point (s) et pendant le temps (tk - t_s).

Cette relation montre que durant la phase d'avancement, la somme des volumes infiltrés de la nappe en surface est égale à la somme des volumes entrés.

35

4.2 : Les composantes du bilan de volume

4.2.1 : L'infiltration

L'infiltration de l'eau dans le sol se définit comme étant le processus d'entrée de l'eau dans le sol à travers une surface déterminée. Dans l'application de la technique du bilan du volume, le comportement de l'infiltration de l'eau dans le sol reste inconnu. Vu sa variabilité dans l'espace et dans le temps, l'infiltration demeure difficile à quantifier. Plusieurs se sont penchés sur la question et ont fournis différentes techniques du bilan de volume qui sont des approches permettant une intégration de la masse de l'infiltration.

L'équation la plus utilisée est celle de KOSTIAKOV :

I=a×t ^b (42)

Avec : I = infiltration cumulé, en mm ;

t = durée de séjour de l'eau à la surface du sol, en mm ; a, b = constantes d'ajustement.

4.2.2 : L'avancement

La durée d'avancement est le temps tx que met la nappe d'eau pour atteindre la distance x de la raie.

L'avancement de l'eau à la surface du sol dépend de plusieurs facteurs :

1- Facteurs variables le débit d'apport ; l'humidité initiale.

2- Facteurs fixes la pente de la raie ; la rugosité de la surface (coefficient de MANNING « n ») ;

la texture du sol.

Recherche de loi d'avancement

A- Forme puissance (parabole) L'équation s'écrit sous la forme :

Tx = P × X (43)

r

P et r sont des constantes. LogTx = LogP+ r× LogX

36

Trois méthodes d'ajustements ont été introduites par BERTHOME « 1985 ».

· Méthode des deux points.

· Méthode de régression log-linéaire.

· Méthode du minimum des écarts.

1- Méthode des deux points

Dans l'avancement de l'eau, cette méthode consiste à choisir uniquement deux points qui sont généralement au milieu de la raie (L/2) et à l'extrémité aval de la raie (L), puis résoudre le système :

TL/2 tL/2 L/2 _(TL/2, L/2)

TL tL L (TL, L)

(TL/2, L/2) TL/2 = P(L/2)^r

(TL, L) TL = P(L)^r

Transformation logarithmique

Log (TL/2) = Log P + r Log (L/2) .(1)

Log (TL) = Log P + r Log (L) ..(2)

(2) - (1) Log (TL) - Log (TL/2) = r [Log (L) - Log (L/2)
Log (TL/TL/2) = r Log 2

T_L

_Lr

P=

Log T T

( / / 2 )

L L

r = et

Log 2

2- Méthode de régression log-linéaire

Cette méthode consiste à faire une linéarisation de la fonction d'avancement après transformation logarithmique des couples (t_x, xi).

Cette linéarisation permet d'ajuster la droite des couples (Log t_x, log xi)

37

X

tx	Log tx = y	0 x1 . . xi . . L
0 tx1 . . txi . . tL	- Log txi . . Log tx1 . . Log tL

X=PXX r

LogTx = LogP+ rX LogX

La droite issue de la linéarisation de la fonction d'ajustement est de la forme y = m + r.x

3- Méthode du minimum des carrés

Cette méthode est trop compliquée par rapports aux premières. Elle est rarement utilisée. Mais elle est plus précise. Elle consiste à rechercher les coefficients X et B qui rendent minimal l'écart type entre les temps observés et les temps calculés.

tx = a X x b B- Forme exponentielle (SCS)

(44)

Le Soil Conservation Service (SCS) propose une deuxième équation du type (ASAE, 1983 ; BERTHOME 1984).

Xl_ g X xl

tx = exp (45)

' ?

F 1 / 2

L qXs J

38

Avec : tx = temps d'avancement à la distance x

q = débit d'alimentation, en l/s;

s = pente en m/m ;

g et F = coefficients constants fonction de la texture ;

x = abscisse.

4.2.3 : La récession

C'est le temps tr de disparition totale de l'eau de la surface du sol de l'amont vers l'aval de la raie. Une loi du type puissance caractérise cette phase :

X = c' (tr)

^b tr = c ' x ' b ' (46)

Avec: tr = temps de récession au point (x) ;

c, b, c', b' = coefficients d'ajustement calculé par la méthode des deux points et par la méthode de la régression log-linéaire.

4.2.4 : Le volume entré

C'est le volume total apporté pendant la durée d'application. Il constitue une partie importante du bilan de volume. Ce volume peut être obtenu par l'intégration de l'hydrogramme des débits d'entrée.

4.2.5 : Le volume stocké

C'est le volume d'eau stocké à la surface de la raie, on peut l'estimer en multipliant la hauteur moyenne de la section mouillée par un facteur de forme. Durant l'avancement, ce facteur varie entre 0,7 et 0,8.

4.2.6 : Le volume infiltré

Le volume infiltré durant les trois phases d'arrosage est défini par l'expression suivante :

Vi(t) = Ve(t) - Vc(t) - Vs(t) (47)

Avec : Vi (t) = volume infiltré, en l ; Ve (t) = volume entré, en l ; Vc (t) = volume écoulé en colature, en l ; Vs (t) = volume stocké, en l.

39

4.2.7 : Le coefficient d'infiltration (Ci)

C'est le rapport du volume infiltré au volume d'eau apporté pendant le temps d'apport

Volume d'eau infiltré

Ci = ×100 (48)
Volume d'eau apporté

Il est donné en pourcentage. 4.3 : Conclusion

Ce chapitre montre que, les objectifs du bilan de volume reposent sur l'estimation de la vitesse d'infiltration et sur ses caractéristiques.

Le débit d'une raie et la durée d'infiltration sont tous les deux, influencés par la conduite des arrosages à suivre. Les calculs se basent sur un arrosage-type et sont ajustés en fonction des variations de la durée d'infiltration, de la dose, et des débits propres à chaque arrosage pendant la saison d'irrigation.

40

CHAPITRE I : PRESENTATION DU MILIEU

L'étude a été conduite à la ferme expérimentale de l'université de Mostaganem à

Mazagran dont les coordonnées géographiques sont les suivantes :

- Altitude : 126 à 130 m

- Latitude : 35° Nord

- Longitude : 06° Est.

Les conditions climatiques de l'essai sont caractérisées par un hiver assez froid et

pluvieux, un été chaud et sec de type semi-aride méditerranéen.

Les caractéristiques physiques et hydriques du sol se résume comme suit dans le

tableau ci-après :

Tableau 8 : Caractéristiques physiques et hydriques du sol

Texture	Densité apparente	Humidité équivalente		Profondeur	Sablo limoneux
da = 1,35	He = 0,13%	Z = 300mm

Atelier agriculture de l'université

I.1 : Caractéristiques générales

L'évolution d'un arrosage peut porter soit sur la totalité d'une parcelle, soit sur une raie.

Dans notre essai, l'évolution de l'arrosage se porte sur quatre (04) raies bouchées de même longueur (12 m). Pour se rapprocher des conditions réelles d'arrosage, les raies expérimentales sont complétées par une raie de garde pour la fixation et la détermination des débits.

I.2 : Caractéristiques des raies étudiées

Après un labour effectué par la charrue à soc, nous avons tracé cinq raies

nécessaires pour l'expérimentation dont quatre (04) expérimentales et une (01) de

garde.

Les caractéristiques des raies sont les suivantes :

- Longueur : 12 m

- Ecartement : 0,80 m

41

- Largeur : 0,25 m

- Section : Trapézoïdale

- Pente : 1,25%

- Extrémité avale : Fermée.

I.3 : Réglage du débit

L'alimentation en eau est assurée par le puits de la ferme à partir duquel est remplie une citerne de 3000 litres. Le débit choisi a été réglé à l'aide d'un dispositif de réglage de débit ; ce dispositif est constitué d'un grand sceau d'une capacité de 90 litres qui comporte des orifices de différents diamètres.

Le diamètre de l'orifice permet la sélection du débit désiré.

I.4 : Caractéristiques de l'essai

Le débit d'alimentation est constant sur la totalité de l'arrosage pour chaque raie et pour chaque débit. Les débits choisis sont :

Q = 0,2 l/s ; Q = 0,4 l/s ; Q = 0,6 l/s ; Q = 0,8 l/s

42

L'irrigation est répétée deux fois pour chaque débit et le temps d'application est fixé à 1,5TL (temps d'avancement).

I.5 : Protocole de mesure

Il consiste à mesurer l'avancement de l'eau dans la raie ne notant le tems de passage de l'eau au niveau des différents jalons espacés de 2 m. De la même façon, la récession est mesurée en notant le temps de disparition totale de l'eau à chaque jalon. La détermination des tirants d'eau dans les sections situées au niveau des jalons est donnée par leur mesure à différents temps au cours de l'arrosage.

43

CHAPITRE II : ETUDE PRATIQUE DE L'INFILTRATION

II.1 : Etude de l'avancement

II.1.1 : Mesure de l'avancement

Les jalons ont été placés avant l'arrosage et sont distants de 2m ; c'est-à-dire :

x0=0m ; x1=2m ; x2=4m ; x3=6 m ; x4=8m ; x5=10m ; x6=12m.

En cours d'arrosage, on note à l'aide d'un chronomètre les temps de passage t_n aux

abscisses x_n à partir du début de l'arrosage.

Les temps de passage au niveau des différents jalons sont consignés au tableau

suivant :

Tableau 9 : Mesure de l'avancement

xn (m)		Temps d'avancement (min)
		Irrigation n° 2
		Raie B	Raie C	Raie D	Raie A	Raie B	Raie C	Raie D
		Q=0.4l/ s	Q=0.6l/ s	Q=0.8l/ s	Q=0.2l/ s	Q=0.4l/ s	Q=0.6l/ s	Q=0.8l/ s	2
0.38		0.23	0.14	0.10	0.30	0.18	0.20	0.13	4
0.85		0.60	0.42	0.28	0.93	0.47	0.45	0.35	6
1.32		0.98	0.62	0.42	1.40	0.77	0.60	0.57	8
2.53		1.68	0.98	0.68	2.12	1.77	0.87	0.90	10
4.78		2.88	1.58	1.12	3.48	1.93	1.40	1.18	12
7.25		4.83	2.92	1.95	5.28	2.62	2.13	1.45	Tap p
8.75		6.33	4.42	3.45	6.78	4.12	3.63	2.95

44

II.1.2 : Détermination de la loi d'avancement

Deus types de loi d'avancement sont généralement utilisées en irrigation à la raie à débit constant :

- La loi de type puissance : c'est la loi la plus courante

X(t) = p . t ou

^r T(x) = a.x

b

Avec : t : temps d'avancement à l'abscisse x, en min ; p, r, a et b : coefficients d'ajustement.

- la loi de SCS (Soil Conservation Service) de type :

g.x

( 1 / 2 )
.

t x =

( ) . Qo S

x e (50)

f

Avec : Qo : débit d'apport au niveau de l'unité d'arrosage, en l/s ; S : pente de la raie, en m/m ;

x : abscisse qui est atteinte par l'eau durant tx

45

g et f sont des constantes qui dépendent de la texture du sol.

La détermination de la loi d'avancement consiste à ajuster les mesures de terrain à

l'une des deux lois citées précédemment.

Dans le cas de notre expérimentation, nous avons utilisé la loi de type puissance. Pour

faire cet ajustement, les méthodes utilisées ont été :

- La méthode des deux points

- La méthode de régression log-linéaire

Après application des deux méthodes, nous avons obtenus les résultats illustrés au

tableau suivant :

Tableau 10 : Détermination de la loi d'avancement par les deux méthodes (Méthode des deux points et méthode de régression log-linéaire)

Irrigation n°	Débit (l/s)	Raie	Méthode des deux points				Méthode de régression log-linéaire
			b		T(x) = a.x ^b	a	b	r	b T(x) = a.x	01
0.2	A	0.016	2.457		2 , 457 T ( x ) = 0.0 1 6 x	0.066	1.790	0.97	1 ,790 T ( x ) = 0.066 x
	B	0.016	2.301		T(x) = 0.0 1 6x	0.042	2 , 30 1 1.783	0.98	1,783 T(x) = 0.042x
	C	0.011	2.236		T(x) = 0.0 1 1x	0.027	2 , 236 1.849	0.97	1, 849 T(x) = 0.027x
	D	0.008	2.215		T(x) = 0.008x	0.023	2 , 2 15 1.934	0.99	1, 934 T(x) = 0.023x	02
0.2	A	0.045	1.915		1, 9 1 5 T ( x ) = 0.045 x	0.158	1.513	0.97	1 ,5 1 3 T ( x ) = 0. 1 5 8 x
	B	0.032	1.766		T(x) = 0.032x	0.068	1, 766 1.422	0.98	1, 422 T(x) = 0.068x
	C	0.023	1.828		T(x) = 0.023x	0.102	1 , 828 1.207	0.98	T(x) = 0. 1 02x1, 207
	D	0.051	1.347		T(x) = 0.05 1x	0.032	1, 347 1.526	0.98	1,526 T(x) = 0.032x

46

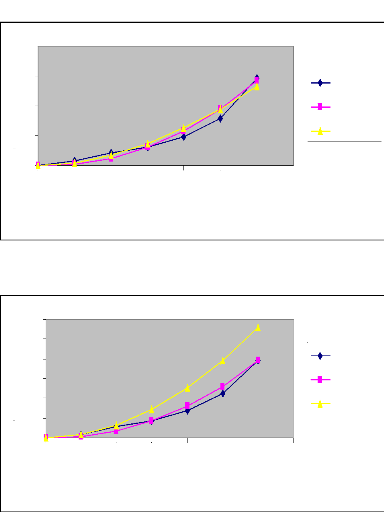
L'évolution de l'avancement le long de la raie en fonction du temps est représentée par les graphes suivants :

47

Figure 7 : Courbes d'avancement ajustées par les deux méthodes (Irrigation N° 1)

Raie B (Q=0.4l/s)

6

5

Tem O s ( m n )

4

3

2

1

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

8

Tem O s ( m n )

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log_lin

Raie A (Q=0.2l/s)

Raie C (Q=0.6l/s)

Raie D (Q=0.8l/s)

4

Tem p s (m n )

3

2

1

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

3

2,5

Tem p s (m n )

2

1,5

1

0,5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

48

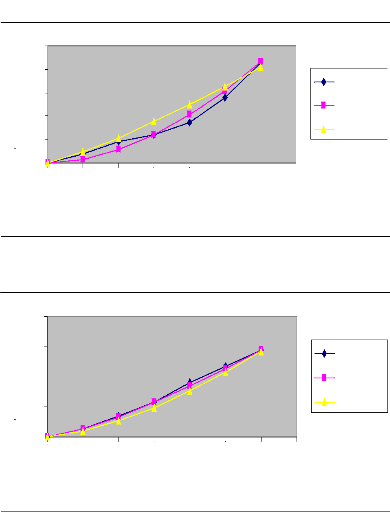
49

Figure 8 : Courbes d'avancement ajustées par les deux méthodes (Irrigation N° 2)

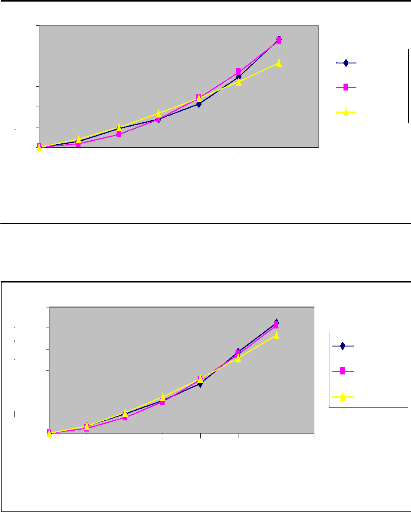
Raie B (Q=0.4l/s)

3

2,5

Tem p s (m i n )

2

1,5

1

0,5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

6

5

Tem p s ( m n )

4

3

2

1

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

Raie A (Q=0.2l/s)

Raie C (Q=0.6l/s)

Raie D (Q=0.8l/s)

2

Tem p s (m n )

1,5

1

0,5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

2,5

Tem p s (m i n )

2

1,5

1

0,5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

50

Tem p s (m n )

8

4

2

6

0

0 2 4 6 8 10 12 14

Longueur (m)

Q=0 2l/s Q=0 4l/s Q=0 6l/s Q=0 8l/s

51

Commentaire

En procédant à une analyse comparative des courbes d'avancement des deux irrigations au niveau des mêmes raies avec les mêmes débits, nous constatons que le temps d'avancement diminue de la première irrigation à la deuxième irrigation. Nous déduisons donc que l'eau s'écoule plus rapidement sur un terrain humide que sur un terrain sec. En effet, l'humidité du sol augmente à chaque irrigation sur la même raie. Par ailleurs, nous constatons que la méthode des deux points donne des résultats plus proches de ceux expérimentaux que la méthode de régression log-linéaire.

Pour obtenir l'évolution du temps d'avancement en fonction de la longueur de la raie, nous avons tracé le graphe suivant qui donne le temps d'avancement en fonction de la longueur de la raie pour les différents débits utilisés et pour les deux irrigations.

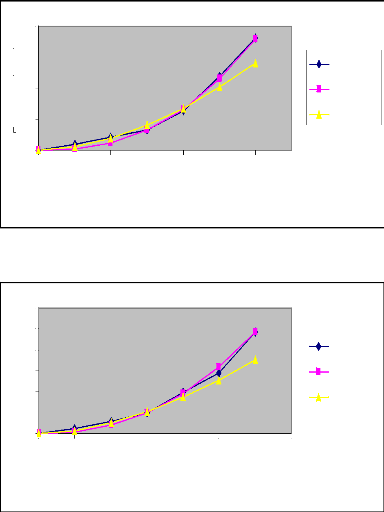
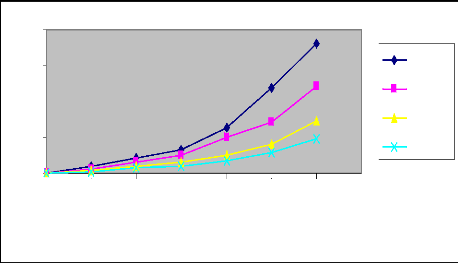
Figure 9 : Courbes de l'évolution du temps d'avancement en fonction de la longueur de la raie pour les différents débits (Irrigation N° 1)

52

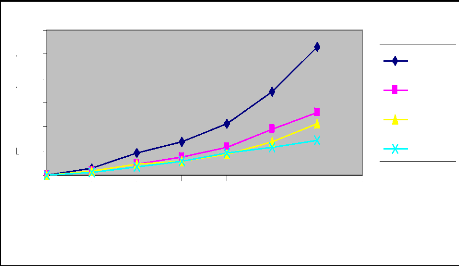
Figure 10 : Courbes de l'évolution du temps d'avancement en fonction de la longueur de la raie pour les différents débits (Irrigation N° 2)

Tem i s (m n )

5

4

3

2

6

0

1

0 2 4 6 8 10 12 14

Longueur (m)

Q=0 2l/s Q=0 4l/s Q=0 6l/s Q=0 8l/s

Commentaire

L'analyse comparative des différents débits au niveau des deux irrigations nous amène à conclure que le temps d'avancement décroît avec le débit d'apport.

II.2 : Etude de la récession

II.2.1 : Mesure de la récession

La récession représente le temps de disparition complète de l'eau en chaque point de la raie.

En théorie, on doit observer un front de récession progressive mais en pratique, l'eau ne disparaît de la surface du sol que d'une façon progressive de l'amont vers l'aval de la raie ; du fait de l'existence de points bas des abscisses intermédiaires. On convient donc que le temps de récession au niveau d'un jalon donné correspond à l'arrêt du mouvement de l'eau à cet endroit précis, même s'il subsiste encore quelques flaques d'eau aux environs du jalon.

53

Le tableau suivant donne les différents temps de récession correspondant aux jalons utilisés pour la phase d'avancement.

Tableau 11 : Mesure de la récession

xn (m)		Temps de récession (min)
		Irrigation n° 2
		Raie B	Raie C	Raie D	Raie A	Raie B	Raie C	Raie D
		Q=0.4l/s	Q=0.6l/s	Q=0.8l/s	Q=0.2l/s	Q=0.4l/s	Q=0.6l/s	Q=0.8l/s	2
1.4		1.23	2.06	1.78	1.22	1.36	1.75	1.13	4
2.07		4.18	2.28	2.05	1.98	4.23	2.82	2.06	6
4.05		12.21	6.30	7.06	3.95	13.43	6.60	6.10	8
5.27		13.85	7.16	7.72	4.92	15.85	7.52	9.97	10
6.12		14.20	8.16	8.29	6.15	16.85	8.80	8.76	12
7.09		14.66	8.92	10.13	7.83	17.55	9.50	10.24

II.2.2 : Détermination de la loi de récession

La récession est caractérisée par une loi de type puissance :

X(t)=a.t_r (51)

b

Avec : tr : temps écoulé après l'arrêt de l'alimentation en tête de la raie, correspondant à l'arrivée du front de récession à l'abscisse Xi

a et b : coefficients d'ajustement

L'application des deux méthodes (méthodes des deux points et méthode de régression log-linéaire) donne les résultats suivants :

54

Tableau 12 : Détermination de la loi de récession par les deux méthodes

Irrigation n°	Débit (l/s)	Raie	Méthode des deux points				Méthode de régression log-linéaire
			b		T(x) = a.x ^b	a	b	r	b T(x) = a.x	01
0.2	A	0.952	0.808		0, 808 T ( x ) = 0.952 x	1.612	0.547	0.97	0, 547 T ( x ) = 1 .6 1 2 x
	B	7.607	0.264		0 , 264 T(x) = 7 .607 x	0.411	1.391	0.97	1, 39 1 T(x) = 0.4 1 1x
	C	2.562	0.502		0 , 502 T(x) = 2.562 x	1.123	0.839	0.99	0, 839 T(x) = 1 . 1 23x
	D	2.775	0.521		0, 52 1 T(x) = 2.775 x	1.091	0.905	0.99	0,905 T(x) = 1 .09 1x	02
0.2	A	0.674	0.987		0, 987 T ( x ) = 0.674 x	1.536	0.626	0.98	0, 626 T ( x ) = 1 .5 36 x
	B	6.725	0.386		0 , 386 T(x) = 6.725 x	0.812	1.223	0.97	1, 223 T(x) = 0. 8 1 2x
	C	2.577	0.525		0 ,525 T(x) = 2.577 x	0.892	0.942	0.98	0, 942 T(x) = 0.892x
	D	1.600	0.747		0, 747 T(x) = 1 .600 x	1.218	0.817	0.97	0,8 17 T(x) = 1 .2 1 8x

L'évolution de la récession en fonction du temps est donnée par les graphes suivants :

55

Figure 11 : Courbes de récession ajustées par les deux méthodes (Irrigation N° 1)

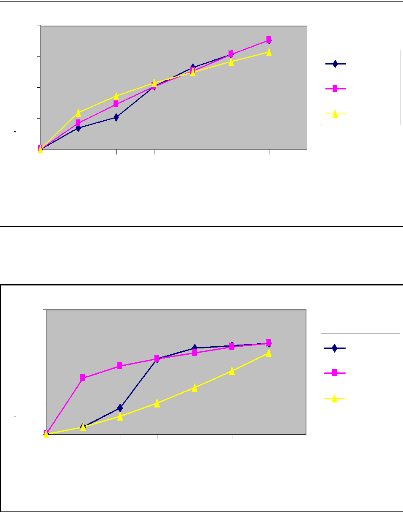
Raie B (Q=0.4l/s)

20

Tem p s (m n )

15

10

5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

8

Tem p s (m n )

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

Raie A (Q=0.2l/s)

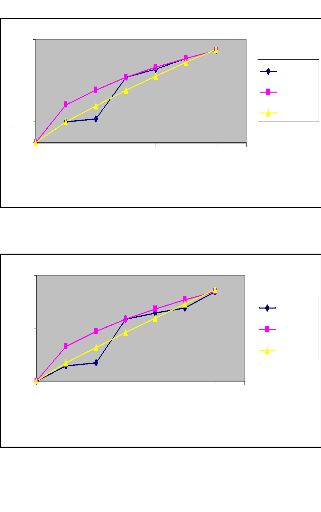
56

Raie C (Q=0.6l/s)

Raie D (Q=0.8l/s)

12

10

Tem D s ( m n i

8

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

10

8

Tem D s ( m n i

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

57

Figure 12 : Courbes de récession ajustées par les deux méthodes (Irrigation N°2)

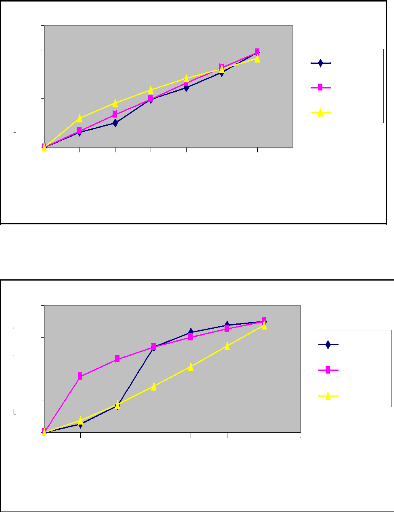
Raie B (Q=0.4l/s)

20

Tem D s ₁ ( m ₁ n i

15

10

5

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

10

Tem D s ( m m n i

8

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

Raie A (Q=0.2l/s)

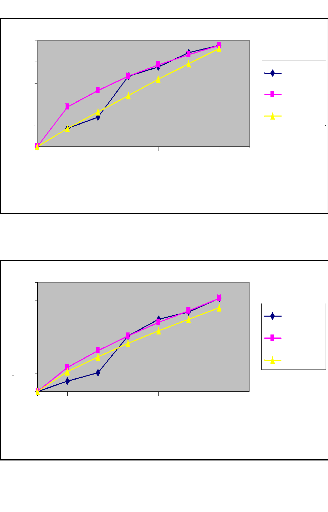
58

Raie C (Q=0.6l/s)

Raie D (Q=0.8l/s)

12

10

Tem D s ( m n )

8

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

10

8

Tem D s ( m n )

6

4

2

0

0 2 4 6 8 10 12 14

Longueur (m)

exp

deux points log-lin

59

Commentaire

L'analyse des courbes de récession nous permet de constater que l'infiltration est plus ou moins rapide au niveau des deux premiers jalons (x1=2m et x2=4m).Au troisième jalon nous avons noté une infiltration assez lente par rapport à celui des autres et ceci dans les deux cas d'irrigation. Ceci s'explique par l'existence d'une pente estimée à 1.25% sur le terrain. Nous remarquons notamment que dans la raie B, l'infiltration est particulièrement lente à compter du troisième jalon. Ce phénomène peut s'expliquer par la nature du sol qui devrait être à ce niveau de beaucoup plus sèche en surface.

De cette analyse, il ressort tout de même que le temps d'infiltration augmente de la première à la deuxième irrigation parce que l'infiltration dans une zone humide est plus lente que celle dans une zone sèche.

Par ailleurs, l'ajustement des temps de récession en fonction des abscisses de la forme puissance (T(x)=a.x^b) montre que pour tous les arrosages, le coefficient de corrélation « r » est hautement significatif selon la méthode de régression log-linéaire. Quand nous comparons les résultats des deux méthodes, nous remarquons que l'ajustement de la durée de récession par la méthode des deux points est plus précis car elle donne des résultats plus proches de la courbe expérimentale.

Les graphes suivants donne l'évolution tu temps de récession en fonction de la longueur de la raie pour les différents débits et pour les deux arrosages.

Figure 13 : Courbes de l'évolution du temps de récession en fonction de la longueur de la raie pour les différents débits (Irrigation N° 1)

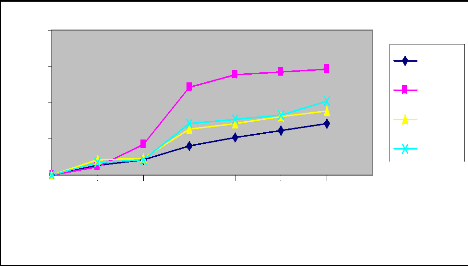
Tem p s (m n )

20

15

10

5

0

0 2 4 6 8 10 12 14

Longueur (m)

Q=0,2l/s Q=0,4l/s Q=0,6l/s Q=0,8l/s

Figure 14 : Courbes de l'évolution du temps de récession en fonction de la longueur de la raie pour les différents débits (Irrigation N° 2)

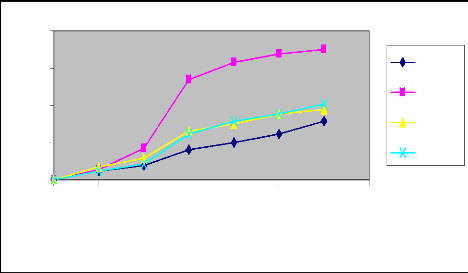
Tem p s (m n )

20

15

10

5

0

0 2 4 6 8 10 12 14

Longueur (m)

Q=0,2l/s Q=0,4l/s Q=0,6l/s Q=0,8l/s

60

61

Commentaire

Dans les deux arrosages, la comparaison entre les différents débits (0.2l/s, 0.6l/s, 0.8l/s) permet de conclure que le temps de récession croit avec le débit d'apport. Cependant pour le débit d'apport de 0.4l/s, nous remarquons que la récession est plus lente du fait de la nature sèche du sol en surface dans cette partie de la raie.

II.3 : Mesure du volume stocké

Les volumes stockés durant les différentes phases sont déduits à partir de la section mouillée correspondant aux différentes phases.

II.3.1 : Mesure de la section mouillée

La section mouillée est la surface hydraulique en un point déterminé de la raie. Elle se calcule par la mesure des tirants d'eau au niveau des repères qui sont placés durant les différentes phases d'arrosage. Ces mesures ont été faites de la façon suivante :

Au niveau de chaque repère yi, on mesure les tirants d'eau dans la raie avec le point y_o ayant une valeur nulle, comme le montre la figure ci-après :

y_o y1 y2 y_n

hn h1 h2

y (cm)

h (cm)

Figure 15 : Mesure du tirant d'eau au niveau de chaque repère

Soient y_o, y1, y2,... _yn-1, y_n les points de mesure équidistants de 2 cm. Chaque point de mesure yi correspond à une hauteur hydraulique h(yi). La section mouillée est donnée par la formule

yn

Sm h ( y ) dy (52)

= ?

y

II.3.2 : Calcul du volume stocké

Le volume stocké à la surface de la raie varie d'une phase à une autre.

· Pendant la phase d'avancement : durant cette phase, on peut calculer le volume stocké par la formule suivante :

Vs = 0,1 .K.Sm.L (53)

Avec : Vs : volume stocké, en l ;

Sm : section mouillée moyenne entre deux points successifs, en cm² ;

K : facteur de forme variant entre 0,7 et 0,8 ; généralement on prend K = 0,77

L : longueur de la raie, en m.

· Pendant la phase d'entretien : durant cette phase, le volume stocké est déterminé par la formule suivante :

(x) dx (54)

L

?

=

Vs

Sm

62

0

II.3.3 : Estimation de la valeur de la section mouillée

Dans notre cas, les raies ont une section mouillée trapézoïdale façonnée par l'eau d'arrosage. Il suffit de déterminer à l'aide d'une règle graduée placée entre deux bûchettes délimitant le niveau d'eau dans la raie, le tirant d'eau écoulé à différentes abscisses correspondant à différents tronçons. Cette opération est répétée pour chaque phase.

II.4 : Etude de l'infiltration

II.4.1 : Calcul des volumes infiltrés

Les volumes infiltrés cumulés (Vi) se déduisent des mesures des volumes stockés en surface (Vs) par la relation du bilan du volume au temps t.

Vi(t) = Ve(t) - Vs(t) (55)

63

Avec : Vi : volume infiltré, en l ;

Ve : volume entré, en l ;

Vs : volume stocké, en l.

Dans notre étude, nous avons estimé que le volume écoulé en colature est nul étant

donné que le débit est resté constant et que l'extrémité aval de la raie est fermée.

Le volume infiltré cumulé représente le volume total apporté pendant la durée

d'application. Il est donné par la formule suivante :

Ve(t) = 60.Qo.t (56)
Avec : Ve : volume entré cumulé, en l ;

Qo : débit en tête de la raie, en l/s ;

t : temps écoulé pendant la durée d'apport

64

Tableau 13 : Calcul des volumes infiltrés expérimentaux pour les différents débits dans le cas de l'irrigation N° 1

Raie A : Q=0.2l/s

	Avancement	Avan+Ent	Récession
T(min)	7.25	8.75	10.15	10.82	12.80	14.02	14.87	15.84
Ve(l)	87	105	105	105	105	105	105	105
Vs(l)	19.42	33.30	25.64	20.51	15.38	10.26	8.97	0
Vi (l)	67.58	71.70	79.36	84.49	89.62	94.74	96.03	105

Raie B : Q=0.4l/s

	Avancement	Avan+Ent	Récession
T(min)	4.83	6.33	7.56	10.51	18.54	20.18	20.53	20.99
Ve (l)	115.92	151.92	151.92	151.92	151.92	151.92	151.92	151.92
Vs (l)	38.46	71.79	53.85	43.59	24.97	16.66	7.69	0
Vi (l)	77.46	80.13	98.07	108.33	126.95	135.26	144.23	151.92

Raie C : Q=0.6l/s

	Avancement	Avan+Ent	Récession
T(min)	2.92	4.42	6.48	6.7	10.72	11.58	12.58	13.34
Ve (l)	105.12	159.12	159.12	159.12	159.12	159.12	159.12	159.12
Vs (l)	44.87	79.49	66.66	56.41	28.20	19.23	14.10	0
Vi (l)	60.25	79.63	92.46	102.71	130.92	139.89	145.02	159.12

Raie D : Q=0.8l/s

	Avancement	Avan+Ent	Récession
T(min)	1.95	3.45	5.23	5.5	10.51	11.17	11.74	13.58
Ve (l)	93.6	165.6	165.6	165.6	165.6	165.6	165.6	165.6
Vs (l)	61.54	107.69	84.64	69.23	30.77	24.36	18.46	0
Vi (l)	32.06	57.91	80.96	96.37	134.83	141.24	147.14	165.6

65

Tableau 14 : Calcul des volumes infiltrés expérimentaux pour les différents débits dans le cas de l'irrigation N° 2

Raie A : Q=0.2l/s

	Avancement	Avan+Ent	Récession
T(min)	5.28	6.78	8.00	8.76	10.73	11.7	12.93	14.61
Ve (l)	63.36	81.36	81.36	81.36	81.36	81.36	81.36	81.36
Vs (l)	20.51	35.89	28.20	23.08	17.95	12.82	11.54	0
Vi (l)	42.85	45.47	53.16	58.28	63.41	68.54	69.82	81.36

Raie B : Q=0.4l/s

	Avancement	Avan+Ent	Récession
T(min)	2.62	4.12	5.48	8.35	17.55	19.97	20.97	21.67
Ve (l)	62.88	98.88	98.88	98.88	98.88	98.88	98.88	98.88
Vs (l)	41.02	74.36	53.85	46.15	20.51	16.66	10.26	0
Vi (l)	21.86	24.52	45.03	52.73	78.37	82.22	88.62	98.88

Raie C : Q=0.6l/s

	Avancement	Avan+Ent	Récession
T(min)	2.13	3.63	5.38	6.45	10.23	11.15	12.43	13.13
Ve (l)	76.68	130.68	130.68	130.68	130.68	130.68	130.68	130.68
Vs (l)	57.69	92.31	79.49	69.23	41.02	32.05	26.92	0
Vi (l)	18.99	38.37	51.19	61.45	89.66	98.63	103.76	130.68

Raie D : Q=0.8l/s

	Avancement	Avan+Ent	Récession
T(min)	1.45	2.95	4.08	5.01	9.05	10.92	11.71	13.19
Ve (l)	69.6	141.6	141.6	141.6	141.6	141.6	141.6	141.6
Vs (l)	53.85	110.26	87.18	71.79	33.33	26.92	21.03	0
Vi (l)	15.75	31.34	54.42	69.81	108.27	114.68	120.57	141.6

66

II.4.2 : Détermination de la loi d'infiltration

La détermination de la loi d'avancement consiste à calculer les coefficients a et b tels que les volumes infiltrés observés se rapprochent le plus possible des volumes infiltrés estimés par la loi de KOSTIAKOV modifiée.

La formule de KOSTIAKOV modifiée est donnée par :

I = K.t^C + f₀.t (57)

Avec : I : volume infiltré, en mm ;

K et C : coefficient d'ajustement ;

t : temps d'infiltration, en mn ;

f0 : représente l'infiltration stabilisée. Elle est déterminée à partir de la formule

suivante :

Volume infiltré pendant le temps d'apport

f0= (58)

(Temps d'apport).(Longueur)

Pour déterminer les coefficients K et C, on utilise la méthode des deux points. Les valeurs de K, C et f0 sont données dans le tableau suivant.

Tableau 14 : les valeurs de K, C et f0 de la loi de KOSTIAKOV modifiée

Irrigation	Raie	Débit (l/s)	K	C	f0	I = K.t^C + f0.t
01	A	0.2	14.80	0.67	0.68	I = 1 4.80t0, ^67 + 0.68t
	B	0.4	1.27	1.52	1.05	I = 1.27t 1 ,52 + 1.05t
	C	0.6	14.24	0.88	1.50	I = 1 4.24t0, 8 8 +1.50t
	D	0.8	19.17	0.78	1.40	I = 1 9. 1 7t0, ^79 +1.40t
02	A	0.2	8.80	0.79	0.56	I = 8. 80t0, ^79 + 0.56t
	B	0.4	2.81	1.12	0.50	I = 2.8 1t 1 , 12 + 0.50t
	C	0.6	2.14	1.56	0.88	I = 2. 1 4t1, ^56 + 0.88t
	D	0.8	21.90	0.69	0.89	I = 2 1.90t^0,69 + 0.89t

Les volumes infiltrés théoriques calculés avec la loi de KOSTIAKOV et ceux expérimentaux se résument dans les tableaux suivants :

67

Tableau 15 : Calcul des volumes infiltrés théoriques pour les différents débits dans le cas de l'irrigation N° 1

Raie A : Q=0.2l/s

T (mn)	7.25	8.75	10.15	10.82	12.80	14.02	14.87	15.84
Vi exp (l)	67.58	71.70	79.36	84.49	89.62	94.74	96.03	105
Vi théo (l)	60.74	69.25	76.82	80.34	90.38	96.34	100.42	105

Raie B : Q=0.4l/s

T (mn)	4.83	6.33	7.56	10.51	18.54	20.18	20.53	20.99
Vi exp (l)	77.46	80.13	98.07	108.33	126.95	135.26	144.23	151.92
Vi théo (l)	18.98	27.63	35.42	56.39	126.95	143.45	147.05	151.83

Raie C : Q=0.6l/s

T (mn)	2.92	4.42	6.48	6.70	10.72	11.58	12.58	13.34
Vi exp (l)	60.25	79.63	92.46	102.71	130.92	138.89	145.02	159.12
Vi théo (l)	40.94	52.29	83.46	85.99	130.92	140.28	151.07	159.21

Raie D : Q=0.8l/s

T (mn)	1.95	3.45	5.23	5.50	10.51	11.17	11.74	13.58
Vi exp (l)	32.06	57.91	80.96	96.37	134.83	141.24	147.14	165.60
Vi théo (l)	35.00	55.19	76.99	80.16	134.79	141.56	147.34	165.66

68

Tableau 16 : Calcul des volumes infiltrés théoriques pour les différents débits dans le cas de l'irrigation N° 2

Raie A : Q=0.2l/s

T (mn)	5.28	6.78	8.00	8.76	10.73	11.70	12.93	14.61
Vi exp (l)	42.85	45.47	53.16	58.28	63.41	68.54	69.82	81.36
Vi théo (l)	35.72	43.71	49.79	53.78	63.37	67.98	73.71	81.39

Raie B : Q=0.4l/s

T (mn)	2.62	4.12	5.48	8.35	17.55	19.97	20.97	21.67
Vi exp (l)	21.86	24.52	45.03	52.73	78.37	82.22	88.62	98.88
Vi théo (l)	9.57	15.78	21.63	34.44	78.32	90.36	95.38	98.91

Raie C : Q=0.6l/s

T (mn)	2.13	3.63	5.38	6.45	10.23	11.15	12.43	13.13
Vi exp (l)	18.99	38.37	51.19	61.45	89.66	98.63	103.76	130.68
Vi théo (l)	8.83	19.18	34.28	44.88	89.51	101.89	120.03	130.38

Raie D : Q=0.8l/s

T (mn)	1.45	2.95	4.08	5.01	9.05	10.92	11.71	13.19
Vi exp (l)	15.75	31.34	54.42	69.81	108.27	114.68	120.57	141.60
Vi théo (l)	29.59	48.82	61.41	71.04	108.18	123.69	130.3	141.58

Les courbes des volumes infiltrés expérimentaux et théoriques des deux arrosages sont données par les graphes suivants :

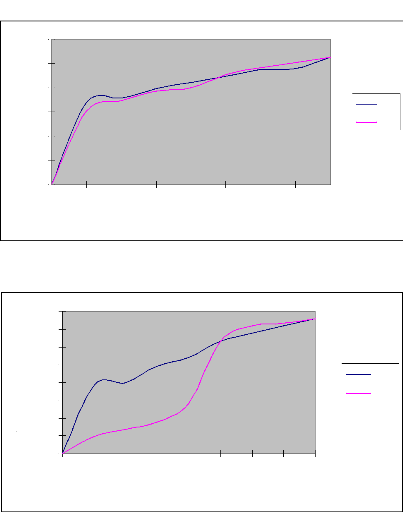
Raie A : Q=0.2l/s

Raie B : Q=0.4l/s

120

100

Volume infiltré (l)

80

exp théo

60

40

20

0

0 7,25 8,75 10,15 10,82 12,8 14,02 14,87 15,84

Temps (mn)

160

140

Volume infiltré (l)

120

100

80

60

40

20

0

0 4,83 6,33 7,56 10,5 18,5 20,2 20,5 21 Temps (mn)

exp théo

69

Figure 16 : Courbes des volumes infiltrés expérimentaux et théoriques (Irrigation N° 1)

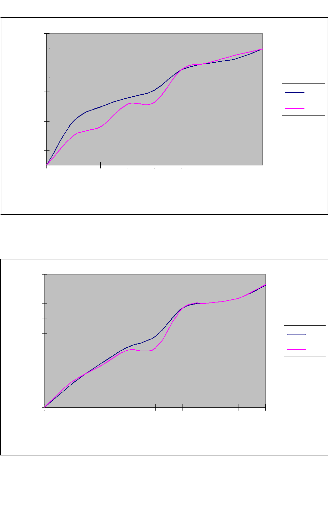
70

Raie C : Q=0.6l/s

Raie D : Q=0.8l/s

180

160

140

Volume infiltré (l)

120

100

exp théo

80

60

40

20

0

0 2,92 4,42 6,48 6,7 10,72 11,58 12,58 13,34

Temps (mn)

180

160

140

Volume infiltré (l)

120

100

exp théo

80

60

40

20

0

0 1,95 3,45 5,23 5,5 10,51 11,17 11,74 13,58

Temps (min)

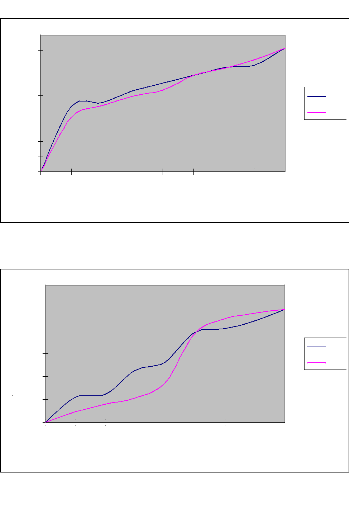
Raie A : Q=0.2l/s

Raie B : Q=0.4l/s

71

90

80

70

Volume infiltré (l)

60

50

exp théo

40

30

20

10

0

0 5,28 6,78 8 8,76 10,73 11,7 12,93 14,61

Temps (mn)

120

100

Volume infiltré (l)

80

exp théo

60

40

20

0

0 2,62 4,12 5,48 8,35 17,55 19,97 20,97 21,67

Temps (mn)

Figure 17 : Courbes des volumes infiltrés expérimentaux et théoriques (Irrigation N°2)

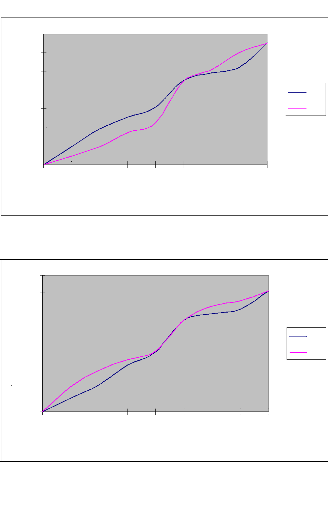
72

Raie C : Q=0.6l/s

Raie D : Q=0.8l/s

160

140

Volume infiltré (l)

120

100

exp théo

80

60

40

20

0

0 1,45 2,95 4,08 5,01 9,05 10,92 11,71 13,19

Temps (mn)

140

120

Volume infiltré (l)

100

80

exp théo

60

40

20

0

0 2,13 3,63 5,38 6,45 10,23 11,15 12,43 13,13

Temps (mn)

73

Commentaire

Nous remarquons à travers l'analyse des graphes des deux irrigations, que les courbes des volumes infiltrés expérimentaux et théoriques ne sont pas les mêmes. Il existe donc un écart plus ou moins important entre ces deux courbes suivant qu'on est dans la phase d'entretien ou dans la phase de récession.

Par ailleurs, une comparaison entre différents débits pour les deux irrigations nous permet d'observer que le volume infiltré est supérieur pour l'arrosage dont le débit est grand.

II.5 : Calcul des paramètres de performance

Les résultats du rendement hydraulique et du coefficient d'uniformité sont résumés dans le tableau suivant :

Tableau 17 : Calcul des paramètres de performance

Irrigation	01				02
Raie	A	B	C	D	A	B	C	D
Débits (l/s)	0.2	0.4	0.6	0.8	0.2	0.4	0.6	0.8
Tapp (mn)	8.75	6.33	4.42	3.45	6.78	4.12	3.63	2.95
dn (mm)	15.8	15.8	15.8	15.8	15.8	15.8	15.8	15.8
db (mm)	26.51	28.13	29.21	30.02	25.32	27.09	28.26	29.66
Rh (%)	59.60	56.17	54.09	52.63	62.40	58.32	55.91	53.27
Cu (%)	92.30	87.18	84.02	79.62	88.63	77.18	75.41	74.11

Commentaire

Les résultats de notre étude montrent à travers ce tableau que, pour un même débit, le rendement hydraulique varie en sens inverse par rapport au temps d'apport ; c'est-à-dire que plus le temps augmente, plus le rendement hydraulique diminue. Nous retenons que le rendement hydraulique est fonction du temps d'arrosage.

Pour ce qui est de l'uniformité de l'arrosage, les résultats obtenus montrent que le débit de 0.2l/s donne la meilleure uniformité par rapport aux autres débits.

74

Nous retenons également que les valeurs des différents coefficients d'uniformité obtenus sont comprises entre celles recommandées par CHRISTIANSEN : (0.5=Cu=1).

Nous pouvons conclure que la distribution de l'eau est meilleure pour toutes les irrigations du fait que l'uniformité d'arrosage est bonne.

75

CHAPITRE III : LA MODELISATION

La modélisation est un processus qui vise à optimiser le temps d'arrosage avec la quantité d'eau infiltré. Il s'agit en fait d'obtenir le meilleur couple avancement-infiltration, pour une irrigation économique, rapide et à rendement optimum.

Pour réduire l'écart entre les résultats expérimentaux et théoriques, nous avons élaboré un modèle qui donnerait un compromis entre les deux résultats.

La modélisation que nous faisons, a pour but de rapprocher le plus possible la courbe modèle de la courbe expérimentale ; autrement dit réajuster la loi d'ajustement. C'est dans cet objectif que nous utilisons un mini-programme « Quick basic » qui se résume par les étapes suivantes :

- Nous fixons « K » et nous faisons varier « C » jusqu'à obtenir un volume infiltré modèle _I(t)mod proche du volume infiltré expérimental _I(t)exp. On note C=C_m.

- Nous fixons « C » à « C_m » et nous faisons varier « K » jusqu'à obtenir un volume infiltré modèle _I(t)mod proche du volume infiltré expérimental _I(t)exp. On note K=K_m.

L'équation modèle s'écrira alors de la manière suivante :

I t

( ) mod = m . + ₀ . (59)
K t ^Cm f t

L'algorithme utilisé est schématisé par l'organigramme suivant :

Figure 18 : Schéma de l'organigramme

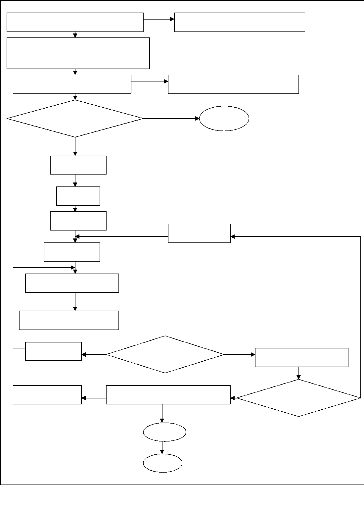
Courbe expérimentale I(t)exp

Expérimentation : I (t) exp. = f (t)

Equation de KOSTIAKOV modifiée I(t) = K.t^c + f0.t

Calcul de K, C et f0

Courbe calculée I(t)= K.t^e + f0.t

Oui

I(t) cal = ? I(t)exp Fin

Non

Modèle

f0 = ?

Choix de K

Autre K

Choix de C

Choix de tc [0,...,t_n]

I(t)mod = Km. t^cm + _f0. t

Non

Oui

Autre C

I(t)mod = ? I(t)exp

I(t)mod = K_m.t^cm + f0 .t

Oui

non

Courbe modèle

Imprimer I(t)mod = K_m.t^cm + f0.t

I(t)mod = ? I(t)exp

Stop

Fin

76

77

Sur la base de l'organigramme précédent, nous avons obtenu les résultats suivants : Tableau 19 : Les nouveaux paramètres d'ajustement K_m et C_m

Irrigation	Raie	Débit (l/s)	Km	Cm	f0	I K t ^Cm f t = m . + 0 .
01	A	0.2	17.68	0.61	0.68	I = 1 7.68t0,6 ^1 + 0.68t
	B	0.4	4.27	1.14	1.05	I = 4.27t 1, 1 4 +1.05t
	C	0.6	18.52	0.78	1.50	I = 1 8.52t0, ^78 + 1.50t
	D	0.8	19.25	0.79	1.40	I = 1 9.25t^0,79 + 1.40t
02	A	0.2	9.05	0.80	0.56	I = 9.05t0, ^80 + 0.56t
	B	0.4	3.14	1.12	0.50	I=3. 1 4t1 . 1 2+0.50t
	C	0.6	5.43	1.21	0.88	I = 5.43t 1 .2 1 + 0.88t
	D	0.8	12.27	0.91	0.89	I = 1 2.27t0, 9 1 + 0. 89t

Les volumes infiltrés modèles calculés à base des nouveaux paramètres K_m et C_m à l'aide de la loi de KOSTIAKOV modifiée sont donnés dans les tableaux suivants :

Tableau 20 : Volumes infiltrés modèles pour les différents débits (Irrigation N° 1)

Raie A : Q=0.2l/s

T (mn)	7.25	8.75	10.15	10.82	12.80	14.02	14.87	15.84
Vi exp (l)	67.58	71.70	79.36	84.49	89.62	94.74	96.03	105
Vi théo (l)	60.74	69.25	76.82	80.34	90.38	96.34	100.42	105
Vi mod (l)	64.13	72.34	79.58	82.93	92.43	98.04	101.86	106.12

Raie B : Q=0.4l/s

T (mn)	4.83	6.33	7.56	10.51	18.54	20.18	20.53	20.99
Vi exp (l)	77.46	80.13	98.07	108.33	126.95	135.26	144.23	151.92
Vi théo (l)	18.98	27.63	35.42	56.39	126.95	143.45	147.05	151.83
Vi mod (l)	30.78	41.64	50.79	73.42	138.61	152.42	155.39	159.29

78

Raie C : Q=0.6l/s

T (mn)	2.92	4.42	6.48	6.70	10.72	11.58	12.58	13.34
Vi exp (l)	60.25	79.63	92.46	102.71	130.92	138.89	145.02	159.12
Vi théo (l)	40.94	52.29	83.46	85.99	130.92	140.28	151.07	159.21
Vi mod (l)	47.10	65.66	89.27	91.70	133.89	142.49	152.34	159.73

Raie D : Q=0.8l/s

T (mn)	1.95	3.45	5.23	5.50	10.51	11.17	11.74	13.58
Vi exp (l)	32.06	57.91	80.96	96.37	134.83	141.24	147.14	165.60
Vi théo (l)	35.00	55.19	76.99	80.16	134.79	141.56	147.34	165.66
Vi mod (l)	35.35	57.44	78.45	81.71	138.16	145.17	151.17	170.16

Tableau 21 : Volumes infiltrés modèles pour les différents débits (Irrigation N° 2)

Raie A : Q=0.2l/s

T (mn)	5.28	6.78	8.00	8.76	10.73	11.70	12.93	14.61
Vi exp (l)	42.85	45.47	53.16	58.28	63.41	68.54	69.82	81.36
Vi théo (l)	35.72	43.71	49.79	53.78	63.37	67.98	73.71	81.39
Vi mod (l)	37.21	45.64	52.25	56.27	66.42	71.29	77.37	85.51

Raie B : Q=0.4l/s

T (mn)	2.62	4.12	5.48	8.35	17.55	19.97	20.97	21.67
Vi exp (l)	21.86	24.52	45.03	52.73	78.37	82.22	88.62	98.88
Vi théo (l)	9.57	15.78	21.63	34.44	78.32	90.36	95.38	98.91
Vi mod (l)	10.54	17.39	23.84	38.00	86.49	99.80	105.35	109.26

79

Raie C : Q=0.6l/s

T (mn)	2.13	3.63	5.38	6.45	10.23	11.15	12.43	13.13
Vi exp (l)	18.99	38.37	51.19	61.45	89.66	98.63	103.76	130.68
Vi théo (l)	8.83	19.18	34.28	44.88	89.51	101.89	120.03	130.38
Vi mod (l)	15.43	29.03	46.33	57.48	99.52	110.27	125.52	133.99

Raie D : Q=0.8l/s

T (mn)	1.45	2.95	4.08	5.01	9.05	10.92	11.71	13.19
Vi exp (l)	15.75	31.34	54.42	69.81	108.27	114.68	120.57	141.60
Vi théo (l)	29.59	48.82	61.41	71.04	108.18	123.69	130.3	141.58
Vi mod (l)	18.49	35.46	47.74	57.63	99.13	117.77	125.56	140.05

Les courbes des volumes infiltrés expérimentaux, théoriques et modèles des deux arrosages sont données par les graphes suivants :

Figure 19 : Courbes des volumes infiltrés expérimentaux, théoriques et modèles en fonction du temps (Irrigation N° 1)

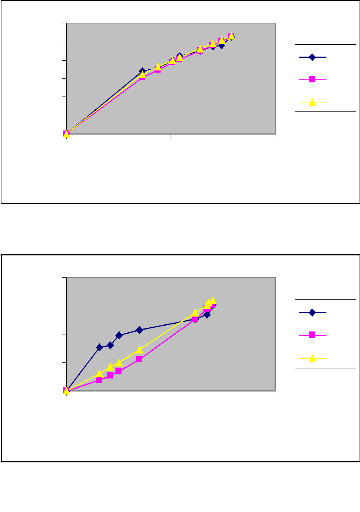
Raie B : Q=0.4l/s

Raie C : Q=0.6l/s

80

120

Volume infiltré (l)

100

80

60

40

20

0

0 5 10 15 20

Temps (mn)

exp
théo
mod

200

Volume infiltré (l)

150

100

50

0

0 10 20 30

Temps (mn)

exp
théo
mod

Raie A : Q=0.2l/s

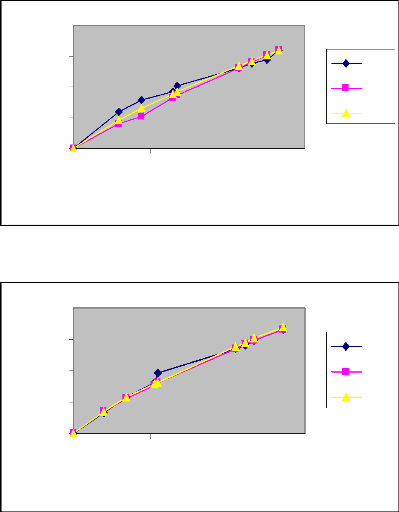
Raie D : Q=0.8l/s

200

Volume infiltré (l)

150

100

50

0

0 5 10 15

Temps (mn)

exp
théo
mod

200

Volume infiltré (l)

150

100

50

0

0 5 10 15

Temps (mn)

exp
théo
mod

81

Figure 20 : Courbes des volumes infiltrés expérimentaux, théoriques et modèles en fonction du temps (Irrigation N°2)

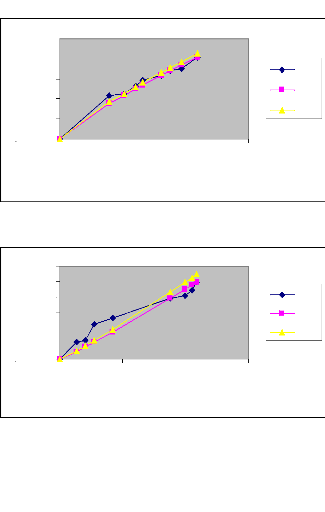
82

Raie A : Q=0.2l/s

Raie B : Q=0.4l/s

Raie C : Q=0.6l/s

100

Volume infiltré (l)

80

60

40

20

0

0 5 10 15 20

Temps (mn)

exp
théo
mod

120

Volume infiltré (l)

100

80

60

40

20

0

0 10 20 30

Temps (mn)

exp
théo
mod

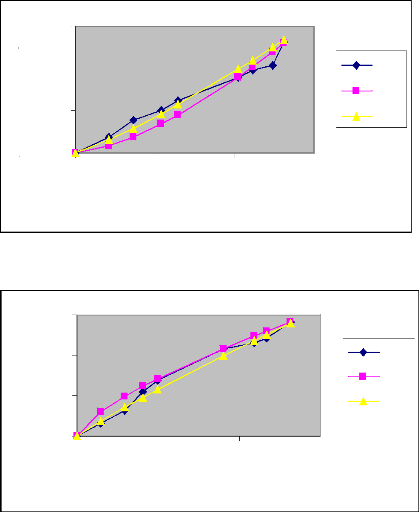
150

Volume infiltré (l)

100

50

0

0 5 10 15

Temps (mn)

exp
théo
mod

Raie D : Q=0.8l/s

150

Volume infiltré (l)

100

50

0

0 5 10 15

Temps (mn)

exp
théo
mod

83

84

Commentaire

Au vu des graphes des figures précédentes, nous constatons que les courbes modèles aux débits Q=0.2l/s, Q=0.6l/s, Q=0.8l/s sont plus proches des courbes expérimentales que des courbes théoriques. Ceci s'explique par le fait que le calcul du volume infiltré théorique ne prend pas en considération certains paramètres dont dépend le processus d'infiltration, tels que la nature du sol, sa texture et sa structure. De même, nous remarquons que, le volume infiltré pour les trois types de courbes (expérimentales, théoriques et modèles) demeure le même dans certains cas comme celui du débit Q=0.2l/s dans la première irrigation. Nous disons dans ce cas que le processus d'infiltration obéit fidèlement à la loi de KOSTIAKOV modifiée.

Par ailleurs, nous constatons dans les deux types d'irrigation pour le débit Q=0.4l/s, qu'il subsiste toujours un écart entre les courbes expérimentales et modèles. Les paramètres de réajustement « K » et « C » ne pourront pas être affectés à ce type de sol qui a servi de base à notre essai. Ceci peut s'expliquer par le fait que le sol, au niveau de cette raie pourrait contenir une couche peu imperméable et dont la présence a affecté la bonne conduite de l'expérimentation.

Nous pouvons conclure à l'issue de ces résultats que la modélisation du processus d'infiltration permet d'obtenir des résultats plus proches des valeurs expérimentales. Toutefois, elle serait meilleure si les résultats expérimentaux étaient plus précis.

Pour voir l'évolution des volumes infiltrés en fonction des débits, nous allons tracer les graphes donnant les volumes infiltrés expérimentaux, théoriques et modèles en fonction des différents débits pour chaque phase (avancement, durée d'apport et récession).

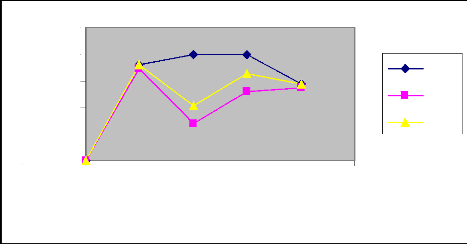
Volume infiltré (l)

100

40

80

60

20

0

0 0,5 1

Débit (l/s)

exp
théo
mod

85

Figure 21 : Volumes infiltrés expérimentaux, théoriques et modèles en fonction des débits pour chaque phase (Irrigation 1).

Phase d'avancement

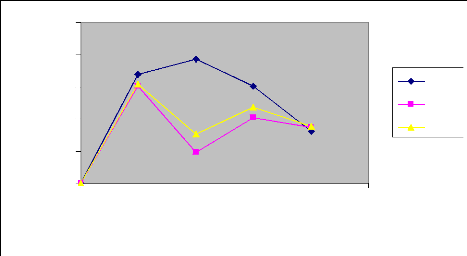
Volume infiltré (l)

100

40

80

60

20

0

0 0,5 1

Débit (l/s)

exp
théo
mod

Phase correspondante à la durée d'apport

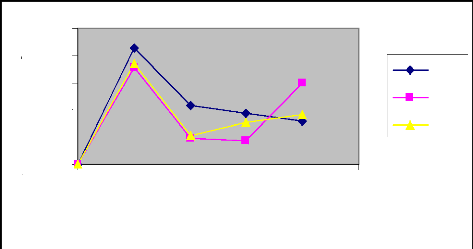
Volume infiltré (l/s)

40

50

30

20

10

0

0 0,5 1

Débit (l/s)

exp
théo
mod

86

Phase de récession

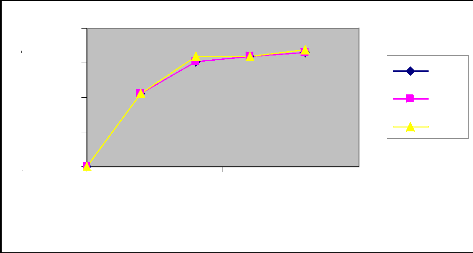
Volume infiltré (l)

200

150

100

50

0

0 0,5 1

Débit (l/s)

exp
théo
mod

Figure 22 : Volumes infiltrés expérimentaux, théoriques et modèles en fonction des débits pour chaque phase (Irrigation 2).

Phase d'avancement

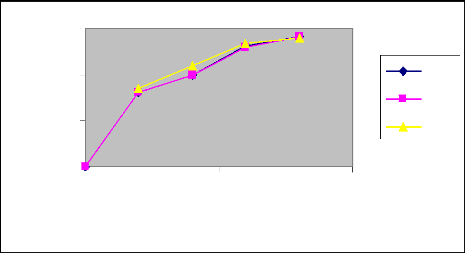
Volume infltré (l)

150

100

50

0

0 0,5 1

Débit (l/s)

exp
théo
mod

87

Phase correspondante à la durée d'apport

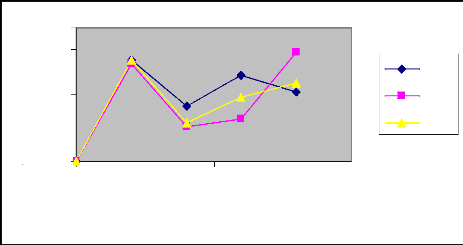
Volume infiltré (l)

40

60

50

30

20

10

0

0 0,5 1

Débit (l/s)

exp
théo
mod

Phase de récession

88

Commentaire

Dans les deux arrosages, nous remarquons au niveau de la phase d'avancement, que les courbes des volumes infiltrés en fonction des débits varient presque de la même manière que les mêmes courbes pendant la phase correspondante à la durée d'apport. Toutefois, il est à noté au débit Q=0.4l/s, que la courbe des volumes expérimentaux est bien écarté de celles deux autres volumes.

A la récession, nous constatons que les trois courbes ont presque la même allure notamment celles des volumes infiltrés expérimentaux et modèles.

Au vu de ces résultats, nous disons que la modélisation est plus précise surtout dans la phase de récession. Ainsi donc, ces résultats pourront permettre dans le temps d'optimiser le rendement hydraulique et de minimiser les pertes.

Par comparaison des graphes des deux arrosages, nous constatons que les valeurs expérimentales dans l'irrigation N° 2 sont nettement plus précises que celles dans l'irrigation N°1. Cet état de chose pourrait s'expliquer par le simple fait qu'un sol humide (pendant l'irrigation N° 2) s'infiltre plus rapidement qu'un sol sec (pendant l'irrigation N°2).

CONCLUSION GENERALE

Cette étude a permis de mettre en évidence le processus de l'infiltration de l'eau dans le sol en se basant sur l'outil informatique. Ainsi, une utilisation des théories relatives à ce processus n'étant pas indispensable, il a été question d'évoquer les différents paramètres physiques qui le régissent.

Il en ressort que la méthode des deux points paraît meilleure que la méthode log-linéaire. Les résultats obtenus au niveau de certaines raies demeurent incohérents vu que certains points en aval de la raie se ressuient plus rapidement que ceux en amont au cours de l'infiltration, pour raison d'hétérogénéité de la pente.

Le meilleur rendement hydraulique est obtenu à la deuxième irrigation pour Q=0.2l/s et est estimé à 62.40%.

Le coefficient d'uniformité reste meilleure dans les différents temps et dépasse 80%, d'où la meilleure homogénéité de la distribution de l'eau le long de la raie.

89

L'ajustement des volumes infiltrés en fonction du temps par la loi de KOSTIAKOV modifiée donne des résultats comparables à ceux issus de l'expérimentation surtout dans la deuxième irrigation.

Enfin, si l'on peut dire que l'un des buts principaux de cette étude consiste en la détermination des paramètres « K » et « C » qui pourraient être affectés à chaque type de sol, il n'en demeure pas moins que la modélisation du processus d'infiltration doit être prise en considération par l'agriculteur, dans la recherche de l'économie en eau.