Impact de la structure de treillis dans le domaine de fouille de données et la représentation des connaissances.

4.3 L'Analyse Formelle des Concepts

L'analyse formelle des concepts est une branche de la théorie des treillis qui permet la génération de concepts, de treillis de concepts et à partir de là, des règles d'associations. A cet effet, elle s'est avéré être un cadre théorique intéressant pour la fouille de données. Elle a été introduite par Wille en 1980 et appliquée à « l'acquisi-tion automatique de connaissances », elle a donc pour objectif d'étudier le problème de l'extraction et de la représentation des connaissances sous l'angle de la théorie mathématique des treillis.[19][11][1]

4.3.1 L'extraction de motifs fréquents

L'extraction de motifs fréquents est une technique très utilisée en fouille de données son objectif est de trouver les motifs que apparaissent fréquemment dans une

45

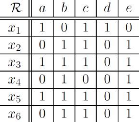
TABLE 4.1 - Exemple de base de données formelle

base de données formelle dont les valeurs sont des booleens indiquant la présence ou l'absence d'une proprieté.[11][14][16]

Définition 1(base de données formelle)

Une base de données formelle est la donnée d'un triplet O, P, R où :

1. O est un ensemble fini d'objets;

2. P est un ensemble fini de proprietés;

3. R est une relation sur OxP qui permet d'indiquer si un objet x a une proprieté P

Considérons la base de données formelle telle que montrée à la table 4.1 : Où

- O = {x1, x2, x3, x4, x5, x6};

- P = {a, b, c, d, e};

- xRp si et seulement si la ligne de x et la colonne de p se croisent sur un 1.[11]

Définition 2 (motif)

Un motif d'une base de données formelle (O, P, R) est un sous ensemble de P.On dit qu'un objet contient un motif si l'objet contient chacun des attributs du motif. La longueur d'un motif est le nombre d'attributs de ce motif. L'image d'un motif est des objets possédant ce motif. Ainsi l'ensemble de tous les motifs d'une base noté 2|P| est donc l'ensemble de partie de P.[11][19]

Un objet x ? O possède un motif in si ?p ? P, xRp. Pour la base de donnée montrée à la table 4.1 :

1. 1 motif de taille 0 : 0.

2. 5 motif de taille 1 : {a}, {b}, {c}, {d}et{e} ou pour simplifier l'écriture, on notera a, b, c, d, e.

3. 10 motif de taille 2 : ab, ac, ad, ae, bc, bd, be, cd, ce, ed.

4. 10 motif de taille 3 : abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

5. 5 motif de taille 4 : abcd, abce, abde, acde, bcde

6. 1 motif de taille 5 : abcde

Ainsi on peut dire que x1 possède les motifs 0, a, c, d, ac, ad, cd, acd

On cherchera ensuite parmi l'ensemble de 2|^P| motifs ceux qui apparaissent fréquemment. Pour cela on va introduire les notions de connexion de Galois et de support d'un motif

46

Définition 3 (connexion de Galois)

Soient f et g deux fonctions définies par :[22][1]

f : 2^P -? 2O

in 7-? f(in) = {x ? O | x possède in}

g : 2^O -? 2P

X 7-? g(X) = {p ? P | ?x ? X,xRp}

f représente l'ensemble de tous les attributs communs à un groupe d'objets O (on parle d'intension) et g l'ensemble des objets qui possèdent tous les attributs de P (extension). Le couple (f, g) définit la connexion de Galois entre P et O associée à une base de donnée formelle (O, P, R). Les opérateurs de la fermeture de Galois sont définis par : h = f ? g et h^' = g ? f.

Le terme de connexion est motivé par le fait que la relation binaire R de la base de donnée formelle connecte chaque attribut à chaque objet et vice-verca.[6][11][1]

Définition 4 (support d'un motif)

Soit in ? 2|^P|, un motif. Le support de in est la proportion d'objets dans O qui possèdent le motif:

support: 2^P -? [0; 1]

in 7-? support(in) = |f(m)|

|O|

Exemple : soit la base de données (cfr table 4.1)

support(a) = 3 ₆, support(b) = 5 ₆, support(ab) = 2 ₆, support(P) = 1

Proprieté 1

Si in est un sous motif de in⁰ (in ? in⁰) alors support(in) = support(in⁰).

Le support mesure la fréquence d'un motif, plus il est élevé, plus le motif est fréquent. Ainsi le seuil d'un motif u₅ marque la différence entre ceux qui sont fréquents de ceux qui ne le sont pas.

Motif fréquent

Une observation o ? O supporte un motif in si tous les attributs de in apparaissent dans l'observation o. Un motif m est fréquent relativement à un support minimal minsup si support(m) = u₅. Avec u₅ le seuil( ou support minimal) qui est une valeur à partir de laquelle un motif sera fréquent ou non selon qu'il est supérieur ou non au seuil. [25][27]