|
EPIGRAPHE
DEDICACE
AVANT - PROPOS
I INTRODUCTION
1.1 Problématique et limite du sujet
1.2 Intérêt du sujet
1.3 Méthode d'approche
1.4 Canevas du travail
II GENERALITES
II.1 Le mécanisme de fixation des prix des carburants
terrestres
II.2 Les Séries chronologiques et processus
stochastiques
II.3 Les prévisions
II.4 La méthode de prévision de BOX et
JENKINS
III APPLICATION DU MODELE D'ANALYSE D'INTERVENTIONS A LA
PREVISION DU VOLUME DES CARBURANTS TERRESTRES
III.1 Familiarisation des données
III.2 Analyse préliminaire
III.3 Spécification du modèle
III.4 Analyse des interventions
III.5 Prévision
III.6 Intervention des résultats
IV CONCLUSION
" Nous nous jugeons nous-même d'après ce
que nous nous sentons capable de faire, alors que les autres nous jugent
d'après ce que nous avons déjà fait ".
Henry WADSWORTH LONGFELLOW.
DEDICACE
A l'Eternel Dieu Tout-Puissant,
A toi mon père Melchior NGANDU KALALA ainsi
qu'à vous mes frères et soeurs actuellement à Beni (Nord
KIVU) occupé,
A toi ma mère Agnès MASENGO wa
NDEKA,
A toi ma future épouse, NDAYA KALONGA
Daddy,
Je dédie ce
travail.
AVANT-PROPOS
Cet ouvrage constitue un travail de fin d'études
présenté et défendu à l'Université de
Kinshasa. Il est ainsi élaboré conformément aux pratiques
de l'Enseignement Supérieur et Universitaire qui recommandent, pour tout
étudiant, la rédaction d'un mémoire à la fin de ses
études.
Ce travail ne demeure pas une oeuvre parfaite, il est
susceptible de critiques en vue de la perfection. Néanmoins, marquant
mes débuts dans le monde de la recherche, il constitue un essai dans ce
vaste domaine.
Non seulement, il est le fruit des connaissances
emmagasinées au cours de ma formation depuis l'école primaire, il
est également celui de l'assistance tant morale que matérielle
rencontrée auprès de certaines personnes à qui nous devons
absolument adresser nos remerciements.
Mes sentiments de gratitude vont droit à l'endroit
du Professeur BOSONGA BOFEKI Jean-Pierre ainsi qu'à l'Assistant BOFOYA
KOMBA Beaujaulais pour lesquels l'encadrement a été des meilleurs
dans l'élaboration de ce travail.
Ma reconnaissance s'adresse au Professeur BANYAKU LUAPE
pour toutes les connaissances en matières pétrolières
qu'il m' a transmises.
Ma reconnaissance s'adresse également à tous
les Professeurs et Assistants de l'Université de Kinshasa pour les
connaissances théoriques qu'ils m'ont transmises, lesquelles m'ont
permis de me défendre dans certaines circonstances.
A toute la profession pétrolière qui a pu
mettre à ma disposition certaines informations et données utiles
à la réalisation de ce travail, j'adresse également mes
remerciements.
Que tous mes parents, frères, soeurs, amis et
connaissances dont les douloureuses privations, véritables
investissements humains, leur ont souvent permis de financer mes années
d'études et parfois ruiné leur santé, trouvent dans ce
travail l'aboutissement de leurs sacrifices et peines.
Que tous ceux qui, de loin ou de près, m'ont
aidé à atteindre cette étape de ma vie, trouvent ici
l'expression de mes sentiments de gratitude.
Ainsi, à tous, je dirai qu'à l'origine des
grandes réalisations, se trouve non seulement la force de la
volonté, mais également la main de l'Eternel Tout
Puissant.
Serge KABONGO wa NTITA.
I.
INTRODUCTION
I.1
PROBLEMATIQUE
Dans bien de pays tant développés qu'en voie de
développement, les carburants terrestres sont des produits
stratégiques. De leurs prix dépendent les prix de plusieurs
produits, surtout les produits de première nécessité.
Les Gouvernements de ces pays, dans leur mission d'assurer le
bien-être social des populations, cherchent dans une large mesure
à maîtriser ces prix.
Ce qui fait qu'en pratique, ces prix sont des "prix
administrés" à travers lesquels l'Etat poursuit certains
objectifs sociaux, politiques ou économiques. Aussi, à travers le
maintien de ces prix des produits pétroliers, il peut également
contenir les conséquences de leur variation sur les prix des autres
produits qu'ils influencent.
La République Démocratique du Congo, pays en
voie de développement, n'échappe pas à cette pratique, car
les prix des carburants terrestres y sont administrés. Cette
administration ne s'y effectuant pas sans heurt ni malheur.
Dans le système de fixation de prix en vigueur en
République Démocratique du Congo, le paramètre
« volume » servant comme base de calcul des autres
éléments de la structure de prix est prévisionnel. Par
conséquent, d'énormes difficultés surgissent lorsque les
écarts importants se dégagent entre les prévisions et les
réalisations.
Par exemple, les objectifs arrêtés lors de
l'établissement de la structure des prix risquent de ne pas être
atteints, d'autant plus que la plupart des prélèvements
autorisés dans la structure des prix et accordés à
différentes institutions le sont sur base de ce volume.
Dès lors, il apparaît nécessaire voire
impératif que, dans ce système de fixation de prix, soit
utilisée une bonne méthode de prévision donnant lieu
à un volume de vente prévisionnel vraisemblable, chaque fois
qu'il sera question d'élaboration d'une structure de prix.
Pour ce faire, nous avons opté pour la méthode
prévision de BOX et JENKINS par l'exploitation de son modèle
d'analyse d'interventions qui en compte les données atypiques
occasionnées par les perturbations que connaît sans cesse notre
espace économique.
I.2 INTERET DU SUJET
Le but visé dans notre étude est de
réaliser les prévisions à partir d'un processus sur base
de l'information qualitative et quantitative qu'il contient soit en terme de
réalisations, soit en terme d'erreurs.
Ainsi, le modèle d'analyse d'interventions que nous
préconisons cherche plutôt à modéliser ces
données afin de conserver et d'utiliser l'information qu'elles
contiennent.
I.3 METHODE D'APPROCHE
La méthode d'approche utilisée consiste en une
étude systématique des séries chronologiques à
partir de leurs caractéristiques afin, dans un premier temps, de
déterminer dans la famille des modèles ARMA, le plus
adapté à représenter le phénomène
étudié ; et ensuite, d'élaborer les prévisions
avec le modèle ainsi obtenu.
Pour effectuer les différents calculs et estimations,
nous avons utilisé les logiciels Econometric Views version 1.1c et Excel
version 8.
I.4 CANEVAS DU TRAVAIL
Outre l'introduction et la conclusion, notre travail comporte
en deux parties.
Dans la première partie, intitulée
Généralités, nous allons parcourir certains concepts
relatifs au mécanisme de détermination des prix des carburants
terrestres, aux séries chronologiques et processus stochastiques, aux
méthodes de prévision ainsi qu'à la méthode de
prévision de BOX et JENKINS
Dans la deuxième, Application du modèle
d'analyse d'interventions à la prévision du volume des
carburants terrestres, il s'agira de la construction du modèle à
utiliser pour les prévisions ainsi que la réalisation des
prévisions proprement dites.
II. GENERALITES
II.1 LE MECANISME DE FIXATION DES PRIX DES CARBURANTS TERRESTRES
II.1.1
INTRODUCTION
Le Décret-Loi du 20 mars 1961 relatif aux prix, tel que
modifié par l'Ordonnance Loi n° 83-026 du 12 septembre 1983,
stipule qu'en République Démocratique du Congo, la fixation des
prix des biens et services relève du domaine des propriétaires de
ces dits biens et services. Toutefois, exception est faite pour certains
produits parmi lesquels nous citons les carburants terrestres. Par le fait de
leur caractère stratégique dans l'économie nationale,
leurs prix sont régentés par l'Etat qui s'en réserve un
droit de regard et le monopole de publication car en fait les prix des
carburants terrestres sont publiés par Arrêté
Ministériel.
Le regard de l'Etat sur les prix des carburants terrestres se
réalise non seulement par le Ministère du Pétrole
ministère tutélaire du secteur, mais également par le
Ministère de l'Economie à travers le Comité de Suivi de la
Structure de prix.
Les prix de carburants sont déterminés et
présentés dans un tableau appelé Structure de
prix des carburants qui comprend plusieurs rubriques. Il existe,
en République Démocratique du Congo, deux types de structures de
prix des carburants ; l'un pour les carburants terrestres notamment
l'essence, le pétrole, le Gasoil, le Fomi et le Gaz ; et l'autres
pour les carburants aériens : le jet A1 et l'Avgas.
La structure de prix des carburants terrestres qui fait
l'objet de notre étude donne les prix des différents types de
carburants terrestres utilisés dans le pays selon que ces types de
carburants seront vendus dans l'une des trois zones territoriales retenues dans
les calculs des prix.
II.1.2 STRUCTURE DE
PRIX DES CARBURANTS TERRESTRES
II.1.2.1 DÉFINITION
La structure de prix des carburants terrestres, telle
qu'élaborée en République Démocratique du Congo,
peut être définie comme un tableau qui donne :
- les prix de l'essence, du pétrole, du gasoil, du
Fomi et du Gaz, pour les trois différentes zones géographiques
retenues qui sont l'Ouest, l'Est et le Sud;
- les quotités prévisionnelles par
m3 ou par Kg (pour le gaz)perçues par les différents
intervenants dans la structure.
Par ses différentes rubriques, la structure de prix des
carburants terrestres rémunère les différents intervenants
dans les prix de ces carburants. Elle permet aussi à l'Etat la
constitution de certaines réserves sous des rubriques telles que Stock
stratégique, Effort de reconstruction, ...
Lorsque la structure est élaborée, la structure
de prix est élaborée, on utilise alors le volume
prévisionnel pour déterminer les quotités que les
différents intervenants prélèveraient par M3
sur les produits vendus.
Ceci donne un caractère prévisionnel aux
enveloppes de prélèvements accordés étant
donné l'utilisation d'une grandeur prévisionnelle pour le calcul
des quotités à prélever par M3. Il sied de
noter que pour certains intervenants, les prélèvements se
réalisent sous forme de pourcentage.
II.1.2.2 ELÉMENTS COMPOSANTS
Ce tableau est composé de sept grandes rubriques :
a. Prix Moyen Frontière (PMF) : C'est la
moyenne des prix des différentes cargaisons de carburants
importés par divers fournisseurs pondérés par les
quantités de ces cargaisons. Pour chaque fournisseur, le prix de la
cargaison comprend les éléments suivants :
· le Prix Platt's qui est un des prix du carburant de
référence tel que coté sur un des marchés mondiaux
des produits pétroliers de référence;
· le Différentiel qui est un ensemble
composé des frais occasionnés pour l'acheminement des produits
jusqu'aux frontières du pays. Il est constitué du fret, de
l'assurance, des frais d'expertise, des frais SOCIR, ...
b. Frais de Distribution : ils sont
constitués d'une part des quotes-parts des différents
intervenants autre que l'Etat : la SOCIR, la Commission Nationale de
l'Energie et SEP CONGO ; et de l'autre les ressources des
sociétés pétrolières commerciales,
c'est-à-dire leurs charges commerciales et leur marge
bénéficiaire.
c. Stock Stratégique / Effort de
reconstruction : C'est une forme de réserve soit en nature
(produits stockés chez SEP CONGO), soit en espèce (Compte dans
une Banque de la place) que l'Etat réalise en vue de faire face à
une situation donnée.
d. Fiscalité : Elle comprend :
· le Droit d'entrée : taxe qui
relève de la fiscalité, il est défini comme un type
d'impôts particuliers sur la dépense ; il est perçu
à l'occasion de l'importation ou de l'exportation des
marchandises.1(*) Il
représente 15 % du Prix moyen frontière fiscal qui est un forfait
institué comme base de calcul des éléments de la
Fiscalité & Parafiscalité.
· Le Droit d'accises qui est également
une taxe relevant de la fiscalité. Il est défini comme un type
d'impôt sur la dépense qui frappe séparément la
consommation de certains produits.2(*) Mais celui-ci représente 15 % de la somme PMF
Fiscal et Droit d'Entrée.
e. Parafiscalité : elle est composée
essentiellement de la surtaxe de transport. Le taux de celle-ci varie suivant
les produits. Pour l'essence, il est de 55 %; pour le pétrole de 15 % et
pour les autres produits, elle représente 45 % du PMF Fiscal. Il sied de
noter qu'il n'est pas appliqué une parafiscalité sur le FOMI.
f. Prix de Référence Réel :
c'est la rubrique des prix tels qu'ils devraient s'appliquer en tenant compte
des différents éléments de coûts.
g. Prix à la pompe : cette rubrique indique
les prix des carburants tels qu'appliqués à la pompe dans les
différentes zones du pays.
II.2 LES SERIES CHRONOLOGIQUES ET PROCESSUS STOCHASTIQUES
II.2.1 SERIES
CHRONOLOGIQUES
II.2.1.1 DÉFINITION
On appelle série chronologique, série
temporelle ou plus simplement, chronique, une suite
d'observations ordonnées dans le temps, habituellement à
intervalles égaux.3(*)
II.2.1.2 COMPOSANTES D'UNE SÉRIE
TEMPORELLE
Une série temporelle est caractérisée par
un certain nombre de mouvements ou de variations caractéristiques qui
peuvent se manifester à des degrés variés.
On distingue principalement quatre catégories de
mouvements pour les séries temporelles, appelés souvent
composantes de la série :
a. Les mouvements à grande période ou
séculaire (tendance séculaire ou Trend) : ils
caractérisent les séries temporelles dont la direction
générale du graphique s'étend sur un grand intervalle de
temps. Ces mouvements produisent une orientation persistante de la vie
économique pendant une longue période de temps.
b. Les mouvements cycliques (mouvements
oscillatoires d'amplitude et de périodicité variable). Ils
regroupent les variations autour de la tendance avec des alternances
d'époques ou de phases d'expansion et de contraction. Le facteur
cyclique de la série suit en général une forme
d'ondulation passant d'une valeur élevée à une valeur
faible, puis revenant à une valeur élevée.
c. Les mouvements saisonniers : ils
représentent la tendance de la série chronologique à
reproduire un mouvement aux intervalles de temps réguliers
appelés « saisons »4(*).
Ceux-ci sont des fluctuations périodiques qui
correspondent aux variations qui se réalisent
régulièrement au cours soit de la semaine, du mois, du trimestre,
... soit de l'année et se produisant plus ou moins de la même
façon d'une période à l'autre.
d. Les mouvements irréguliers ou
aléatoires : Ce sont des mouvements des séries
chronologiques irréguliers, imprévisibles et dus aux
événements du hasard. Ils ne produisent de variations durables
que pendant un temps court.
II.2.2 PROCESSUS
STOCHASTIQUE
II.2.2.1 DÉFINITION5(*)
Un processus stochastique est un ensemble des variables
aléatoires Yt définies par t = ...-1, 0, 1, ... (l'indice se
référant au temps).
..., Y-1, Y0, Y1, ... qui
peut encore être désigné de façon plus concise
Yt tT ou simplement Yt où T désigne alors
la suite de tous les nombres entiers positifs et négatifs.
Ceci revient à considérer un processus
stochastique comme une population qui a la dimension
« temps », c'est-à-dire que les
éléments de cette population sont fonction du temps ou encore
qu'il y a une population en chaque temps t.
Donc Yo est une variable aléatoire
différente par exemple de Y-1 ou Y1. Dans ce
cadre, une série chronologique sera considérée comme un
échantillon de cette population ou autrement dit, une réalisation
de ce processus stochastique ;
Connaissant ce processus et la loi de probabilité qui
le gouverne nous pouvons prévoir les réalisations de celui-ci
sous certaines probabilités.
II.2.2.2 CONCEPTS
II.2.2.2.1 Notion de stationnarité
Soit un processus aléatoire {Xt}. Ce
processus est dit stationnaire, s'il remplit les conditions
ci-après :
- E(Xt) ne dépend pas de t et
vaut m;
- Var(Xt) = E[(Xt - m)] ne
dépend pas de t et vaut o;
- Cov(Xt; Xt-1) = E[(Xt -
m)(Xt-1 - m)] ne dépend pas de t
et vaut k.
II.2.2.2.2 Notion d'inversibilité
Cette notion nous permet de trouver les coefficients du
polynôme Moyenne Mobile, connaissant les autocorrélations simples
du processus.
Soit le processus Moyenne Mobile d'ordre 1 suivant :
Xt = et - et-1. Nous aurons :
Xt = -et-1 + et
= -(Xt-1 + et-2) + et
= ...
= -Xt-1 - 2Xt-2 - ... -
et
Si 1 ou -1, le poids du passé ira en grandissant.
Ceci est absurde, car il se produira une explosion des valeurs. Par
conséquent, nous ne pouvons accepter comme valeurs de que les valeurs
comprises dans l'intervalle [-1 ; 1 ]. Ainsi, cette condition s'appelle la
« condition d'inversibilité ».
II.2.2.2.3 Processus Bruit Blanc (White Noice Process ou Purely
random process)
On appelle Processus Bruit Blanc, une suite de
variables aléatoires ayant une même distribution et mutuellement
indépendantes telle que :
- E(et) = 0
- E(e2t) = 2
- E(et es) = 0 avec t s
- k = Corr(et , et-k
) = 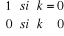
Le terme Bruit blanc traduit l'idée d'une absence
d'information dans les résidus du modèle retenu.
II.2.2.3 OUTILS D'ANALYSE
II.2.2.3.1 Fonction d'autocovariance
Elle est définie par la relation :
k =
Cov(Xt ; Xt+k) = E[(Xt -
)(Xt+k - )] où k
Propriétés :
- k = -k k
- o = k2 = E[(Xt
- )2]
La matrice variance-covariance qui est définie positive
est donnée par :
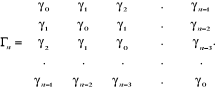
Elle fournit simultanément de l'information sur la
variabilité de la série et sur les liaisons temporelles de
celle-ci.
II.2.2.3.2 Fonction d'autocorrélation
La fonction d'autocorrélation est celle qui mesure la
corrélation entre les variables Xt et Xt-k . Elle
est définie par :
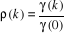 avec
- k Z avec
- k Z
- 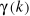 =
Cov(Xt ; Xt+k) =
Cov(Xt ; Xt+k)
- 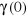 =
Var(Xt) = Var(Xt+k) =
Var(Xt) = Var(Xt+k)
Propriétés :
- k = -k
- 0 = 1
- k = 1, k
Les autocorrélations donnent une idée de
dépendance temporelle qui existe au sein d'un processus donné.
Elles sont particulièrement intéressantes pour des raisons de
comparaisons, car elles sont dépourvues de dimensions et par
conséquent, elles sont indépendantes de la dispersion du
processus.6(*)
On appelle corrélogramme, la
représentation graphique des différentes valeurs prises au temps
t par cette fonction.
Si nous considérons m observations successives
Xt, Xt+1, ... Xt+m, nous pouvons introduire la
matrice d'autocorrélation du vecteur des observations Xt,
Xt+1, ... Xt+m.
Cette matrice est donnée par :
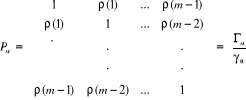
II.2.2.3.3 Fonction d'autocorrélation partielle
Soit Xt une variable aléatoire. On appelle
Fonction d'autocorrélation partielle, celle qui,
mesurant la liaison linéaire entre Xt et Xt-k une
fois retirés les liens transitant par les variables
intermédiaires Xt-1, ... Xt-k+1.
Les autocorrélations partielles sont
notées :
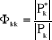
où 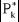 est le
déterminant de la matrice des autocorrélations dans laquelle la
k-ième colonne est remplacée par le vecteur
[1,2,... k]' est le
déterminant de la matrice des autocorrélations dans laquelle la
k-ième colonne est remplacée par le vecteur
[1,2,... k]'
Le corrélogramme partiel est une représentation
graphique des valeurs prises par cette fonction.
II.2.3 MODELE
LINEAIRE GENERAL
II.2.3.1 MODÈLES POUR SERIES
STATIONNAIRES
Ils sont caractérisés par la modélisation
ARMA qui se généralise simultanément les modèles
Autorégressifs et Moyennes mobiles purs. Cette modélisation
présente comme avantage d'être souple d'utilisation et de fournir
généralement de bonnes approximations des séries
réelles avec moins de paramètres que les modèles
Autorégressifs ou Moyennes mobiles purs7(*).
II.2.3.1.1 Définition
Un processus stationnaire Xt admet une
représentation ARMA(p, q) s'il satisfait l'équation :
(1-1B
-...-pBp)Xt =
(1-1B -...-qBq)et
ou (B)Xt = (B)et
où : - p 0, q
0 ;
- les polynômes et ont leurs racines de modules
strictement supérieures à 1 ;
- et n'ont pas de racines communes ;
- {et} est le processus d'innovation, un
processus bruit blanc.
II.2.3.1.2 Propriétés
Si Xt est un processus stationnaire de
représentation ARMA(p, q) :
(B)Xt =
(B)et
i) Xt admet la représentation MA() :
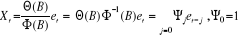
ii) Xt admet la représentation AR() :
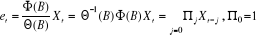
iii) Xt admet pour innovation t.
II.2.3.1.3 Caractéristiques
Etant donné que le processus ARMA(p, q) est un
regroupement des processus AR(p) et MA(q), nous présenterons dans un
tableau unique les caractéristiques de tous ces processus.
Les caractéristiques des processus ARMA(p, q) sont
différentes de celles des processus autorégressifs et des
processus moyenne mobile, comme nous le montre le tableau ci-dessous.
|
Bruit blanc
|
AR(p)
|
MA(q)
|
ARMA(p, q)
|
|
Condition de stationnarité
|
Non
|
Oui*
|
Non
|
Oui*
|
|
Condition d'inversibilité
|
Non
|
Non
|
Oui**
|
Oui**
|
|
Fonction d'autocorrélation rk
tronquée
|
Oui
(pour k 0)
|
Non
|
Oui
(pour k q)
|
Non
|
|
Fonction d'autocor. partielle pk
Tronquée
|
Oui
(pour k 0)
|
Oui
(pour k p)
|
Non
|
Non
|
|
* La condition de stationnarité porte sur les racines
de polynôme 1 - 1B - ... -
pBp
** La condition d'inversibilité porte sur les racines
de polynôme 1 - 1B - ... -
qBq
|
Pour établir une liaison entre les processus AR(p),
MA(q) et ARMA(p, q), il faut d'abord assurer l'inversibilité des
polynômes autorégressifs et polynômes moyennes mobiles des
processus AR(p) et MA(q). Ainsi, d'une part, les processus AR(p) et ARMA(p, q)
peuvent être mis sous forme de processus MA() ; et de l'autre, les
processus MA(q) et ARMA(p, q) peuvent être mis sous forme de processus
AR().
II.2.3.2 MODÈLE POUR SERIES NON
STATIONNAIRES
En général, les séries chronologiques ont
non seulement une moyenne non nulle, mais elles ne sont pas stationnaires :
elles comportent également une tendance, une saisonnalité ou
même une structure plus complexe. Par conséquent,
l'intérêt pour les modèles ARMA semble assez
limité.
Aussi, il est évident que, pour la plupart des
séries économiques, l'hypothèse de stationnarité
n'est pas tenable ; mais que si l'on considère la
désaisonnalisation, les différences premières de telles
séries, l'hypothèse de stationnarité devient souvent
vraisemblable.
Il est donc naturel de considérer la classe des
processus dont désaisonnalisation ou la différence d'un certain
ordre satisferait une représentation ARMA, et par conséquent le
traitement du processus comme un processus stationnaire.
Cette classe des modèles prend la forme
générale des Processus Autorégressifs Moyennes Mobiles
Intégrés avec saisonnalité, SARIMA(p,d,q)(P,D,Q) :
(B)(Bs)d2D(Xt - m) =
(B)(Bs)et
où :
(B) : polynôme autorégressif ordinaire de
degré p ;
(Bs) : polynôme autorégressif
saisonnier de degré P en Bs ;
d : opérateur de différence ordinaire
de degré d ;
sD : opérateur de
différence saisonnière de degré D et de
périodicité S;
(B) : polynôme moyenne mobile ordinaire de degré
q ;
(Bs) : polynôme moyenne mobile saisonnier de
degré Q en Bs.
II.2.4 MODELE D'ANALYSE D'INTERVENTIONS
II.2.4.1 INTRODUCTION
Il arrive fréquemment que les séries
chronologiques soient affectées par des interventions : changement de
définition de la grandeur étudiée, changement de
réglementation qui affecte sa valeur, circonstances particulières
(accidents, grèves, promotion, etc.). Ces phénomènes se
traduisent par des données atypiques ou aberrantes dans les
séries statistiques.
Ces données conduisent généralement
à des estimations erronées des paramètres du modèle
pouvant à leur tour conduire à des mauvaises prévisions.
Face à ces données atypiques, bien d'auteurs
préconisent soit leur élimination, soit leur lissage. Ces
opérations ont comme conséquence le perte ou la
déformation de l'information contenue dans les séries.
Pour palier ce problème, on utilise le modèle
d'interventions ou modèle ARMA incluant des variables binaires.
II.2.4.2 ANALYSE DES INTERVENTIONS
Les modèles d'analyse d'interventions permettent de
représenter l'influence d'information qualitative en plus de
l'information quantitative. En fait, dans leur démarche, ces
modèles utilisent les variables binaires pour saisir l'information
qualitative supposée contenue dans les données atypiques.
II.2.4.3 FORMES D'INTERVENTIONS
Il existe plusieurs formes d'interventions dont le choix et
l'identification de l'instant s'effectuent à partir du graphe de la
série chronologique. Il est aussi possible de combiner sur une
même série différentes formes d'interventions.
Plus généralement, on définit quatre
formes d'impacts :
1. Impulsion de o au temps
· Définition de la variable à
introduire
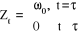 ; la
fonction de la variable est ; la
fonction de la variable est  avec avec 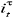 la variable
binaire telle que la variable
binaire telle que 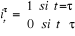 . .
Z
0
0
t
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
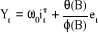
2. Saut de o au temps
· Définition de la variable à
introduire
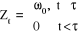 , la
fonction de la variable est : , la
fonction de la variable est :
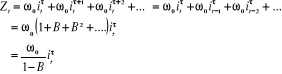
Z
0
0
t
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
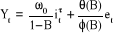
3. Accroissement o au temps ,
exponentiellement dégressif au taux
· Définition de la variable à
introduire
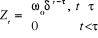 ; la
fonction de la variable est : ; la
fonction de la variable est :
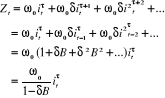
Z
0
t
0
- 1 + 1
· Insertion des effets des interventions dans le
modèle ARMA :
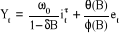
4. Rampe de pente 1 au temps
· Définition de la variable à
introduire
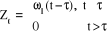 ; la
fonction de la variable est : ; la
fonction de la variable est :
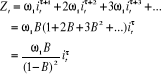
Z
0
1
0
- 1 + 1
t
· Insertion des effets des interventions dans le
modèle ARMA :
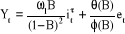
II.2.4.4 PROCÉDURE D'APPLICATION
DU MODÈLE D'ANALYSE D'INTERVENTIONS
La mise en application de cette méthode passe, dans un
premier temps, par la détermination du modèle ARMA de la
série sous étude, et ensuite par l'analyse des interventions
proprement dites.
La détermination du modèle ARMA du processus
sous étude se réalise par la l'exécution des quatre
premières étapes de la méthode classique de BOX &
JENKINS. L'utilisation, à la quatrième étape, de l'une
des procédures de spécification doit aboutir au choix d'un
certain nombre de modèles parmi lesquels nous retiendrons le
modèle définitif.
En fait, la partie analyse d'interventions rajoute, aux
étapes traditionnelles de la méthode de BOX & JENKINS, les
étapes supplémentaires suivantes :
- La création des variables d'intervention pour les
points représentant les données aberrantes;
- La reestimation des modèles retenus avec
également les variables binaires comme variables explicatives.
II.3 LES PREVISIONS
II.3.1 INTRODUCTION
La prévision est l'art de prévoir les valeurs
futures de certaines variables en dehors d'un échantillon original et
donné.8(*)
Pour pouvoir planifier ses activités, toute
organisation est pratiquement obligée de faire de la prévision
d'une manière ou d'une autre9(*).
Nous recourons ainsi à la prévision pour deux
raisons : d'abord, le futur est incertain; ensuite, il existe souvent un
décalage de temps entre la perception d'un événement ou
d'un besoin et la réalisation effective de cet événement.
10(*)
Etant donné la survenance dans le futur de certains
facteurs influant sur nos activités, la prévision se justifie
parce qu'elle nous permettrait, elle permettrait aux décideurs de
prendre, dans la mesure du possible, certaines mesures qui puissent assurer les
lendemains meilleurs.
L'activité de prévision peut donner lieu
à :
- une prévision ponctuelle : lorsqu'elle
est donnée par un nombre;
- une prévision par intervalle : lorsque la
valeur est sensée se trouver dans un intervalle donné;
- une prévision conditionnelle : lorsque la
prévision est réalisée conditionnellement
à la réalisation d'un autre événement;
- une prévision inconditionnelle : lorsque la
prévision n'est pas soumise à la
réalisation d'un quelconque événement;
- une prévision à court terme : la
prévision est réalisée pour une inférieure ou
égale à douze mois;
- une prévision à long terme : lorsque
l'horizon de la prévision dépasse quatre années.
II.3.2 TYPES DE
METHODES DE PREVISION
Il existe plusieurs méthodes de prévisions. Le
tableau suivant donne un classement basé sur la technique de
prévision, la distinction entre méthodes statistiques et
méthodes non statistiques, la distinction entre méthodes
chronologiques et méthodes causales, ou encore la distinction entre
méthodes quantitatives et méthodes qualitatives.
|
Méthodes informelles
|
Méthodes ad hoc subjectives ou intuitives
|
|
Méthodes formalisées de
prévision
|
Méthodes quantitatives
|
Causale
ou régressive
|
Régression simple
|
Les variations des variables dépendantes sont
expliquées par les variations de la (ou des ) variable(s)
indépendantes.
|
|
Modèles économétriques
|
Système d'équations simultanées de
régression multiple.
|
|
Séries chronologiques
|
Méthodes élémentaires (naïves)
|
Application des règles simples telles que la
prévision est égale à la réalisation la plus
récente, ou à celle du même mois un an avant + 5 %.
|
|
Extrapolation de tendance
|
Projection linéaire, exponentielle, en forme d'S, ou
d'autres formes.
|
|
Lissage exponentiel
|
Calcul des moyennes et lissage de façon linéaire
ou exponentielle.
|
|
Décomposition
|
Une série chronologique est décomposée en
tendance, saisonnier, cycle et aléa.
|
|
Filtres
|
Les prévisions résultant d'une combinaison
linéaire de valeurs passées - présentes - paramètre
modèle pouvant s'adapter aux modifications des données.
|
|
Modèles Autorégressifs
Moyennes mobiles ARMA,
Méthode de BOX et JENKINS
|
Les prévisions résultant d'une combinaison
linéaire de valeurs passées et présentes et/ou d'erreurs
passées.
|
|
Méthodes qualitatives
|
Combinaisons subjectives
|
Arbre de décision
|
On assigne une probabilité subjective à quelques
éléments et on utilise l'approche statistique bayesienne.
|
|
Estimation par les vendeurs
|
Approche ascendante de la base au sommet, regroupant les
prévisions des vendeurs.
|
|
Commission d'Evaluation des cadres
|
Des cadres de marketing, de production et financiers
préparent ensemble des prévisions.
|
|
Etudes anticipatives du marché
|
Etudes des intentions d'achats des clients potentiels ou des
bilans d'entreprises.
|
|
Technologiques
|
Exploratoires
|
A partir d'une base de connaissance actuelle, on évalue
dans les grandes lignes l'état futur.
|
|
Normatives
|
On commence par évaluer les objectifs, besoins ou
souhaits futurs et on remonte pour déterminer les développements
nécessaires pour atteindre les objectifs, etc.
|
Source : KAMIANTAKO A., op. cit.
II.3.3 VALIDITE DES METHODES DE PREVISION
Toute prévision donne lieu aux valeurs dégageant
des écarts par rapport aux réalisations. L'exactitude
prévisionnelle peut se mesurer de plusieurs manières. Examinons
à présent quelques critères de validité de
méthodes de prévision.
II.3.3.1 CRITÈRES USUELS11(*)
Supposons qu'on dispose de n prévisions 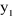 , ..., , ...,
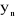 qui correspondent aux données y1, ...,
yn, et soit donc de n erreurs de prévision
e1,..., en. Les critères suivants sont
utilisés pour juger de la validité des méthodes de
prévision.
qui correspondent aux données y1, ...,
yn, et soit donc de n erreurs de prévision
e1,..., en. Les critères suivants sont
utilisés pour juger de la validité des méthodes de
prévision.
· l'Erreur moyenne ("Mean Error") :
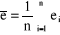
· la Variance :
var(e) = 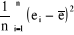
· l'Ecart-type ("Standard Deviation") :
std(e) =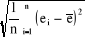
· l'Ecart absolu moyen ("Mean Absolute
Deviation") :
MAD(e) =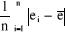
· le Carré moyen des erreurs ("Mean
Square Error") :
MSE(e) =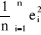
· l'Erreur quadratique moyenne ("Root Mean
Square Error") :
RMSE(e) =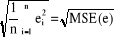
· l'Erreur absolue moyenne ("Mean Absolute
Error") :
MAE(e) = 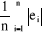
· l'Erreur absolue moyenne en pourcentage
("Mean Absolute Percent") :
MAPE(e) =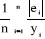
II.3.3.2 CRITÈRES
ADDITIONNELS12(*)
Ces critères servent soit à comparer la
méthode de prévision sous étude à une
méthode de prévision de référence, souvent la
méthode naïve ; soit à comparer deux ou plusieurs
méthodes de prévision.
· Estimation non biaisée de la variance
:
VarNb(e) =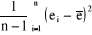
· Critère MAPE de la prévision
naïve 1 ("naive forecast") :
NF1 = 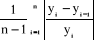
· Critère de U de Theil :
U = 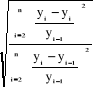
Si U = 0 : Les prévisions sont parfaites;
Si U = 1 : La méthode naïve est aussi bonne
que la prévision examinée;
Si 0 U 1 : la méthode étudiée est
meilleure que la méthode naïve;
Si U 1 : La méthode de prévision naïve
donne de meilleurs résultats.
· Critère AIC (Akaike Information
Criterion) :
AIC(e) = n ln[MSE(e)] + 2p
où p : nombre de paramètres estimés
Ce critère, basé sur la théorie de
l'information, réalise un compromis en pénalisant les
paramètres introduits sans nécessité.
· Critère SBIC, BIC ou SBC (Schwarz Bayesian
Information Criterion)
SBIC(e) = n ln[MSE(e)] + ln(n)p
où p : nombre de paramètres estimés
Ce critère a des propriétés statistiques
plus intéressantes que AIC. On considère
généralement qu'il pénalise les paramètres en
nombre excessif encore plus fortement que AIC.
II.3.4 CHOIX D'UNE METHODE DE PREVISION
Le choix d'une méthode de prévision
dépend de plusieurs facteurs notamment, le type de données,
l'horizon temporel de la prévision, la loi d'évolution des
données à prédire, le coût d'utilisation de la
méthode de prévision, l'exactitude prévisionnelle
souhaitée et son application.13(*)
Ainsi la prévision d'une grandeur donnée
réalisée par deux prévisionnistes donnerait
peut-être deux résultats différents suivant que tel ou tel
prévisionniste disposait ou pas de tel ou tel moyen, suivant qu'il
réalisait sa prévision sur tel ou tel horizon temporel, suivant
que l'exactitude souhaitée était de tel ou tel pourcentage,...
II.4 LA METHODE DE PREVISION DE BOX ET
JENKINS
II.4.1 INTRODUCTION
L'approche de BOX et JENKINS (1976) consiste en une
méthodologie d'étude systématique des séries
chronologiques à partir de leurs caractéristiques. L'objectif
est de déterminer dans la famille des modèles ARIMA, le plus
adapté à représenter le phénomène
étudié.14(*)
Il s'agit, dans sa version originelle, d'une méthode de
prévision extrapolative puisque seul le passé de la variable est
utilisé à cette fin, sans apport d'information extérieure.
Dans sa version évoluée, elle peut être utilisée
dans le cadre plus général des méthodes de
prévision explicatives en permettant l'inclusion de variables
explicatives et d'information extérieure dans un modèle de
séries chronologiques. Cette méthode est recommandée pour
les prévisions à court terme.
II.4.2 ETAPES DE LA METHODE DE BOX & JENKINS
Cette approche comporte, en principe, 3 étapes
fondamentales :
* le choix du Modèle (spécification ou
identification);
* l'ajustement du Modèle (estimation);
* la validation du Modèle (adéquation).
Le diagramme suivant présente ces trois phases en
parallèle avec les étapes de la démarche scientifique,
où l'analyse exploratoire conduit à l'élaboration d'un
modèle, et où l'analyse confirmatoire permet de confirmer ou
d'infirmer la validité de celui-ci.15(*)
DONNEES
Choix d'un
Modèle
Analyse
exploratoire
= = SPECIFICATION
Ajustement du
Modèle
MODELISATION
= ESTIMATION
Analyse
confirmatoire
= = ADEQUATION
Validation du
Modèle
Si Mauvais
Recommencer
Si Bon
Conclure
CONCLUSION
Figure 1 : Illustration de la démarche de
BOX & JENKINS
En fait, il est préférable de voir la
méthode constituée de sept étapes qui sont
généralement répétées jusqu'à
satisfaction 16(*):
- la familiarisation avec les données;
- l'analyse préliminaire;
- la spécification du modèle (ou
identification);
- l'estimation des paramètres;
- l'adéquation du modèle (ou validation);
- la prévision;
- l'interprétation des résultats.
II.4.2.1 LA FAMILIARISATION AVEC LES
DONNEES
Connaissant le domaine dont relèvent les
données, les théories existantes, les objectifs poursuivis
(prévision ponctuelle ou par intervalle, détection d'un
changement de comportement, etc.) et la qualité des données
(précision, exactitude, périodicité inhérente au
phénomène étudié, homogénéité
dans le temps, événements qui ont pu influencer la série),
nous devons représenter graphiquement les données.
Ensuite, nous examinerons cette représentation
graphique (graphe en fonction du temps avec points reliés,
éventuellement avec codification des trimestres ou des mois) qui, dans
notre cas, peut nous révéler des conséquences
d'interventions (changements législatifs ou économiques,
accidents majeurs, grèves, etc.), des changements de structure dans la
série, ...
II.4.2.2 L'ANALYSE PRELIMINAIRE
Les options suivantes peuvent être prises : abandonner
une partie des données au début de la série, corriger les
données aberrantes, suppléer les données manquantes,
transformer les données (transformation logarithmique, inversé,
racine carrée, etc.), changer de variable (division par une série
tel qu'un indice de prix, les nombres mensuels de jours ouvrables, etc.).
Dans le cadre ce travail, les données atypiques ou
aberrantes ne seront pas corrigées, mais elles seront plutôt
modéliser afin d'éviter toute perte ou déformation
d'information conséquente à leur traitement.
Puisqu'il faudra souvent se ramener à un modèle
ARMA stationnaire, l'option peut être prise de travailler avec les
différences ordinaires et/ou saisonnières. Ce choix sera
dicté par l'allure graphique de la série.
Il est conseillé de comparer les variances (ou des
écarts-types) des séries qu'on veut modéliser. La
série avec la plus petite variance (ou le plus petit écart-type)
conduit souvent à la modélisation la plus simple. Typiquement,
les autocorrélations décroissent de manière
linéaire (et non exponentielle) quand une différence
première est nécessaire.
La nécessité d'une différence
saisonnière se manifeste par des autocorrélations de retard
s, 2s, etc., qui sont proches de 1 et décroissent
linéairement.17(*)
II.4.2.3 LA SPECIFICATION DU MODELE
Il existe plusieurs méthodes d'identification, parmi
lesquelles nous citons :
· La méthode des corrélogrammes ou
graphique18(*)
Cette méthode, la plus utilisée, consiste
à se baser sur la forme des fonctions d'autocorrélation simple
et partielle de la série étudiée (éventuellement
différenciée) {Yt} afin de choisir un
modèle ARMA ou éventuellement plusieurs modèles qui seront
examinés à tour de rôle.
On commence par réaliser les tests de bruit blanc.
Si la série {Yt} paraît
être la réalisation d'un bruit blanc, le modèle sera
Yt = et (en effet les autocorrélations sont
généralement calculées sur la série centrée,
donc après avoir soustrait la moyenne).
S'il y a un grand nombre d'autocorrélations
significatives, nous déterminerons le modèle sachant que les
autocorrélations d'un processus MA(q) sont nulles pour un retard
supérieur à q et que les autocorrélations
partielles d'un processus AR(p) sont nulles pour un retard supérieur
à p.
Si, compte tenu des variations statistiques, on ne
reconnaît ni l'un ni l'autre processus, nous sommes donc en
présence d'une structure d'autocorrélation plus complexe, on peut
examiner la saisonnalité à travers la significativté des
autocorrélations des lags correspondants.
· La procédure de spécification
autorégressive
Elle consiste à estimer successivement les
paramètres des modèles AR(1), AR(2), ainsi de suite sur la
série étudiée, et à examiner les
autocorrélations des séries résiduelles. Si l'ajustement
d'un modèle AR(p) conduit à une série résiduelle
dont les autocorrélations sont tronquées au-delà du retard
q, cette série résiduelle pourra être
représentée par un modèle MA(q), d'où ressort
un modèle global ARMA(p, q) pour la série. On peut simplifier le
modèle en écartant certains termes en B pour lesquels les
coefficients sont non significatifs.19(*)
II.4.2.4 L'ESTIMATION DES PARAMETRES
Cette phase d'estimation utilise des techniques classiques de
statistique. Les paramètres i, i et 2
sont généralement estimés en utilisant l'approche du
maximum de vraisemblance ou la technique des moindres carrés.
Avec le développement de l'informatique, nous trouvons
plusieurs logiciels spécialisés qui nous aident à
réaliser ce travail d'estimation en donnant directement les valeurs
estimées et toutes les statistiques nécessaires aux
différents tests.
II.4.2.5 L'ADEQUATION DU MODELE (OU
VALIDATION)
Il faut vérifier si les coefficients estimés
satisfont aux conditions de stationnarité et d'inversibilité et
s'il n'y a pas de simplification possible entre les facteurs constituant le
polynôme autorégressif et ceux relatifs au polynôme moyenne
mobile.
Ensuite, on peut examiner les résidus du modèle;
c'est l'analyse des résidus :
. leur moyenne est-elle nulle ? (le contraire indiquerait le
besoin d'ajouter une moyenne m au modèle);
. reste-t-il de l'autocorrélation résiduelle ?
(tests individuels et tests globaux Q de Box et Pierce ou encore mieux Q' de
Ljung et Box) ;
. reste-t-il de l'autocorrélation partielle
résiduelle ?
. y a-t-il indication de la présence de données
aberrantes ? (regarder les résidus qui sortent de l'intervalle
+2...).
Pour les tests globaux de Box-Pierce et de Ljung-Box, le
nombre de degrés de liberté à prendre en
considération est le nombre de retards diminué du nombre de
paramètres autorégressifs ou moyenne mobile estimés.
Pour le test individuel, en vue d'effectuer un examen plus
précis de la significativité des autocorrélations simples
et partielles, il faudra utiliser le facteur d'erreur type suivant : 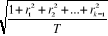 avec T la
taille de la série sous étude. avec T la
taille de la série sous étude.
De la sorte, les limites seront données par :
1,96. 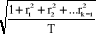
Il se peut que plusieurs modèles franchissent la phase
de vérification ou d'identification et qu'il faille choisir dans cet
ensemble. Il existe cependant un certain nombre de critères de
choix qu'on peut utiliser pour ce faire.
Si le modèle n'est pas valable, il y a lieu de
reprendre l'analyse à partir d'une des étapes
précédentes, de préférence en exploitant
l'information acquise.
II.4.2.6 LA PREVISION
La prévision se réalise par une fonction de
prévision que l'on doit construire.
Après validation du modèle, la prévision
peut alors être calculée à un horizon de quelques
périodes limitées car la variance de l'erreur de prévision
croît très vite avec l'horizon20(*). Il est ainsi préférable que la
prévision réalisée soit à court terme.
Soit un modèle ARMA(p, q) :
(1-1B
-...-pBp)Yt =
(1-1B -...-qBq)et
ou
Yt = 1Yt-1 +
2Yt-2 +...+ pYt-p + et +
1et-1 + 2et-2 + ... +
qet-q
et plaçons-nous au temps T où la dernière
observation est disponible.
Pour calculer les prévisions 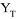 (1), (1), 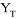 (2), ... (2), ...
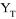 (h),
écrivons l'équation aux temps T+1, T+2, ...T+h. (h),
écrivons l'équation aux temps T+1, T+2, ...T+h.
Nous obtiendrons :
Au temps T+1 :
YT+1 = 1YT +
2YT-1 +...+ pYT-p+1 +
eT+1 + 1eT + 2eT-1 + ...
+ qeT-q+1
Au temps T+2 :
YT+2 = 1YT+1 +
2YT +...+ pYT-p+2 + eT+2
+ 1eT+1 + 2eT + ... +
qeT-q+2
...
Au temps T+h :
YT+h =
1YT+h-1+2YT+h-2+...+pYT+h-p+eT+h+1eT+h-1+2eT+h-2+...+qeT+h-q
Nous constatons que, pour un horizon h
supérieur à l'ordre p du modèle, les prévisions de
la partie AR(p) ne font plus intervenir directement les valeurs
observées. Mais pour la partie MA(q) du modèle, si h>q, les
prévisions deviennent nulles.21(*)
II.4.2.7 L'INTERPRETATION DES
RESULTATS
Elle n'est pas toujours aisée. Les
éléments les plus importants, pour lesquels il faudra trouver une
explication, sont les opérateurs de différence utilisés et
éventuellement les constantes. Ceux-ci déterminent en effet le
comportement de la prévision à long terme.
Le polynôme autorégressif joue également
un rôle essentiel sur la fonction de prévision. En effet, pour
celui-ci, les racines réelles induisent une composante amortie dans la
fonction de prévision. Mais, les racines complexes donnent lieu à
une composante pseudo-périodique amortie.
III.
APPLICATION DU MODELE D'ANALYSE D'INTERVENTIONS A LA PREVISION DU VOLUME DES
CARBURANTS TERRESTRES
III.1 Familiarisation avec les
données
La figure ci-dessous illustre, à travers la
série Yt, l'évolution des volumes des carburants
terrestres consommés en République Démocratique du Congo
de janvier 1982 à avril 199922(*).
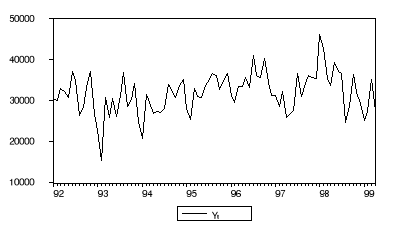
L'analyse de cette série nous conduit à
réaliser les observations suivantes :
- Février 1993 : une chute remarquable
de l'ordre de 68 % est observée. Cette chute, dans la consommation des
carburants terrestres, est attribuée aux deuxièmes pillages qui
ont eu lieu dans la ville de Kinshasa, principal centre de consommation avec
près de 80 % de la consommation totale.
- Août 1998 : une seconde chute de
consommation est observée. Elle correspond à la rébellion
menée par les BANYAMULENGE qui a commencé par leur révolte
à Kinshasa.
- De juin 1997 à janvier 1998 : un
accroissement de la consommation est observé pendant cette
période. Il peut être attribué aussi bien à la
relance des activités économiques enregistrée après
la prise du pouvoir par l'AFDL, qu'au retournement de tendance des prix Platt's
qui ont commencé aussi à chuter.
- De février 1998 à avril 1999 :
Il a été observée une décroissance de la
consommation attribuable au fait que le pays a commencé à avoir
non seulement des problèmes politiques, mais surtout des
problèmes économiques dus à l'absence de l'aide
extérieure qui devait relayer la timide relance enregistrée du
fait de l'effet psychologique causé par la chute de la dictature
mobutienne.
III.2
Analyse préliminaire
L'intérêt des séries stationnaires
étant démontré, nous devons tester si notre série
sous étude est stationnaire.
La stationnarité de notre série est clairement
traduite par le graphique ci haut qui illustre son évolution à
travers le temps.
Cette stationnarité est confirmée par la lecture
du corrélogramme de la série. En effet, lorsque nous observons le
corrélogramme simple, nous remarquons qu'il y a une chute rapide des
valeurs des coefficients au fur de l'évolution des lags.
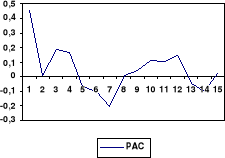
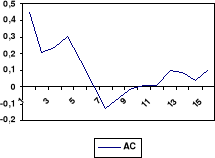
Un autre moyen
de vérifier la stationnarité des séries reste le test
Augmented Dickey-Fuller de stationnarité. Effectué sur la
série Yt, celui-ci nous conduit également à
confirmer la stationnarité de cette série. En effet, la
statistique du test ADF qui est de -3,376079 est supérieure, en valeur
absolue, à la valeur critique au seuil de 5 % qui est de -2,8955.
ADF Test Statistic -3.376079 1% Critical Value*
-3.5082
5% Critical Value -2.8955
10% Critical Value -2.5846
*MacKinnon critical values for rejection of hypothesis of a
unit root.
III.3
Spécification du modèle
Le corrélogramme de notre série Yt
indique que celle-ci est générée par un processus
ARMA(1,1).
Toutefois, l'exploration des voisinages de ce modèle
nous permet de trouver également d'autres bons modèles auxquels
la série Yt peut être ajustée :
1. Yt = 31.790 +
0,45*Yt-1
(0,00) (0,00)
R2 = 0,20 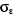 = 4339.25 = 4339.25
2. Yt = 31.773 +
0,42*et-1
(0,00) (0,00)
R2 = 0,18 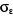 = 3638.48 = 3638.48
3. Yt = 31.791 +
0,46*Yt-1 -
0,01*et-1
(0,00) (0,03) (0,96)
R2 = 0,20 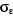 = 4339.20 = 4339.20
4. Yt = 31.808
+ 0,09*Yt-1 +
0,14*Yt-2 +
0,77*et-1
(0,00) (0,00) (0,00)
(0,00)
R2 = 0,21 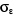 = 4357.43 = 4357.43
5. Yt = 31.749 +
0,81*Yt-1 - 0,35*et-1 -
0,19*et-2
(0,00) (0,00) (0,16) (0,27)
R2 = 0,22 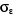 = 4284.74 = 4284.74
Ces modèles sont résumés dans le tableau
suivant avec certains critères de choix de modèles :
|
Modèles ARMA(p,q)
|
Résidus
|
SBIC
|
|
Observations
|
|
(1, 0)
|
BB
|
16 ,84
|
4.339,25
|
-
|
|
(0, 1)
|
BB
|
16,85
|
4.370,56
|
-
|
|
(1, 1)
|
BB
|
16,89
|
4.339,20
|
Le coefficient Ma(1) non significatif
|
|
(2, 1)
|
BB
|
16,95
|
4.357,43
|
Tous les coefficients non significatifs, sauf la constante.
|
|
(1, 2)
|
BB
|
16,91
|
4.284,74
|
Tous les coefficients Ma(q) non significatifs
|
Le terme BB dans la deuxième colonne indique que la
série est un bruit blanc. La troisième colonne donne le
critère de SCHWARTZ indiquant la bonté d'un modèle
comparativement à un autre.
Ce critère a des propriétés statistiques
plus intéressantes que le critère AIC23(*). Ainsi, un modèle sera
meilleur par rapport à un autre lorsque la valeur de son SBIC est
inférieure.
III.4 ANALYSE DES INTERVENTIONS
Les modèles estimés ci-haut peuvent cependant
être améliorés en essayant de prendre en compte les
« points aberrants » apparaissant dans la série des
résidus par le traitement utilisant la méthode dite des
interventions.24(*)
III.4.1 Détermination des points aberrants
Pour chacun des modèles estimés, et avec un
intervalle de confiance de 95 %, nous avons comparé le double de
écart-type de la série des résidus aux différents
résidus de cette série. Pour l'ensemble des modèles, nous
avons trouvé les données aberrantes aux dates suivantes :
- - Fév. 1993
- Juillet 1996
- Janv. 1998
- Août 1998
L'observation du graphique de la série confirme que ces
données se caractérisent par des interventions en forme
d'impulsion.
Ainsi, pour chacune de ces dates, nous avons
créé une variable binaire reflétant la structure
liée aux interventions en forme d'impulsion :
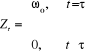
III.4.2
Intervention et Identification du modèle
L'intervention se réalise par l'introduction, dans les
différents modèles retenus ci-haut, des variables binaires
créées relatives aux dates également retenues.
Cette insertion des variables binaires se réalisera
sous la forme suivante :
Yt = ARMA(p, q) +
0it
La reestimation des modèles ci-haut retenus avec
introduction des variables binaires nous donne les résultats
suivants :
1. Yt = 31.843 -
12.692*I293 + 7.251*I796 +
8.913*I198 - 7.848*I898 +
0,43*Yt-1
(0,00) (0,00) (0,04)
(0,01) (0,03 ) (0,00)
R2 = 0,41 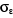 = 3734.37 = 3734.37
2. Yt = 31.826 -
15.212*I293 + 7.292*I796 +
8.350*I198 - 6.267*I898 -
0,58*et-1
(0,00) (0,00) (0,03) (0,01)
(0,04 ) (0,00)
R2 = 0,43 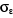 = 3638.48 = 3638.48
3. Yt = 31.781 -
16.864*I293 + 11.256*I796 +
14.215*I198 - 6.556*I898 +
0,49*Yt-1 +
0,98*et-1
(0,00) (0,00) (0,00)
(0,00) (0,02 ) (0,00) (0,00)
R2 = 0,46 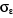 = 3578.72 = 3578.72
4. Yt = 31.782
-16.032*I293+11.076*I796+
13.095*I198 - 7.608*I898 -
0,42*Yt-1 + 0,15*Yt-2 +
0,97*et-1
(0,00) (0,00) (0,00) (0,00)
(0,01 ) (0,00) (0,20) (0,00)
R2 = 0,47 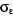 = 3571.11 = 3571.11
5. Yt = 31.818 -
14.190*I293 + 7.004*I796 +
7.924*I198 - 6.849*I898 +
0,87*Yt-1 - 0,29*et-1 -
0,39*et-2
(0,00) (0,00) (0,03)
(0,01) (0,04 ) (0,00) (0,26) (0,04)
R2 = 0,45 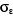 = 3620.27 = 3620.27
Le tableau suivant donne le résumé de ces
modèles sur base de certains critères de choix de
modèles :
|
Modèles ARMA(p, q)
|
Résidus
|
SBIC
|
|
Observations
|
|
(1, 0)
|
BB
|
16,74
|
3.734,37
|
-
|
|
(0, 1)
|
BB
|
16,69
|
3.638,48
|
-
|
|
(1, 1)
|
BB
|
16,71
|
3.578,72
|
-
|
|
(2, 1)
|
BB
|
16,76
|
3.571,11
|
-
|
|
(1, 2)
|
BB
|
16,78
|
3.620,27
|
Coefficient Ma(1) non significatif
|
Etant donné notre objectif de prévision à
un horizon supérieur à un, nous abandonnons le modèle
ARMA(0, 1) parce qu'avec ce modèle les prévisions
au-delà de période T+1 sont nulles.
Par conséquent, des modèles ainsi
identifiés sortira le modèle définitif qui sera retenu
après l'étape d'adéquation.
III.5 Adéquation du modèle
1. Modèle ARMA( 1, 0)
(a) Condition de stationnarité
Pour un processus autorégressif d'ordre 1, la condition
de stationnarité entraîne que le coefficient autorégressif
soit compris dans l'intervalle ]-1 ;1[.
Dans le cas du modèle présent, ce coefficient
qui est égal à 0,43 appartient à cet intervalle. Donc, ce
processus est stationnaire.
(b) Analyse des résidus
Les résidus ont une valeur presque nulle :
-0,0002. Le test individuel et collectif de bruit blanc indique que les
résidus de la série donne lieu à un bruit blanc, comme le
traduit la série des statistiques Q de BOX et PIERCE. En effet, les
coefficients des corrélations simples et partielles calculées
pour la série des résidus de la régression de ce
modèle sont inférieures aux statistiques Q théoriques au
seuil = 5 %.
(c) Corrélogramme des résidus
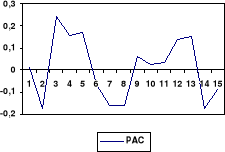
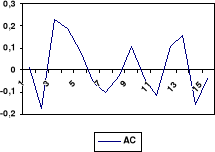
2.
Modèle ARMA(1, 1)
(a) Condition de stationnarité
Le coefficient du polynôme autorégressif du
modèle est égal à -0,4912. La condition de
stationnarité est vérifiée pour ce processus, car -1 <
-0,4912 < 1.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a comme
coefficient : 0,9751. Comme la valeur de cette racine se situe dans
l'intervalle [-1 ; 1], nous concluons que la condition
d'inversibilité est vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 5,91. Le test individuel
et collectif de bruit blanc indique que les résidus de la série
donne lieu à un bruit blanc, comme le traduit la série des
statistiques Q de BOX et PIERCE. Les coefficients des corrélations
simples et partielles calculées pour la série des résidus
de la régression de ce modèle sont inférieures aux
statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
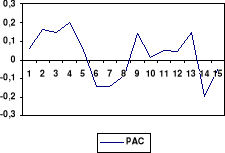

3. Modèle ARMA(2, 1)
(a) Condition de stationnarité
Le polynôme autorégressif du modèle donne
comme racines : 0,23 et -0,66. Le module de cette racine ayant une valeur de
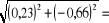 0,698
qui est inférieur à l'unité, nous concluons que la
condition de stationnarité n'est pas vérifiée pour ce
processus. 0,698
qui est inférieur à l'unité, nous concluons que la
condition de stationnarité n'est pas vérifiée pour ce
processus.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a comme
coefficient : 0,95. Comme la valeur de cette racine se situe dans l'intervalle
[-1 ; 1], nous concluons que la condition d'inversibilité est
vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 9,96. Le test individuel
et collectif de bruit blanc indique que les résidus de la série
donne lieu à un bruit blanc, comme le traduit la série des
statistiques Q de BOX et PIERCE. Les coefficients des corrélations
simples et partielles calculées pour la série des résidus
de la régression de ce modèle sont inférieures aux
statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
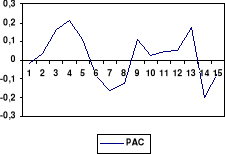
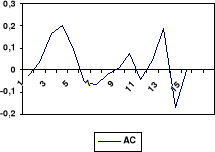
Ce modèle doit être rejeté par qu'il n'est
pas stationnaire.
4. Modèle ARMA(1, 2)
(a) Condition de stationnarité
Le coefficient du polynôme autorégressif du
modèle est égal à 0,8689. La condition de
stationnarité est vérifiée pour ce processus parce que -1
< -0,4912 < 1.
(b) Condition d'inversibilité
Le polynôme moyenne mobile du modèle a pour
coefficient : -0,2879 et
-0,3889. Comme les valeurs de ces coefficients se situent dans
l'intervalle [-1 ; 1], nous concluons que la condition
d'inversibilité est vérifiée pour ce processus.
(c) Analyse des résidus
La moyenne des résidus est de 15,07. Le test
individuel et collectif de bruit blanc indique que les résidus de la
série donne lieu à un bruit blanc, comme le traduit la
série des statistiques Q de BOX et PIERCE. Les coefficients des
corrélations simples et partielles calculées pour la série
des résidus de la régression de ce modèle sont
inférieures aux statistiques Q théoriques au seuil = 5 %.
(d) Corrélogramme des résidus
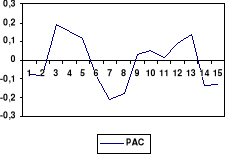
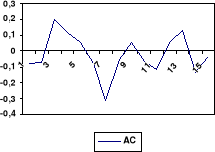
Après adéquation des modèles ci-dessus,
nous retenons le modèle ARMA(1, 1), pour les raisons suivantes :
- il présente le plus faible écart-type des
résidus ;
- il donne la plus faible valeur du critère de
SCHWARTZ (SBIC)
III.6 Prévision
III.6.1 Calcul des prévisions
Nous avons choisi, dans le cas de notre étude, de
réaliser une prévision sur une période égale T+12.
Le modèle retenu est donné par l'expression
suivante :
Yt = 31781 -
16864*I293 + 11256*I796 +
14215*I198 - 6556*I898 - 0.491*
Yt-1 + 0.975*et-1
(0,00) (0,00) (0,00)
(0,00) (0,02 ) (0,00) (0,00)
R2 = 0,46 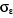 = 3578.72 = 3578.72
Etant donné que la structure des variables binaires
ainsi créées est telle que celles-ci n'ont de valeurs non nulles
qu'aux dates pour lesquelles elles ont été
générées, nous les éliminons. Par
conséquent, notre modèle se réduit à :
Yt = 31781.21 - 0.491*
Yt-1 + 0.975* et-1
a. Fonctions de prévisions
Pour les prévisions d'horizon T+1 à T+ 12, nous
aurons les fonctions reprises dans le tableau suivant :
|
C
|
Yt
|
et
|
|
Ypt+1
|
31781
|
-0,491
|
0,975
|
|
Ypt+2
|
16177
|
0,241
|
-0,479
|
|
Ypt+3
|
23838
|
-0,118
|
0,235
|
|
Ypt+4
|
20077
|
0,058
|
-0,115
|
|
Ypt+5
|
21924
|
-0,029
|
0,057
|
|
Ypt+6
|
21017
|
0,014
|
-0,028
|
|
Ypt+7
|
21462
|
-0,007
|
0,014
|
|
Ypt+8
|
21243
|
0,003
|
-0,007
|
|
Ypt+9
|
21351
|
-0,002
|
0,003
|
|
Ypt+10
|
21298
|
0,001
|
-0,002
|
|
Ypt+11
|
21324
|
0,000
|
0,001
|
|
Ypt+12
|
21311
|
0,000
|
0,000
|
b. Erreurs de prévision
Elles sont obtenues par la différence entre les
observations à la période t+n et les prévisions à
cette même période ; soit : et+n =
Yt+n -
YPt+n.
Les fonctions des observations sont présentées
dans le tableau suivant :
|
C
|
Yt
|
et
|
et+1
|
et+2
|
et+3
|
et+4
|
et+5
|
et+6
|
et+7
|
et+8
|
et+9
|
et+10
|
et+11
|
et+12
|
|
Yt+1
|
31781
|
-0,491
|
0,975
|
1,000
|
|
|
|
|
|
|
|
|
|
|
|
|
Yt+2
|
16177
|
0,241
|
-0,479
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
|
|
Yt+3
|
23838
|
-0,118
|
0,235
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
|
Yt+4
|
20077
|
0,058
|
-0,115
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
Yt+5
|
21924
|
-0,029
|
0,057
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
Yt+6
|
21017
|
0,014
|
-0,028
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
Yt+7
|
21462
|
-0,007
|
0,014
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
Yt+8
|
21243
|
0,003
|
-0,007
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
Yt+9
|
21351
|
-0,002
|
0,003
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
Yt+10
|
21298
|
0,001
|
-0,002
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
Yt+11
|
21324
|
0,000
|
0,001
|
-0,001
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
Yt+12
|
21311
|
0,000
|
0,000
|
0,000
|
-0,001
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
Les différents résultats des calculs des erreurs
par la formule et+n = Yt+n -
YPt+n sont
donnés dans le tableau suivant :
|
et+1
|
et+2
|
et+3
|
et+4
|
et+5
|
et+6
|
et+7
|
et+8
|
et+9
|
et+10
|
et+11
|
et+12
|
|
t+1
|
1,000
|
|
|
|
|
|
|
|
|
|
|
|
|
t+2
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
|
|
t+3
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
|
t+4
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
|
t+5
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
|
t+6
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
|
t+7
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
|
t+8
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
|
t+9
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
|
t+10
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
|
t+11
|
-0,001
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
|
|
t+12
|
0,000
|
-0,001
|
0,002
|
-0,003
|
0,007
|
-0,014
|
0,028
|
-0,057
|
0,117
|
-0,238
|
0,484
|
1,000
|
c. Espérance mathématique
E(t+1) = E(t+2) = ... =
E(t+12) = 0
d. Variances (Ecarts-types)
Etant donné 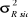 =
12.807.165, les variances et écarts-types aux différents temps
sont donnés dans le tableau suivant : =
12.807.165, les variances et écarts-types aux différents temps
sont donnés dans le tableau suivant :
|
|
Variance
|
Ecart-type
|
|
T+1
|
1,000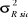
|
12.807.165
|
3.578,71
|
|
T+2
|
1,484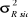
|
19.005.833
|
4.359,57
|
|
T+3
|
1,246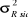
|
15.962.287
|
3.995,28
|
|
T+4
|
1,363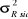
|
17.456.668
|
4.178,12
|
|
T+5
|
1,306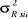
|
16.722.927
|
4.089,37
|
|
T+6
|
1,334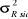
|
17.083.194
|
4.133,18
|
|
T+7
|
1,320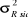
|
16.906.303
|
4.111,73
|
|
T+8
|
1,327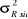
|
16.993.157
|
4.122,28
|
|
T+9
|
1,324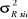
|
16.950.512
|
4.117,10
|
|
T+10
|
1,325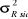
|
16.971.450
|
4.119,64
|
|
T+11
|
1,324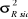
|
16.961.169
|
4.118,39
|
|
T+12
|
1,325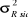
|
16.966.217
|
4.119,01
|
e. Calcul des prévisions
· Valeurs exactes
Ces valeurs sont données dans le tableau suivant :
|
Périodes
|
Yt
|
et-1
|
|
T
|
Avril-1999
|
27.500
|
-4.595
|
|
T+1
|
Mai-1999
|
13.776
|
-
|
|
T+2
|
Juin-1999
|
25.017
|
-
|
|
T+3
|
Juillet-1999
|
19.498
|
-
|
|
T+4
|
Août-1999
|
22.208
|
-
|
|
T+5
|
Sept-1999
|
20.877
|
-
|
|
T+6
|
Oct-1999
|
21.531
|
-
|
|
T+7
|
Nov-1999
|
21.210
|
-
|
|
T+8
|
Déc-1999
|
21.367
|
-
|
|
T+9
|
Janv-2000
|
21.290
|
-
|
|
T+10
|
Féf-2000
|
21.328
|
-
|
|
T+11
|
Mars-2000
|
21.309
|
-
|
|
T+12
|
Avril-2000
|
21.318
|
-
|
· Intervalle de prévision
Lorsque les résidus sont normalement distribués,
l'erreur de prévision suit une loi normale d'espérance nulle.
L'expression 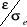 suit alors une loi de Student suit alors une loi de Student 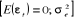 à
(T-p-q) degrés de liberté. Soit pour notre modèle (T-2)
degré de liberté. à
(T-p-q) degrés de liberté. Soit pour notre modèle (T-2)
degré de liberté. 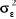 sera
estimé à partir des résidus d'estimation par : sera
estimé à partir des résidus d'estimation par : 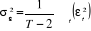 . .
Au niveau 95 %, l'intervalle de confiance s'obtient par :
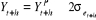 auquel
appartiendrait la vraie valeur de Yt+h avec une probabilité
approximative de 0,95. auquel
appartiendrait la vraie valeur de Yt+h avec une probabilité
approximative de 0,95.
Etant donné les écarts-types, les intervalles de
confiances pour les prévisions sont donnés par le tableau
suivant :
|
Mois
|
Limite inf.
|
Limite Sup.
|
|
T+1
|
Mai-1999
|
6.618
|
20.933
|
|
T+2
|
Juin-1999
|
16.298
|
33.737
|
|
T+3
|
Juillet-1999
|
11.507
|
27.488
|
|
T+4
|
Août-1999
|
13.852
|
30.564
|
|
T+5
|
Sept-1999
|
12.698
|
29.056
|
|
T+6
|
Oct-1999
|
13.264
|
29.797
|
|
T+7
|
Nov-1999
|
12.986
|
29.433
|
|
T+8
|
Déc-1999
|
13.123
|
29.612
|
|
T+9
|
Janv-2000
|
13.056
|
29.524
|
|
T+10
|
Féf-2000
|
13.089
|
29.567
|
|
T+11
|
Mars-2000
|
13.072
|
29.546
|
|
T+12
|
Avril-2000
|
13.080
|
29.556
|
III.6.2 Evaluation des prévisions
Dans cette partie nous procédons à
l'évaluation de la bonté de nos prévisions. Cette mesure
porte sur la comparaison des prévisions réalisées à
partir d'une partie de la série observée avec les valeurs
réelles de la série en réserve.25(*)
Pour effectuer cette mesure, nous utilisons les observations
allant d'avril 1998 à avril 1999 pour lesquelles nous allons calculer
certaines statistiques (le Mean Absolute Error, le Mean Absolute Percentage
Error et le Theil Inequality Coefficient) qui nous permettrons de
décider.
· l'Erreur absolue moyenne ("Mean Absolute
Error") :
MAE(e) = 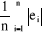 = 3805,75
M = 3805,75
M
· l'Erreur absolue moyenne en pourcentage
("Mean Absolute Percent") :
MAPE(e) =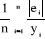 = 12,02
% = 12,02
%
· Critère de U de Theil :
U = 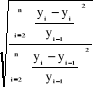 = 0.067
0 < U=0,067 < 1 = 0.067
0 < U=0,067 < 1
Au vu des résultats fournis par les statistiques
ci-haut, nous affirmons que nos prévisions sont assez bonnes. En effet,
le MAE représente 12 % ; ce qui est passable, car la limite (marge
de tolérance) étant généralement établie
à 15 %. Par ailleurs, le coefficient de Theil qui est proche de
zéro confirme également la bonté de nos
prévisions.
Actual: SER1 Forecast: SER1F
Sample: 1998:04 1999:04
Include observations: 13
Root Mean Squared Error 4270.008
Mean Absolute Error 3805.750
Mean Absolute Percentage Error 12.02121
Theil Inequality Coefficient 0.067427
Bias Proportion 0.011420
Variance Proportion 0.478842
Covariance Proportion 0.509738
III.7
Interprétation des résultats
Le modèle ARMA(1,1) que nous avons construit nous
renseigne que :
- il existe une consommation mensuelle de 31.781 M qui ne
dépend ni du niveau des consommations antérieures (t-1), ni des
aléas antérieurs (t-1).
- 49,12 % des consommations mensuelles antérieures
(t-1) influent négativement sur les 31.781 M structurels. De la sorte,
nous pouvons affirmer que 49,12 % consommations mensuelles actuelles
constituent des achats anticipatifs du mois suivants.
- Les consommations mensuelles actuelles (t) sont
également influencées, mais cette fois ci positivement, par les
aléas du mois précédent (t-1), à la hauteur de 97,5
% de ceux-ci.
Les prévisions (Ypt) ainsi
réalisées sont représentées par la figure
ci-dessous.
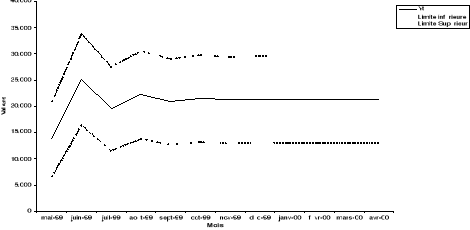
L'observation de ce graphe montre que la série des
prévisions convergence vers une certaine valeur. En fait cela peut
s'expliquer par le fait :
- Que le processus qui génère cette
série est stationnaire ;
- Que les racines du polynôme autorégressif sont
des valeurs réelles.
IV. CONCLUSION
Au cours de ce travail nous avons eu à illustrer
l'emploi du modèle d'analyse d'interventions, un des modèles de
la méthode de BOX & JENKINS, pour la prévision du volume des
carburants terrestres consommés en République Démocratique
du Congo, et ce, en utilisant une série allant de janvier 1992 à
avril 1999.
Cela nous a conduit aux résultats suivant lesquels la
série du volume des carburants terrestres consommés en
République Démocratique du Congo est généré
par un modèle ARMA(1,1), expliquant le fait que les valeurs de ce volume
observées au temps t dépendent des valeurs et des chocs
aléatoires de la période t-1.
C'est donc non seulement dans la mémoire de notre
série chronologique sous étude, mais également dans les
variables binaires par lesquelles nous avons saisi l'information qualitative
que nous avons dégagé le modèle qui représente le
mieux le processus stochastique par lequel notre série est
générée.
Certes, ce modèle est complexe à mettre au
point ; mais une fois élaboré, la détermination des
prévisions devient automatique et les intervalles de prévision
aisément obtenus.
Aussi, nous recommandons son utilisation dans toutes les
prévisions portant sur des variables d'intérêt
stratégique.
BIBLIOGRAPHIE
1. G.E.P. BOX et G.M. JENKINS, Time series analysis,
forecasting and control, San Francisco, Holden day, 1970.
2. Gérard CORNU, Vocabulaire juridique, P.U.F.,
Paris, 1987.
3. Guy MELARD, Méthodes de prévision
à court terme, Ed. de l'Université de Bruxelles, Bruxelles,
1999.
4. BOSONGA BOFEKI, Cours de Statistique Approfondie,
Première Licence Economie Mathématique, Université de
Kinshasa, Année académique 1997-98
5. Christian GOURIEROUX et Alain MONFORT, Séries
temporelles et modèles dynamiques, 2è Ed, Ed. Economica,
Paris, 1995.
6. MURRAY R. SPIEGEL, Théorie et applications de la
Statistique, Série Schaum, Ed. McGraw-Hill, Paris, 1987.
7. KAMIANTAKO A., Cours de Théorie et Pratique des
prévisions, Première Licence Economie Mathématique,
Université de Kinshasa, année académique 1997-98.
8. BOURBONNAIS Régis, Econométrie :
Cours et exercices corrigés, Ed. Dunod, Paris, 1993
9. SEP CONGO : Département Finances, Tableaux
des quantités livrées à la clientèle en
mètres-cube à température ambiante, Janvier 1992 -
Décembre 1998.
10. NSA BAKINDO, Analyse prévisionnelle des ventes des
produits pétroliers par la méthode de BOX & JENKINS,
Mémoires de fin d'études, UNIKIN, 1996-1997, p. 45
TABLE DES MATIERES
SOMMAIRE
......................................................................................................1
EPIGRAPHE
.....................................................................................................2
DEDICACE........................................................................................................3
AVANT- PROPOS
..............................................................................................4
I. INTRODUCTION
0
I.1 PROBLEMATIQUE
0
I.2 INTERET DU SUJET
0
I.3 METHODE D'APPROCHE
0
I.4 CANEVAS DU TRAVAIL
0
II. GENERALITES
0
II.1 LE MECANISME DE FIXATION DES PRIX DES CARBURANTS
TERRESTRES
0
II.1.1 INTRODUCTION
0
II.1.2 STRUCTURE DE PRIX DES CARBURANTS TERRESTRES
0
II.1.2.1 DÉFINITION
0
II.1.2.2 ELÉMENTS COMPOSANTS
0
II.2 LES SERIES CHRONOLOGIQUES ET PROCESSUS STOCHASTIQUES
0
II.2.1 SERIES CHRONOLOGIQUES
0
II.2.1.1 DÉFINITION
0
II.2.1.2 COMPOSANTES D'UNE SÉRIE TEMPORELLE
0
II.2.2 PROCESSUS STOCHASTIQUE
0
II.2.2.1 DÉFINITION
0
II.2.2.2 CONCEPTS
0
II.2.2.2.1 Notion de stationnarité
0
II.2.2.2.2 Notion d'inversibilité
0
II.2.2.2.3 Processus Bruit Blanc (White Noice Process ou
Purely random process)
0
II.2.2.3 OUTILS D'ANALYSE
0
II.2.2.3.1 Fonction d'autocovariance
0
II.2.2.3.2 Fonction d'autocorrélation
0
II.2.2.3.3 Fonction d'autocorrélation partielle
0
II.2.3 MODELE LINEAIRE GENERAL
0
II.2.3.1 MODÈLES POUR SERIES STATIONNAIRES
0
II.2.3.1.1 Définition
0
II.2.3.1.2 Propriétés
0
II.2.3.1.3 Caractéristiques
0
II.2.3.2 MODÈLE POUR SERIES NON STATIONNAIRES
0
II.2.4 MODELE D'ANALYSE D'INTERVENTIONS
0
II.2.4.1 INTRODUCTION
0
II.2.4.2 ANALYSE DES INTERVENTIONS
0
II.2.4.3 FORMES D'INTERVENTIONS
0
II.2.4.4 PROCÉDURE D'APPLICATION DU MODÈLE
D'ANALYSE D'INTERVENTIONS
0
II.3 LES PREVISIONS
0
II.3.1 INTRODUCTION
0
II.3.2 TYPES DE METHODES DE PREVISION
0
II.3.3 VALIDITE DES METHODES DE PREVISION
0
II.3.3.1 CRITÈRES USUELS
0
II.3.3.2 CRITÈRES ADDITIONNELS
0
II.3.4 CHOIX D'UNE METHODE DE PREVISION
0
II.4 LA METHODE DE PREVISION DE BOX ET JENKINS
0
II.4.1 INTRODUCTION
0
II.4.2 ETAPES DE LA METHODE DE BOX & JENKINS
0
II.4.2.1 LA FAMILIARISATION AVEC LES DONNEES
0
II.4.2.2 L'ANALYSE PRELIMINAIRE
0
II.4.2.3 LA SPECIFICATION DU MODELE (OU IDENTIFICATION)
0
II.4.2.4 L'ESTIMATION DES PARAMETRES
0
II.4.2.5 L'ADEQUATION DU MODELE (OU VALIDATION)
0
II.4.2.6 LA PREVISION
0
II.4.2.7 L'INTERPRETATION DES RESULTATS
0
III. APPLICATION DU MODELE D'ANALYSE D'INTERVENTIONS A
LA PREVISION DU VOLUME DES CARBURANTS TERRESTRES
0
III.1 FAMILIARISATION AVEC LES DONNÉES
0
III.2 ANALYSE PRÉLIMINAIRE
0
III.3 SPÉCIFICATION DU MODÈLE
0
III.4 ANALYSE DES INTERVENTIONS
0
III.4.1 Détermination des points aberrants
0
III.4.2 Intervention et Identification du modèle
0
III.5 ADÉQUATION DU MODÈLE
0
III.6 PRÉVISION
0
III.6.1 Calcul des prévisions
0
III.6.2 Evaluation des prévisions
0
III.7 INTERPRÉTATION DES RÉSULTATS
0
IV. CONCLUSION
0
BIBLIOGRAPHIE
.............................................................................................48
TABLE DES MATIERES
....................................................................................49
* 1 Gérard CORNU,
Vocabulaire juridique, P.U.F., Paris, 1987, p. 286
* 2 Gérard CORNU,
op. cit., p. 9
* 3 MURRAY R. SPIEGEL,
Théorie et applications de la Statistique, Série Schaum,
Ed. McGraw-Hill, Paris, 1987, p. 283.
* 4 BOSONGA BOFEKI, Cours
de Statistique Approfondie, Première Licence Economie
Mathématique, Université de
Kinshasa, Année académique 1997-98.
* 5 NSA BAKINDO, Analyse
prévisionnelle des ventes des produits pétroliers par la
méthode de BOX & JENKINS,
Mémoires de fin
d'études, UNIKIN, 1996-1997, p. 12.
* 6 Guy MELARD, op.
cit., p. 373
* 7 Christian GOURIEROUX et
Alain MONFORT, Séries temporelles et modèles dynamiques,
2è Ed, Ed. Economica,
Paris, 1995, p. 159.
* 8 Idem, p. 1.
* 9 KAMIANTAKO A., Cours
de Théorie et Pratique des prévisions, L1 Economie
Mathématique, Université de Kinshasa, Année
académique 1997-98, p. 1.
* 10 Idem, p. 1.
* 11 Guy MELARD, op.
cit., p. 25.
* 12 Guy MELARD, op.
cit., p. 26.
* 13 KAMIANTAKO A., op.
cit., p. 8.
* 14 BOURBONNAIS
Régis, Econométrie : Cours et exercices
corrigés, Ed. Dunod, Paris, 1993, p. 249.
* 15 Idem, p. 348.
* 16 Guy MELARD, op.
cit., p. 348.
* 17 Guy MELARD, op.
cit., p. 353.
* 18 Guy MELARD, op.
cit., p. 362.
* 19 Guy MELARD, op.
cit., p. 373.
* 20 BOURBONAIS, op.
cit., p. 256.
* 21 Guy MELARD, op.
cit., p. 327.
* 22 SEP CONGO :
Département Finances, Tableaux des quantités livrées
à la clientèle en mètres cubes à température
ambiante, Janvier 1992 - avril 1999.
* 23 Guy MELARD, op.
cit., p. 15.
* 24 Christian GOURIEROUX et
Alain MONFORT, op. cit., p. 211.
* 25 NSA BAKINDO, op.
cit., p. 45.
| 


