|
\adeff0
DEDICACE
A nos regrettés parents,
A nos frères et soeurs,
A nos amis,
A tous ceux qui nous sont chers,
A la famille BASHONGA Evariste
REMERCIEMENTS
La réalisation de ce travail n'aurait jamais pris fin
sans le concours précieux de plusieurs personnes à qui nous
devons des remerciements sincères et cordiaux. Qu'il soit
remercié Dieu le père tout puissant car c'est celui qui guide la
sagesse et dirige les sages.
Nous remercions particulièrement Dr Jean de Dieu
BAZIRUWIHA qui a accepté sans ambages d'assurer la direction de notre
travail. Nos remerciements distingués s'adressent à tous les
autorités et les professeurs de K.I.E, plus particulièrement
ceux des départements de Mathématiques-physique, de
Biologie-chimie et de l'Education physique, qui nous ont donné la
formation intellectuelle et morale.
Nous remercions tous les collègues d'études,
plus particulièrement Emmanuel KAMANA, Albert KWIZERA, Jean de Dieu
HAKIZAYEZU, Didace NSHIMIYIMANA, Fidèle RUGIRAMANZI et Zéphanie
NIYONKURU pour leurs collaboration et encouragement durant nos études
universitaires.
Nous remercions également les membres de notre
famille, surtout à Patricie MUKAGASANA pour son aide, assistance,
affection et prières ; à Martin NIYIBIGENA, HAVUGIMANA et
Théoneste MUHINYUZI pour leur aide ; vous autres de près ou
de loin qui avez contribué matériellement et moralement à
la réalisation du présent travail, nous vous remercions. Que Dieu
vous bénisse.
TABLE DE MATIERE
DEDICACE
i
REMERCIEMENTS
ii
TABLE DE MATIERE
iii
INTRODUCTION GENERALE
1
CHAPITRE I : LA POSITION DU PROBLEME
ET LA REVUE DE LA LITTERATURE
2
I.1.Introduction
2
I.2. Valeurs moyennes et fluctuations
3
I.2.1 Valeur moyenne
3
I.2.2. Fluctuation
5
I.3. Gaz parfait
6
I.4. Distribution grand canonique de Gibbs
7
CHAPITRE II: CALCUL DE LA FLUCTUATION DU
NOMBRE DE REMPLISSAGE DES NIVEAUX ENERGETIQUES POUR UN GAZ PARFAIT QUANTIQUE EN
UTILISANT LA DISTRIBUTION GRAND CANONIQUE DE GIBBS
8
II.1. Calcul de la valeur moyenne du nombre de
remplissage des niveaux énergétiques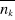 , pour un gaz parfait quantique
8 , pour un gaz parfait quantique
8
II.2.Calcul de la fluctuation du nombre moyen
de remplissage des niveaux énergétiques pour un gaz parfait
quantique en utilisant la distribution grand canonique de Gibbs
13
CONCLUSION
19
BIBLIOGRAPHIE
20
INTRODUCTION GENERALE
Un gaz parfait quantique est un système quantique avec
un grand nombre de degrés de liberté et son étude oblige
à recourir à la physique statistique quantique, qui se construit
sur les principes fondamentaux de la mécanique quantique.
Notre travail a comme objectif la détermination de
l'écart quadratique moyen (fluctuation) du nombre de remplissage des
niveaux énergétiques pour un gaz parfait quantique.
Ce travail est subdivisé en deux chapitres :
Le premier chapitre porte sur la position du problème
et la revue de la littérature. Dans ce chapitre nous présentons
l'approche de la physique statistique en utilisant le modèle quantique
lors de la description d'un système possédant un grand nombre de
degrés de libertés de liberté. Dans cette approche nous
insistons sur le calcul de la valeur moyenne et de la fluctuation. Nous parlons
aussi de la distribution grand canonique de Gibbs.
Le second chapitre concerne le calcul de la fluctuation du
nombre de remplissage des niveaux énergétiques pour un gaz
parfait quantique en utilisant la distribution grand canonique de Gibbs.
CHAPITRE I : LA POSITION DU PROBLEME ET LA REVUE DE LA
LITTERATURE
I.1.Introduction
Dans la pratique, nous avons affaire aux systèmes
macroscopiques, c'est-à-dire constitués par un grand nombre de
particules (atomes, molécules, etc.). D'où l'importance de
l'application des méthodes statistiques pour l'étude de tels
systèmes.
Par ailleurs, c'est la mécanique quantique qui
décrit correctement le comportement des microparticules constituant un
macrosystème. Le modèle du gaz parfait joue un rôle
important en théorie statistique et sert de départ pour
l'étude des systèmes plus compliqués. La distribution
grand canonique de Gibbs, quoique conceptuellement plus élaborée,
simplifie les calculs physiques sur les systèmes quantiques.
Nous savons que n'importe quel système possède
des grandeurs le caractérisant, qui varient en oscillant autour de leurs
valeurs moyennes. La fluctuation nous permet de connaître les
écarts à la moyenne.
Lors de l'étude du comportement et des
propriétés des corps macroscopiques formant des systèmes
simples, on utilise les modèles de la mécanique classique ou de
la mécanique quantique. D'après les études faites, il
s'avère que la description complète du comportement et les
propriétés des systèmes constitués par un grand
nombre de particules (c'est-à-dire ayant un grand nombre de
degrés de liberté) en utilisant ces modèles est
pratiquement impossible. Il est donc nécessaire de recourir à une
théorie permettant d'étudier le comportement d'un système
avec un grand nombre de degrés de liberté.
Pour appliquer les méthodes de la mécanique,
bien que nous puissions utiliser la mécanique classique, il est
indispensable d'écrire et de résoudre un nombre égal
à N équations différentielles ordinaires du
deuxième ordre, ce qui est pratiquement impossible lorsque N est
très grand.
Remarquons que même si l'on pouvait écrire la
solution générale de ces équations différentielles,
il serait absolument impossible d'y introduire les conditions initiales pour
les vitesses et les coordonnées de particules, ne serait-ce qu'à
cause du temps et de la quantité de papiers nécessaires.
La question ne se pose pas uniquement au niveau pratique, mais
aussi du côté technique, nous ne pouvons pas trouver un programme
dans l'ordinateur qui peut résoudre ce problème, du moins
à l'heure actuelle[5] et [6].
La physique statistique ou mécanique statistique est
une branche de la physique théorique qui étudie les lois
particulières régissant le comportement et les
propriétés des corps macroscopiques, c'est-à-dire des
corps composés d'une énorme quantité de particules
(atomes, molécules, etc.) en utilisant le modèle
microscopique.
Donc, lorsque le nombre de particules augmente les
propriétés du système mécanique deviennent
essentiellement compliquées et il y a l'apparition des lois statistiques
dont leur caractère diffère essentiellement de celui de lois
mécaniques. L'importance de la physique statistique au sein de la
physique théorique provient du fait que, le plus souvent, dans la
nature, nous avons affaire à des corps macroscopiques qui peuvent
être eux- mêmes composites en molécules, atomes,
électrons, quarks, etc. dont le comportement ne peut être
complètement décrit par des méthodes purement
mécaniques. On dit que ces corps obéissent aux lois statistiques.
La description selon les lois statistiques utilise deux
modèles :
Le modèle classique qui est un
système de N points matériels en mouvement selon les lois de la
mécanique classique. La physique statistique classique est construite
sur les principes fondamentaux de la théorie classique des états
d'équilibre.
Le modèle quantique qui est un
système de N points matériels en mouvement selon les lois de la
mécanique quantique. Donc, la physique statistique quantique se
construit sur les principes fondamentaux de la mécanique quantique
[6].
La physique statistique quantique doit être
étudiée en considérant la physique classique comme un cas
limite qui ne serait approximativement exacte que dans les conditions
déterminées. La physique statistique ne fournit des
résultats corrects que dans le cas d'un choix heureux du modèle
du système, ce choix ne pouvant souvent être justifié
qu'après recours aux conceptions quantiques [7].
I.2. Valeurs moyennes et fluctuations
I.2.1 Valeur moyenne
Un grand système peut être subdivisé en
sous-systèmes qui forment de nouveaux systèmes mécaniques
mais qui ne sont pas isolés, le grand système
considéré est isolé. La physique statistique se rapporte
à un système se trouvant en équilibre.
D'habitude est isolé cette condition d'équilibre
est vérifiée ; au contraire, les sous-systèmes sont
soumis à des actions diverses de la part des autres parties des
systèmes. A cause du grand nombre de degrés de liberté de
ces autres parties, les interactions ont un caractère compliqués
et enchevêtrés.
Ceci rend impossible les méthodes de la
mécanique. Par conséquent, la méthode statistique repose
essentiellement sur une certaine distribution statistique permettant de
calculer la valeur d'une grandeur quelconque.
En statistique classique, la valeur moyenne d'une grandeur
quelconque f(p,q) est donnée par la
formule :
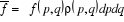 (1.1)
(1.1)
Où 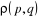 est la fonction de distribution statistique qui est égale
à la probabilité pour les coordonnées
qi et les impulsions
pi de prendre les valeurs se
trouvant dans les intervalles infiniment petits qi,
pi et qi+dqi,
pi+dpi est la fonction de distribution statistique qui est égale
à la probabilité pour les coordonnées
qi et les impulsions
pi de prendre les valeurs se
trouvant dans les intervalles infiniment petits qi,
pi et qi+dqi,
pi+dpi
(avec i =1,2,...,N)
q = (q1,q2,...,qN)
est l'ensemble des coordonnées généralisées,
p = (p1,p2,...,pN)
est l'ensemble des impulsions généralisées
dq = dq1dq2...dqN ;
dp = dp1dp2...dpN,
N est le nombre de degrés de liberté
La moyenne trouvée 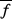 à l'aide de la fonction de distribution est appelée
statistique. La statistique permet de faire les
prédictions se réalisant avec une grande précision pour la
majeure partie d'un intervalle de temps suffisamment long pour que l'influence
des conditions initiales disparaisse. En ce sens, les prédictions de la
statistique ont un caractère non pas aléatoire mais pratiquement
déterminé. On dit qu'un système se trouve en
équilibre statistique, de même qu'en équilibre
thermodynamique ou thermique, si les grandeurs physiques macroscopiques
caractérisant chacune de ses parties sont égales, avec une
précision relativement grande à leurs moyennes. à l'aide de la fonction de distribution est appelée
statistique. La statistique permet de faire les
prédictions se réalisant avec une grande précision pour la
majeure partie d'un intervalle de temps suffisamment long pour que l'influence
des conditions initiales disparaisse. En ce sens, les prédictions de la
statistique ont un caractère non pas aléatoire mais pratiquement
déterminé. On dit qu'un système se trouve en
équilibre statistique, de même qu'en équilibre
thermodynamique ou thermique, si les grandeurs physiques macroscopiques
caractérisant chacune de ses parties sont égales, avec une
précision relativement grande à leurs moyennes.
En mécanique quantique, la valeur moyenne de toute
grandeur caractérisant le système, ainsi que les
probabilités des différentes valeurs de ces grandeurs sont
déterminées à l'aide de la matrice densité.
Ainsi, la valeur moyenne de toute grandeur f à
l'état donné est :
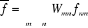 ` (1.2) ` (1.2)
Où 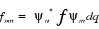 sont les éléments matriciels de la grandeur f sont les éléments matriciels de la grandeur f
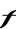 est l'opérateur correspondant et est l'opérateur correspondant et 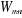 dépendant généralement du temps, est l'ensemble des
grandeurs qui représentent la matrice densité. [5] dépendant généralement du temps, est l'ensemble des
grandeurs qui représentent la matrice densité. [5]
Les distributions statistiques des sous-systèmes
doivent, par définition de l'équilibre statistique, être
stationnaires. Par conséquent, les matrices statistiques 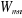 de tous sous-systèmes sont diagonales ; la
grandeur de tous sous-systèmes sont diagonales ; la
grandeur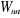 , notée aussi par , notée aussi par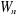 , est la distribution de probabilité. , est la distribution de probabilité.
Par suite, la formule déterminant la valeur moyenne
d'une grandeur f se trouve ainsi simplifiée.
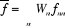 (1.3) (1.3)
Avec 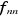 les éléments matriciels diagonaux. les éléments matriciels diagonaux.
I.2.2. Fluctuation
On appelle fluctuation d'une grandeur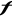 , caractérisant le système, l'écart de la valeur
réelle , caractérisant le système, l'écart de la valeur
réelle 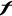 de sa valeur moyenne de sa valeur moyenne 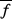 conditionné par l'agitation thermique chaotique des particules du
système. Le carré moyen de la différence conditionné par l'agitation thermique chaotique des particules du
système. Le carré moyen de la différence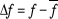 , appelé fluctuation quadratique,
représente la mesure de la fluctuation : , appelé fluctuation quadratique,
représente la mesure de la fluctuation :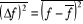 [3]. [3].
On peut calculer la fluctuation d'une grandeur qui varie en
oscillant autour de sa valeur moyenne dans le temps comme suit :
Considérons une grandeur quelconque 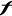 se rapportant à un certain corps macroscopique ou à une
de ses parties. se rapportant à un certain corps macroscopique ou à une
de ses parties.
Dans le temps, cette grandeur varie en oscillant autour de
sa valeur moyenne : la valeur moyenne de la différence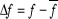 , où , où 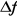 est la largeur de l'intervalle de cette variation. est la largeur de l'intervalle de cette variation.
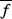 la valeur moyenne, ne peut être prise pour une telle
caractéristique, car la grandeur la valeur moyenne, ne peut être prise pour une telle
caractéristique, car la grandeur 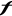 s'écarte de sa valeur moyenne, tant d'un côté que
l'autre, c'est-à-dire tantôt en haut, tantôt en bas de cette
valeur moyenne, et la valeur moyenne da la différence s'écarte de sa valeur moyenne, tant d'un côté que
l'autre, c'est-à-dire tantôt en haut, tantôt en bas de cette
valeur moyenne, et la valeur moyenne da la différence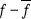 qui est tantôt positive, tantôt négative se trouve
être nulle, quel que soit le nombre des écarts notables de qui est tantôt positive, tantôt négative se trouve
être nulle, quel que soit le nombre des écarts notables de 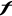 à sa valeur moyenne. à sa valeur moyenne.
Il est commode de prendre pour la caractéristique
cherchée la valeur moyenne du carré de cette différence.
La grandeur 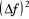 étant toujours positive, sa valeur moyenne ne tend pas vers
zéro, en d'autres termes elle se trouve être petite seulement si
des écarts notables de étant toujours positive, sa valeur moyenne ne tend pas vers
zéro, en d'autres termes elle se trouve être petite seulement si
des écarts notables de 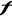 à à 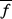 sont peu probables. sont peu probables.
La grandeur 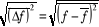 (1.4) (1.4)
est appelée écart quadratique moyen
de la grandeur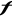 ou fluctuation de ou fluctuation de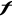 [6]. [6].
Remarquons que :
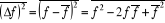
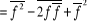
Mais 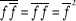 (1.5) (1.5)
C'est-à-dire que la fluctuation est
déterminée par la différence entre le carré moyen
de la grandeur et le carré de sa valeur moyenne.
Le rapport 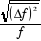 est appelé fluctuation relative de la grandeur
f. est appelé fluctuation relative de la grandeur
f.
I.3. Gaz parfait
Un gaz parfait est un gaz dont la pression est si basse que
ses atomes ou ses molécules se déplacent indépendamment
l'un de l'autre. En d'autres termes, un gaz parfait peut être
considéré comme un ensemble des boules (molécules) en
mouvement chaotique. Les molécules doivent avoir un volume propre
négligeable et n'interagissent pas l'une de l'autre à distance.
Ces molécules entrent continuellement en collision avec d'autres
molécules du gaz parfait et avec des parois du récipient en
exerçant sur elles une certaine pression [3] et [8].
Pour un gaz parfait classique, les particules identiques le
constituant peuvent être distinguées (sont discernables) tandis
que pour un gaz parfait quantique, les particules identiques le constituant ne
peuvent pas être distinguées (sont indiscernables).
I.4. Distribution grand canonique de Gibbs
Dans la pratique, nous avons affaire aux systèmes
macroscopiques, c'est-à-dire constitués par un grand nombre de
particules (atomes, molécules, etc.). D'où l'importance de
l'application des méthodes statistiques pour l'étude de tels
systèmes. Nous pouvons définir la distribution grand canonique
pour un système macroscopique.
La distribution grand canonique quoi que conceptuellement plus
élaborée, simplifie les calculs physiques sur les systèmes
quantiques. [4] et [5]
La distribution grand canonique de Gibbs
s'écrit :
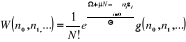 (1.6) (1.6)
Où 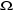 est le potentiel généralisé ou le grand
potentiel, est le potentiel généralisé ou le grand
potentiel,
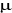 est le potentiel chimique, est le potentiel chimique,
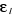 est le niveau énergétique, est le niveau énergétique,
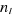 est le nombre de particules occupant le niveau énergétique est le nombre de particules occupant le niveau énergétique
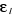 , ,
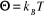 avec avec 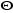 est le module de la distribution canonique, est le module de la distribution canonique,
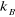 est la constante de Boltzmann, est la constante de Boltzmann,
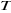 est la température du système, est la température du système,
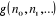 est une grandeur exprimant le degré de
dégénérescence des niveaux énergétiques est une grandeur exprimant le degré de
dégénérescence des niveaux énergétiques
Sachant que 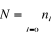 et en notant et en notant
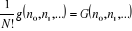 (1.7) (1.7)
L'équation (1.6) prend de la forme :
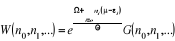 (1.8) (1.8)
CHAPITRE II: CALCUL DE LA
FLUCTUATION DU NOMBRE DE REMPLISSAGE DES NIVEAUX ENERGETIQUES POUR UN GAZ
PARFAIT QUANTIQUE EN UTILISANT LA DISTRIBUTION GRAND CANONIQUE DE GIBBS
II.1. Calcul de la valeur moyenne du nombre de remplissage des
niveaux énergétiques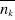 , pour un gaz parfait quantique , pour un gaz parfait quantique
A l'aide de l'expression (1.8), on peut
calculer les valeurs de n'importe quelle fonction des nombres de remplissages
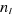 si on connaît si on connaît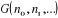 . On peut par exemple calculer : . On peut par exemple calculer :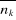 , , 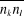 , , 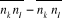 , , 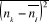 . .
Pour la raison de commodité, nous allons utiliser
l'astuce mathématique suivant : nous allons considérer comme
si le gaz parfait ne possède pas un seul potentiel chimique u mais tout
un ensemble de potentiels chimiques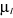 . A la fin des calculs, nous allons supposer que tous les
potentiels chimiques ul sont les mêmes et sont égaux
à u. Donc nous pouvons écrire à partir de l'expression
(1.8) . A la fin des calculs, nous allons supposer que tous les
potentiels chimiques ul sont les mêmes et sont égaux
à u. Donc nous pouvons écrire à partir de l'expression
(1.8)
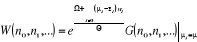 (2.1) (2.1)
La condition de normalisation conduit
à :
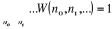 (2.2) (2.2)
C'est-à-dire :
 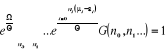 (2.3) (2.3)
En posant
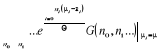 (2.4) (2.4)
L'équation (2.3) prend de la forme :
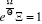 ou ou 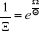 (2.5) (2.5)
et nous obtenons :
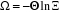 (2.6) (2.6)
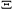 est la fonction de partition grand canonique ou somme des états
quantique ou somme statistique pour un système à nombre variable
de particules. est la fonction de partition grand canonique ou somme des états
quantique ou somme statistique pour un système à nombre variable
de particules.
En mettant l'équation (2.4) dans l'équation
(2.6) puis en dérivant l'équation (2.6) par rapport à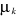 , nous arrivons à la valeur du nombre de remplissage , nous arrivons à la valeur du nombre de remplissage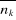 . .
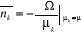 (2.7) (2.7)
L'équation (2.7) représente la valeur moyenne du
nombre de remplissage des niveaux énergétiques. Le calcul concret
de 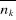 en utilisant la formule (2.7) nécessite une connaissance
précise de la grandeur en utilisant la formule (2.7) nécessite une connaissance
précise de la grandeur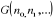 . .
Un gaz parfait quantique de particules identiques peut
être constitué, soit par les particules avec spin demi-entier
appelées fermions, soit par les particules de spin
entier appelées bosons.
Pour les fermions est valable le principe d'exclusion de
Pauli : deux ou plusieurs particules identiques ne peuvent pas se trouver
exactement dans un même état quantique. Ce fait peut être
considéré de la façon suivante. Il faut poser
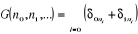 (2.8) (2.8)
Dans ce cas :
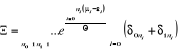  (2.9) (2.9)
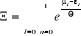
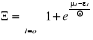 (2.10) (2.10)
D'où 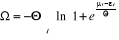 (2.11) (2.11)
Le nombre moyen de remplissage des niveaux
énergétiques est obtenu en remplaçant l'expression (2.11)
dans l'équation (2.7), ce qui donne :
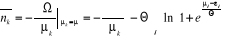
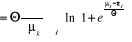 (2.12) (2.12)
Comme la dérivé de la somme est égale
à la somme des dérivés, l'expression (2.12) peut
s'écrire :
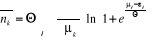
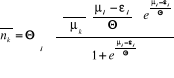
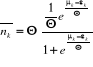
En posant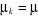 , on obtient : , on obtient :
 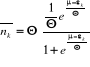 (2.13) (2.13)
En multipliant le dénominateur et le numérateur
de l'expression (2.13) par 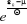 , on obtient : , on obtient :
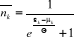 (2.14) (2.14)
Avec 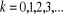
L'expression (2.14) c'est le nombre moyen de remplissage des
niveaux énergétiques pour un gaz parfait constitué par les
particules avec un spin demi-entier.
Dans le cas des bosons, il faut poser
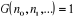 (2.15) (2.15)
ce qui va nous conduire à la statistique de Bose
Einstein, dans ce cas :
 (2.16) (2.16)
Avec 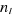 quelconque : quelconque : 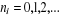 et et 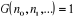
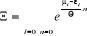
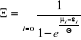 (2.17) (2.17)
Ce qui conduit à :
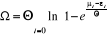 (2.18) (2.18)
En remplaçant l'expression (2.18) dans l'expression
(2.7), nous obtenons :
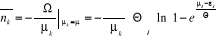
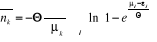 (2.19) (2.19)
Comme la dérivé de la somme est égale
à la somme des dérivés, l'expression (2.19) peut
s'écrire comme suit :
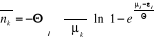
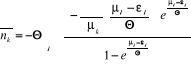
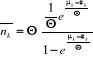
En posant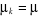 , on obtient : , on obtient :
 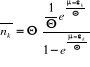 (2.20) (2.20)
En multipliant le dénominateur et le numérateur
de l'expression (2.20) par 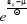 , on obtient : , on obtient :
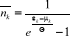 (2.21) (2.21)
Avec 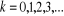
L'expression (2.21) n'est rien d'autre que le nombre moyen de
remplissage des niveaux énergétiques pour un gaz parfait
quantique constitué par les particules de spin entier.
A la limite, lorsque 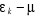 >>È, de (2.14) et (2.21) on trouve : >>È, de (2.14) et (2.21) on trouve :
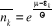 (2.22) (2.22)
Les formules (2.14), (2.21) et (2.22) peuvent s'écrire
sous la forme unique suivante :
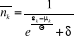 (2.23) (2.23)
où 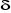 est une constante, qui est égale soit : est une constante, qui est égale soit :
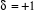 pour un gaz parfait de Fermi, pour un gaz parfait de Fermi,
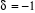 pour un gaz parfait de Bose, pour un gaz parfait de Bose,
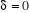 pour un gaz parfait de Boltzmann [1], [2] et [5]. pour un gaz parfait de Boltzmann [1], [2] et [5].
II.2.Calcul de la fluctuation du nombre moyen de remplissage
des niveaux énergétiques pour un gaz parfait quantique en
utilisant la distribution grand canonique de Gibbs
La formule (1.8) de la distribution grand canonique
quantique, lorsque la grandeur 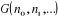 est concrètement connue, permet de calculer les fonctions des
nombres de remplissage est concrètement connue, permet de calculer les fonctions des
nombres de remplissage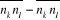 , en utilisant l'astuce mathématique, comme nous l'avons fait au
sous-chapitre II.1, lors du calcul de , en utilisant l'astuce mathématique, comme nous l'avons fait au
sous-chapitre II.1, lors du calcul de 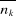 (voir 2.7) (voir 2.7)
Trouvons 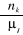 : :
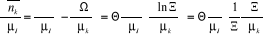
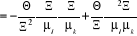
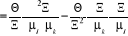 (2.24) (2.24)
Mais 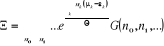 (2.25) (2.25)
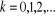
En tenant compte de (2.24) et (2.25), nous
écrivons :
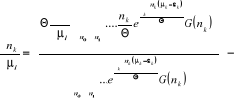
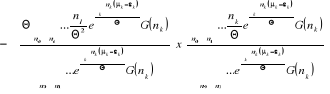
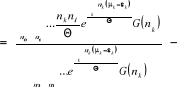
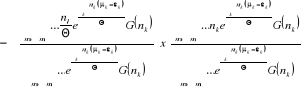 (2.26) (2.26)
De (2.25), on sait que le dénominateur dans
l'équation (2.26) est égale à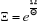 , ce qui donne : , ce qui donne :
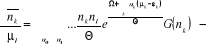
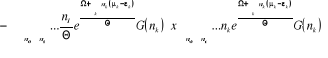
(2.27)
En posant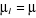 , on obtient : , on obtient :
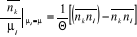 (2.28) (2.28)
C'est-à-dire :
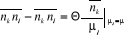 (2.29) (2.29)
Dans le cas particulier où les niveaux
énergétiques k et l sont égaux, de la formule (2.29), on
obtient :
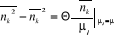 (2.30) (2.30)
Avec 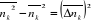 qui présente la dispersion du nombre de remplissage des niveaux
énergétiques. qui présente la dispersion du nombre de remplissage des niveaux
énergétiques.
La valeur moyenne du nombre de remplissage des niveaux
énergétiques pour un gaz parfait quantique est donnée
par :
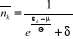 (2.31) (2.31)
En utilisant l'expression (2.31) dans l'expression (2.30), on
obtient :
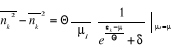
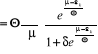
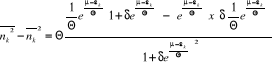
 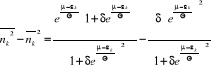
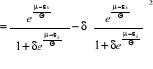
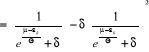
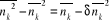 (2.32) (2.32)
L'expression (2.32), est la formule de la dispersion du
nombre de remplissage des niveaux énergétiques pour un gaz
parfait quantique en général.
La fluctuation du nombre de remplissage des niveaux
d'énergie s'obtient à partir de la dispersion par la
relation :
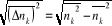 (2.33) (2.33)
En utilisant l'expression (2.32) dans l'expression (2.33), on
obtient :
 
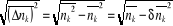 (2.34) (2.34)
L'expression (2.34), est la fluctuation du nombre de
remplissage des niveaux énergétiques pour un gaz parfait
quantique.
Pour un gaz parfait de Bose, on obtient :
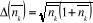
Pour un gaz parfait de Fermi, on obtient :
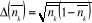
Pour un gaz régi par la statistique de Boltzmann, on
obtient : 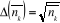 .Ainsi, on voit que l'expression pour l'écart quadratique moyen
du nombre de remplissage des niveaux énergétiques dans le cas
d'un gaz parfait est la même que l'expression obtenue dans le cas
classique. .Ainsi, on voit que l'expression pour l'écart quadratique moyen
du nombre de remplissage des niveaux énergétiques dans le cas
d'un gaz parfait est la même que l'expression obtenue dans le cas
classique.
Cette expression classique est obtenue comme suit :
Dans le cas classique, il n'y a pas de niveaux
énergétiques. La valeur moyenne de particules se trouvant dans
l'intervalle d'énergie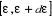 est obtenue à partir de la distribution classique de
Maxwell-Boltzmann. Cette valeur est sous la forme : est obtenue à partir de la distribution classique de
Maxwell-Boltzmann. Cette valeur est sous la forme :
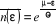
La dispersion du nombre de particules se trouvant dans
l'intervalle d'énergie 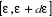 est calculée comme suit : est calculée comme suit :
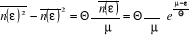
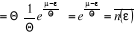
La fluctuation du nombre de particules se trouvant dans
l'intervalle de l'énergie 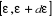 est calculée comme suit : est calculée comme suit :
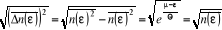
CONCLUSION
En appliquant la distribution grand canonique de Gibbs, nous
avons trouvé la formule de la fluctuation du nombre de remplissage des
niveaux énergétiques pour un gaz parfait quantique
suivante :
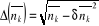 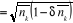
Où 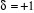 pour un gaz de fermions, pour un gaz de fermions,
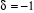 pour un gaz de bosons pour un gaz de bosons
A la limite lorsque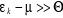 , , 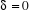 et on obtient l'expression analogue à l'expression classique. et on obtient l'expression analogue à l'expression classique.
BIBLIOGRAPHIE
[1] Arthur Beiser. Concepts of modern physics, fifth
edition. Mc Graw-Hill. USA, 1995
[2] B.M Yavorsky and A.A Pinsky. Fundamentals of
physics volume I. Mir Publishers.
Moscow, 1987.
[3] B. Yavorski, A. Detlaf. Aide mémoire de
physique, 3e édition. Editions MIR, Moscou,
1975.
[4]
http://fr.wikipekia:ébouche
physique.physique statistique. 25/03/2007.
[5] L. Landau et E. Lifshitz. Physique
théorique vol 5 : Physique statistique tome 1.
Editions MIR, Moscou, 1973.
[6] L. Landau et E. Lifchitz. Physique
statistique. Editions MIR, Moscou, 1967
[7] M. Leontovitch. Introduction à la
thermodynamique, physique statistique. Editions
MIR, Moscou, 1986.
[8] S. P. KASHINJE, Jean de Dieu BAZIRUWIHA. Module 6
de physique:
Thermodynamique. K.I.E, Kigali, 2003.
| 


