Chapitre 4
Géométrie presque riemannienne
[MS.2,8,15]
Soient M une variété lisse de
dimension deux et X, Y deux champs de vecteurs lisses sur
M. Si {X, Y } est Lie bracket generating,
alors le système de contrôle
qÿ =
uX(q) + vY
(q), u2 +
v2 = 1, q ? M ,
(4.1)
est commandable et la fonction valeur pour le temps minimum
définit une distance continue sur M. Dans le cas
où X et Y sont partout
linéairement indépendants (ce qui peut arriver seulement si
M est parallélisable), la distance ainsi obtenue est
riemannienne et correspond à la métrique pour laquelle
(X, Y ) est un repère mobile orthonormal.
Dans cette section, nous nous intéressons à la
géométrie obtenue dans le cas où les deux champs de
vecteurs peuvent être colinéaires à certains points.
Une structure métrique sur une surface M
est dite presque riemannienne si elle peut être
définie localement par un couple de champs de vecteurs (X, Y
) grâce à (4.1). De façon plus intrinsèque,
une structure presque riemannienne S est un couple (E,
f), où E est un fibré euclidien de rang
deux sur M et f : E ? TM est
un morphisme de fibrés vectoriels tel que
f(Eq) ? TqM
et l'évaluation en q de l'algèbre de
Lie engendrée par
L = {f ? ó | ó section de
E}
est égale à TqM pour
tout q ? M. (La notion de structure presque riemannienne
s'étend naturellement au cas d'une variété
différentielle de dimension supérieure à deux).
Si E est orientable, nous disons que S
est orientable. Si E est équivalent
au fibré euclidien trivial M × R2, nous
disons que la structure presque riemannienne est trivialisable.
Notons par Z, dit ensemble
singulier, l'ensemble des points q de M
tels que f(Eq) est de
dimension un. Sous des hypothèses de généricité sur
f, l'ensemble Z est une
sous-variété de dimension un de M. Une structure
presque riemannienne est riemannienne si et seulement si Z =
Ø, c'est-à-dire, f est un
isomorphisme de fibrés vectoriels. Un couple de champs de vecteurs
(X, Y ) de L est dit une base orthonormale de
S sur un ouvert 11 de M si X
= f ? ó et Y =
f?ñ avec (ó, ñ) une base
orthonormale pour E sur 11. Les bases orthonormales de
S forment un système de générateurs
locaux de L. Remarquons que S est trivialisable si et
seulement s'il existe une base orthonormale globale de S.
Un exemple célèbre de structure presque
riemannienne est le plan de Grushin, obtenu globalement sur M
= R2 avec X(x,y) =
(1,0) et Y (x,y) =
(0,x). (Cf. [25, 37, 57, 62].) D'autres structures presque
riemanniennes ont été obtenues dans des problèmes de
contrôle quantique avec M =
S2 ([35, 36]) et pour d'autres surfaces de
révolution ([33]).
Une structure presque riemannienne sur une surface
s'écrit localement à l'aide d'une des formes normales
suivantes.
Théorème 4.1
Génériquement par rapport à f,
pour tout point q ? M, il existe une base
orthonormale (X, Y ) pour S
sur un voisinage de q et un système de
coordonnées locales tels que (q, X, Y ) admet
l'une des représentations suivantes :
(F1) q = (0,0),
X(x, y) = (1,0), Y
(x, y) = (0,
eö(x,y)),
(F2) q = (0,0),
X(x, y) = (1, 0), Y
(x, y) = (0,
xeö(x,y)),
(F3) q = (0,0),
X(x, y) = (1,0), Y
(x, y) = (0, (y -
x2ø(x))eî(x,y)),
avec ö, ø et
î lisses et
ö(0,y) = 0,
ø(0) =6 0.
Nous disons dans la suite qu'une structure presque
riemannienne S vérifie l'hypothèse
(H0) si elle peut se mettre localement en chaque point sous
l'une des formes normales présentées dans le
théorème 4.1. On dit que une structure presque
riemannienne S vérifiant l'hypothèse
(H0) n'a pas de points de tangence si elle peut
s'écrire localement sous la forme (F1) ou (F2) seulement. Un point
de tangence est, par définition, un point pour lequel
S est décrite localement par (F3).
Soit M compacte, orientée et munie
d'une structure presque riemannienne orientable. Soit K
: M \ Z ? R la courbure gaussienne définie par la
structure presque riemannienne et dAs le
pushforward par f d'une forme de volume sur
E.
Notons Må = {q ? M |
d(q, Z) > å}. Soit
M+ (respectivement, M--) le
sous-ensemble de M \Z sur lequel l'orientation définie
par dAs coïncide avec (respectivement, est
opposée à) celle de M.
Nous pouvons démontrer le résultat suivant, qui
généralise la formule de Gauss-Bonnet. (D'autres
généralisations dans des domaines proches ont été
obtenues pour des structures sousriemanniennes [4], finsleriennes [17] et pour
des pseudo-métriques singulières [92].)
Théorème 4.2
Soit M compacte et orientée. Pour une
structure presque riemannienne orientée, sans points de tangence et
vérifiant l'hypothèse (H0), la limite
limå\0 f Må
K(q)dAs existe et est
égale à
2ð(÷(M+)
- ÷(M--)), oft
÷ est la caractéristique d'Euler.
Étant donné un fibré vectoriel
orienté E de rang deux sur une variété
différentielle compacte orientée M de dimension
deux, le numéro d'Euler de E, noté
par e(E), est défini par
e(E) = E
i(p, ó),
p | ó(p)=0
oil ó : M ? E est une
section transverse à la section nulle et i(p,
ó) = 1 (respectivement, -1) si
dpó : TpM ?
Tó(p)E préserve
(respectivement, reverse) l'orientation.
Remarquons que, en changeant l'orientation sur
M ou sur E, le signe de
e(E) change. Par conséquent,
e(E) est défini au signe près. Par
contre, le numéro d'Euler de TM est défini sans
ambiguïté et est égal à
÷(M). Remarquons aussi que si (E,
f) est trivialisable, alors
e(E) = 0.
Nous avons la caractérisation topologique suivante.
Théorème 4.3
Soit M compacte et orientée dotée d'une
structure presque riemannienne orientée et vérifiant
l'hypothèse (H0). Alors
÷(M+) -
÷(M--) + ô
= e(E), oft
ô est le nombre de révolutions de A
sur Z calculé par rapport à
l'orientation induite par M+
sur Z.
Comme conséquence directe des théorèmes
4.2 et 4.3, nous avons que, pour une structure presque
riemannienne
trivialisable, sans points de tangence, et vérifiant l'hypothèse
(H0), définie sur une
surface M
compacte et orientable, la limite limå\0 f
Må
K(q)dAs existe et est
égale à zéro. Nous
pouvons donner l'interprétation suivante de cette
propriété : pour une structure riemannienne, la topologie de la
surface donne une contrainte sur la courbure totale (formule de Gauss-Bonnet) ;
dans le cas d'une structure presque riemannienne trivialisable, par contre, la
courbure totale est égale à zéro et la topologie de la
surface force la métrique à devenir singulière sur un
ensemble de topologie appropriée.
Il est intéressant de remarquer que toute surface
orientable compacte peut être équipée d'une structure
presque riemannienne trivialisable, sans points de tangence et vérifiant
l'hypothèse (H0) (voir figures 4.1 et 4.2).
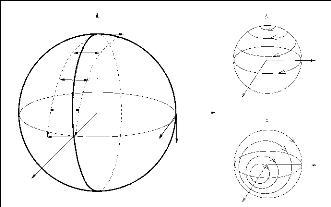
X
X
X
X
Y
Y
Y
Y
X
Y
courbes intégrales de X
courbes intégrales de Y
FIGURE 4.1 --- Exemple de structure presque riemannienne
trivialisable sans points de tangence sur une sphère.
Pour étendre le théorème 4.2 au cas des
variétés à bord, nous introduisons une notion de domaine
admissible de M.
Définition 4.4 Soit
U un domaine borné d'une surface
M munie d'une structure presque riemannienne orientable et
vérifiant l'hypothèse (H0). Nous disons
que U est admissible si
U ne contient pas de points de tangence et si le
bord de U est l'union des supports d'un
ensemble fini de courbes ã1, .
. . ,ãm telles que chaque
ãl : [0, Tl]
M satisfait les conditions suivantes :
ãl est C2
sur [0, Tl] ;
ãl est localement solution de (4.1) (en
particulier a longueur finie) ;
ãl a la même orientation que celle induite
sur par U.
Théorème 4.5
Soit U un domaine admissible d'une
surface M munie d'une structure
presque
riemannienne orientable et vérifiant l'hypothèse
(H0). Soient
ã1, . . . ,
ãm comme dans la défini-
tion
4.4. Pour tout å > 0, soit
M#177;å = M#177; fl
Må et
U#177;å =
M#177;å fl U. Soient
tj1, . . . ,
tjlj les temps
pour lesquels ãj
traverse i. Associons à chaque
tjl la quantité
Ó+(tjl ) de la
façon suivante : si,
pour å > 0
suffisamment petit, le support de ãj|(tj l
,tj l +å) est contenu
dans M+, alors
Ó+(tjl ) =
1,
sinon
Ó+(tjl) =
--1. De façon similaire, si pour å
> 0 suffisamment petit le support de
ãj|(tjl
-å,tjl )
est contenu dans M+
alors posons
Ó-(tjl ) =
1, sinon
Ó-(tjl )
= --1. Notons par
kjg(t) la courbure
géodésique de ãj en
ãj(t). Définissons
Î
Õ(Î) =2V 1
--
Î2 + arccos(Î) 41
|
|
X=
Y=
|
A
|
|
|
|
|
|
|
X
de Y
|
|
|
|
|
|
|
|
|
|
zéros de
zéros
|
|
|
|
|
B lieu singulier
|
FIGURE 4.2 --- Exemple de structure presque riemannienne
trivialisable sans points de tangence sur la somme connexe de plusieurs
tores.
et
|
Î#177;(tjl
) = lim
t?tj l #177;
|
kj g(t)|t -
tj l |,á(tjl ) =
Ó-(tjl
)Õ(Î-(tjl
)) + Ó+(tjl
)Õ(Î+(tjl
)).
|
Alors
m
lim KdAs+ k
do-
g kgdo-) =
271-(x(U+)
-- x(U))--
á(tjl),
å?0
(fk?U,
frn?Uk frn?U
j=1 l=1
oft nous interprétons chaque
intégrale fn?U#177;
å kgdó comme la somme des
intégrales le long des portions lisses de n
?U#177;å plus la somme des angles aux
points oft n'est pas C1.
Si, de plus, est
C2 dans un voisinage de Z,
alors
ZU
oft
KdAs + f kgdós
=
2ð(÷(U+)
- ÷(U)),
aU
ZU
KdAs = lim
KdAs,
å?0
fukå?U-å
|
kgdós =
faU å?0 (f
rn?Uk å
|
k dó -
k dó) .
frn?U
|
Le théorème 4.5 peut être utilisé
pour démontrer une version du théorème 4.2 dans laquelle
les points de tangence sont admis. L'idée est que, contrairement
à ce qui arrive aux points de type (F2), près des points de
tangence, le bord de Må converge vers
Z, pour å ? 0, avec un taux de convergence
différent de å (par rapport à un
système de coordonnées quelconque). Nous devons
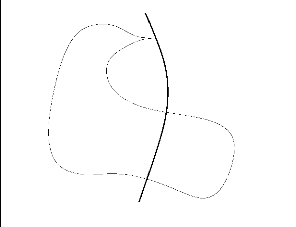
U
Z
FIGURE 4.3 - Un domaine admissible U.
alors isoler les points de tangence grâce au calcul de
l'intégrale de K sur une région qui
dépend de plusieurs paramètres qui convergent vers zéro
sur différentes échelles de temps. Plus
précisément, soit T l'ensemble des point de
tangence de la structure presque riemannienne. Associons à tout
q ? T un voisinage « rectangulaire » Bq
ä1,ä2 dépendant de deux
paramètres ä1 et ä2, qui
jouent le rôle des longueurs des cotés du rectangle, avec la
construction suivante : considérons une courbe lisse
(-1, 1) ? s 7?
w(s) qui passe par le point de tangence
w(0) = q et qui est transverse à z en
q ; pour tout s ?
(-1, 1), soit
ãs la géodésique
paramétrée par son abscisse curviligne telle que
ãs(0) =
w(s) et qui minimise localement la distance
à {w(s) | s ?
(-1, 1)}
(ãs est bien définie en
raison de la transversalité de w); pour
ä1 et ä2 suffisamment petits, le
rectangle Bq ä1,ä2 est le
sous-ensemble de M qui contient le point q et
dont le bord est
ãä2([-ä1,
ä1]) ?
ã[-ä2,ä2](ä1)
? ã-ä2([-ä1,
ä1]) ?
ã[-ä2,ä2](-ä1)
(voir figure 4.4).
Soit Må ä1,ä2 =
Må \ Uq?T Bq
ä1,ä2. Nous pouvons démontrer le
résultat suivant, qui généralise le théorème
4.2 et, par conséquent, la formule de Gauss-Bonnet.
Théorème 4.6 Soit
M compacte et orientée. Pour une structure
presque riemannienne orientée qui vérifie l'hypothèse
(H0), la limite
f
uim uim uim
K(q)dAs (4.2)
ä1?0
ä2?0 å?0
Må
ä1,ä2
existe et est égale à
2ð(÷(M+)
- ÷(M-) + ô) =
2ðe(E). En particulier, la limite
vaut zéro si et seulement si la structure est trivialisable.
Remarquons que la construction de Må
ä1,ä2 dépend du choix des courbes
w transverses à z aux points de T et
de leur paramétrage. Le théorème 4.6 affirme que la valeur
de la limite (4.2) est, néanmoins, intrinsèque.
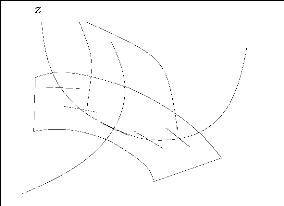
ãä2(-ä1)
ã-ä2(-ä1)
A
w(-ä2)
q
w(ä2)
ã-ä2(ä1)
M+
ãä2(ä1)
M-
FIGURE 4.4 -- La construction de
Bq
ä1,ä2.
Nous terminons ce chapitre avec l'analyse de ce qui arrive si
l'on essaye de calculer (4.2) en remplaçant
Måä1,ä2 par
Må, en analogie avec l'enonce du theorème
4.2.
D'abord, grâce à la formule de Gauss-Bonnet
riemannienne et en supposant que å est
petit,
K(q)dA5
=
2ð(÷(ME+)
- ÷(ME)) - f
kgds + f kgds
Lå aW f å
=
2ð(÷(M+)
- ÷(M-)) - f kgds
+ f kgds
aMå + aM;
où nos avons utilise la notation
M#177;å = M#177; n
Må. Il n'est pas difficile de verifier, en utilisant
la forme normale (F2), que les contributions des courbures geodesiques
de ?M+å
et ?M-å s'annulent reciproquement loin des
points de tangence quand å tend vers zero. Nous allons
donc argumenter que la presence de points de tangence peut conduire à la
divergence de limå?0 fMå
K(q)dAs, en calculant
numeriquement la courbure geodesique de
?M+å et
?M-å dans un voisinage d'un tel point. Nous prenons
donc la forme normale (F3) avec ø = 1 et
î = 0, pour laquelle K est donne
explicitement par la formule
K=
-2
(3x2 + y)
(x2 - y)2
.
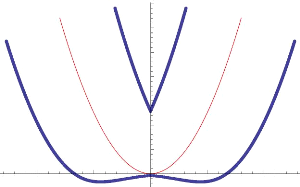
Le graphe de K est represente en figure 4.5.
Remarquons que lim
supq?(0,0)
K(q) = +8 et lim
infq?(0,0)
K(q) = -8. La situation est
differente de celle que l'on retrouve autour des points ayant pour forme
normale (F2), pour lesquels K(q) diverge
à -8 quand q approche
Z.
Le comportement de ?Må est
illustre en figure 4.6.
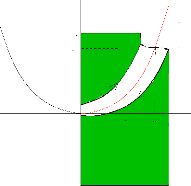
Fixons 0 < a < 1 et considerons la
geodesique passant par (a, a2) qui minimise
(localement) la distance à Z. Notons par
P+ et P- les deux points le long de cette
geodesique à distance å de
Z et par ã+ et
ã- les portions de
?M+å et
?M-å joignant l'axe vertical avec les deux points
P+ et P- (voir figure 4.7). La
figure 4.8 montre la valeur de
å (f Kgds - f
Kgds)
7+ f
pour a = 0.1 et
å variant dans l'intervalle
[0.01, 0.04] (calcule
à l'aide du logiciel Mathematica).
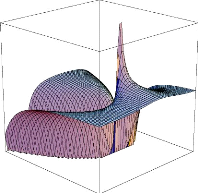
FIGURE 4.5 - Graphe de K pour Ä =
span((1, 0), (0, y -
x2))
-1.0 -0.5
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.5 1.0
FIGURE 4.6 - Bord de Må avec
å = 1 2.
La fonction paraît converger vers une valeur finie non
nulle quand å tend à zéro, permettant
ainsi de conjecturer que fMå
K(q)dAs diverge.



Ì
Ì+
å
å
P
Ù+
+
ã
ã
a
Ù
-a
a
2
a
-2.07
-2.08
FIGURE 4.7 - Construction de
ã+ et ã-


-2.04




-2.05

-2.06


0.010 0.015 0.020 0.025 0.030 0.035 0.040
(f )
ã+ Kgds -
f
FIGURE 4.8 Graphe de å
ã- Kgdspour a
= 0.1
Perspectives de recherche
De nombreux sujets de recherche sont laissés ouverts
par les activités présentées dans les quatre chapitres
précédents. Certains de ces sujets sont déjà en
cours avancé de développement, d'autres font l'objet
d'activités de recherche programmées dans un futur proche,
d'autres encore à plus long terme.
Concernant les activités présentées dans
le premier chapitre, dédié à la commande des
systèmes non linéaires de dimension finie, le
développement du sujet de la section 1.2 (suivi de trajectoire pour un
sous-marin) a donné lieu à l'encadrement du post-doc de
María Barbero Liñán sur une généralisation
de l'approche backstepping à une classe beaucoup plus vaste de
systèmes mécaniques. Il s'agissait en particulier de faire le
lien entre nos résultats de suivi de trajectoire et ceux
présentés dans [40] dans le cadre abstrait des systèmes de
contrôle dits à connexion affine. Dans un travail en
cours de rédaction, nous avons pu étendre les résultats de
[40] en généralisant au cadre de la connexion affine l'approche
utilisé dans [MS.7] pour étudier le suivi de trajectoire d'un
sous-marin. Nous avons aussi rendu la construction plus algorithmique, en
étudiant comment les pas successifs de la procédure par
backstepping doivent être hiérarchisés. Plus
précisément, nous avons analysé les rapports quantitatifs
entre les paramètres correspondant aux différents pas,
aboutissant ainsi à des familles de lois de commande, dépendant
d'un seul paramètre, qui réalisent le suivi de trajectoire
désiré.
Des perspectives de développement de ce sujet qui
m'intéressent beaucoup sont celles liées à l'analyse de
complexité des commandes obtenues par les algorithmes de suivi de
trajectoire. Il s'agit en général de lois de commande qui
oscillent fortement. Pour pouvoir obtenir des bonnes performances sur des
modèles réels, il faut minimiser la fréquence des
oscillations des lois de commande en préservant la même
tolérance par rapport à la trajectoire cible.
Dans la même thématique des systèmes non
linéaires de dimension finie, je suis en train de collaborer avec
François Alouges et Karine Beauchard sur un problème d'inversion
de la magnétisation de micro-aimants ellipsoïdaux ayant des
applications dans le développement de systèmes de stockage de
type MRAM. La magnétisation m à
l'intérieur du corps ferromagnétique Ù c
R est un champs de vecteurs de norme constante, régi par
l'équation de Landau-Lifschitz
?m ?t =
á(H(m) --
(H(m),m)m) -- m A
H(m), x E
Ù,
oil H(m) indique le champs
magnétique total. Nous nous intéressons à la planification
des trajectoires pour des réductions de dimension finie de ce
modèle.
Le thème qui sera probablement au centre de mes
activités de recherche dans les prochaines années est celui issu
des travaux sur le contrôle quantique présentés dans le
chapitre 2. Il s'agit d'abord d'améliorer les résultats
déjà obtenus en relaxant les hypothèses suffisantes de
contrôlabilité approchée de l'équation de
Schrödinger bilinéaire présentées en section 2.1. Si
notre intuition concernant les hypothèses minimales qui garantissent la
contrôlabilité approchée est correcte, il sera alors
possible d'utiliser la construction à la base de notre preuve
d'existence pour déterminer des algorithmes explicites de planification
de trajectoires. En collaboration avec des physiciens expérimentaux de
Dijon (en particulier Dominique Sugny) nous voulons alors tester
nos algorithmes sur des problèmes d'orientation et
alignement de molécules. Ces problèmes méritent
d'être aussi étudiés ultérieurement du point de vue
théorique, en étendant les résultats que nous avons
obtenus pour les rotations sur un cercle d'une molécule linéaire
rigide. Dans ce contexte, le prochain cas à considérer est, sans
doute, celui des rotations sur une sphère de R3.
En collaboration avec Ugo Boscain, Thomas Chambrion et Paolo
Mason nous voudrions aussi transférer, si possible, les résultats
que nous avons obtenu pour le contrôle des matrices de densité au
cas où le spectre de l'opérateur n'est pas discret, en
étudiant, en particulier, l'évolution dans l'espace
engendré par les états propres qui correspondent à la
partie discrète du spectre. Nous pourrions alors compléter les
résultats de commandabilité approchée obtenus par
Mirraihimi dans ce contexte dans (cf. [82]).
Nous voudrions aussi nous pencher sur les modèles
quantiques non linéaires, en commençant par l'équation de
Gross-Pitaevski. Il ne nous parait pas impossible d'adapter un cas non
linéaire la partie finie dimensionnelle des arguments à la base
de nos résultats de commandabilité approchée. Une
contrainte importante pour l'application complète de notre
méthode nous semble plutôt physique, à savoir le domaine de
validité de l'équation de Gross-Pitaevski, qu'il ne faut bien
sûr pas forcer au delà de ses limites.
Un autre sujet très intéressant est celui de la
commande adiabatique des systèmes quantiques (cf. [112]). L'objectif
dans ce domaine est de développer dans un cadre mathématique
général les techniques de commande proposées par les
physiciens et étudiées du point de vue du contrôle, dans
des situations spécifiques, par Adami et Boscain dans [1]. On vise ici
des équations de Schrödinger avec au moins deux contrôles
scalaires qui varient très lentement. Un des outils importants pour
estimer l'évolution de ces systèmes est l'analyse de comment le
spectre d'un opérateur de Schrödinger perd sa simplicité et
de son développement paramétrique autour d'un point de non
simplicité. On sait donner à l'ensemble des potentiels
correspondants à des opérateurs de Schrödinger ayant spectre
non simple une structure différentielle (cf. [48, 71, 76]). Il faudra
alors utiliser des arguments de transversalité pour garantir,
génériquement, l'applicabilité des méthodes
adiabatiques. Pour cette raison, cette thématique de recherche rejoint
celle des sections 2.3 et 2.4.
En restant dans le domaine du contrôle des
systèmes quantiques, je voudrais aussi m'intéresser à la
question de la description des obstructions à la commandabilité
exacte de l'équation de Schrödinger. Les travaux de Beauchard [22]
et Beauchard et Coron [24] ont donné une description assez
précise de l'ensemble atteignable d'une équation de
Schrödinger particulière. Il est remarquable que les états
propres de l'opérateur non contrôlé sont exactement
joignables par des trajectoires admissibles pour une large classe
d'opérateurs de contrôle (cf. [23]). Cela donne l'espoir qu'il
soit possible d'isoler des propriétés générales des
ensembles atteignables des systèmes quantiques.
Concernant le chapitre 3, dédié à la
stabilité des systèmes hybrides, je voudrais d'abord poursuivre
les collaborations déjà entamées avec Pierre Riedinger,
Jamal Daafouz, Ulysse Serres et Jean-Claude Vivalda sur la commande des
convertisseurs de puissance multicellulaires. Ce sont des systèmes
électriques qui peuvent atteindre des puissances de quelques
mégawatts et emploient généralement des tensions de
plusieurs kilovolts. Ces systèmes sont particulièrement
intéressants pour des applications de forte puissance avec des hautes
tensions (cf. [79]). L'objectif est de proposer des solutions originales et
intrinsèquement hybrides dans le cadre de l'amélioration des
performances dynamiques de cette classe de systèmes ainsi que la
diminution du nombre de capteurs nécessaires.
J'envisage aussi de développer ma recherche sur les
systèmes linéaires à commutations en temps discret,
présentée en section 3.3. Dans ce contexte, en collaboration avec
Jamal Daafouz, un premier objectif est de caractériser les lois de
commutation ne permettant pas de converger vers l'origine et la structure des
ensembles limites. Cette caractérisation pourrait ensuite être
ex-
ploitée pour l'analyse d'observabilité et la
synthèse d'observateurs des systèmes à commutations en
temps discret. L'extension des résultats de stabilité au cas non
linéaire planaire est également envisagée. D'autres
extensions possibles des résultats de la section 3.3 concernent des
contraintes de type lipschitz que l'on peut ajouter à la variation des
paramètres de commutation, ou bien des dépendances plus
élaborées de la fonction de Liapounov par rapport à
l'évolution passée de ces mêmes paramètres.
Un autre thème de recherche que je souhaite
développer en collaboration avec Yacine Chitour et Paolo Mason dans le
cadre des systèmes dynamiques hybrides est celui de la
caractérisation de l'instabilité maximale d'un système
linéaire à commutations à temps continu. Cette
caractérisation passe à la fois par la description des
systèmes à commutations dont l'instabilité est polynomiale
et par la recherche des trajectoires périodiques des systèmes
marginalement stables (cf. [18, 19, 77]).
Une autre activité de recherche en cours de lancement,
en collaboration avec Martin Gugat, concerne l'analyse de stabilité de
systèmes de contrôle de dimension infinie modélisant des
réseaux de cordes (cf. [51]). L'idée est de développer une
approche similaire à celle présentée en section 3.2. Le
passage à la dimension infinie donne naissance à des nouveaux
phénomènes d'instabilité, comme il a été
remarqué dans [63].
Relativement au quatrième axe, l'étude de la
géométrie presque riemannienne présentée dans le
chapitre 4, nous sommes en train d'établir, en collaboration avec Ugo
Boscain, Grégoire Char-lot et Roberta Ghezzi, une caractérisation
complète des classes d'équivalence des structures presque
riemanniennes en dimension deux, où l'équivalence est
considérée par rapport à l'existence de transformations
bi-lipschitiennes. Cette caractérisation se fait en associant à
chaque structure presque riemannienne un graphe libellé qui contient
tous ses invariants. Nous étudions aussi la construction d'une forme
normale intrinsèque autour d'un point de tangence. En reprenant la
démonstration du théorème 4.1, on s'aperçoit que
cela revient à construire de façon intrinsèque une courbe
paramétrée, transverse à l'ensemble singulier au point de
tangence.
| 

