Contribution à l'optimisation complexe par des techniques de swarm intelligence

UNIVERSITÉ MOHAMMED V - AGDAL FACULTÉ DES SCIENCES Rabat

N° d'ordre: 2493

THÈSE DE DOCTORAT
Présentée par :
Lamia Benameur
Discipline : Sciences de l'Ingénieur
Spécialité : Informatique et Télécommunications

Titre : Contribution à l'optimisation complexe par des techniques
de swarm intelligence

Soutenue le : 13 Mai 2010 Devant le jury

Président :

D. Aboutajdine, Professeur, Faculté des Sciences de Rabat.

Examinateurs :

A.A. El Imrani, Professeur, Faculté des Sciences de Rabat

B. El Ouahidi, Professeur, Faculté des Sciences de Rabat

A. Sekkaki, Professeur, Faculté des Sciences Ain Chock de Casablanca J. Benabdelouahab, Professeur, Faculté des Sciences de Tanger

Y. El Amrani, Professeur Assistant, Faculté des Sciences de Rabat

Faculté des Sciences, 4 Avenue Ibn Battouta B.P. 1014 RP, Rabat - Maroc
Tel [phone]/38, Fax : [phone], http://www.fsr.ac.ma

Avant-Propos

Les travaux présentés dans ce mémoire ont été effectués au Laboratoire Conception et Systèmes (LCS) de la Faculté des Sciences de Rabat (Equipe de Soft Computing et aide a la décision) sous la direction du Professeur A. A. El Imrani.

J'exprime, tout d'abord, ma vive reconnaissance a Monsieur A. Ettouhami, Directeur du LCS, pour la confiance qu'il m'a accordée en m'autorisant a mener mes travaux de recherche dans ce laboratoire.

Je ne saurai témoigner toute ma gratitude a Monsieur A. A. El Imrani, Professeur a la Faculté des Sciences de Rabat, pour ses qualités humaines et scientifiques. Je suis heureuse de lui adresser mes vifs remerciements pour l'intérêt qu'il a manifesté a ce travail en acceptant la charge de suivre de près ces travaux. Je voudrais lui exprimer ma profonde reconnaissance pour l'aide qu'il m'a constamment octroyée tout au long de ce travail, qu'il trouve, en ce mémoire, le témoignage de mes sincères remerciements.

Je présente a Monsieur D. Aboutajdine, Professeur a la Faculté des sciences de Rabat, l'expression de ma profonde reconnaissance, pour l'honneur qu'il me fait en acceptant de présider ce jury de thèse.

Je tiens a remercier Monsieur B. El Ouahidi, Professeur a la Faculté des Sciences de Rabat, de l'intérêt qu'il a porté a ce travail en acceptant d'en être rapporteur et de sa participation au jury de cette thèse.

Je suis particulièrement reconnaissante a Monsieur J. Benabdelouahab, Professeur a la Faculté des Sciences et Techniques de Tanger, qui a bien voulu consacrer une part de son temps pour s'intéresser a ce travail, d'en être le rapporteur et qui me fait l'honneur de siéger dans le jury de cette thèse.

Que Monsieur A. Sekkaki, Professeur a la Faculté des Sciences Ain Chock de Casablanca, accepte mes vifs remerciements pour avoir bien voulu juger ce travail et pour sa participation au jury de cette thèse.

Mes remerciements et ma haute considération vont également a Monsieur Y. El Amrani, Professeur assistant a la Faculté des Sciences de Rabat, pour ses remarques, ses nombreux conseils et pour l'intérêt qu'il a porté a ce travail.

Je n'oublierai pas d'exprimer mon amitié et ma reconnaissance a Mademoiselle J. Alami Chentoufi, docteur chercheur et membre de l'équipe Soft computing et aide a la décision du laboratoire LCS, qui m'a initié au sujet de thèse. Elle m'a fait bénéficier de ses encouragements, de son soutien amical et moral et de son aide scientifique de tous les instants qu'elle n'a cessés de me témoigner.

Je tiens à remercier tous les membres du Laboratoire Conception et Systèmes, Professeurs et Doctorants, pour leur esprit de groupe. Qu'ils trouvent ici le témoignage de toute mon estime et ma sincère sympathie.

Je tiens finalement à souligner que la partie de ce travail, portant sur le problème d'affectation de fréquences mobiles, entre dans le cadre du projet "Résolution du problème d'affectation de fréquences par des méthodes de Soft Computing" soutenu par la Direction de la technologie du Ministère de l'Enseignement Supérieur.

"Durant les trois dernières années de mes études doctorales, j'ai bénéficié d'une bourse d'excellence octroyée par le Centre National de Recherche Scientifique et Technique (CNRST) et ce dans le cadre du programme des bourses de recherche initié par le ministère de l'Education Nationale de l'Enseignement Supérieur, de la Formation des Cadres et de la Recherche Scientifique".

Table des matières

Introduction générale 1

I Application de l'algorithme d'optimisation par essaims particulaires à des problèmes réels 5

1 Techniques de calcul "intelligent" 7

1.1 Introduction 8

1.2 Techniques de Calcul "Intelligent" 10

1.2.1 Les réseaux de neurones (Neural Networks) 10

1.2.2 La logique floue (Fuzzy Logic) 12

1.2.3 Les techniques de calcul évolutif (Evolutionary Computation) 13 1.3 Conclusion 24

2 Application de l'algorithme d'optimisation par essaims particulaires aux problèmes MSAP et PAF 25

2.1 Introduction 26
2.2 Commande en vitesse des machines synchrones à aimant permanent

(MSAP) 27

2.2.1 Modélisation d'une machine synchrone à aimant permanent 27

2.2.2 Conception d'un contrôleur PI basé sur les essaims particulaires 29
2.2.3 Résultats de simulation 31

2.3 Problème d'affectation de fréquences (PAF) 38

2.3.1 Problématique 38

2.3.2 Formulation du FS-FAP 39

2.3.3 Implémentation de l'algorithme d'optimisation par essaims

particulaires à la résolution de FS-FAP 40

2.3.4 Etude expérimentale 42

2.3.5 Comparaison avec d'autres techniques 47

2.4 Conclusion 49

II Conception de nouveaux modèles pour l'optimisation multimodale et l'optimisation multiobjectif 50

3 Conception d'un nouveau modèle d'optimisation multimodale (Multipopulation Particle Swarms Optimization MPSO) 52

3.1 Introduction 53

3.2 Problématique de l'optimisation multimodale 54

3.3 Techniques de l'optimisation multimodale 55

3.3.1 Les méthodes de niche 55

3.3.2 Les systèmes basés sur l'intelligence des essaims particulaires

(PSO) 61

3.3.3 Les systèmes immunitaires artificiels 62

3.4 Synthèse 63

3.5 Conception d'un nouveau modèle d'optimisation multimodale (MPSO) 64

3.5.1 Le principe du modèle 64

3.5.2 La couche de classification automatique floue 64

3.5.3 La couche de séparation spatiale 67

3.5.4 Le concept de migration 68

3.5.5 Fonctionnement du modèle 68

3.5.6 Complexité temporelle de l'algorithme 69

3.6 Etude expérimentale 69

3.6.1 Fonctions tests 70

3.6.2 Résultats numériques 71

3.6.3 Comparaisons avec d'autres techniques 79

3.7 Conclusion 82

4 Conception d'un nouveau modèle pour l'optimisation multiobjectif 83

4.1 Introduction 84

4.2 Principe de l'optimisation multiobjectif 85

4.2.1 Formulation d'un problème multiobjectif 85

4.2.2 Exemple de problème multiobjectif 86

4.3 L'optimisation multiobjectif 86

4.3.1 Choix utilisateur 87

4.3.2 Choix concepteur 87

4.3.3 Les méthodes agrégées 88

4.3.4 Les méthodes non agrégées, non Pareto 90

4.3.5 Les méthodes Pareto 92

4.3.6 Les techniques non élitistes 94

4.3.7 Les techniques élitistes 96

4.3.8 Difficultés des méthodes d'optimisation multiobjectif 99

4.4 Optimisation multiobjectif par essaims particulaires 100

4.4.1 Leaders dans l'optimisation multiobjectif 102

4.4.2 Conservation et propagation des solutions non-dominées . . 104

4.4.3 Maintien de la diversité par création de nouvelles solutions . 105

4.4.4 Classification des différentes approches 107

4.5 Synthèse 109

4.6 Optimisation multiobjectif par essaims particulaires basée sur la Clas-

sification Floue 110

4.6.1 Implémentation de la couche PSOMO 110

4.6.2 Fonctionnement du modèle 111

4.7 Etude expérimentale 112

4.7.1 Problèmes tests 113

4.7.2 Résultats numériques 115

4.7.3 Comparaisons avec d'autres techniques 115

4.8 Conclusion 118

Conclusion générale 119

Références Bibliographiques 122

Introduction générale

Les ingénieurs et les décideurs sont confrontés quotidiennement à des problèmes de complexité grandissante, relatifs à des secteurs techniques très divers, comme dans la conception de systèmes mécaniques, le traitement des images, l'électronique, les télécommunications, les transports urbains, etc. Généralement, les problèmes à résoudre peuvent souvent s'exprimer sous forme de problèmes d'optimisation. Ces problèmes sont le plus souvent caractérisés en plus de leur complexité, d'exigences qui doivent tenir compte de plusieurs contraintes spécifiques au problème à traiter.

L'optimisation est actuellement un des sujets les plus en vue en " soft computing". En effet, un grand nombre de problèmes d'aide à la décision peuvent être décrits sous forme de problèmes d'optimisation. Les problèmes d'identification, d'apprentissage supervisé de réseaux de neurones ou encore la recherche du plus court chemin sont, par exemple, des problèmes d'optimisation.

Pour modéliser un problème, on définit une fonction objectif, ou fonction de coût (voire plusieurs), que l'on cherche à minimiser ou à maximiser par rapport à tous les paramètres concernés. La définition d'un problème d'optimisation est souvent complétée par la donnée de contraintes : tous les paramètres des solutions retenues doivent respecter ces contraintes, faute de quoi ces solutions ne sont pas réalisables.

On distingue en réalité deux types de problèmes d'optimisation : les problèmes "discrets" et les problèmes à variables continues. Parmi les problèmes discrets, on trouve le problème d'affectation de fréquences à spectre fixe : il s'agit de trouver des solutions acceptables en minimisant le niveau global d'interférence de fréquences affectées. Un exemple classique de problème continu est celui de la recherche des valeurs à affecter aux paramètres d'un modèle numérique de processus, pour que ce modèle reproduise au mieux le comportement réel observé. En pratique, on rencontre aussi des "problèmes mixtes", qui comportent à la fois des variables discrètes et des variables continues.

Cette différenciation est nécessaire pour cerner le domaine de l'optimisation difficile. En effet, deux sortes de problèmes reçoivent, dans la littérature, cette appellation :

Certains problèmes d'optimisation discrète, pour lesquels on ne connaît pas d'algorithme exact polynomial. C'est le cas, en particulier, des problèmes dits "NP-difficiles".

Certains problèmes d'optimisation à variables continues, pour lesquels on ne
connaît pas d'algorithme permettant de repérer un optimum global (c'est-à-
dire la meilleure solution possible) à coup sûr et en un nombre fini de calculs.

Des efforts ont longtemps été menés pour résoudre ces deux types de problèmes, dans le domaine de l'optimisation continue, il existe ainsi un arsenal important de méthodes classiques dites d'optimisation globales, mais ces techniques sont souvent inefficaces si la fonction objectif ne possède pas une propriété structurelle particulière, telle que la convexité. Dans le domaine de l'optimisation discrète, un grand nombre d'heuristiques, qui produisent des solutions proches de l'optimum, ont été développées; mais la plupart d'entre elles ont été conçues spécifiquement pour un problème donné.

Face à cette difficulté, il en a résulté un besoin d'outils informatiques nouveaux, dont la conception ne pouvait manquer de tirer parti de l'essor des technologies de l'information et du développement des mathématiques de la cognition.

Dans ce contexte, un nouveau thème de recherche dans le domaine des sciences de l'information a été récemment suggéré. Cette voie regroupe des approches possédant des caractéristiques ou des comportements "intelligents". Bien que ces techniques aient été développées indépendamment, elles sont regroupées sous un nouveau thème de recherche baptisé "Techniques de calcul intelligent" (Computational Intelligence). Ce thème, introduit par Bezdek (1994), inclut la logique floue, les réseaux de neurones artificiels et les méthodes de calcul évolutif. Ces différents champs ont prouvé, durant ces dernières années, leur performance en résistant à l'imperfection et à l'imprécision, en offrant une grande rapidité de traitement et en donnant des solutions satisfaisantes, non nécessairement optimales, pour de nombreux processus industriels complexes.

Par ailleurs, les techniques de calcul "intelligent" peuvent être vues comme un ensemble de concepts, de paradigmes et d'algorithmes, permettant d'avoir des actions appropriées (comportements "intelligents") pour des environnements variables et complexes.

Selon Fogel, ces nouvelles techniques représentent, de façon générale, des méthodes, de calculs "intelligents", qui peuvent être utilisées pour adapter les solutions aux nouveaux problèmes et qui ne requièrent pas d'informations explicites. Par la suite, Zadeh a introduit le terme Soft Computing qui désigne également les mêmes techniques [Zadeh, 1994].

Les méthodes de calcul évolutif "Evolutionary Computation" constituent l'un des thèmes majeurs des techniques de calcul "intelligent". Ces méthodes qui s'inspirent de métaphores biologiques (programmation évolutive, stratégie évolutive, programmation génétique, algorithmes génétiques), d'évolution culturelle des populations

(algorithmes culturels), ou du comportement collectif des insectes (colonies de fourmis, oiseaux migrateurs), etc., sont très utilisées dans le domaine de l'optimisation difficile.

A la différence des méthodes traditionnelles (Hard Computing), qui cherchent des solutions exactes au détriment du temps de calcul nécessaire et qui nécessitent une formulation analytique de la fonction à optimiser, les méthodes de calcul évolutif permettent l'étude, la modélisation et l'analyse des phénomènes plus ou moins complexes pour lesquels les méthodes classiques ne fournissent pas de bonnes performances, en termes de coût de calcul et de leur aptitude à fournir des solutions au problème étudié.

Une autre richesse de ces métaheuristiques est qu'elles se prêtent à toutes sortes d'extensions. Citons, en particulier :

- L'optimisation multiobjectif [Collette et Siarry, 2002], oil il s'agit d'optimiser simultanément plusieurs objectifs contradictoires;

- L'optimisation multimodale, oil l'on s'efforce de repérer tout un jeu d'optima globaux ou locaux;

- L'optimisation dynamique, qui fait face à des variations temporelles de la fonction objectif.

Dans ce contexte, les travaux présentés dans ce mémoire présentent dans un premier temps l'adaptation de l'une des techniques de calcul évolutif, qui s'inspire du comportement collectif des insectes : l'optimisation par essaims particulaires (Particle Swarm Optimization PSO), à l'optimisation de problèmes réels tels que machine synchrone à aimant permanent et le problème d'affectation de fréquences à spectre fixe.

La seconde partie de ce travail sera consacrée à une investigation de l'optimisation multimodale et l'optimisation multiobjectif par essaims particulaires.

Dans cet ordre d'idée, le présent travail propose une nouvelle méthode d'optimisation multimodale par essaims particulaires, le modèle MPSO (Multipopulation Particle Swarms Optimization).

Dans le cadre de l'optimisation multiobjectif, une nouvelle approche, basée sur PSO, la dominance de Pareto et la classification floue, est proposée. Le but principal de cette approche est de surmonter la limitation associée à l'optimisation multiobjectif par essaims particulaires standard. Cette limitation est liée à l'utilisation des archives qui fournit des complexités temporelles et spatiales additionnelles.

Les travaux présentés dans ce mémoire sont structurés selon quatre chapitres :

Nous évoquerons dans le premier chapitre un concis rappel sur les différentes techniques de calcul "intelligent". Un intérêt tout particulier est destiné aux techniques de calcul évolutif qui s'inscrivent dans le cadre de l'optimisation globale.

Le deuxième chapitre illustre la performance de l'algorithme d'optimisation par essaims particulaires dans l'optimisation globale de problèmes réels. Les différentes implémentations effectuées nécessitent une phase d'adaptation de la méthode adoptée ainsi qu'un bon réglage des paramètres. Les problèmes traités dans ce chapitre sont de nature combinatoire, e.g., le problème d'affectation de fréquences dans les réseaux cellulaires, ou des problèmes de prise de décision, e.g., la commande en vitesse des machines synchrones à aimant permanent.

Le troisième chapitre présente, dans un premier temps, l'état de l'art dans le domaine d'optimisation multimodale, et s'intéresse particulièrement aux techniques de niche, basées sur les algorithmes génétiques, les algorithmes culturels et sur les essaims particulaires. Les différentes couches du modèle présenté (MPSO) seront en-suite décrites plus en détail. Enfin, les performances du modèle MPSO sont validées sur plusieurs fonctions tests et comparées à d'autres modèles.

Dans le quatrième chapitre nous commencerons par présenter les différentes techniques d'optimisation multiobjectif proposées dans la littérature. Le modèle proposé FC-MOPSO (Fuzzy Clustering Multi-objective Particle Swarm Optimizer) est en-suite présenté et décrit en détail. Les performances du modèle seront enfin évaluées sur plusieurs fonctions tests et comparées à d'autres modèles.

Première partie

Application de l'algorithme

d'optimisation par essaims

particulaires à des problèmes réels

Résumé

Cette partie introduit les différentes techniques de calcul "Intelligent". Les techniques de calcul évolutif tels que les systèmes immunitaires artificiels, les algorithmes évolutifs et les systèmes basés sur l'intelligence collective sont décrites. Dans un deuxième temps, nous présentons l'application de l'algorithme d'optimisation par essaims particulaires sur deux problèmes réels, un problème continu : la commande d'une machine synchrone à aimant permanent (MSAP), et un autre discrèt : le problème d'affectation de fréquences dans les réseaux cellulaires (PAF).

Chapitre 1

Techniques de calcul "intelligent"

1.1 Introduction

La recherche de la solution optimale d'un problème est une préoccupation importante dans le monde actuel, qu'il s'agisse d'optimiser le temps, le confort, la sécurité, les coûts ou les gains. Beaucoup de problèmes d'optimisation sont difficiles à résoudre, la difficulté ne vient pas seulement de la complexité du problème mais également de la taille excessive de l'espace des solutions. Par exemple, le problème du voyageur de commerce a une taille de l'espace de solutions qui varie en factorielle (n-1) où n est le nombre de villes où il faut passer; On s'aperçoit qu'à seulement 100 villes, il y a ~ 9· 10¹⁵³ solutions possibles. Il est alors impensable de pouvoir les tester toutes pour trouver la meilleure [Amat et Yahyaoui, 1996].

En général, un problème d'optimisation revient à trouver un vecteur ?- v ? M, tel qu'un certain critère de qualité, appelé fonction objectif, f : M ? R, soit maximisé (ou minimisé). La solution du problème d'optimisation globale nécessite donc de trouver un vecteur ?-v * tel que

?-? v ? M : f(-^? v ) = f(-^? v ^*)(resp. =)

Nous assistons ces dernières années à l'émergence de nouvelles techniques d'optimisation. Le principe de ces techniques repose sur la recherche de solutions en tenant compte de l'incertitude, de l'imprécision de l'information réelle et utilisant l'apprentissage. Le but n'est plus de trouver des solutions exactes, mais des solutions satisfaisantes à coût convenable.

Sur la base de ces nouvelles techniques, le concept de "Computational Intelligence" (calcul "Intelligent") a été introduit par Bezdek [Bezdek, 1994] pour définir une nouvelle orientation de l'informatique. Ce nouveau thème de recherche considère les programmes comme des entités (ou agents) capables de gérer des incertitudes, avec une aptitude à apprendre et à évoluer.

Le terme "Soft Computing", a été également proposé par Zadeh [Zadeh, 1994] qui se réfère à un ensemble de techniques de calcul (Computational techniques) utilisées dans plusieurs domaines, notamment l'informatique, l'intelligence artificielle et dans certaines disciplines des sciences de l'ingénieur.

Les techniques de soft computing regroupent diverses méthodes de différentes inspirations, notamment la logique floue, les réseaux de neurones et les techniques de calcul évolutif. En général, ces méthodes reposent particulièrement sur les processus biologiques et sociologiques et considèrent les être vivants comme modèles d'inspiration. À la différence des méthodes traditionnelles (Hard Computing), qui cherchent des solutions exactes au détriment du temps de calcul nécessaire et qui nécessitent une formulation analytique de la fonction à optimiser, les méthodes de calcul "intelligent" permettent l'étude, la modélisation et l'analyse des phénomènes plus ou moins complexes pour lesquels les méthodes classiques ne fournissent pas de bonnes performances, en termes du coût de calcul et de leur aptitude à fournir une solution au problème étudié.

L'objectif visé dans ce chapitre est de présenter les différentes techniques de calcul "intelligent". Un intérêt tout particulier est adressé aux techniques évolutives utilisées dans le cadre de l'optimisation.

1.2 Techniques de Calcul "Intelligent"

Le principe de base des méthodes de Calcul "Intelligent" consiste à considérer les êtres vivants comme modèles d'inspiration, le but étant de simuler à l'aide des machines leur comportement.

En général, ces techniques peuvent être regroupées en trois grandes classes : les réseaux de neurones artificiels qui utilisent l'apprentissage pour résoudre des problèmes complexes tels que la reconnaissance des formes ou le traitement du langage naturel, la logique floue utilisée dans des applications d'intelligence artificielle, dans lesquelles les variables ont des degrés de vérité représentés par une gamme de valeurs situées entre 1 (vrai) et 0 (faux), et les méthodes de calcul évolutif pour la recherche et l'optimisation (figure 1.1). Ces différentes classes seront présentées dans les sections suivantes.















FIG. 1.1 - Techniques de calcul "Intelligent"

1.2.1 Les réseaux de neurones (Neural Networks)

Un réseau de neurones (Artificial Neural Network) est un modèle de calcul dont la conception est schématiquement inspirée du fonctionnement de vrais neurones. Les réseaux de neurones sont généralement optimisés par des méthodes d'apprentissage de type statistique, si bien qu'ils sont placés d'une part dans la famille des applications statistiques, qu'ils enrichissent avec un ensemble de paradigmes permettant de générer de vastes espaces fonctionnels, souples et partiellement structurés, et d'autre part dans la famille des méthodes de l'intelligence artificielle qu'ils enrichissent en permettant de prendre des décisions s'appuyant d'avantage sur la perception que sur le raisonnement logique formel.

Ce sont les deux neurologues Warren McCulloch et Walter Pitts [McCulloch et Pitts, 1943] qui ont mené les premiers travaux sur les réseaux de neurones. Ils constituèrent un modèle simplifié de neurone biologique communément appelé neurone

formel. Ils montrèrent également théoriquement que des réseaux de neurones formels simples peuvent réaliser des fonctions logiques, arithmétiques et symboliques complexes.

La fonction des réseaux de neurones formels à l'instar du modèle vrai est de résoudre divers problèmes. A la différence des méthodes traditionnelles de résolution informatique, on ne doit pas construire un programme pas à pas en fonction de la compréhension de celui-ci. Les paramètres les plus importants de ce modèle sont les coefficients synaptiques. Ce sont eux qui construisent le modèle de résolution en fonction des informations données au réseau. Il faut donc trouver un mécanisme, qui permet de les calculer à partir des grandeurs acquises du problème, c'est le principe fondamental de l'apprentissage. Dans un modèle de réseau de neurones formels, apprendre, c'est d'abord calculer les valeurs des coefficients synaptiques en fonction des exemples disponibles. La structure d'un réseau de neurones artificiel est donnée par la figure (1.2).

Le neurone calcule la somme de ses entrées puis cette valeur passe à travers la fonction d'activation pour produire sa sortie. La fonction d'activation (ou fonction de seuillage) sert à introduire une non linéarité dans le fonctionnement du neurone.





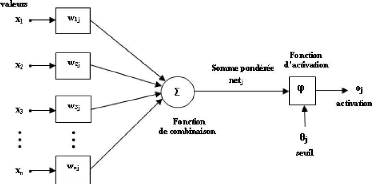
FIG. 1.2 Structure d'un neurone artificiel

Les fonctions de seuillage présentent généralement trois intervalles :

1. en dessous du seuil, le neurone est non-actif (souvent dans ce cas, sa sortie vaut 0 ou 1),

2. au voisinage du seuil, une phase de transition,

3. au-dessus du seuil, le neurone est actif (souvent dans ce cas, sa sortie vaut 1).

En général, un réseau de neurone est composé d'une succession de couches dont chacune prend ses entrées à partir des sorties de la couche précédente. Chaque couche i est composée de Ni neurones, prenant leurs entrées sur les _{Ni_1} neurones de la couche précédente. A chaque synapse est associé un poids synaptique, de sorte que les _{Ni_1} sont multipliés par ce poids, puis additionnés par les neurones de niveau i, ce qui est équivalent à multiplier le vecteur d'entrée par une matrice de transformation. Mettre l'une derrière l'autre, les différentes couches d'un réseau de neurones, reviendrait à mettre en cascade plusieurs matrices de transformation et pourrait se ramener à une seule matrice, produit des autres, s'il n'y avait à chaque couche, la fonction de sortie qui introduit une non linéarité à chaque étape. Ceci montre l'importance du choix judicieux d'une bonne fonction de sortie : un réseau de neurones dont les sorties seraient linéaires n'aurait aucun intérêt.

Plusieurs types de réseaux de neurones ont été reportés dans la littérature, notamment le perceptron proposé par Rosenblatt [Rosenblatt, 1958], les cartes autoorganisatrices de Kohonen [Kohonen, 1989], le modèle neural-gas [Martinez et Schulten, 1991] et les réseaux basés sur le modèle de Hopfield [Hopfield, 1982], etc, [Jedra, 1999].

Grâce à leur capacité de classification et de généralisation, les réseaux de neurones sont généralement utilisés dans des problèmes de nature statistique, tels que la classification automatique, reconnaissance de motif, approximation d'une fonction inconnue, etc.

1.2.2 La logique floue (Fuzzy Logic)

La théorie des sous ensembles flous a été introduite par Lotfi Zadeh en 1965 [Zadeh, 1965] et utilisée dans des domaines aussi variés que l'automatisme, la robotique (reconnaissance de formes), la gestion de la circulation routière, le contrôle aérien, l'environnement (météorologie, climatologie, sismologie), la médecine (aide au diagnostic), l'assurance (sélection et prévention des risques) et bien d'autres. Elle constitue une généralisation de la théorie des ensembles classiques, l'une des structures de base sous-jacente à de nombreux modèles mathématiques et informatiques [Bezdek, 1992].

La logique floue s'appuie sur la théorie mathématique des sous ensembles flous. Cette théorie, introduite par Zadeh, est une extension de la théorie des ensembles classiques pour la prise en compte des sous ensembles définis de façon imprécise. C'est une théorie formelle et mathématique dans le sens oil Zadeh, en partant du concept de fonction d'appartenance pour modéliser la définition d'un sous-ensemble d'un univers donné, a élaboré un modèle complet de propriétés et de définitions formelles. Il a aussi montré que la théorie des sous-ensembles flous se réduit effectivement à la théorie des sous-ensembles classiques dans le cas oil les fonctions d'appartenance considérées prennent des valeurs binaires (0, 1).

À l'inverse de la logique booléenne, la logique floue permet à une condition d'être en un autre état que vrai ou faux. Il y a des degrés dans la vérification d'une condition. La logique floue tient compte de l'imprécision de la forme des connaissances et propose un formalisme rigoureux afin d'inférer de nouvelles connaissances.

Ainsi, la notion d'un sous ensemble flou permet de considérer des classes d'objets, dont les frontières ne sont pas clairement définies, par l'introduction d'une fonction caractéristique (fonction d'appartenance des objets à la classe) prenant des valeurs entre 0 et 1, contrairement aux ensemble "booléens" dont la fonction caractéristique ne prend que deux valeurs possibles 0 et 1.

La capacité des sous ensembles flous à modéliser des propriétés graduelles, des contraintes souples, des informations incomplètes, vagues, linguistiques, les rend aptes à faciliter la résolution d'un grand nombre de problèmes tels que : la commande floue, les systèmes à base de connaissances, le regroupement et la classification floue, etc.

Mathématiquement, un sous ensemble floue F sera défini sur un référentiel H par une fonction d'appartenance, notée u, qui, appliquée à un élément u ? H, retourne un degré d'appartenance uF(u) de u à F, uF(u) = 0 et uF(u) = 1 correspondent respectivement à l'appartenance et à la non appartenance.

1.2.3 Les techniques de calcul évolutif (Evolutionary Computation)

Les techniques de calcul évolutif (EC) représentent un ensemble de techniques. Ces techniques sont regroupées en quatre grandes classes : les systèmes immunitaires artificiels, l'intelligence collective, les algorithmes évolutifs et les algorithmes culturels (figure 1.1).

1.2.3.1. Les systèmes immunitaires artificiels

Les algorithmes basés sur les systèmes immunitaires artificiels (AIS Artificial Immune Systems) ont été conçus pour résoudre des problèmes aussi variés que la robotique, la détection d'anomalies ou l'optimisation [De Castro et Von Zuben, 1999], [De Castro et Von Zuben, 2000].

Le système immunitaire est responsable de la protection de l'organisme contre les agressions d'organismes extérieurs. La métaphore dont sont issus les algorithmes AIS mettent l'accent sur les aspects d'apprentissage et de mémoire du système immunitaire dit adaptatif. En effet, les cellules vivantes disposent sur leurs membranes de molécules spécifiques dites antigènes. Chaque organisme dispose ainsi d'une identité unique, déterminée par l'ensemble des antigènes présents sur ses cellules. Les lymphocytes (un type de globule blanc) sont des cellules du système immunitaire qui possèdent des récepteurs capables de se lier spécifiquement à un antigène unique, permettant ainsi de reconnaître une cellule étrangère à l'organisme. Un lymphocyte

ayant ainsi reconnu une cellule "étrangère" va être stimulé à proliférer (en produisant des clones de lui-même) et à se différencier en cellule permettant de garder en mémoire l'antigène, ou de combattre les agressions. Dans le premier cas, il sera capable de réagir plus rapidement à une nouvelle attaque à l'antigène. Dans le second cas, le combat contre les agressions est possible grâce à la production d'anticorps. Il faut également noter que la diversité des récepteurs dans l'ensemble de la population des lymphocytes est quant à elle produite par un mécanisme d'hyper-mutation des cellules clonées [Forrest et al., 1993], [Hofmeyr et Forrest, 1999].

L'approche utilisée dans les algorithmes AIS est voisine de celle des algorithmes évolutionnaires, mais a également été comparée à celle des réseaux de neurones. On peut, dans le cadre de l'optimisation difficile, considérer les AIS comme une forme d'algorithme évolutionnaire présentant des opérateurs particuliers. Pour opérer la sélection, on se fonde par exemple sur une mesure d'affinité entre le récepteur d'un lymphocyte et un antigène; la mutation s'opère quant à elle via un opérateur d'hypermutation directement issu de la métaphore.

1.2.3.2. Les algorithmes évolutifs (AE)

Les algorithmes évolutifs (Evolutionary Algorithms) sont des techniques de recherche inspirées de l'évolution biologique des espèces, apparues à la fin des années 1950. Parmi plusieurs approches [Holland, 1962], [Fogel et al, 1966], [Rechenberg, 1965], les algorithmes génétiques (AG) constituent certainement les algorithmes les plus connus [Goldberg, 1989a].

Le principe d'un algorithme évolutionnaire est très simple. Un ensemble de N points dans un espace de recherche, choisi a priori au hasard, constituent la population initiale; chaque individu x de la population possède une certaine performance, qui mesure son degré d'adaptation à l'objectif visé : dans le cas de la minimisation d'une fonction objectif f, x est d'autant plus performant que f(x) est plus petit. Un AE consiste à faire évoluer progressivement, par générations successives, la composition de la population, en maintenant sa taille constante. Au cours des générations, l'objectif est d'améliorer globalement la performance des individus; le but étant d'obtenir un tel résultat en imitant les deux principaux mécanismes qui régissent l'évolution des êtres vivants, selon la théorie de Darwin :

la sélection, qui favorise la reproduction et la survie des individus les plus performants,

la reproduction, qui permet le brassage, la recombinaison et les variations des caractères héréditaires des parents, pour former des descendants aux potentialités nouvelles.

En fonction des types d'opérateurs, i.e., sélection et reproduction génétique, employés dans un algorithme évolutif, quatre approches différentes ont été proposées [Bäck et al, 1997] : les algorithmes génétiques (AG), la programmation génétique (PG), les stratégies d'évolution (SE) et la programmation évolutive (PE) que nous

allons décrire par la suite. La structure générale d'un AE est donnée par le pseudo code (7).

algorithme 1 Structure de base d'un algorithme évolutif

Algorithme évolutif

t 4-- 0

Initialiser la population P(t)

Evaluer P(t)

Répéter

t 4-- t + 1

Sélectionner les parents

Appliquer les opérateurs génétiques

Evaluer la population des enfants crées

Créer par une stratégie de sélection la nouvelle population P(t) Tant que (condition d'arrêt n'est pas satisfaite)

a. Les algorithmes génétiques (Genetic Algorithms)

Les algorithmes génétiques sont des techniques de recherche stochastiques dont les fondements théoriques ont été établis par Holland [Holland, 1975]. Ils sont inspirés de la théorie Darwinienne : l'évolution naturelle des espèces vivantes. Celles-ci évoluent grâce à deux mécanismes : la sélection naturelle et la reproduction. La sélection naturelle, l'élément propulseur de l'évolution, favorise les individus, d'une population, les plus adaptés à leur environnement. La sélection est suivie de la reproduction, réalisée à l'aide de croisements et de mutations au niveau du patrimoine génétique des individus. Ainsi, deux individus parents, qui se croisent, transmettent une partie de leur patrimoine génétique à leurs progénitures. En plus, quelques gènes des individus, peuvent être mutés pendant la phase de reproduction. La combinaison de ces deux mécanismes, conduit, génération après génération, à des populations d'individus de plus en plus adaptés à leur environnement. Le principe des AG est décrit par le pseudo code (8).

algorithme 2 Structure de base d'un algorithme génétique

Algorithme Génétique

t 4-- 0

Initialiser la population P(t)

Evaluer P(t)

Répéter

t 4-- t + 1

P(t) = Sélectionner (P(t - 1)) Croiser (P(t))

Muter (P(t))

Evaluer P(t)

Jusqu'à (condition d'arrêt validée)

Dans leur version canonique, les AG présentent des limites qui conduisent le plus souvent à des problèmes de convergences lente ou prématurée. Pour pallier à ces inconvénients, des améliorations ont été apportées : e.g, codage, opérateurs biologiques, stratégie élitiste, etc. les détails de fonctionnement de ces algorithmes peuvent être trouvés dans plusieurs références principalement : [El Imrani, 2000], [Michalewicz, 1996].

b. Programmation génétique (Genetic Programming)

La programmation génétique est une variante, des algorithmes génétiques, destinée à manipuler des programmes [Koza, 1992] pour implémenter un modèle d'apprentissage automatique. Les programmes sont généralement codés par des arbres qui peuvent être vus comme des chaînes de bits de longueur variable. Une grande partie des techniques et des résultats concernant les algorithmes génétiques peuvent donc également s'appliquer à la programmation génétique.

c. Stratégies d'évolution (Evolutionary Strategy)

Les stratégies d'évolution forment une famille de métaheuristiques d'optimisation. Elles sont inspirées de la théorie de l'évolution. Ce modèle fut initialement proposé par Rencherberg [Rechenberg, 1965]. il constitue, à ce titre, la première véritable métaheuristique et le premier algorithme évolutif.

Dans sa version de base, l'algorithme manipule itérativement un ensemble de vecteurs de variables réelles, à l'aide d'opérateurs de mutation et de sélection. L'étape de mutation est classiquement effectuée par l'ajout d'une valeur aléatoire, tirée au sein d'une distribution normale. La sélection s'effectue par un choix déterministe des meilleurs individus, selon la valeur de la fonction d'adaptation.

Les strategies d'évolution utilisent un ensemble de u "parents" pour produire A "enfants". Pour produire chaque enfant, p parents se "recombinent". Une fois produits, les enfants sont mutés. L'étape de sélection peut s'appliquer, soit uniquement aux enfants, soit à l'ensemble (enfants + parents). Dans le premier cas, l'algorithme est noté (u, A)--ES, dans le second (u + A)--ES [Schoenauer et Michalewicz, 1997].

À l'origine, l'étape de recombinaison était inexistante, les algorithmes étant alors notés ((u, A)--ES ou (u + A)--ES. Les méthodes actuelles utilisent l'opérateur de recombinaison, comme les autres algorithmes évolutifs, afin d'éviter d'être piégées dans des optima locaux.

Une itération de l'algorithme général procède comme suit :

1. À partir d'un ensemble de u parents,

2. produire une population de A enfants:

a. choisir p parents,

b. recombiner les parents pour former un unique individu,

c. muter l'individu ainsi crée,

3. sélectionner les i meilleurs individus.

d. Programmation évolutive (Evolutionary Programming)

La programmation évolutive a été introduite par Laurence Fogel en 1966 [Fogel et al, 1966] dans la perspective de créer des machines à état fini (Finite State Machine) dans le but de prédire des événements futurs sur la base d'observations antérieures.

La programmation évolutive suit le schéma classique des algorithmes évolutifs de la façon suivante :

1. on génère aléatoirement une population de n individus qui sont ensuite évalués;

2. chaque individu produit un fils par l'application d'un opérateur de mutation suivant une distribution normale;

3. les nouveaux individus sont évalués et on sélectionne de manière stochastique une nouvelle population de taille n (les mieux adaptés) parmi les 2m individus de la population courante (parents + enfants);

4. on réitère, à partir de la deuxième étape, jusqu'à ce que le critère d'arrêt choisi soit valide.

La programmation évolutive partage de nombreuses similitudes avec les stratégies d'évolution : les individus sont, a priori, des variables multidimensionnelles réelles et il n'y a pas d'opérateur de recombinaison. La sélection suit une stratégie de type

(i + A).

1.2.3.3. Les systèmes de classifieurs (Learning Classifier Systems)

Les classifieurs sont des machines, d'apprentissage automatique, basées sur la génétique et l'apprentissage renforcé, mais sont d'une complexité et d'une richesse bien plus grande. Ils sont capables de s'adapter par apprentissage à un environnement dans lequel ils évoluent. Ils reçoivent des entrées de leur environnement et réagissent en fournissant des sorties. Ces sorties sont les conséquences de règles déclenchées directement ou indirectement par les entrées. Un système classifieur est constitué de trois composantes principales :

1. Un système de règles et de messages,

2. Un système de répartition de crédits,

3. Un algorithme évolutif.

Le système de règles et de messages est un type particulier de système de production (SP). Un SP est un procédé qui utilise des règles comme unique outil algorithmique. Une règle stipule que quand une condition est satisfaite une action peut être réalisée (règle déclenchée) [Goldberg, 1989a].

Notons que l'environnement dans lequel évolue le système de classifieurs peut changer au cours de l'évolution. Le système s'adapte alors remettant éventuellement en cause des règles. D'une manière générale, les systèmes classifieurs sont capables d'induire de nouvelles règles par généralisation à partir d'exemples [Holland et al, 1986]. Les systèmes de classifieurs sont utilisés pour résoudre des problèmes réels en biologie, en médecine, en sciences de l'ingénieur, etc.

1.2.3.4. Les systèmes basés sur l'intelligence collective (Swarm Intelligence)

L'intelligence collective désigne les capacités cognitives d'une communauté résultant des interactions multiples entre les membres (ou agents) de la communauté. Des agents, au comportement très simple, peuvent ainsi accomplir des tâches complexes grâce à un mécanisme fondamental appelé synergie. Sous certaines conditions particulières, la synergie créée, par la collaboration entre individus, fait émerger des possibilités de représentation, de création et d'apprentissage supérieures à celles des individus isolés.

Les formes d'intelligence collective sont très diverses selon les types de communauté et les membres qu'elles réunissent. Les systèmes collectifs sont en effet plus ou moins sophistiqués. Les sociétés humaines en particulier n'obéissent pas à des règles aussi mécaniques que d'autres systèmes naturels, par exemple du monde animal. Pour des systèmes simples les principales caractéristiques sont :

1. L'information locale : Chaque individu ne possède qu'une connaissance partielle de l'environnement et n'a pas conscience de la totalité des éléments qui influencent le groupe,

2. L'ensemble de règles : Chaque individu obéit à un ensemble restreint de règles simples par rapport au comportement du système global,

3. Les interactions multiples : Chaque individu est en relation avec un ou plusieurs autres individus du groupe,

4. La collectivité : les individus trouvent un bénéfice à collaborer (parfois instinctivement) et leur performance est meilleure que s'ils avaient été seuls.

L'intelligence collective est observée notamment chez les insectes sociaux (fourmis, termites et abeilles) et les animaux en mouvement (oiseaux migrateurs, bancs de poissons). En conséquence, plusieurs algorithmes basés sur le principe d'intelligence collective ont été introduits : on peut citer les colonies de fourmis et les essaims particulaires [Hoffmeyer, 1994], [Ramos et al., 2005].

a. Les colonies de fourmis (Ants Colony)

Une colonie de fourmis, dans son ensemble, est un système complexe stable et autorégulé capable de s'adapter très facilement aux variations environnementales les plus imprévisibles, mais aussi de résoudre des problèmes, sans contrôle externe ou mécanisme de coordination central, de manière totalement distribuée.

L'optimisation par colonies de fourmis (ACO "Ants Colony Optimisation") s'inspire du comportement des fourmis lorsque celles-ci sont à la recherche de nourriture [Deneubourg et al, 1983], [Deneubourg et Goss, 1989], [Goss et al, 1990]. Il a ainsi été démontré qu'en plaçant une source de nourriture reliée au nid par une passerelle, formée d'une branche courte et d'une branche longue, les fourmis choisissaient toutes le chemin le plus court après un certain laps de temps [Beckers et al, 1992]. En effet, chaque fourmi se dirige en tenant compte des traces de phéromone déposées par les autres membres de la colonie qui la précèdent.

Comme cette phéromone s'évapore, ce choix probabiliste évolue continuellement. Ce comportement collectif, basé sur une sorte de mémoire partagée entre tous les individus de la colonie, peut être adapté et utilisé pour la résolution de problèmes d'optimisation combinatoire surtout les problèmes du parcours des graphes.

D'une façon générale, les algorithmes de colonies de fourmis sont considérés comme des métaheuristiques à population, oil chaque solution est représentée par une fourmi se déplaçant dans l'espace de recherche. Les fourmis marquent les meilleures solutions, et tiennent compte des marquages précédents pour optimiser leur recherche.

Ces algorithmes utilisent une distribution de probabilité implicite pour effectuer la transition entre chaque itération. Dans leurs versions adaptées à des problèmes combinatoires, ils utilisent une construction itérative des solutions.

La différence qui existe entre les algorithmes de colonies de fourmis et les autres métaheuristiques proches (telles que les essaims particulaires) réside dans leur aspect constructif. En effet, dans le cas des problèmes combinatoires, il est possible que la meilleure solution soit trouvée, alors même qu'aucune fourmi ne l'aura découverte effectivement. Ainsi, dans l'exemple du problème du voyageur de commerce, il n'est pas nécessaire qu'une fourmi parcoure effectivement le chemin le plus court, i.e., celui-ci peut être construit à partir des segments les plus renforcés des meilleures solutions. Cependant, cette définition peut poser problème dans le cas des problèmes à variables réelles, oil aucune structure de voisinage n'existe.

b. Les essaims particulaires (Particle Swarm Optimization PSO)

L'optimisation par essaims particulaires est une métaheuristique d'optimisation, proposée par Russel Ebenhart et James Kennedy en 1995 [Eberhart et Kennedy, 1995], [Kennedy et Eberhart, 1995]. Cette métaheuristique s'appuie notamment sur un modèle développé par le biologiste Craig Reynolds à la fin des années 1980, permettant de simuler le déplacement d'un groupe d'oiseaux.

Cette méthode d'optimisation se base sur la collaboration des particules entre elles. Elle a d'ailleurs des similarités avec les algorithmes de colonies de fourmis, qui s'appuient eux aussi sur le concept d'auto-organisation.

Ainsi, grâce à des règles de déplacement très simples (dans l'espace de solutions), les particules peuvent converger progressivement vers un optimum. Cette métaheuristique semble cependant mieux fonctionner pour des espaces en variables continues.

Au départ de l'algorithme, un essaim est réparti au hasard dans l'espace de recherche de dimension D, chaque particule p est aléatoirement placée dans la position xp de l'espace de recherche, chaque particule possède également une vitesse aléatoire. Ensuite, à chaque pas de temps:

chaque particule est capable d'évaluer la qualité de sa position et de garder en mémoire sa meilleure performance P i : la meilleure position qu'elle a atteinte jusqu'ici (qui peut en fait être parfois la position courante) et sa qualité (la valeur en cette position de la fonction à optimiser),

chaque particule est capable d'interroger un certain nombre de ses congénères (ses informatrices, dont elle-même) et d'obtenir de chacune d'entre elles sa propre meilleure performance Pg (et la qualité afférente),

à chaque pas de temps, chaque particule choisit la meilleure des meilleures performances dont elle a connaissance, modifie sa vitesse V en fonction de cette information et de ses propres données et se déplace en conséquence.

La modification de la vitesse est une simple combinaison linéaire de trois ten-dances, à l'aide de coéfficients de confiance :

- la tendance « aventureuse », consistant à continuer selon la vitesse actuelle,

la tendance « conservatrice », ramenant plus ou moins vers la meilleure position déjà trouvée,

la tendance « panurgienne », orientant approximativement vers la meilleure informatrice.

La mise à jour des deux vecteurs vitesse et position, de chaque particule p dans l'essaim, est donnée par les équations (1.1) et (1.2) :

v_j (t + 1) = r(t)v^p

p j (t) + uw1j(t)(P ⁱ _j(t) - x^p _j(t)) + uw2j(t)(P _j ^g(t) - x^p _j(t)) (1.1)

xp _j(t + 1) = x^p _j(t) + vp j (t + 1) (1.2)

Où j = 1. . . , D, r(t) est le facteur d'inertie, u représente le paramètre cognitif et u le paramètre social. w1j(t) et w2j(t) sont des nombres aléatoires compris entre 0 et 1.

Lors de l'évolution de l'essaim, il peut arriver qu'une particule sorte de l'espace de recherche initialement défini. Pour rester dans un espace de recherche fini donné, on ajoute un mécanisme pour éviter qu'une particule ne sorte de cet espace.

le plus fréquent est le confinement d'intervalle. Supposons, par simplicité, que l'espace de recherche soit [xmin, xmax]^D. Alors ce mécanisme stipule que si une coordonnée xj, calculée selon les équations de mouvement, sort de l'intervalle [xmin, xmax],on lui attribue en fait la valeur du point frontière le plus proche. En pratique, celà revient donc à remplacer la deuxième équation de mouvement (équation 1.2) par:

xj(t + 1) = min(max(xj(t) + vj(t + 1), xmin), xmax) (1.3)

De plus, on complète souvent le mécanisme de confinement par une modification de la vitesse, soit en remplaçant la composante qui pose problème par son opposée, souvent pondérée par un coefficient inférieur à 1, soit, tout simplement, en l'annulant. Donc le principe du confinement consiste à ramener la particule qui sort de l'espace de recherche au point le plus proche qui soit dans cet espace et modifier sa vitesse en conséquence. Le pseudo code de l'algorithme PSO de base est donné par l'algorithme (3), [De Falco et al, 2007].

Principales caractéristiques

Ce modèle présente quelques propriétés intéressantes, qui en font un bon outil pour de nombreux problèmes d'optimisation, particulièrement les problèmes fortement non linéaires, continus ou mixtes (certaines variables étant réelles et d'autres entières) :

il est facle à programmer, quelques lignes de code suffisent dans n'importe quel langage évolué,

il est robuste (de mauvais choix de paramètres dégradent les performances, mais n'empêchent pas d'obtenir une solution).

algorithme 3 Pseudo code de l'algorithme PSO

t 4-- 0

Pour chaque particule

Initialiser sa position et sa vitesse.

Initialiser P ⁱ(t)

Fin pour

Répéter

Choisir la particule P g(t) ayant la meilleure fitness dans l'itération courante

Pour chaque particule p

Calculer la vitesse vp(t + 1) utilisant l'équation (1.1).

Mettre à jour le vecteur position xp(t + 1) selon l'équation (1.2).

Calculer la valeur de la fitness f(xp(t))

Si f(xp(t)) > f(P ⁱ(t))

P ⁱ(t + 1) 4-- xp(t)

Fin si

Fin pour t 4-- t + 1

Tant que (critère d'arrêt n'est pas validé)

1.2.3.5. Les algorithmes culturels (Cultural Algorithms CA) a. Principes de base

Les algorithmes culturels sont des techniques évolutives modélisant l'évolution culturelle des populations [Reynolds, 1994]. Ces algorithmes supportent les mécanismes de base de changement culturel [Durham, 1994]. Certains sociologues ont proposé des modèles oil les cultures peuvent être codées et transmises à l'intérieur et entre les populations [Durham, 1994], [Renfrew, 1994]. En se basant sur cette idée, Reynolds a développé un modèle évolutif dans lequel l'évolution culturelle est considérée comme un processus d'héritage qui agit sur deux niveaux évolutifs différents : le niveau microévolutif (espace population) et le niveau macro-évolutif (espace de connaissance) [Reynolds, 1994].



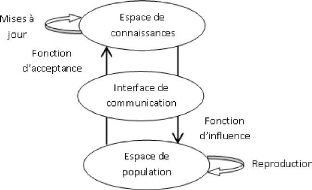
FIG. 1.3 - Les composants principaux d'un algorithme culturel

Ces algorithmes agissent donc sur deux espaces : l'espace de population qui contient un ensemble d'individus qui évoluent grâce à un modèle évolutif, et l'espace de connaissances qui contient les informations et les connaissances, spécifiques au problème à résoudre, utilisées pour guider et influencer l'évolution des individus des populations au cours des générations. De ce fait, un protocole de communication est indispensable pour établir une interaction entre ces deux espaces (figure 1.3).

Ce protocole a, en fait, une double mission, il détermine d'une part quels individus de la population peuvent influencer l'espace de connaissances (fonction d'acceptance), et d'autre part quelles connaissances peuvent influencer l'évolution des populations (fonction d'influence). Le pseudo code (4) représente la structure de base d'un AC [Zhu et Reynolds, 1998].

Plusieurs versions d'algorithmes culturels ont été développées avec différentes implémentations des deux espaces évolutifs. VGA (Version space guided Genetic Algorithm) se sert d'un algorithme génétique comme modèle micro-évolutif et de "Version

algorithme 4 Structure de base d'un Algorithme Culturel

t 4-- 0

Initialiser la population P(t);

Initialiser l'espace de connaissances B(t); Répéter

Evaluer P(t);

Ajuster (B(t), acceptance P(t)); Evaluer (P(t), influence B(t));

t 4-- t + 1;

Jusqu'à (condition d'arrêt valide);

Spaces" pour le niveau macro-évolutif [Reynolds et Zannoni, 1994], d'autres implémentations utilisent la programmation génétique pour le niveau micro évolutif et "Program segments" pour le niveau macro-évolutif [Zannoni et Reynolds, 1997].

1.3 Conclusion

Dans ce chapitre, nous avons présenté les différentes techniques de calcul "intelligent". Ces méthodes s'avèrent utiles dans divers domaines de recherche: l'apprentissage, la classification, l'optimisation, etc. Un intérêt tout particulier est adressé aux problèmes d'optimisation, qui constitue l'un des principaux objectifs de cette étude.

Dans ce contexte, nous avons choisi de nous intéresser aux techniques de calcul évolutif (Evolutionary Computation EC) en raison de leur efficacité dans le cadre de l'optimisation globale. Ces techniques qui s'inspirent des métaphores biologiques (Programmation Evolutive, Stratégie d'Evolution, Programmation Génétique, Algorithmes Génétiques), de l'évolution culturelle des populations (Algorithmes Culturels), ou du comportement collectif (Colonies de Fourmis et Essaims particulaires), etc., offrent la possibilité de trouver des solutions optimales en un temps de calcul raisonnable.

En général, les techniques EC ont été conçues initialement, dans leur version de base, pour traiter un certain type de problèmes. Par exemple, les AG canoniques ont été proposés pour l'optimisation de fonctions, les algorithmes d'optimisation par colonies de fourmis pour les problèmes de parcours de graphe, etc. En général, ces méthodes ont prouvé leur efficacité à résoudre des problèmes analogues à ceux pour lesquelles elles ont été conçues à l'origine.

En conclusion, bien qu'on dispose d'une panoplie de méthodes utiles à l'optimisation globale, leur application directe à un problème donné est quasiment impossible. En effet, une phase d'adaptation de ces techniques au problème à résoudre reste une démarche indispensable pour obtenir de meilleures performances.

Chapitre 2

Application de l'algorithme

d'optimisation par essaims

particulaires aux problèmes MSAP

et PAF

2.1 Introduction

La résolution d'un problème d'optimisation consiste à explorer un espace de recherche afin de maximiser (ou minimiser) une fonction objectif. En effet, dans la vie courante nous sommes fréquemment confrontés à des problèmes réels d'optimisation plus ou moins complexes.

En général, deux sortes de problèmes reçoivent, dans la littérature, cette appellation :

Certains problèmes d'optimisation discrets, pour lesquels on ne connait pas d'algorithme exact polynomial (NP-difficiles),

Certains problèmes d'optimisation à variables continues, pour lesquels on ne connait pas d'algorithme permettant de repérer un optimum global à coup sûr et en un nombre fini de calculs.

Des efforts ont été longtemps menés, séparément, pour résoudre ces deux types de problèmes. Dans le domaine de l'optimisation continue, il existe un arsenal de méthodes classiques, mais ces techniques se trouvent souvent limitées. Cette limitation est due soit à l'absence de modèles analytiques, soit à l'inadéquation des techniques de résolution. Dans le domaine de l'optimisation discrète, un grand nombre d'heuristiques, qui produisent des solutions proches de l'optimum, ont été développées, mais la plupart d'entre elles ont été conçues spécifiquement pour un problème donné.

L'arrivée des métaheuristiques marque une réconciliation des deux domaines : en effet, celles-ci s'appliquent à toutes sortes de problèmes discrèts et elles peuvent s'adapter aussi aux problèmes continus.

L'algorithme d'optimisation par essaims particulaires (PSO) fait partie de ces métaheuristiques. cet algorithme est basé sur la notion de coopération entre des agents (les particules qui peuvent être vues comme des « animaux » aux capacités assez limitées : peu de mémoire et de facultés de raisonnement). L'échange d'information entre les agents fait que, globalement, ils arrivent néanmoins à résoudre des problèmes difficiles voire complexes.

Dans ce chapitre, l'algorithme d'optimisation par essaims particulaires est implémenté pour résoudre deux problèmes réels, un problème continu : la commande d'une machine synchrone à aimant permanent, et un autre discret : le problème d'affectation de fréquences dans les réseaux cellulaires.

2.2 Commande en vitesse des machines synchrones à aimant permanent (MSAP)

Les machines synchrones à aimant permanent (MSAP) sont de grand intérêt, particulièrement dans les applications industrielles de faible et moyenne puissance, puisqu'elles possèdent de bonnes caractéristiques telles que la compacité de la dimension, bons rapports couple/poids et couple/inertie et l'absence des pertes dans le rotor [Slemon, 1994]. Cependant, la performance de MSAP est très sensible aux variations de paramètres et aux perturbations externes de charge dans le système.

La conception du contrôleur conventionnel, i.e., Proportionnel-Intégrateur (PI), est basée sur un modèle mathématique du dispositif utilisé, qui peut souvent être inconnu, non-linéaire, complexe et multi-variable avec variation de paramètres. De ce fait, le contrôleur conventionnel PI ne présente pas, en général, une solution utile pour la commande du moteur MSAP. Pour surmonter ces problèmes, plusieurs stratégies de commande ont été proposées pour la commande en vitesse des MSAP, notamment par : la logique floue [Lee, 1990], [Akcayol et al, 2002], les réseaux de neurones artificiels [Lin et Lee, 1991] [Rahman et Hoque, 1998], les algorithmes génétiques [Loukdache et al, 2007], et par les essaims particulaires [Benameur et al, 2007].

Dans les sections suivantes nous décrivons la modélisation des MSAP, nous présentons les résultats de simulation relatifs à l'utilisation d'un PI basé sur les essaims particulaires (PIPSO) [Benameur et al, 2007] et nous comparons enfin les résultats avec ceux obtenus par l'utilisation des algorithmes génétiques (PIGA) [Loukdache et al, 2007].

2.2.1 Modélisation d'une machine synchrone à aimant permanent

La configuration du système de commande des MSAP est donnée par la figure (2.1). Le système de commande se compose d'un contrôleur de vitesse, d'un régulateur de courant, d'un contrôleur de courant à bande d'hystérésis, d'un onduleur triphasé et d'un capteur de position.

è_r représente la position du rotor, w_r est la vitesse actuelle, i^* a, i^* b, i^* _c, sont les courants de phase de référence et e_w désigne l'erreur en vitesse. e_w est la différence entre la vitesse de référence w* r et la vitesse actuelle w_r. Utilisant l'erreur en vitesse e_w, le contrôleur de vitesse génère un courant appelé courant de référence ou courant de contrôle I^*.

La figure (2.2) illustre le circuit équivalent de MSAP et de l'onduleur triphasé.



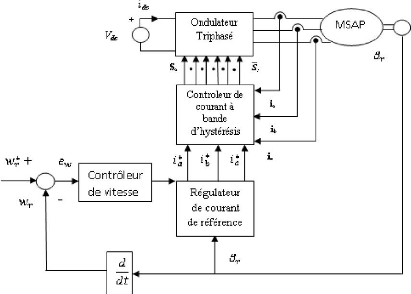
FIG. 2.1 - Schéma de la commande en vitesse de MSAP



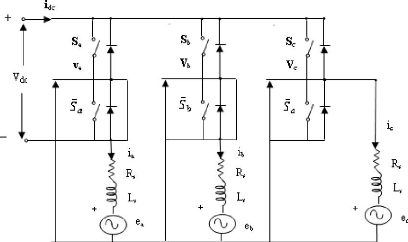
FIG. 2.2 Circuit équivalent de MSAP et de l'onduleur triphasé

Les équations de tension au niveau du stator de la MSAP sous forme matricielle sont données par l'équation (2.1).

?
?

V_a

Vb

V_c

? ? ? ? ? ? ? ? ? ? ?

R_s 0 0 i_a L_s 0 0 i_a e_a

d

? = ? 0 R_s 0 ? ? ib ? ? 0 L_s 0 ? ? ib ? + ? eb ? (2.1)

0 0 R_s i_c 0 0 Ls ^dt i_c ec

Les équations d'état associées à l'équation (3.1) peuvent être écrites selon la formule (2.2) :

d I ^ia 1 = I L_{0 s L}0 0 1-1 {[ s 1[ 1 -- [ -R_s 0 0 i_a e_a Va 1

0 -R 0 ib eb 1 [ V } (2.2)

dt I_ i_c j I_ 0 0 L_s i 0 0 -R_s i_c ec #177; Vcb

La vitesse du rotor et le couple électrique T_e peuvent être formulés selon les équations (2.3) et (2.4) :

d dtùr =

p2 (Te -- TL -- B (^2) ùr) /J (2.3) p

T_e = K I^* (2.4)

Où K = -₄ 3p ëf et ëf est le flux dû à l'aimant permanent du rotor. L'équation du contrôleur de courant de bande d'hystérésis est donnée par l'équation (2.5).

(

h_x = 1 si i^*-- i_x < 0.5h_rb

(2.5)

0 si i^* _x-- i_x > --0.5h_rb

Où, x représente a, b, c respectivement. h_x désigne la fonction du contrôleur de courant à bande d'hystérésis h_a, hb, h_c. h_rb est le rang du contrôleur de courant à bande d'hystérésis. En utilisant la fonction h_x, l'équation (2.2) peut être formulée de la façon donnée en équation (2.6) :

[ ia _{i i}

0 0 L_s 0 0 --R_s e_c

ib = [ 0 L 0

Ls s 0 -1 [ ₀

--R_s

--R_s 0¹ [ib-- [ ee:+ (-ha+²hb-hc_gb )

(-ha --F2hc)

d
dt

(2h_a

[vdc]



3

(2.6)

2.2.2 Conception d'un contrôleur PI basé sur les essaims particulaires

Le nouveau contrôleur proposé intègre le modèle PSO [Benameur et al, 2007] (figure 2.3). L'objectif principal est d'identifier les meilleurs paramètres du contrôleur conventionnel de vitesse PI (K_p et Ki), qui optimisent une fonction objectif et qui dépend particulièrement de l'erreur en vitesse reçue.

e_w représente l'erreur en vitesse et ù^* est la vitesse de référence. La fonction objective que nous souhaitons minimiser est donnée par l'équation (2.7) :

F(K_p, Ki) = a1
· e²_w(k) + a2
· (K_p
· e_w(k) + Ki
· e_w(k)
· T)² (2.7)

Où a1 et a2 représentent le poids d'importance du premier et du second terme de l'équation (2.7) respectivement, T est le temps d'échantillonnage et K_p, Ki sont les paramètres (ou les gains) du contrôleur PI.





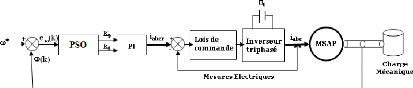
FIG. 2.3 - Contrôleur PI basé sur PSO pour la commande de MSAP

Dans cette application, les signaux de retour représentent respectivement la position 0 et les courants de phase. Le signal relatif à la position est 0 utilisé pour calculer la vitesse.

La figure (2.3) montre que le bloc (PSO) reçoit l'erreur en vitesse e_ù et fournit les paramètres optimaux (K_p, Ki) au bloc suivant PI. Ce bloc exploite ces paramètres pour générer les courants de référence optimaux _abcr. Une boucle de courants, composée d'un onduleur triphasé, produit ensuite les courants optimaux _abc qui vont être injectés dans le bloc de la machine MSAP pour qu'elle puisse atteindre la vitesse w* requise.

2.2.2.1. Implémentation de PSO pour la commande de MSAP La configuration des paramètres de l'algorithme PSO est donnée par:

- Taille de l'essaim : la première étape d'un algorithme PSO est de créer l'essaim de particules initial. La taille de l'essaim utilisée est de 50. La position et la vitesse de chaque particule sont représentées par des valeurs réelles;

Intervalle de variables : l'algorithme PSO est utilisé pour chercher les valeurs des gains du K_p et Ki contrôleur PI. Par conséquent, chaque particule aura deux positions associées à ces deux gains. Chaque position doit appartenir à un intervalle de recherche spécifique. Pour cette application, le premier paramètre (K_p) peut varier dans l'intervalle [50, 100], alors que les valeurs permises de (K_p) appartiennent à l'intervalle [1, 10];

Le facteur d'inertie ô(t) utilisé est donné par l'équation (2.8)

ô(t) = 0.9 - t * (0.5/(t + 1)) (2.8)

Les paramètres u et u, utilisés dans l'équation de la mise à jour du vecteur vitesse (équation (1.1)), sont initialisés à 2.

2.2.3 Résultats de simulation

Dans cette section, les résultats de simulation relatifs au contrôleur proposé PIPSO pour la commande en vitesse d'une machine synchrone à aimant permanent seront présentés et comparés avec ceux obtenus par l'utilisation du contrôleur conventionnel PI et des algorithmes génétiques (PIGA) [Loukdache et al, 2007].

Les paramètres, de la MSAP étudiée dans cette application, sont les suivants : - Résistance du stator : R_s = 2.875 I;

- Inductance Ld = L_q = 8.5e^-3H ;

- Inertie = 0.8e^-3kg · m² ;

- Nombre de paires de pôles = 4.

L'objectif principal de cette application étant de fournir comme entrée une vitesse de référence que la MSAP doit asservir. Pour cela, deux cas d'exemple sont étudiés. Dans le premier cas, la vitesse de référence est définie par un échelon qui varie entre 200 et 700 rd/s (figure 2.4), le couple de charge mécanique varie entre 0 et 6 N.m (figure 2.5). Pour le deuxième cas, la vitesse de référence est représentée par séquence répétitive de trapézoïdes (figure 2.6), le couple de charge mécanique étant maintenu constant durant le temps de simulation (T_m = 4 N.m) (figure 2.7).



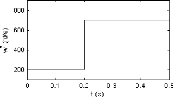
FIG. 2.4 - Vitesse de référence



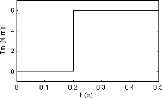
FIG. 2.5 Couple de charge mécanique



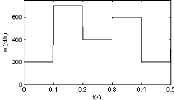
FIG. 2.6 - Vitesse de référence



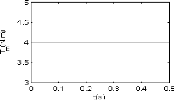
FIG. 2.7 - Couple de charge mécanique

2.2.3.1. Premier cas : Commande par échelon

Dans ce cas, la vitesse de référence et le couple de charge mécanique sont définis par des échelons (figures 2.4 et 2.5). La figure (2.8) représente la réponse temporelle de la machine à la vitesse de référence utilisant les trois stratégies de commande (contrôleurs) : le PI conventionnel (figure 2.8(a)), PIGA (figure 2.8(b)) et PIPSO (figure 2.8(c)).

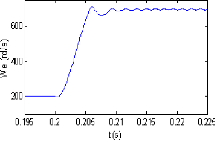
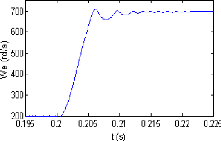
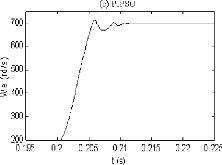
La figure (2.8(a)) montre que le temps de réponse, à la vitesse de référence utilisée, n'est pas atteint en utilisant le contrôleur conventionnel PI. Cependant, la réponse temporelle relative à PIGA est obtenue à l'instant t 0.222s (figure 2.8(b)) alors que à l'instant t 0.21s, la réponse en vitesse est atteinte utilisant PIPSO (figure 2.8(c)). Par conséquent, le contrôleur PIPSO est 94% plus rapide que la stratégie de commande PIGA.

Il est clair que la performance du contrôleur PIPSO relative à la réponse en vitesse est meilleure que celles des deux contrôleurs PIGA et du PI conventionnel.

De plus, pour illustrer la performance et l'efficacité du modèle proposé, la figure (2.9) présente la réponse en couples électromagnétiques fournie par ces trois contrôleurs.

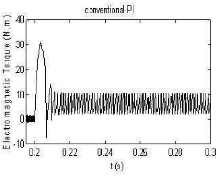
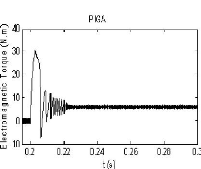
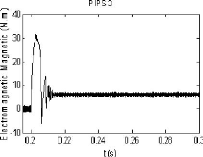
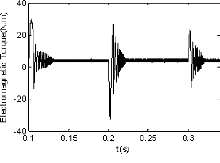
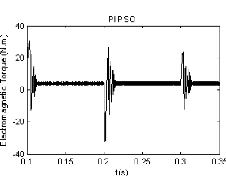
La réponse en couple électromagnétique présentée par la figure (2.9(a)), relative au contrôleur conventionnel PI, montre que les oscillations ne sont pas atténuées durant





(a)





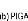
(b)



(c) FIG. 2.8 Réponse en vitesse électrique



(a)



(b)



(c) FIG. 2.9 Réponse en couple électromagnétique

tout le temps de simulation. Dans la figure (2.9(b)), les oscillations sont presque atténuées à l'instant t 0.221s utilisant le contrôleur PIGA, tandis qu'avec la stratégie de commande PIPSO, ces oscillations se réduisent à t 0.218s (figure 2.9(c)). Dans ce cas, le rapport du temps de réponse est donné par: PIGA/PIPSO = 101.4%.

2.2.3.2. Second cas : Commande par une séquence trapézoïdale

Pour ce cas, la vitesse de référence est définie par une séquence répétitive de trapézoïdes (figure 2.6), le couple est fixé à 4 N.m (figure 2.7).

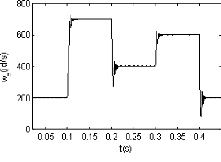
La figure (2.10) représente les réponses en vitesse relatives aux trois stratégies de commande utilisées.

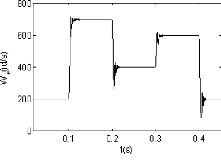
Comme illustré dans la figure (2.10), la stratégie de commande par essaims particulaires PIPSO est plus appropriée que les autres stratégies (PI Conventionnel et PIGA), dans les différentes phases de la commande de la MSAP, en termes de stabilité et de temps de réponse requis.

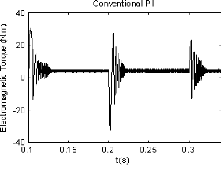
La figure (2.11) présente la réponse en couple électromagnétique. Cette figure confirme aussi les résultats conclus antérieurement.

En conclusion, à cause du comportement non linéaire du système, des perturbations, de la variation des paramètres et du couple de charge, la stratégie de commande conventionnelle s'avère inadéquate pour la commande des MSAP. En effet, utilisant le contrôleur conventionnel PI, la convergence est occasionnellement obtenue et dépend généralement d'un bon réglage des paramètres de PI.

De ce fait, le contrôleur basé sur les essaims particulaires est proposé et comparé avec celui basé sur les algorithmes génétiques. Selon les résultats de simulation obtenus, il est clair que la stratégie PIPSO fournie de meilleures réponses en vitesse et de précision que les autres stratégies.





(a)





(b)



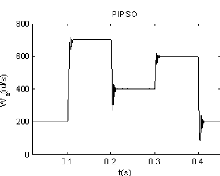
(c) FIG. 2.10 Réponse en vitesse de la MSAP



(a)





(b)



(c) FIG. 2.11 Réponse en couple électromagnétique

2.3 Problème d'affectation de fréquences (PAF)

La gestion efficace, du spectre de fréquences disponibles, est d'une importance capitale pour les opérateurs des systèmes de téléphonie cellulaire. Le coût d'exploitation du réseau et par conséquent la marge de profit dépendent en grande partie, de la capacité à réutiliser de façon optimale les canaux.

Le principe fondamental de la téléphonie cellulaire consiste à subdiviser l'espace desservi en un ensemble de cellules ou zones géographiques, et à réutiliser, chaque fois que les contraintes de compatibilité électromagnétique le permettent, les mêmes canaux à travers ces différentes cellules. Plus les canaux disponibles sont bien utilisés, moins on investira pour de nouveaux équipements dans le but d'éliminer des interférences potentielles, ou de pouvoir desservir un plus grand nombre de clients.

Il y a quelques années, le problème d'affectation de canaux se formulait comme un problème d'optimisation avec pour objectif la minimisation du nombre de canaux distincts utilisés ou la minimisation de la largeur de bande [Hale, 1981], [Hurley et al, 1997]. Ces objectifs étaient appropriés parce qu'il était encore possible d'assigner des fréquences sans engendrer des interférences. Actuellement, il s'agit de trouver des solutions acceptables en minimisant le niveau global d'interférence de fréquences affectées. Dans ce cas on parle de problème d'affectation de fréquences à spectre fixe (Fixed Spectrum Frequency Assignment Problem FS-FAP). Le fait de garder les différents types d'interférences, à un niveau minimal, conduit à un faible taux de blocage des appels, une plus grande capacité en termes du nombre de clients, une meilleure qualité de communication et des économies en investissement pour de nouveaux équipements.

2.3.1 Problématique

Le problème d'allocation de fréquences (FS-FAP) est classé dans la catégorie des problèmes NP-Complets [Kunz, 1991], [Mathar et Mattfeldt, 1993]. Ce problème peut être modélisé en un problème d'optimisation ayant la forme suivante : étant donné une bande de fréquence [fmin, fmax] subdivisée en un ensemble m de canaux (de même largeur de bande z) numérotés de 1 à un nombre maximum m donné, où m = (fmax ^-fmin)/z et un ensemble de cellules auxquelles on doit attribuer des fréquences, il s'agit de trouver une affectation qui satisfait un ensemble de contraintes et qui minimise le niveau global d'interférence des affectations de fréquences proposées.

L'allocation de canaux, aux domaines cellulaires dans un réseau radio mobile, est susceptible d'engendrer des interférences radio de sources internes. Ces interférences apparaissent entre deux canaux proches d'un point de vu spectral dans le domaine fréquentiel et émettant à partir d'émetteurs géographiquement proches. Les types d'interférences internes considérées dans le problème d'affectation de fréquences sont les suivantes :

Interférence co-cellule : représente l'interférence entre deux canaux identiques alloués à la même cellule.

Interférence co-canal : c'est l'interférence entre deux cellules auxquelles on a alloué le même canal. Typiquement, cette interférence décroît quand la distance géographique entre les deux cellules croît;

Interférence du canal adjacent : c'est l'interférence entre deux cellules adjacentes auxquelles on a alloué des canaux proches l'un de l'autre dans le plan spectral.

Ces interférences peuvent être représentées par une matrice appelée matrice de compatibilités électromagnétiques C de taille m × m, oil n est le nombre de cellules dans un réseau. Les éléments _cij de la matrice indiquent la contrainte de séparation spectrale des canaux alloués aux cellules i et j. Les éléments diagonaux _cii de la matrice de la compatibilité représentent les interférences co-cellules et les éléments non diagonaux _cij représentent soit les interférences co-canal soit les interférences de canaux adjacents.

Du fait de la nature combinatoire du problème d'affectation de fréquences, l'utilisation de méthodes de recherche exactes "Hard Computing" s'avère inexploitable, en termes de temps de calcul requis [Aardal et al, 1995], [Maniezzo et Montemanni, 1999]. De ce fait, des techniques plus appropriées ont été appliquées pour la résolution de ce problème. Ces méthodes incluent la méthode de recherche par Tabou [Montemanni et al, 2003], recuit simulé [Duque-Anton et al, 1993], algorithmes génétiques [Crompton et al, 1994], réseaux de neurones [Kunz, 1991], programmation dynamique [Shirazi et Amindavar, 2005], colonie de fourmis [Alami et El Imrani, 2006], algorithmes culturels [Alami et El Imrani, 2007] et essaims particulaires [Benameur et al, 2009a].

Dans les paragraphes suivants, nous présenterons l'implémentation d' algorithme d'optimisation discrète par essaims particulaires (DPSO) adaptés à la résolution du FS-FAP [Benameur et al, 2009b]. Les résultats de simulation, relatifs aux différentes instances utilisées dans la littérature, seront présentés et comparés ensuite avec d'autres modèles.

2.3.2 Formulation du FS-FAP

On considère un système de n cellules représenté par n vecteurs X =x1, x2,. . . , x_n. On suppose que les canaux disponibles sont numérotés de 1 à m. Une matrice de compatibilité de l'ordre m × m est utilisée pour représenter les différents types d'interférence. Soit R = r1, r2, . . . , r_n un vecteur représentant la demande en fréquence pour chaque cellule. Chaque élément ri de R représente le nombre, minimal de canaux, qui doit être assigné à la cellule xi.

Le problème FS-FAP est décrit par le triplet (X, R, C), oil X est le système cellulaire, R est le vecteur de demande et C la matrice de compatibilité. Supposons que N = 1, 2, ... ,m représente l'ensemble de canaux disponibles et Hi un sous ensemble de N assigné à la cellule xi. L'objectif principal de FS-FAP est d'identifier la meilleure affectation H = H1, H2, . . . , H_n satisfaisant les trois conditions suivantes :

|Hi| = ri, ?1 = i = n	(2.9)
|h - h^:|= cij,?h ? Hi, h^: ? Hj,?1 = i,j = n, i =6 j	(2.10)
|h - h^:| = cii,?h,h^: ? Hi, ?1 = i = n, h =6 h^:	(2.11)

Oil |Hi|désigne le nombre de canaux présents dans l'ensemble Hi.

Par conséquent, la résolution de FS-FAP consiste à identifier la meilleure combinaison qui minimise le nombre total de violation de contraintes. De façon formelle nous avons l'équation (2.12) :

_Xn
i=1

Min

_Xm
a=1

_Xn
j=1

_Xm
b=1

oil :

p(i, a)c(i, a, j, b)p(j, b) (2.12)

{

0 si |a - b| = cij c(i, a, j, b) = (2.13)
1 sinon et

(

1 si le canal a est assigné à la cellule

p(i, a) = ^,(2.14)

0 sinon

c(i, a, j, b) est égal à 1 si l'assignation du canal a à la i^ème celule et le canal b à la jème cellule viole les contraintes de compatibilité électromagnétique.

2.3.3 Implémentation de l'algorithme d'optimisation par essaims particulaires à la résolution de FS-FAP

Le FS-FAP [Benameur et al, 2010] opère uniquement sur des valeurs entières, la représentation d'une solution de FS-FAP se compose d'une séquence ordonnée de nombres entiers. De ce fait, il peut être considéré comme un problème de programmation discrète (Integer Programming IP) . Ce type de problèmes est souvent difficile à résoudre. Le but de cette étude consiste en l'application de l'algorithme d'optimisation discrète par essaims particulaires pour la résolution de FS-FAP.

PSO a été à l'origine conçu pour traiter des problèmes dont l'espace de recherche est réel multidimensionnel. Pour pouvoir appliquer PSO à la résolution de FS-FAP, le modèle utilisé doit être adapté à ce type de représentation de solution ( c-à-d. la position d'une particule est maintenant une séquance ordonnée de nombres entiers).

Le codage utilisé nécessite la redéfinition des éléments (position et vitesse) et des opérations (multiplication externe d'un coefficient par une vitesse, la somme de vitesses et la somme d'une vitesse et une position) des équations (1.1) et (1.2) du chapitre 1. En plus, il est nécessaire de déterminer comment la population initiale doit être choisie et de définir les critères d'arrêt les plus adéquats.

- Position de la particule : Une position se compose d'une solution qui représente des affectations de fréquences. Chaque membre de l'essaim se compose de Dtot paramètres entiers, oil Dtot est le nombre total de fréquences demandées dans le système cellulaire. Par exemple, une position peut être une séquence (1, 6, 10, 2, 8, 3).

- Vitesse de la particule : L' expression X2 - X1 oil X1 et X2 sont deux positions, représente la différence entre deux positions et la vitesse demandée pour aller de X1 à X2. Cette vitesse est une liste ordonnée de transformations (appelées mouvements) qui doivent être appliquées séquentiellement à la particule pour passer de sa position courante X1 en une autre X2. Un mouvement est une paire de valeurs a/j.

Pour chaque position u dans la séquence X1, l'algorithme détermine si l'unité qui est en position u de la séquence X1 est la même unité qui est en position u de la séquence X2. Si les unités sont différentes, a est l'unité en position u de X2 et j est égal à la position u. Ainsi, ce mouvement dénote que pour aller de la séquence X1 à la séquence X2, l'unité en position j doit être échangée par l'unité a. Par exemple soient X1 = (A1, B1, C2, C1, B2, C4, A2, C3) et X2 = (A1, C1, B2, C2, A2, C4, B1, C3), donc la vitesse X2 - X1 est constituée par la liste de mouvement : {(C1/2), (B2/3), (C2/4), (A2/5), (B1/7)}

X1	=	(A1, B1, C2, C1, B2, C4, A2, C3)
(C1/2)	?	(A1,C1,C2,B1,B2,C4,A2,C3)
(B2/3)	?	(A1, C1, B2, B1, C2, C4, A2, C3)
(C2/4)	?	(A1, C1, B2, C2, B1, C4, A2, C3)
(A2/5)	?	(A1,C1,B2,C2,A2,C4,B1,C3)
(B1/7)	?	(A1, C1, B2, C2, A2, C4, B1, C3) = X2

- Multiplication externe d'un coefficient par une vitesse : Les valeurs des coefficients des ô(t), u et u utilisés dans l'équation de la mise à jour du vecteur vitesse (équation (1.1) du chapitre 1) sont entre 0 et 1. Lorsqu'un coefficient est multiplié par une vitesse, il indique la probabilité de chaque mouvement à être appliquer. Par exemple, si on multiplie le coefficient 0.6 par la vitesse [(C1/2), (B2/3), (C2/4), (A2/5), (B1/7)], cinq nombres aléatoires entre 0 et 1 sont génerés pour la comparaison avec la valeur 0.6. Si le nombre aléatoire est inférieur à 0.6, le mouvement est appliqué. Par conséquent, si les valeurs des nombres aléatoires sont 0.8, 0.3, 0.7, 0.4 et 0.2, les mouvements (B2/3), (A2/5) et(B1/7) sont appliqués, tandis que les mouvements (C1/2) et (C2/4) ne sont pas appliqués. La

vitesse résultante de la multiplication est donc [(B2/3), (A2/5), (B1/7)], qui, comme précédemment indiqué, représente une liste de mouvements qu'on va appliquer à un point.

- Somme de vitesses : La somme de deux vitesses est simplement la concaténation de leur propre liste de mouvements.

- Somme de vitesse et une position : La somme d'une vitesse et une position donne le résultat d'appliquer séquentiellement chaque mouvement de la vitesse à la position.

- Population initiale : La population initiale est produite en plaçant une vitesse vide et une position aléatoire pour chaque particule.

- Critère d'arrêt : L'algorithme s'arrête après avoir effectuer un nombre prédéfini d'itérations.

2.3.4 Etude expérimentale

Afin d'améliorer les performances de DPSO, une procédure de recherche locale déterministe est appliquée à chaque itération. L'idée de base est de ramener chaque solution à son minimum local utilisant une heuristique d'optimisation locale déterministe [Li, 1995]. Cette heuristique consiste en le choix, pour chaque cellule violant les contraintes électromagnétiques, d'un canal qui valide les différentes contraintes. Les nouvelles solutions constituent les particules de la génération courante.

Le Tableau (2.1) présente les différentes caractéristiques des problèmes étudiés. Ces caractéristiques incluent le vecteur de demande en canaux (D), la matrice de contraintes électromagnétiques (C), le nombre de cellules et le nombre de fréquences disponibles. Le vecteur de demande spécifie le nombre de canaux requis par chaque cellule. Le nombre total de demande (Dtot) représente la somme des éléments de D. Ces différents vecteurs caractéristiques sont illustrés par la figure (2.12).

TAB. 2.1 - Caractéristiques des problèmes étudiés

Probleme #	No. de cellules	No. de canaux valables	Matrice de Compatibilités (C)	Vecteur de demande (D)
1	4	11	C1	D1
2	25	73		D2
3	21	381	C3	D3
4	21	533	C4	D3
5	21	533	C5	D3
6	21	221	C3	D4
7	21	309	C4	D4
8	21	309	C5	D4



FIG. 2.12 - Vecteurs caractéristiques des problèmes étudiés

Les résultats de simulation obtenus pour quelques instances des problèmes spécifiés ci-dessus sont présentés. Il faut noter que les paramètres de l'algorithme sont donnés par la taille de population et le nombre maximum de générations.

Problème #1

Ce problème est relativement simple à résoudre, l'algorithme DPSO est appliqué à une population de 10 individus évoluant durant 10 générations. Le tableau (2.2) présente les différentes affectations de fréquences associées à chaque cellule. Les solutions obtenues montrent que les contraintes de compatibilités électromagnétiques sont toutes validées. Il faut noter que plusieurs solutions ont été obtenues pour ce problème, ces solutions diffèrent uniquement par l'affectation de fréquences des trois premières cellules. En effet, l'affectation de fréquences pour la quatrième cellule illustrée par le tableau (2.2) représente la solution unique qui ne viole pas les interférences de type co-cellule.

TAB. 2.2 Fréquences affectées aux différentes cellules du problème #1

Cel.#	Canaux affectés
1	3
2	7
3	2
4	10	5	0

Problème #2

Le tableau (2.3) représente la solution associée au problème #2. Ce problème est caractérisé par 25 cellules dont le nombre total de demande en fréquences est de 167, alors que le nombre de fréquences disponibles est 73. Pour ce problème, 10 individus qui évoluent durant 10 générations sont utilisés pour l'exécution de l'algorithme DPSO.

TAB. 2.3 - Canaux alloués aux différentes cellules du problème #2

Cel.#	Canaux affectés
1	53	44	57	0	2	4	6	8	10	12
2	3	5	7	9	11	13	15	17	20	22	24
3	14	19	23	28	30	21	32	26	34
4	0	2	4	6	9
5	1	27	29	33	35	41	43	38	46
6	0	2	4	6
7	27	29	31	33	35
8	36	38	41	1	46	52	54
9	3	5	11	7
10	42	40	55	63	67	48	50	69
11	8	12	22	17	51	59	49	62
12	18	49	51	64	68	58	62	45	70
13	56	44	53	61	16	65	44	44	71	57
14	52	36	39	54	47	60	66
15	14	21	23	18	25	28	31
16	0	2	4	6	9	11
17	3	1	5	7
18	10	13	15	19	26
19	20	29	34	32	37
20	3	7	24	33	35	38	40
21	6	13	4	16	19	9
22	0	2	10	26
23	1	11	18	14	21
24	13	19	15	23	25	27	29
25	16	24	28	30	32

Problème #3

Ce problème est plus compliqué que les autres instances en termes du nombre total de demande en fréquences (= 481 canaux requis). En plus, les contraintes cocellule, données par les éléments diagonaux de la matrice, sont peu élevées (=5). Le nombre d'individus utilisé dans ce cas est fixé à 40 et le nombre maximum de générations égal à 30. Le tableau (2.4) présente les canaux affectés à chacune des 21

cellules. Les fréquences allouées à chaque cellule valident toutes les contraintes de compatibilités électromagnétiques.

TAB. 2.4 - Canaux alloués aux différentes cellules du problème #3

Cel.#	Canaux affectés
1	127	1	6	11	16	21	26	31
2	187	2	7	12	17	22	27	37	42	47	52	57	62	67
	72	77	82	87	92	97	102	107	112	117
3	122	3	8	13	18	23	28	33
4	61	1	6	11	16	21	26	31
5	40	0	5	10	15	20	25	30
6	79	0	5	10	15	20	25	30	35	40	45	50	55	60
	65
7	122	3	8	13	18	23	28	33	38	43	48	53	58	63
	68	73	78	83
8	284	4	9	14	19	41	46	51	56	61	66	71	76	81
	86	91	96	101	106	111	116	121	126	131	136	141	146	151
	156	161	166	171	176	181	186	191	196	201	206	211	216	221
	226	231	236	241	246	251	256	261	266	271
9	0	5	10	15	20	25	30	35	40	45	50	55	60	65
	70	75	80	85	90	95	100	105	110	115	120	125	130	135
	140	145	150	155	160	165	170	175	180	185	190	195	200	205
	210	215	220	225	230	235	240	245	250	255	260	265	270	275
	280	285	290	295	300	305	310	315	320	325	330	335	340	345
	350	355	360	365	370	375	380
10	36	43	48	53	58	63	68	73	78	83	88	93	98	103
	108	113	118	123	128	133	138	143	148	153	158	163	168	173
11	67	2	7	12	17	22	27	32	37	42	47	52	57
12	79	3	8	13	18	23	28	33	38	44	49	54	59	64
	69
13	156	1	6	11	16	21	26	31	36	41	46	51	56	61
	66	71	76	81	86	91	96	101	106	111	116	121	126	131
	136	141	146
14	32	2	7	12	17	22	27	37	52	57	62	67	72	77
	82
15	88	207	212	217	222	227	232	237	242	247	252	257	262	267
	272	93	98	103	108	113	118	123	128	133	138	143	148	153
	158	163	168	173	178	183	188	193
16	301	306	24	29	34	39	44	49	54	59	64	69	74	79
	84	89	94	99	104	109	114	119	124	129	134	139	144	149
	154	159	164	169	174	179	184	189	194	199	204	209	214	219
	224	229	234	239	244	249	254	259	264	269	274	311	279	286
	291
17	192	127	132	137	142	147	152	157	162	167	172	177	182	197
	202	208	213	218	223	228	233	238	243	248	253	258	263	268
18	66	4	9	14	19	41	46	51
19	87	1	6	11	16	21	26	31	36	42
20	47	2	7	12	17	22	27	32	37	52	57	62	67
21	56	3	8	13	18	23	28	33

On peut constater que la 9^ème cellule (tableau 2.4), caractérisée par le plus grand nombre de demande en fréquences (=77), exploite l'ensemble du spectre disponible sans violer les contraintes de compatibilités. En effet, la complexité de ce problème réside dans le fait que pour la neuvième cellule, il existe une solution unique qui évite toute violation de contraintes de type co-cellule, alors que le reste des contraintes doivent être validées par les autres cellules.

Problème #6

Pour ce problème, Le nombre de cellules est 21, le spectre disponible est [0...220], le nombre total de demande en canaux est 470. L'algorithme DPSO est appliqué à une population de 60 individus évoluant durant 30 générations. La solution finale obtenue à la convergence de DPSO est présentée dans le tableau (2.5).

TAB. 2.5 - Canaux alloués aux différentes cellules du problème #6

Cel.#	Canaux affectés
1	20	53	0	5	10
2	23	49	1	6	13
3	63	68	2	8	14
4	36	41	3	9	48	16	21	26
5	73	51	58	66	1	6	11	18	23	28	33	38
6	135	120	1	6	125	12	17	22	27	32	37	42	47	52
	57	62	67	72	77	82	87	92	97	102	107
7	96	63	2	7	14	19	24	29	34	39	44	50	55	68
	73	78	83	88	101	108	117	122	127	132	137	142	147	152
	157	162
8	136	76	3	9	16	21	26	31	36	41	46	51	56	61
	66	71	81	86	91	141	146	103	111	116	121
9	190	185	4	11	25	30	35	40	45	70	75	80	85	90
	95	100	105	110	115	120	125	130	135	140	145	150	155	160
	165	170
10	197	202	207	7	12	17	22	27	32	37	42	47	52	57
	62	67	72	77	82	87	92	97	102	107	112	117	122	127
	132	137	142	147	152	157	162	167	172	177	182	187
11	13	19	24	29	219	44	49	54	59	64	69	74	79	84
	89	94	99	104	109	114	119	124	129	134	139	144	149	154
	159	164	169	174	179	184	189	194	199	204	209	214
12	0	5	10	15	20	25	30	35	40	45	50	55	60	65
	70	75	80	85	90	95	100	105	110	115	120	125	130	135
	140	145	150	155	160	165	170	175	180	185	190	195	200	205
	210	215	220
13	98	103	0	5	10	15	20	25	30	35	40	45	51	56
	61	66	71	76	81	86
14	174	179	4	11	18	23	49	54	59	64	69	74	79	84
	89	94	99	104	109	114	119	124	129	134	139	144	149	154
	159	164
15	188	106	8	58	65	193	198	203	208	213	218	112	118	123
	128	133	138	143	148	153	158	163	168	173	178
16	151	60	131	28	33	38	43	48	156	161	166	171	180	189
	194
17	93	98	0	5	10	15	20	50	55	175	181	186	191	196
	201
18	61	76	81	34	39	86	46	188	53	193	198	71	203	208
	91	213	218	103	111	116	121	126	136	141	146	153	158	163
	168	173
19	97	102	1	6	12	17	22	27	32	37	42	47	52	57
	62	67	72	77	82	87
20	119	109	2	13	18	23	29	44	49	54	59	64	69	74
	79	84	89	94	99	104
21	143	96	3	8	14	21	26	31	36	41	51	56	63	68
	73	78	83	88	101	106	113	118	123	128	133

Problème #8

Pour ce système cellulaire de 21 cellules, le spectre disponible est [0...308], le nombre total de demande en canaux est 470. Le nombre des contraintes co-cellule est égal à 7. Le tableau (2.6) présente la solution obtenue utilisant une population de 60 individus qui évolue durant 30 générations.

TAB. 2.6 - Canaux alloués aux différentes cellules du problème #8

Cel.#	Canaux affectés
1	47	5	12	19	26
2	0	7	14	23	30
3	69	76	41	48	55
4	22	29	89	96	103	117	1	8
5	173	180	187	31	110	17	3	10	24	61	68	75
6	200	156	193	165	172	182	0	8	15	22	29	36	43	50
	57	64	71	78	85	92	99	106	117	124	131
7	138	145	152	159	238	250	2	10	17	24	31	38	45	52
	59	66	73	80	87	94	101	108	115	180	187	195	202	209
	216	223
8	28	229	21	56	35	42	49	63	70	77	84	91	98	111
	118	128	161	168	175	236	286	243	252	259	266
9	172	179	186	263	270	256	249	4	11	18	25	32	39	46
	53	60	67	74	81	88	95	102	109	116	123	130	137	144
	151	158
10	36	288	6	13	295	302	43	50	57	64	71	78	85	92
	99	113	120	127	134	141	148	155	162	169	176	183	190	197
	204	211	267	274	281
11	269	276	283	290	19	297	304	26	38	45	52	59	66	73
	80	87	94	101	108	115	122	129	136	143	150	157	164	171
	178	185	241	248	255
12	0	7	14	21	28	35	42	49	56	63	70	77	84	91
	98	105	112	119	126	133	140	147	154	161	168	175	182	189
	196	203	259	266	273	280	287	294	301	308
13	121	128	135	142	149	102	3	11	18	25	32	39	46	53
	60	67	74	81	88	95
14	225	190	197	204	211	218	6	13	20	27	34	41	48	55
	62	69	76	83	90	97	104	112	119	126	133	140	147	154
	162	169
15	248	122	136	143	150	157	164	171	178	185	192	199	206	213
	220	227	234	241	255	262	269	276	283	290	297
16	273	245	125	132	139	181	1	8	15	189	196	203	210	217
	224
17	174	277	284	291	193	200	20	27	62	207	214	221	105	228
	235
18	293	286	188	131	138	124	195	2	9	16	23	202	33	40
	47	54	209	216	223	230	237	244	251	258	265	272	279	145
	152	159
19	113	120	127	134	141	148	5	12	19	26	33	40	47	54
	61	71	78	85	92	99
20	108	115	129	160	146	153	3	10	17	24	31	38	45	52
	59	66	73	80	87	94
21	163	170	177	184	191	198	0	7	14	29	42	49	56	68
	75	82	89	96	103	110	117	126	133	140	149

2.3.5 Comparaison avec d'autres techniques

Le tableau (2.7) présente la comparaison entre les résultats obtenus par DPSO [Benameur et al, 2009b] et différentes techniques reportées dans la littérature, [Cheng et al, 2005], [Alami et El Imrani, 2007], [Funabiki et Takefuji, 1992], [Kim et al, 1997].

Pour pouvoir comparer les performances des techniques employées, deux critères de performances sont utilisés. Ces critères incluent le nombre d'itérations requis pour la convergence ainsi que le taux de convergence à la solution optimale. Le tableau (2.7) illustre la moyenne de ces deux critères obtenue à la suite de 100 exécutions des différentes techniques.

TAB. 2.7 - Comparaison des performances des différentes techniques pour les 8 problèmes

Méthodes	Problème #	1	2	3	4	5	6	7	8
DPSO	# d'itérations	1	5	30	40	55	60	50	60
	Taux de	100	100	100	100	100	100	100	100
	Convergence%
[Cheng et	# d'itérations	1	5	3	1	5	8.6	4	5
al, 2005]	Taux de	100	100	100	100	100	100	100	100
	Convergence%
[Alami et	# d'itérations	1	2	2	2	2.25	2.75	3.52	4
El Imrani, 2008]	Taux de Convergence%	100	100	100	100	100	100	100	100
[Funabiki	# d'itérations	212	294	147.8	117.5	100.3	234.8	85.6	305.6
et Takefuji, 1992]	Taux de Convergence%	100	9	93	100	100	79	100	24
[Kim et al, 1997]	# d'itérations Taux de	- -	279.9 62	67.4 99	64.2 100	126.8 98	62.4 97	127.7 99	151.9 52
	Convergence%

Le tableau (2.7) montre que l'implémentation de l'algorithme DPSO sur les différentes instances du problème étudié est exploitable. En effet, l'algorithme de base DPSO converge, à chaque exécution, vers une solution pour les différentes instances du problème.

Même si le nombre moyen d'itérations nécessaire à la convergence de DPSO est plus grand relativement à celui requis par les autres modèles pour quelques instances, l'application de cet algorithme reste plus adéquate du fait que la complexité de l'algorithme PSO est plus petite que celle des autres algorithmes utilisés (algorithmes culturels, réseaux de neurone).

2.4 Conclusion

L'objectif principal de ce chapitre étant d'appliquer l'algorithme d'optimisation par essaims particulaires à des problèmes d'optimisation réels, à savoir un problème continu : la commande d'une machine synchrone à aimant permanent (MSAP), et un autre discret : le problème d'affectation de fréquences dans les réseaux cellulaires.

Le problème d'optimisation MSAP est très sensible aux variations de paramètres et aux perturbations externes de charge dans le système. dans ce contexte, l'algorithme PSO a été utilisé pour surmonter les problèmes liés à l'utilisation du contrôleur conventionnel. Les résultats de simulation montre que la stratégie PIPSO fournie de meilleures réponses en vitesse et de précision que les autres stratégies (le contrôleur PIPSO est 94% plus rapide que la stratégie de commande PIGA, le rapport du temps de réponse donné par: PIGA/PIPSO est égal à 101.4%.).

D'autre part, l'algorithme PSO a été utilisé pour la résolution de problème d'allocation de fréquences, qui est classé dans la catégorie des problèmes NP-Complets. Du fait de la nature discrète de FS-FAP, les paramètres du modèle PSO doivent être adapter à la résolution de ce problème. Les résultats de simulation montrent que l'algorithme DPSO a donné de meilleurs résultats pour les différentes instances du problème étudié (en termes du nombre de taux de convergence qui est égal à 100% pour toutes les instances et en terme de temps de calcul).

Nous pouvons conclure que l'algorithme PSO est très utile dans l'optimisation globale de problèmes continu ou discret plus ou moins compliqués. Ces performances peuvent être expliquées par la nature stochastique de cette méthode et par l'équilibre qu'elle assure entre exploration/exploitation de l'espace de recherche.

Deuxième partie

Conception de nouveaux modèles

pour l'optimisation multimodale et

l'optimisation multiobjectif

Résumé

Dans la plupart des cas réels, on est confronté à deux types de problèmes difficiles : les problèmes d'optimisation multimodale, caractérisés par des domaines multimodaux, la résolution de ces problèmes requière la recherche de toutes les solutions, aussi bien locales que globales, et les problèmes multiobjectifs, caractérisés par la présence simultanée de plusieurs objectifs, souvent contradictoires. Dans ce contexte, nous avons conçu de nouvelles approches basées sur PSO et la classification floue pour résoudre ces deux types de problèmes d'optimisation difficile.

Chapitre 3

Conception d'un nouveau modèle

d'optimisation multimodale

(Multipopulation Particle Swarms

Optimization MPSO)

3.1 Introduction

Dans la pratique, on est souvent confronté à des problèmes oil on désire identifier tous les optima. Les problèmes réels, généralement caractérisés par des domaines multimodaux, requièrent, de ce fait, la recherche de toutes les solutions, aussi bien locales que globales.

L'algorithme PSO standard ne permet de localiser qu'un seul optimum dans l'espace de recherche [Kennedy et Eberhart, 1995]. Afin d'adapter l'algorithme PSO à la résolution de ce genre de problèmes, nous avons conçu un nouveau modèle MPSO (Multipopulation Particle Swarms Optimization) qui permet de créer et de maintenir des sous-populations d'essaims, de sorte que chaque sous-essaim effectue une recherche locale dans son propre espace de recherche afin de localiser la meilleure position globale qui représente un optimum.

En effet, le modèle proposé permet la formation et la maintenance de sous-populations de solutions ainsi que leur sous-espace de recherches et implémente un processus de migration en vue d'échanger des informations entre les sous-essaims voisins. Une procédure de classification automatique floue permet de générer des classes de solutions et de regrouper ainsi les solutions similaires sous forme de sous-population.

L'intérêt de la procédure de classification automatique floue réside dans le fait qu'elle permet de mieux traduire la réalité et de tenir compte de l'ambiguïté qui survient quand un même objet semble appartenir à plusieurs classes, mais avec des degrés d'appartenance différents. Aussi, cette technique n'exige aucune information préalable sur la distribution de données.

Dans ce chapitre, les différentes techniques utilisées dans le contexte d'optimisation multimodale seront décrites. Enfin la structure de base, de modèle proposé, sera présentée en détail et validée par plusieurs fonctions tests.

3.2 Problématique de l'optimisation multimodale

Lorsqu'une fonction admet plusieurs optima locaux, elle est dite multimodale (elle est unimodale dans le cas contraire). Le plus petit (respectivement le plus grand) optimum local d'une fonction multimodale, est appelé optimum global.

La figure (3.1) présente, à titre d'exemple, une distribution possible des optima d'une fonction unidimensionnelle et multimodale, ainsi que certains points particuliers, tels que les points d'inflexion et de discontinuité, pouvant poser des difficultés aux méthodes de résolution.



FIG. 3.1 - Points singuliers d'une fonction unidimensionnelle multimodale

Lorsqu'un tel problème est traité par des techniques d'optimisation (chapitre 1), l'un des optima sera découvert. Cependant, dans la pratique, on est souvent confronté à des problèmes oil on désire identifier tous les optima. Les problèmes réels, généralement caractérisés par des domaines multimodaux, requièrent, de ce fait, la recherche de toutes les solutions, aussi bien locales que globales. Dans ce contexte, plusieurs techniques ont été développées, soit pour améliorer les techniques de base en intégrant des procédures de recherche multimodale, soit en concevant de nouvelles heuristiques.

La stratégie la plus simple consiste à exécuter l'algorithme de recherche autant de fois que possible pour localiser tous les optima requis. Si tous les optima ont la même probabilité d'être trouvés, le nombre d'exécutions indépendantes est donné

approximativement par [Beasley et al, 1993] :

X p p i=1

1 i

p(ã + logp) (3.1)

Où p : nombres d'optima,ã : constante d'Euler.

Par ailleurs, dans la pratique, les optima n'ont pas la même chance d'être trouvés, de sorte que le nombre d'exécutions indépendantes est beaucoup plus élevé. D'autre part, dès que le nombre d'optima devient important, cette méthode devient très coûteuse en temps de calcul.

3.3 Techniques de l'optimisation multimodale

Plusieurs méthodes d'optimisation multimodale ont été reportées dans la littérature, ces methodes incluent les techniques de niche, qui ont été initialement introduites dans les algorithmes génétiques, afin de limiter la dérive génétique due à l'opérateur de sélection et d'explorer en parallèle différentes solutions, locales ou globales, situées dans des régions éloignées de l'espace [Säreni, 1999]. Ces caractéristiques permettent enfin d'éviter le piégeage de l'algorithme dans un optimum local.

D'autres méthodes ont été développées utilisant d'autres concepts, telles que les systèmes immunitaires artificiels [De Castro et Timmis, 2002] et les systèmes basés sur des stratégies financières [Goldberg et Wang, 1997].

3.3.1 Les méthodes de niche

Les méthodes de niche reposent sur une analogie entre les domaines de recherche en optimisation et les écosystèmes naturels. Dans la nature, Chaque espèce évolue de façon à remplir une niche écologique. Une espèce représente un groupe d'organismes identiques de caractéristiques biologiques semblables. Dans chaque niche, les ressources naturelles sont limitées et doivent être partagées entre les représentants des espèces qui l'occupent.

Par analogie, une niche se réfère typiquement à un optimum de la fonction objectif et la qualité de l'optimum représente les ressources de cette niche [Goldberg et Richardson, 1987]. Les espèces sont constituées par des groupes d'individus similaires. La mesure de la similarité entre individus est effectuée à partir d'un critère de distance et d'un seuil de dissimilarité (ou seuil de voisinage).

En principe, les techniques de niche utilisent deux stratégies. La première est basée sur la modification de la structure de certaines régions de l'espace de recherche pour prévenir la convergence de l'algorithme vers ces sections. Cette approche englobe les techniques de surpeuplement, de remplissage ou de partage. La seconde approche

impose des contraintes géographiques à la population pour prévenir la prolifération rapide d'individus très performants. Les modèles des 'îlots' et de populations isolées utilisent en général cette seconde stratégie [El Imrani, 20001.

Plusieurs méthodes de niche ont été reportées dans la littérature, incluant les méthodes : de partage [Goldberg et Richardson, 19871 et de sa version améliorée [El Imrani et al, 1999a1, [El Imrani et al, 1999b1, de niche séquentielle [Beasley et al, 19931, de niche dynamique [Miller et Shaw, 19961 ou de procédure d'éclaircissement (clearing) [Petrowski, 19961, de surpeuplement (Crowding) [Mahfoud, 19941, [Qing et al, 20081. D'autres méthodes ont été développées utilisant d'autres concepts, telles que les systèmes immunitaires artificiels [De Castro et Timmis, 20021 et les systèmes basés sur des stratégies financières [Goldberg et Wang, 19971.

Plus récemment, le concept de niche écologique a été également étendu à d'autres modèles (e.g., les essaims particulaires (PSO)). On peut citer : Nbest PSO [Brits et al, 2002a1, Niche PSO [Brits et al, 2002b1, SPSO [Li, 20041 qui améliore la technique proposée par [Kennedy, 20001, les techniques basées sur des opérations vectorielles [Schoeman et Engelbrecht, 20051. Une technique basée sur le concept de nichage séquentiel et la technique d'essaims particulaires PSO (ASNPSO), a été récemment proposée dans [Zhang et al, 20061.

3.3.1.1. La technique de partage (fitness sharing)

La méthode de partage constitue probablement la technique de niche la plus utilisée. Cette technique a été initialement introduite par Goldberg et Richardson en 1987 [Goldberg et Richardson, 19871. Elle consiste à réajuster l'adaptation de chaque individu en fonction des ressources disponibles dans son environnement local, et du nombre de congénères voisins susceptibles de lutter pour ces ressources. Le partage a pour effet de modifier l'espace de recherche en pénalisant les régions à forte densité de population. Il permet, par conséquent, de réduire la fonction fitness de chaque élément de la population par une quantité proportionnelle au nombre d'individus similaires. Cet effet incite les individus à migrer vers d'autres points de l'espace et favorise, par conséquent, l'exploration des régions inoccupées [Mahfoud, 19951. En pratique, la mise en oeuvre de la méthode de partage se fait de la façon suivante :

L'adaptation brute f(i) d'un individu i est réduite d'un facteur correspondant approximativement au nombre d'éléments, qui lui sont similaires, qui représente son compteur de niche. La fonction d'adaptation réajustée f_sh(i) d'un individu i s'écrit alors :

f(i)

f_sh(i) = _PN (3.2)

j=1 sh(d(i, j))

Le compteur de niche est calculé en sommant la fonction de partage de tous les membres de la population. N définit la taille de la population totale et d(i, j) une mesure de distance entre les individus i et j. La fonction de partage (sh) mesure le niveau de similarité entre deux individus de la population. Elle retourne 1 si les

individus sont identiques et 0 si la distance d(i, j) est plus grande qu'un certain seuil de dissimilarité [Säreni et Krähenbühl, 1998].

I 1 - (d(i,j) as )á si d(i, j) < ós sh(d(i, j)) = 0 autrement

(3.3)

où á est un paramètre qui modifie la forme de la fonction de partage. á est habituellement fixé à 1, donnant comme fonction résultante la fonction de partage triangulaire.

La distance d(i, j) peut être caractérisée par une similarité métrique génotypique (distance de Hamming) dans le cas binaire ou phénotypique (distance euclidienne par exemple) reliée directement aux paramètres réels de l'espace de recherche. Deb et Goldberg [Deb et Goldberg, 1989] montrent que l'utilisation de distance phénotypique donne des résultats légèrement meilleurs.

A l'aide de cette technique, plusieurs optima peuvent donc être découverts en même temps. Cependant, la grande difficulté de l'application de la méthode consiste dans la définition de la distance d. En effet, des individus très proches au niveau de leur génotype peuvent différer complètement au niveau de leur position dans l'espace, donc ne pas partager la même ressource. De même, des individus ayant des performances proches peuvent très bien être différents au niveau de leur génotype et donc se trouver sur des optima différents. De plus, cette technique présente un inconvénient majeur relatif au réglage du seuil de similarité.

3.3.1.2. Nichage dynamique (Dynamic Niching)

le nichage dynamique (Dynamic Niching) a été proposé par Miller et Shaw [Miller et Shaw, 1996]. Elle consiste à faire précéder le partage d'une phase de regroupement (Clustering), qui a pour rôle de rassembler et de classer les individus similaires à l'intérieur de groupes (ou niches) représentant une même sous-population. Une fois la séparation explicite des niches est effectuée, chaque individu se trouve affecté à une sous-population donnée. Le partage est alors réalisé en prenant un facteur nichage défini à partir des caractéristiques des sous-populations qui est égal au nombre d'individus appartenant à la même sous-population.

L'inconvénient majeur de cette méthode est l'utilisation de partage fixe en dehors des niches dynamiques [Goldberg et Wang, 1997].

3.3.1.3. Nichage séquentiel (Sequential Niching)

Le nichage séquentiel exécute de façon séquentielle un algorithme d'optimisation unimodal en utilisant les connaissances acquises à chaque itération pour éviter la réexploration des régions où des solutions ont déjà été trouvées [Beasley et al, 1993].

Cette méthode consiste à réajuster la fonction objectif à l'aide d'une fonction de pénalisation lorsque l'algorithme converge. L'algorithme est ensuite relancé en écartant l'optimum trouvé avec une nouvelle fonction objectif.

L'un des problèmes majeurs de la technique de nichage séquentiel est l'apparition de solutions locales inexistantes à la suite du réajustement de la fonction d'adaptation.

3.3.1.4. Méthode de sous-populations (Sub-populations Schemes)

Cette méthode introduite par Spears [Spears, 1994] consiste à associer à chaque individu un identificateur (ou label) représentatif de la sous-population à laquelle il appartient. Ces labels sont initialisés aléatoirement à la première génération selon le nombre désiré de sous-populations.

Cette technique est une variante de la méthode de partage standard, le facteur de nichage d'un individu est simplement donné par le nombre d'éléments de la sous-population à laquelle il appartient.

L'avantage de cette méthode réside dans le fait que la technique de croisement restrictif est facilement appliquée, en autorisant uniquement les croisements entre individus de la même sous-population, i.e., qui ont le même label.

Cependant, cette technique n'offre aucune garantie de détecter tous les optima de la fonction objectif, puisque plusieurs sous-populations distinctes peuvent converger vers le même optima. Cela impose le choix d'un nombre de sous-populations très supérieur au nombre d'optima requis.

3.3.1.5. La méthode d'éclaircissement (Clearing)

La méthode d'éclaircissement, similaire au schéma de partage standard, est basée sur le principe des ressources limitées dans l'environnement [Petrowski, 1996]. Elle consiste à n'attribuer les ressources d'une niche qu'aux meilleurs représentants.

En pratique, la capacité k d'une niche spécifie le nombre maximal d'individus qu'une niche peut accepter. Après avoir évalué la performance des individus dans chaque niche, cette méthode préserve les k meilleurs représentants des sous-populations respectives (dominants) et exclut les autres (dominés) de la population en réinitialisant leur adaptation.

Comme dans le cas de la méthode de partage, les individus appartiennent à une même niche si la distance qui les sépare est inférieure au seuil de similarité (Clearing radius) [Petrowski, 1996]. Cette méthode est caractérisée par une complexité temporelle moindre comparativement à la méthode de partage, mais souffre des mêmes limitations, principalement en ce qui concerne la définition du rayon de niche.

3.3.1.6. Méthode de surpeuplement (Crowding Method)

Cette méthode insère de nouveaux éléments dans la population en remplaçant des éléments similaires. Dans sa version standard, une fraction seulement de la population spécifiée par un pourcentage G se reproduit et meurt à chaque génération. Dans ce schéma, un individu remplace l'individu le plus similaire à partir d'une sous-population aléatoire de taille CF (Crowding factor). A cause des nombreuses erreurs de remplacement, cette technique a montré ses limites, l'inconvénient majeur est qu'elle retarde l'exploration de domaines qui ne sont pas proches (similaires) de la distribution initiale. D'autre part, cette méthode ne permet pas de maintenir plus de 2 niches [Mahfoud, 1992] et donc de découvrir plus de deux optima.

Ce schéma standard a été amélioré par Mahfoud en s'inspirant directement de la présélection de Cavicchio (Cavicchio 1970). Le principe est basé sur le concept de compétition entre parents et enfants descendants de la même niche. Après les opérations de croisement et éventuellement de mutation, un enfant remplace un parent s'il est mieux adapté [Mahfoud, 1994].

Cette méthode présente un avantage du fait qu'elle est caractérisée par une complexité linéaire d'ordre N. Toutefois, elle souffre du problème de dérive génétique due aux éventuelles erreurs de remplacement.

3.3.1.7. Populations co-évolutives

Ce modèle, basé sur l'interaction commerçants-clients [Goldberg et Wang, 1997], est inspiré de la compétition monopoliste. Il utilise deux populations : des clients et des commerçants. Les clients sont servis par le commerçant les plus proches. Utilisant une fonction de partage, la fitness d'un commerçant est réduite en fonction du nombre total d'autres clients servis par le commerçant le plus proche. La population des clients évolue sous un AG classique. Par contre, les commerçants tentent de maximiser le nombre de clients servis. Plus ce nombre est élevé plus la fitness du commerçant augmente.

Pour prévenir la convergence de la population de commerçants vers un seul optimum, les commerçants doivent être séparés par une distance minimale _dmin. Cette population évolue selon un mécanisme qui permet aux meilleurs clients de devenir commerçants. Pour chaque commerçant, n clients sont sélectionnés aléatoirement. Le premier client qui a la meilleure fitness, et est situé à _dmin des autres commerçants, remplace alors le commerçant d'origine dans la population [Watson, 1999].

3.3.1.8. Algorithme Génétique Co-évolutif basé sur la Classification Floue (AGCoCF)

Le modèle AGCoCF, proposé par [El Imrani et al, 1999a], est une technique qui combine la technique de partage et une méthode de classification floue, en vue d'améliorer les performances des algorithmes génétiques dans l'optimisation des fonctions multimodales.



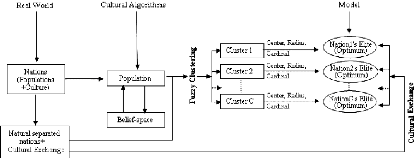
Le principe de cette technique repose sur différents concepts. D'une part, elle intègre une procédure de classification floue afin d'identifier les différentes classes, pouvant exister dans une population, correspondant à des niches. D'autre part, elle utilise une stratégie de séparation spatiale dont l'objectif est de créer des sous populations stables et de guider la recherche vers de multiples niveaux d'exploration et d'exploitation de l'espace de recherche. Pour promouvoir une certaine diversité au sein des sous populations, ce modèle implémente le concept de migration d'individus entre sous populations voisines.

Quoique le modèle AGCoCF ait fourni des performances de recherche plus élevées que le schéma de partage standard, aussi bien en terme de qualité des solutions identifiées, que par sa capacité à localiser de nouvelles solutions, il présente toutefois une complexité de l'ordre O(N²), oil N est le nombre d'individus de la population.

3.3.1.9. Multipopulation Algorithme Culturel basé sur la Classification Floue (MCAFC)

MCAFC (Multipopulation Cultural Algorithm using Fuzzy Clustering) est un nouveau modèle inspiré de l'environnement social comme représenté (Figure 3.2) [Alami et al, 2007]. Cette figure présente l'analogie entre le modèle proposé avec le monde réel. En effet, dans l'environnement réel, il y a différentes nations naturellement séparées, qui peuvent évoluer et échanger leurs cultures .

Basé sur cette analogie, le modèle MCAFC implémente un algorithme culturel de base pour faire évoluer les sous-populations de solutions et intègre une procédure de classification automatique floue, qui permet de créer les sous-populations à partir de la population initiale. Ces sous-populations sont caractérisées par leur centre ou prototype, rayon et cardinal. Dans le contexte du modèle proposé, une classe représente une nation, c.-à-d., une population ayant son propre espace de connaissance, et le centre indique l'élite de chaque nation qui correspond au meilleur individu dans la nation et donc l'optimum requis.

FIG. 3.2 - Analogie entre le monde réel, AC et MCAFC
60

3.3.2 Les systèmes basés sur l'intelligence des essaims particulaires (PSO)

Les méthodes de niche ont été étendues récemment pour pallier aux limitations que présente la méthode de base PSO, dans le contexte d'optimisation multimodale. De ce fait, plusieurs techniques ont été proposées dans la littérature.

3.3.2.1. Nbest PSO

La technique Nbest PSO a été développée par Brits, Engelbrecht et van den Bergh. Cette méthode redéfinit la meilleure position du voisinage pour augmenter la diversité pendant le partage d'informations entre les particules. En effet, pour chaque particule i, K particules voisines sont déterminées, et la meilleure position du voisinage sera définie comme le centre de masse des meilleures positions visitées par ces K particules [Brits et al, 2002a].

3.3.2.2. Niche PSO

Dans cette technique, l'essaim initial, est généré uniformément dans l'espace de recherche. La performance des particules est examinée durant les itérations. Si la fitness d'une particule reste inchangée durant quelques itérations, sa position est convertie en une solution candidat. La particule est ensuite retirée de l'essaim et un nouvel sous-essaim est crée. Durant l'évolution de cette procédure, l'essaim a tendance à perdre ses membres alors que de nouveaux sous-essaims sont générés. Ces sous-essaims, dynamiquement crées, sont censés identifier en parallèle tous les optima aussi bien globaux que locaux [Brits et al, 2002b].

3.3.2.3. PSO basé sur le concept des espèces (SPSO)

La méthode SPSO (Species Particle Swarm Optimization) proposée dans [Li, 2004] consiste à rassembler les particules semblables dans des sous-essaims appelés espèces (Species). Cette technique utilise la distance Euclidienne comme mesure de similarité. La meilleure particule dans une espèce s'appelle le noyau de l'espèce (Species Seed), et la frontière des espèces est le cercle dont le centre est le noyau de cette espèce et de rayon r₅. A chaque itération, les particules de l'essaim se déplacent dans leur propre espace du sous-essaim. Ensuite, ces particules sont évaluées et les espèces sont redéfinies. Dans cette technique, les différents optima sont maintenus d'une façon parallèle.

La performance de SPSO dépend du choix du paramètre r₅ qui représente le centre de l'espace occupé par le sous-essaim. Ce paramètre est de grande importance, puisqu' il permet d'affecter chaque particule à un sous-essaim.

3.3.2.4. PSO basé sur les opérations vectorielles

La technique de base proposée dans [Schoeman et Engelbrecht, 2004], repose principalement sur des opérations vectorielles (Vector-Based PSO : VPSO). Le principe de base réside dans le fait que le produit scalaire de deux vecteurs se dirigeant dans

différentes directions sera négatif, alors que deux vecteurs ayant la même direction auront un produit scalaire positif.

Puisque la technique de base PSO exploite les meilleurs vecteurs de position locale et du voisinage, le produit scalaire des deux vecteurs est donc calculé pour déterminer si la particule va se diriger ou s'éloigner de la meilleure position. En outre, un rayon de niche est calculé en cherchant la distance entre la meilleure position du voisinage et la particule la plus proche, qui assure un produit scalaire négatif.

Dans la version VPSO, les niches sont séquentiellement optimisées une fois qu'elles sont identifiées durant l'évolution du processus. Lorsque les niches ne sont pas symétriques, par rapport au meilleur voisinage, des niches auxiliaires peuvent être formées entre les niches déjà identifiées. De ce fait, et vue la nature des espaces de recherche qui ne sont pas nécessairement symétriques, le nombre de niches, pouvant être identifié, peut être supérieur au nombre de niches requis. Pour cela, une autre version a été introduite pour pallier aux limites de VPSO.

Cette nouvelle technique, introduite par Schoeman et Engelbrecht [Schoeman et Engelbrecht, 2005], applique un ensemble d'opérations vectorielles en parallèle pour la formation des niches dans l'espace de recherche (Parallel Vector-based PSO : PVPSO). Dans PVPSO, les niches initiales sont identifiées comme dans VPSO, mais toutes les particules sont évaluées simultanément. La mise à jour de la vitesse est accomplie en utilisant la meilleure position locale et celle du voisinage.

3.3.2.5. PSO basé sur la méthode de nichage séquentiel (ASNPSO)

L'algorithme proposé utilise plusieurs sous-essaims pour détecter séquentiellement les solutions optimales [Zhang et al, 2006], tel que chaque sous-essaim est responsable d'identifier une solution à la fois. En outre, une fonction de pénalisation 'hill valley' proposée dans [Ursem, 1999] est implémentée dans cet algorithme pour modifier la fitness des particules dans le sous-essaim actuel. Cette fonction permet d'éviter la localisation d'une solution déjà identifiée par un sous-essaim.

Il est clair que le nombre de sous-essaims, qui vont effectuer la recherche des solutions, dépend du nombre d'optima (globaux et locaux) de la fonction à optimiser. Cependant, pour des problèmes réels, on ne dispose pas du nombre de solutions optimales.

3.3.3 Les systèmes immunitaires artificiels

Ces systèmes ont été étudiés par la communauté des chercheurs en "vie artificielle" aussi bien pour leur intérêt scientifique intrinsèque, que pour l'application des concepts d'immunologie adaptés aux problèmes de calcul scientifique [Mitchell et Forrest, 1993]. Ces systèmes ont été simulés en se basant sur deux populations différentes, qui interagissent, représentées par des chaînes de bits : antigènes et anticorps.

Le principe du modèle proposé par Mitchell et Forrest est le suivant : tous les individus possèdent initialement une fitness égale à zéro. Un antigène et un ensemble d'individus sont ensuite aléatoirement choisis. L'individu le plus similaire à l'antigène remportera la compétition et sa fitness sera incrémentée [Smith et al, 1993]. L'effet de cette technique est analogue à celui du partage dans le sens oil les individus les plus similaires devraient souvent partager le coût fourni par les antigènes qui leur sont parfaitement similaires.

Ce modèle s'adresse principalement aux problèmes pratiques tels que la détection des intrusions dans les réseaux [Hofmeyr et Forrest, 1999]. Pour cela, Une version adaptée à la technique de base a été proposée [De Castro et Timmis, 2002], dont le but est de résoudre le problème d'optimisation de fonctions multimodales .

3.4 Synthèse

L'efficacité des méthodes de niche requiert souvent des connaissances a priori du rayon de niche et de la disposition spatiale des optima. Ces limitations peuvent influencer le nombre d'optima recherchés et dégrader la qualité des solutions désirées. On peut par exemple, choisir un rayon de niche assez petit pour séparer les niches, mais cela nécessite une taille de population très grande et peut conduire par conséquent à définir un grand nombre de niches sans grande importance.

La section suivante, présente les principes de base du modèle proposé basé sur l'algorithme d'optimisation par essaims particulaires et une méthode de classification floue. Cette approche surmonte les problèmes que présentent les méthodes de niches. En effet, elle ne requiert aucune information a priori sur l'espace de recherche.

3.5 Conception d'un nouveau modèle d'optimisation multimodale (MPSO)

3.5.1 Le principe du modèle

L'idée principale de ce modèle est d'encourager et maintenir la formation de sous populations d'essaims, le modèle proposé intègre une technique de classification floue permettant d'identifier les differentes sous populations. Ainsi, chaque classe de particule (ou essaim) effectue une recherche locale dans son propre espace de recherche et cherche à localiser les differents optima.

Le principe du modèle MPSO est basé sur une stratégie à trois-couches (figure 3.3) [Alami et al, 2009]. La première couche intègre un algorithme d'optimisation par essaims particulaires de base. La sortie de ce niveau constitue l'entrée de la deuxième couche (FC). Cette couche est basée sur un algorithme de classification floue non supervisé, qui permet de partitionner la population en un ensemble de (C) classes. Chaque classe identifiée correspond à un essaim (sous-population). La dernière couche implémente le principe de la séparation spatiale pour créer les différents sous-essaims à partir des caractéristiques fournies par la couche FC, i.e., centre, rayon et cardinal de chaque classe identifiée. Une fois les sous essaims sont crées, une stratégie de migration est appliquée afin de promouvoir un certain degré de diversité au sein des essaims et d'améliorer la qualité des solutions trouvées. Les sous-essaims ainsi engendrés vont co-évoluer en utilsant l'algorithme de base PSO.











FIG. 3.3 MPSO strategy

Dans la section suivante, les différentes couches du modèle sont présentées, le fonctionnement du modèle est ensuite décrit plus en détail. Un ensemble de fonctions tests permet enfin de valider le modèle et de comparer les résultats obtenus avec d'autres méthodes d'optimisation multimodale.

3.5.2 La couche de classification automatique floue

C'est une approche qui cherche à détecter la présence éventuelle de classes homo-
gènes au sein d'un ensemble d'observations multidimensionnelles X = {x1, x2, ..., x_n} ?

Rp, de structure totalement inconnue a priori. Elle ne fait aucune hypothèse préalable sur le nombre de classes à détecter et suppose que les données sont entièrement non étiquetées.

Cette méthode est constituée de deux étapes [Bouroumi et al, 2000]. La première étape est une procédure d'apprentissage flou qui explore les données de X, moyennant une mesure de similarité inter-objets et un seuil associé S_mi_n, en vue d'y détecter la présence éventuelle de classes plus au moins séparées. Elle fournit, en plus du nombre c de classes détectées dans X, une bonne estimation des prototypes V = {v1, v2, . . . , v_c} ? R^c × Rp et de la matrice des degrés d'appartenance U = {u1, u2, . . . , u_c} ? R^c × Rⁿ. La seconde étape est une procédure d'optimisation qui applique l'algorithme des C-moyens flous, initialisé avec les résultats de la première étape, notamment le nombre de classes c et la matrice des prototypes V.

Phase d'apprentissage

Cette procédure cherche à exploiter l'information, apportée par les vecteurs de X, dans le but de détecter la présence éventuelle de groupements homogènes au sein de X. Pour cela, elle commence par générer une première classe dont le prototype (centre) est initialisé avec le premier vecteur objet analysé. Ensuite, les (n-1) autres vecteurs objets sont séquentiellement examinés. Une nouvelle classe est automatiquement créée chaque fois que l'objet traité présente un faible degré de similarité, i.e., inférieur à un seuil donné S_mi_n, par rapport aux différents centres de classes déjà créées.

Pour mesurer la similarité entre deux vecteurs xi et xj de Rp, l'expression (3.4) est utilisée :

s(i, j) = 1 - d(xi, xj) vp

= VEio=1 11xik - xjk11^2 1 - (3.4) vp

oil d(xi, xj) est une mesure de distance Euclidienne, calculée à partir des valeurs normalisées de xi et xj. Pour normaliser la K^ème composante de chaque vecteur (1 = k = p), oil p est la dimension de l'espace des objets (nombre total de paramètres), la relation suivante a été utilisée :

x i ? max(k) - min(k) xi - min(k)

(3.5)

x^k_i représente le K^ème composante (valeur) du i^ème vecteur objet, max(k) et min(k) désignent respectivement les valeurs maximale et minimale prises par cette composante sur l'ensemble des vecteurs de X.

En remplaçant, dans l'équation (3.4), xj par le représentant (prototype) de la classe j (vj), la relation peut également être interprétée comme le degré d'appartenance de l'objet xj à la classe j.

d(xi, vj)

uij = 1 - (3.6)

vp

Lors du processus d'apprentissage, l'équation (3.6) est effectivement utilisée à chaque itération pour évaluer le degré d'appartenance de l'objet courant à chacune des c classes existantes (avec c variable). La condition de création d'une nouvelle classe peut alors s'exprimer sous la forme :

max(uij) < Smin (3.7)

i=j=c

Lorsque la condition (3.7) n'est pas vérifiée, les C prototypes des classes précédemment créées sont actualisés selon la règle d'apprentissage donnée par l'équation (3.8) :

vi(k) = vi(k - 1) + uik

çi(k)[xk - vi(k - 1)] (3.8)

oil çi(k) dénote le cardinal flou de la i^ème classe à l'itération k, soit :

çi(k) = _Xk uij (3.9)

j=1

Il est clair que le choix du paramètre _Smin joue un rôle essentiel dans le processus d'apprentissage. Théoriquement, si à la limite _Smin est très faible ( 0%), une seule classe, formée des n objets de X, peut être obtenue (C = 1). Inversement, si _Smin est trop élevé ( 100%), chaque objet peut former une classe à part et on aura (C = n).

Intuitivement, pour découvrir les groupements naturels supposés présents dans X, une valeur adéquate de _Smin doit être typiquement inférieure aux similarités inter-classes et supérieure aux similarités intra-classes. Il sera donc plus commode de faire varier _Smin entre 2 valeurs S1 et S2 qui dépendent de l'ensemble X et qui sont automatiquement déterminées par l'algorithme selon les équations suivantes :

S1 = min{S(xi, xk)} (3.10a)

i6=k

S2 = max i6=k

{S(xi, xk)} (3.10b)

Généralement, lorsqu'un algorithme produit une C-partition des données, plusieurs questions surviennent à propos de la qualité de la partition obtenue, du degré de confiance qu'on peut lui attribuer, de la possibilité de trouver une partition meilleure, etc. C'est le problème de validation des résultats qui constitue le dernier stade du modèle. Ce problème est intimement lié à toute classification automatique et traite de la validité de la structure des données produite par un algorithme.

Pour valider les résultats de classification, plusieurs critères de validité ont été testés. Ceux-ci incluent le coefficient de partition [Bezdek, 1981], l'indice de Xie et de Beni [Xie et Beni, 1991], l'indice de Fukuyama et de Sugeno, l'indice de Bensaid et le critère d'entropie [Bezdek, 1981]. Les résultats expérimentaux ont prouvé que, dans cette étude, le critère de l'entropie (h) est l'index le plus fiable. Ce critère

dépend uniquement de la matrice des degrés d'appartenance U et est donné par la formule (3.11) :

1 1

h(U) = -- ÓC j=1uij log(uij) (3.11)
log(C) n

Phase d'optimisation

La seconde phase de l'approche de classification floue sert à améliorer la partition apprise, générée lors de la phase d'apprentissage. En général, la procédure utilisée est basée sur l'algorithme C-moyennes (C-means) floues (CMF) [Bezdeck, 1981].

L'algorithme des C-moyennes floues est une extension directe de l'algorithme classique, oil la notion d'ensemble flou est introduite dans la définition des classes. L'algorithme des C-moyennes est l'exemple type des algorithmes de "clustering" (regroupement). Le principe de base, qui reste inchangé dans la version floue, est de former C groupes qui soient les plus homogènes et naturels possibles. CMF est une technique d'optimisation qui cherche à minimiser la somme pondérée des carrées des distances interclasses.

Dans l'algorithme des C-moyennes, on suppose que le nombre de classes C est connu. En fait, l'implémentation de cet algorithme présuppose que le nombre de classe est déterminé préalablement lors de la phase d'auto-apprentissage.

Les étapes de l'algorithme des C-moyennes se déroulent de la manière suivante (C fixé) :

1. Utiliser la matrice d'appartenance générée par la phase d'apprentissage,

2. Calculer les centres des classes,

3. Réajuster la matrice d'appartenance suivant la position des centres,

4. Calculer le critère d'arrêt : s'il n'a pas convergé, retourner à l'étape 1.

Enfin, une procédure de "defuzzification" est utilisée pour affecter définitivement chaque objet à sa classe naturelle, i.e., pour laquelle il présente le degré d'appartenance le plus élevé. On obtient ainsi une partition classique à C classes représentées par leurs centres (prototypes) vi, (1 i C).

3.5.3 La couche de séparation spatiale

Le concept de séparation spatiale est implémenté dans MPSO pour deux raisons. D'une part, dans la nature, les essaims sont divisés en un certain nombre de sousessaims qui peuvent interagir. D'autre part, le fait d'avoir plusieurs sous-essaims permet d'avoir une bonne implémentation parallèle du modèle et donc une efficacité vis-à-vis du temps de calcul [Pelikan et Goldberg, 2001].

Dans le modèle que nous avons proposé, l'objectif principal de cette couche est d'induire une géographie locale dans l'essaim et de forcer une coopération locale au sein de cette structure. Elle consiste en la formation de sous-essaims en utilisant les résultats de la procédure de classification. À chaque cycle, un sous-essaim est formé en utilisant le centre et le rayon de la classe correspondante.

3.5.4 Le concept de migration

Une fois les sous essaims sont crées, une stratégie de migration est appliquée afin de promouvoir un certain degré de diversité au sein des essaims et d'améliorer la qualité des solutions trouvées. Le processus de migration permet d'avoir un échange entre les sous-essaims dans la structure multi-essaims. Les paramètres les plus importants de la migration sont la topologie de connection entre les sous-essaims, le taux de migration,(la fraction de la population qui va migrer), la fréquence de migration, et la règle pour choisir les migrateurs et pour remplacer les individus existants. La stratégie utilisée dans cette étude est définie comme suit :

1. Définir une structure de voisinage en utilisant la distance entre les différents centres de classes;

2. Pour chaque sous-essaim

Choisir aléatoirement in particule qui vont migrer au sous-essaim voisin, Recevoir in particules venant des sous-essaims voisins.

Il existe deux manière de choisir les particules qui vont migrer d'un sous-essaim, on peut les choisir aléatoirement ou sélectionner les meilleurs particules de sous-essaim. Aussi il y'en a deux choix pour remplacer les particules existantes dans un sousessaim par les particules migrantes des autres sous-essaim : choisir aléatoirement ou remplacer les plus mauvaises. Dans cette étude, les particules migrantes et les particules qu'elles remplacent sont choisies aléatoirement.

3.5.5 Fonctionnement du modèle

Le modèle MPSO commence par générer un essaim aléatoire S(t = 0), Les particules sont définies par leurs positions et leurs vitesses , cet essaim évolue en utilisant l'algorithme PSO. L'algorithme de classification floue non supervisée permet de partitionner l'essaim en C classes, et détermine pour chaque classe ses caractéristiques principales. De nouveaux sous-essaims sont ensuite générés en utilisant le centre et le rayon de chaque classe, cette stratégie de réinitialisation permet d'introduire une nouvelle diversité au sein des sous-essaims.

La séparation spatiale permet d'engendrer une coopération locale au niveau de chaque sous-essaim. Un processus de migration est appliqué ensuite en vue d'échanger des informations entre les sous-essaims voisins, les sous-essaims vont donc coévoluer séparément et à la fin un nouveau essaim est formée à partir des différents sous-essaims. Le processus est itéré jusqu'à ce que l'entropie (h), utilisée comme critère de validation, atteigne un minimum prédéfini (h < 10^-3). L'essaim S(t) est initialisé une seule fois dans tout le processus à la première itération t = 0. Pendant

les itérations intermédiaires, S(t + 1) = UC i=1 Si(t) oil C est le nombre de classes déterminées.

Le pseudo code du modèle proposé est donné par l'algorithme 7 [Alami et al, 2009]

algorithme 5 Pseudo-code du modèle MPSO

t - 0

Initialiser l'essaim S(t)

S(t) - PSO(S(t))

Répéter

{

FC(S(t))

Pour i = 1 to C /*C nombre de classes identifiées

Créer les sous-essaims Si(t)

Appliquer le processus de migration

Si(t) - PSO(Si(t))

Fin pour

S(t + 1) - UC i=1 Si(t)

t - t + 1 }

Tant que (h < hmin)

3.5.6 Complexité temporelle de l'algorithme

Le modèle proposé, présente une complexité additionnelle , par rapport à l'algorithme de base PSO, induite par la procédure de classification floue. Cette complexité correspond aux étapes de calcul des C centres de classes ainsi que par la distance entre chaque vecteur (n vecteurs de dimension p) et le centre de chaque classe. Ces deux étapes peuvent être effectuées en O(np). De plus, la détermination de chaque nouvelle partition, durant le cycle itératif, nécessite le calcul du degré d'appartenance de chaque vecteur à chaque classe, processus pouvant s'effectuer en O(npC). Puisque le processus est itéré jusqu'à ce que l'algorithme converge, la complexité de l'algorithme de classification flou est donc de l'ordre de O(npCt), oil t est le nombre d'itérations.

3.6 Etude expérimentale

Plusieurs fonctions tests ont été utilisées pour valider les performances du modèle proposé. Ces fonctions ont plusieurs caractéristiques, qui les rendent idéales pour tester la capacité de l'approche proposée à identifier différents optima dans un domaine multimodal. Sachant que la localisation de chaque optimum, dans l'espace de recherche, est connue a priori, il est facile de comparer la distribution de la population à la convergence à la distribution idéale des optima théoriques. Il faut noter que durant la procédure de classification floue, les objets sont représentés par les particules de l'essaim et par leur fitness.

2186 -- (x² + y -- 11)² -- (x + y² -- 7)² F6(x, y) = 2186

1

F7(x, y) = 500

_v-.24 1

+ 2_,

0.002 i=0 1+i+(x-a(i))⁶+(y-b(i))⁶

a(i) = 16[(i mod 5) -- 2] et b(i) = 16(Li/5] -- 2)



;

F8(x) =

Xn i=1

(x^2i -- 10 cos(2ðxi) + 10)

Pour pouvoir comparer les performances du modèle propose à d'autres modèles, trois critères sont utilises. Ces critères incluent :

- Le rapport maximum de pics détectés (Maximum Peaks Ratio : MPR) : determine le nombre et la qualite des optima. Il est defini par la somme des optima identifies divisee par la somme des optima reels.

_PC

MP R = Pq i=1 f(i) (3.12)

k=1 f(k)

Oil f(i) est la fonction "fitness" d'un optimum i, C represente le nombre de classes identifiees dont le centre represente l'optimum i. f(k) etant la fitness de l'optimum reel k, et q le nombre de ces optima.

- Le nombre effectif des pics maintenus (NPM) : represente la capacite d'une technique à localiser et maintenir des individus au niveau des pics pour une duree determinee.

Le nombre effectif d'évaluations de "fitness" (Number of Fitness Evaluations : NFE) : designe le nombre d'evaluations requis pour la convergence de l'algorithme. Dans cette etude, l'algorithme converge lorsque la valeur d'entropie est inferieure à 10^-3.

3.6.1 Fonctions tests

Dans cette section, les differentes fonctions tests utilisees pour illustrer les performances du modèle propose sont presentees.

F1(x) = sin⁶(5ðx)

2100)(^x₍1⁰₈^.1

F2(x) = exp^- sin⁶(5ðx)

F3(x) = sin⁶(5ð(x³⁴ -- 0.05))

2 log(2) ( xa_i0₄82 ) _sin6 _(57(x

F4(x) = exp^{- 4} -- 0.05))

F5(x) =

? ???????? ? ?????????

x + 1 si 0 < x < 1 0.4(x -- 1) si 1 < x < 2 0.24x -- 0.08 si 2 < x < 3 0.24x + 1.36 si 3 < x < 4 0.4x + 2 si 4 < x < 5 x -- 5 si 5 < x < 6

La fonction F1 admet 5 maxima uniformément espacés ayant une même valeur 1, la fonction F2 admet cinq pics de hauteurs différentes dans l'intervalle [0,1]. Les pics sont localisés approximativement aux valeurs de x : 0.1, 0.3, 0.5, 0.7 et 0.9. Les maxima sont respectivement 1.0, 0.917, 0.707, 0.459 et 0.250. La fonction F3 a cinq pics de hauteurs identiques (= 1). La fonction F4 admet cinq pics de hauteurs différentes dans l'intervalle [0, 1]. Les pics sont localisés approximativement aux valeurs de x : 0.08, 0.247, 0.451, 0.681 et 0.934. Les maxima sont respectivement 1.0, 0.948, 0.770, 0.503 et 0.250. F5 a deux maxima globaux de hauteurs 1, aussi bien qu'un maximum local localisé en x = 3 et dont la valeur est 0.64. La fonction modifiée d'Himmelblau F6 est une fonction bidimensionnelle, les variables (x et y) sont définies dans l'intervalle [-6,6]. La fonction modifiée de Himmelblau F6 contient quatre pics de hauteurs identiques (= 1) localisés approximativement en (3.58, - 1.86), (3.0, 2.0), (- 2.815, -3.125) et (- 3.78, 3.28). F7 (Shekel's Foxholes) est une fonction bidimensionnelle ayant 25 pics, oil les variables (x et y) [- 65.536, 65.536]. Les maxima de F7 sont situés en (x, y) dont les coordonnées sont (16i, 16j) oil i et j représentent tous les nombres entiers compris dans [- 2, 2], les 25 optima ont tous différentes valeurs, s'étendant de 476.191 à 499.002, l'optimum global est localisé en (- 32, 32). Enfin, la fonction de Rastrigin F8, oil --5.12 xi 5.12, i = 1, . . . , 30, a un seul minimum global ((0, 0) pour une dimension= 2), et plusieurs minima locaux. F8 avec des dimensions (de 2 à 6) est utilisée pour tester la capacité de l'approche proposée.

3.6.2 Résultats numériques

Les paramètres u et u, utilisés dans l'équation de la mise à jour du vecteur vitesse (équation (1.1)), sont initialisés à 1.02 pour toutes les fonctions tests, ô(t) varie linéairement de 0.7 à 0.2 pendant les différentes itérations. Le modèle est appliqué à un essaim de 80 particules pour les fonctions F1, F2, F3, F4 et F5. Pour la fonction F6, la taille de l'essaim est 100. Des différentes tailles de l'essaim sont testées pour détecter les optimums de la fonction F7 et les meilleurs résultats sont trouvés pour un essaim de 400 particules.

Fonction F1

Le modèle converge à la quatrième itération. Le tableau (3.1) représente l'évolution de l'entropie h et le nombre de classes détectées (C) à la première itération pour différents seuils de similarité. La meilleure partition correspond à la plus petite valeur de l'entropie.

Comme le montre le tableau (3.1), la valeur 50.6% de similarité fournit la meilleur partition (C = 5) qui correspond à la plus petite valeur d'entropie (h = 4.11E --02).

Le tableau (3.2) montre l'évolution des optima détectés, il faut noter que les centres des classes sont définis par leurs coordonnés et leurs fitness, C représente le nombre de classes identifiées.

TAB. 3.1 - Evolution de la valeur d'entropie et du nombre de classes pour les différentes valeurs de similarité

Smin(%)	C	h
31.6	2	0.417
40.6	3	0.392
50.6	5	4.11E-02
57.6	6	6.67E-02
60.6	7	4.14E-02
64.6	8	6.03E-02
67.6	10	0.138

TAB. 3.2 - Evolution de la valeur d'entropie, des centres et des rayons de classes de la fonction F1.

1^erCycle(C = 5)		2^èmeCycle(C = 5)		3^èmeCycle(C = 5)		4^èmeCycle(C = 5)
Centre Rayon		Centre	Rayon	Centre	Rayon	Centre	Rayon
(0.097, 0.917)	0.037	(0.101,0.985)	0.009	(0.1, 0.999)	0.0016	(0.1,1)	0
(0.301,0.961)	0.038	(0.299,0.989)	0.016	(0.3, 0.998)	0.004	(0.3,1)	0
(0.501,0.982)	0.010	(0.500,0.999)	0.002	(0.5,1)	0	(0.5,1)	0
(0.697, 0.955)	0.073	(0.699, 0.94)	0.019	(0.7, 0.997)	0.005	(0.7,1)	0
(0.899,0.953)	0.027	(0.899,0.992)	0.006	(0.9,0.999)	0.003	(0.9,1)	0
h	0.041		0.010		0.002		3E-06
MRP	0.954		0.981		0.999		1

L'analyse de ces résultats montre que les cinq classes détectées, au premier cycle, ne sont pas chevauchée et chaque classe contient un seul optimum. Même si les cinq optima ont été trouvés au premier cycle, les cycles suivants du processus permettent un ajustement local fin de ces optima, cet effet tend évidemment à améliorer la qualité des solutions. Ceci est confirmé par la valeur de MRP, qui vaut 0.954 au premier cycle et 1 au dernier.

La figure (3.4) représente la distribution des particules dans l'espace de recherche durant chaque cycle du processus d'évolution.

Fonction F2

Les résultats de simulation obtenus sont présentés dans le tableau (3.3).

TAB. 3.3 - Evolution de la valeur d'entropie, des centres et des rayons de classes de la fonction F2.

1^erCycle(C = 6)		2^èmeCycle(C = 5)		3^èmeCycle(C = 5)		4^èmeCycle(C = 5)
Centre	Rayon	Centre	Rayon	Centre	Rayon	Centre	Rayon
(0.144,0.122)	0.009	(0.104,0.939)	0.028	(0.101,0.988)	0.008	(0.1,1)	0
(0.298,0.889)	0.019	(0.298,0.913)	0.006	(0.299,0.916)	0.002	(0.3,0.917)	0
(0.499,0.678)	0.054	(0.499,0.691)	0.014	(0.499,0.707)	0.003	(0.5,0.707)	0
(0.698,0.440)	0.031	(0.698,0.457)	0.006	(0.698,0.459)	0.002	(0.7,0.459)	0
(0.962,0.942)	0.067	(0.897,0.251)	0.002	(0.9,0.25)	0	(0.9,0.250)	0
(0.897,0.241)	0.013	-		-		-
h	0.076		0.014		2.7 E-06		1E-05

L'analyse des classes et des rayons montre que la cinquième et la dernière classe sont chevauchées, et toutes les deux contient le même optimum au point x = 0.9.



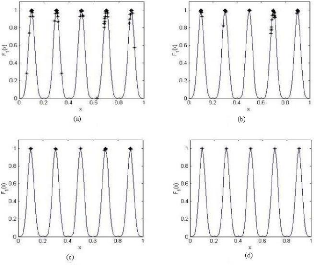
FIG. 3.4 - Placement des individus dans l'espace de recherche durant l'évolution de MPSO pour la fonction F1

Ces deux classes se recouvrent et forment une classe unique à l'itération suivante. A ce stade, même si les cinq optima sont déjà identifiés, la valeur d'entropie continue à diminuer, l'algorithme converge au quatrième cycle (h = 1E - 05). Dans ce cas, toutes les particules de même sous-essaim sont identiques et ont la même fitness (figure 3.5), ce qui correspond à un rayon de classe égal à zéro.

Fonction F3

Pour cette fonction, l'algorithme converge à la troisième itération et tous les optima sont localisés. La valeur d'entropie à la convergence du processus est égale à 6.9E - 04.

La distribution des particules dans l'espace de recherche durant chaque cycle du processus d'évolution est représentée dans la figure (3.6).

A la première itération, les particules sont aléatoirement placées dans l'espace de recherche. Ces particules se regroupent progressivement autour du plus proche pic. A la convergence de l'algorithme, toutes les particules de même sous-essaim sont identiques et ont la même fitness.



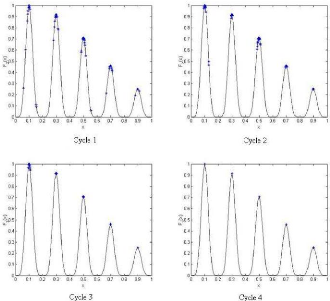
FIG. 3.5 - Distribution des individus dans l'espace de recherche durant l'évolution de MPSO pour la fonction F2



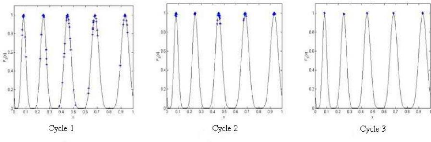
FIG. 3.6 Placement des individus dans l'espace de recherche durant l'évolution de MPSO pour la fonction F3

Fonction F4

Le processus converge à la quatrième itération quand la valeur d'entropie est égale à 9.82E - 04. La figure (3.7) représente la distribution des particules dans l'espace de recherche durant l'évolution de MPSO pour la fonction F4.



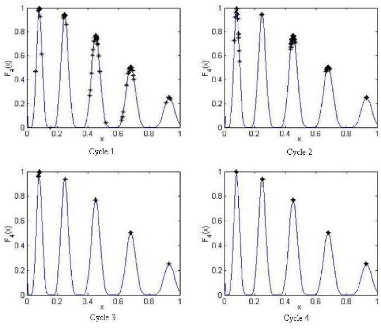
FIG. 3.7 - Placement des individus dans l'espace de recherche durant l'évolution de MPSO pour la fonction F4

Fonction F5

La figure (3.8) représente la distribution des particules dans l'espace de recherche durant les différentes itérations. A la première itération, la valeur d'entropie est proche de 0.13E - 01, quand l'algorithme converge, l'entropie prend une valeur plus petite que 2E - 04.



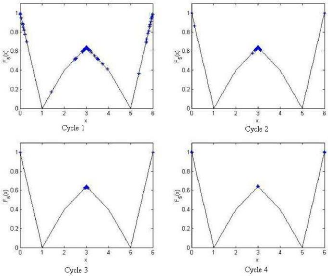
FIG. 3.8 - Placement des individus dans l'espace de recherche durant l'évolution de MPSO pour la fonction F5

Fonction d'Himmelblau F6

Les résultats obtenus sont récapitulés dans le tableau (3.4). On peut noter que le centre de chaque classe détectée est décrit par ses coordonnées (x, y).

L'analyse de ces résultats montre que, dans la première itération, les quatre classes identifiées ne se chevauchent pas et que la valeur de l'entropie est relativement grande. Dans la dernière itération, les optima identifiés sont proche des optima réel (entropie = 1E - 04). Ceci est confirmé également en suivant l'évolution de la distribution des particules dans l'espace de recherche au cours des différents cycles (figure 3.9).

TAB. 3.4 Evolution de la valeur d'entropie, des centres et des rayons de classes de la fonction F6.

1^erCycle(C = 6)		2^èmeCycle(C = 5)		3^èmeCycle(C = 5)		4^èmeCycle(C = 5)
Centre	Rayon	Centre	Rayon	Centre	Rayon	Centre	Rayon
(2.50,2.49)	(2.25,1.62)	(3.03, 1.95)	(0.59,0.07)	(3.02,1.99)	(0.16, 0.01)	(3.0, 2.00)	(0.04, 0)
(3.52,-1.91)	(2.28,0.56)	(3.64,-1.84)	(0.31,0.01)	(3.58,-1.80)	(0.08, 0.00)	(3.58, -1.80)	(0, 0)
(-3.42,-2.53)	(3.33,0.69)	(-3.77,-3.11)	(0.62,0.07)	(-3.78,-3.19)	(0.12,0.01)	(-3.77,-3.28)	(0, 0)
(-2.39,3.00)	(1.98,2.67)	(-2.79, 3.17)	(0.22,1.05)	(-2.81,3.12)	(0.02, 0.23)	(-2.8, 3.10)	(0, 0.02)
h	0.387		0.05		6.2E-03		1E-04



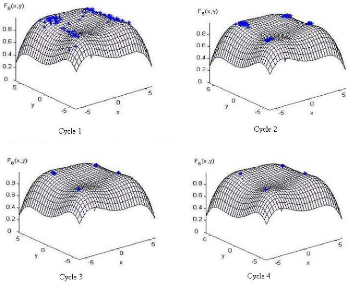
FIG. 3.9 - Placement des individus au cours les différents cycles du processus d'évolution pour la fonction F6

Fonction de Shekel F7

Le tableau (3.5) représente les résultats obtenus durant l'évolution du processus.

TAB. 3.5 - Evolution de la valeur d'entropie de la fonction F7.

	1er cycle C = 38	2^ème cycle C = 35	3^ème cycle C = 29	4^ème cycle C = 26	5^ème cycle C = 25	6^ème cycle C = 25
h	0.436	0.177	0.01	6.2E-03	2.3E-03	1.12E-05

L'analyse de ces résultats montre que 38 classes ont été détectées à la première itération, ces classes sont chevauchées et la valeur de l'entropie est relativement élevée. Au cours de la deuxième itération, 35 classes sont détectées et l'entropie continue à décroître. A partir de cinquième itération, les 25 optima sont localisés.

L'évolution des populations, durant chaque cycle du processus, est illustrée par la figure (3.10). Au premier cycle, les particules sont aléatoirement distribuées dans l'espace de recherche, durant l'évolution du processus, les particules du sous-essaim sont progressivement groupées autour de plus grand pic de la fonction F7 (figure 3.11).



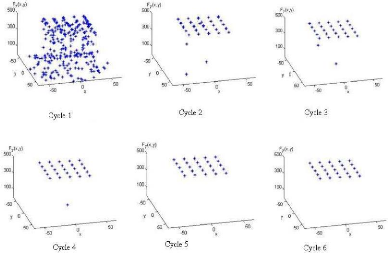
FIG. 3.10 - Placement des individus au cours les différents cycles du processus d'évolution pour la fonction F7



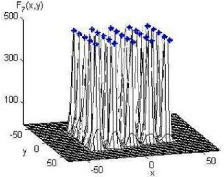
FIG. 3.11 Représentation 3-D de la distribution finale des individus dans l'espace de recherche de la fonction F7

3.6.3 Comparaisons avec d'autres techniques

Dans cette section, la comparaison entre les résultats obtenus par le modèle proposé MPSO, le modèle MCAFC et les techniques de partage, Nichage séquentiel SNGA (Sequential Niched Genetic Algorithm) [Beasley et al, 1993], SPSO (Species Particle Swarm Optimization) [Li, 2004] , Niche PSO [Brits et al 2007], nbestPSO [Brits et al 2002a] et SCGA (Species Conserving Genetic Algorithm) [Li et al, 2002] est présentée.

3.6.3.1. Comparaison entre le modèle MPSO, MCAFC et la méthode de partage

L'efficacité des méthodes d'optimisation multimodale est relative à leur capacité à maintenir les maximums des fonctions, à identifier les solutions qui sont plus proches des optima théoriques et à voir le plus petit temps de calcul. Ces performances peuvent être résumées en leurs capacités à assurer le meilleur rapport qualité-prix.

Le tableau (3.6) présente la valeur moyenne des 3 critères de performance (MPR, NPM et NFE), des modèles MPSO, MCAFC et la technique de partage, relatives aux quatre fonctions tests F4, F5, F6, et F7. Ces valeurs moyennes sont obtenues en exécutant les deux techniques 10 fois.

TAB. 3.6 - Comparaison entre le modèle MPSO, MCAFC et la méthode de partage

	Nombre de Pics Maintenus(NPM)				Rapport de pics maintenus(MPR)				Nombre Effectif d'Evaluations (NFE)
Techniques	F4	F5	F6	F7	F4	F5	F6	F7	F4	F5	F6	F7
MPSO	5	3	4	25	1	1	1	1	1600	1720	1880	17600
MCAFC	5	3	4	25	1	1	1	1	2700	1280	1800	13800
Partage	5	2.3	4	20.2	0.99	0.73	0.89	0.79	20000	40000	12150	73000

Le tableau (3.6) montre que la technique de partage est capable d'identifier tous les optima de F4 à chaque exécution. Cependant, pour quelques exécutions, elle n'arrive pas à localiser toutes les solutions possibles de F5, F6 et F7. Par contre, la moyenne du critère NPM indique que les modèles MPSO et MCAFC ont pu localiser tous les optima des 4 fonctions tests pour les différentes exécutions.

De plus, la valeur moyenne du critère MPR relative aux trois techniques, indique que la qualité des optima identifiés par les approches PMSO et MCAFC est meilleure que celle obtenue par la technique de partage.

Il est évident que les deux approches PMSO et MCAFC convergent plus rapide que la technique de partage pour toutes les fonctions. On peut remarquer que MCAFC converge légèrement plus rapide que PMSO pour les fonctions F5, F6 et F7.

En conclusion, la comparaison entre les résultats obtenus par la méthode de partage, MPSO et MCAFC confirme l'utilité et la capacité des approches MPSO et MCAFC d'assurer un meilleur rapport qualité/coût.

3.6.3.2. Comparaison entre les modèles MPSO, MCAFC, SNGA et SCGA

Pour permettre la comparaison entre le modèle proposé, MCAFC, SNGA [Beasley et al, 1993] et SCGA [Li et al, 2002], cette section présente les résultats obtenus relatifs aux fonctions F1 et F6. Le tableau (3.7) présente la valeur moyenne, calculée après 30 exécutions, du critère NFE et le taux de réussite des quatre méthodes à identifier tous les optima.

TAB. 3.7 - Comparaison des critères de performance pour les fonctions F1 et F6.

		SNGA		SCGA		MCAFC		MPSO
Fonction	Nombre d'optima	NFE	Taux de réussite	NFE	Taux de réussite	NFE	Taux de réussite	NFE	Taux de réussite
F1	5	1900	99%	3310	100%	1120	100%	1583.33	100%
F6	4	5500	76%	-	-	1800	100%	1880	100%

Comme montré dans le tableau (3.7), les deux techniques MCAFC et MPSO sont capables d'identifier toutes les solutions optimales des fonctions F1 et F6 avec un taux de 100% à chaque exécution. Toutefois, le nombre d'évaluations, requis pour la convergence du modèle MCAFC est inférieur à celui requis par la technique MPSO.

3.6.3.3. Comparaison de MPSO avec les méthodes de nichage basées sur PSO

Cette section présente la comparaison entre les résultats obtenus par le modèle proposé MPSO et les techniques : niche PSO, gbest PSO, nbest PSO et SPSO, relatives aux cinq fonctions tests F1, F2, F3, F4 et F6.

Le tableau (3.8) présente la valeur moyenne, calculée après 30 exécutions, du critère NFE et le taux de réussite des quatre méthodes à identifier tous les optima.

TAB. 3.8 - Comparaison des critères de performance pour les fonctions F1, F2, F3, F4 et F6

Fonctions tests	NichePSO		nbestPSO		MPSO
	NFE #177; dev	Taux de réussite	NFE #177; dev	Taux de réussite	NFE #177; dev	Taux de réussite
F1	2372#177; 109	100	4769#177; 45	93	1583.33#177; 135.55	100
F2	2934#177; 475	93	-	-	1670#177; 106.66	100
F3	2404#177; 195	100	4789#177; 51	93	1560#177; 293.33	100
F4	2820#177; 517	93	-	-	1600#177; 53.33	100
F6	2151#177; 200	100	5008#177; 562	100	1800#177; 66.66	100
Average	2536.2	97.2	4855.34	95.34	1642.66	100

Selon le tableau (3.8), nous constatons que le modèle proposé et NichePSO sont capables d'identifier toutes les solutions des fonctions _F1,F2 et F6 avec un taux de 100% pour toutes les exécutions. de plus, le nombre d'évaluations, requis pour la convergence, du modèle MPSO est inférieur à celui requis par les techniques NichePSO et nbestPSO.

La performance du modèle proposé est également confirmée par les résultats obtenus pour la fonction F8 (avec une dimension variante entre 2 et 6).

Le tableau (3.9) présente la moyenne des critères de performance correspondants aux modèles MPSO et SPSO.

TAB. 3.9 - Comparaison des critères de performance associés à F8

	SPSO		MPSO
Dimension	NFE (Moyen #177; stand. dev.)	Taux de succés	NFE (Moyen #177; stand. dev.)	Taux de succés	Nombre d'optima identifiés
2	3711.67#177; 911.87	100%	3120 #177; 812	100%	32.3
3	9766.67#177; 4433.86	100%	6760 #177; 3150.67	100%	25.6
4	36606.67#177; 14662.38	33.3%	30660 #177; 13568.33	100%	31
5	44001.67#177; 10859.84	26.7%	43100 #177; 11000.5	90%	29.5
6	50000.00#177; 0.00	0%	51100 #177; 10325	85%	22

D'après le tableau (3.9), l'efficacité de la nouvelle approche MPSO est validée par la valeur moyenne du nombre d'évaluations nécessaire pour la convergence, ainsi que par le nombre d'optima localisés, aussi bien globaux que locaux, et ce même lorsque la dimension de la fonction augmente. Cependant, la technique SPSO cherche seulement les minimums globaux et elle n'arrive pas à les localiser quand la dimension de la fonction augmente. Par exemple, pour la fonction F8 de dimension 6, MPSO identifie 22 optima avec un taux de succès de 85% tandis que SPSO ne localise aucun optima.

3.7 Conclusion

Dans ce chapitre, nous avons présenté une nouvelle technique d'optimisation multimodale basée sur l'intelligence collective des essaims particulaires. Cette nouvelle technique est proposée pour deux raisons : 1) soit pour pallier aux limitations des algorithmes de base, soit 2) pour résoudre les problèmes liés au réglage des paramètres, lorsqu'on est confronté à un problème d'optimisation multimodale.

Cette technique utilise une procédure de classification automatique floue pour promouvoir la formation de multiples sous-essaims et par conséquent la localisation simultanée des différents optima. Une stratégie de migration est aussi appliquée afin de promouvoir un certain degré de diversité au sein des essaims et d'améliorer la qualité des solutions trouvées.

L'objectif étant d'améliorer les performances des techniques de niche reportées dans la littérature, basées sur PSO, ces techniques sont limitées par le réglage des paramètres qui peut influencer la qualité et le nombre de solutions escomptées.

Les résultats de simulation montre que l'algorithme MPSO accompli les meilleurs performances par rapport aux autres méthodes de nichage basées sur PSO, celà est expliqué par le fait que cette approche utilise un mécanisme qui permet de subdiviser l'essaim en des sous-essaim sans avoir aucune information préalable sur la distribution de données, et ainsi, le rayon de niche est automatiquement calculé. L'algorithme MPSO permet donc de surmonter le problème majeur des autres techniques de nichage, basées sur PSO, qui réside dans l'estimation de rayon de niche.

En conclusion, l'algorithme MPSO fournit de meilleures performances comparativement aux autres modèles en assurant un meilleur rapport qualité/prix. Le prix reflète le temps de calcul nécessaire pour la localisation de toutes les solutions requises.

Chapitre 4

Conception d'un nouveau modèle

pour l'optimisation multiobjectif

4.1 Introduction

Les problèmes d'optimisation multiobjectifs (POMs) sont très fréquents dans le monde réel. Dans un tel problème, les objectifs à optimiser sont normalement en conflit entre eux, ce qui signifie qu'il n'y a pas une seule solution de ce problème. Un POM est résolu lorsque toutes ses solutions Pareto optimales sont trouvées. Cependant, il est impossible de trouver l'ensemble total de solutions Pareto-optimales, parce que le nombre de solutions, non-dominées, augmente très rapidement avec l'augmentation des objectives [Deb, 2001; DiPierro et al, 2007; Farina et Amato, 2004]. En pratique, l'utilisateur n'a besoin que d'un nombre limité de solutions bien distribuées le long de la frontière optimale de Pareto, ce qui rend la tâche d'un POM relativement plus facile.

Plusieurs algorithmes d'optimisation multiobjectifs par essaims particulaires ont été récemment proposés [Sierra et Coello, 2006], la plupart de ces algorithmes utilisent des archives externes pour stocker les solutions non-dominées trouvées le long du processus de recherche. Cependant, l'utilisation des archives fournit des complexités temporelles et spatiales additionnelles. Les derniers travaux proposent l'utilisation de méthodes inspirées des stratégies d'évolution pour améliorer les performances de ces algorithmes, cette idée a portant un prix: l'augmentation du nombre des paramètres de réglages et la complexification de l'écriture des algorithmes.

Dans ce chapitre, un nouveau modèle, l'algorithme d'optimisation multiobjectif par essaims particulaires FC-MOPSO (Fuzzy Clustering Multi-objective Particle Swarm Optimizer), basée sur PSO, la dominance de Pareto et la classification floue, est proposé. La nouveauté principale de ce modèle consiste en utilisation d'un mécanisme qui permet de fournir une meilleure distribution des solutions dans l'espace de recherche.

Le but principal du modèle proposé est de surmonter la limitation associée à l'optimisation multiobjectif par essaims particulaires standard. L'idée fondamentale, derrière cette approche est de promouvoir et maintenir la formation de sous-populations d'essaims en utilisant la technique FC. Chaque sous-essaim a son propre ensemble de leaders (les particules non-dominées) et évolue en utilisant l'algorithme PSO et le concept de la dominance de Pareto. Le concept de migration est également implémenté pour maintenir la diversité des sous-essaims, et améliorer la qualité des solutions trouvées.

Dans ce chapitre, les différentes techniques utilisées dans le contexte d'optimisation multiobjectif seront décrites. Enfin la structure de base, du modèle proposé, sera présentée en détail, validée par plusieurs fonctions tests et comparée à d'autres modèles.



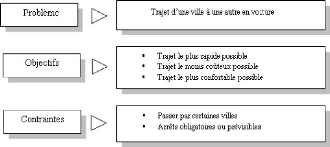
4.2 Principe de l'optimisation multiobjectif

Dans la vie quotidienne, nous résolvons des problèmes d'optimisation plus ou moins complexes. Nos achats, notre organisation, nos déplacements ne sont pas faits sans avoir réfléchi au préalable aux multiples options dont nous disposons pour aboutir à la décision nous semblant la plus appropriée. Par exemple, en prévision d'un trajet en véhicule, nous pouvons être amenés à résoudre la problématique présentée à la figure (4.1). Ces raisonnements, même s'ils paraissent anodins, font appel au concept de compromis, en ce sens que les décisions prises le sont rarement dans un contexte d'objectif unique.

Plusieurs critères sont simultanément intégrés à la réflexion, afin de dégager un choix final présentant le meilleur compromis entre tous les objectifs. cette approche nous conduit à considérer une autre catégorie de problèmes d'optimisation : les problèmes multicritères ou multiobjectifs.



FIG. 4.1 - Exemple de problème multicritère de la vie courante

4.2.1 Formulation d'un problème multiobjectif

Un problème multicritère P peut se formuler de la manière suivante : F1(X)

min[F(X)] = Fj(X) j = 1...Nobjectif

...

FNobjectif (X)

oil X = [X1...Xi...XNp_aram] , i = 1...Nparam avec gk(X) 0 , k = 1...Ncontrainte

Il s'agit de minimiser simultanément _Nobjectf objectifs Fi(X), sous un ensemble de _Ncontrainte contraintes gk(X). Le vecteur X représente l'ensemble des _Nparam variables de conception associées au problème. Dans la formulation, on ne considère

que des contraintes d'inégalité. En effet, sans perte de généralité, on remarque qu'une contrainte d'égalité de type h(X) = 0 est équivalente à deux contraintes d'inégalité h(X) = 0 et -h(X) = 0. Par ailleurs, tout problème défini en terme de maximisation peut aisément se ramener à la formulation précédente au prix de quelques transformations mathématiques.

L'union des domaines de définition de chaque variable et les contraintes forment un ensemble E qu'on appelle l'ensemble des actions réalisables. F est l'ensemble des objectifs réalisables.

La difficulté principale, de l'optimisation multicritère, est liée à la présence de conflits entre les divers objectifs. En effet, les solutions optimales, pour un objectif donné, ne correspondent généralement pas à celles des autres objectifs pris indépendamment. De ce fait, il n'existe, la plupart du temps, aucun point de l'espace de recherche oil toutes les fonctions objectifs sont optimales simultanément. Ainsi, contrairement à l'optimisation monocritère, la solution d'un problème d'optimisation multicritère est rarement unique. Elle est constituée de différentes solutions, représentant l'ensemble des meilleurs compromis vis-à-vis des objectifs du problème.

4.2.2 Exemple de problème multiobjectif

Le problème de [Schaffer, 1985] constitue un exemple simple de référence pour les problèmes multicritères. Il est défini de la manière suivante :

[ F1(X) = x2 ] min[F (X)] = F2(X) = (x - 2)^2 avec x ? [-1,3]

(4.1)

Les deux fonctions à optimiser sont tracées sur la figure (4.2), par rapport à la variable x. Comme on peut le constater, les deux objectifs du problème sont antagonistes, dans la mesure oil il n'existe aucune zone de l'espace de recherche pour laquelle leur minimisation simultanée est possible. A l'intérieur de l'intervalle [0, 2], nous notons qu'une des fonctions (F1(x)) s'éloigne de sa valeur minimale (obtenue pour x = 0) tandis que la deuxième décroit vers sa valeur optimale, en x = 2. Il n'est donc pas possible, dans cet intervalle, de minimiser un critère sans détériorer l'autre.

4.3 L'optimisation multiobjectif

En général, on rencontre deux classifications différentes des méthodes de résolution de problèmes multiobjectifs. Le premier classement adopte un point de vue utilisateur, les méthodes sont classées en fonction de l'usage que l'on désire en faire. Le deuxième classement est plus théorique, plus conceptuel, les méthodes sont triées en fonction de leur façon de traiter les fonctions objectifs.



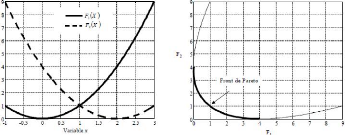
FIG. 4.2 - Problème multicritère de Schaffer

4.3.1 Choix utilisateur

Cette classification est essentiellement utilisée en recherche opérationnelle. Les décisions étant considérées comme un compromis entre les objectifs et les choix spécifiques du décideur (contraintes de cout, de temps, etc.), un décideur choisit une méthode en fonction de l'aide qu'elle va lui apporter.

les méthodes dites a priori, pour lesquelles l'utilisateur définit le compromis qu'il désire réaliser avant de lancer la méthode de résolution. On trouve dans cette famille la plupart des méthodes agrégatives, ou méthodes scalaires. Elles transforment le problème multicritère en un problème monocritère, en pondérant l'ensemble des critères initiaux.

Les méthodes progressives, pour lesquelles l'utilisateur affine son choix des compromis au fur et à mesure du déroulement de l'optimisation. Comme cela est signalé dans [Colette, 2002], ces méthodes ont l'inconvénient de monopoliser l'attention du décideur tout au long du processus d'optimisation. Cet aspect peut être pénalisant si l'évaluation, des fonctions objectifs est longue et que les sollicitations imposées au concepteur sont fréquentes.

Les méthodes dites a posteriori, pour lesquelles il n'est plus nécessaire, pour le concepteur, de modéliser ces préférences avant l'optimisation. Ces méthodes se contentent de produire un ensemble de solutions directement transmises au décideur. Il pourra alors a posteriori choisir une solution de compromis parmi celles obtenues lors de la résolution du problème.

4.3.2 Choix concepteur

Ce classement adopte un point de vue plus théorique articulé autour des notions d'agrégation et d'optimum de Pareto. Ces notions sont développées dans les paragraphes suivants, nous adoptons cette classification pour présenter les différentes méthodes.

Les méthodes agrégées : Ces méthodes transforment un problème multiobjectif en un problème simple objectif.

Les méthodes fondées sur Pareto : Ces méthodes sont fondées sur la notion de dominance au sens de Pareto qui privilégie une recherche satisfaisant au mieux tous les objectifs.

Les méthodes non agrégées et non Pareto : Certaines méthodes n'utilisent aucun des deux concepts précédents. Alors que l'agrégation ou l'utilisation de la dominance de Pareto traitent les objectifs simultanément, en général, les méthodes dites non agrégées et non Pareto possèdent un processus de recherche qui traite séparément les objectifs.

4.3.3 Les méthodes agrégées

L'ensemble de ces méthodes repose sur l'axiome suivant : tout décideur essaye inconsciemment de maximiser une fonction d'utilité U.

U = U(f1,f2,...,fK) (4.2)

Les modèles les plus couramment utilisées sont :

- le modèle additif

U = _Xk Ui(fi) (4.3)

i=1

oil Ui est la fonction de mise à l'échelle du i^èmecritère.

- le modèle multplicatif

U = _Yk Ui(fi) (4.4)

i=1

L'utilisation de ces modèles impose que les objectifs soient commensurables. Il est donc très difficile d'utiliser ces techniques lorsque l'ensemble des critères est composé à la fois de critères qualitatifs et quantitatifs.

4.3.3.1. La moyenne pondérée

Cette méthode consiste à additionner tous les objectifs en affectant à chacun un coefficient de poids. Ce coefficient représente l'importance relative que le décideur attribue à l'objectif. Cela modifie un problème multiobjectif en un problème simple objectif de la forme :

min _Xk wifi(x) avec wi = 0 (4.5)

i=1

wi représente le poids affecté au crtère i et k i=1 wi = 1

4.3.3.2. Le modèle "Goal programming"

Cette méthode est également appelée "Target Vector Optimisation" [Coello 1996, Van Veldhuizen 1999]. Le décideur fixe un but Ti à atteindre pour chaque objectif fi [Charnes 1961]. Ces valeurs sont ensuite ajoutées au problème comme des contraintes supplémentaires. La nouvelle fonction objectif est modifiée de façon à minimiser la somme des écarts entre les résultats et les buts à atteindre :

k

min i=1 |fi(x) -- Ti| avec x E F (4.6)

Ti représente la valeur à atteindre pour le i^ème objectif. F représente l'espace complet des objectifs.

Différentes variantes et applications de ces techniques ont été proposées [Ignizo, 1981; Van Veldhuizen, 1999].

4.3.3.3. Le modèle min-max

Cette méthode est assez proche de la précédente, elle minimise le maximum de l'écart relatif entre un objectif et son but associé par le décideur.

min max i

ufi(x) -- Ti) Ti )

avec i = 1, ..., k (4.7)

Ti le but à atteindre pour le i^èmeobjectif.

Dans [Coello, 1995], l'auteur présente précisément plusieurs variantes de la méthode min-max ainsi que diverses applications de celles-ci.

4.3.3.4. L'approche "Goal attainment"

Dans cette approche le décideur spécifie l'ensemble des buts Ti qu'il souhaite atteindre et les poids associés wi. La solution optimale est trouvée en résolvant le problème suivant :

minmiser á tel que (4.8)

Ti + á
· wi > fi(x)

k

avec i=0 wi = 1 4.3.3.5. La méthode e-- contrainte

Cette méthode est basée sur la minimisation d'un objectif fi en considérant que les autres objectifs fj avec j =6 i qui doivent être inférieurs à une valeur ej. En général, l'objectif choisi est celui que le décideur souhaite optimiser en priorité.

minimiser fi(x) avec (4.9)

fj(x) ej, Vj =6 i

De cette manière, un problème simple objectif sous contraintes peut être résolu. Le décideur peut ensuite réitérer ce processus sur un objectif différent jusqu'à ce qu'il trouve une solution satisfaisante. Cette méthode a été testée avec un algorithme génétique dans [Ritzel, 1994] avec différentes valeurs de c pour générer différentes valeurs Pareto-optimales.

4.3.4 Les méthodes non agrégées, non Pareto

En général, les méthodes dites non agrégées et non Pareto possèdent un processus de recherche qui traite séparément les objectifs.

4.3.4.1. Algorithme VEGA (Vector Evaluated Genetic Algorithm)

Cette méthode a été introduite par Schaffer en 1985 dans la perspective d'adapter un algorithme génétique canonique à la résolution d'un problème multiobjectif [Schaffer, 1985]. Appelée Vector Evaluated Genetic Algorithm, cette technique se différencie de l'algorithme de base uniquement par le type de sélection utilisé. L'idée est simple, si nous avons k objectifs et une population de n individus, une sélection de n/k individus est effectuée pour chaque objectif. Ainsi K sous-populations vont être crées, chacune d'entre elles contenant les n/k meilleurs individus pour un objectif particulier. Une nouvelle population de taille n est ensuite formée à partir des K sous populations. Le processus se termine par l'application des opérateurs génétiques de base (croisement et mutation).

De nombreuses variantes de cette technique ont été proposées :

Mélange de VEGA avec dominance de Pareto [Tanaki, 1995],

Paramètre pour contrôler le taux de sélection [Ritzel, 1994],

Application à un problème contraint [surry, 1995],

Utilisation d'un vecteur contenant les probabilités d'utiliser un certain objectif lors de la sélection [Kurwase, 1984].

4.3.4.2. Utilisation des genres

Cette méthode introduite par Allenson [Allenson, 1992] utilise la notion de genre et d'attracteur sexuel pour traiter un problème à deux objectifs. Une des applications de ce modèle consiste à minimiser la longueur d'un pipeline tout en réduisant l'impact écologique de sa construction. En affectant un objectif à chaque genre, l'auteur espère minimiser les deux objectifs simultanément car un genre sera toujours jugé d'après l'objectif qui lui a été associé.

Allenson utilise un algorithme génétique canonique dans lequel un nombre égal d'individus des deux genres sera maintenu. La population est initialisée avec autant de males que de femelles, puis à chaque génération, les enfants remplacent les plus mauvais individus du même genre. La création des enfants s'effectue par croisement

mais leur genre est choisi aléatoirement et leur attracteur est crée en fonction de plusieurs heuristiques différentes (aléatoire, clonage ou croisement).

En 1996, Lis et Eiben ont également réalisé un algorithme basé sur l'utilisation des genres, mais dans ce cas l'algorithme n'est pas limité à deux genres [Lis et Eiben 1996]. Il peut y avoir autant de genres que d'objectifs du problème. Ils ont également modifié le principe de croisement. Pour générer un enfant, un parent de chaque genre est sélectionné. Ensuite un croisement multipoint est effectué et le parent ayant participé le plus, en nombre de gènes, à l'élaboration de l'enfant transmet son genre. En cas d'égalité le choix s'effectue aléatoirement entre les parents égaux. L'opérateur de mutation effectue un simple changement de genre.

4.3.4.3. La méthode lexicographique

La méthode lexicographique, proposée par Fourman [fourman, 1985], consiste à ranger les objectifs par ordre d'importance déterminé par le décideur. Ensuite, l'optimum est obtenu en minimisant tout d'abord la fonction objectif la plus importante puis la deuxième et ainsi de suite.

Soient les fonctions objectifs fi avec i = 1, ..., k, supposons un ordre tel que :

f1 Â f2 Â ... Â fk

Il faut :

minimiser f1(x)

avec gj(x) satisfait ?j = 1, ..., m

Soit x^* ₁, la meilleure solution trouvée avec f* 1 = f1(x*1). f* 1 devient alors une nouvelle contrainte.

L'expression du nouveau problème est donc :

minimiser f2(x)

avec gj(x) satisfait ?j = 1, ..., m et f1(x) = f* ₁

Soit x* 2 la solution de ce problème. Le i^èmeproblème sera le suivant :

minimiser fi(x)

avec gj(x) satisfait ?j = 1, ..., m

et f1(x) = f* 1 , f2(x) = f* 2 , ..., f(i-1)(x) = f* (i-1)

La procédure est répétée jusqu'à ce que tous les objectifs soient traités. La solution obtenue à l'étape k sera la solution du problème.



Fourman a proposé une autre version de cet algorithme qui choisit aléatoirement la fonction objectif devant être prise en compte. Il en déduit que cela marche aussi bien. Cette façon de procéder équivaut à une somme pondérée dans laquelle un poids correspond à la probabilité que la fonction objectif associée soit sélectionnée.

4.3.4.4. Algorithme NGGA (A Non Generational Genetic Algorithm)

Valenzuela et Uresti ont proposé une méthode de sélection des individus non générationnelle dans laquelle la fitness est calculée de façon incrémentale [Valenzuela et Uresti, 1997]. La méthode est appliquée pour la conception de matériel électronique, l'objectif de cette application est de maximiser la performance du matériel, minimiser le temps moyen entre deux erreurs et minimiser le coût de revient. Le principe retenu consiste à utiliser un algorithme non générationnel comme dans le cas des systèmes de classifieurs [Goldberg, 1989b].

4.3.4.5. Le modèle élitiste

L'algorithme proposé dans [Ishibuchi et Murata, 1996] est basé sur une sélection de type min-max, les solutions non dominées trouvées à chaque génération forment une population externe. Les auteurs utilisent également une méthode de recherche locale pour générer de meilleurs individus.

L'utilisation d'une population externe d'individus non dominés et d'une technique de recherche locale apporte à cette méthode une capacité élitiste très importante.

Nous allons voir dans la section suivante que l'introduction de ce mécanisme de stockage associé aux stratégies de mise à jour de cette population externe et de réinjection des individus dans la population courante va inspirer beaucoup de chercheurs.

4.3.5 Les méthodes Pareto

L'idée d'utiliser la dominance au sens de Pareto a été proposée par Goldberg [Goldberg, 1989b] pour résoudre les problèmes proposés par Schaffer [Schaffer, 1985]. L'auteur suggère d'utiliser le concept d'optimalité de Pareto pour respecter l'intégralité de chaque critère au lieu de comparer a priori les valeurs de différentes critères. L'utilisation d'une sélection basée sur la notion de dominance de Pareto entraine la convergence de la population vers un ensemble de solutions efficaces. Ce concept ne permet pas de choisir une alternative plutôt qu'une autre mais il apporte une aide précieuse au décideur.

Dans les paragraphes suivants, nous définissons tout d'abord la notion de dominance au sens de Pareto et la frontière de Pareto, ensuite, nous présentons les techniques évolutionnaires utilisant cette notion.

4.3.5.1. Optimum de Pareto

Au XIX^ème siècle, Vilfredo Pareto, formule le concept suivant [Pareto, 1896] : dans un problème multiobjectif, il existe un équilibre tel que l'on ne peut pas améliorer un critère sans détériorer au moins un des autres critères.

Cet équilibre a été appelé optimum de Pareto. Un point x est dit Pareto-optimal s'il n'est dominé par aucun autre point appartenant à l'espace de recherche E. Ces points sont également appelés solutions non inférieures ou non dominées.

4.3.5.2. Notion de dominance Un point x E E domine x^' E E si :

Vi, fi(x) fi(x^') avec (4.10)

au moins un i tel que fi(x) < fi(x^')

Dans l'exemple (figure 4.3), les points 1, 3 et 5 ne sont dominés par aucun autre point. Alors que le point 2 est dominé par le point 3, et le point 4 est dominé par 3 et 5.



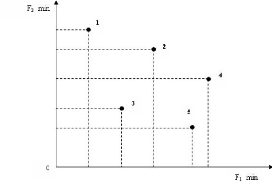
FIG. 4.3 - Exemple de dominance

Un point x E E est dit faiblement non dominé, s'il n'existe pas de point x^' E E tel que :

fi(x^') < fi(x),Vi = 1, ...,k

Un point x E E est dit fortement non dominé, s'il n'existe pas de point x^' E E tel que :

fi(x^') fi(x),Vi = 1, ...,k avec

au moins un i tel que, fi(x^') < fi(x)

4.3.5.3. Frontière de Pareto

La frontière de Pareto est l'ensemble de tous les points Pareto-optimaux. La figure (4.4) présente la frontière de Pareto pour un problème à deux objectifs.





FIG. 4.4 - Exemple de frontière de Pareto

4.3.6 Les techniques non élitistes

4.3.6.1. Algorithme MOGA (Multiple Objective Genetic Algorithm)

En 1993 Fonseca et Fleming ont proposé une méthode, dans laquelle chaque individu de la population est rangé en fonction du nombre d'individus qui le dominent [Fonseca et Fleming, 1993]. Ensuite; ils utilisent une fonction de notation permettant de prendre en compte le rang de l'individu et le nombre d'individus ayant le même rang.

Soit un individu x à la génération t, dominé par p (t) individus. Le rang de cet individu est :

rang(x ,t) = 1 + p (t) (4.11)

Tous les individus non dominés sont de rang 1. Les auteurs calculent la fitness de chaque individu de la façon suivante :

Calcul du rang de chaque individu.

Affectation de la fitness de chaque individu par application d'une fonction de changement d'échelle sur la valeur de son rang. Cette fonction est en général linéaire. Suivant le problème, d'autres types de fonction pourront être envisagés afin d'augmenter ou de diminuer l'importance des meilleurs rangs ou d'atténuer la largueur de l'espace entre les individus de plus fort rang et de plus bas rang.

L'utilisation de la sélection par rang a tendance à répartir la population autour d'un même optimum. Or cela n'est pas satisfaisant pour un décideur car cette méthode ne lui proposera qu'une seule solution. Pour éviter cette dérive, les auteurs utilisent une fonction de partage. L'objectif est de répartir la population sur l'ensemble de la frontière de Pareto.

La technique de partage agit sur l'espace des objectifs. Cela suppose que deux actions qui ont le même résultat dans l'espace des objectifs ne pourront pas être présentes dans la population.

Cette méthode obtient des solutions de bonne qualité et son implémentation est facile. Mais les performances dépendent de la valeur du paramètre _óshare utilisé dans la technique de partage. Dans leur article Fonseca et Flaming proposent une méthode de sélection de la meilleure valeur de óshare.

4.3.6.2. Algorithme NSGA (Non dominated Sorting Genetic Algorithm)

Dans la méthode proposée par [Srivinas et Deb 1993], le calcul de fitness s'effectue en séparant la population en plusieurs groupes en fonction du degré de domination au sens de Pareto de chaque individu.

1. Dans la population entière, on recherche les individus non dominés. Ces derniers constituent la première frontière de Pareto.

2. On leur attribue une valeur de fitness factice, cette valeur est supposée donner une chance égale de reproduction à tous ces individus. Cependant pour maintenir la diversité dans la population, il est nécessaire d'appliquer une fonction de partage sur cette valeur.

3. Ce premier groupe d'individu est ensuite supprimé de la population.

4. On recommence cette procédure pour déterminer la seconde frontière de Pareto. La valeur factice de fitness attribuée à ce second groupe est inférieure à la plus petite fitness après application de la fonction de partage sur le premier groupe. Ce mécanisme est répété jusqu'à ce que l'on ait traité tous les individus de la population.

L'algorithme se déroule ensuite comme un algorithme génétique classique. Srivinas et Deb utilisent une sélection basée sur le reste stochastique. Mais leur méthode peut être utilisée avec d'autres heuristiques de sélections (tournoi, roulette pipée, etc.).

4.3.6.3. Algorithme NPGA (Niched Pareto Genetic Algorithm)

Cette méthode proposée par Horn et Napfliotis utilise un tournoi basé sur la 95

notion de dominance de Pareto [Horn et Napfliotis, 1993]. Elle compare deux individus pris au hasard avec une sous-population de taille _tdom également choisie au hasard. Si un seul de ces deux individus domine le sous-groupe, il est positionné dans la population suivante. Dans les autres cas une fonction de partage est appliquée pour sélectionner l'individu.

4.3.7 Les techniques élitistes

Les approches que nous venons de voir sont dites non élitistes car:

1. Elles ne conservent pas les individus Pareto-optimaux trouvés au cours de l'évolution.

2. Elles maintiennent difficilement la diversité sur la frontière de Pareto.

3. La convergence des solutions vers la frontière de Pareto est lente. Pour résoudre ces difficultés, de nouvelles techniques ont été appliquées.

1. Introduction d'une population externe ou archive permettant de stocker les individus Pareto-optimaux.

2. Utilisation de techniques de nichage, classification et "grid-based" pour répartir efficacement les solutions sur la frontière de Pareto.

3. Préférence pour les solutions non dominées.

Les paragraphes suivants présentent différents modèles intégrants des méthodes élitistes.

4.3.7.1. Algorithme SPEA (Strength Pareto Evolutionary Algorithm)

En 1998 Zitzler et Thiele ont proposé une nouvelle méthode d'optimisation multiobjectif qui possède les caractéristiques suivantes [Zitzler et Thiele, 1998] :

Utilisation du concept de Pareto pour comparer les solutions.

Un ensemble de solutions Pareto-optimales est maintenu dans une mémoire externe appelée archive.

La fitness de chaque individu est calculée par rapport aux solutions stockées dans l'archive.

Toutes les solutions de l'archive participent à la sélection.

Une méthode de classification est utilisée pour réduire l'ensemble de Pareto sans supprimer ses caractéristiques.

Une nouvelle méthode de niche, basée sur Pareto, est utilisée afin de préserver la diversité. L'avantage essentiel est qu'elle n'exige pas de réglage de paramètres de la méthode de partage.

4.3.7.2. Algorithme PAES (Pareto Archived Evolution Strategy)

Cette méthode a été développée initialement comme méthode de recherche locale dans un problème de routage d'information off-line. Les premiers travaux de

Knowles et Corne ont montré que cette méthode simple objectif fournissait des résultats supérieurs aux méthodes de recherche basées sur une population [Knowles et Corne, 1999]. Par conséquent, les auteurs ont adapté cette méthode aux problèmes multiobjectifs. Les particularités de cette méthode sont les suivantes :

Elle n'est pas basée sur une population. Elle n'utilise qu'un seul individu à la fois pour la recherche des solutions.

Elle utilise une population annexe de taille déterminée permettant de stocker les solutions temporairement Pareto-optimales.

L'algorithme utilisé est plus simple et inspiré d'une stratégie d'évolution [Rechenberg, 1973].

Elle utilise une technique de remplissage basée sur un découpage en hypercubes de l'espace des objectifs.

4.3.7.3. Algorithme PESA (Pareto Envelope based Selection Algorithm)

La méthode PESA a été également proposée par Knowles et corne [Knowles et al., 2000]. Elle reprend approximativement le principe de crowding développé dans PAES et définit un paramètre appelé "squeeze_factor" qui représente la mesure d'encombrement d'une zone de l'espace. Alors que PAES est basé sur une stratégie d'évolution, PESA est une méthode basée sur les algorithmes génétiques. Elle définit deux paramètres concernant la taille des populations d'individus : PI (taille de la population interne) et PE (taille de la population externe ou archive).

4.3.7.4. Modèle NSGA II

Dans cette deuxième version de NSGA [Deb, 2000]; l'auteur tente de résoudre les problèmes liés à l'approche NSGA : complexité, non élitisme et utilisation du partage.

La complexité de l'algorithme NSGA est notamment due à la procédure de création des différentes frontières. Pour diminuer la complexité de calcul de NSGA, Deb propose une modification de la procédure de tri de la population en plusieurs frontières.

La deuxième difficulté liée à l'approche NSGA est l'utilisation de la méthode de partage qui exige le réglage d'un ou plusieurs paramètre(s) et qui nécessite un temps de calcul important. Dans NSGA II, Deb remplace la fonction de partage par une fonction de remplissage.

Enfin, le modèle proposé utilise une sélection par tournoi pour permettre la conservation des meilleurs individus d'une génération à l'autre.

4.3.7.5. Modèle PESA II (Region-based Selection)

PESA II est une technique de sélection basée sur l'utilisation d'hypercubes dans l'espace des objectifs [Corne, 2001]. Au lieu d'effectuer une sélection en fonction de la fitness des individus comme dans PESA, cette méthode effectue une sélection par rapport aux hypercubes occupés par au moins un individu. Après avoir sélectionné l'hypercube, on choisit aléatoirement l'individu dans l'hypercube. Cette méthode se montre plus efficace à repartir les solutions sur la frontière de Pareto. Cela est dû à sa capacité de choisir avec une plus grande probabilité que le tournoi classique, des individus situés dans des zones désertiques.

4.3.7.6. Algorithme Micro-GA (Micro-Genetic Algorithm)

Coello trouve que les recherches actuelles n'accordent pas assez d'importance à l'efficience des méthodes d'optimisation multiobjectifs. Dans [Coello et al., 2001], il propose une méthode basée sur une population avec un nombre très faible d'individus. Cette technique se base sur les résultats théoriques obtenus par Goldberg [Goldberg, 1989b].

Coello applique le mécanisme suggéré par Goldberg aux problèmes d'optimisation multiobjectifs en utilisant un algorithme génétique avec une petite taille de population associée à une archive et une heuristique de distribution géographique. Il définit une population extérieure divisée en deux parties : une partie remplaçable et une partie non remplaçable. La portion non remplaçable ne change pas durant le processus de modification et sert à maintenir la diversité. Elle ne sera mise à jour que lorsque le micro algorithme génétique aura convergé. La portion remplaçable est totalement modifiée à intervalle régulier. Ce dernier est défini en nombre de cycles du micro GA.

Au début de l'algorithme du micro GA, la population est constituée à l'aide d'individus sélectionnés aléatoirement dans la population externe. Ensuite l'algorithme se déroule de manière classique. En fin de cycle, lorsque la population du micro GA a perdu sa diversité, deux individus non dominés sont sélectionnés pour mettre à jour l'archive. L'approche utilisée est similaire à celle de PAES. Ensuite ces deux mêmes individus sont comparés à deux individus de la partie non remplaçable. Si l'un des deux premiers domine l'un des deux autres alors il le remplace dans la partie non remplaçable.

Les tests effectués par l'auteur montrent que cette approche est capable de converger plus rapidement vers la surface de Pareto (en terme de temps CPU). Mais pour le cas de fonctions avec contraintes, la méthode a été moins bonne que NSGA II. Dans quelque cas, cette méthode produit une meilleure distribution des points sur la surface de Pareto.

4.3.8 Difficultés des méthodes d'optimisation multiobjectif

Un processus d'optimisation multiobjectif doit résoudre les deux tâches suivantes :

- Guider le processus de recherche vers la frontière de Pareto,

- Maintenir une diversité des solutions pour assurer une bonne répartition sur la frontière de Pareto.

L'accomplissement de ces tâches est très délicat car les difficultés rencontrées dans un problème multiobjectif sont identiques à celles d'un problème simple objectif mais elles sont amplifiées par la présence d'objectifs dépendants les un des autres.

Le processus de recherche est souvent ralenti ou totalement dérouté par des fonctions possédant une des caractéristiques suivantes : multimodalité, isolation d'un optimum ou optimum trompeur.

-La multimodalité : Comme déjà sité dans le chapitre 3, Une fonction est dite multimodale si elle possède plusieurs optima-globaux. Dès lors, chaque optimum exerce sur les individus d'une population une attraction différente qui peut piéger le processus de convergence de l'algorithme. Ce problème peut être éviter en utilisant une technique de répartition des individus de type partage ou remplissage [Mahfoud, 1995].

-L'isolation d'un optimum : Il existe des problèmes dans lesquels un optimum peut être entouré de grandes zones pratiquement plates. Cet optimum se trouve alors isolé car l'espace de recherche qui l'entoure ne peut pas guider vers lui les individus de la population.

-Les problèmes trompeurs : Un problème est dit trompeur lorsqu'il guide la convergence vers une zone non optimale de la fonction.

Pour éviter ce problème, Deb et Goldberg recommandent l'utilisation de techniques de répartition individus en niches [Goldberg et Deb, 1992]. Ils établissent également que le choix d'une taille appropriée de la population est primordial pour éviter ce problème.

La difficulté à maintenir une bonne répartition des solutions sur la frontière de Pareto résulte principalement des caractéristiques suivantes : convexité ou non convexité de la frontière de Pareto, discontinuité de cette frontière et non uniformité de la distribution.

- non convexité de la frontière de Pareto : Certains problèmes ont une frontière de Pareto non convexe. Les méthodes dont le calcul de la fitness est basé sur le nombre d'individus dominés (MOGA, SPEA) vont être moins efficaces.

-Discontinuité de la frontière de Pareto : Si une frontière de Pareto est discontinue, on retrouve le même principe que pour une fonction multimodale. Les différentes parties de cette frontière vont exercer, proportionnellement à leur taille, une attraction plus ou moins importante sur les individus d'une population. Certaines parties pourront donc ne pas être découvertes. Les méthodes basées sur les algorithmes génétiques sont plus sensibles à ce phénomène que les méthodes utilisant des stratégies d'évolution.

-Non uniformité de répartition sur la frontière : Les solutions sur la frontière de Pareto peuvent ne pas être réparties uniformément. La raison principale vient du choix des fonctions objectifs. Par exemple; si une des fonctions objectifs est multimodale, elle va influencer de manière très différente la répartition des solutions sur la frontière de Pareto.

4.4 Optimisation multiobjectif par essaims particulaires

Il est évident que l'algorithme original PSO doit être modifié pour être adapté à la résolution des problèmes d'optimisation multiobjectifs. Comme on a vu, l'ensemble des solutions d'un problème avec multiples objectifs ne se compose pas d'une seule solution (comme dans l'optimisation globale).

Cependant, dans l'optimisation multiobjectif, il est nécessaire de trouver un ensemble de solutions (l'ensemble Pareto-optimal). Généralement pour résoudre un problème multiobjectif, il y' a trois objectifs principaux à réaliser [Zitzler et al, 2000] :

1. Maximiser le nombre des éléments de l'ensemble Pareto-optimal trouvé.

2. Minimiser la distance entre le front de Pareto trouvé par l'algorithme et le vrai (global) front de Pareto (supposant qu'on connait son endroit).

3. Maximiser la répartition des solutions trouvées, de sorte que nous puissions avoir une distribution des vecteurs la plus uniforme.

Etant donné la structure de la population de PSO, il est souhaitable de produire plusieurs (différentes) solutions non-dominées avec une seule itération. Ainsi, comme avec tout autre algorithme évolutionnaire, les trois questions posés lors de l'adaptation de PSO à l'optimisation multiobjectif sont [Coello et al, 2002] :

1. Comment choisir les particules (employées comme leader) afin de donner plus de préférence aux solutions non-dominées.

2. Comment maintenir les solutions non-dominées trouvées pendant le processus de recherche afin de rapporter les solutions non-dominées, en tenant compte de toutes les anciennes populations et non seulement de la population courante. Aussi, il est souhaitable que ces solutions soient bien réparties sur le front de Pareto.

3. Comment maintenir la diversité dans l'essaim afin d'éviter la convergence prématurée vers une seule solution.

Comme nous l'avons déjà vu, en résolvant les problèmes d'optimisation à un seul objectif, pour chaque particule, le leader qui a la meilleure des meilleures performances dont elle a connaissance, est complètement déterminé une fois une topologie de voisinage est établie. Cependant, dans le cas des problèmes d'optimisation multiobjectif, chaque particule pourrait communiquer avec différents leaders, un seul étant choisi afin de mettre à jour sa position. Un tel ensemble de leaders est habituellement stocké dans une mémoire appelée archive externe. Les solutions contenues dans les archives externes sont employées comme leaders quand les positions des particules de l'essaim doivent être mises à jour. En outre, le contenu des archives externes est souvent rapporté comme résultat final de l'algorithme.

L'algorithme général de MOPSO est décrit par le pseudo code (6). Nous avons marqué en italique les processus qui rendent cet algorithme différent de l'algorithme PSO de base de l'optimisation à un seul objectif.

algorithme 6 Pseudo code de l'algorithme général de MOPSO

Initialiser l'essaim

Initialiser l'ensemble de leaders

mesurer la qualité de leaders

t 4-- 0

tant que (t < tmax)

Pour chaque particule

Sélectionner un leader

Calculer la vitesse

Mettre à jour la position

Effectuer la mutation si c'est nécessaire Mettre à jour pbest

Fin pour

Mettre à jour les leaders dans l'archive externe mesure la qualité de leaders

t 4-- t + 1

Fin tant que

Retourner les résultats de l'archive externe

Après l'initialisation de l'essaim, un ensemble de leaders est également initialisé avec les particules non-dominées de l'essaim. Comme nous avons déjà mentionné,

l'ensemble de leaders est souvent stocké dans des archives externes. Ensuite, une mesure de qualité est calculée pour tous les leaders afin de choisir (souvent) un leader pour chaque particule de l'essaim. A chaque génération, pour chaque particule, un leader est choisi et le vol est exécuté. La plupart des MOPSOs existants applique un opérateur de mutation après l'exécution du vol. La particule est ensuite évaluée et la valeur de pbest (la meilleure position qu'elle a atteinte jusqu'ici) correspondante est mise à jour. Une nouvelle position de particule remplace sa pbest habituellement quand cette position de particule domine sa pbest ou si elles sont toutes les deux non-dominée l'une de l'autre. Après la mise à jour de toutes les particules, l'ensemble de leaders est mise à jour aussi. Finalement, la mesure de qualité de l'ensemble de guides est recalculée. Ce processus est répété pour un certain nombre d'itérations.

En résumé, pour adapter l'algorithme de base PSO à la résolution des problèmes multiobjectifs, on est confronté à deux difficultés majeures [Pulido, 2005] :

1. Choix et mise à jour des leaders

- Comment choisir un seul guide de l'ensemble des solutions non-dominées qui sont toutes bonnes, on peut le choisir d'une manière aléatoire ou on doit utiliser un critère additionnel (pour favoriser la diversité, par exemple).

Comment choisir les particules qui devraient demeurer dans les archives externes d'une itération à l'autre.

2. Création de nouvelles solutions

Comment favoriser la diversité en utilisant deux mécanismes pour créer de nouvelles solutions : mise à jour de positions et mutation. Ces concepts sont discutés en détail dans les prochains paragraphes.

4.4.1 Leaders dans l'optimisation multiobjectif

Puisque la solution d'un problème multiobjectif se compose d'un ensemble de bonnes solutions, il est évident que le concept de leader traditionnellement adopté dans PSO doit être changé. Afin d'éviter la définition d'un nouveau concept de leader pour des problèmes multiobjectifs, certaines méthodes utilisent des fonctions d'agrégation (sommes pondérées des objectifs) ou approches qui optimisent chaque objectif séparément. Cependant, il est important d'indiquer que la majorité des approches actuellement proposées de MOPSO redéfinissent le concept de leader.

Comme mentionné plus haut, le choix d'un leader est une composante importante dans la conception de MOPSO. L'approche la plus directe est de considérer chaque solution non-dominée comme un nouveau leader et puis, un seul leader étant choisi. De cette façon, une mesure de qualité qui indique la qualité d'un leader est très importante. Evidemment, une telle approche peut être définie de différentes manières. Des différentes propositions, pour traiter ce problème, seront présentées plus loin.

Une manière possible de définir une telle mesure de qualité peut être les mesures de densité. La promotion de la diversité peut être faite par ce processus au moyen de mécanismes basés sur quelques mesures de qualité qui indiquent la proximité des particules dans l'essaim. Plusieurs auteurs ont proposé des techniques de choix de leader qui sont basées sur des mesures de densité, nous présentons ici deux des plus important mesures de densité utilisées dans le domaine de l'optimisation multiobjectif :

- Estimateur de densité de voisin le plus proche : L'estimateur de densité de voisin le plus proche nous donne une idée de la façon dont les voisins les plus proches d'une particule donnée sont distribués, dans l'espace de fonction objectif [Deb et al, 2002]. Cette mesure estime le périmètre du cuboïde formé en employant le plus proche voisin comme sommet (figure 4.5).





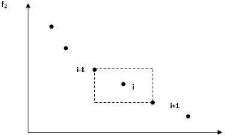
FIG. 4.5 - Exemple d'estimateur de densité de voisin le plus proche

- Estimateur de densité de grain: Quand une particule partage les ressources avec d'autres particules, sa fitness est dégradée proportionnellement au nombre et proximité des particules qui l'entourent avec un certain périmètre seuil [Goldberg et Richardson, 1987; Deb et Goldberg, 1989]. Un voisinage d'une particule est défini en termes de paramètre noté _óshare qui indique le rayon de voisinage. De tels voisinages s'appellent niches écologiques (figure 4.6).



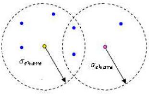
FIG. 4.6 Niches de particules

4.4.2 Conservation et propagation des solutions non-dominées

Comme déjà mentionné, il est important de maintenir les solutions non-dominées trouvées le long de tout le processus de recherche et ainsi pouvoir retourner à la fin ces solutions non-dominées en tenant compte de toutes les populations précédentes. Ceci est important non seulement pour des raisons pragmatiques, mais également pour les raisons théoriques [Rudolph, 1998].

La manière la plus directe de maintenir des solutions non-dominées, en prenant en considérations toutes les populations précédentes (ou essaims), est d'employer des archives externes. De telles archives permettra l'ajout d'une solution seulement si elle est non-dominée par une solution enregistrée dans l'archive ou si elle domine une des solutions de l'archive (dans ce cas, les solutions dominées doivent être supprimés de l'archive).

L'inconvénient de cette approche est l'augmentation très rapide de la taille des archives. C'est un point important parce que les archives doivent être mises à jour à chaque génération. Ainsi, cette mise à jour peut devenir très coûteuse en temps de calcul si la taille des archives est importante. Dans le pire des cas, tous les membres de l'essaim peuvent entrer dans l'archive, à chaque génération. Ainsi, le processus de la mise à jour correspondant, à chaque génération, aura une complexité de o(kN²), oil N est la taille de l'essaim et k le nombre des objectifs. De cette façon, la complexité du processus de mise à jour pour l'exécution complète de l'algorithme est de o(kMN²), oil M est le nombre total d'itérations.

Cependant, il est nécessaire d'ajouter un critère pour décider quelles solutions non-dominées doivent être maintenues dans le cas oil l'archive est pleine. Dans l'optimisation multiobjectif évolutionnaire, les chercheurs ont adopté différentes techniques pour réduire la taille des archives. D'autres concepts ont été introduits pour l'utilisation des archives, par exemple, pour ajouter les éléments dans l'archive, la distribution des solutions a été utilisée comme critère additionnel au lieu d'utiliser uniquement le concept de non dominance.

Il faut noter qu'on doit utiliser trois archives pour adapter PSO à l'optimisation multiobjectif : une pour stocker les meilleures solutions globales, une pour les meilleures valeurs pbest et une troisième pour stocker la meilleure solution locale. Cependant, dans la pratique, quelques auteurs rapportent l'utilisation de plus d'une archive dans leur MOPSOs. Plus récemment, d'autres chercheurs ont proposé l'utilisation de formes relaxées de dominance. La plus principale a été la méthode c-dominance [Laumanns et al, 2002]. Le but était de sauvegarder les solutions non dominées dans des archives externes. En utilisant le paramètre c, on définit un ensemble de cases de taille epsilon, une seule solution non-dominée est maintenue pour chaque case (située à la limite gauche et inférieure de chaque case). Comme illustré dans la figure (4.7).



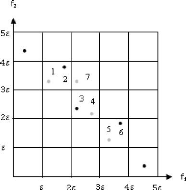
FIG. 4.7 - Exemple d'utilisation de € dominance dans un archive externe

Comme le montre la figure (4.7), la solution 1 domine la solution 2; donc la solution 1 est maintenue. Les solutions 3 et 4 sont non dominées l'une de l'autre, mais solution 3 est mieux que 4, puisque solution 3 est le plus proche au coin à gauche inférieur représenté par le point (2€, 2€). Solution 5 domine solution 6, donc solution 5 est maintenue. Solution 7 est non accepté puisque sa case représentée par le point (2€, 3€) est dominée par la case représentée par le point (2€, 2€).

Pour un cas Bi-objectif, l'utilisation du c--dominance, comme proposé dans [Laumanns et al, 2002], garantit que les solutions maintenues sont non-dominées en tenant compte de toutes les solutions produites pendant l'exécution.

En utilisant c-dominance, la taille de l'archive externe final dépend de la valeur c, qui est normalement un paramètre défini par l'utilisateur [Laumanns et al, 2002].

4.4.3 Maintien de la diversité par création de nouvelles solutions

La convergence rapide est l'une des caractéristiques les plus importantes de l'algorithme PSO. Ce pendant, il est primordial de maintenir un certain degré de diversité pour éviter que l'algorithme soit piégé.

La convergence prématurée est provoquée par la perte rapide de diversité dans l'essaim. Ainsi, le maintien de la diversité dans PSO est un point très important afin de contrôler sa convergence (normalement rapide). Comme mentionné précédemment, en adoptant PSO pour résoudre des problèmes d'optimisation multiobjectifs, il est possible de favoriser la diversité par le choix de leaders. Cela peut être également fait par les deux principaux mécanismes utilisés pour créer de nouvelles solutions :

a. Mise à jour des positions

L'utilisation de différentes topologies de voisinage détermine la vitesse du processus de transfert de l'information à travers l'essaim. Cependant, dans une topologie entièrement reliée, toutes les particules sont reliées les unes avec les autres, l'information est transférée plus rapidement que dans le cas de topologie locale best ou d'arbre. Aussi, une topologie spécifique de voisinage détermine également la vitesse de perte de diversité dans l'essaim. Puisque dans une topologie entièrement reliée le transfert d'information est rapide, en employant cette topologie, la diversité dans l'essaim est également perdue rapidement. De cette façon, les topologies qui définissent des voisinages plus petits que l'essaim global pour chaque particule peuvent également préserver la diversité dans l'essaim.

D'autre part, la diversité peut également être favorisée par le facteur d'inertie (ô(t) de l'équation (1.1)). Le facteur d'inertie est utilisé pour contrôler l'impact des vitesses antérieures sur la vitesse courante. Ainsi, le poids d'inertie influence la différence entre les capacités d'exploration globales et locales [Shi et Eberhart, 1998]. Un grand facteur d'inertie facilite l'exploration globale tandis qu'un plus petit facteur d'inertie tend à faciliter l'exploration locale. La valeur du facteur d'inertie peut varier pendant le processus d'optimisation. Shi [Shi et Eberhart, 1998] a montré qu'en diminuant linéairement le poids d'inertie d'une valeur relativement grande à une petite valeur durant l'exécution de PSO, l'algorithme favorise une recherche globale au début de son exécution et une recherche locale à la fin.

L'addition de la vitesse à la position actuelle pour produire la prochaine position est semblable à l'opérateur de mutation dans des algorithmes évolutionnaires, sauf que la mutation dans PSO est guidée par l'expérience d'une particule et de celle de ses voisines.

b. L'utilisation d'un opérateur de mutation (ou turbulence)

Quand une particule met à jour sa position, une mutation se produit. Parfois, une turbulence est aussi nécessaire. La turbulance reflète le changement du vol des particules qui est hors de son control [Fieldsend et Singh, 2002].

En général, quand un essaim stagne, c-à-d., quand les vitesses des particules sont pratiquement nulles, il devient incapable de produire de nouvelles solutions qui pourraient mener l'essaim hors de cet état. Ce comportement peut mener l'essaim entier à être emprisonné dans un optimum local duquel il est impossible de s'échapper. Puisque le meilleur individu global attire tous les membres de l'essaim, il est possible de mener l'essaim loin d'un endroit courant grâce à la mutation d'une particule simple si la particule mutée devient le nouveau leader. Ce mécanisme permet à la fois de s'échapper des optima locaux et d'accélérer la recherche [ Stacey et al, 2003].

De cette façon, l'utilisation d'un opérateur de mutation est très importante afin de s'échapper des optima locaux et d'améliorer les capacités d'exploration de PSO. En fait, différents opérateurs de mutation ont été proposés qui permettent la mutation des composants de la position ou de la vitesse d'une particule.

Le choix d'un bon opérateur de mutation est une tâche difficile qui a un impact significatif sur l'exécution. D'autre part, une fois un opérateur spécifique de mutation est choisi, une autre tâche difficile est de savoir le nombre de mutation à appliquer : avec quelle probabilité, dans quelle étape du processus, dans quel élément spécifique d'une particule, etc.

Plusieurs approches proposées ont employé des opérateurs de mutation, néanmoins, d'autres approches qui n'utilisent pas d'opérateurs de mutation ont donné de bonnes performances.

4.4.4 Classification des différentes approches

On peut classifier les MOPSOs de la manière suivante :

- Approches agrégées.

- Ordre lexicographique.

- Approches de sous-population. - Approches basées sur Pareto. - Approches combinées.

Ces différents modèles seront présentés dans les paragraphes suivants.

4.4.4.1. Approches agrégées

Sous cette catégorie nous considérons les approches qui combinent tous les objectifs du problème en un seul objectif. En d'autres termes, le problème à multiples objectifs est transformé en un seul-objectif.

a. L'algorithme de Parsopoulos et Vrahatis : Cet algorithme adopte trois types de fonctions d'agrégation : les fonctions d'agrégation linéaire conventionnelle, les fonctions d'agrégation dynamique et l'approche moyenne pondérée [Parsopolous et Vrahatis, 2002].

b. L'approche de Baumgartner, Magele et Renhart : Basé sur la topologie entièrement reliée, cette approche utilise les fonctions d'agrégation linéaire. Dans ce cas l'essaim est divisé en n sous-essaims, chaque sous-essaim utilise un ensemble de poids et se déplace en direction de leader. L'approche adopte une technique de gradient pour identifier les solutions Pareto optimales [Baumgarter et al, 2004].

4.4.4.2. Ordre lexicographique

Dans cette méthode, l'utilisateur est invité à ranger les objectifs par ordre d'importance. La solution optimale est alors obtenue par minimisation des fonctions objectifs séparément, commençant par la plus importante et procédant selon l'ordre d'importance assigné aux objectifs [ Miettinen, 1999]. L'ordre lexicographique tend à être utile seulement quand peu d'objectifs sont employés (deux ou trois), et il peut être sensible à l'ordre choisi des objectifs [Coello, 1999].

a. L'approche de Hu et Eberhart : Dans cet algorithme, chaque objectif est optimisé séparément en utilisant un schéma similaire à l'ordre lexicographique. Cette approche n'utilise pas d'archive externe [Hu et Eberhat, 2002].

b. Interactif Multi-essaims PSO : Cette approche prend en considération l'ordre d'importance déterminé par le décideur durant le processus d'optimisation. L'approche utilise la structure multi-essaims, la population est composée de l'essaim principal et de plusieurs essaims assistants, chaque objectif est optimisé par un essaim assistant correspondant et tous les objectifs sont optimisés simultanément dans l'essaim principal. Une nouvelle équation de la mise à jour de vitesse est introduite afin de partager l'information entre les essaims assistants et l'essaim principal [Wang et Yang, 2008].

4.4.4.3. Approches de sous-population

Ces approches concernent l'utilisation de plusieurs sous-populations en tant que problème à un seul-objectif. Les sous-populations effectuent ensuite un échange d'information ou une recombinaison visant à produire la diversité entre les différentes solutions précédemment produites pour les objectifs qui ont été séparément optimisés.

a. Approche VEPSO (Parallel Vector Evaluated Particle Swarm Optimization) : Cette approche [Parsopoulos et al., 2004] est une multi-essaim variante de PSO, qui est inspirée de l'algorithme " Evaluated Genetic Algorithm" (VEGA) [Schaffer, 1985]. En VEPSO, chaque essaim est évalué en prenant seulement un seul objectif en considération, et l'information qu'il possède est échangée avec d'autres essaim à travers l'échange de sa meilleure expérience (gbest).

4.4.4.4. Approches basées sur Pareto

Ces approches utilisent des techniques, de choix de leader, basées sur la dominance de Pareto. L'idée fondamentale de toutes ces approches est de choisir comme leaders les particules non-dominées de l'essaim. Cependant, plusieurs variations de la sélection de leader sont possibles puisque la plupart des auteurs adoptent des informations supplémentaires pour choisir les leaders (par exemple, l'information fournie par un estimateur de densité) afin d'éviter un choix aléatoire d'un leader de l'ensemble courant de solutions non-dominées.

a. L'Algorithme de Ray et Liew : Cet algorithme utilise la dominance de Pareto et combine le concept de techniques évolutionnaires avec les essaims particulaires. Cette approche utilise l'estimateur de densité de voisin le plus proche pour maintenir la diversité. L'ensemble de leaders maintenus est sauvegarder dans une archive externe [Ray et Liew, 2002].

b. L'optimisation multiobjective par essaims particulaires (Multiple Objective Particle Swarm Optimization) : Cette approche est basée sur l'idée d'avoir une archive externe dans laquelle chaque particule déposera son expérience après chaque itération. Le système basé sur la position géographique des particules est appliqué lors de la mise à jour d'archive. L'espace de recherche est divisé en des hypercubes. Cette approche emploie également un opérateur de mutation [Coello et al, 2004].

c. Approche AMOPSO (Another Multi-objective Particle Swarm Optimization ) : Cette approche utilise : (1) le rang de Pareto, (2) une technique de classification qui permet une subdivision de l'espace de recherche en plusieurs sous-essaims , afin de fournir une meilleure distribution des solutions dans l'espace de recherche. Dans chaque sous-essaim, un algorithme de PSO est exécuté et, au même temps, les différents sous-essaims échangent l'information [Pulido et Coello, 2004].

4.4.4.5. Approches combinées

Il y a des approches qui combinent quelques catégories décrites précédemment comme l'algorithme adaptive weighted PSO[Mahfouf et al, 2004] et l'algorithme d'optimisation intelligente par essaims particulaire (IPSO)[ Xiao-hua et al, 2005]. Aussi des approches qui ne peuvent pas rentrer dans les catégories principales, telle que l'approche maximinPSO [Li, 2004]

4.5 Synthèse

Plusieurs algorithmes d'optimisation multiobjectif par essaims particulaires ont été proposés, les inconvénients majeurs de ces differents algorithmes sont :(1) le nombre élevé de paramètres de réglages, (2) l'utilisation des archives. Cependant, l'utilisation des archives introduit des complexités temporelles et spatiales additionnelles, ce qui dégrade les performances de ces algorithmes.

Pour pallier ce problème, la section suivante, présente les principes de base du modèle proposé basé sur la notion de dominance de Pareto et une méthode de classification floue. Cette approche surmonte les problèmes que présentent les méthodes d'optimisation multiobjectif par essaims particulaires, en effet, elle n'utilise aucune archive externe et ainsi les complexités temporelles et spatiales sont réduites.

4.6 Optimisation multiobjectif par essaims particulaires basée sur la Classification Floue

FC-MOPSO (Fuzzy Clustering Multi-objective Particle Swarm Optimizer) est un nouveau modèle d'optimisation multiobjectif par essaims particulaires basé sur Pareto dominance et classification floue [Benameur et al, 2009c]. La nouveauté principale de cette méthode est l'utilisation de la classification floue afin d'identifier les différentes classes de l'essaim. Ainsi, chaque classe de particules (ou essaim) a son propre ensemble de leaders et évolue utilisant l'algorithme PSO et le concept de dominance de Pareto, le concept de migration est intégré afin de maintenir la diversité des sous-essaims et d'améliorer en conséquence la qualité des solutions trouvées.

Le principe du modèle FC-MOPSO est basé sur une stratégie à trois-couches (figure 4.8). La première couche intègre un algorithme d'optimisation multiobjectif par essaims Particulaires (PSOMO) qui n'utilise pas d'archives externes pour maintenir les solutions non-dominées trouvées le long de tout le processus de recherche. La sortie de ce niveau constitue l'entrée de la deuxième couche (FC), cette couche est basée sur un algorithme de classification floue non supervisé, qui permet de partitionner la population en un ensemble de (C) classes, chaque classe identifiée correspond à un sous essaim. Cette couche permet de calculer automatiquement le nombre de classes (C), le cardinal (Ni), le centre (Vi) et le rayon (ri) de chaque classe. La dernière couche implémente le principe de la séparation spatiale pour créer les différentes sous essaims à partir des caractéristiques fournies par la couche FC. Les sous-essaims ainsi engendrés vont co-évoluer en utilisant l'algorithme de base PSOMO.

Dans le paragraphe suivant, la première couche du modèle est présentée, les autres couches sont détaillées dans le chapitre 3, le fonctionnement du modèle est ensuite décrit plus en détail. Un ensemble de fonctions tests permet enfin de valider le modèle et de comparer les résultats obtenus avec d'autres méthodes d'optimisation multiobjectif par essaim particulaire.



FIG. 4.8 Structure en couches du modèle FC-MOPSO

4.6.1 Implémentation de la couche PSOMO

Le PSOMO est un algorithme d'optimisation multiobjectif par essaims particulaires qu'on peut décrire comme suit : Une fois l'essaim est initialisé, un ensemble

de leaders est également initialisé avec les particules non-dominées de l'essaim. A` chaque génération, pour chaque particule, un leader est aléatoirement choisi parmi l'ensemble de leaders et le vol est exécuté. Ensuite, la fitness de particule est évaluée et la valeur de pbest correspondante est mise à jour. Une nouvelle particule rem-place sa pbest particule quand cette pbest est dominée ou si toutes les deux sont incomparables. Après la mise à jour de toutes les particules, l'ensemble de leaders est mis à jour aussi. Le principe de PSOMO est décrit par le pseudo code (7).

algorithme 7 Pseudo code de l'algorithme PSOMO utilisé

Initialiser l'essaim

Initialiser l'ensemble de leaders (en utilisant la dominance au sens de Pareto)

t 4-- 0

tant que (t < tmax)

Pour chaque particule

Sélectionner un leader

Calculer la vitesse

Mettre à jour la position

Mettre à jour pbest

Mettre à jour l'ensemble de leaders

Fin pour
t 4-- t + 1
Fin tant que

4.6.2 Fonctionnement du modèle

Le modèle FC-MOPSO [Benameur et al, 2009d] est initialisé avec un essaim aléatoire de particules S(t = 0) définies par leurs positions et leur vitesses. Cet essaim évolue utilisant l'algorithme PSOMO, l'algorithme de classification floue non supervisée permet de partitionner l'essaim en C classes, et détermine pour chaque classe ses caractéristiques principales. De nouveaux sous-essaims, ainsi que leur sousespace de recherche, sont ensuite générés en utilisant le centre et le rayon de chaque classe. Cette stratégie de réinitialisation permet d'introduire une nouvelle diversité au sein des sous-essaims.

Utilisant le principe de séparation spatiale, une coopération locale est ensuite engendrée au niveau de chaque sous-essaim. Après avoir généré les sous-essaims et les sous espaces de recherche correspondants, un processus de migration est appliqué en vue d'échanger des informations entre les sous-essaims voisins. Les sous essaims vont donc co-évoluer séparément, et à la fin de cette évolution une nouvelle population est formée à partir des différentes sous essaims. Le processus est itéré jusqu'à ce que l'entropie (h) utilisée comme critère de validation, atteigne un minimum prédéfini (h < 10^-3). L'essaim S(t) est initialisé une seule fois dans tout le processus à la première itération (t = 0). Pendant les cycles intermédiaires S(t + 1) = Uc i=1 Si(t) oil C est le nombre de classes identifiées.

Le principe du modèle proposé est donné par le pseudo code (8).

algorithme 8 Pseudo code de l'algorithme FC-MOPSO

t - 0

Initialiser l'essaim (S(t))

S(t) - PSOMO(S(t))

Répéter

FC(S(t))

Pour i = 1 to C /*C nombre de classes identifiées

Créer les sous-essaims Si(t)

Appliquer le processus de migration

Si(t) - PSOMO(Si(t))

Fin pour

S(t + 1) - UC i=1 Si(t)

t - t + 1

Tant que (h < hmin)

4.7 Etude expérimentale

Plusieurs fonctions tests ont été utilisées pour valider les performances du modèle proposé. Ces fonctions ont plusieurs caractéristiques qui les rendent idéales pour tester la capacité de l'approche proposée à identifier la frontière optimale de Pareto. Il faut noter que ce sont les fonctions de benchmark les plus utilisées dans la littérature.

Pour pouvoir comparer les performances du modèle proposé avec d'autres modèles, deux critères sont utilisés. Ces critères incluent :

La distance générationnelle (Generational Distance GD) : Cette métrique a été proposée par Deb et Jain [Deb et Jain, 2002] pour mesurer la distance entre les éléments de l'ensemble des solutions non-dominées trouvées et les éléments de l'ensemble Pareto optimal.

IPn i=1 d2 i GD = m

(4.12)

oil m est le nombre des éléments de l'ensemble des solutions non-dominées trouvées et di est la distance euclidienne (mesurée dans l'espace des objectifs) entre chacune de ces solutions et le plus proche élément de l'ensemble Pareto optimal.

L'espacement (Spacing :SP) : On désire par SP mesurer la distribution des solutions trouvées. Puisque le début et la fin de front de Pareto sont connus, une métrique convenable peut montrer si les solutions sont bien réparties sur le front de Pareto trouvé. Schott [Schott, 1995] a proposé une telle métrique

qui mesure la variance de distance entre les solutions voisines de l'ensemble des solutions non-dominées trouvée. Cette métrique est définie par :

SP =	tu u v	1	Xn i=1	( d - di)^2 (4.13)
		n - 1

di est défini comme suit :

di = min j

XM m=1

|f^i m(x) - f^j m(x)|, i,j = 1,...,n,

oil d est la moyenne de tous les di, M est le nombre d'objectifs et n est le nombre de solutions non-dominées trouvées. La valeur zéro de cette métrique indique que tous les membres du front de Pareto trouvé sont tous espacés de la même distance.

4.7.1 Problèmes tests

Pour valider un algorithme, nous avons besoin d'un ensemble de fonctions tests. Cet ensemble doit être soigneusement choisi de façon à mettre à l'épreuve l'efficacité des méthodes étudiées dans diverses situations difficiles. En effet, un "bon" test doit être tel que :

1. il représente un danger particulier pour la convergence ou pour la diversité;

2. la forme et la position de la surface de Pareto soient connues et les valeurs des variables de décisions correspondantes soient faciles à trouver.

Dans la suite, nous utilisons le générateur de tests de Deb [Deb, 1999]. L'idée consiste à construire des tests à M objectifs, pour M = 2. Nous commençons par partitionner le vecteur des variables de décision en M groupes.

x = (x1, x2,··· , xM)

Ensuite, à partir de M -1 fonctions f1,··· , _fM-1, d'une fonction g positive et d'une fonction h à M variables, on construit la fonction fM par :

fM(x) = g(xM)h(f1(x1),··· , _fM-1(xM-1), g(xM))

avec x_m ? R^m pour in = 1, · · · , M - 1. Enfin, le problème d'optimisation est défini par:

minimiser fm(xm)m=1,··· ,M-1, fM(x)

La surface optimale correspond ici aux solutions sur lesquelles la fonction g atteint son minimum e elle est donc décrite comme :

fM = g^*h(f1, · · · , _fM-1, g^*)
Dans les paragraphes qui suivent nous présentons quatre fonction tests bi-objectif

ZDT1, ZDT2, ZDT3, ZDT6 et une à quatre objectif DTLZ7 que nous utilisons pour valider l'approche proposée. Notre choix s'est fixé sur ces fonctions tests car elles ont servi comme une base commune pour la comparaison des algorithmes evolutionnaires multi-Objectifs existants et pour l'évaluation des nouvelles techniques.

Fonction ZDT1

La fonction ZDT1 est la plus simple de cette ensemble, le front de Pareto correspondant étant continu, convexe et avec la distribution uniforme des solutions le long du front.

ZDT1 :

? ?? ??

f1(x) = x1 g(x2) = 1 + ^9_1 E7 n =2 xi (4.14) h(f1, g) = 1 - V ^91

oil xi ? [0, 1] pour tout i = 1, · · · , n et n = 30. Fonction ZDT2

La difficulté de cette fonction se présente dans la non-convexité du front de Pareto.

ZDT2 :

? ? ?

f1(x) = x1 Pn g(x2) = 1 + 9 i=2 xi n_1 h(f1, g) = 1 - (f g )^2

(4.15)

oil xi ? [0, 1] pour tout i = 1, · · · , n et n = 30.

Fonction ZDT3

La difficulté de cette fonction réside dans la discontinuité du front de Pareto.

ZDT3 :

? ?? ??

f1(x) = x1 g(x2) = 1 + ^9_1E7 n =2 xi (4.16) h(f1, g) = 1 - 91 - (f g )sin(10ðf1)

oil xi ? [0, 1] pour tout i = 1, · · · , n et n = 30. Fonction ZDT6

La particularité de ce problème est que les solutions optimales ne sont pas uniformément distribuées le long du front de Pareto. Cet effet est due à la non-linéarité de la fonction f1.

ZDT6 :

? ? ?

f1(x) =^1 - exp(-4x1) sin^6(4ðx1) g(x2) = 1 + ^9(E7=2 n^x21)^1/4 h(f1, g) = 1 - (^f g)^2

(4.17)

oil xi ? [0, 1], pour tout i = 1, · · · , n et n = 10.

Fonction DTLZ7

Dans cette étude, nous utilisons une fonction DTLZ7 à 4 objectifs, le front de Pareto de cette fonction est discontinu et formé de 8 régions séparées dans l'espace de recherche,

DTLZ7 :

? ????? ?????

f1(x1) = x1 f2(x2) = x2 f3(x3) = x3 Pn g(x4) = 1 + 9 i=4 xi h(f1, f2, f3, g) = 4 - I23 |x4| i=1[^fi 1+g(1 + sin(3ðfi))]

(4.18)

oil xi ? [0, 1] pour tout i = 1,··· , m et m = 23.

4.7.2 Résultats numériques

Les paramètres u et u, utilisés dans l'équation de la mise à jour du vecteur vitesse (équation 1.1), sont initialisés à 1.5 et 2.5 respectivement pour toutes les fonctions tests, la valeur de facteur d'inertie r(t) se réduit pendant le processus [Venter et Sobieski, 2004] selon l'équation (4.19)

r(t + 1) = r(t)c_ô (4.19)

c_ô est une constante entre 0 et 1, la valeur de c_ô utilisée est 0.975, r est intialisé à 1.4 et la taille de l'essaim est 200.

La figure (4.9) représente les fronts de Pareto des quatre fonctions tests ZDT1, ZDT2, ZDT3 et ZDT6 trouvés en utilisant l'algorithme FC-MOPSO. Il est clair que l'algorithme proposé peut produire presque un front de Pareto uniforme et complet pour chaque fonction.

4.7.3 Comparaisons avec d'autres techniques

Dans cette section, la comparaison entre les résultats obtenus par le modèle proposé FC-MOPSO et les techniques : interactive multi-swarm PSO [Wang et Yang, 2008], MOPSO [Coello et al, 2004] et MOPSO-CD [Raquel et Naval, 2005].

Le tabeau (4.1) représente la valeur moyenne et l'écart type des valeurs de GD concernant le modèle FC-MOPSO et les techniques : interactive multi-swarm PSO, MOPSO et MOPSO-CD.

D'après le tableau (4.1), La valeur de GD indique que l'algorithme proposé a obtenue la meilleure convergence pour toutes les fonctions par rapport aux algorithmes multi-swarm, MOPSO et MOPSO-CD. Ceci est confirmé par le paramètre GD, qui est égal à 3.6E -05 (fonction ZDT1) pour l'algorithme FC-MOPSO et égal à 8.4E - 05, 2.5E - 02 et 1.0E - 02 pour l'interactive multiswarm PSO, MOPSO et MOPSO-CD respectivement. La même analyse peut être faite pour les fonctions ZDT2, ZDT3 et ZDT6.



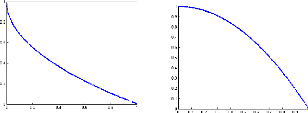
(a) ZDT1 (b) ZDT2



(c) ZDT3 (d) ZDT6

FIG. 4.9 - Le front de Pareto final généré par l'algorithme FC-MOPSO.

TAB. 4.1 - La moyenne et l'ecart type de la valeur de GD

Algorithme	ZDT1	ZDT2	ZDT3	ZDT6	DTLZ7
	Moyenne
FC-MOPSO	3.6E-05	9.3E-08	4.5E-06	5.7E-08	8.7E-03
Interactive multiswarm PSO	8.4E-05	1.1E-07	8.2E-06	1.1E-07	1.2E-02
MOPSO	2.5E-02	4.0E-03	7.3E-03	6.9E-03	1.8E-02
MOPSO-CD	1.0E-02	1.1E-02	1.3E-02	2.8E-02	1.9E-02
	Ecart type
FC-MOPSO	1.88E-04	3.5E-07	8.4E-06	2.9E-07	1.2E-04
Interactive multiswarm PSO	2.6E-04	4.6E-07	2.2E-05	4.2E-07	3.2E-04
MOPSO	2.3E-03	6.0E-07	4.8E-04	1.0E-02	8.4E-02
MOPSO-CD	3.4E-03	4.9E-05	1.5E-04	1.5E-03	8.5E-04

Puisque le front de Pareto de DTLZ7 est l'intersection de la droite avec l'hyperplan, la convergence est difficile. Cependant, FC-PSOMO arrive à améliorer la valeur de GD par rapport aux autres algorithmes.

Le tableau (4.2) représente la moyenne et l'écart type des valeurs de SP pour les quatre MOPSO algorithmes appliqués aux cinq fonctions tests. La valeur de SP montre que les solutions générées par l'algorithme proposé sont mieux distribuée que celles obtenues par les autres trois algorithmes pour toutes les fonctions tests.

TAB. 4.2 - La moyenne et l'écart type de la valeur de SP

Algorithme	ZDT1	ZDT2	ZDT3	ZDT6	DTLZ7
	Moyenne
FC-MOPSO	3.4E-04	8.7E-05	6.3E-04	1.19E-04	1.1E-02
Interactive multiswarm PSO	3.2E-03	3.8E-04	4.2E-03	8.8E-04	1.3E-02
MOPSO	1.1E-02	1.0E-02	2.3E-02	2.4E-03	8.4E-02
MOPSO-CD	1.6E-02	1.0E-02	1.6E-02	2.8E-03	4.8E-02
	Ecart type
FC-MOPSO	6.5E-03	2.56E-04	2.3E-03	7.3E-04	1.4E-04
Interactive multiswarm PSO	7.3E-03	3.4E-04	1.4E-03	5.7E-04	1.9E-02
MOPSO	6.8E-03	8.4E-03	4.8E-04	9.5E-04	2.8E-02
MOPSO-CD	3.3E-03	3.4E-03	4.3E-03	5.7E-04	6.3E-02

Puisque le front de Pareto de ZDT3 n'est pas uniformément distribué, cette fonction peut être utilisée pour étudier la capacité de l'algorithme à maintenir une bonne distribution de solution. D'après les résultats obtenus pour la fonction ZDT3, on peut conclure que la distribution des solutions est améliorée par l'utilisation de FCMOPSO. En fait, la vaeur de SP est égal à 6.3E -04 pour le modèle FC-MOPSO et égal à 4.2E-03, 2.3E-02 et 1.6E-02 pour interactive multi-swarm PSO, MOPSO et MOPSO-CD respectivement. La même analyse peut être faite pour les fonctions ZDT1, ZDT2, ZDT6 et DTLZ7.

Les résultats de simulation montre que l'algorithme proposé accompli les meilleurs performances par rapport aux autres méthodes en terme de la qualité des solutions trouvées, prouvée par les valeurs de GD et de SP.

4.8 Conclusion

Dans ce chapitre, une nouvelle approche d'optimisation multiobjectif par essaims particulaires basé sur classification floue est présentée. Cette approche incorpore la dominance de Pareto, la classification floue, la séparation spatiale et la procédure de migration.

L'avantage principal de cette approche est qu'elle permet de former des sousessaims sans information à priori sur la distribution de données en employant la technique de classification floue, un mécanisme de séparation spatiale est implémenté afin d'introduire une géographie locale dans l'espace de recherche permettant à chaque sous essaim une recherche locale dans son propre sous espace, une procédure de migration est également implémenté pour maintenir une diversité au sein des sous essaims, permettant ainsi l'amélioration de la qualité des solutions.

L'implémentation de cette technique, pour la résolution de différentes fonctions multiobjectives, montre que le modèle FC-MOPSO fournit de meilleures performances, comparativement aux autres modèles tels que : interactive multi-swarm PSO, MOPSO et MOPSO-CD, en terme de la qualité des solutions trouvées. Ceci est due d'une part à l'utilisation de classification floue qui permet de partitionner l'essaim en un ensemble de sous-essaims, chaque sous-essaim est traitée par un PSOMO, et d'autre part à l'application de procédure de migration qui permet de promouvoir une certaine diversité au sein des sous-essaims.

Cette approche surmonte les problèmes que présentent les méthodes d'optimisation multiobjectif par essaims particulaires, en effet, elle n'utilise aucune archive externe et ainsi les complexités temporelles et spatiales sont réduites.

En conclusion, généralement, pour des problèmes réels, dans lesquels on ne dispose d'aucune information sur l'espace de recherche, l'approche proposée peut être efficacement appliquée. En fait, elle exige moins de connaissances sur le problèmes à résoudre par rapport aux autres techniques multiobjectives.

Conclusion générale

L'essor de l'informatique et des techniques d'intelligence artificielle a conduit ces dernières années à un développement sans précédent des procédés d'optimisation automatique qui peuvent aujourd'hui prendre en compte de plusieurs paramètres. En particulier, les méthodes évolutionnistes ont connu depuis le début des années soixante une croissance exponentielle en s'affirmant peu à peu comme des techniques performantes comparativement aux techniques traditionnelles. Cette performance est due à leur aptitude à apprendre, évoluer et effectuer des traitements en un temps de calcul réduit, et à leur capacité à gérer avec efficacité des incertitudes et des imprécisions dans un environnement donné.

Sur la base de ce nouveau thème de recherche, cette thèse a consisté, en une investigation de l'algorithme d'optimisation par essaims particulaires, d'une part, en optimisation globale, de problèmes difficilement solubles exactement. D'autre part, elle a porté sur l'étude de l'optimisation multimodale et multiobjectif.

Dans un premier temps, une étude exhaustive des différentes techniques de calculs 'intelligent', notamment les techniques de calcul évolutif qui s'inscrivent dans le cadre de l'optimisation, a été effectuée. Cela nous a permis de maîtriser le fonctionnement de ces techniques et de les implémenter pour résoudre des problèmes réels.

L'application de PSO, pour l'optimisation globale, n'était pas une tâche évidente. En effet, elle a nécessité une phase préliminaire d'adaptation de la méthode utilisée au problème étudiée, notamment, pour le problème d'affectation de fréquence dans les réseaux cellulaires qui a nécessité une adaptation de l'algorithme à l'optimisation discrète. De plus, un bon réglage des paramètres est toujours indispensable pour l'obtention de bonnes solutions.

Les performances de PSO ont été aussi validées sur un problème continu, qui consistait à optimiser la commande d'une machine synchrone à aimant permanent. Les résultats obtenus montrent que la maitrise de ces différents modèles et un bon réglage des paramètres permettent de fournir de très bonnes performances.

Cependant, dans leur version de base, les techniques d'optimisation sont incapables de gérer efficacement des domaines caractérisés par plusieurs optima (ce qui est le cas généralement dans la plupart des applications réelles), puisque à l'origine

elles ont été conçues pour l'optimisation globale. Par ailleurs, il est souvent indispensable d'identifier toutes les solutions possibles, aussi bien globales que locales. En effet, l'utilisateur a généralement besoin de l'ensemble de solutions possibles afin de choisir la meilleure solution qui fournit un bon rapport qualité/prix.

De ce fait, plusieurs techniques d'optimisation multimodale, basées sur l'analogie avec les niches écologiques, ont été proposées dans la littérature pour ce type de problèmes. Toutefois, de nombreuses limitations apparaissent dans l'utilisation de ces modèles. Elles sont liées principalement aux paramètres spécifiés par l'utilisateur, i.e., rayon de niche, disposition des niches dans l'espace, etc. Ces difficultés peuvent souvent induire des résultats erronés.

Dans ce contexte, le présent travail a porté sur la conception de nouvelle technique, basée sur l'algorithme d'optimisation par essaims particulaires et une procédure de classification floue MPSO, a été proposé. Cette approche permet l'exploration parallèle de plusieurs régions de l'espace de recherche en partitionnant la population en plusieurs sous-populations d'essaims, chaque sous-essaim étant traité indépendamment par un algorithme PSO.

Pour localiser les différentes solutions, une procédure de classification floue non supervisée a été intégrée. Cette procédure permet, en effet, de regrouper les solutions en différentes classes. Le représentant de chaque classe identifiée étant l'optimum requis. L'intérêt de cette stratégie réside dans le fait qu'elle n'a besoin d'aucune information a priori sur le problème à résoudre, notamment le nombre d'optima recherché, la séparabilité des classes, etc.

Une stratégie de migration, qui permet d'avoir un échange entre les sous-essaims dans la structure multi-essaims, est appliquée afin de promouvoir un certain degré de diversité au sein des essaims et d'améliorer la qualité des solutions trouvées.

Les résultats d'optimisation relatifs aux différentes fonctions tests, et les comparaisons avec d'autres modèles montrent l'efficacité du modèle proposé, plus spécifiquement, en termes de la qualité des solutions identifiées et du nombre d'évaluations de la fonction fitness requis pour la convergence. Cela peut être expliqué par le fait que ce modèle fournit un bon équilibre entre exploitation/exploration des différentes régions prometteuses de l'espace de recherche.

La dernière partie du présent travail a consisté en conception d'un nouveau modèle d'optimisation multiobjectif par essaims particulaires FC-MOPSO, basée sur PSO, la dominance de Pareto et la classification floue. La nouveauté principale de ce modèle consiste en utilisation d'un mécanisme qui permet de fournir une meilleure distribution des solutions sur l'ensemble Pareto-optimal.

Grace à l'utilisation de la technique FC, cette approche permet de promouvoir et maintenir la formation de sous-populations d'essaims. Chaque sous-essaim a son

propre ensemble de leaders (les particules non-dominées) et évolue en utilisant l'algorithme PSO et le concept de la dominance de Pareto. Le concept de migration est également implémenté pour maintenir la diversité des sous-essaims, et améliorer la qualité des solutions trouvées.

Les résultats de simulation obtenus ont prouvé les performances du modèle proposé. Cependant, la plupart des techniques d'optimisation multiobjectif basées sur PSO, reportées dans la littérature, ont été limitées au choix de paramètres de réglage, et l'utilisation d'archives externes, ce qui introduit des complexités temporelles et spatiales additionnelles.

Références Bibliographiques

1. Aardal K. I., Hipolito A., Van Hoesel S., Jansen B., (1995). A Branch-and-Cut Algorithm for the Frequency Assignment Problem, Technical Report Annex T-2.2.1 A, CALMA project, T.U. Eindhoven and T.U. Delft.

2. Akcayol M. A., Cetin A., Elmas C., (2002). An Educational Tool for Fuzzy Logic-Controlled BDCM, IEEE Transactions On Education, Vol. 45, No. 1, pp. 33-42.

3. Alami J., Benameur L., El Imrani A., (2007). Fuzzy clustering based parallel cultural algorithm. International Journal of Soft Computing Vol.2(4), 562-571.

4. Alami J., Benameur L., El Imrani A. (2009) A Fuzzy Clustering based Particle Swarms for Multimodal Function Optimization. International Journal of Computational Intelligence Research, ISSN 0974-1259. Vol.5, No.2 (2009), pp. 96-107.

5. Alami J., El Imrani A., Bouroumi A., (2007). A multipopulation cultural algorithm using fuzzy clustering. In journal of Applied Soft Computing Vol.7 (2), 506-519.

6. Alami J., El Imrani A., (2006). A Hybrid Ants Colony Optimization for Fixed-Spectrum Frequency Assignment Problem, Colloque International sur l'Informatique et ses Applications IA 2006, 231-235, Oujda, Maroc.

7. Alami J., El Imrani A., (2007). Using Cultural Algorithm for the Fixed-Spectrum Frequency Assignment Problem. in the Journal of Mobile Communications.

8. Allenson R., (1992). Cenetic Algorithm with Gender for Multi-Function Optimisation, TR. EPCC-SS92-01, Edinburgh Parallel Computing Center, Edinburgh, Scotland.

9. Alvarez-Benitez J. E., Everson R.M., Fieldsend J. E. (2005). A MOPSO algorithm based exclusively on pareto dominance concepts. In Third International

Conference on Evolutionary Multi-Criterion Optimization, EMO2005, pp 459- 473, Guanajuato, México, LNCS3410, Springer-Verlag.

10. Amat J.L., Yahyaoui G.,(1996). Techniques avancées pour le traitement de l'information. Cépadués Editions.

11. Arias M. A. V, Pulido G. T. , C. A. C. Coello (2005). A proposal to use stripes to maintain diversity in a multi-objective particle swarm optimizer. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, pp 22-29, Pasadena,California, USA, June.

12. Bäck T., Hammel U., Schweffel F-P., (1997). Evolutionary Computation : Comments on the history and current state. IEEE transactions on Evolutionary Computation, 1(1), 3-17.

13. Bartz T.B., Limbourg P., Parsopoulos K. E., Vrahatis M. N., Mehnen J., Schmitt K., (2003). Particle swarm optimizers for pareto optimization with enhanced archiving techniques. In Congress on Evolutionary Computation (CEC'2003), volume 3, pages 1780-1787, Canberra,Australia,December.

14. Baumgartner U., Magele Ch., Renhart W., (2004). Pareto optimality and particle swarm optimization. IEEE Transactions on Magnetics, 40(2) :1172-1175, March.

15. Beasley D., Bull D.R., Martin R.R., (1993 ). A sequential niche technique for multimodal function optimization. Evolutionary Computation 1(2), 101-125.

16. Beckers R., Deneubourg. J.L. Goss. S., (1992). Trails and U-turns in the selection of the shortest path by the ant Lasius Niger. Journal of Theoretical Biology, vol. 159, pp. 397-415.

17. Benameur L., Alami J., Loukdache A., El Imrani A., (2007). Particle Swarm Based PI Controller for Permanent Magnet Synchronous Machine. Journal of Engineering and Applied Sciences 2 (9) : 1387-1393.

18. Benameur L., Alami J., El Imrani A. (2009a). Frequency Assignment Problem Using Discrete Particle Swarm model. International Conference on Multimedia Computing and Systems ICMCS/IEEE 09. Avril 02-04 Ouarzazate.

19. Benameur L., Alami J., El Imrani A. (2009b). A New Discrete Particle Swarm model for the Frequency Assignment Problem. In proced. of IEEE/AICCSA 2009, pp. 139-144. Rabat, Morocco, May 10-13.

20. Benameur L., Alami J., El Imrani A., (2009c). A New Hybrid Particle Swarm Optimization Algorithm for Handling Multiobjective Problem Using Fuzzy

Clustering Technique. In proced. of the International Conference on Computational Intelligence, Modelling and Simulation, Brno,czech republic : 48-53.

21. Benameur L., Alami J., El Imrani A., (2009d). Using fuzzy clustering Techniques to improve the performance of a multiobjective particle swarm optimizer.International Journal of Computational Science 3(4) : 436-455. .

22. Benameur L., Alami J., El Imrani A., (2010). A hybrid discrete particle swarm algorithm for solving the fixed-spectrum frequency assignment problem. International Journal of Computational Science and Engineering. 5(1) :68-73.

23. Bezdek J. C., (1981). Pattern recognition with fuzzy objective function algorithms. (Plenum Press, New York).

24. Bezdek J. C., (1992). On the relationship between neural networks, pattern recognition and intelligence. International journal of approximate reasoning, (6), 85-107.

25. Bezdek K., (1994). On affine subspaces that illuminate a convex set, Contributions to Alg. and Geom. 35/1, 131-139.

26. Bouroumi A., Limouri M., Essaid A., (2000). Unsupervised fuzzy learning and cluster seeking. Intelligent Data Analysis journal 4 (3-4), 241-253.

27. Brits R., Engelbrecht A., Van den Bergh F., (2002a). Solving systems of unconstrained equations using particle swarm optimization. Proceedings of the IEEE Conf. on Systems, Man, and Cybernetics, Tunisa, Vol.3, no.pp.6.

28. Brits R., Engelbrecht A., Van den Bergh F., (2002b). A niching particle swarm optimizer. Wang, L., Tan, K.C., Furuhashi, T., Kim, J.H., Yao, X., eds., Proceedings of the 4^th Asia-Pacific Conf. on Simulated Evolution and Learning, Vol. 2, (Singapore) 692-696.

29. Brits R., Engelbrecht A., van den Bergh F.,(2007). Locating multiple optima using particle swarm optimization, Applied Mathematics and Computation, 189, pp 1859-1883.

30. Charnes A., Cooper W., (1961). Management Models and Industrial Applications of Linear Programming, vol 1, John Wiley, New-york.

31. Cheng R-H., Yu C. W., Wu T-K., (2005). A Novel Approach to the Fixed Channel Assignment Problem. Journal of Information Science and Engineering 21, 39-58.

32. Chow C.k. , Tsui H.t., (2004). Autonomous agent Response learning by a multi-species particle swarm optimization. In Congress on Evolutionary Computation (CEC'2004), volume 1, pp 778-785, Portland, Oregon,USA, June. IEEE Service Center.

33. Chung. C. J., (1997). Knowledge Based Approaches to Self Adaptation in Cultural Algorithms. PhD thesis, Wayne State University, Detroit, Michigan.

34. Coello C. A.C., (1995). Multiobjective design Optimization of Counterweight Balancing of a Robot Arm using genetic Algorithm, Seventh International Conference on Tools with Artificial Intelligence, p. 20-23.

35. Coello C. A.C., (1996). An Empirical study of Evolutionary Techniques for Multiobjective Optimization in Engineering Design, Ph.D. Thesis, Department of Computer sciences, Tulane University, New Orleans.

36. Coello C. A. C., (1999). A comprehensive survey of evolutionary based multiobjective optimization techniques. Knowledge and Information Systems. An International Journal, 1(3) :269-308, August.

37. Coello C. A.C., Pulido G.T., (2001). Multiobjective Optimization using a Micro-genetic Algorithm, In proceedings of the Genetic and Evolutionary Computation Conference (GECCO'2001), pp. 274-282, San Francisco, California.

38. Coello C.A.C.,.Veldhuizen D.A.V, Lamont G. B, (2002). Evolutionary Algorithms for Solving Multi-Objective Problems. Kluwer Academic Publishers, NewYork,May.

39. Coello C. A. C., Lechuga M. S, (2002). MOPSO : A proposal for multiple objective particle swarm optimization. InCongressonEvolutionary Computation (CEC'2002), volume 2, pp. 1051-1056, Piscataway, New Jersey, May.

40. Coello, C. A., Pulido, G. T., Lechuga, M. S, (2004). Handling Multiple Objectives with Particle Swarm Optimization, IEEE Transactions on Evolutionary Computation 8(3), pp. 256-279.

41. Colette Y., Siarry P., (2002). Optimisation multiobjectif, Edition Eyrolles.

42. Corne D.W, (2001). PESA II : Region-based Selection in Evolutionary Multiobjective Optimization, In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO'2001), pp. 283-290, San Francisco, California.

43. Crompton W., Hurley S., Stephens N. M., (1994). A parallel genetic algorithm for frequency assignment problems, in Proceedings of the IMACS, IEEE Conference on Signal Processing, Robotics and Neural Networks, Lille, France, pp. 81 -84.

44. Deb K., Goldberg D. E. (1989). An investigation of niche and species formation in genetic function optimization. In J. David Schaffer, editor, Proceedings of the Third International Conference on Genetic Algorithms, pp. 42-50, San Mateo, California, June. George Mason University, Morgan Kaufmann Publishers.

45. Deb K.,(1999). Multi-objective genetic algorithms : Problem difficulties and construction of test problems. Evolutionary Computation Journal, 7(3), pp. 311-338.

46. Deb, K., (2000). A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multiobjective Optimization : NSGA II, Parallel problem Solving form Nature-PPSN VI, Springer lecture Notes in computing Science, p. 849-858.

47. Deb, K., (2001). Multiobjective Optimization Using Evolutionary Algorithms, John Wiley and Sons.

48. Deb K., Jain S., (2002). Running Performance Metrics for Evolutionary Multi-objective Optimization, Tech. rep, KanGAL Report.

49. Deb K., Pratap A., Agarwal S., Meyarivan T., (2002). A fast and elitist multiobjective genetic algorithm : NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), pp. 182-197, April.

50. De Castro L. N, Von Zuben F., (1999). Artificial Immune Systems: Part I : Basic Theory and Applications. Technical Report TR-DCA 01/99, Department of Computer Engineering and Industrial Automation, School of Electrical and Computer Engineering, State University of Campinas, Brazil.

51. De Castro L. N, Von Zuben F., (2000). Artificial Immune Systems : Part II : A Survey of Applications. Technical Report DCA-RT 02/00, Department of Computer Engineering and Industrial Automation, School of Electrical and Computer Engineering, State University of Campinas, Brazil.

52. De Castro L. N., Timmis J., (2002). An artificial Immune Network for multimodal function optimization. The IEEE World Congress on Computational Intelligence.

53. De Falco I., Della Cioppa A., Tarantino E., (2007). Facing classification problems with Particle Swarm Optimization. Applied Soft Computing 7, pp. 652-

658.

54. Deneubourg J. L., Goss S. (1989). Collective patterns and decision-making, Ethology and Evolution, (1), pp. 295-311.

55. Deneubourg J.L., Pasteels J.M., Verhaeghe J.C. (1983). Probabilistic behaviour in ants : A strategy of errors, Journal of Theoretical Biology, 105, pp. 259-271.

56. DiPierro F., Khu S., Savi D., (2007). An Investigation on Preference Order Ranking Scheme for Multiobjective Evolutionary Optimization, IEEE Transactions on Evolutionary Computation 11(1), pp. 17-45.

57. Duque-Anton M., Kunz D., Ruber B., (1993). Channel assignment for cellular radio using simulated annealing. IEEE Trans.Vehicular Technol.42, pp. 14 -21.

58. Durham W. H., (1994). Co-evolution : Genes, Culture, and Human Diversity. Stanford University Press, Stanford, California.

59. Eberhart, R. Kennedy, J. (1995). New optimizers using particle swarm theory. In Proceedings of the 6^th International Sysmposium on Micro Machine and Human Science, pp. 39-43.

60. El Imrani A.A., (2000). Conception d'un Algorithme Génétique Coévolutif. Application à l'optimisation des Histoires Thermiques. Thèse de Doctorat d'Etat. Faculté des Sciences, Rabat.

61. El Imrani A. A., Bouroumi A., Zine El Abidine H., Limouri M., Essaïd A., (1999a). A Fuzzy Clustering-based Niching Approach to Multimodal Function Optimization. Journal Cognitive Systems research, Volume (1) issue (2) 2000, pp. 119-133.

62. El Imrani A. A., Bouroumi A., Limouri M., Essaïd A., (1999b). A Coevolutionary Genetic Algorithm using Fuzzy Clustering. International Journal of Intelligent Data Analysis, Vol 4(2000), pp. 183-193.

63. Farina M., Amato P., (2004). A Fuzzy Definition of Optimality for Many-criteria Optimization Problems, IEEE Transactions on Systems, Man and Cybernetics, Part A 34 (3), pp. 315-326.

64. Fieldsend J. E., Singh S., (2002). A multiobjective algorithm based upon particle swarm optimisation, an efficient data structure and turbulence. In Proceedings of the 2002 U.K. Workshop on Computational Intelligence, pp. 37-44,

Birmingham, UK, September.

65. Fogel D. B., (1995). A comparison of evolutionary programming and genetic algorithms on selected constrained optimization problems, Simulation, pp. 397-403, June 1995.

66. Fogel, L. J., Owens, A. J., Walsh, M. J., (1966). Artificial Intelligence through Simulated Evolution.

67. Fonseca C.M., Fleming P.J, (1993). Genetic Algorithms for Multiobjective Optimization : formulation, discussion and Generalization, In Proceeding of the Fifth International Conference on Genetic Algorithms. San Mateo, California, pp. 416-423.

68. Forrest S., Javornik B., Smith R.E., Perelson A.S.,(1993). Using genetic algorithms to explore pattern recognition in the immune system, Evol. Comput. 1 (3) 191-211.

69. Fourman, (1985). Compaction of symbolic Layout using Genetic Algorithms. In Genetic Algorithms and their Applications : Proceedings of the First International Conference on Genetic Algorithm, pp. 141-153.

70. Funabiki N., Takefuji Y., (1992). A neural network parallel algorithm for channel assignment problems in cellular radio networks. IEEE Transactions on Vehicular Technology, Vol. 41, pp. 430-436.

71. Goldberg D. E., (1989a). Genetic Algorithms in search, optimization and machine learning. Addison-wesley Publishing Inc.

72. Goldberg D.E, (1989b). Sizing Populations for Serial and Parallel Genetic Algorithms, Proceedings of the Third International Conference on Genetic Algorithm, pp. 70-97, San-Mateo, California.

73. Goldberg D.E, Deb D., Horn H., (1992). Massive multiomodality and genetic algorithms, Ed. R. Manner, B. Manderick, parallel problem solving from nature 2, Brussels, pp. 37-46.

74. Goldberg D. E., Richardson J., (1987). Genetic algorithms with sharing for multimodal function optimization. Proceedings of the Second International Conference on Genetic Algorithms, pp. 41-49.

75. Goldberg D. E., Wang L., (1997). Adaptative niching via coevolutionary sharing. Quagliarella et al.(Eds.). Genetic Algorithms in Engineering and Computer Science (John Wiley and Sons, Ltd). pp. 21-38.

76. Goss S., Beckers R., Deneubourg J.L., Aron S., Pasteels J.M. (1990). How trail lying and trail following can solve foraging problems for ant colonies. In : Behavioural Mechanisms of Food Selection, R.N. Hughes ed., NATO-ASI Series, vol. G20, Berlin : Springer verlag.

77. Hale W. K., (1981). New spectrum management tools. Proceedings IEEE Int. Symp. Electromag. Compatibility, pp. 47- 53, Aug.

78. Ho S.L, Shiyou Y., Guangzheng N., Lo E. W.C., Wong H.C, (2005). A particle swarm optimization based method for multiobjective design optimizations. IEEE Transactions on Magnetics, 41(5), pp. 1756-1759, May.

79. Hoffmeyer J.,(1994). The Swarming Body. In I. Rauch and G.F. Carr, editors, Semiotics Around the World, Proceedings of the Fifth Congress of the International Association for Semiotic Studies, pp. 937-940.

80. Hofmeyr S.A., Forrest S., (1999). Immunity by Design : An Artificial Immune System, in : Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Morgan Kaufmann, San Francisco, CA, pp. 1289-1296.

81. Holland, J. H. , (1962). Outline for logical theory of adaptive systems. J. Assoc. Comput. March, 3, pp. 297-314.

82. Holland, J. H. , (1975). Adaptation in Natural and Artificial Systems. The University of Michigan Press, Ann Arbor, MI.

83. Holland J.H., Holyoak K.J., Nisbett R.E., Thagard P.R., (1986). Induction : Processes of Inference, learning and discovery. MIT Press, Cambridge, MA, USA.

84. Hopfield J. J., (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the national academy of sciences, USA, pp. 2554-2558.

85. Horn J., Nafpliotis N., (1993). Multiobjective Optimization using the Niched Pareto Genetic Algorithm, Illigal TR. 93005, July.

86. Hu X. , Eberhart R, (2002). Multiobjective optimization using dynamic neighborhood particle swarm optimization. In Congress on Evolutionary Computation (CEC'2002), volume 2, pp. 1677-1681, Piscataway, New Jersey, May.

87. Hu X., Eberhart R., Shi Y, (2003). Particle swarm with extended memory for multiobjective optimization. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, pp. 193-197, Indianapolis, Indiana,USA, April.

88. Hurley S., Smith D. H., Thiel S. U., (1997). FASoft : A system for discrete channel frequency assignment. Radio Science, vol. 32, no. 5, pp. 1921- 1939.

89. Ignizio J.P., (1981). The Determination of a Subset of Efficient Solutions via Goal Programming, Computing and Operations Research 3, pp. 9-16.

90. Ishibuchi H., Murata T., (1996). Multi-objective Genetic Local Search Algorithm. In Toshio Fukuda and Takesshi Furuhashi editors, Proceedings of the 1996 International conference on Evolutionary Computation, pp. 119-124, Nagoya, Japan.

91. Janson S., Merkle D., (2005). A new multiobjective particle swarm optimization algorithm using clustering applied to automated docking. In Maria J. Blesa, Christian Blum, Andrea Roli, and Michael Sampels, editors, Hybrid Metaheuristics, Second International Workshop, HM2005, pp. 128-142, Barcelona, Spain, August. Springer. Lecture Notes in ComputerScience Vol.3636.

92. Jedra M., (1999). Modèles connexionnistes temporels, Application à la reconnaissance des variétés de semences et à l'analyse de contexte des caractères arabes. Thèse de Doctorat d'Etat, Faculté des sciences, Rabat.

93. Kennedy J., Eberhart R. C., (1995). Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, pages 1942- 1948, Piscataway, New Jersey, 1995. IEEE Service Center.

94. Kennedy J., (2000). Stereotyping : Improving particle swarm performance with cluster analysis. Proceedings of the IEEE Congress on Evol. Comput. (San Diego, California, U.S.A.), pp. 1507-1512.

95. Kim J. S., Park S. H., Dowd P. W., Nasrabadi N. M., (1997). Cellular radio channel assignment using a modified Hopfield network. IEEE Transactions on Vehicular Technology, Vol. 46, pp. 957-967.

96. Knowles J.D., Corne D.W., (1999). The Pareto Archived Evolution Strategy: A New Baseline Algorithm for Multiobjective Optimisation, Congress on Evolutionary Computation, pp. 98-105, Washington, July.

97. Knowles J.D., Corne D.W., Oates M.J., (2000). The Pareto-Envelope based Selection Algorithm for Multiobjective Optimization, In Proceeding of the Sixth International Conference on Parallel Problem Solving from Nature (PPSN VI), pp.839-848, Berlin, September.

98. Kohonen T., (1989). Self organization and associative memory. Springer series in information sciences, springer verlag, 3^rd edition.

99. Koza J.R., (1992). Genetic Programming. MIT Press, ISBN : 0-262-11170-5.

100. Kunz D., (1991). Channel assignment for cellular radio using neural network. IEEE Transactions on Vehicular Technology, Vol. 40, pp. 188-193.

101. Kurwase F., (1984). A variant of Evolution Strategies for Vector optimization, Ph. D Thesis, Vanderbilt University, Nashville, Tennessee.

102. Laumanns M., Thiele L., Deb K., Zitzler E, (2002). Combining convergence and diversity in Evolutionary multi-objective optimization. Evolutionary Computation, 10(3), pp. 263-282.

103. Lechuga M.S, Rowe J, (2005). Particle swarm optimization and fitness sharing to solve multi-objective optimization problems. In Congresson Evolutionary Computation (CEC'2005), pp. 1204- 1211,Edinburgh,Scotland,UK,September.IEEE Press.

104. Lee C.C., (1990). Fuzzy logic in control systems : Fuzzy logic controller, Part I, Part II. IEEE Trans. on Syst., Man, and Cyber., Vol. 20, No.2, pp. 404- 435.

105. Li S. Z., (1995). Markov Random Field, Modeling in computer vision. Spring Verlag, 1995.

106. Li J. P., Balazs M. E., Parks G., Clarkson P. J., (2002). A species conserving genetic algorithm for multimodal function optimization, Evolutionary Computation, 10(3), pp. 207-234.

107. Li X., (2003). A non-dominated sorting particle swarm optimizer for multiobjective optimization. In Erick Cantu-Paz et al., editor, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO'2003), pp 37-48. Springer. Lecture Notes in Computer Science Vol.2723, July.

108. Li X., (2004). Adaptively choosing neighborhood bests using species in swarm optimizer for multimodal function optimization. GECCO, pp. 105-116.

109. Lin C.T., Lee C.S.G., (1991). Neural-network-based Fuzzy logic control and decision system. IEEE Trans. On Comp., Vol.40, No. 12, pp. 1320-1336.

110. Lis J., Eiben A.E., (1996). A Multi-Sexual Genetic Algorithm for Multiobjective Optimization, In T.Fukuda and T. Furuhashi ed., Proceedings of the 1996 International Conference on Evolutionary Computation, Nagoya, Japan, pp.59-64.

111. Loukdache A., Alami J., El Belkacemi M., El Imrani A., (2007). New control approach for permanent magnet synchronous machine. International Journal

of Electrical and Power Engineering 1(4), pp. 455 -462.

112. Mahfoud, S. W., (1992). Crowding and preselection revisited. Parallel Problem Solving from Nature. North-Holland, Amsterdam, (2), pp. 27-36.

113. Mahfoud S.W, (1994). Crossover Interactions Among niches. Proceedings of the 1st IEEE Conference on Evolutionary Computation, pp. 188-193.

114. Mahfoud S. W, (1995). Niching Methods for Genetic Algorithms. PhD Thesis, University of Illinois.

115. Mahfouf, M., Chen, M. Y., Linkens, D. A., (2004). Adaptive Weighted Particle Swarm Optimization for Multi- objective Optimal Design of Alloy Steels, Parallel Problem Solving from Nature - PPSN VIII, pp. 762-771, Birmingham, UK, Springer-Verlag. Lecture Notes in Computer Science Vol. 3242.

116. Maniezzo V., Montemanni R., (1999). An exact algorithm for the radio link frequency assignment problem. Report CSR 99-02, Computer Science, Univ. of Bologna.

117. Martinez T. M., Schulten K. J., (1991). A "neural-gas" network learns topologies. Artificial neural network, Rédacteurs : T. Kohonen, K. Mäkisara, O. Simula et J. Kanges, pp. 397-402, Elsevier Science Publishers, B. V(North Holland).

118. Mathar R., Mattfeldt J., (1993). Channel assignment in cellular radio networks. IEEE Transactions on Vehicular Technology, Vol. 42, pp. 647-656.

119. McCulloch W. S., Pitts W., (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5, pp. 115-133.

120. Michalewicz Z., (1996). Genetic Algorithms + Data Structures = Evolution Programs. Springer-Verlag, New York.

121. Miettinen K., (1999). Nonlinear Multiobjective Optimization. Kluwer Academic Publishers, Boston, Massachusetts.

122. Miller B.L., Shaw M.J., (1996). Genetic Algorithms with Dynamic Niche Sharing for Multimodal Function Optimization. IlliGAL Report no. 95010.

123. Mitchell M., Forrest S., (1993). Genetic Algorithms and Artificial Life. Paper 93-11-072.

124. Montemanni R., Moon Jim N. J., Smith D. H., (2003). An improved Tabu search algorithm for the fixed spectrum frequency assignment problem. IEEE Transactions on Vehicular Technology, vol. 52, No.3, May.

125. Moore J., Chapman R., (1999). Application of particle swarm to multiobjective optimization. Department of Computer Science and Software Engineering, Auburn University.

126. Mostaghim S., Teich J., 2003(a). Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO). In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, pp. 26-33, Indianapolis, Indiana, USA, April.

127. Mostaghim S., Teich J., 2003(b). The role of c-- dominance in multi objective particle swarm optimization methods. In Congress on Evolutionary Computation (CEC'2003), volume 3, pp. 1764-1771, Canberra, Australia, December.

128. Mostaghim S., Teich J., (2004). Covering pareto-optimal fronts by subswarms in multi-objective particle swarm optimization. In Congress on Evolutionary Computation (CEC'2004), volume 2, pp. 1404- 1411, Portland, Oregon, USA, June.

129. Pareto V., (1896). Cours d'économie politique, vol. 1 et 2, F. Rouge, Lausanne.

130. Parsopoulos K. E., Vrahatis M. N., (2002). Particle swarm optimization method in multiobjective problems. In Proceedings of the 2002 ACM Symposium on Applied Computing (SAC'2002), pp. 603-607, Madrid, Spain.

131. Parsopoulos K. E., Tasoulis D., Vrahatis M. N., (2004). Multiobjective optimization using parallel vector evaluated particle swarm optimization. In Proceedings of the IASTED International Conference on Artificial Intelligence and Applications (AIA 2004), volume 2, pp. 823-828, Innsbruck, Austria, February.

132. Pelikan M., Goldberg D. E., (2001). Escaping hierarchical traps with competent genetic algorithms. In Proceeding. of the Genetic and Evolutionary Computation Conference, pp. 511- 518.

133. Petrowsky A., (1996). A clearing procedure as a niching method for Genetic Algorithms. Proceedings of IEEE International Conference of Evolutionary Computation, (Nagoya-Japan), pp. 798-803.

134. Pulido G. T., (2005). On the Use of Self-Adaptation and Elitism for Multiobjective Particle Swarm Optimization. PhD thesis, Computer Science Section, Department of Electrical Engineering, CINVESTAV-IPN, Mexico, September.

135. Pulido, G. T., Coello, C. A., (2004). Using Clustering Techniques to Improve the Performance of a Particle Swarm Optimizer, In Kalyanmoy Deb et al., editor, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO'2004), pp. 225-237, Seattle, Washington, USA, Springer-Verlag, Lecture Notes in Computer Science Vol. 3102.

136. Qing L., Gang W., Zaiyue Y., Qiuping W., (2008). Crowding clustering genetic algorithm for multimodal function optimization, Applied Soft Computing 8, pp. 88-95.

137. Rahman M.A., Hoque M. A., (1998). On-line adaptive artificial neural network based vector control of permanent magnet synchronous motors. IEEE Trans. On Energy Conversion, Vol.13, No. 4, pp. 311-318, 1998.

138. Ramos V., Fernandes C., Rosa A.C., (2005). Social Cognitive Maps, Swarm Collective Perception and Distributed Search on Dynamic Landscapes. Technical report, Instituto Superior Técnico, Lisboa, Portugal, http ://alfa.ist.utl.pt/ cvrm/staff/vram 58.html.

139. Raquel C. R., Naval Jr. P. C., (2005). An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO2005), pp 257-264, Washington, DC, USA, June.

140. Ray T., Liew K.M., (2002). A swarm metaphor for multiobjective design optimization. Engineering Optimization, 34(2), pp. 141-153, March.

141. Rechenberg, I., (1965). Cybernetic Solution Path of an Experimental Problem. Royal Aircraft Establishment Library Translation.

142. Rechenberg I., (1973). Evolutionsstrategie : Optimierung technischer Systeme nach Prinzipien der biologischen Evolution, Stuttgart.

143. Renfrew A. C., (1994). Dynamic Modeling in Archaeology : What, When, and Where? In S. E. van der Leeuw, editor, Dynamical Modeling and the Study of Change in Archaelogy. Edinburgh University Press, Edinburgh, Scotland.

144. Reyes M. S., Coello C. A. C., (2005). Improving PSO-based multi-objective optimization using crowding, mutation and c--dominance. In Third International Conference on Evolutionary Multi-Criterion Optimization, EMO 2005, pp. 505-519, Guanajuato, México. LNCS 3410, Springer- Verlag.

145. Reynolds R. G., (1994). An Introduction to Cultural Algorithms. In Antony V, Sebald and Lawrence J. Fogel, editors, Proceedings of the Third Annual

Conference on Evolutionary Programming, pp. 131- 139. World Scientific.

146. Reynolds R. G., (1997). Using Cultural Algorithms to support Re-Engineering of Rule-Based Expert Systems in Dynamic Performance Environments : A Case Study in Fraud Detection. IEEE Transactions on Evolutionary Computation, volume 1 No.4, November.

147. Reynolds R. G., Zannoni E., (1994). Learning to Understand Software Using Cultural Algorithms. In Antony V, Sebald and Lawrence J. Fogel, editors, Proceedings of the Third Annual Conference on Evolutionary Programming. World Scientific.

148. Ritzel B., (1994). Using Genetic Algorithms to Solve a Multiple Objective Groundwater Pollution Containment Problem. Water Resources Research 30, pp. 1589-1603.

149. Rosenblatt F., (1958). The perceptron : a probabilistic model for information storage and organization in the brain. Psychological review, 65, pp. 386-408.

150. Rudolph G., (1998). On a multi-objective evolutionary algorithm and its convergence to the Pareto set. In Proceedings of the 5th IEEE Conference on Evolutionary Computation, pp. 511-516, Piscataway, New Jersey.

151. Säreni B., Krähenbühl L., (1998). Fitness sharing and niching methods revisited. IEEE transactions on Evolutionary Computation vol. 2, No. 3, pp. 97-106.

152. Säreni B., (1999). Méthodes d'optimisation multimodales associées à la modélisation numérique en électromagnétisme. Thèse de doctorat, l'école centrale de Lyon.

153. Schaffer J.D., (1985). Multiple objective optimization with vector evaluated genetic algorithms, In J.J. Grefenstette ed., Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, pp. 93-100.

154. Schoeman, I.L., Engelbrecht, A.P., (2004). Using vector operations to identify niches for particle swarm optimization. Proceedings of the conference on cybernetics and intelligent systems.

155. Schoeman I.L., Engelbrecht A., (2005). A parallel vector-based particle swarm optimizer. International Conf. on Artificial Neural Networks and Genetic Algorithms (ICANNGA), Portugal.

156. Schoenauer M., Michalewicz Z., (1997). Evolutionary Computation. Control and Cybernetics, 26(3), pp. 307-338.

157. Schott J. R., (1995). Fault tolerant design using single and multi-criteria genetic algorithms. Master's thesis, Departement of Aeronautics and Astronautics, Boston.

158. Shi Y., Eberhart R., (1998). Parameter selection in particle swarm optimization. In Evolutionary Programming VII : Proceedings of the Seventh annual Conference on Evolutionary Programming, pp. 591-600, NewYork, USA. Springer-Verlag.

159. Shirazi S. A. G., Amindavar H., (2005). Fixed channel assignment using new dynamic programming approach in cellular radio networks. Computers and Electrical Engineering 31, pp. 303-333.

160. Sierra, M. R., Coello C., (2006). Multi-objective Particle Swarm Optimizers : A Survey of the State-of-the-art, Inter-national Journal of Computational Intelligence Research 2 (3), pp. 287-308.

161. Slemon G. R., (1994). Electrical machines for variable-frequency drives. Proceeding of IEEE, Vol.82, No.8, pp. 1123-1139.

162. Smith R., Forrest S., Perelson A. S., (1993). Searching for diverse, cooperative populations with genetic algorithms. Evolutionary Computation 1(2), pp. 127-149.

163. Spears W.M., (1994). Simple sub-populations schemes. Proceedings of the 3rd Annual Conference on Evolutionary Programming, World Scientific, pp. 296- 307.

164. Srivinas N., Deb K., (1993). Multiobjective Optimization using Non dominated Sorting in Genetic Algorithms, technical Report, Departement of Mechanical Engineering, Institute of Technology, India.

165. Stacey A., Jancic M., Grundy I., (2003). Particle swarm optimization with mutation. In Proceedings of the Congress on Evolutionary Computation, pp. 1425-1430,Camberra, Australia.

166. Surry P., (1995). A Multiobjective Approach to Constrained Optimisation of Gas Supply Networks : The COMOGA Method, Evolutionary Computing AISB Workshop Selected Papers, Lecture Notes in Computing Sciences, pp. 166-180.

167. Tanaki H., (1995). Multicriteria optimization by Genetic Algorithms : a case of scheduling in hot rolling process, In Proceeding of the Third APORS, pp. 374-381.

168. Ursem R.K., (1999). Multinational evolutionary algorithms. Proceedings of Congress of Evolutionary Computation (CEC-99), vol. 3, Washington, DC, USA, pp. 1633-1640.

169. Van Veldhuizen D.A., (1999). Multiobjective, evolutionary algorithms : classification, analyses and new innovation, air force institute of Technology, United States.

170. Valenzuela M., Uresti-Charre E., (1997). A Non- Cenerational Genetic Algorithm for Multiobjective Optimization, Proceedings of the Seventh International Conference on Genetic Algorithms, pp. 658-665.

171. Wang, Y., Yang, Y., (2008). Handling Multiobjective Problem with a Novel Interactive Multi-swarm PSO, Proceedings of the 4^th International Conference on Intelligent Computing : Advanced Intelligent Computing Theories and Applications 5227, pp. 575-582.

172. Watson J.P., (1999). A performance assessment of modern niching methods for parameter optimization problems. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO) (Morgan- Kaufmann, San Francisco).

173. Xie L. X, BENI G., (1991). A Validity Measure for Fuzzy Clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 13 No 8.

174. Xiao-hua Z, Hong-yun M., Li-cheng J., (2005). Intelligent particle swarm optimization in multiobjective optimization. In Congress on Evolutionary Computation (CEC'2005), pp. 714-719, Edinburgh, Scotland,UK, September.

175. Zadeh L.A., (1965). Fuzzy Sets. Information and control, 8, pp. 338-353.

176. Zadeh L.A., (1994). Soft Computing, LIFE lecture, Japan.

177. Zannoni E., Reynolds R. G., (1997). Extracting Design Knowledge from Genetic Programs Using Cultural Algorithms. Full version in Journal Evolutionary Computation.

178. Zhang J., Huang De-Shuang, Lok T., Lyu M. R., (2006). A novel adaptive sequential niche technique for multimodal function optimization. Neurocomputing 69, pp. 2396-2401.

179. Zhang L.B., Zhou C.G., Liu X.H., Ma Z.Q., Liang Y.C., (2003). Solving multi objective optimization problems using particle swarm optimization. In Congress on Evolutionary Computation (CEC'2003), volume 3, pp. 2400-2405,

Canberra, Australia, December.

180. Zhao B., Cao Y., (2005). Multiple objective particle swarm optimization technique for economic load dispatch. Journal of Zhejiang University SCIENCE, 6A (5), pp. 420-427.

181. Zhu. S., Reynolds. R.G., (1998). The Design of Fully Fuzzy Cultural Algoritms with Evolutionary Programming for Function Optimization. International Conference GP May.

182. Zitzler E.,. Deb k., Thiele L., (2000).Comparison of Multiobjective Evolutionary Algorithms : Empirical Results. Evolutionary Computation, 8(2), pp. 173-195.

183. Zitzler E., Thiele L., (1998). An Evolutionary Algorithm for Multiobjective optimization : The Strength Pareto Approach, TIK-Report 43.

Discipline : Sciences de l'ingénieur

Spécialité : Informatique et Télécommunications

UFR : Informatique et Télécommunications

Responsable de l'UFR : Driss Aboutajdine Période d'accréditation : 2005- 2008

Titre de la thèse : Contribution à l'optimisation complexe par des techniques de Swarm Intelligence

Prénom, Nom : Lamia Benameur

Résumé

Les travaux de recherche présentés dans ce mémoire consistent en l'étude des techniques de calcul «Intelligent», et tout particulièrement les algorithmes basés sur l'intelligence collective des agents.

L'algorithme d'optimisation par essaims particulaires PSO de base est ensuite mis en oeuvre pour l'optimisation globale de problèmes réels. Les problèmes étudiés, dans ce mémoire, sont: le problème d'affectation de fréquences dans les réseaux cellulaires et la commande en vitesse d'une machine synchrone à aimant permanent. L'implémentation de cette technique nécessitait une phase d'adaptation et un réglage fin de paramètres.

Dans un deuxième temps, le modèle de base n'étant pas adapté à l'optimisation de problème nécessitant la localisation de plusieurs optima, un nouveau modèle MPSO (Multipopulation Particle Swarms Optimization) est proposé. Ce modèle permet de créer et de maintenir des sous-populations d'essaims, afin d'effectuer des recherches locales dans différentes régions de l'espace de recherche dans le but de localiser la meilleure position globale qui représente un optimum. L'intégration d'une procédure de classification floue permet, dans ce contexte, d'échantillonner la population en différentes classes constituant les différents sous-essaims.

Dans le cadre de l'optimisation multiobjectif, où il s'agit d'optimiser simultanément plusieurs objectifs contradictoires, une nouvelle approche, basée sur l'algorithme PSO, la dominance de Pareto et la classification floue FCMOPSO (Fuzzy Clustering Multi-objective Particle Swarm Optimizer), est également proposée. Le but principal de cette approche est de surmonter la limitation associée à l'optimisation multiobjectif par essaims particulaires standard. Cette limitation est liée à l'utilisation des archives qui fournit des complexités temporelles et spatiales additionnelles.

Mots-clefs

Techniques de calcul «Intelligent», Optimisation multimodale, Optimisation multiobjectif, Algorithme d'optimisation par essaims particulaires, Classification floue.