3.2 Problématique de l'optimisation
multimodale
Lorsqu'une fonction admet plusieurs optima locaux, elle est
dite multimodale (elle est unimodale dans le cas contraire). Le plus petit
(respectivement le plus grand) optimum local d'une fonction multimodale, est
appelé optimum global.
La figure (3.1) présente, à titre d'exemple, une
distribution possible des optima d'une fonction unidimensionnelle et
multimodale, ainsi que certains points particuliers, tels que les points
d'inflexion et de discontinuité, pouvant poser des difficultés
aux méthodes de résolution.
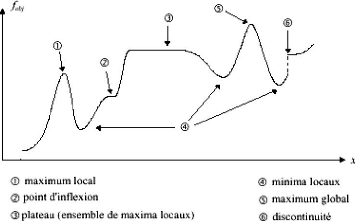
FIG. 3.1 - Points singuliers d'une fonction unidimensionnelle
multimodale
Lorsqu'un tel problème est traité par des
techniques d'optimisation (chapitre 1), l'un des optima sera découvert.
Cependant, dans la pratique, on est souvent confronté à des
problèmes oil on désire identifier tous les optima. Les
problèmes réels, généralement
caractérisés par des domaines multimodaux, requièrent, de
ce fait, la recherche de toutes les solutions, aussi bien locales que globales.
Dans ce contexte, plusieurs techniques ont été
développées, soit pour améliorer les techniques de base en
intégrant des procédures de recherche multimodale, soit en
concevant de nouvelles heuristiques.
La stratégie la plus simple consiste à
exécuter l'algorithme de recherche autant de fois que possible pour
localiser tous les optima requis. Si tous les optima ont la même
probabilité d'être trouvés, le nombre d'exécutions
indépendantes est donné
approximativement par [Beasley et al, 1993] :
|
X p
p
i=1
|
1
i
|
p(ã + logp) (3.1)
|
Où p : nombres d'optima,ã : constante
d'Euler.
Par ailleurs, dans la pratique, les optima n'ont pas la
même chance d'être trouvés, de sorte que le nombre
d'exécutions indépendantes est beaucoup plus élevé.
D'autre part, dès que le nombre d'optima devient important, cette
méthode devient très coûteuse en temps de calcul.
3.3 Techniques de l'optimisation multimodale
Plusieurs méthodes d'optimisation multimodale ont
été reportées dans la littérature, ces methodes
incluent les techniques de niche, qui ont été initialement
introduites dans les algorithmes génétiques, afin de limiter la
dérive génétique due à l'opérateur de
sélection et d'explorer en parallèle différentes
solutions, locales ou globales, situées dans des régions
éloignées de l'espace [Säreni, 1999]. Ces
caractéristiques permettent enfin d'éviter le piégeage de
l'algorithme dans un optimum local.
D'autres méthodes ont été
développées utilisant d'autres concepts, telles que les
systèmes immunitaires artificiels [De Castro et Timmis, 2002] et les
systèmes basés sur des stratégies financières
[Goldberg et Wang, 1997].
3.3.1 Les méthodes de niche
Les méthodes de niche reposent sur une analogie entre
les domaines de recherche en optimisation et les écosystèmes
naturels. Dans la nature, Chaque espèce évolue de façon
à remplir une niche écologique. Une espèce
représente un groupe d'organismes identiques de caractéristiques
biologiques semblables. Dans chaque niche, les ressources naturelles sont
limitées et doivent être partagées entre les
représentants des espèces qui l'occupent.
Par analogie, une niche se réfère typiquement
à un optimum de la fonction objectif et la qualité de l'optimum
représente les ressources de cette niche [Goldberg et Richardson, 1987].
Les espèces sont constituées par des groupes d'individus
similaires. La mesure de la similarité entre individus est
effectuée à partir d'un critère de distance et d'un seuil
de dissimilarité (ou seuil de voisinage).
En principe, les techniques de niche utilisent deux
stratégies. La première est basée sur la modification de
la structure de certaines régions de l'espace de recherche pour
prévenir la convergence de l'algorithme vers ces sections. Cette
approche englobe les techniques de surpeuplement, de remplissage ou de partage.
La seconde approche
impose des contraintes géographiques à la
population pour prévenir la prolifération rapide d'individus
très performants. Les modèles des 'îlots' et de populations
isolées utilisent en général cette seconde
stratégie [El Imrani, 20001.
Plusieurs méthodes de niche ont été
reportées dans la littérature, incluant les méthodes : de
partage [Goldberg et Richardson, 19871 et de sa version améliorée
[El Imrani et al, 1999a1, [El Imrani et al, 1999b1, de niche
séquentielle [Beasley et al, 19931, de niche dynamique [Miller et Shaw,
19961 ou de procédure d'éclaircissement (clearing) [Petrowski,
19961, de surpeuplement (Crowding) [Mahfoud, 19941, [Qing et al, 20081.
D'autres méthodes ont été développées
utilisant d'autres concepts, telles que les systèmes immunitaires
artificiels [De Castro et Timmis, 20021 et les systèmes basés sur
des stratégies financières [Goldberg et Wang, 19971.
Plus récemment, le concept de niche écologique a
été également étendu à d'autres
modèles (e.g., les essaims particulaires (PSO)). On peut citer : Nbest
PSO [Brits et al, 2002a1, Niche PSO [Brits et al, 2002b1, SPSO [Li, 20041 qui
améliore la technique proposée par [Kennedy, 20001, les
techniques basées sur des opérations vectorielles [Schoeman et
Engelbrecht, 20051. Une technique basée sur le concept de nichage
séquentiel et la technique d'essaims particulaires PSO (ASNPSO), a
été récemment proposée dans [Zhang et al, 20061.
3.3.1.1. La technique de partage (fitness sharing)
La méthode de partage constitue probablement la
technique de niche la plus utilisée. Cette technique a été
initialement introduite par Goldberg et Richardson en 1987 [Goldberg et
Richardson, 19871. Elle consiste à réajuster l'adaptation de
chaque individu en fonction des ressources disponibles dans son environnement
local, et du nombre de congénères voisins susceptibles de lutter
pour ces ressources. Le partage a pour effet de modifier l'espace de recherche
en pénalisant les régions à forte densité de
population. Il permet, par conséquent, de réduire la fonction
fitness de chaque élément de la population par une
quantité proportionnelle au nombre d'individus similaires. Cet effet
incite les individus à migrer vers d'autres points de l'espace et
favorise, par conséquent, l'exploration des régions
inoccupées [Mahfoud, 19951. En pratique, la mise en oeuvre de la
méthode de partage se fait de la façon suivante :
L'adaptation brute f(i) d'un individu i
est réduite d'un facteur correspondant approximativement au nombre
d'éléments, qui lui sont similaires, qui représente son
compteur de niche. La fonction d'adaptation réajustée
fsh(i) d'un individu i s'écrit
alors :
f(i)
fsh(i) =
PN (3.2)
j=1 sh(d(i, j))
Le compteur de niche est calculé en sommant la fonction
de partage de tous les membres de la population. N définit la
taille de la population totale et d(i, j) une mesure de
distance entre les individus i et j. La fonction de partage
(sh) mesure le niveau de similarité entre deux individus de la
population. Elle retourne 1 si les
individus sont identiques et 0 si la distance d(i,
j) est plus grande qu'un certain seuil de dissimilarité
[Säreni et Krähenbühl, 1998].
|
I
1 - (d(i,j)
as )á si d(i, j)
< ós
sh(d(i, j)) =
0 autrement
|
(3.3)
|
où á est un paramètre qui
modifie la forme de la fonction de partage. á est
habituellement fixé à 1, donnant comme fonction résultante
la fonction de partage triangulaire.
La distance d(i, j) peut être
caractérisée par une similarité métrique
génotypique (distance de Hamming) dans le cas binaire ou
phénotypique (distance euclidienne par exemple) reliée
directement aux paramètres réels de l'espace de recherche. Deb et
Goldberg [Deb et Goldberg, 1989] montrent que l'utilisation de distance
phénotypique donne des résultats légèrement
meilleurs.
A l'aide de cette technique, plusieurs optima peuvent donc
être découverts en même temps. Cependant, la grande
difficulté de l'application de la méthode consiste dans la
définition de la distance d. En effet, des individus
très proches au niveau de leur génotype peuvent différer
complètement au niveau de leur position dans l'espace, donc ne pas
partager la même ressource. De même, des individus ayant des
performances proches peuvent très bien être différents au
niveau de leur génotype et donc se trouver sur des optima
différents. De plus, cette technique présente un
inconvénient majeur relatif au réglage du seuil de
similarité.
| 


