Contribution à l'optimisation complexe par des techniques de swarm intelligence

1.2.3.3. Les systèmes de classifieurs (Learning Classifier Systems)

Les classifieurs sont des machines, d'apprentissage automatique, basées sur la génétique et l'apprentissage renforcé, mais sont d'une complexité et d'une richesse bien plus grande. Ils sont capables de s'adapter par apprentissage à un environnement dans lequel ils évoluent. Ils reçoivent des entrées de leur environnement et réagissent en fournissant des sorties. Ces sorties sont les conséquences de règles déclenchées directement ou indirectement par les entrées. Un système classifieur est constitué de trois composantes principales :

1. Un système de règles et de messages,

2. Un système de répartition de crédits,

3. Un algorithme évolutif.

Le système de règles et de messages est un type particulier de système de production (SP). Un SP est un procédé qui utilise des règles comme unique outil algorithmique. Une règle stipule que quand une condition est satisfaite une action peut être réalisée (règle déclenchée) [Goldberg, 1989a].

Notons que l'environnement dans lequel évolue le système de classifieurs peut changer au cours de l'évolution. Le système s'adapte alors remettant éventuellement en cause des règles. D'une manière générale, les systèmes classifieurs sont capables d'induire de nouvelles règles par généralisation à partir d'exemples [Holland et al, 1986]. Les systèmes de classifieurs sont utilisés pour résoudre des problèmes réels en biologie, en médecine, en sciences de l'ingénieur, etc.

1.2.3.4. Les systèmes basés sur l'intelligence collective (Swarm Intelligence)

L'intelligence collective désigne les capacités cognitives d'une communauté résultant des interactions multiples entre les membres (ou agents) de la communauté. Des agents, au comportement très simple, peuvent ainsi accomplir des tâches complexes grâce à un mécanisme fondamental appelé synergie. Sous certaines conditions particulières, la synergie créée, par la collaboration entre individus, fait émerger des possibilités de représentation, de création et d'apprentissage supérieures à celles des individus isolés.

Les formes d'intelligence collective sont très diverses selon les types de communauté et les membres qu'elles réunissent. Les systèmes collectifs sont en effet plus ou moins sophistiqués. Les sociétés humaines en particulier n'obéissent pas à des règles aussi mécaniques que d'autres systèmes naturels, par exemple du monde animal. Pour des systèmes simples les principales caractéristiques sont :

1. L'information locale : Chaque individu ne possède qu'une connaissance partielle de l'environnement et n'a pas conscience de la totalité des éléments qui influencent le groupe,

2. L'ensemble de règles : Chaque individu obéit à un ensemble restreint de règles simples par rapport au comportement du système global,

3. Les interactions multiples : Chaque individu est en relation avec un ou plusieurs autres individus du groupe,

4. La collectivité : les individus trouvent un bénéfice à collaborer (parfois instinctivement) et leur performance est meilleure que s'ils avaient été seuls.

L'intelligence collective est observée notamment chez les insectes sociaux (fourmis, termites et abeilles) et les animaux en mouvement (oiseaux migrateurs, bancs de poissons). En conséquence, plusieurs algorithmes basés sur le principe d'intelligence collective ont été introduits : on peut citer les colonies de fourmis et les essaims particulaires [Hoffmeyer, 1994], [Ramos et al., 2005].

a. Les colonies de fourmis (Ants Colony)

Une colonie de fourmis, dans son ensemble, est un système complexe stable et autorégulé capable de s'adapter très facilement aux variations environnementales les plus imprévisibles, mais aussi de résoudre des problèmes, sans contrôle externe ou mécanisme de coordination central, de manière totalement distribuée.

L'optimisation par colonies de fourmis (ACO "Ants Colony Optimisation") s'inspire du comportement des fourmis lorsque celles-ci sont à la recherche de nourriture [Deneubourg et al, 1983], [Deneubourg et Goss, 1989], [Goss et al, 1990]. Il a ainsi été démontré qu'en plaçant une source de nourriture reliée au nid par une passerelle, formée d'une branche courte et d'une branche longue, les fourmis choisissaient toutes le chemin le plus court après un certain laps de temps [Beckers et al, 1992]. En effet, chaque fourmi se dirige en tenant compte des traces de phéromone déposées par les autres membres de la colonie qui la précèdent.

Comme cette phéromone s'évapore, ce choix probabiliste évolue continuellement. Ce comportement collectif, basé sur une sorte de mémoire partagée entre tous les individus de la colonie, peut être adapté et utilisé pour la résolution de problèmes d'optimisation combinatoire surtout les problèmes du parcours des graphes.

D'une façon générale, les algorithmes de colonies de fourmis sont considérés comme des métaheuristiques à population, oil chaque solution est représentée par une fourmi se déplaçant dans l'espace de recherche. Les fourmis marquent les meilleures solutions, et tiennent compte des marquages précédents pour optimiser leur recherche.

Ces algorithmes utilisent une distribution de probabilité implicite pour effectuer la transition entre chaque itération. Dans leurs versions adaptées à des problèmes combinatoires, ils utilisent une construction itérative des solutions.

La différence qui existe entre les algorithmes de colonies de fourmis et les autres métaheuristiques proches (telles que les essaims particulaires) réside dans leur aspect constructif. En effet, dans le cas des problèmes combinatoires, il est possible que la meilleure solution soit trouvée, alors même qu'aucune fourmi ne l'aura découverte effectivement. Ainsi, dans l'exemple du problème du voyageur de commerce, il n'est pas nécessaire qu'une fourmi parcoure effectivement le chemin le plus court, i.e., celui-ci peut être construit à partir des segments les plus renforcés des meilleures solutions. Cependant, cette définition peut poser problème dans le cas des problèmes à variables réelles, oil aucune structure de voisinage n'existe.

b. Les essaims particulaires (Particle Swarm Optimization PSO)

L'optimisation par essaims particulaires est une métaheuristique d'optimisation, proposée par Russel Ebenhart et James Kennedy en 1995 [Eberhart et Kennedy, 1995], [Kennedy et Eberhart, 1995]. Cette métaheuristique s'appuie notamment sur un modèle développé par le biologiste Craig Reynolds à la fin des années 1980, permettant de simuler le déplacement d'un groupe d'oiseaux.

Cette méthode d'optimisation se base sur la collaboration des particules entre elles. Elle a d'ailleurs des similarités avec les algorithmes de colonies de fourmis, qui s'appuient eux aussi sur le concept d'auto-organisation.

Ainsi, grâce à des règles de déplacement très simples (dans l'espace de solutions), les particules peuvent converger progressivement vers un optimum. Cette métaheuristique semble cependant mieux fonctionner pour des espaces en variables continues.

Au départ de l'algorithme, un essaim est réparti au hasard dans l'espace de recherche de dimension D, chaque particule p est aléatoirement placée dans la position xp de l'espace de recherche, chaque particule possède également une vitesse aléatoire. Ensuite, à chaque pas de temps:

chaque particule est capable d'évaluer la qualité de sa position et de garder en mémoire sa meilleure performance P i : la meilleure position qu'elle a atteinte jusqu'ici (qui peut en fait être parfois la position courante) et sa qualité (la valeur en cette position de la fonction à optimiser),

chaque particule est capable d'interroger un certain nombre de ses congénères (ses informatrices, dont elle-même) et d'obtenir de chacune d'entre elles sa propre meilleure performance Pg (et la qualité afférente),

à chaque pas de temps, chaque particule choisit la meilleure des meilleures performances dont elle a connaissance, modifie sa vitesse V en fonction de cette information et de ses propres données et se déplace en conséquence.

La modification de la vitesse est une simple combinaison linéaire de trois ten-dances, à l'aide de coéfficients de confiance :

- la tendance « aventureuse », consistant à continuer selon la vitesse actuelle,

la tendance « conservatrice », ramenant plus ou moins vers la meilleure position déjà trouvée,

la tendance « panurgienne », orientant approximativement vers la meilleure informatrice.

La mise à jour des deux vecteurs vitesse et position, de chaque particule p dans l'essaim, est donnée par les équations (1.1) et (1.2) :

v_j (t + 1) = r(t)v^p

p j (t) + uw1j(t)(P ⁱ _j(t) - x^p _j(t)) + uw2j(t)(P _j ^g(t) - x^p _j(t)) (1.1)

xp _j(t + 1) = x^p _j(t) + vp j (t + 1) (1.2)

Où j = 1. . . , D, r(t) est le facteur d'inertie, u représente le paramètre cognitif et u le paramètre social. w1j(t) et w2j(t) sont des nombres aléatoires compris entre 0 et 1.

Lors de l'évolution de l'essaim, il peut arriver qu'une particule sorte de l'espace de recherche initialement défini. Pour rester dans un espace de recherche fini donné, on ajoute un mécanisme pour éviter qu'une particule ne sorte de cet espace.

le plus fréquent est le confinement d'intervalle. Supposons, par simplicité, que l'espace de recherche soit [xmin, xmax]^D. Alors ce mécanisme stipule que si une coordonnée xj, calculée selon les équations de mouvement, sort de l'intervalle [xmin, xmax],on lui attribue en fait la valeur du point frontière le plus proche. En pratique, celà revient donc à remplacer la deuxième équation de mouvement (équation 1.2) par:

xj(t + 1) = min(max(xj(t) + vj(t + 1), xmin), xmax) (1.3)

De plus, on complète souvent le mécanisme de confinement par une modification de la vitesse, soit en remplaçant la composante qui pose problème par son opposée, souvent pondérée par un coefficient inférieur à 1, soit, tout simplement, en l'annulant. Donc le principe du confinement consiste à ramener la particule qui sort de l'espace de recherche au point le plus proche qui soit dans cet espace et modifier sa vitesse en conséquence. Le pseudo code de l'algorithme PSO de base est donné par l'algorithme (3), [De Falco et al, 2007].

Principales caractéristiques

Ce modèle présente quelques propriétés intéressantes, qui en font un bon outil pour de nombreux problèmes d'optimisation, particulièrement les problèmes fortement non linéaires, continus ou mixtes (certaines variables étant réelles et d'autres entières) :

il est facle à programmer, quelques lignes de code suffisent dans n'importe quel langage évolué,

il est robuste (de mauvais choix de paramètres dégradent les performances, mais n'empêchent pas d'obtenir une solution).

algorithme 3 Pseudo code de l'algorithme PSO

t 4-- 0

Pour chaque particule

Initialiser sa position et sa vitesse.

Initialiser P ⁱ(t)

Fin pour

Répéter

Choisir la particule P g(t) ayant la meilleure fitness dans l'itération courante

Pour chaque particule p

Calculer la vitesse vp(t + 1) utilisant l'équation (1.1).

Mettre à jour le vecteur position xp(t + 1) selon l'équation (1.2).

Calculer la valeur de la fitness f(xp(t))

Si f(xp(t)) > f(P ⁱ(t))

P ⁱ(t + 1) 4-- xp(t)

Fin si

Fin pour t 4-- t + 1

Tant que (critère d'arrêt n'est pas validé)

1.2.3.5. Les algorithmes culturels (Cultural Algorithms CA) a. Principes de base

Les algorithmes culturels sont des techniques évolutives modélisant l'évolution culturelle des populations [Reynolds, 1994]. Ces algorithmes supportent les mécanismes de base de changement culturel [Durham, 1994]. Certains sociologues ont proposé des modèles oil les cultures peuvent être codées et transmises à l'intérieur et entre les populations [Durham, 1994], [Renfrew, 1994]. En se basant sur cette idée, Reynolds a développé un modèle évolutif dans lequel l'évolution culturelle est considérée comme un processus d'héritage qui agit sur deux niveaux évolutifs différents : le niveau microévolutif (espace population) et le niveau macro-évolutif (espace de connaissance) [Reynolds, 1994].

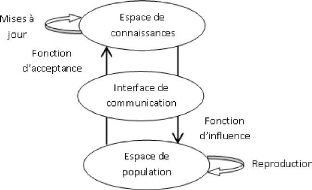
FIG. 1.3 - Les composants principaux d'un algorithme culturel

Ces algorithmes agissent donc sur deux espaces : l'espace de population qui contient un ensemble d'individus qui évoluent grâce à un modèle évolutif, et l'espace de connaissances qui contient les informations et les connaissances, spécifiques au problème à résoudre, utilisées pour guider et influencer l'évolution des individus des populations au cours des générations. De ce fait, un protocole de communication est indispensable pour établir une interaction entre ces deux espaces (figure 1.3).

Ce protocole a, en fait, une double mission, il détermine d'une part quels individus de la population peuvent influencer l'espace de connaissances (fonction d'acceptance), et d'autre part quelles connaissances peuvent influencer l'évolution des populations (fonction d'influence). Le pseudo code (4) représente la structure de base d'un AC [Zhu et Reynolds, 1998].

Plusieurs versions d'algorithmes culturels ont été développées avec différentes implémentations des deux espaces évolutifs. VGA (Version space guided Genetic Algorithm) se sert d'un algorithme génétique comme modèle micro-évolutif et de "Version

algorithme 4 Structure de base d'un Algorithme Culturel

t 4-- 0

Initialiser la population P(t);

Initialiser l'espace de connaissances B(t); Répéter

Evaluer P(t);

Ajuster (B(t), acceptance P(t)); Evaluer (P(t), influence B(t));

t 4-- t + 1;

Jusqu'à (condition d'arrêt valide);

Spaces" pour le niveau macro-évolutif [Reynolds et Zannoni, 1994], d'autres implémentations utilisent la programmation génétique pour le niveau micro évolutif et "Program segments" pour le niveau macro-évolutif [Zannoni et Reynolds, 1997].