Conditions aux limites transparentes et modélisation des vagues de surface dans un écoulement

redéfinition des noms chapitres spéciaux

CoNsERvAToiRE NATioNAL DEs ARTs ET METiERs
LABoRAToiRE DE CALcuL SciENTiFiQuE

MEMOIRE D'INGENIEUR

EN INFORMATIQUE

Spécialité : Modélisation Ingénierie Mathématique
par
Denis-Maxime BISSENGUE

CoNDiTioNs AuX LiMiTEs
TRANspARENTEs ET MoDELisATioN DEs

vAGuEs DE suRFAcE DANs uN

EcouLEMENT.

	Rapport soutenu le : 11 Janvier 2012 devant le jury composé de :
Mr.	PHiLippE DESTUYNDER	Professeur au C.N.A.M	(Président)
Mr.	THiERRy HORSIN	Professeur au C.N.A.M	(Membre)
Mr.	ALEXis HERAULT	Maître de conférence au C.N.A.M	(Membre)
Mr.	OLiviER WILK	Ingénieur au C.N.A.M	(Membre)
Mr.	THoMAs GAZZOLA	Ingénieur au BUREAU VERITAS	(Membre)
Mr.	SLiMANE AMARA	Ingénieur Université de Troyes	(Membre)

REMERCIEMENTS

M

Es premiers remerciements sont adressés à Monsieur Philippe Destuynder, qui m'a accueilli au sein de la chaire de calcul sci-

entifique m'a proposé ce mémoire d'ingénieur et a dirigé mon travail. Je suis spécialement sensible à la confiance qu'il a toujours eu en moi. J'exprime ma profonde gratitude aux membres du jury, en particulier :

- messieurs Thierry Horsin et Alexis Herault qui ont accepté de faire

parti du jury de ce travail,

- monsieur Thomas Gazzola du Bureau Veritas qui a bien voulu s'associer au jury,

- monsieur Olivier Wilk dont l'aide amicale a été un atout précieux tout au long de l'élaboration de ce memoire.

J'ai eu de la chance de bénéfier d'un environnement de travail excep-

tionnel au laboratoire, je remercie particulièrement, Janine Laurent , Christiane Morel, Aurélien Latouche ainsi que tous les membres du département d'ingénierie mathématique.

Enfin, je ne peux en aucun cas oublier ma tendre épouse et ma fille pour le soutien moral dont elles ont fait preuve au cours de mes études, je remercie tout spécialement celle qui par son abnégation et son dévouement a permis que ces études se concrétisent.

Lieu, le 26 février 2012.

TABLE DEs MATièREs

1 2	Introduction Les Modèles 2.1 MoDèLE DANs L'EAu		1 5 6
		2.1.1 Hypothèses de petites pertubations	7
	2.2	MoDèLE à LA suRFAcE	10
	2.3	TRAiTEMENT DEs coNDiTioNs LiMiTEs Aux BoRDs	11
	2.4	CoNDiTioNs Aux LiMiTEs TRANspARENTEs	13
		2.4.1 Condition aux limites transparentes en dimension n =1 .	14
		2.4.2 Condition aux limites transparente en dimension n=2; 3 .	24
		2.4.3 Conclusion	28
3	Propriétés des modèles		31
	3.1	FoRMuLATioN vARiATioNNELLE	31
		3.1.1 Formulation variationnelle du modèle Hydroacoustique
		avec écoulement	31
		3.1.2 Formulation variationnelle du modèle de vagues . . . .	38
		3.1.3 Stabilité du modèle	41
		3.1.4 Existence et unicité d'une solution	43
		3.1.5 Conclusion	48
4	Schémas numériques		49
	4.1	MAiLLAgE	49
		4.1.1 Description du logiciel Gmsh	50
		4.1.2 Présentation du logiciel Getfem + +	51
	4.2	DiscRéTisATioN EN EspAcE	51
	4.3	DiscRéTisATioN EN TEMps	54
	4.4	ETuDE DE LA sTABiLiTé Du schéMA D'iNTégRATioN EN TEMps	54
5	Expériences numériques		57
		5.0.1 Solution stationnaire	58
		5.0.2 Frontières adaptées	60
		5.0.3 Conclusion	62
6	Résultats numériques		63
		6.0.4 Modèle sans couplage avec les vagues	64
		6.0.5 Résultats numériques	64
		6.0.6 Conclusion	69
		6.0.7 Modèle avec couplage avec les vagues	70
		6.0.8 Résultats numériques	71
		6.0.9 Stabilité du modèle	87

7 Conclusion et perspectives 89

8 Annexe 91

8.1 RAPPEL DEs OUTILs MATHéMATIQUEs 91

8.2 EQUATIONs DE LA MécANIQUE DEs FLUIDEs 95

LIsTE DEs FIGUREs

2.1 Modèle. 5

2.2 Equilibre d'une colonne d'eau à la surface. 10

2.3 Représentation des quantités caractéristiques au travers des frontières ouvertes. 16

3.1 les équipotentielles sont orthogonales aux lignes de courant. 36

5.1 Résultat avec stucture symétrique : une ellipse . 59

5.2 Résultat avec stucture non symétrique :un sous-marin. . . 60

5.3 Exemple d'iso-potentiel pour U= 0.01m.s-¹. 60

5.4 Maillage du domaine découpé avec une ellipse à l'intérieur 61

5.5 Maillage du domaine découpé avec un sous-marin à l'intérieur. 62

6.1 Schema de fonctionnement 63

6.2 Step 1-2 :Ecoulement transitiore, avec condition aux limites

transparentes sur les frontières latérales. 65
6.3 Step 3-4 :Ecoulement transitiore, avec condition aux limites

transparentes sur les frontières latérales. 65
6.4 Step 5-6 :Ecoulement transitiore, avec condition aux limites

transparentes sur les frontières latérales. 65
6.5 Step 7-8 :Ecoulement transitiore, avec condition aux limites

transparentes sur les frontières latérales. 65
6.6 Step 9-10 :Ecoulement transitiore, avec condition aux limites

transparentes sur les frontières latérales. 66
6.7 Step 11-12 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 66
6.8 Step 13-14 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 66
6.9 Step 15-16 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 67
6.10 Step 17-18 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 67
6.11 Step 19-20 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 67
6.12 Step 21-22 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 68

6.13 Step 23-24 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 68
6.14 Step 25-26 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 68
6.15 Step 27-28 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 68
6.16 Step 29-30 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 69
6.17 Step 31-32 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 69
6.18 Step 33-34 :Ecoulement transitiore, avec condition aux lim-

ites transparentes sur les frontières latérales. 69

6.19 Step 1-2 : couplage avec les vagues 71

6.20 Step 3-4 : couplage avec les vagues 71

6.21 Step 5-6 : couplage avec les vagues 72

6.22 Step 7-8 : couplage avec les vagues 72

6.23 Step 9-10 : couplage avec les vagues 72

6.24 Step 7-8 : couplage avec les vagues 72

6.25 Step 13-14 : couplage avec les vagues 73

6.26 Step 15-16 : couplage avec les vagues 73

6.27 Step 17-18 : couplage avec les vagues 73

6.28 Step 9-10 : couplage avec les vagues 73

6.29 Step 21-22 : couplage avec les vagues 74

6.30 Step 11-12 : couplage avec les vagues 74

6.31 Step 13-14 : couplage avec les vagues 74

6.32 Step 15-16 : couplage avec les vagues 74

6.33 Step 29-30 : couplage avec les vagues 75

6.34 Step 31-32 : couplage avec les vagues 75

6.35 Step 17-18 : couplage avec les vagues 75

6.36 Step 19-20 : couplage avec les vagues 75

6.37 Step 37-38 : couplage avec les vagues 76

6.38 Step 21-22 : couplage avec les vagues 76

6.39 Step 23-24 : couplage avec les vagues 76

6.40 Step 43-44 : couplage avec les vagues 76

6.41 Step 25-26 : couplage avec les vagues 77

6.42 Step 27-28 : couplage avec les vagues 77

6.43 Step 29-30 : couplage avec les vagues 77

6.44 Step 29-30 : couplage avec les vagues 77

6.45 Courbe des valeurs propres en fonction des vitesses 79

6.46 Step 1-2 : couplage avec les vagues 80

6.47 Step 3-4 : couplage avec les vagues 80

6.48 Step 5-6 : couplage avec les vagues 80

6.49 Step 7-8 : couplage avec les vagues 81

6.50 Step 7-8 : couplage avec les vagues 81

6.51 Step 11-12 : couplage avec les vagues 81

6.52 Step 9-10 : couplage avec les vagues 81

6.53 Step 15-16 : couplage avec les vagues 82

6.54 Step 17-18 : couplage avec les vagues 82

6.55 Step 11-12 : couplage avec les vagues 82

6.56 Step 21-22 : couplage avec les vagues 82

6.57 Step 13-14 : couplage avec les vagues 83

6.58 Step 25-26 : couplage avec les vagues 83

6.59 Step 15-16 : couplage avec les vagues 83

6.60 Step 29-30 : couplage avec les vagues 83

6.61 Step 31-32 : couplage avec les vagues 84

6.62 Step 17-18 : couplage avec les vagues 84

6.63 Step 19-20 : couplage avec les vagues 84

6.64 Step 37-38 : couplage avec les vagues 84

6.65 Step 21-22 : couplage avec les vagues 85

6.66 Step 41-42 : couplage avec les vagues 85

6.67 Step 23-24 : couplage avec les vagues 85

6.68 Step 45-46 : couplage avec les vagues 85

6.69 Step 25-26 : couplage avec les vagues 86

6.70 Step 49-50 : couplage avec les vagues 86

6.71 Courbe des valeurs propres en fonction des vitesses 87

1

INTRODUCTION

L

ES VAGUES et la mer en général, ont toujours exercé un mystérieux attrait sur les hommes. Et malgré cette apparente monotonie, nous

avons beaucoup de mal à comprendre leur naissance et leur évolution. Ainsi le mécanisme de vague s'est progressivement laissé découvrir ce dernier siècle après d'instantes recherches faites de façon complémentaire par les physiciens et les mathématiciens qui se sont succédés jusqu'à nos jours. Ces derniers ont montré que c'est l'action du vent à la surface de l'eau qui est responsable de la formation de ces vagues obéissant aux mêmes règles depuis des millénaires interpellant navigateurs et chercheurs.

Une vague est une onde mécanique qui se propage à la surface de l'eau entre deux fluides en l'occurence l'eau et l'air.

Depuis les travaux de Kelvin [1], de noubreuses contributions et simulations numériques ont été publiées pour la modélisation des vagues de surface. Dans la plupart d'entre eux, les auteurs [3,4] considèrent que la capillarité est négligeable par rapport aux forces en présence à la surface de la mer.

Malheureusement, comme il a été souligné dans les articles [9] et par d'autres auteurs[5], que le modèle est mal posé dans le sens oil l'existence d'ondes à la surface de l'eau est due d'une part à la pesanteur qui tend à maintenir l'interface air-eau horizontale (ondes de gravité) et d'autre part à la tension de surface qui tend à maintenir l'interface plane (ondes capillaires).

Dans ce document, nous considérons d'une part un écoulement capillaire possédant une surface libre dans un domaine incluant un sous-marin et d'autre part, nous-nous intéressons à la propagation acoustique dans ce domaine contenant l'eau en écoulement uniforme et soumis à de petites perturbations autour d'un écoulement moyen initial réalisant l'équilibre statique de la surface libre.

Bien qu'étant à la base de la majorité des modèles présents dans la littérature, l'étude de la propagation acoustiques dans des écoulements reste un problème d'actualité et difficile à appréhender dont les principales applications se rencontent dans les secteurs de l'industrie maritime et de l'aéronautique.

En se limitant au cadre de la propagation linéaire dans un domaine con-tenant un sous-marin en présence d'un écoulement, nous nous sommes proposé d'étudier l'acoustique sous-marine qui a pour objet l'étude et l'utilisation de modèles mathématiques décrivant la propagation des ondes acoustiques dans la mer.

Pour le modèle de surface, il est connu que dans le cadre linéaire simple des ondes progressives dans un domaine borné modélisé par le modèle de Neumann-Kelvin des instabilités numériques apparaissent. Ainsi, nous avons choisi de prendre comme modèle d'ondes progressives à la surface de la mer, le modèle traduisant l'équilibre de la surface libre en présence de la tension superficielle et de la gravité. Modèle défini dans l'article de Philippe Destuynder et Caroline Fabre [9].

Par ailleurs, les problèmes de propagation d'ondes sont souvent posés en domaine non borné et une des questions importantes pour leur résolution numérique est de savoir borner artificiellement le domaine de calcul. Afin de construire ces limites articielles de sorte que le problème aux conditions initiales et aux limites soit "bien-posé" et que les frontières latérales du domaine soient "transparentes" vis-a-vis des ondes entrantes et sortantes, B. Engquist et Majda (1977) ont mis au point une méthode théorique pour rendre les limites transparentes à un niveau d'approximation clairement défini.

Leur théorie générale de construction des conditions transparentes s'appuie sur l'analyse modale des équations du mouvement linéarisées autour d'un état de référence et ré-écrites aux bords sous la forme d'une condition qui peut en général s'exprimer à l'aide de l'opérateur de DirichletNeumann. En générale, la forme de cette opérateur n'est pas toujours commode (pratique), l'essentiel du travail de construction des conditions transparentes consiste donc à trouver une bonne approximation de ce dernier.

Dans ce travail, un autre thème important abordé dans ce travail est celui du traitement des conditions aux limites non réfléchissantes (ou transparentes) pour l'acoustique en écoulement.

Celles-ci sont à la fois indispensables du fait du caractère nécessairement borné du domaine de calcul et cruciales pour l'obtention de résultats numériques pertinents.

Ces conditions transparentes doivent être en mesure de simuler une condition de rayonnement à l'infini, tout en veillant à ne pas créer de réflection aux frontières du domaine de calcul.

Ce sujet reste aujourd'hui un important axe de recherche dans l'étude et la simulation numérique de l'ensemble des phénomènes de propagation d'ondes.

La méthode des équations intégrales qui est utilisée par la plupart des codes de calcul industriels, ne permet pas de traiter ces aspects de façon satisfaisante et nécessitent des hypothèses simplificatrices incompatibles avec une représentation réaliste des phénomènes physiques en présences. Les difficultés sont multiples : d'une part le modèle linéaire est naturellement instable et seul la présence de termes non linéaires à la surface de l'eau permet de la stabiliser et d'autre part, il apparait trois types d'ondes couplés (ondes de gravité, ondes acoustiques et ondes de capillarité ).

La grande disparité des vitesses d'ondes et de celle du sous-marin conduisent à des difficultés numériques qu'il a fallu surmonter en utilisant un schéma d'intégration en temps adapté et qui ne dissimule pas l'un des phénomènes en présence.

La pertinence de ce travail est justifiée en particulier par la construction

3

d'un modèle de condition aux limites transparentes évitant les réflexions d'ondes.

Ce mémoire s'articule autour de six chapitres suivant les points d'étude précedemment évoqués.

Ainsi, dans le deuxième chapitre nous définissons les modèles, présentons les lois physiques et les principales hypothèses permettant d'aborder le problème et nous donnons les équations gouvernant les écoulements considéres.

Le principal résultat de ce chapitre est l'écriture mathématique de la condition aux limites transparentes sur les frontières représentant respectivement la section d'entrée du fluide et la section de sortie du fluide. Cette condition aux limites est obtenue et est valable seulement pour les frontières planes perpendiculaires à la direction de l'écoulement.

Une validation numérique sur un cas test (dimension 1) de cette condition aux limites est effectuée afin de vérifier l'efficacité de la méthode.

Le troisième chapitre est consacré à l'étude des différentes formulations variationnelles et au modèle couplé fluide-vague à la surface. Pour cet étude, nous-nous sommes intéressé à la determination d'une nouvelle frontière du domaine.

Il s'agit de frontières adaptées évitant des ondes tangentielles à la frontière qui diffracteraient.

Nous proposons aussi dans ce chapitre une étude du système couplé approché obtenu afin d'établir des résultats d'existence, d'unicité et de stabilité a priori du modèle. Nous déduisons de cette étude qu'en présence d'une capillarité, nous avons une vitisse critique, vitesse au dessus de laquelle le modèle peut être instable.

Dans le quatrième chapitre, nous présentons les logiciels et la méthode numérique utilisés. La méthode numérique appropriée pour la prise en compte des conditions aux limites que nous avions choisi est celle des éléments finis.

Le cinquième et le sixième chapitres sont consacrés à la vérification numériques de la validité du modèle numérique présenté dans le quatrième chapitre.

L

'ouvERt tridimensionnel sur lequel est posé le problème d'écoulement sera noté Ù ? R³. Il correspond à un bassin rempli d'eau dans

lequel un corps immergé est animé d'un mouvement rectiligne uniforme. Pour la mise en équation, on se placera dans le référentiel lié au corps, cela revient à supposer qu'il est fixe et soumis à un écoulement que l'on supposera uniforme et irrotationel. La vitesse à l'infini amant est u.

Notons que la frontière de ce bassin est partitionnée en cinq parties:

- une surface libre notée _s,

- le fond du bassin que l'on note 0, est supposé imperméable, - deux côtés latéraux 1 et 2 par lesquels l'eau rentre et sort, - et b la surface arbitraire entourant le corp immergé (un sous-marin)

et ne rencontrant pas la surface libre.

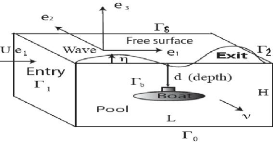
FiGuRE 2.1 - Modèle.

Afin de bien rendre compte de l'intéraction fluide-modèle de vague, nous allons analyser séparément les équations régissant le comportement du fluide dans le bassin et celles qui régissent celui de la surface libre en prenant en compte l'effet de la capillarité .

Ensuite, une formulation mathématique et physique des conditions aux limites transparentes sera faite pour les frontières latérales entrante 1 et sortante 2 .

Nous ferons des hypothèses classiques permettant de construire un modèle sur lequel il est possible d'obtenir de nombreux résultats opérationnels. On suppose que :

1. le fluide est parfait et compressible et il n'est soumis qu'à des forces de gravité et de pression.

2. Le champ de vitesses u des particules fluides est supposé irrotationnel :

rot(u) = 0,

et la circulation du champ de vitesses sur chaque composante connexe de la frontière de l'ouvert occupé par le fluide est supposée nulle.

Ceci permet d'assurer l'existence d'une fonction potentielle de vitesses notée ö définie à une constante additive près telle que :

u = Vö.

2.1 MoDèle DANs l'eAu

Etant donné ñ_e la masse volumique de l'eau, le principe de conservation de la masse (2.7.1) s'écrit :

?ñ_e

?t + div(ñ_eVö) = 0 dans n×]0, T[. (2.1)

L'équation traduisant le théorème de la conservation de la quantité de mouvement s'écrit :

?u

ñe( ?t + uvu) = ñ_eg - Grp dans n×]0, T[. (2.2)

Afin de simplifier cette relation et de trouver une intégrale première, nous introduisons un potentiel de barotropie notée F(ñ_e) et qui est défini par : F(ñ_e) = fe ñe 1 ?p 0 ñ ?ñe(ñe)dñ + c(x), (2.3)

d'où

?F 1 ?p rF(ñe) = .rñe + rc = . ?ñe (ñe).rñe ?ñe ñe Vp

+Vc,

Par conséquent, le gradient de (2.3) est donné par :

1

VF(ñ_e) = .rp(ñ_e) + rc (2.4)

ñ_e

En négligeant la gravité dans (2.2), et en tenant compte de l'hypothèse de fluide non visqueux, on obtient une formulation plus simple de la relation fondamentale :

?ö 1

v ( _?t + ₂ |Vö|² + F(ñ_e)) =0 dans n×]0, T[. (2.5)

Et comme le potentiel des vitesses ö est définie à une constante spatiale additive près, en choisissant convenablement cette constante on obtient :

?ö +

?t 2 |Vö|² + F(ñ_e) = 0 dans n×]0, T[, (2.6a)

1

2.1.1 Hypothèses de petites pertubations

Dans le cadre de la théorie linéaire de l'acoustique, les pertubations (pour une particule donnée à un instant donné) des quantités caractérisant l'écoulement sont supposées suffisamment petites pour pouvoir limiter au premier ordre les développements (en puissances d'un paramètre caractéristique e, sans dimension, de l'ordre de grandeur de la pertubation et petit devant l'unité) de ces quantités autour de l'état non pertubé.

Cette hypothèse consiste donc à envisager des mouvements de faible amplitude autour d'un état moyen défini par un écoulement permanent représenté par le potentiel de ?0, solution du problème de Neumann:

? -A?0	= 0 dans 1, et R 1 ?0	= 0,
?????????
??0	= 0 sur F0 ? Fb ? Fs,		(2.7)
?í
????????? ??0	= u(e1, í) sur F1 ? F2.
?í

Dans ce système, u est l'amplitude de la vitesse d'écoulement suivant la direction e1.

Et le champs de vitesse constant est donné par le gradient de ?0.

D'autre part, pour des raisons de simplification, nous supposons que ?0 est suffisament régulière et de classe C^°°(1) pour justifier les calculs dans la suite.

Nous écrivons ensuite :

Equation traduisant la conservation de la masse

La linéarisation de l'équation de continuité (2.1) :

?ñ_e

ö(x, t) = ?0(x) + ?(x, t), ñ_e(x, t) = ñ0 + ñ(x, t) x ? R³,

?t + Vñ_e
· Vö + ñ_eAö = 0 dans 1x]0, T[.

autour de ?0 et ñ0 donne:

?ñ ?t + V?0
· Vñ + ñ0A? = 0 dans 1x]0, T[. (2.8)

d'ou :

?ñ ?t

= -V?0 · Vñ - ñ0A? dans 1x]0, T[. (2.9)

Equation de conservation de la quantité de mouvement

De même pour la deuxième équation du système précédent, la linéarisation se fait en deux étapes (cf :[10]).

- Etape 1 : On dérive par rapport au temps l'équation (2.6a)

?^2ö ?t2 +

1 ?t(|Vö|^2) + ?F ? ?ñe (ñe)?ñe ?t = 0, 2

?F 1 ?p

?ñe (ñ_e) = ñ_e ?ñe (ñe),

et on linéarise autour de l'état permanent :

?²? ?p

?t2 + r?0
· r(?? _?t ) + 1 ?ñ0 (ñe)?ñ ?t = 0,

ñ0

ensuite, on remplace ?ñ par l'expression précedente : ?t

?2, ?? 1 ?p ?p

?t; + V?0
· v( _?t ) - ñ0 ?ñe (ñ0)(V?0
· Vñ) - , (ñ0)6? = 0.

uñe

(2.10)

- Etape 2 : On applique l'opérateur V?0V(
·) à l'équation (2.6a)

G?0
· V(^?ö) + 1 (Gr?0
· V(|Vö|²)) + (V?0
· V (F(ñ_e)) =0,

?t 2

comme

v(|vö|²) = 2V.(V?0
· V?) et V(F(ñ_e) = 1 ?p

ñ_e ?ñe (ñe).rñe,

alors

V?0 · V (F(ñe) = ñ10

?p ?ñe

(ñ0).(V?0 · Vñ).

On obtient alors la relation suivante :

r?0
· r.(?? _?t ) + r?0
· r.(r?0
· r?)) + 1 ?p

?ñe (ñ0).(rñ0
· rñ) = 0.

ñ0

(2.11) Et pour conclure, on additionne les deux relations (2.10) et (2.11) ce qui donne alors l'équation des ondes :

?²?

?t2 + 2r?0
· r(?? _?t ) + V?0
· V(V?0
· V?) - c²f6? = 0 dans I/×]0, T[.

(2.12)

avec

?p

cf 2 = ?ñe (ñ0), vitesse du son dans le fluide.

Modèle dans l'ouvert U.

- un écoulement stationnaire problème stationnaire ? ????????? ?????????	: --Ä?0 ??0	de potentiel de vitesse ?0 solution du = 0 dans Ù, = 0 sur 0 U b U s, = u(e1, í) sur 1 U 2.
	?í ??0
	?í

Où ?0 est définie à constante près, que nous fixons en prenant par exemple la condition de moyenne nulle sur _s :

Z

?0 = 0, _s - et un écoulement transitoire représenté par le potentiel ? solution de :

?²?

?t2 +2V?0 .V.(?? _?t )+V?0 .V(V?0 .V?)-- c2 f Ä? = 0 dans Ùx]0, T[.

2.2 ModèLe à La suRFace

Dans cette partie, nous discutons d'une propriété des interfaces entre un liquide et un gaz (air). Cette interface joue un rôle très important dans l'équilibre et l'écoulement des fluides, dès lors qu'ils ont des surfaces

libres et ne sont plus simplement en contact avec des parois solides.

Sur la frontière _s représentant une surface libre perpendiculaire à la direction de la gravité locale, nous avons l'équilibre local d'une colonne d'eau au voisinage de cette surface (cf schéma ci-dessous).

En désignant par ?_s la frontière de _s, et par í_s la normale unitaire sortante à _s dans son plan le long de ?_s.

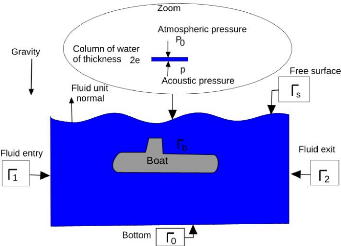
FiGuRe 2.2 - Equilibre d'une colonne d'eau à la surface.

Nous notons par ç le déplacement normal à _s compté positivement suivant la normale sortante à Ù.

Et nous désignons par:

1. p la pression du fluide qui est en dessous du milieu considéré,

2. ó la constante de capillarité,

3. g l'accélération de la pesanteur .

L'équation d'équilibre local d'une colonne d'eau d'épaisseur 2e soumise à la pression atmosphérique P0 constante, à la pression de fluide et à la tension capillaire de la surface s'écrit :

2åñ[^?2ç (2.13)

?t2 + . . .] = -P0 + p - ñgç + ó ? ?s^(?ç ?s ).

La pression du fluide p est définie par la relation de Bernouilli :

après développement du terme :

(Vö)² = (V?0 + V?)² = |V?0|² + 2V?0
· V? + |V?|², et comme :

?ö

ñe ?t

= (ñ0 + ñ) ? ?t(?0 + ?) = ñ0 ?? ?t ,

on obtient après substitution dans (2.14), l'expression linéairisée de la pression :

?? p = -ñ0 ?t

ñ0V?0 · V? - ñ02 |V?0|^2. (2.15)

Et l'equation traduisant l'équilibre de la surface libre devient (après avoir remplacer p par son expression trouvée précédemment) :

?²ç ??

2åñ0 - MO + _poo + po at + povspo
· vsp =-^ñ0 | v ?0 |².

?t² 2

En résumé : Sur la frontière I'_s, le mouvement de la surface libre est décrit par l'équation :

ate ??

2åñ0 ' MO + poo + po at + povspo
· vsp = ñ0 |vs?0|2.

at² 2

(2.16)

2.3 TRAITEMENT DES CONDITIONS LIMITES AUX BORDS

Le traitement des conditions aux limites est la principale difficulté dans les codes de calcul.

Un mauvais traitement de ces conditions limites peut mener à des instabilités numériques causées par le traitement des bords. Afin d'obtenir des résultats gouvernés par la physique et non par les instabilités numériques, il est donc important de recourir à une méthode de traitement des conditions aux limites éfficaces.

Sur la surface libre I'_s

La condition aux limites qu'il faut adopter à l'interface entre l'eau et l'air doit être formulée dans la configuration physique instantanée en représentation eulerienne et ensuite ramenée sur une configuration de référence (représentation de Lagrange).

Pour cela, nous désignons par í⁰ la normale à la frontière déformée I's . Elle est différente de la normale í dans le cas d'une rotation de la surface libre, ce qui est le cas pour une vague.

Et le couplage entre la rotation de í et le déplacement d'un point géométrique de la surface libre notée ç conduit à des forces gyroscopiques.

Et un simple calcul de géométrie différentielle permet d'exprimer au pre-
mier ordre la normale í⁰ à la surface déformée en fonction de í et V_sç :

í 0 = í - V_sç
ou V_s est le gradient surfacique, c'est-à-dire par rapport aux coordonnées

0

variants sur la frontière _s. De ce fait, la normale ín'est plus unitaire. Par ailleurs, la continuité géométrique des déplacements à la traversée de la surface _s déformée s'écrit donc au premier ordre :

?ç (vs(? + ?0) - ?t í)
· í⁰ = 0,

et

?ç

(r_s? + rs?0 - ?t í)
· (í - Vsç) = 0,

ce qui donne après développement

?ç ?ç ?ç

r_s?
· í + rs?0
· í - ?t - r_s?
· r_sç - rs?0
· r_sç + ?t
· = 0,

?s

??0

et puisque : (s) = 0 sur _s.

?í

?? = ?í

?ç

On obtient au premier ordre l'équation :

?t + Vs?0
· V_sç, sur _s. (2.17)

Cette équation traduit le couplage entre le potentiel de vitesse de l'écoulement ? et le déplacement de la surface libre ç.

Sur le fond du bassin noté 0

Nous supposons dans un premier temps que le fond de notre bassin est étanche, dans ce cas la condition de non pénétrabilité du fluide s'écrit :

??

= 0.

?í

Ensuite, une étude pratique d'une autre condition aux limites sera faite dans la partie numérique. Cette condition aux limites est une condition aux limites transparentes que nous définirons dans la suite, elle permet de limiter les phénomènes de réflexion d'onde qui apparaissent au fond lorsqu'on considère un domaine délimité par une frontière bornée.

Sur la structure immergée représentant le sous-marin notée b

Dans ce travail, la structure (un sous-marin) est supposée animée d'un mouvement rectiligne uniforme à la vitesse : -u-^?e1 dans un repère lié à notre bassin rempli d'eau.

Et en se plaçant dans le référentiel lié à la structure, cela revient à supposer qu'il est fixe et parcouru par un écoulement uniforme de vitesse u-^?e1 ,

venant de x = -8 .

En désignant par d, le déplacement du sous-marin dans le référentiel qui lui est lié, et par íb la normale unitaire sortante à la frontière b délimitant le sous-marin.

L'équation linéaire de son mouvement est d'une manière génerale donné par:

?d?t + Vb?0
· Vbd,

?? = ?íb

ou Vb représente le gradient par rapport aux coordonnées variant sur la frontière b.

Et comme dans ce référentiel le sous-marin est immobile, on a : d = 0 ce qui implique que :

?? = 0, sur b. ?í

Sur les frontières latérales 1 et 2

Sur les frontières 1 et 2, on veut introduire des conditions particulières d'entrée et de sortie pour simuler l'écoulement à l'infini. Sur ces deux frontières un traitement particulier sera fait.

Nous présentons dans la section suivante une méthode permettant de répondre à cette problématique : ce sont les conditions aux limites transparentes.

2.4 CONDITIONS AUX LIMITES TRANSPARENTES

De nombreux problèmes de propagation d'ondes se posent en milieu

non borné ou du moins très grand par rapport à la zone d'intérêt.

Pour des raisons pratiques évidentes, on est amené à réduire les calculs effectifs à un domaine borné en espace. Se pose alors le problème du traitement de la frontière artificielle ainsi introduite afin de simuler le fait que le milieu de propagation réel est infinie.

C'est ce qui nous amène à introduire les notions de conditions aux limites transparentes appliquée à notre modèle hydroacoustique.

La méthode consiste à borner latéralement notre domaine de calcul par des frontières découpées selon les isopotentielles sur lesquelles on écrit une condition aux limites dite transparente, c'est-à-dire une condition exacte qui prend en compte le comportement à l'infini des ondes sortantes sans réflexion parasites, et qui n'influence pas la solution.

Nous traitons successivement deux cas de difficultés croissantes dans cette section, d'abord la formulation monodimensionnelle décrivant la condition aux limites transparentes pour la propagation des ondes acoustiques qui est un cas classique mais dont l'étude a des vertus pédagogiques et ensuite la généralisation en dimension n = 2,3 de cette formulation, toujours pour les ondes acoustiques.

2.4.1 Condition aux limites transparentes en dimension n =1 Considerons une equation d'ondes homogène en dimension 1.

{

a2 au at2u (x, t) -- c^2f ax2 (x, t) = 0 pour x E IR et t > 0, u(x, 0) = u0(x) pour x E IR, ' at au (x 0) = u1(x) pour x E IR.

(2.18)

On cherche la solution generale de cette equation differentielles aux derivees partielles en effectuant le changement de variable :

{	X = x + cft, Y = x -- cft.

En posant

u(x, t) = U(X, Y),

l'equation des ondes (2.18) en variable X, Y s'ecrit sous la forme :

a^2U		= 0.
aXaY

Par integration, on obtient :

U(X, Y) = F(X) + G(Y) <=> u(x, t) = F(x + cft) + G(x -- cft). (2.19)

Les fonctions F et G sont arbitraires et au moins de classe C² et dependent du choix des conditions initiales en vitesse, en positions et aux limites à l'infini :

on obtient le système :

{	F(x) + G(x) = u0(x), F^i(x) -- G^i(x) = u1(x).

La solution du problème (2.18)avec des conditions initiales donnees est donc la superposition de deux ondes progressives, l'une se propageant vers la droite à la vitesse cf, l'autre vers la gauche à la vitesse --cf. Cette solution est donnee par la relation :

c ,. f x-t x+ t

u(x, t) = 1 [u0(x + cf t) + u0(x -- cf t)] + ' u1 (s)ds. (2.20)

2

au
at

Nous allons maintenant etudier la façon dont l'onde propage l'information. Pour cela, nous definissons les courbes caracteristiques en posons : 41= --cf ax au et x =

En remplaçant dans l'équation (2.18), on obtient :

? (ø

?t

) ? 0 cf ?

÷ + 0?

cf 0 x

) at = 0

] ,

L'équation des ondes est hyperbolique donc on peut diagonaliser la ma-trice qui intervient dans l'équation differentielle .

On obtient un système d'équations différentielles découplées d'ordre 1 :

?

?

?

?t

? ?

C- ? ? ?

-cf 0 C-

?

? + ? ? ? ? = 0

_C+ ?t

0 cf C+

Les vecteurs propres associés aux valeurs propres cf et -cf sont :

? v1 = ?

1 -cf

et ? ) v2 = ?cf1.

donc les composantes dans la bases des vecteurs propres sont :

?

??? ?

????

?u cf ?x

C+ = ?u

?t

?u
?x

?u

C- = ?t + cf

Les quantitées C- et C⁺ sont conservées le long des courbes caractéristiques :

x - cft = constante et x + cft = constante

Ce sont les quantitées entrantes et sortantes, respectivement aux vitesses : -cf et cf au travers des frontières lorsqu'on limite le domaine.

Conditions limites

D'après ce qui précède, C- et C⁺ sont invariantes le long des courbes caractéristiques, donc ce sont les quantités entrantes et sortantes du domaine.

Supposons que l'on place une frontière ouverte, c'est-à-dire transparente, en x = L (cf figure 2.2). On se place dans l'hypothèse oil l'influence extérieure est nulle. La quantité entrante est donc nulle :

C⁺ = 0,

le même raisonnement en x = -L, mène à la condition :

C- = 0.

En tenant compte des expressions de C- et C⁺ données précédemment, on obtient que les conditions aux limites naturelles pour u pour les frontières ouvertes sont définies par :

? ???? ????

?u ?u ?t (-L, t) - cf ?x (-L, t) = 0?uu?u ?t (L, t) + cf ?x (L, t) = 0 '

(2.21)

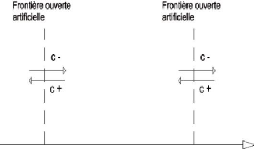
FIGURE 2.3 - Représentation des quantités caractéristiques au travers des frontières ouvertes.

Mise en oeuvre et résultats numérique en dimension 1

La mise en oeuvre numérique en dimension un du problème concernant la condition aux limites transparentes est la suivante.

Dans un premier temps, nous considérons le problème suivant :

?^2u ?t2 - c2 ?2u ?x^2

= 0 xE]0, L[×]0, T[,

conditions initiales :

u(x,0) = u0 x E]0, L[,

?

???????????????????????? ?

?????????????????????????

?u

(2.22)

?t (x,0) = u1 x E]0, L[,

conditions aux limites :

u(0, t) = 0 ?t > 0,

?u ?u

?t (L, t) + c_?x (L, t) = 0 ?t > 0.

Ou c représente la vitesse d'onde en mètre par seconde.

Ce problème sera mis sous sa forme variationnelle que nous décrivons ci-après. Ensuite, nous présentons les résultats numériques obtenus.

Formulation variationnelle

On considère l'espace :

V = {v E H¹(]0, L[), v(0) = 0}

Le problème devient après multiplication par v :

L ?2u L ?2u

o

?x2

v(x)dx = 0,

? v ? V; f_?t2 v(x)dx - c2

en intégrant ensuite par parties le deuxième terme entre 0 et L , on obtient :

?v, at² 0 ax

fL ?2u L ?u (x_' t) J (x,t)v(x)dx + c² I ?u (L, t)v(L) = 0,

0 ??v

x ^(x)dx c?t

On approche l'espace V par l'espace des fonctions affines par morceaux et continues wi :

L

Vh = {wi : wi(xj) =äij,?i = 1, ...N - 1 , ?j = 1, ...N - 1 et xj =j N } Le problème approché dans V^h est donc :

trouver uh ? V^h tel que ? vh ? V^h : L ?2uhL? ax ?x ?t ax ?vh uh ?t2 (x, t)vh(x)dx + c^2 I (x, t) (x)dx c^a (L, t)vh(L) = 0. o

Le modèle peut donc s'écrire formellement sous forme d'une équation différentielle matricielle à coefficients constants :

?????

trouver X(t) tel que : M ^·X(t) + C ^ÿX(t) + AX(t) = 0,

(2.23)

où :

- M est une matrice de masse,

- A une matrice de raideur,

- C une matrice contenant un seul élément .

Et l'équation différentielle du second ordre (2.23) est résolue, en introduisant un découpage en temps, ou nAt est le pas de temps et tⁿ = nAt. Pour obtenir un schéma totalement discrétisé, on approche en temps par :

- ^ÿX(nAt) =

Xn+1 Xn At

- ^·X(nAt) =

Xn+1 - 2X^n + )0-1 At^2

Et pour améliorer la stabilité, il est préférable de moyenner les termes de raideur en posant :

X(nAt) = Xn+1 + Xn

2

ce qui conduit au schéma suivant :

M Xⁿ⁺¹ - 2Xⁿ + Xn-1 + C Xn+1 - Xn + _AXⁿ⁺¹ + Xn = 0, (2.24)

Ät² Ät 2

équivalent au schéma :

Ät²

2 A]Xⁿ⁺¹ = [2M + ÄtC - Ät2

[M + ÄtC + 2 A]Xⁿ - MXⁿ-¹. (2.25)

Analyse de la stabilité

Nous ferons l'analyse de la stabilité de ce schéma en utilisant les techniques de l'énergie.

Pour cela, nous considérons le schéma (2.24) précedent :

Xn+1 - 2Xⁿ + _Xn-1 Xn+1 - _Xn Xn+1 + Xn

M + C + A = 0,

Ät² Ät 2

ce qui donne :

M( Xn+1 - Xn

Ät2 ) - M( Xn+1 - Xn

Ät2 ) + C( Xn+1 - Xn

Ät ) + A( Xn+1 + Xn

2 ) = 0

En multipliant scalairement par : Xⁿ⁺¹ - Xⁿ,

M(

Xn+1 - Xn Ät , Xn+1 - Xn

Ät ) + ¹ _ÄtC(Xⁿ⁺¹ - Xn, Xⁿ⁺¹ - Xⁿ) + ¹ ₂(AXⁿ⁺¹, Xⁿ⁺¹)

= M( Xn - Xn-1

Ät , Xn+1 - Xn

Ät ) + ¹ ₂(AXⁿ, Xⁿ).

(2.26)

L'inégalitée de Cauchy-Schwarz suivante :

(MX, Y) =<¹₂(MX,, X) + ¹₂(MY,, Y),

appliquéee au premier terme du second membre de l'égalitée (2.26), donne :M( Xn - Xn-1 Ät , Xn+1 - Xn

Ät ) = 1 2 M( Xn - Xn-1

Ät , Xn - Xn-1

Ät ) t1 1Xn+1 1_- --XnnXn+1 i- --Xnn+ +2M((Ät t^, 'Ätt ),'

on obtient ensuite :

1 1_(MX^{n+1 1}- --XnnX+1 1- _Xnn11112Ät

^,

'

Ät

⁾

⁾

⁺

⁺

^ÄtC(Xn+1

¹

^-

^--

^Xn,

^,

^Xn+1

¹

^-

^--

2

t

^t

⁺ ₂ A(Xn+1, Xn+1))

^Xn)

⁾

⁺

11Xnn-_Xn-11Xn n- _^Xn-11=<₂M(( _Ät t, _'Ätt ).
·

(2.27)

Et comme la matrice C contient seulement un seul terme positif, alors le terme suivant est positif :

Ätt

1 C(Xⁿ⁺¹¹ --- Xn, _Xn+11 --- _Xn)) => 0,

l'inégalité (2.27) donne l'inégalité :

2 M( Xn+1 - Xn

1 Ät , Xn+1 - Xn

Ät ) + 1 2 A(Xⁿ⁺¹, Xn+1) =1 2 M( Xn - Xn-1

Ät , Xn - Xn-1

Ät )

+ ₂ A(Xⁿ, Xⁿ).

1

On définit l'énergie mécanique par:

1 Ät , Xn - Xn-1

En = 2 M( Xn - Xn-1 Ät ) + 1 2 A(Xⁿ, Xⁿ),

d'où

En+1 = Eⁿ.

L'énergie mécanique totale est décroissante au sens large au cours du temps, ce qui assure la stabilité de ce schéma numérique dès que la solution est elle-même stable.

Résultats numériques

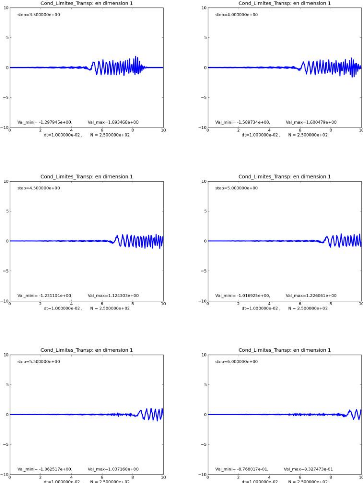
Pour cette application numérique, nous considérons une onde se propageant sur un segment de longueur L = 10 m, que nous maillons en 250 points.

La célérité de l'onde est égale c = 340 m/s.

Les figures suivantes représentent la solution numérique du modèle (2.29) qui est une onde progressive.

Dans cet exemple, la condition aux limites est appliquée sur la frontière
représentant la section de sortie du fluide afin de vérifier sa transparence,
dans le sens où celle ci laisse sortir les ondes et ne provoque pas de retours.

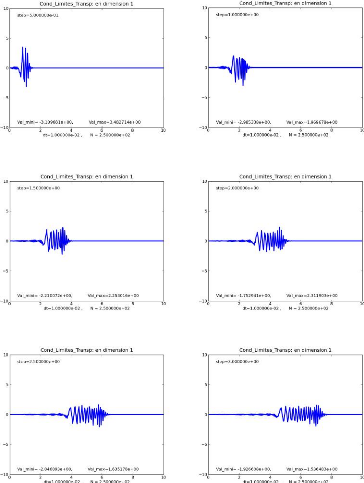
Sur ces figures, nous avons l'onde longitudinale se propageant vers la frontière droite. Sur cette frontière, nous avons défini une condition aux limites transparentes pour laisser sortir l'onde sans réflexion parasite.

Les figures suivantes confirment bien le caractère transparent de cette condition.

Conclusion

En effet, comme le montre ces différentes figures nos résultats sont en parfaits accord avec le modèle physique et l' approximation est justifiée pour une équation d'onde acoustique en dimension un.

L'étape suivante de l'étude est de formuler analytiquement et de tester cette condition de manière genérale.

2.4.2 Condition aux limites transparente en dimension n=2; 3 Nous considérons une équation d'ondes non-homogène

???? ?

???? u(x, 0) = u0(x), ?t (x, 0) = u1(x) pour tout x ? Rⁿ,

?²u

?t2(x, t) - c2 f Äu(x, t) = f (x, t), pour tout x ? Rⁿ et t ?]0, 8[, ?u

(2.28)

dont les termes sources

f : R+ × Rⁿ ? Rⁿ, u0 : R+ ? Rⁿ et u1 : R+ ? Rn

sont des fonctions de classe C⁸ et dont les supports sont inclus dans le borné :

Ù = [-L, L]ⁿ avec L > 0.

Et

f (x, t) = 0, u0(x) = 0 et u1(x) = 0 pourx ?6 Ù = [-L, L]ⁿ et t = 0.

Cherchons maintenant à calculer les valeurs de la fonction u, solution du système (2.28) dans le domaine Ù = [-L, L]ⁿ, tout en modélisant le comportement de cette pour tout

x ? Ù^c = {x ? Rⁿ : |x| > L}

à l'aide des conditions aux limites en espace posées à une interface entre Ù et Ù^c définie par :

= {x ? Rⁿ : |x| = L}

Comme en dimension un, nous faisons une étude pour les ondes planes. Désignons par í, la normale unitaire sortante à .

Ensuite, considérons la relation (2.21) en dimension 1, nous envisageons une condition aux limites à l'interface du type :

?u

?x ? , _?t (x, t) + (cf
· í)^?u

?í (x, t) = 0 t ?]0, 8[. (2.29)

?

??????????????????? ?

????????????????????

Trouver une fonction u(x, t) : Ù × [0, 8[? R telle que :

?t2(x, t) - c2 f Äu(x, t) = 0, pour tout x ? Ù et t ?]0, 8[,

?²u

On est alors amené à resoudre le problème équivalent

?u

(2.30)

u(x, 0) = u0(x), ?t (x, 0) = u1(x) pour tout x ? Ù,

et les conditions aux limites,

?u

?t (x, t) + (cf
· í)_?^u (x, t) = 0 sur et t ?]0, 8[.

La restriction de la solution du problème (2.28) à x ? Ù, vérifie (2.30). Pour montrer que l'on peut calculer cette restriction en résolvant (2.30), il nous suffit de montrer que ce problème admet une unique solution. Commençons par définir l'espace admissible sur lequel, une formulation variationnelle du problème (2.30) sera établie. Nous considérons pour cela, l'espace

V = {v ? H¹(Ù) : Äu ? L²(Ù) et ?u ?t + (cf
· í).^?u

?í = 0 sur }

En multipliant la première équation du système (2.30), par une fonction test arbitraire de l'espace V, on peut construire formellement la formalution variationnelle de ce système :

at?v ? V, I_{n at} (x, t)v(x) - äu(x, t)v(x) = f (x, t)v(x)dx.

Appliquons, toujours formellement (car nous ne connaissons pas la régularité de la solution éventuelle) la formule de Green et compte tenu des conditions aux limites sur , cela conduit à :

?l i ?t u ?u (x, t)v(x)d

r

= f (x, t)v(x)dx.

On place cette écriture dans un cadre général en introduisant les formes bilinéaires suivantes :

fr)

?t (x, t)v(x)dx + cf2

I

u(x, t)
·

V

v(x)dx + (cf
· í)

(2.31)

?

????????? ? ??????????

?v, w ? V, a(w, v) = cfI w(x, t) · Vv(x)dx, ?v, w ? V, m(w, v) = cw(x)v(x)dx, ?v, w ? V, c(w, v) = (cf · í) frw(x)v(x)dx,

ainsi que la forme linéaire :

?v ? V, L(v) = I f (x, t)v(x)dx.

L'équation que nous avons obtenue se formule de la façon suivante avec ces notations :

? ?? ??

trouver u telle que à chaque instant t on ait u(x, t) ? V : et vérifiant, ?v ? V, m( ·u, v) + c( ÿu, v) + a(u, v) = L(v).

(2.32)

L'espace des fonctions admissibles V étant un espace de Hilbert. Il existe donc une famille totale {wⁿ}, de cet espace qui forme une base de V. Nous désignons par V^N le sous espace de V engendré par les N premiers vecteurs de cette famille.

Pour établir l'existence d'une solution à l'équation (2.32),nous utilisons

une suite de problèmes approchés construits à partir de V^N .

Nous montrons alors que cette suite converge vers une solution de (2.32) lorsque N tend vers l'infini, et cela dans un espace Hilbert ad hoc, que nous introduisons a priori par

W(0T) = {v = (vi); v E L²(0T; V) ; ?v ?t E L²(0T; (L²(Ù))³)}, muni de la norme définie à partir du produit scalaire :

Z _{T Z} Z _T Z ?u ?u

(u, v) = _Ù(Vu
· Vv + uv) + ?t .

0 0 Ù ?t

Nous lui associons le sous espace :

W^N(0T) = {v E W(0T) ; v(t) E V^N}, A chaque entier N, on associe le problème :

? ?? ??

trouver u^N E W^N(0T) tel que : ?v E V^N, m( ·u^N, v) + c( ÿu^N, v) + a(u^N, v) = L(v).

(2.33)

auquel on adjoint les conditions initiales :

u^N(t = 0) = ð^Nu0(x) et ÿu^N(t = 0) = ð^Nu1(x).

ðN désignant l'opérateur d'interpolation (ou d'approximation) de V dans V^N.

Il vérifie la propriété

lim IIu0 - ð^Nu0llV = 0.

N?8

Choisissons dans (2.33)

v = ÿu^N,

On obtient

1 d

2 dt

[m( ÿu^N, ÿu^N) + a(u^N, u^N)] + c( ÿu^N, ÿu^N) = L( ÿu^N). La forme bilinéaire c vérifie

j1? ÿu^N E V^N, |c( ÿu^N, ÿu^N)| = |(cf .í)| |ÿu^N|²dx = 0, cela permet d'obtenir l'inégalité suivante :

Z t

2[m(

ÿuN, ÿu^N) + a(u^N, u^N)](t) = 1 1 ₂[m( ÿu^N, ÿu^N) + a(u^N, u^N)](0) + ₀ L( ÿu^N).
On fait alors l'hypothèse que L(.) définit une forme linéaire continue sur (L²(Ù))³, de telle façon que :

Z t

| 0 L( ÿu^N)| = IILIIL²(0t;(L²(Ù))³).II ^ÿu^NIIL²(0t;(L²(Ù))³).

Et comme les formes m(., .) et a(., .), sont continues et coercives sur l'espace V, on deduit qu'il existe une constante positive C, independante du temps et telle que :

I ÿuNk20,Ù(t) + Iu^NI²_1,Ù(t) = C[I ÿuNl20,Ù(0) + IuNI21,Ù(0) + ll II²

I^, ..L²(0t;(L²(Ù))³)] t

I

+ C I ÿuNl20,Ù.

En appliquant le lemme de Gronwall à la fonction

t

((f MÿuNaÙ) + 1114N1120,Ù(t)) C,

((f

on en deduit alors l'estimation

Iu^NiW(0T) = C,

Puisque l'espace W(0T) est reflexif, on peut extraire de u^N, une sous suite notee u^N, telle que :

u^Ni ? u^* ? W(0T) (convergence faible dans W(0T)),

Par un passage à la limite (faible) dans l'equation (2.33), nous obtenons l'existence d'une solution dans l'espace W(0T) à l'equation (2.32).

L'unicite decoule de l'inegalite suivante :

si u¹ et u² sont deux solutions de (2.32), alors

2[m(

^ÿu¹ - ÿu², ÿu¹ - ÿu²) + a(u¹ - u2, u¹ - u²)](t) = -c( ÿu¹ - ÿu², ÿu¹ - ÿu²) = 0. 1

ce qui implique

₂[m( ÿu¹ - ÿu², ÿu1 ÿ2

- u ) + a(u¹ - u2, u¹ - u2)](t) = 0,

1

et

1 2

u = u .

En conclusion, la restriction de la solution du problème (2.28) admet bien une solution unique. Ce qui montre que le problème (2.30) est bien pose.

Conditions aux limites sur 1 et sur 2

D'après ce qui precede, on peut construire une condition aux limites transparentes conduisant à des problèmes bien poses dans le cas d'ondes acoustiques. Cette condition aux limites, fournit un comportement le plus "transparent" possible, c'est-à-dire qu'elle laisse passer les ondes entrantes et sortantes.

Ainsi le traitement aux frontières, 1 et 2 du domaine Ù ne se fait pas sur les grandeurs physiques, mais sur des variables calculees à partir de celles-ci en supposant que les ondes se propagent orthogonalement aux frontières considerees.

Dans le cas oil les ondes se propagent suivant des directions quelconques

aux frontières considerées, des difficultés supplémentaires apparaissent à cause des dérivées tangentielles de la vitesse sur ces frontières. Ce cas ne sera pas abordé dans ce travail, nous traiterons uniquement le cas oü les ondes se propagent orthogonalement aux frontières.

Définissons la frontière 1 comme étant l'ensemble :

1 = {x ? R³; e1
· í(x) = 0}

oü í(x) est la normale unitaire sortante à l'ouvert Ù et au point de coordonnées x et e1 est le vecteur directeur de la direction de l'écoulement

sur laquelle le champ de vitesse des particules fluides est imposé. On a,

u = ue1, u > 0 sur 1, et u = 0 sur b,

et le produit scalaire intervenant dans la formulation analytique des conditions aux limites (2.29) devient :

cf.(e1
· í(x)) = -cf

Nous définissons de même la face sortante de l'écoulement notée 2, par:

2 = {x ? R³; e1
· í(x) = 0}

Sur cette dernière, nous laissons l'écoulement sortir librement sans reflex-ion. Et comme la normale sortante à cette frontière est supposée colinéaire au champs de vitesse, le produit scalaire intervenant dans (2.29) s'écrit

cf.(e1
· í(x)) = cf.

Ainsi en tenant compte de l'écoulement et de l'onde acoustique, il est naturel de considérer sur ces deux frontières les conditions suivantes :

?? + (u - cf)^?? ?í = 0, sur 1, ?t (2.34) ?? ?t + (u + cf )?? ?í = 0, sur 2.

2.4.3 Conclusion

Ce chapitre a été consacré à la présentation et la définition mathématique des modèles utilisés dans cette étude.

Le travail reporté dans ce chapitre porte aussi sur la construction mathématique d'une condition aux limites particulière sur les frontières verticales 1 et 2 du domaine Ù .

Cette condition aux limites dite transparente, qui prend en compte le comportement à l'infini de l'onde et qui la laisse passer sans réflexion est étudiée dans ce chapitre pour une propagation d'onde acoustique dans un écoulement uniforme.

Nous avons ensuite réalisé un test numérique de validation en dimension

un, les résultats obtenus sont en très bon accord avec le modèle physique. Le chapitre suivant concerne la formulation variationnelle en dimension deux du modèle. Nous allons dans un premier temps établir la formulation variationnelle du modèle fluide et ensuite du modèle de surface. Puis une étude d'existence et d'unicité du modèle couplé fluide-vague de surface dans un espace des fonctions admissibles approprié sera faite.

3

PRopRiéTés DEs MoDèLEs

D

Epuis l'avènement des ordinateurs, la simulation numérique a parfois remplacé l'expérimentation directe trop coûteuse et longue à mettre en oeuvre.

Sur le plan mathématique, la simulation numérique nécessite essentiellement la résolution numérique d'équations aux dérivées partielles qui conduisent à l'obtention de solutions approchées.

Il existe de nombreuses méthodes d'approximation qui présentent toutes des avantages et des inconvénients; citons à titre illustratif, la méthode des différences finis, la méthode des volumes finis, les méthodes spectrales, la méthode des élèments finis...

Dans ce rapport, nous nous intéressons à la méthode des éléments finis qui est très utilisée dans l'industrie. Cette méthode est intéressante, compte tenu de sa souplesse d'utilisation, en particulier vis-a-vis de l'approximation des divers opérateurs modélisant des phènomènes en physiquemathématique et également pour la prise en compte de conditions aux limites portant sur les gradients de la fonction à calculer.

La méthode des éléments finis est une méthode d'approximation des solutions d'équations aux dérivées partielles qui est construite à partir d'une formulation équivalente du problème à résoudre; cette dernière est appelée formulation variationnelle du problème et nécessite le minimun de régularité de la solution.

Cette phase de transformation du problème est la plus délicate et la plus difficile à traiter car, en toute rigeur, elle nécessite l'utilisation de notions mathématiques très fines et très abstraites.

Dans cette section, nous-nous efforcerons d'aplanir les difficultés en établissant séparemment la formulation variationnelle du modèle hydroacoustique et celle du modèle de vague.

3.1 FoRMuLATioN vARiATioNNELLE

3.1.1 Formulation variationnelle du modèle Hydroacoustique avec écoulement

Nous supposons que la géométrie de l'ouvert 1 est celle de la Figure 2.2 (modèle). Sur les frontières latérales F1 ou F2, on utilisera les conditions aux limites transparentes définies par (2.34).

Et sur F_s qui représente la surface libre, nous avons le couplage entre le potentiel de vitesse du fluide et le déplacement d'un point de la surface libre défini par l'équation (2.17).

On considère comme espace des fonctions admissibles, l'espace : H¹(Ù) = {v | v ? L²(Ù) | ?kv ? L²(Ù) k = 1,2}

En multipliant l'équation ci-dessous par une fonction test arbitraire ø de l'espace H¹(Ù), nous obtenons :

?

(?t ? 2V^rp_o
· v(^?? ) + v?0
· v(v?0
· v?)-c_.1.Ä?).ø= 0 dans Ù×]0, T[,

?t

puis après intégration sur l'ouvert Ù :

_{Z Z Z Z}

?²?

?t2 ø + 2 _Ù r?0
· r(?? _?t )ø + _Ù G?0
· V(V?0
· V?)ø- c² _ÙÄ?ø = 0,

f

Ù

qui s'écrit

Z Z Z ?^2? ?t2 ø + Ù r?0 · r(?? ?t )ø + Ù r?0 · r(?? ?t ).ø Ù | {z } *

Z + Ù V?0 · V(V?0 · v?).ø | Sys. **

= 0.

_Z

- c2 Ù Ä?.ø a

_Nos.

***

On utilise la formule d'intégration par partie de Green aux intégrales suivantes :

_{Z Z Z}

* Ù r?0
· r(?? _?t ).ø = - _Ù(r?0
· rø)?? _?t + _?Ù(r?0
· í)?? _?t ø,

_{Z Z Z}

* * Ù r?0
· r(r?0
· r?)ø = - _Ù(r?0
· r?)(r?0
· rø) + _?Ù(r?0
· V?)(V?0
· í)ø,

_{Z Z Z}

* * * Ù Ä?ø = - Ù r?
· rø + ?Ù(r?
· í)ø,

et comme :

?

??? ?

????

?0

Gr?0
· í = ? ?í ,

??

'?
· í = ?í .

En remplaçant dans l'équation précédente , on obtient :

Z Z f ?^2? ?t2 ø + Ù V?0 · V(?? ?t )ø - Ù(V?0 · Vø)^?? Ù ?t

ZÙ

(V?0 · V?)(V?0 · Vø)

_Z

+ c2 Ù V?
· Vø = L(ø),

a

Le second membre est une somme des intégrales sur la frontière de notre domaine.

Il est defini de la façon suivante :

_{Z Z Z}

?? ??0 ??

L(ø) = c2 f ?í ø - ?t ø - _?Ù(r?0
· r?)^??0

?í ø.

?Ù ?Ù ?í

Or, nous savons que l'un des avantages de la formulation variationnelle des équations de la physique, est de permettre la prise en compte des conditions aux limites dans les termes frontières.

L'expression explicite de ce second membre est obtenue en évaluant ces différentes intégrales sur la frontière du domaine Ù découpée en 5 parties :

?Ù = 0 ? 1 ? 2 ? _s ? b,

ce qui nous amène à faire une évaluation de L(ø) sur chaque sous frontière en commençant par:

Le fond du bassin noté 0,

Nous supposons d'abord que le fond de notre bassin est étanche, dans ce cas la condition de non pénétrabilité du fluide s'écrit :

?? = 0.

?í

où í est la normale unitaire sortante à l'ouvert Ù, et dirigée vers le bas. Nous précisons par ailleurs que pour les applications numériques, nous utiliserons une condition aux limites transparentes. Elle permettent d'éviter les rebonds, les ondes piègées et de laisser sortir les ondes.

Ensuite, sur la frontière latérale gauche 1,

nous appliquons la condition limite transparente pour modéliser la sortie des ondes en présence dans le fluide.

Pour un écoulement permanent représenté par le potentiel de vitesse : ?0(x) = ux1, nous auront donc une condition aux limites dite condition transparente de type:

?? ?t + (??0

?í - cf)^??

?í = 0, sur 1.

Et la frontière latérale droite 2,

pour la même raison que précedemment, la condition aux limites sur 2 est :

?? ?t + (??0

?í + cf )??

?í = 0, sur 2.

Pour la surface libre du liquide notée _s,

la condition aux limites n'est nullement évidente car les deux composantes (air et eau) sont en mouvement, mais pour assurer le couplage entre le fluide et le déplacement transverse de la surface libre, nous considérons l'équation :

??

?í =

?ç

?t +Vs?0
· V_sç, sur _s×]0, T[.

Enfin sur la structure immergée délimitée par la frontière notée b,

nous avons d'après l'analyse faite sur le traitement des différentes conditions limites dans la section précedent, une condition de type Neumann homogène :

??

= 0,

?í

traduisant l'immobilité de notre structure dans le repère qui lui est lié, et la non pénétrabilité du fluide à travers sa surface.

Ainsi le terme L(ø), devient en tenant compte d'abord des conditions sur 0 et b :

L(ø) = c2ffr, av^ø I

??0 ap ?t . ??

(Vp_o
· Vp)

1?2?_s av r1?2?s ?í fr1?2?s ?⁰í

c'est-à-dire

_Z L(ø) = cf_?í vy+cf 2 ?

r₁urí riur2

?? 2 f ?? ^4' I ??0 ??ø I ?

riur2(Vq)o
· Vp)? ?í 0

?í
· ?t

or sur _s, nous avons :

?? ?ç

= + rs?0
· r_sç,

?í ?t

et dans la base local, nous avons par définition

V?0 =	? ??? ? ????	??0	et	? ??
		?í ??0		??? ? ?í , V? = ???? ??
		?s		?s .

L'apparition des dérivées tangentielles de ?0 sur les frontières latérales entraînent des difficultés supplémentaires pour la prise en compte de condition aux limites transparentes.

De ce fait, nous proposons dans la partie suivante une construction des nouvelles frontières latérales F1 et F2 suivant les équipotentielles telle que toutes les dérivées tangentielles de la vitesse d'écoulement du fluide soient nulles.

Nouvelles frontières F1 et F2

Intéressons nous aux profils des vitesses (lignes de courants) autour de la structure.

Dans le domaine contenant la structure (le sous-marin) le fluide est considéré comme incompressible et irrotationnel, l'écoulement étant uniforme. La recherche du potentiel des vitesses pour un tel écoulement autour de la structure doit satisfaire uniquement deux conditions : loin de l'obstacle, on doit retrouver un écoulement presque uniforme avec un potentiel de vitesse

?0 = Ux,

et sur l'obstacle, la vitesse normale à la paroi doit être nulle. Ainsi la structure constituant une perturbation de l'écoulement uniforme.

Nous obtenons à partir du potentiel de vitesse et de la relation,

U~ =

^~V?0,

les composantes du vecteur vitesse

U_x = U et U_y = 0,

en chaque noeud du maillage éloigné de la structure. Et au voisinage de la structure dans 1), nous avons cette fois

U_x =6 0 et U_y =6 0.

Les lignes de courant au voisinage de la structure sont alors définies comme des lignes tangentes aux vecteurs vitesses en chaque noeud du maillage. Ce sont des courbes qui ne se croisent jamais (sinon il y aurait deux directions différentes d'écoulement pour une même particule de fluide à un instant donné).

Elles sont définies par l'équation,

dx = Ux

dy Uy

= Uxdy - Uydx = 0. (3.1)

Au même titre que la fonction potentiel, nous introduisant au voisinage la structure la fonction de courant que nous notons ø à partir des composantes de la vitesse. Pour cela nous posons :

?ø ??0

? ?

y x
?ø ??0

U_y = -=

?x ?y

U_x = =

En utilisant la relation (3.1) et les deux équations précédentes on a,

?ø ?ø

dy + dx = 0 = ø = constante.

?y ?x

ce qui signifie qu'en chacun de ses points, la courbe est orthogonale au vecteur vitesse (voir figure 3-1). Il en résulte par ailleurs que les équipotentielles sont partout orthogonales aux lignes de courant.

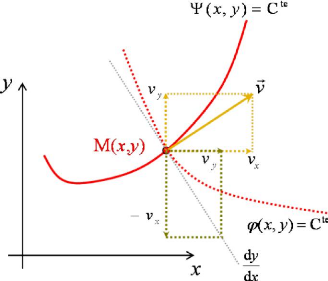
FIGURE 3.1 - les équipotentielles sont orthogonales aux lignes de courant.

Ainsi, nous pouvons à partir des lignes de courant construire deux équipotentielles représentant respectivement la frontière latérale gauche et droite du domaine. Ces deux frontières sont construites de façon à éviter les ondes tangentielles, l'expression du gradient de ?0 dans le repère local devient :

?

????

????

V?0 =

??0 =6 0 ?í

= 0.

??0
?s

L(ø) = c² I (^?ç + V_spo
· vs/)1p+ f_r ø[c2??- ^??0.??- (??0)2??]

r_s ?t 1?2f ?í ?í ?t ?í ?í

_r2

(?ç + v (p
· v 11.1 _t??0 ^v?? __L ??0 ?? ??ith

= cf ?t s , 0 n1

s , fr1?2 ?í L ?t ?í . ?í - (a^te) ?í `r .

2 is

L'écoulement permanent est caracterisé par le potentiel de vitesse

??0

?0 tel que =6 0 ,

?í

alors

L() = c (( ??0 )?0 2 c2)

??0 f _r?? kk ?í f??_]

øf ?t + vspo
· vs0p ?í r1?2 L _?t + ? ?í

2 I (?ç

?í

En prenant en compte les expressions des conditions aux limites transparentes sur 1 et 2 décrite dans la section précedent, on a :

??

?t sur

((^??0

?í ) - cf)

- 1

- 1

((???í ⁰) + cf)

??

?t sur 2.

?

????? ?

??????

??

?v

??

=

?v

Ce qui donne, après remplacement et simplication dans L(ø), une expression de la forme :

? ??o _f ?_t ((?:)-cf) act

⁹)

L(ø) = c2I (^?ç + vspo
· vs1) 4¹ ø(

I^-_s ?t ?í r1 ? ??0 at

?í

??0 f ø( ?? ?í cf) ??)]

2

§ ?í r ?t ??0 ?t

?í

qui s'écrit encore de manière plus simplifiée :

ZL(ø) = c²:_t ø+ q. f_r Vs?0
· Vsçø + cf fr1 ??? t ø-cf ^??^q): fr₂ ^??^q;^ø.

Finalement la formulation variationnelle du modèle hydroacoustique devient : ?ø ? H¹(Ù)

_{Z Z Z Z}

?²?

?t2 ø + _ÙG?0
· V(^??_?t )ø - _Ù(G?0
· vø)^??_?t - c2 vs?0
· r_sçø

f

Ù _s

- _ca(cr?0
· V?)(V?0
· vø) + q^./ 'Cr?
· vrø

2 I c ??0 I ??4'+ c ??0 I ?? = 0

cf r_s ^f ?í rl ?t ^f ?í r2 ?t ø .

(3.2)

3.1.2 Formulation variationnelle du modèle de vagues

Intéressons nous maintenant, à la formulation variationnelle du modèle de vague à la surface qui s'écrit :

?²ç ??

2åñ?t2 - óÄ_sç + ñgç + ñ?t + ñV?0
· V? = -ñ 2|V?0|2.

La frontière de _s sera notée ?_s et í_s est la normale unitaire sortante à _s dans son plan le long de ?_s.

En bidimensionnel, cette frontière se réduit en des points définissant des angles géométriques aux deux coins supérieurs gauche et droit.

Ainsi, pour des raisons de simplification des calculs nous supposons que :

?ç

- à gauche : ?ís = 0 ,

= 0

?ç ?ç

- et à droite : + c_r

?t í_s

où

c_r représente la vitesse de ride à la surface _s.

Ainsi, pour la formulation variationnelle on prendra comme espace des fonctions tests, l'espace suivant :

H¹(_s) = {v | v ? L²(_s) | ?v

?x ? L²(_s)},

nous obtenons après multiplication et intégration par une fonction arbitraire v ? H¹(_s) :

?2 ?

v - ó I p + pg Içv+ ñ_e I ^?v+pf ?0
· V ?v

2åñ fr_s ?t2 ç Ts Asi Ts I^- ?t Ts^V

2JrI |v. ?0|²v.

s

On applique la formule de Green à l'intégrale :

ó I Ä_sip = ó ^?çv - ó I
· Vv,

T_s fas ?í_s T_s

on obtient alors la formulation variationnelle du modèle de vague à la surface :

2åñ ,",;

?2n v+p ? ? I v + ñg I ipo^- + I Vç
· Vv + ñ I V?0
· V?v

fr_s ot_ T_s ?t T_s T_s T_s

ó + cr

?t (L, t)v(L) = -ñ2 frs|v?0|2v. (3.3)

Introduisons quelques notations utiles pour simplifier les écritures. Pour le système couplé, il y a en tout deux champs d'inconnues.

- le potentiel de vitesse dans le fluide noté ?,

- le déplacement transverse d'un point géométrique de la surface noté

Nous pouvons alors formuler le couplage de nos deux modèle, en considérant comme inconnu de notre problème le couple

X = (?, ç) ? H¹(Ù) × H¹(_s).

élément de l'espace admissible H¹(Ù) × H¹(_s) produit de deux espaces dans lesquels sont définis respectivement le potentiel des vitesses et le déplacement d'un point de la surface libre.

Et pour obtenir les symétries et antisymétries physiques, nous multiplions l'équation de la capillarité (3.3) par le coefficient :

c²

a = f

ñ

ce qui donne

2

2åc ç 2 I ?? #177; 2

2 f V #177; Cf v gcf I p+ óa Vrç
· 'crv + c²Gr?0
· V?v

f r_s ?t² r_s ?t Ts i

_{s s}

c_f f

2 Jr |V?0|2v.

s

(3.4)

En rappelant que :

- cf : est la vitesse du son dans le fluide (eau ),

- ñ : la masse volumique du fluide (eau).

Afin de rendre l'expression plus lisible, nous définissons à partir des deux équations (3.2) et (3.4) suivantes :

_Z Z Z^?_?t^?ø+V?0
· V(^?_?^q_t ⁾)ø-(V?0
· vø):_t + ?
· vø

f

Ù- q ^{f ?ç41--} I (vpo
· Vp)(Vpo
· VC -- qf vs?0
· vsçø
r_s ?t f

^a" I 441#177;c ?" I ?P

cf f = 0, (3.2)

?í ri ?t ?í r2 ?t

et

2 Is 2çv 2 I ??v+ c2 Içv + óa1 vç
· vv + q I Gr?0
· Vr?v

2åcf r ?t2 + cf rs ?t g f

T_s T_s

c2 2 Jrs |v?0|²v, (3.4)

Et nous définissons alors les différentes formes bilinaires suivantes sur H¹(Ù) × H¹(_s) :

M(X,Y) = I ?(x)ø(x)dx + 2åq f ç(s)v(s)ds, (3.5)

Ts

C(X,Y) = f_rI[r?0(x)
· r?(x)ø(x) - r?0(x)
· rø(x)?(x)]dx

+ _cffrs [?(s)v(s) - ç(s)ø(s)]ds + cf?:: fr1n2

(3.6)

K(X,Y) = f_rl[c_.1-r ?(x)
· rø(x) - (r?0(x)
· r?(x))(r?0(x)
· rø(x))]dx

f_rs[rs?0(s)
· r_s?(s)v(s) - r_s?0(s)
· r_sç(s)ø(s)]ds

Is ç(s)v(s)ds + óa kr_sç(s)
· r _sv(s)ds,

(3.7)

plus une forme linéaire obtenue à partir du second membre

_c2 L(Y) = - f 2 j1 |r?0(s)|²v(s)ds. (3.8)

,

Et le problème consiste alors à trouver un potentiel de vitesse ? et un champ de déplacement d'un point de la surface libre ç vérifiant d'une part, les conditions initiales suivante :

1. déplacement ?(t = 0, x) = ?0(x) et ç(t = 0, s) = ç0(s)

2. vitesse ÿ?(t = 0, x) = ÿ?0(x) et ÿç(t = 0, s) = ÿç0(s)

et d'autre part, l'équation :

? ??

??

Trouver X(t) ? H¹(Ù) × H¹(_s) tel que :

M( ^·X,Y) + C( ^ÿX,Y) + K(X, Y) = L(Y), ?Y ? H¹(Ù) × H¹(_s).

(3.9)

Avant d'étudier l'existence et l'unicité d'une solution de cette équation différentielle matricielle, intéressons-nous d'abord à la positivité de l'opérateur K(.,.) .

3.1.3 Stabilité du modèle

Commençons par examiner la coercivité de la forme quradratique :

ZK(X, Y) = Ù[c2 _f r?(x)
· Vø(x) - (V?0(x)
· V?(x))(V?0(x)
· Vø(x))]dx

+ q f_rs[Vs?0(s)
· V'_s?(s)v(s) - Vs?0(s)
· V_sç(s)ø(s)]ds

_{Z Z}

+ gc² ç(s)v(s)ds + óa r_sç(s)
· r_sv(s)ds,

f _{s s}

Pour cela, considerons un élément quelconque X de H¹(Ù) × H¹(_s) , on a

_{Z Z}

K(X, X) = c2 Ù |r?(x)|²dx - Ù |r?0(x)|2|r?(x)|2dx f

_{Z Z}

+ c² r_s?0(s)
· r_s?(s)ç(s) - c² r_s?0(s)
· r_sç(s)?(s)ds

f f

_{s s}

_{Z Z}

+ gc² |ç(s)|²ds + óa |r_sç(s)|²ds,

f _s s ,

(3.10)

u , le nombre de Mach

cff

posons m ₌

et

max_x?Ù|V?0|²² = u² = m²c²f,,

alors (3.10)) est minorée par :Z Z

K(X, X) = (c2 f - u2) _Ù |r?(x)|²dx + c² r_s?0(s)
· r_s?(s)ç(s)

f s )Z _{Z Z}

- c² r_s?0(s)
· r_sç(s)?(s)ds + gc² |ç(s)|²ds + óa |r_sç(s)|²ds,

f f

_{s s s s}

d'oùu

K(X ,X) => (c²fq--- u²)i?ii_,Ù, +in f (gc2 _f , óa)kç(s)k2 1,_s sZ Z

+ c² r_s?0(s)
· r_s?(s)ç(s)ds - c² r_s?0(s)
· r_sç(s)?(s)ds.

f f

_s s .

Et puisque nous-nous sommes placéss dans le cas oùl :

?p = 0 sur ?s..

la formule de Green permet d'obtenirr pour ?0(x)) = ux1i :

Äs?0) = 0 sur s..

Ainsi,

_{Z Z}

r_s?0(s)
· r_s?(s)ç(s)ds = - Ä_s?0(s)?(s)ç(s)ds

_{s s}

Z

rs?0(s)
· r_sç(s)?(s)ds _{s Z}
= - r_s?0(s)
· r_sç(s)?(s)ds,

_s

ce qui permet d'obtenir une minoration de l'opérateur K(., .) de la forme :

K(X, X) = (c² f- u2) ?k²1,Ù + inf (gc²f, óa)Iç(s)k2 1,s

_Z

- 2c² r_s?0(s)
· r_sç(s)?(s)ds,

f s

et comme le gradient de ?0 est égale à :

Vs?0 = 0,

l'inégalité de Cauchy-Schwarz appliquée au troisième terme de gauche impose l'existence d'un nombre réel positif noté á tel que :

_{Z Z c}2 _Z

f

2c² r_s?0(s)r_sç(s)?(s)ds = áu²c² |r_sç(s)|²ds + |?(s)|²ds.

f f

_{s s} á _s

l'inégalité précedente devient donc : K(X, X) = (c^2 f- u^2)i?i^21,Ù + inf (gc^2f, óa)kç(s)k2 1,s - áu^2c^2 fkçk2 1,s -

cá ^f k?k2 0,s. á

L'application trace étant continue, en désignant par c0 la constante de continuité on a,

?? ? H¹(Ù); I?I0,_s = c0l?i1,Ù,

et l'opérateur K(., .) est bornée inférieurement par un terme defini en fonction du paramètre á

c0c2 f

K(X, X) = (c2 f - u² - )k?k2 _1,Ù + (in f (gc2 _f , óa) - áu2c2 _f )kç(s)k2 1,s.

á

?

????? ?

??????

c0c2 f

á = (c2 f - u²)

Et pour que K(., .) puisse être est définie positve, il suffit que l'on puisse choisir á > 0 tel que :

ñ )

f

in f (gc2 _f , ó c2

á = ,

u²c²_f

ou encore sous forme plus explicite en simplifiant par c² f:

c0c²f

(c² u2) = á = f ceci etant possible si :

in f (gc2 _f , óc2 ñ f )

,

_u2 2

c_f

u2 ₌1 - c2 m2 inf (g, ó

Cette inégalité nous donne une condition suffisante de stabilité.

En effet, en choisissant Y = X^ÿ dans le système matriciel, et puisque la matrice C définie une forme bilinéaire antisymétrique :

C( ^ÿX, ^ÿX) = 0

et on obtient :

d 1 ÿ ÿ ¹K(X, X)] = L(^ÿX),

[_ M(X, X) + 2

dt 'z

par conséquent, lorsque L(.) = 0, le système est conservatif vis-à-vis de l'énergie définie par :

1 ÿ ÿ

= 2 M( X, X) + ¹ ₂K(X, X).

Il apparaît donc clairement que la solution du système mécanique reste uniformement bornée en temps. La valeur exacte (au sens numérique) de u notée u_c pour laquelle la forme bilinéaire K(., .) perd sa positivité sera calculée par une méthode numérique à la suite de ce travail. Reste à montrer l'existence et l'unicité d'une solution de l'équation (3.9).

3.1.4 Existence et unicité d'une solution

:

La recherche de modes propres du système couplé est un problème difficile, nous considérons une approche utilisant les modes propres de chaque composantes mécanique pris séparement.

- Pour la surface libre (capillarité) : désignons par ù^s_n les modes propres de la surface capillaire (tension superficielle) associés aux valeurs propres ë^s .

Le problème aux valeurs propres s'écrit :

?

????????????? ?

??????????????

trouver (ù^s, ë^s) ? H¹(I'_s) × IR⁺,

?ù^s
í_s

-Aù^s + gù^s = ë^sù^s sur Fs,

= 0 le long de ?F_s,

IFs |ù^s|²(s)ds = 1 condition de normalisation.

?

?????????????????? ?

???????????????????

- Et pour le fluide compressible : le problème s'écrit
trouver (ùf, ëf) E H¹(Ù) x R⁺,

--c2 _f Äù ^f + V?0
· V(V?0
· Vùf) = ëf ù ^f dans Ù,

?ù f = 0 sur _s,

í

ù f = 0 sur ?Ù -- _s,

ZÙ |ù ^f |²(x)dx = 1 condition de normalisation.

ou ù ^f désigne les modes propres du fluide associés aux valeurs propres ëf .

L'existence et l'unicité d'une solution au modèle (3.9) s'obtiennent en construisant une suite de problèmes approchés obtenus en utilisant une base réduite constituée de modes propres du fluide et du modèle de vague obtenus précedemment c'est-à-dire sans couplage.

Commençons par définir les espaces de dimensions finies dans lesquels on va rechercher une approximation des solutions en ? et ç.

Nous considérons pour cela des sous-espaces de H¹(Ù) et de H¹(_s) engendrés par les N premiers vecteurs propres de la surface capillaire de l'eau et du fluide, notés respectivement :

N

WN = {ç^N / ç^N = ? ánùs n } pour la surface capillaire de l'eau

n=1

VN = {ø^N / ø^N =

N ? n=1

ânù f n } pour le fluide.

Notons :

VN = V^N x W^N.

La solution approchée X^N(t) = (?^N(t), ç^N(t)) du système (3.9) est
définie comme l'unique solution du système différentiel matriciel ci-

après :

? ????????????????????? ? ??????????????????????

trouver X^N(t) = (?^N(t), ç^N(t)) ? VN tel que : ?Y ? H^1(Ù) × H^1(s) n L^2(s) M( ^·X^N, Y) + C( ^ÿXN, Y) + K(X^N, Y) = 0 satisfaisant les conditions initiales suivantes : X^N(0) = (?^N0 , ç^N0 )^ÿXN(0) = (?^N1 , ç^N1 )

(3.11)

ou :

(?^N0 , ç^N0 ) ? H¹(Ù) × H¹(_s), et (?^N1 ; ç^N1 ) ? H¹(Ù) × H¹(_s) et vérifiant respectivement d'une part

? lim

N?8 11?t; - ?011 = 0,

+

? lim 11 ?^l1 ^v - ?1 11 = 0,

? N?+ 8

d'autre part

? lim

N?8 11çtlⁱ - ç011 = 0,

+

?

N?lim811ç1 N - ç111 = 0. ? +

Remarquons que, lorsque N (nombre des modes retenus) évolue, les coefficients de X^N dans la base naturelle de l'espace de dimension fini V^N changent.

De ce fait, pour montrer l'existence d'une solution, nous ne pouvions pas procéder comme dans le cas classique oil nous disposions d'une base de vecteurs propres qui permettait de diagonaliser les opérateurs associés aux différentes formes bilinéaires.

Et par rapport à la vitesse critique notée u_c, nous envisageons deux méthodes d'étude d'existence d'une solution au modèle continue.

Cas ou u < u_c : l'existence d'une solution au modèle continu, s'obtient en montrant que la suite des solutions approchées construite à partir de V^N converge vers une solution de (3.9) lorsque N tend vers l'infini, et cela dans un espace défini a priori.

Ainsi a chaque entier N, associons le problème suivant :

? ??????? ???????

trouver X^N(t) = (?^N, ç^N) ? V^N tel que : ?Y ? V^N, M( ^·X^N,Y) + C(^ÿX^N,Y) + K(X^N,Y) = 0, XN(0) = (?^N0 , ç^N0 )^ÿXN(0) = (?^N1 , ç^N1 ).

(3.12)

Choisissons dans (3.12) :

Y = ÿXN

on obtient :

dt^[1

^d₂M(^ÿX^N, ^ÿX^N) + ¹₂K(X^N, X^N)] + C(^ÿX^N, ^ÿX^N) = 0. (3.13)

Notons que l'opérateur,

C(X,Y) = u f [V?0(x)
· V?(x)ø(x) - V?0(x)
· Vø(x)?(x)]dx

+ q1

_rs [?(s)v(s) - ç(s)ø(s)]ds + ucf I

r1?r2

est définie par une forme bilinéaire symétrique plus une forme bilinéaire antisymétrique, nous pouvons le décomposé sous la forme :

C(X,Y) = C_s(X, Y) + C_a(X, Y)

avec

- C_s(X, Y) opérateur symétrique,

- C_a(X, Y) opérateur antisymétrique.

Finalement l'expression (3.13),se réduit sous forme :

d 1 .

dt 2 ^M(XN,XN) 2

K( X^N X^N)] + C_s (^ÿX^N X^N) = 0.

[

et comme

C_s( ^ÿX^N, ^ÿX^N) = 0.

Des propriétés des formes M(., .) et K(., .) , on déduit par un calcul clas-
sique qu'il existe une constante positive c, indépendante du temps et telle

que :

+ IIXNII2V(t)) r t

c[lIg^NIIV(⁰) + IIXNIIV(0)1+c ₀I ^ÿX^Nk²_V(s)ds.

Une application de l'inégalité de Gronwall, permet alors de déduire une estimation a priori :

( ^ÿX^N0_f(t) +₀ k^ÿX^Nk²_V(s)ds) = c.

La suite X^N est donc bornée dans l'espace : H¹(0, T; H¹) n L²(0, T; V) , qui est un espace de Hilbert.

On peut alors extraire de X^N, une sous suite notée X^N telle que :

XN X^* ? H¹(0, T; H¹) n L²(0, T; V) (convergence faible)
Ensuite on peut utiliser une formulation faible satisfaite par la solution approchée X^N afin de caractériser X^*. On a alors,

pour tout Y ? H¹(0, T; H¹) n L²(0, T; V) tel que Y(T) = 0

_T

M( X^N,Y)dt + ^IT C( ^ÿXN, + K(X^N, = 0,

10^T 0

(3.¹4)

et par une intégration par partie, on a

Z0

TM ( ^·XN , Y) = -M( ^ÿX^N(0), Y(0)) -

0 T M( ^ÿX^N, ^ÿY)dt,

eton obtient

1₀^T M( ^ÿXN , ^ÿY)dt + f T C ( XN ,Y)dt + f T K(X^N,Y)dt = M( ^ÿX^N(0),Y(0)).

Alors le passage à la limite faible montre que X^* est une solution de la formulation faible pour tout X E H¹(0, T; H¹) n L²(0, T; V).

Nous avons donc établi l'existence d'une solution dans l'espace H¹(0, T; H¹) n L²(0, T; V) à l'équation (3.9).

Pour ce qui est de l'unicité, on peut procéder de la façon suivante : supposons qu'il y'ait deux solutions X1 et X2 à l'équation (3.9). Notons par X = X2 - X1 leur différence.

En supposant que ces deux solutions soient suffisamment régulières, nous obtenons en choisissant Y = X^ÿ dans l'équation variationnelle satisfaite par X :

d 1 ÿ ÿ

dt[2M(X, X) + ¹ ₂K(X, X)] = -C_s(X, X) < 0. Ceci permet de conclure que, X = 0, c'est-à-dire X2 = X1.

Cas ou u > u_c : nous avons un modèle d'onde instable pour lequel l'hypothèse o^- > 0 est essentielle pour prouver un résultat d'existence. Pour une vitesse u donnée, il y'a seulement un nombre fini de modes propres instables pour lesquels l'opérateur de raideur est négatif.

Décomposons l'espace W en somme direct de deux sous espace Vi et V_s ou

- Vi :est un sous espace de dimension finie engendré par les modes propres instables,

- V_s :un sous espace de dimension finie engendré par les modes propres stables.

On a

W = Vi e Vs

Soit k une constante strictement positive et de valeur très élévée, et posons
X(t) = ekteX(t),

on a

^ÿX(t) = k^eX(t)e^kt + ^ÿeX(t)e^kt,

^·X(t) = k^2eX(t)e^kt + 2k ^ÿeX(t)e^kt + ^·eX(t)e^kt,

ce qui donne, en remplaçant dans la formulation variationnelle de modèle (3.9) :

La forme bilinéaire définie par l'opérateur K(., .) est continue et vérifie,
pour tout X ? V_s, il existe une constante c0 = 0 tel que :

K(X, X) = c0IIXIIW.

Nous avons supposé v > 0 alors toutes les normes définies sur l'espace Vi de dimension finie engendré par les modes propres instables sont équivalentes.

Et pour une valeur très grande de k, le terme

K(^eX, Y) + kC(^eX, Y) + k²M(^eX, Y), est tel qu'il existe une constante c1 positive telle que :

VX^e ? Vi, K( ^eX, ^eX) + kC(^eX, ^eX) + k²M(^eX, ^eX) = c1k ^eXk² _W.

Afin d'obtenir une estimation a priori sur la solution ^eX^N du modèle approximatif, choisissons Y = .5e dans léquation (3.14). Ce qui donne :

N

^;·^,NM(

A.,N X Cs ,^A.,N ) \ I, X^N ) k^2Mae^N , X^N ) A-N (3.15) = -2kM( X , X) - kCP^-e^N , X )

Des propriétés de M(., .), il existe une constante notée c3 indépendante du temps telleque :

1

2

d

dt[M( X , X ) + C_s (X^N , ie^N) + K(X^N , fe^N) + k² MPe^N , fe^N )]

= c3k ^ÿeX^NkW + kC(^eX^N, ^ÿeX^N).

Ce qui permet par simple application du lemme de Gronwall, d'obtenir

une estimation a priori sur X^N ainsi que sur ^ÿeX^N.

On peut alors extraire une sous-suite qui converge faiblement, vers une solution faible du modèle (3.11).

On en deduit que l'existence et l'unicité d'une solution sont encore vraies, même si des instabilités apparaissent. Les détails complémentaires de la démonstration se trouvent dans [9].

3.1.5 Conclusion

L'étude présentée dans ce chapitre est essentiellement basée sur l'établissement de la formulation variationnelle du modèle et sur les propriétés des différents oprérateurs linéaires obtenus.

Nous avons aussi étudié l'existence et l'unicité d'une solution du modèle. Pour cette étude, nous avons considéré une suite de problèmes approchés obtenus en utilisant une base réduite constituée de modes propres du fluide et du modèle de vague sans couplage.

Cela nous a permis d'introduire la notion de vitesse critique, vitesse au dessus de laquelle le modèle peut être instable.

L'étape suivante sera consacré à la validation numérique cette formulation variationnelle.

4

SCHéMAS NUMéRIQUFS

L

F besoin de recourir aux simulations numériques est aujourd'hui omniprésent dans de multiples domaines d'applications (automobile, aéronautique et thermique...) et ce pour plusieurs raisons.

Tout d'abord, les simulations numériques permettent de tester l'influence de certains paramètres et de comprendre les phénomènes impliqués dans un écoulement : l'accès à certaines informations est rendu possible, l'écoulement peut être calculé et donc visualisé en 2D ou 3D.

Dans ce chapitre, nous décrivons les moyens que nous avons mis en oeuvre pour implémenter les différents concepts théoriques présentés auparavant et concevoir un code de calcul pour la simulation de nos modèles. Nous avons choisi de travailler avec le langage Python pour l'implémentation et ceci pour plusieurs raisons, c'est un langage :

- interprété car il est directement exécuté sans passer par une phase de compilation qui traduit le programme en langage machine, comme c'est le cas pour le langage C,

- orienté objet de haut niveau car il propose des fonctionnalités avancées et automatiques.

- modulaire car de nombreux modules et librairies ont été développées,

- et à syntaxe positionnelle en ce sens que l'indentation fait partie du langage. Alors que le point virgule permet de séparer les instruction en langage C, l'accolade permet de commencer un bloc d'instruction. En Python, seule l'indentation permet de marquer le début et la fin d'un bloc.

Ainsi la syntaxe de Python est beaucoup plus simple que celle des autres langage, ce qui améliore de façon très significative les temps de développement.

4.1 MAILLAGF

La méthode des éléments finis repose sur un découpage du domaine selon un maillage. L'étape du maillage est une étape clé pour s'assurer de la validité des simulations. Et nous utilisons le logiciel Gmsh développé par Christophe Geuzaine et Jean-François Remacle pour réaliser les maillages bidimensionnels sur lesquels nous tavaillons.

4.1.1 Description du logiciel Gmsh

Le logiciel Gmsh est doté de 3 fonctionnalités principales. C'est un logiciel assez développé, permettant la manupulation de champs de nature variées ( scalaire, vectorielle, tensorielle, continu ou non), et dispose d'un volume de visualisation de résultats de calculs scientifiques.

Les fonctions

Il possède différents modules. Trois de ceux-ci nous sont particulièrement utiles : les modules de la géométrie, du maillage et du post-processing.

Géométie : Gmsh nous permet de produire une grande variété de formes géométriques. La construction d'une géométrie permet l'emploi de paramètre sur les longueurs d'arêtes, le nombre de mailles, la longueur des mailles,...ce qui rend facile l'adaptation d'un maillage à un nouveau problème.

Tout élément, surface, ligne ou point peut être considéré comme étant «physique» c'est-à-dire qu'une information supplémentaire appelé tag correspondant à une propriété physique sera attribuée à l'entité, et transmise dans le fichier contenant le maillage fini. Cela permet de différencier physiquement les différents point, arêtes, surfaces et volumes s'ils ont des propriétés particulières.

Mailleur : le Logiciel permet de produire un maillage de triangles sur les surfaces définies par la géométrie. Le nombre et la taille des mailles sont définis via des paramètres attachés aux frontières de ces surfaces. Le maillage peut se faire suivant certaines contraintes de régularité des mailles (lignes et surfaces dites transfinies) avec un nombre de noeuds imposé sur une arête, ou bien par la définition d'une longueur approximative de côté de mailles.

Le mailleur permet de mailler dans une, deux ou trois dimensions, en formant successivement des éléments linéaires surfaciques et volumiques. Post-processing : les résultats peuvent être visualisés via le postprocesseur de Gmsh.

Le maillage produit est traduit généralement en termes de noeuds, lignes, surfaces et volumes dans un fichier.msh.

La forme de fichier est décrit ci-dessous :

NOD

Nombre de Noeuds

numéro du noeud1 Xnoeud1 , Ynoeud1 , Znoeud1 ... ... ... ...

ENDNOD

ELM

Nbr elem

num elem type elem physical reg elem nbr noeuds num noeuds ... ... ... ...

ENDELM

où :

- Nbr elem = nombre d'élements (lignes, arêtes, triangles et/ ou quadrangles),

- num elem = numéro de l'élement,

- type elem = type d'élément ( 1 = arête, 2 = triangle, 3 = quadrangle), - physical = tag attribué à l'élement,

- reg elem = numéro de l'entité élementaire auquel appartient l'élement,

- nbr noeuds = nombre de noeuds de l'élement,

- num noeuds = les numéros des noeuds de l'élement.

Dans ce travail, nous considérons deux domaines de même dimensions pour nos différents calculs, dans les quelles nous incluons deux structures différentes.

1. un domaine avec stucture symétrique de type : une ellipse L'avantage de ce cas est de permettre une étude de sensibilité au maillage. Cela consiste à faire des simulations avec un nombre de mailles différent, et aussi de vérifier la cohérence et la symétrie de nos résultats.

2. et un autre domaine avec stucture non symétrique : le sous-marin Ce domaine sera notre véritable domaine d'étude, nous ferons plusieurs simulations avec différents maillages, et pour différentes hauteurs du sous-marin dans le domaine.

Après avoir créer nos différents maillages avec le logiciel Gmsh aux formats « fichier.msh », nous les importerons pour un autre logiciel afin de pouvoir effectuer les calculs des matrices élementaires en vu de les assemblées pour nos simulations. Nous utiliserons pour cela le logiciel Getfem + + , que nous décrivons brièvement dans le paragraphe qui suit.

4.1.2 Présentation du logiciel Getfem + +

Le logiciel Getfem est à la base une bibliothèque d'élements finis génériques en C++ dont l'objectif est d'offrir une gamme d'élements la plus large possible et un calcul de matrices élèmentaires également la plus large possible pour l'approximation de problème linéaires ou nonlinéaires.

La bibliothèque Getfem comprend des outils habituels pour les éléments finis tels que des procédures d'assemblages pour les équations aux dérivées partielles classiques. Ses objectifs sont :

- fournir des outils de base pour le développement de méthodes éléments finis nouvelles,

- séparer clairement les concepts de transformation géométrique, de

méthode de quadrature, de méthodes des élément fini et de modèles.

- mettre en oeuvre des méthodes d'assemblage génériques; - proposer une interface simple sous Matlab et Python.

4.2 DiscrétisatioN eN espace

Soit une triangulation donnée du domaine Ù telle que Ù = S K?g-K.

Le paramètre h, caractérise la finesse du maillage, et est défini de la manière suivante :

h = maxK?g-hK,

avec hK le diamètre de la plus petite sphère contenant l'élèment K. Nous introduisons ensuite l'espace d'approximation

Vh = {vh ? C⁰(Ù)/ vh/K ? (P1)³, ?K ?

qui est le sous-espace vectoriel des fonctions à valeurs vectorielles continues sur Ù et de restrictions affines sur chaque élément et correspond à l'utilisation d'éléments finis de Lagrange de type P1.

Celui-ci constitue une approximation conforme de l'espace H¹(Ù)³ et sa dimension est égale au nombre de degré de liberté du problème, soit 3Nh où Nh désigne le nombre de noeuds de la triangulation g^- appartenant à Ù.

A chaque noeud ni , i = 1, Nh, de la triangulation sont alors associées

trois fonctions de bases : wi1, wi2, wi3 appartenant à Vh et vérifiant :

1 0 0

wi1(nj) = (0) äi,j , wi2(nj) = (1) äi,j , et wi3(nj) = (0) äi,j, j = 1, ...., Nh

0 0 1

Où äi_,jdésigne le symbole de Kronecker.

Et tout champ vh de Vh se décompose alors sous la forme :

Nh 3

vh = ? ? vhá(ni)wiá.

i=1 á=1

Ainsi, tout élément de Vh peut être identifié à un vecteur colonne formé des valeurs réelles _vhá(ni) , i = 1, Nh et á = 1,2,3 des composantes de vh aux noeuds du maillage.

A l'aide de cette base, on peut à partir de chacune des formes bilinéaires M(., .), C(.,.) et K(.,.), obtenir les matrices notées respectivement M^s, Mf, Cf, Cs, Kf , K^s appelées matrices des masses, des raideurs, d'amortissements et de couplages définissant la discretisation spaciale du système (3.9).

ZÙ ?iøj

Mf =

i,j

= fI r?i
· røP- u2 I (r?0
· r?i)(rñ0
· røj)

i,j

C = u I (r ?0
· r - u _I (r?0
· røj)?i + cf f ?iø

i,j

?2

et

_Z

Ms i,j = 2åñ çivj,

_s

_{Z Z}

Ks i,j = ñg _çivj + ó rsçi
· rsvj

_{s s}

_{Z Z}

Cc1

i,j = c2 çiøj et Cc2

i,j = ñf ?ivj

f _{s s}

Bz) = uq f vs?0
· vsçiøj et B^c_i²= uñ I Vs?0
· vs?ivj

rs ^,jrs

Et le problème approché consiste alors à trouver un élèment X^h de Vh tel que :

?Y ? H¹(Ù) × H¹(_s) M( ^·X^h,Y) + C( ^ÿX^h,Y) + K(X^h,Y) = L(Y),

ce qui s'écrit de manière détaillée sous forme matricielle, en considérant pour tout :

~

? ~X ? H¹(Ù) × H¹(_s) et Y = (^ø) ? H¹(Ù) × H¹(_s) : ç v

? ?

Mf 0 0 Ms

?? ? ?

? +? Cf -C^c^1 ??ÿ? +? e^. -Bc1 ?? =?0? ? Cc2 T ?çÿ? ? Bc2 Ks ?Id F

Notons que la matrice T est explicitée après, dans la section Résultats Numériques.

Ainsi nous obtenons en posant respectivement :

? M = ?

Mf 0 0 M^s

? ? ? ? ?

Cf _-Cc1 Kf -Bc1

? , C = ? ? , K = ? ?

Cc2 T Bc2 _Ks

et F = [F^0,

une équation différentielle matricielle du second ordre en temps. M kt ozh KX^h = F

Pour pouvoir la résoudre, il faut prendre en compte les conditions initiales en vitesses et en déplacements.

Pour cela, on construit un interpolé dans Vh du champ de déplacements initial, X^0h, et du champ à vitesse initial, soit ÿX⁰h

On impose alors à t = 0 :

X^h(0, x) = X^0h(x),
^ÿX^h(0, x) = 10^h(x).

4.3 DiscréTisATioN eN TeMps

Dans cette partie, nous allons décrire et analyser la methode d'intégration numérique de l'équation différentielle matricielle du second ordre (3.9) avec les conditions initiales. Nous nous contenterons d'une méthode parmi les plus usitées.

L'intervalle de temps [0, T] sur lequel on souhaite évaluer la solution de (3.9) , est partagé en sous intervalles supposés égaux pour simplifier et de longueur At .

En posant Xⁿ l'approximation obtenue par le calcul du vecteur X(nAt) à l'instant nAt on a :

Xn+1 + Xn

X(nAt) =

2

On utilise ensuite différentes estimations des dérivées X^ÿ et ^X· à l'instant nAt :

Xn+1 - Xn

^ÿX(nAt) =

At

^·X(nAt) = Xn+1 - 2Xⁿ + Xn-1

At²

L'équation différentielle du second ordre est résolue par un schéma au différences.

)0+1 - 2Xⁿ + Xn-1 )0+1 - )0 Xn+1 + X M ) + C( ) + K( ) = F .

(

At² At 2

L'avantage de telles méthodes est qu'elles sont moins coûteuse puisqu'elles ne nécessitent l'évaluation des inconnues fluide et vague qu'une seule fois par itération en temps.

(At)² ₊1 (At)²

[M + AtC + ₂ K]Xⁿ [2M + AtC - 2 K]Xⁿ + [M]Xⁿ-¹ = (At)²F

(4.¹)

4.4 ETuDe De LA sTAbiLiTé Du scHéMA D'iNTégrATioN eN TeMps

ment, on a :

?

???????????? ?

?????????????

trouver X^N ? Vh tel que ?Y ? Vh, M( Xⁿ⁺¹ - 2Xⁿ + ^Xn-1,Y) +C( Xn+1-Xn

(4.2)

Ät , Y)

Ät²

+K( Xⁿ⁺¹₂ +Xn , Y) = F(Y).

Posons

Y = Xⁿ⁺¹ - Xn,

Une démarche similaire que celle de la section 2.4.1, tout en remarquant que l'opérateur C(.,.) contient des termes symétriques et des antisymétriques conduit A :

M( Xn+1 - Xn Ät , Xn+1 - Xn

Ät ) + ¹ _Ät(C(Xⁿ⁺¹ - Xn, Xⁿ⁺¹ - Xⁿ)) + ¹ ₂(KXⁿ⁺¹, Xⁿ⁺¹)

= M( Xn - Xn-1

Ät , Xn+1 - Xn

Ät ) + ¹ ₂(KXⁿ, Xⁿ).

(4.3) Les termes antisymétriquess de l'opérateurr C(.,.) s'annulent,, et les termes symétriquess sont tels que

1 (C_s(Xⁿ⁺¹¹ --- Xn,, _Xn+11 --- Xn)) => ,

Ätt

L'inégalitée de Cauchy-Schwarz suivante :

(MX, Y) =<₂₂¹¹₂₂(MX,,X))++¹¹(MY,, Y),

appliquéee au premier terme du second membre de l'égalitée (4.3), donne :M( Xn - Xn-1

Ät , Xn+1 - Xn

Ät ) = 1 2 M( Xn - Xn-1

Ät , Xn - _Xn-1 'Ätt )1 1Xn+1 i_- _XnnXn+1 i- _Xnn+ +2M((Ät t^, 'Ätt ),'

on obtient ensuite :2 M( Xn+1 - Xn

+ 2K(Xn+1 ,Xn+1)

1 Ät , Xn+1 - Xn

Ät ) + ¹ _Ät(C(Xⁿ⁺¹ - Xn, Xⁿ⁺¹ - Xⁿ)) + ¹

11Xnn-_Xn-11Xn n- _^Xn-11=<₂M(( _Ät t, _'Ätt ).
·

(4.4) Et comme l'opérateurr symétriquee C_s(.,, .) est positif, alors l'inégalitée (4.4) donne l'inégalitée :2 M( Xn+1 - Xn

1 Ät , Xn+1 - Xn

Ät ) + ¹ ₂K(Xⁿ⁺¹, Xn+1) =1 2 M( Xn - Xn-1

Ät , Xn - _Xn-1 'Ätt )

+ 12 K(Xⁿ,, Xⁿ).

Considérons l'énergie mécanique est définie par l'expression :

1 Ät , Xn -- Xn--1

En = 2 M( Xn -- Xn--1 Ät ) + ¹ ₂K(Xⁿ, Xⁿ),

nous aboutissons à la même conclusion que dans le cas dimension c'est-àdire :

En+1 En.

L'energie mécanique totale est décroissante au sens large au cours du temps, ce qui assure la stabilité de ce schéma numérique.

N

ous décrivons maintenant les différentes étapes et l'algorithme de résolution de notre problème.

- Une première étape consiste à determiner les frontières optimales sur les quelles seront appliqueés les conditions transparentes. Pour cela, nous allons d'abord chercher la solution stationnaire q'0 du système (2.7).

Nous pouvons ensuite obtenir à partir des gradients de cette solution stationnaire la vitesse de l'écoulement. Les lignes de courants peuvent être defini par la suite en observant au même instant l'ensemble des points de l'écoulement pendant une durée assez courte en description lagrangien.

Les frontières optimales seront obtenues alors par découpage du domaine suivant les courbes équipotentielles orthogonales aux lignes de courant.

Rappelons que, les deux conditions aux limites (2.34), ne sont valables que pour une frontière perpendiculaire à la direction de l'écoulement, c'est-à-dire pour des écoulements dont les champs de vecteurs vitesses sont colinéaires à la normale sortante de la frontière considerée. Ainsi, pour un écoulement quelconque avec une frontière curviligne quelconque, l'apparition des composantes tangentielles de la vitesse de l'écoulement sur la frontière considérée entraîne des difficultés supplémentaires que nous n'abordons pas dans ce travail.

- Dans un second temps, nous appliquons la condition aux limites au cas d'un écoulement transitoire.

- Et enfin, une extension au équations des vagues progressives sera étudiée. Les calculs sont effectués dans un cadre bidimensionnel et les scripts de simulation sont développés en langage Python.

5.0.1 Solution stationnaire

Nous nous plaçons dans le cas d'écoulement potentiel et incompressible. Nous avons donc à resoudre le système suivant définit au (2.7) :

? ?????????

?????????{

-Ä?0o = ⁰ dans ^Ù,,_???0o₌ =0 0sur r0 o? Ub b? us,,??0" = (e1,, U) sur 1i ?u 2,,

^?ív

ou ?0 est définie à constante près, que nous fixons en prenant la condition de moyenne nulle sur _s :

Z

?0 = 0. s .L'espace des fonctions test consideré pour la formulation variationnelle de

ce problème sera :

H¹(Ù)) = {v/v ?E L²(Ù)// ?kvv ?E L2(Ù)}}

et la formulation variationnelle est :

_{Z Z} Z ??0

?ø ? H¹(Ù); - Ù Ä?0ø = Ù r?0rø - ?í ø,

?Ù

??0

en tenant compte des valeurs de sur les frontières de l'ouvert Ù, on

?í

a :

Z Z

?ø ? H1(Ù); _Ù r?0rø = u ø,

1?2 '

Le problème à resoudre devient :

? ??? ???{

Trouver ?0o ?E H^1(Ù)) telle que : Z Z Ù r?0rø = u ø , ?ø ? H^1(Ù). 1?2 2

Ce problèmee admet bien une solution unique. Pour s'enn assurer, nous vérifionss les hypothèsess du théorèmee de Lax-Milgram.

Commençonss par montrer :_Z

la continuité de la forme bilinéaire : a(?0, ø) = Ù r?0rø l_Z

|a(?0, ø)| = | Ù r?0rø| = kr?0kL²(Ù) × krøkL²(Ù) = |?0H¹(Ù)||øH¹(Ù)| l
= 1?01L2(Ù)1ø1L2(Ù).
·

Ainsi :

La forme bilinéaire a(.,.) est donc continue sur H × H et elle est H-coercive.

Montrons maintenant la continuité de la fonctionnelle

_Z

l(ø) = u ø :

1?2

|l(ø)|= ~ ~u(f ₂ ø - f 1 ø) ~~~ = u(k Z øIIL²(Ù) + 11 øIIL²(Ù))

1 2

= u(køkL2(1) + IøIIL2(2)) Cauchy-Schwarz

= u(c1 + _{c2)IIøIIH1(Ù)} par l'inégalité de Trace

d'où :

|l(ø)| = u(c1 + _{c2)IIøIIH1(Ù),} avec c1 , c2 et u des constantes

Ainsi l'existence et l'unicité de solution au problème (2.7) sont démontrées.

Les figures (5.1) et (5.2) montrent les solutions obtenues avec deux maillages contenant respectivement une structure symétrique et non symétrique. Pour ce calcul nous avons considérer une vitesse d'écoulement de U = 0.01m.s-¹.

FIGURE 5.1 - Résultat avec stucture symétrique : une ellipse.

La différence est significative au niveau de la répartition des champs de vitesse autour des structures.

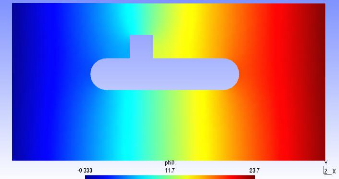
FIGURE 5.2 - Résultat avec stucture non symétrique :un sous-marin.

5.0.2 Frontières adaptées

Dans cette section nous nous intéressons à la construction numérique des nouvelles frontières adaptées définies dans le troisième chapitre. En partant d'un noeud du mailage situe à l'interface représentant la surface libre du domaine, calculer le gradient de la solution stationnaire q'0, déterminer l'intersection du vecteur directeur de la droite orthogonale à la ligne de courant passant par ce noeud avec les segments des éléments P1 ( triangles) ayant en commun ce noeud.

Ensuite à partir de ce point, nous calculons à nouveau le gradient q'0 et déterminons l'intersection du vecteur directeur de la droite orthogonale à la ligne de courant passant par ce noeud avec les autres segments de l'élément ainsi de suite jusqu'à la frontière représentant le fond du domaine. En partant d'un noeud de la surface libre non loin de la structure, nous obtenons une courbe représentant la courbe équipotentielle.

La figure (5.3) présente un exemple d'équipotentielles obtenus pour une vitesse d'écoulement U = 0.01m.s-¹, avec un domaine contenant un sousmarin.

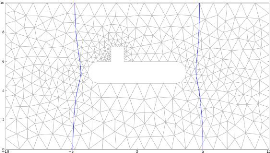
sont presque parallèles aux frontières latérales du domaines, ce qui est normal car l'écoulement est presque uniforme .

Nous pouvons alors découper nos domaines de calcul suivant les équipotentielles. Ce choix permet d'obtenir des frontières adaptées que nous notons respectivement par 1 et 2 sur les quelles nous pouvons désormais appliquées la condition aux limites transparentes.

Notons que sur ces frontières la composante tangentielle du gradient de q'0 dans le repère local lié à ces frontières est nulle. De ce fait, la vitesse d'écoulement est supposée orthogonale à ces frontières.

Les figures (5.4) et (5.5) présentent les maillages obtenus avec les nouveaux domaines découpés suivant les frontières optimales pour une vitesse d'écoulement U = 0.01m.s-¹.

FIGURE 5.4 - Maillage du domaine découpé avec une ellipse à l'intérieur.

FIGURE 5.5 - Maillage du domaine découpé avec un sous-marin à l'intérieur.

5.0.3 Conclusion

Ces deux chapitres sont consacrés à la présentation des outils numériques Gmsh et Getfem++ utilisés dans cette étude.

Au cours de ces chapitres, nous avons détaillé le schéma permettant de résoudre numériquement l'équation du modèle.

Nous avons aussi explicité la méthode utilisée pour le découpage du domaine de calcul suivant les frontières obtenues à partir des lignes de courant et des équipotentielles de l'écoulement potentiel autour d'une ellipse et d'un sous-marin.

Deux maillages du domaine contenant ces deux structures (une ellipse et un sous-marin) sont obtenus.

Dans le dernier chapitre, nous présentons les résultats numériques obtenus avec ces deux maillages.

N

ous présentons ici l'algorithme permettant de passer, d'un maillage produit par le logiciel Gmsh à partir d'un domaine optimal, au

calcul des différentes matrices par le logiciel Getfem + + à un résulat sous forme d'un écoulement autour d'une structure et d'une déformation ondulatoire de la surface libre au cours du temps.

Le code est articulé autour d'un programme principal Main.py , qui fait appel à chaque fragment de programme nécessaire.

La figure ci-dessous en montre le fonctionnement général.

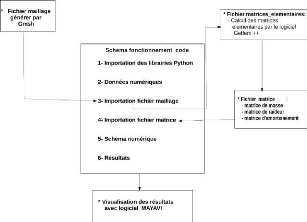
FiGuRE 6.1 - Schema de fonctionnement.

Dans un premier temps, Main.py fait appel aux différentes librairies de calcul scientifique de Python . Il réalise ensuite les opérations suivantes : - importation du maillage,

- calcul des matrices globales de, masse, raideur, d'amortissement, - initialisation des variables.

Le programme lance ensuite le processus itératif. Et au cours d'une itération les opérations suivantes sont effectuées :

- calcul du potentiel de vitesse ? ,

- calcul du déplacement normale de la surface libre ç .

6.0.4 Modèle sans couplage avec les vagues

Avant d'utiliser notre conditions aux limites transparentes dans un procédé de couplage avec les équations de vagues progressives, il convient de la tester à un modèle d'écoulement transitoire autour d'une structure avec une condition de type equation de vague:

?? ??

g?í (s, t) + _?t (s, t) = 0, sur _s×]0, T[. (6.1)

appliquée à la surface libre _s.

Cela permet non seulement de se rassurer quant à la validité de cette condition aux limites et aussi de bien comprendre l'influence de certains paramètres tels que, la profondeur de la structure dans le fluide et la qualité des maillages utilisés.

6.0.5 Résultats numériques

Notre exemple donné ci-après est obtenu avec le domaine optimale représenté par la Figure 5.4

Le domaine est discrétisé en 42020 points et les frontières en 1027 points. La résolution du problème à potentiel par la méthode des élèments finis nous donne le potentiel des vitesses.

Pour cette application numérique, la célérité de l'onde dans le fluide est cf = 1000m.s-¹ , la vitesse d'écoulement uniforme en amont à l'infini est u = 1.5m.s-¹,

Les conditions initiales concernant le fluide, imposées à la surface sont les suivantes :

IIx-x011²

L si 0 = IIx - x011² = R,

Ae

?

øinit(x) = ??????? ???????

0 si IIx - x011² = (R + A),

(1 - Mx-x0M2

(R+A) )e- IIx-x0II2

L si R = lix - x011² = (R + A).

Avec x = (x1, x2) ? ², A et R des constantes et L, représente la longueur du bassin.

Les figures ci-après illustrent une représentation du potentiel de vitesse instationnaire caractérisant l'écoulement dans le fluide.

FIGURE 6.2 - Step 1-2 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

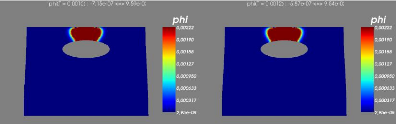
FIGURE 6.3 - Step 3-4 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

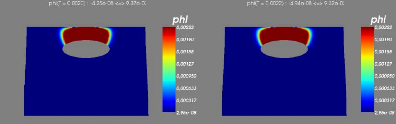
FIGURE 6.4 - Step 5-6 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

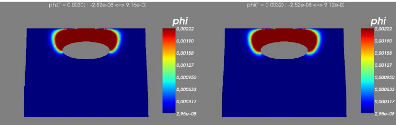
FIGURE 6.5 - Step 7-8 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

Les premières série de tests, montrent une symétrie du sillage de l'écoulement de par et d'autre de la structure.

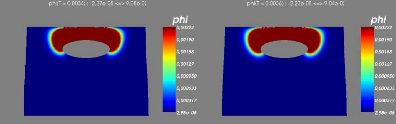
FIGURE 6.6 - Step 9-10 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

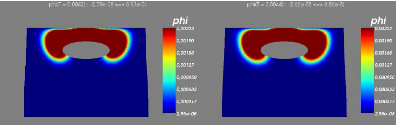
FIGURE 6.7 - Step 11-12 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

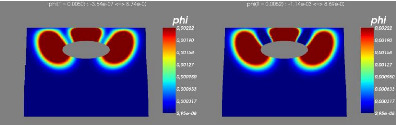
FIGURE 6.8 - Step 13-14 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

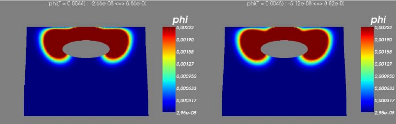
FIGURE 6.9 - Step 15-16 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

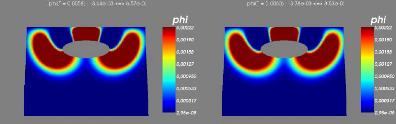
FIGURE 6.10 - Step 17-18 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

FIGURE 6.11 - Step 19-20 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

Nous remarquons que la forme géométrique du silage de l'écoulement n'est pas modifiée aux bords des frontières latérales.

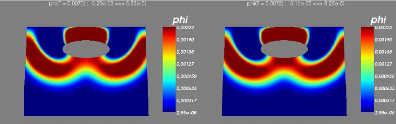
FIGURE 6.12 - Step 21-22 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

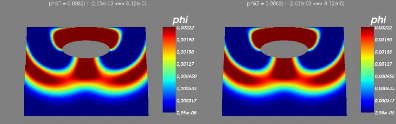
FIGURE 6.13 - Step 23-24 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

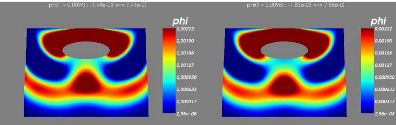
FIGURE 6.14 - Step 25-26 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

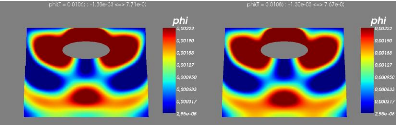
FIGURE 6.15 - Step 27-28 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

Les figures précedentes confirment parfaitement bien la notion de "limite transparente" sur les frontières latérales. On observe en effet, la non réflexion d'onde sur ces frontières.

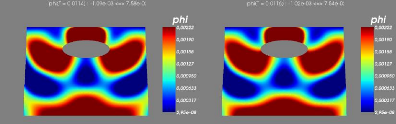
FIGURE 6.16 - Step 29-30 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

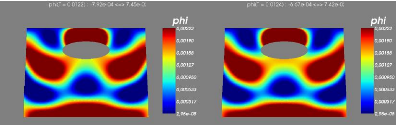
FIGURE 6.17 - Step 31-32 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

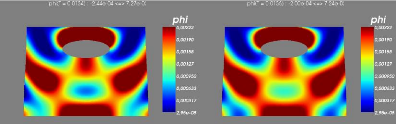
FIGURE 6.18 - Step 33-34 :Ecoulement transitiore, avec condition aux limites transparentes sur les frontières latérales.

Sur ces résultats, nous avons une réflexion d'onde au fond du domaine et nous visualisons bien les ondes piègées entre la structure et le fond du domaine . Ceci est dû à la condition de Neumann appliquée au fond dans cette application.

6.0.6 Conclusion

Cette étude a montré la faisabiité de la mise en oeuvre de la condition aux limites transparentes sur un cas transitoire. Les solutions obtenues

sont satisfaisantes.

Le choix de l'utilisation de la condition de Neumann au fond du bassin plutôt qu'une condition transparente à permis de visualiser d'une par les ondes piègées et d'autre part de vérifier l'algorithme développé.

6.0.7 Modèle avec couplage avec les vagues

L'objectif suivant est de coupler ce modèle avec le modèle de vague à la surface.

Cependant, ce objectif ne peut pas être atteint sans difficulté. Premièrement, les frontières de la surface libre F_s sont réduit en des points géometrique conduisant à une singularité. Ainsi il est difficile de définir analytiquement une conditions aux limites adaptée en ce deux points.

Et par soucis de simplification, nous appliquons pour les differentes expériences numériques, une condition aux limite de type:

= 0 au point géometrique situé à gauche de la frontière

?ç

-

?í_s

?F_s de F_s ,

- et au point géometrique situé à droite de cette frontière, nous im-

?ç ?ç

posons : + c_r = 0 .

?t í_s

c_r est la vitesse de ride et determinée par la relation:

r ó

cr =2eñ,

avec

- ó = 7.5 × 10-³ : la constante de capillarité,

- ñ = 10³ : masse volumique de l'eau.

De cette relation, nous obtenons une valeur numérique de l'épaisser de la surface capillaire, en supposant que la vitesse de ride est égale à la vitesse de l'écoulement du fluide u.

Ce qui nous donne une expression de la constante e sous la forme:

e =

ó

2u²ñ

De ce fait, la matrice T intervenant dans la matrice d'amortissement notée C est une matrice carrée dont la dimension est égale au carré du nombre de noeud sur la frontière F_s et contenant un seul élement définie comme suit:

0 ... 0 0

T= ... ... ...

0 ... 0 0
0 ... 0 u

Deuxièment, la présence des différentes ondes (ondes de gravité , on-des acoustique et ondes de capillarité) entrainent une grande disparité des vitesses d'ondes et de celle du bateau conduit à des difficultés numériques, que nous surmontons en utilisant un schéma d'intégration en temps adapté (4.1).

6.0.8 Résultats numériques

L'algorithme des simulations numériques que nous présentons ciaprès sont très similaires aux précedentes, la différence majeur étant le couplage avec les équations de vagues et l'application d'une condition aux limites transparentes au fond du bassin (I'0) pour éviter les ondes piègées entre le fond de la structure et le fond du bassin.

Dans un premier temps, nous utilisons le même maillage que dans le cas précedent avec la même structure (une ellipse) et les mêmes données numériques. La condition initiale étant la même, mais cette fois-ci définie sur la structure.

Ensuite, nous présentons les résultats numériques pour un domaine con-tenant un sous-marin.

FIGURE 6.19 - Step 1-2 : couplage avec les vagues

FIGURE 6.20 - Step 3-4 : couplage avec les vagues

Pour le domaine contenant une ellipse, nous avons les figures suivantes

FIGURE 6.21 - Step 5-6 : couplage avec les vagues FIGURE 6.22 - Step 7-8 : couplage avec les vagues FIGURE 6.23 - Step 9-10 : couplage avec les vagues FIGURE 6.24 - Step 7-8 : couplage avec les vagues

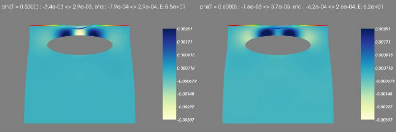
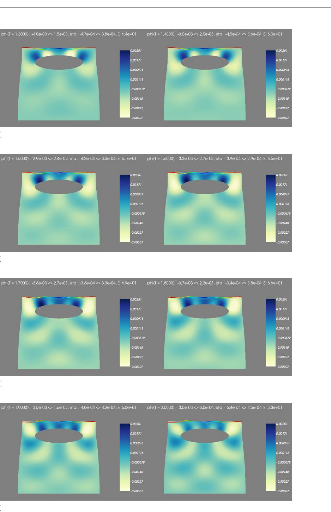
73

FIGURE 6.25 - Step 13-14 : couplage avec les vagues FIGURE 6.26 - Step 15-16 : couplage avec les vagues FIGURE 6.27 - Step 17-18 : couplage avec les vagues FIGURE 6.28 - Step 9-10 : couplage avec les vagues

FIGURE 6.29 - Step 21-22 : couplage avec les vagues FIGURE 6.30 - Step 11-12 : couplage avec les vagues FIGURE 6.31 - Step 13-14 : couplage avec les vagues FIGURE 6.32 - Step 15-16 : couplage avec les vagues

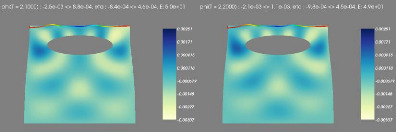
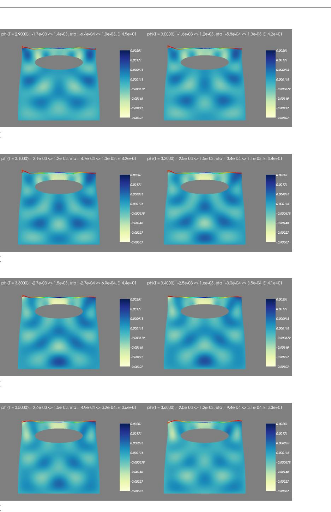
FIGURE 6.33 - Step 29-30 : couplage avec les vagues FIGURE 6.34 - Step 31-32 : couplage avec les vagues FIGURE 6.35 - Step 17-18 : couplage avec les vagues FIGURE 6.36 - Step 19-20 : couplage avec les vagues

FIGURE 6.37 - Step 37-38 : couplage avec les vagues FIGURE 6.38 - Step 21-22 : couplage avec les vagues FIGURE 6.39 - Step 23-24 : couplage avec les vagues FIGURE 6.40 - Step 43-44 : couplage avec les vagues

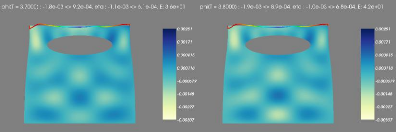
FIGURE 6.41 - Step 25-26 : couplage avec les vagues FIGURE 6.42 - Step 27-28 : couplage avec les vagues FIGURE 6.43 - Step 29-30 : couplage avec les vagues FIGURE 6.44 - Step 29-30 : couplage avec les vagues

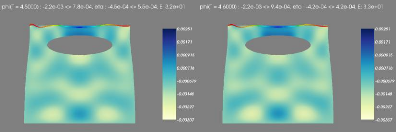
dynamique produit par la source et la forme de la structure.

Nous avons aussi l'existence d'ondes à la surface de l'eau (les vagues) due, d'une part à la pesanteur qui tend à maintenir l'interface air-eau horizontale (ondes de gravité), et d'autre part à la tension de surface qui tend à maintenir l'interface plane (onde capillaires).

D'autre part, l'amplitude des réflexions parasites des ondes sur les frontières latérales sont minimiser par l'effet transparent de la condition aux limites transparentes appliquées sur ces frontières.

Valeurs propres

Considérons toujours le domaine contenant une ellipse avec les frontières adaptées (cas précédent). L'étude de la stabilité du système consiste à étudier les valeurs propres de l'opérateur de raideur K(.,.) obtenu après couplage :

ZK(X, Y) = Ù[c2 _f V?(x)
· Vø(x) - (V?0(x)
· V?(x))(V?0(x)
· Vø(x))]dx

_Z

+ c² [V_s?0(s)
· V_s?(s)v(s) - V_s?0(s)
· V_sç(s)ø(s)]ds

f s

_{Z Z}

+ gc² ç(s)v(s)ds + óa V_sç(s)
· V_sv(s)ds,

f _{s s}

dont la matrice est :

? K = ?

Kf -Bc1 Bc2 Ks

? ? .

Pour cette étude, nous-nous intéressons à la première valeur de la vitesse de l'écoulement u, pour laquelle la plus petite valeur propre notée ëmin est négative (ëmin = 0). Nous avons appelée cette vitesse, vitesse critique et notée u_c.

Des simulations numériques montrent l'instabilité du modèle lorsque la vitesse u est supérieure à la vitesse critique.

C'est la vitesse à partir de laquelle le modèle peut devenir instable.

La figure suivante donne l'allure de la courbe représentant les valeurs de la plus petite valeur propre obtenue en fonction des vitesses d'écoulement.

Les calculs sont faits pour des données suivantes :

fluide

- masse volumique du fluide ñ = 1000 kg.m-³ - intensité pésanteur g = 9.8 m.s-²

- coefficient de tension superficiel ó = 0.075 N.m-¹ Le domaine plus la structure (ellispe) est maillé en :

- 85075 élèments triangles

- contient 42020 noeuds intérieurs

- et 1027 noeuds sur les frontières.

On observe que u_c 0.18m.s-¹ ce qui signifie qu'au dessus de cette valeur le modèle peut être instable.

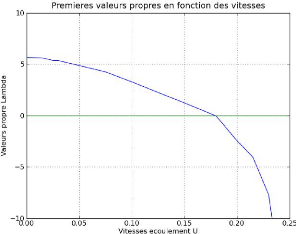
FIGURE 6.45 - Courbe des valeurs propres en fonction des vitesses

FIGURE 6.46 - Step 1-2 : couplage avec les vagues

FIGURE 6.47 - Step 3-4 : couplage avec les vagues

Pour le domaine contenant un sous-marin.

Les simulations numériques que nous présentons dans cette section sont très similaires aux précedentes, la différence majeure étant que la structure immergée est remplacée par un sous-marin.

Ainsi, nous avons les figures suivantes :

FIGURE 6.48 - Step 5-6 : couplage avec les vagues

Nous observons sur les premières figures l'apparition des ondes de surface

81

FIGURE 6.49 - Step 7-8 : couplage avec les vagues

FIGURE 6.50 - Step 7-8 : couplage avec les vagues

FIGURE 6.51 - Step 11-12 : couplage avec les vagues

FIGURE 6.52 - Step 9-10 : couplage avec les vagues

FIGURE 6.53 - Step 15-16 : couplage avec les vagues FIGURE 6.54 - Step 17-18 : couplage avec les vagues FIGURE 6.55 - Step 11-12 : couplage avec les vagues FIGURE 6.56 - Step 21-22 : couplage avec les vagues

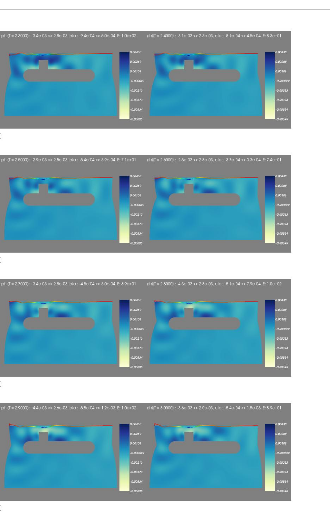
FIGURE 6.57 - Step 13-14 : couplage avec les vagues FIGURE 6.58 - Step 25-26 : couplage avec les vagues FIGURE 6.59 - Step 15-16 : couplage avec les vagues FIGURE 6.60 - Step 29-30 : couplage avec les vagues

FIGURE 6.61 - Step 31-32 : couplage avec les vagues FIGURE 6.62 - Step 17-18 : couplage avec les vagues FIGURE 6.63 - Step 19-20 : couplage avec les vagues FIGURE 6.64 - Step 37-38 : couplage avec les vagues

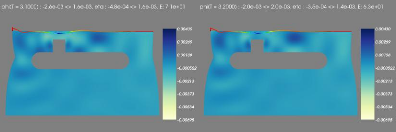
85

FIGURE 6.65 - Step 21-22 : couplage avec les vagues FIGURE 6.66 - Step 41-42 : couplage avec les vagues FIGURE 6.67 - Step 23-24 : couplage avec les vagues FIGURE 6.68 - Step 45-46 : couplage avec les vagues

86 Chapitre 6. Résultats numériques

FIGURE 6.69 - Step 25-26 : couplage avec les vagues
FIGURE 6.70 - Step 49-50 : couplage avec les vagues

Conclusion

Ici encore les résultats sont concluantes et sont presques analogues à ceux obtenus dans la simulation précedente.

En effet, on observe les sillages hydrodynamiques autour du sous-marin
et les vagues à la surface, ce qui semble correct du point de vue physique.

6.0.9 Stabilité du modèle : modes propres

Nous nous intéressons au problème des valeurs propres obtenu à partir de l'opérateur de raideur K(.,.), qui consiste à :

? ?? ??

trouver (A, X) E R x H^1(Ù) x H^1(s) tel que : (K0 + U K1 - U^2 K2)X = AX,

C'est une équation matricielle du second ordre en U, avec

_{Z Z Z}

K0 = c2 Ù Vq(x)
· Vp(x)dx + gc² ij(s)v(s)ds + aa V_sij(s)
· V_sv(s)ds,

f f _{s s}

_{Z Z}

K1 = c² V_sq(s)v(s)ds - c² V_sij(s)p(s)ds,

f f

Z _{s s}

K2 = c2 Ù Vq(x)
· Vp(x)dx. f

On a tracé plusieurs courbes en fonction de U

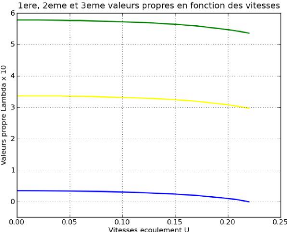
FIGURE 6.71 - Courbe des valeurs propres en fonction des vitesses

D

Ans ce travail d'ingénieur, nous nous sommes intéressés de la modélisation d'une condition aux limites transparentes pour un écoulement

transitoire permetttant de mettre en oeuvre un modèle de simulation hydrodynamique de sillage de bateau en milieu infini.

L'intérêt de ce travail est de permettre une modélisation non-lineaire du comportement de la surface de l'eau tout en évitant les phénomènes de réflections d'ondes qui apparaissent habituellement lorsqu'on utilise une modélisation classique, sur un ouvert de calcul borné.

Pour réaliser cette étude nous avons suivi la démarche suivante :

- tout d'abord, une modélisation mathématique du problème acoustique en écoulement uniforme et du modèle de Kelvin-Neumann en prenant en compte la capillarité, la gravité et pression de l'eau, a été établie.

- Puis une analyse mathématique de la condition aux limites transpar-
entes sur les frontières verticales en amont et en aval a été réalisée.

- Enfin, la simulation numérique du modèle fluide-vague à la surface avec une condition aux limites transparentes sur les frontières a été mise en oeuvre.

Nous avons appliqué cette méthode aux problèmes de la propaga-

tion acoustique dans un domaine contenant de l'eau en écoulement uniforme dans lequel est immergé une structure à section constante. Une formulation variationnelle du problème considéré avec la condition aux limites transparentes sur les frontières optimales du domaine a été faite. Ensuite l'existence et l'unicité de la solution de ce problème sont établies en fonction de la vitesse critique.

Une approche numérique a enfin été présentée. Dans un premier temps, nous avons considéré une structure à section symétrique (une ellipse) pour vérifier nos modèles puis nous avons élargi le problème à un sous-marin. Cette approche numérique a permis d'une part, dans le cadre du problème couplé de mettre en évidence les phénomènes suivants :

- les ondes de surfaces qui apparaissent grâce d'une part à la pesanteur qui tend à maintenir l'interface air-eau horizontale et d'autre part la tension de surface qui tend à maintenir l'interface plane.

- Le phénomène de non réflection d'onde en amont et en aval de l'é-

coulement , ce qui se traduit le comportement à l'infini de l'onde.
D'autre part de montrer que le système est stable tant que la vitesse

de l'écoulement est inférieure à la vitesse dite critique.

Enfin, Une seconde poursuite à ce travail pourrait évidemment porter
sur l'extension au cas tridimensionnel. Cela nécessitera en particulier la

généralisation de ces résultats à un écoulement non uniforme sur des domaines de différentes configurations.

Il serait également intéressant d'étendre ces résultats au cas d'un bateau de surface avec tossage (Th. Gazzola [13]).

8

ANNEXE

8.1 RAppEL DEs OutiLs mAthémAtiquEs Les espaces fonctionnels

Commençons par rappeler les définitions classiques des espaces fonctionnels les plus courants.

Nous noterons Ù un ouvert borné de IRⁿ (n = 1,2, ou 3). Sa frontière est désignée par ?Ù et supposée au moins de classe C¹ par morceaux et globalement lipschitzienne.

- Espace de Banach L¹(Ù)

Il s'agit de l'espace des fonctions à valeurs réelles, mesurables au sens de Lebesgue sur l'ouvert Ù et dont l'intégrale du module sur Ù est finie.

L¹(Ù) = {v : Ù ? Rⁿ mesurable / I| v| (x)dx < 8}

ca

Cet espace est muni de la norme :

v ? L¹ (Ù)

ilvil0,1,Ù = f

?

_ca |v|(x)dx

- Espace L²(Ù)

Il s'agit de l'espace des fonctions à valeurs réelles, mesurables au sens de Lebesgue sur l'ouvert Ù et dont l'intégrale du carré du module est finie sur Ù.

L²(Ù) = {v : Ù ? Rⁿ mesurable / I|v(x)|²dx < 8}

ca

Cet espace est un espace de Hilbert muni du produit scalaire :

u, v ? L²(Ù) ? (u, v)0,Ù = I

_cu(x)v(x)dx

et dont la norme associée est :

v ? L²(Ù) ? 11v110,Ù = (I_. |v(x)|²dx)^12.

- Espace H^k(Ù)

On désigne par H^k(Ù) l'espace de Sobolev d'ordre k définit par : H^k(Ù) = {v ? L²(Ù)/D^áv ? L²(Ù), |á| < k}

où D^áv est la dérivée de v au sens de distributions . De plus on notera

H^k₀(Ù) = {v ? H^k(Ù)/v = 0 sur ?Ù}

- Espace H¹(Ù) Il est défini par :

H¹(Ù) = {v/v ? L²(Ù)/ ?kv ? L²(Ù)}

où ?k est la dérivée partielle par rapport à xk et est muni de la norme :

v ? H¹(Ù), ? kvk1,Ù = {lv1²0,Ù + ? k?kvk2 0,Ù}1 2

k=1,n

C'est un espace de Hilbert dont le produit scalaire est :

u, v ? H¹(Ù) = f u(x)v(x)dx + ? f ?ku(x)?kv(x)dx

k=1,n

On a, aussi l'espace : - Espace H²(Ù)

Il est défini par :

H²(Ù) = {v/v ? H¹(Ù) / ?ikv ? L²(Ù) i, k ? {1,2,3}} Théorème de trace

Dans la mesure où nous cherchons à étudier des problèmes aux limites, nous aurons besoin de connaître le comportement des fonctions de H¹(Ù) au voisinage du bord de Ù.

Il n'est pas évident que cette question ait un sens les fonctions de L¹(Ù) sont définies presque partout.

Or le bord est une « variété »de dimension n - 1 si Ù ? IRⁿ.

Disons simplement que dans le cas qui nous intéresse, il s'agit de la généralisation d'une surface dans 1R³.

En particulier, est de mesure nulle, et il n'est pas possible de définir la restriction d'une fonction quelconque de L²(Ù) à .

Toutefois, la régularité supplémentaire des fonctions de H¹(Ù) permet de définir cette restriction. Plus précisément, nous avons le résultat suivant. Théorème de trace

Soit Ù un ouvert borné régulier, de frontière . On définit l'application trace ã0 :

H¹(Ù) n C(Ù) ? L²() n C()

v ? ã0(v) = v (8.1)

Cette application se prolonge par continuité en une application linéaire continue de H¹(Ù) dans L²(), encore notée ã0.

En particulier, il existe une constante c > 0 telle que, pour toute fonction v ? H¹(Ù), on a

Iv/IL²() = cIvIH¹(Ù) (8.2)

Il est naturel de vouloir identifier le noyau de l'application trace ã0, noté usuellement H¹0(Ù).

En effet, H¹0(Ù) est le sous-espace des fonctions de H¹(Ù) «qui s'annulent sur le bord ».

H¹0(Ù) = {v/v ? H¹(Ù)/ v=0 sur }

C'est un espace de Hilbert, muni de la semi-norme définie sur H¹0(Ù)

par :

_Z

2

|v|H1 0(Ù) = ( _Ù |rv(x)|2dx)1

qui est une norme sur H¹0(Ù) ,équivalente à la norme de H¹(Ù) Théorème de Green

Le flux d'un champs de vecteurs, sortant d'une surface fermée S, est égal à l'intégrale de la divergence de ce champ étendue au volume Ù limité par S :

ZS

Vnds = I _Ù div(V)dv (Stokes)

LEMME DE GREEN

Soient u,v deux fonctions telles que u ? H²(Ù) et v ? H¹(Ù). On a alors

ZÙ

_{Z Z}

Äuv = (8.3)

?Ù v?u

?í - Ù ru.rv,

où ?í désigne la dérivée normale le long de la frontière ?Ù de l'ouvert ?

Ù.

Théorème de Reynolds

La formule de Leibniz permet de différencier par rapport au temps des intégrales, dont les bornes sont fonctions du temps.

En dimension un, cette formule s'écrit :

Z b(t) Z b(t)

d ? f (x, t)

a(t) f (x, t)dx = ?t dx + f (b(t))^db

dt - f (a(t))^da

dt a(t) dt

Elle se généralise à des intégrales multiples (c'est-à-dire des intégrales sur des volumes au lieu d'intégrales sur des intervalles).

On obtient la relation suivante appelée « théorème de transport».

_{Z Z Z}

d ? f

V f dV = ?t dV + _S f u.ídS, (8.4)

dt V

- où V est un volume de contrôle contenant une certaine masse de fluide,

- S est la surface enveloppant ce volume,

- et v est la normale à la surface S,

- la normale v est unitaire (|v| = 1) et orientée vers l'extérieur. Cette relation peut s'interpréter de la façon suivante :

La variation temporelle d'une quantité f définie sur un volume de contrôle V est égale à la somme de :

1. la variation de f au cours du temps au sein du volume de contrôle (variation dite locale);

2. le flux de f à travers la surface S enveloppant le volume de contrôle ( flux = ce qui entre - ce qui sort de V).

Autre formulation du théorème de transport en utilisant le théorème de Green-Ostrogradski :

d fdV = I (a + (2.4.2)

d t iv v at (8.5)

Théorème de Lax-Milgram

Soit V un espace de Hilbert réel dont la norme est notée k.kV et a(.,.) une forme bilinéaire sur V vérifiant :

i- Continuité : ?M > 0, ?u, v ? V, |a(u, v)| = MIulVIvIV,

ii- V-coercivité : ?a > 0, ?v ? V, a(v, v) = aIvI²_V

Alors pour tout forme linéaire continue sur l'espace V (c'est-a-dire dans l'espace dual V^' de V ), notée l , il existe une solution unique u dans V du modèle variationnel suivant :

?v ? V, a(u, v) = l(v).

En outre nous avons l'inégalité suivante :

.

klk_V0

kukV = a

oil la norme sur V^I est définie par :

IlvIlV^.

11l11v = supv?V l(v)

Théorème spectral

Soient :

- a(., .) une forme bilinéaire symétrique positive et équivalente au carré de la norme sur un espace de Hilbert V,

- m(., .) une forme bilinéaire symétrique positive et équivalente au carré de la norme sur un espace de Hilbert H.

On considère le problème de valeurs propres :

(u, A) ? V × IR, ?v ? V, a(u, v) = Am(u, v), m(u, u) = 1.

8.2 EQuATioNs DE LA mécANiQuE DEs fLuiDEs

Les lois de la mécanique s'écrivent selon le type de description choisie, mais elles expriment les mêmes principes. Ces principes sont au nombre de trois :

- la masse se conserve;

- la variation de quantité de mouvement (masse× vitesse) est égale à la somme des forces appliquées ;

- l'énergie totale se conserve : c'est le premier principe de la thermodynamique.

Nous ferons un rappel de ces principes pour des systèmes fluides. Il existe une multitude de formulations possible du mème principe :

- formulation sur un volume de contrôle (formulation dite globale ou intégrale) ou bien pour un volume infinitésimal (équation dite local);

- formulation sur des volumes de contrôle ouverts ou fermés. Cette multitude s'avère fort pratique car cela permet une meilleure compréhension physique et une résolution plus simple des problèmes.

Conservation de la masse

On applique le théorème de transport (8.4) à la fonction scalaire : f =

ñ.

On déduit :

d t ap(x, t)

_jvñdV = iv ?t dV + I ñu.ídS,

d

avec V un volume matériel et la la surface enveloppant ce volume. En

utilisant le théorème de la divergence (Théorème de Green), on tire :

Z d

dtV v t ñdV = I_a

₍?ñ(x, t)

+ div(ñu))dV,

De plus, si ñ est continue, alors on a l'équation de conservation local de la masse (ou équation de continuité) :

?ñ(x, t)

+ div(ñu) = 0. (8.6)

?t

Conservation de la quantité de mouvement

On applique a nouveau le théorème de transport (8.4) à la fonction vectorielle représentant la quantité de mouvement local : f = ñu.

d t v

_jvñudV = I ^?ñ_at^udV + I ñu(u.í)dS.

d

En utilisant le théorème de la divergence, on obtient :

d t

_jv I pudV = (^?ñ_at^u + div(ñu.u))dV,

d

et en utilisant l'equation de continuite on obtient :

dt

ipudV = I p(^?u + div(uu))dV. v v ?t
Le principe fondamental de la dynamique montre que toute variaton de

quantite de mouvement resulte de l'application de forces. Donc, on peut ecrire une relation generale de la forme :

d

dt _jV ñudV = mg |{z}

poids

is ódS

force de surface

= I ñgdS + I E.ndS.

- ó = E.n designe la contrainte,

- et E le tenseur des contraintes qui se decompose en tenseur des pressions -pId et tenseur des extra-contraintes T :

E = -pId + T, avec Id tenseur identite.

Le tenseur T depend de la nature du fluide etudie ou du niveau d'approximation :

- T= 0 correspond au cas des fluides parfaits (ou non visqueux),

- T= 2uD correspond au cas des fluides newtoniens,

- T= g^-(D) correspond au cas des fluides non newtoniens, avec g^- la loi du comportement du fluide.

Et une application de Theorème de Green-Ostrogradski, permet d'aboutir à la formulation locale des equations de la quantite de mouvement :

?ñu

?t

+ div(ñu.u) = ñg - Vp + div(T), (8.7)

ou bien :

?u

ñ ?t + ñuvu = ñg - Vp + div(T).

Conservation de l'énergie

Pour l'energie, rappelons que le premier principe de la thermodynamique enonce que l'energie totale E varie au cours du temps, à cause du travail des forces exterieures et du flux de chaleur :

äE

ät =

äQ ät .

äW + ät

avec :

- SE = (k + pe) : la variation d'énergie totale, c'est-à-dire l'intégrale sur le volume de contrôle de l'énergie cinétique k et de l'énergie interne pe ( e étant l'énergie interne massique );

- Sw : le travail des forces extérieures au sein du volume de contrôle,

- SQ = jQ = -KV'T : la quantité de chaleur à travers la surface de contrôle S , et K la conductibilité thermique T la température,

- St : incrément de temps En faisant tendre St vers 0 , on obtient :

. (8.9)

dt f_v(k + pe)dV = I pg.udV + f o-.udS - f jQ.vdS

s | {z 0.
· | _{z }

Qÿ

Wÿ

La puissance des forces extérieures comprend des termes positifs (puissances fournie au volume de contrôle) et négatifs (puissance dissipée au sein du volume ou aux frontières) :

_Z

+

S

pg.udV

ZW^ÿ =

| _{z }

V

puissances fournies au volume V

o^-.udS

| _{z }

puissances dissipées aux frontières et dans V

Par définition de la contrainte via le tenseur des contraintes E , on a o^- = E.v = (-pId + T).v = -pn + T.v,

ce qui permet d'écrire

ZV pg.udV + I u.(-pn + T.v)dS,

pg.udV + I (-pu + T.u).vdS,.

Wÿ =

=

ZV

Et la formulation du premier principe de la thermodynamique est donc le suivant :

dt _iv(k + pe)dV = I pg.udV + I (-pu + T.u - jQ).vdS,

L'application du théorème de Stokes fournit immédiatement

dt _iV(k + pe)dV = I pg.udV + I div(-pu + T.u - jQ)dV,

Et on , obtient finalement l'équation locale de conservation de l'énergie totale :

d(k + pe) dt

= pg.u + div(-pu + T.u - jQ). (8.10)

BIBLIOGRAPHIE

[1] L. KELVIN (SIR THOMSON), On the waves produced by a single input in water of any depth, or in a dispersive medium, Proc. Roy.Soc. Lond. A 42 (1887), pp. 80-85.

[2] M. LIVSHITS AND V. MAZ'YA, Solvability of the two-dimensional Neumann-Kelvin's problem for a submerged circular cylinder, Appl.Anal.64(1997), pp.1-5.

[3] J.J. STOKER, Water Waves, Pure and Applied mathematics, Vol.IV, inter Science publishers, Inc., New York, 1957

[4] Y. DOUTRELEAU, Résonances pour le problème de Neumann-Kelvin tridimensionnel dans le cas d'un corps immergé, 5th Journ de l'Hydrodynamique, Rouen, Mars,1995.

[5] X. CHEN, On the singular and highly oscillatory properties of the Green function for ship motions, J. Fluid Mechs. 445(2001), pp.77-91.

[6] E.F CAMPANA AND A. IAFRATI, Direct numerical simulation of surface tension dominated and non-dominated breaking waves, 24th Symposium on Naval Hydrodynamics, Fukuoka, Japan, July 2002.

[7] D.S. MOAK, The q-analogue of the Laguerre polynomials, J. Math. Anal. Appl. 81(1981), pp.20-47.

[8] PH. DESTUYNDER AND C. FABRE, A modelling of springing, whipping and slamming for ships, Commun. Pure Appl. Anal. 8(1)(2008), pp. 209- 228.

[9] PH. DESTUYNDER AND C. FABRE, A discussion on Neumann-Kelvin's model for progressive water waves, Applicable Analysis, First published on : 30 March 2011.

[10] PH. DESTUYNDER , Vibrations des structures et des systèmes couplés, Hermès Sciense, Lavoisier, 2007.

[11] PH. DESTUYNDER , Introduction à l'Aéroélasticité et à l'Aéroacoustique, Hermès Sciense, Lavoisier, 2007.

[12] PH. DESTUYNDER , Introduction au calcul des Structures, Cours cycle C , Calcul scientifique, IAT/CNAM, 1990.

[13] TH. GAZZOLA, A. KOROBKIN, S. MALENICA, AND Y.M. SCOLAN, Three-dimensional Wagner problem using variational inequalities, Proceedings of the 20th International Workshop on Water Waves and Floating Bodies, Longyearbyen, Norway, pp. 77-81, 2005.

[14] W. ArTilEs AND A. NAcHbiN, Asymptotic nonlinear wave modeling through the Dirichlet to Neumann operateur, Methods Appl. Anal. 11(3)(2004), p.001018.

[15] D. LANNEs, Well posedness of the water waves equations, J.Amer.Math.Soc. 13(3)(2005),pp.605-654.

[16] W. CrAig AND C. SulEM, Numerical simulation of gravity waves, J. Comput. Phys. 108(1) (1993), pp. 73-83.

[17] R. CoifMAN AND Y. MEyEr, Nonlinear Harmonic Analytic and Analytic Dependence, Pseudodifferential Operators and Applications, AMS, Providence, RI, 1985.

[18] J. NEcAs, Les Méthodes Directes en Théorie des Equations Elliptiques, Masson, Paris, 1967.

[19] P. GrisvArD, Singularities in Boundary Value Problems, Masson, Paris, 1992.

[20] M. Borsuk AND V. KoNDrATiEv, Elliptic Boundary Value Problems of Second Order in Priecewise Smooth Domains, North Holland, Mathematical Library, Amsterdam, 2006.

[21] R. ADAMs, Sobolev Spaces, Academic Press, New York, 1975.

[22] J.L. LioNs AND E. MAgENEs, Problèmes aux Limites Non-homogènes et Applications, Tome 1, Dunod, Paris, 1968.

[23] G. DuvAuT, Mécanique des Milieux Continus, Dunod, Paris, 1990.

[24] L. LANDAu AND E. lifcHiTz, Mécanique des fluides, J. Eng. Math. 58(2007), pp. 121-139.

[25] P.A. RAviArT AND J.M. THoMAs, Introduction à l'Analyse Numérique des Equations aux Dérivées Partielles, Masson, Paris, 1983.

[26] X. CHEN, Role of the surface tension in modelling ship waves, in Proceedings of the 17th International Workshop on Water Waves and Floating Bodies, R.C. Rayney and S.F. Lee, eds.,Peterhouse, Cambridge, UK, 14-17 April 2002, pp. 25-28.

[27] J.L. LioNs, Quelques Méthodes de Résolution des Problèmes aux limites Non-linéaires, Dunod, Paris, 1969.

[28] K. KircHgAssNEr, Nonlinear resonant surface waves and homoclinic bifurcation, Adv.Appl. Math. 26(1988), p.135181.

[29] BATHE K.J., Finite element procedures in engineering analysis, Prentice-Hall, New-York, 1982.

[30] Bourlè H., Systèmes linéaires, Hermès, Lavoisier,2006.

[31] Brézis H., Analyse fonctionnelle, Masson, Paris, 1983.

[32] CiArlET P. G., The finite element method for elliptic problems, Elsevier, Amsterdam, 1978.

[33] CiARlET P. G., Analyse numérique matricielle et optimisation, Dunod, Paris, 1982.

[34] DuNfoRT N., SchwARz J. T., Linear operators Part II : Spectral theory, John Wiley, Londres, 1988.

[35] SchwARz L., Analyse fonctionnelle, Hermann Paris, 1969.

[36] SchwARz L., Méthodes mathématiques pour les sciences physiques, Hermann Paris, 1965.

[37] B. ENgquisT AND MAjDA., Absorbing boundary conditions for the numerical simulation of waves, Maths. Comp,31(139) : 629-651, 1977.

[38] RoBERT L. HigDoN, Absorbing boundary conditions for difference approximations to the muldimensional wave equation,Math. Comp 47(176) : 437- 459, 1986.

Ce document a été préparé aide de l'éditeur de texte Gedit et du logiciel de
composition typographique LATEX 2å.

Titre Conditions aux limites transparentes et modélisation des vagues de surface dans un écoulement.

Résumé Dans ce travail, nous présentons une formulation de condition aux limites transparentes permettant de réaliser la simulation hydrodynamique de sillage de bateau en milieu infini.

L'intérêt est de permettre une modélisation linéaire transitoire du comportement de la surface de l'eau, tout en évitant les phénomènes de réflections d'ondes qui apparaissent habituellement lorsqu'on utilise une modélisation classique, sur un ouvert de calcul borné. Par ailleurs, la méthode des équations intégrales qui est utilisée dans la plupart des codes industriels, ne permet pas de traiter ces aspects transitoire de façon satisfaisante et nécessitent des hypothèses simplificatrices incompatibles avec une représentation des phénomènes physiques en présences.

Les difficultés sont multiples : d'une part, le modèle linéaire est naturellement instable et seule la présence de termes non-linéaires à la surface de l'eau permet éventuellement de les stabiliser. D'autre part, il apparait trois types d'ondes couplés (ondes de gravité, ondes acoustique, et ondes de capillarité), ce qui rend la méthode intégrale très délicate. En outre, la grande disparité des vitesses d'ondes et de celle du bateau conduit à des difficultés numériques, qui nécessite l'utilisation d'un schéma d'intégration en temps adapté ne dissimulant pas l'un des mécanismes en présence.

Mots-clés Conditions limites transparentes, ondes de capillarité, vagues progressives, instabilite surface, interaction fluide-fluide, schéma numérique.

Title Transparent boundary conditions and wave modeling surface in a flow.

Abstract In this paper, we present a formulation of transparent boundary condition for achieving the hydrodynamic simulation of wake boat in an infinite medium. The interest is to allow a linear modeling of transient behavior of the surface of the water, while avoiding the phenomena of wave reflections that usually appear when using a classical model, on an open bounded computation. Moreover, the method of integral equations is used in most industrial codes, does not address them satisfactorily transient and require simplifying assumptions inconsistent with a representation of physical phenomena involved. The challenges are multiple: first, the linear model is naturally unstable and only the presence of nonlinear terms on the surface of water can eventually stabilize. On the other hand, it appears three types of coupled waves (gravity waves, acoustic waves and capillary waves), which makes the integral method very difficult. In addition, the wide disparity of wave speeds and that the ship led to numerical difficulties, which requires the use of a time integration scheme suitable not concealing one of the mechanisms presence.