|
UNIVERSITE ADVENTISTE DE LUKANGA
(UNILUK)
B.P. 180
BUTEMBO, NORD-KIVU
REPUBLIQUE DEMOCRATIQUE DU CONGO

FACULTE DES SCIENCES ECONOMIQUES ET DE
GESTION
DEPARTEMENT DE GESTION INFORMATIQUE
OPTIMISATION HEURISTIQUE DU PROBLEME
D'ENTREPOSAGE
D'OBJETS EN TROIS
DIMENSIONS
par :
RUHAMYA MULINDWA Chirac
Mémoire présenté et
défendu en vue de l'obtention du grade de Licencié en Sciences
économiques et de gestion
Option : Gestion Informatique Directeur
: Dr. Osée M. MASIVI
Année académique : 2012/2013

i
Epigraphe
`' Souvent le monde de l'industrie préfère une
réponse approximative mais rapide et
efficace plutôt qu'une
réponse parfaite »
Anonyme
`' La connaissance commence par la tension entre savoir et
non-savoir : -pas de
problème sans savoir -pas de problème
sans non-savoir »
Popper, 1979
`' Les ordinateurs sont comme les dieux de l'Ancien Testament :
avec beaucoup de règles, et sans pitié `'
Joseph Campbell
ii
DEDICACE
A mes chers parents ;
A toute ma Famille proche ;
A tous ceux qui m'ont soutenu et témoigné leur
amour ;
Chirac RUHAMYA MULINDWA
REMERCIEMENTS
Personne ne peut tout faire seul. Sans le concours de bien de
gens de bonne foi, nous ne serions pas là où nous sommes
aujourd'hui. De ce fait, nous serons ingrat de finir ce modeste travail sans
remercier tout effort autre que le nôtre à avoir concouru à
la réussite de ce mémoire.
Je tiens tout d'abord à remercier Mr. le Docteur
Osée MUHINDO MASIVI. Je le remercie pour l'intérêt qu'il a
porté à mon travail, pour toutes ces discussions scientifiques et
autres, qui m'ont permis d'avancer dans mes travaux, qui m'ont fait
réfléchir et qui m'ont inspiré. Je voudrais encore le
remercier infiniment pour avoir accepté d'être le directeur de ce
travail de recherche.
Toute ma gratitude s'adresse à la famille RUHAMYA car
c'est grâce à son soutient, sa patience et son amour que je suis
là aujourd'hui. Je n'oublierais pas tous mes oncles, frères,
soeurs, neveux et cousins pour les sacrifices qu'ils ont pu faire pendant mes
longues années d'études et d'absence.
Aux camarades étudiants, compagnons de lutte avec qui
nous avons partagé peines et joies, nous disons également merci
pour l'ambiance chaleureuse de travail qu'ils maintiennent au quotidien.
Ce travail ne serait pas ce qu'il est sans la présence,
la générosité, l'enthousiasme et les précieux
conseils de tous mes amis dont je ne pourrais lister les noms qui m'ont
toujours encouragés, soutenus et permis de travailler dans les
meilleures conditions.
iii
Chirac RUHAMYA MULINDWA
iv
SIGLES ET ABBREVIATIONS
1D : Une dimension
2D : Deux dimensions
3D : Trois dimensions
3DBPP : 3D Bin Packing Problem
HI-BHA : Human Intelligence Based on a Heuristic Approach
IDE : Integrated Development Environment
LAFF : Largest Area First-Fit
NP : Non Determinist Polynomial
NP-C : Non Determinist Polynomial Complete
OUT : Output File
SI : Système d'information
v
TABLE DES MATIERES
Epigraphe i
DEDICACE ii
REMERCIEMENTS iii
SIGLES ET ABBREVIATIONS iv
TABLE DES MATIERES v
LISTE DES FIGURES vii
LISTE DES TABLEAUX vii
RESUME viii
ABSTRACT ix
INTRODUCTION GENERALE 1
0. Problématique de recherche 1
1. But et Objectif de recherche 3
2. Choix et intérêt du travail 4
3. Délimitation du sujet 4
4. Méthodes et technique de recherche 5
5. Subdivision du travail 5
Chapitre premier : REVUE DE LA LITTERATURE 7
I.1. Optimisation 7
I.2. Entrepôt et Entreposage 12
I.3. Les objets 12
I.3.1. Objet en une dimension 13
I.3.2. Objet en deux dimensions 13
I.3.3. Objet en trois dimensions 13
I.4. Quelques travaux de recherche étudiés 14
I.5. Conclusion partielle 16
Chapitre deuxième : METHODOLOGIE DU TRAVAIL 17
II.1.Methode Algorithmique 17
vi
II.1.1. Problèmes algorithmiques 17
II.1.2. Classes de Complexité 18
II.2. Le Prototypage 20
II.3. L'Expérimentation 20
II.4. L'Argumentation 21
Chapitre Troisième : APPROCHES METHODOLOGIQUES 22
III.1. Modélisation algorithmique du problème de
3DBP 22
III.1.1. Formulation du problème 22
III.1.2. Méthodes exactes 24
III.1.3. Méthodes approximatives (heuristiques) 26
Chapitre Quatrième : PROTOTYPAGE, EXPERIMENTATION ET
ARGUMENTATION
DES RESULTATS 42
VI.1. Prototypage 42
VI.1.1. Les fonctions du programme 42
IV.1.2. Formulaire d'entrées des données 45
IV.1.3. Les rapports 46
IV.2. Expérimentation et Argumentation 49
IV.2.1. Environnement de travail 49
IV.2.2. Données de test 50
IV.2.3. Résultat de l'algorithme HI-BHA 50
IV.2.4. Argumentation sur les résultats de l'algorithme
HI-BHA 51
IV.3. DIFFICULTES RENCONTREES 52
CONCLUSION 53
BIBLIOGRAPHIE 55
ANNEXES 56
vii
LISTE DES FIGURES
Figure 1 : exemple d'un objet en une dimension 13
Figure 2 : exemple d'un objet en deux dimensions 13
Figure 3 : exemple d'un objet en trois dimensions 14
Figure 4 : Dimensions d'articles commerciaux qui nous
intéressent. 23
Figure 5 : Ordinogramme de l'algorithme HI-BHA 32
Figure 6 : Première méthode de placement des
boîtes avec LAFF 38
Figure 7 : seconde méthode de placement des boîtes
avec LAFF 39
Figure 8 : solution possible avec LAFF 40
Figure 9 : Paramètres de la fonction FindBox() 43
Figure 10 : Fichier des variables entrantes 45
Figure 11 : Fenêtre console avant exécution du
programme 46
Figure 12 : Fenêtre après exécution du
programme 47
Figure 13 : fichier `'Rapport de la meilleure solution du
programme`' 48
Figure 14 : Fichier des variables entrantes de l'interface
graphique du programme 49
LISTE DES TABLEAUX
Tableau 1 : Liste des champs dans le `'BoxList[] Array `' 28
Tableau 2 : Liste de champs dans le `'Layers[] Array `'. 29
Tableau 3 : Création du tableau BOXLIST[] 32
Tableau 4 : Création du tableau Layers[] 34
Tableau 5 : les fonctions de l'algorithme HI-BHA 42
Tableau 6 : Résultat du test de l'algorithme HI-BHA
51
RESUME
L'obtention d'une grande surface pour l'entreposage des
produits est un facteur très important pour les entreprises. De nos
jours, la plus part d'entreprises commerciales et industrielles dispose des
espaces de stockage qui valent la peine d'être utilisé avec
délicatesse. Dans ce travail nous traitons le problème de
maximisation de l'utilisation d'espaces de stockage tridimensionnels par les
articles en trois dimensions. Nous faisons allusion dans ce travail aux
entrepôts et articles possédant chacun une longueur, une largeur
et une hauteur. L'objectif est d'utiliser de la meilleure façon possible
l'espace de stockage disponible.
Ce problème étant du type NP-C, nous avons
utilisé un heuristique pour le résoudre vu que l'algorithme
exacte exigerait plus de ressources temporelles. Pour résoudre ce
problème, nous avons utilisé l'algorithme `'Human Intelligence
Based on Heuristic Approach`', ce modèle nous a permis de trouver une
réponse près de l'optimum en temps raisonnable. Nous avons
ensuite implémenté cet algorithme en langage C. Le test et
l'argumentation des résultats nous ont permis de vérifier notre
objectif que nous avons jugé atteint.
viii
Mots clés : 3D Bin packing, Heuristiques,
optimisation combinatoire, Entreposage.
ix
ABSTRACT
Getting more space for storage of products is a very important
factor for the companies. Nowadays, more commercial and industrial companies
have spaces for storage of goods that are to be used tactfully. This study
addresses the problem of maximization of the three dimensional storage spaces
of three dimensions sized goods. This study considers length, width and height
of each article. The objective is to maximize used volume and minimize wasted
space.
In order to resolve this problem a heuristic method is
applied, since the exact algorithm would require more temporal resources. The
"Human Intelligence Based on Heuristic Approach" algorithm is applied. This
model lead to an answer close to the optimum in reasonable time. Then the
algorithm is implemented in C language. The test and argumentations of results
permitted to verify objective set for the study.
Keywords: 3D Bin packing problem, Heuristics,
combinatorial optimization, storage
INTRODUCTION GENERALE
0. Problématique de recherche
`' On assiste aujourd'hui à l'émergence d'une
nouvelle économie dite de l'information ou « Nouvelle
économie », où le travail en rapport avec l'information est
devenu plus important que le travail en rapport avec les autres secteurs. Ceci
sous-entend donc la mise en place d'un système représentant
l'ensemble des ressources (les hommes, le matériel, les logiciels)
utilisées pour collecter, stocker, traiter et communiquer les
informations au sein de l'entreprise : « Le système d'information
(SI) » de l'entreprise `' (Sanni, 2009). Les Systèmes d'information
peuvent mettre en jeu le succès et même la survie de l'entreprise,
par conséquent une gestion saine des systèmes d'information
constitue un défi pour les dirigeants. A nos jours, La croissance d'une
entreprise passe forcément par un grand volume d'activités et
donc une grande quantité d'informations à gérer et dont il
faudra tirer le meilleur parti pour prendre les bonnes décisions.
L'entreposage des marchandises est une des principales
tâches du commerce et de l'industrie. Afin qu'ils comprennent toutes les
connexions du flux des marchandises, les commerçants ainsi que les
industriels doivent disposer des connaissances de base à tous les
niveaux, même si les différentes activités sont
exécutées par des spécialistes. En effet, les
différentes compagnies et entreprises fournissent de grands efforts dans
le but de détecter des possibilités de réduction des
coûts associés aux entreposages de tous les produits
(Matières première, produits semi-ouvrés et
2
produits finis). C'est dans cette optique qu'une optimisation
d'entreposage d'articles tridimensionnels dans des aires de stockage permettra
sûrement aux entreprises tant commerciales qu'industrielles de
réduire au maximum les coûts liés au stockage des produits
(coûts de l'entrepôt ou de l'espace, coût des marchandises,
coûts des machines et autres instruments de travail utilisés,...),
ce qui engendra une amélioration de profits pour enfin rester flexible
et compétitive sur un marché ouvert.
En effet, la minimisation d'espaces d'entreposage peut induire
à la réduction des coûts liés aux investissements en
espace de stockage, à l'amortissement pour la dépréciation
des espaces de stockage, aux primes d'assurances des entrepôts, à
l'approvisionnement et entretien des équipements, à la
réduction des temps morts ou mouvements inutiles durant le processus de
déchargement, de stockage et des chargement des entrepôts et
à l'organisation du rangement des marchandises reçues. En effet,
pour être compétitif, les entreprises doivent baisser au maximum
l'ensemble des coûts liés à ses services.
Apparemment le problème d'optimisation d'entreposage
d'articles que nous tentons de modéliser fait partie de la classe des
problèmes NP-Difficile, il nous semble que c'est un problème qui
ne peut donc pas être résolu à l'aide d'un algorithme de
complexité polynomiale. En effet, ce problème peut être
rattaché au problème classique de remplissage de panier
appelé communément problème de Bin packing. Ce
problème relève de la recherche opérationnelle et de
l'optimisation combinatoire. Il s'agit en fait de trouver le rangement le plus
économique possible pour un ensemble d'articles dans des boîtes.
Le problème classique se définit en une dimension.
De ce fait, le travail se base sur les interrogations
suivantes :
3
- Existe-t-il les algorithmes exactes et les heuristique
pouvant être utilisés pour : assurer un meilleur entreposage de
marchandises, minimiser les retards et augmenter les capacités de
stockage des entrepôts ?
- Et, quel est l'algorithme le plus effectif en termes de
complexité temporelle et spatiale pour résoudre notre
problème ?
Toutes ces questions se posent au niveau des
différentes activités s'exerçant dans des entreprises
disposant des locaux d'entreposage, et constituent des objectifs soucieux des
théoriciens, praticiens et également les responsables de la
gestion de stock.
1. But et Objectif de recherche
Notre but dans la réalisation de ce travail de
recherche est de répondre à la question posée ci-haut dans
notre problématique, c'est-à-dire, de trouver une ou plusieurs
méthode capable de modéliser et résoudre le
problème lié à l'optimisation d'objets tridimensionnels
dans des aires de stockage le plus effectivement possible. A la fin de ce
travail nous devons aussi mettre en place un logiciel informatique
d'entreposage d'objets en 3 dimensions.
Vu notre hypothèse de croire que le problème qui
nous intéresse ici est une variante du problème de bin packing en
trois dimensions, notre objectif principal est de : trouver l'algorithme le
plus effectif au problème d'entreposage d'objet en 3 dimensions et
capable de fournir des solutions réalisables de qualité
acceptable, proches de l'optimal et déterminées en un temps
raisonnable (complexité polynomiale).
En tant qu'objectifs spécifiques, nous tenterons de
:
- Lister un ou plusieurs algorithmes exactes pour les
problèmes de même nature que le nôtre ;
4
- Trouver et analyser les heuristiques capables de
résoudre notre problème en temps raisonnable ;
- Après que nous aurons jugé ces algorithmes
optimaux, nous pourront traduire un de ces algorithmes en logiciel
d'application pouvant représenter une potentialité
d'amélioration intéressante.
2. Choix et intérêt du travail
Toute entreprise aspire à l'amélioration de sa
trésorerie pour diverses raisons dont l'augmentation de sa
capacité d'autofinancement. En vue d'aider nos entreprises nous avons
jugé faire ce qui est à nos pouvoir pour contribuer à
l'atteinte de cet objectif ; et c'est ainsi que nous avons eu l'idée de
mettre à la disposition de tout responsable de la gestion des stocks cet
outils qui pourra leur permettre de réduire les difficultés
qu'ils rencontrent face au rangement des articles dans des entrepôts et
la maximisation des espaces à utiliser.
Le choix de ce sujet a été motivé par
notre souci de guider les prises de décisions des entreprises
congolaises en particulier, et ceux de partout ailleurs en
générale, quant à l'utilisation efficace des ressources
toujours limitées qu'ont les entreprises, en vue d'accroître leurs
niveaux d'activité.
3. Délimitation du sujet
Le monde de recherche étant assez vaste, nous
limiterons ce travail à la gestion optimum des espaces de stockage des
articles en trois dimensions dans des entrepôts afin d'en maximiser
l'usage. Nous nous contenterons donc d'étudier et appliquer quelques
heuristiques du problème classique de bin packing (remplissage de
panier) en trois dimensions.
5
4. Méthodes et technique de recherche
Aktouf, (1992) a dit que toute recherche doit en principe
aboutir à modéliser ce qu'elle a pris comme objet d'étude.
Le principe directeur qui peut y mener, c'est ce qu'il est convenu d'appeler
méthode. La méthode se définit donc, comme étant la
procédure logique d'une science ; c'est-à-dire l'ensemble de
pratiques particulières mises en oeuvre pour que le cheminement de ses
démonstrations et de ses théorisations soit clair, évident
et irréfutable. Les techniques quant à elles sont des moyens
précis pour atteindre un résultat partiel, à un niveau et
à un moment donné de la recherche. Elles ne sont que des outils
mis à la disposition du chercheur et organisées par la
méthode dans un but précis. Elles ne peuvent donc qu'être
momentanées, conjoncturelles et limitées dans le cheminement de
la recherche. La technique représente ces différentes phases
d'opérations limitées, liées à des
éléments pratiques concrets, adaptés à un but
défini, alors que la méthode est une conception intellectuelle
coordonnant un ensemble d'opération, en général plusieurs
techniques.
Comme méthode, nous utiliserons la méthode
algorithmique, ce qui nous permettra d'analyser notre problème et de
transformer les entrées (valeurs entrées par l'utilisateur) en
sorties (résultats). Les techniques documentaires nous aiderons à
récupérer la plupart des documentations sur l'internet et dans
des documents (livres, notes des cours, mémoires,...) pour nous
permettre d'aboutir à nos objectifs.
5. Subdivision du travail
Cette recherche suit une progression ordonnée. Ce
travail se décompose en effet en quatre chapitres mis à part
cette introduction et la conclusion qui viendra plus tard acheminer notre
démarche scientifique. Il s'agit de la revue de la littérature,
la méthodologie du travail, les approches méthodologiques et la
présentation et
6
discussion des résultats constitué du
prototypage, des tests et de l'argumentation des résultats.
Chapitre premier : REVUE DE LA LITTERATURE
Des nombreux chercheurs avant nous se sont
intéressés au domaine d'optimisation combinatoire, plus
particulièrement dans la conception des logiciels d'optimisation de la
coupe et entreposages des articles. Plusieurs méthodes ont
été utilisées pour résoudre ce problème.
Cette revue de littérature nous permettra de situer notre sujet par
rapport à des recherches antérieures afin d'établir un
créneau unique pour notre recherche. En plus de ça, cette partie
sera pour nous, une occasion de fournir les informations de fond en ce qui
concerne notre sujet pour comprendre les termes clés qui constituent
notre thème.
I.1. Optimisation
D'après le petit Larousse (1980), l'optimisation c'est
l'action de donner à un investissement, une entreprise ou une machine un
rendement maximale. Selon Microsoft Encarta (2008), l'optimisation est une
action de réguler (quelque chose) dans le but d'obtenir la plus grande
efficacité possible.
Pour Nzalamingi (2012), l'optimisation est une branche des
mathématiques, cherchant à analyser et à résoudre
analytiquement ou numériquement les problèmes qui consistent
à déterminer le meilleur élément d'un ensemble en
fonction d'un critère quantitatif donné. Aujourd'hui, nombreux
des systèmes susceptibles d'être décrits par un
modèle mathématique sont optimisés. Ils sont
extrêmement variés : optimisation d'un trajet, de la forme d'un
objet, d'un prix de vente, d'une réaction chimique, du contrôle
aérien, du rendement d'un appareil, du fonctionnement d'un moteur, de
la
8
gestion des lignes ferroviaires, du choix des investissements
économiques, de la construction d'un navire jusqu'à
l'optimisation des espaces de stockage et de la coupe de matériel.
L'optimisation de ces systèmes permet de trouver une configuration
idéale, d'obtenir un gain d'effort, de temps, d'argent,
d'énergie, de matière première, de satisfaction, des rebus
ou encore d'espaces. Très loin de constituer une liste exhaustive, ces
quelques exemples attestent la variété des formulations et
préfigurent la diversité des outils mathématiques
susceptibles de résoudre ces problèmes.
En termes simples et pratiques, l'optimisation des processus
consiste à améliorer les procédures d'usage et les
manières de réaliser les tâches de manière à
atteindre une productivité maximale l'entreprise. Cette optimisation
vise donc à minimiser les couts et contraintes restreignant la
productivité et à maximiser les gains favorisant
l'efficacité. Pour ce qui concerne ce travail les contraintes sont
constituées des places inutilisables dans les dépôts alors
que les gains sont constitués des place ou case bien utilisées
aux entrepôts.
La qualité des résultats et des
prédictions du système optimisé dépendent de la
pertinence du modèle, de l'efficacité de l'algorithme et des
moyens pour le traitement numérique. Et ce travail est concerné
par le modèle et l'algorithme du système de découpage et
entreposage d'article.
D'après Nzalamingi (2012), les modèles
d'optimisation sont repartis en plusieurs classes dont nous pouvons relever
:
- L'optimisation linéaire qui étudie le cas
où la fonction objectif et les contraintes caractérisant
l'ensemble de possibilités sont linéaires. C'est une
méthode très employée pour établir les programmes
des raffineries pétrolières, mais aussi pour
9
déterminer la composition la plus rentable d'un
mélange salé, sous contraintes, à partir des prix de
marché du moment.
- L'optimisation linéaire en nombres entiers
étudie les problèmes d'optimisation linéaire dans lesquels
certaines ou toutes les variables sont contraintes de prendre des valeurs
entières.
- L'optimisation quadratique étudie le cas où la
fonction objectif est une forme quadratique (avec contraintes
linéaires)
- L'optimisation non linéaire étudie le cas
général dans lequel l'objectif ou les contraintes (ou les deux)
contiennent des parties non linéaires, éventuellement
non-convexes.
- L'optimisation stochastique étudie le cas dans lequel
certaines des contraintes dépendent de variables aléatoires. En
optimisation robuste, les aléas sont supposés être
situés dans des intervalles autour de positions nominales et on cherche
à optimiser le système soumis à de tels aléas, dans
le pire des cas.
- L'optimisation combinatoire (optimisation discrète)
consiste à trouver dans un ensemble discret un parmi les meilleurs
sous-ensembles (ou solutions) réalisables, la notion de meilleure
solution étant définie par une fonction objectif.
Comme lu dans Wikimedia Foundation (2013), l'optimisation
combinatoire est en fait une branche de l'optimisation en mathématiques
appliquées et en informatique, également liée à la
recherche opérationnelle, l'algorithmique et la théorie de la
complexité. On parle également d'optimisation discrète.
Dans sa forme la plus générale, un problème
d'optimisation combinatoire (on dit aussi
d'optimisation discrète) consiste à trouver dans
un ensemble discret un parmi les meilleurs sous-ensembles (ou
solutions) réalisables, la notion de meilleure solution
étant définie par une fonction objectif. Formellement,
étant donnés :
10
- un ensemble discret N,
- une fonction d'ensemble f : 2N ?
R, dite fonction objectif, et
- un ensemble R sous-ensembles de N, dont les
éléments sont appelés les
solutions réalisables,
Un problème d'optimisation combinatoire consiste à
déterminer
L'ensemble des solutions réalisables ne saurait
être décrit par une liste exhaustive car la difficulté
réside ici précisément dans le fait que le nombre des
solutions réalisables rend son énumération impossible, ou
bien qu'il est NP-complet de dire s'il en existe ou non. La description de
R est donc implicite, il s'agit en général de la
liste, relativement courte, des propriétés des
solutions réalisables. La plupart du temps on est dans les cas
particuliers suivants :
- et R = X n Z n où X €
R n et la cardinalité de R est
exponentielle en n,
- R = conv (n) n Z n donc les
propriétés de R se traduisent en contraintes
linéaires,
c'est-à-dire que X est un polyèdre de R
n,
L' Optimisation combinatoire consiste à trouver le
meilleur entre un nombre fini de choix. Autrement dit, minimiser une fonction,
avec contraintes, sur un ensemble fini. Quand le nombre de choix est
exponentiel (par rapport à la taille du problème), mais que les
choix et les contraintes sont bien structurées, des méthodes
mathématiques doivent et peuvent intervenir, comme dans le cas " continu
", pour permettre de trouver la solution en temps polynomial (par rapport
à la taille du problème). Le travail de l'équipe consiste
à développer des algorithmes polynomiaux
11
et des théorèmes sur des structures
discrètes qui permettent de résoudre ces problèmes.
Trouver une solution optimale dans un ensemble discret et fini
est un problème facile en théorie : il suffit d'essayer toutes
les solutions, et de comparer leurs qualités pour voir la meilleure.
Cependant, en pratique, l'énumération de toutes les solutions
peut prendre trop de temps ; or, le temps de recherche de la solution optimale
est un facteur très important et c'est à cause de lui que les
problèmes d'optimisation combinatoire sont réputés si
difficiles. La théorie de la complexité donne des outils pour
mesurer ce temps de recherche. De plus, comme l'ensemble des solutions
réalisables est défini de manière implicite, il est aussi
parfois très difficile de trouver ne serait-ce qu'une solution
réalisable.
Quelques problèmes d'optimisation combinatoire peuvent
être résolus (de manière exacte) en temps polynomial par
exemple par un algorithme glouton, un algorithme de programmation dynamique ou
en montrant que le problème peut être formulé comme un
problème d'optimisation linéaire en variables réelles.
Dans la plupart des cas, le problème est NP-difficile
et, pour le résoudre, il faut faire appel à des algorithmes de
branch and bound, à l'optimisation linéaire en nombres entiers ou
encore à la programmation par contraintes. En pratique, on se contente
très souvent d'avoir une solution approchée, obtenue par une
heuristique ou une métaheuristique. Pour certains problèmes, on
peut prouver une garantie de performance, c'est-à-dire que
l'écart entre la solution obtenue et la solution optimale est
borné. Chacune de ces méthodes sera exploitée d'avantage
dans le deuxième chapitre de notre travail.
12
I.2. Entrepôt et Entreposage
`' Un entrepôt est un bâtiment logistique
destiné au stockage de biens en vue de leur expédition vers un
client (interne ou externe à l'entreprise). Il peut être
détenu et géré en propre par l'entreprise ou faire l'objet
d'une sous-traitance auprès d'un prestataire logistique `' (Wikimedia
Foundation, 2013).
La nature des biens entreposables dépend de
l'activité de l'entreprise, on trouvera : - activités de
production :
? matières premières, encours de production,
produits semi-finis destinés à la régulation du processus
de production (de l'entreprise ou de son client : cas des entrepôts
avancés fournisseurs dans l'automobile par exemple)
? emballages
? mais aussi produits finis destinés au processus
commercial...
- activités commerciales et de négoce :
? produits dont l'entreprise a fait l'acquisition et qui ne
subiront aucune transformation en vue de leur vente
? pièces de rechanges en cas d'activité
après-vente.
L'entreposage est une étape très importante dans
la chaine logistique. L'entreposage est le fait d'entreposer (donc de stocker
et d'emmagasiner) des marchandises, des matières premières et des
produits en très grande quantité. Afin de faciliter les
opérations de manutention des marchandises, on trouvera
fréquemment dans les entrepôt les engins de manutention suivants :
transpalettes, chariots élévateurs, gerbeurs, préparateurs
de commande, nacelles, diables,...
I.3. Les objets
Dans notre travail, nous considérons comme objets les
articles qui constituent le stock dont nous optimiserons l'espace.
13
I.3.1. Objet en une dimension
Un objet en une dimension (1D), c'est un objet ne comprenant
que la dimension de la longueur.

Longueur
Figure 1 : exemple d'un objet en une dimension
I.3.2. Objet en deux dimensions
On dit qu'un objet est en deux dimensions (2D) lorsqu'il ne
comportant que les dimensions de la longueur et de la largeur.

Largeur
Longueur
Figure 2 : exemple d'un objet en deux dimensions
I.3.3. Objet en trois dimensions
Trois dimensions (3D), se dit de tout objet ou espace
possédant une longueur, une largeur et une épaisseur, tout en
sachant que la largeur peut aussi être appelée profondeur et
l'épaisseur est aussi désigné par la hauteur. Ce sont ces
objets qui nous intéressent dans ce travail.
14
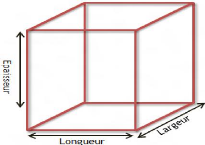
Figure 3 : exemple d'un objet en trois dimensions
I.4. Quelques travaux de recherche
étudiés
Dans cette section nous passeront en revue les
mémoires, thèses et logiciels déjà proposés
pour résoudre le problème d'optimisation d'aires d'entreposage
des articles en différentes dimensions pour enfin apporter quelque chose
d'originale à notre recherche.
Nzalamingi (2012), dans son travail intitulé
"Optimisation de la coupe et entreposage en une et deux dimensions" est parvenu
à de trouver un modèle mathématique d'optimisation du
découpage et d'emmagasinage d'objets en une et deux dimensions pour les
entreprises. Il a finalement traduit ce modelé mathématique en
algorithme et mis en oeuvre un logiciel informatique pouvant être
exploité pour la productivité des entreprises tant industrielles
que commerciales en général et des Ets Tsang en particulier.
Gazdar (2009), a lui dans sa thèse d' "Optimisation
Heuristique Distribuée du Problème de Stockage de Conteneurs dans
un Port" étudié dans un contexte bien déterminé et
selon les motivations et les enjeux qu'elle a défini, le modèle
COSAH (COntainer Stacking via multi-Agent approach and Heuristic method), ce
qui lui a permis d'optimiser le placement des conteneurs dans la zone de
stockage (statique ou
15
dynamique selon les départs ou les arrivées de
navires ou camions ou de conteneurs en import ou en export) en minimisant le
nombre de mouvements improductifs respectant un nombre de contraintes
spatio-temporelles et tenant compte de plusieurs paramètres pouvant
catégoriser les conteneurs et définir une certaine
priorité entre eux (destination, taille, date de départ, horizon
des arrivées des barges ou navires associés).
Perrot (2005), dans sa thèse intitulée "Integer
programming column generation strategies for the cutting stock problem and its
variants", s'est intéressé au problème de découpe
unidimensionnel où elle a présenté une formulation pour la
minimisation du nombre de plans de découpe distincts jusqu'à ce
que le déchet soit fixé à sa valeur optimale. Son objectif
est principalement de réduire au minimum la perte correspondant à
la partie inutilisée des rouleaux. Elle a proposé une solution
donnée par un ensemble de plans de découpe réalisables,
c'est à dire des façons de couper les petites pièces sur
les rouleaux, de sorte que leur production totale couvre les demandes.
Le logiciel 3D Load Packer (2011), est l'optimiseur de
l'espace conçu par Nikita Yurchenko pour aider à planifier
rapidement et facilement le meilleur arrangement compact d'un certain nombre de
différentes tailles d'objets 3D rectangulaire (dénommé
"Boxes") dans une ou plusieurs enceintes rectangulaires (dénommé
"conteneurs"). 3DLoad Parker peut être utilisé pour optimiser la
charge multi-produit des plans pour tous les contenants rectangulaires
(camions, remorques, wagons, palettes et caisses).
VitragePro (2007) est un logiciel d'optimisation de
découpe de vitrage, développé par Patrice Rozet. Il est
destiné aux vitriers, miroitiers et à tous les professionnels qui
doivent régulièrement effectuer des découpes de vitrages.
Il vous permet de générer
16
aisément et rapidement les plans de découpe. Il
réalise en effet les plans de découpe en prenant en compte
plusieurs matériaux d'épaisseurs différentes.
CubeMaster (2012) est une application destinée au monde
de la logistique et de la supply chain. C'est une solution logicielle
permettant de réduire les coûts et d'optimiser le chargement des
camions, containers et autres contenants.
I.5. Conclusion partielle
Nous n'avons pas touché tous les travaux
spécifiquement liés au nôtre. Mais, d'après ces
quelques exemples, il est sied de noter que notre travail n'est pas le premier
à aborder le problème d'optimisation d'espaces. Tous ces travaux
répondent au problème d'optimisation d'entreposage mais dont les
contextes d'utilisation et les conditions de stockage ne sont pas
forcément les mêmes ni adaptées à celles que nous
abordons dans le présent travail.
Chapitre deuxième : METHODOLOGIE DU TRAVAIL
Ce chapitre de notre travail nous permettra de donner une
présentation générale des différentes
méthodes que nous aurons à utiliser pour trouver solution
à l'énoncé théorique de notre problème. Les
concepts qui nous intéresserons dans ce chapitre sont : la
méthode algorithmique, le prototypage, l'expérimentation et
l'argumentation.
II.1.Methode Algorithmique
Un algorithme répond à un problème. Il
est composé d'un ensemble d'étapes simples nécessaires
à la résolution d'un problème, dont le nombre varie en
fonction du nombre d'éléments à traiter. D'autre part,
plusieurs algorithmes peuvent répondre à un même
problème. Pour savoir quelle méthode est plus efficace il faut
les comparer. Pour cela, on utilise une mesure que l'on appelle la
complexité. Elle représente le nombre
d'étapes qui seront nécessaires pour résoudre le
problème pour une entrée de taille donnée.
II.1.1. Problèmes algorithmiques
Un problème algorithmique est un problème
posé de façon mathématique, c'est-à-dire qu'il est
énoncé rigoureusement dans le langage des mathématiques.
On distingue deux types de problèmes :
- Les problèmes de décision :
ils posent une question dont la réponse est oui ou non
;
18
- Les problèmes d'optimisation : ils
comportent une question ou plutôt une injonction de la forme «
trouver un élément tel que ...» dont la réponse
consiste à fournir un tel élément.
La théorie de la complexité étudie
principalement (mais pas uniquement) les problèmes de décisions.
Dans ce travail le type de problème dont nous aurons à traiter
est celui d'optimisation.
II.1.2. Classes de Complexité
La théorie de la complexité est
un domaine des mathématiques, et plus précisément de
l'informatique théorique, qui étudie formellement la
quantité de ressources (en temps et en espace)
nécessaire pour la résolution de problèmes au
moyen de l'exécution d'un algorithme. Il s'agit donc d'étudier la
difficulté intrinsèque de problèmes posés
mathématiquement.
Les classes de complexité sont des ensembles de
problèmes qui ont la même complexité selon un certain
critère. Dans ce qui suit nous allons définir trois classes de
complexité les plus étudiées en une liste qui va de la
complexité la plus basse à la complexité la plus haute :
la classe P, la classe NP et la classe NP-C.
a. La classe P
Un problème de décision est dans P
s'il peut être décidé sur une machine
déterministe en temps polynomial par rapport à la taille
de la donnée. On qualifie
alors le problème de polynomial. C'est un
problème de complexité O(nk),
pour un certain k. On admet, en
général, que les problèmes dans P sont ceux qui sont
faciles à
résoudre.
b. La classe NP
La classe NP possède une
définition moins naturelle que celle de P, et ne
signifie pas "non polynomial", mais polynomial
non-déterministe. La classe NP est donc une
19
extension de la classe P, en
autorisant des choix non déterministes pendant l'exécution de
l'algorithme. Si le modèle de calcul est celui des machines de Turing,
on autorise plusieurs transitions à partir d'un état et d'un
symbole lu sur la bande.
c. La classe NP-Complet
En théorie de la complexité, un
problème NP-complet est un problème
vérifiant les propriétés suivantes :
- Il est possible de vérifier une solution efficacement
(en temps polynomial) ; la classe des problèmes vérifiant cette
propriété est notée NP.
- Tous les problèmes de la classe NP se ramènent
à celui-ci via une réduction polynomiale ; cela signifie que le
problème est au moins aussi difficile que tous les autres
problèmes de la classe NP.
Un problème NP-difficile est un
problème qui remplit la seconde condition, et donc peut être dans
une classe de problème plus large et donc plus difficile que la classe
NP.
Bien qu'on puisse vérifier rapidement toute
solution proposée d'un problème NP-complet, on ne sait pas en
trouver efficacement. C'est le cas, par exemple, du problème du
voyageur de commerce, celui du sac à dos ou encore celui de remplissage
des paniers.
Une question reste ouverte et fait partie des problèmes
non résolus en mathématiques les plus importants à ce
jour. Celui de prouver s'il existe un algorithme polynomial pour
résoudre un quelconque des problèmes NP-complets, si oui, alors
tous les problèmes de la classe NP peuvent être résolus en
temps polynomial. Trouver un algorithme polynomial pour un problème
NP-complet ou prouver qu'il n'en existe pas permettrait de savoir si P
= NP ou P ? NP.
20
En pratique, les informaticiens et les développeurs
sont souvent confrontés à des problèmes NP-complets, ce
qui est d'ailleurs le cas pour nous dans ce travail. Savoir que le
problème sur lequel on travaille est NP-complet est une indication du
fait que le problème est difficile à résoudre, donc qu'il
vaut mieux chercher des solutions approchées en utilisant des
algorithmes d'approximation ou des
heuristiques pour trouver des solutions approximatives.
II.2. Le Prototypage
Même si la construction des programmes est au centre de
l'informatique, il est surprenant que la programmation en elle seule ne
constitue pas de recherche scientifique. Il y a après tout, des milliers
de programmeurs qui, quelle que soit la haute technicité de leur
travaux, écrivent des programmes sans nécessairement être
des chercheurs.
Le prototypage des programmes est écrit à la fin
d'une recherche en informatique pour démontrer que le modèle
produit dans la recherche peut être implémenté dans un
langage de programmation. Ainsi, les prototypes servent de véhicule
d'expérimentation et leur construction fournit des nouveaux
aperçus sur le modèle prototypé (Masivi, 2013).
II.3. L'Expérimentation
L'idée derrière la méthode
expérimentale en informatique est de tester la modèle
et d'en noter les effets. L'expérimentation peut donc
avoir pour objectif :
- Chercher à trouver quelque chose d'intéressant :
expérimentation exploratoire ;
- Tester une théorie ou un modèle :
expérimentation de test ;
- Prouver une théorie ou un modèle :
expérimentation de preuve.
En ce qui nous concerne, seule l'expérimentation de test
nous sera utile car elle
nous permettra de tester le modèle que allons analyser au
troisième chapitre.
21
II.4. L'Argumentation
Selon Masivi (2013), l'argumentation est
généralement utilisée quand deux ou plusieurs alternatives
sont comparées. L'objectif est donc de présenter certains
arguments permettant le choix d'une solution en dépend de l'autre. Cette
argumentation peut être présentée des faits évidents
ou un raisonnement relevant et combinant des issues subtiles. Dans notre
travail, nous utiliserons l'argumentation, si et seulement si on aura à
utiliser deux ou plusieurs algorithmes de résolution d'un
problème d'optimisation d'un espace de stockage.
Chapitre Troisième : APPROCHES
METHODOLOGIQUES
Dans ce travail nous traitons un problème
d'optimisation combinatoire appliqué au problème concret
d'entreposage d'objets 3D dans un espace de stockage. De ce fait, nous aurons
besoin d'au moins un algorithme pouvant nous permettre d'atteindre notre
objectif, celui d'utiliser de la meilleure façon possible l'espace de
stockage disponible.
Ce chapitre est consacré à la
représentation et l'analyse des algorithmes pouvant résoudre le
problème de 3DBP. De prime à bord, nous avons
procédé à la présentation des algorithmes qui ont
constitués notre objet de recherche, nous avons commencé par la
présentation d'un algorithme exacte du problème de remplissage de
paniers puis les algorithmes d'approximations qui nous ont permis de
résoudre ce problème en donnant une solution acceptable en un
temps convenable.
III.1. Modélisation algorithmique du
problème de 3DBP
III.1.1. Formulation du problème
Le problème de 3D bin packing relève de la
recherche opérationnelle et de l'optimisation combinatoire. Il s'agit de
trouver le rangement le plus économique possible pour un ensemble
d'articles dans des boîtes. Le problème classique se
définit en une dimension, mais il existe de nombreuses variantes en deux
ou trois dimensions.
Le problème de chargement d'entrepôts que nous
tentons de modéliser est une variante du problème en trois
dimensions. En fait, dans ce travail nous ne faisons
23
allusion qu'aux articles possédant chacun une largeur,
une longueur (ou profondeur) et une hauteur c'est de là d'ailleurs que
vient de concept 3D (figure 4).
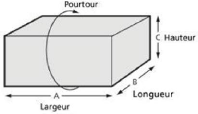
Figure 4 : Dimensions d'articles commerciaux qui nous
intéressent.
Dans le problème classique, les données sont : Un
nombre infini de paniers de taille C
Une liste 1,2,.......,n d'objets i de taille
ci
On cherche à trouver le rangement valide pour tous ces
objets de façon à minimiser le nombre de paniers à
utiliser. Pour qu'un rangement soit valide, la
somme des tailles des objets affectés à un panier
doit être inférieure ou égale à C.
Pour décrire une solution, on peut utiliser un codage
binaire pour indiquer dans quel panier un objet est rangé.
La variable vaudra si l'article est rangé dans le panier ,
et sinon.
La variable binaire est égale à si la boîte
est utilisée, sinon.
On cherche donc à minimiser le nombre de
panier :
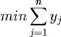
Sous les contraintes suivantes :
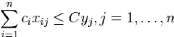
24
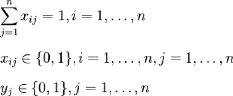
Source : Wikimedia Foundation (2013).
La première inégalité signifie qu'on ne peut
dépasser la taille d'un panier pour un
rangement. À noter que la partie droite de
l'inégalité oblige à prendre la valeur
dès qu'un article est rangé dans le panier . La
deuxième inégalité impose à chaque objet
d'être rangés dans une boîte et une seule. Toute solution
pour laquelle la famille d'équations précédente est
vérifiée est dite réalisable. (Kantorovitch,
1960).
Le problème de bin packing a été
largement étudié dans la communauté de recherche
opérationnelle. Il existe des heuristiques
très efficaces pour le résoudre, et des
méthodes exactes utilisant l'optimisation
linéaire en nombre entiers, la formulation de Kantorovich, une
résolution par génération de colonnes, la procédure
par séparation et évaluation,... Les méthodes exactes
permettent d'obtenir la solution optimale à chaque fois, mais le temps
de calcul peut être long si le problème est compliqué
à résoudre. Les méthodes approchées, encore
appelées heuristiques, permettent d'obtenir rapidement une solution
approchée, donc pas nécessairement optimale. Nous n'allons pas
vraiment parler de toutes ces méthodes car ce qui nous intéresse
dans ce travail c'est plutôt trouver une heuristique qui donne une
solution acceptable en un temps convenable.
III.1.2. Méthodes exactes
Le problème de chargement d'entrepôt que nous
tentons de modéliser dans ce chapitre est en fait rattachable au
problème de 3D bin packing, une extension au problème de
remplissage de sacs, ce qui explique son NP complétude.
25
Tous les algorithmes exactes connus pour résoudre des
problèmes NP-complets ont un temps d'exécution exponentiel en la
taille des données d'entrée dans le pire cas, ils sont donc
inexploitables en pratique car bien qu'ils résolvent les
problèmes NP-C en donnant des réponses exactes, ils sont couteux
en terme de temps d'exécution.
L'algorithme exact consiste à essayer toutes les
combinaisons d'objets et choisir celle qui minimise le nombre de panier. Il
faut d'abord deviner toutes les solutions réalisables puis
vérifier chaque alternative. On parle alors d'un divin et d'un
vérificateur, le divin propose un certificat, c'est-à-dire, une
réponse probable ou encore un candidat-réponse et le
vérificateur teste si le certificat remplit les conditions d'être
une réponse.
En ce qui nous concerne ici, l'algorithme exact est donc celui
dont le divin fournit plusieurs ensembles d'articles (caisses ou boîtes)
provenant d'une liste de plusieurs articles. Il essaie toutes les combinaisons
possibles, chaque ensemble constitue un candidat-réponse à la
question de savoir quel ensemble d'articles maximise l'utilisation de
l'entrepôt. Le vérificateur vérifie si chaque ensemble
remplit les contraintes en se posant les questions ci-après :
- Dans un ensemble d'articles ni existe-t-il un article dont
la hauteur (hi), la largeur (li) ou la profondeur (pi) est supérieur
à la hauteur (H), la largeur (L) ou la profondeur (P) de
l'entrepôt ? Tout en sachant que l'objet peut être roté et
donc, on considère comme hi, li ou pi finale, sa valeur après
dernière rotation.
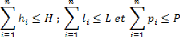
- Est-ce que la taille (volume) d'un ensemble d'articles (ni)
dépasse la taille de l'espace de stockage ?
26
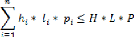
Tout en sachant que l'objectif est de minimiser l'espace non
utilisé, c'est-à-dire la différence entre le volume de
l'espace de stockage et le volume de toutes les boîtes
chargées.
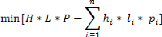
Cette solution donne une réponse exacte mais
malheureusement il est couteux. Pour pallier à ce problème
lié au temps d'exécution, il existe les algorithmes
d'approximation. Ceux-ci qui permettent de résoudre un problème
NP-complet en donnant une solution presque optimale en temps polynomial.
III.1.3. Méthodes approximatives (heuristiques)
Les algorithmes d'approximations sont utilisés pour
réduire la complexité des problèmes de classe NP-Hard.
Comme nous l'avons déjà dit dans notre
introduction, nous présentons dans ce travail quelques algorithmes
d'approximation que nous allons ensuite implémenter dans un langage de
programmation et les soumettre à une expérimentation pour trouver
le plus performant en terme de temps d'exécution et d'espace de
l'entrepôt utilisé. Notre objectif est donc de répertorier
quelques algorithmes existants pour le problème de 3D Bin packing et
trouver le plus performant.
Dans cette section nous allons présenter 2 algorithmes
de 3D Bin packing : l'algorithme HI-BHA (A Human Intelligence-Based
Heuristic Approach) proposé par (Baltacioglu, 2002) et le LAFF
(Largest Area First-Fit) développé par
(Gürbüz, Akyokuþ, Emiroðlu, & Güran, 2009).
27
1. A Human Intelligence Based Heuristic
Approach
Le problème de 3DBP est toujours résolu en
utilisant les algorithmes optimums et les méthodes heuristiques. Voici
une méthode heuristique parmi plusieurs qui essaie de résoudre le
problème en un temps polynomiale.
Cette approche a été qualifiée d'une
approche basée sur l'intelligence humaine par son auteur du fait qu'elle
simule l'intelligence humaine en chargeant les boîtes dans
l'entrepôt comme un humain, de bas à haut et en construisant des
couches.
Ce modèle utilise un outil puissant de l'heuristique et
une structure de données dynamique qui lui permet d'imiter
l'intelligence humaine. L'avantage de cet algorithme est qu'il est capable de
charger l'article dans n'importe quelle orientation, tout en sachant qu'un
article peut être roté de six manières différentes.
Cette approche est basée sur la construction des couches ou murs.
L'idée est qu'après la création d'une couche, avant qu'une
boîte soit chargée dans la couche, l'algorithme analyse toutes les
boîtes non chargées pour trouver celle qui conviendra le mieux au
sein de la couche selon son épaisseur (hauteur) pour minimiser l'espace
perdu. Cependant, l'épaisseur de la couche sélectionnée
est flexible et peut augmenter pour s'adapter à la hauteur de la
boîte sélectionnée.
Variables entrantes (inputs)
Les premières variables entrants sont les
coordonnées x, y et z qui représentent les dimensions de l'espace
de stockage. Les informations suivantes représentent les
caractéristiques des boîtes à entreposer. Dans chaque ligne
le premier élément représente l'étiquette de la
boîte contenant les articles, ces étiquettes n'ont aucun effet sur
l'algorithme, ce n'est qu'une façon d'identifier chaque boîte,
elles sont facultatives, le deuxième, troisième et
quatrième élément correspondent respectivement aux
coordonnées x, y et z de chaque boîte. Le cinquième
élément
28
représente le nombre de boîte de même type,
c'est-à-dire le nombre de boîtes ayant la même largeur (x),
la même hauteur (y) et la même profondeur (z).
Structuration des données
La structure de données est un critère assez
important dans un programme, elle affecte de manière directe le
résultat de la solution d'un algorithme que ce soit en terme de temps
d'exécution ou en terme d'espace utilisé.
Cet algorithme utilise deux tableaux : la premier tableau est
celui de la liste des boîtes dénommé `'BoxList[]
Array`', il sert à garder toutes les dimensions, les
coordonnées et d'autres informations nécessaires relatives aux
boîtes dans une liste. Il a au total douze champs :
Tableau 1 : Liste des champs dans le `'BoxList[] Array `'
Noms du champs Descriptions
Packst L'état du chargement {0:Non chargé,
1:Chargé)
N Nombre de boîtes identiques
Dim1 La taille d'une des trois dimensions
Dim2 La taille d'une autre dimension parmi les trois
Dim3 La taille d'une autre dimension parmi les trois
Cox La coordonnée x de l'emplacement de la boîte
chargée
Coy La coordonnée y de l'emplacement de la boîte
chargé
Coz La coordonnée z de l'emplacement de la boîte
chargé
Packx La dimension x de la boîte après rotation
Packy La dimension y de la boîte après rotation
Packz La dimension z de la boîte après rotation
Vol Le volume de la boîte (Dim1*Dim2*Dim3)
Cet algorithme stocke aussi le volume de chaque boîte,
ainsi on n'a pas besoin de le recalculer à chaque instant qu'on en a
besoin. Les champs 6 à 11 n'ont pas de sens si le premier (Packst) a
comme valeur 0, ils deviennent importants une fois qu'on a chargé la
première boîte et Packst devient égal à 1. Chaque
boîte constitue une ligne d'enregistrement dans le tableau `'BoxList[]
`'.
29
Un autre tableau est le `'Layers[]`'. Ce
tableau stocke les différentes tailles de toutes les dimensions des
boîtes. Chaque champ dénommé Layerdim représente
l'épaisseur d'une couche créée au sein de l'espace de
stockage. Avant le commencement de chaque boucle (itération), les
différentes valeurs des dimensions des boîtes sont stockées
dans ce tableau. Le deuxième champ de ce tableau est le Layereval, la
valeur de ce champ est calculée par la fonction Listcanditlayers que
nous allons expliquer plus tard dans le quatrième chapitre de ce
travail. Voici donc les deux champs du tableau Layereval :
Tableau 2 : Liste de champs dans le `'Layers[] Array `'.
Noms Descriptions
Layerdim La valeur d'une dimension
Layereval Evaluation de la valeur correspondante du Layerdim
Contraintes de l'algorithme
Les limites de l'algorithme HI-BHA sont d'après le
concepteur dues à la capacité
moyenne de mémoires des ordinateurs et à l'ampleur
du problème réel de
chargement d'entrepôt. Voici donc les limites à ne
pas franchir :
Nombre maximal de boîtes dans un ensemble de boîtes :
5000
Nombre total des boîtes ayant des caractéristiques
différentes : 1000
Tous les nombres doivent être en entier.
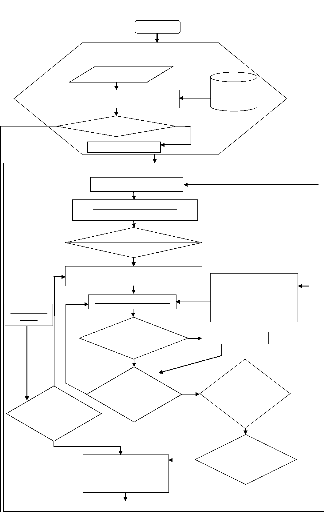
Ordinogramme
Ceci est une représentation graphique de l'enchainement
des opérations de ce qui
constituera le fruit de l'implémentation de l'algorithme
HI-BHA (le programme
proprement dit). Il nous permet donc d'analyser notre
problème.
Avant l'exécution de l'algorithme, on doit s'assurer du
respect des critères ci-
après :
30
- Chaque espace de stockage doit posséder une largeur et
une profondeur et une hauteur bien finie ;
- Chaque boîte à entreposer doit aussi avoir une
largeur, une profondeur et une hauteur ;
- Toutes les boîtes peuvent être rotée et
placée dans n'importe quel angle dans l'entrepôt ;
- Les boîtes peuvent se supporter les unes sur les autres
sans créer des dommages.
31
Début
INITIALISATION
Entrées des variables
INPUT BOXLIST Lecture du fichier
Fichier des
variables
entrantes
Si variables Incorrectes
Non
Initialisation des variables
EXECITERATIONS
Essaie d'une orientation de la boîte
LISTCANDIDATETLAYERS Creation de
Layers[]Array
QSORT
Trie du Layers[]
Prise en compte d'un enregistrement du Layers[] comme
l'épaisseur (hauteur) de la couche
PACKLAYER(laverthickness)
PACKLAYER (space)
FINDLAYER(remainpy)
Trouve la couche ayant la
hauteur la plus convenable en
examinant les boîtes
non
chargées.
Il y a un espace pour la
création d'une
couche
dans la couche ?
OUI
PACKLAYER(space)
NON
NON
OUI
NON
OUI
Il y a un espace pour
le chargement d'une
boîte
dans la
couche ?
Toutes les layers[]
sont
déjà
utilisées ?
Il y a un espace
pour le chargement
d'une boîte
dans
l'espace de
stockage ?
NON
OUI
OUI
NON
Toutes orientations
des boîtes ont
déjà
été testées ?
Meilleur utilisation de l'espace de stockage garde l'orientation
de la boîte et la hauteur de la couche
Msg : Les Données entrées incorrectes, veuillez
entrer les vraies valeurs
Saisie de `O'
Fichier du rapport de la meilleure solution
FIN
32
Figure 5 : Ordinogramme de l'algorithme HI-BHA
Fonctionnement de l'algorithme
HI-BHA
Nous allons expliquer dans ce point le fonctionnement et
l'obtention des valeurs de différents champs des tableaux
détaillés un peu plus haut dans ce troisième chapitre, il
s'agit de `'BoxList[]» et de `'Layers[]». Ceci en nous basant d'un
exemple typique.
Exemple : soit un entrepôt de 104 dm de long, 96 dm de haut
et 84 dm de profondeur. On décide de ranger 9 caisses dans cet
entrepôt dont 4 de dimensions (70, 104, 84), 2 de dimensions (14, 104,
48) et 3 de dimensions (40, 52, 36). BOXLIST[]Array
Tableau 3 : Création du tableau BOXLIST[]
Taille de l'entrepôt : XX=104
; YY=96 ; ZZ=84
|
Boxlist[x]
|
Packst
|
N
|
Dim1
|
Dim2
|
Dim3
|
Cox
|
Coy
|
Coz
|
Packx
|
Packy
|
Packz
|
Vol
|
|
Boxlist[1]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[2]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[3]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[4]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[5]
|
0
|
2
|
14
|
104
|
48
|
0
|
0
|
0
|
0
|
0
|
0
|
69888
|
|
Boxlist[6]
|
0
|
2
|
14
|
104
|
48
|
0
|
0
|
0
|
0
|
0
|
0
|
69888
|
|
Boxlist[7]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
|
Boxlist[8]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
|
Boxlist[9]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
33
Après avoir entrée les variables entrantes, le
modèle détermine les hauteurs des couches et les entre dans un
tableau, le `'Layers[]». Ce tableau contient une dimension de chaque
boîte moins la dimension y de l'espace de stockage. Le tableau LAYERS[]
est créé après l'examen de chaque orientation des
boîtes.
Avec le même exemple, voyons maintenant comment obtenir
les valeurs des champs dans le tableau Layers[].
XX=104 ; YY=96 ; ZZ=84
Layers[x]=(Layerdim, Layereval)
Layers[X]=(Layerdim, Layereval)
Abs(70-70) + Abs(70-70) + Abs(70-70) + Abs(70-48) + Abs(70-48) +
Abs(70-52) +
Abs(70-52) + Abs(70-52) = 98
Layers[l]=(70, 98)
Abs(24-24) + Abs(24-24) + Abs(24-24) + Abs(24-14) + Abs(24-14) +
Abs(24-36) +
Abs(24-36) + Abs(24-36) = 56
Layers[2]=(24, 56)
Abs(14-24) + Abs(14-24) + Abs(14-24) + Abs(14-24) + Abs(14-14) +
Abs(14-40) +
Abs(14-40) + Abs(14-40) = 106
Layers[3]=(14,106)
Abs(48-70) + Abs(48-70) + Abs(48-70) + Abs(48-70) + Abs(48-48) +
Abs(48-40) +
Abs(48-40) + Abs(48-40) = 100
Layers[4]=(48,100)
Abs(40-24) + Abs(40-24) + Abs(40-24) + Abs(40-24) + Abs(40-48) +
Abs(40-48) +
Abs(40-40) + Abs(40-40) = 80
Layers[5]=(40, 80)
Abs(52-70) + Abs(52-70) + Abs(52-70) + Abs(52-70) + Abs(52-48) +
Abs(52-48) +
Abs(52-52) + Abs(52-52) = 80
Layers[6]=(52, 80)
Abs(36-24) + Abs(36-24) + Abs(36-24) + Abs(36-24) + Abs(36-48) +
Abs(36-48) +
Abs(36-36) + Abs(36-36) = 72
Layers[7]=(36, 72)
34
Normalement il y aurait 8 valeurs au total, mais comme la
dimension y de certaines boîtes est supérieure à celle de
l'espace de stockage, on ne peut pas évaluer ça comme une hauteur
de la couche.
Après l'obtention des valeurs du Layer[], on les trie
dans l'ordre croissant d'après chaque Layereval.
Tableau 4 : Création du tableau Layers[]
|
Layers[X]=(Layerdim, Layereval) Layer[1]=(24, 56)
Layer[2]=(36, 72) Layer[3]=(52, 80) Layer[4]=(40, 80) Layer[5]=(70, 98)
Layer[6]=(48, 100) Layer[7]=(14, 106)
|
Comme la plus petite Layereval peut être la hauteur la
plus convenable pour une couche, trier la liste de ces champs selon l'ordre
croissant est un facteur important dans le but de réduire le temps
d'exécution d'une solution, spécialement lorsqu'on veut charger
un nombre élevé de boîte de différentes tailles.
Complexité de l'algorithme
HI-BHA
Les itérations de cet algorithme sont liées aux
six orientations possibles que peut prendre une boîte. Pendant les
itérations, les boîtes sont d'abord chargées dans toutes
les six orientations. Chaque orientation de la boîte est
considérée comme une solution de chargement. Evidemment si toutes
les trois dimensions d'une boîte sont identiques, c'est-à-dire si
la boîte est carrée, il n'y a qu'une seule orientation possible.
Généralement on a soit un, deux ou six orientations
respectivement pour un, deux ou trois dimensions différentes. Dans
chaque itération, chaque orientation de la boîte est chargé
une fois dans chaque champs du tableau `'Layers[]».
Ainsi, comme dans notre exemple, nous avons sept
différentes dimensions dans notre tableau `'Layers[]`' et que toutes nos
boîtes on trois dimensions uniques,
35
l'algorithme va effectuer 6*7=42 itérations. Ainsi, le
temps d'exécution de cet algorithme dépend du type de boîte
(celles avec une dimension, deux dimensions ou trois dimensions) et du nombre
total des boîtes à charger. Le nombre de boîtes identiques
(celle avec les mêmes dimensions) n'affecte pas directement le temps
d'exécution de cet algorithme.
Maintenant, nous pouvons déterminer la
complexité de l'algorithme HI-BHA. Supposons que nous avons n
boîtes dans un ensemble de boîtes et d, la valeur des dimensions de
toutes les boîtes. Dans le pire de cas, le temps d'exécution sera
:
1'(t)=6 n d P(t) ; (1)
Où P(t) est le temps utilisé pour trouver et ranger
chaque boîte.
P(t)=6 n E(t) ; (2)
Où E(t) est le temps utilisé pour examiner
l'orientation d'une boîte. E(t) dépend
d'un ordinateur à un autre.
Ainsi, dans le pire de cas, la complexité de cet
algorithme est :
1'(t)=36 n2 d E(t).
Ainsi, la complexité de cet algorithme est
Ø(nk) avec comme k une constante et toujours
égale à 2.
2. Largest Area First-Fit
Dans cette section de notre travail, nous présentons un
autre algorithme heuristique que nous n'allons pas implémenter suite au
temps qui nous est insuffisant mais dont les résultats seront
comparés au premier. Le LAFF algorithme résout lui aussi le 3DBPP
en un temps polynomial. Nous allons présenter cet algorithme en
définissant de prime à bord les variables entrantes et sortantes.
Cet algorithme est
36
appelé LAFF minimizing heigth. Il place les
boîtes à une plus grande surface en minimisant la hauteur du
container.
Variables entrantes (inputs)
La première variable à entrer est le nombre de
boîtes de taille différentes noté N. La deuxième
entrée c'est les dimensions de chaque type des boites de tailles
différentes. Nous notons cela par quatre paramètres (an, bn, cn,
kn) où an est la largeur, bn est la profondeur, cn est la hauteur et kn,
le nombre de boîtes pour une dimension donnée.
Comme vous pouvez le voir sur une boîte, chaque
dimension peut être considérée en largeur, en hauteur ou
profondeur. Si vous prenez bn comme la largeur, les autres dimensions
c'est-à-dire an et cn peuvent être acceptés comme hauteur
ou profondeur. Parce que, la boîte est tridimensionnelle et elle peut
être roté et peut être envisagé en des perspectives
différentes. La liste suivante montre les paramètres à
entrer proposés par l'algorithme :
Nombre des boîtes de tailles différentes : : N
Largeur de la boîte : : an
Profondeur de la boîte : : bn
Hauteur de la boîte : : cn
Nombre de boîte par dimension : : kn
Variables sortantes (outputs)
Après l'exécution de l'algorithme LAFF, le
programme doit produire les outputs ci-après :
O1: Le volume de l'espace
O2: L'espace utilisé (Le volume de toutes les
boîtes déjà placées)
O3: L'espace non utilisé
37
O4: Le temps d'exécution (exprimée en
millisecondes).
Fonctionnement de l'algorithme
LAFF
Comme déjà signalé le problème de
3D bin packing est du genre NP-Complet, c'est-à-dire que la solution
optimum pour ce problème ne peut être trouvée
qu'après avoir essayé toutes les combinaisons possibles. C'est
donc un problème difficile. Cependant, si le nombre de boîtes
augmente au fur et à mesure, le nombre d'itérations augmentent
aussi au point qu'il ne peut pas être résolu en temps polynomial
même par l'ordinateur le plus rapide possible qui puisse exister à
nos jours. Mais alors, avec quelques suppositions, ces genres de
problèmes peuvent être résolus par des algorithmes
heuristiques en un temps presque polynomial et fournir une solution près
de l'optimum.
L'algorithme LAFF minimizing hieght proposé ci-dessus
utilise une heuristique qui place la boîte dans le container en ne
prenant pas en compte sa hauteur. Cet algorithme fonctionne de la
manière ci-après :
De prime à bord, la largeur et la profondeur de
l'espace de stockage doivent être déterminées. Ainsi, en
donnant un ensemble de boîtes de tailles différentes, on calcule
la profondeur et la largeur de l'espace de stockage et on trouve le plus long
des deux bords des boîtes. La largeur et la profondeur de l'espace sont
déterminées au début de l'algorithme et restent fixes
jusqu'à la fin de son exécution. On suppose ici que la hauteur
reste illimitée, elle augmente au fur et à mesure que
l'algorithme s'exécute.
Etant ainsi, la largeur (ak) et la profondeur (bk) de l'espace
sont trouvées en sélectionnant le premier et deuxième plus
long bord des boîtes (ai, bi et ci). Le plus long est pris comme largeur
(ak) et le deuxième comme profondeur (bk). Donc ak et bk ne changent
jamais.
38
Après avoir déterminé les valeurs de la
largeur et de la profondeur de l'espace de stockage, les boîtes peuvent
être placées dans le contenant. Dans cet algorithme, deux
méthodes de placement sont utilisés. Le premier est alloue un
espace à chaque boîte entrante, ce qui augmente la hauteur du
contenant. La deuxième méthode alloue un espace aux boîtes
restantes s'il y a une boîte qui convient parfaitement dans l'espace
encore disponible autour des boîtes déjà placées
sans dépasser la hauteur de la boîte placé.
Dans la première méthode de placement, les
boîtes ayant la plus grande surface sont déterminées, les
boîtes sont sélectionnées pour essayer de trouver la
boîte qui a la hauteur minimum dans toutes boîtes
sélectionnées. Ainsi, la boîte ayant la hauteur minimum est
placée dans le contenant. La plus grande boite
sélectionnée doit être en parallèle avec le fond du
contenant.
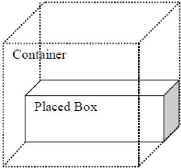
Figure 6 : Première méthode de placement des
boîtes avec LAFF
Dans la seconde méthode, les objets sont placés
dans un ordre et l'algorithme essaie d'allouer un espace aux boîtes
restantes autour de la boîte déjà placée (selon la
première méthode). Ainsi, pour les espaces restants autour de la
boîte déjà placée comme le montre la figure 7,
l'algorithme essaie de les remplir d'après la deuxième
méthode de placement. Selon cette méthode, étant
donné que les boîtes ont des
39
dimensions ai, bi et ci sur un niveau, l'espace de stockage
aura deux espaces vides autour de la boîte déjà
placé avec les dimensions ((ak-ai),bk,ci) et (ak,(bk-bi),ci). Donc s'il
y a une boîte qui convient parfaitement dans l'espace non alloué,
ça peut être une boîte ou plus, on place la boîte qui
a le volume maximum à côté de la boîte comme le
montre la figure 7. Cette répétition continue jusqu'à ce
qu'il n'y ait aucune boîte qui convient dans l'espace vide.
Dans la deuxième méthode de placement, s'il n'y
a pas d'espace autour de la boîte placée, alors l'algorithme
continue d'après la première méthode.
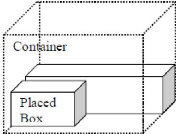
Figure 7 : seconde méthode de placement des
boîtes avec LAFF
A chaque fois qu'il y a des boîtes non encore
placées, l'algorithme va à la première méthode de
placement et ainsi de suite jusqu'à ce que toutes les boîtes
soient placées. À la fin de l'algorithme, une solution possible
comme le montre la figure 8 est produite.
40
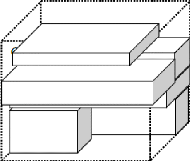
Figure 8 : solution possible avec LAFF
Etapes de l'algorithme LAFF
Les principales étapes de l'algorithme LAFF sont
résumées comme suit :
Etape 1 : Entrer les dimensions et nombres des boîtes
N : Nombre de boîtes uniques
Etape 2 : Déterminer la largeur (ak) et la profondeur (bk)
de l'espace de stockage
ak : le bord le plus long de toutes les boîtes
bk : le deuxième bord long des boîtes
ck : 0 (zéro)
Etape 3 : choisir la boîte la plus volumineuse. S'il y en a
beaucoup, choisir celle
ayant la plus petite hauteur. Placer cette boîte (ith)
à l'endroit le plus large en
parallèle avec la base du contenant.
Etape 3.1 : Déterminer la hauteur de l'espace de stockage
et décrémenter le nombre
de boîtes (ith).
ck=ck+ci
ki=ki-1
Etape 3.2 : si le nombre de boîte est égal à
0 alors terminer
41
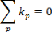
Etape 3.3 : si l'espace (ak-ai)=0 et (bk-bi)=0 aller à
l'étape 3. Par contre, choisir la boîte capable de remplir
convenablement l'espace restant. S'il y a plus d'une boîte capable de
convenir dans l'espace restant, choisir la boîte la plus volumineuse.
Cette boîte est appelée jth.
Etape 3.3.1 : déterminer la dimension de l'espace.
as=max(ak-ai, ak-aj) and bs=bk-bi-bj
Etape 3.3.2 : Décrémenter le nombre des
boîtes ith
kj=kj-1
Etape 3.3.3 : si le nombre des boîtes devient
égal à 0 alors terminer. Sinon, aller à l'étape
3.3.
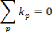
Complexité de l'algorithme
LAFF
Si on considère n comme le nombre de toutes les
boîtes à être placées dans l'espace de stockage et k
comme le type de différentes boîtes de tailles différentes,
la durée d'exécution pour le cas le pire de cette
exécution est exprimé de la manière suivante :
T(n) = n (nk)
T(n) = kn2 où k est une constante.
Au final, la complexité de cet algorithme est
O(n2).
Chapitre Quatrième : PROTOTYPAGE,
EXPERIMENTATION
ET ARGUMENTATION DES RESULTATS
Ce chapitre sera pour nous une opportunité de
présenter la traduction de l'algorithme HI-BHA dans le langage C, nous
allons présenter les fonctions utilisées dans le programme et les
fichiers des données. Cette partie de notre travail sera pour nous aussi
une occasion de présenter le test de l'algorithme HI-BHA et
l'argumentation du résultat, c'est-à-dire l'évaluation de
celui-ci par rapport au LAFF algorithme.
VI.1. Prototypage
VI.1.1. Les fonctions du programme
Le prototype du programme comporte les fonctions suivantes :
Tableau 5 : les fonctions de l'algorithme HI-BHA
Nom de la Fonction Description
Packlayer Met à jours le `'Boxlist[]Array`' quand une
boîte est rangée
Findsmallestz Détermine le vide ayant la valeur z le plus
petite dans la courante
couche
Findbox Sert à trouver la boîte qui remplit le
mieux le vide courant dans la
couche
Analyzebox Cette fonction est utilisée par la
précédente pour analyser les
dimensions des boîtes
Checkfound Détermine quelle boîte charger
d'après sa capacité à remplir le
vide
Execiterations Exécute les itérations en appelant
les fonctions appropriées
Report Stocke la meilleure solution de chargement
Outputboxlist Ecrit les informations de la solution de chargement
dans un fichier
Graphunpackedout Ecrit l'ordre de rangement des articles pour la
visualisation
43
La fonction `'Findbox» analyse les boîtes non encore
chargées en utilisant la fonction `'Analyzebox». Pour chaque
orientation de la boîte non encore chargée, la fonction Analyzebox
utilise les paramètres suivants :
Hmx : longueur maximum (dimension x) disponible pour le
chargement
Hy : hauteur (dimension y) de la courante couche
Hmy : hauteur maximum (dimension y) disponible pour le
chargement
Hz : profondeur (dimension z) de la courante couche pour le
chargement
Hmz : profondeur maximum (dimension z) disponible pour le
chargement
Dim1 : dimension x de la boîte à examiner
après orientation
Dim2 : dimension y de la boîte à examiner
après orientation Dim1 : dimension z de la boîte à examiner
après orientation
X
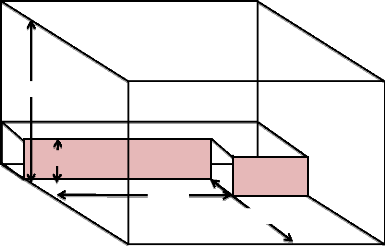
Hmy
Z
Hy
Y
Hmx
Hmz
Figure 9 : Paramètres de la fonction FindBox()
La fonction AnalyzeBox cherche, par ordre de priorité,
une boîte ayant une hauteur qui est proche de Hy mais pas
supérieur à Hmy, une longueur proche mais pas supérieure
à Hmx et une largeur proche de Hz mais pas supérieur à
Hmz. Ceci
44
veut dire que cette fonction considère d'abord la
hauteur (y dimension), donc, parmi les boîtes qui ont une même
hauteur, elle vérifie les longueurs (x dimension) et finalement parmi
les boîtes ayant la même longueur et la même hauteur, elle
vérifie la profondeur (z dimension). Cette fonction calcule les
différences entre le volume encore disponible dans la couche
(c'est-à-dire le vide) et le volume de chaque boîte, à la
fin, elle récupère la boîte qui génère une
moindre différence pour un meilleure remplissage. Elle cherche aussi les
boîtes ayant une y-dimension supérieure mais proche de la hauteur
de la couche courante. Les boîtes qui conviennent, celle qui ont la
hauteur appropriée sont chargées. Celles qui ne conviennent pas
nécessitent, en effet, une autre considération.
Dans l'algorithme HI-BHA, une méthode appelée
`'Layer-in-layer packing`' ceci pour dire chargement d'une couche dans une
couche. Layer-in-Layer est une fonction qui crée une couche au sein
d'une autre. Cette fonction permet de loger la boîte ayant la hauteur qui
ne convient pas à la couche. Si aucune boîte de convient dans le
vide, ce vide est considérée comme perdue.
Dans la fonction `'FindBox`', la hauteur de la couche est
adaptée au y-dimension de la plus haute boîte. Quand la hauteur de
la courante couche augmente, le total des incrémentations de la couche
du début à la fin du chargement des boîtes dans cette
couche est stocké dans la variable layerinlayer. A la fin du chargement
des boites dans cette couche, si la variable layerinlayer est supérieure
à zéro, un autre chargement dans la couche est entrepris. Quand,
le Layer-in-layer packing`' est utilisé, le modèle utilise
beaucoup de volume.
Après chaque chargement, le volume des boîtes
chargées ainsi que le volume des boîtes non chargé sont
calculés afin d'obtenir le taux d'utilisation de l'entrepôt et
la
45
pourcentage du volume des boîtes chargées. La
solution avec un meilleur taux d'utilisation est considérée comme
la solution finale.
Après qu'on ait obtenu tous les paramètres de la
meilleure solution, la fonction `'Report`' est appelée. Cette fonction
ré exécute le chargement avec les paramètres de la
meilleure solution trouvée et appelle la fonction `'Outputboxlist`' pour
générer le rapport (fichier) et `'Graphunpackedout`' pour
générer le fichier input de la visualisation. Les informations
sur les boîtes non chargées sont affichées à la fin
du rapport.
IV.1.2. Formulaire d'entrées des données
Avant de lancer le programme console codé en C, il faut
s'assurer que toutes les informations concernant l'entrepôt et les
articles (boîtes 3D) à entreposé sont déjà
spécifiées par l'utilisateur dans un fichier texte (avec
l'extension .txt). Ce fichier doit être enregistré dans le
même répertoire que l'exécutable (fichier .exe).
Voici un exemple du formulaire d'entrée des
données :
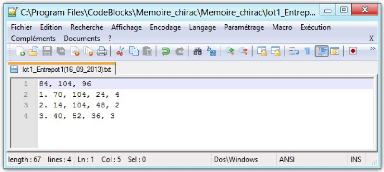
Figure 10 : Fichier des variables entrantes
paramètres x, y et z qui sont respectivement la longueur,
la hauteur et la profondeur
La première ligne contient les informations sur
l'entrepôt, elle comprend les
46
de l'entrepôt. L'ordre la succession de ces valeurs est
d'une importance capitale. Toutes les lignes suivantes comportent les
informations concernant les boîtes. Dans chaque ligne, la première
valeur représente l'étiquette de la boîte, cette valeur n'a
aucun effet sur l'algorithme. La deuxième, troisième et
quatrième valeur sont les dimensions x, y et z de la boîte. Ces
valeurs sont prises comme tel lorsque le programme aura jugé une
orientation comme étant convenable. Le cinquième
élément c'est le nombre de boîte de ce type. De toute
façon, les virgules entre les chiffres ne sont pas obligatoires,
même un simple espacement peut délimiter deux valeurs.
IV.1.3. Les rapports
Ce programme génère au total trois
fenêtres. Le premier c'est le console, elle nous permet d'entrer le nom
du fichier (.txt) à traiter.
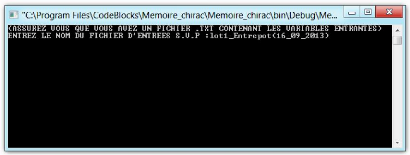
Figure 11 : Fenêtre console avant exécution du
programme
47
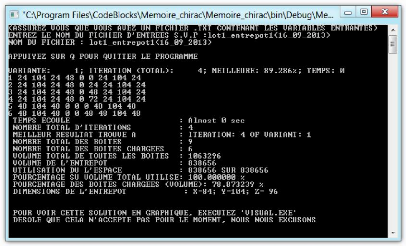
Figure 12 : Fenêtre après exécution du
programme
La deuxième fenêtre contient le rapport de la
meilleure solution et l'orientation de chaque boîte après
chargement. A la fin de ce rapport, on trouve la liste de toutes les
boîtes qui n'ont pas eu de place dans l'entrepôt. Ce rapport est du
type .OUT, il peut être ouvert avec Mozilla firefox, google chrome, etc,
il est créé après exécution du fichier des
variables entrantes dans le même dossier que le fichier exécutable
du programme et porte le même nom que le fichier d'entrées des
variables. Il comporte toutes les informations nécessaires sur le
chargement.
48
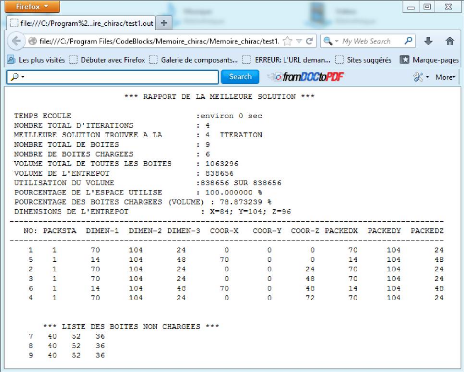
Figure 13 : fichier `'Rapport de la meilleure solution du
programme`'
La troisième fenêtre est un fichier du type
(.txt) qui est créée lui aussi après exécution d'un
cas. Elle comporte les coordonnées et les orientations des boites
chargées et celles de l'entrepôt. C'est ce qui fichier qui permet
à l'interface graphique que nous n'avons pu créer d'avoir une vue
3D de la solution. Il comporte, en effet, toutes les variables entrantes dont
le programme de l'interface graphique a besoin. Il est enregistré dans
le même répertoire que le fichier exécutable et porte le
nom du fichier d'entrée des données privé de la
première initiale pour éviter le doublon.
49
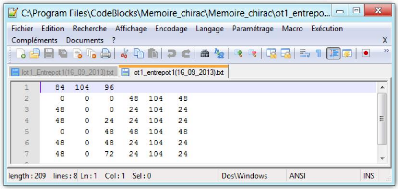
Figure 14 : Fichier des variables entrantes de l'interface
graphique du programme
IV.2. Expérimentation et Argumentation
L'informatique reste une science de l'ingénieur, ce qui
signifie ici, que malgré toutes les études ou les critères
théoriques permettant de comparer l'efficacité de deux
algorithmes dans l'absolu, dans la pratique nous ne pourrons pas dire qu'il y a
un meilleur algorithme pour résoudre tel type de problème. Une
méthode pouvant être lente pour certaines configurations de
données et dans une autre application qui travaille
systématiquement sur une configuration de données favorables la
méthode peut s'avérer être la "meilleure".
IV.2.1. Environnement de travail
L'efficacité d'un algorithme est directement
liée au programme à implémenter sur un ordinateur. Le
programme va s'exécuter en un temps fini et va mobiliser des ressources
mémoires pendant son exécution; ces deux paramètres se
dénomment complexité temporelle et complexité spatiale.
50
Le programme de résolution du problème
d'optimisation d'entreposage des articles 3D a été conçu
en utilisant le langage de programmation C. L'expérimentation a
été effectuée sur une machine de configuration suivante
:
- Type de processeur : Genuine Intel(R) CPU 1.83 GHZ
- Mémoire installée (RAM) : 2,00 Go
- Système d'exploitation : Windows 8 Consumer Preview 32
Bits
- Nous avons utilisé Cod::Blocks 8.02 comme environnement
de développement
(IDE), nous l'avons trouvé idéal parce qu'il
combine en lui seul l'éditeur de code, le compilateur et le
débugger, il nous a permis d'écrire facilement le code source du
programme (en C), de transformer ("compiler") notre code source en code binaire
et de traquer les erreurs dans notre code.
IV.2.2. Données de test
Nous avons testé notre problème en utilisant
douze ensembles différents d'articles. Nous avons pris ces ensembles
aléatoirement, mais en respectant les limites numériques de
l'algorithme et nous nous sommes arrangés de manière à ce
que les boites à entreposer contiennent exactement dans l'espace de
stockage pour mieux tester la performance de l'algorithme. Vous pouvez trouver
en annexe 1, les détails sur chaque cas que nous avons testé
comprenant la liste d'articles et les dimensions de l'entrepôt.
IV.2.3. Résultat de l'algorithme HI-BHA
Apres usage du logiciel issu de cette recherche les
résultats suivants ont été observés des chacun des
algorithmes (Tableau 6).
Vous pouvez trouver en annexe 1, les détails sur chaque
cas que nous avons testé.
51
Tableau 6 : Résultat du test de l'algorithme HI-BHA
|
Ens. De boite Nbre
de boite
|
Nbre de
type de
boite
|
Nbre
de
boites
chargées
|
Utilisation
de l'espace
(%)
|
Temps
d'exécution
(sec)
|
Ens. N° 1 307 5 291 89,46 1
Ens. N° 2 1728 5 1714 97,46 41
Ens. N° 3 637 11 591 92,40 13
Ens. N° 4 1493 21 1472 96,37 57
Ens. N° 5 86 7 82 91,59 0
Ens. N° 6 12 4 12 100 0
Ens. N° 7 39 15 35 84,47 0
|
Ens. N° 8 (pire des cas)
|
31 31 26 68,65 1
|
IV.2.4. Argumentation sur les résultats de
l'algorithme HI-BHA
De ce tableau, nous constatons que cet algorithme donne des
bons résultats par apport aux facteurs temps et espace
utilisé. En effet, pour presque toutes les instances, les temps
d'exécution de l'algorithme sont tous inférieurs à une
minute, et les pourcentages de l'espace utilisé sont
généralement supérieurs à 85%, sauf pour le pire de
cas où, la performance de l'algorithme baisse mais reste acceptable.
Donc, Plus le nombre de types de boîtes augmente, plus la performance de
l'algorithme diminue et son temps d'exécution augmente. Nous avons
jeté un coup d'oeil sur les résultats de l'algorithme LAFF et
avons constaté que les deux algorithmes semblent identiques au point de
vue temps d'exécution et espace utilisé, ce qui est normal vu
leurs complexités qui sont toutes d'ordre n2. Mais alors, un
autre paramètre comme le non pris en charge de la hauteur de l'espace
d'entreposage nous pousse à opter pour l'algorithme HI-BHA vu que les
entrepôts dont nous faisons allusion dans ce travail sont tous en 3
dimensions, c'est-à-dire qu'ils possèdent tous une longueur, une
largeur et une hauteur finie.
52
IV.3. DIFFICULTES RENCONTREES
Au cours de l'élaboration de ce travail nous nous
sommes heurtés à des difficultés ci-après :
- Nous n'avons pas pu implémenter l'algorithme LAFF,
faute de ressources temporelles, mais nous avons pris les résultats de
cet algorithme testé sur un environnement presque similaire au
nôtre à partir de l'article de (Gürbüz, Akyokuþ,
Emiroðlu, & Güran, 2009), ce qui nous a permis d'avoir une
idée sur les performances de l'algorithme.
- Nous avons eu du mal à produire l'interface graphique
du modèle HI-BHA, faute du compilateur qui manquait les
bibliothèques graphics.h et Xlib.h que nous n'avons pas pu nous
procurer. Mais nous avons réussi à générer un
fichier (.OUT) où une zone présentant une sélection de
colis avec leurs positions et leurs orientation, qui remplit plutôt bien
l'entrepôt est disponible.
- Nous n'avons pas pu tester l'algorithme en fonction des cas
réels de la ville de Butembo. Nous nous sommes heurtés à
des difficultés dans la récolte des données, en fait,
beaucoup de magasinier d'ont aucune idée sur les dimensions des
entrepôts, moins encore des articles. Mais nous avons testé
l'algorithme sur des données générées
aléatoirement tout en respectant les contraintes liées à
l'algorithme.
CONCLUSION
L'optimisation d'entreposages des articles tridimensionnels
dans des aires d'entreposage est un facteur assez important pour réduire
les coûts liés à l'emmagasinage des produits commerciaux et
industriels. Afin d'être compétitif sur le marché, les
entreprises ont besoin d'un outil puissant pour réduire l'ensemble de
leurs dépenses.
Dans ce travail intitulé `'Optimisation heuristique du
problème d'entreposage d'objets en trois dimensions`', notre soucis
était de trouver réponse à la question de savoir s'il
existe une méthode capable de ranger les objets 3D dans des espaces de
stockage 3D de manière maximiser l'espace disponible, le but
étant de proposer une méthode efficace pour optimiser le
chargement des boîtes. La grande complexité de ce problème
et la présence de nombreuses littératures dans ce domaine nous
ont dissuadées de construire nos idées à partir des
méthodes déjà prouvés et jugés
performantes.
Etant donné que le problème d'entreposage que
nous traitons dans ce travail est un problème NP-Difficile et par
conséquent très complexe à résoudre en un temps
polynomiale, nous avons proposé dans ce travail une méthode
heuristique du problème 3D Bin packing. Nous avons analysé deux
algorithmes d'approximation, le Largest Area First-Fit et le fameux Human
Intelligence-Based Heuristic Approach. Tous les deux algorithmes ont
été jugés polynomiaux. Mais alors, nous avons
proposé un seul algorithme qui est le Human Intelligence-Based Heuristic
Approach
54
pour les avantages qu'il offre, entre autre la prise en compte
des rotations d'articles et la considération de la hauteur du
contenant.
Nous avons proposé l'algorithme HI-BHA qui est une
méthode d'approximation qui résout le problème 3DBP ; nous
l'avons présenté sous forme d'ordinogramme. Un prototype
d'application codé en langage C a été mis en place pour
traduire l'algorithme en programme d'application. Nous avons testé ce
modèle et les résultats nous ont montré que le
modèle est bel et bien efficace en donnant des réponses
près de l'optimum allant jusqu'à utiliser 100% de l'espace de
stockage en temps très réduit. Si le modèle proposé
venait à être concrétisé dans les entreprises
commerciales et industriels qui sont concernées par les entreposages
d'objets en 3D, nous osons croire qu'il sera capable de résoudre le
problème ci-haut évoque, celui de permettre à chaque
entrepôt de contenir plus d'articles 3D possible et ainsi réduire
les coûts liés à l'entreposage d'articles.
Loin d'imaginer avoir touché tous les aspects, nous
restons ouverts à toutes les avancées sur ce domaine. En effet,
nous ne prétendons pas avoir proposé le modèle le plus
parfait qui puisse exister. Ainsi donc, tout autre chercheur
intéressé dans ce domaine pourra trouver une autre méthode
plus efficace que celui-ci. Nous suggérons aussi à tous les
travaux futurs de prendre en compte d'autres paramètres comme le poids
des boîtes, le prix et la durée de vie des produits qui est
limitée, l'idéal serait de pouvoir ranger d'abord les
boîtes avec un prix élevé et une courte durée de vie
dans l'entrepôt. Ainsi, nous invitons tous les autres chercheurs à
nous emboîter le pas et restons réceptifs à toutes les
remarques et suggestion.
Wikimepia Foundation. (2008). Optimisation combinatoire.
Consulté en Janvier 2013, sur wikipedia:
http://fr.wikipedia.org/optimisation_combinatoire
55
BIBLIOGRAPHIE
Baltacioglu, E. (2002). The distributer's Three-dimensional
pallet-packing. Washington DC: Air force institute of technologie.
Clautiaux, F. (2010). New collaborative approaches for
bin-packing problems. Lille, France: Université des sciences et
technologies de Lille.
Cordeau, B. (2006). Cours d'algorithme et Langage C.
IUT d'Orsay.
Divay, M. (2004). Algorithmes et structures de
données génériques. Paris, France: Dunod.
Dube, E., & Kanavathy, L. R. (2006). Optimizing
three-dimensional bin packing through simulation. Durban, South Africa:
University of KwaZulu-Natal.
Gazdar, M. (2008). Optimisation heuristique
distribuée du problème de stockage de conteneurs dans un port.
Lille, France: Ecole centrale de lille.
Gürbüz, Z., Akyokuþ, S., Emiroðlu, t.,
& Güran, A. (2009). An efficient Algorithm for 3D Rectangular Box
packing. Republic of Macedonia: Society for ETAI.
Masivi, O. (2012). Cours de Laboratoire informatique II.
Butembo, RDC: UNILUK.
Masivi, O. (2013). Approches méthodologiques de la
recherche scientifique en informatique. Butembo, RDC: UNILUK.
Nebra, M. (2010). Apprenez à programmer en C.
Paris, France: Simple IT.
Nzalamingi, F. (2012). Optimisation de la coupe et
entreposage en une et deux dimensions.(memoire) Butembo, RDC: UNILUK.
Perrot, N. (2005). Integer Programming column generation
strategies for the cutting stock problem and its variants. Bordeaux,
France: University Bordeaux I.
Rohaut, S. (2007). Algorithmique: Techniques fondamentales
de programmation. Edition ENI.
Sanni, L. (2009). Le rôle du système
d'information dans les entreprises d'aujourd'hui. Consulté en Mars
2013, sur lookouster:
http://www.lookouster.org/blog/
role_systeme_information
Scala, R. d. (2004). Les bases de l'informatique et de la
programmation. Alger: Edition Berti.
Wattebled, P. (2010). Résolution heuristique d'un
problème de conception de modules automatiques de rangement. Lille,
France: INRIA.
Wikimedia Foundation. (2000). Problème de
Bin-Packing. Consulté en Mai 2013, sur Wikipedia:
http://fr.wikipedia.org/bin_packing
56
ANNEXES
ANNEXE A : DONNEES DE TEST
Ensemble N° 1
104, 96, 84
1. 3, 5, 7, 51
2. 20, 4, 6, 90
3. 11, 21, 16, 80
4. 51, 2, 60, 80
5. 6, 17, 8, 6
Ensemble N°
3
104, 96, 84
1. 3, 5, 7, 200
2. 9, 11, 2, 29
3. 14, 6, 8, 30
4. 1, 4, 19, 51
5. 10, 13, 21, 12
6. 27, 23, 34, 5
7. 12, 9, 13, 10
8. 24, 15, 19, 50
9. 5, 16, 9, 100
10. 10, 20, 5, 100
11. 9, 18, 15, 50
Ensemble N°
2
104, 96, 84
1. 3, 5, 7, 200
2. 9, 11, 2, 290
3. 14, 6, 8, 300
4. 1, 4, 19, 748
5. 10, 13, 21, 190
Ensemble N°
4
104, 96, 84
1. 1, 2, 3, 200
2. 2, 4, 5, 200
3. 6, 7, 1, 200
4. 6, 8, 2, 29
5. 11, 2, 3, 29
6. 9, 4, 2, 29
7. 14, 5, 3, 30
8. 10, 4, 6, 30
9. 11, 8, 3, 30
10. 1, 2, 19, 50
11. 8, 13, 11, 50
12. 1, 3, 21, 10
13. 8, 9, 10, 30
14. 7, 13, 31, 115
15. 12, 66, 3, 30
16. 4, 15, 19, 90
17. 5, 16, 9, 100
18. 10, 2, 5, 100
19. 10, 10, 1, 90
20. 9, 18, 15, 50
21. 6, 9, 14, 1
Ensemble N°
5
104, 96, 84
1. 28, 32, 18, 9
2. 24, 21, 35, 16
3. 19, 26, 20, 4
4. 19, 26, 16, 16
5. 16, 26, 20, 4
6. 20, 20, 26, 1
7. 16, 14, 25, 36
Ensemble N°
6
104, 96, 84
1. 70, 45, 24, 4
2. 70, 59, 24, 4
3. 14, 40, 48, 2
4. 14, 64, 48, 2
57
|
Ensemble N°
7
|
|
|
Ensemble N°
8
|
|
|
104, 96, 84
|
|
104, 96, 84
|
|
|
1. 19, 20, 42,
|
2
|
|
1.
|
1, 2, 3, 1
|
|
|
2.
|
25, 20, 30,
|
1
|
|
2.
|
4, 5, 6, 1
|
|
3.
|
|
25, 20, 25,
|
1
|
|
3.
|
7, 8, 9, 1
|
|
|
|
4.
|
25, 20, 29,
|
1
|
|
4.
|
10,
|
11, 12,
|
1
|
|
5.
|
8, 20, 21, 4
|
|
|
5.
|
13,
|
14, 15,
|
1
|
|
6.
|
36, 46, 84,
|
1
|
|
6.
|
16,
|
17, 18,
|
1
|
|
7.
|
16, 46, 10,
|
2
|
|
7.
|
19,
|
20, 21,
|
1
|
|
8.
|
16, 46, 32,
|
2
|
|
8.
|
22,
|
23, 24,
|
1
|
|
9.
|
20, 30, 15,
|
1
|
|
9.
|
25,
|
26, 27,
|
1
|
|
10.
|
20, 30, 69,
|
1
|
|
10.
|
28,
|
29, 30,
|
1
|
|
11.
|
20, 30, 21,
|
4
|
|
11.
|
31,
|
32, 33,
|
1
|
|
12.
|
12, 30, 7,
|
12
|
|
12.
|
34,
|
35, 36,
|
1
|
|
13.
|
52, 60, 42,
|
2
|
|
13.
|
37,
|
38, 39,
|
1
|
|
14.
|
26, 36, 21,
|
4
|
|
14.
|
40,
|
41, 42,
|
1
|
|
15.
|
26, 36, 84,
|
1
|
|
15.
|
43,
|
44, 45,
|
1
|
|
|
|
|
16.
|
46,
|
47, 48,
|
1
|
|
17.
|
2,
|
3, 4, 1
|
|
|
|
|
|
|
|
18.
|
5,
|
6, 7, 1
|
|
|
|
|
19.
|
8,
|
9, 10, 1
|
|
|
|
|
20.
|
11,
|
12, 13,
|
1
|
|
|
|
21.
|
14,
|
15, 16,
|
1
|
|
|
|
22.
|
17,
|
18, 19,
|
1
|
|
|
|
23.
|
20,
|
21, 22,
|
1
|
|
|
|
24.
|
23,
|
24, 25,
|
1
|
|
|
|
25.
|
26,
|
27, 28,
|
1
|
|
|
|
26.
|
29,
|
30, 31,
|
1
|
|
|
|
27.
|
32,
|
33, 34,
|
1
|
|
|
|
28.
|
35,
|
36, 37,
|
1
|
|
|
|
29.
|
38,
|
39, 40,
|
1
|
|
|
|
30.
|
41,
|
42, 43,
|
1
|
|
|
|
31.
|
44,
|
45, 46,
|
1
|
58
ANNEXE B : CODES C DE QUELQUES FONCTIONS DE L'ALGORITHME
HUMAN INTELLIGENCE - BASED HEURISTIC APPROACH
//les directives du préprocesseur
#include <time.h>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <malloc.h>
#include <conio.h>
//fonction main
int main(int argc, char *argv[]) j
if (argc == 1) j
printf("(ASSUREZ VOUS QUE VOUS AVEZ UN FICHIER .TXT
CONTENANT LES VARIABLES ENTRANTES)\n");
printf ("ENTREZ LE NOM DU FICHIER D'ENTREES S.V.P :");
scanf ("%s",filename);
}
else
j
printf("%s", argv[1]);
strcpy(filename, argv[1]);
}
initialize();
time(&start);
printf("\nAPPUIYEZ SUR Q POUR ARRETER
L'ITERATION\n\n");
execiterations();
time(&finish);
report();
getch();
return 0;
}
//lectures des coordonnées largeur, hauteur et
profondeur entrées dans le fichier txt
void inputboxlist(void)j
short int n;
char lbl[5], dim1[5], dim2[5], dim3[5], boxn[5],
strxx[5], stryy[5], strzz[5];
strcpy(strtemp, filename);
strcat(strtemp,".txt");
if ((ifp=fopen(strtemp,"r"))==NULL) j
printf("Impossible d'ouvrir le fichier %s",
strtemp);
exit(1);
}
tbn=1;
if (fscanf(ifp,"%s %s %s",strxx, stryy, strzz)==EOF)j
exit(1);
}
xx=atoi(strxx); yy=atoi(stryy);
zz=atoi(strzz);
59
while (fscanf(ifp,"%s %s %s
%s",lbl,dim1,dim2,dim3,boxn)!=EOF){
boxlist[tbn].dim1=atoi(dim1); boxlist[tbn].dim2=atoi(dim2);
boxlist[tbn].dim3=atoi(dim3);
boxlist[tbn].vol=boxlist[tbn].dim1*boxlist[tbn].dim2*boxlist[t
bn].dim3;
n=atoi(boxn);
boxlist[tbn].n=n;
while (--n){
boxlist[tbn+n]=boxlist[tbn];
}
tbn=tbn+atoi(boxn);
}
--tbn;
fclose(ifp);
return;
}
//recherche de la caisse la plus appropriée en cherchant
toutes les
//six orientations possibles, l'espace vide
donnée, les caisses
//adjacentes et la limite de l'entrepôt
void findbox(short int hmx, short int hy, short int hmy, short
int hz, short int hmz)
{
short int y;
bfx = 32767; bfy = 32767; bfz = 32767;
bbfx = 32767; bbfy = 32767; bbfz = 32767;
boxi = 0; bboxi = 0;
for (y = 1; y <= tbn; y = y + boxlist[y].n)
{
for (x = y; x < x + boxlist[y].n - 1; x++)
{
if (!boxlist[x].packst) break;
}
if (boxlist[x].packst) continue;
if (x > tbn) return;
analyzebox(hmx, hy, hmy, hz, hmz,
boxlist[x].dim1,
boxlist[x].dim2, boxlist[x].dim3);
if ( (boxlist[x].dim1 == boxlist[x].dim3) &&
(boxlist[x].dim3 == boxlist[x].dim2) ) continue;
analyzebox(hmx, hy, hmy, hz, hmz, boxlist[x].dim1,
boxlist[x].dim3, boxlist[x].dim2);
analyzebox(hmx, hy, hmy, hz, hmz, boxlist[x].dim2,
boxlist[x].dim1, boxlist[x].dim3);
analyzebox(hmx, hy, hmy, hz, hmz, boxlist[x].dim2,
boxlist[x].dim3, boxlist[x].dim1);
analyzebox(hmx, hy, hmy, hz, hmz, boxlist[x].dim3,
boxlist[x].dim1, boxlist[x].dim2);
analyzebox(hmx, hy, hmy, hz, hmz,
boxlist[x].dim3,
boxlist[x].dim2, boxlist[x].dim1);
}
}
//analyses de chaque caisse non chargée pour trouver
le meilleure
//emplacement dans l'entrepôt
//recherche de la couche ayant la hauteur la plus
appropriées
60
void analyzebox (short int hmx, short int hy, short int
hmy,
short int hz, short int hmz, short int dim1, short int
dim2,
short int dim3)j
if (dim1<=hmx && dim2<=hmy &&
dim3<=hmz)j
if (dim2<=hy) j
if (hy-dim2<bfy) j
boxx=dim1;
boxy=dim2;
boxz=dim3;
bfx=hmx-dim1;
bfy=hy-dim2;
bfz=abs(hz-dim3);
boxi=x;
}
else if (hy-dim2==bfy && hmx-dim1<bfx)
j
boxx=dim1;
boxy=dim2;
boxz=dim3;
bfx=hmx-dim1;
bfy=hy-dim2;
bfz=abs(hz-dim3);
boxi=x;
}
else if (hy-dim2==bfy && hmx-dim1==bfx &&
abs(hz-
dim3)<bfz) j
boxx=dim1;
boxy=dim2;
boxz=dim3;
bfx=hmx-dim1;
bfy=hy-dim2;
bfz=abs(hz-dim3);
boxi=x;
}
}
else j
if (dim2-hy<bbfy) j
bboxx=dim1; bboxy=dim2; bboxz=dim3; bbfx=hmx-dim1;
bbfy=dim2-hy; bbfz=abs(hz-dim3); bboxi=x;
}
else if (dim2-hy==bbfy && hmx-dim1<bbfx) j
bboxx=dim1; bboxy=dim2; bboxz=dim3; bbfx=hmx-dim1; bbfy=dim2-hy;
bbfz=abs(hz-dim3); bboxi=x;
}
else if (dim2-hy==bbfy && hmx-dim1==bbfx
&& abs(hz-dim3)<bbfz) j
bboxx=dim1; bboxy=dim2; bboxz=dim3; bbfx=hmx-dim1;
bbfy=dim2-hy; bbfz=abs(hz-dim3); bboxi=x;
}
}
}
}
//fonction exigée pour le fonctionnement de la
fonction QSORT int complayerlist(const void *i, const void *j)j
return *(long int*)i-*(long int*)j;
}
}
61
//en cherchant les boites non encore chargées
et l'espace vide //encore disponible
int findlayer( short int thickness) j
short int exdim,dimdif,dimen2,dimen3,y,z; long int
layereval, eval;
layerthickness=0;
eval=1000000;
for(x=1;x<=tbn;x++)j
if (boxlist(x].packst) continue;
for(y=1;y<=3;y++)j
switch(y) j
case 1:
exdim=boxlist(x].dim1; dimen2=boxlist(x].dim2;
dimen3=boxlist(x].dim3; break;
case 2:
exdim=boxlist(x].dim2; dimen2=boxlist(x].dim1;
dimen3=boxlist(x].dim3; break;
case 3:
exdim=boxlist(x].dim3; dimen2=boxlist(x].dim1;
dimen3=boxlist(x].dim2; break;
}
layereval=0;
if ((exdim<=thickness) && (((dimen2<=px)
&& (dimen3<=pz)) || ((dimen3<=px) && (dimen2<=pz)))) j
for(z=1;z<=tbn;z++)j
if (!(x==z) && !(boxlist(z].packst))j
dimdif=abs(exdim-boxlist(z].dim1); if (abs(exdim-
boxlist(z].dim2)<dimdif)j
dimdif=abs(exdim-
boxlist(z].dim2);
}
if (abs(exdim-
boxlist(z].dim3)<dimdif)j
dimdif=abs(exdim-
boxlist(z].dim3);
}
layereval=layereval+dimdif;
}
}
if (layereval<eval) j
eval=layereval;
layerthickness=exdim;
}
}
}
}
if (layerthickness==0 || layerthickness>remainpy)
packing=0;
return 0;
62
//recherche du premier vide à être
chargée
//au bord de la couche
void findsmallestz(void) j
scrapmemb=scrapfirst;
smallestz=scrapmemb;
while (!((*scrapmemb).pos==NULL)) j
if((*((*scrapmemb).pos)).cumz<(*smallestz).cumz)j
smallestz=(*scrapmemb).pos;
}
scrapmemb=(*scrapmemb).pos;
}
return;
}
//utilisation des paramètres trouvées pour
le chargement de la
meilleure solution trouvée et envoie du rapport
à la console
et au fichier OUT
void report(void)j
quit=0;
switch(bestvariant) j
case 1:
px=xx; py=yy; pz=zz;
break;
case 2:
px=zz; py=yy; pz=xx;
break;
case 3:
px=zz; py=xx; pz=yy;
break;
case 4:
px=yy; py=xx; pz=zz;
break;
case 5:
px=xx; py=zz; pz=yy;
break;
case 6:
px=yy; py=zz; pz=xx;
break;
}
packingbest=1;
if ((gfp=fopen(graphout,"w"))==NULL) j
printf("Impossible de lire le fichier %s", filename);
exit(1);
}
itoa(px, strpx, 10); itoa(py, strpy, 10); itoa(pz, strpz,
10); fprintf(gfp,"%5s%5s%5s\n",strpx,strpy,strpz); strcat(filename,".out"); if
((ofp=fopen(filename,"w"))==NULL) j
printf("Impossible d'ouvrir le fichier %s", filename);
exit(1);
}
percentagepackedbox=bestvolume*100/totalboxvol;
percentageused=bestvolume*100/totalvolume;
elapsedtime = difftime( finish, start);
fprintf(ofp," *** RAPPORT DE LA MEILLEURE SOLUTION
***\n\n");
fprintf(ofp," TEMPS ECOULE
:environ %.0f sec\n", elapsedtime);
}
63
|
fprintf(ofp," itenum);
fprintf(ofp,"
|
NOMBRE TOTAL D'ITERATIONS MEILLEURE SOLUTION TROUVEE A
LA
|
:
:
|
%d\n", %d
|
|
ITERATION\n", bestite);
fprintf(ofp," NOMBRE TOTAL DE BOITES tbn);
fprintf(ofp," NOMBRE DE BOITES CHARGEES
bestpackednum);
|
:
:
|
%d\n", %d\n",
|
|
fprintf(ofp,"
|
VOLUME TOTAL DE TOUTES LES BOITES:
|
|
%.0f\n",totalboxvol);
fprintf(ofp," VOLUME DE L'ENTREPOT
:
%.0f\n",totalvolume);
fprintf(ofp," UTILISATION DU VOLUME :%.0f
SUR %.0f\n",
bestvolume, totalvolume);
fprintf(ofp," POURCENTAGE DE L'ESPACE UTILISE :
%.6f
%%\n", percentageused);
fprintf(ofp," DIMENSIONS DE L'ENTREPOT :
X=%d; Y=%d; Z=%d\n", px, py, pz);
fprintf(ofp,"
fprintf(ofp," POURCENTAGE DES BOITES CHARGEES (VOLUME) :
%.6f %%\n",percentagepackedbox);
\n");
fprintf(ofp," NO: PACKSTA DIMEN-1 DIMEN-2 DIMEN-3 COOR-X
COOR-Y COOR-Z PACKEDX PACKEDY PACKEDZ\n");
fprintf(ofp," \n");
listcanditlayers();
layers[0].layereval=-1;
qsort(layers,layerlistlen+1,sizeof(struct
layerlist),complayerlist);
packedvolume=0.0;
packedy=0;
packing=1;
layerthickness=layers[bestite].layerdim;
remainpy=py;
remainpz=pz;
for (x=1; x<=tbn; x++){
boxlist[x].packst=0;
}
do{
layerinlayer=0; layerdone=0;
packlayer();
packedy=packedy+layerthickness;
remainpy=py-packedy;
if(layerinlayer){
prepackedy=packedy;
preremainpy=remainpy;
remainpy=layerthickness-prelayer;
packedy=packedy-layerthickness+prelayer; remainpz=lilz;
layerthickness=layerinlayer;
layerdone=0; packlayer();
packedy=prepackedy;
remainpy=preremainpy;
remainpz=pz;
}
if (!quit){
findlayer(remainpy);
}
64
while (packing && !quit);
fprintf(ofp,"\n\n*** LISTE DES BOITES NON CHARGEES ***\n");
unpacked=1;
for (cboxi=1; cboxi<=tbn; cboxi++)j
if(!boxlist[cboxi].packst)j
graphunpackedout();
}
}
unpacked=0;
fclose(ofp);
fclose(gfp);
printf("\n");
for (n=1; n<=tbn; n++)
if (boxlist[n].packst)
printf("%d %d %d %d %d %d %d %d %d %d\n",n,
boxlist[n].dim1,boxlist[n].dim2,boxlist[n].dim3,boxlist[n].cox
,boxlist[n].coy,boxlist[n].coz,boxlist[n].packx,boxlist[n].pac
ky,boxlist[n].packz);
printf(" TEMPS ECOULE : environ
%.0f sec\n",elapsedtime);
printf(" NOMBRE TOTAL D'ITERATIONS : %d\n",
itenum);
printf(" MEILLEUR RESULTAT TROUVE A :
ITERATION: %d\n", bestite);
printf(" NOMBRE TOTAL DES BOITES : %d\n",
tbn);
printf(" NOMBRE TOTAL DES BOITES CHARGEES :
%d\n",bestpackednum);
printf(" VOLUME TOTAL DE TOUTES LES BOITES :
%.0f\n",totalboxvol);
printf(" VOLUME DE L'ENTREPOT : %.0f\n",
totalvolume);
printf(" UTILISATION DU L'ESPACE : %.0f SUR
%.0f\n",
bestvolume, totalvolume);
printf(" POURCENTAGE SU VOLUME TOTAL UTILISE: %.6f
%%\n",percentageused);
printf(" POURCENTAGE DES BOITES CHARGEES (VOLUME): %.6f
%%\n",percentagepackedbox);
printf(" DIMENSIONS DE L'ENTREPOT : X=%d;
Y=%d; Z=
%d\n\n\n", px, py, pz);
printf(" POUR VOIR CETTE SOLUTION EN GRAPHIQUE, EXECUTEZ
'VISUAL.EXE'\n");
}
printf(" DESOLE QUE CELA N'ACCEPTE PAS POUR LE MOMENT, NOUS
NOUS EXCUSONS\n");
| 


