III.1.2. Méthodes exactes
Le problème de chargement d'entrepôt que nous
tentons de modéliser dans ce chapitre est en fait rattachable au
problème de 3D bin packing, une extension au problème de
remplissage de sacs, ce qui explique son NP complétude.
25
Tous les algorithmes exactes connus pour résoudre des
problèmes NP-complets ont un temps d'exécution exponentiel en la
taille des données d'entrée dans le pire cas, ils sont donc
inexploitables en pratique car bien qu'ils résolvent les
problèmes NP-C en donnant des réponses exactes, ils sont couteux
en terme de temps d'exécution.
L'algorithme exact consiste à essayer toutes les
combinaisons d'objets et choisir celle qui minimise le nombre de panier. Il
faut d'abord deviner toutes les solutions réalisables puis
vérifier chaque alternative. On parle alors d'un divin et d'un
vérificateur, le divin propose un certificat, c'est-à-dire, une
réponse probable ou encore un candidat-réponse et le
vérificateur teste si le certificat remplit les conditions d'être
une réponse.
En ce qui nous concerne ici, l'algorithme exact est donc celui
dont le divin fournit plusieurs ensembles d'articles (caisses ou boîtes)
provenant d'une liste de plusieurs articles. Il essaie toutes les combinaisons
possibles, chaque ensemble constitue un candidat-réponse à la
question de savoir quel ensemble d'articles maximise l'utilisation de
l'entrepôt. Le vérificateur vérifie si chaque ensemble
remplit les contraintes en se posant les questions ci-après :
- Dans un ensemble d'articles ni existe-t-il un article dont
la hauteur (hi), la largeur (li) ou la profondeur (pi) est supérieur
à la hauteur (H), la largeur (L) ou la profondeur (P) de
l'entrepôt ? Tout en sachant que l'objet peut être roté et
donc, on considère comme hi, li ou pi finale, sa valeur après
dernière rotation.
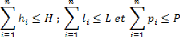
- Est-ce que la taille (volume) d'un ensemble d'articles (ni)
dépasse la taille de l'espace de stockage ?
26
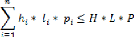
Tout en sachant que l'objectif est de minimiser l'espace non
utilisé, c'est-à-dire la différence entre le volume de
l'espace de stockage et le volume de toutes les boîtes
chargées.
Cette solution donne une réponse exacte mais
malheureusement il est couteux. Pour pallier à ce problème
lié au temps d'exécution, il existe les algorithmes
d'approximation. Ceux-ci qui permettent de résoudre un problème
NP-complet en donnant une solution presque optimale en temps polynomial.
III.1.3. Méthodes approximatives (heuristiques)
Les algorithmes d'approximations sont utilisés pour
réduire la complexité des problèmes de classe NP-Hard.
Comme nous l'avons déjà dit dans notre
introduction, nous présentons dans ce travail quelques algorithmes
d'approximation que nous allons ensuite implémenter dans un langage de
programmation et les soumettre à une expérimentation pour trouver
le plus performant en terme de temps d'exécution et d'espace de
l'entrepôt utilisé. Notre objectif est donc de répertorier
quelques algorithmes existants pour le problème de 3D Bin packing et
trouver le plus performant.
Dans cette section nous allons présenter 2 algorithmes
de 3D Bin packing : l'algorithme HI-BHA (A Human Intelligence-Based
Heuristic Approach) proposé par (Baltacioglu, 2002) et le LAFF
(Largest Area First-Fit) développé par
(Gürbüz, Akyokuþ, Emiroðlu, & Güran, 2009).
27
1. A Human Intelligence Based Heuristic
Approach
Le problème de 3DBP est toujours résolu en
utilisant les algorithmes optimums et les méthodes heuristiques. Voici
une méthode heuristique parmi plusieurs qui essaie de résoudre le
problème en un temps polynomiale.
Cette approche a été qualifiée d'une
approche basée sur l'intelligence humaine par son auteur du fait qu'elle
simule l'intelligence humaine en chargeant les boîtes dans
l'entrepôt comme un humain, de bas à haut et en construisant des
couches.
Ce modèle utilise un outil puissant de l'heuristique et
une structure de données dynamique qui lui permet d'imiter
l'intelligence humaine. L'avantage de cet algorithme est qu'il est capable de
charger l'article dans n'importe quelle orientation, tout en sachant qu'un
article peut être roté de six manières différentes.
Cette approche est basée sur la construction des couches ou murs.
L'idée est qu'après la création d'une couche, avant qu'une
boîte soit chargée dans la couche, l'algorithme analyse toutes les
boîtes non chargées pour trouver celle qui conviendra le mieux au
sein de la couche selon son épaisseur (hauteur) pour minimiser l'espace
perdu. Cependant, l'épaisseur de la couche sélectionnée
est flexible et peut augmenter pour s'adapter à la hauteur de la
boîte sélectionnée.
Variables entrantes (inputs)
Les premières variables entrants sont les
coordonnées x, y et z qui représentent les dimensions de l'espace
de stockage. Les informations suivantes représentent les
caractéristiques des boîtes à entreposer. Dans chaque ligne
le premier élément représente l'étiquette de la
boîte contenant les articles, ces étiquettes n'ont aucun effet sur
l'algorithme, ce n'est qu'une façon d'identifier chaque boîte,
elles sont facultatives, le deuxième, troisième et
quatrième élément correspondent respectivement aux
coordonnées x, y et z de chaque boîte. Le cinquième
élément
28
représente le nombre de boîte de même type,
c'est-à-dire le nombre de boîtes ayant la même largeur (x),
la même hauteur (y) et la même profondeur (z).
Structuration des données
La structure de données est un critère assez
important dans un programme, elle affecte de manière directe le
résultat de la solution d'un algorithme que ce soit en terme de temps
d'exécution ou en terme d'espace utilisé.
Cet algorithme utilise deux tableaux : la premier tableau est
celui de la liste des boîtes dénommé `'BoxList[]
Array`', il sert à garder toutes les dimensions, les
coordonnées et d'autres informations nécessaires relatives aux
boîtes dans une liste. Il a au total douze champs :
Tableau 1 : Liste des champs dans le `'BoxList[] Array `'
Noms du champs Descriptions
Packst L'état du chargement {0:Non chargé,
1:Chargé)
N Nombre de boîtes identiques
Dim1 La taille d'une des trois dimensions
Dim2 La taille d'une autre dimension parmi les trois
Dim3 La taille d'une autre dimension parmi les trois
Cox La coordonnée x de l'emplacement de la boîte
chargée
Coy La coordonnée y de l'emplacement de la boîte
chargé
Coz La coordonnée z de l'emplacement de la boîte
chargé
Packx La dimension x de la boîte après rotation
Packy La dimension y de la boîte après rotation
Packz La dimension z de la boîte après rotation
Vol Le volume de la boîte (Dim1*Dim2*Dim3)
Cet algorithme stocke aussi le volume de chaque boîte,
ainsi on n'a pas besoin de le recalculer à chaque instant qu'on en a
besoin. Les champs 6 à 11 n'ont pas de sens si le premier (Packst) a
comme valeur 0, ils deviennent importants une fois qu'on a chargé la
première boîte et Packst devient égal à 1. Chaque
boîte constitue une ligne d'enregistrement dans le tableau `'BoxList[]
`'.
29
Un autre tableau est le `'Layers[]`'. Ce
tableau stocke les différentes tailles de toutes les dimensions des
boîtes. Chaque champ dénommé Layerdim représente
l'épaisseur d'une couche créée au sein de l'espace de
stockage. Avant le commencement de chaque boucle (itération), les
différentes valeurs des dimensions des boîtes sont stockées
dans ce tableau. Le deuxième champ de ce tableau est le Layereval, la
valeur de ce champ est calculée par la fonction Listcanditlayers que
nous allons expliquer plus tard dans le quatrième chapitre de ce
travail. Voici donc les deux champs du tableau Layereval :
Tableau 2 : Liste de champs dans le `'Layers[] Array `'.
Noms Descriptions
Layerdim La valeur d'une dimension
Layereval Evaluation de la valeur correspondante du Layerdim
Contraintes de l'algorithme
Les limites de l'algorithme HI-BHA sont d'après le
concepteur dues à la capacité
moyenne de mémoires des ordinateurs et à l'ampleur
du problème réel de
chargement d'entrepôt. Voici donc les limites à ne
pas franchir :
Nombre maximal de boîtes dans un ensemble de boîtes :
5000
Nombre total des boîtes ayant des caractéristiques
différentes : 1000
Tous les nombres doivent être en entier.
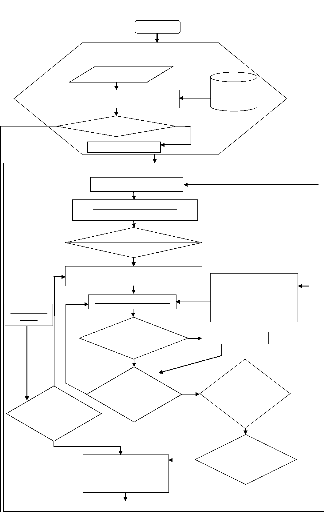
Ordinogramme
Ceci est une représentation graphique de l'enchainement
des opérations de ce qui
constituera le fruit de l'implémentation de l'algorithme
HI-BHA (le programme
proprement dit). Il nous permet donc d'analyser notre
problème.
Avant l'exécution de l'algorithme, on doit s'assurer du
respect des critères ci-
après :
30
- Chaque espace de stockage doit posséder une largeur et
une profondeur et une hauteur bien finie ;
- Chaque boîte à entreposer doit aussi avoir une
largeur, une profondeur et une hauteur ;
- Toutes les boîtes peuvent être rotée et
placée dans n'importe quel angle dans l'entrepôt ;
- Les boîtes peuvent se supporter les unes sur les autres
sans créer des dommages.
31
Début
INITIALISATION
Entrées des variables
INPUT BOXLIST Lecture du fichier
Fichier des
variables
entrantes
Si variables Incorrectes
Non
Initialisation des variables
EXECITERATIONS
Essaie d'une orientation de la boîte
LISTCANDIDATETLAYERS Creation de
Layers[]Array
QSORT
Trie du Layers[]
Prise en compte d'un enregistrement du Layers[] comme
l'épaisseur (hauteur) de la couche
PACKLAYER(laverthickness)
PACKLAYER (space)
FINDLAYER(remainpy)
Trouve la couche ayant la
hauteur la plus convenable en
examinant les boîtes
non
chargées.
Il y a un espace pour la
création d'une
couche
dans la couche ?
OUI
PACKLAYER(space)
NON
NON
OUI
NON
OUI
Il y a un espace pour
le chargement d'une
boîte
dans la
couche ?
Toutes les layers[]
sont
déjà
utilisées ?
Il y a un espace
pour le chargement
d'une boîte
dans
l'espace de
stockage ?
NON
OUI
OUI
NON
Toutes orientations
des boîtes ont
déjà
été testées ?
Meilleur utilisation de l'espace de stockage garde l'orientation
de la boîte et la hauteur de la couche
Msg : Les Données entrées incorrectes, veuillez
entrer les vraies valeurs
Saisie de `O'
Fichier du rapport de la meilleure solution
FIN
32
Figure 5 : Ordinogramme de l'algorithme HI-BHA
Fonctionnement de l'algorithme
HI-BHA
Nous allons expliquer dans ce point le fonctionnement et
l'obtention des valeurs de différents champs des tableaux
détaillés un peu plus haut dans ce troisième chapitre, il
s'agit de `'BoxList[]» et de `'Layers[]». Ceci en nous basant d'un
exemple typique.
Exemple : soit un entrepôt de 104 dm de long, 96 dm de haut
et 84 dm de profondeur. On décide de ranger 9 caisses dans cet
entrepôt dont 4 de dimensions (70, 104, 84), 2 de dimensions (14, 104,
48) et 3 de dimensions (40, 52, 36). BOXLIST[]Array
Tableau 3 : Création du tableau BOXLIST[]
Taille de l'entrepôt : XX=104
; YY=96 ; ZZ=84
|
Boxlist[x]
|
Packst
|
N
|
Dim1
|
Dim2
|
Dim3
|
Cox
|
Coy
|
Coz
|
Packx
|
Packy
|
Packz
|
Vol
|
|
Boxlist[1]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[2]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[3]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[4]
|
0
|
4
|
70
|
104
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
174720
|
|
Boxlist[5]
|
0
|
2
|
14
|
104
|
48
|
0
|
0
|
0
|
0
|
0
|
0
|
69888
|
|
Boxlist[6]
|
0
|
2
|
14
|
104
|
48
|
0
|
0
|
0
|
0
|
0
|
0
|
69888
|
|
Boxlist[7]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
|
Boxlist[8]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
|
Boxlist[9]
|
0
|
3
|
40
|
52
|
36
|
0
|
0
|
0
|
0
|
0
|
0
|
74880
|
33
Après avoir entrée les variables entrantes, le
modèle détermine les hauteurs des couches et les entre dans un
tableau, le `'Layers[]». Ce tableau contient une dimension de chaque
boîte moins la dimension y de l'espace de stockage. Le tableau LAYERS[]
est créé après l'examen de chaque orientation des
boîtes.
Avec le même exemple, voyons maintenant comment obtenir
les valeurs des champs dans le tableau Layers[].
XX=104 ; YY=96 ; ZZ=84
Layers[x]=(Layerdim, Layereval)
Layers[X]=(Layerdim, Layereval)
Abs(70-70) + Abs(70-70) + Abs(70-70) + Abs(70-48) + Abs(70-48) +
Abs(70-52) +
Abs(70-52) + Abs(70-52) = 98
Layers[l]=(70, 98)
Abs(24-24) + Abs(24-24) + Abs(24-24) + Abs(24-14) + Abs(24-14) +
Abs(24-36) +
Abs(24-36) + Abs(24-36) = 56
Layers[2]=(24, 56)
Abs(14-24) + Abs(14-24) + Abs(14-24) + Abs(14-24) + Abs(14-14) +
Abs(14-40) +
Abs(14-40) + Abs(14-40) = 106
Layers[3]=(14,106)
Abs(48-70) + Abs(48-70) + Abs(48-70) + Abs(48-70) + Abs(48-48) +
Abs(48-40) +
Abs(48-40) + Abs(48-40) = 100
Layers[4]=(48,100)
Abs(40-24) + Abs(40-24) + Abs(40-24) + Abs(40-24) + Abs(40-48) +
Abs(40-48) +
Abs(40-40) + Abs(40-40) = 80
Layers[5]=(40, 80)
Abs(52-70) + Abs(52-70) + Abs(52-70) + Abs(52-70) + Abs(52-48) +
Abs(52-48) +
Abs(52-52) + Abs(52-52) = 80
Layers[6]=(52, 80)
Abs(36-24) + Abs(36-24) + Abs(36-24) + Abs(36-24) + Abs(36-48) +
Abs(36-48) +
Abs(36-36) + Abs(36-36) = 72
Layers[7]=(36, 72)
34
Normalement il y aurait 8 valeurs au total, mais comme la
dimension y de certaines boîtes est supérieure à celle de
l'espace de stockage, on ne peut pas évaluer ça comme une hauteur
de la couche.
Après l'obtention des valeurs du Layer[], on les trie
dans l'ordre croissant d'après chaque Layereval.
Tableau 4 : Création du tableau Layers[]
|
Layers[X]=(Layerdim, Layereval) Layer[1]=(24, 56)
Layer[2]=(36, 72) Layer[3]=(52, 80) Layer[4]=(40, 80) Layer[5]=(70, 98)
Layer[6]=(48, 100) Layer[7]=(14, 106)
|
Comme la plus petite Layereval peut être la hauteur la
plus convenable pour une couche, trier la liste de ces champs selon l'ordre
croissant est un facteur important dans le but de réduire le temps
d'exécution d'une solution, spécialement lorsqu'on veut charger
un nombre élevé de boîte de différentes tailles.
Complexité de l'algorithme
HI-BHA
Les itérations de cet algorithme sont liées aux
six orientations possibles que peut prendre une boîte. Pendant les
itérations, les boîtes sont d'abord chargées dans toutes
les six orientations. Chaque orientation de la boîte est
considérée comme une solution de chargement. Evidemment si toutes
les trois dimensions d'une boîte sont identiques, c'est-à-dire si
la boîte est carrée, il n'y a qu'une seule orientation possible.
Généralement on a soit un, deux ou six orientations
respectivement pour un, deux ou trois dimensions différentes. Dans
chaque itération, chaque orientation de la boîte est chargé
une fois dans chaque champs du tableau `'Layers[]».
Ainsi, comme dans notre exemple, nous avons sept
différentes dimensions dans notre tableau `'Layers[]`' et que toutes nos
boîtes on trois dimensions uniques,
35
l'algorithme va effectuer 6*7=42 itérations. Ainsi, le
temps d'exécution de cet algorithme dépend du type de boîte
(celles avec une dimension, deux dimensions ou trois dimensions) et du nombre
total des boîtes à charger. Le nombre de boîtes identiques
(celle avec les mêmes dimensions) n'affecte pas directement le temps
d'exécution de cet algorithme.
Maintenant, nous pouvons déterminer la
complexité de l'algorithme HI-BHA. Supposons que nous avons n
boîtes dans un ensemble de boîtes et d, la valeur des dimensions de
toutes les boîtes. Dans le pire de cas, le temps d'exécution sera
:
1'(t)=6 n d P(t) ; (1)
Où P(t) est le temps utilisé pour trouver et ranger
chaque boîte.
P(t)=6 n E(t) ; (2)
Où E(t) est le temps utilisé pour examiner
l'orientation d'une boîte. E(t) dépend
d'un ordinateur à un autre.
Ainsi, dans le pire de cas, la complexité de cet
algorithme est :
1'(t)=36 n2 d E(t).
Ainsi, la complexité de cet algorithme est
Ø(nk) avec comme k une constante et toujours
égale à 2.
2. Largest Area First-Fit
Dans cette section de notre travail, nous présentons un
autre algorithme heuristique que nous n'allons pas implémenter suite au
temps qui nous est insuffisant mais dont les résultats seront
comparés au premier. Le LAFF algorithme résout lui aussi le 3DBPP
en un temps polynomial. Nous allons présenter cet algorithme en
définissant de prime à bord les variables entrantes et sortantes.
Cet algorithme est
36
appelé LAFF minimizing heigth. Il place les
boîtes à une plus grande surface en minimisant la hauteur du
container.
Variables entrantes (inputs)
La première variable à entrer est le nombre de
boîtes de taille différentes noté N. La deuxième
entrée c'est les dimensions de chaque type des boites de tailles
différentes. Nous notons cela par quatre paramètres (an, bn, cn,
kn) où an est la largeur, bn est la profondeur, cn est la hauteur et kn,
le nombre de boîtes pour une dimension donnée.
Comme vous pouvez le voir sur une boîte, chaque
dimension peut être considérée en largeur, en hauteur ou
profondeur. Si vous prenez bn comme la largeur, les autres dimensions
c'est-à-dire an et cn peuvent être acceptés comme hauteur
ou profondeur. Parce que, la boîte est tridimensionnelle et elle peut
être roté et peut être envisagé en des perspectives
différentes. La liste suivante montre les paramètres à
entrer proposés par l'algorithme :
Nombre des boîtes de tailles différentes : : N
Largeur de la boîte : : an
Profondeur de la boîte : : bn
Hauteur de la boîte : : cn
Nombre de boîte par dimension : : kn
Variables sortantes (outputs)
Après l'exécution de l'algorithme LAFF, le
programme doit produire les outputs ci-après :
O1: Le volume de l'espace
O2: L'espace utilisé (Le volume de toutes les
boîtes déjà placées)
O3: L'espace non utilisé
37
O4: Le temps d'exécution (exprimée en
millisecondes).
Fonctionnement de l'algorithme
LAFF
Comme déjà signalé le problème de
3D bin packing est du genre NP-Complet, c'est-à-dire que la solution
optimum pour ce problème ne peut être trouvée
qu'après avoir essayé toutes les combinaisons possibles. C'est
donc un problème difficile. Cependant, si le nombre de boîtes
augmente au fur et à mesure, le nombre d'itérations augmentent
aussi au point qu'il ne peut pas être résolu en temps polynomial
même par l'ordinateur le plus rapide possible qui puisse exister à
nos jours. Mais alors, avec quelques suppositions, ces genres de
problèmes peuvent être résolus par des algorithmes
heuristiques en un temps presque polynomial et fournir une solution près
de l'optimum.
L'algorithme LAFF minimizing hieght proposé ci-dessus
utilise une heuristique qui place la boîte dans le container en ne
prenant pas en compte sa hauteur. Cet algorithme fonctionne de la
manière ci-après :
De prime à bord, la largeur et la profondeur de
l'espace de stockage doivent être déterminées. Ainsi, en
donnant un ensemble de boîtes de tailles différentes, on calcule
la profondeur et la largeur de l'espace de stockage et on trouve le plus long
des deux bords des boîtes. La largeur et la profondeur de l'espace sont
déterminées au début de l'algorithme et restent fixes
jusqu'à la fin de son exécution. On suppose ici que la hauteur
reste illimitée, elle augmente au fur et à mesure que
l'algorithme s'exécute.
Etant ainsi, la largeur (ak) et la profondeur (bk) de l'espace
sont trouvées en sélectionnant le premier et deuxième plus
long bord des boîtes (ai, bi et ci). Le plus long est pris comme largeur
(ak) et le deuxième comme profondeur (bk). Donc ak et bk ne changent
jamais.
38
Après avoir déterminé les valeurs de la
largeur et de la profondeur de l'espace de stockage, les boîtes peuvent
être placées dans le contenant. Dans cet algorithme, deux
méthodes de placement sont utilisés. Le premier est alloue un
espace à chaque boîte entrante, ce qui augmente la hauteur du
contenant. La deuxième méthode alloue un espace aux boîtes
restantes s'il y a une boîte qui convient parfaitement dans l'espace
encore disponible autour des boîtes déjà placées
sans dépasser la hauteur de la boîte placé.
Dans la première méthode de placement, les
boîtes ayant la plus grande surface sont déterminées, les
boîtes sont sélectionnées pour essayer de trouver la
boîte qui a la hauteur minimum dans toutes boîtes
sélectionnées. Ainsi, la boîte ayant la hauteur minimum est
placée dans le contenant. La plus grande boite
sélectionnée doit être en parallèle avec le fond du
contenant.
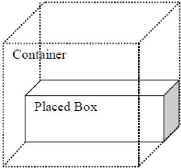
Figure 6 : Première méthode de placement des
boîtes avec LAFF
Dans la seconde méthode, les objets sont placés
dans un ordre et l'algorithme essaie d'allouer un espace aux boîtes
restantes autour de la boîte déjà placée (selon la
première méthode). Ainsi, pour les espaces restants autour de la
boîte déjà placée comme le montre la figure 7,
l'algorithme essaie de les remplir d'après la deuxième
méthode de placement. Selon cette méthode, étant
donné que les boîtes ont des
39
dimensions ai, bi et ci sur un niveau, l'espace de stockage
aura deux espaces vides autour de la boîte déjà
placé avec les dimensions ((ak-ai),bk,ci) et (ak,(bk-bi),ci). Donc s'il
y a une boîte qui convient parfaitement dans l'espace non alloué,
ça peut être une boîte ou plus, on place la boîte qui
a le volume maximum à côté de la boîte comme le
montre la figure 7. Cette répétition continue jusqu'à ce
qu'il n'y ait aucune boîte qui convient dans l'espace vide.
Dans la deuxième méthode de placement, s'il n'y
a pas d'espace autour de la boîte placée, alors l'algorithme
continue d'après la première méthode.
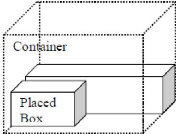
Figure 7 : seconde méthode de placement des
boîtes avec LAFF
A chaque fois qu'il y a des boîtes non encore
placées, l'algorithme va à la première méthode de
placement et ainsi de suite jusqu'à ce que toutes les boîtes
soient placées. À la fin de l'algorithme, une solution possible
comme le montre la figure 8 est produite.
40
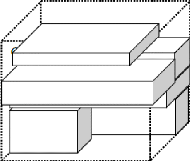
Figure 8 : solution possible avec LAFF
Etapes de l'algorithme LAFF
Les principales étapes de l'algorithme LAFF sont
résumées comme suit :
Etape 1 : Entrer les dimensions et nombres des boîtes
N : Nombre de boîtes uniques
Etape 2 : Déterminer la largeur (ak) et la profondeur (bk)
de l'espace de stockage
ak : le bord le plus long de toutes les boîtes
bk : le deuxième bord long des boîtes
ck : 0 (zéro)
Etape 3 : choisir la boîte la plus volumineuse. S'il y en a
beaucoup, choisir celle
ayant la plus petite hauteur. Placer cette boîte (ith)
à l'endroit le plus large en
parallèle avec la base du contenant.
Etape 3.1 : Déterminer la hauteur de l'espace de stockage
et décrémenter le nombre
de boîtes (ith).
ck=ck+ci
ki=ki-1
Etape 3.2 : si le nombre de boîte est égal à
0 alors terminer
41
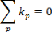
Etape 3.3 : si l'espace (ak-ai)=0 et (bk-bi)=0 aller à
l'étape 3. Par contre, choisir la boîte capable de remplir
convenablement l'espace restant. S'il y a plus d'une boîte capable de
convenir dans l'espace restant, choisir la boîte la plus volumineuse.
Cette boîte est appelée jth.
Etape 3.3.1 : déterminer la dimension de l'espace.
as=max(ak-ai, ak-aj) and bs=bk-bi-bj
Etape 3.3.2 : Décrémenter le nombre des
boîtes ith
kj=kj-1
Etape 3.3.3 : si le nombre des boîtes devient
égal à 0 alors terminer. Sinon, aller à l'étape
3.3.
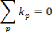
Complexité de l'algorithme
LAFF
Si on considère n comme le nombre de toutes les
boîtes à être placées dans l'espace de stockage et k
comme le type de différentes boîtes de tailles différentes,
la durée d'exécution pour le cas le pire de cette
exécution est exprimé de la manière suivante :
T(n) = n (nk)
T(n) = kn2 où k est une constante.
Au final, la complexité de cet algorithme est
O(n2).
| 


