Marchandage et partage d'objets

1

Mémoire - Marchandage et partage d'objets

Bastien Ibanez - Lucas Bugeaud - (Valentin Autie)
5 mai 2021

Table des matières

1 2	Introduction au principe de marchandage 1.1 Motivations 1.2 Quelques exemples de marchandages 1.3 Exemple d'étude Les jeux de marchandage selon J.F Nash		3 3 3 4 5
	2.1	Mise en place du modèle	5
		2.1.1 Notations	5
		2.1.2 Théorie de l'utilité	5
		2.1.3 Définition du modèle	6
		2.1.4 Les propriétés de Nash	6
	2.2	Existence et unicité de la solution de Nash	7
	2.3	Exemple d'application réelle de cette théorie	9
	2.4	Conclusion sur la partie théorique de la solution de Nash	10
3	Développement numérique du jeu de marchandage		11
	3.1	De la théorie au numérique	11
	3.2	Exhibition de la frontière de Pareto	11
	3.3	Solution du jeu de Nash	14
4	Étude numérique : voiture partagée "uberisée"		19
	4.1	Rappel introductif	19
	4.2	Notations	20
	4.3	Choix de la dimension 1	20
	4.4	Perspectives d'études	20
	4.5	Application de l'algorithme à un cas simple	21
	4.6	La problématique du mensonge	23
		4.6.1 Jeu à information parfaite	23
		4.6.2 Nombre d'occurrence de chaque solution en information parfaite	25
		4.6.3 Jeu à information imparfaite	26
	4.7	Étude statistique de la nature de la solution de Nash dans notre modèle	29
	4.8	Conclusion de la partie numérique sur la solution de Nash	32

2

5

	La solution de Nash : une solution faisant débat 5.1 Remise en cause de la solution de Nash via l'axiome d'indépendance aux alterna- tives non pertinentes 5.2 Axiome de monotonicité de Kalai-Smorodinsky		34 34 37
6	Conclusion		42
7	Bibliographie		43
8	Appendice		44
	8.1 Codes et résultats consoles annexe de la partie 4		44
	8.2 Code réalisé tout au long de ce mémoire		48
	8.2.1 Fichier	Nash_solver.py	48
	8.2.2 Fichier	Fonctions_distances.py	54
	8.2.3 Fichier	Etude_probleme_voiture_partagee 56
	8.2.4 Fichier	Applications_theorie_des_jeux.py	72
	8.2.5 Fichier	Applications_statistiques.py	82

3

Ce mémoire traite la notion de jeu de marchandage apparue en 1950 suite aux recherches faites par le mathématicien J.F Nash qui s'intéressait à la collaboration pour un profit mutuel entre deux individus. Il se décompose en trois parties majeures. Dans la première, nous introduisons, expliquons et démontrons la démarche suivie par J.F Nash pour trouver une solution à cette collaboration entre deux individus. La deuxième partie nous donne l'occasion d'implémenter une telle solution et de la mettre en pratique dans un problème que nous avons imaginé. Le problème consiste à étudier une situation lors de laquelle une voiture doit rendre service à deux usagers en les amenant à la destination qu'il souhaite tout en ayant la possibilité de les prendre conjointement. L'enjeu de cette partie est d'étudier la viabilité de la solution de Nash appliquée à une problématique actuelle. Enfin dans la troisième partie, nous allons voir que la démarche consistant à se reposer sur l'utilisation d'axiomes pour trouver une solution n'est pas unique et qu'il est possible de proposer d'autres axiomes permettant de trouver une solution différente et dans certains cas plus pertinente.

1 Introduction au principe de marchandage

1.1 Motivations

Un jeu de marchandage s'intéresse à la manière dont deux agents (ou plusieurs par extension du jeu initial) se partagent leurs biens. Il peut s'agir d'une production agricole, d'un bien matériel tel que du mobilier, un objet de valeur,... voire d'un bien "immatériel" tel que de l'argent, du temps, de l'énergie... Un jeu de marchandage est donc un jeu de négociation, où chacun des agents a un intérêt pour ce que l'autre possède et est prêt à céder tout ou une partie de ce qu'il possède. Un exemple simple est le cas d'un acheteur et d'un vendeur négociant le prix d'un objet auquel le premier attribut plus de valeur que le second. Il n'existe alors pas qu'un prix sur lequel les joueurs peuvent trouver un arrangement "convenable".

Plus généralement, on se posera la question de savoir s'il est possible, lorsque les agents ont une multitude de partages possibles, de parvenir à une répartition unique qui ne souffre pas de meilleures alternatives possibles.

Cette première partie présente la solution proposée par John Nash en 1953. La démarche entreprise est axiomatique, elle consiste donc à poser un certain nombre d'axiomes que la solution doit satisfaire. Bien choisis, ces axiomes permettent de révéler l'existence voire l'unicité d'une solution.

1.2 Quelques exemples de marchandages

Afin de se familiariser avec la notion de marchandage, il est utile d'expliciter quelques exemples simples de jeu de marchandage. Un premier jeu de marchandage fait par exemple intervenir le lègue d'un héritage entre les individus d'une même famille. Ces derniers doivent se répartir des biens matériels (maisons, mobiliers, objets de valeurs) ainsi que des biens immatériels (argent, actions) auxquels ils n'attribuent pas la même utilité. Les possibilités de partage sont dénombrables et chacune d'elle attribue une certaine utilité à chacun des individus. Un jeu de marchandage consiste dans ce cas à trouver le "meilleur" partage parmi tous ceux possibles. La question logique qui s'ensuit consiste à se demander ce qui définit un partage comme étant le "meilleur". La démarche axiomatique proposée par J.F Nash pour résoudre ce type de jeu consiste justement à définir cela.

Prenons un autre exemple simple faisant intervenir un artiste et son client potentiel. L'artiste a peint un tableau qu'il souhaite désormais vendre, et le client souhaite l'acheter. Les deux protagonistes doivent s'entendre sur un prix. En fonction du montant, chacun éprouve une utilité qui

4

lui est propre. Pour évaluer le prix de son oeuvre, l'artiste prend en considération le temps qu'il a mis a faire l'oeuvre, son attrait pour l'argent ainsi qu'un tas d'autres facteurs. Il en va de même pour le client qui considère le temps qu'il a mis à gagner cet argent, son niveau de satisfaction s'il arrive à prendre possession de l'oeuvre etc... Le jeu de marchandage consiste donc ici à trouver le prix sur lequel les deux personnes devraient arriver à s'entendre sous peine de ne pas faire affaire.

1.3 Exemple d'étude

Parmi les jeux de marchandages que nous avons pu imaginer, nous en avons choisi un qui deviendra notre objet d'étude principal. Nous l'avons construit et amélioré au fur et à mesure. Le processus de modélisation s'est donc fait en plusieurs étapes. A l'origine, nous voulions prendre l'exemple d'une voiture autonome qui était un bien partagé entre plusieurs utilisateurs. Le jeu se développait de la façon suivante : à tout moment, deux utilisateurs de la voiture pouvaient simultanément avoir recours à son utilisation pour se rendre quelque part. L'utilisation de la voiture était donc évidemment un gain de temps pour les deux usagers dont l'utilité dépendait du temps nécessaire pour se rendre à leur destination. La voiture étant un bien partagé entre ces deux utilisateurs, chacun était donc obligé de concéder un peu de son utilité. L'utilisation de la voiture utilisée séparément était un gain de temps pour les deux usagers. Cependant, le fait que la voiture soit un bien partagé implique un devoir moral à chacun des utilisateurs, ces derniers sont donc obligés de concéder un peu de leur utilité afin que l'autre puisse profiter de l'utilisation de la voiture. On peut dénombrer neuf alternatives possibles, nous en listerons 4 d'entre-elles, les autres se devinant facilement :

-- la voiture vient chercher J1 puis J2, dépose J1 puis J2

-- la voiture va chercher J1, le dépose, elle va ensuite chercher J2 pour le déposer

-- la voiture va chercher J1 et J2 doit se rendre à pied à destination

-- chacun des joueurs se rend à pied à sa destination.

Finalement, après avoir calculé les couples utilités procurées par chacune des alternatives, il revenait au logiciel de la voiture la responsabilité de faire l'arbitrage entre les alternatives et choisir la plus pertinente au sens du jeu de marchandage, ce choix sera d'ailleurs l'enjeu de la première partie qui consistera à présenter la solution proposée par J.F Nash.

Le jeu tel que présenté représentait quelques limites. En effet, nous verrons par la suite, que la résolution du jeu selon Nash répond à une logique précise qui implique qu'en connaissance de tous les facteurs intervenant dans un jeu, il est facile pour le joueur de connaître la solution induite. Le mensonge fait donc partie intégrante du jeu de marchandage si un joueur souhaite tourner le résultat à son avantage. Or, conceptuellement, une voiture partagée induit une entente préalable entre les utilisateurs, la malhonnêteté n'est donc pas un facteur très réaliste. Un autre facteur un peu limitant concernait le positionnement de la voiture. On imaginait que la voiture non-utilisée se trouvait en permanence à un endroit fixe (tel un parking), or le fait de rajouter un facteur aléatoire concernant le positionnement de la voiture qui influerait sur la stratégie des joueurs était un aspect intéressant à rajouter dans le modèle.

C'est pour cela que le modèle s'est tourné vers un exemple de compagnie VTC (voiture de transport avec chauffeur, bien que la notion de chauffeur ne soit pas essentielle ici) comme peut l'être Uber. Les principes fondamentaux du modèle ne change pas, la voiture Uber reçoit deux demandes simultanées et doit déterminer quelle option parmi les 9 disponibles est la plus pertinente, encore une fois du point de vue d'un jeu de marchandage. Le modèle ainsi posé offre davantage de possibilités quant à l'introduction de jeux de mensonges/vérités notamment.

Bien entendu, le modèle possède des limites que nous exposeront ultérieurement.

5

2 Les jeux de marchandage selon J.F Nash 2.1 Mise en place du modèle

2.1.1 Notations

On adoptera dans la suite les notations suivantes : -- pour x, y E II8², on note :

x y lorsque x1 y1 et x2 y2

x « y lorsque x1 < y1 et x2 < y2

x < y lorsque x y et x y

xy E 1I8² le produit terme à terme de x et y

2.1.2 Théorie de l'utilité

Nous verrons par la suite que pour résoudre un jeu de marchandage, il est nécessaire de mesurer l'utilité que chacun des agents obtient à chaque issue possible du jeu. Ainsi, la théorie de l'utilité théorisée par John von Neumann et Oskar Morgenstern dans Theory of Games and Economic Behavior (1944) permet de modéliser les préférences d'un agent par une fonction d'utilité.

Soit C := {c1, ...cN} l'ensemble des issues pour N co, et L := (p1, ...,pN) une loterie quelconque, avec _øNi«1 pi = 1, où p_n représente la probabilité de la réalisation de l'issue c_n. Le choix présenté à un agent peut ainsi être représenté comme une liste de probabilités associées à chaque issue possible du jeu. On note L l'ensemble des loteries simples sur l'ensemble des issues C. On considère à présent la relation de préférence > sur les L, cette dernière doit vérifier les axiomes suivants :

1. Complétude :

VL,L^' E L, L L^' L

On peut toujours déterminer la préférence ou l'indifférence de l'individu entre deux loteries

2. Transitivité :

VL,L^',L^" E L, (L>L^'etL^'>L^") L > L"

Elle traduit l'ordre de préférence entre différentes loteries de manière cohérente.

3. Continuité : Pour les loteries L, L' et L», les ensembles

{á E [0,1], áL + (1 -- á)L^' > L^"} {á E [0, 1], áL + (1 -- á)L^' < L^"}

sont fermés.

Cet axiome traduit le fait que pour un changement très faible de probabilité, l'agent garde les mêmes préférences.

4. Indépendance :

VL,L^',L^" E L,á E]0,1[, L > L^' e=> áL^' + (1 -- á)L^"

Grâce à ces axiomes, il est possible de montrer l'existence d'une fonction d'utilité associée à la relation de préférence >. A fortiori, on pourra l'écrire comme une fonction d'utilité de type vNM.

6

Définition 1 (Fonction d'utilité vNM) La fonction d'utilité U : G ]8 a une forme

d'espérance d'utilité s'il existe un vecteur (u1, ...uN) tel que pour toute loterie simple L = (p1, ...,pN) E G on a : U(L) = ø^Ni«1 piui. Une fonction d'utilité respectant cette propriété est dite fonction d'utilité von Neumann-Morgenstern (vNM).

On peut à présent exposer le théorème de Von Neumann et Morgenstern :

Théorème 2.1 (von Neumann-Morgenstern) Supposons qu'une relation de préférence ¾ sur les loteries satisfassent les 4 axiomes précédents; alors ¾ peut être représentée par une fonction d'utilité de type vNM.

Ajoutons quelques propriétés cohérentes et utiles qui découlent de la construction d'une telle fonction :

u(L) > u(L^') H L L^'.

u(L) < u(L^') H L ã L^'.

u(L) = u(L^') H L L^'.

d 0 p 1, u[pL + (1 -- p)L^'] = pu(L) + (1 -- p)u(L^')

Remarque 1 Une fonction d'utilité représentant une relation de préférence ¾ ainsi définie n'est pas unique.

2.1.3 Définition du modèle

Définition 2 Un jeu de marchandage à deux joueurs est un couple (A, d) tel que :

A est une partie convexe et compacte de ]]8², appelée l'ensemble des alternatives

d est un élément de A, appelé point de désaccord

il existe x E A tel que x » d On note J l'ensemble de ces jeux.

Dans la suite, on écrira simplement jeu pour désigner un jeu de marchandage à deux joueurs. On note

Définition 3 Une règle de marchandage est une application qui à tout jeu (A, d) E J associe un unique point de A.

2.1.4 Les propriétés de Nash

Dans cette partie, on se donne une règle de marchandage. On tentera également d'expliquer la légitimité du choix de tels axiomes dans la construction d'une solution.

1. L'efficacité

Définition 4 (b est dite efficace lorsque pour tout jeu (A, d) E J , il n'existe aucun x E A tel que x > (b(A, d).

L'efficacité de la solution semble être un pré-requis indispensable à sa construction. L'objectif est en effet d'améliorer la situation des deux joueurs, l'existence d'une solution meilleure n'a donc pas lieu d'être.

2. La symétrie

Définition 5 (b est dite symétrique lorsque pour tout jeu (A, d) E J tel que

si (x1, x2) E A alors (x2, x1) E A

d1 = d2

7

on a 01(A,d) = 02(A,d)

La symétrie sous-entend que l'arbitre ne donne de préférence à aucun des deux joueurs lorsque le jeu est symétrique.

3. L'invariance par transformation affine

Définition 6 0 est dite invariante par transformation affine lorsque pour tout jeu (A, d) E J , et pour tous a, b E R² avec a » (0, 0),

0(aA + b, ad + b) = a0(A, d) + b

L'invariance par transformation affine signifie que l'en modifiant de la même manière l'ensemble des alternatives et le point de désaccord, la solution obtenue sera identique à la solution initiale modifiée similairement.

4. L'indépendance des alternatives non pertinentes

Définition 7 0 est dite indépendante des alternatives non pertinentes lorsque pour tout jeu (A, d) E J et A^' c R²,

(A c A^' et 0(A^', d) E A) 0(A^', d) = 0(A, d)

Cette notion peut être illustré par le fait qu'en retirant une alternative non pertinente à A^', la solution restera la même.

2.2 Existence et unicité de la solution de Nash

Lemme 1 Soit (A, d) un jeu. La fonction

f : x E R² 1--0' x1x2.

admet un unique maximiseur sur Ad := {x -- d | x E A, x . d}. Preuve 1 Ad est :

non vide car (A, d) est un jeu,

fermé car intersection des fermés A -- d et {y E R² | y . (0, 0)},

borné car inclus dans le borné A -- d.

f étant continue, elle admet donc un maximum sur A--d. Montrons à présent que ce maximum est unique.

On suppose que f admet deux maximiseurs distincts x et y sur Ad.^x`y

2 E Ad, car Ad convexe

par intersection de d'ensembles convexes. Or on a :

_f(x+y) (x1 + y1l (x2 + y2) (1)

11\\ ₂ J 2 J 2 J
1

= ₄(x1x2 + y1y2 + x1y2 + x2y2) (2)

1

= ₄(2x1x2 + 2y1y2 + (x1 -- y1)(y2 -- x2)) > f(x) (3)

Ceci contredit le fait que x est maximiseur de f sur Ad. Justifions l'inégalité (3). D'une part, par hypothèse, f(y) = f(x), d'où

1 1

₄(2x1x2 + 2y1y2) = ₄(2f(x) + 2f(y)) = f(x).

D'autre part, comme (A, d) est un jeu, il existe z E A tel que z » d. Alors (z1 -- d1)(z2 -- d2) > 0, et donc f(x), f(y) > f(z -- d) > 0. En particulier, x1, x2, y1, y2 > 0 et y2 = x1

y1 x2. De plus, si

y1 = x1, alors y2 = x2 et donc y = x : comme x et y sont distincts, on doit avoir y1 0 x1. On en conclut que :

(x1 -- y1)(y2 -- x2) = (x1 -- y1)(^x1

x2 -- x2)

y1

8

^x2(x1 -- y1)² y1

> 0

Théorème 2.2 Il existe unique règle de marchandage à la fois efficace, symétrique, invariante par transformation affine et indépendante des alternatives non pertinentes. Elle est donnée par :

(A, d) E J argmax (x1 -- d1)(x2 -- d2)

xEA, x,,d

Preuve 2 Soit ? une règle respectant les quatre propriétés et (A, d) un jeu. On pose m := argmaxxEA, x,,d(x1 -- d1)(x2 -- d2). On va montrer que ?(A, d) = m.

Étape 1

On rappelle que m » (0, 0). L'invariance de ? par transformation affine assure que :

?(A, d) = ?(A -- d, (0, 0))

= m?( 1 (A -- d), (0, 0)) m

Posons A^m_d := ¹_m(A -- d). Il suffit donc de montrer que ?(A^m_d , (0, 0)) = (1, 1).

Étape 2 Montrons que

sup x1x2 1. xEAd , x,,(0,0)

Soit x E A^m_d tel que x . (0, 0). Alors il existe y E A -- d tel que x = ¹_my. Mais alors, y . (0,0) et il existe z E A tel que z -- d = y. On a alors z . d et donc, d'après le lemme 1, (z1 -- d1)(z2 -- d2) _m1m2. ^D'où x1x2 = m11 (z1 -- d1) _m21 (z2 -- d2) 1.

Étape 3

Montrons que

dx E A^m_d , x1 + x2 2.

Supposons qu'il existe x E A^m_d tel que x1+x2 > 2. A^m_d étant convexe, il contient l'ensemble des points du segment entre (1,1) et x. Considérons la fonction

Q : p E [0;1] f(p(1,1) + (1 -- p)x)

où, pour rappel, f est la fonction qui à tout élément de 118² associe le produit de ses composantes. On calcule :

dp E [0;1], Q(p) = (p + (1 -- p)x1)(p + (1 -- p)x2)

= p² + (x1 + x2)p(1 -- p) + x1x2(1 -- p)²

= (1 -- 2(x1 + x2) + x1x2)p² + 2((x1 + x2) -- 2x1x2)p + x1x2

9

On remarque que Q est un trinôme, donc dérivable, et que Q'(0) = 2((x1 + x2) -- 2x1x2). On distingue alors deux cas :

soit x . (0, 0), auquel cas x1x2 = f(x) 1 d'après le résultat de l'étape 2 ;

soit l'une des composantes de x est strictement négative, auquel cas l'autre doit être supérieure à 2, car x1 + x2 > 2 et alors x1x2 < 0.

Dans tous les cas, Q'(0) > 0. Q' étant continue, il existe e > 0 tel que Q' est strictement positive et donc strictement croissante sur [0; e]. On suppose aussi e assez petit pour que y := f(1,1)+(1--e)x » (0, 0). Mais alors f(y) = Q(e) > Q(0) = 1, ce qui contredit l'étape 3.

Étape 4

A^m_d est compact, car image du compact A par la fonction continue x E 1I8^{2 1}_m(x -- d).
En particulier, A^m_d est borné, et par équivalence des normes sur 1R²,

3c > 0, dx E A^m_d , |x1| + |x2| c.

On en déduit que pour tout x E A^m_d , par inégalité triangulaire,

|x1 -- x2| |x1| + |x2| c

|x1 + x2| |x1| + |x2| c, et en particulier x1 + x2 . --c.

En ajoutant le résultat de l'étape 3, on peut dire que A^m_d est contenu dans R := {x E JR² | x1 + x2 2, |x1 -- x2| c, x1 + x2 . --c}.

Étape 5

On vérifie que (R,(0,0)) est un jeu :

on vérifie aisément que R est convexe, fermé et borné,

on a bien (0,0) E R,

enfin, (1,1) E R et (1,1) » (0, 0).

Or pour tout (x1, x2) E R, on a (x2, x1) E R. Par symétrie de ?, il existe á E 1I8 tel que ?(R, (0,0)) = (á, á). Si á < 1, alors (á, á) « (1,1), ce qui est exclu par efficacité de ?. Si á > 1, alors á + á > 2, ce qui est aussi exclu car (á, á) E R. On a donc á = 1. On conclut grâce à l'indépendance de ? des alternatives non pertinentes : comme A^m_d c R et ?(R, (0,0)) = (1,1) E A^m_d , alors

?(A^m_d , (0,0)) = ?(R, (0, 0)) = (1, 1).

2.3 Exemple d'application réelle de cette théorie

Pour conclure cette partie théorique voici un exemple de jeu de marchandage faisant intervenir les concepts développés jusqu'à maintenant et qui puisse s'appliquer à une situation réelle, tout en mettant en évidence certaines limites.

Prenons le cadre de l'Union Européenne. Supposons que la commission européenne ait pour mission de répartir des vaccins aux États membres dans le cadre de la crise du COVID-19. Elle se doit d'avoir un jugement impartial entre les pays, elle joue donc le rôle du juge. Les pays sont les joueurs qui veulent maximiser les vaccins reçus, et donc maximiser leur utilité. Cette utilité liée aux vaccins est d'autant plus grande que l'état du système de santé du pays en question est sous-développé et que le nombre de cas positifs au COVID-19 y résidant est grand. Si les pays ne se mettent pas d'accord, personne n'aura de vaccin car ceux-ci ont entre temps été achetés aux laboratoires par d'autres pays hors Union Européenne. La solution de Nash appliquée à ce problème permettrait d'avoir une répartition des vaccins juste et la plus efficace possible.

10

Cette utilisation de la solution de Nash est imaginable, il faut néanmoins en énoncer certaines limites. Il se peut en effet que dans la réalité elle soit politiquement inapplicable. Par exemple si la France et l'Allemagne ne reçoivent que très peu de vaccins en raison de leurs bons systèmes de santé, ils seront davantage à même de bloquer cette décision car ils font partie des pays ayant le plus d'influence au sein de l'Union Européenne. Malgré tout, la solution de Nash pourrait servir d'indicateur sur la voie à suivre. Par ailleurs, on peut aussi imaginer que des pays choisissent de mentir à la commission sur l'état de leur système de santé ainsi que le nombre de cas de COVID dans leur pays. Ce mensonge influerait sur la solution de Nash et augmenterait le nombre de doses reçues par le pays. On peut imaginer encore une fois que pour dissuader cette éventualité, la commission enverrait des inspecteurs européens dans les différents pays pour vérifier l'utilité annoncée et en cas de duperie la pays se verrait infliger une amende.

Cette exemple met en lumière la grande applicabilité de cette théorie, bien qu'à première vue elle paraisse plutôt théorique.

2.4 Conclusion sur la partie théorique de la solution de Nash

Cette partie a été l'occasion de présenter la démarche axiomatique entreprise par J.F Nash pour trouver une solution au problème de marchandage ainsi qu'à démontrer l'existence de la solution qu'induit ce choix des axiomes. On remarque que le choix des axiomes relève avant tout d'un choix arbitraire destiné à faire émerger une solution, il n'est pas exclu que certains de ces axiomes fassent l'objet de remises en question. De plus, le dernier exemple évoqué donne un premier aperçu des difficultés que peut rencontrer l'application de cette théorie à des cas pratiques. L'enjeu de notre mémoire consiste désormais à numériser une telle solution pour pouvoir l'appliquer à des cas concrets, en valider certains aspects et en montrer ses limites.

11

3 Développement numérique du jeu de marchandage

Remarque : Toute cette partie numérique fait référence au fichier "Nash_solver" Il est aussi possible de se référer aux sections 8.2.1 et 8.2.2 mises en annexe.

3.1 De la théorie au numérique

Nous avons montré comment il était possible de trouver la solution de Nash pour un jeu (A,d). Afin de pouvoir implémenter et développer l'exemple décrit en introduction, il est nécessaire de construire l'algorithme permettant la résolution d'un jeu de marchandage. On a vu que tout jeu était décrit à l'aide du couple (A,d), où A est un ensemble convexe et d est le point de désutilité. Dans un jeu à deux joueurs, l'ensemble A est l'enveloppe convexe des couples d'utilités des joueurs. L'ensemble A sera donc du type list (voire même list de list où cette dernière comporte les utilités de chacun des joueurs). Le point de désutilité d sera quant à lui du type array qui permet des manipulations plus faciles, notamment quant il s'agit de translater les points d'un ensemble selon le vecteur d afin de centrer l'ensemble A en [0,0].

Nous allons dans un premier temps présenter les étapes clés qui ont permis la construction de l'algorithme de résolution du jeu de Nash. Nous illustrerons ces parties grâce aux données suivantes, tirées au hasard :

L = [[444, 968], [261, 220], [646, 985], [815, 878], [929, 122],

[638,	136],	[536,	550],	[435,	992],	[346, 161],	[372,	283],
[608,	674],	[569,	491],	[255,	962],	[670,198],	[958,	304]]

d = [1,28]

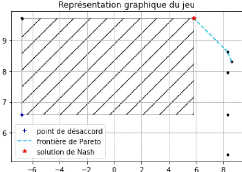
Voici premier plot de nos points, le point de désaccord est mis en évidence en rouge.

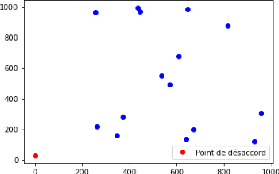
FIGURE 1 - Ensemble des points choisis pour l'illustration

3.2 Exhibition de la frontière de Pareto

En premier lieu, la solution de Nash se trouve nécessairement sur la frontière de Pareto qui constitue l'ensemble des meilleures alternatives possibles pour les joueurs. Il convient donc de

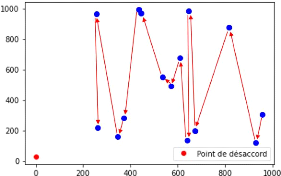
12

FIGURE 2 - Premier tri de la liste (de droite à gauche et bas en haut)

trier la liste des couples d'utilité pour garder uniquement ceux constituant cette frontière.

1. Première étape: trier la liste

Il est tout d'abord nécessaire de faire un premier tri afin de pouvoir facilement manipuler la liste de points. La figure montre bien le choix de tri qui a été fait. On remarque que tous les points désignés par une flèche orientée vers le bas ne seront pas retenus car strictement Pareto-dominés par ceux qui l'entourent (ce ne sont pas les seuls, nous le verrons par la suite) Voici les fonctions utiles à ce premier tri :

1

2 def first_component(a): # renvoie l'abscisse d'un point de R2

3 return a[0]

4 def second_component(a): # renvoie l'ordonnee d'un point de R2

5 return a[1]

6

7 def double_sort(L):

8 S = sorted(L, key = second_component, reverse = True)

9 S.sort(key = first_component, reverse = True) # la méthode "sort"
ãÑ conserve l'ordre lorsque la cle est la meme

10 return S

11 # prend en entree une liste de points de R2 renvoie

12 # la liste triee par ordre decroissant par rapport a la premiere

ãÑ composante

13 # les points de premiere composante egale sont tries par rapport a la

ãÑ seconde

Voici l'état de la liste qui en résulte :

L = [[958, 304], [929, 122], [815, 878], [670, 198], [646, 985], [638, 136], [608, 674], [569,

491], [536, 550], [444, 968], [435, 992], [372, 283], [346, 161], [261, 220], [255, 962]]

2. Seconde étape : Frontière de Pareto

Après avoir trié intelligemment la liste, il nous faut exclure les points Pareto-dominés de notre liste. Dans un premier temps, la fonction first_selection élimine les points désignés

13

par les flèches orientées vers le bas, qui sont comme évoqué précédemment, Pareto-dominés par leurs voisins. Cela ne suffit pas, car parmi les points restants, certains peuvent se situer en-dessous de la droite reliant ses deux voisins, auquel cas, il est dominé par toutes combinaisons linéaires de ces derniers. Les fonctions above et second_selection permettent de terminer d'exhiber de la frontière de Pareto.

14 def first_selection(L):

15 S = [L[0]] # L etant triee par "double_sort", L[0] sera forcement le
ãÑ premier element de la sous-liste

16 n = len(L)

17 i = 1

18 j = 0

19 while i < n:

20 if L[i][0] < S[j][0] and L[i][1] > S[j][1]:

21 S.append(L[i])

22 j+=1

23 i+=1

24 return S

25 # prend en entree une liste triee par la fonction "double_sort"

26 # renvoie une sous-liste strictement décroissante pour la premiere

27 # composante et strictement croissante pour la seconde

28

29 def above(a,b,c):

30 return b[1] > (a[1]*(b[0]-c[0])/(a[0]-c[0])) +
ãÑ (c[1]*(a[0]-b[0])/(a[0]-c[0]))

31 # prend en entree trois points strictement decroissants/croissants

32 # pour la premiere/seconde composante renvoie "True" ssi le point du ãÑ milieu

33 # est strictement au-dessus de la droite passant par les deux autres

34

35 def second_selection(L):

36 if len(L) == 1: return L

37 S = [L[0],L[1]]

38 n = len(L)

39 i = 2

40 j = 0

41 while i < n:

42 if above(S[j],S[j+1],L[i]):

43 S.append(L[i])

44 j+=1

45 i+=1

46 else:

47 S.pop()

48 if j == 0:

49 S.append(L[i])

50 i+=1

51 else:

52 j-=1

53 return(S)

14

54 # prend en entree une liste strictement decroissante/croissante pour la

ãÑ premiere/

55 # seconde composante renvoie la sous-liste privee des points ãÑ Pareto-domines

56 # par une combinaison d'autres points

Notre exemple de liste n'étant pas assez exhaustif, il ne met pas en avant la différence apportée par la fonction second_selection, voici donc deux print tirés d'une liste plus

exhaustive, et qui illustre bien le passage de la première à la seconde sélection.

On exhibe par ailleurs la frontière de Pareto de notre liste initiale sur la figure. Voici la liste finale :

L = [[958,304], [815,878], [646,985], [435,992]]

3.3 Solution du jeu de Nash

Après avoir réussi à réduire la liste en incluant uniquement les points appartenant à la frontière de Pareto, il nous est désormais possible de trouver la solution du problème selon Nash. On rappelle pour cela que la solution de Nash maximise la fonction produit de la frontière de Pareto. Autrement dit, il faut trouver la combinaison linéaire de deux points appartenant à la frontière (ou un point appartenant directement à la frontière s'il s'agit du maximiseur) qui maximise l'aire du rectangle dont une des diagonales rejoint le point de désaccord et le maximiseur en question. Pour cela, les fonctions x_max et y_max sont utilisées afin de trouver l'abscisse et l'ordonnée respectives du point qui maximise la fonction produit sur une droite passant par deux points. Le maximum ne se situe pas nécessairement entre les deux points.

57 def y_max(a,b): # a est sous la forme [x1,y1]

58 a_1, a_2, b_1, b_2 = a[0], a[1] ,b[0] ,b[1]

59 p_cut = b_1/(b_1-a_1)

60 return (p_cut*a_2 + (1-p_cut)*b_2)/2

61

62 def x_max(a,b):

63 a_1, a_2 ,b_1 ,b_2 = a[0], a[1] ,b[0] ,b[1]

64 p_cut = b_2/(b_2-a_2)

65 return (p_cut*a_1 + (1-p_cut)*b_1)/2

Il est à présent possible de trouver la solution de Nash par dichotomie. Brièvement, nous comparons deux points de l'enveloppe :

1. Soit le maximum de la fonction produit se trouve entre les deux points, dans ce cas le point représente la solution de Nash

2. Soit le maximum de la fonction produit se trouve à gauche du segment reliant les deux points, deux possibilités s'ouvrent à nous:

(a) Il reste plus de deux points étudiables sur la frontière de Pareto se trouvant à gauche des points actuels, dans ce cas on continue de procéder par dichotomie sur l'ensemble des points à gauche

(b) Autrement, le point de gauche constitue la solution de Nash

3. Le raisonnement est similaire pour le cas où le maximum de la fonction produit se trouve à droite du segment reliant les deux points

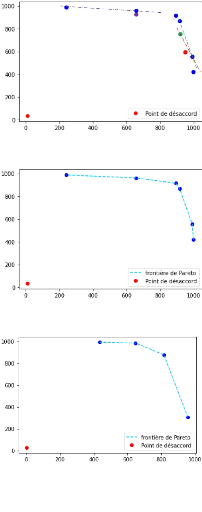
FIGURE 3 - Ensemble L après first_selection

FIGURE 4 - Ensemble L après second_selection

FIGURE 5 - Frontière de Pareto de notre liste initiale

15

16

Voici les fonctions qui nous permettent de trouver la solution finale :

(à noter que la fonction solution_rec renvoie un array avec: la solution, les deux points issus de la combinaison amenant au résultat ainsi que les coefficients de la combinaison ([1,0] si le point appartient à l'enveloppe))

66 def y_max(a,b): # a est sous la forme [x1,y1]

67 a_1, a_2, b_1, b_2 = a[0], a[1] ,b[0] ,b[1]

68 p_cut = b_1/(b_1-a_1)

69 return (p_cut*a_2 + (1-p_cut)*b_2)/2

70 # prend en entree deux points strictement decroissants/croissants pour la

ãÑ premiere

71 # /seconde composante renvoie l'ordonnee du maximiseur de la "fonction produit"

ãÑ

sur

72 # la droite passant par ces deux points

73

74 def x_max(a,b):

75 a_1, a_2 ,b_1 ,b_2 = a[0], a[1] ,b[0] ,b[1]

76 p_cut = b_2/(b_2-a_2)

77 return (p_cut*a_1 + (1-p_cut)*b_1)/2

78

79 # prend en entrée une liste traitee par "frontier_points"

80 # renvoie le point de l'enveloppe convexe de la liste qui maximise la "fonction

ãÑ produit"

81 def solution_rec(L):

82 n = len(L)

83 if n == 0:

84 print("Echec de la recurrence")

85 if n == 1:

86 return np.array([[L[0][0],L[0][1]],[0,0],[0,0],[1,0]])

87 else:

88 m = n//2

89 a, b = L[m-1], L[m]

90 y = y_max(a,b)

91 if y < a[1]:

92 if n > 2:

93 return solution_rec(L[:m])

94 else:

95 s = np.array([a[0],a[1]])

96 a = np.array([a[0],a[1]])

97 b = np.array([b[0],b[1]])

98 c = np.array([1,0])

99 return np.array([s,a,b,c])

100 if y > b[1]:

101 if n > 2:

102 return solution_rec(L[m:])

103 else:

104 s = np.array([b[0],b[1]])

105 a = np.array([a[0],a[1]])

106 b = np.array([b[0],b[1]])

107 c = np.array([0,1])

108 return np.array([s,a,b,c])

109 else:

110 x = x_max(a,b)

111 p = (x - b[0]) / (a[0]-b[0])

112 s = np.array([x,y])

113 a = np.array([a[0],a[1]])

114 b = np.array([b[0],b[1]])

115 c = np.array([p,1-p])

116 return np.array([s,a,b,c])

117

Important : Dans ce dernier paragraphe, la solution de Nash était avant tout le maximum de la fonction produit de la frontière de Pareto dans un ensemble centré en [0,0], c'est à dire que le point de désaccord est nécessairement [0,0]. Pour trouver la solution de Nash d'un problème quelconque, il est nécessaire d'introduire une fonction shift qui permet de centrer l'ensemble, d'en exhiber le maximum de la fonction produit, et de l'incrémenter à nouveau de la valeur du point de désaccord. Voici les fonctions en question :

118 def shift(L,v):

119 L_shifted = []

120 for i in range(len(L)):

121

P = np.array([ L[i][0] + v[0], L[i][1] + v[1] ])

17

122 L_shifted.append(P)

123 return L_shifted

124

125 def true_solution(A,d):

126 L = shift(A+[d], (-1)*d)

127 F = frontier_points(L)

128 s = solution_rec(F)

129 s_list =[]

130 for i in range (3):

131 s_list.append(shift(to_list(s[i]),d)) # la fonction shift prends en
ãÑ argument des listes, d'où l'utilisation de la fonction "to_list"

132 # le point solution, le point a et le point b sont incrémentés du point d

L=[]

133

134 for i in range (len(s_list)): # on remet les valeurs de la solution

ãÑ incrémentées par le point d

135 p = [s_list[i][0][0], s_list[i][0][1]]

136 L.append(p)

137 L.append([s[3][0],s[3][1]])

138 return L

Nous avons désormais les outils nécessaires permettant de trouver la solution de Nash à notre exemple de départ : la solution est le point de la liste initiale : [815, 878]

Voici un autre résultat d'un exemple quelconque où la solution est une combinaison de deux points : La solution est une combinaison linéaire du point [955.0, 779.0] chargé du poids 0.29 et du point [819.0, 913.0] chargé du poids 0.71

La solution est le point [859.1, 873.49]

18

On peut maintenant écrire une fonction qui permet d'afficher un plot de notre solution, voici le résultat de notre exemple :

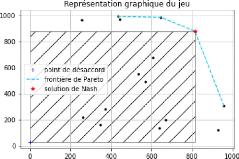
FIGURE 6 - Plot final de la solution de Nash

19

4 Étude numérique : voiture partagée "uberisée" 4.1 Rappel introductif

Dans un premier temps, remettons en contexte l'exemple décrit en introduction. Le jeu s'articule autour de deux joueurs se trouvant chacun à un endroit et souhaitant se rendre à un endroit différent. Une voiture reçoit les requêtes des joueurs, à peu près simultanément par soucis de simplification et neuf possibilités s'offrent à elle, parmi lesquelles notamment :

-- la voiture vient chercher J1 puis J2, dépose J1 puis J2

-- la voiture va chercher J1, le dépose, elle va ensuite chercher J2 pour le déposer

-- la voiture va chercher J1 et J2 doit se rendre à pied à destination

-- chacun des joueurs se rend à pied à sa destination.

Cet exemple ne correspond pas exactement à ce à quoi on pourrait s'attendre intuitivement d'un jeu de marchandage. Le schéma de pensée s'orienterait davantage autour d'une discussion entre deux joueurs au sujet du partage de biens disponibles, le partage serait tranché par un arbitre désintéressé en suivant les 4 axiomes décrits pas J.F Nash. Le partage d'un héritage entre plusieurs membres d'une famille se prête bien à cette description. Ces exemples ont été évoqués dans la partie 1.2

Remettons donc en place les différents paramètres constituant un jeu de marchandage qui se prêtent ici à notre modèle.

L'utilité des joueurs est sûrement le point le plus contestable. En effet, dans un jeu de marchandage classique, deux options sont imaginables : les acteurs ont soit, chacun quelque chose à partager (exemple: un agriculteur partage avec le supermarché local une partie de sa récolte contre de l'argent), soit un ensemble de biens qui leur ait collectivement légué et qu'ils se répartissent entre eux (l'exemple déjà cité précédemment d'un héritage).

Ici, les biens partageables ne sont pas matériels mais plutôt immatériels voire idéologiques. En effet, la première ressource que les acteurs se partagent est le temps. Aller chercher un joueur puis prendre le suivant dans la foulée est, dans la plupart du temps, une perte de temps pour le premier. On peut alors imaginer que l'utilité d'un joueur soit maximale à condition qu'il soit le seul client du chauffeur. Dans un cas pareil, le jeu de marchandage n'a pas de raison d'être car un joueur ne rentre dans un jeu de marchandage que s'il y trouve un intérêt. Il est donc nécessaire de conceptualiser cet intérêt par un facteur supplémentaire qui incite le joueur à participer au jeu. Le facteur imaginé ici, est idéologique, il se matérialise sous la forme d'un marqueur de bonne volonté pour lequel les joueurs consentiraient à contribuer au principe de partage de l'utilisation d'une même voiture. Les raisons seraient par exemple, soit écologiques ou soit de l'ordre d'une solidarité exprimée vis-à-vis d'une petite entreprise ne possédant pas encore beaucoup de véhicules. Ce postulat ne constitue pas un frein majeur à la transposition de notre exemple dans la réalité étant donné que des principes de covoiturages et autres façons diverses de partager des voitures sont déjà implantés dans notre société.

On s'autorise à modéliser l'utilité des joueurs en fonction uniquement du temps qu'ils mettent à se rendre à l'endroit désiré. Le facteur de bonne volonté est implicitement suggéré dans l'existence même du jeu par le fait que chacun des joueurs accepte de concéder un peu de leur temps pour en faire gagner à l'autre. Des fonctions d'utilité concaves en la variable de temporalité permettent le bon fonctionnement de l'exemple. En effet, les joueurs souhaitent malgré tout minimiser leurs temps de trajet, ainsi la composition d'une fonction concave avec le temps de trajet permet d'obtenir un ensemble convexe.

20

A présent loti de notre ensemble convexe, il convient de fixer le point de désaccord indispensable au jeu de marchandage. Il parait naturel que l'une des alternatives suggérant le fait que les deux joueurs soient obligés de se rendre à pied à leur destination constitue le point de désaccord évident de notre jeu. On complète la théorie en attribuant à la voiture (ou indifféremment au chauffeur) le rôle d'arbitre désintéressé du jeu dont le rôle est de prendre la meilleure décision en connaissance des utilités des joueurs, de leurs positions et leur endroit d'arrivée.

4.2 Notations

Les notations en dimension 1 sont les suivantes :

-- x1 = la position de départ du joueur 1

-- x2 = la position de départ du joueur 2

-- y1 = l'endroit d'arrivée du joueur 1

-- y2 = l'endroit d'arrivée du joueur 2

-- v = la position de départ de la voiture.

Nous allons étudier un cas simplifié de notre exemple en nous concentrant sur le segment [0,1]. L'utilité attribuée à chaque joueur est une fonction concave qui va dépendre du temps. On choisit arbitrairement la fonction uipt1, t2q « 't2 _i . On distingue également le temps parcouru en voiture t_v et le temps parcouru à pied t_m :

tipx, yq « tm,ipx, yq ` tv,ipx, yq où 4.3 Choix de la dimension 1

"tv,ipx, yq « d1px, yq « |x ' y| tm,ipx,yq « Ktv,ipx,yq

Ce choix simplifie légèrement le calcul des distances mais a pour défaut de recourir souvent aux mêmes alternatives. Il faut par exemple que deux points x1 et x2 soient complètement opposés pour que la voiture choisissent d'en prendre un et de le déposer avant de prendre le second.

Exemple : dans cette configuration, mise à part

un changement majeur, la solution sera quasi-

systématiquement : La voiture ira chercher J2 puis J1,

déposera J1 puis J2

Un choix de dimension 2 sur une grille aurait sûrement permis à d'autres alternatives de ressortir

plus régulièrement.

4.4 Perspectives d'études

Ce jeu nous offre plusieurs possibilités. Dans un premier temps, il nous faut coder les solutions du jeu en fonction des paramètres initiaux. Nous allons laisser apparaître les résultats de la console ainsi que les graphiques qui permettent d'illustrer le fonctionnement de certaines fonctions. Le code dans son intégralité est laissé disponible en annexe.

Rendre possible le calcul numérique de ces solutions nous permet également d'en tester les limites. En effet, nous avons laissé entendre en introduction qu'un joueur (ou les deux) pouvait choisir de mentir sur la position d'arrivée qu'il indiquait à la voiture, cela induit inévitablement le calcul d'une solution différente lui permettant dans certains cas d'obtenir davantage d'utilité, au détriment parfois de l'utilité de l'autre joueur. Le recours à des concepts de théorie des jeux vont nous permettre d'étudier les effets ainsi que la récurrence de cet aspect du modèle.

Il est également intéressant de se mettre à la place de la compagnie. En effet, sa problématique consiste à traiter au mieux la gestion de ses voitures afin d'en utiliser le moins possible, en prenant

21

en charge plusieurs utilisateurs à la fois. Cette dernière envisage de considérer la solution de Nash pour résoudre cette problématique.

L'étude des comportements tel que le mensonge peut lui permettre de juger la pertinence de l'application d'un jeu de marchandage à son business (qui consiste dans la mesure de ses capacités à satisfaire ses clients).

On a vu également que la solution théorique n'aboutissait pas systématiquement sur un point appartenant à l'ensemble des alternatives. Cela implique le recours au hasard lorsque la solution est issue de la combinaison de deux possibilités. On peut imaginer que la compagnie souhaiterait savoir si avec une probabilité raisonnable elle peut espérer obtenir des solutions pures.

4.5 Application de l'algorithme à un cas simple

Remarque: Cette partie numérique fait référence aux fichiers "Etude_probleme_voiture_partagee" et "Applications_theorie_des_jeux" Il est aussi possible de se référer aux sections 8.2.3 et 8.2.4 mises en annexe..

Dans un premier temps, nous allons étudier un cas fixé nous permettant d'imager les résultats renvoyés par notre code. Pour cela, imaginons la situation suivante pour laquelle les deux joueurs se situent dans des quartiers différents délimités par les sous-segments [0,0.2] et [0.3,0.35] et souhaitent tous deux se rendre sur leur lieu de travail se situant dans une zone industrielle située dans [0.7,1.0]. Les joueurs sont positionnés arbitrairement en x1 = 0.02 et x2 = 0.34. Ils souhaitent se rendre en y1 = 0.84 et en y2 = 0.71. La voiture est placée en v = 0.5. Rappelons également que la fonction d'utilité est la même pour les deux joueurs à savoir: ui(t1, t2) = 10--t2 i et que le temps de marche est défini comme _tm,i(x, y) = Ktv,i(x, y) où on choisira K = 5. La marche est donc un facteur pénalisant dans le calcul de l'utilité du joueur même si elle n'intervient pas encore car les deux joueurs annonce ici l'endroit où ils souhaitent véritablement se rendre en voiture.

Voici le message affiché par la console ainsi que le plot de la résolution :

139

140 Solution du jeu classique

141

142 La voiture est placée en 0.5 sur [0,1]

143

144 Le joueur 1 est placée en 0.02 sur [0,1] et souhaite se rendre en 0.84

à

145

146 Le joueur 2 est placée en 0.34 sur [0,1] et souhaite se rendre en 0.71

147

148 Le point de désaccord correspondant au fait que les deux joueurs se rendent

ãÑ pied

149 est [-6.81 6.578]

150 Avec une réalisation classique du jeu, l'action suivante sera choisie :

151 La voiture ira chercher J2, le déposera, puis ira chercher J1 et le déposera

152

153 J1 en retire une utilité de 5.838

154

155 J2 en retire une utilité de 9.719

156

22

FIGURE 7 - Plot de notre solution simple

On remarque qu'une autre configuration peut également nous donner une solution mixte. On imagine que dans un tel cas, l'entreprise serait obligée de tirer une des deux solutions au hasard. D'un point de vue pratique, ce n'est pas une configuration souhaitable pour l'entreprise qui préfère obtenir une solution simple parmi les alternatives proposées.

157 Solution du jeu classique

158

159 La voiture est placée en 0.2 sur [0,1]

160

161 Le joueur 1 est placée en 0.05 sur [0,1] et souhaite se rendre en 0.89

162

163 Le joueur 2 est placée en 0.6 sur [0,1] et souhaite se rendre en 0.91

164

165 Le point de désaccord correspondant au fait que les deux joueurs se rendent à ãÑ pied est [-7.64 7.6 ]

166 Avec une réalisation classique du jeu, l'action suivante sera choisie :

167 0.6 fois du temps, on aura l'action : La voiture ira chercher .31 puis .32, ãÑ déposera .31 puis .32

168

169 0.4 fois du temps, on aura l'action : La voiture ira chercher .32, le déposera, ãÑ puis ira chercher .31 et le déposera

170

171 .31 en retire une utilité de 7.1

172

173 .32 en retire une utilité de 9.19

23

4.6 La problématique du mensonge

4.6.1 Jeu à information parfaite

Continuons l'analyse en donnant la possibilité au joueur de mentir sur sa position d'arrivée. S'il décide de mentir, le joueur est déposé à l'endroit qu'il a annoncé et doit donc parcourir la distance restante à pied. Le joueur cherche donc d'abord à connaître le point d'arrivée le plus favorable qui lui permette de maximiser son utilité.

Pour implémenter la recherche de ce y et limiter le nombre et le temps de calcul, nous avons opté pour une méthode de dichotomie à trois variables permettant de trouver une bonne approximation de l'utilité maximum en fonction du point d'arrivée du joueur sur le segment. On choisit d'ajouter une variable à la méthode de dichotomie à deux variables car cette dernière n'est pas adaptée en tant que tel pour trouver un extrema. La méthode consiste ici à évaluer l'utilité (recherche sollicitant beaucoup de calculs) en 3 points :

a < p < m < q < b

Ainsi, chercher le maximum a sur l'intervalle [a,b] se réduit aux 3 possibilités suivantes :

u(p) > u(m) alors a E]a, m[

u(m) < u(q) alors a E]m, b[

u(p) . u(m) et u(m) . u(q) alors a E]p, q[

Le schéma suivant illustre deux des trois possibilités évoquées, l'intervalle [a,b] est divisé par deux à chaque itération. (La fonction de dichotomie codée pour ce problème apparaît dans l'appendice)

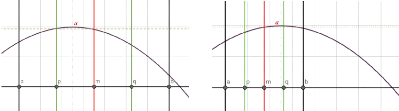
(a) u(p) > u(m) et donc a Psa, mr (b) u(m) < u(q) et donc a Psm, br

FIGURE 8 - Illustration de la méthode de dichotomie à 3 variables

Maintenant que le choix de la méthode a été expliqué, nous pouvons présenter les résultats correspondant à notre exemple initial.

Dans un jeu à information parfaite, les joueurs savent si l'autre ment ou non. Dans ce cas il est possible pour le joueur jouant en second de déterminer la destination annoncée par le premier joueur quand il décide de mentir et donc de trouver le meilleur endroit pour mentir en conséquence. On construit deux modèles, un premier dans lequel le joueur 1 joue en premier, et un second où c'est le joueur 2 qui prend la main. Les différents résultats sur les utilités des joueurs permettent de construire un arbre décisionnel permettant de trouver la solution de Nash grâce à un raisonnement par induction à rebours. Les résultats de la console sont présentés ci-contre, on joint également en appendice, les graphiques illustrant la recherche des y optimaux, ces derniers laissent apparaître les points qui ont été calculés durant la compilation.

24

174 Valeurs du jeu à

information parfaite

175

176 Quand les deux joueurs disent la vérité :

177 Utilité de .31 : 5.838

178 Utilité de .32 : 9.719

179

180 Quand .31 ment et que .32 dit la vérité :

181 Utilité de .31 : 6.464

182 Utilité de .32 : 9.181

183 .31 annonce vouloir aller en 0.546 au lieu de 0.84

184 La différence d'utilité de .31 équivaut à : 0.626

185 La différence d'utilité de .32 équivaut à : -0.538

186

187 Quand .32 ment et que .31 dit la vérité :

188 Utilité de .31 : 6.024

189 Utilité de .32 : 9.73

190 .32 annonce vouloir aller en 0.687 au lieu de 0.71

191 La différence d'utilité de .31 équivaut à : 0.186

192 La différence d'utilité de .32 équivaut à : 0.011

193

194 Quand les deux joueurs mentent de manière ingénue (ils se contentent de faire ãÑ leur meilleur mensonge quand l'autre dit la vérité') :

195 Utilité de .31 : 7.539

196 Utilité de .32 : 9.501

197 .31 annonce vouloir aller en 0.546 au lieu de 0.84

198 .32 annonce vouloir aller en 0.687 au lieu de 0.71

199 La différence d'utilité de .31 équivaut à : 1.701

200 La différence d'utilité de .32 équivaut à : -0.218

201

202 Quand le joueur 2 a décidé de mentir alors qu'il savait que le joueur 1 mentait

ãÑ :

203 Utilité de .31 : 7.238

204 Utilité de .32 : 9.718

205 .31 annonce vouloir aller en 0.766 au lieu de 0.84

206 .32 annonce vouloir aller en 0.687 au lieu de 0.71

207 La différence d'utilité de .31 équivaut à : 1.4

208 La différence d'utilité de .32 équivaut à : -0.001

209

210 Quand le joueur 1 a décidé de mentir alors qu'il savait que le joueur 2 mentait

ãÑ :

211 Utilité de .31 : 6.177

212 Utilité de .32 : 9.743

213 .31 annonce vouloir aller en 0.546 au lieu de 0.84

214 .32 annonce vouloir aller en 0.668 au lieu de 0.71

215 La différence d'utilité de .31 équivaut à : 0.339

216 La différence d'utilité de .32 équivaut à : 0.024

Ces résultats permettent donc de construire l'arbre décisionnel suivant, cet arbre est une des manières de trouver la solution de Nash au jeu. La fonction print_jeu_decouvert (jointe en appendice) permet également cela quand on lui fournit des couples d'utilité. On remarque que

dans les deux cas quand ils ont connaissances de toutes les informations, et surtout du choix de l'autre, les joueurs décident de mentir. Ce résultat semble logique étant donné que mentir est, par construction, plus avantageux que de dire la vérité. L'enjeu est d'étudier si cette décision reste rationnelle quand on prive le joueur de certaines informations. Ça sera l'objet d'une partie ultérieure.

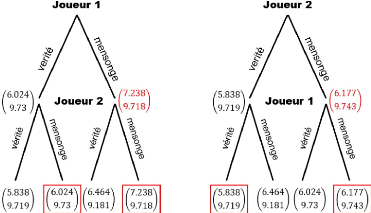
25

(a) Arbre décisionnel quand J1 joue en premier (b) Arbre décisionnel quand J2 joue en premier

FIGURE 9 - Arbres décisionnel et résolution à rebours

4.6.2 Nombre d'occurrence de chaque solution en information parfaite

Afin de compléter l'analyse du jeu à information parfaite, on peut s'intéresser au taux d'apparition des solutions. En effet, quatre solutions sont possibles, deux où un seul joueur ment, une où les deux mentent ainsi qu'une dernière où les deux ne mentent pas. On peut vraisemblablement supposer que la seconde n'apparaîtra presque jamais étant donné la manière dont a été construit le problème. Effectivement, compte tenu de la pénalité relative accordée au fait de marcher (le facteur K=5 fixé plus haut), un joueur qui sait que le premier n'a pas menti devrait pouvoir trouver une solution qui l'avantage. Dans le cas contraire, aucun des deux joueurs ne ment, mais cette éventualité devrait survenir de façon marginale.

L'algorithme destiné à compter le nombre de ces occurrences est décomposé en deux fonctions majeures (mises en appendice), la première fonction nash_joueur_i_premier_joueur permet de calculer une solution par induction à rebours, la fonction est d'ailleurs déjà utilisée dans la fonction print_jeu_decouvert qu'on a utilisé précédemment, la seconde fonction occur-rence_type_solution_jeu_decouvert retourne quant à elle une liste de valeurs s P {0, 1, 2, 3} correspondant aux 4 possibilités. Sur deux échantillons de 200 valeurs toutes comprises entre 0 et 3 (un échantillon correspondant à un des joueurs jouant en premier) on obtient les résultats suivant :

217 Quand le joueur 1 joue en premier

218 Nombre de fois oil les deux individus mentent : 179

26

219

Nombre de fois oil le premier ment et que le second ne ment pas	:	15	220
Nombre de fois oil le premier ne ment pas et que le second ment	:	4	221
Nombre de fois oil les deux disent la vérité : 2			222
Quand le joueur 2 joue en premier			223
Nombre de fois oil les deux individus mentent : 130			224
Nombre de fois oil le premier ment et que le second ne ment pas	:	44	225
Nombre de fois oil le premier ne ment pas et que le second ment	:	7	226
Nombre de fois oil les deux disent la vérité : 19

On constate dans ce modèle que presque 9 fois sur 10 les joueurs trouvent un intérêt à mentir. Cet exemple reflète une première limite à la solution de Nash. Cette dernière est en effet très sensible à l'utilité que les individus indiquent à l'arbitre, c'est d'ailleurs un problème déjà soulevé lorsque l'exemple 2.3 sur l'union européenne avait été proposé. Un joueur peut donc influer sur le calcul de son utilité (ici en jouant sur le temps de parcours), pour en changer le résultat et améliorer ses gains.

4.6.3 Jeu à information imparfaite

Le jeu à information parfaite présente l'avantage d'être simple à calculer, mais il reflète mal la réalité, en effet, il n'existe pas à priori de raisons pour un joueur de connaître la position de départ de l'autre ainsi que sa destination et encore moins son choix de mentir ou de dire la vérité. C'est la raison qui nous pousse à introduire et utiliser la notion de jeux à information imparfaite. La notion de "jeux" fait ici écho aux choix des joueurs de mentir ou de dire la vérité, le fait d'ignorer la position de l'autre joueur ainsi que sa destination relève quant à lui en partie de la notion de "croyance", on appuiera un peu plus précisément ce phénomène dans l'exemple suivant.

Considérons ici un jeu reprenant certains éléments du précédent. Le joueur 1 est au courant que le joueur 2 habite sur [0.3,0.35] (0.34 en réalité), le joueur 2, lui, sait que le joueur 1 se trouve sur [0,0.2] (0.02 en réalité). Tout deux souhaitent se rendre sur le segment [0.7,1] (0.84 pour le joueur 1 et 0.71 pour le joueur 2) et sont au courant de ce fait, tout en ignorant précisément la destination précise.

La difficulté est de choisir les deux points sur lesquels les joueurs hésitent à mentir sachant qu'ils ignorent beaucoup d'informations. Il n'y a pas de meilleures façons de faire, on a opté pour un calcul empirique des yi. Nous proposons de décrire une des itération qui sera répétée plusieurs fois : pour trouver l'endroit où le joueur 1 ment, on prend les valeurs de x1 « 0.02 et y1 « 0.84 qu'il connaît puis on tire aléatoirement x2 et y2 sur leur intervalle respectif (selon une loi uniforme) et finalement on calcule les deux y1 optimaux dans le jeu à information parfaite, c'est à dire ceux choisis par le joueur quand il sait que l'autre dit la vérité et également quand il ment. On obtient deux y correspondant à chacune des deux situations.

Ce processus est itéré n fois et produit deux échantillons de yi. Le y choisi pour le joueur 1 est celui obtenu en faisant la moyenne sur les 2n valeurs de y générées. On procède de manière similaire pour trouver le y du joueur 2.

En résumé, on a donc calculé la moyenne des destinations choisies par un joueur quand il sait que l'autre dit la vérité ainsi que lorsqu'il sait que l'autre ment. On pourrait continuer longtemps en s'intéressant à la destination choisie quand le joueur sait que l'autre sait qu'il ment et qu'il va mentir en conséquence etc... le processus est à la fois infini et devient de plus en plus complexe au fur et à mesure que l'on rajoute des stratégies. Sur un échantillon de 300 tirages, on obtient les valeurs suivantes (remarque : un jeu de données a également été fourni pour trouver les mêmes

y)

27

-- y1 quand J1 ment simplement vaut en moyenne: 0.787

-- y1 quand J1 ment en sachant que J2 ment vaut en moyenne: 0.678

-- y2 quand J2 ment simplement vaut en moyenne: 0.685

-- y2 quand J2 ment en sachant que J2 ment vaut en moyenne: 0.659 En prenant la moyenne respective des y1 et y2, on en vient à prendre :

-- y1 « 0.732

-- y2 « 0.679

On rappelle qu'initialement le joueur 1 souhaite se rendre en 0.84 et le joueur 2 en 0.71. On remarque que le joueur 1 doit concéder plus de distance de marche s'il veut influencer le jeu à sa faveur. C'est un résultat logique intuitivement étant donné qu'il se trouve plus loin de la voiture et souhaite se rendre plus loin que le joueur 2. En appliquant notre algorithme aux valeurs trouvées, nous trouvons les nos 4 couples d'utilités répertoriés dans le jeu mis sous forme normale :

Les résultats quant aux utilités obtenues sont les suivants :

6.27

9.72

Vérité

J1

J2

Mensonge

Vérité

5.84

9.72

9.76

9.69

9.76

6.14

Mensonge

On observe l'existence d'une solution de Nash unique pour laquelle les deux joueurs préfèrent encore une fois mentir en permanence.

Un autre test a été fait en diminuant encore davantage l'utilité due au fait de marcher. En effet nous avons fait passer le facteur K de 5 à 10, et pour autant les résultats ne diffèrent que marginalement comme en atteste le tableau suivant.

5.94

9.72

Vérité

J1

J2

Mensonge

Vérité

5.84

9.72

9.6

9.73

9.73

5.94

Mensonge

Ce résultat unanime s'explique en grande partie par les paramètres établis initialement. En effet, on s'aperçoit que lorsque le joueur 2 ment, il augmente considérablement l'utilité du joueur 1. Quand il ment, il rapproche son point de destination, et ce phénomène "arrange" le joueur 1 car il participe à changer les paramètres initiaux qui n'étaient pas à la base favorable au premier joueur.

Le fait que le jeu précédent soit à information imparfaite n'apporte pas de changement radical vis à vis du fait qu'on ait enlevé de l'information aux joueurs. C'est pourquoi nous allons changer le jeu en ajoutant des facteurs de désinformation aux joueurs. Considérons donc la situation suivante :

-- Une première zone d'habitation se trouve en [0,0.1]

-- Une seconde zone d'habitation se trouve en [0.9,1]

-- Une zone industrielle se trouve en [0.5,0.6]

28

A présent les joueurs 1 et 2 n'ont respectivement pas connaissance de X2 et X1, ils savent néanmoins que l'autre joueur se situe nécessairement dans l'une des deux zones d'habitation. On considère le jeu suivant : chacun des joueurs se situe dans l'une des deux zones d'habitation avec une probabilité p pour la zone [0,0.1] et 1-p pour la zone [0.9,1], distribués selon une loi uniforme sur chacun de ces intervalles. En introduisant ces facteurs p et 1-p, on introduit le concept de croyance mentionné plus haut. Ainsi, les deux joueurs souhaitent se rendre dans la zone industrielle mais ignorent où se trouve le second joueur. On s'intéresse au comportement des deux joueurs.

Afin d'obtenir des valeurs numériques, nous procédons de la manière suivante : un joueur ne trouve un intérêt à mentir que si l'autre joueur se trouve dans l'autre zone d'habitation, ainsi son choix de y se fait en considérant que l'autre joueur est soit en 0.05 soit en 0.95 (correspondant aux moyennes des deux segments d'habitation) selon que lui-même soit dans la zone 2 ou la zone 1 (choix possible grâce à notre fonction permettant de trouver un y optimal par dichotomie). Nous sommes ainsi capable de calculer les différentes destinations optimales des deux joueurs en fonction de la zone où ils se trouvent.

Afin de rester dans un cadre généraliste, on prend X1 et X2 égaux aux moyennes des segments sur lesquels ils se trouvent. Grâce aux valeurs numériques on obtient donc l'arbre suivant :

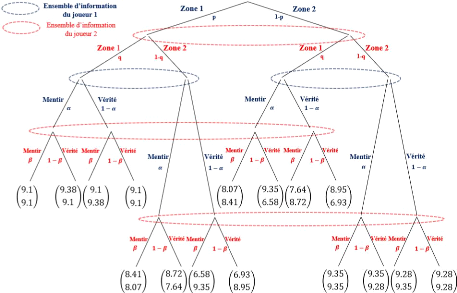
FIGURE 10 - Arbre décisionnel quand J1 et J2 ignorent où se trouve le second joueurs

La stratégie d'équilibre est facilement identifiable dans cet arbre. On observe en effet que pour chacun des noeuds terminaux du joueur 2, le mensonge domine la stratégie de dire la vérité

29

(strictement à un noeud près tout à gauche). Il ne reste plus qu'à considérer les noeuds terminaux où le joueur 2 ment pour s'apercevoir que le joueur 1 a toujours intérêt à mentir. La stratégie d'équilibre consiste donc à mentir peu importe les croyances p et q de chacun des deux joueurs. Cet équilibre est en fait un équilibre bayésien parfait.

4.7 Étude statistique de la nature de la solution de Nash dans notre modèle

Remarque: Cette partie numérique fait référence aux fichiers "Etude_probleme_voiture_partagee" et "Applications_statistiques", un jeu de donnée à également été fourni pour trouver les mêmes p-valeurs. Il est aussi possible de se référer à la section 8.2.5 mise en annexe.

Introduisons le nouveau cadre d'étude suivant : le patron de l'entreprise de VTC souhaite prendre connaissance de la part des cas où la solution de Nash induirait le recours à un tirage au sort entre deux possibilités. En effet, en ayant recours à la solution de Nash d'un modèle de marchandage, son objectif ne consiste pas à recourir au tirage au sort entre deux alternatives existantes, mais bel et bien à sélectionner une alternative existante. C'est pourquoi nous allons faire une étude statistique pour étudier la redondance de l'utilisation du tirage au sort dans le modèle. Si cette dernière devait prendre une part trop importante dans les résultats, l'entreprise serait sûrement contrainte de changer de méthode. Nous différencierons une solution comme étant mixte ou pure si elle a recours ou non au tirage au sort.

Notre entreprise a décidé qu'elle ne souhaitait pas que le modèle lui fournisse une solution mixte plus de 10% du temps. Nous allons par l'utilisation du test de Student juger si l'utilisation du jeu de marchandage satisfait les contraintes de l'entreprise.

Pour notre test, nous utilisons un échantillon Xi P t0, 1uⁿ ({Xi « 1u :« {la i^ème solution est pure}) de n variables aléatoires indépendantes générées par le calcul de la solution de Nash à partir des variables x1, x2, y1, y2, v tirées selon la loi Upr0, 1sq.

Nous avons choisi d'utiliser le test paramétrique de Student qui a l'avantage d'être plus puissant qu'un test non paramétrique tel que le test de la moyenne (dont les résultats n'étaient pas satisfaisant) afin de nous permettre d'estimer la fréquence d'obtention d'une solution pure. Nous allons donc effectuer notre test sur les hypothèses suivantes :

f

H0 : u à 90% H1 : u ï 90% Étant donné que nous cherchons un estimateur de la moyenne, il convient de prendre l'estima-

teur empirique ^ÏX_n « 1 øn i«0 Xi qui d'après la loi forte des grands nombres est un estimateur n

consistant de u. Au seuil á, la région de rejet du test est donc la suivante :

R_á « ^ÏX_n ã k_á(

Tandis que l'erreur de première espèce est définie par :

á :« sup P_up ^ÏX_n ã k_áq( « sup P_up ^ÏX_n ã k_áq(

H0 u90%

N'ayant pas de loi évident sur X_n et afin de trouver le k_á adéquat nous allons nous ramener à une statistique de Student et en évaluer le quantile. Rappelons la chose suivante:

Studentpn ' 1q

ç0

T « _a

X{pn ' 1q

Expression pour laquelle :

ç0 Np0,1q et X ÷2n-1

Premièrement, d'après le théorème central limite :

ç0 :« ?n à	^ÏXn ' u			Np0,1q

Ensuite, pour le calcul de la loi Khi-2 nous aurons besoin de l'estimateur ó, noté ó², encore une fois choisi par estimation empirique de part sa consistance :

pó^2 « 1 n ' 1

ÿn i=1

pXi ' ^ÏXnq^2

Nous pouvons ainsi calculer notre X :

X « pn ' 1qpó²

_ó2

Par simplification, nous pouvons réécrire notre statistique de test de la façon suivante :

?np

T «

^ÏX_n ' uq

b 1

ó (n-1)pó²

Studentpn ' 1q

?np ^ÏX_n ' uq

1

«

óp

.

Étant donné que nous avons transformé notre statistique de test, il convient de redéfinir notre erreur de première espèce :

á :« sup P_up ^ÏX_nã k_áq( (4)

%0

á « sup "_upT ã ^?npká'^uqq*(5) óp

óp

á « Pu=90%pT ã

?npk_á ' 0.9q

q (6)

30

En effet le passage de (5) à (6) se justifie par le fait que la probabilité est d'autant plus grande que le terme %/n(k_Q -u) est élevé et donc que u est petit, c'est pourquoi le sup est atteint en u « 0.9.

Étant donné que nous connaissons la loi de T, il est possible de trouver le quantile associé, on a donc :

qá (n-1) « ?npk_á ' 0.9q

óp

óp

_?n

Et donc :

k_á « 0.9 ` _qT (n-1)

á

Et notre zone de rejet s'écrit donc :

R_á « { ã 0.9 + qâ ^(T-1)

l ?n

Grâce à ça, on est désormais capable de trouver la p-valeur de notre test :

31

p-valeur « â :« inf }á P r0; 1s | X_n ã 0.9 ` _qa pn'1q ::n } (7)

_l

« inf }á P r0;1s |l p^ÏX_n ' 0.9q ã _qa pn'1q } (8)

« inf }á P r0;1s | _FT pn'1qp~n p^ÏX_n ' 0.9qq ã _FTpn'1qp_q« pn'1qq } (9)

" _?n *

« inf á P r0;1s | FTpn'1qp óp p ^ÏX_n ' 0.9qq ã á (10)

?n áà « FTpn'1qp óp

p Xn ' 0.9qq (11)

Le passage de (8) à (9) se justifie par la stricte croissance de la fonction de répartition de la loi de Student.

Pour notre échantillon de taille 1000, nous obtenons une p-valeur de 0.999

Cette très grande p-valeur nous conforte dans le fait de ne pas rejeter 1-10 et de conclure que l'entreprise peut raisonnablement entreprendre d'utiliser la solution de Nash pour répondre à sa problématique compte tenu de son seuil d'exigence. Malgré tout, elle devra accepter de recourir à l'aléatoire un nombre non négligeable de fois, ce qui est constitue assurément une limite à l'utilisation de la solution de Nash.

Encore une fois, étant donnée la formulation de notre hypothèse nulle, la p-valeur élevée nous prête à penser que nous ne devons pas rejeter 1-10. Par conséquent, étant données les exigences de l'entreprise, la solution de Nash semble y répondre efficacement.

Les p-valeurs de notre test précédent sont critiquables car elles dépendent très largement de l'échantillon qui a été généré aléatoirement. Ainsi, elles sont susceptibles de beaucoup fluctuer en fonction de l'échantillon généré. Il nous est même possible d'influencer le résultat en faveur de ce qu'on souhaite montrer en faisant simplement varier la taille de cet échantillon car la p-valeur est croissante et tend vers 1 quand la taille de l'échantillon grandit. De plus, l'écart qu'on peut constater entre les différents calculs de p-valeurs s'explique par la grande sensibilité du test. Ainsi un écart léger écart en dessous du seuil fixé se traduit immédiatement par une très faible p-valeur. Or la moyenne des échantillons générés tend à se distribuer selon une loi gaussienne autour de 90%, il n'est donc pas rare que certaines moyennes soit inférieures à ce seuil. En couplant le résultat donné par la p-valeur (qu'on a par ailleurs calculé 1000 fois et dont on a affiché un histogramme pour se rendre compte de sa distribution) et la moyenne de l'échantillon, on peut affirmer que 9 fois sur 10 en moyenne, la solution donnée à l'entreprise est une solution pure.

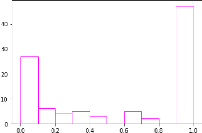
32

FIGURE 11 - Histogramme de 1000 p-valeur issues du test de Student

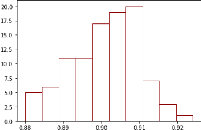
FIGURE 12 - Histogramme de 1000 moyennes résultant de solutions différentes

4.8 Conclusion de la partie numérique sur la solution de Nash

L'application de la solution de Nash décrite en première partie à notre étude numérique au sujet de la voiture partagée est riche d'enseignements. On a d'abord pu constater que la solution était assez facilement implémentable grâce à des fonctions judicieusement choisies. L'algorithme a par ailleurs l'avantage d'être stable dans son utilisation. Un autre avantage de la solution de Nash est le fait qu'elle se transpose aisément à notre étude à condition de poser les bonnes hypothèses, concernant notamment son applicabilité dans la réalité. Enfin, l'avantage majeur de cette solution est présent avant tout dans son existence ainsi que dans son unicité, il aurait été compliqué d'envisager un modèle vraisemblable et applicable si la solution fournie n'était pas unique.

Malgré ces avantages, cet exemple a mis en lumière deux limites à la solution de Nash. Le premier concerne la construction de l'ensemble des possibilités sur lequel la solution de Nash doit trancher. Cette dernière joue un rôle essentiel qui détermine entièrement la solution et rend la solution sensible à tout modification. On a vu que l'utilisateur de la voiture partagée pouvait trouver un intérêt à modifier des paramètres qui le concernait pour tourner la solution à son avantage. La seconde concerne la possibilité d'obtenir une solution mixte. Cette possibilité est indispensable pour être certain d'obtenir une solution, elle reste néanmoins difficilement exploitable quand on essaie de transposer le modèle à la réalité et contraint ses utilisateurs à recourir à l'aléa.

Cette partie nous a donc éclairé sur certaines problématiques qu'on pouvait rencontrer avec

33

l'utilisation pratique de la solution de Nash. Par ailleurs, on peut se demander si la construction même de cette solution n'est pas susceptible d'être remise en question. La démarche axiomatique permet certes de trouver l'existence d'une solution, mais le choix des axiomes relève avant tout d'une décision arbitraire de celui qui les incorpore au modèle. N'existe-t-il pas d'autres axiomes permettant de trouver également une solution unique, différente de celle trouvée jusqu'à présent? Cette question est l'objet de la partie suivante.

34

5 La solution de Nash : une solution faisant débat

5.1 Remise en cause de la solution de Nash via l'axiome d'indépendance aux alternatives non pertinentes

Nous avons vu précédemment que la solution de Nash au problème de marchandage à 2 joueurs est applicable dans nombre de domaines. En effet nous avons pu l'employer dans des situations tel le partage de voiture, un problème qui semble pertinent dans un monde où l'écologie prend de plus en plus d'importance. Cette solution, unique de par les conditions qui lui sont appliquées, se heurte à des problèmes de cohésion lorsque nous l'utilisons dans certaines situations. Nous nous proposons dans cette partie d'explorer ces situations, de réfléchir à pourquoi la solution de Nash est non pertinente dans ces cas et de finalement proposer une solution alternative qui serait mieux adaptée.

Pour mieux pouvoir illustrer nos propos, nous allons dans un premier temps rappeler les caractéristiques de la solution de Nash dans un jeu de marchandage à 2 joueurs.

A chaque jeu de marchandage opposant deux joueurs, on associe la paire (A, d). A est un sous-espace du plan. d = (d1, d2) sera le point de désaccord où di est le niveau d'utilité du joueur i si les deux n'arrivent pas à coopérer.

(A,d) doit au préalable vérifier 4 conditions :

Il existe au moins un point x de A tel que xi > di pour i = 1,2. Le marchandage doit donc être profitable aux 2 joueurs.

A est convexe : Si deux solutions de A permettent de construire la solution alors on peut ajouter des probabilités pour le choix entre ces deux événements pour parvenir à la solution.

A est compact.

d , x Vx E A. Si ce n'est pas le cas on peut ignorer tout point de A ne satisfaisant pas cette condition.

On va appeler J l'ensemble des couples (A,d) remplissant les conditions ci-dessus.

On peut à présent énoncer les axiomes qui permettent d'obtenir une fonction 0(A, d) qui renvoie l'unique solution de Nash au problème :

Pareto optimalité : V (A, d) E J, y E A tq y . 0(A, d) et y 0(A, d)

Symétrie : V T : 118² 118² définie par T (x1, x2) = (x2, x1), V (A, d) E J,
0(T(A),T(d)) = T(0(A, d))

Invariance par transformation affine : V(A, d) E J , et pour tous a, b E 118² avec a » (0, 0), 0(aA + b, ad + b) = a0(A, d) + b

Nous arrivons maintenant à l'axiome en question dont on va étudier la pertinence :

Indépendance des alternatives non pertinentes : V (A, d) E J , VA' c 118², A c A' et 0(A', d) E A 0(A', d) = 0(A, d)

C'est ce ^4ième axiome qui définit la solution de Nash ainsi que son unicité.

35

Cet axiome signifie que si la solution de Nash n'est pas modifiée lorsque l'on retire une alternative de l'ensemble des alternatives possible , cela signifie que l'accord trouvé entre les 2 joueurs restera le même que l'on prenne l'ensemble avec ou sans cette alternative. Celle-ci est considérée comme non pertinente.

Supposons par exemple que chaque année Lucas et Bastien doivent faire un choix sur le jour de départ de leurs vacances. Ayant le choix entre lundi, mardi et mercredi, ils ne choisissent jamais mercredi. Ils choisissent donc un mélange entre des départs le lundi et le mardi. Alors, d'après ce 4ième axiome de Nash, l'accord passé pour la date de départ sera le même qu'ils aient le choix entre les 3 jours ou juste lundi et mardi.

Bien que cet axiome puisse paraître dans un premier temps raisonnable, une multitude de cas démontrent facilement sa limite. Avant de pouvoir présenter un exemple qui exhibe une solution dont la pertinence puisse être remise en question, nous allons devoir introduire de nouvelles notations.

Soit (A, d) E J et soit M(A) = (M1(A), M2(A)) tel que :

M1(A) = sup{x E R : 3y E R, (x,y) E A} M2(A) = sup{y E R : 3x E R,(x,y) E A}

On définit la fonction gA(x) définie pour x M1(A) par :

" y si (x, y) est le point Pareto-optimal de (A, d) gA(x) = M2(A) sinon

Ici gA(x) est le maximum que le joueur 2 peut obtenir si le joueur 1 obtient au moins x. Grâce à la première condition vérifiée par (A,d), nous avons bien Mi(A) > di pour i=1,2. . Ainsi par compacité de A, M1(A) et M2(A) sont finis et atteints par des points de A.

Avec ces nouvelles notations observons ensemble un exemple concret.

Prenons 2 étudiants passant 2 épreuves. Ils représenterons nos 2 joueurs pour le jeu de marchandage suivant. L'un ne connaît que la première matière et l'autre que la seconde. A moins de s'entraider ils ne valideront pas et donc le point de désaccord sera d=(0,0).

Prenons 2 ensembles des alternatives différents A1 et A2 avec A1 = {(20, 0), (0, 20), (15, 15)} et A2 = {(20, 0), (0, 20), (20, 14)} tel que (A1, d) et (A2, d) appartiennent bien à J . On peut supposer ici que l'utilité des joueurs correspond à leur moyenne à ces examens avec 20 étant la note maximale. Par exemple si l'on prend le point ²¹ x (20, 0) + ²¹ x (0, 20) cela représente le fait que chaque joueur va aider l'autre de tel sorte à ce qu'ils ont tous les deux 10 de moyenne. Le fait de faire réviser l'autre entraîne une désutilité aux étudiants car cela leur prend du temps qu'ils auraient pu utiliser eux-mêmes pour réviser.

Si x est l'utilité du Joueur 1 et y celle du Joueur 2, on peut remarquer que :

" V x E [0 20] 3 y tel que (x, y) E A2

^,,Si 3 y' E 1R tel que (x,y^') E A1 alors y > y'

Donc gA₁(x) est ici inférieure à gA₂(x). En d'autres termes le maximum que le joueur 2 peut obtenir si le joueur 1 obtient au moins x est supérieur avec l'ensemble d'alternatives A2 plutôt qu'avec A1.

Nous pouvons donc logiquement émettre l'idée que l'étudiant 2 va demander un arrangement plus avantageux avec l'ensemble A2 par rapport à l'ensemble A1 car celui-ci peut y obtenir une

36

meilleure note sans que celle du joueur 1 ne change.

Si pour tout niveau d'utilité que pourrait demander le joueur 1, le maximum possible pour le joueur 2 peut en même temps être supérieur, alors le niveau d'utilité assigné au joueur 2 devrait logiquement se voir grandir.

Nous allons maintenant, grâce à notre algorithme, calculer les 2 solutions de Nash de ce jeu avec les ensembles d'alternatives A1 et A2.

Voici ce que nous obtenons :

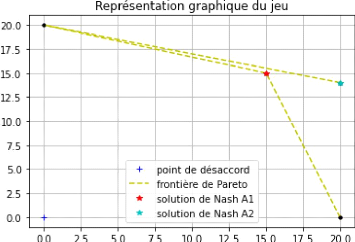
FIGURE 13 - Solution de Nash avec A1 et A2

Comme nous pouvons l'observer sur le graphique ci-dessus, la solution de Nash en prenant A1 est (15,15) tandis qu'avec A2 la solution est (20,14). En utilisant la solution de Nash et donc l'axiome d'indépendance des alternatives non pertinentes, l'étudiant 2 obtient une utilité inférieure avec A2 comparé à A1, ce qui contredit ce que nous avons dit précédemment. En effet ces solutions ne remplissent pas l'attente du Joueur 2 qui voulait pouvoir avoir une meilleure utilité avec A2 comparé à A1. Cet exemple met en lumière le fait que la solution au jeu de marchandage à 2 joueurs trouvé par Nash peut ne pas avoir de sens dans certains problèmes.

Nous pouvons maintenant nous poser la question : existe-il une solution unique au problème de marchandage qui donnerait un aboutissement du marchandage rationnel même dans les cas comme l'exemple ci-dessus?

37

5.2 Axiome de monotonicité de Kalai-Smorodinsky

25 ans après que Nash ait proposé ses axiomes pour trouver une unique solution au problème de marchandage, les économistes Ehud Kalai et Meir Smorodinsky ont proposé un ^4ième axiome alternatif : l'axiome de monotonicité.

-- Axiome de monotonicité : Si (A1, d) et (A2, d) E J tel que M1(A1) = M1(A2) et

gA₁ gA₂ alors 02(A1, d) 02(A2, d) avec 0(A, d) = (01(A, d), 02(A, d))

Cet axiome explique que si l'utilité maximum atteignable du Joueur 2 ( 02(A1, d) étant l'utilité du joueur 2 avec l'ensemble des alternatives A1 et le point de désutilité d ) est améliorée alors le niveau d'utilité du joueur 2 de la solution doit aussi être amélioré, et cela que pour toute utilité que le joueur 1 puisse demander. A travers l'axiome de monotonicité, Kalai et Smoro-dinsky affirment que la solution au problème de marchandage doit dépendre de tout l'ensemble des alternatives, c'est-à-dire qu'aucune alternative ne doit être considéré comme insignifiante et doit donc être prise en compte pour l'obtention de la solution.

Retournons à Lucas et Bastien qui marchandent sur les dates de leur départ en vacances chaque année. Reprenons les mêmes jours qu'avant mais cette fois-ci supposons que Bastien préfère largement partir mercredi plutôt que mardi et préfère légèrement partir mardi plutôt que lundi (mercredi » mardi > lundi). Lucas, lui, prèfère largement lundi à mardi lui-même préféré largement à mercredi (lundi »mardi » mercredi). Supposons qu'ils ont conclu un certain marché qui consiste à ne partir que des lundis et des mardis. Si l'on retire mercredi des choix possibles, l'accord peut tout à fait changer car mercredi pouvait servir d'outil de négotiation à Bastien : "J'accepte de ne jamais partir mercredi, le jour qui m'arrange le plus, mais alors je veux partir plus souvent mardi en conséquence.". Cette logique contredit Nash et son axiome d'indépendance des alternatives non pertinentes. En effet, pour Nash, la répartition entre les lundis et les mardis reste la même, que Bastien ait accès à son jour préféré ou non.

Je pense que la solution de Kalai est plus réaliste dans la société d'aujourd'hui. En effet, une stratégie connue en marketing est d'ajouter des alternatives pour pouvoir rendre les alternatives recherchées plus acceptables au client. Si on me propose une maison à un certain prix, je vais penser que le prix est correct si l'agence me propose pour le même prix une maison beaucoup plus petite.

C'est pour cela que les économistes Kalai et Smorodinsky remplace le ^4ième axiome de Nash par l'axiome de monotonicité ci-dessus. Désormais, un joueur ayant de meilleures options devrait obtenir un meilleur accord. Ce nouvel axiome, en remplaçant l'axiome d'indépendance des alternatives non pertinentes, permet en gardant les 3 autres axiomes ainsi que les conditions sur (A,d) de trouver une nouvelle solution unique au jeu de marchandage à 2 joueurs.

Théorème 5.1 (Unicité de la solution monotonique) Il existe une unique solution u qui satisfait l'axiome de monotonicité.

Soit (A, d) E J et L(M(A), d) la droite joignant d à M(A). L'élément maximum de A sur cette droite est u(A, d) avec M(A) = (M1(A), M2(A)).

On obtient donc la relation suivante :

u1 -- d1

=

u2 -- d2

38

M1(A) -- d1

M2(A) -- d2

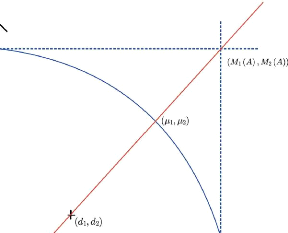
FIGURE 14 - Solution monotonique (u1,u2)

Preuve 3 Nous allons prouver ici que u est bien solution unique du problème de marchandage à 2 joueurs.

-- Étape 1

Montrons dans un premier temps que la solution monotonique est bien définie.

Fixons (A, d) E J un jeu normalisé.

(A, d) est normalisé si (d1, d2) = (0,0) et (M1(A), M2(A)) = (1,1). Il n'y a pas perte de généralité car grâce à l'axiome d'invariance par transformation affine, nous pouvons facilement retrouver la solution dans le cadre général.

L(M(A), d) a une pente positive de sorte que l'ordre partiel sur R² induit un ordre total sur L(M(A), d). Cela implique que si L(M(A), d) coupe A, alors il y a un unique élément maximum de A dans lui-même, et u(A) est bien défini. L(M(A), d) coupant A vient du fait qu'il existe un point (M1(A), y) E A tel que y . d2, qu'il existe un point (x, M2(A)) E A tel que x . d1, que d < M(A) et A est convexe.

On rappelle qu'une relation binaire . est un ordre partiel sur l'ensemble A si pour tous

39

éléments x, y et z de A :

x ï y et y ï z ñ x ï z (transitivité)

x ï x (réflexivité)

x ï y et y ï x ñ x « y (antisymétrie)

Si, de plus, x ï y ou y ï x, alors la relation est un ordre total sur A.

Étape 2

Nous allons maintenant montrer que u est une solution au problème de marchandage à 2 joueurs et qu'elle satisfait l'axiome de monotonicité.

u est symétrique : en effet pour tout jeu pA, dq P J , si px, yq P A ñ py, xq P A et d1 « d2, alors u1pA, dq « u2pA, dq.

De plus, u satisfait l'axiome d'optimalité de Pareto car A est convexe et compact.

u est invariante par transformation affine car pour tout jeu pA, dq P J , pour tous a, b P R2 avec a " p0, 0q, upaA ` b, ad ` bq « aupA, dq ` b.

La monotonicité va se prouver géométriquement.

Soit L_á est une droite de pente a avec 0 ï a ï ² passant par d. Si po1paq, o2paqq est le point d'intersection de L_á avec la frontière de tx P R² : Dy P A, x ì 0 et x ï yu, alors si /3 a, o2p/3q ì o2paq et si po1²'paq,o₂²'paqq est le point correspondant pour pA2,dq, on a que o₁ páq ì op1'

p2' 1 . On rappelle que dans le cadre de cet axiome gA₁ ^ï gA₂.

Étape 3

Prouvons finalement que u est l'unique solution qui satisfait la condition de monotonicité. Soit pA, 0q un jeu normalisé et f une solution monotonique.

p1, 0q, upA^', 0qu un

Soit A^' « tx P R² : Dy P A tel que x ì 0 et x ï yu. pA^', 0q est bien un jeu normalisé avec A A^' tel qu'il n'existe pas de point y tel que y ì fpA^', 0q et y %o fpA^', 0q. Donc fpA, 0q « fpA^', 0q. Les points p0,1q et p1,0q sont dans A^'. Soit A^'' « tp0,1q,

convexe. Alors pA^'', 0q est un jeu normalisé symétrique pour les 2 joueurs avec A^'' A^'. Nous avons donc fpA^'', 0q « upA^', 0q.

On remarque aussi que A^' ne contient aucun point y tel que y ì fpA^'', 0q et y %o fpA^'', 0q. Donc fpA, 0q « upA^', 0q « upA, 0q.

Revenons à notre exemple des étudiants. Ceux-ci doivent se mettre d'accord pour de l'entraide concernant 2 examens à passer. Dans ce problème notre point de désaccord était d « p0, 0q et on avait à notre disposition deux ensembles d'alternatives : A1 « tp20, 0q, p0, 20q, p15, 15qu et A2 « tp20, 0q, p0, 20q, p20, 14qu. Les solutions de Nash avec A1 et A2 étaient respectivement p15, 15q et p20, 14q. D'après Kalai et Smorodinsky, la solution du Joueur 2 devrait être supérieure avec A2 car la moyenne maximum atteignable par le joueur 2 peut obtenir si le joueur 1 obtient au moins la moyenne x est supérieure avec A2. Calculons les solutions monotoniques de ce problème et voyons si cela résout notre problème concernant la solution de Nash.

Tout d'abord pour A1 nous devons donc résoudre le problème suivant :

" « M1pA1q ' d1

'

p

1q '

u2

d2 M2

A

d2

max pu1, u2q P ]I82 + | u1 ' d1

En remplaçant on obtient :

" max px, y, zq P ]I8³ 120x ` 15z « 20 }

20y ` 15z 20

40

sachant que x + y + z = 1 et que x, y, z 0

On obtient donc :

max { (x, y, z) E 118³ | x = y}

sachant que x + y + z = 1 et que x, y, z 0 De façon similaire pour A2 nous obtenons :

"max (u1,u2) E 118₊ |

2 1

u1 -- d1 M1(A2) -- d1

=

u2 -- d2 M2(A2) -- d2

En remplaçant on obtient :

"

3 20x + 20z 20

max (x, y, z) E 118 I =

20y + 14z 20

sachant que x + y + z = 1 et que x, y, z 0

On obtient ainsi :

max { (x, y, z) E 118³ | 20x + 6z = 20y}

sachant que x + y + z = 1 et que x, y, z 0

Pour A1 nous obtenons encore une fois (15, 15) mais pour A2 nous trouvons ici (15.38, 15.38). Nous constatons bien que l'utilité du Joueur 2 est supérieure pour A2 avec son utilité obtenue via la solution de Nash pour le même ensemble d'alternatives. Cela résout en effet la problématique soulevée par Ehud Kalai et Meir Smorodinsky, le joueur 2 ayant une meilleure utilité dans le cas où il a plus de choix possibles.

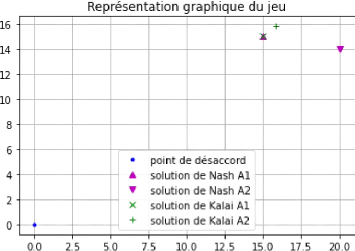
41

FIGURE 15 - Solutions de Nash et Kalai avec A1 et A2

Dans ce problème en question la solution de Kalai paraît beaucoup plus logique que la solution de Nash. En effet dans l'ensemble des alternatives A2, l'étudiant 1 peut se permettre d'aider l'étudiant 2 à avoir 14 de moyenne tout en gardant 20 de moyenne. Avec l'ensemble des alternatives A1, il lui est impossible d'atteindre 20 de moyenne tout en aidant l'étudiant 2 à avoir 14. Avec A2, l'étudiant peut "gratuitement" avoir 14 de moyenne, le joueur 1 étant indifférent entre l'aider où non vu qu'il a 20 de toute façon. Cela devrait donc se traduire par un avantage pour le joueur 2 au moment des négociations, ce que la solution de Nash manque de prendre en compte.

Après cette partie il est légitime de se demander laquelle de ces 2 solutions est la plus juste. Cela va dépendre de notre préférence pour l'un des axiomes interchangeables. Si nous considérons que l'ajout d'une alternative qui ne sera jamais choisie ne va pas modifier l'accord trouvé entre les 2 joueurs, alors la solution de Nash est pertinente via l'axiome d'indépendance des alternatives non pertinentes. Si au contraire nous acceptons le fait que bien que cette alternative ne soit pas choisie, elle modifie le pouvoir de négociation des joueurs, il sera intéressant de choisir la solution de Kalai avec l'axiome de monotonicité. Dans ce cas là, si l'utilité maximum d'un joueur augmente, et cela pour toute utilité que l'autre joueur puisse demander, alors son utilité augmentera. Nous pouvons faire l'interprétation qu'un juge, dont le rôle est de trouver l'accord entre les deux joueurs, va être impartial entre les deux joueurs mais partial sur le choix des axiomes utilisés et donc sur la solution choisie. Cela pourrait représenter sa propre notion de ce qui est juste. Ces préférences peuvent être apparenté au type de société dans lequel l'échange prend place, celle-ci ayant des caractéristiques sociales et morales spécifiques.

42

6 Conclusion

Nous avons vu avec ce mémoire que le principe de marchandage est un cadre créé par J.F Nash pour pouvoir rigoureusement développer une théorie permettant d'encadrer l'échange entre 2 agents. Il a essayé de décrire le comportement de ces agents au travers d'axiomes mathématiques, lesquels ont été soigneusement choisis pour qu'ils puissent permettre, ensemble, l'acquisition de certaines propriétés essentielles concernant l'arrangement trouvé entre les deux individus. Incorporés au modèle développé par J.F Nash, ces axiomes rendent l'existence d'un accord systématique et unique, deux caractéristiques indispensables à l'application concrète du principe de marchandage.

Ces axiomes procurent à la solution des propriétés géométriques avantageant sa construction algorithmique et permettant ainsi une étude approfondie de ses applications à des exemples concrets. L'étude du concept de voiture partagée géré par une entreprise était un exemple, original, de l'application concrète qu'il était possible de faire avec la solution obtenue par J.F Nash. Néanmoins, elle n'est pas une solution "miracle" car elle comporte certains défauts à une application dans la réalité. La possible malhonnêteté d'un ou des agents en est un premier. En effet, de la véracité des informations qu'il soumet à l'arbitre (ici l'entreprise) dépend la solution obtenue. On a vu que lorsque l'agent choisit de modifier légèrement des paramètres sur lesquels il a un pouvoir de décision, à savoir sa destination dans notre cas, le résultat pouvait changer radicalement, au point que mentir formait souvent une stratégie dominante. Le deuxième défaut étudié a été le fait que la solution n'appartenait pas forcément à un élément du cadre initial mais pouvait être le mixte entre deux d'entre eux. Le cadre théorique ne se soucie pas de cette éventualité, par contre elle peut rendre difficile une application concrète du principe de marchandage. C'est la raison pour laquelle on a étudié le fait que l'entreprise devait prendre en compte cette éventualité avant de décider si elle devait ou non appliquer le principe de marchandage à sa problématique initiale. Il est nécessaire malgré tout de préciser que le fait de ne pas appliquer cette solution ne signifie pas que dans le cadre imaginé, il en existe une meilleure. On a vu par la suite que la solution de Nash pouvait être confrontée à celle de Kalai, mais parfois (et c'est le cas nous le pensons ici) il vaut mieux changer le cadre plutôt que d'essayer de trouver une meilleure solution (positionnement plus stratégique des voitures par l'entreprise par exemple).

Nous avons pu mettre en lumière la différence entre la solution de Nash et la solution de Ka-lai pour un jeu de marchandages à 2 joueurs. Ceci est fort intéressant car nous constatons que contrairement à d'autres champs comme les mathématiques, les sciences économiques tel que celle des jeux de marchandages sont relativement récentes (1950 pour Nash et 1975 pour Kalai). Nous avons constaté que le choix des axiomes dépendait non pas d'une vérité universelle mais de la vision de son créateur et de certaines propriétés à appliquer à leur solution. En effet, au cours de l'étude de leurs travaux, nous avons constaté que ces économistes étaient autant préoccupés par les caractéristiques mathématiques avantageuses de leur solution, comme l'unicité, que par la vraisemblance de cette solution à la réalité. Les axiomes choisis servent à décrire la manière de réfléchir des agents, mais surtout à créer un modèle mathématique qui a du sens. Nous avons vu via l'exemple de la distribution de vaccins dans l'Union Européenne qu'en réalité il y a beaucoup plus de paramètres à prendre en compte et que la solution de Nash ou de Kalai sont difficiles à appliquer. Néanmoins, ces 2 solutions restent pertinentes et peuvent servir de repères pour prendre une décision. Il serait intéressant pour des décideurs de prendre en compte plusieurs solutions différentes comme les solutions de Nash et Kalai pour ensuite prendre une décision concernant un jeu de marchandage. Bien qu'ils soient différents, les axiomes mis en place par les différents économistes ont tous du sens et peuvent mettre en lumière certains comportements.

43

Avis personnels :

Lucas : Ayant eu la matière Théorie des Jeux durant ma Licence de Mathématiques puis Théorie des Contrats au premier semestre de cette année, j'étais d'avis à choisir un sujet de mémoire dans ce domaine ayant aimé ces matières. Le sujet Marchandage et partage d'objets a donc été le choix évident pour moi. Ce mémoire nous a appris à nous organiser à plusieurs autour d'un projet. Chercher par soi-même des concepts théoriques sans avoir un cours à l'Université sur lequel on peut se baser n'est pas chose évidente, et avoir appris à lire et comprendre des papiers de chercheurs est, je pense, un outil pertinent à avoir pour la suite de mes études et surtout pour ma future carrière professionnelle. Les concepts étant parfois compliqué à saisir, j'ai compris l'importance des exemples de de la "vulgarisation scientifique" des notions avancées. En effet ce mémoire ne s'adresse pas forcément aux personnes déjà compétentes dans ce domaine d'étude et donc, comme nous au départ, vont avoir besoin de de contexte pour bien saisir toutes les nuances du modèle créé par Nash. C'est cela qui, à mon avis, rend le sujet intéressant.

Bastien : Ce mémoire a été enrichissant à bien des égards. Il m'a permis de comprendre la démarche que pouvait entreprendre un scientifique lorsqu'il souhaitait trouver une solution à un problème posé. J'ai donc éprouvé un réel intérêt envers ce procédé axiomatique qui relève parfois d'une logique personnelle pouvant être remise en question sans pour autant être fausse. Ce mémoire a aussi été l'occasion pour moi de beaucoup coder avec certaines problématiques en tête, la première étant le fait d'essayer de rendre un code le plus intelligible possible, tâche ô combien ardue. Une deuxième consistait à découper un gros problème en plusieurs plus petits et plus facilement réalisables. Enfin, une dernière problématique concernait l'application d'algorithmes sur des cas pratiques à des fins théoriques. Face à toutes les idées d'applications qu'on pouvait imaginer, il a fallu à chaque fois penser des façons de procéder et choisir celle qui nous semblait être la meilleure. On a malheureusement dû se séparer de beaucoup d'idées intéressantes mais également très chronophages.

7 Bibliographie

Nash, J. (1950). The Bargaining Problem. Consulté sur https :// www.semanticscholar.org/paper/The-Bargaining-Problem-Nash/c38e70179b9c33a19824fd157adb8291cfbef1c2

Nash, J. (1953). Two-Person Cooperative Games. Consulté sur https :// www.jstor.org/stable/1906951 ?seq=1

Kalai, E., & Smorodinsky, M. (1975). Other Solutions to Nash's Bargaining Problem. Consulté sur https :// www.semanticscholar.org/paper/OTHER-SOLUTIONS-TO-NASH%27S-BARGAINING-PROBLEM-Kalai-Smorodinsky/ea620f7be68a48d3bcc9b260fecdfd6e54f14270 ?p2df

Ozdaglar, A. (2010). Game Theory with Engineering Applications Lecture 14 : Nash Bargaining Solution. Consulté sur https :// ocw.mit.edu/courses/electrical-engineering-and-computer-

science/6-254-game-theory-with-engineering-applications-spring-2010/lecture-notes/MIT6_254S10_lec14.pdf

44

8 Appendice

8.1 Codes et résultats consoles annexe de la partie 4

1. Fonction de dichotomie pour la recherche d'extrema 3 Lien pour retourner sur la page contenant la référence 23

227 def joueur_ment_y_maximum_dichotomie

ãÑ (joueur,a,b,x1,x2,y1,y2,v,decimale,tolerance) :

228 u_et_y = [[],[]]

229 if joueur == 1 : # le while suivant trouve le max quand J2 ment,

ãÑ on inverse donc si c'est J1 qui ment

230 c = x1

231 x1 = x2

232 x2 = c

233 d = y1

234 y1 = y2

235 y2 = d

236 i = 0

237 while (b-a) > 10**(-tolerance) and (i < 50):

238 p = a + (b-a)/4

239 m = a + (b-a)/2

240 q = a + 3*(b-a)/4

241

242 u_p = solution_rapide(x1,x2,y1,p,v,decimale)[0][1] -
ãÑ abs(utilite_marche(p, y2, decimale))

243 u_q = solution_rapide(x1,x2,y1,q,v,decimale)[0][1] -
ãÑ abs(utilite_marche(q, y2, decimale))

244 u_m = solution_rapide(x1,x2,y1,m,v,decimale)[0][1] -
ãÑ abs(utilite_marche(m, y2, decimale))

245

246 u_et_y[0].append(u_p), u_et_y[0].append(u_q),
ãÑ u_et_y[0].append(u_m)

247 u_et_y[1].append(p), u_et_y[1].append(q), u_et_y[1].append(m)

248

249 if u_p > u_m:

250 b = m

251 elif u_m < u_q:

252 a = m

253 else:

254 a = p

255 b = q

256 i+=1

257 y_sol = (a+b)/2

258 u_sol = solution_rapide (x1,x2,y1,y_sol,v,decimale)[0][1] -

ãÑ abs(utilite_marche(y_sol, y2, decimale))

259

260 u_et_y[0].append(u_sol)

261 u_et_y[1].append(y_sol)

262 return [y_sol,u_sol,u_et_y] # u_et_y sert au plot

45

2. Fonction print_jeu_decouvert

Lien pour retourner sur la page contenant la référence 24

263 def print_jeu_decouvert (x1,x2,y1,y2,v,decimale):

264 B=[]

265 B.append(str("\nQuand .31 est le premier à jouer, .31 décidera de

ãÑ mentir et .32 également"))

266 B.append(str("\nQuand .31 est le premier à jouer, .31 décidera de
ãÑ mentir mais .32 préférera dire la vérité"))

267 B.append(str("\nQuand .31 est le premier à jouer, .31 décidera de dire
ãÑ la vérité mais .32 préférera mentir"))

268 B.append(str("\nQuand .31 est le premier à jouer, .31 décidera de dire
ãÑ la vérité et .32 également"))

269

270 B.append(str("\nQuand .32 est le premier à jouer, .32 décidera de
ãÑ mentir et .31 également"))

271 B.append(str("\nQuand .32 est le premier à jouer, .32 décidera de
ãÑ mentir mais .31 préférera dire la vérité"))

272 B.append(str("\nQuand .32 est le premier à jouer, .32 décidera de dire
ãÑ la vérité mais .31 préférera mentir"))

273 B.append(str("\nQuand .32 est le premier à jouer, .32 décidera de dire
ãÑ la vérité et .31 également"))

274 print(" \n Solution de Nash du jeu à découvert

		")
ãÑ

275 liste_1 = creation_4_couples_utilites

ãÑ (1,x1,x2,y1,y2,v,decimale,tolerance)

276 s_1,i_1 = nash_joueur_i_premier_joueur(1, liste_1)[:2]

277 print(B[i_1])

278 liste_2 = creation_4_couples_utilites

ãÑ (1,x1,x2,y1,y2,v,decimale,tolerance)

279 s_2,i_2 = nash_joueur_i_premier_joueur(2, liste_2)[:2]

280 print(B[i_2+4])

3. Cliquer pour revenir à la page correspondante

281 def nash_info_parfaite (premier_joueur,S): # prend en argument le

ãÑ return de creation_4_couples_utilites

282 s_mm,s_vm,s_mv,s_vv = S[0], S[1], S[2], S[3]

283 if premier_joueur == 1 :

284 joueur = 2

285 s_1 = comparaison(joueur,s_mv,s_vv)

286 s_2 = comparaison(joueur,s_mm,s_vm)

287 s = comparaison(premier_joueur, s_1, s_2)

288 else :

289 joueur = 1

290 s_1 = comparaison(joueur,s_mv,s_vv)

291 s_2 = comparaison(joueur,s_mm,s_vm)

292 s = comparaison(premier_joueur, s_1, s_2)

293 return s

4. Cliquer pour revenir à la page correspondante

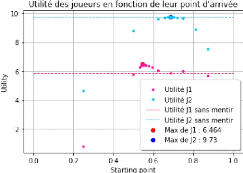
46

FIGURE 16 - Graphique : recherche par dichotomie quand aucun des joueurs ment

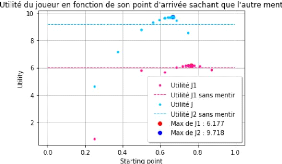
FIGURE 17 - Graphique: recherche par dichotomie quand un joueur sait que l'autre ment

47

294 def occurrence_type_solution_jeu_decouvert (taille_echantillon = 100, ãÑ decimale = 2, tolerance = 100, joueur = 1): # joueur ==> premier à

ãÑ

jouer

295 occurrence_J1 = []

296 for i in range (taille_echantillon):

297 x1, x2, y1, y2, v = random_5_points(decimale) # random_5_points
ãÑ -> 5 points x1,x2,y1,y2,v en évitant que x1=y1 et x2=y2 car ãÑ problématique

298 liste = creation_4_couples_utilites

ãÑ (joueur,x1,x2,y1,y2,v,decimale,tolerance) # -> créer les 4 ãÑ couples d'utilité

299

ãÑ occurrence_J1.append(nash_joueur_i_premier_joueur(joueur,liste)[1])

300 return occurrence_J1

48

8.2 Code réalisé tout au long de ce mémoire

Le code a été écrit sur spyder, certaines syntaxe sont donc propres à cet IDE. 8.2.1 Fichier "Nash_solver.py"

301 # Le programme suivant vise a calculer la solution de Nash d'un jeu de ãÑ marchandage a deux joueurs dont l'ensemble d'alternatives est l'enveloppe ãÑ convexe d'un nombre fini de points.

302

303 from numpy import array

304 from matplotlib.pyplot import plot, figure, title, grid, legend, show

305 from matplotlib.patches import Rectangle

306

307

308 # renvoie l'abscisse d'un point de R2

309 def first_component(a):

310 return a[0]

311

312 # renvoie l'ordonnee d'un point de R2

313 def second_component(a):

314 return a[1]

315

316 # prend en entree une liste de points de R2 renvoie

317 # la liste triee par ordre decroissant par rapport a la premiere composante

318 # les points de premiere composante egale sont tries par rapport a la seconde

319 def double_sort(L):

320 S = sorted(L, key = second_component, reverse = True)

321 S.sort(key = first_component, reverse = True) # la méthode "sort"

ãÑ conserve

322 # l'ordre lorque la cle est

ãÑ la meme

323 return S #O(len(L))

324

325 # prend en entree une liste triee par la fonction "double_sort"

326 # renvoie une sous-liste strictement décroissante pour la premiere

327 # composante et strictement croissante pour la seconde

328 def first_selection(L):

329 S = [L[0]] # L etant triee par "double_sort", L[0] sera forcement

330 # le premier element de la sous-liste

331 n = len(L)

332 i = 1

333 j = 0

334 while i < n:

335 if L[i][0] < S[j][0] and L[i][1] > S[j][1]:

336 S.append(L[i])

337 j+=1

338 i+=1

339 return S #O(len(L))

340

49

341 # prend en entree trois points strictement decroissants/croissants

342 # pour la premiere/seconde composante renvoie "True" ssi le point du milieu

343 # est strictement au-dessus de la droite passant par les deux autres

344 def above(a,b,c):

345 return b[1] > (a[1]*(b[0]-c[0])/(a[0]-c[0])) +
ãÑ (c[1]*(a[0]-b[0])/(a[0]-c[0]))

346

347 # prend en entree une liste strictement decroissante/croissante pour la ãÑ premiere/

348 # seconde composante renvoie la sous-liste privee des points Pareto-domines

349 # par une combinaison d'autres points

350 def second_selection(L):

351 if len(L) == 1: return L

352 S = [L[0],L[1]]

353 n = len(L)

354 i = 2

355 j = 0

356 while i < n:

357 if above(S[j],S[j+1],L[i]):

358 S.append(L[i])

359 j+=1

360 i+=1

361 else:

362 S.pop()

363 if j == 0:

364 S.append(L[i])

365 i+=1

366 else:

367 j-=1

368 return(S) # O(len(L))

369

370 # prend en entree une liste de points de R2

371 # renvoie la liste triee des points constituant la frontiere de Pareto de ãÑ l'enveloppe convexe de l'ensemble des points

372 def frontier_points(L):

373 S_0 = double_sort(L)

374 S_1 = first_selection(S_0)

375 S_2 = second_selection(S_1)

376 return S_2 # O(len(L))

377

378 # prend en entree deux points strictement decroissants/croissants pour la

ãÑ premiere

379 # /seconde composante renvoie l'ordonnee du maximiseur de la "fonction produit"

ãÑ

sur

380 # la droite passant par ces deux points

381

382 def y_max(a,b): # a est sous la forme [x1,y1]

383 a_1, a_2, b_1, b_2 = a[0], a[1] ,b[0] ,b[1]

384 p_cut = b_1/(b_1-a_1)

50

385 return (p_cut*a_2 + (1-p_cut)*b_2)/2

386

387 # idem "y_max"; renvoie l'abscisse

388 def x_max(a,b):

389 a_1, a_2 ,b_1 ,b_2 = a[0], a[1] ,b[0] ,b[1]

390 p_cut = b_2/(b_2-a_2)

391 return (p_cut*a_1 + (1-p_cut)*b_1)/2

392

393 # prend en entrée une liste traitee par "frontier_points"

394 # renvoie le point de l'enveloppe convexe de la liste qui maximise la "fonction

ãÑ produit"

395 def solution_rec(L):

396 n = len(L)

397 if n == 0:

398 print("Echec de la recurrence")

399 if n == 1:

400 return array([[L[0][0],L[0][1]],[0,0],[0,0],[1,0]])

401 else:

402 m = n//2

403 a, b = L[m-1], L[m]

404 y = y_max(a,b)

405 if y < a[1]:

406 if n > 2:

407 return solution_rec(L[:m])

408 else:

409 s = array([a[0],a[1]])

410 a = array([a[0],a[1]])

411 b = array([b[0],b[1]])

412 c = array([1,0])

413 return array([s,a,b,c])

414 if y > b[1]:

415 if n > 2:

416 return solution_rec(L[m:])

417 else:

418 s = array([b[0],b[1]])

419 a = array([a[0],a[1]])

421 c = array([0,1])

422 return array([s,a,b,c])

423 else:

424 x = x_max(a,b)

425

420 b = array([b[0],b[1]])

p = (x - b[0]) / (a[0]-b[0])

426 s = array([x,y])

427 a = array([a[0],a[1]])

428 b = array([b[0],b[1]])

429 c = array([p,1-p])

430 return array([s,a,b,c]) # O(len(L))

431

432 # prend en entree une liste de points et un vecteur de R2

51

433 # renvoie la liste decalee par le vecteur

434 def shift(L,v):

435 L_shifted = []

436 for i in range(len(L)):

437 P = array([ L[i][0] + v[0], L[i][1] + v[1] ])

438 L_shifted.append(P)

439 return L_shifted # O(len(L))

440

441 # prend en entree une liste de points de R2

442 # renvoie deux listes constituees respectivement de ses abscisses et ordonnees

443 def get_lists(L):

444 X = []

445 Y = []

446 for i in range(len(L)):

447 tmp = L[i]

448 X.append(tmp[0])

449 Y.append(tmp[1])

450 return [X,Y] # O(len(L))

451

452 # prend en entree une liste d'alternatives et un point de desaccord

453 # affiche la representation du jeu sur le plan ainsi que sa solution de Nash

454 def plot_solution(A,d):

455 L = shift(A+[d], (-1)*d)

456 F = frontier_points(L)

457 s = solution_rec(F)[0]

458 A_lists = get_lists(A)

459 F_lists = get_lists(shift(F,d))

460 fig = figure()

461 ax = fig.add_subplot(111)

462 plot(A_lists[0], A_lists[1], '.k')

463 plot(d[0], d[1], '+b', label="point de désaccord")

464 plot(F_lists[0], F_lists[1], '--y', c = "deepskyblue", label="frontière de

ãÑ Pareto")

465 plot(s[0]+d[0], s[1]+d[1], '*r', label="solution de Nash")

466 ax.add_patch(Rectangle(d,s[0], s[1], linewidth = 0.5, edgecolor = 'black',

ãÑ fill = False,hatch='/'))

467 grid()

468 title("Représentation graphique du jeu")

469 legend()

470 show()

471

472 def to_list (s):

473 n = len(s)

474 if n%2 != 0:

475 print('Raté')

476 return 0

477 m = int(n/2)

478 L = []

479 for i in range (m):

52

480 x = [s[2*i],s[2*i+1]]

481 L.append(x)

482 return L # O(len(L))

483

484 def true_solution(A,d):

485 L = shift(A+[d], (-1)*d)

486 F = frontier_points(L)

487 s = solution_rec(F)

488 s_list =[]

489 for i in range (3):

490 s_list.append(shift(to_list(s[i]),d))

491

492 L=[]

493 for i in range (len(s_list)):

494 p = [s_list[i][0][0], s_list[i][0][1]]

495 L.append(p)

496 L.append([s[3][0],s[3][1]])

497 return L # O(len(L))

498

499

500 def print_solution(s): # prend en entrée le résultat de true_solution

501 sol = [round(s[0][0],2),round(s[0][1],2)]

502 a = [round(s[1][0],2),round(s[1][1],2)]

503 b = [round(s[2][0],2),round(s[2][1],2)]

504 p = round(s[3][0],2)

505 q = round(1 - p,2)

506

507 if p == 1:

508 print ("La solution est le point de la liste initiale : ", sol)

509 elif p == 0:

510 print ("La solution est le point de la liste initiale : ", sol)

511 else :

512 print("La solution est une combinaison linéaire du point " + str(a)\

513 + " chargé du poids " + str(p) + " et du point " + str(b) + \

514 " chargé du poids " + str(q))

515 print("La solution est le point ", sol)

516

517

518

519

520

521

522

523

524

525

#%%

#'''	'''				Partie 3					'''
L =	[[444,	968],	[261,	220],	[646,	985],	[815,	878],	[929,	122],\
	[638,	136],	[536,	550],	[435,	992],	[346,	161],	[372,	283],\
	[608,	674],	[569,	491],	[255,	962],	[670,	198],	[958,	304]]
d =	[1, 28]

526

527 L_list = get_lists (L)

528

53

529 figure()

530 plot(L_list[0],L_list[1],'o', c = 'b')

531 plot(d[0],d[1],'o', c = 'r')

532

533 L_double_sort = double_sort(L)

534 L_double_sort_list = get_lists(L_double_sort)

535 figure()

536 plot(L_double_sort_list[0],L_double_sort_list[1],'o', c = 'b')

537 plot(d[0],d[1],'o', c = 'r')

538 title('Points restants après le triage par "double sort"')

539

540 L_frontier = frontier_points(L_double_sort)

541 L_frontier_list = get_lists(L_frontier)

542 figure()

543 plot(L_frontier_list[0],L_frontier_list[1],'o', c = 'b')

544 plot(d[0],d[1],'o', c = 'r')

545 title('Points restants après le triage par "frontier point"')

546

547 d = array([d[0],d[1]])

548 S = true_solution(L,d)

549 print_solution(S)

550 plot_solution(L, d) #'''

54

8.2.2 Fichier "Fonctions_distances.py"

551 from numpy import array

552

553 def marche(x):

554 return 5*x

555

556 def dist(x,y): # simple calcul de la distance euclidienne

557 return abs(y-x)

558

559 def cp3 (x,z,y): # calcul de la distance entre deux points en imposant un

ãÑ checkpoint

560 return dist(x,z) + dist(z,y)

561

562 def cp4 (x,v,w,y):

563 return cp3(x,v,w)+dist(w,y)

564

565 def cp5 (x,u,v,w,y):

566 return cp4(x,u,v,w)+dist(w,y)

567

568 def dist_v(x,y): # calcul de la distance parcourue en voiture en faisant

ãÑ x -> y

569 return dist(x,y)

570

571 def cp3_v (x,z,y): # calcul de la distance parcourue en voiture

572 return cp3(x,z,y)

573

574 def cp4_v (x,v,w,y):

575 return cp4(x,v,w,y)

576

577 def cp5_v (x,u,v,w,y):

578 return cp5(x,u,v,w,y)

579

580 def dist_m(x,y): # calcul de la distance parcourue en marchant, en
ãÑ considérant que dist_m = marche(d_v)

581 return marche(dist_v(x,y))

582

583 def cp3_m (x,z,y): # calcul de la distance parcourue en marchant en

ãÑ faisant x -> z -> y

584 return marche(cp3_v(x,z,y))

585

586 def cp4_m (x,v,w,y): # calcul de la distance parcourue en marchant en

ãÑ faisant x -> v -> w -> y

587 return marche(cp4_v(x,v,w,y))

588

589 def cp5_m (x,u,v,w,y):

590 return marche(cp5_v(x,u,v,w,y))

591

592 #%%

55

593 # renvoie un vecteur de dimension 2x9 des distances négatives

594 # quand on est dans le cas à 9 solutions sur un segment [0,1]

595 # le premier vecteur est celui des 9 distances du joueur 1

596 # le second vecteur est celui des 9 distances du joueur 2

597

598 def vect_temps (v,x1,x2,y1,y2):

599

600 d11 = cp4_v (v,x1,x2,y1)

601 d12 = d11 + dist_v (y1,y2)

602

603 d22 = cp4_v (v,x1,x2,y2)

604 d21 = d22 + dist_v (y2,y1)

605

606 d31 = cp4_v (v,x2,x1,y1)

607 d32 = d31 + dist_v (y1,y2)

608

609 d41 = cp4_v (v,x2,x1,y2)

610 d42 = d41 + dist_v (y2,y1)

611

612 d52 = cp3_v (v,x2,y2)

613 d51 = d52 + cp3_v(y2,x1,y1)

614

615 d61 = cp3_v (v,x1,y1)

616 d62 = d61 + cp3_v(y1,x2,y2)

617

618 d71 = dist_m (x1,y1) # le joueur 1 y va à pied

619 d72 = cp3_v (v,x2,y2)

620

621 d81 = cp3_v (v,x1,y1) # le joueur 2 y va à pied

622 d82 = dist_m (x2,y2)

623

624 d91 = dist_m(x1, y1) # les deux joueurs y vont à pied

625 d92 = dist_m(x2, y2)

626

627 D =

ãÑ array([[d11,d21,d31,d41,d51,d61,d71,d81,d91],[d12,d22,d32,d42,d52,d62,d72,d82,d92]])

628

629 return D

56

8.2.3 Fichier "Etude_probleme_voiture_partagee"

630 from numpy import array

631 from matplotlib import pyplot as plt

632 from random import randint

633 from sympy import symbols, solve

634

635 import Nash_solver as ns

636 import Fonctions_distances as fd

637 #%%

638

639 ''' Jeu classique '''

640 v = 0.21

641 x1 = 0.2

642 x2 = 0.1

643 y1 = 0.98

644 y2 = 0.66

645 decimale = 2

646 a = 0

647 b = 1

648 tolerance = 100

649

650 n = 4

651 m = 1000

652 joueur = 1

653 i = 0

654

655 #%%

656 ''' Fonctions "utilitaires" '''

657

658 # fonctions pour transformer un array de coordonnées de points en liste

659 # on entre neuf points (correspondands aux alternatives) sous forme d'array de ãÑ dimension 2

660 # dimension 1 : abcisses des 9 alternatives

661 # dimension 2 : ordonnées des 9 alternatives

662 def array_to_list_simple (D):

663 C = []

664 for i in range (9): # on remplit la liste

665 C.append([D[0][i],D[1][i]])

666 return C

667

668 # même fonction ou on entre plusieurs combinaisons de 9 points

669 # exemple : si on veut entrer 1000 combinaisons différentes on aura un array

670 # de dimension 2000

671 def array_to_list (D):

672 lengthD = int(len(D)/2) # on prend la partie entière divisée par deux, les
ãÑ paires de lignes sont regroupées

673 C = []

674 for i in range(lengthD): # création de la liste sour le format qui

675

57

C.append([]) # nous intéresse pour le calcul de la solution

ãÑ de Nash

676 for j in range (9):

677 C[i].append([])

678 for i in range (lengthD): # on remplit la liste

679 for j in range (9):

C[i][j] = [D[2*i][j],D[2*i+1][j]]

680

681 return C

682

683

684 def round_list_coordonnees_nx2 (D,decimale = 2): # D =

ãÑ ((2.1223,3.3314],(2.44141,4.43134],...]

685 for i in range (len(D)):

686 D[i][0] = round(D[i][0],decimale)

687 D[i][1] = round(D[i][1],decimale)

688 return D # D =

ãÑ ((2.12,3.33],(2.44,4.43],...]

689

690 def get_coordonnees (L): # L = ((x1,x2,x3,...],(y1,y2,y3,...]]

691 M = []

692 for i in range (len(L[0])):

M.append([L[0][i],L[1][i]])

693

694 return M # M = ((x1,y1],(x2,y2],(x3,y3],...]

695

696 #%%

697 ''' Fonctions servant à l'affichage de la solution de Nash
'''

ãÑ

698

699 def print_donnees (x1,x2,y1,y2,v = 0.5):

700 print("v = ",v)

701 print("x1 = ",x1)

702 print("x2 = ",x2)

703 print("y1 = ",y1)

704 print("y2 = ",y2)

705

706 def utilite (x):

707 return 5-x*x

708

709 def utilite_list_couple (L):

710 D = []

711 for i in range (len(L)):

712 A1 = utilite(L[i][0])

713 A2 = utilite(L[i][1])

714 A = [A1,A2]

715 D.append(A)

716 return D # O(len(L))

717

718 def coordonnees_utilites (x1,x2,y1,y2,v = 0.5,decimale = 2):

719 D = fd.vect_temps(v,x1,x2,y1,y2) # sans mensonges

58

720 D1 = array_to_list_simple(D) # rappel : liste de coordonnées de 9 points

721 D2 = utilite_list_couple(D1) # application de la fonction d'utilité

722 D_f = round_list_coordonnees_nx2(D2,decimale) # on essaye de garder n

ãÑ décimales

723 return D_f # D_f = [[u_x_1,u_y_1],[u_x_2,u_y_2],[u_x_3,u_y_3],...]

724

725 def desaccord (D): # prend en argument la solution de coordonnees_utilites

726 return array([D[8][0],D[8][1]]) # point de désaccord

727

728 def solution (D, d):

729 return ns.true_solution(D,d)

730 # array([[x_sol,y_sol],[x_a,y_a],[x_b,y_b], [p,1-p]])

731 # x_sol = utilité joueur 1, y_sol = utilité joueur 2

732

733 def solution_rounded (s, decimale = 2): # prend en argument la solution de la

ãÑ fonction "solution"

734 for i in range (4): # s = array(solution = [3.2313,3.234], a

ãÑ =[2.2313,4.1414], b =[.,.], p=[.,.])

735 s[i][0] = round(s[i][0],decimale)

736 s[i][1] = round(s[i][1],decimale)

737 return s # s = array(solution = [3.23,3.23], a =[2.23,4.14], b =[.,.],
ãÑ p=[.,.])

738

739 ''' Fonction "résumé" du cas d'étude de la voiture partagée

'''

ãÑ

740

741 def solution_rapide (x1,x2,y1,y2,v = 0.5,decimale = 2):

742 D = coordonnees_utilites (x1,x2,y1,y2,v,decimale)

743 d = desaccord (D)

744 s = solution (D, d)

745 s = solution_rounded (s) # s = array(solution = [3.23,3.23], a

ãÑ =[2.23,4.14], b =[.,.], p=[.,.])

746 return s

747

748 def print_solution_voiture(s,D): # prend en entrée le résultat de true_solution ãÑ et la liste des 9 coordonnées d'utilité

749 sol = [s[0][0],s[0][1]]

750 a = [s[1][0],s[1][1]]

751 b = [s[2][0],s[2][1]]

752 p = round(s[3][0],2)

753 q = round(1 - p,2)

754 B=[]

755 B.append(str("La voiture ira chercher J1 puis J2, déposera J1 puis J2"))

756 B.append(str("La voiture ira chercher J1 puis J2, déposera J2 puis J1"))

757 B.append(str("La voiture ira chercher J2 puis J1, déposera J1 puis J2"))

758 B.append(str("La voiture ira chercher J2 puis J1, déposera J2 puis J1") )

759 B.append(str("La voiture ira chercher J2, le déposera, puis ira chercher J1

ãÑ et le déposera"))

760 B.append(str("La voiture ira chercher .31, le déposera, puis ira chercher .32

59

ãÑ et le déposera"))

761 B.append(str("La voiture ira chercher .32 et le déposera, .31 se rendra à

ãÑ pied"))

762 B.append(str("La voiture ira chercher .31 et le déposera, .32 se rendra à

ãÑ pied"))

763 B.append(str("La voiture n'ira chercher personne, les deux joueurs se

ãÑ rendront à pied à leur destination"))

764

765 if sol in D:

766 i = 0

767 while sol != D[i]:

768 i+= 1

769 if i>=9 :

770 print("Soucis 1")

771 break

772 print(B[i])

773 else :

774 i = 0

775 j = 0

776 while a != D[i]:

777 i+= 1

778 if i>=9 :

779 print("Soucis 2")

780 break

781 while b != D[j]:

782 j+= 1

783 if j>=9 :

784 print("Soucis 3")

785 break

786 print(str(p) + " fois du temps, on aura l'action : " + B[i] + "\n \n" +

787 str(q) + " fois du temps, on aura l'action : " + B[j])

788

789

790 def print_solution_jeu_classique (x1,x2,y1,y2,v = 0.5,decimale = 2):

791

792 print_donnees (x1,x2,y1,y2,v)

793 print("\n Solution du jeu classique
ãÑ \n")

794

795 print("La voiture est placée en " + str(v) + " sur [0,1] \n")

796

797 print("Le joueur 1 est placée en " + str(x1) + \

798 " sur [0,1] et souhaite se rendre en " + str(y1) + " \n")

799 print("Le joueur 2 est placée en " + str(x2) + \

800 " sur [0,1] et souhaite se rendre en " + str(y2) + " \n")

801

802 D = coordonnees_utilites (x1,x2,y1,y2,v,decimale)

803 d = desaccord(D)

60

804 s = solution(D,d)

805 s = solution_rounded(s)

806 u1 = s[0][0]

807 u2 = s[0][1]

808

809 print("Le point de désaccord correspondant au fait que les deux joueurs se
ãÑ rendent à pied est ",\

810 d)

811 print("Avec une réalisation classique du jeu, l'action suivante sera
ãÑ choisie : ")

812 print_solution_voiture(s,D)

813 print("\nJ1 en retire une utilité de ", u1)

814 print("\nJ2 en retire une utilité de ", u2)

815 ns.plot_solution(D,d)

816

817

818 ''' Jeu mensonge '''

819

820 def desutilite_marche (x,y,decimale = 2):

821 return round(-(fd.dist_m(x,y))**(2),decimale)

822

823 def y_max_joueur_quand_il_ment (joueur,a,b,x1,x2,y1,y2,v = 0.5,decimale = ãÑ 2,tolerance = 100) :

824 u_et_y = [[],[]]

825 if joueur == 1 : # le while suivant trouve le max quand J2 ment, on

ãÑ inverse donc si c'est J1 qui ment

826 c = x1

827 x1 = x2

828 x2 = c

829 d = y1

830 y1 = y2

831 y2 = d

832 i = 0

833 while (b-a) > 10**(-tolerance) and (i < 50):

834 p = a + (b-a)/4

835 m = a + (b-a)/2

836 q = a + 3*(b-a)/4

837

838 u_p = solution_rapide(x1,x2,y1,p,v,decimale)[0][1] +
ãÑ desutilite_marche(p, y2, decimale)

839 u_q = solution_rapide(x1,x2,y1,q,v,decimale)[0][1] +
ãÑ desutilite_marche(q, y2, decimale)

840 u_m = solution_rapide(x1,x2,y1,m,v,decimale)[0][1] +
ãÑ desutilite_marche(m, y2, decimale)

841

842 u_et_y[0].append(u_p), u_et_y[0].append(u_q), u_et_y[0].append(u_m)

843 u_et_y[1].append(p), u_et_y[1].append(q), u_et_y[1].append(m)

844

845 if u_p > u_m:

61

846 b = m

847 elif u_m < u_q:

848 a = m

849 else:

850 a = p

851 b = q

852 i+=1

853 y_sol = (a+b)/2

854 u_sol = solution_rapide (x1,x2,y1,y_sol,v,decimale)[0][1] +

ãÑ desutilite_marche(y_sol, y2, decimale)

855

856 u_et_y[0].append(u_sol)

857 u_et_y[1].append(y_sol)

858 return [y_sol,u_sol,u_et_y] # u_et_y sert au plot

859

860

861 def plot_recherche_max_joueur1et2 (x1,x2,y1,y2,v = 0.5,decimale = 2,tolerance = ãÑ 100,titre = "Utilité des joueurs en fonction de leur point ãÑ d'arrivée",a=0,b=1):

862 s1 = y_max_joueur_quand_il_ment (1,a,b,x1,x2,y1,y2,v,decimale,tolerance)

863 s2 = y_max_joueur_quand_il_ment (2,a,b,x1,x2,y1,y2,v,decimale,tolerance)

864

865 u_verite = solution_rapide (x1,x2,y1,y2,v,decimale)[0]

866

867 plt.figure(0)

868 plt.plot(s1[2][1],s1[2][0], '.k',color = "deeppink", label = "Utilité J1")

869 plt.plot(s2[2][1],s2[2][0], '.k',color = "deepskyblue", label = "Utilité

ãÑ J2")

870 plt.scatter(s1[0], s1[1], c = 'red', label = 'Max de J1 : ' +

ãÑ str(round(s1[1],decimale)))

871 plt.scatter(s2[0], s2[1], c = 'blue', label = 'Max de J2 : ' +
ãÑ str(round(s2[1],decimale)))

872 plt.plot([a, b], [u_verite[0], u_verite[0]], '--', label = 'Utilité J1 sans

ãÑ mentir', c = 'deeppink', lw=1)

873 plt.plot([a, b], [u_verite[1], u_verite[1]], '--', label = 'Utilité J2 sans

ãÑ mentir', c = 'deepskyblue', lw=1)

874 plt.xlabel ('Starting point')

875 plt.ylabel ('Utility')

876 plt.title (titre)

877 plt.legend(loc = 'best', shadow=True, borderpad=1)

878 plt.grid()

879 plt.show()

880

881 # similaire a la fonction précédente mais concerne seulement 1 joueur

882 def plot_recherche_max_joueur1 (x1,x2,y1,y2,v = 0.5,decimale = 2,tolerance = ãÑ 100,titre = "Utilité du joueur en fonction de son point ãÑ d'arrivée",a=0,b=1):

883 s1 = y_max_joueur_quand_il_ment (1,a,b,x1,x2,y1,y2,v,decimale,tolerance)

884

62

885 u_verite = solution_rapide (x1,x2,y1,y2,v,decimale)[0]

886

887 plt.figure(1)

888 plt.plot(s1[2][1],s1[2][0], '.k',color = "deeppink", label = "Utilité J1")

889 plt.scatter(s1[0], s1[1], c = 'red', label = 'Max de J1 : ' +

ãÑ str(round(s1[1],decimale)))

890 plt.plot([a, b], [u_verite[0], u_verite[0]], '--', label = 'Utilité J1 sans
ãÑ mentir', c = 'deeppink', lw=1)

891 plt.xlabel ('Starting point')

892 plt.ylabel ('Utility')

893 plt.title (titre)

894 plt.legend(loc = 'best', shadow=True, borderpad=1)

895

896

897 def plot_recherche_max_joueur2 (x1,x2,y1,y2,v = 0.5,decimale = 2,tolerance = ãÑ 100,titre = "Utilité du joueur en fonction de son point ãÑ d'arrivée",a=0,b=1):

898 s2 = y_max_joueur_quand_il_ment (2,a,b,x1,x2,y1,y2,v,decimale,tolerance)

899

900 u_verite = solution_rapide (x1,x2,y1,y2,v,decimale)[0]

901

902 plt.figure(1)

903 plt.plot(s2[2][1],s2[2][0], '.k',color = "deepskyblue", label = "Utilité

ãÑ J")

904 plt.scatter(s2[0], s2[1], c = 'blue', label = 'Max de J2 : ' +

ãÑ str(round(s2[1],decimale)))

905 plt.plot([a, b], [u_verite[1], u_verite[1]], '--', label = 'Utilité J2 sans

ãÑ mentir', c = 'deepskyblue', lw=1)

906 plt.xlabel ('Starting point')

907 plt.ylabel ('Utility')

908 plt.title (titre)

909 plt.legend(loc = 'best', shadow=True, borderpad=1)

910 plt.grid()

911

912 def J1_et_J2_verite (x1,x2,y1,y2,v = 0.5,decimale = 2):

913 u_verite = solution_rapide (x1,x2,y1,y2,v,decimale)

914 return u_verite # array([[x_sol,y_sol],[x_a,y_a],[x_b,y_b], [p,1-p]])

915

916 def J1_ment (x1,x2,y1,y2,v = 0.5,decimale = 2,tolerance = 100):

917 s_J1_ment = y_max_joueur_quand_il_ment
ãÑ (1,a,b,x1,x2,y1,y2,v,decimale,tolerance)

918 y_J1_ment = s_J1_ment[0]

919 s_J1_ment_bis = solution_rapide (x1,x2,s_J1_ment[0],y2,v,decimale)

920 u1_J1_menteur = s_J1_ment[1] # utilité de J1 quand il ment

921 u2_J1_ment = s_J1_ment_bis[0][1] # utilité de J2 quand J1 ment et que J2 ne

ãÑ ment pas

922 return [u1_J1_menteur, u2_J1_ment, y_J1_ment]

923

924 def J2_ment (x1,x2,y1,y2,v,decimale,tolerance):

63

925 s_J2_ment = y_max_joueur_quand_il_ment

ãÑ (2,a,b,x1,x2,y1,y2,v,decimale,tolerance)

926 y_J2_ment = s_J2_ment[0]

927 s_J2_ment_bis = solution_rapide (x1,x2,y1,s_J2_ment[0],v,decimale)

928 u1_J2_ment = s_J2_ment_bis[0][0] # utilité de J1 quand J2 ment et que J1 ne

ãÑ ment pas

929 u2_J2_menteur = s_J2_ment[1] # utilité de J2 quand il ment

930 return [u1_J2_ment, u2_J2_menteur, y_J2_ment]

931

932 def J1_et_J2_mentent_ingenument (J1_ment_obj,J2_ment_obj):

933 y_J1_ment = J1_ment_obj [2]

934 y_J2_ment = J2_ment_obj [2]

935 solution = solution_rapide(x1, x2, y_J1_ment, y_J2_ment, v, decimale)

936 u1 = solution[0][0]

937 u2 = solution[0][1]

938 return [u1,u2,y_J1_ment,y_J2_ment]

939

940 def J1_et_J2_mentent_decouvert (x1,x2,y1,y2,v = 0.5,decimale = 2,tolerance = ãÑ 100,a=0,b=1):

941 s_J1_ment = y_max_joueur_quand_il_ment

ãÑ (1,a,b,x1,x2,y1,y2,v,decimale,tolerance)

942 s_J2_ment = y_max_joueur_quand_il_ment
ãÑ (2,a,b,x1,x2,y1,y2,v,decimale,tolerance)

943 y_J1_ment = s_J1_ment[0] # choix du point d'arrivée de J1 quand il ment

944 y_J2_ment = s_J2_ment[0] # choix du point d'arrivée de J2 quand il ment

945

946 s_J2_ment_sachant_J1_ment = y_max_joueur_quand_il_ment
ãÑ(2,a,b,x1,x2,y_J1_ment,y2,v,decimale,tolerance)

947 y2_J2_ment_sachant_J1_ment = s_J2_ment_sachant_J1_ment[0]

948 s_J2_ment_sachant_J1_ment_bis = solution_rapide

ãÑ (x1,x2,y_J1_ment,y2_J2_ment_sachant_J1_ment,v,decimale)

949 u1_J2_ment_sachant_J1_ment = s_J2_ment_sachant_J1_ment_bis[0][0]

950 u2_J2_ment_sachant_J1_ment = s_J2_ment_sachant_J1_ment[1]

951

952 s_J1_ment_sachant_J2_ment = y_max_joueur_quand_il_ment
ãÑ(1,a,b,x1,x2,y1,y_J2_ment,v,decimale,tolerance)

953 y1_J1_ment_sachant_J2_ment = s_J1_ment_sachant_J2_ment[0]

954 s_J1_ment_sachant_J2_ment_bis = solution_rapide

ãÑ (x1,x2,y1_J1_ment_sachant_J2_ment,y_J2_ment,v,decimale)

955 u1_J1_ment_sachant_J2_ment = s_J1_ment_sachant_J2_ment[1]

956 u2_J1_ment_sachant_J2_ment = s_J1_ment_sachant_J2_ment_bis[0][1]

957

958

ãÑ #plot_recherche_max_joueur1(x1,x2,y1,y_J2_ment,v,decimale,tolerance,"Utilité ãÑ du joueur en fonction de son point d'arrivée sachant que l'autre ment")

959 #plot_recherche_max_joueur2(x1,x2,y_J1_ment,y2,v,decimale,tolerance)

960

64

961 return

ãÑ [[u1_J2_ment_sachant_J1_ment,u2_J2_ment_sachant_J1_ment],[u1_J1_ment_sachant_J2_ment,u2_

ãÑ [y_J1_ment,y2_J2_ment_sachant_J1_ment],[y1_J1_ment_sachant_J2_ment,y_J2_ment]]

962

963 def print_utilites_jeu_info_parfaite (x1,x2,y1,y2,v = 0.5,decimale = 2):

964 J1_et_J2_verite_var = J1_et_J2_verite (x1,x2,y1,y2,v,decimale)

965 J1_ment_var = J1_ment (x1,x2,y1,y2,v,decimale,tolerance)

966 J2_ment_var = J2_ment (x1,x2,y1,y2,v,decimale,tolerance)

967 J1_et_J2_mentent_ingenument_var = J1_et_J2_mentent_ingenument(J1_ment_var,

ãÑ J2_ment_var)

968 J1_et_J2_mentent_decouvert_var = J1_et_J2_mentent_decouvert
ãÑ (x1,x2,y1,y2,v,decimale,tolerance)

969

970 u1 = J1_et_J2_verite_var [0][0]

971 u2 = J1_et_J2_verite_var [0][1]

972 u1_J1_ment = J1_ment_var [0]

973 u2_J1_ment = J1_ment_var [1]

974 u1_J2_ment = J2_ment_var [0]

975 u2_J2_ment = J2_ment_var [1]

976 u1_J1_ment_J2_ment = J1_et_J2_mentent_ingenument_var [0]

977 u2_J1_ment_J2_ment = J1_et_J2_mentent_ingenument_var [1]

978 u1_J1_ment_sachant_J2_ment = J1_et_J2_mentent_decouvert_var [1][0]

979 u2_J1_ment_sachant_J2_ment = J1_et_J2_mentent_decouvert_var [1][1]

980 u1_J2_ment_sachant_J1_ment = J1_et_J2_mentent_decouvert_var [0][0]

981 u2_J2_ment_sachant_J1_ment = J1_et_J2_mentent_decouvert_var [0][1]

982

983 y1_J1_ment = round(J1_ment_var [2],decimale)

984 y2_J2_ment = round(J2_ment_var [2],decimale)

985 y1_J1_ment_J2_ment = round(J1_et_J2_mentent_ingenument_var [2],decimale)

986 y2_J1_ment_J2_ment = round(J1_et_J2_mentent_ingenument_var [3],decimale)

987 y1_J1_ment_sachant_J2_ment = round(J1_et_J2_mentent_decouvert_var

ãÑ [2][0],decimale)

988 y2_J1_ment_sachant_J2_ment = round(J1_et_J2_mentent_decouvert_var
ãÑ [2][1],decimale)

989 y1_J2_ment_sachant_J1_ment = round(J1_et_J2_mentent_decouvert_var
ãÑ [3][0],decimale)

990 y2_J2_ment_sachant_J1_ment = round(J1_et_J2_mentent_decouvert_var
ãÑ [3][1],decimale)

991

992

993 print("\n Valeurs du jeu à information parfaite

ãÑ \n")

994

995 print("\nQuand les deux joueurs disent la vérité : ")

996 print("Utilité de J1 : ", u1)

997 print("Utilité de J2 : ", u2)

998

999 print("\nQuand J1 ment et que J2 dit la vérité : ")

1000 print("Utilité de J1 : ", u1_J1_ment)

65

1001 print("Utilité de J2 : ", u2_J1_ment)

1002 print("J1 annonce vouloir aller en " + str(y1_J1_ment) + " au lieu de " +

ãÑ str(y1))

1003 print("La différence d'utilité de J1 équivaut à : " , round(u1_J1_ment -
ãÑ u1, decimale))

1004 print("La différence d'utilité de J2 équivaut à : " , round(u2_J1_ment -
ãÑ u2, decimale))

1005

1006 print("\nQuand J2 ment et que J1 dit la vérité : ")

1007 print("Utilité de J1 : ", u1_J2_ment)

1008 print("Utilité de J2 : ", u2_J2_ment)

1009 print("J2 annonce vouloir aller en " + str(y2_J2_ment) + " au lieu de " +

ãÑ str(y2))

1010 print("La différence d'utilité de J1 équivaut à : " , round(u1_J2_ment -

ãÑ u1, decimale))

1011 print("La différence d'utilité de J2 équivaut à : " , round(u2_J2_ment -

ãÑ u2, decimale))

1012

1013 print("\nQuand les deux joueurs mentent de manière ingénue (ils se
ãÑ contentent de faire leur meilleur mensonge quand l'autre dit la ãÑ vérité') : ")

1014 print("Utilité de J1 : ", u1_J1_ment_J2_ment)

1015 print("Utilité de J2 : ", u2_J1_ment_J2_ment)

1016 print("J1 annonce vouloir aller en " + str(y1_J1_ment_J2_ment) + " au lieu

ãÑ de " + str(y1))

1017 print("J2 annonce vouloir aller en " + str(y2_J1_ment_J2_ment) + " au lieu

ãÑ de " + str(y2))

1018 print("La différence d'utilité de J1 équivaut à : " ,

ãÑ round(u1_J1_ment_J2_ment - u1, decimale))

1019 print("La différence d'utilité de J2 équivaut à : " ,

ãÑ round(u2_J1_ment_J2_ment - u2, decimale))

1020

1021

1022 print("\nQuand le joueur 2 a décidé de mentir alors qu'il savait que le
ãÑ joueur 1 mentait : ")

1023 print("Utilité de J1 : ", u1_J2_ment_sachant_J1_ment)

1024 print("Utilité de J2 : ", u2_J2_ment_sachant_J1_ment)

1025 print("J1 annonce vouloir aller en " + str(y1_J2_ment_sachant_J1_ment) + "

ãÑ au lieu de " + str(y1))

1026 print("J2 annonce vouloir aller en " + str(y2_J2_ment_sachant_J1_ment) + "

ãÑ au lieu de " + str(y2))

1027 print("La différence d'utilité de J1 équivaut à : " ,

ãÑ round(u1_J2_ment_sachant_J1_ment - u1, decimale))

1028 print("La différence d'utilité de J2 équivaut à : " ,

ãÑ round(u2_J2_ment_sachant_J1_ment - u2, decimale))

1029

1030

1031 print("\nQuand le joueur 1 a décidé de mentir alors qu'il savait que le
ãÑ joueur 2 mentait : ")

66

1032 print("Utilité de J1 : ", u1_J1_ment_sachant_J2_ment)

1033 print("Utilité de J2 : ", u2_J1_ment_sachant_J2_ment)

1034 print("J1 annonce vouloir aller en " + str(y1_J1_ment_sachant_J2_ment) + "

ãÑ au lieu de " + str(y1))

1035 print("J2 annonce vouloir aller en " + str(y2_J1_ment_sachant_J2_ment) + "

ãÑ au lieu de " + str(y2))

1036 print("La différence d'utilité de J1 équivaut à : " ,

ãÑ round(u1_J1_ment_sachant_J2_ment - u1, decimale))

1037 print("La différence d'utilité de J2 équivaut à : " ,

ãÑ round(u2_J1_ment_sachant_J2_ment - u2, decimale))

1038

1039

1040 ''' Fonctions permettant de trouver la solution de Nash au

ãÑ jeu à info parfaite '''

1041

1042 def comparaison (joueur,s1,s2):

1043 if s1[joueur-1] <= s2[joueur-1] :

1044 return s2

1045 elif s1[joueur-1] > s2[joueur-1] : # pourquoi le -1 : indice de J1 = 0,

ãÑ indice de J2 = 1

1046 return s1

1047 # on compare deux couples d'utilité pour le joueur 1 ou 2

1048 # on prend en argument 1 ou 2 correspondant au joueur

1049 # ainsi que les deux couples (u11, u12) et (u21, u22) d'utilité qu'on souhaite

ãÑ comparer

1050

1051 def nash_info_parfaite (premier_joueur,S): # prend en argument le return de
ãÑ creation_4_couples_utilites

1052 s_mm,s_vm,s_mv,s_vv = S[0], S[1], S[2], S[3]

1053 if premier_joueur == 1 :

1054 joueur = 2

1055 s_1 = comparaison(joueur,s_mv,s_vv)

1056 s_2 = comparaison(joueur,s_mm,s_vm)

1057 s = comparaison(premier_joueur, s_1, s_2)

1058 else :

1059 joueur = 1

1060 s_1 = comparaison(joueur,s_mv,s_vv)

1061 s_2 = comparaison(joueur,s_mm,s_vm)

1062 s = comparaison(premier_joueur, s_1, s_2)

1063 return s

1064 # Pour trouver toutes les solutions de Nash il faut faire tourner la fonction ãÑ quand J1 joue en premier

1065 # et quand J2 joue en premier, si on trouve la meme elle est unique, sinon il y

ãÑ a en a deux.

1066

1067 def indice (s,L):

1068 i = 0

1069 while (s != L[i]):

1070 if i >= len(L):

67

1071 break

1072 i+=1

1073 return i

1074

1075 # Fonction très utile permettant de calculer directement les 4 couples ãÑ d'utilité du problème

1076 # en fonction des paramètres de base

1077 def creation_4_couples_utilites (joueur,x1,x2,y1,y2,v = 0.5,decimale = ãÑ 2,tolerance = 100) :

1078 if joueur == 1:

1079 s_mm = J1_et_J2_mentent_decouvert(x1,x2,y1,y2,v,decimale,tolerance)[0]

1080 s_vm = J1_ment(x1,x2,y1,y2,v,decimale,tolerance)[:2]

1081 s_mv = J2_ment(x1,x2,y1,y2,v,decimale,tolerance)[:2]

1082 s_vv = J1_et_J2_verite(x1,x2,y1,y2,v,decimale)[0]

1083 list_sol = [s_mm,s_vm,s_mv,s_vv]

1084 else :

1085 s_mm = J1_et_J2_mentent_decouvert(x1,x2,y1,y2,v,decimale,tolerance)[1]

1086 s_vm = J2_ment(x1,x2,y1,y2,v,decimale,tolerance)

1087 s_mv = J1_ment(x1,x2,y1,y2,v,decimale,tolerance)

1088 s_vv = J1_et_J2_verite(x1,x2,y1,y2,v,decimale)[0]

1089 list_sol = [s_mm,s_vm,s_mv,s_vv]

1090 return list_sol

1091

1092 ''' Jeu info parfaite, solution de Nash en fonction du

ãÑ joueur qui joue en premier '''

1093

1094 def nash_joueur_i_premier_joueur (joueur,liste):

1095 sol = nash_info_parfaite(joueur,liste)

1096 i = indice(sol,liste) # on prend un indice pour la fonction print

ãÑ suivante

1097 return [sol,i]

1098 # sol = couple d'utilité solution 1099 # i = indice de la réponse (0 3) :

1100 # 0 : mensonge puis mensonge

1101 # 1 : verité puis mensonge

1102 # 2 : mensonge puis verite

1103 # 3 : verite puis verite

1104

1105 # Un utilise le principe d'indifference quand une solution mixte existe 1106 # la fonction n'a pas été utilisée durant le mémoire malheureusement 1107 def solution_mixte_nash (S):

1108 s1 = nash_info_parfaite(1, S)

1109 s2 = nash_info_parfaite(2, S)

1110 if s1 == s2:

1111 return s1

1112 elif s1!=s2 and (abs(indice(s1,S) - indice(s2,S))%2 != 0):

1113 x = symbols('x')

1114 eq1 = x*S[0][1] + (1-x)*S[1][1] - (x*S[2][1] + (1-x)*S[3][1])

1115 p = solve(eq1)

68

1116

1117 y = symbols('y')

1118 eq2 = y*S[0][0] + (1-y)*S[2][0] - (y*S[1][0] + (1-y)*S[3][0])

1119 q = solve(eq2)

1120 return p,q

1121 '''

1122 S = [[3,2],[2,3],[2,3],[3,2]]

1123 #S = [[5,3],[2,2],[1,1],[4,6]]

1124 print(solution_mixte_nash(S)) #'''

1125

1126 # fonction "print" affichant la solution de Nash lorsqu'on a le choix entre 4

ãÑ couples d'utilité

1127 def print_jeu_decouvert (x1,x2,y1,y2,v = 0.5,decimale = 2):

1128 B=[]

1129 B.append(str("\nQuand J1 est le premier à jouer, J1 décidera de mentir et

ãÑ J2 également"))

1130 B.append(str("\nQuand J1 est le premier à jouer, J1 décidera de mentir mais

ãÑ J2 préfèrera dire la vérité"))

1131 B.append(str("\nQuand J1 est le premier à jouer, J1 décidera de dire la

ãÑ vérité mais J2 préfèrera mentir"))

1132 B.append(str("\nQuand J1 est le premier à jouer, J1 décidera de dire la
ãÑ vérité et J2 également"))

1133

1134 B.append(str("\nQuand J2 est le premier à jouer, J2 décidera de mentir et
ãÑ J1 également"))

1135 B.append(str("\nQuand J2 est le premier à jouer, J2 décidera de mentir mais
ãÑ J1 préfèrera dire la vérité"))

1136 B.append(str("\nQuand J2 est le premier à jouer, J2 décidera de dire la
ãÑ vérité mais J1 préfèrera mentir"))

1137 B.append(str("\nQuand J2 est le premier à jouer, J2 décidera de dire la
ãÑ vérité et J1 également"))

1138

1139 print(" \n Solution de Nash du jeu à découvert

ãÑ ")

1140 liste_1 = creation_4_couples_utilites (1,x1,x2,y1,y2,v,decimale,tolerance)

1141 s_1,i_1 = nash_joueur_i_premier_joueur(1, liste_1)[:2]

1142 print(B[i_1])

1143 liste_2 = creation_4_couples_utilites (1,x1,x2,y1,y2,v,decimale,tolerance)

1144 s_2,i_2 = nash_joueur_i_premier_joueur(2, liste_2)[:2]

1145 print(B[i_2+4])

1146

1147 # fonction pour définir 5 points aléatoires, on veut éviter d'avoir x1 = y1 et

ãÑ x2 = y2, car

1148 # ils n'ont pas d'interêt dans le problème et le font planter. 1149 def random_5_points(decimale = 2):

1150 x1 = randint(0,10**decimale)/10**decimale

1151 x2 = randint(0,10**decimale)/10**decimale

1152 y1 = x1

1153 y2 = x2

69

1154 v = x1

1155 while (y1 == x1) or (y2 == x2) or (v == x1):

1156 y1 = randint(0,10**decimale)/10**decimale

1157 y2 = randint(0,10**decimale)/10**decimale

1158 v = randint(0,10**decimale)/10**decimale #'''

1159 return x1, x2, y1, y2, v

1160

1161 # fonction servant la partie théorie des jeux pour compter le nombre de fois
ãÑ qu'un individu ment

1162 def occurrence_type_solution_jeu_decouvert (taille_echantillon = 100, decimale ãÑ = 2, tolerance = 100, joueur = 1):

1163 occurrence_J1 = []

1164 for i in range (taille_echantillon):

1165 x1, x2, y1, y2, v = random_5_points(decimale)

1166 liste = creation_4_couples_utilites

ãÑ (joueur,x1,x2,y1,y2,v,decimale,tolerance)

1167 occurrence_J1.append(nash_joueur_i_premier_joueur(joueur,liste)[1])

1168 return occurrence_J1

1169

1170 # fonction servant la partie statistique du mémoire, on ne s'intéressera que
ãÑ au premier élément renvoyé par la fonction

1171 # qui n'est autre qu'une liste de 0 et 1 suivant le fait que la solution est ãÑ pure ou mixte

1172 def echantillon_test_stat_solution_pure (m): # taille de l'échantillon

1173 liste, s_list, s_pure, s_mixte, x1_pure, x2_pure, y1_pure, y2_pure, v_pure,

ãÑ \

1174 x1_mixte, x2_mixte, y1_mixte, y2_mixte, v_mixte =

ãÑ [],[],[],[],[],[],[],\

1175 [],[],[],[],[],[],[]

1176 for i in range (m):

1177 x1, x2, y1, y2, v = random_5_points(decimale)

1178 s = solution_rapide(x1,x2,y1,y2,v,decimale)

1179 s_list.append(s)

1180 if (s[3][0] == 0.0) or (s[3][0] == 1.0) :

1181 liste.append(1), s_pure.append(s), x1_pure.append(x1), \

1182 x2_pure.append(x2), y1_pure.append(y1), y2_pure.append(y2),

ãÑ v_pure.append(v)

1183 else:

1184 liste.append(0), s_mixte.append(s), x1_mixte.append(x1), \

1185 x2_mixte.append(x2), y1_mixte.append(y1), y2_mixte.append(y2),

ãÑ v_mixte.append(v)

1186 return liste,s_list, s_pure, x1_pure, x2_pure, y1_pure, y2_pure, v_pure, \

1187 s_mixte, x1_mixte, x2_mixte, y1_mixte, y2_mixte, v_mixte

1188 # 0 : liste de 0 et de 1 correspondant des solutions mixtes ou pures

1189 # 1 : liste de toutes les solutions : [point solution, point A, point B, le

ãÑ facteur p]

1190 # 2 : liste des solutions uniquement pures

1191 # 3 - 7 : valeurs des coordonnées quand la solution est pure 1192 # 8 : liste des solutions uniquement mixtes

70

1193 # 9 - 13 : valeurs des coordonnées quand la solution est mixte 1194

1195 def n_echantillon (m,n):

1196 L_liste_pure_mixte = [J

1197 L_s_list = [J

1198 L_s_pure = [J

1199 L_x1_pure = [J

1200 L_x2_pure = [J

1201 L_y1_pure = [J

1202 L_y2_pure = [J

1203 L_v_pure = [J

1204 L_s_mixte = [J

1205 L_x1_mixte = [J

1206 L_x2_mixte = [J

1207 L_y1_mixte = [J

1208 L_y2_mixte = [J

1209 L_v_mixte = [J

1210

1211 for i in range (n):

1212 liste_pure_mixte, s_list, s_pure, x1_pure, x2_pure, y1_pure, y2_pure,
ãÑ v_pure, s_mixte, x1_mixte, x2_mixte, y1_mixte, y2_mixte, v_mixte = ãÑ echantillon_test_stat_solution_pure (m)

1213

1214 L_liste_pure_mixte.append(liste_pure_mixte)

1215 L_s_list.append(s_list)

1216 L_s_pure.append(s_pure)

1217 L_x1_pure.append(x1_pure)

1218 L_x2_pure.append(x2_pure)

1219 L_y1_pure.append(y1_pure)

1220 L_y2_pure.append(y2_pure)

1221 L_v_pure.append(v_pure)

1222 L_s_mixte.append(s_mixte)

1223 L_x1_mixte.append(x1_mixte)

1224 L_x2_mixte.append(x2_mixte)

1225 L_y1_mixte.append(y1_mixte)

1226 L_y2_mixte.append(y2_mixte)

1227 L_v_mixte.append(v_mixte)

1228

1229 return L_liste_pure_mixte,L_s_list, L_s_pure, L_x1_pure, L_x2_pure, \

1230 L_y1_pure, L_y2_pure, L_v_pure, L_s_mixte, L_x1_mixte, L_x2_mixte,
ãÑ L_y1_mixte, \

1231 L_y2_mixte, L_v_mixte

1232 # Nous renvoie 14 listes contenant chacunes les n sous-listes suivantes :

1233

1234 # 0 : liste de 0 et de 1 correspondant à des solutions mixtes ou pures

1235 # 1 : liste de toutes les solutions : [point solution, point A, point B, le

ãÑ facteur p]

1236 # 2 : liste des solutions uniquement pures

1237 # 3 - 7 : valeurs des coordonnées quand la solution est pure

71

1238

	#	8	: liste des solutions uniquement mixtes
1239	#	9	- 13 : valeurs des coordonnées quand la solution est mixte

72

8.2.4 Fichier "Applications_theorie_des_jeux.py"

1240 from random import uniform

1241 from numpy import mean

1242

1243 import Etude_probleme_voiture_partagee as ev

1244

1245 #%%

1246 ''' Partie 4.5 - Cas simple n°1

'''

ãÑ

1247

1248 x1, x2, y1, y2, v = 0.02, 0.34, 0.84, 0.71, 0.5

1249 tolerance = 100

1250

1251

1252 s = ev.solution_rapide (x1,x2,y1,y2,v)

1253

1254 D = ev.coordonnees_utilites(x1, x2, y1, y2, v)

1255 ev.print_solution_voiture(s, D)

1256 ev.print_solution_jeu_classique (x1,x2,y1,y2,v)

1257

1258 #%%

1259 ''' Partie 4.5 - Cas simple n°2

'''

ãÑ

1260

1261 x1, x2, y1, y2, v = 0.05, 0.60, 0.89, 0.91, 0.2

1262 tolerance = 100

1263

1264 #'''

1265 s = ev.solution_rapide (x1,x2,y1,y2,v)

1266

1267 D = ev.coordonnees_utilites(x1, x2, y1, y2, v)

1268 ev.print_solution_voiture(s, D)

1269 ev.print_solution_jeu_classique (x1,x2,y1,y2,v)

1270

1271 #%%

1272 ''' Partie 4.6.1 - infos parfaites

'''

ãÑ

1273 #'''

1274 x1, x2, y1, y2, v = 0.02, 0.34, 0.84, 0.71, 0.5

1275 decimale, tolerance = 2, 100

1276 a, b = 0, 1

1277

1278

1279 #s =

ãÑ ev.joueur_ment_y_maximum_dichotomie(1,a,b,x1,x2,y1,y2,v,decimale,tolerance)

1280 #print(s)

1281 #ev.plot_solution_menteur(a,b,x1,x2,y1,y2,v,decimale,tolerance)

1282

73

1283 s = ev.solution_rapide (x1,x2,y1,y2,v,decimale)

1284

1285 D = ev.coordonnees_utilites(x1, x2, y1, y2, v, decimale)

1286

1287 ev.print_solution_voiture(s, D)

1288 ev.print_solution_jeu_classique (x1,x2,y1,y2,v,decimale)

1289 ev.print_jeu_decouvert(x1,x2,y1,y2,v,decimale)

1290 ev.plot_recherche_max_joueur1et2 (x1,x2,y1,y2,v,decimale,tolerance,"Utilité des

ãÑ joueurs en fonction de leur point d'arrivée",a,b)

1291 ev.print_utilites_jeu_info_parfaite(x1,x2,y1,y2,v,decimale) #''' 1292 1293 1294 #%%

1295 ''' Partie 4.6.2 - occurrence des mensonges

'''

ãÑ

1296 #'''

1297 L = ev.occurrence_type_solution_jeu_decouvert(taille_echantillon = 200, joueur

ãÑ = 1)

1298

1299 print(" Quand le joueur 1 joue en premier

")

1300 zero1 = L.count(0)

1301 print("Nombre de fois oil les deux individus mentent : ", zero1)

1302 un1 = L.count(1)

1303 print("Nombre de fois oil le premier ment et que le second ne ment pas : ", un1)

1304 deux1 = L.count(2)

1305 print("Nombre de fois oil le premier ne ment pas et que le second ment : ",

ãÑ deux1)

1306 trois1 = L.count(3)

1307 print("Nombre de fois oil les deux disent la vérité : ", trois1)

1308

1309 L = ev.occurrence_type_solution_jeu_decouvert(taille_echantillon = 200, joueur

ãÑ = 2)

1310

1311 print(" Quand le joueur 2 joue en premier

")

1312 zero2 = L.count(0)

1313 print("Nombre de fois oil les deux individus mentent : ", zero2)

1314 un2 = L.count(1)

1315 print("Nombre de fois oil le premier ment et que le second ne ment pas : ", un2)

1316 deux2 = L.count(2)

1317 print("Nombre de fois oil le premier ne ment pas et que le second ment : ",

ãÑ deux2)

1318 trois2 = L.count(3)

1319 print("Nombre de fois oil les deux disent la vérité : ", trois2) #'''

1320

1321 #%%

1322 ''' Partie 4.6.3 - infos imparfaites

'''

ãÑ

1323 #'''

1324 m = 300

74

1325 i = 0

1326 decimale, tolerance = 3, 100

1327 a, b = 0, 1

1328

1329 y1_les_deux_mentent = []

1330 y2_les_deux_mentent = []

1331 y1_J1_ment_sachant_J2_ment_List = []

1332 y2_J2_ment_sachant_J1_ment_List = []

1333

1334 for i in range (m):

1335 x1_u, x2_u = uniform(0,0.2), uniform(0.3,0.35)

1336 x1_v, x2_v = 0.02, 0.34 # correspond l'endroit où se trouve vraiment le

ãÑ joueur

1337

1338 y1_u, y2_u = uniform(0.7,1.0), uniform(0.7,1.0)

1339 y1_v, y2_v = 0.84, 0.71 # correspond la vraie destination du joueur

1340 v = 0.5
1341

1342 # Calcul de l'approximation de y1 #
1343

1344 J1_et_J2_verite = ev.J1_et_J2_verite (x1_v,x2_u,y1_v,y2_u,v,decimale) #
ãÑ y1_v correspond au vrai y, y2_u correspond un y tiré uniformément

1345 J1_ment = ev.J1_ment (x1_v,x2_u,y1_v,y2_u,v,decimale,tolerance)

1346 J2_ment = ev.J2_ment (x1_v,x2_u,y1_v,y2_u,v,decimale,tolerance)

1347 J1_et_J2_mentent_ingenument = ev.J1_et_J2_mentent_ingenument(J1_ment,

ãÑ J2_ment)

1348 J1_et_J2_mentent_decouvert = ev.J1_et_J2_mentent_decouvert
ãÑ (x1_v,x2_u,y1_v,y2_u,v,decimale,tolerance)

1349

1350 y1_J1_ment_J2_ment = round(J1_et_J2_mentent_ingenument [2],decimale)

1351 y1_J1_ment_sachant_J2_ment = round(J1_et_J2_mentent_decouvert

ãÑ [3][0],decimale)

1352

1353 y1_les_deux_mentent.append(y1_J1_ment_J2_ment)

1354 y1_J1_ment_sachant_J2_ment_List.append(y1_J1_ment_sachant_J2_ment)

1355

1356 # Calcul de l'approximation de y2 #
1357

1358 J1_et_J2_verite = ev.J1_et_J2_verite (x1_u,x2_v,y1_u,y2_v,v,decimale) #
ãÑ y2_v correspond au vrai y, y1_u correspond un y tiré uniformément

1359 J1_ment = ev.J1_ment (x1_u,x2_v,y1_u,y2_v,v,decimale,tolerance)

1360 J2_ment = ev.J2_ment (x1_u,x2_v,y1_u,y2_v,v,decimale,tolerance)

1361 J1_et_J2_mentent_ingenument = ev.J1_et_J2_mentent_ingenument(J1_ment,

ãÑ J2_ment)

1362 J1_et_J2_mentent_decouvert = ev.J1_et_J2_mentent_decouvert
ãÑ (x1_u,x2_v,y1_u,y2_v,v,decimale,tolerance)

1363

1364 y2_J1_ment_J2_ment = round(J1_et_J2_mentent_ingenument [3],decimale)

1365 y2_J2_ment_sachant_J1_ment = round(J1_et_J2_mentent_decouvert

75

ãÑ [2][1],decimale)

1366

1367 y2_les_deux_mentent.append(y2_J1_ment_J2_ment)

1368 y2_J2_ment_sachant_J1_ment_List.append(y2_J2_ment_sachant_J1_ment) #'''

1369 #'''

1370 MOYENNE_y1_les_deux_mentent = mean(y1_les_deux_mentent)

1371 MOYENNE_y2_les_deux_mentent = mean(y2_les_deux_mentent)

1372 MOYENNE_y1_J1_ment_sachant_J2_ment_List = mean(y1_J1_ment_sachant_J2_ment_List)

1373 MOYENNE_y2_J2_ment_sachant_J1_ment_List = mean(y2_J2_ment_sachant_J1_ment_List)

1374

1375 print("Moyenne des y1 quand J1 ment et que J2 dit la vérité = ",

ãÑ round(MOYENNE_y1_les_deux_mentent,3))

1376 print("Moyenne des y2 quand J2 ment et que J1 dit la vérité = ",

ãÑ round(MOYENNE_y2_les_deux_mentent,3))

1377 print("Moyenne des y1 quand J1 ment et qu'il sait que J2 ment = ",

ãÑ round(MOYENNE_y1_J1_ment_sachant_J2_ment_List,3))

1378 print("Moyenne des y2 quand J2 ment et qu'il sait que J1 ment = ",

ãÑ round(MOYENNE_y2_J2_ment_sachant_J1_ment_List,3)) #''' 1379 #%%

1380 #'''

1381

1382 y_1_app = (1/2)*(MOYENNE_y1_les_deux_mentent +

ãÑ MOYENNE_y1_J1_ment_sachant_J2_ment_List) 1383 y_2_app = (1/2)*(MOYENNE_y2_les_deux_mentent +

ãÑ MOYENNE_y2_J2_ment_sachant_J1_ment_List) 1384 v = 0.5

1385

1386 y1, y2 = 0.84, 0.71

1387 print("On prend donc comme valeur de y1 : ", y_1_app)

1388 print("On prend donc comme valeur de y2 : ", y_2_app) #'''

1389

1390

1391 #%%

1392 #'''

1393 y_1_app = 0.7323850000000001 1394 y_2_app = 0.671815

1395 v = 0.5 #'''

1396

1397 x1, x2 = 0.02, 0.34 # correspond l'endroit où se trouve vraiment le joueur

1398 y1, y2 = 0.84, 0.71 # correspond la vraie destination du joueur

1399

1400 # Solution du jeu info imparfaite #

1401

1402 VV = ev.solution_rapide(x1,x2,y1,y2,v = 0.5,decimale = 2)

1403 VM = ev.solution_rapide(x1,x2,y1,y_2_app,v = 0.5,decimale = 2)

1404 MV = ev.solution_rapide(x1,x2,y_1_app,y2,v = 0.5,decimale = 2)

1405 MM = ev.solution_rapide(x2,x2,y_1_app,y_2_app,v = 0.5,decimale = 2)

1406

76

1407

1408 print("\n Solution du jeu à info imparfaite

ãÑ \n")

1409

1410 print("\n Quand les deux joueurs disent la vérité : \n")

1411 print("J1 obtient une utilité de :", VV[0][0])

1412 print("J2 obtient une utilité de :", VV[0][1])

1413

1414 print("\n Quand J1 dit la vérité et que J2 ment : \n")

1415 print("J1 obtient une utilité de :", VM[0][0])

1416 print("J2 obtient une utilité de :", VM[0][1])

1417

1418 print("\n Quand J2 dit la vérité et que J1 ment : \n")

1419 print("J1 obtient une utilité de :", MV[0][0])

1420 print("J2 obtient une utilité de :", MV[0][1])

1421

1422 print("\n Quand les deux joueurs mentent : \n")

1423 print("J1 obtient une utilité de :", MM[0][0])

1424 print("J2 obtient une utilité de :", MM[0][1])

1425

1426 #print(ev.solution_mixte_nash ([VV[0],VM[0],MV[0],MM[0]])) #'''

1427

1428 #%%

1429 a = 0

1430 b = 1

1431 v = 0.5

1432 zonehab11 = 0

1433 zonehab12 = 0.1

1434 zonehab21 = 0.9

1435 zonehab22 = 1

1436 zone1 = [zonehab11,zonehab12]

1437 zone2 = [zonehab21,zonehab22]

1438

1439 p_zone1 = 0.3

1440 p_zone2 = 1-p_zone1

1441

1442 zoneind1 = 0.5

1443 zoneind2 = 0.6

1444 zoneindustielle = [zoneind1,zoneind2]

1445

1446 x_zone1_moyen, x_zone2_moyen = mean(zone1), mean(zone2)

1447 y_moyen = mean(zoneindustielle)

1448

1449

1450 ''' Première étude '''

1451

1452 ''' Un a ici 16 couples d'utilités à trouver, il faut distinguer les cas en

ãÑ fonction

77

1453 de la zone où se trouve le joueur, il faut également penser que les endroits où

ãÑ ils

1454 décident de mentir dépend de là où ils se trouvent (ex: si J1 est dans la zone

ãÑ 1, l'endroit

1455 de son mensonge sera choisi en considérant que J2 est dans la zone opposée, ie.

ãÑ la zone 2 '''

1456

1457 y1,y2 = y_moyen, y_moyen

1458

1459 ''' '''

1460 ''' J1 zone 1 - J2 zone 1 = K1 '''

1461 ''' '''

1462 x1 = x_zone1_moyen 1463 x2 = x_zone1_moyen

1464 ''' Aucun joueur ne ment '''

1465

1466 solution_verite_K1 = ev.solution_rapide (x1,x2,y1,y2,v) 1467 u1_verite_K1 = solution_verite_K1[0][0] 1468 u2_verite_K1 = solution_verite_K1[0][1]

1469

1470 ''' J1 ment, J2 vérité '''
1471 y1_J1ment_J2zone2 = ev.y_max_joueur_quand_il_ment

ãÑ (1,a,b,x1,x_zone2_moyen,y1,y2,v)[0]

1472

1473 solution_J1ment_J2verite_K1 = ev.solution_rapide (x1,x2,y1_J1ment_J2zone2,y2,v)

1474 u1_J1ment_J2verite_K1 = solution_J1ment_J2verite_K1[0][0]

1475 u2_J1ment_J2verite_K1 = solution_J1ment_J2verite_K1[0][1]

1476

1477 ''' J1 vérité, J2 ment '''
1478 y2_J2ment_J1zone2 = ev.y_max_joueur_quand_il_ment ãÑ (2,a,b,x_zone2_moyen,x2,y1,y2,v)[0]

1479

1480 solution_J2ment_J1verite_K1 = ev.solution_rapide (x1,x2,y1,y2_J2ment_J1zone2,v) 1481 u1_J2ment_J1verite_K1 = solution_J2ment_J1verite_K1[0][0] 1482 u2_J2ment_J1verite_K1 = solution_J2ment_J1verite_K1[0][1]

1483

1484 ''' J1 ment, J2 ment '''

1485

1486 solution_J1ment_J2ment_K1 = ev.solution_rapide

ãÑ (x1,x2,y1_J1ment_J2zone2,y2_J2ment_J1zone2,v)

1487 u1_J1ment_J2ment_K1 = solution_J1ment_J2ment_K1[0][0]

1488 u2_J1ment_J2ment_K1 = solution_J1ment_J2ment_K1[0][1]

1489 print ("\n ")
1490 print ("Quand les joueurs se situe dans la même zone 1")

1491 print (" ")
1492 print ("\nSi les deux joueurs décident de dire la vérité") 1493 print ("J1 aura une utilité de :", u1_verite_K1) 1494 print ("J2 aura une utilité de :", u2_verite_K1) 1495 print ("\nSi J1 décide de mentir et J2 dire la vérité")

78

1496 print ("J1 aura une utilité de :", u1_J1ment_J2verite_K1) 1497 print ("J2 aura une utilité de :", u2_J1ment_J2verite_K1) 1498 print ("\nSi J1 décide de dire la vérité et J2 mentir") 1499 print ("J1 aura une utilité de :", u1_J2ment_J1verite_K1) 1500 print ("J2 aura une utilité de :", u2_J2ment_J1verite_K1) 1501 print ("\nSi les deux joueurs décident de mentir") 1502 print ("J1 aura une utilité de :", u1_J1ment_J2ment_K1) 1503 print ("J2 aura une utilité de :", u2_J1ment_J2ment_K1) 1504

1505 ''' '''

1506 ''' J1 zone 1 - J2 zone 2 = K2 '''

1507 ''' '''

1508 x1 = x_zone1_moyen 1509 x2 = x_zone2_moyen

1510 ''' Aucun joueur ne ment '''

1511

1512 solution_verite_K2 = ev.solution_rapide (x1,x2,y1,y2,v) 1513 u1_verite_K2 = solution_verite_K2[0][0] 1514 u2_verite_K2 = solution_verite_K2[0][1]

1515

1516 ''' J1 ment, J2 vérité '''
1517 y1_J1ment_J2zone2 = ev.y_max_joueur_quand_il_ment

ãÑ (1,a,b,x1,x_zone2_moyen,y1,y2,v)[0]

1518

1519 solution_J1ment_J2verite_K2 = ev.solution_rapide (x1,x2,y1_J1ment_J2zone2,y2,v)

1520 u1_J1ment_J2verite_K2 = solution_J1ment_J2verite_K2[0][0]

1521 u2_J1ment_J2verite_K2 = solution_J1ment_J2verite_K2[0][1]

1522

1523 ''' J1 vérité, J2 ment '''
1524 y2_J2ment_J1zone1 = ev.y_max_joueur_quand_il_ment ãÑ (2,a,b,x_zone1_moyen,x2,y1,y2,v)[0]

1525

1526 solution_J2ment_J1verite_K2 = ev.solution_rapide (x1,x2,y1,y2_J2ment_J1zone1,v) 1527 u1_J2ment_J1verite_K2 = solution_J2ment_J1verite_K2[0][0] 1528 u2_J2ment_J1verite_K2 = solution_J2ment_J1verite_K2[0][1]

1529

1530 ''' J1 ment, J2 ment '''

1531

1532 solution_J1ment_J2ment_K2 = ev.solution_rapide

ãÑ (x1,x2,y1_J1ment_J2zone2,y2_J2ment_J1zone1,v) 1533 u1_J1ment_J2ment_K2 = solution_J1ment_J2ment_K2[0][0] 1534 u2_J1ment_J2ment_K2 = solution_J1ment_J2ment_K2[0][1] 1535

1536 print ("\n ")

1537 print ("Quand le joueur 1 se trouve dans la zone 1 et le joueur 2 dans la zone

ãÑ 2")

1538 print (" ")

1539 print ("\nSi les deux joueurs décident de dire la vérité") 1540 print ("J1 aura une utilité de :", u1_verite_K2)

79

1541 print ("J2 aura une utilité de :", u2_verite_K2)

1542 print ("\nSi J1 décide de mentir et J2 dire la vérité") 1543 print ("J1 aura une utilité de :", u1_J1ment_J2verite_K2) 1544 print ("J2 aura une utilité de :", u2_J1ment_J2verite_K2) 1545 print ("\nSi J1 décide de dire la vérité et J2 mentir") 1546 print ("J1 aura une utilité de :", u1_J2ment_J1verite_K2) 1547 print ("J2 aura une utilité de :", u2_J2ment_J1verite_K2) 1548 print ("\nSi les deux joueurs décident de mentir") 1549 print ("J1 aura une utilité de :", u1_J1ment_J2ment_K2) 1550 print ("J2 aura une utilité de :", u2_J1ment_J2ment_K2)

1551

1552 ''' '''

1553 ''' J1 zone 2 - J2 zone 1 = K3 '''

1554 ''' '''

1555 x1 = x_zone2_moyen 1556 x2 = x_zone1_moyen

1557 ''' Aucun joueur ne ment '''

1558

1559 solution_verite_K3 = ev.solution_rapide (x1,x2,y1,y2,v) 1560 u1_verite_K3 = solution_verite_K3[0][0] 1561 u2_verite_K3 = solution_verite_K3[0][1]

1562

1563 ''' J1 ment, J2 vérité '''
1564 y1_J1ment_J2zone1 = ev.y_max_joueur_quand_il_ment

ãÑ (1,a,b,x1,x_zone1_moyen,y1,y2,v)[0]

1565

1566 solution_J1ment_J2verite_K3 = ev.solution_rapide (x1,x2,y1_J1ment_J2zone1,y2,v)

1567 u1_J1ment_J2verite_K3 = solution_J1ment_J2verite_K3[0][0]

1568 u2_J1ment_J2verite_K3 = solution_J1ment_J2verite_K3[0][1]

1569

1570 ''' J1 vérité, J2 ment '''
1571 y2_J2ment_J1zone2 = ev.y_max_joueur_quand_il_ment ãÑ (2,a,b,x_zone2_moyen,x2,y1,y2,v)[0]

1572

1573 solution_J2ment_J1verite_K3 = ev.solution_rapide (x1,x2,y1,y2_J2ment_J1zone2,v) 1574 u1_J2ment_J1verite_K3 = solution_J2ment_J1verite_K3[0][0] 1575 u2_J2ment_J1verite_K3 = solution_J2ment_J1verite_K3[0][1]

1576

1577 ''' J1 ment, J2 ment '''

1578

1579 solution_J1ment_J2ment_K3 = ev.solution_rapide

ãÑ (x1,x2,y1_J1ment_J2zone1,y2_J2ment_J1zone2,v) 1580 u1_J1ment_J2ment_K3 = solution_J1ment_J2ment_K3[0][0] 1581 u2_J1ment_J2ment_K3 = solution_J1ment_J2ment_K3[0][1] 1582

1583 print ("\n ")

1584 print ("Quand le joueur 1 se trouve dans la zone 2 et le joueur 2 dans la zone

ãÑ 1")

1585 print (" ")

80

1586 print ("\nSi les deux joueurs décident de dire la vérité") 1587 print ("J1 aura une utilité de :", u1_verite_K3)

1588 print ("J2 aura une utilité de :", u2_verite_K3)

1589 print ("\nSi J1 décide de mentir et J2 dire la vérité") 1590 print ("J1 aura une utilité de :", u1_J1ment_J2verite_K3) 1591 print ("J2 aura une utilité de :", u2_J1ment_J2verite_K3) 1592 print ("\nSi J1 décide de dire la vérité et J2 mentir") 1593 print ("J1 aura une utilité de :", u1_J2ment_J1verite_K3) 1594 print ("J2 aura une utilité de :", u2_J2ment_J1verite_K3) 1595 print ("\nSi les deux joueurs décident de mentir") 1596 print ("J1 aura une utilité de :", u1_J1ment_J2ment_K3) 1597 print ("J2 aura une utilité de :", u2_J1ment_J2ment_K3)

1598

1599 ''' '''

1600 ''' J1 zone 2 - J2 zone 2 = K4 '''

1601 ''' '''

1602 x1 = x_zone2_moyen 1603 x2 = x_zone2_moyen

1604 ''' Aucun joueur ne ment '''

1605

1606 solution_verite_K4 = ev.solution_rapide (x1,x2,y1,y2,v) 1607 u1_verite_K4 = solution_verite_K4[0][0] 1608 u2_verite_K4 = solution_verite_K4[0][1]

1609

1610 ''' J1 ment, J2 vérité '''
1611 y1_J1ment_J2zone1 = ev.y_max_joueur_quand_il_ment

ãÑ (1,a,b,x1,x_zone1_moyen,y1,y2,v)[0]

1612

1613 solution_J1ment_J2verite_K4 = ev.solution_rapide (x1,x2,y1_J1ment_J2zone1,y2,v)

1614 u1_J1ment_J2verite_K4 = solution_J1ment_J2verite_K4[0][0]

1615 u2_J1ment_J2verite_K4 = solution_J1ment_J2verite_K4[0][1]

1616

1617 ''' J1 vérité, J2 ment '''
1618 y2_J2ment_J1zone1 = ev.y_max_joueur_quand_il_ment ãÑ (2,a,b,x_zone1_moyen,x2,y1,y2,v)[0]

1619

1620 solution_J2ment_J1verite_K4 = ev.solution_rapide (x1,x2,y1,y2_J2ment_J1zone1,v) 1621 u1_J2ment_J1verite_K4 = solution_J2ment_J1verite_K4[0][0] 1622 u2_J2ment_J1verite_K4 = solution_J2ment_J1verite_K4[0][1]

1623

1624 ''' J1 ment, J2 ment '''

1625

1626 solution_J1ment_J2ment_K4 = ev.solution_rapide

ãÑ (x1,x2,y1_J1ment_J2zone1,y2_J2ment_J1zone1,v) 1627 u1_J1ment_J2ment_K4 = solution_J1ment_J2ment_K4[0][0] 1628 u2_J1ment_J2ment_K4 = solution_J1ment_J2ment_K4[0][1] 1629

1630 print ("\n ")

1631 print ("Quand les joueurs se situe dans la même zone 2")

81

1632 1633 1634 1635

	print print print	print (" ") ("\nSi les deux joueurs décident de dire la vérité") ("J1 aura une utilité de :", u1_verite_K4) ("J2 aura une utilité de :", u2_verite_K4)
1636	print	("\nSi J1 décide de mentir et J2 dire la vérité")
1637	print	("J1 aura une utilité de :",	u1_J1ment_J2verite_K4)
1638	print	("J2 aura une utilité de :",	u2_J1ment_J2verite_K4)
1639	print	("\nSi J1 décide de dire la vérité et J2 mentir")
1640	print	("J1 aura une utilité de :",	u1_J2ment_J1verite_K4)
1641	print	("J2 aura une utilité de :",	u2_J2ment_J1verite_K4)
1642	print	("\nSi les deux joueurs décident de mentir")
1643	print	("J1 aura une utilité de :",	u1_J1ment_J2ment_K4)
1644	print	("J2 aura une utilité de :",	u2_J1ment_J2ment_K4)

82

8.2.5 Fichier "Applications_statistiques.py"

1645 from numpy import zeros

1646 from matplotlib import pyplot as plt

1647 from scipy.stats import binom, t

1648 from math import sqrt

1649

1650 import Etude_probleme_voiture_partagee as ev

1651

1652 #%%

1653 n = 100

1654

1655 def list_to_array(L):

1656 n = len(L)

1657 X = zeros(n)

1658 for i in range (n):

X[i]=L[i]

1659

1660 return X

1661

1662 liste = ev.echantillon_test_stat_solution_pure (n)[0]

1663

1664 X_sample = list_to_array(liste)

1665 #%%

1666 p=1/2

1667

1668 stat_test_mediane = sum(X_sample)

1669

1670 moyenne_empirique = (1/n)*sum(X_sample)

1671

1672 variance_empirique = (1/(n-1))*sum((X_sample-moyenne_empirique)**2)

1673

1674 quantile_p_valeur = (sqrt(n)/variance_empirique)*(moyenne_empirique-0.90)

1675

1676 p_valeur_mediane = binom.cdf(stat_test_mediane,n,p)

1677 p_valeur_student = t.cdf(quantile_p_valeur,n-1)

1678

1679 print("stat_test_mediane = ",stat_test_mediane)

1680 print("stat_test_mediane = ",moyenne_empirique)

1681

1682 print("p_valeur_mediane = ",p_valeur_mediane)

1683 print("p_valeur_student = ",p_valeur_student)

1684

1685 #%%

1686

1687 def m_p_valeur (n,m):

1688 p_mediane = [] # on rentre les p-valeurs du test 1 de la médiane

1689 p_student = [] # on rentre les p-valeurs du test 2 de Student

1690 moyenne = [] # on rentre les valeurs des moyennes

1691 save_nb_solutions_mixtes = [] # sert étudier les moyennes quand les
ãÑ p-valeurs sont inférieures un seuil choisi

83

1692

1693 for i in range (m):

1694 liste = ev.echantillon_test_stat_solution_pure (n)[0]

1695

1696 X_sample = list_to_array(liste)

1697 stat_test_mediane = sum(X_sample)

1698

1699 moyenne_empirique = (1/n)*stat_test_mediane

1700 moyenne.append(moyenne_empirique)

1701

1702 variance_empirique = (1/(n-1))*sum((X_sample-moyenne_empirique)**2)

1703

1704 quantile_p_valeur =

ãÑ (sqrt(n)/variance_empirique)*(moyenne_empirique-0.90)

1705 p = 1/2

1706 p_valeur_mediane = binom.cdf(stat_test_mediane,n,p)

1707 p_valeur_student = t.cdf(quantile_p_valeur,n-1)

1708 if p_valeur_student < 0.8:

1709

ãÑ save_nb_solutions_mixtes.append([p_valeur_student,moyenne_empirique])

1710 p_mediane.append(p_valeur_mediane)

1711 p_student.append(p_valeur_student)

1712

1713 return p_mediane, p_student, moyenne, save_nb_solutions_mixtes

1714 n, m = 100, 100

1715 p_mediane, p_student, moyenne, etude_p_valeur = m_p_valeur(n,m)

1716

1717

1718 plt.figure()

1719 plt.hist(p_mediane, edgecolor = "black", color = "white")

1720 plt.title("Histogramme de " + str(n) + " p-valeurs correspondant au test de la

ãÑ médiane")

1721

1722 plt.figure()

1723 plt.hist(p_student, edgecolor = "magenta", color = "white")

1724 plt.title("Histogramme de " + str(n) + " p-valeurs correspondant au test de

ãÑ Student")

1725

1726 plt.figure()

1727 plt.hist(moyenne, edgecolor = "darkred", color = "white")

1728 plt.title("Histogramme de " + str(n) + " moyennes")